Small area estimation under a measurement error bivariate Fay–Herriot model

Abstract

The bivariate Fay–Herriot model is an area-level linear mixed model that can be used for estimating the domain means of two correlated target variables. Under this model, the dependent variables are direct estimators calculated from survey data and the auxiliary variables are true domain means obtained from external data sources. Administrative registers do not always give good auxiliary variables, so that statisticians sometimes take them from alternative surveys and therefore they are measured with error. We introduce a variant of the bivariate Fay–Herriot model that takes into account the measurement error of the auxiliary variables and we give fitting algorithms to estimate the model parameters. Based on the new model, we introduce empirical best predictors of domain means and we propose a parametric bootstrap procedure for estimating the mean squared error. We finally give an application to estimate poverty proportions and gaps in the Spanish Living Condition Survey, with auxiliary information from the Spanish Labour Force Survey.

1 Introduction

Survey sample sizes are generally calculated to obtain precise direct estimates of target parameters in planned territories, but they might be not large enough for obtaining reliable estimates in unplanned smaller regions or small areas. Small area estimation (SAE) theory introduces indirect model-based or model-assisted estimators for treating these situations. SAE is an important part of statistical inference in finite populations with applications to social and economic statistics. The monograph of Rao and Molina (2015) contains a general description of SAE.

When auxiliary variables related to the target variable are available at the small area level, the most widely used area-level model in SAE is the Fay–Herriot (FH) model. This model was first proposed by Fay and Herriot (1979) to obtain estimates of mean per capita income in U.S. small areas using survey data. Esteban et al. (2012a, b), Marhuenda et al. (2013) and Morales et al. (2015) apply variants of the basic FH model to the small area estimation of poverty indicators in the Spanish Living Condition Survey (SLCS), with auxiliary information from the Spanish Labour Force Survey (SLFS).

If there is more than one target variables, multivariate area-level mixed models can take into account their correlations. These correlations can be an important additional information for the estimation. Fay (1987) and Datta et al. (1991) showed that small area estimators obtained from multivariate models have, in general, better precision than the ones obtained from univariate models for each response variable. Molina et al. (2007) and López-Vizcaíno et al. (2013), López-Vizcaíno et al. (2015) made use of this idea and applied it to estimate labour force indicators. Several other authors have investigated and applied multivariate Fay–Herriot (MFH) models in the SAE setup, e.g. Datta et al. (1996), González-Manteiga et al. (2008), Porter et al. (2015) or Benavent and Morales (2016).

Under the MFH model, the values of the dependent variable are direct estimates calculated from survey data and the auxiliary variables are “true” domain means obtained from administrative registers. However, it is not always possible to find good auxiliary variables in administrative registers and MFH models are sometimes applied with auxiliary variables measured with errors. Oftentimes, direct estimates obtained from a sample of a different survey are used. The aforementioned applications do not take into account the measurement error of the auxiliary variables. This manuscript addresses this practical issue.

Concerning the contributions to area-level linear mixed models with covariates measured with error, Ybarra and Lohr (2008) introduced a functional measurement error model where the underlying true values of the covariates are fixed but unknown quantities. Their model can be viewed as a generalization of the Fay–Herriot model. They also introduced a new small area estimator that accounts for sampling variability in the auxiliary information, and derive its properties, in particular showing that it is approximately unbiased. They applied their estimator to predict quantities measured in the U.S. National Health and Nutrition Examination Survey, with auxiliary information from the U.S. National Health Interview Survey. Marchetti et al. (2015) presented an application where measures derived from Big Data are used as covariates in a Fay–Herriot model to estimate poverty indicators, accounting for the presence of measurement error in the covariates. Polettini and Arima (2015) introduced predictors of small area means based on area-level linear mixed models with covariates perturbed for disclosure limitation.

Adopting a Bayesian approach, Arima et al. (2015) rewrote the Ybarra-Lohr measurement error model as a hierarchical model and introduced Bayes predictors. This last work was later extended by Arima et al. (2017) proposing multivariate Fay–Herriot Bayesian predictors of small area means under functional measurement error. On the other hand, Burgard et al. (2019) followed a likelihood-based approach for extending the Ybarra-Lohr model. They proposed residual maximum likelihood (REML) estimators of the model parameters and introduced empirical best predictors and a mean squared error analytical approximation.

Concerning unit-level models, further contributions to the Bayesian SAE literature on measurement error models are Ghosh et al. (2006), Ghosh and Sinha (2007), Torabi et al. (2009), Datta et al. (2010) and Arima et al. (2012). More recently, Torabi (2013) presented an application of data cloning conducting a frequentist analysis of GLMM with covariates subject to the measurement error model.

This paper introduces a three-step bivariate Fay–Herriot model by assuming that the vector of true domain means of auxiliary variables differ from the corresponding vector of direct estimators in a zero-mean multivariate normally distributed random error. The introduced functional measurement error model can be considered as a multivariate adaptation of the Ybarra-Lohr univariate model to a parametric inference setup with multivariate normal measurement errors. The proposed approach can also be considered as the non Bayesian counterpart of the statistical methodology introduced by Arima et al. (2017).

Ybarra and Lohr (2008) did not assume the normality of the measurement errors and they proposed a weighted least squared approach to estimate the model parameters. Arima et al. (2017) assumed the multivariate normality of the measurement errors and they considered a Bayesian approach. They simulated the posterior distributions of the model parameters and calculated the hierarchical Bayes predictors of domain means by applying Markov Chain Monte Carlo algorithms. This paper preserves the likelihood modelling of Arima et al., but applies a non Bayesian approach. The main target is to calculate empirical best predictors of domain means and to estimate the corresponding mean squared errors (MSE).

Assuming that measurement errors have a multivariate normal distribution is a natural choice in practice, as due to the central limit theorem, the distribution of the auxiliary variable estimators has an asymptotic multivariate normal distribution. This adaption, besides giving another motivation of the empirical best predictor provided by Ybarra and Lohr (2008), has two mayor advantages. First, we derive Fisher-scoring algorithms for calculating maximum likelihood (ML) and pseudo-residual maximum likelihood (pseudo-REML) estimators of model parameters. Second, we provide a parametric bootstrap procedure for estimating the mean squared errors.

The rest of the paper is organized as follows. Section 2 introduces the measurement error bivariate Fay–Herriot model. Section 3 derives the best predictors of random effects and target domain parameters. It also calculates the MSEs of the best predictors. Section 4 presents the relative efficiency matrix of the best predictors that takes into account that variables are measured with error compared to the corresponding ones that ignores this information. Section 5 proposes a parametric bootstrap procedure for estimating the mean squared error of the empirical best predictors. Section 6 describes the pseudo-REML method for estimating the model parameters. Section 7 carries out simulation experiments to investigate the behavior of the pseudo-REML fitting algorithm, the empirical best predictors and the bootstrap estimator of the mean squared error of the empirical best predictors. Section 8 gives an application to real data where the target is the small area estimation of poverty proportions and gaps in the SLCS, with auxiliary information from the SLFS. Sections 9 summarizes some conclusions. The paper contains three appendixes that are provided as supplementary file. Appendix A gives some auxiliary results for the calculation of the best predictors and their MSEs. Appendix B shows some tables with results of the application to SLCS data. Appendix C presents the Fisher scoring algorithm for calculating the ML estimators of the model parameters.

2 The measurement error bivariate Fay–Herriot model

Let U be a finite population partitioned into D domains $U_1,\ldots ,U_D$. Let $\mu _{d}=\left( \mu _{d1},\mu _{d2}\right) ^{\prime }$ be a vector of characteristics of interest in the domain d and let ${y}_{d}=\left( {y}_{d1},{y}_{d2}\right) ^{\prime }$ be a vector of direct estimators of $\mu _d$ calculated by using the data of the target survey sample. The measurement error bivariate Fay–Herriot (MEBFH) model is defined in three steps. The first step indicates that direct estimators are unbiased and follow the sampling model

$$\begin{aligned} {y}_{d}=\mu _{d}+{e}_{d},\quad d=1,\ldots ,D, \end{aligned}$$

(1)

where the vectors ${e}_{d}=(e_{d1},e_{d2})^\prime \sim N_2\left( 0,{V}_{ed}\right)$ are independent and the $2\times 2$ covariance matrices ${V}_{ed}$ are known. In most cases, ${V}_{ed}$ is taken to be the design-based covariance matrix of the direct estimator $y_d$, $d=1,\ldots ,D$.

In the second step the true area characteristic $\mu _{dk}$ is assumed to be linearly related to $p_k+q_k$ explanatory variables, $k=1,2$, $d=1,\ldots ,D$. Let $\tilde{x}_{dk}^\prime =(\tilde{x}_{dk1},\ldots ,\tilde{x}_{dkp_k})$ be a row vector containing the true aggregated (population) values of $p_k$ explanatory variables for $\mu _{dk}$ and let $\tilde{X}_{d}=\text{ diag }(\tilde{x}_{d1}^\prime ,\tilde{x}_{d2}^\prime )$ be a ${2\times p}$ block-diagonal matrix with $p=p_1+p_2$. Let $\lambda _{k}=(\lambda _{k1},\ldots ,\lambda _{kp_k})^\prime$ be a column vector of size $p_k$ containing regression parameters for $\mu _{dk}$ and let $\lambda =\left( \lambda _{1}^{\prime },\lambda _{2}^{\prime }\right) ^{\prime }_{p\times 1}$. Let $z_{dk}^\prime =(z_{dk1},\ldots ,z_{dkq_k})$ be a row vector containing the true aggregated (population) values of $q_k$ explanatory variables for $\mu _{dk}$ and let $Z_{d}=\text{ diag }(z_{d1}^\prime ,z_{d2}^\prime )$ be a ${2\times q}$ block-diagonal matrix with $q=q_1+q_2$. Let $\eta _{k}=(\eta _{k1},\ldots ,\eta _{kq_k})^\prime$ be a column vector of size $q_k$ containing regression parameters for $\mu _{dk}$ and let $\eta =\left( \eta _{1}^{\prime },\eta _{2}^{\prime }\right) ^{\prime }_{q\times 1}$.

The linking model is

$$\begin{aligned} \mu _{d}=Z_d\eta +\tilde{X}_{d}\lambda +{u}_{d},\quad {u}_{d}=(u_{d1},u_{d2})^\prime \sim N_2(0,{V}_{ud}),\quad d=1,\ldots ,D, \end{aligned}$$

(2)

where the vectors ${u}_{d}$’s are independent of the vectors ${e}_{d}$’s. The $2\times 2$ covariance matrices ${V}_{ud}$ depend on 3 unknown parameters, $\theta _{1}=\sigma _{u1}^2$, $\theta _{2}=\sigma _{u2}^2$ and $\theta _{3}=\rho$, i.e.

$$\begin{aligned} {V}_{ud}= \left( \begin{array}{cc} \sigma _{u1}^2 & \rho \sigma _{u1}\sigma _{u2}\\ \rho \sigma _{u1}\sigma _{u2}&\sigma _{u2}^2\end{array}\right) . \end{aligned}$$

This manuscript assumes that the $\tilde{x}_{dk}$’s are unknown random vectors that are predicted from independent data sources. These data sources could be administrative registers or other surveys with larger sample sizes than the target survey. For $k=1,2$, let us define the random measurement error vectors $v_{dk}^\prime =(v_{dk1},\ldots ,v_{dkp_k})$. We assume that the vectors ${v}_{d}=(v_{d1}^\prime ,v_{d2}^\prime )^\prime$ are independent with distributions ${v}_{d}\sim N_p(0,\Sigma _d)$ and known $p\times p$ covariance matrices

$$\begin{aligned} \Sigma _d=\Big (\begin{array}{cc}\Sigma _{d11}&\Sigma _{d12}\\ \Sigma _{d21}&\Sigma _{d22}\end{array}\Big ),\quad \Sigma _{dk_1k_2}=\text{ cov }(v_{dk_1},v_{dk_2}),\,\,\,k_1,k_2=1,2,\,d=1,\ldots ,D. \end{aligned}$$

The third step considers the functional measurement error model

$$\begin{aligned} \tilde{x}_{dk}={x}_{dk}+v_{dk},\quad d=1,\ldots ,D,\,\, k=1,2, \end{aligned}$$

(3)

where $x_{dk}^\prime$ is a row vector containing the unbiased predictors of the components of $\tilde{x}_{dk}^\prime$ and the vectors ${v}_{d}$ and ${x}_{d}=(x_{d1}^\prime ,x_{d2}^\prime )^\prime$, $d=1,\ldots ,D$, are independent. In most cases, $x_{dk}$ is a vector of direct estimators calculated from data of a different survey and $\Sigma _{dk_1k_2}$ is taken to be the design-based covariance matrix of vectors $x_{dk_1}$ and $x_{dk_2}$, $k_1,k_2=1,2$.

Let us also define the $2\times p$ block diagonal matrices $B_d=\text{ diag }(\lambda _{1}^\prime ,\lambda _{2}^\prime )$ and ${X}_{d}=\text{ diag }({x}_{d1}^\prime ,{x}_{d2}^\prime )$.

The measurement error bivariate Fay–Herriot (MEBFH) model can be expressed as a single model in the form

$$\begin{aligned} y_d=Z_d\eta +X_d\lambda +B_dv_d+u_d+e_d, \quad d=1,\ldots , D, \end{aligned}$$

(4)

or in the matrix form

$$\begin{aligned} y=Z\eta +X\lambda +Bv+u+e, \end{aligned}$$

where $B=\underset{1\le d \le D}{\hbox {diag}}(B_d)$, $X=\underset{1\le d \le D}{\hbox {col}}({X}_{d})$, $Z=\underset{1\le d \le D}{\hbox {col}}({Z}_{d})$ and

$$\begin{aligned} {y}=\underset{1\le d \le D}{\hbox {col}}({y}_{d}),\,\,\, {u}=\underset{1\le d \le D}{\hbox {col}}({u}_{d}),\,\,\, {v}=\underset{1\le d \le D}{\hbox {col}}({v}_{d}),\,\,\, {e}=\underset{1\le d \le D}{\hbox {col}}({e}_{d}). \end{aligned}$$

We finally assume that matrices $V_{ud}$, $\Sigma _d$ and $V_{ed}$ are invertible and that $x_d$, $v_d$, $u_d$, $e_d$, $d=1,\ldots ,D$, are independent, but we only introduce inference procedures conditionally on X. If there are no measurement errors, then the $v_d$’s are null vectors and the bivariate Fay–Herriot (BFH) model is obtained as a special case of (4). The MEBFH model can be considered as a multivariate generalization of the Fay–Herriot model with measurement error studied by Ybarra and Lohr (2008) or by Burgard et al. (2019). This approach was also considered by Arima et al. (2017) in a Bayesian context. Note that the MEBFH model is not a linear mixed model as the matrix B depends on the vector $\lambda$ of model parameters. Therefore, the MEBFH model cannot be expressed in the standard form $Y=X\beta +Zu+e$.

It holds that

$$\begin{aligned} V_{\lambda d}=\text{ var }(B_dv_d)&=B_d\text{ var }(v_d)B_d^\prime =\text{ diag }(\lambda _1^\prime ,\lambda _2^\prime )\Sigma _d\text{ diag }(\lambda _1,\lambda _2)\\&=\left( \begin{array}{cc}\lambda _1^\prime \Sigma _{d11}\lambda _1 & \lambda _1^\prime \Sigma _{d12}\lambda _2\\ \lambda _2^\prime \Sigma _{d21}\lambda _1&\lambda _2^\prime \Sigma _{d22}\lambda _2\end{array}\right) . \end{aligned}$$

Therefore, $V_u=\text{ var }(u)=\underset{1\le d \le D}{\hbox {diag}}(V_{ud})$, $V_e=\text{ var }(e)=\underset{1\le d \le D}{\hbox {diag}}(V_{ed})$ and $\text{ var }(Bv)=\underset{1\le d \le D}{\hbox {diag}}(V_{\lambda d})$. Conditioned to $x_d$, $d=1,\ldots ,D$, the covariance matrix of y is

$$\begin{aligned} V=V(\theta ,\lambda )=\text{ var }(y|X)=\underset{1\le d \le D}{\hbox {diag}}(V_d)=\underset{1\le d \le D}{\hbox {diag}}(V_{\lambda d}+V_{ud}+V_{ed}). \end{aligned}$$

(5)

Further, it holds that $y_d|_{x_d}\sim N_2\big (Z_d\eta +X_d\lambda ,V_{\lambda d}+V_{ud}+V_{ed}\big )$,

$$\begin{aligned} y_d|_{x_d,v_d}\sim N_2\big (Z_d\eta +X_d\lambda +B_dv_d,V_{ud}+V_{ed}\big ), \quad \text {and}\quad \end{aligned}$$

$$\begin{aligned} y_d|_{x_d,u_d}\sim N_2\big (Z_d\eta +X_d\lambda +u_d,V_{\lambda d}+V_{ed}\big ). \end{aligned}$$

3 Best predictors under the MEBFH model

This section derives the best predictors (BP) of the random effects $v_d$ and $u_d$ and of the target parameter $\mu _d$. It also calculates variances and expectations of cross products. The proofs of the following propositions are based on the properties of the multivariate normal distribution. We recall that the kernel of the n-variate normal distribution is

$$\begin{aligned} f(y|\mu ,\Sigma )&=\frac{1}{(2\pi )^{n/2}|\Sigma |^{1/2}}\exp \big \{-\frac{1}{2}(y-\mu )^\prime \Sigma ^{-1}(y-\mu )\big \}\\&\propto \exp \big \{-\frac{1}{2} y^\prime \Sigma ^{-1}y+\mu ^\prime \Sigma ^{-1}y\big \}. \end{aligned}$$

The first two propositions deal with the BP of $v_d$ and its basic properties.

Proposition 1

Under model (4), the best predictor of $v_d$ is

$$\begin{aligned} \hat{v}_d^{bp}=E[v_d|x_d,y_d]= \Psi _d\,B_d^{\prime }\big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ), \end{aligned}$$

(6)

where

$$\begin{aligned} \Psi _d=\left( B_d^{\prime }\big (V_{ud}+V_{ed}\big )^{-1}B_d+\Sigma _d^{-1}\right) ^{-1} =\Sigma _d-\Sigma _d\,B_d^{\prime }(V_{\lambda d}+V_{ud}+V_{ed})^{-1}B_d\Sigma _d. \end{aligned}$$

Proof

The conditional distribution of $v_d$, given the estimators $x_d$ and $y_d$, is

$$\begin{aligned} f_{v_d}&= f(v_d|x_d,y_{d}) \propto f(y_d|x_d,v_d) f(v_d) =\big (2\pi |V_{ud}+V_{ed}|^{1/2}\big )^{-1} \\&\quad\cdot \exp \Big \{-\frac{1}{2}(y_d-Z_d\eta -X_d\lambda -B_dv_d)^\prime (V_{ud}+V_{ed})^{-1}(y_d-Z_d\eta -X_d\lambda -B_dv_d)\Big \} \\&\quad\cdot \big ((2\pi )^{p/2}|\Sigma _d|^{1/2}\big )^{-1}\exp \Big \{-\frac{1}{2}v_d^\prime \Sigma _d^{-1}v_d\Big \} \\\propto & \exp \Big \{-\frac{1}{2}(v_{d1}^\prime \lambda _1,v_{d2}^\prime \lambda _2)(V_{ud}+V_{ed})^{-1} \Big (\begin{array}{c}\lambda _1^\prime v_{d1}\\ \lambda _2^\prime v_{d2}\end{array}\Big ) \\&\quad +\,(v_{d1}\lambda _1^\prime ,v_{d2}^\prime \lambda _2)(V_{ud}+V_{ed})^{-1}(y_d-Z_d\eta -X_d\lambda )\Big \} \exp \Big \{-\frac{1}{2}v_d^\prime \Sigma _d^{-1}v_d\Big \}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} f_{v_d}&= \exp \Big \{-\frac{1}{2}(v_{d1}^\prime ,v_{d2}^\prime )\left( B_d^\prime \big (V_{ud}+V_{ed}\big )^{-1}B_d+\Sigma _d^{-1}\right) \Big (\begin{array}{c}v_{d1}\\ v_{d2}\end{array}\Big ) \\&\quad +\,(v_{d1}^\prime ,v_{d2}^\prime )\Psi _d^{-1}\Big [\Psi _d\, B_d^\prime \big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda )\Big ]\Big \}. \end{aligned}$$

We have proved that $f(v_d|x_d,y_{d})$ is a multivariate normal distribution with parameters

$$\begin{aligned} \text{ var }(v_d|x_d,y_{d})&= \left( B_d^{\prime }\big (V_{ud}+V_{ed}\big )^{-1}B_d+\Sigma _d^{-1}\right) ^{-1}=\Psi _d,\\ E[v_d|x_d,y_{d}]&= \Psi _dB_d^{\prime }\big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ). \end{aligned}$$

By applying Lemma A.1 of Appendix A in the supplementary file, the results follows. $\square$

Proposition 2

Under model ( 4 ), it holds that $E[\hat{v}_d^{bp}|x_d]=0$ and

$$\begin{aligned} \text{ var }(\hat{v}_d^{bp}|x_d)=E\big [\hat{v}_d^{bp}\hat{v}_d^{bp\,\prime }|x_d\big ] =\Psi _dB_d^{\prime }(V_{ud}+V_{ed})^{-1} (V_{\lambda d}+V_{ud}+V_{ed})(V_{ud}+V_{ed})^{-1}B_d\Psi _d. \end{aligned}$$

Proof

We recall that $y_d-Z_d\eta -X_d\lambda =B_dv_d+u_d+e_d$. Therefore, we have

$$\begin{aligned} \text{ var }(\hat{v}_d^{bp}|x_d)&= \Psi _dB_d^{\prime }(V_{ud}+V_{ed})^{-1}E\big [(B_dv_d+u_d+e_d)(B_dv_d+u_d+e_d)^\prime |x_d\big ] \\&\quad\cdot (V_{ud}+V_{ed})^{-1}B_d\Psi _d \\&= \Psi _dB_d^{\prime }(V_{ud}+V_{ed})^{-1} (V_{\lambda d}+V_{ud}+V_{ed})(V_{ud}+V_{ed})^{-1}B_d\Psi _d. \end{aligned}$$

$\square$

The following two propositions derive the BP of $u_d$, show that it is predictively unbiased and calculate its variance.

Proposition 3

Under model ( 4 ), the best predictor of $u_d$ is

$$\begin{aligned} \hat{u}_d^{bp}=E[u_d|x_d,y_d]= \Phi _d\big (V_{\lambda d}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ),\nonumber \\ \Phi _d=\left( \big (V_{\lambda d}+V_{ed}\big )^{-1}+V_{ud}^{-1}\right) ^{-1}. \end{aligned}$$

(7)

Proof

The conditional distribution of $u_d$, given $x_d$ and $y_d$, is

$$\begin{aligned} f_{u_d}&= f(u_d|x_d,y_{d})\varpropto f(y_d|x_d,u_d)f(u_d)= \\&= \frac{1}{2\pi |V_{\lambda d}+V_{ed}|^{1/2}} \\&\quad\cdot \exp \Big \{-\frac{1}{2}(y_d-Z_d\eta -X_d\lambda -u_d)^\prime (V_{\lambda d}+V_{ed})^{-1}(y_d-Z_d\eta -X_d\lambda -u_d)\Big \} \\&\quad\cdot \frac{1}{2\pi |V_{ud}|^{1/2}}\exp \Big \{-\frac{1}{2}u_d^\prime V_{ud}^{-1}u_d\Big \} \\\propto & \exp \Big \{-\frac{1}{2}u_d^\prime (V_{\lambda d}+V_{ed})^{-1}u_d+u_d^\prime (V_{\lambda d}+V_{ed})^{-1}(y_d-Z_d\eta -X_d\lambda )\Big \} \\&\quad\cdot \exp \Big \{-\frac{1}{2}u_d^\prime V_{ud}^{-1}u_d\Big \} \\&= \exp \Big \{-\frac{1}{2}u_d^\prime \Big (\big (V_{\lambda d}+V_{ed}\big )^{-1}+V_{ud}^{-1}\Big )u_d \\&\quad +\,u_d^\prime \Phi _d^{-1}\Big [\Phi _d\, \big (V_{\lambda d}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda )\Big ]\Big \}. \end{aligned}$$

Therefore $f(u_d|x_d,y_{d})$ is a multivariate normal distribution with parameters

$$\begin{aligned} \text{ var }(u_d|x_d,y_{d})&= \left( \big (V_{\lambda d}+V_{ed}\big )^{-1}+V_{ud}^{-1}\right) ^{-1}=\Phi _d, \\ E[u_d|x_d,y_{d}]&= \Phi _d\,\big (V_{\lambda d}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ). \end{aligned}$$

$\square$

Proposition 4

Under model (4), it holds that $E[\hat{u}_d^{bp}|x_d]=0$ and

$$\begin{aligned} \text{ var }(\hat{u}_d^{bp}|x_d)=E\big [\hat{u}_d^{bp}\hat{u}_d^{bp\,\prime }|x_d\big ] =\Phi _d(V_{\lambda d}+V_{ed})^{-1}(V_{\lambda d}+V_{ud}+V_{ed})(V_{\lambda d}+V_{ed})^{-1}\Phi _d. \end{aligned}$$

Proof

As $y_d-Z_d\eta -X_d\lambda =B_dv_d+u_d+e_d$, we have

$$\begin{aligned} \text{ var }(\hat{u}_d^{bp}|x_d)&= \Phi _d(V_{\lambda d}+V_{ed})^{-1}E\big [(B_dv_d+u_d+e_d)(B_dv_d+u_d+e_d)^\prime |x_d\big ] \\&\quad\cdot (V_{\lambda d}+V_{ed})^{-1}\Phi _d \\&= \Phi _d(V_{\lambda d}+V_{ed})^{-1}(V_{\lambda d}+V_{ud}+V_{ed})(V_{\lambda d}+V_{ed})^{-1}\Phi _d. \end{aligned}$$

$\square$The following two propositions give the best predictor of $\mu _d$ and its MSE. This section ends by defining the empirical best predictor of $\mu _d.$

Proposition 5

Under model ( 4 ), the best predictor (MEBFH-BP) of $\mu _d$ is

$$\begin{aligned} \hat{\mu }_d^{bp}&= Z_d\eta +X_{d}\lambda +V_{\lambda d}\big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ) \nonumber \\&\quad -\,V_{\lambda d}(V_{\lambda d}+V_{ud}+V_{ed})^{-1}V_{\lambda d}\big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ) \nonumber \\&\quad +\,\Phi _d\big (V_{\lambda d}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ) \end{aligned}$$

(8)

Proof

As $\mu _d=Z_d\eta +X_{d}\lambda +B_dv_d+u_d$, $\Psi _d=\Sigma _d-\Sigma _d\,B_d^{\prime }(V_{\lambda d}+V_{ud}+V_{ed})^{-1}B_d\Sigma _d$ and $V_{\lambda d}=B_d\Sigma _dB_d^{\prime }$, we have

$$\begin{aligned} \hat{\mu }_d^{bp}&= E[\mu _d|x_d,y_d]=Z_d\eta +X_{d}\lambda +B_d\hat{v}_d^{bp}+\hat{u}_d^{bp} \\&= Z_d\eta +X_{d}\lambda +B_d\Psi _d\,B_d^{\prime }\big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ) \\&\quad +\,\Phi _d\big (V_{\lambda d}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ) \\&= Z_d\eta +X_{d}\lambda +V_{\lambda d}\big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ) \\&\quad -\,V_{\lambda d}(V_{\lambda d}+V_{ud}+V_{ed})^{-1}V_{\lambda d}\big (V_{ud}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ) \\&\quad +\,\Phi _d\big (V_{\lambda d}+V_{ed}\big )^{-1}(y_d-Z_d\eta -X_d\lambda ). \end{aligned}$$

$\square$

Proposition 6

Under the model ( 4 ), the MSE of $\hat{\mu }_d^{bp}$ is

$$\begin{aligned} MSE(\hat{\mu }_d^{bp}|x_d)&= \Big \{B_d\Psi _dB_d^{\prime }(V_{ud}+V_{ed})^{-1} (V_{\lambda d}+V_{ud}+V_{ed})(V_{ud}+V_{ed})^{-1}B_d\Psi _dB_d^\prime \\&\quad +\,\Phi _d(V_{\lambda d}+V_{ed})^{-1}(V_{\lambda d}+V_{ud}+V_{ed})(V_{\lambda d}+V_{ed})^{-1}\Phi _d \\&\quad +\,B_d\Psi _dB_d^\prime (V_{ud}+V_{ed})^{-1}(V_{\lambda d}+V_{ud}+V_{ed})(V_{\lambda d}+V_{ed})^{-1}\Phi _d \\&\quad +\, \Phi _d(V_{\lambda d}+V_{ed})^{-1}(V_{\lambda d}+V_{ud}+V_{ed})(V_{ud}+V_{ed})^{-1}B_d\Psi _dB_d^\prime \Big \} \\&\quad +\,\big \{V_{\lambda d}+V_{ud}\big \} \\&\quad -\, \Big \{V_{\lambda d}(V_{ud}+V_{ed})^{-1}B_d\Psi _dB_d^\prime +V_{ud}(V_{\lambda d}+V_{ed})^{-1}\Phi _d \\&\quad +\,V_{\lambda d}(V_{\lambda d}+V_{ed})^{-1}\Phi _d +V_{ud}(V_{ud}+V_{ed})^{-1}B_d\Psi _dB_d^\prime \Big \} \\&\quad -\, \Big \{B_d\Psi _dB_d^\prime (V_{ud}+V_{ed})^{-1}B_d\Sigma _dB_d^\prime +\Phi _d(V_{\lambda d}+V_{ed})^{-1}V_{ud} \\&\quad +\,\Phi _d(V_{\lambda d}+V_{ed})^{-1}B_d\Sigma _dB_d^\prime +B_d\Psi _dB_d^\prime (V_{ud}+V_{ed})^{-1}V_{ud}\Big \}. \end{aligned}$$

Proof

It hold that

$$\begin{aligned} MSE(\hat{\mu }_d^{bp}|x_d)&= E\big [(\hat{\mu }_d^{bp}-\mu _d)(\hat{\mu }_d^{bp}-\mu _d)^\prime |x_d\big ] \\&= E\big [\hat{\mu }_d^{bp}\hat{\mu }_d^{bp\,\prime }|x_d\big ] +E\big [\mu _d\mu _d^\prime |x_d\big ] -E\big [\mu _d\hat{\mu }_d^{bp\,\prime }|x_d\big ] -E\big [\hat{\mu }_d^{bp}\mu _d^\prime |x_d\big ]. \end{aligned}$$

where $E\big [\mu _d\mu _d^\prime |x_d\big ]=V_{\lambda d}+V_{ud}$.

The remaining expectations are calculated in Propositions A.2 and A.3 from Appendix A in the supplementary file. By doing the corresponding substitutions, the result follows. $\square$

In practice, the BPs are not calculable because the model parameters are not known.

Under model (4), the empirical best predictors (MEBFH-EBP) of $v_d$, $u_d$ and $\mu _d$ are obtained from formulas (6), (7) and (8) by plugging estimators $\hat{\varvec{\beta }}$, $\hat{\sigma }_{u1}^2$, $\hat{\sigma }_{u2}^2$ and $\hat{\rho }$ in the place of $\varvec{\beta }$, $\sigma _{u1}^2$, $\sigma _{u2}^2$ and $\rho$ respectively. The MEBFH-EBP of $\mu _d$ is

$$\begin{aligned} \hat{\mu }_d^{ebp}=E[\mu _d|x_d,y_d]=Z_d\hat{\eta }+X_{d}\hat{\lambda }+\text{ diag }(\hat{\lambda }_{1}^\prime ,\hat{\lambda }_{2}^\prime )\hat{v}_d^{ebp}+\hat{u}_d^{ebp}. \end{aligned}$$

(9)

Section 6 introduces the maximum likelihood and the pseudo-REML of estimators of model parameters. In the application to real data, the MEBFH-EBP of $\mu _d$ is calculated by plugging pseudo-REML estimators.

4 Relative efficiency matrix of best predictors

An important question is, when using estimated auxiliary variables, how much efficiency can be gained by using the MEBFH-BP instead of the BFH-BLUP. We recall that MEBFH-BP denotes the BP of $\mu _d$ calculated by assuming that the MEBFH model is the true model. Similarly, BFH-BLUP denotes the best linear unbiased predictor of $\mu _d$ calculated by assuming that the BFH model (with no measurement errors) is the true model. The gain in efficiency is measured as the relative reduction of the MSE when using the MEBFH-BP instead of the BFH-BLUP, under the assumption that all model parameters are known and the true model is MEBFH.

We first derive the BFH-BLUP of $\mu _d$ and its MSE under the true MEBFH model. If we equate $V_\lambda$ to the null matrix in (8), we obtain the BFH-BLUP, i.e.

$$\begin{aligned} \hat{\mu }_d^{bp_0}=Z_d\eta +X_d\lambda +(V_{ud}^{-1}+V_{ed}^{-1})^{-1}V_{ed}^{-1}\xi _d = Z_d\eta +X_d\lambda +V_{ud}(V_{ud}+V_{ed})^{-1}\xi _d, \end{aligned}$$

(10)

where $\xi _d=y_d-Z_d\eta -X_d\lambda =B_dv_d+u_d+e_d.$ The prediction error of the BFH-BLUP is

$$\begin{aligned} \hat{\mu }_d^{bp_0}-\mu _d&= Z_d\eta +X_d\lambda +V_{ud}(V_{ud}+V_{ed})^{-1}\xi _d-\big (Z_d\eta +X_d\lambda +B_dv_d+u_d\big ) \\&= V_{ud}(V_{ud}+V_{ed})^{-1}\xi _d-B_dv_d-u_d. \end{aligned}$$

Under the MEBFH model, the BFH-BLUP is predictively unbiased. It holds that

$$\begin{aligned} E\big [\xi _d|x_d\big ]=E\big [B_dv_d+u_d+e_d\big ]=0,\quad E\big [\hat{\mu }_d^{bp_0}-\mu _d|x_d\big ]=0. \end{aligned}$$

Under the MEBFH model, we have

$$\begin{aligned} E\big [\xi _d\xi _d^\prime |x_d\big ]&= B_dE\big [v_dv_d^\prime |x_d\big ]B_d^\prime +E\big [u_du_d^\prime |x_d\big ]+E\big [e_de_d^\prime |x_d\big ] \\&= V_{\lambda _d}+V_{u_d}+V_{e_d}=V_d, \\ E\big [\xi _dv_d^\prime |x_d\big ]B_d^\prime&= E\big [(B_dv_d+u_d+e_d)v_d^\prime |x_d\big ]B_d^\prime =B_dE\big [v_dv_d^\prime |x_d\big ]B_d^\prime =V_{\lambda _d}, \\ E\big [\xi _du_d^\prime |x_d\big ]&= E\big [(B_dv_d+u_d+e_d)u_d^\prime |x_d\big ]=E\big [u_du_d^\prime |x_d\big ]=V_{u_d}. \end{aligned}$$

Under the MEBFH model, with all model parameters known, the MSE of the BFH-BLUP is

$$\begin{aligned} MSE(\hat{\mu }_d^{bp_0}|x_d)&= E\big [(\hat{\mu }_d^{bp_0}-\mu _d)(\hat{\mu }_d^{bp_0}-\mu _d)^\prime |x_d\big ]\\&= V_{ud}(V_{ud}+V_{ed})^{-1}E\big [\xi _d\xi _d^\prime |x_d\big ](V_{ud}+V_{ed})^{-1}V_{ud} \\&\quad +\,B_dE\big [v_dv_d^\prime |x_d\big ]B_d^\prime +E\big [u_du_d^\prime |x_d\big ] \\&\quad -\,V_{ud}(V_{ud}+V_{ed})^{-1}E\big [\xi _dv_d^\prime |x_d\big ]B_d^\prime \\&\quad -\,V_{ud}(V_{ud}+V_{ed})^{-1}E\big [\xi _du_d^\prime |x_d\big ] -B_dE\big [v_du_d^\prime |x_d\big ] \\&\quad -\,B_dE\big [v_d\xi _d^\prime |x_d\big ](V_{ud}+V_{ed})^{-1}V_{ud} \\&\quad -\,E\big [u_d\xi _d^\prime |x_d\big ](V_{ud}+V_{ed})^{-1}V_{ud} -E\big [u_dv_d^\prime |x_d\big ]B_d^\prime \\&= V_{ud}(V_{ud}+V_{ed})^{-1}V_d(V_{ud}+V_{ed})^{-1}V_{ud}+V_{\lambda _d}+V_{u_d} \\&\quad -\,2V_{ud}(V_{ud}+V_{ed})^{-1}V_{u_d} \\&\quad -\,V_{ud}(V_{ud}+V_{ed})^{-1}V_{\lambda _d} -V_{\lambda _d}(V_{ud}+V_{ed})^{-1}V_{ud}. \end{aligned}$$

If all MEBFH model parameters are known, the relative efficiency matrix of the MEBFH-BP compared to the BFH-BLUP is

$$\begin{aligned} RE_d=\left( \begin{array}{cc}RE_{d11} & RE_{d12}\\ RE_{d21} & RE_{d22}\end{array}\right) =\frac{MSE(\hat{\mu }_d^{bp}|x_d)}{MSE(\hat{\mu }_d^{bp_0}|x_d)},\quad d=1,\ldots ,D, \end{aligned}$$

(11)

where the division of the $2\times 2$ matrices $MSE(\hat{\mu }_d^{bp}|x_d)$ and $MSE(\hat{\mu }_d^{bp_0}|x_d)$ is done component by component. We are mainly interested in the diagonal components $RE_{d11}$ and $RE_{d11}$; this is to say, in the relative efficiencies when predicting $\mu _{d1}$ and $\mu _{d2}$ respectively. We further remark that $RE_d$ does not depend on $x_d$, $\eta$ or D.

In what follows, we presents some numerical calculations of the relative efficiencies of the MEBFH model with respect to the BFH model. Let us consider a MEBFH model (4) with $q_1=q_2=p_1=p_2=1$, so that the model elements are $Z_d=\text{ diag }(z_{d1},z_{d2})$, $\eta =(\eta _1,\eta _2)^\prime$, $X_d=\text{ diag }(x_{d1},x_{d2})$, $\lambda =(\lambda _1,\lambda _2)^\prime$, $B=\text{ diag }(\lambda _1,\lambda _2)$, $v_d=(v_{d1},v_{d2})^\prime$, $u_d=(u_{d1},u_{d2})^\prime$, $e_d=(e_{d1},e_{d2})^\prime$. For $d=1,\ldots ,D$, define $\tau _{d11}=\Sigma _{d11}$, $\tau _{d21}=\tau _{d12}=\Sigma _{d12}$, $\tau _{d22}=\Sigma _{d22}$ and

$$\begin{aligned} \Sigma _{d}=\left( \begin{array}{cc} \tau _{d11}&\tau _{d12}\\ \tau _{d12}&\tau _{d22}\\ \end{array}\right) , \quad V_{ud}=\left( \begin{array}{cc} \theta _1&\theta _3\sqrt{\theta _1}\sqrt{\theta _2}\\ \theta _3\sqrt{\theta _1}\sqrt{\theta _2}&\theta _2\\ \end{array}\right) , \quad V_{ed}=\left( \begin{array}{cc} 1&c\\ c&1\\ \end{array}\right) , \end{aligned}$$

where $\tau _{d12}=\rho _{\tau }\tau _{d11}^{1/2}\tau _{d22}^{1/2}$. Take $\lambda _1=\lambda _2=1$, $\tau =\tau _{d11}=\tau _{d22}$, $\theta _1=1$ and $\theta _2=3/2$.

Table 1 presents the relative efficiencies $RE_{d11}$ (top) and $RE_{d22}$ (bottom) for the 45 scenarios 1A,...,9E. All the scenarios take $\theta _1=1$, $\theta _2=3/2$. The row cases A, B, C, D, E take $\tau =1.81, 1.41, 1.01, 0,61, 0.21$ respectively. Scenarios 1–9 take the parameters $\rho _{\tau }$, c and $\theta _3$ given by the rows 2, 3 and 4 of Table 1. We observe that the relative efficiencies decrease as $\tau$ increases from case E to case A. This is to say, the greater the measurement error variance of the auxiliary variables is, the greater gain of efficiency is obtained by using the best predictor based on the MEBFH model. On the other hand, if the measurement errors are negligible ($\tau \approx 0$), then the gain of efficiency almost null.

The greater values of $RE_{d11}$ and $RE_{d22}$ are in the column case 5. Therefore, the efficiency gain when using the MEBFH model is smaller when the correlations $\rho _{\tau }$, c and $\theta _3$ of the components of the measurement errors $v_d$, the sampling errors $e_d$ and the random effects $u_d$ respectively, are close to zero. In the limit $\rho _{\tau }=c=\theta _3=0$, we get two independent measurement error univariate Fay–Herriot models and it is not possible to transport information from one component to other.

Figure 1 plots the relative efficiencies $RE_{d11}$ and $RE_{d22}$ for $\theta _3\in \{-0.75,0.85\}$ and any $\rho _{\tau }$ and c. The case $\theta _3=-0.75$ covers the Scenarios 2A and 3A and any other scenario with $\theta _3=-0.75$, $-0.5\le \rho _\tau \le 0.5$ and $-0.5\le c\le 0.5$. The case $\theta _3=0.85$ contains the scenarios 8A and 9A as individual points in the right-hand printed surfaces.

In summary, Table 1 and Figure 1 show some scenarios where the MSE of the MEBFH-BP is around a half of the MSE of the BFH-EBLUP. They also show some other scenarios where the gain of efficiency is rather small. This information is useful to decide in what situations it is more profitable to use the more complex EBP based on the MEBFH model.

Table 1 $RE_{d11}$ (top) and $RE_{d22}$ (bottom) for $\theta _1=1$, $\theta _2=3/2$ and scenarios 1A,..., 9E.

Fig. 1

Relative efficiencies for $\tau =1.81$, $\theta _1=1$, $\theta _2=3/2$

5 Mean squared error estimation

Obtaining an approximation to the MSE of the EBP of $\mu _d$ under the MEBFH model requires tedious calculations. Unlike the case of no measurement errors, the obtained approximation will be quite awkward and not very useful to introduce analytic MSE estimators. This is why we propose applying a parametric bootstrap procedure, like the one introduced by González-Manteiga et al. (2008) and later extended by González-Manteiga et al. (2010) to semi-parametric Fay–Herriot models.

Let $\psi =(\eta ^\prime ,\lambda ^\prime ,\theta ^\prime )^\prime$ be the vector of model parameters, where $\theta =(\sigma _{u1}^2,\sigma _{u2}^2,\rho )^\prime$. The following parametric bootstrap procedure estimates $MSE(\hat{\mu }^{ebp}_d)$.

• 1. Calculate the estimates $\hat{\psi }$ and $\hat{V}_{ud}=V_{ud}(\hat{\psi })$ by using the data $(y_d,Z_d,X_d)$, $d=1,\ldots ,D$.

• 2. Repeat B times

  • 2.1. For $d=1,\ldots ,D$, generate $u_d^{*(b)}\sim N_2(0,\hat{V}_{ud})$, $e_d^{*(b)}\sim N_2(0,V_{ed})$ ${v}_{d}^{*(b)}\sim N_2(0,\Sigma _d)$, $y_d^{*(b)}=\mu _d^{*(b)}+e_{d}^{*(b)}$ and$\mu _d^{*(b)}=Z_d\hat{\eta }^{(i)}+X_d\lambda ^{(i)}+ \text{ diag }(\hat{\lambda }_1^{(i)},\hat{\lambda }_2^{(i)})v_d^{*(b)}+u_d^{*(b)}$.

  • 2.2. Calculate the estimator $\hat{\psi }^{*(b)}$ by using the data $(y_d^{*(b)},Z_d,X_d)$, $d=1,\ldots ,D$.

  • 2.3 Calculate the EBPs $\hat{\mu }^{*(b)}_{dk}$, $d=1,\ldots ,D$, $k=1,2$, under the model of Step 2.1.

• 3 For $d=1,\ldots ,D$, $k=1,2$, calculate the MSE estimator of the EBP; i.e.

  $$\begin{aligned} mse_{dk}^{*}=\frac{1}{B}\sum _{b=1}^B\big (\hat{\mu }^{*(b)}_{dk}-\mu ^{*(b)}_{dk}\big )^2. \end{aligned}$$

6 Estimation of model parameters

We consider two methods for estimating $\eta$, $\lambda$, $\sigma _{u1}^2$, $\sigma _{u2}^2$ and $\rho$ under model (4): (1) pseudo-residual maximum likelihood, and (2) maximum likelihood. Both method are based on the distribution of y|X. Appendix C in the supplementary file gives the Fisher-scoring algorithm to calculate the maximum likelihood estimators of the model parameters. However, we we do not implement this last algorithm because it has a greater computational complexity. This section describes the pseudo-residual maximum likelihood method.

ML estimators of model parameters have well known asymptotic properties. Under regularity conditions on the auxiliary variables, they are consistent and asymptotically normal. The Fisher-scoring algorithm maximizes the log-likelihood of y|X by solving the corresponding system of nonlinear equation, i.e. first partial derivatives equated to zero. It is a system with $p+q+3$ equations and the Fisher-scoring algorithm inverts matrices of that dimension. If p or q are big, then the algorithm speed decreases and it might have convergence problems when the number of domains D is not big enough.

The REML estimators of the parameters of a linear mixed model are quite attractive. They have similar good asymptotic properties as ML estimators, but their calculation has a lower computational cost because the REML log-likelihood involves only the variance component parameters. Nevertheless, the MEBFH model is not a linear mixed model and the REML method is thus not applicable. This is why, we introduce pseudo-REML approach by treating the components of matrix $B_d$ in (4) as known constants. In that case, the MEBFH model becomes a linear mixed model and the REML method can be applied yielding to the maximization of the derived REML log-likelihood. However, the components of $B_d$ depends on the unknown vector of parameters $\lambda$ and, therefore, we are not applying the REML method but a pseudo-REML approach. The small sample properties of the pseudo-REML are empirically investigated in Simulation 1.

Let us define ${T}=[Z,X]=\underset{1\le d \le D}{\hbox {col}}({T}_{d})$, ${T}_{d}=[Z_d,X_d]$ and $\beta =(\eta ^\prime ,\lambda ^\prime )^\prime$, so that model (4) can be written in the form

$$\begin{aligned} y_d={T}\beta +Bv_d+u_d+e_d, \quad d=1,\ldots , D, \end{aligned}$$

(12)

The pseudo-REML log-likelihood of model (12) is

$$\begin{aligned} {l}_{reml}(\theta )=-\frac{2D-p-q}{2}\log 2\pi +\frac{1}{2}\log |{{T}}^{\prime }{{T}}|-\frac{1}{2}\log |{V}| - \frac{1}{2}\log |{{T}}^{\prime }{V}^{-1}{{T}}| -\frac{1}{2}\,{y}^{\prime }{P}{y}, \end{aligned}$$

where $\theta =(\theta _1,\theta _2,\theta _3)$, $\theta _1=\sigma _{u1}^2$, $\theta _2=\sigma _{u2}^2$, $\theta _3=\rho$, ${P}{V}{P}={P}$, ${P}{{T}}=0$, ${P}={V}^{-1}-{V}^{-1}{{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}$, and V is defined in (5). By applying the formulas

$$\begin{aligned} \frac{\partial \log |V|}{\partial \theta }=\text{ tr }\Big (V^{-1}\frac{\partial V}{\partial \theta }\Big ),\quad \frac{\partial V^{-1}}{\partial \theta }=-V^{-1}\frac{\partial V}{\partial \theta }V^{-1}, \end{aligned}$$

we calculate the first partial derivatives of ${l}_{reml}$ with respect to $\theta _{\ell }$, i.e.

$$\begin{aligned} \frac{\partial {l}_{reml}(\theta )}{\partial \theta _{\ell }}&= -\frac{1}{2}\,\text{ tr }\Big (V^{-1}\frac{\partial V}{\partial \theta _\ell }\Big ) +\frac{1}{2}\,\text{ tr }\Big (({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1}{{T}}\Big ) -\frac{1}{2}\,{y}^{\prime }\frac{\partial {P}}{\partial \theta _{\ell }}{y}\\&= -\frac{1}{2}\,\text{ tr }\Big (V^{-1}\frac{\partial V}{\partial \theta _\ell }\Big ) +\frac{1}{2}\,\text{ tr }\Big ({V}^{-1}{{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}\frac{\partial V}{\partial \theta _\ell }\Big ) -\frac{1}{2}\,{y}^{\prime }\frac{\partial {P}}{\partial \theta _{\ell }}{y}\\&= -\frac{1}{2}\,\text{ tr }\Big (\big [{V}^{-1}-{V}^{-1}{{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}\big ]\frac{\partial V}{\partial \theta _\ell }\Big ) -\frac{1}{2}\,{y}^{\prime }\frac{\partial {P}}{\partial \theta _{\ell }}{y}\\&= -\frac{1}{2}\,\text{ tr }\Big (P\frac{\partial V}{\partial \theta _\ell }\Big )-\frac{1}{2}\,{y}^{\prime }\frac{\partial {P}}{\partial \theta _{\ell }}{y},\quad \ell =1,2,3. \end{aligned}$$

Let us define $G=V^{-1}{T}({T}^{\prime }V^{-1}{T})^{-1}$, so that $P=(I-{G}{{T}}^{\prime }){V}^{-1}=V^{-1}(I-{T} G^\prime )$. The first partial derivatives of $P={V}^{-1}-{V}^{-1}{{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}$ with respect to $\theta _{\ell }$ are

$$\begin{aligned} \frac{\partial P}{\partial \theta _{\ell }}&= -{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1} +{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1}{{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}\\&\quad +\, {V}^{-1}{{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1}\\&\quad -\, {V}^{-1}{{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1} {{T}}({{T}}^{\prime }{V}^{-1}{{T}})^{-1}{{T}}^{\prime }{V}^{-1}\\&= -{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1} +{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1}{{T}}{G}^{\prime } +{G}{{T}}^{\prime }{V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1} \\&\quad -\,{G}{{T}}^{\prime } {V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1}{{T}}{G}^{\prime } \\&= -(I-{G}{{T}}^{\prime }){V}^{-1}\frac{\partial V}{\partial \theta _\ell }{V}^{-1}(I-{G}{{T}}^{\prime })^{\prime }=-P\frac{\partial V}{\partial \theta _\ell }P,\quad \ell =1,2,3. \end{aligned}$$

Therefore, the score vector for $\ell =1,2,3$ is

$$\begin{aligned} S(\theta ,\beta )=(S_1,S_2,S_3)^\prime ,\,\, S_{\ell }=S_{\ell }(\theta ,\beta )=\frac{\partial {l}_{reml}}{\partial \theta _{\ell }}= -\frac{1}{2}\,\hbox {tr}({P}{V}_{\ell })+\frac{1}{2}\,{y}^{\prime }{P}{V}_{\ell }{P}{y},\quad \end{aligned}$$

where $P=P(\theta ,\beta )=\big (P_{d_1d_2}\big )_{d_1,d_2=1,\ldots ,D}$, $V_\ell =V_\ell (\theta )=\frac{\partial {V}}{\partial \theta _{\ell }}=\underset{1\le d \le D}{\hbox {diag}}({V}_{ud\ell })$ and

$$\begin{aligned} P_{dd}=V_d^{-1}-V_d^{-1}{{T}}_dQ{{T}}_d^\prime V_d^{-1},\quad P_{d_1d_2}=-V_{d_1}^{-1}{{T}}_{d_1}Q{{T}}_{d_2}^\prime V_{d_2}^{-1},\quad Q=\big ({{T}}^\prime V^{-1}{{T}}\big )^{-1}, \end{aligned}$$

$$\begin{aligned} V_{ud1}&= \frac{\partial V_{ud}}{\partial \sigma _{u1}^2}= \left( \begin{array}{cc} 1&\frac{\rho _{12}\sigma _{u2}}{2\sigma _{u1}}\\ \frac{\rho _{12}\sigma _{u2}}{2\sigma _{u1}}&0\\ \end{array}\right) ,\quad V_{ud2}=\frac{\partial V_{ud}}{\partial \sigma _{u2}^2}= \left( \begin{array}{cc} 0&\frac{\rho _{12}\sigma _{u1}}{2\sigma _{u2}}\\ \frac{\rho _{12}\sigma _{u1}}{2\sigma _{u2}}&1\\ \end{array}\right) , \\ V_{ud3}&= \frac{\partial V_{ud}}{\partial \rho _{12}}= \left( \begin{array}{cc} 0&\sigma _{u1}\sigma _{u2}\\ \sigma _{u1}\sigma _{u2}&0\\ \end{array}\right) . \end{aligned}$$

For $\ell =1,2,3$, we have

$$\begin{aligned} {P}{V}_\ell&= \Big [\underset{1\le d \le D}{\hbox {diag}}({V}_{d}^{-1})- \underset{1\le d \le D}{\hbox {col}}({V}_{d}^{-1}{{T}}_d)Q\underset{1\le d \le D}{\hbox {col}^\prime }({{T}}_d^{\prime }{V}_{d}^{-1})\Big ] \underset{1\le d \le D}{\hbox {diag}}({V}_{ud\ell }) \\&= \underset{1\le d \le D}{\hbox {diag}}({V}_{d}^{-1}{V}_{ud\ell })- \underset{1\le d \le D}{\hbox {col}}({V}_{d}^{-1}{{T}}_d)Q\underset{1\le d \le D}{\hbox {col}^\prime }({{T}}_d^{\prime }{V}_{d}^{-1}{V}_{ud\ell }). \end{aligned}$$

For $a,b=1,2,3$, we have

$$\begin{aligned} {P}{V}_a{P}{V}_b&= \Big [\underset{1\le d \le D}{\hbox {diag}}({V}_{d}^{-1}{V}_{uda})- \underset{1\le d \le D}{\hbox {col}}({V}_{d}^{-1}{{T}}_d)Q\underset{1\le d \le D}{\hbox {col}^\prime }({{T}}_d^{\prime }{V}_{d}^{-1}{V}_{uda})\Big ] \\&\quad\cdot \Big [\underset{1\le d \le D}{\hbox {diag}}({V}_{d}^{-1}{V}_{udb})- \underset{1\le d \le D}{\hbox {col}}({V}_{d}^{-1}{{T}}_d)Q\underset{1\le d \le D}{\hbox {col}^\prime }({{T}}_d^{\prime }{V}_{d}^{-1}{V}_{udb})\Big ] \\&= \underset{1\le d \le D}{\hbox {diag}}({V}_{d}^{-1}{V}_{uda}{V}_{d}^{-1}{V}_{udb}) \\&\quad -\,\underset{1\le d \le D}{\hbox {col}}({V}_{d}^{-1}{V}_{uda}{V}_{d}^{-1}{{T}}_d)Q \underset{1\le d \le D}{\hbox {col}^\prime }({{T}}_d^{\prime }{V}_{d}^{-1}{V}_{udb}) \\&\quad -\, \underset{1\le d \le D}{\hbox {col}}({V}_{d}^{-1}{{T}}_d)Q \underset{1\le d \le D}{\hbox {col}^\prime }({{T}}_d^{\prime }{V}_{d}^{-1}{V}_{uda}{V}_{d}^{-1}{V}_{udb}) \\&\quad +\,\underset{1\le d \le D}{\hbox {col}}({V}_{d}^{-1}{{T}}_d)Q \Big (\sum _{d=1}^D{{T}}_d^{\prime }{V}_{d}^{-1}{V}_{uda}{V}_{d}^{-1}{{T}}_d\Big )Q \underset{1\le d \le D}{\hbox {col}^\prime }({{T}}_d^{\prime }{V}_{d}^{-1}{V}_{udb}). \end{aligned}$$

For $\ell =1,2,3$, we have

$$\begin{aligned} \text{ tr }({P}{V}_{\ell })&= \sum _{d=1}^D\text{ tr }({V}_{d}^{-1}{V}_{ud\ell })-\sum _{d=1}^D\text{ tr }({V}_{d}^{-1}{{T}}_dQ{{T}}_d^{\prime }{V}_{d}^{-1}{V}_{ud\ell }) =\sum _{d=1}^D\text{ tr }({P}_{dd}{V}_{ud\ell }), \\ y^\prime PV_{\ell }P y&= \sum _{d=1}^Dy_d^\prime V_d^{-1}V_{ud\ell }V_d^{-1}y_d -2\sum _{d_1=1}^D\sum _{d_2=1}^Dy_{d_1}^\prime V_{d_1}^{-1}{V}_{ud_1\ell }V_{d_1}^{-1}{{T}}_{d_1}Q{{T}}_{d_2}^{\prime }V_{d_2}^{-1}y_{d_2} \\&\quad +\,\sum _{d_1=1}^D\sum _{d_2=1}^Dy_{d_1}^\prime V_{d_1}^{-1}{{T}}_{d_1}Q\Big (\sum _{d_1=1}^D{{T}}_{d}^{\prime }V_{d}^{-1}V_{ud\ell }V_{d}^{-1}{{T}}_d\Big )Q {{T}}_{d_2}^{\prime }V_{d_2}^{-1}y_{d_2}. \end{aligned}$$

For $a,b=1,2,3$, the second partial derivatives of the REML log-likelihood function are

$$\begin{aligned} \frac{\partial {l}_{reml}^2(\theta )}{\partial \theta _a\partial \theta _b}&= \frac{1}{2}\,\text{ tr }\big (PV_bPV_a\big )-\frac{1}{2}\,{y}^{\prime }(PV_bPV_aP+PV_aPV_bP){y} \\&= \frac{1}{2}\,\text{ tr }\big (PV_aPV_b\big )-{y}^{\prime }PV_aPV_bPy, \end{aligned}$$

where the last equality follows from the fact that $V_\ell$ is symmetric, $\ell =1,2,3$. By changing the sign, taking expectations and applying $P{T}=0$, $PV=I-V^{-1}{T} Q{T}^\prime$ and the formula

$$\begin{aligned} E\big [y^\prime Ay\big ]=\text{ tr }\big (A\text{ var }(y)\big )+E[y]^\prime AE[y], \end{aligned}$$

we get the components of the Fisher information matrix, i.e.

$$\begin{aligned} F_{ab}&= F_{ab}(\theta )=-\frac{1}{2}\,\text{ tr }\big (PV_aPV_b\big )+ \text{ tr }\big (PV_aPV_bPV\big )+\beta ^\prime {T}^\prime V_aPV_bP{T}\beta \\&= -\frac{1}{2}\,\text{ tr }\big (PV_aPV_b\big )+\text{ tr }\big (PV_aPV_b[I-V^{-1}{{T}}Q{{T}}^\prime ]\big ) \\&= \frac{1}{2}\,\text{ tr }\big (PV_aPV_b\big )+\text{ tr }\big (PV_aPV_bV^{-1}{{T}}Q{{T}}^\prime \big ) =\frac{1}{2}\,\text{ tr }\big (PV_aPV_b\big ),\quad a,b=1,2,3. \end{aligned}$$

Therefore, the Fisher information matrix is

$$\begin{aligned} F(\theta ,\beta )=\big (F_{a,b}\big )_{a,b=1,2,3},\quad F_{ab}=F_{ab}(\theta ,\beta )=\frac{1}{2}\text{ tr }({P}{V}_a{P}{V}_b),\quad a,b=1,2,3. \end{aligned}$$

The trace of ${P}{V}_a{P}{V}_b$ can be calculated as

$$\begin{aligned} \text{ tr }({P}{V}_a{P}{V}_b)&= \sum _{d=1}^D\text{ tr }\big ({V}_{d}^{-1}{V}_{uda}{V}_{d}^{-1}{V}_{udb}\big ) -\sum _{d=1}^D\text{ tr }\big ({V}_{udb}{V}_{d}^{-1}{V}_{uda}{V}_{d}^{-1}{{T}}_dQ{{T}}_d^{\prime }{V}_{d}^{-1}\big ) \\&\quad -\,\sum _{d=1}^D\text{ tr }\big ({V}_{uda}{V}_{d}^{-1}{V}_{udb}{V}_{d}^{-1}{{T}}_dQ{{T}}_d^{\prime }{V}_{d}^{-1}\big ) \\&\quad +\, \text{ tr }\Big (\Big \{\sum _{d=1}^D{{T}}_d^{\prime }{V}_{d}^{-1}{V}_{udb}{V}_{d}^{-1}{{T}}_{d}\Big \}Q \Big \{\sum _{d=1}^D{{T}}_d^{\prime }{V}_{d}^{-1}{V}_{uda}{V}_{d}^{-1}{{T}}_{d}\Big \}Q\Big ). \end{aligned}$$

The pseudo-REML Fisher-scoring algorithm is

• 1. Set the initial values $\beta ^{(0)}$, $\theta ^{(0)}$, and $\varepsilon _j>0$, $j=1,\ldots ,p+q+3$.

• 2. Repeat the following steps until the tolerance or the boundary conditions are fulfilled.

  • (a) Updating equation for $\theta$: Do $\theta ^{(i+1)}=\theta ^{(i)}+{F}^{-1}(\theta ^{(i)},\beta ^{(i)}){S}(\theta ^{(i)},\beta ^{(i)})$.

  • (b) Boundary condition: If $\theta _1^{(i+1)}>0$, $\theta _2^{(i+1)}>0$ and $\big |\theta _3^{(i+1)}\big |<1$, continue. Otherwise, do $\hat{\theta }=\theta ^{(i)}$ and stop.

  • (c) Updating equation for $\beta$:Do $\beta ^{(i+1)}=\big ({{T}}^\prime {V}^{-1}(\theta ^{(i+1)},\beta ^{(i)}){{T}}\big )^{-1}{{T}}^\prime {V}^{-1}(\theta ^{(i+1)},\beta ^{(i)})y$.

  • (d) Tolerance condition: If $\big |\theta _\ell ^{(i+1)}-\theta _\ell ^{(i)}\big |<\varepsilon _{p+q+\ell }$, $\big |\beta _j^{(i+1)}-\beta _j^{(i)}\big |<\varepsilon _j$, $j=1,\ldots ,p+q$, $\ell =1,2,3$, do $\hat{\theta }_\ell =\theta _\ell ^{(i+1)}$, $\hat{\beta }=\beta ^{(i+1)}$ and stop. Otherwise, continue.

• 3. Output: $\hat{\theta }$, $\hat{\beta }$, ${F}^{-1}(\hat{\theta },\hat{\beta })$.

The asymptotic distributions of the REML estimators $\hat{\theta }$ and $\hat{\beta }$,

$$\begin{aligned} \hat{\theta }\sim N_2\big (\theta , {F}^{-1}(\theta ,\beta )\big ),\quad \hat{\beta }\sim N_{p+q}\big (\beta , ({{T}}^{\prime }{V}^{-1}(\theta ,\beta ){{T}})^{-1}\big ), \end{aligned}$$

can be used to construct $(1-\alpha )$-level confidence intervals for the components $\theta _{\ell }$ of $\theta$ and $\beta _j$ of $\beta$, i.e.

$$\begin{aligned} \hat{\theta }_{\ell }\pm z_{\alpha /2}\,\nu _{\ell \ell }^{1/2},\,\, \ell =1,2,3,\quad \hat{\beta }_{j}\pm z_{\alpha /2}\,g_{jj}^{1/2},\,\, j=1,\ldots ,p+q, \end{aligned}$$

(13)

where ${F}^{-1}(\hat{\theta },\hat{\beta })=(\nu _{ab})_{a,b=1,2,3}$, $({{T}}^{\prime }{V}^{-1}(\hat{\theta },\hat{\beta }){{T}})^{-1}=(g_{ab})_{a,b=1,\ldots ,p+q}$ and $z_{\alpha }$ is the $\alpha$-quantile of the N(0, 1) distribution. For $\hat{\beta }_j=\beta _0$, the p-value for testing the hypothesis $H_0:\,\beta _j=0$ is

$$\begin{aligned} \text{ p-value }=2P_{H_0}(\hat{\beta }_j>|\beta _0|)=2P(N(0,1)> |\beta _0|/\sqrt{g_{jj}}). \end{aligned}$$

(14)

We remark that we have changed the notation in (13) and (14), where $\beta _j$ denotes the j-th component of the vector $\beta$ and not the vector of regression parameters of the j-th category.

7 Simulations

This section presents simulation experiments for assessing the performance of the fitting method, the EBP estimator, and the MSE estimator. The objective is to show how the new methodology works in realistic (not extreme) scenarios. In practice, some explanatory variables can be taken from an auxiliary survey that is different from the target survey and that has bigger sample sizes. This is the case of the SLCS (target survey) and the SLFS (auxiliary survey). The second one has bigger sample sizes than the first. Therefore, it is natural to choose scenarios where the variances of the measurement errors are lower than the variances of the sampling errors and lower than the variances of the random effects.

In the calculation of Sect. 4, the variances of the sampling errors are $\sigma _{e1}^2=\sigma _{e2}^2=1$ and the variances of the random effects are $\sigma _{u1}^2=\theta _1=1$ and $\sigma _{u2}^2=\theta _2=3/2=0.66$. Therefore, it is quite natural to choose scenario E, where the measurement error variances are $\tau _{d11}=\tau _{d22}=0.21$ Concerning the random effect correlations, we are mainly interested in the case $\theta _3=\text{ corr }(u_{d1},u_{d2})=0.45$ because $\theta _3$ is positive in the application to real data. This is why, we consider that the scenario 6E is the most close to the application to real data presented in Sect. 8. For the sake of completeness, we also run simulations under the scenarios 5E and 4E with correlations $\theta _3=0.05$ and $\theta _3=-0.55$.

The data for the simulation experiments is generated as follows. We take $q_1=q_2=p_1=p_2=1$, so that the elements of the MEBFH model (4) are $Z_d=\text{ diag }(z_{d1},z_{d2})$, $\eta =(\eta _1,\eta _2)^\prime$, $X_d=\text{ diag }(x_{d1},x_{d2})$, $\lambda =(\lambda _1,\lambda _2)^\prime$, $B=\text{ diag }(\lambda _1,\lambda _2)$, $v_d=(v_{d1},v_{d2})^\prime$, $u_d=(u_{d1},u_{d2})^\prime$, $e_d=(e_{d1},e_{d2})^\prime$. Take $z_{d1}=z_{d2}=1$, $\eta _1=\eta _2=\lambda _1=\lambda _2=1$ and

$$\begin{aligned} x_{d1}=\mu _{x1}+\sigma _{x1}^{1/2}S_{d1},\quad x_{d2}=\mu _{x2}+\sigma _{x2}^{1/2}S_{d2},\quad S_{dk}\overset{\text{ ind }}{\sim }U(0,1),\quad k=1,2,\,\, d=1,\ldots ,D, \end{aligned}$$

with $\mu _{x1}=\mu _{x2}=1$, $\sigma _{x1}=1.2$ and $\sigma _{x2}=2.4$. Note that

$$\begin{aligned} \text{ var }_{U(0,1)}({x}_{d12})=\frac{\sigma _{x1}}{12}=0.1,\quad \text{ var }_{U(0,1)}({x}_{d22})=\frac{\sigma _{x2}}{12}=0.2. \end{aligned}$$

For $d=1,\ldots ,D$, generate $v_d\sim N_{2}(0,\Sigma _{d})$, ${u}_{d}\sim N_{2}(0,{V}_{ud})$ and ${e}_d\sim N_{2}(0,{V}_{ed})$, where

$$\begin{aligned} \Sigma _{d}=\left( \begin{array}{ll} \tau _{d11}&\tau _{d12}\\ \tau _{d21}&\tau _{d22}\\ \end{array}\right) , \quad V_{ud}=\left( \begin{array}{ll} \theta _1&\theta _3\sqrt{\theta _1}\sqrt{\theta _2}\\ \theta _3\sqrt{\theta _1}\sqrt{\theta _2}&\theta _2\\ \end{array}\right) , \quad V_{ed}=\left( \begin{array}{cc} 1&c\\ c&1\\ \end{array}\right) \end{aligned}$$

$\tau _{d12}=\rho _{\tau }\tau _{d11}^{1/2}\tau _{d22}^{1/2}$, $\tau _{d11}=\tau _{d22}=\tau =0.21$, $\rho _\tau =c=-0.35$, $\theta _1=1$ and $\theta _2=1.5$. Concerning the random effect correlation, we consider $\theta _3=0.45$, $\theta _3=0.05$ and $\theta _3=-0.55$. This is to say, we take the same model parameters as in Scenarios 6E, 5E and 4E of Sect. 4.

7.1 Simulation 1

The target of Simulation 1 is to check the behavior of the pseudo-REML Fisher-scoring algorithm for fitting the MEBFH model. The steps of Simulation 1 are

• 1. Generate $z_{dk}$, $x_{dk}$, $d=1,\ldots ,D$, $k=1,2$.

• 2. Repeat $I=1000$ times ($i=1,\ldots ,1000$)

  • 2.1. Generate $v_d^{(i)}\sim N_2(0,\Sigma _{d})$, $u_d^{(i)}\sim N_2(0,V_{ud})$, $e_d^{(i)}\sim N_2(0,V_{ed})$ and

    $$\begin{aligned} y_d^{(i)}=Z_d\eta +X_d\lambda +Bv_d^{(i)}+u_d^{(i)}+e_d^{(i)}, \quad d=1,\ldots ,D. \end{aligned}$$

    (15)

  • 2.2. For every model parameter $\gamma \in \{\eta _1,\lambda _1,\eta _2,\lambda _2,\theta _1,\theta _2,\theta _3\}$, calculate the corresponding REML estimator $\hat{\gamma }^{(i)}\in \{\hat{\eta }_1^{(i)},\hat{\lambda }_1^{(i)},\hat{\eta }_2^{(i)},\hat{\lambda }_2^{(i)}, \hat{\theta }_{1}^{(i)},\hat{\theta }_{2}^{(i)},\hat{\theta }_{3}^{(i)}\}$.

• 3. Output (empirical biases and root-MSEs):

  $$\begin{aligned} BIAS(\hat{\gamma })=\frac{1}{I}\sum _{i=1}^{I}(\hat{\gamma }^{(i)}-\gamma ),\quad RMSE(\hat{\gamma })=\left( \frac{1}{I}\sum _{i=1}^{I}(\hat{\gamma }^{(i)}-\gamma )^2\right) ^{1/2}. \end{aligned}$$

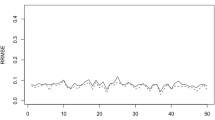
For the sake of brevity, Table 2 presents only the results of Simulation 1 under Scenario 6E. The column labeled by $\gamma$ contains the values of the true model parameters. Simulation 1 shows that the REML Fisher scoring algorithm works properly because BIAS and RMSE decrease as D increases. Similar results are obtained under Scenarios 4E and 5E.

Table 2 Empirical biases (left) and root-MSEs (right) for scenario 6E

7.2 Simulation 2

Simulation 2 investigates the performance of the EBPs of the mean parameters $\mu _{dk}$. The steps of Simulation 2 are

• 1. Generate $z_{dk}$, $x_{dk}$, $d=1,\ldots ,D$, $k=1,2$. Take $D\in {\mathcal{D}}=\{50, 100, 200\}$.

• 2. Repeat $I=10^4$ times ($i=1,\ldots ,I$)

  • 2.1. Generate $\{(e_{d}^{(i)},u_{d}^{(i)},v_{d}^{(i)},y_{d}^{(i)}): d=1,\ldots ,D\}$ from the MEBFH model (15).

  • 2.2. Calculate the true means $\mu _{d}^{(i)}=Z_d\eta +X_d\lambda +Bv_d^{(i)}+u_d^{(i)}$, $d=1,\ldots ,D$.

  • 2.3. Fit the MEBFH model to the simulated data $(y_{d}^{(i)},Z_d,X_d)$, $d=1,\ldots ,D$. Calculate the EBP $\hat{\mu }^{(i)}_{d}$ under the MEBFH model.

• 3. For $d=1,\ldots ,D$, $k=1,2$, calculate the relative performance measures

  • 3.1 $E_{dk}=\Big (\frac{1}{I}\sum _{i=1}^{I}(\hat{\mu }_{dk}^{(i)}-\mu _{dk}^{(i)})^2\Big )^{1/2}$, $B_{dk}=\frac{1}{I}\sum _{i=1}^{I}(\hat{\mu }_{dk}^{(i)}-\mu _{dk}^{(i)})$,

    $\mu _{dk}=\frac{1}{I}\sum _{i=1}^{I}\mu _{dk}^{(i)}$.

  • 3.2. $RE_{dk}=100\frac{E_{dk}}{\mu _{dk}}$, $RB_{dk}=100\frac{B_{dk}}{\mu _{dk}}$, $RE_{k}=\frac{1}{D}\sum _{d=1}^DRE_{dk}$,

    $RB_{k}=\frac{1}{D}\sum _{d=1}^D|RB_{dk}|$.

Table 3 presents the relative performance measures $RB_{k}$ (left) and $RE_{k}$ (right) of EBPs under Scenarios 4E, 5E and 6E. As expected, the EBPs have almost no bias in all cases. We also note that root-MSEs decrease slowly as the number of domains increases. This is somewhat reasonable, since increasing D also increases the number of quantities $\mu _d$ to be predicted.

Table 3 Relative measures $RB_{k}$ (left) and $RE_{k}$ (right) of EBPs (in %)

7.3 Simulation 3

Simulation 3 investigates the performance of the parametric bootstrap estimator of the MSE of the EBPs. For $D=100$, the steps of Simulation 3 are

• 1. Take $mse_{dk}=E_{dk}^2$, $k=0,1$, $d=1,\ldots ,D$, from the output of Simulation 2.

• 2. Generate $z_{dk}$, $x_{dk}$, $d=1,\ldots ,D$, $k=1,2$.

• 3. Repeat $I=10^2$ times ($i=1,\ldots ,I$)

  • 3.1. Generate $\{(e_{d}^{(i)},u_{d}^{(i)},v_{d}^{(i)},y_{d}^{(i)}): d=1,\ldots ,D\}$ from the MEBFH model (15).

  • 3.2. Calculate the REML estimators $\hat{\gamma }^{(i)}\in \{\hat{\eta }_1^{(i)},\hat{\lambda }_1^{(i)},\hat{\eta }_2^{(i)},\hat{\lambda }_2^{(i)}, \hat{\theta }_{1}^{(i)},\hat{\theta }_{2}^{(i)},\hat{\theta }_{3}^{(i)}\}$ by using the sample data $(y_{d}^{(i)},Z_d,X_d)$, $d=1,\ldots ,D$.

  • 3.3. Repeat B times

    • (a) Generate $u_d^{*(ib)}\sim N_2(0,\hat{V}_{ud}^{(i)})$, $e_d^{*(ib)}\sim N_2(0,V_{ed})$, ${v}_{d}^{*(ib)}\sim N_2(0,\Sigma _d)$ and

      $$\begin{aligned} y_{d}^{*(ib)}&= \mu _d^{*(ib)}+e_{d}^{*(ib)}, \\ \mu _d^{*(ib)}&= Z_d\hat{\eta }^{(i)}+X_d\lambda ^{(i)}+ \text{ diag }(\hat{\lambda }_1^{(i)},\hat{\lambda }_2^{(i)})v_d^{*(ib)}+u_d^{*(ib)},\,\,\, d=1,\ldots ,D. \nonumber \end{aligned}$$

      (16)

    • (b) Calculate the REML estimators $\hat{\eta }_1^{*(ib)},\hat{\lambda }_1^{*(ib)},\hat{\eta }_2^{*(ib)},\hat{\lambda }_2^{*(ib)}, \hat{\theta }_{1}^{*(ib)},\hat{\theta }_{2}^{*(ib)},\hat{\theta }_{3}^{*(ib)}$ by using the sample data $(y_d^{*(ib)},Z_d,X_d)$, $d=1,\ldots ,D$.

    • (c) Calculate the EBP $\hat{\mu }^{*(ib)}_{dk}$ under the MEBFH model (16).

  • 3.4. For $d=1,\ldots ,D$, $k=1,2$, calculate the bootstrap MSE estimator of the EBP, i.e.

    $$\begin{aligned} mse_{dk}^{*(i)}=\frac{1}{B}\sum _{b=1}^B\big (\hat{\mu }^{*(ib)}_{dk}-\mu ^{*(ib)}_{dk}\big )^2. \end{aligned}$$

• 4. For $d=1,\ldots ,D$, $k=1,2$, calculate the relative performance measures $RE_{dk}^{*}=100E_{dk}^{*}/mse_{dk}$ and $RB_{dk}^{*}=100B_{dk}^{*}/mse_{dk}$, where

  $$\begin{aligned} E_{dk}^{*}=\Big (\frac{1}{I}\sum _{i=1}^{I}(mse_{dk}^{*(i)}-mse_{dk})^2\Big )^{1/2},\,\,\, B_{dk}^{*}=\frac{1}{I}\sum _{i=1}^{I}(mse_{dk}^{*(i)}-mse_{dk}). \end{aligned}$$

• 5. For $k=1,2$, calculate the averages across domains of the relative performance measures, i.e. $RB_{k}^*=\frac{1}{D}\sum _{d=1}^D|RB_{dk}^*|$, $RE_{k}^*=\frac{1}{D}\sum _{d=1}^DRE_{dk}^*$.

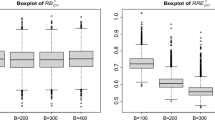
Table 4 presents the relative performance measures $RB_k^*$ and $E B_k^*$ (in %) under Scenarios 4E, 5E and 6E, for $D=100$. Figures 2 and 3 presents the boxplots of the absolute performance measures $B_{dk}^*$’s and $E_{dk}^*$’s respectively under scenario 6E. Similar boxplots are constructed for Scenarios 4E and 5E, but they are not presented here. They show that the parametric bootstrap estimators of the MSEs of the EBPs have a negative bias in the simulated scenarios. Nevertheless, the observed biases are rather small in comparison with the calculated empirical root-MSEs. Simulation 3 suggests that running a parametric bootstrap algorithm with a number of replicates B between 200 and 400 give a considerably good approximation to estimate the MSE of the EBP.

Table 4 Relative measures of MSE estimators for $D=100$ (in %)

Fig. 2

Boxplots of biases $\{B_{dk}^*: d=1,\ldots ,D\}$, $k=1,2$

Fig. 3

Boxplots of root-MSEs $\{E_{dk}^*: d=1,\ldots ,D\}$, $k=1,2$

8 Estimation of poverty proportions and gaps in Spanish provinces

This manuscript presents an application of the MEBFH model to the estimation of poverty proportions and gaps in Spanish provinces by sex. Spain is divided in 52 provinces (including the autonomous cities of Ceuta and Melilla) leading to $D=104$ target domains (provinces crossed by sex) of known sizes $N_d$, $d=1,\ldots ,D$.

Let $z_{dj}$ be the normalized net annual income of the household where the individual j of domain d lives. Let $z_0$ be the poverty line, so that individuals with $z_{dj}<z_0$ are considered as poor. The main goal of this section is to jointly estimate poverty proportions and gaps

$$\begin{aligned} \bar{Y}_{d1}=\frac{1}{N_{d}}\sum _{j=1}^{N_{d}}y_{d1j},\quad \bar{Y}_{d2}=\frac{1}{N_{d}}\sum _{j=1}^{N_{d}}y_{d2j},\quad d=1,\ldots ,D, \end{aligned}$$

(17)

where $y_{d1j}=I(z_{dj}<z_0)$, $I(z_{dj}<z_0)=1$ if $z_{dj}<z_0$, $I(z_{dj}<z_0)=0$ otherwise and $y_{d2j}=z_0^{-1}(z_0-z_{dj})I(z_{dj}<z_0)$.

The Spanish Statistical Office calculates $z_{dj}$ by summing up the net annual incomes of the household members and by dividing by its normalized size. Later, the same value of the normalized net annual income of the household is assigned to all the individuals j of the household. Therefore $z_{dj}$ is constant within the household. The aim of normalizing the household income is to adjust for the varying size and composition of households. The definition of the total number of normalized household members is the modified OECD scale used by EUROSTAT. This scale gives a weight of 1.0 to the first adult, 0.5 to the second and each subsequent person aged 14 and over and 0.3 to each child aged under 14 in the household h. The normalized size of a household is the sum of the weights assigned to each person. So the total number of normalized household members is

$$\begin{aligned} H_{dh}=1+0.5 (H_{dh\ge 14}-1)+0.3 H_{dh< 14}, \end{aligned}$$

where $H_{dh\ge 14}$ is the number of people aged 14 and over and $H_{dh< 14}$ is the number of children aged under 14. Following the standards of the Spanish Statistical Office, the poverty threshold is fixed as the 60% of the median of the normalized net annual incomes in Spanish households. The Spanish poverty threshold (in euros) in 2008 is $z_{2008}=7488.65$. We deal with data from the SLCS of 2008 with sample size 35967. This is an annual survey where the planned domains are the regions (autonomous communities), so that sample sizes are selected to obtain precise direct estimates at the region level. As Spain is hierarchically partitioned in regions, provinces, counties (comarcas) and municipalities, estimating province-sex poverty proportions is a small area estimation problem.

The direct estimators of the size $N_d$, the total $Y_{dk}=\sum _{j=1}^{N_{d}}y_{dkj}$ and the mean $\bar{Y}_{dk}=Y_{dk}/N_{d}$ are

$$\begin{aligned} \hat{N}_{d}^{dir}=\sum _{j\in s_{d}}w_{dj},\quad \hat{Y}_{dk}^{dir}=\sum _{j\in s_{d}}w_{dj}\, y_{dkj},\quad \hat{\bar{Y}}_{dk}^{dir}=\hat{Y}_{dk}^{dir}/\hat{N}_{d}^{dir},\quad k=1,2, \end{aligned}$$

where $s_{d}$ is the domain sample of size $n_d$ and the $w_{dj}$’s are the official calibrated sampling weights which take non response into account. The direct estimates of the domain means are used as responses in the area-level Fay–Herriot model. The design-based covariance between $\hat{\bar{Y}}_{dk_1}^{dir}$ and $\hat{\bar{Y}}_{dk_2}^{dir}$, $k_1,k_2=1,2$, can be estimated by

$$\begin{aligned} \hat{\text{ cov }}_\pi (\hat{\bar{Y}}_{dk_1}^{dir},\hat{\bar{Y}}_{dk_2}^{dir})= \frac{1}{\big (\hat{N}_d^{dir}\big )^2} \sum _{j\in s_{d}}w_{dj}(w_{dj}-1)(y_{dk_1j}-\hat{\bar{Y}}_{dk_1}^{dir})(y_{dk_2j}-\hat{\bar{Y}}_{dk_2}^{dir}), \end{aligned}$$

(18)

where the case $k_1=k_2=k$ denotes estimated variance, i.e. $\hat{\text{ var }}_\pi (\hat{\bar{Y}}_{dk}^{dir})=$ $\hat{\text{ cov }}_\pi (\hat{\bar{Y}}_{dk}^{dir},\hat{\bar{Y}}_{dk}^{dir})$. The last formulas are obtained from Särndal et al. (1992), pp. 43, 185 and 391, with the simplifications $w_{dj}=1/\pi _{dj}$, $\pi _{dj,dj}=\pi _{dj}$ and $\pi _{di,dj}=\pi _{di} \pi _{dj}$, $i\ne j$ in the second order inclusion probabilities.

We take data from the SLFS of 2008 to construct the data file of aggregated auxiliary variables. The SLFS is a quarterly survey with provinces as planned domains. Within each quarter, the SLFS sample sizes at the province level are fixed a priori. They are selected high enough to have precise direct estimates. By putting together the data files of the 4 quarters, the SLFS direct estimators of means at domain (province crossed by sex) level are even more precise for 2008 than using only the data of one quarter. Additionally, by doing this aggregation all the calculated SLFS direct estimators of domain means have non zero estimated variances.

The file of auxiliary variables is constructed from the SLFS data of 2008 (SLFS2008). It contains the direct estimates of the domain means by the categories of the considered auxiliary variables. It also contains the variance and covariance estimates of the calculated direct estimators. The auxiliary variables are:

Nationality, with categories Spanish and Foreigner.

Education, with categories LowEdu (less than secondary level completed), HighEdu (secondary or superior level completed)

Age, with categories age1 ($\le 15$), age2 (16-24), age3 (25-49), age4 (50-64), age5 ($>64$).

Labour situation, with categories $\le 15$, Employed, Unemployed, Inactive.

Table 5 presents the pseudo-REML estimates of the regression parameters of the selected MEBFH model. It also contains the corresponding p-values. We note that domains with higher proportions of Spanish or unemployed people tends to have higher poverty proportions. On the other hand, the level of education is negatively related with the poverty proportion. We note that foreigners tend to live and work in rich provinces. Therefore, the obtained results are in agreement with the Spanish socioeconomic situation of 2008.

Table 5 Regression parameters

Table 6 contains the estimates of the variance component parameters and the corresponding asymptotic 95% confidence intervals.

Table 6 Variance component parameters

Figure 4 (left) plots the MEBFH model residuals of poverty proportions versus the corresponding EBPs. Figure 4 (right) plots the MEBFH model residuals of poverty gaps versus their EBPs.

We observe that the residuals present greater variability on the right hand side of the OX axis. This is a natural phenomenon, as the EBPs have to smooth the behavior of the direct estimators. The plots show that EBPs tend to be smaller than direct estimates when direct estimates are large. This is due to two main reasons. First, it is part of the smoothing work that EBPs have to do. Second, the variance of the directly estimated proportion is approximately $(1-n_d/N_d)/(n_d-1)\hat{\bar{Y}}_{dk}^{dir}(1-\hat{\bar{Y}}_{dk}^{dir})$, which takes its maximum at $\hat{\bar{Y}}_{dk}^{dir}=0.5$, for $n_d, N_d$ fixed. Allowing in this context area specific $V_{ud}$ is an interesting future research task, that possibly could further reduce the MSE of the EBP.

Figure 5 plots the EBPs and direct estimates of poverty proportions (left) and gaps (right) for men and women. We observe that both estimators tend to coincide as the sample size increases.

Fig. 4

Model residuals versus EBPs of poverty proportions (left) and gaps (right)

Fig. 5

EBPs and direct estimates of men (left) and women (right) poverty proportions

Figure 6 plots the estimated model-based root-MSEs of the EBPs and the estimated design-based root-MSEs of the direct estimators of poverty proportions (left) and gaps (right) for men and women. The first root-MSE is estimated by parametric bootstrap under the fitted MEBFH model. The second one is calculated by applying the estimator (18) for design-based variances. The EBPs have lower root-MSEs than the direct estimators. When the sample size increases the root-MSEs of all the estimators become almost equal.

Fig. 6

Root-MSEs of EBPs and direct estimators for men (left) and women (right)

Figures 7 and 8 plot the Spanish provinces in 4 colors depending on the values of the EBPs of the poverty proportions and poverty gaps in $\%$. We observe that the Spanish provinces where the proportion of the population under the poverty line is smallest are those situated in the north and east. On the other hand, the Spanish provinces with higher poverty proportions are those situated in the center and south.

Fig. 7

Estimated poverty proportions for men (left) and women (right) in 2008

Fig. 8

Estimated poverty gaps for men (left) and women (right) in 2008

Appendix B in the supplementary file contains 2 tables with basic numerical results. To give a brief summary of the obtained numerical results, we order the Spanish provinces (including the cities of Ceuta and Melilla) by sample size and we select one in five. Table B.1 presents the EBPs and direct (dir) estimates of poverty proportions for men and women respectively. Table B.2 presents the EBPs and direct (dir) estimates of poverty gaps for men and women respectively. These tables also give the estimated root-MSEs (rmse.eblup and rmse.dir), for both types of estimators. The column $N_d$ presents the estimates of the domain sizes calculated by using the data of the 4 quarters of the SLFS in 2008. The columns province and $n_d$ contain the province name and the sample size respectively.

9 Conclusions

In many applications the auxiliary information used in bivariate Fay–Herriot models is not measured exactly. Under this setting, the EBLUP based on the bivariate Fay–Herriot model is not the EBP anymore, as this model assumes the exact measurement of the auxiliary variables.

By calculating relative efficiencies, we showed that not taking into account the measurement errors may lead to predictions of target parameters with greater mean squared errors. Therefore, we extended the bivariate Fay–Herriot model by allowing for multivariate normal distributed random error on the auxiliary variables. This reflects the typical situation of estimated auxiliary information. Both, the mean squared error and the bias of the new EBP are reduced with respect to the classical EBLUP.

For fitting the new model, the pseudo-REML estimation procedure showed to be stable. Further a second fitting algorithm was introduced but not implemented. In the case of exactly measured auxiliary variables, the measurement error bivariate Fay–Herriot model reduces to the classical bivariate Fay–Herriot model and, therefore, they basically give the same predictions. Finally, we recommend to use the proposed measurement error Fay–Herriot model when the auxiliary variables are estimated.