Measuring spatial price differentials at the basic heading level: a comparison of stochastic index number methods

Abstract

Spatial price comparisons rely to a high degree on the quality of the underlying price data that are collected within or across countries. Below the basic heading level, these price data often exhibit large gaps. Therefore, stochastic index number methods like the Country–Product–Dummy (CPD) method and the Gini–Eltetö–Köves–Szulc (GEKS) method are utilised for the aggregation of the price data into higher-level indices. Although the two index number methods produce differing price level estimates when prices are missing, the present paper demonstrates that both can be derived from exactly the same stochastic model. For a specific case of missing prices, it is shown that the formula underlying these price level estimates differs between the two methods only in weighting. The impact of missing prices on the efficiency of the price level estimates is analysed in two simulation studies. It can be shown that the CPD method slightly outperforms the GEKS method. Using micro data of Germany’s Consumer Price Index, it can be observed that more narrowly defined products improve estimation efficiency.

1 Introduction

In general, index number theory is divided into three primary strands: the test approach (e.g. Balk 1995), which relies on a framework of desirable properties for the valuation of index number methods; the economic approach (e.g. Diewert 1995), which builds on microeconomic theory in the context of cost and utility functions; and the stochastic approach (e.g. Clements et al. 2006), which embeds the index number theory into a statistical framework. The stochastic approach to index numbers has especially gained increasing attention in recent years.

Within the International Comparison Program (ICP), for example, stochastic index number methods are used for the compilation of Purchasing Power Parities (PPPs) in the participating countries (see World Bank 2020, p. 82 for the ICP round in 2017 and World Bank 2015, pp. 256–257 for the ICP rounds in 2005 and 2011). In the first stage of aggregation, PPPs are calculated by the two probably best-known index number methods of the stochastic approach: the Country–Product–Dummy (CPD) method, originally developed by Summers (1973), and the GEKS method, named after its authors Gini (1924, 1931), Eltetö and Köves (1964) and Szulc (1964). Strictly speaking, the CPD method is used by all countries except those belonging to the Commonwealth of Independent States (CIS) and those participating in the Eurostat-OECD PPP programme.¹ The latter rely on the GEKS method. This heterogeneous choice among countries seems to be due to historical reasons, although a consistent usage would be desirable from a statistical perspective.² Whether one of the two index number methods is actually better suited for price comparisons at this first stage of aggregation is not evident (e.g. Diewert 2010, pp. S17–S18). Further analysis of their statistical properties thus might provide additional guidance in this regard.

The CPD method is a simple case of a hedonic regression. It explains the price of some product by the product itself and the region where that price was observed. In the literature, it is well-known that the GEKS method can be put into a regression approach as well (e.g. Rao and Timmer 2003, pp. 498–500). Initially, however, it was designed as a technique to adjust a set of bilateral index numbers such that these satisfy internal consistency in a multilateral context. The CPD and GEKS methods might be complemented by the much less prominent Country–Dummy (CD) method, which reaches back to Summers (1973) as well. Similarly, within a regression framework, it explains the regional price ratio of some product by the general price level of the regions. A comprehensive survey of these stochastic index number methods is provided, for example, by Balk (2008) and Auer (2012).

In the literature, the CPD and GEKS methods are typically considered independently of each other. This, in fact, makes sense because of the different rationale behind their model specifications. Balk (1981, p. 75), however, points out that both methods are closely related.³ In our paper, we demonstrate that both the CPD and the GEKS methods can be derived from the same stochastic model originally introduced by Summers (1973, p. 5) and Selvanathan and Rao (1992, pp. 338–340). Moreover, we show that the CD method also traces back to this model. This deeper anchoring of the three multilateral index number methods into the stochastic approach is this paper’s first contribution.

At the basic heading level, a spatial price comparison relies exclusively on the prices that were collected in different regions for a number of products.⁴ If the price of each product is observed in each region, then the available price matrix is said to be complete. For a complete price matrix, it is known that the CPD method and the GEKS method generate exactly the same estimates for the regional price levels (e.g. World Bank 2013, pp. 115–116). Strictly speaking, this is true when the bilateral price index numbers underlying the GEKS method are calculated as a Jevons index (henceforth, we use the term GEKS-Jevons method for this setting). A complete price matrix, however, is rarely available in practice. More often there are large gaps in the price data due to missing prices. In this case, the CPD and GEKS-Jevons methods no longer produce the same results, although it would be helpful to know how these differences evolve.

For this purpose, Ferrari et al. (1996) consider a price matrix with two groups of regions. For the first group of regions, the matrix is complete, and for each region of the second group, the same prices are missing. The authors show that in this case, the CPD method and the GEKS-Jevons method generate different results, and that the differences are due to different weights in a correction term. We extend the work of Ferrari et al. (1996) by a more general scenario of missing prices where all regions exhibit gaps. We show that their results also remain valid in this new setting. Now, however, the price level estimates rely not on one but on two correction terms that are weighted differently between the CPD and the GEKS-Jevons methods. Moreover, it can be shown that the price levels differ between intragroup comparisons (the prices of two regions that belong to the same group of regions are compared) and intergroup comparisons. For intragroup comparisons, the CPD price levels correspond to the Jevons index of the two regions under consideration. These further insights into the calculation of price levels in the case of missing prices are the paper’s second contribution.

Our theoretical derivations draw on a specific case of an incomplete price matrix. To evaluate the impact of missing prices on the price level estimates also in a more general setting, we conduct a Monte Carlo analysis. For that purpose, we build artificial price data, randomly introduce gaps into these data sets and apply the CPD and GEKS-Jevons methods (a similar approach was undertaken by Dikhanov 2010). This enables us to evaluate the impact of missing prices on the estimation efficiency separately for both index number methods and, in addition, to analyse possible differences between them. Not surprisingly, it turns out that the estimation efficiency in general suffers from an increasing number of gaps. Moreover, the CPD method slightly outperforms the GEKS-Jevons method under different tested scenarios. These findings are the paper’s third contribution.

We also adopt our simulation strategy to more realistic price data. For that purpose, we draw on a subset of the micro price data underlying the official Consumer Price Index (CPI) of Germany. On the basis of these data, we are able to confirm the findings of our first simulation study. Moreover, we use the product descriptions provided in the data to analyse how the estimation efficiency reacts to narrower product definitions. This issue has practical relevance for two reasons. First, with respect to our simulation results, it shows that one may increase the estimation efficiency with a narrower product definition. Second, it also reveals that this gain in the efficiency is closely related to the regional volatility of the prices. More specifically, with low regional price fluctuations, one could rely on relatively loose product definitions as narrower ones do not significantly improve estimation efficiency. This finding may have an important implication for the compilation of regional price indices in practice. A narrow product definition using CPI data usually entails a lot of data preprocessing (e.g. Weinand and Auer 2020, pp. 420–421). Our results indicate that this extensive workload can be reduced when the regional volatility of prices within a basic heading is taken into account. This is the paper’s fourth contribution.

The remainder of the paper is laid out as follows. Section 2 provides an overview of the stochastic approach to index numbers in the context of spatial price comparisons at the basic heading level. Section 3 discusses appropriate error term specifications in the light of empirical studies on spatial price comparisons. Section 4 presents the theoretical derivations for a specific case of incomplete price data and the results of our simulation studies, while Sect. 5 concludes.

2 Stochastic approach to spatial price index numbers

Two central requirements for spatial price comparisons are transitivity and characteristicity of the price index numbers. They are defined in Sect. 2.1, along with some other basic concepts. In Sect. 2.2, we derive the CPD and CD methods from a stochastic model initially proposed by Summers (1973) and Selvanathan and Rao (1992) in the context of spatial price comparisons. Likewise, in Sect. 2.3, we derive the GEKS-Jevons method from this model.

2.1 Basic concepts and definitions

Usually, the price levels of more than two regions are compared. A basic requirement of such multilateral price comparisons is called transitivity. It postulates that $P^{sr}$, the relative price level between the regions r and s, should be equal to the product of the price levels $P^{st}$ and $P^{tr}$, where t is some arbitrary third region that serves as a bridge (e.g. Rao and Banerjee 1986, p. 304). Consequently, transitivity ensures the internal consistency of some multilateral system of index numbers. A second postulate, initially advocated by Drechsler (1973), is denoted as characteristicity. It states that the price comparison between two regions r and s should be based exclusively on information relating to these two regions. Both requirements play a central role for spatial price comparisons.

Below the basic heading level, neither expenditure weights nor quantity information are available. In this case, elementary price indices are used for the aggregation of prices into higher-level (or: basic heading) indices. An elementary index number formula widely used among statistical offices is the Jevons (1865) index (e.g. OECD 2018, pp. 8–9). For the regions r and s, it is defined by:

$$\begin{aligned} {\dot{P}}_{\mathrm {J}}^{sr} = \prod _{i=1}^{N} \left( p_{i}^{r} / p_{i}^{s} \right) ^{\frac{1}{N}}, \end{aligned}$$

(1)

where $p_{i}^{r}$ is the price of product i in region r and N the number of products.⁵

The Jevons index outperforms most other elementary index number formulas under the axiomatic approach to index numbers and is also (weakly) supported under the economic approach (e.g. Diewert 1995, pp. 5–20). In particular, Hill and Hill (2009, p. 198) point out that the Jevons index numbers are transitive if prices are available for each product and region. Moreover, from (1), it is obvious that each index number on its own is characteristic. In practice, however, price information for individual products is frequently missing below the basic heading level. Equation (1) shows that the Jevons index is only applicable to regionally matched price observations. Thus, price comparisons between different pairs of regions (e.g. ${\dot{P}}^{st}$ vs. ${\dot{P}}^{sr}$) might stem from varying sets of matched prices. Consequently, a multilateral system of bilateral Jevons index numbers would still be characteristic, but no longer transitive. Taking into account the trade-off between transitivity and characteristicity, the stochastic approach to index numbers offers alternatives to ensure transitivity even in the event that prices are missing.

Following the stochastic model advocated by Summers (1973, p. 5) and Selvanathan and Rao (1992, pp. 338–340), the price ratio of product i for regions r and s is defined by the multiplicative relationship of two terms: the general price level of region r relative to region s, $P^{sr}$, and a random component, $\epsilon _{i}^{rs}$. If transitivity is assumed, $P^{sr}$ can be written as $P^{r}/P^{s}$ (e.g. Rao and Banerjee 1986, pp. 304–306). Hence, the logarithm of this multiplicative relationship can be expressed by

$$\begin{aligned} \ln \left( p_{i}^{r} / p_{i}^{s} \right) = \ln \left( P^{r} / P^{s} \right) + u_{i}^{sr}, \end{aligned}$$

(2)

where $u_{i}^{sr} = \ln \epsilon _{i}^{sr}$ is assumed to be some normally distributed random variable with expected value 0 and variance $\sigma ^{2}$ for all products $i=1,2,\ldots,N$ and regions $s,r=1,2,\ldots,R$.⁶ In the following, we show that the stochastic model in (2) serves as a starting point for the derivation of the CD, the CPD and the GEKS-Jevons methods, respectively.

2.2 CPD method and Country–Dummy method

CPD method Taking the sum over all regions $s=1,\ldots,R$ in Eq. (2) and rearranging leads to

$$\begin{aligned} \ln p_{i}^{r} = \ln P^{r} + \frac{1}{R} \sum _{s=1}^{R} \ln \left( p_{i}^{s} / P^{s} \right) + \frac{1}{R} \sum _{s=1}^{R} u_{i}^{sr}. \end{aligned}$$

(3)

Although the price $p_{i}^{s}$ on the right-hand side of the equation is initially known, the price level $P^{s}$ is not. Therefore, the arithmetic average of the logarithmic price to price level ratios, $\frac{1}{R} \sum _{s=1}^{R} \ln \left( p_{i}^{s} / P^{s} \right)$, is also unknown. We denote this term by $\ln \pi _{i}$. From an economic point of view, it represents the average deflated price of product i. This interpretation reveals similarities to the “international price” of the Geary–Khamis method.⁷ In addition, we define $\frac{1}{R} \sum _{s=1}^{R} u_{i}^{sr} = u_{i}^{r}$. Consequently, Eq. (3) can be rewritten as

$$\begin{aligned} \ln p_{i}^{r} = \ln P^{r} + \ln \pi _{i} + u_{i}^{r}. \end{aligned}$$

(4)

Equation (4) represents the logarithmic form of the CPD method’s underlying model (Summers 1973, p. 10). It explains the price of product i in region r, $p_{i}^{r}$, by region r’s general price level ${P}^{r}$ and product i’s general value $\pi _{i}$. Because $u_{i}^{r}$ is a linear combination of the disturbances $u_{i}^{sr}$ in (2), it follows a normal distribution with expected value 0. The variance of the disturbances is assumed to be identical among the regions and products in the original form of the CPD method.

In order to transform (4) into a standard regression model, we introduce for each region t $(t=1,\ldots,R)$ the dummy variable ${{ region }}^{t}$ and for every product j $(j=1,\ldots,N)$ the dummy variable ${{ product }}_{j}$:

$$\begin{aligned} {{ region }}^{t} = {\left\{ \begin{array}{ll} 1 &{} \text {if}\; r=t \\ 0 &{} \text {if}\; r \ne t \end{array}\right. } \quad \text {and} \quad {{ product }}_{j}= {\left\{ \begin{array}{ll} 1 &{} \text {if}\; i=j \\ 0 &{} \text {if}\; i \ne j \end{array}\right. }. \end{aligned}$$

(5)

Defining $\alpha ^{t}=\ln \left( P^{t} / k \right)$ and $\beta _{j}=\ln \left( k \cdot \pi _{j} \right)$, with k being some constant, we can express Eq. (4) by

$$\begin{aligned} \ln p_{i}^{r}= \sum ^{R}_{t=1} \alpha ^{t} { region }^{t} + \sum ^{N}_{j=1} \beta _{j} \; { product }_{j} + u_{i}^{r} \quad \forall \ r = 1,\ldots,R \ \text {and} \ i = 1,\ldots,N. \end{aligned}$$

(6)

Equation (6) can be viewed as a linear regression model, albeit one suffering from perfect multicollinearity. Furthermore, we are interested in estimates of the price levels $P^{t}$. Since $\alpha ^{t}=\ln \left( P^{t} / k \right)$, we first need to specify k. Both problems can be simultaneously solved by specifying k in terms of the parameter $\alpha ^{t}$.

If we define region $t=1$ (or some other region) as the base region that serves as a reference for the price levels of the other regions, that is, $k=P^{1}$, it follows that $\alpha ^{1} = \ln \left( P^{1} / P^{1} \right) = 0$. As a consequence, $\alpha ^{1} { region }^{1}=0$ for all observations. Therefore, the term $\alpha ^{1} { region }^{1}$ can be dropped from Eq. (6):

$$\begin{aligned} \ln p_{i}^{r}= \sum ^{R}_{t=2} \alpha ^{t} { region }^{t} + \sum ^{N}_{j=1} \beta _{j} \; { product }_{j} + u_{i}^{r} \quad \forall \ r = 1,\ldots,R \ \text {and} \ i = 1,\ldots,N. \end{aligned}$$

(7)

Perfect multicollinearity is removed. The parameters $\alpha ^{t}$ are estimated using ordinary least squares (OLS). The corresponding estimator, ${\widehat{\alpha }}^{t}$, is defined as the logarithmic price level relative between region t and the base region. By definition, these estimated price levels satisfy the requirement of transitivity (e.g. Rao and Banerjee 1986, pp. 304–306). Alternatively, we could avoid perfect multicollinearity in (6) by setting $\sum _{t=1}^{R}\alpha ^{t}=0$. Consequently, ${\widehat{\alpha }}^{t}$ would express the logarithmic price level of region t relative to the unweighted average price level of all regions. Diewert (2004, pp. 6–8) describes an elegant way of estimating the parameters $\alpha ^{t}$ in this setting.

Country–Dummy method Alternatively to the approach outlined above, one can set in Eq. (2) region s as a fix reference for product i’s price ratios:

$$\begin{aligned} \ln \left( p_{i}^{r} / p_{i}^{s} \right) = \ln \left( P^{r} / P^{s} \right) + u_{i}^{sr} \quad \forall \ r \in R_{s}^{*} \ \text {and} \ i = 1,\ldots,N \; \end{aligned}$$

(8)

where $R_{s}^{*} = \{ r \in {\mathbb {N}}^{+} \; | \; r \le R, \; r \ne s \}$. Equation (8) represents the Country–Dummy method. It assumes that any product-specific price ratio between two regions r and s can be explained by the overall price level relative of these regions. The disturbances $u_{i}^{sr}$ remain a normally distributed random variable with expected value 0 and variance $\sigma ^{2}$. However, as pointed out by Summers (1973, pp. 6 and 10), $u_{i}^{sr}$ is not mutually independent. Instead, $u_{i}^{sr} = u_{i}^{sv} - u_{i}^{rv}$ applies. From this it follows that $\text {cov} \left( u_{i}^{sr}, \ u_{i}^{sv} \right) = \frac{1}{2} \sigma ^{2}$ for regions $r \ne v$. If $\text {cov} \left( u_{i}^{sr}, \ u_{j}^{sr} \right) = \text {cov} \left( u_{i}^{sr}, \ u_{j}^{sv} \right) = 0$ for products $i \ne j$ is additionally assumed, then the disturbances are autocorrelated block-wise (see also Online Appendix A.2).

In addition to the dummy variable ${ region }^{t}$ in (5), we need to define a second dummy variable that refers to the price of region s in the price ratio $\ln \left( p_{i}^{r}/p_{i}^{s} \right)$. For that purpose, we introduce for each region t $\left( t=1,\ldots,R \right)$ the dummy variable

$$\begin{aligned} \widetilde{{ region }^{t}} = {\left\{ \begin{array}{ll} 1 &{} \text {if}\; s=t \\ 0 &{} \text {if}\; s \ne t \end{array}\right. }. \end{aligned}$$

(9)

The two dummy variables, ${\textit{region}}^{t}$ and $\widetilde{{ region }^{t}}$, are complemented by the additional parameter of region t’s logarithmic price level, $\alpha ^{t}$. Defining $\alpha ^{t}=\ln \left( P^{t}/P^{1} \right)$, the regression model of the CD method can be expressed by

$$\begin{aligned} \ln \left( p_{i}^{r} / p_{i}^{s} \right) = \sum ^{R}_{t=2} \alpha ^{t} \left( {\textit{region}}^{t} - \widetilde{{ region }^{t}} \right) + u_{i}^{sr} \quad \forall \ r \in R_{s}^{*} \ \text {and} \ i = 1,\ldots,N. \end{aligned}$$

(10)

Since $\alpha ^{1}= \ln \left( P^{1}/P^{1} \right) = 0$, it follows that $\alpha ^{1} \left( {\textit{region}}^{1} - \widetilde{{ region }^{1}} \right)$ is not included in (10). Due to the known autocorrelation structure, the remaining parameters $\alpha ^{2},\ldots,\alpha ^{R}$ are estimated by generalised least squares (GLS). They indicate the price level difference compared to base region $t=1$. Moreover, they are transitive in a multilateral context. In comparison to (7), it is worthwhile to note that the lower number of model parameters is exactly compensated by a lower number of observations. As a result, the degrees of freedom in models (7) and (10) are identical.

Subtracting the definition of product i’s price in region $r=1$, $\ln p_{i}^{1} = \ln P^{1} + \ln \pi _{i} + u_{i}^{1}$, from Equation (4) and rearranging yields the CPD’s regional price level with

$$\begin{aligned} \ln \left( P^{r} /P^{1} \right) = \ln \left( p_{i}^{r} / p_{i}^{1} \right) - \left( u_{i}^{r} - u_{i}^{1} \right). \end{aligned}$$

From (4), it is known that $u_{i}^{r} = \frac{1}{R} \sum _{s=1}^{R} u_{i}^{sr}$ and $u_{i}^{1} = \frac{1}{R} \sum _{s=1}^{R} u_{i}^{s1}$. Consequently, $u_{i}^{r} - u_{i}^{1}$ can be written as $\frac{1}{R} \sum _{s=1}^{R} \left( u_{i}^{sr} - u_{i}^{s1} \right)$. Because $u_{i}^{sr} - u_{i}^{s1} = u_{i}^{1r}$ applies, the previous equation can be rewritten as (8), which defines the CD method’s price level for region $s=1$, $\ln \left( P^{r} / P^{1} \right)$. This suggests that the CPD and CD methods are equivalent approaches and, therefore, should give equal price level estimates.

In the case of a complete price matrix, the CPD and CD method’s price level estimator, $\exp \left( {\widehat{\alpha }}^{t} \right)$, is defined as a geometric average of the price ratios between region t and the base region (see, for example, Rao and Hajargasht 2016, pp. 418–419 and Online Appendix A for the derivation of this result).⁸ Consequently, the estimated price levels coincide with the Jevons index in (1). Furthermore, it follows that the CPD estimator for product j’s general value, ${\widehat{\beta }}_{j}$, is defined by $\frac{1}{R} \sum _{t=1}^{R} \ln \left( p_{j}^{t} / \exp \left( {\widehat{\alpha }}^{t} \right) \right).$⁹ This expression is already known from (3). It reveals that the prices of product j are deflated by the respective regional price levels.

2.3 GEKS-Jevons method

Following Hill (2008, p. 3), the general GEKS method is not a price index in the proper sense. Strictly speaking, it is a two-stage technique to convert a set of bilateral price index numbers into a multilateral system of transitive index numbers. The first stage encompasses the calculation of the bilateral index numbers, ${\dot{P}}^{sr}$, for each regional pair r and s. If each ${\dot{P}}^{sr}$ is calculated, for example, by (1), it would be more precise to speak of the GEKS-Jevons method.¹⁰ The bilateral index numbers, however, may lack transitivity, with the result that they differ from the multilateral index numbers, $P^{sr}$. For that reason, the second stage incorporates an adjustment of the characteristic bilateral into transitive multilateral index numbers. Drechsler (1973, p. 28) points out that the GEKS method is designed with the aim of keeping this adjustment as small as possible with respect to the trade-off between characteristicity and transitivity. A mathematical formulation of this optimisation problem can be found in Hill and Timmer (2006, pp. 368–369) and Rao and Timmer (2003, pp. 497–500).

In the following, we demonstrate that the multilateral GEKS-Jevons method, like the CPD method, can be derived from the stochastic model defined in (2). Taking the sum over all products $i=1,\ldots,N$ in (2) and rearranging yields

$$\begin{aligned} \frac{1}{N} \sum _{i=1}^{N} \ln \left( p_{i}^{r} / p_{i}^{s} \right) = \ln \left( P^{r} / P^{s} \right) + \frac{1}{N} \sum _{i=1}^{N} u_{i}^{sr}. \end{aligned}$$

(11)

The term on the left-hand side of the equation is the logarithmic form of the Jevons index in (1).¹¹ Therefore, we denote it by $\ln {\dot{P}}^{sr}_{\text {J}}$. In addition, we define $\frac{1}{N} \sum _{i=1}^{N} u_{i}^{sr} = u^{sr}$. Consequently, (11) can be rewritten as

$$\begin{aligned} \ln {\dot{P}}^{sr}_{\text {J}} = \ln \left( P^{r} / P^{s} \right) + u^{sr}. \end{aligned}$$

(12)

This model specification of the GEKS-Jevons method is widely documented (e.g. Hill 2016, p. 408). It states that the bilateral Jevons index numbers, $\ln {\dot{P}}^{sr}_{\text {J}}$, and the corresponding transitive index numbers, $\ln \left( P^{r}/P^{s} \right)$, differ only with respect to the disturbances $u^{sr}$. Since the disturbances $u^{sr}$ are a linear combination of $u_{i}^{sr}$ in (2), they follow a normal distribution with expected value 0. Their variance is assumed to be identical.

In order to transform (12) into a standard regression model, we introduce for each region t ($t=1,\ldots,R$) the two dummy variables ${ region }^{t}$ and $\widetilde{{ region }^{t}}$. Their definitions can be found in (5) and (9). Defining $\alpha ^{t} = \ln \left( P^{t} / P^{1} \right)$, Eq. (12) can be written as

$$\begin{aligned} \ln {\dot{P}}^{sr}_{\text {J}} = \sum ^{R}_{t=2} \alpha ^{t} \left( { region }^{t} - \widetilde{{ region }^{t}} \right) + u^{sr} \quad \forall \ s=1,\ldots,R-1 \ \text {and} \ r=s+1,\ldots,R. \end{aligned}$$

(13)

Regression model (13) draws on non-redundant bilateral price index numbers only. Because $\alpha ^{1} = \ln \left( P^{1} / P^{1} \right) = 0$, it follows that $\alpha ^{1}\left( { region }^{1} - \widetilde{{ region }^{1}} \right)$ is not included in (13). The remaining parameters $\alpha ^{2},\ldots,\alpha ^{R}$ are estimated using OLS. In Online Appendix A.3, it is shown that the corresponding estimator, $\exp \left( {\widehat{\alpha }}^{t} \right)$, is defined by

$$\begin{aligned} \exp \left( {\widehat{\alpha }}^{t} \right) = \prod ^{R}_{r=1} \left( {\dot{P}}^{1r}_{\text {J}} \cdot {\dot{P}}^{rt}_{\text {J}} \right) ^\frac{1}{R} \, \end{aligned}$$

(14)

which is the typical presentation of the GEKS-Jevons method (e.g. ILO et al. 2020, p. 446). Moreover, when we insert the definitions of ${\dot{P}}^{1r}_{\text {J}}$ and ${\dot{P}}^{rt}_{\text {J}}$ into (14), it simplifies to

$$\begin{aligned} \exp \left( {\widehat{\alpha }}^{t} \right) = \prod _{i=1}^{N} \left( p_{i}^{t} / p_{i}^{1} \right) ^{\frac{1}{N}} = {\dot{P}}^{1t}_{\text {J}} \end{aligned}$$

in the case of a complete price matrix. Thus, the estimated price levels of the GEKS-Jevons method, $\exp \left( {\widehat{\alpha }}^{t} \right)$, are defined as ordinary Jevons indices (e.g. Hill 2016, p. 408). This is due to the fact that the bilateral Jevons index numbers are transitive when no product prices are missing. As a consequence, no adjustment of the bilateral index numbers is necessary.

3 Discussion on the error term specification

In the previous section, it was shown that the stochastic approach to index numbers provides point estimates for the price level of some region. The reliability of these estimates depends to a high degree on the quality of the collected price data. In particular, differences in the quality of products, missing prices across regions or selection bias may lead to distortions in the regional price levels and a loss in representativity. These “non-stochastic” sources of error are widely discussed in the literature (e.g. Balk and Kersten 1986; Kokoski et al. 1999; Silver 2009).

As one of its main advantages over the economic and the test approach, the stochastic approach to index numbers provides measures of precision for the estimated price levels (e.g. standard errors, confidence intervals). Even if price level estimates are unbiased, the interpretation of these measures relies highly on the choice of model specification and the assumptions on the error term.¹² Model (2), for example, postulates that the price ratio of regions r and s for product i solely deviates from the general relative price level by a random error term. This is a simple but plausible assumption. The assumption that the error term’s variance is identical among the regions and products, however, is rather restrictive (e.g. Summers 1973, p. 6). In particular, it is not only restrictive but might be false when it does not fit to the underlying empirical data. As a consequence, the measures of precision would be biased and, thus, meaningless. In the following, we address the importance of appropriate error term specifications in light of empirical studies on spatial price comparisons.

Variance of the disturbances The error term in (2) is assumed to be homoskedastic. This assumption, however, might be inappropriate when the price ratios behave systematically different among the regions and/or products (e.g. due to pricing policies that differ among the products). For example, suppose that some basic heading consists of two products i and j. Product i is uniformly priced in the regions, while product j is not. Following (2), the error terms would be realised by

$$\begin{aligned} \exp \left( u_{i}^{sr} \right) = P^{s}/P^{r} \quad \text {and} \quad \exp \left( u_{j}^{sr} \right) = \left( P^{s}/P^{r} \right) \cdot \left( p_{j}^{r} / p_{j}^{s} \right), \end{aligned}$$

suggesting a higher dispersion of product j’s error term. The assumption of homoskedastic rather than heteroskedastic disturbances would be difficult to defend in this case.¹³

Moreover, from a statistical viewpoint, some of the price ratios might be more reliable than others. Several researchers have stressed this issue by incorporating more plausible specifications on the error term into the CPD and GEKS methods.¹⁴ Rao (2001, pp. 4–8) introduced a weighting concept into the GEKS method where the variance of the error term, $\text {var} \left( u^{sr} \right)$, depends on individual weights, $w^{sr}$, for the underlying bilateral price index numbers. Consequently, with $\text {var} \left( u^{sr} \right) = \sigma ^{2} / w^{sr}$, it is possible to discriminate between different pairs of regions. Within this framework, Rao and Timmer (2003, pp. 498–500) developed and tested various weighting schemes (e.g. weights based on the number of product matches or the economic distance of regions) while Hill and Timmer (2006, pp. 370–371) derived standard errors as a weighting factor that “penalizes bilateral comparisons where the overlap of products is small”. Similarly, Rao (2001, pp. 15–16), Rao (2005, pp. 574–575) and Diewert (2005) incorporated weights into the CPD method that reflect the importance of a single price observation. In the absence of expenditure share data within a basic heading, the ICP uses “importance weights” that distinguish between important (weight of 3) and unimportant (weight of 1) price observations (see World Bank 2013, p. 110). In this scenario, the price levels are estimated by weighted rather than ordinary least squares.

Covariance of the disturbances among regions The covariance of different regions (CPD method) or different pairs of regions (GEKS method) is usually assumed to be zero, meaning that the error terms are spatially uncorrelated. Empirical studies, however, have shown that spatial autocorrelation can be found in prices as well as price levels. Aten (1997, 1996) was the first to explore the spatial nature in price levels. Using household consumption data for 64 countries in 1985, Aten (1996, pp. 160–162) reported for 15 out of 23 product categories “significantly spatially autocorrelated residuals”. Rao (2001, pp. 18–20) found for seven out of eight highly aggregated product categories, such as food and furniture, significant spatial autocorrelation. These findings have been confirmed in more recent studies that used the price data underlying the official CPI. Biggeri et al. (2017, pp. 109–111) computed sub-national price levels on the basis of official CPI data for seven basic headings that were collected in Italy in 2014. They reported that “an autocorrelation among disturbances was observed for all the BHs [basic headings] under analysis even if Moran’s I is quite low in some cases.” Similarly, Weinand and Auer (2020, pp. 428–432) computed a regional price index with price data underlying the German CPI in 2016. They found positive spatial autocorrelation in the regional price levels which is mainly driven by housing and, to a much lesser degree, by services and goods.

The empirical studies show that spatial autocorrelation plays an important role in spatial price comparisons. More specifically, from a statistical viewpoint, ordinary least squares would no longer provide efficient estimates when the disturbances are spatially autocorrelated. Therefore, various concepts have been proposed to address this issue. Rao (2004, pp. 8–11) reformulated the original CPD model into a spatial error model (e.g. Anselin 2003, p. 316). In this modified version, the disturbances are assumed to be spatially autocorrelated, with $\text {cov} \left( u_{i}^{r}, \ u_{i}^{s} \right) \ne 0$ for regions $r \ne s$. In contrast, Montero et al. (2020, pp. 519–521) propose a spatially-penalised version of the CPD method where a penalty for the differences in the price levels of neighbouring regions is included in the CPD model. For the GEKS method, Cuthbert (2003, pp. 77–78) recommended on the basis of an OECD data set the use of an “idealised“ variance–covariance–matrix with constant variances and covariances that are defined by $\text {cov} \left( u^{sr}, \ u^{st} \right) > 0$ and $\text {cov} \left( u^{sr}, \ u^{ut} \right) = 0$ for different regions r, s, t and u.

Covariance of the disturbances among products A relatively new field in price statistics is the collection of online price data using web scraping techniques. Empirical studies show that many online retailers are characterised by uniform pricing policies, meaning that the prices on their website do not depend on the buyers’ location (e.g. Cavallo 2018, pp. 15–21). Thus, spatial autocorrelation might not play a dominant role in online price data. However, with web scraped price data, new issues might arise that affect the error term specification in multilateral index number methods. More specifically, online prices that are adjusted by algorithms in response to competitors’ price changes for the same product or for a substitute might lead to correlated disturbances among the products. A survey of the European Commission (2017, pp. 175–177) on e-commerce strengthens this assumption. It revealed that “53% of the respondent retailers track the online prices of competitors [...]” while the “majority of those retailers that use software to track prices subsequently adjust their own prices to those of their competitors (78%)”. Moreover, Chen et al. (2016, pp. 1344–1346) found evidence of dynamic pricing in the online marketplaces of Amazon while Calvano et al. (2020) and Klein (2018) studied experimentally Q-learning algorithms and showed, broadly speaking, that these are able to coordinate on price setting.

The issue of correlated product prices is likely to be of more concern for the CPD method rather than for the GEKS method. From (12), it is obvious that the latter does not rely on individual product prices. Consequently, possible correlations among the prices of products vanish in the calculation of the bilateral index numbers. In contrast, for the CPD method, it would imply that $\text {cov} \left( u_{i}^{r}, \ u_{j}^{r} \right) \ne 0$ for products $i \ne j$. Furthermore, taking into account the findings on regionally uniform pricing of online retailers by Cavallo (2018), this might be extended to $\text {cov} \left( u_{i}^{r}, \ u_{j}^{s} \right) \ne 0$ for products $i \ne j$ and regions $r \ne s$. Lastly, it is worthwhile noting that correlated product prices are likely to have more relevance in temporal price comparisons as the algorithmic adjustment of prices to those of competitors is more of a temporal rather than a spatial issue. Nevertheless, the considerations may give rise to future research in this field.

4 Price level estimates when prices are missing

In Sect. 2, it is shown that the CPD, CD and GEKS-Jevons methods yield identical price level estimates under suitable assumptions on the error terms and in the case of complete price data. Strictly speaking, the price levels are defined by Eq. (1) as a Jevons index. It is well known that this equivalence no longer applies when prices are missing (e.g. World Bank 2013, p. 108), although there is little knowledge about how price level estimates change. One exception is the work of Ferrari et al. (1996). They consider the case where prices for exactly the same products are missing in some regions, while prices are fully available in the remaining regions. It turns out that the CPD and GEKS-Jevons price level estimators are still defined as a geometric average of those price ratios that are commonly available in the regions to be compared, though multiplied with a correction term. The correction term is weighted differently in both methods.

4.1 Some insights from a specific case of missing prices

In the following, we expand the case considered by Ferrari et al. (1996). For that purpose, we randomly divide the regions into the nonempty and disjoint subsets $R_{k}$ and the products into the disjoint subsets $N_{k}$ (henceforth, we will refer to region and product groups).¹⁵ We suppose that our price data consist of two groups of regions and products, respectively, that is, $k \in \{1,2\}$. Furthermore, we assume that the prices of products $i \in N_{k}$ are only available in regions $r \in R_{k}$. Thus, we have two complete, but non-connected blocks of prices (e.g. World Bank 2013, p. 98). Using graph-theoretic concepts, Rao (2004, pp. 11–17) shows that the computation of price levels with the CPD method, however, requires a connected price data graph.¹⁶ This is a remarkable result that also applies to the stochastic GEKS approach (e.g. Ferrari and Riani 1998, pp. 102–105). Therefore, we introduce an additional, nonempty set of products, $N_{0}$, whose prices are fully available in all regions. As a consequence, our price data are said to be connected since all regions are linked either through direct or indirect comparisons of product prices.¹⁷ In total, the price data encompass $\sum _{k=1}^{2} |R_{k}|=R$ regions and $\sum _{k=0}^{2} |N_{k}|=N$ products, where $|R_{k}|$ is the number of regions and $|N_{k}|$ the number of products in group k, respectively. The corresponding price incidence matrix is sketched in Table 1. For illustration purposes, its entries are ordered column-wise by the product group and row-wise by the region group.

Table 1 Price incidence matrix of blockwise missing prices, indicating whether a specific price is available in the data ($=1$) or not ($=0$)

We denote the price level estimator of region t compared to some arbitrary base region s by ${\widehat{P}}^{st}_{m}$. The subscript m indicates if the price level stems from the CPD or the GEKS-Jevons method. In Online Appendix B, it is shown that the formula underlying the price level estimator is given by

$$\begin{aligned} {\widehat{P}}^{st}_{m} = \prod _{i \in N_{0}} \left( \frac{p_{i}^{t}}{p_{i}^{s}} \right) ^{\frac{1}{|N_{0}|}} \cdot \left( \displaystyle \prod \limits _{r \in R_{1}} \varLambda _{1}^{sr} \right) ^{\frac{1}{\lambda _{m,1}}} \cdot \left\{ \begin{array}{ll} \left( \prod \limits _{r \in R_{1}} \varLambda _{1}^{rt} \right) ^{\frac{1}{\lambda _{m,1}}} &{} \text {if} \ s, t \in R_{1} \\ \left( \prod \limits _{r \in R_{2}} \varLambda _{2}^{rt} \right) ^{\frac{1}{\lambda _{m,2}}} &{} \text {if} \ s \in R_{1} \wedge t \in R_{2} \end{array} \right. \end{aligned}$$

(15)

where the correction term of product group $N_{k}$ for regions r and t, $\varLambda _{k}^{rt}$, as well as its weighting factor, $\lambda _{m,k}$, are defined by

$$\begin{aligned} \varLambda _{k}^{rt} = \frac{ \displaystyle \prod \limits _{i \in N_{0} \cup N_{k}} \left( p_{i}^{t} / p_{i}^{r} \right) ^{\frac{1}{|N_{0}| + |N_{k}|}}}{\displaystyle \prod \limits _{i \in N_{0}} \left( p_{i}^{t} / p_{i}^{r} \right) ^{\frac{1}{|N_{0}|}}} \quad \ \text {and} \quad \ \lambda _{m,k} = {\left\{ \begin{array}{ll} |R_{k}| &{} \text {if} \ m=\text {CPD} \\ \ R &{} \text {if} \ m=\text {GEKS-J} \end{array}\right. } \end{aligned}$$

for $k \in \{1,2\}$.¹⁸ The correction term $\varLambda _{1}^{sr}$ for regions s and r is defined in the same way.

The basic structure of the correction term is obviously the same for the CPD and GEKS-Jevons methods. Consequently, the price levels ${\widehat{P}}^{st}_{\text {CPD}}$ and ${\widehat{P}}^{st}_{\text {GEKS-J}}$ differ only due to a different weighting of the two correction terms. Since $|R_{k}|<R$ for all k, the CPD method assigns greater weights to the correction terms than the GEKS-Jevons method. One could say that the CPD method’s weights are somewhat plutocratic (Diewert 1986, pp. 18–19) because they differ with respect to the regional group sizes. In contrast, the correction terms of the GEKS-Jevons method are weighted independently of the regional group sizes and, thus, more or less “democratic”.

Equation (15) reveals that the calculation of ${\widehat{P}}^{st}_{m}$ distinguishes between a price comparison involving two regions of the same (intragroup comparisons) or of a different regional group (intergroup comparisons). For intragroup comparisons, it actually simplifies to

$$\begin{aligned} {\widehat{P}}^{st}_{m} = \prod _{i \in N_{0}} \left( \frac{p_{i}^{t}}{p_{i}^{s}} \right) ^{\frac{1}{|N_{0}|}} \cdot \left( \varLambda _{1}^{st} \right) ^{\frac{|R_{1}|}{\lambda _{m,1}}} \quad \text {if} \ s,t \in R_{1}. \end{aligned}$$

(16)

The price level solely relies on the prices of the two regions under consideration.¹⁹ Therefore, it is fully characteristic. In contrast, the price levels of intergroup comparisons, ${\widehat{P}}^{st}_{m}$ (with $s \in R_{1} \wedge t \in R_{2}$), are defined in (15) by a geometric average of those prices that are commonly available in regions s and t (first term), multiplied with two regional sequences of the correction terms, $\varLambda _{1}^{sr}$ and $\varLambda _{2}^{rt}$ (second and third term). The latter two put the prices of regions s and t in relation to those of other regions r in the same regional group. As a result, intragroup comparisons generate characteristic price levels, while intergroup comparisons do not.

The GEKS-Jevons price levels are generated such that the overall quadratic deviation to the initial Jevons price levels, ${\dot{P}}^{st}_{\text {J}}$, is kept at a minimum (e.g. Rao and Timmer 2003, p. 499; Laureti and Rao 2018, p. 126). Therefore, it would be the natural choice to use the GEKS-Jevons method in every situation in order to approximate ${\dot{P}}^{st}_{\text {J}}$ on average as close as possible. Equation (15) shows that this might be appropriate when intergroup comparisons are of relevance, due to the smoother weighting of the correction terms, $\varLambda _{1}^{sr}$ and $\varLambda _{2}^{rt}$, by the GEKS-Jevons method.²⁰ For intragroup comparisons, however, this is not the case. With $\lambda _{\text {CPD},1} = |R_{1}|$, the CPD price level estimator, ${\widehat{P}}^{st}_{\mathrm {CPD}}$, in (16) simplifies to

$$\begin{aligned} {\widehat{P}}^{st}_{\mathrm {CPD}} = \prod _{i \in N_{0} \cup N_{1}} \left( p_{i}^{t} / p_{i}^{s} \right) ^{\frac{1}{|N_{0}|+|N_{1}|}} = {\dot{P}}^{st}_{\text {J}} \quad \text {if} \ s, t \in R_{1} \end{aligned}$$

and, thus, corresponds to the bilateral Jevons price level of regions s and t, ${\dot{P}}^{st}_{\text {J}}$. In contrast, the GEKS-Jevons price level estimator, ${\widehat{P}}^{st}_{\mathrm {GEKS-J}}$, equals ${\dot{P}}^{st}_{\text {J}}$ only if $p_{i}^{t} = p_{i}^{s}$ for all products $i \in N_{0} \cup N_{1}$. As a result, it seems that the CPD method assigns a higher priority on the “accuracy” of intragroup price levels, while the GEKS-Jevons method treats intragroup and intergroup price levels as equally important. This leads to the question of how the CPD and GEKS-Jevons price level estimators behave in a generalised setting, namely when prices are randomly rather than group-wise missing.

4.2 A generalised setting: simulation of artificial price data

In Sect. 2, it was shown that the CPD method as well as the GEKS-Jevons method can be derived from the same data generating process (DGP) in Equation (2). In the following, we exploit the DGP to create artificial price data that can be used for a deeper comparison between the CPD and the GEKS-Jevons price level estimators. Kackar and Harville (1984, p. 860) recommend including a relatively simple estimator into the comparison of the error metrics. In our case, the logarithm of the Jevons index, ${\dot{\alpha }}_{\text {J}}^{t} = \ln {\dot{P}}^{1t}_{\text {J}}$, would be a natural choice that serves as our baseline in the following.

We conduct a Monte Carlo analysis with $L=\text {2000}$ iterations ($l=1,\ldots,L$).²¹ We set the number of regions in each iteration to $R=30$ in order to receive a constant amount of price level estimates. In each region, there are the same $N=50$ products $(i=1,\ldots,N)$ available. The price levels, $P^{t} \; (t=2,\ldots,R)$, are drawn independently for each region and iteration from a log-normal distribution with $P^{t} \sim {\textit{LN}} \left( \mu =0, \sigma ^{2}=0.02 \right)$. In addition, we exogenously fix the price level of the base region to one, i.e. $P^{1}=1$. This setting ensures a sufficient fluctuation around the base region’s price level, while the maximum price level spread between the most expensive and the cheapest region is roughly four. Furthermore, we assume that the error term is iid with $u_{i}^{sr} = \ln \epsilon _{i}^{sr} \sim N \left( \mu =0, \sigma ^{2}=0.04\right)$. As a result, we obtain $L=\text {2000}$ data sets with regional price ratios at the product level.

We apply the GEKS-Jevons method to each of these simulated data sets and obtain a set of transitive price levels, ${\widehat{\alpha }}^{t}_{\text {GEKS-J}}$. The CPD method, however, requires absolute prices rather than price ratios. Therefore, we additionally assume to know the price for each product in at least one region. This enables us to compute all of the remaining absolute prices, to transform these into a full price matrix and, consequently, to apply the CPD method as well. As a result, we receive the logarithmic price level estimators, ${\widehat{\alpha }}^{t}_{\text {CPD}}$ and ${\widehat{\alpha }}^{t}_{\text {GEKS-J}}$ ($t=2,\ldots,R$), that were computed from exactly the same price data. Moreover, from the DGP, we also know the “true” logarithmic price levels, $\alpha ^{t} = \ln \left( P^{t} / P^{1} \right)$, that were used within the simulation of each data set. Thus, we are able to evaluate the performance of the estimators in terms of bias and root mean squared error (RMSE):

$$\begin{aligned} \text {Bias} \left( {\widehat{\alpha }}^{t}_{m} \right) = \frac{1}{L} \cdot \sum _{l=1}^{L} \left( {\widehat{\alpha }}^{t}_{m,l} - \alpha ^{t}_{l} \right) \quad \text {and} \quad \text {RMSE} \left( {\widehat{\alpha }}^{t}_{m} \right) = \sqrt{\frac{1}{L} \cdot \sum _{l=1}^{L} \left( {\widehat{\alpha }}^{t}_{m,l} - \alpha ^{t}_{l} \right) ^{2}} \;, \end{aligned}$$

where $L=\text {2000}$ is the number of simulation runs and $m \in \{\text {CPD}, \; \text {GEKS-J}, \; \text {Jevons} \}.$

We know from Sect. 2 that the CPD and GEKS-Jevons price level estimators, ${\widehat{\alpha }}^{t}_{\text {CPD}}$ and ${\widehat{\alpha }}^{t}_{\text {GEKS-J}}$, coincide when no prices are missing. Moreover, we know that they also coincide with the logarithm of the Jevons index, ${\dot{\alpha }}_{\text {J}}^{t}$. Consequently, regardless of how many simulations we would run, the estimated bias as well as the estimated RMSE is the same for these three estimators. However, when prices are missing, it is well known that the simple Jevons index no longer generates transitive price levels (e.g. ILO et al. 2020, p. 446). In addition, it is shown in Sect. 4.1 that the transitive price levels produced by the CPD and GEKS-Jevons methods differ. Therefore, in order to evaluate the performance of the price level estimators under these circumstances, we incorporate gaps into our simulated price data by dropping prices for certain products and regions. The selection of the prices that are removed happens randomly, but is restricted to three conditions. First, no matter how many prices are removed, the price data must stay connected in order to ensure the feasibility of price level computations. Second, for each product, prices are always available in at least two different regions. Third, the deletion of prices is path-dependent for a single price data set.²²

Table 2 contains the simulation results in terms of bias and RMSE for the three estimators. It further illustrates how the two error metrics change when the gaps in our artificial price data gradually increase from $0\%$ (no missing prices) to $80\%$ (highly fragmented). As can be seen, the estimated bias is roughly zero and, thus, indicates that the estimators are unbiased. The estimated RMSE, on the other hand, increases for each estimator in reaction to an increased share of gaps in our price data. Not surprisingly, it is the highest for the simple Jevons index. The CPD and GEKS-Jevons estimators clearly outperform the Jevons index in terms of efficiency.

Table 2 Estimated bias and RMSE by percentage of missing prices for the CPD, GEKS-Jevons and Jevons price level estimators, respectively. Calculations on the basis of $L=\text {2000}$ simulated price data sets with $R=30$ regions and $N=50$ products

The simulation setting leading to the results in Table 2 represents the case when all regions may exhibit gaps in the price data (including the base region s and the comparison region t of some estimated price level, ${\widehat{\alpha }}^{t}_{m} = \ln {\widehat{P}}^{st}_{m}$). Nevertheless, it neglects scenarios where either the base region, the comparison region or both of them provide full price information, while the other regions do not. Therefore, the simulation study is extended to these scenarios.²³

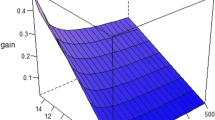
As expected, it turns out that the estimated bias is still roughly zero in all scenarios. The simulation results for the RMSE, in contrast, reveal differences between the scenarios. These are shown in Fig. 1. The first panel depicts the RMSE that arises when both, the base as well as the comparison region, provide full price information, while all other regions in the data set may exhibit gaps (scenario I). As can be seen, the RMSE of the CPD method and the simple Jevons index coincide.²⁴ Moreover, it does not change when prices are missing in other regions (represented by the horizontal line). This, in contrast, is not true for the RMSE of the GEKS-Jevons method. The second and third panels highlight the case when either the comparison (scenario II) or the base region (scenario III) is the only region that provides full price information. Interestingly, both the CPD and GEKS-Jevons estimators perform far better when the prices are fully available in the comparison region rather than in the base region. Lastly, the fourth panel captures the RMSE values of Table 2 where all regions may exhibit gaps (scenario IV).

Fig. 1

RMSE (vertical axis) by percentage of missing prices (in %, horizontal axis), index method and scenario (four panels). Calculations on the basis of $L=\text {2000}$ simulated price data sets with $R=30$ regions and $N=50$ products

Overall, Fig. 1 shows that the baseline RMSE of the Jevons index vastly increases as soon as prices are missing in at least one of the two regions under consideration (see dotted line in panels two to four). Moreover, the RMSE of the CPD price level estimator lies slightly below that of the GEKS-Jevons estimator in all four scenarios. The change associated with an increased share of missing prices, however, is fairly similar. This result is not surprising for two reasons. First, from Equation (15), we know that the CPD and GEKS-Jevons price level estimates differ only due to a different weighting of the correction terms. Now, even in this more general setting, the estimators ${\widehat{\alpha }}^{t}_{\text {CPD}}$ and ${\widehat{\alpha }}^{t}_{\text {GEKS-J}}$ are almost perfectly correlated.²⁵ Second, and perhaps more importantly, the deletion of prices within the simulation happened randomly, with the result that the gaps in our price data are uniformly distributed among the regions and products. In practice, however, this is a rather unrealistic situation as regions provide price information at varying frequencies. Similarly, specific products are less frequently available across regions than others. Therefore, we adapt our simulation study in the next section to a more realistic setting.

4.3 A more realistic setting with official micro price data

The official CPI in Germany is constructed as a stratified, non-random sample.²⁶ The prices of narrowly defined products are collected on a monthly basis in different regions, outlet types (e.g. supermarkets, discount stores) and basic headings (e.g. rice, milk). The actual collection of the price data is mainly carried out by the Statistical Offices of the Federal States (Statistische Landesämter) in selected regions of Germany. These data are supplemented by the Federal Statistical Office (Statistisches Bundesamt) which gathers the prices of products that are known to be regionally identical (e.g. books and cigarettes) or affected by particularly complex pricing policies (e.g. package holidays).

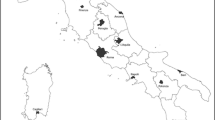
We have the privilege to work with a subset of these CPI data that was provided to us by the Research Data Centre (RDC) of the Federal Statistical Office and Statistical Offices of the Federal States. The price data were collected in $R=19$ Bavarian regions in May 2011 (see left panel of Fig. 2). They contain 23,642 consumer prices for goods, services and rents that are divided at the lowest classification level into 607 basic headings. The basic headings’ expenditure weights add up to 71.79% of the German consumption basket.²⁷ Moreover, the data set contains information about the region where a price was collected. A unique identifier of the product for which that price was observed, however, is missing. Instead, semi-structured product descriptions are available (e.g. Behrmann et al. 2009, pp. 5–6; Zimmer 2016, pp. 44–45). These include information about the product’s amount (e.g. the weight or quantity), the respective unit of measurement (e.g. litre) and, subject to the basic heading, a number of supplementary characteristics like the brand or the packaging. In addition, special offer prices and the outlet type where the price was observed are indicated.

Fig. 2

Bavarian regions where prices were collected in 2011 (left panel, grey shaded areas) and relationship between population density and number of collected prices across those regions (right panel, logarithmic scale). Source RDC of the Federal Statistical Office and Statistical Offices of the Federal States, Consumer Price Index, May 2011, own calculations

The collected rents for flats and single-family houses in the data set are accompanied by much richer “product descriptions” compared to those for goods and services. Therefore, one would typically draw on more sophisticated methods for the computation of regional price levels than the simple CPD and GEKS-Jevons methods (e.g. more complex hedonic regressions). However, since our simulation analysis concentrates on the latter two, we omit the rent data from that analysis. As a result, 21,783 price observations in $B=601$ basic headings (expenditure weight: 51.05%) remain. For those basic headings, we rely on the product descriptions to define directly comparable products as precisely as possible. The choice of how narrowly we define such a product, however, is left to us and is thus more or less subjective. Therefore, we distinguish the following evaluation of the estimators’ performances by the level of product definition. For price comparisons at the product level (a product is defined as narrowly as possible by all available characteristics), we identify 1291 unique products that are priced in at least two different regions. In contrast, this number reduces to 652 at the outlet level (a product is defined only by the outlet type within a basic heading) and to 371 at the basic heading level (no product definition; all prices within a basic heading are assumed to be directly comparable). Weinand and Auer (2020, pp. 432–433) speak in this context of “simplified compilation procedures”, since a definition at the outlet or at the basic heading level does not require any prior processing of the product descriptions.

As in the previous section, we perform a Monte Carlo analysis with $L=\text {2000}$ iterations ($l=1,2,\ldots,L$). This time, however, we do not randomly introduce gaps into our price data. Instead, we mimic the underlying structure of the CPI data set, i.e., we create artificial basic headings that adopt the observed basic headings’ structure. In this way, we take into account that the number of collected prices varies by region (see right panel of Fig. 2). More specifically, it is positively correlated with the population density. Those regions with a relatively low population density do not provide prices for each basic heading. As a result, most of the basic headings in the data set are incomplete.

Our simulation strategy is as follows. First, we randomly choose one of Eurostat’s main HICP special aggregates.²⁸ Second, within the aggregate, we randomly select $N=10$ specific products from the original CPI data set without replacement. This setting ensures that unprocessed food, say, is not mixed up with services. Third, we add to these products the corresponding regions that originally collected prices. Consequently, we receive a new composition of products and regions. The regional distribution of available product prices, however, is adopted from the original price data. Lastly, we add artificial prices. For this purpose, we sample independently for each iteration the true regional price levels, $P^{t} \; (t=1,\ldots,R)$, and error terms, $u_{i}^{sr}$, in line with the DGP in (2):

$$\begin{aligned} P^{t} \sim {\textit{LN}} \left( \mu =0, \sigma ^{2}=0.02 \right) \quad \text {and} \quad u_{i}^{sr} = \ln \epsilon _{i}^{sr} \sim N \left( \mu =0, \sigma ^{2}=0.04 \right). \end{aligned}$$

In this way, we generate $L=\text {2000}$ data sets. On average, 66.7% of the prices are missing within these data sets. The distribution of available prices across the regions is highly correlated with that of the original CPI data $\left( \rho =0.78 \right)$. We apply the CPD, the GEKS-Jevons and the simple Jevons estimators to each of these data sets. Their performance in terms of bias and RMSE is documented in Table 3.

Table 3 Simulation results in terms of bias and RMSE for the CPD, GEKS-Jevons and Jevons price level estimators, respectively. Calculations on the basis of $L=\text {2000}$ incomplete price data sets with $N=10$ products

The simulation results show how the regional price level estimators perform on “real world data”. Moreover, they demonstrate the relevance of the product definition level for the estimation efficiency. As can be seen, the estimated bias and RMSE are the same for the three estimators when there is no product differentiation within a basic heading (see line “Basic heading level”). Otherwise, with a product differentiation, the RMSEs differ. Strictly speaking, they slightly decrease for product definitions at the outlet level and considerably at the much narrower product level. In both cases, the RMSE is the lowest for the CPD method.

Lastly, it is worthwhile to note that the RMSE comparison between the different levels of product definition also depends on the regional volatility of prices, that is, how much the prices of some product fluctuate across the regions. Unsurprisingly, when we lowered the regional volatility of the prices in our simulation study, the RMSE values dropped to roughly 0.22, including for product definitions at the outlet and basic heading level.²⁹ As a consequence, in future work with official CPI data, one could rely on product definitions at the outlet level for those basic headings with low regional price fluctuations. In contrast, for those basic headings with high regional price fluctuations, the estimation efficiency clearly benefits from a narrow product definition. This mixed strategy would heavily reduce the costly data preprocessing reported by Weinand and Auer (2020, pp. 420–421).

5 Concluding remarks

The main goal of this paper was to extend the theoretical foundations of the stochastic approach to index numbers in light of spatial price comparisons. To this end, we examined the most prominent representatives of the stochastic approach: the CPD method and the GEKS(-Jevons) method. In particular, we analysed the impact of missing prices below the basic heading on the estimation of regional price levels. For a specific case of missing prices, we derived the formula underlying the price level estimates and showed that differences between the CPD and GEKS-Jevons methods stem solely from the assignment of a different weighting pattern. Moreover, using simulation techniques, we studied the statistical properties of the CPD and GEKS-Jevons price level estimators in terms of bias and RMSE. Our results reveal lower RMSE values for the CPD method in four tested scenarios. For spatial price comparisons, it is worthwhile keeping in mind that the estimation efficiency improves, especially in cases where the comparison region provides complete prices.

Notwithstanding these differences, our results demonstrate that the regional price level estimates of the CPD and the GEKS-Jevons methods are closely related. Therefore, we do not want to speak generally in favour of one of the two methods. However, two thoughts are worth mentioning. First, from a practical point of view, statistical offices collect absolute prices rather than price ratios or price index numbers. These price data form the building blocks for CPI measurement purposes and would be a unique data source for the calculation of regional price levels as well. The application of standard regression techniques to these raw data (CPD method), therefore, seems more straightforward than first converting prices into bilateral index numbers (general GEKS approach). In addition, the regression approach underlying the CPD method allows for extensions in the sense of more careful quality adjustments, for example, by including additional product characteristics (e.g. Balk 2008, p. 258). Second, from a statistical point of view, we showed in Sect. 4 that the estimation efficiency of the CPD method outperforms that of the GEKS-Jevons method, especially in the case of substantial gaps in the price data. This result strengthens the application of the CPD method below the basic heading level where data gaps are frequently an issue.

In our second simulation study, we used a subset of the price data underlying Germany’s CPI. These price data come with precise but relatively unstructured product descriptions. The importance of these product descriptions for spatial price comparisons is widely documented in the literature (e.g. ILO et al. 2020, p. 68; World Bank 2013, p. 590), as they enable price statisticians to identify directly comparable products as precisely as possible. Utilising the product descriptions would be a natural choice for statistical offices to compare only like with like across regions and thereby avoid any distortions in their estimates of regional price levels. However, one drawback that statistical offices would face is the extensive preprocessing of the product descriptions. Our findings have practical relevance for two reasons as they address both issues and may therefore serve as guidance for statistical offices carrying out spatial price comparisons. First, our simulation results underline the importance of the product definition for the estimation efficiency. In particular, they show an improvement in the estimation efficiency owing to more narrowly defined products, though this is usually accompanied by more gaps in the price data. Second, our simulation results reveal that statistical offices may reduce the workload associated with preprocessing the product descriptions by following a mixed strategy that takes into account the regional price volatilities of the basic headings.³⁰ For those basic headings with a low regional price volatility, statistical offices could rely on looser product definitions, such as the outlet level, which do not require any data preprocessing.

We conclude with two points that are worth mentioning but beyond the focus of this paper. First of all, Hajargasht and Rao (2019) recently examined the theory on multilateral index numbers in light of graph theory. Although they do not explicitly mention the CPD and GEKS-Jevons methods, their derivations might be relevant to our setting as well. Basically, not only does the percentage of missing prices directly influence the efficiency of the price level estimates, the manner in which the prices and thus the gaps within the collected data are distributed among the regions (“degree of connectedness”) is also relevant. This consideration may give rise to future research. Second, with respect to simulation studies, greater attention in future work could be focused towards different patterns in the price data (e.g. spatially correlated prices). Also, the adoption of various extensions of multilateral index number methods into the simulation framework would be valuable. This particularly applies to the weighted CPD and GEKS-Jevons methods as well as the variants used in the last ICP rounds in 2011 and 2017 at the basic heading level.³¹