Abstract
Distance sampling and capture–recapture are the two most widely used wildlife abundance estimation methods. capture–recapture methods have only recently incorporated models for spatial distribution and there is an increasing tendency for distance sampling methods to incorporated spatial models rather than to rely on partly design-based spatial inference. In this overview we show how spatial models are central to modern distance sampling and that spatial capture–recapture models arise as an extension of distance sampling methods. Depending on the type of data recorded, they can be viewed as particular kinds of hierarchical binary regression, Poisson regression, survival or time-to-event models, with individuals’ locations as latent variables and a spatial model as the latent variable distribution. Incorporation of spatial models in these two methods provides new opportunities for drawing explicitly spatial inferences. Areas of likely future development include more sophisticated spatial and spatio-temporal modelling of individuals’ locations and movements, new methods for integrating spatial capture–recapture and other kinds of ecological survey data, and methods for dealing with the recapture uncertainty that often arise when “capture” consists of detection by a remote device like a camera trap or microphone.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The need to account for imperfect detection in wildlife surveys has long been recognized. The best way to do this, and the effects of not accounting for it, are often discussed in the ecological literature (Kellner and Swihart 2014). Distance sampling (DS) and capture–recapture (CR) methods are the most commonly used methods of estimating abundance (see Buckland et al. 2001; Williams et al. 2002 for overviews of DS and CR, respectively).
The two main types of distance sampling are line transect (in which observers traverse lines while searching, and the line is the “sampler”) and point transect (in which observers search from a point, and the point is the “sampler”). As their name suggests, DS methods use distances to detected individuals to draw inferences about detection probability. If the distribution of individuals in the vicinity of samplers (i.e., close to the lines or points) is known, changes in detection frequency as a function of distance from sampler can be used to estimate the relative detectability of individuals as a function of distance. And if all individuals at distance zero are detected, estimates of relative detectability can be converted into estimates of absolute detection probability. This is what DS methods do. Because detection probability is modelled as a function of distance, individuals’ inclusion probabilities (the probability of an individual appearing in the sample) can be estimated as a function of their locations.
By contrast, capture–recapture methods took no account of the location of individuals before the advent of spatial capture–recapture. Classical CR methods were classified by Otis et al. (1978) according to the form of dependence of capture probability on explanatory variables: \(\hbox {M}_0\) for none, \(\hbox {M}_t\) for occasion (time), \(\hbox {M}_b\) for individual trap-response (behaviour avoidance or attraction after being captured) and \(\hbox {M}_h\) for individual heterogeneity. None of these models include anything to do with individuals’ locations. As a result classical CR methods can not draw inferences about detection probability as a function of location, and so, unlike distance sampling methods, are not able to draw inferences about detection (or capture) range. And a consequence of this is that they are not able to draw inferences about density, only about abundance in some unknown region. The region is unknown because CR data contain no spatial information and so no information on how far away individuals are detectable. A variety of methods using data external to the CR survey and/or additional assumptions about detection range have been used to try to get density estimates out of non-spatial CR data, but these do not in general perform well (see Efford and Fewster 2013).
Spatial capture–recapture (SCR) methods rectified this situation by incorporating distance sampling detection functions in CR methods. Actually, that is not quite true, distance sampling detection functions had been used with CR survey methods for at least two decades prior to the advent of SCR, in the form of “mark-recapture distance sampling” (MRDS) methods (see Borchers et al. 1998, and references therein). What SCR added to MRDS was the ability to deal with unobserved individual locations.
Both DS and CR methods involve spatial sampling, i.e. placing samplers randomly or systematically in space and detecting individuals in a population on the basis of their proximity to the samplers. And yet conventional DS and CR models base inference either on very simplistic spatial models (independent, uniform distribution in space, typically) or conduct inference without an explicit spatial model. With the advent of SCR models, this situation is rapidly changing in the case of CR, and there is a parallel tendency for DS models to incorporate an explicit model for the spatial distribution of animals in the region of interest. That said, the kinds of spatial models used in DS and SCR tend to be very simple compared to those used in the field of spatial modelling itself. In particular, they tend to neglect spatial correlation—something that is so central to the field of spatial modelling that many in that field would say that the model is not a spatial model unless it incorporates spatial correlation.
Spatial modelling in a DS and SCR context presents new challenges because the probability of including individuals in the sample depends on their location relative to the samplers and this probability is unknown and must be estimated from the same data used to estimate the parameters of the spatial model. As a result, spatial modelling in DS, and SCR in particular, is in its infancy and there is much scope for methodological development. Development of realistically complex spatial and spatio-temporal models for use with DS and SCR could provide new ways of addressing questions of a fundamentally spatial nature, such as species distribution, habitat preference, movement patterns, spatial connectivity and spatial aspects of population dynamics.
We do not develop such models here, but by formulating DS and SCR models as thinned point process models with unknown thinning probabilities in this paper, we provide a framework that unites the two methods and can serve as a basis for the development of realistically complex spatial models for these two most widely used methods in ecological sampling.
The remainder of this review is organized as follows: We build on a description of the modeling framework (Sect. 2) with sections placing conventional distance sampling (Sect. 3) and mark-recapture distance sampling (Sect. 4) within that framework. We then move to spatial capture recapture models (Sect. 5) and some of their extensions (Sect. 6). We conclude in Sect. 7 with a brief discussion noting relevant topics that we neglected for the sake of brevity and the key areas that we anticipate will be the focus of future research effort.
2 Modelling framework
We use the terms capture or detection interchangeably, depending on context. Unless we say otherwise, we assume that animals are, or can be, uniquely marked, and that they are identified as marked when recaptured. Any feature that uniquely identifies an animal, allowing previous captured animals to be recognized, can be used to “mark” the animal. Examples of such “natural” marks include DNA fingerprinting (Puechmaille and Petit 2007), dorsal fin contours (Currey et al. 2008), fur patterns (Rich et al. 2014) or distinctive scars or other marks. We use “traps” and “detectors” somewhat interchangeably, preferring “detectors” to convey the idea that animals do not need to be physically trapped.
To avoid more complicated notation than is essential, we do not distinguish in our notation between random variables and realisations of random variables. This is usually apparent from the context.
2.1 The meaning of “location”
We denote the location of individual i in a population of interest by \(\varvec{s}_i\), and the locations of all individuals in the population by \(\varvec{S}=(\varvec{s}_1,\ldots ,\varvec{s}_N)\).
The meaning of “location” is survey dependent. “Location” may be an abstract thing and need not have any biological relevance. On a distance sampling survey in which animals are detected by eye, “location” is the point in the plane that the animal is at when it is first detected. For a tiger that is detected by moving in front of a camera trap, “location” for the purposes of SCR is the centre of its movements over the duration of the survey (its “activity centre”), not its location at time of detection. In this case detection comes about as a consequence of the tiger’s movement. For a frog sitting still and making sounds that are detected by microphones, “location” is the position of the frog. In this case detection comes about as a consequence of the frog’s vocalization, not its movement. For a bird moving about and making calls that are detected by microphones, “location” is its activity centre over the period that microphones operated. In this case detection comes about as a consequence of both the bird’s movement and its vocalization. We use the words “location” and “activity centre” interchangeably.
2.2 The model hierarchy
Distance sampling and spatial capture–recapture models are hierarchical. The lowest level of the hierarchy is a point process model for the locations of individuals in the population. On top of this is a detection probability model for individuals that is conditional on the individuals’ locations. Because CR surveys involve repeat detections, the basic observation for the ith individual on a CR survey is a “capture history”, \(\varvec{\omega }_i=(\omega _{i1},\ldots ,\omega _{iJ})\), being a vector of J binary random variables for a survey with J occasions, in which \(\omega _{ij}=1\) if individual i was detected on occasion j and \(\omega _{ij}=0\) otherwise. And since SCR surveys involve multiple detectors per occasion, SCR capture histories are slightly more complex, being \(\varvec{\omega }_i=(\omega _{i11},\ldots ,\omega _{iJ1},\ldots ,\omega _{i1K},\ldots ,\omega _{iJK})\) for a survey with K detectors on each occasion. We denote the full set of capture histories \(\varOmega =(\varvec{\omega }_1,\ldots ,\varvec{\omega }_N)\).
The basic SCR hierarchy is therefore
- \(f_S(\varvec{S};{\phi })\) :
-
This is a point process model for the number (N) and locations \(\varvec{S}\) of the N individuals in the population. Here \({\phi }\) is a vector of (typically unknown) parameters of this model.
- \(f_\varOmega (\varOmega {\mid }\varvec{S};\varvec{\theta })\) :
-
This is a probability model for the capture histories, given individuals’ locations, \(\varvec{S}\). Here \(\varvec{\theta }\) is a vector of (typically unknown) parameters of the spatial detection probability model.
2.3 The point process model
While other point process models are possible, with very few exceptions, the point process model governing the number and locations of individuals is assumed to be a Poisson process model:
where \(D(\varvec{s};{\phi })\) is the density of individuals at location \(\varvec{s}\) and \(E(N;{\phi })=\int _\mathcal{A}D(\varvec{s};{\phi })\mathrm{d}\varvec{s}\), with integration being over the survey region \(\mathcal A\).
It is not uncommon for DS and SCR models to condition on N, i.e. to treat the number of individuals in the survey region as a fixed (but unknown) number, not a random variable, in a frequentist context. In this case the locations of the N individuals in the population follows a non-homogeneous binomial point process: \(f_S(\varvec{S}_N;{\phi })=D(\varvec{s}_i;{\phi })/\int _\mathcal{A}D(\varvec{s};{\phi })\mathrm{d}\varvec{s}\), where the N subscript on \(\varvec{S}_N\) indicates that N is fixed in this case (whereas with \(\varvec{S}\), N is a random variable). In this review we use the Poisson point process model rather than the binomial point process model. We can factorise Eq. (1) as the product of a Poisson distribution for N (the first term in square brackets below) and a binomial point process model for \(\varvec{S}\), given N (the second term in square brackets below):
2.4 The observation model
It is convenient to separate the observation process into the probability of observing an individual at all, and the probability of obtaining a capture history, given observation or not. We define a random vector \(\varDelta =(\delta _1,\ldots ,\delta _N)\) such that \(\delta _i=1\) if individual i was observed at all on the survey, and \(\delta _i=0\) otherwise (\(i=1,\ldots ,N\)). In the case of unobserved individuals there is only one possible capture history, comprising KJ zeros, so there is no random process operating for capture histories of unobserved individuals. In the case of observed individuals, we do have a random process operating. We use \(\varOmega _n\) to denote the capture histories of detected individuals.
It is useful to construct a hierarchy of random processes within the observation process, thus:
- \(f_\varDelta (\varDelta {\mid }\varvec{S};\varvec{\theta })\) :
-
This is the detection probability model, conditional on \(\varvec{S}\), in which the \(\delta _i\)s are typically assumed to be independent so that \(f_\varDelta (\varDelta {\mid }\varvec{S};\varvec{\theta })=\prod _if_\delta (\delta _i{\mid }\varvec{s}_i;\varvec{\theta })\), and \(f_\delta (\delta _i{\mid }\varvec{s}_i;\varvec{\theta })\) is a binary regression model with parameter vector \(\varvec{\theta }\) and explanatory variable \(\varvec{s}\). (Typically there would also be other explanatory variables, but we omit these for simplicity.)
- \(f_{\varOmega _n}(\varOmega _n{\mid }\varDelta ,\varvec{S};\varvec{\theta })\) :
-
This is a probability model for the capture histories of detected individuals, given detection or not (\(\varDelta \)) and locations \(\varvec{S}\).
The above observation models depend on the locations of the detectors as well as the locations of the individuals in the population of interest. Both models are therefore conditional on the locations of detectors, but for simplicity of exposition we do not make these locations explicit at this stage.
3 Conventional distance sampling models
Let \(d_{ik}=d_{ik}(\varvec{s}_i)\) be the distance of individual i, located at \(\varvec{s}_i\), from detector k, and let p(d) be the probability that an individual at distance d from detector k is detected. Conventional distance sampling (CDS) models assume that \(p(0)=1\). (The CDS literature usually refers to this probability as g(0), not p(0). We use p(0) for consistency with CR literature.) A common form for p(d) is the half-normal:
where \(\varvec{\theta }\equiv \sigma ^2\). Another common form is the hazard rate form of Hayes and Buckland (1983). Additional flexibility can be obtained by adding “adjustment terms”, which involves adding scaled cosine or polynomial basis functions to the half-normal, hazard-rate or uniform p(d) model (see Buckland 1992).
CDS surveys typically involve only one distance per detected individual (\(d(\varvec{s}_i)\) for individual i), so that
3.1 Distance sampling as a latent variable regression model
The above looks like a binary regression model, with explanatory variable \(d(\varvec{s}_i)\) and a non-standard form for the binary “success” probability \(p(d(\varvec{s}_i);\varvec{\theta })\) (namely one that has \(p(0;\varvec{\theta })=1\)). Unfortunately, it can not be implemented as such—because we do not observe the “failures” (when \(\delta _i=0\)) and as a consequence we do not know how many binary “trials” there were.
The way DS methods deal with this is by treating the number of trials (N here) as a latent variable, or unknown parameter. More specifically, the spatial nonhomogeneous Poisson process (NHPP) of the previous section provides a probability mass function for the latent variable N, namely \(N\sim \hbox {Po}(E(N;{\phi }))\), as per the first term in square brackets in Eq. (2), and for \(\varvec{S}\) given N, as per the second term in square brackets in Eq. (2). So one can think of distance sampling models as binary regression models with a random number of trials, governed by a probability density for N, and partially observed latent variables \(\varvec{S}\) (observed only for detected individuals).
If N is treated as a fixed but unknown parameter, and \(\varvec{S}\) as a draw from a binomial point process model, then the distance sampling model can be thought of as a binary regression model with an unknown number of trials (N) and partially observed latent variables \(\varvec{S}\). The focus of inference in this case is on the number of trials, N. Inference about N is only possible because the value of \(p(d_k(\varvec{s}_i);\varvec{\theta })\) is known for some \(d(\varvec{s})\), namely \(p(0;\varvec{\theta })=1\) (see below too).
3.2 Distance sampling as a thinned point process
Although most distance sampling methods are not fully model-based (i.e based on a model of the sort outlined above), there is an increasing trend towards fully model-based inference (see Buckland et al. 2016) and that is what we focus on here. Johnson et al. (2010) is a recent example of this approach. Like Johnson et al. (2010), we assume that \([\varvec{S};{\phi }]\) is a nonhomogeneous Poisson process (NHPP), as in Eq. (1). As a consequence, the locations \(\varvec{S}_n\) of the n observed individuals (those with \(\delta _i=1\)) is a thinned NHPP, thinned according to Eq. (4), i.e.
with \(E(n;\varvec{\theta }),{\phi }=\int _\mathcal{A}p(d(\varvec{s});\varvec{\theta })D(\varvec{s};{\phi })\mathrm{d}\varvec{s}\). Note that on DS surveys, \(\varvec{S}_n\) is observed. This kind of thinning is called “p(x)-thinning” by Illian et al. (2009), because the thinning depends on some covariate x (\(d(\varvec{s})\) in our case). A notable feature of thinning in a distance sampling context is that the thinning function \(p(d(\varvec{s});\varvec{\theta })\) is unknown.
When considered as a function of \(\varvec{\theta }\) and \({\phi }\), given the observations \(\varvec{S}_n\) obtained on a survey, Eq. (5) is a distance sampling likelihood function.
Notice that multiplying \(p(d(\varvec{s});\varvec{\theta })\) by any constant and dividing \(D(\varvec{s};{\phi })\) by this constant gives the same likelihood. As a consequence, \(p(d(\varvec{s});\varvec{\theta })\) and \(D(\varvec{s};{\phi })\) cannot be separately estimated from distance sampling data. Distance sampling methods avoid this problem by assuming that \(p(0;\varvec{\theta })=1\) (as in Eq. (3), example) and modelling \(D(\varvec{s};{\phi })\) as a smooth function of function of spatial covariates. Providing that samplers span a range of these covariate values, separate estimation of and \(D(\varvec{s};{\phi })\) is possible , although confounding of the two functions is still possible. Confounding will manifest itself in analysis as a ridge in the likelihood. In conventional distance sampling, \((\varvec{s};{\phi })\) is assumed constant and in this case there is no confounding.
We can rewrite Eq. (5) as
where f(n) is a Poisson distribution and \(f(\varvec{s}_i{\mid }\delta _i=1)\) is the conditional distribution of the observed location \(\varvec{s}_i\), given that individual i was detected. This is the form in which CDS likelihoods appear in the DS literature (see Appendix), although more commonly with binomial rather than Poisson f(n) (see Buckland et al. 2016).
3.3 Distance sampling hybrid model
Most CDS estimators are not fully model-based, in that they do not involve a spatial point process model for the whole survey region. They typically assume uniform distribution in the vicinity of the samplers, i.e. within some specified distance W such that \(p(W;\varvec{\theta })>0\) (typically \(0.1\le p(W;\varvec{\theta })\le 0.15\)) and then use design-based inference to estimate density and abundance in the whole survey region, conditional on estimates within distance W of samplers. Buckland et al. (2004) refer to this as a “hybrid” model; see Buckland et al. (2001, 2004) for details.
4 Mark-recapture distance sampling
Mark-recapture distance sampling (MRDS) is distance sampling with more than one detector, with detectors acting independently. The logistic constraints imposed by having more than one detector at the same location (which usually means on the same survey boat, plane or other survey platform) are such that no more than two detectors are used (i.e., \(K=2\)) although in principle more could be used. “Recaptures” are detections of the same individual by both detectors. (They are usually called “duplicates” in the context of MRDS surveys.) Viewed from a CR perspective, MRDS surveys are two-occasion surveys, with detectors playing the role of occasion, individuals’ locations are individual random effects that affect capture probability, and \(D(\varvec{s};{\phi })/\int _\mathcal{A}D(\varvec{s};{\phi })\mathrm{d}\varvec{s}\) is the random effect distribution. The random effect is partially observed, insofar as individuals’ locations are observed for detected individuals but not undetected individuals. (This is also true for CDS models.)
MRDS surveys generate capture history data \(\varOmega _n\) (\(\varvec{\omega }_i\in \{(1,0), (0,1), (1,1)\}\) with \(K=2\) detectors; \(i=1,\ldots ,n\)). We assume that individuals are detected independently and we write the probability of observing capture history \(\varvec{\omega }_i\) as \({\mathbb {P}}(\varvec{\omega }_i;\varvec{\theta })\). A MRDS likelihood function is obtained by multiplying the CDS likelihood Eq. (5) by a capture–recapture probability component:
The MRDS likelihood is then as follows (for readability we usually omit the parameter vectors \({\phi }\) and \(\varvec{\theta }\) from the equations from now on):
If we also assume (as is commonly done) that detection of an individual by one observer is independent of its detection by another, and we let \(p_k(d(\varvec{s}_i))\) be the probability that observer k (\(k=1,2)\) detects individual i, then the probability of detecting individual i at all is \(p(d(\varvec{s}_i))=1-\prod _{k=1}^2\left[ 1-p_k(d(\varvec{s}_i))\right] \) and the capture history probability is
In this case, Eq. (7) is the conditional capture–recapture model of Alho (1990) and Huggins (1989), with \(d(\varvec{s})\) as an explanatory variable. Unlike CDS detection functions, MRDS and CR models typically use standard binary regression model forms for \(p_k(d(\varvec{s}))\) (most often logistic) and do not assume that \(p_k(0)=1\). Unlike CDS models, this does not result in confounding between \(D(\varvec{s}_i)\) (or N) and \(p_k(d(\varvec{s}))\), because \(p_k(d(\varvec{s}))\) is estimable from the conditional capture history likelihood Eq. (7) alone, as demonstrated by Alho (1990) and Huggins (1989).
By similar arguments to those used to show that CDS models are latent variable binary regression models, MRDS models are latent variable binary regression models, but with each subject having \(K=2\) regressions with the same explanatory variable (\(\varvec{s}_i\) for subject i).
5 Spatial capture–recapture methods
SCR surveys typically involve \(K>2\) detectors placed at different locations (unlike MRDS surveys which usually have \(K=2\) detectors at the same location, although the location can move over time). This might, for example, be an array of camera traps (which photograph animals as they pass), an array of microphones or hydrophones, or an array of traps of some sort. It is assumed that individuals can be recognised (by natural markings, acoustic signature, DNA, attached tag, or some other means) so that recaptures are identified as such. Like MRDS surveys, SCR surveys generate capture histories of length K, indicating detection or not at each detector. Unlike MRDS surveys, they most often also have capture histories through time at each detector. The capture history for individual i is \(\varvec{\omega }_i=(\omega _{i11},\ldots ,\omega _{i1K},\omega _{i21},\ldots ,\omega _{iJK})\), with \(\omega _{ijk}=1\) if the individual was detected on occasion j (of J occasions) by detector k (of K detectors), and \(\omega _{ijk}=0\) otherwise. Here j indexes discrete times (occasions). SCR models that use continuous time have also been developed (Borchers et al. 2014). We cover these briefly below, but begin by dealing with discrete occasions.
Having more detectors and more occasions than MRDS surveys, as SCR surveys do, requires only very minor extension of the MRDS survey models described above. When detections by each detector are independent, as with MRDS, Eq. (8) still applies, but with the following equation replacing Eq. (9):
where \(p_{jk}(d(\varvec{s}_i))\) is the probability of individual i being detected by detector k on occasion j.
The feature that really distinguishes SCR models from MRDS models is that on SCR surveys no locations of individuals are observed (remembering that when animals are detected wholly or partly because of their movement into the proximity of a detector, “location” refers to their activity centre, not the location at which they were detected): \(\varvec{s}_1,\ldots ,\varvec{s}_n\) are unknown. This makes inference a bit more difficult. From a Bayesian perspective, it adds \(\varvec{s}_1,\ldots ,\varvec{s}_n\) to the vector of parameters to be estimated (with \(D(\varvec{s})/\int _\mathcal{A}D(\varvec{s})\mathrm{d}\varvec{s}\) being regarded as an independent prior for each of \(\varvec{s}_1,\ldots ,\varvec{s}_n\), given n). From a frequentist perspective, it requires \(\varvec{S}_n\) to be integrated out of the likelihood:
The density function \(D(\varvec{s})\) is typically quite smooth in space, so that fast and accurate numerical integration is usually quite feasible.
5.1 SCR detection hazards and detection functions
Consider a point process in time in which the hazard of detection by detector k of an individual at \(\varvec{s}\) at time t on occasion j is \(h_{jk}(t,\varvec{s})\), and the integrated hazard is \(H_{jk}(\varvec{s})=\int _0^{T_j}h_{jk}(t,\varvec{s})\mathrm{d}t\), where \(T_j\) is the length of occasion j. Assuming independent detections over time, the \(m_{ijk}\) times that individual i is detected at detector k on occasion j (contained in the vector \(\varvec{t}_{ijk}=(t_{ijk1},\ldots ,t_{ijkm_{ijk}})\)) can be modelled as a temporal Poisson process:
from which it follows that the probability that individual i is detected at all by detector k on the occasion is \(1-f_m(\varvec{0}{\mid }\varvec{s}_i)\), where \(\varvec{0}\) represents a zero capture history, i.e. the capture history of an individual that is missed altogether, and for which \(m_{ijk}=0\)):
If \(H_{jk}(\varvec{s}_i)\) is modelled as a half-normal function of \(d(\varvec{s}_i)\): \(H_{jk}(\varvec{s}_i) =e^{\theta _{0jk}-\theta _{djk}d(\varvec{s}_i)^2}\) (with \(\theta _{djk}=1/(2\sigma _{jk}^2)\)), then Eq. (13) has complimentary log–log form with linear predictor \(\theta _{0jk}-\theta _{djk}d(\varvec{s}_i)^2\).
The probability of detector k not detecting individual i on occasion j is the survival function \(S_{ijk}(\varvec{s})=e^{-H_{ijk}(\varvec{s})}\).
Not all SCR detection function models are formulated in terms of detection hazards, but formulating them in this way does provide a versatile framework for dealing with all kinds of SCR data, as we will see in the next section. And any detection function can be reformulated in terms of integrated hazards. For example, the half-normal detection function of Eq. (3) is quite commonly used in SCR models, albeit with an intercept term, \(g_0\), that may be less than 1: \(p_{jk}(d(\varvec{s}_i))=g_0\exp \left\{ -d^2/2\sigma ^2\right\} \). If we define a cumulative hazard as \(H_{jk}(\varvec{s}_i)=-\log (1-g_0\exp \left\{ -d^2/2\sigma ^2\right\} )\), then Eq. (13) is \(g_0\exp \left\{ -d^2/2\sigma ^2\right\} \).
5.2 SCR detection and capture models
Binary capture histories of the sort dealt with thus far are not the only possible kind of capture histories that arise from SCR surveys. Some kinds of detector (camera traps being an example) record not only whether or not an individual is detected on an occasion, but also how many times it is detected. In this case, the response variable is a count: the number of times individual i is detected on occasion j by detector k. Some kinds of detector (camera traps again being a good example), record not only the number of times that an individual is detected on each occasion but the times of each detection. And when detectors are actual traps that detain individuals until the surveyor releases them, the response is binary and the appropriate probability model depends on whether or not traps are taken out of action when they catch an individual. We consider each of these cases below:
-
Binary detection data This is the case in which the response is the binary random variable \(\omega _{ijk}\) and detection does not involve catching the individual, so that detections by different detectors within occasions are independent. \({\mathbb {P}}(\varvec{\omega }_i{\mid }\varvec{s}_i)\) is as in Eq. (10). Detection of individuals by hair snags (Efford et al. 2008 for example) is an example of detectors that necessarily generate binary data. In this case, individual identification is by DNA matching.
-
Binary capture data The response is again the binary random variable \(\omega _{ijk}\) but because detection involves trapping and holding the individual, detections by different detectors within occasions are not independent: when an individual is caught in one trap on any occasion, it cannot be caught in any other trap within that occasion. We need to distinguish further between “single-catch” traps and “multi-catch” traps. The former are taken out of action as soon as an individual is caught (snap traps are an example) (see Efford et al. 2008), the latter have nominally infinite capacity (mist nets are an example, see Borchers and Efford 2008).
In the case of multi-catch traps, we can model the detection process as a competing risks survival model, where “death” corresponds to capture, and traps “compete” to catch individuals. In this case
$$\begin{aligned} {\mathbb {P}}(\varvec{\omega }_i{\mid }\varvec{s}_i)= & {} \prod _{j=1}^J S_j(\varvec{s}_i)^{1-\sum _k\omega _{ijk}} \prod _{k=1}^K \left[ \frac{H_{jk}(\varvec{s}_i)}{H_{j\cdot }(\varvec{s}_i)} p_{j}(d(\varvec{s}_i)) \right] ^{\omega _{ijk}}, \end{aligned}$$(14)where \(H_{jk}(\varvec{s}_i)\) is the integrated hazard of detection (see Sect. 5.1) and \(H_{j\cdot }(\varvec{s}_i)=\sum _{k=1}^KH_{jk}(\varvec{s}_i)\). (Note that only one of \(\omega _{ij1},\ldots ,\omega _{ijK}\) can be non-zero because an individual can only be caught in one trap on any one occasion.)
Unlike SCR models with binary detection data or MRDS models, the SCR model for multi-catch trap data can not be viewed as a binary regression model with latent variables, because Eq. (14) is not a binary regression model. It could be viewed as a survival model with latent variables \(\varvec{S}_n\), an unknown number of right-censored subjects (the undetected individuals) and unknown times of death (capture times). And if the integrated hazard is modelled using a half-normal shape, as in Eq. (13), it is a survival model with complimentary log–log link function.
In the case of single-catch traps, traps “compete” to catch individuals and as soon as a trap does catch an individual, it is taken out of action. A computationally tractable expression for the probability of the observations from single-catch traps remains to be developed. Efford (2004) developed a simulation-based inverse prediction method that is currently the only method that is able to deal explicitly with this case. Multi-catch estimation methods have been shown to perform well when used with single-catch traps, providing that trap saturation (the proportion of traps taken out of action by catching individuals) is not very high (see Efford et al. 2008).
-
Count detection data This is the case in which the response variable is a count: \(m_{ijk}\in \{0,1,\ldots ,\infty \}\) is the number of times individual i was detected on occasion j by detector k. Detection does not involve catching the individual, so that detections by different detectors within occasions are independent (given \(\varvec{s})\). The Poisson distribution, \(f_m(m_{ijk})\) of Eq. (12) was proposed by Royle et al. (2009) for modelling \(m_{ijk}\), and it is to date the only model that has been used, although overdispersed count models have been suggested. With this model, \({\mathbb {P}}(\varvec{\omega }_i{\mid }\varvec{s}_i)\) in Eq. (11) is replaced by
$$\begin{aligned} {\mathbb {P}}(\varvec{m}_i{\mid }\varvec{s}_i)= & {} \prod _{j=1}^J\prod _{k=1}^K \frac{H_{ijk}(\varvec{s})^{m_{ijk}}e^{-H_{ijk}(\varvec{s})}}{m_{ijk}!}, \end{aligned}$$(15)where \(\varvec{m}_i=(m_{i11},\ldots ,m_{i1K},m_{i21},\ldots ,m_{iJK})\). This is a Poisson regression model in which the number of subjects (n) is itself a Poisson random variable and subjects have latent random variables \(\varvec{S}_n\) that are governed by the spatial NHPP.
-
Time of detection data SCR models with detection time as response were proposed by Borchers et al. (2014). In this case, the response is a vector of detection times \(\varvec{t}_i=(\varvec{t}_{i11},\ldots ,\varvec{t}_{i1K},\varvec{t}_{i21},\ldots ,\varvec{t}_{iJK})\) for individual i, where \(\varvec{t}_{ijk}=(t_{ijk1},\ldots ,t_{ijkm_{ijk}})\). In this case, \({\mathbb {P}}(\varvec{\omega }_i{\mid }\varvec{s}_i)\) of Eq. (11) is replaced by
$$\begin{aligned} f_{t_i}(\varvec{t}_i{\mid }\varvec{s}_i)= & {} \prod _{j=1}^J\prod _{k=1}^Kf_{t_{ijk}}(\varvec{t}_{ijk}{\mid }\varvec{s}_i) \nonumber \\= & {} \prod _{j=1}^J\prod _{k=1}^K\left( e^{-H_{jk}(\varvec{s}_i)}\prod _{m=1}^R h_{jk}(t_{ijkm},\varvec{s}_i)\right) \end{aligned}$$(16)where \(f_{t_{ijk}}(\varvec{t}_i{\mid }\varvec{s}_i)\) is given by Eq. (12). This is a temporal Poisson process regression model with latent regressor variable \(\varvec{s}_i\) for process i, and the number n of processes is a Poisson random variable.
6 More complex SCR models
The above development covers the basic DS, MRDS and SCR models for closed populations (i.e. without birth, death, immigration or emigration). These methods can be extended in a number of ways (see below), including incorporating additional covariates in the spatial model, incorporating covariates and random effects in the observation model, incorporating additional data on individuals’ locations, dealing with situations in which not all individuals are identifiable, and incorporating population dynamics and movement.
6.1 Extending the point process model
Although Borchers and Efford (2008) developed the analytic framework for modelling locations using a NHPP, almost all published analyses use a homogeneous Poisson process model (or if treating N as a parameter, a homogeneous binomial point process model) for locations, largely because it was not obvious how to implement a NHPP model with a sufficiently flexible intensity function \(D(\varvec{s})\). Borchers and Kidney (2014) proposed using regression splines to model \(D(\varvec{s})\) in a flexible way and this method is implemented in Efford (2010). It allows spatial covariates to be included as explanatory variables in the intensity function (as well as covariates that are not spatially referenced).
Reich and Gardner (2014) developed a point process model applicable with territorial animals using a Strauss process (in which points tend to repel one another), but with a constant intensity throughout the survey region.
6.2 Extending the observation model
Detection probability models have been extended in a number of ways, the simplest of which is incorporating covariates into the detection function, or detection hazard function. There are many ways of doing this. One that will be familiar to statisticians is to extend the linear predictor of the complimentary log–log model to include observed covariates (if the complimentary log–log model is used). In a similar vein, the cumulative hazard of a Poisson observation model for count data or the detection hazard for detection time models (see Sect. 5.2) can be made to depend on covariates through a log link function. If the detection function is not formulated using detection hazards, the \(g_0\) parameter (see Sect. 5.1) or the range or scale parameter (\(\sigma \) with a half-normal detection function form) can be made to depend on covariates (the former with a logit link function, the latter with a log link function).
Unobserved latent variables or random effects other than \(\varvec{s}\) can be included in similar ways. For example, Borchers and Efford (2008) incorporated the finite mixture model of Pledger (2000) in SCR models. Probability density or mass functions for the latent variables or random effects must obviously be introduced for all latent variables. Frequentist inference methods require marginalising over the latent variables or random effects, which can become difficult. Bayesian methods deal with additional latent variables and random effects seamlessly.
In some cases latent variables are partially observed. The sex of individuals is an example. Royle et al. (2015) and Efford (2010) developed methods for this case.
While not strictly an extension of the basic methods described above, being rather an illustration of the utility of the detection hazard formulation, Efford et al. (2013) demonstrate how detection function models parameterised in terms of detection hazards can accommodate covariates quantifying detection effort. By doing so they are able to explicitly and parsimoniously model detection probability on surveys in which detectors operate for different lengths of time.
6.2.1 Modelling movement
In applications using detectors such as camera traps, in which individuals are detected by virtue of movement that results in encounters with detectors, data from time series of observed locations from telemetry data obtained from a sample of tagged animals can be used to inform the detection probability model (see Sollmann et al. 2013a, b, for example).
Royle et al. (2013b) proposed a model that incorporates both telemetry and camera trap data. Aspects of the model relating to inferences about resource selection (rather than incorporation of the telemetry data per se) were criticized by Efford (2014) because the detection function model and resource selection models used were not consistent with one another.
Royle et al. (2013b) and Sutherland et al. (2014) developed a detection function model that allows detection probability to depend on a least-cost distance (“ecological distance”) rather than the more usual Euclidian distance from individuals’ locations to detectors. The cost is parameterised as a function of habitat (some habitats having lower costs for movement of individuals than others) and allows the cost function to be estimated simultaneously with other SCR model parameters. In addition to providing a flexible way of modelling habitat-dependent movement, the model is useful for drawing inferences about how individuals move through heterogeneous habitats, and hence about landscape connectivity. An example of an application of the ecological distance detection probability model can be found in Fuller et al. (2016).
Royle et al. (2016) developed and tested by simulation models that allow some animals’ activity centres to move in the course of the survey. They found that estimators of abundance that assume stationary activity centres remained approximately unbiased in this case but that detection function parameters were biased, and cautioned against over-interpretation of detection function parameters.
6.2.2 Alternative \(p(\varvec{s})\) forms
Efford and Mowat (2014) and Efford et al. (2015) suggest two forms of re-parameterised half-normal detection function models, motivated in the first case by the fact that the range and the intercept of detection functions tend to be negatively correlated when individuals are detected by virtue of their movement (if they move a lot, the range increases and the intercept decreases, and vice-versa) and in the second case by the fact that individuals’ territory sizes tend to be smaller when density is higher.
Efford et al. (2009) and Stevenson et al. (2015) proposed detection function forms specifically for acoustic surveys, which implicity model the loss in acoustic signal strength with distance from source.
6.3 Supplementary location data
Received signal strength on an acoustic SCR survey is an example of supplementary data (i.e. an observed response other than capture history) that is informative about location: the weaker the received signal strength, the farther away the source is likely to be. Efford et al. (2009), Borchers et al. (2015) and Stevenson et al. (2015) develop SCR models that use received signal strength to improve inference.
There are other supplementary location data sources on acoustic surveys too. These include exact times of arrival of acoustic signals at detectors (the signal arrives earlier at those closer to the source) and estimates of angles to source and/or distance to source when human listeners or sonobuoyes are the detectors. Borchers et al. (2015) and Stevenson et al. (2015) showed that these can reduce bias and increase precision substantially on acoustic SCR surveys.
A common problem with acoustic SCR data is uncertain recapture identification. A similar problem arises with non-invasive genetic data when there is partial identity or in camera trapping data when recapture is difficult to ascertain if only one side of an individual is detected on the camera initially and the opposite side for the recapture. While in the case of acoustic surveys, it may not be difficult to identify received signals at different detectors as the same vocalization, it is often difficult to identify different vocalizations from the same individual as such. Supplementary location data should help resolve this problem (as the more we know about the location of the sound source, the less uncertainty there is about recapture identity) but as yet no method has been developed to do this.
6.4 Unmarked individuals
Chandler and Royle (2013) developed a method without capture histories but the quality of inferences from this method is poor. They also considered situations in which only a fraction of the population is marked, which leads to much more reliable inference. This method is likely to be very useful for many camera trap datasets in which a fraction of a population of individuals that are otherwise not individually identifiable, can be marked. Sollmann et al. (2013a) and Sollmann et al. (2013b) extended this method to accommodate a tagged sample with telemetry data.
6.5 Open population models
Two kinds of open population model with SCR have been developed. The first involves estimation of population trajectory by modelling temporal trend in \(D(\varvec{s})\) using some smooth function, without explicitly modelling demographic parameters driving the trend. This approach with monotonic temporal trend was developed by Borchers and Efford (2008) and extended to model trend using regression splines by Borchers and Kidney (2014).
Open population models in which birth, death and movement are modelled at the individual level have been developed by Gardner et al. (2010), Royle et al. (2013a), Ergon and Gardner (2014) and Sollmann et al. (2015). Schaub and Royle (2013) develop a similar model to that of Ergon and Gardner (2014) but estimate only movement and survival of a marked subset of the population. Aside from Ergon and Gardner (2014) and Schaub and Royle (2013), these models assume either that individuals’ activity centres do not change over time, or that they are independently located across time. Ergon and Gardner (2014) and Schaub and Royle (2013) model individual movement over time as a dispersal process.
7 Discussion
We have tried to present an overview of SCR methods for statisticians who are unfamiliar with methods in statistical ecology, starting from distance sampling methods (a spatial sampling method in which individuals are observed) and showing how the addition of capture–recapture data and then the loss of observed locations leads to SCR methods. In doing this we have focussed on SCR models and how they relate to some models in mainstream (non-ecological) statistics, and this has been at the cost of not describing of how SCR is applied in practice.
For example, we have not covered survey design issues, which is an important area in which relatively little research has been done. And the only detectors we have mentioned are detectors like camera traps, snap traps, microphones and other detectors that are effectively points in space, but SCR methods also accommodate detectors that span areas or transects (see Royle and Young 2008; Royle et al. 2011; Efford 2011). We have also not had space to illustrate the many and various applications of SCR to wildlife populations
We have only touched in passing on inference methods. While the first SCR method was frequentist (the inverse prediction method of Efford 2004), the first methods with explicit likelihood functions were developed simultaneously for Bayesian (Royle and Young 2008) and frequentist (Borchers and Efford 2008) inference methods. The two approaches have developed in parallel since then and it is largely a matter of the preference of the analyst that leads to one or the other approach being used. Frequentist inference tends to be faster, because the data augmentation Markov chain Monte Carlo methods implemented for Bayesian inference can be much more computationally demanding. This may change with the advent of a more efficient Bayesian method by King et al. (2016). Bayesian methods are more easily able to deal with open population models in which there is temporal dependence in the state of the population, with situations in which only a fraction of the population is marked, and in which there is spatial correlation in individuals’ locations. Indeed the only current methods for dealing with these cases are Bayesian.
SCR methods are relatively new and growing fast (see Royle et al. 2013a). We are only beginning to appreciate and explore the possibilities that the extension of capture–recapture into spatial dimensions provides, and this is a field of research ripe for innovative method development by applied statisticians. Areas of likely future development include more sophisticated spatial and spatio-temporal modelling of individuals’ locations for closed and open populations, new methods for integrating spatial capture–recapture and other kinds of ecological survey data, and methods of dealing with recapture uncertainty.
References
Alho, J.M.: Logistic regression in capture–recapture models. Biometrics 46, 623–635 (1990)
Borchers, D.L., Efford, M.G.: Spatially explicit maximum likelihood methods for capture–recapture studies. Biometrics 64, 377–385 (2008)
Borchers, D.L., Kidney, D.: Flexible density surface estimation for spatially explicit capture–recapture surveys. Technical report, University of St Andrews (2014)
Borchers, D.L., Zucchini, W., Fewster, R.: Mark-recapture models for line transect surveys. Biometrics 54, 1207–1220 (1998)
Borchers, D.L., Distiller, G., Foster, R., Harmsen, B., Milazzo, L.: Continuous-time spatially explicit capture–recapture models, with an application to a jaguar camera-trap survey. Methods Ecol. Evol. 5, 656–665 (2014)
Borchers, D.L., Stevenson, B.C., Kidney, D., Thomas, L., Marques, T.A.: A unifying model for capture–recapture and distance sampling. J. Am. Stat. Assoc. 201, 195–204 (2015)
Buckland, S., Oedekoven, C., Borchers, D.: Model-based distance sampling. J. Agric. Biol. Environ. Stat. 21, 58–75 (2016)
Buckland, S.T.: Fitting density functions with polynomials. Appl. Stat. 41, 63–76 (1992)
Buckland, S.T., Anderson, D.R., Burnham, K.P., Laake, J.L., Borchers, D.L., Thomas, L.: Introduction to Distance Sampling: Estimating Abundance of Biological Populations. Oxford University Press, Oxford (2001)
Buckland, S.T., Anderson, D.R., Burnham, K.P., Laake, J.L., Borchers, D.L., Thomas, L.: Advanced Distance Sampling. Oxford University Press, Oxford (2004)
Chandler, R.B., Royle, J.A.: Spatially explicit models for inference about density in unmarked or partially marked populations. Ann. Appl. Stat. 7, 936–954 (2013)
Currey, R.J.C., Rowe, L.E., Dawson, S.M.: Abundance and demography of bottlenose dolphins in Dusky Sound, New Zealand, inferred from dorsal fin photographs. N. Z. J. Mar. Freshw. Res. 42, 439–449 (2008)
Efford, M.: secr: Spatially Explicit Capture–Recapture in R. R package version, vol. 1, no. (4) (2010)
Efford, M.: Estimation of population density by spatially explicit capture–recapture analysis of data from area searches. Ecology 92, 2202–2207 (2011)
Efford, M., Borchers, D., Mowat, G.: Varying effort in capture–recapture studies. Methods Ecol. Evol. 4, 629–636 (2013)
Efford, M., Dawson, D.K., Jhala, Y., Qureshi, Q.: Density-dependent home-range size revealed by spatially explicit capture–recapture. Ecography 38, 1–13 (2015)
Efford, M.G.: Density estimation in live-trapping studies. Oikos 106, 598–610 (2004)
Efford, M.G.: Bias from heterogeneous usage of space in spatially explicit capture–recapture analyses. Methods Ecol. Evol. 5, 599–602 (2014)
Efford, M.G., Fewster, R.M.: Estimating population size by spatially explicit capture–recapture. Oikos 122, 918–928 (2013)
Efford, M.G., Mowat, G.: Compensatory heterogeneity in spatially explicit capture–recapture data. Ecology 95, 1341–1348 (2014)
Efford, M.G., Borchers, D.L., Byrom, A.E.: Modeling Demographic Processes in Marked Populations, chapter Density estimation by spatially explicit capture-recapture: likelihood-based methods. Environmental and Ecological Statistics. Springer, New York (2008)
Efford, M.G., Dawson, D.K., Borchers, D.L.: Population density estimated from locations of individuals on a passive detector array. Ecology 90, 2676–2682 (2009)
Ergon, T., Gardner, B.: Separating mortality and emigration: modelling space use, dispersal and survival with robust-design spatial capture-recapture data. Methods Ecol. Evol. 5, 1327–1336 (2014)
Fuller, A.K., Sutherland, C.S., Royle, A.J., Hare, M.P.: Estimating population density and connectivity of American mink using spatial capture–recapture. Ecol. Appl. 26, 1125–1135 (2016)
Gardner, B., Reppucci, J., Lucherini, M., Royle, J.A.: Spatially explicit inference for open populations: estimating demographic parameters from camera-trap studies. Ecology 91, 3376–3383 (2010)
Hayes, R.J., Buckland, S.T.: Radial-distance models for the line-transect method. Biometrics 39, 29–42 (1983)
Huggins, R.M.: On the statistical analysis of capture experiments. Biometrika 76, 133–140 (1989)
Illian, J., Penttinen, A., Stoyan, H., Stoyan, D.: Statistical Analysis and Modelling of Spatial Point Patterns. Wiley, New York (2009)
Johnson, D.S., Laake, J.L., Ver Hoef, J.M.: A model-based approach for making ecological inference from distance sampling data. Biometrics 66, 310–318 (2010)
Kellner, K.F., Swihart, R.K.: Accounting for imperfect detection in ecology: a quantitative review. PLoS One 9, e111436 (2014)
King, R., McClintock, B., Kidney, D., Borchers, D.: Capture-recapture abundance estimation using a semi-complete data likelihood approach. Ann. Appl. Stat. 10, 264–285 (2016)
Otis, D.L., Burnham, K.P., White, G.C., Anderson, D.R.: Statistical inference from capture data on closed animal populations. Wildl. Monogr. 62, 1–135 (1978)
Pledger, S.: Unified maximum likelihood estimates for closed capture-recapture models using mixtures. Biometrics 56, 434–442 (2000)
Puechmaille, S.J., Petit, E.J.: Empirical evaluation of non-invasive capture-mark–recapture estimation of population size based on a single sampling session. J. Appl. Ecol. 44, 843–852 (2007)
Reich, B., Gardner, B.: A spatial capture–recapture model for territorial species. Environmetrics 25, 630–637 (2014)
Rich, L.N., Kelly, M.J., Sollmann, R., Noss, A.J., Maffei, L., Arispe, R.L., Paviolo, A., De Angelo, C.D., Di Blanco, Y.E., Di Bitetti, M.S.: Comparing capture–recapture, mark-resight, and spatial mark-resight models for estimating puma densities via camera traps. J. Mammal. 95, 382–391 (2014)
Royle, J.A., Young, K.V.: A hierarchical model for spatial capture–recapture data. Ecology 89, 2281–2289 (2008)
Royle, J.A., Karanth, K.U., Gopalaswamy, A.M., Kumar, N.S.: Bayesian inference in camera trapping studies for a class of spatial capture–recapture models. Ecology 90, 3233–3244 (2009)
Royle, J.A., Kéry, M., Guilat, J.: Spatial capture–recapture models for search-encounter data. Methods Ecol. Evol. 2, 602–611 (2011)
Royle, J.A., Chandler, R.B., Sollmann, R., Gardner, B.: Spatial Capture–Recapture. Academic Press, Oxford (2013a)
Royle, J.A., Chandler, R.B., Gazenski, K.D., Graves, T.A.: Spatial capture–recapture models for jointly estimating population density and landscape connectivity. Ecology 94, 287–294 (2013b)
Royle, J.A., Sutherland, C., Fuller, A.K., Sun, C.C.: Likelihood analysis of spatial capture–recapture models for stratified or class structured populations. Ecosphere 6, 1–11 (2015)
Royle, J.A., Fuller, A.K., Sutherland, C.: Spatial capture–recapture models allowing Markovian transience or dispersal. Popul. Ecol. 58, 53–62 (2016)
Schaub, M., Royle, J.A.: Estimating true instead of apparent survival using spatial Cormack–Jolly–Seber models. Methods Ecol. Evol. 5, 1316–1326 (2013)
Sollmann, R., Gardner, B., Parsons, A.W., Stocking, J.J., McClintock, B.T., Simons, T.R., Pollock, K.H., O’Connell, A.F.: A spatial mark-resight model augmented with telemetry data. Ecology 94, 553–559 (2013a)
Sollmann, R., Gardner, B., Chandler, R.B., Shindle, D.B., Onorato, D.P., Royle, J.A., O’Connell, A.F.: Using multiple data sources provides density estimates for endangered Florida panther. J. Appl. Ecol. 50, 961–968 (2013b)
Sollmann, R., Gardner, B., Chandler, R.B., Royle, J.A., Sillett, T.S.: An open population hierarchical distance sampling model. Ecology 96, 325–331 (2015)
Stevenson, B.C., Borchers, D.L., Altwegg, R., Swift, R.J., Gillespie, D.M., Measey, G.J.: A general framework for animal density estimation from acoustic detections across a fixed microphone array. Methods Ecol. Evol. 6, 38–48 (2015)
Sutherland, C., Fuller, A.K., Royle, J.A.: Modelling non-Euclidean movement and landscape connectivity in highly structured ecological networks. Methods Ecol, Evol (2014)
Williams, B.K., Nichols, J.D., Conroy, M.J.: Analysis and Management of Animal Populations. Academic Press, San Diego, California (2002)
Acknowledgements
TAM thanks support by CEAUL (funded by FCT—Fundação para a Ciência e a Tecnologia, Portugal, through the Project UID/MAT/00006/2013).
Author information
Authors and Affiliations
Corresponding author
Appendix: Distance sampling models
Appendix: Distance sampling models
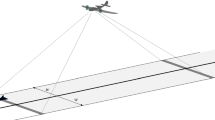
As noted in Sect. 3.3, DS methods are usually model-based only within distance W of samplers, relying on design-based methods to draw inferences beyond W. And most DS methods assume uniform distribution of individuals with distance W. In this case, the pdf of individuals’ locations within the searched region is \(D(\varvec{s};{\phi })=1/(\pi W^2)\) for point transect surveys (when a circle of radius W is searched—see Fig. 1) and \(D(\varvec{s};{\phi })=1/(2WL)\) for line line transect surveys (when a rectangle with sides L and 2W is searched—see Fig. 1).
Point transect (left) and line transect (right) survey schematics. With point transects, a circle of radius W is searched, while with line transects a rectangle of width W and length L is searched by transiting the line up its centre. The coordinate system is centred on the observer, at the solid circle. The figures show coordinates for an individual detected at Cartesian coordinates (x, y)
If we write \(\varvec{s}\) in terms of Cartesian coordinates (x, y) and transform from Cartesian to polar coordinates for the point transect case: \(r=\sqrt{x^2+y^2}, \theta =\tan ^{-1}(y/x)\) and \(x=r\sin (\theta ), y=r\cos (\theta )\), with Jacobian =\(-1\), and then marginalise over \(\theta \), we get \(D(r)=2r/W^2\).
In the case of point transect surveys, detection probability is modelled as a function of radial distance only, so that \(p(d(\varvec{s}_i);\varvec{\theta })=p(r_i;\varvec{\theta })\). In the case of line transect surveys, detection probability is modelled as a function of perpendicular distance only, so that \(p(d(\varvec{s}_i);\varvec{\theta })=p(x_i;\varvec{\theta })\). Inference is usually based only on \(r_i\) for point transects and \(x_i\) for line transects (\(i=1,\ldots ,n\)), so that we use \(f(r_i{\mid },\delta _i=1)\) and \(f(x_i{\mid },\delta _i=1)\) in place of \(f(\varvec{s}_i{\mid },\delta _i=1)\). These are obtained using \(D(\varvec{s};{\phi })=1/(\pi W^2)\) and integrating out \(\theta \) for point transects and using \(D(\varvec{s};{\phi })=1/(2WL)\) and integrating out y for line transects, as follows:
These are the forms found in the conventional distance sampling literature.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Borchers, D.L., Marques, T.A. From distance sampling to spatial capture–recapture. AStA Adv Stat Anal 101, 475–494 (2017). https://doi.org/10.1007/s10182-016-0287-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10182-016-0287-7