Abstract
Theory shows that polyandry (mating with multiple males within a reproductive season) works as bet-hedging to increase the geometric mean fitness (GMF) of polyandrous genotype over generations and avoid extinction but it was rarely tested empirically. In this study, we distributed the eggs of Gryllus bimaculatus females mated with 1–4 males (mating treatment) into 4 petri dishes with different conditions: 25 °C/fresh water, 37 °C/fresh water, 25 °C/salt water, 37 °C/salt water, simulating 4 clutches laid at the different sites are suffered environmental change. The egg hatching rate was obtained over 7 blocks with different females for each mating treatment. In general, significantly more eggs hatched in 25 °C than 37 °C and in fresh water than salt water. The reproductive failure (no hatched eggs per petri dish) frequently occurred in monandry and 2-male polyandry. Next, we considered 7 blocks as the successive 7 virtual generations and calculated the within-generation arithmetic mean fitness (AMF) among females of the same treatment and the between-generation GMF of the AMF across 7 generations. Randomization test shows that the GMF of 3- and 4-male polyandry were significantly higher than monandry. This study shows that the risk from mating only once can be avoided by polyandrous mating as bet-hedging.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In general, male fitness is positively correlated with the number of mates that he acquires, and thus, the adaptive significance of male multiple mating (polygyny) is easily understandable (Thornhill and Alcock 1983; Shuker and Simmons 2014; Simmons 2019). However, the relationship between female fitness and her mating frequency is not straightforward (Bateman 1948; Tang-Martínez 2019) because female multiple mating with different males (polyandry) or sometimes repeated matings with the same male seem unnecessary to secure fertilization of the limited number of eggs and often costly (e.g. loss of energy and time, predation and infection risks; Birkhead and Møller 1992; Arnqvist and Rowe 2005). Thus, the causes and consequences of polyandry have stimulated many researchers as an unsolved enigma in evolutionary biology (Walker 1980; Thornhill and Alcock 1983; Birkhead and Møller 1992; Yasui 1997, 1998, 2001; Arnqvist and Nilsson 2000; Simmons 2005; Jennions and Petrie 2007; Garcia-Gonzalez et al. 2015; Yasui and Garcia-Gonzalez 2016; Yasui and Yoshimura 2018).
The reasons that females mate with more than one male are classified into (1) female benefit, in which females obtain some benefits from males, which are larger than the remating cost (Thornhill and Alcock 1983; Birkhead and Møller 1992; Arnqvist and Nilsson 2000) and (2) female coercion, in which females are coerced superfluous copulation by males (Arnqvist and Rowe 2005). From the female viewpoint, (1) is adaptive but (2) is maladaptive explanation. Among the adaptive hypotheses, direct or environmental benefits (e.g., replenishment of sperm supply, nutritional nuptial gift, paternal care of offspring and protection against predators or sexual harassment from other males; Arnqvist and Nilsson 2000) are convincing because the cost for females are paid within generation (Yasui 1998). However, in the species lacking obvious direct benefits, indirect or genetic benefits (e.g., acquisition of good or compatible genes and genetic diversity among offspring; Yasui 1998; Jennions and Petrie 2007) are supposed. Despite several theoretical models (Curtsinger 1991; Yasui 1997, 1998, 2001; Yasui and Garcia-Gonzalez 2016; Yasui and Yoshimura 2018) showed that genetic benefits are possible, they remain still controversial because the sufficient return at the offspring generations is difficult to detect empirically in many cases (Yasui 1998; Jennions and Petrie 2007).
Female multiple mating can be understood as a form of non-simultaneous female mate choice and the problem for the females mating multiply is the uncertainty of information regarding male quality (Yasui 1998, 2001). For a given female, population would contain “unsuitable males”, which cause the total reproductive failure as a result for various reasons (Sheldon 1994; Palumbi 1999; Tregenza and Wedell 2000; Preston et al. 2001; Wedell et al. 2002; García-González 2004; Hasson and Stone 2009; Rhainds 2010; Tyler and Tregenza 2013; Forbes 2014; Greenway et al. 2015; Greenway and Shuker 2015; Balfour et al. 2020). The males may have unsuitable genetic factors such as intrinsically bad genes, deleterious mutations or incompatible genetic element (Tregenza and Wedell 2000). More importantly, even in any high genetic quality males, accidental mating failure is always possible (García-González 2004; Tyler and Tregenza 2013; Balfour et al. 2020). If genital coupling normally occurs, sperm transfer is not necessarily successful (Tyler and Tregenza 2013). The male may temporally deplete sperm store and some damage or disease on his copulatory organ may disturb normal ejaculation (Sheldon 1994; Preston et al. 2001; Wedell et al. 2002). Moreover, under the sexual conflict (Arnqvist and Rowe 2005), such defective males would conceal their low quality and mating failure from females, so that the females possibly cannot detect infertile mating even after its occurrence (Yasui and Garcia-Gonzalez 2016; Yasui and Yoshimura 2018). If these females have mated only once, they cannot leave offspring at all.
In such situations, indiscriminative polyandry can operate as bet-hedging, in which females spread the risk of reproductive failure over multiple males (Yasui and Garcia-Gonzalez 2016). When the bad male frequency in population or the occurrence probability of mating failure is p (1 ≥ p ≥ 0) and females mate with n males, the probability that all n males mating to a female fail is pn. Thus, even if 1/5 of males are infertile, the females to mate with 4 males (supposing even paternity share) can greatly decrease the total reproductive failure to 0.24 = 0.0016. In large populations these benefits arising from sampling more males are not likely to drive higher mating frequencies but that theory shows that bet-hedging polyandry effectively works in small female populations or small subpopulations in the structured metapopulations (for the rationale see Yasui and Garcia-Gonzalez 2016).
In the life-history evolutionary theory, bet-hedging traits such as egg dispersal, seed dormancy and iteroparity are the adaptations against unpredictable environmental fluctuation (Cohen 1966; Slatkin 1974; Gillespie 1977; Philippi and Seger 1989; Sterns 1992; Alekseev and Lampert 2001). In the context of female mating strategy of insects such as crickets laying eggs in the soil, if hatching environments of eggs (e.g., temperature, salinity or pH of the soil) changed after oviposition, polyandrous strategy may help to cope with the unpredictable changes by producing genetically or phenotypically diverse offspring (Yasui 1998) in addition to the insurance against male-caused reproductive failures.
In this study, we tested the bet-hedging polyandry hypothesis using the field cricket Gryllus bimaculatus. In this study, we intended to incorporate any possible accidents into the results: such as the change of salt concentration among blocks, the fewer number of eggs laid by some females, age variance, male’s mating experience and empty spermatophore (nonsperm representation in García-González 2004; Balfour et al. 2020), etc. Females face these potential threats of reproductive failures. In our experiment, females mated with 1–4 males (1 mating in each pair, thus monandry means single mating) and the eggs were allocated to good or bad hatching conditions. The egg hatching rate was compared among monandry, 2-, 3- and 4-male polyandry.
Materials and methods
Insects
Two strains of laboratory cultures of Gryllus bimaculatus were used in the experiments. One was a wild-type (black eye: B) population which was pooled from multiple sources such as a long-term mass rearing culture (being sold as prey of reptile pets) and wild-caught individuals in Ishigaki island (Okinawa Prefecture, Japan). The other was a white-eye mutant strain (W) that shows recessive inheritance against black eye (i.e., the hybrid BW expresses black eye). Each stock culture was maintained in a plastic container (L41 × W32 × H24 cm) under room temperature (ca. 25 °C) and natural photoperiod. The containers were partially heated by a bottom heater plate in winter season. The crickets were fed with Koi-fish (carp) food and water ad libitum.
Virgin females of W morph were obtained by the sexing and isolation at the final instar nymphal stage. Seven- to 14-day-old virgin females were used in pairing. Natural male population of such highly promiscuous species as G. bimaculatus contains individuals of various ages, conditions and mating experiences. Most males would be non-virgin, which exhaust more or less sperm stores and may be suffered injuries on genital organs compared to newly emerged virgin males. If only virgin males are used in mating experiments, the male condition may bias the results (about the overestimation of the benefits that females receive from multiple virgin males, see Wilson and Tomkins 2014). In this study, because we expect that females encounter males with various qualities/conditions and indiscriminately mate with them, the experimental males were randomly chosen from the stock cultures.
Mating experiments
Table 1 shows an example of the pairing. We set the four mating treatments (monandry, 2-male polyandry, 3-male polyandry and 4-male polyandry (hereafter abbreviated as M, 2P, 3P and 4P) as the different female strategies (virtual genotypes). Single block consisted of several virgin females (W) and a dozen or so males (B and W) (Table 1). In each block, the mating order of females and males was randomized to avoid possible systematic bias: for example, if every block starts by monandrous mating, it follows that younger females tend to be allocated to monandry treatment and if the B males are always used as the first mating role, higher paternity of B morph and that of the first mating male cannot be discriminated. Pairing was carried out in a plastic container (L150 × W90 × H130 mm). In cricket copulation, males attach a spermatophore outside the female genital opening (Simmons 1986). Then, sperm move from spermatophore to female spermatheca via narrow tube (Simmons 1986). The number of sperm transferred is positively correlated with the duration of spermatophore attachment and the sufficient transfer needs 30 min (Simmons 1986). In our experiments, during 30 min after successful spermatophore attachment, the mating pairs were cohabitated to avoid early spermatophore removal by females (males guard their spermatophores). Then, spermatophores were removed using fine forceps to adjust the maximum insemination duration. After the spermatophore was successfully transferred the male was no longer used in further matings. Even if spermatophore transfer succeeded, early detachment within 30 min (not removal by females) of spermatophore frequently occurred, but these cases were treated as mating itself was completed. In polyandrous treatments, females finished all (2–4) matings within 3 days. Females were allowed to lay eggs in a plastic cup (60 mm diameter and 25 mm depth) filled with wet sand for ca. 7 days.
Egg hatching conditions
Eggs were washed out from the sand with 25 °C water in a 500-ml glass beaker. Up to 200 eggs were collected from a single female and divided into 4 plastic petri dishes (90 mm diameter and 15 mm depth, equipped wet filter paper) using a soft fine brush. Petri dishes each containing up to 50 eggs (5 rows of 10 eggs with ca. 5 mm distance) were allocated to 4 different conditions (normal 25 °C or hot 37 °C temperatures/fresh or salty water). Salt concentration was varied among blocks from 0.6 to 12 wt%. This treatment simulated the disaster that an unpredictable storm surge covers the coastal oviposition sites. The petri dishes were checked every day and filter papers were always kept wet until all eggs hatched or were confirmed dead. Egg fertilization rate was calculated as (no. eggs swelled with water/no. eggs collected) and paternity was judged by eye-spot color of the developing embryos before hatching (as the same manner in Garcia-Gonzalez and Simmons 2007).
Calculation of fitness
Female fitness was evaluated mainly as the arcsine-transformed egg hatching rate. This transformation does not intend to normalize the distribution but to avoid the product of fitness values across multiple blocks at the calculation of geometric mean (see below) becoming complicate large decimal place (e.g., 0.5 × 0.5 × 0.5 × 0.5 × 0.5 × 0.5 × 0.5 = 0.0078125). When comparing geometric mean fitness (our main concern), we used randomization test, which is not affected by the transformation. The appropriate fitness index to evaluate adaptability of bet-hedging traits is the geometric mean fitness across generations (Yasui 1998, 2001; Yasui and Garcia-Gonzalez 2016). In this study, different blocks were considered as the successive virtual generations of each mating strategy (for example, the females of 2P treatment can be considered as the same strategists mating in different generations). In each block, we calculated the egg hatching rate (HR) for each petri dish, and then, arithmetic mean of HR across 4 petri dishes from each female (individual fitness; IF). Next, arithmetic mean (AM) of IF across all females of the same strategy was calculated. Finally, geometric mean (GM) of AM across all blocks for each strategy was evaluated (about calculation example, see Appendix 1). If all females of the same strategy fail reproduction in a single generation (AM = 0), then the GM of that strategy necessarily becomes zero, meaning the extinction of the genotype at that generation (Slatkin 1974; Philippi and Seger 1989; Yasui 1998, 2001; Hopper 1999; Yasui and Garcia-Gonzalez 2016). Because we wished to know which female strategy most likely led to extinction, zero-hatching rate was replaced with 0.000001 to compare GM among strategies (Yasui and Yoshimura 2018; Matsumura et al. 2021). For statistical analyses based on arithmetic mean, we used JMP ver.10.0.2. There is no appropriate statistical package to analyze geometric mean fitness. Instead, resampling and randomization tests using PopTools version 3.2 (Hood 2010) were conducted as follows: when two mating strategies such as 4P and M were compared, observed GM differences (4P-M) was used as the test statistic. Resampling (100,000 iterations) from the pooled samples (all petri dishes in the 4 mating strategies) produced null-hypothesis distribution of the test statistic. The location of the observed test statistic in the null-hypothesis distribution indicates the significance level (2-sided test) (see Appendix 1 for the calculation details). For multiple comparisons among M, 2P, 3P and 4P strategies (6 combinations), the probabilities were corrected by Holm-Bonferroni sequential correction.
Blocks
The seven blocks of the experiments were carried out from April to December in 2019 at the Laboratory of Entomology, Faculty of Agriculture of Kagawa University (Table 2). Thirty-four females in total were investigated. Block means the set of mating individuals at the same period. The collection of eggs and tracing embryo development need a few weeks so mating experiments were able to be performed only intermittently. The uneven sample size was due to the difficulty to mate all pairs according to the plan. In particular, because to complete 3- or 4-male mating by the same female within a few days was hard task, the sample sizes of these treatments are smaller than the fewer-mating treatments (n = 10 females in 7 blocks for M; n = 9 females in 6 blocks for 2P; n = 7 females in 4 blocks for 3P and n = 7 females in 5 blocks for 4P: Table 2). The change of salt concentration was the result of trials and errors to find moderately-harsh conditions where only a fraction of the total number of embryos, and not all of them, die. We incorporated these accidents to dataset.
Results
Occurrence of reproductive failure
Female 3–1 (Table 2) was unable to mount a male because of the lack of both hind legs. Female 5–5 copulated with 4 males but did not lay eggs and died. These females were omitted from the analyses as the female-caused reproductive failure (not attributable to males). Although most females laid more than 200 eggs, female 3–4 (4P), 3–5 (3P) and 5–1 (4P) laid less than 200 eggs, which could not be allocated to all 4 treatments (see Table 2). Males often failed the spermatophore attachment. In such case, we retried the pairing with the same male after ca. 1 h rest or replaced the male with another one. Female 4–2 (2P), 5–4 (M), 7–5 (M) successfully copulated and normally laid eggs but all of 200 eggs collected from each female were unfertilized. Such fertilization failure was not observed in the 3- and 4-male polyandry treatments. Out of 200 eggs each collected from female 6–2 (2P), 6–3 (2P), 7–3 (2P) and 7–4 (3P), 100 eggs allocated to the salinity conditions were dead before the swelling but remaining 100 eggs allocated to the fresh water condition were developed further. Because the allocation to 4 petri dishes was random, these mortalities had must occur after fertilization. Even under extremely high salinity (12%) conditions, eggs from female 2–1 (2P), 2–2 (2P), 2–3 (M) and 2–4 (3P) developed until the eye-spot stage but did not hatch.
Figure 1 shows the developmental process of the collected eggs. The high temperature and salinity caused earlier decline of the number of surviving embryos but the 4-male polyandry could tolerate such harsh conditions in many cases. In fact, the total reproductive failure (0 hatching rate) in the 4-male polyandry treatment occurred only in one petri dish (37 °C and salt in 4–4: Fig. 1d). The fertilization failures (unfertilized eggs) occurred significantly differently among the mating treatments (contingency analysis in JMP10.0.2, Chi-square = 14.498, p = 0.0023; Table 3a) but the significance greatly decreased after fertilization (Chi-square = 8.115, p = 0.0437; Table 3b). Throughout all embryonic developments, the probability of reproductive failures significantly differs among the mating treatments (Chi-square = 11.521, p = 0.0092; Table 3c).
Embryonic development in monandry and polyandry. The number of eggs that passed through each developmental stage are shown (7 blocks are pooled). Incubating conditions: 25 °C and fresh water (solid blue, n = 36), 25 °C and salt water (dotted blue, n = 40), 37 °C and fresh water (solid red, n = 25) and 37 °C and salt water (dotted red, n = 22). Overlapping lines: a each 4 petri-dishes of 5–4(M) and 7–5(M), b 4 petri-dishes of 4–2(2P) and each 2 petri-dishes (salt water) of 6–2(2P), 6–3(2P) and 7–3(2P), c 2 petri-dishes (salt water) of 7–4(3P)
Egg hatching rate varied among mating treatments and among environments of egg incubation (Fig. 2). Least square fitting (JMP 10.0.2) incorporating the number of mates, temperature and water conditions as the fixed effect and female’s ID as the random factor shows significantly (p < 0.05) higher hatching rate in 25 °C than 37 °C (p = 0.0009) as well as in fresh water than salt water (p < 0.0001). However, although egg hatching rate tended to increase with the number of mates, the differences among mating frequencies were not significant (p = 0.1028).
Within-generation arithmetic mean fitness
For each of 7 virtual generations, within-generation arithmetic mean fitness of 4 mating treatments is calculated (Fig. 3). The differences among the treatments were significant in some blocks but not in others. This experiment simulates a metapopulation structure, in which females lay eggs at 4 different sites whose environments (temperature and salinity) unpredictably changed after oviposition. Because low hatching rate in bad environments (e.g., salt water in block 2, see Fig. 2) was offset by high hatching rate in good environment (e.g., fresh water in block 2), the individual fitness (IF) of the female, and thus, arithmetic mean of IF among the females of the same strategy kept positive value (e.g., block 2 in Fig. 3).
Arithmetic mean fitness in 7 blocks. Arcsine transformed egg hatching rates are averaged among females of the same mating strategy in each block. The same letters in each block indicate non-significant differences (p > 0.05) in randomization test and post-hoc test with Holm–Bonferroni sequential correction. “No sample” means that no female was allocated to this treatment. In block 5, only one female (5–4) was allocated to monandrous treatment and this female laid 200 unfertilized eggs, so that its arithmetic mean fitness is set as 0.000001 instead of 0 to avoid that the geometric mean across blocks (generations) becomes 0
Between-generation geometric mean fitness
With the increase of number of mates, geometric mean fitness across available blocks (i.e., virtual generations) increased but their SE decreased (Fig. 4). The total reproductive failure (AM = 0.000001) of female 5–4 in block 5 drastically reduced the geometric mean of monandry. The randomization tests detect the significant differences between 4P and M and between 3P and M (Fig. 4).
Geometric mean fitness across blocks. Geometric mean (GM) is calculated as the n-th root of the products of each arithmetic mean fitness of n blocks (n = 7, 6, 6 and 5 in M, 2P, 3P and 4P treatments, respectively). To create null-hypothesis distribution in randomization test, egg-hatching rates in 123 petri dishes (consist of 36, 40, 25 and 22 petri dishes in M, 2P, 3P and 4P treatments, respectively) were resampled (bootstrapping). Two out of 6 possible comparison pairs show the significant differences (two-sided test) after Holm-Bonferroni sequential correction
Paternity skew
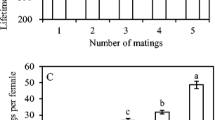
Black-eyed males fathered significantly more offspring than the expected frequency (1/2) under random fertilization in 2P and 4P treatments (2P; Mantel–Haenszel Chi-square = 11.368, p = 0.000747: 4P; Mantel–Haenszel Chi-square = 55.322, p < 0.000001) but there was no significant deviation from the expected ratio (1/3 or 2/3) in 3P treatment (Mantel–Haenszel Chi-square = 0.85878, p = 0.354081) (Fig. 5).
Paternity in polyandrous clutch. The observed paternity share (the number of black-eyed and white-eyed offspring) in each polyandrous female is compared with the expected ratio (Table 1) under the random fertilization (complete sperm mixing). Each column shows the frequencies of black-eyed and white-eyed offspring produced from a polyandrously-mated female. For example, doubly-mated 7–3 female (upper right) was expected to produce 50% black-eyed offspring and 50% white-eyed offspring but only black-eyed offspring were observed
Discussion
How to compare geometric mean fitness
This study is a rare case comparing geometric mean fitness in empirical studies to test the bet-hedging polyandry hypothesis (but see Fox and Rauter 2003; Garcia-Gonzalez et al. 2015; Matsumura et al. 2021). Fox and Rauter (2003) did a pioneer study of this issue, however, their calculations of geometric mean fitness are not entirely correct in our view because their method tends to produce higher geometric mean in polyandry than monandry (see Appendix 1). We have established the correct method to evaluate geometric mean fitness in this paper.
Bet-hedging in the field crickets
This study shows that 3 different types of bet-hedging worked in the crickets as follows: (1) the bet-hedging polyandry to avoid male-caused reproductive failures, (2) metapopulation bet-hedging to spread the extinction risks over multiple habitats and (3) reproduction itself as bet-hedging.
Polyandry as bet-hedging
Compared to monandry, mating with 3 or more males reduced the occurrence of total reproductive failures (Table 3c) and achieved higher geometric mean fitness over multiple blocks (Fig. 4). This means that polyandry works as bet-hedging to reduce extinction risk of the female “genotype” over multiple “generations” (Yasui 2001; Yasui and Garcia-Gonzalez 2016; Yasui and Yoshimura 2018) although to separate the effects of bet-hedging (stochastic process) from that of sexual selection (deterministic process) is difficult (we discuss this issue later). The trade-off between the mean and variance of fitness, a definition of bet-hedging (Slatkin 1974; Gillespie 1977; Philippi and Seger 1989) was not detected because the polyandrous treatments showed higher arithmetic mean fitness than monandry in some blocks (Fig. 3). The rationale of this definition is that the bet-hedging traits (e.g., seed dormancy; Cohen 1966) suppressing intergenerational fitness fluctuation, which necessarily increases between-generation geometric mean fitness (GMF; the long-term persistence), should be costly in the term of within-generation arithmetic mean fitness (AMF; moment rate of increase). Consequently, the trade-off (negative correlation) appears between AMF and GMF via AMF variance across generations. This is, traditionally, a prerequisite to invoke bet-hedging strategies. However, this requirement needs further theoretical testing. Such theoretical investigations are not the scope of the current study, but, in short, the negative correlation between AMF and GMF should be genetic but would not be necessarily realized at the phenotype level because an individual of bet-hedger genotype with good conditions would be superior to that of non-bet-hedger genotype with bad condition in single generation. Moreover, even if the AMF of monandry is greater than that of polyandry as expected from the trade-off assumption, it can be also explained by the fitness cost of remating (cost associated with sexual selection). Therefore, we hold that the trade-off is not a necessary condition to confirm bet-hedging in empirical studies.
We focused the accidental mating failures and male infertility at the phenotype level. The compensation of mating failure by multiple mating might have occurred in the following cases: 5–2, 6–3, 7–3, 5–3, 7–1, 7–4 and 5–1 (see Table 2). In these cases, offspring of only one morph (black eye or white eye) were born. If such absence of paternity share of a part of the mates was caused by his (their) mating failure (especially early spermatophore separation), it follows that it was compensated by the existence of other partner(s).
Polyandry corresponds to “within-generation bet-hedging” (Hopper 1999; Hopper et al. 2003) and its efficiency depends on the female population size (Yasui 2001; Yasui and Garcia-Gonzalez 2016). If the sufficient number of monandrous females exist in a large panmictic population, the probability that all monandrous females unluckily encounter unsuitable males is low, and thus, the GMF of monandry is not inferior to that of polyandry (Yasui 2001; Yasui and Garcia-Gonzalez 2016). However, many organisms live in more or less structured population (Levin 1974; Hanski 1999; Marsh and Trenham 2001). In metapopulations that consists of small patches, polyandry is favored (Yasui and Garcia-Gonzalez 2016). Even in single large population containing many males, if the opportunity of mate choice for a single female may be limited to a few males, bet-hedging polyandry can work (Yasui and Garcia-Gonzalez 2016; Yasui and Yoshimura 2018). In this study, where each block can be taken as corresponding to a single small population, this theory is applicable.
Metapopulation bet-hedging
The egg allocation to the 4 petri dishes with different conditions (temperature and salinity) can be interpreted not only as the unpredictable environmental changes after oviposition but also as the female strategy to migrate and distribute eggs to 4 different patches (i.e., metapopulation bet-hedging; Hopper 1999). In metapopulations, if some patches crashed completely by unpredictable catastrophe (e.g., pesticide spraying) but others were unaffected (i.e., spatial fine-grained environments), migration strategies can spread the risk of extinction. In fact, the 0-hatching rate in the block 2 salt water was compensated with the success of the eggs of the same genotype allocated to fresh water (Fig. 2). Thus, even monandrous females can tolerate the environmental fluctuation if they distribute offspring to multiple environments, suggesting metapopulation bet-hedging is more powerful than within-generation bet-hedging (Hopper 1999; Hopper et al. 2003).
Reproduction is bet-hedging
Moreover, the existence of multiple females of the same strategy (i.e., homologous individuals descended from single mutant) in the population offsets the fitness fluctuation among females. Thus, reproduction itself can be considered as bet-hedging to make spare individuals to offset fitness variance among mothers. There are no organisms lacking the intrinsic tendency to increase. Indeed, numbers are power.
The risk of small population when spare individual of the same strategy (genotype) is absent was also detected. Considering each block as a population in a discrete generation, block 5 contained only one monandrous female (5–4) and this female failed reproduction (0-hatching rate in all petri dishes), resulting in the extinction of the monandrous “genotype”. On the other hand, the fertilization failure of 7–5(M) was compensated by 7–2(M) within the same population. The blocks in this study can be also interpreted as the small population of endangered species. Yasui and Garcia-Gonzalez (2016) suggested that the bet-hedging polyandry can delay the extinction of demes. Therefore, the present study provides good verifications of various aspects of the bet-hedging theory.
What causes the reproductive failures
The standard way of polyandry study has adopting the repeated mating with the same male as “monandry” treatment (Tregenza and Wedell 1998; Simmons 2001; Garcia-Gonzalez and Simmons 2007). It surely adjusts the number of mating between polyandry and monandry. However, in natural environment, a female of solitary insect usually does not mate repeatedly with the same male. In such design, even if the male fails single copulation, he can be eventually successful via the repeated mating. In the bet-hedging theory, we should focus accidental mating failure which is unpredictable and thus unavoidable for females. If we use the repeated mating design as monandry, the mating failure risk in single mating would be underestimated. Although some studies (Rodríguez-Muñoz et al. 2010, 2011) have shown the congeneric field cricket Gryllus campestris females frequently mate repeatedly with the same male sharing the same burrow, as well as showing high degrees of polyandry, our study does not focus cricket biology but the empirical test of the hypothesis using the cricket as the model system. If mating failure in a single mating can be compensated with repeated mating, such cohabitation behavior as like as pair-bonding in birds and mammals can be interpreted as bet-hedging against mating failure and temporal infertility. Therefore, the G. campestris example enhances the bet-hedging hypothesis.
This study shows that even in the laboratory conditions, which are more favorably controlled regarding, e.g., food supply than natural populations, reproductive failures frequently occurs. Out of 34 females investigated, one was unable to copulate due to physical disability (loss of hind legs) and another one mated with four males but did not lay eggs. Out of 123 petri dishes obtained from the remaining 32 females, 31 dishes (3 out of which was under the “best”, 25 °C fresh water condition) recorded the 0-hatching rate. Because such reproductive failures are usually not reported in the literature as they are most of the times deemed inconvenient or non-informative for the purpose of particular studies conducted, their prevalence and evolutionary significance are greatly underestimated (García-González 2004; Greenway et al. 2015; Balfour et al. 2020). Considering the publication bias against negative data, analysis including negative data like as this study is necessary to test this hypothesis.
Among the various causes of reproductive failures (García-González 2004; Balfour et al. 2020), this study focused on the infertile mating (fertilization failure) and developing environments after fertilization. Causes of the infertile mating may come from female-side, male-side or their interaction (García-González 2004). Of course, if females are permanently infertile because of new mutations and some postnatal (nongenetic) disabilities such as loss of legs observed at female 3–1, and obstruction of oviducts etc. (Rhainds 2010), polyandry cannot rescue it. The male-side causes are genetic (e.g., deleterious mutations and genetic incompatibilities) or environmental (e.g., abnormal spermatophore attachment, spermatophore aplasia, empty spermatophore and early detachment of spermatophore) are possible (García-González 2004). Bet-hedging polyandry can cope with most of them.
When analyzing the early (from copulation to egg swelling) and late (from swelling to hatch) embryonic development separately, the compensation by multiple mating functioned especially in the early stage (Table 3). Hence, in this experiment, the bet-hedging polyandry mainly worked to offset mating failure but could not deal with the postfertilization environmental changes. To tolerate such environmental changes, genetic variance about e.g., temperature adaptability and salinity tolerance is needed in male genes (i.e., genotype-by-environment interaction within multiply-sired clutches; Yasui 1998). Because the small laboratory population of G. bimaculatus unlikely sustains the enough genetic variance, our results are reasonable. However, in natural populations maintaining genetic diversity, bet-hedging polyandry possibly works against unpredictable fluctuation of egg-hatching conditions.
Remained problem
A serious and very difficult-to-handle issue with the design of the study is that in the polyandry groups, females that failed to mate the designated number of times were discarded from the treatment of original plan. This means that in the higher-degree polyandry groups only those females willing to mate a set number of times were used, these are unlikely to be a random sample of the population and indeed it is easy to imagine they might be the healthier individuals. This will tend to create a bias in favor of the polyandry treatments. Unless using artificial insemination, it is impossible to coerce the unwilling female to mate. The future development of such technique is awaited.
Conclusion: bet-hedging is ubiquitous background of sexual selection
Some authors pointed out that to test bet-hedging polyandry hypothesis separately from sexual selection process such as sperm competition and cryptic female choice is difficult especially in internal fertilizer species (Garcia-Gonzalez et al. 2015; Matsumura et al. 2021). In this study, paternity in clutches of the polyandrous females significantly biased toward black-eye males from the expectation under random fertilization (Fig. 5). The black-eye strain is the wild type and superior than the mutant white-eye strain about the intrinsic genetic quality and competitiveness (unpublished data). Thus, good-sperm hypothesis (Yasui 1997), in which polyandrous females can indirectly choose genetically-superior male via his higher sperm competitiveness may explain the results. Alternatively, females (white eye) possibly store more sperm from non-kin black-eye males than the related white-eye males (our white-eye strain is single matriline and cryptic female choice toward sperm of unrelated males was suggested by Tregenza and Wedell 1998). However, whenever females mate with multiple males and some matings possibly result in reproductive failure, the bet-hedging effect always works. Thus, bet-hedging is a general background on which other specific mechanisms may work (Yasui and Yoshimura 2018). Therefore, the truth is the opposite: ones cannot evaluate sexual selection processes without considering about the bet-hedging effect working simultaneously. Even if the sexual selection processes choose good or compatible males, as long as uncertainty exists in their mating success (a good-gene male may fail fertilization), females need bet-hedging polyandry as insurance. Anyway, certainly we need future studies focusing on how sexually selected mechanisms and bet-hedging mechanisms may work together, possibly synergistically.
Data availability
Data are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.0zpc866xf.
Change history
08 December 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10164-021-00734-x
References
Alekseev V, Lampert W (2001) Maternal control of resting-egg production in Daphnia. Nature 414:899–901
Arnqvist G, Nilsson T (2000) The evolution of polyandry: multiple mating and female fitness in insects. Anim Behav 60:145–164
Arnqvist G, Rowe L (2005) Sexual conflict. Princeton University Press, Princeton
Balfour VL, Black D, Shuker DM (2020) Mating failure shapes the patterns of sperm precedence in an insect. Behav Ecol Sociobiol. https://doi.org/10.1007/s00265-020-2801-x
Bateman AJ (1948) Intra-sexual selection in Drosophila. Heredity (edinb) 2:349–368
Birkhead TR, Møller AP (1992) Sperm competition in birds: evolutionary causes and consequences. Academic Press, London
Cohen D (1966) Optimizing reproduction in a randomly varying environment. J Theor Biol 12:119–129
Curtsinger JW (1991) Sperm competition and the evolution of multiple mating. Am Nat 138:93–102
Forbes S (2014) Partial fertility and polyandry: a benefit of multiple mating hiding in plain sight? Behav Ecol Sociobiol 68:1329–1334
Fox CW, Rauter CM (2003) Bet-hedging and the evolution of multiple mating. Evol Ecol Res 5:273–286
García-González F (2004) Infertile matings and sperm competition: The effect of “nonsperm representation” on intraspecific variation in sperm precedence patterns. Am Nat 164:457–472
Garcia-Gonzalez F, Simmons LW (2007) Paternal indirect genetic effects on offspring viability and the benefits of polyandry. Curr Biol 17:32–36
Garcia-Gonzalez F, Yasui Y, Evans JP (2015) Mating portfolios: bet-hedging, sexual selection and female multiple mating. Proc Biol Sci 282:20141525
Gillespie JH (1977) Natural selection for variances in offspring numbers: a new evolutionary principle. Am Nat 111:1010–1014
Greenway EV, Dougherty LR, Shuker DM (2015) Mating failure. Curr Biol 25:R534-536
Greenway EVG, Shuker DM (2015) The repeatability of mating failure in a polyandrous bug. J Evol Biol 28:1578–1582
Hanski I (1999) Metapopulation ecology. Oxford Univ Press, Oxford
Hasson O, Stone L (2009) Male infertility, female fertility and extrapair copulations. Biol Rev Camb Philos Soc 84:225–244
Hood GM (2010) PopTools version 3.2.3. Available on the internet. http://www.poptools.org
Hopper KR (1999) Risk-spreading and bet-hedging in insect population biology. Annu Rev Entomol 44:535–560
Hopper KR, Rosenheim JA, Prout T, Oppenheim SJ (2003) Within-generation bet hedging: a seductive explanation? Oikos 101:219–222
Jennions MD, Petrie M (2007) Why do females mate multiply? A review of the genetic benefits. Biol Rev 75:21–64
Levin SA (1974) Dispersion and population interactions. Am Nat 108:207–228
Marsh DM, Trenham PC (2001) Metapopulation dynamics and amphibian conservation. Conserv Biol 15:40–49
Matsumura K, Miyatake T, Yasui Y (2021) An empirical test of the bet-hedging polyandry hypothesis: female red flour beetles avoid extinction via multiple mating. Ecol Evol. https://doi.org/10.1002/ece3.7418
Palumbi SR (1999) All males are not created equal: fertility differences depend on gamete recognition polymorphisms in sea urchins. Proc Natl Acad Sci USA 96:12632–12637
Philippi T, Seger J (1989) Hedging one’s evolutionary bets, revisited. Trends Ecol Evol 4:41–44
Preston BT, Stevenson IR, Pemberton JM, Wilson K (2001) Dominant rams lose out by sperm depletion. Nature 409:681–682
Rhainds M (2010) Female mating failures in insects. Entomol Exp Appl 136:211–226
Rodríguez-Muñoz R, Bretman A, Slate J, Walling CA, Tregenza T (2010) Natural and sexual selection in a wild insect population. Science 328:1269
Rodríguez-Muñoz R, Bretman A, Tregenza T (2011) Guarding males protect females from predation in a wild insect. Curr Biol 21:1716–1719
Sheldon BC (1994) Male phenotype, fertility, and the pursuit of extra-pair copulations by female birds. Proc R Soc B Biol Sci 257:25–30
Shuker DM, Simmons LW (2014) The evolution of insect mating systems. Oxford University Press
Simmons LW (1986) Female choice in the field cricket Gryllus bimaculatus (De Geer). Anim Behav 34:1463–1470
Simmons LW (2001) The evolution of polyandry: an examination of the genetic incompatibility and good-sperm hypotheses. J Evol Biol 14:585–594
Simmons LW (2005) The evolution of polyandry: sperm competition, sperm selection, and offspring viability. Annu Rev Ecol Evol Syst 36:125–146
Simmons LW (2019) Sperm competition and its evolutionary consequences in the insects. Princeton University Press
Slatkin M (1974) Hedging one’s evolutionary bets. Nature 250:704–705
Sterns SC (1992) The evolution of life histories. Oxford University Press, Oxford
Tang-Martínez Z (2019) Bateman's principles: original experiment and modern data for and against. In: Choe JC (ed) Encyclopedia of animal behavior, 2nd edn. Academic Press, pp 472–483. ISBN 9780128132524. https://doi.org/10.1016/B978-0-12-809633-8.01276-0
Thornhill R, Alcock J (1983) The evolution of insect mating systems. Harvard University Press, Cambridge
Tregenza T, Wedell N (1998) Benefits of multiple mates in the cricket Gryllus bimaculatus. Evolution 52:1726–1730
Tregenza T, Wedell N (2000) Genetic compatibility, mate choice and patterns of parentage: invited review. Mol Ecol 9:1013–1027
Tyler F, Tregenza T (2013) Why do so many flour beetle copulations fail? Entomol Exp Appl 146:199–206
Walker WF (1980) Sperm utilization strategies in nonsocial insects. Am Nat 115:780–799
Wedell N, Gage MJG, Parker GA (2002) Sperm competition, male prudence and sperm-limited females. Trends Ecol Evol 17:313–320
Wilson CJ, Tomkins JL (2014) Female Callosobruchus maculatus can maximize long-term fitness through polyandry. Behav Ecol 26:502–509
Yasui Y (1997) A “Good-Sperm” model can explain the evolution of costly multiple mating by females. Am Nat 149:573–584
Yasui Y (1998) The ‘genetic benefits’ of female multiple mating reconsidered. Trend Ecol Evol 13:246–250
Yasui Y (2001) Female multiple mating as a genetic bet-hedging strategy when mate choice criteria are unreliable. Ecol Res 16:605–616
Yasui Y, Garcia-Gonzalez F (2016) Bet-hedging as a mechanism for the evolution of polyandry, revisited. Evolution 70:385–397
Yasui Y, Yoshimura J (2018) Bet-hedging against male-caused reproductive failures may explain ubiquitous cuckoldry in female birds. J Theor Biol 437:214–221
Acknowledgements
We thank Mr. Daigo Nagamori for collecting a part of data. Dr. Francisco Garcia-Gonzalez read the earlier version of the manuscript critically and gave valuable comments. We also thank two anonymous reviewers. This work was partly supported by Grants-in-Aid from the Ministry of Education, Culture, Sports Science and Technology of Japan to Yukio Yasui, Japan Society for the Promotion of Science (nos. 26440241and 19K06839).
Author information
Authors and Affiliations
Contributions
Both authors contributed to the study. Conceptualization was done by Yasui (Ys). Data collection was mainly performed by Yamamoto (Ym). Manuscript was mainly written by Ys and checked by Ym. Statistical analysis was performed by Ys.
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interest to declare. All applicable international, national, and/or institutional guidelines for the care and use of animals were followed.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to a retrospective Open Access order.
Appendix 1: Correct calculation method of between-generation geometric mean fitness
Appendix 1: Correct calculation method of between-generation geometric mean fitness
We show the correct way to evaluate bet-hedging efficiency as the geometric mean fitness using a hypothetical dataset (Appendix Table
4). The essence of within-generation bet-hedging (classified by Hopper et al. 2003 that corresponds to bet-hedging by polyandry) is that the failure of an individual is offset by the success of the other individual (with the same genotype) in each generation. As implicitly suggested by Hopper et al. 2003, bet-hedging is not individual (or linage)-based selection but genotype-based selection. One should not ask how many offspring a lineage produced but how many offspring a genotype produced in total in each generation. Therefore, the correct way is to calculate: (1) arithmetic mean fitness among all individuals with the same genotype (polyandry or monandry) in each generation; (2) geometric mean fitness across generations for each genotype; and (3) compare polyandry genotype and monandry genotype by randomization test, as we have done in this paper.
Our method (See Table 4):
Within-generation arithmetic mean fitness of a strategy (genotype) in generation 1.
Between-generation geometric mean fitness of a strategy (genotype) across 3 generations.
Randomization test (PopTools)
To calculate null-hypothesis test statistic, first, we pooled all samples (from a to z of 3 generations) and shuffled them. Next, the shuffled samples were redistributed to all data points. A test statistic \({\mathrm{GM}}_{\mathrm{poly}}-{\mathrm{GM}}_{\mathrm{mono}}\) was calculated from this randomized dataset. Finally, we repeated this procedure 100,000 times to produce the null-hypothesis distribution of the test statistic. The location of the observed test statistic in the null-hypothesis distribution (n = 100,000) indicates the statistical significance (p value). If the observed value locates within the largest 2500 or the smallest 2500 samples in the null- hypothesis distribution, it is significant at p < 0.05 in the two-side test.
Method by Fox and Rauter (2003)
Fox and Rauter (2003) adopted an elaborate experimental design of male multiple mating (polygyny) instead of polyandry because they equated them in statistical treatment. The calculation procedure according to their method is as follows:
-
1.
Calculating geometric mean across females in the same generation:
$${\mathrm{Mean}}_{\mathrm{mono}}G1=\sqrt[3]{\mathrm{IF}1\times \mathrm{IF}2\times \mathrm{IF}3}=0.471769398$$$${\mathrm{Mean}}_{\mathrm{poly}}G1=\sqrt[3]{\mathrm{IF}10\times \mathrm{IF}11\times \mathrm{IF}12}=0.498327747$$ -
2.
Performing paired t test (the pair is made within each generation):
Pair 1 (\({\mathrm{Mean}}_{\mathrm{mono}}G1\) vs \({\mathrm{Mean}}_{\mathrm{poly}}G1\))\(=(0.471769398\mathrm{ vs }0.498327747)\)
Pair 2 (\({\mathrm{Mean}}_{\mathrm{mono}}G2\) vs \({\mathrm{Mean}}_{\mathrm{poly}}G2\))\(=(0.471769398\mathrm{ vs }0.498327747)\)
Pair 3 (\({\mathrm{Mean}}_{\mathrm{mono}}G3\) vs \({\mathrm{Mean}}_{\mathrm{poly}}G3\))\(=(0.471769398\mathrm{ vs }0.498327747)\)
The dataset (a–z) is exactly equal between monandry and polyandry. It consists of four 0.3 s, four 0.5 s and four 0.7 s in each strategy except for the different order. Any fitness index must coincide between the two strategies. Our method creates the same geometric mean fitness between monandry and polyandry because the averaging (AMmono) absorbs the larger variance of IF in monandry (than polyandry) within each generation. Unless stochastic fluctuation in small population creates larger variance in monandry (e.g., 0.1, 0.5 and 0.9), bet-hedging does not work. In this dataset, male-sample size of monandry is 1/3 of polyandry but the stochastic fluctuation is not incorporated. This compensation by the arithmetic averaging in monandry does not work in Fox and Rauter’s (2003) method because they calculated geometric mean within generation (not across generations after the calculation of the within-generation, across-female arithmetic mean). Thus, Meanpoly is always larger than Meanmono in the same dataset. Therefore, their conclusion was an artifact overestimating their “bet-hedging” effect.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Yasui, Y., Yamamoto, Y. An empirical test of bet-hedging polyandry hypothesis in the field cricket Gryllus bimaculatus. J Ethol 39, 329–342 (2021). https://doi.org/10.1007/s10164-021-00707-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10164-021-00707-0