Abstract
The field of process mining focuses on distilling knowledge of the (historical) execution of a process based on the operational event data generated and stored during its execution. Most existing process mining techniques assume that the event data describe activity executions as degenerate time intervals, i.e., intervals of the form [t, t], yielding a strict total order on the observed activity instances. However, for various practical use cases, e.g., the logging of activity executions with a nonzero duration and uncertainty on the correctness of the recorded timestamps of the activity executions, assuming a partial order on the observed activity instances is more appropriate. Using partial orders to represent process executions, i.e., based on recorded event data, allows for new classes of process mining algorithms, i.e., aware of parallelism and robust to uncertainty. Yet, interestingly, only a limited number of studies consider using intermediate data abstractions that explicitly assume a partial order over a collection of observed activity instances. Considering recent developments in process mining, e.g., the prevalence of high-quality event data and techniques for event data abstraction, the need for algorithms designed to handle partially ordered event data is expected to grow in the upcoming years. Therefore, this paper presents a survey of process mining techniques that explicitly use partial orders to represent recorded process behavior. We performed a keyword search, followed by a snowball sampling strategy, yielding 68 relevant articles in the field. We observe a recent uptake in works covering partial-order-based process mining, e.g., due to the current trend of process mining based on uncertain event data. Furthermore, we outline promising novel research directions for the use of partial orders in the context of process mining algorithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the recent years, the field of process mining [1] gained attention in both academia and industry, i.e., witnessed by the IEEE International Conference on Process Mining SeriesFootnote 1 and several commercial process mining solutions, e.g., among others, CelonisFootnote 2 and UI Path Process Mining.Footnote 3 Process mining can be considered a collection of tools, techniques, methods, and algorithms designed to translate recorded operational event data, generated during the execution of processes, into actionable knowledge. In this context, the different types of processes that can be analyzed using process mining techniques are vast, e.g., administrative processes, logistic processes, medical processes, and production processes. As a prerequisite for applying process mining, processes are assumed to leave a digital trace in a company’s information systems.
Three major sub-fields are identified in process mining. Process discovery techniques [2] aim to translate the recorded event data into a (graphical) process model, e.g., a BPMN model [3]. The process modeling formalisms used, i.e., either automatically discovered or designed manually, often compactly represent all the process’s possible (parallel) executions. The goal of a discovered process model is to accurately describe the behavior observed in the event data, reasonably generalize w.r.t. the behavior observed in the data, and to be human interpretable. The first two goals are imperative for many data-driven algorithms, yet, the third requirement is less common. The second branch of techniques is referred to as conformance checking techniques [4]. The techniques in this branch aim to relate the observed event data w.r.t. a given reference process model. Here, the complexity lies in the fact that a process model often describes vast amounts of different executions (possibly infinite). Finally, process enhancement techniques aim to find possible improvement points for the process. Examples of such techniques are decision point mining [5] and performance prediction [6].
The event data analyzed by process mining algorithms are stored in event logs. In its simplest form, such an event log is a data table consisting of three columns. Consider Table 1, which describes a simplified example of an event log. The first column records the instance of the process, e.g., the customer for which the process was executed. The second column captures what activity has been performed for the process instance. The third column records at what point in time the activity was performed. A row in Table 1 is an event. The same activity can be executed several times (i.e., repetition of activities) in the context of the same instance of a process, i.e., the explicit differentiation between events (recordings) and activities (task performed) captures this.
In practice, more data attributes are recorded for events, e.g., the start and end timestamp of the executed activities and the resource performing the activity. Despite the simplistic nature of Table 1, most process mining algorithms adopt a corresponding mathematical formalization of their input: sequences of atomically executed activities. However, activities executed in real processes are often not atomic, i.e., the instances of executed activities typically have a nonzero duration. Consequently, multiple activities may overlap during their execution. It is hard to represent such an overlapping when using sequences of activities as a mathematical representation of the process, i.e., without explicit differentiation between activity start and end times. Even if we accurately differentiate between events describing activity start and end times, respectively, assuming a total order among these events requires us to observe all possible interleaving of the parallel activities to conclude their parallel relationship. Rather than formalizing the recorded event data as an input, an alternative mathematical formalism closer to the underlying phenomenon, i.e., the process itself, is of interest. In this context, some authors use the notion of partial orders as a suitable intermediate representation. The use of partial orders naturally supports capturing activities’ start and end timestamps. Additionally, it serves as a basis for several other problems, e.g., arbitrary ordering of activity instances with the same timestamp and general uncertainty in event logging.
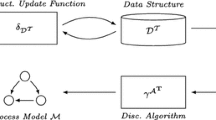
Whereas partial orders have been considered the context of process mining (and are promising for future work in the field), an overview of their use in process mining is lacking. Hence, in this paper, we present a survey and outlook of work in the field of partial-order-based process mining. We performed a keyword search, followed by a snowball sampling strategy, yielding 68 relevant articles in the field. The works considered roughly follow the general architecture depicted in Fig. 1, i.e., the recorded operational event data are translated into a partial-order-based representation, which is subsequently used as algorithmic input. We study how partial orders are extracted from event data and present an in-depth study of the different use cases of partial orders in both process discovery and conformance checking. Additionally, we discuss other use cases of partial orders (i.e., outside of process discovery and conformance checking) and highlight novel research directions where partial orders are expected to be particularly impactful.
The remainder of this paper is structured as follows. In Sect. 2, we briefly present background concepts that ease the readability of this paper. In Sect. 3, we present the survey methodology adopted. In Sect. 4, we present the survey results. In Sect. 5, we discuss other application areas of partial orders and interesting future research directions. Section 6 concludes this paper.
2 Background
In this section, we introduce background concepts that ease the overall readability of this paper. We discuss partial orders, event data, process modeling formalisms, and the different semantics under which partial orders can be considered.
2.1 Partial orders
A strict partial order \((X,\prec )\) is an irreflexive (\(x{\nprec }x\)), anti-symmetric (\(x{\prec }y{\wedge }y{\prec }x{\implies }x{=}y\)) and transitive (\(x{\prec }y{\wedge }y{\prec }z{\implies }x{\prec }z\)) binary relation over a set X. For example, consider Fig. 2 visualizing a simple example partial order over the nodes \(\{a,b,c,e,g,h\}\). Whereas we focus on strict partial orders, we simply refer to partial orders in the remainder of the paper. Note that due to the transitivity property, in Fig. 2, node a is preceding each other node.
Labeled partial order corresponding to the activity instances of case 7 in Table 2 (we only show \(\ell \)-values)
In some cases, we associate the elements of a partial order with a label, e.g., to represent the fact that the same activity can be executed multiple times for a single process instance. To this end, we use the notion of a Labeled Partial Order (LPO), where given some partial order \((X,\prec )\), an arbitrary set of labels \(\Sigma \) and labeling function \(\ell {:}X{\rightarrow }\Sigma \). Tuple \((X,\prec ,\ell )\) represents a labeled partial order over X.
2.2 Event data
The information systems employed in companies, e.g., Enterprise Resource Planning (ERP) systems such as SAPFootnote 4 and Customer Relationship Management (CRM) systems such as Salesforce,Footnote 5 track the execution of the activities performed in the context of the processes they support. For example, an insurance provider can extract an insurance claim’s exact historical course of action from such a system. Every activity executed, including various details such as the customer ID, vehicle type, total claim, and involved resources, is available. When analyzed correctly, such a rich source of data can significantly enhance the overall knowledge of the process and can thus be used to improve the process.
Consider Table 2, in which we present a simplified example of an event log. Even though Table 2 is still simplified, it is more realistic than the event log shown in Table 1.
Each row represents an activity instance of the process. For example, the first row in the table records that employee Bob executed the Register Defect activity for a process instance with ID 7. The activity took 2 min and had an associated cost of 25 U.S. Dollars. Multiple rows have the same value for the Process Instance ID-column, i.e., allowing us to capture all activity instances executed for the same customer, patient, insurance claim, or, in this case, for the same repair. We refer to the digital recording of a process instance as a case. Hence, an event log describes a collection of cases.
A partial order over the activity instances, i.e., as recorded by the events, can be defined. The relation holds for two events \(e\) and \(e'\) if the completion timestamp of \(e\) is strictly smaller than the start time of event \(e'\).Footnote 6 Reconsider Fig. 2, which captures a labeled partial order corresponding to the activities recorded for case 7 in Table 2. There are, however, various other ways in which partial orders can be defined for a given event log, which we discuss in more detail in Sect. 4.1.
2.3 Process modeling formalisms
A process model describes how cases flow through a (business) process and denotes which activities (captured by the universe of activity names \({\mathcal {A}}\)) can be executed and in what order. Formally, a process model expresses a, possibly infinite, set of process behavior, i.e., defined either as a sequence or a partial order.
As an example, we briefly describe the notion of Petri nets [7], i.e., an often-used process modeling formalism in process mining that compactly represents concurrent behavior. Additionally, many high-level process modeling formalisms, e.g., BPMN [8], can be transformed to Petri nets. A Petri net is a bipartite graph connecting a set of places, used to represent the model’s state (visualized as circles), to a set of transitions, used to manipulate the state of the described process (visualized as boxes). For example, consider Fig. 3, depicting an example Petri net consisting of 9 places (circles) and 9 transitions (boxes).
A Petri net describing the partial order in Fig. 2
A Petri net is described by a tuple \((P, T, F, \lambda , M_I, M_O)\) in which P is a set of places, T is a set of transitions, \(F{\subseteq } (P{\times }T){\cup }(T{\times }P)\) is a set of arcs, \(\lambda {:}T{\nrightarrow }{\mathcal {A}}\) is a labeling function and  are multisets of places, indicating the desired initial and final state of the Petri net.Footnote 7 The labeling function \(\lambda \) (in Fig. 3, the label function values are visualized within the transitions) allows us to let different transitions describe the same activity \(a{\in }{\mathcal {A}}\). Furthermore, in certain cases, e.g., when a transition is used for “routing purposes”, we have \(\lambda (t){=}\tau \) (transition \(t_8\) in Fig. 3) indicating that no corresponding activity exists for the transition.
are multisets of places, indicating the desired initial and final state of the Petri net.Footnote 7 The labeling function \(\lambda \) (in Fig. 3, the label function values are visualized within the transitions) allows us to let different transitions describe the same activity \(a{\in }{\mathcal {A}}\). Furthermore, in certain cases, e.g., when a transition is used for “routing purposes”, we have \(\lambda (t){=}\tau \) (transition \(t_8\) in Fig. 3) indicating that no corresponding activity exists for the transition.
Places can hold tokens, which together determine the state (the marking) of the Petri net. For example, in Fig. 3, place \(p_1\) holds one token. If all places with arcs to a transition t contain a token in a marking (e.g., \(t_1\) in Fig. 3), then the transition can fire, which consumes these tokens from the incoming places \(\{p{\mid } (p, t){\in }F\}\) and produces tokens on outgoing places \(\{p{\mid }(t, p){\in }F\}\). Firing a transition t may correspond to the execution of an activity \(\lambda (t){\in }{\mathcal {A}}\). The net starts in the initial marking \(M_I\), and by a sequence of transition firings, changes state until the final marking \(M_O\) is reached. For example, in the marking depicted in Fig. 3, i.e., \([p_1]\), transition \(t_1\) is the only transition that is allowed to fire, i.e., describing activity a. After firing transition \(t_1\) and correspondingly observing activity a, the new marking of the net is \([p_2]\), i.e., one token in place \(p_2\). The labeled transitions in a transition sequence describe the activity instances that are expected to be observed for a case of the process that the model represents.
The firing rule (described in the previous paragraph) generates sequences of transitions which can be converted into sequences of activities by applying the \(\lambda \)-function. However, partially ordered semantics can be expressed by several process modeling formalisms as well, including BPMN [8], Message Sequence Charts [9] and Petri nets [10]. In most process modeling formalisms, the execution of two activities \(a, b{\in }{\mathcal {A}}\) may be independent, that is, the execution of a does not directly influence the execution of b and vice versa. If the execution of activities does not take time (i.e., is atomic), then a and b are interleaved. If a process model does specify activity duration (e.g., Petri nets can be extended to include such a time-perspective [11]), the activities are assumed to be executed concurrently. For example, consider the marking \([p_3, p_4]\) in Fig. 3, reachable after the consecutive firing of transitions \(t_1\) and \(t_2\) (activities a and b, respectively). Depending on whether we assume transitions to have a certain duration, transition \(t_3\) (activity g) can be executed either interleaved or concurrent with transition \(t_4\) or \(t_5\) (activities c or d). Observe that the partial order depicted in Fig. 2 is also described by the Petri net in Fig. 3.
2.4 Partially ordered trace semantics
We assume that a partial order can be either derived from a process model (cf. Sect. 2.3) or extracted from an event log (studied in Sect. 4.1). In contrast to a total order, partially ordered behavior does not express an ordering relation between all of its described events (or activity instances). Such absence of an ordering between events does not mean that a corresponding total order representation of the partial order behavior does not exist. The existence of a corresponding total order representation, i.e., derived from a partial order, is of use, e.g., it allows one to apply any existing process mining algorithm on partial-order based event data. Note that transforming an event log to a partial order representation and subsequently deriving total order sequences may yield more behavioral total orders compared to directly deriving total orders from the event log.
The total order representation of a partial order depends on the interpretation of the absence of a relation between two events describing activities a and b, yielding different partial order trace semantics (i.e., either defined by a process model or recorded in an event log). We observe the following semantics (schematically visualized in Fig. 4).
-
In Certain Semantics (CS), the unordered activities are assumed to occur and are executable in any order. We distinguish two sub-types of certain semantics:
-
The observed activity instances a and b are Interleaved (CS-I) if they may be executed or may have been executed in any order (e.g., a followed by b or b followed by a), but they cannot overlap in time.
-
The observed activity instances a, and b are concurrent (CS-C) if they may overlap or may have overlapped in time during execution. For concurrent semantics, activity executions cannot be atomic and must take time.
-
-
In the Uncertain Semantics (US), unordered activities are assumed to have been executed, or may be performed, in one particular unknown order. We know that a and b can be executed or were executed in a particular order, but we do not know which order.
We use the three semantics identified to structure our survey presented in Sect. 4.
3 Methodology
In this section, we briefly discuss the review methodology adopted. The goal of this work is to provide a comprehensive overview of the use of partial orders as a primary citizen in process mining techniques. As such, we adopt a semi-systematic literature review approach [12] aiming to provide a qualitative overview of the state-of-art. A semi-systematic literature review is intended to study topics that have been conceptualized differently and studied by different researchers, possibly within different fields. Said literature review type allows one, e.g., to detect novel research directions and themes. A typical outcome is, as is the case in this article, a synthesis of the current state of knowledge. In the remainder of this section, we discuss the literature collection strategy (Sect. 3.1) and the corresponding search results (Sect. 3.2).
3.1 Literature collection
In this section, we briefly present the literature collection strategy adopted. The literature collection strategy, consists of three separate phases:
-
1.
Keyword Search; To identify relevant literature, we query three databases: Scopus (https://scopus.com), ACM Digital Library (https://dl.acm.org/), and SpringerLink (https://link.spinger.com). We use the search term TITLE-ABS-KEY ( “process mining” AND ( “partial order” OR “partial orders” ) ) in Scopus. We use the same logical query for the other databases (the exact syntax differs per database). All data related to the literature collection, i.e., collected papers, filtered collections, etc., are publicly available.Footnote 8 The search results include conference/journal papers, collections (books/proceedings), and encyclopedia entries. We only consider journal and conference papers.
-
2.
Author Knowledge; We augment the results of the keyword search by addition of relevant articles known to the authors.
-
3.
Snowball Sampling [13]; We apply snowball sampling on the selected papers (outputs of Step 1. and 2.). We consult the references of the selected papers and further select articles that are of relevance to the survey. Snowball sampling is iteratively applied, i.e., results of a previous round that are included in the survey form the input for the next round of sampling, until a fix-point is reached.
3.2 Search results
In this section, we present the results of the literature search. Consider Table 3, which schematically presents the outputs of the different steps of the literature collection step.
The initial keyword search yielded a total of 210 articles, i.e., Scopus: 15, ACM: 15, and SpringerLink: 185 (some articles exist in multiple sources). On the keyword results, we performed a global search for all papers on the terms partial, partial order and event data. All papers that yielded no match were excluded directly. For the remaining papers, we investigated the definition of event data and assessed the use of partial orders in this context. Various papers that mention the notion of partial orders (e.g., in the related work section) use the “classical notion of event logs” in the technique(s) they describe (cf. Table 1). These papers are removed from the selection. Additionally, various works do not consider the notion of event data at all, e.g., describing process model formalisms that support partial orders. Such works have been excluded from the selection as well. After careful selection, 39 papers remained. We augmented the selection with papers that are known to the authors. In total, 16 papers known to the authors (yet not part of the results of the literature search) have been assessed, out of which 14 have been included. Snowball sampling was iteratively applied on the selected 53 articles, yielding an additional 61 potential articles out of which 15 were included in the survey. As such, in total, 68 articles are identified in the context of partial-order-based process mining.
4 Partial-order-based process mining: a survey
In this section, we present the results of our survey. First, in Sect. 4.1, we a review the different types of partial order extraction techniques. We structure the remaining works along the lines of different application domains of partial orders rather than structuring it chronologically, with the aim of providing a global overview of the performed research in the respective domains. We do so, as for both process discovery (discussed in Sect. 4.2) and conformance checking (discussed in Sect. 4.3), a major share of work can be identified. Both sections are structured along the lines of the different semantics identified (certain versus uncertain, cf. Sect. 2.4). Works covering other domains in process mining are discussed separately in Sect. 4.4 (Other Application Areas).
4.1 Partial order extraction
In this section, we cover the primary step of any partial-order-based process mining technique, i.e., partial order extraction based on the event data stored in an information system (cf. Fig. 1). A few techniques have been proposed to convert sequences of recorded events into partial orders of events. In this section, we discuss these different techniques, structuring the discussion using the following two criteria:
-
1.
Which information captured in the event log is used to derive a partial order?
-
2.
Which of the certain and uncertain relations are captured by the partial order?
Existing approaches derive partial order traces using two types of information. The first type concerns internal information that is already stored in the event data to infer partial orders. Within this stream of approaches, three types of event attributes are typically used: the sequential ordering of events in a log, the timestamps of events, the activity life-cycle information, and the data attributes of events. In contrast, the second type concerns the external knowledge that is available to derive concurrent activities, namely domain knowledge or a normative process model. Using these types of information, the existing approaches then obtain partial order traces, based on one of the identified semantics (cf. Sect. 2.4): certain (concurrent or interleaved) or uncertain. In the following, we discuss existing approaches with respect to these two criteria.
4.1.1 Exploiting information within an event log
Traditional process mining techniques assume that an event log is available and that the event log consists of a set of sequences of events. The sequential ordering of events is used to derive causal relations between the activities that the events represent. If there is information that indicates otherwise, the other types of relations, such as concurrency or interleaved, are concluded. In the following, we discuss these techniques and the information they use to derive partial orders.
Total order and log based
A common approach to derive partially ordered traces is to leverage different total ordering of events in a log. Most discovery algorithms use the total ordering of event data to infer a process model which includes causal and concurrency relations. These types of relations have a certain semantics. Among these relations, the concurrency relations can be used as a concurrency oracle. Such a concurrency oracle indicates which activities are executed concurrently. This information is subsequently used to convert a sequence of events into a partial order. For example, a classical process discovery algorithm, i.e., the \(\alpha \)-miner [14], uses the total order of events to compute a direct succession relation. Built on the direct successions, the \(\alpha \)-miner infers the causality, parallel, and choice relations between activities. The set of parallel relations can be seen as a concurrency oracle. The resulting partial orders inherit the concurrency relations and the semantics induced by the discovery algorithm. These concurrency relations have a interleaved semantic in nature (instead of uncertain). For example, given two traces \(\langle a, b, c, d\rangle \) and \(\langle a, c, b, d \rangle \), the \(\alpha \)-miner returns b and c to be parallel. This concurrency oracle can then be used to construct a partial order \((X,\prec )\), where \({\prec }{=}\{(a,b), (a,c), (b,d), (c,d), (a,d)\}\).
In [15], the authors use such an oracle-based approach to transform the traces into event structures [16], which are used to compare different subsequent groups of process executions in order to detect concept drift, i.e., changes in the execution of the process. In [17], a similar approach is adopted for general process comparison. (Here, groups of execution do not need to be close in time-proximity.) Another example is [18], in which the authors propose to build instance graphs based on classical event logs. In an instance graph, each vertex represents an activity instance. Two vertices may only be connected using an arc if there is a causal relationship between the source and target node, i.e., according to some causal relation oracle. In an instance graph, transitive relations are explicitly forbidden, i.e., an instance graph resembles the transitive reduction of a partial order.
Total order and time/data based
Another commonly used type of information to derive partial orders is to use other data attributes in the event data, such as the timestamp of events or the life-cycle information. The timestamps of events indicate when individual events occurred, e.g., starting or finishing the execution of an activity. However, in some instances, these timestamps are recorded at a coarse-granular level, e.g., only the days are recorded, the hours and minutes are missing, or are known to be unreliable [19, 20]. The events may also be recorded simultaneously, having the same timestamp. These works describe the corresponding construction of behavior graphs [21], which are transitive reductions of partial orders based on the uncertain event data. Lu et al. [22] propose to use this information to consider the events that have identical timestamps as having an uncertain ordering and creating the partial order accordingly.
When events contain timestamps that indicate the start and completion time of an activity, one may use such information to derive true concurrency relations between the events and use these to obtain partial orders that have a certain-concurrency semantics. Interestingly, when using start and end timestamps of events to derive partial orders of activity instances, the partial orders derived are interval orders [23], i.e., describing the additional property that if \(x{\prec }y\) and \(w{\prec }z\), then either \(x{\prec }z\) or \(w{\prec }y\), i.e., concurrency between sequential behavior of x and y, and, w and z, respectively, is not observed.
Leemans et al. [24] propose a technique that leverages the \(\alpha \)-miner and uses start and complete information to derive partial orders and concurrence information. In [25], the authors propose to learn a temporal network representation of an event log. Such a network is based on Allen’s interval algebra [26] and captures how frequently a specific relation is present in the event log. Various (existing/commonly used) relations can be derived from the network that can be subsequently used, e.g., for process discovery.
4.1.2 Using external knowledge
In addition to the information within an event log, external knowledge regarding the relations may also be used to convert sequences into partial orders. Most work either uses a external concurrency oracle, or, a reference process model.
External concurrency oracle
Some techniques assume the existence of an external concurrency oracle that indicates the possible concurrent or interleaved activities. The exact procedures to obtain such an oracle are left open and may vary, e.g., a domain expert may be used. Dumas et al. [27] propose a two-step approach to derive partial orders enriched with conflict relations, i.e., labeled prime event structures (PESs), using a given external concurrency oracle. Observe that as a fallback method, the log-based concurrency oracle can be used.
Process model
When a normative process model is available, the certain information regarding concurrent or interleaved activities in the process model can be used to convert total orders into partial orders. The resulting partial orders have the same semantics as the process models used. Fahland and van der Aalst [28] propose to replay traces on a model to obtain partially ordered runs to simplify process models.
4.2 Discovering process models from partial orders
This section discusses process discovery techniques that use partial orders directly or explicitly exploit the notion of concurrency. We first briefly discuss classical process discovery algorithms. Secondly, we cover techniques that explicitly assume activity lifecycles, i.e., enabling these techniques to observe true concurrency. Thereafter, we focus on partial-order-based process discovery algorithms.
4.2.1 Classical process discovery
Most classical discovery techniques (see [2] for a detailed overview) use the total order of events in an event log and derive concurrency based on the context of events, i.e., as covered in Sect. 4.1. It has been shown that concurrency can be reliably discovered [29], as long as the concurrency involves more complex structures than just activities, i.e., otherwise classical process discovery techniques cannot distinguish between activities being concurrent (i.e., potentially overlapping) and being interleaved (i.e., both being executed yet non-overlapping).
Nevertheless, discovering concurrency remains challenging due to the information required from the event log: a process of 10 concurrent activities has \(10!{=}3\,628\,800\) different orders of execution. In techniques that use the directly follows abstraction, e.g., the previously presented \(\alpha \) miner [14] and its derivatives, this amount of information is alleviated to \(10*9 = 90\) observations. In comparison, the same information can be captured using only one partially ordered trace.
Discovery techniques that detect concurrency using totally ordered traces inherently use uncertain semantics: at least one partially ordered run must match the given totally ordered trace in the discovered model.
In contrast, [30] uses the eventually follows abstraction to directly construct a partially ordered model, which, due to label splitting, supports looping behavior.
4.2.2 Discovery based on lifecycle information
In event logs, events can be annotated with an attribute indicating the life cycle information of that event. In particular, an event can indicate the start of the execution of an activity (an activity instance) and the completion of an activity instance. For instance, the trace \(\langle a_s, b_s, b_c, a_c\rangle \) denotes a trace of two activity instances (a and b), such that a started, after which b started and completed, after which a completed. More elaborate life cycle models, for instance, supporting pausing and resuming execution, have been proposed [31]. However, such models have thus far not been leveraged for process discovery.
In [32], the authors propose to revise the internal data structure used of a classical process discovery algorithm, i.e., the Heuristic Miner [33], to be aware of activity instances. Other examples of techniques that use life cycle information are Tsinghua alpha (T\(\alpha \)) [34] and Inductive Miner—life cycle (IMlc) [24]. IMlc uses the concurrent semantics, whereas T\(\alpha \) uses the interleaved semantics. T\(\alpha \) and IMlc do not need to know which start event belongs to which completion event, as they abstract the behavior in the event log on an activity level (rather than the activity instance level). They only consider when an activity starts and completes, not when a particular activity instance starts or ends. Such techniques do not use this information as it is not available in event logs with life cycle information: for instance, in the trace \(\langle a_s, a_s, a_c, a_c\rangle \) it is unknown which one of the start events \(a_s\) link to which completion event \(a_c\).
In contrast, such information is necessary to construct a partially ordered trace. On the other hand, a partial order cannot express that a should start before b but should end only after b completes. Hence, life cycle information and partially ordered traces are orthogonal and partially ordered traces in which the events are annotated with life cycle information could be defined.
4.2.3 Partial-order-based process discovery
This section considers process discovery techniques that directly work on partial orders. It is important to note that a large amount of works focuses on the Petri net synthesis problem based on labeled partial orders [35,36,37,38,39,40,41,42,43]. These techniques discover a Petri net that describes a (partial order) language that is as close as possible to the input LPOs. Typically, the resulting models are hard to interpret by a human analyst. We divide the work covered in this section,i.e., partial-order-based process discovery techniques, according to the usage of partial orders under certain semantics and uncertain semantics.
Certain semantics
This section covers process discovery techniques that assume certain trace semantics. As this category covers a large amount of work, we order the work chronologically.
In [44, 45], Herbst describes, i.e., as one of the first authors on process discovery, various classes of process discovery problems, explicitly assuming the existence of a partial order over the instances of a workflow. In [46], partial orders are first transformed to eventually follows relations, transitively reduced, de-duplicated and transformed into a process model.
In [47], the authors do not use partial orders as an intermediary object. However, they do account for multiple activity stages, e.g., ready, started, etc. These states are used to detect concurrency among two activities in the process. The relation (and others) is used to construct an execution graph, which can be seen as the transitive closure of a partial order over the observed activities (if activities only occur once). The execution graphs are combined into a workflow graph.
In [48], the authors introduce the Multi-Phase Miner, which aggregates instance graphs (partially ordered traces) into Petri nets. This aggregation first collapses the instance graphs into projected instance graphs. Each activity of the instance graph is a node (rather than each activity instance), and the edges are annotated with how often they appeared in the corresponding instance graph. Second, the union of all projected instance graphs is taken. Third, the union is transformed into an EPC using structural transformation rules. However, the models that preserve all behavior in the input event log tend to be imprecise. The authors show that these steps preserve behavior, and fitness is guaranteed; however, the method might generalize and sacrifice precision.
In [49], the author proposes to discover block-structured workflow models. The algorithm assumes that the event data capture start and end times. In the first step of the algorithm, repeated executions of activities are grouped together by an overarching fresh activity, i.e., representing the repeated behavior. In the second step, the ordering relations between the different activities in the event log are used to create trace clusters. The clusters are merged, e.g., based on observations of interleaving. Every cluster is transformed into a block-structured process model, which are combined together into a single resulting process model.
The authors in [9] use Message Sequence Charts (MSCs), which denote messages sent between processes, with the messages sent for one process being totally ordered. Each MSC is translated into a partially ordered trace. Using a set of these translated MSCs, the Multi Phase Miner can be applied, with two limitations: Each message label must be unique in each trace, and the derived partial orders must be transitively reduced.
In [50], the authors propose to construct Petri nets from partially ordered traces using synthesis: Using linear programming, a Petri net is constructed that can replay at least all partially ordered traces in the log.
In [51], the authors introduce three algorithms to discover process models from partially ordered event logs. To this end, first, a collection of conclusions is derived from the partially ordered runs—a conclusion expresses equality between tokens produced and tokens consumed, corresponding to the edges of the partially ordered trace. Second, a Petri net is constructed that adheres to these conclusions.
In [52], an event log is translated to a first-order logic expression, which is subsequently used to update a workflow model incrementally. In [53, 54], the authors propose to learn labeled partial orders which are subsequently converted into event structures. From the event structures, occurrence nets are deduced, which are subsequently folded into a Petri net (allowing the integration of negative trace information).
In [27], the authors use partial orders enriched with choices and conflict relations (prime event structures (PESs)). Events in these PESes that are equivalent (or equivalent enough to allow for imprecisions to be included) are combined, and the result is translated to a Petri net. Note that to construct partially ordered traces, the presence of a concurrency oracle for each activity is assumed. Thus, duplicate labels are not possible. In [55], a public implementation of the proposal of [27] is presented.
In [56], the authors use conditional partial order graphs (CPOGs) to visualize event data and as an intermediate step towards process mining. In a (potentially cyclic) graph, the edges can be annotated with boolean variables, such that for each combination of boolean variable assignments, a partial order results. The language of a CPOG is the set of total ordered traces resulting from all possible variable assignments. Finding the smallest CPOG given a set of partially ordered traces is called CPOG synthesis, and several approaches have been proposed. A CPOG describes an acyclic partially ordered language and can thus be seen as a process model. Finally, data mining techniques are applied to provide intuition to the variables of the CPOG.
In [57], a more generic approach extending partial orders is adopted. Event logs are defined as a partial order over the events (rather than a total order). Yet, the paper primarily focuses on assigning regions to events that help further decompose the process discovery problem. In this context, since using a process discovery algorithm is seen as a black box in this paper, partial orders have no added benefit over total orders.
Prime Miner [58] first uses life-cycle information to create partially ordered runs. Second, it folds the most frequently (up to varying thresholds) partially ordered runs into a prime event structure. Third, the prime event structure is synthesized into a Petri net using the theory of compact token flow regions.
Uncertain semantics
Interestingly, almost all work in partial-order-based process discovery assumes complete certainty in the event data logging. In [59], the authors assume a partially ordered event log, in which multiple trace notions might be present, i.e., events can be linked to various artifacts. A directly follows-based model is discovered from partially ordered and multi-trace event logs. This approach assumes that a partial order indicates an order’s absence, thus using uncertain semantics.
In [60], the authors assume that event data contains uncertainty. The authors assume simple uncertainty, i.e., the exact activity may not be known, or the exact timestamp may not be known (i.e., an interval is assumed). The authors propose to build behavior graphs as an intermediate representation of the data, which is a transitive reduction of a partial order representation of the behavior.
4.3 Conformance checking
In this section, we cover the area of conformance checking. Recall that conformance checking aims to assess whether the execution of a process, i.e., as recorded in the event data, conforms to a given reference process model. We first briefly cover techniques defined for the classical notion of event data, i.e., totally ordered event data. Subsequently, we briefly cover works considering partial orders within conformance checking. In line with the previous sections, we structure the discussion of the techniques in their usage of partial orders under certain semantics and uncertain semantics.
4.3.1 Classical conformance checking
The first work concerning the conformance checking problem is often referred to as token-based replay [61]. The approach heuristically “replays” the observed behavior in the context of a given process model (usually a Petri net). To accommodate for the heuristic nature of the previous work, the notion of alignments was introduced [62]. An alignment quantifies an observed trace in the context of an execution sequence of a given model. It does so by mapping each observed activity in a trace (if possible) to a corresponding activity in the given process model. An alignment, for example, allows us to pinpoint whether certain activities were skipped or duplicated. For a detailed overview of classical conformance checking techniques, we refer to [4].
4.3.2 Conformance checking using partially ordered event data
A few techniques have been proposed to check conformance between partially ordered traces and normative process models. We identify the same main streams for partial-order-based conformance checking as we observe for process discovery, i.e., certain semantics and uncertain semantics. In the remainder of this section, we discuss works in each category in more detail.
Certain semantics
One of the earliest works in partial-order based conformance checking is the verification module of VipTool [63,64,65], supporting the comparison of a scenario (LPO) with a given Petri net. Lu et al. were the first to consider partial ordered traces for conformance checking [22]. The proposed approach is founded on the notion of alignments. In particular, partial ordered traces are converted to an occurrence net (i.e., a Petri net that describes the observed partial order in the event data), and a synchronous product is computed between the occurrence net and the normative model. From the initial marking of the synchronous product to its final marking, the shortest path of transitions is computed and unfolded into a partially ordered alignment. In [66], this work is formalized and applied in a healthcare case study.
In [27], the authors propose to use event structures [16] as an intermediary data structure for process mining operations. An event structure describes a partial order over a set of events, as well as a conflict relation, i.e., representing the notion of mutually exclusive events. The authors propose to derive an event structure from both the event log and the process model, which they subsequently compare to each other (exploiting the work proposed in [67]).
Senderovich et al. [68] consider conformance checking and process improvement of scheduled processes. The proposed technique assumes that both the schedule and the event log describe a partial order of activity instances. Both artifacts are transformed into a open fork/join network and are used to compare the schedule and true execution from various perspectives.
In [69], the authors adopt a partial order notion for the observed event data. Using this representation, the authors propose to use automated planning algorithms [70] and provide an algorithmic framework in the standardized Planning Domain Definition Language (PDDL) language.
Uncertain semantics
In [71, 72], the authors assume that events are recorded in an atomic fashion, yet, the granularity of the timestamp recordings is coarse-grained. As such, the data describe multiple events occurring at the same point in time. The proposed algorithm computes totally ordered alignments based on the partially ordered event data. Yet, upper and lower bounds for alignments are given, rather than an exact conformance value.
van der Aa et al. [73] represent events recorded in the context of a process instance as a sequence of disjoint sets of events. When the sequences consist of an event set that contains more than one event, that recording is categorized as uncertain. In the work, the authors assume that each event observed in the uncertain set has been executed; however, the ordering of the events is unknown. The authors propose to compute the possible resolutions of the observed event data, i.e., all possible total orderings of the observed events. Furthermore, the probability of a resolution is quantified as well. The general conformance of an observed uncertain process instance is computed by computing the sum of all resolution probabilities multiplied with the corresponding resolution’s conformance (using classical conformance checking over total orders). The authors present three different resolution strategies, i.e., strategies to compute a trace resolution probability distribution. To reduce the computational effort, the authors propose means to compute the expected conformance value and confidence intervals.
4.4 Other application areas
Partial orders have been leveraged in other process mining studies as well. We briefly discuss the following lines of work: deviation detection, behavioral pattern mining, trace clustering, process monitoring, performance measurement and prediction, and process comparison, and we provide a brief overview of each.
4.4.1 Deviation detection
Process-oriented deviation detection aims to detect outliers in terms of process executions. In this context, in [74], partial order representations of event data are used to quantify deviations of primary process behavior. In [75], we present a framework that can detect anomalous behavioral patterns, taking a given reference model as a basis for the anomaly detection. These patterns are represented as partially ordered behavioral graphs. Denisov et al. [76] assume a partial order event log and focus on the repair/augmentation of event logs, i.e., to anticipate the possible occurrence of missing events. However, partial orders are not explicitly used to model the uncertainty.
4.4.2 Behavioral pattern mining
Similar to frequent itemset mining [77], behavioral pattern mining techniques aim to find common behavioral patterns that are shared by sub-fragments of the recorded process instances. In [78], the authors propose to discover episodes, i.e., partial orders defined over events. However, the goal of the work is to find frequent patterns in terms of episodes, i.e., an episode is typically describing a subset of the events in a trace. As an input, classical event logs are used. As such, the work bears great similarity to work from the field of partial-order aware frequent pattern mining [79, 80]. In [81, 82], the authors adopt partial orders on the observed events and use the notion of behavioral patterns to refer to frequently occurring sub-orders of the collection of partial order traces. In [83], the authors propose a semi-supervised approach for pattern detection. The user provides a set of patterns, i.e., specified in a DSL, which are transformed into partial order representations. Subsequently, pattern detection and matching are applied to find meaningful and frequent matches.
4.4.3 Trace clustering
In trace clustering, the goal is to combine process executions that share some form of commonality, i.e., either behavioral or based on other “environment variables.” In [84], a generic framework for trace clustering, i.e., grouping of different recorded traces in an event log, is proposed. The proposed technique assumes the observed event data to be a total order of events. However, it allows the centroids of the clustering method to be arbitrary behavioral artifacts, including partial order runs derived from a process model.
4.4.4 Process monitoring, performance measurement and prediction
In this section, we cover techniques that focus on process monitoring (i.e., covering ongoing cases) and techniques that focus on performance measurement of (ongoing/historical) cases of a process. In [85], the authors assume that event data describe activity instances. The authors propose to learn queueing networks based on the process using schedules and event data as input. The WoMan framework [86] describes a general workflow management framework based on first-order logic that assumes that activity start and end are always recorded. As such, the framework supports the partial ordering of workflow tasks. The framework has also been extended for prediction [87, 88]. In [89], the authors assume that cases describe activity instances with an associated partial order. The orders are, however, used in an implicit manner as the authors assess various optimization strategies to perform “cost-informed” process improvement.
In [90], the authors present an event-interval-based performance measurement approach. The authors assume the potential existence of start and end timestamps and use the intervals to define different notions of time intervals, e.g., case-level intervals, waiting time intervals, etc. However, the proposed measurements do not explicitly exploit the partial order nature of the intervals considered. In [91], the authors propose a performance measurement and prediction framework. The technique assumes that the event data are partially ordered and use partial order alignments to quantify the observed event data and compute alternative execution scenarios using an arbitrary reference model.
A noteworthy sub-field of performance measurement and prediction is queue mining [68, 92, 93]. In these works, the process is assumed to be representable by some form of queueing network. Often, a detailed level of timestamp granularity is assumed, yielding partial orders over the observed events. However, the partial order representation is often not explicitly used or exploited.
4.4.5 Process comparison
In process comparison, the goal is to compare two groups of executions of a process and identify significant commonalities and differences. In [94], the authors define a partial order over the events observed in the event log. The event data are subsequently mapped onto perspective graphs which allows the user to spot significant differences between logs on an arbitrarily chosen data perspective. Similar approaches are presented in [67, 95]; however, said approaches are strictly defined for model-model comparison.
4.4.6 Visualization
Recently, different authors have considered novel ways to visualize partial order event data. In [96], the authors propose a visualization tool that allows the user to group events happening in the same hour, day, month, etc. Clearly, such a grouping yields a partial order on the observed events (even if one timestamp is recorded per event). The technique also supports mixed granularity in the timestamp recording of events. Similarly, in [97], the authors propose a generalization of the “Variant Explorer.”
5 Discussion
In this section, we discuss several interesting dimensions of the use of partial orders in the context of process mining. In Sect. 5.1, we discuss the distribution of the works considered in the context of the different categories discussed (data extraction, process discovery, etc.). Additionally, we present a chronological overview of the development of partial-order-based process mining. In Sect. 5.2, we sketch various novel directions in process mining, where the use of partial orders as a representation of processes may be of explicit benefit. Finally, in Sect. 5.3, we reflect on challenging aspects of the use of partial orders in the context of process mining.
5.1 Overview
In this section, we present a structured overview of the results of our survey, i.e., as discussed in Sect. 4.
Consider Fig. 5, in which we present the general distribution of the work considered, over the different categories identified.Footnote 9
We have separated Petri net synthesis from general process discovery. Additionally, for both process discovery and conformance checking, we differentiate between certain and uncertain semantics. Interestingly, extraction, process discovery and Petri net synthesis together span slightly over half of the works considered. Conformance checking represents 15% of the considered techniques. In both process discovery and conformance checking, the number of works considering the uncertain semantics is relatively low. In the other application areas, the process monitoring, performance measurement and prediction category (represented as Monitoring/Prediction in the figure) stands out, representing roughly 14% of the techniques covered. Conceptually, this (over)representation makes sense since a vast majority of the works considers the process performance dimension (both in monitoring and prediction) which typically requires the use of both start and end timestamps.
In Fig. 6, we plot the chronological development of partial-order-based process mining. We observe that the first work considering event data as a partial order stems from 1998. An initial spike of articles is observed around the year 2009, and later in 2015. In general, after 2015, the number of works supporting partial orders is higher compared to the years before. This is in line with the general increase in event data availability as well as the more recently developed research line on process mining with uncertain data.
5.2 Outlook
As indicated, partial orders are primarily used when either both start and end timestamps of events are present, or, when some form of uncertainty is present in the data. In this section, we highlight other application areas as well as interesting novel lines of work.
5.2.1 Data logging quality
As highlighted by the uncertainty semantics, logging quality is a prominent issue in real event data. The survey shows that tackling various data logging quality issues using partial orders as a representation is a viable solution. However, interestingly, both in process discovery and conformance checking, the vast majority of techniques assume the certain semantics (cf. Sect. 5.1). Hence, more work towards uncertainty in event data and correspondingly using partial order event data as an intermediary representation can be done. In some instances, certain semantics, combined with data quality issues, are also applicable. For example, if the level of detail of logging is limited, e.g., events are recorded on a day level, a partial order can be used to express that the events occurred on the same day.
5.2.2 Event abstraction
Recently, various studies investigated the application of existing process mining techniques, i.e., process discovery, conformance, or enhancement studies, on non-standard event data sources. Examples include, among various others, customer journey analysis [98], various applications in healthcare [99] and the analysis of sensor data [100]. In such contexts, the recorded data are often of a different level of granularity compared to the level at which one aims to analyze the process. The level at which the data are recorded is often more fine-grained than the intended target level of analysis. To accommodate for this mismatch, a novel branch of techniques emerged, focusing on the application of (semi)-automated techniques that lift the recorded event data to the business level, i.e., referred to as event abstraction techniques [101]. Consider Fig. 7, in which the concept of event abstraction is exemplified.
Example visualization of the problem of logging at different granularity levels versus the business activity level (adopted from [101]). Multiple recorded events constitute a high-level business process activity, e.g., the event sequence \(\langle \texttt {reg}\_\texttt {act}\_\texttt {start}, \texttt {opsi}\_\texttt {pp}\_\texttt {open}, \texttt {reg}\_\texttt {act}\_\texttt {end} \rangle \) corresponds to register request
The two high-level business activity instances, i.e., register request and check ticket, are recorded as sequences of lower-level events. Hence, even if recording the process activities occurs in an atomic fashion, when abstracting these recorded activities to a higher level notion, events recording both start and end times of the higher-level business activities appear. As such, analysis of the process data, i.e., at a higher level of abstraction, greatly benefits from techniques that naively support partially ordered event data.
5.2.3 Accurate performance quantification
Performance measures can be improved by taking the partial order of events in an event log into account. That is, waiting time for an activity can be considered to start with the completion of the previous sequential event in the trace—rather than simply the previous event in the trace. That is, an event a that was executed concurrently to an event b should not influence the waiting time for b. The partial order, derived from a process model or otherwise, informs the last sequential event in the trace.
5.3 Challenges
Here, we identify challenges in the context of the use of partial orders as an (intermediate) event data representation. We discuss tool support and standardization, as well as computational complexity.
5.3.1 Tool support and standardization
Whereas totally ordered event logs are well supported by process mining tools and established file-formats such as CSV and XES,Footnote 10 tool support for partially ordered logs is limited and fragmented. To the best of our knowledge, there are no well-established file formats or frameworks for storing partially ordered trace sets or event logs. However, in [59], the notion of Object-Centric Event Logs is presented, i.e., a first conceptual design novel event log format that more explicitly takes the relationship between events and objects (e.g., items belonging to an order) into account. In the definition (Def. 3 of the paper), a partial order over the events is assumed. As such, events are considered to be atomic, yet, may be recorded at the same point in time. Furthermore, when applying partially order-based tools, it is up to the user to verify that the semantics that the tool that produced the partial orders assumes match the semantics that the tool that uses them as an input assumes. Arguably, said semantics of partial orders are, from a cognitive perspective, more challenging to understand, analyze, and reason with than total orders. Hence, we identify a clear need for a standardized framework to support partial orders as an event data representation.
5.3.2 Computational complexity
The computational complexity of partial orders can be prohibitively high. The number of totally ordered traces supported by a partially ordered trace (in the case of certain semantics) is exponential in the length and factorial in the breadth of the trace, where length denotes ordered parts and breadth denotes unordered (i.e., concurrent/interleaved) parts. Figure 4 shows an example, and a completely unordered trace of 10 events has \(10!{=}3\,628\,800\) corresponding totally ordered traces. It is not uncommon for log traces to have over 100 events. This clearly shows the need for optimizations, such as the design of divide and conquer computational strategies [102], to cope with said computational complexity.
6 Conclusion
Existing process mining techniques use total orders of process activities as their primary input. However, the sheer nature of activities, i.e., having a clear start and end point in time, and the inherent uncertainty in process data logging are not supported by a total order assumption. Hence, we advocate the use of partial orders as an intermediary data representation for process mining algorithms. We have evaluated the current state of the art in process mining w.r.t. the use of partial orders. We observe that partial orders are predominantly used in process discovery and conformance checking. Most work focuses on start/end timestamp recording, i.e., handling uncertainty in event logging is a relatively new development. Various works have been identified that cover other interesting application areas of process mining. We have identified different interesting areas in process mining where partial orders are of particular interest. Finally, we have elaborated on the challenges expected in adopting partial orders as a primary citizen in process mining algorithms.
Notes
In case either only the start or end time of an activity is recorded, it is trivial to transform such data to the form presented in Table 2, i.e., by copying the missing timestamp from the available timestamp.
Observe that a Petri net with designated initial and final marking is also referred to as an Accepting Net.
Observe that a minor fraction of the work identified spans multiple categories, e.g., extraction and process discovery.
References
van der Aalst WMP (2016) Process mining: data science in action, 2nd edn
Augusto A, Conforti R, Dumas M, Rosa ML, Maggi FM, Marrella A, Mecella M, Soo A (2019) Automated discovery of process models from event logs: review and benchmark. IEEE Trans Knowl Data Eng 31(4):686–705
Dijkman RM, Dumas M, Ouyang C (2008) Semantics and analysis of business process models in BPMN. Inf Softw Technol 50(12):1281–1294
Carmona J, van Dongen BF, Solti A, Weidlich M (2018) Conformance checking: relating processes and models
de Leoni M, van der Aalst WMP (2013) Data-aware process mining: discovering decisions in processes using alignments. In: Shin SY, Maldonado JC (eds.) Proceedings of the 28th annual ACM symposium on applied computing, SAC ’13. Coimbra, Portugal, March 18–22, 2013, pp 1454–1461
Teinemaa I, Dumas M, Rosa ML, Maggi FM (2019) Outcome-oriented predictive process monitoring: review and benchmark. ACM Trans Knowl Discov Data 13(2):17–11757
Murata T (1989) Petri nets: properties, analysis and applications. Proc IEEE 77(4):541–580
OMG: Business Process Model and Notation (BPMN), Version 2.0.2. Object Management Group
Lassen KB, van Dongen BF (2008) Translating message sequence charts to other process languages using process mining. Trans Petri Nets Other Model Concurr 1:71–85
Vogler W (2002) Partial order semantics and read arcs. Theor Comput Sci 286(1):33–63
Berthomieu B, Diaz M (1991) Modeling and verification of time dependent systems using time petri nets. IEEE Trans Software Eng 17(3):259–273
Snyder H (2019) Literature review as a research methodology: an overview and guidelines. J Bus Res 104:333–339
Goodman LA (1961) Snowball sampling. Ann Math Stat 148–170
van der Aalst WMP, Weijters T, Maruster L (2004) Workflow mining: discovering process models from event logs. IEEE Trans Knowl Data Eng 16(9):1128–1142
Maaradji A, Dumas M, Rosa ML, Ostovar A (2015) Fast and accurate business process drift detection. In: Motahari-Nezhad HR, Recker J, Weidlich M (eds) Business process management—13th international conference, BPM 2015, Innsbruck, Austria, August 31–September 3, 2015, Proceedings. Lecture Notes in Computer Science, vol 9253, pp 406–422
Nielsen M, Plotkin GD, Winskel G (1981) Petri nets, event structures and domains, part I. Theor Comput Sci 13:85–108
van Beest NRTP, Dumas M, García-Bañuelos L, Rosa ML (2015) Log delta analysis: interpretable differencing of business process event logs. In: Motahari-Nezhad HR, Recker J, Weidlich M (eds) Business process management—13th international conference, BPM 2015, Innsbruck, Austria, August 31–September 3, 2015, Proceedings. Lecture Notes in Computer Science, vol 9253, pp 386–405
Diamantini C, Genga L, Potena D, van der Aalst WMP (2016) Building instance graphs for highly variable processes. Expert Syst Appl 59:101–118
Pegoraro M, Uysal MS, van der Aalst WMP (2021) PROVED: A tool for graph representation and analysis of uncertain event data. In: Buchs D, Carmona J (eds) Application and theory of petri nets and concurrency—42nd international conference, PETRI NETS 2021, Virtual Event, June 23–25, 2021, Proceedings. Lecture Notes in Computer Science, vol 12734, pp 476–486
Pegoraro M, Uysal MS, van der Aalst WMP (2020) Efficient time and space representation of uncertain event data. Algorithms 13(11):285
Pegoraro M, Uysal MS, van der Aalst WMP (2020) Efficient construction of behavior graphs for uncertain event data. In: Abramowicz W, Klein G (eds) Business information systems—23rd international conference, BIS 2020, Colorado Springs, CO, USA, June 8–10, 2020, Proceedings. Lecture Notes in Business Information Processing, vol 389, pp 76–88
Lu X, Fahland D, van der Aalst WMP (2014) Conformance checking based on partially ordered event data. In: International conference on business process management—Workshops. LNBIP, vol 202, pp 75–88
Fishburn PC (1970) Intransitive indifference with unequal indifference intervals. J Math Psychol 7(1):144–149
Leemans SJJ, Fahland D, van der Aalst WMP (2015) Using life cycle information in process discovery. In: International conference on business process management—workshops. LNBIP, vol 256, pp 204–217
Senderovich A, Weidlich M, Gal A (2017) Temporal network representation of event logs for improved performance modelling in business processes. In: Carmona J, Engels G, Kumar A (eds) Business process management—15th international conference, BPM 2017, Barcelona, Spain, September 10–15, 2017, Proceedings. Lecture Notes in Computer Science, vol 10445, pp 3–21
Allen JF (1983) Maintaining knowledge about temporal intervals. Commun ACM 26(11):832–843
Dumas M, García-Bañuelos L (2015) Process mining reloaded: Event structures as a unified representation of process models and event logs. In: International conference on application and theory of petri nets and concurrency. LNCS, vol 9115, pp 33–48
Fahland D, van der Aalst WMP (2015) Model repair: aligning process models to reality. Inf Syst 47:220–243
Leemans SJJ, Fahland D (2020) Information-preserving abstractions of event data in process mining. Knowl Inf Syst 62(3):1143–1197
Agrawal R, Gunopulos D, Leymann F (1998) Mining process models from workflow logs. In: Schek H, Saltor F, Ramos I, Alonso G (eds) Advances in database technology—EDBT’98, 6th international conference on extending database technology, Valencia, Spain, March 23–27, 1998, Proceedings. Lecture Notes in Computer Science, vol 1377, pp 469–483
Acampora G, Vitiello A, Di Stefano B, van der Aalst W, Günther C, Verbeek E (2017) IEEE 1849tm: the XES standard. IEEE Comput Intell Mag 4–8
Burattin A, Sperduti A (2010) Heuristics miner for time intervals. In: 18th European symposium on artificial neural networks, ESANN 2010, Bruges, Belgium, April 28–30, 2010, Proceedings
Weijters AJMM, van der Aalst WMP (2003) Rediscovering workflow models from event-based data using little thumb. Integr Comput Aided Eng 10(2):151–162
Wen L, Wang J, van der Aalst WMP, Huang B, Sun J (2009) A novel approach for process mining based on event types. J Intell Inf Syst 32(2):163–190
Lorenz R, Juhás G (2006) Towards synthesis of petri nets from scenarios. In: Donatelli S, Thiagarajan PS (eds) Petri nets and other models of concurrency—ICATPN 2006, 27th International conference on applications and theory of petri nets and other models of concurrency, Turku, Finland, June 26–30, 2006, Proceedings. Lecture Notes in Computer Science, vol 4024, pp 302–321
Lorenz R, Mauser S, Juhás G (2007) How to synthesize nets from languages: a survey. In: Henderson SG, Biller B, Hsieh M, Shortle J, Tew JD, Barton RR (eds) Proceedings of the winter simulation conference, WSC 2007, Washington, DC, USA, December 9–12, 2007, pp 637–647
Bergenthum R, Desel J, Mauser S (2009) Comparison of different algorithms to synthesize a petri net from a partial language. Trans Petri Nets Other Model Concurr 3:216–243
Bergenthum R, Desel J, Lorenz R, Mauser S (2008) Synthesis of petri nets from infinite partial languages. In: Billington J, Duan Z, Koutny M (eds) 8th International conference on application of concurrency to system design (ACSD 2008), Xi’an, China, June 23–27, 2008, pp 170–179
Bergenthum R, Desel J, Lorenz R, Mauser S (2008) Synthesis of petri nets from scenarios with viptool. In: International conference on applications and theory of petri nets. LNCS, vol 5062, pp 388–398
Bergenthum R, Desel J, Lorenz R, Mauser S (2008) Synthesis of petri nets from finite partial languages. Fundam Inform 88(4):437–468
Bergenthum R, Mauser S (2011) Folding partially ordered runs. In: Desel J, Yakovlev A (eds) Proceedings of the workshop applications of region theory 2011, Newcastle upon Tyne, UK, June 21, 2011. CEUR workshop proceedings, vol 725, pp 52–62
Lorenz R, Desel J, Juhás G (2013) Models from scenarios. Trans Petri Nets Other Model Concurr 7:314–371
Bergenthum R (2017) Synthesizing petri nets from Hasse diagrams. In: Carmona J, Engels G, Kumar A (eds) Business process management—15th international conference, BPM 2017, Barcelona, Spain, September 10–15, 2017, Proceedings. Lecture Notes in Computer Science, vol 10445, pp 22–39
Herbst J (2000) A machine learning approach to workflow management. In: de Mántaras RL, Plaza E (eds) Machine learning: ECML 2000, 11th European conference on machine learning, Barcelona, Catalonia, Spain, May 31–June 2, 2000, Proceedings. Lecture Notes in Computer Science, vol 1810, pp 183–194
Herbst J, Karagiannis D (2000) Integrating machine learning and workflow management to support acquisition and adaptation of workflow models. Intell Syst Account Finance Manag 9(2):67–92
Herbst J (2000) Dealing with concurrency in workflow induction. In: European concurrent engineering conference. SCS Europe. Citeseer
Golani M, Pinter SS (2003) Generating a process model from a process audit log. In: van der Aalst WMP, ter Hofstede AHM, Weske M (eds) Business process management, international conference, BPM 2003, Eindhoven, The Netherlands, June 26–27, 2003, Proceedings. Lecture Notes in Computer Science, vol 2678, pp 136–151
van Dongen BF, van der Aalst WMP (2004) Multi-phase process mining: building instance graphs. In: International conference on conceptual modeling. LNCS, vol 3288, pp 362–376
Schimm G (2004) Mining exact models of concurrent workflows. Comput Ind 53(3):265–281
Bergenthum R, Desel J, Mauser S, Lorenz R (2009) Construction of process models from example runs. Trans Petri Nets Other Model Concurr 2:243–259
van Dongen BF, Desel J, van der Aalst WMP (2012) Aggregating causal runs into workflow nets. Trans Petri Nets Other Model Concurr 6:334–363
Ferilli S, Esposito F (2013) A logic framework for incremental learning of process models. Fundam Inform 128(4):413–443
de León HP, Rodríguez C, Carmona J, Heljanko K, Haar S (2015) Unfolding-based process discovery. In: Finkbeiner B, Pu G, Zhang L (eds) Automated technology for verification and analysis—13th international symposium, ATVA 2015, Shanghai, China, October 12–15, 2015, Proceedings. Lecture Notes in Computer Science, vol 9364, pp 31–47
de León HP, Rodríguez C, Carmona J (2015) POD: A tool for process discovery using partial orders and independence information. In: International conference on business process management—Demos. CEUR WP, vol 1418, pp 100–104
Bergenthum R, Meis B (2017) Mining with eve: process discovery and event structures. In: van der Aalst WMP, Bergenthum R, Carmona J (eds) Proceedings of the international workshop on algorithms and theories for the analysis of event data 2017 satellite event of the conferences: 38th international conference on application and theory of petri nets and concurrency petri nets 2017 and 17th international conference on application of concurrency to system design ACSD 2017, Zaragoza, Spain, June 26–27, 2017. CEUR Workshop Proceedings, vol 1847, pp 71–75
Mokhov A, Carmona J (2015) Event log visualisation with conditional partial order graphs: from control flow to data. In: International conference on application and theory of petri nets and concurrency. CEUR WP, vol 1371, pp 16–30
van der Aalst WMP, Kalenkova AA, Rubin VA, Verbeek E (2015) Process discovery using localized events. In: Devillers RR, Valmari A (eds) Application and theory of petri nets and concurrency—36th international conference, PETRI NETS 2015, Brussels, Belgium, June 21–26, 2015, Proceedings. Lecture Notes in Computer Science, vol 9115, pp 287–308
Bergenthum R (2019) Prime miner: process discovery using prime event structures. In: International conference on process mining, pp 41–48
van der Aalst WMP (2019) Object-centric process mining: dealing with divergence and convergence in event data. In: International conference on software engineering and formal methods. LNCS, vol 11724, pp 3–25
Pegoraro M, Uysal MS, van der Aalst WMP (2019) Discovering process models from uncertain event data. In: Francescomarino CD, Dijkman RM, Zdun U (eds) Business process management workshops—BPM 2019 international workshops, Vienna, Austria, September 1–6, 2019, revised selected papers. Lecture Notes in Business Information Processing, vol 362, pp 238–249
Rozinat A, van der Aalst WMP (2008) Conformance checking of processes based on monitoring real behavior. Inf Syst 33(1):64–95
van der Aalst WMP, Adriansyah A, van Dongen BF (2012) Replaying history on process models for conformance checking and performance analysis. Wiley Interdiscip Rev Data Min Knowl Discov 2(2):182–192
Desel J, Juhás G, Lorenz R, Neumair C (2003) Modelling and validation with viptool. In: van der Aalst WMP, ter Hofstede AHM, Weske M (eds) Business process management, international conference, BPM 2003, Eindhoven, The Netherlands, June 26–27, 2003, Proceedings. Lecture Notes in Computer Science, vol 2678, pp 380–389
Juhás G, Lorenz R, Desel J (2005) Can I execute my scenario in your net? In: Ciardo G, Darondeau P (eds) Applications and theory of petri nets 2005, 26th international conference, ICATPN 2005, Miami, USA, June 20–25, 2005, Proceedings. Lecture Notes in Computer Science, vol 3536, pp 289–308
Bergenthum R, Desel J, Juhás G, Lorenz R (2006) Can I execute my scenario in your net? viptool tells you! In: Donatelli S, Thiagarajan PS (eds) Petri nets and other models of concurrency—ICATPN 2006, 27th international conference on applications and theory of petri nets and other models of concurrency, Turku, Finland, June 26–30, 2006, Proceedings. Lecture Notes in Computer Science, vol 4024, pp 381–390
Lu X, Mans R, Fahland D, van der Aalst WMP (2014) Conformance checking in healthcare based on partially ordered event data. In: IEEE emerging technology and factory automation, pp 1–8
Armas-Cervantes A, Baldan P, Dumas M, García-Bañuelos L (2014) Behavioral comparison of process models based on canonically reduced event structures. In: International conference on business process management. LNCS, vol 8659, pp 267–282
Senderovich A, Weidlich M, Yedidsion L, Gal A, Mandelbaum A, Kadish S, Bunnell CA (2016) Conformance checking and performance improvement in scheduled processes: a queueing-network perspective. Inf Syst 62:185–206
de Leoni M, Lanciano G, Marrella A (2018) Aligning partially-ordered process-execution traces and models using automated planning. In: International conference on automated planning and scheduling, pp 321–329
Ghallab M, Nau DS, Traverso P (2004) Automated planning: theory and practice
Pegoraro M, van der Aalst WMP (2019) Mining uncertain event data in process mining. In: International conference on process mining, ICPM 2019, Aachen, Germany, June 24–26, 2019, pp 89–96
Pegoraro M, Uysal MS, van der Aalst WMP (2021) Conformance checking over uncertain event data. Inf Syst 102:101810
van der Aa H, Leopold H, Weidlich M (2020) Partial order resolution of event logs for process conformance checking. Decis Support Syst 136:113347
Lu X, Fahland D, van den Biggelaar FJHM, van der Aalst WMP (2015) Detecting deviating behaviors without models. In: Reichert M, Reijers HA (eds) Business process management workshops—BPM 2015, 13th international workshops, Innsbruck, Austria, August 31–September 3, 2015, Revised Papers. Lecture Notes in Business Information Processing, vol 256, pp 126–139
Genga L, Alizadeh M, Potena D, Diamantini C, Zannone N (2018) Discovering anomalous frequent patterns from partially ordered event logs. J Intell Inf Syst 51(2):257–300
Denisov V, Fahland D, van der Aalst WMP (2020) Repairing event logs with missing events to support performance analysis of systems with shared resources. In: International conference on application and theory of petri nets and concurrency. LNCS, vol 12152, pp 239–259
Borgelt C (2012) Frequent item set mining. WIREs Data Min Knowl Discov 2(6):437–456
Leemans M, van der Aalst WMP (2014) Discovery of frequent episodes in event logs. In: Symposium on data-driven process discovery and analysis. LNBIP, vol 237, pp 1–31
Hwang S, Wei C, Yang W (2004) Discovery of temporal patterns from process instances. Comput Ind 53(3):345–364
Gwadera R, Antonini G, Labbi A (2011) Mining actionable partial orders in collections of sequences. In: Gunopulos D, Hofmann T, Malerba D, Vazirgiannis M (eds) Machine learning and knowledge discovery in databases—European conference, ECML PKDD 2011, Athens, Greece, September 5–9, 2011. Proceedings, Part I. Lecture Notes in Computer Science, vol 6911, pp 613–628
Diamantini C, Genga L, Potena D, Storti E (2014) Discovering behavioural patterns in knowledge-intensive collaborative processes. In: Appice A, Ceci M, Loglisci C, Manco G, Masciari E, Ras ZW (eds) New frontiers in mining complex patterns: third international workshop, NFMCP 2014, Held in conjunction with ECML-PKDD 2014, Nancy, France, September 19, 2014, Revised Selected Papers. Lecture Notes in Computer Science, vol 8983, pp 149–163
Diamantini C, Genga L, Potena D (2016) Behavioral process mining for unstructured processes. J Intell Inf Syst 47(1):5–32
Lu X, Fahland D, Andrews R, Suriadi S, Wynn MT, ter Hofstede AHM, van der Aalst WMP (2017) Semi-supervised log pattern detection and exploration using event concurrence and contextual information. In: On the move to meaningful internet systems. LNCS, vol 10573, pp 154–174
Boltenhagen M, Chatain T, Carmona J (2019) Generalized alignment-based trace clustering of process behavior. In: International conference on application and theory of petri nets and concurrency. LNCS, vol 11522, pp 237–257
Senderovich A, Weidlich M, Gal A, Mandelbaum A, Kadish S, Bunnell CA (2015) Discovery and validation of queueing networks in scheduled processes. In: Zdravkovic J, Kirikova M, Johannesson P (eds) Advanced information systems engineering: 27th international conference, CAiSE 2015, Stockholm, Sweden, June 8–12, 2015, Proceedings. Lecture Notes in Computer Science, vol 9097, pp 417–433
Ferilli S (2016) The woman formalism for expressing process models. In: Perner P (ed) Advances in data mining. applications and theoretical aspects—16th industrial conference, ICDM 2016, New York, NY, USA, July 13–17, 2016. Proceedings. Lecture Notes in Computer Science, vol 9728, pp 363–378
Ferilli S, Redavid D, Angelastro S (2017) Activity prediction in process management using the woman framework. In: Perner P (ed) Advances in data mining. Applications and theoretical aspects—17th industrial conference, ICDM 2017, New York, NY, USA, July 12–13, 2017, Proceedings. Lecture Notes in Computer Science, vol 10357, pp 194–208
Ferilli S, Esposito F, Redavid D, Angelastro S (2017) Extended process models for activity prediction. In: Kryszkiewicz M, Appice A, Slezak D, Rybinski H, Skowron A, Ras ZW (eds) Foundations of intelligent systems: 23rd international symposium, ISMIS 2017, Warsaw, Poland, June 26–29, 2017, Proceedings. Lecture Notes in Computer Science, vol 10352, pp 368–377
Low WZ, vanden Broucke SKLM, Wynn MT, ter Hofstede AHM, Weerdt JD, van der Aalst WMP (2016) Revising history for cost-informed process improvement. Computing 98(9):895–921
Suriadi S, Ouyang C, van der Aalst WMP, ter Hofstede AHM (2015) Event interval analysis: Why do processes take time? Decis Support Syst 79:77–98
van Zelst SJ, Santos LFR, van der Aalst WMP (2021) Data-driven process performance measurement and prediction: a process-tree-based approach. In: Nurcan S, Korthaus A (eds) Intelligent information systems: CAiSE Forum 2021, Melbourne, VIC, Australia, June 28–July 2, 2021, Proceedings. Lecture Notes in Business Information Processing, vol 424, pp 73–81
Senderovich A, Weidlich M, Gal A, Mandelbaum A (2014) Queue mining - predicting delays in service processes. In: Jarke M, Mylopoulos J, Quix C, Rolland C, Manolopoulos Y, Mouratidis H, Horkoff J (eds) Advanced information systems engineering—26th international conference, CAiSE 2014, Thessaloniki, Greece, June 16–20, 2014. Proceedings. Lecture Notes in Computer Science, vol 8484, pp 42–57
Senderovich A, Leemans SJJ, Harel S, Gal A, Mandelbaum A, van der Aalst WMP (2015) Discovering queues from event logs with varying levels of information. In: Reichert M, Reijers HA (eds) Business process management workshops—BPM 2015, 13th international workshops, Innsbruck, Austria, August 31–September 3, 2015, Revised Papers. Lecture Notes in Business Information Processing, vol 256, pp 154–166
Nguyen H, Dumas M, Rosa ML, ter Hofstede AHM (2018) Multi-perspective comparison of business process variants based on event logs. In: Trujillo J, Davis KC, Du X, Li Z, Ling TW, Li G, Lee M (eds) Conceptual modeling—37th international conference, ER 2018, Xi’an, China, October 22–25, 2018, Proceedings. Lecture Notes in Computer Science, vol 11157, pp 449–459
Weidlich M, Mendling J, Weske M (2011) Efficient consistency measurement based on behavioral profiles of process models. IEEE Trans Softw Eng 37(3):410–429
van der Aalst WMP, Santos LFR (2021) May I take your order?—on the interplay between time and order in process mining. In: Marrella A, Weber B (eds) Business process management workshops—BPM 2021 international workshops, Rome, Italy, September 6–10, 2021, revised selected papers. Lecture Notes in Business Information Processing, vol 436, pp 99–110
Schuster D, Schade L, van Zelst SJ, van der Aalst WMP (2021) Visualizing trace variants from partially ordered event data. In: Munoz-Gama J, Lu X (eds) Process mining workshops—ICPM 2021 international workshops, Eindhoven, The Netherlands, October 31–November 4, 2021, revised selected papers. Lecture Notes in Business Information Processing, vol 433, pp 34–46
Spenrath Y, Hassani M, van Dongen BF, Tariq H (2020) Why did my consumer shop? Learning an efficient distance metric for retailer transaction data. In: Machine learning and knowledge discovery in databases—Demos. LNCS, vol 12461, pp 323–338
Munoz-Gama J, Martin N, Fernández-Llatas C, Johnson O, Sepúlveda M (2020) Innovative informatics methods for process mining in health care. J Biomed Inform 109:103551
Koschmider A, Janssen D, Mannhardt F (2020) Framework for process discovery from sensor data. In: International workshop on enterprise modeling and information systems architectures. CEUR WP, vol 2628, pp 32–38
van Zelst SJ, Mannhardt F, de Leoni M, Koschmider A (2021) Event abstraction in process mining: literature review and taxonomy. Granul Comput 6(3):719–736
Verbeek HMW, van der Aalst WMP, Munoz-Gama J (2017) Divide and conquer: a tool framework for supporting decomposed discovery in process mining. Comput J 60(11):1649–1674
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Leemans, S.J.J., van Zelst, S.J. & Lu, X. Partial-order-based process mining: a survey and outlook. Knowl Inf Syst 65, 1–29 (2023). https://doi.org/10.1007/s10115-022-01777-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-022-01777-3