Abstract
Process mining aims at obtaining information about processes by analysing their past executions in event logs, event streams, or databases. Discovering a process model from a finite amount of event data thereby has to correctly infer infinitely many unseen behaviours. Thereby, many process discovery techniques leverage abstractions on the finite event data to infer and preserve behavioural information of the underlying process. However, the fundamental information-preserving properties of these abstractions are not well understood yet. In this paper, we study the information-preserving properties of the “directly follows” abstraction and its limitations. We overcome these by proposing and studying two new abstractions which preserve even more information in the form of finite graphs. We then show how and characterize when process behaviour can be unambiguously recovered through characteristic footprints in these abstractions. Our characterization defines large classes of practically relevant processes covering various complex process patterns. We prove that the information and the footprints preserved in the abstractions suffice to unambiguously rediscover the exact process model from a finite event log. Furthermore, we show that all three abstractions are relevant in practice to infer process models from event logs and outline the implications on process mining techniques.













Similar content being viewed by others
Notes
Available from https://data.4tu.nl/repository/collection:event_logs_real.
The filtered logs are available from http://doi.org/10.4121/uuid:adc42403-9a38-48dc-9f0a-a0a49bfb6371.
NB: if not all activities are present in a process model, PCC might report a negative \(p_n\).
References
van der Aalst WMP (2016) Process mining–data science in action, 2nd edn. Springer, Berlin. https://doi.org/10.1007/978-3-662-49851-4
Buijs JCAM, van Dongen BF, van der Aalst WMP (2014) Quality dimensions in process discovery: the importance of fitness, precision, generalization and simplicity. Int J Cooperative Inf Syst. https://doi.org/10.1142/S0218843014400012
van der Aalst WMP, Weijters AJMM, Maruster L (2004) Workflow mining: discovering process models from event logs. IEEE Trans Knowl Data Eng 16:1128–1142
vanden Broucke SKLM, Weerdt JD (2017) Fodina: a robust and flexible heuristic process discovery technique. Decis Support Syst 100:109–118
Leemans SJJ, Fahland D, van der Aalst WMP (2013) Discovering block-structured process models from event logs—a constructive approach. In: PETRI NETS 2013. Lecture notes in computer science, vol 7927. Springer, pp 311–329. https://doi.org/10.1007/978-3-642-38697-8_17
Augusto A, Conforti R, Dumas M, Rosa ML (2017) Split miner: discovering accurate and simple business process models from event logs. In: ICDM 2017. IEEE Computer Society, pp 1–10. https://doi.org/10.1109/ICDM.2017.9
Weidlich M, van der Werf JMEM (2012) On profiles and footprints—relational semantics for petri nets. In: Petri Nets
Polyvyanyy A, Armas-Cervantes A, Dumas M, García-Bañuelos L (2016) On the expressive power of behavioral profiles. Form Asp Comput 28:597–613
Leemans SJJ, Fahland D, van der Aalst WMP (2014) Discovering block-structured process models from event logs containing infrequent behaviour. In: Lohmann N, Song M, Wohed P (eds) Business process management workshops. Lecture notes in business information processing, vol 171. Springer, pp 66–78
Augusto A, Conforti R, Dumas M, Rosa ML, Maggi FM, Marrella A, Mecella M, Soo A (2018) Automated discovery of process models from event logs: review and benchmark. IEEE Trans Knowl Data Eng. arXiv:1705.02288
OMG (2011) Business Process Model and Notation (BPMN), Version 2.0. http://www.omg.org/spec/BPMN/2.0. Accessed 8 July 2019
van Zelst SJ, van Dongen BF, van der Aalst WMP (2018) Event stream-based process discovery using abstract representations. Knowl Inf Syst 54(2):407–435. https://doi.org/10.1007/s10115-017-1060-2
Syamsiyah A, van Dongen BF, van der Aalst WMP (2016) DB-XES: enabling process discovery in the large. In: SIMPDA 2016. LNBIP, vol 307. Springer, pp 53–77. https://doi.org/10.1007/978-3-319-74161-1_4
Syamsiyah A, van Dongen BF, van der Aalst WMP (2017) Recurrent process mining with live event data. In: BPM Workshops 2017. LNBIP, vol 308. Springer, pp 178–190
Weerdt JD, Backer MD, Vanthienen J, Baesens B (2012) A multi-dimensional quality assessment of state-of-the-art process discovery algorithms using real-life event logs. Inf Syst 37:654–676
Badouel E, Bernardinello L, Darondeau P (2015) Petri net synthesis. Springer, Berlin
de Medeiros, AKA, van Dongen BF, van der Aalst WMP, Weijters AJMM (2004) Process mining for ubiquitous mobile systems: an overview and a concrete algorithm. In: Baresi L, Dustdar S, Gall HC, Matera M (eds) Ubiquitous mobile information and collaboration systems, second CAiSE workshop, UMICS 2004, Riga, Latvia, 7–8 June 2004, Revised selected papers. Lecture notes in computer science, vol 3272. Springer, pp 151–165. https://doi.org/10.1007/978-3-540-30188-2_12
Wen L, Wang J, Sun J (2006) Detecting implicit dependencies between tasks from event logs. In: Zhou X, Li J, Shen HT, Kitsuregawa M, Zhang Y (eds) Frontiers of WWW Research and Development—APWeb 2006, 8th Asia-Pacific Web Conference, Harbin, China, 16–18 January 2006, Proceedings. Lecture notes in computer science, vol 3841. Springer, pp 591–603. https://doi.org/10.1007/11610113_52
Wen L, van der Aalst WMP, Wang J, Sun J (2007) Mining process models with non-free-choice constructs. Data Min Knowl Discov 15(2):145–180. https://doi.org/10.1007/s10618-007-0065-y
Wen L, Wang J, van der Aalst WMP, Huang B, Sun J (2010) Mining process models with prime invisible tasks. Data Knowl Eng 69(10):999–1021. https://doi.org/10.1016/j.datak.2010.06.001
Wen L, Wang J, Sun J (2007) Mining invisible tasks from event logs. In: Dong G, Lin X, Wang W, Yang Y, Yu JX (eds) Advances in data and web management, Joint 9th Asia-Pacific Web Conference, APWeb 2007, and 8th international conference, on web-age information management, WAIM 2007, Huang Shan, China, 16–18 June 2007, Proceedings. Lecture notes in computer science, vol 4505. Springer, pp 358–365. https://doi.org/10.1007/978-3-540-72524-4_38
Guo Q, Wen L, Wang J, Yan Z, Yu PS (2015) Mining invisible tasks in non-free-choice constructs. In: Motahari-Nezhad HR, Recker J, Weidlich M (eds) Business process management—13th international conference, BPM 2015, Innsbruck, Austria, August 31–September 3 2015, Proceedings. Lecture notes in computer science, vol 9253. Springer, pp 109–125. https://doi.org/10.1007/978-3-319-23063-4_7
Leemans SJJ, Fahland D, van der Aalst WMP (2014) Discovering block-structured process models from incomplete event logs. In: Ciardo G, Kindler E (eds) Application and theory of petri nets and concurrency—35th international conference, PETRI NETS 2014, Tunis, Tunisia, 23–27 June 2014. Proceedings. Lecture notes in computer science, vol 8489. Springer, pp 91–110. https://doi.org/10.1007/978-3-319-07734-5_6
Russell N, van der Aalst WMP, ter Hofstede AHM (2016) Workflow patterns: the definitive guide. MIT Press, Cambridge
Zha H, Wang J, Wen L, Wang C, Sun JG (2010) A workflow net similarity measure based on transition adjacency relations. Comput Ind 61:463–471
Sun J, Gu T, Qian J (2017) A behavioral similarity metric for semantic workflows based on semantic task adjacency relations with importance. IEEE Access 5:15609–15618
van Dongen BF, Dijkman RM, Mendling J (2008) Measuring similarity between business process models. In: CAiSE 2008. Lecture notes in computer science, vol 5074. Springer, pp 450–464. https://doi.org/10.1007/978-3-540-69534-9_34
Polyvyanyy A, Weidlich M Conforti R, Rosa ML, ter Hofstede AHM (2014) The 4c spectrum of fundamental behavioral relations for concurrent systems. In: Petri Nets
Wang J, He T, Wen L, Wu N, ter Hofstede AHM, Su J (2010) A behavioral similarity measure between labeled petri nets based on principal transition sequences—(short paper). In: OTM 2010. Lecture notes in computer science, vol 6426. Springer, pp 394–401
Becker M, Laue R (2012) A comparative survey of business process similarity measures. Comput Ind 63(2):148–167
Kunze M, Weidlich M, Weske M (2011) Behavioral similarity—a proper metric. In: Business process management 2011. Lecture Notes in Computer Science, vol 6896. Springer, pp 166–181
Kunze M, Weidlich M, Weske M (2015) Querying process models by behavior inclusion. Softw Syst Model 14(3):1105–1125. https://doi.org/10.1007/s10270-013-0389-6
Polyvyanyy A, Weidlich M, Weske M (2012) Isotactics as a foundation for alignment and abstraction of behavioral models. In: BPM
Weidlich M, Mendling J, Weske M (2012) Propagating changes between aligned process models. J Syst Softw 85:1885–1898
van der Werf JMEM, van Dongen BF, Hurkens CAJ, Serebrenik A (2009) Process discovery using integer linear programming. Fundam Inf 94(3–4):387–412. https://doi.org/10.3233/FI-2009-136
Schunselaar DMM, Verbeek E, van der Aalst WMP, Reijers HA (2013) A framework for efficiently deciding language inclusion for sound unlabelled wf-nets. In: Joint proceedings of the international workshop on petri nets and software engineering (PNSE’13) and the international workshop on modeling and business environments (ModBE’13), Milano, Italy, 24–25 June 2013. CEUR Workshop Proceedings, vol 989. CEUR-WS.org, pp 135–154
Leemans SJJ, Fahland D, van der Aalst WMP (2018) Scalable process discovery and conformance checking. Softw Syst Model 17(2):599–631. https://doi.org/10.1007/s10270-016-0545-x
Buijs JCAM, van Dongen BF, van der Aalst WMP (2012) A genetic algorithm for discovering process trees. In: Proceedings of the IEEE congress on evolutionary computation, CEC 2012, Brisbane, Australia, 10–15 June. IEEE, pp 1–8. https://doi.org/10.1109/CEC.2012.6256458
Molka T, Redlich D, Gilani W, Zeng X, Drobek M (2015) Evolutionary computation based discovery of hierarchical business process models. In: Abramowicz W (ed) Business information systems—18th international conference, BIS 2015, Poznań, Poland, 24–26 June 2015, Proceedings. Lecture notes in business information processing, vol 208. Springer, pp 191–204. https://doi.org/10.1007/978-3-319-19027-3_16
Leemans SJJ (2017) Robust process mining with guarantees. Ph.D. thesis, Eindhoven University of Technology
Polyvyanyy A, Vanhatalo J, Völzer H (2010) Simplified computation and generalization of the refined process structure tree. In: Bravetti M, Bultan T (eds) Web services and formal methods—7th international workshop, WS-FM 2010, Hoboken, NJ, USA, 16–17 September 2010. Revised Selected Papers. Lecture notes in computer science, vol 6551. Springer, pp 25–41. https://doi.org/10.1007/978-3-642-19589-1_2
Reisig W (1985) Petri nets: an introduction. Springer, New York
Gallo G, Longo G, Pallottino S (1993) Directed hypergraphs and applications. Discrete Appl Math 42(2):177–201. https://doi.org/10.1016/0166-218X(93)90045-P
Conforti R, Rosa ML, ter Hofstede AHM (2017) Filtering out infrequent behavior from business process event logs. IEEE Trans Knowl Data Eng 29(2):300–314. https://doi.org/10.1109/TKDE.2016.2614680
Leemans SJ, Fahland, D (2019) dfahland/exp-abstractions-in-pm-KAIS: original experiment. https://doi.org/10.5281/zenodo.3243981
Leemans SJJ, Fahland D (2019) Process models obtained from event logs with different information-preserving abstractions. https://doi.org/10.5281/zenodo.3243988
van Dongen B (2012) BPI challenge 2012 dataset. https://doi.org/10.4121/uuid:3926db30-f712-4394-aebc-75976070e91f
Acknowledgements
We thank Wil van der Aalst for his contribution to earlier versions of the directly follows and minimum self-distance abstractions [5]. Furthermore, we thank Alifah Syamsiyah for her corrections in the examples of the minimum self-distance abstraction.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Semantics of process trees
Definition A.1
(process tree semantics) Let \(\Sigma \) be an alphabet of activities and let \(\oplus _{\mathcal {L}}\) be a language-combination function, then
Then, the semantics of process tree operators can be described by a specific language-combination function \(\oplus _{\mathcal {L}}\), depending on the operator \(\oplus \):
Definition A.2
(process tree operator semantics) Let  be a language shuffle function shuffling the events in traces \(t_1 \ldots t_n\), and languages \(L_1 \ldots L_n\):
be a language shuffle function shuffling the events in traces \(t_1 \ldots t_n\), and languages \(L_1 \ldots L_n\):

Furthermore, let p(n) denote the set of all permutations of the numbers \(1 \ldots n\) and let q(n) denote the set of all subsets of the numbers \(1 \ldots n\). Then,

Footprints
1.1 Directly follows (Definition 5.2)
Let \(\alpha _{\text {dfg}}\) be a directly follows relation and let \(c = (\oplus , \Sigma _1, \ldots \Sigma _n)\) be a cut, consisting of a process tree operator  and a partition of activities with parts \(\Sigma _1 \ldots \Sigma _n\) such that \(\Sigma (\alpha _{\text {dfg}}) = \bigcup _{1 \leqslant i \leqslant n} \Sigma _i\) and \(\forall _{1 \leqslant i < j \leqslant n}~ \Sigma _i \cap \Sigma _j = \emptyset \).
and a partition of activities with parts \(\Sigma _1 \ldots \Sigma _n\) such that \(\Sigma (\alpha _{\text {dfg}}) = \bigcup _{1 \leqslant i \leqslant n} \Sigma _i\) and \(\forall _{1 \leqslant i < j \leqslant n}~ \Sigma _i \cap \Sigma _j = \emptyset \).
Exclusive choice. c is an exclusive choice cut in \(\alpha _{\text {dfg}}\) if
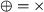 and
and
- x.1:
No part is connected to any other part:
\(\forall _{1 \leqslant i \leqslant n, 1 \leqslant j \leqslant n, i\ne j}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~ \lnot \alpha _{\text {dfg}}(a, b) \wedge \lnot \alpha _{\text {dfg}}(b, a)\):
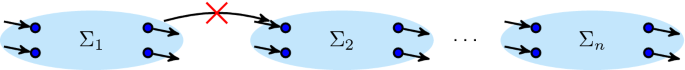
Sequential. c is a sequence cut in \(\alpha _{\text {dfg}}\) if \(\oplus = \rightarrow \) and
- s.1:
Each node in a part is indirectly and only connected to all nodes in the parts “after” it:
\( \forall _{1 \leqslant i < j \leqslant n}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~ \alpha _{\text {dfg}}\!\!^{+}\!(a, b) \wedge \lnot \alpha _{\text {dfg}}\!\!^{+}\!(b, a)\):

Interleaved. c is an interleaved cut in \(\alpha _{\text {dfg}}\) if \(\oplus = \leftrightarrow \) and
- i.1:
Between parts, all and only connections exist from an end to a start activity:
\( \forall _{1 \leqslant i \leqslant n, 1 \leqslant j \leqslant n, i \ne j}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~ \alpha _{\text {dfg}}(a, b) \Leftrightarrow (a \in {{\,\mathrm{End}\,}}\wedge b \in {{\,\mathrm{Start}\,}})\)):

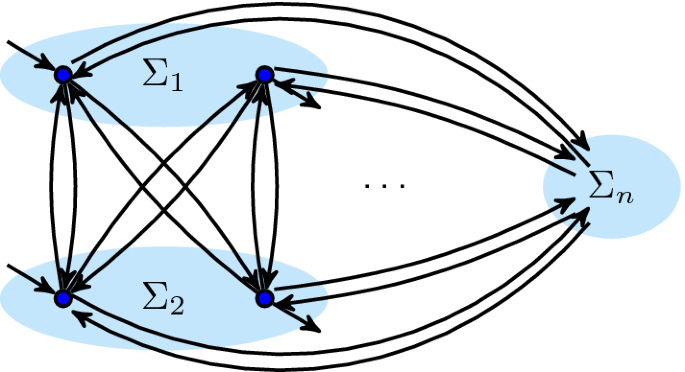
Concurrent. c is a concurrent cut in \(\alpha _{\text {dfg}}\) if \(\oplus = \wedge \) and
- c.1:
Each part contains a start and an end activity:
\(\forall _{1 \leqslant i \leqslant n}~ {{\,\mathrm{Start}\,}}(\alpha _{\text {dfg}}) \cap \Sigma _i \ne \emptyset \wedge {{\,\mathrm{End}\,}}(\alpha _{\text {dfg}}) \cap \Sigma _i \ne \emptyset \)
- c.2:
All parts are fully interconnected:
\( \forall _{1 \leqslant i < n, 1 \leqslant j \leqslant n, i \ne j}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~ \alpha _{\text {dfg}}(a, b) \wedge \alpha _{\text {dfg}}(b, a)\)):
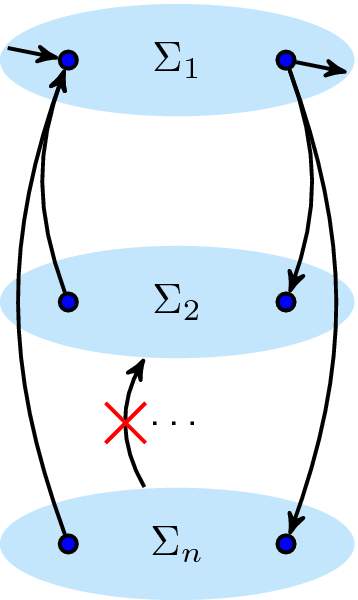
Loop. c is a loop cut in \(\alpha _{\text {dfg}}\) if \(\oplus \,=\,\circlearrowleft \) and
- l.1:
All start and end activities are in the body (i.e. the first) part:
\( {{\,\mathrm{Start}\,}}(\alpha _{\text {dfg}}) \cup {{\,\mathrm{End}\,}}(\alpha _{\text {dfg}}) \subseteq \Sigma _1\)
- l.2:
Only start/end activities in the body part have connections from/to other parts:
\( \forall _{2 \leqslant j \leqslant n}~ \forall _{a \in \Sigma _1, b \in \Sigma _j}~ \alpha _{\text {dfg}}(a, b) \Rightarrow a \in {{\,\mathrm{End}\,}}(\alpha _{\text {dfg}})\)
\( \forall _{2 \leqslant j \leqslant n}~ \forall _{a \in \Sigma _1, b \in \Sigma _j}~ \alpha _{\text {dfg}}(b, a) \Rightarrow a \in {{\,\mathrm{Start}\,}}(\alpha _{\text {dfg}})\)
- l.3:
Redo parts have no connections to other redo parts:
\( \forall _{2 \leqslant i \leqslant n, 2 \leqslant j \leqslant n, i\ne j}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~ \lnot \alpha _{\text {dfg}}(a, b) \wedge \lnot \alpha _{\text {dfg}}(b, a)\)
- l.4:
If an activity from a redo part has a connection to/from the body part, then it has connections to/from all start/end activities:
\( \forall _{2 \leqslant i \leqslant n}~ \forall _{a \in {{\,\mathrm{Start}\,}}, b \in \Sigma _i}~ \alpha _{\text {dfg}}(b, a) \Leftrightarrow \forall _{c \in {{\,\mathrm{Start}\,}}(\alpha _{\text {dfg}})}~ \alpha _{\text {dfg}}(b, c) \)
\( \forall _{2 \leqslant i \leqslant n}~ \forall _{a \in {{\,\mathrm{End}\,}}, b \in \Sigma _i}~ \alpha _{\text {dfg}}(a, b) \Leftrightarrow \forall _{c \in {{\,\mathrm{End}\,}}(\alpha _{\text {dfg}})}~ \alpha _{\text {dfg}}(c, b) \)):
1.2 Minimum self-distance (Definition 6.3)
Let \(\alpha _{\text {msd}}\) be a minimum self-distance graph and let \(c = (\oplus , \Sigma _1, \ldots \Sigma _n)\) be a cut, consisting of a process tree operator  and a partition of activities with parts \(\Sigma _1 \ldots \Sigma _n\) such that \(\Sigma (\alpha _{\text {msd}}) = \bigcup _{1 \leqslant i \leqslant n} \Sigma _i\) and \(\forall _{1 \leqslant i < j \leqslant n}~ \Sigma _i \cap \Sigma _j = \emptyset \).
and a partition of activities with parts \(\Sigma _1 \ldots \Sigma _n\) such that \(\Sigma (\alpha _{\text {msd}}) = \bigcup _{1 \leqslant i \leqslant n} \Sigma _i\) and \(\forall _{1 \leqslant i < j \leqslant n}~ \Sigma _i \cap \Sigma _j = \emptyset \).
Concurrent and interleaved. If \(\oplus = \wedge \) or \(\oplus = \leftrightarrow \), then in \(\alpha _{\text {msd}}\):
- ci.1:
There are no \(\alpha _{\text {msd}}\) connections between parts:
\(\forall _{i \in [1\ldots n], i \ne j \in [1 \ldots n]}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~ \lnot \alpha _{\text {msd}}(a, b)\)):
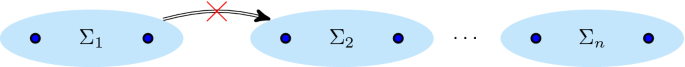
Loop. If \(\oplus = \circlearrowleft \) then in \(\alpha _{\text {msd}}\):
- l.1:
Each activity has an outgoing edge:
\(\forall _{a \in \Sigma (\alpha _{\text {msd}})}~ \exists _{b \in \Sigma (\alpha _{\text {msd}}), b \ne a}~ \alpha _{\text {msd}}(a, b)\)
- l.2:
All redo activities that have a connection to a body activity have connections to the same body activities:
$$\begin{aligned} \forall _{2 \leqslant i \leqslant n, 2 \leqslant j \leqslant n}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~&(\{ c \mid {\alpha _{\text {msd}}(a, c)} \} \cap \Sigma _1 \ne \emptyset \wedge {}\\&\{c \mid {\alpha _{\text {msd}}(b, c)} \} \cap \Sigma _1 \ne \emptyset ) \Rightarrow {}\\&\{c \mid {\alpha _{\text {msd}}(a, c)}\} \cap \Sigma _1 = \{c \mid {\alpha _{\text {msd}}(b, c)}\} \cap \Sigma _1 \end{aligned}$$
- l.3:
All body activities that have a connection to a redo activity have connections to the same redo activities:
$$\begin{aligned} \forall _{a, b \in \Sigma _1}~&(\{ c \mid {\alpha _{\text {msd}}(a, c)} \} \cap \Sigma (\alpha _{\text {msd}}) \setminus \Sigma _1 \ne \emptyset \wedge {}\\&\{ c \mid {\alpha _{\text {msd}}(b, c)} \} \cap \Sigma (\alpha _{\text {msd}}){\setminus }\Sigma _1 \ne \emptyset ) \Rightarrow {}\\&\{ c \mid {\alpha _{\text {msd}}(a, c)} \} \cap \Sigma (\alpha _{\text {msd}}){\setminus }\Sigma _1 = \{ c \mid {\alpha _{\text {msd}}(b, c)} \} \cap \Sigma (\alpha _{\text {msd}}){\setminus }\Sigma _1 \end{aligned}$$
- l.4:
No two activities from different redo children have an \(\alpha _{\text {msd}}\)-connection:
\(\forall _{2 \leqslant i < j \leqslant n}~ \forall _{a \in \Sigma _i, b \in \Sigma _j}~ \lnot \alpha _{\text {msd}}(a, b) \wedge \lnot \alpha _{\text {msd}}(b, a)\)
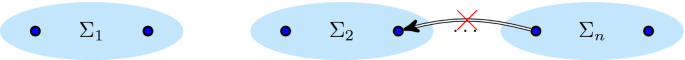
1.3 Sequence with  -constructs: (Definition 7.3)
-constructs: (Definition 7.3)
Let \(\Sigma \) be an alphabet of activities, let \(\alpha _{\text {dfg}}\) be a directly follows graph over \(\Sigma \) and let \(C = (\rightarrow , S_1, \ldots S_m)\) be a \(\rightarrow \)-cut of \(\alpha _{\text {dfg}}\) according to Definition 5.2. Then, a partial cut \((\rightarrow , \Sigma _1, \ldots \Sigma _n)\) is a partial \(\rightarrow \)-cut if there is a pivot\(\Sigma _p\) such that:
- s.1:
The partial cut is a consecutive part of C:
\( \exists _{1 \leqslant s \leqslant m}~ \forall _{1 \leqslant j \leqslant n}~ S_{s + j - 1} = \Sigma _j\)
- s.2:
There are no end activities before the pivot in the partial cut:
\( \forall _{x \in [1 \ldots p - 1]}~ \Sigma _x \cap {{\,\mathrm{End}\,}}(\alpha _{\text {dfg}}) = \emptyset \)
- s.3:
There are no start activities after the pivot in the partial cut:
\( \forall _{x \in [p + 1 \ldots n]}~ \Sigma _x \cap {{\,\mathrm{Start}\,}}(\alpha _{\text {dfg}}) = \emptyset \)
- s.4:
There are no directly follows edges bypassing the pivot in the partial cut:
\( \forall _{x \in [1 \ldots p - 1]}~ \forall _{a \in \Sigma _x}~ \forall _{\alpha _{\text {dfg}}(a, b)}~ \exists _{y \in [1 \ldots p]}~ b \in \Sigma _y \)
\( \forall _{y \in [p + 1 \ldots n]}~ \forall _{b \in \Sigma _y}~ \forall _{\alpha _{\text {dfg}}(a, b)}~ \exists _{x \in [p \ldots n]}~ a \in \Sigma _x \)
- s.5:
The partial cut can be tightly avoided:
$$\begin{aligned} \begin{aligned}&\exists _{1 \leqslant x< s, s + n \leqslant y \leqslant m}~ \exists _{a \in S_x, b \in S_y}~ \alpha _{\text {dfg}}(a, b) \\ {} \vee {}&\exists _{1 \leqslant x < s}~ \exists _{a \in S_x}~ a \in {{\,\mathrm{End}\,}}(\alpha _{\text {dfg}}) \\ {} \vee {}&\exists _{s + n \leqslant y \leqslant m}~ \exists _{b \in S_y}~ b \in {{\,\mathrm{Start}\,}}(\alpha _{\text {dfg}}) \\ {} \vee {}&\epsilon \in \alpha _{\text {dfg}}\end{aligned} \end{aligned}$$
end of definition
Partial cuts are considered only when close enough to the root of the process tree. We formalize this in sequence-optional stems (\({{\,\mathrm{so-stem}\,}}\)s). If we consider a process tree as a graph, then the so-stem is the connected subgraph that starts at the root of the tree and that consists of \(\rightarrow \)- and  -nodes. In addition,
-nodes. In addition,  -nodes are only included if such nodes have two children of which one is a \(\tau \):
-nodes are only included if such nodes have two children of which one is a \(\tau \):
Definition B.1
(sequence-optional tree and stem) A reduced process tree \(M = \oplus (M_1,\ldots M_n)\) is a so-tree if and only if \(\oplus = \rightarrow \), or if  , \(n = 2\) and \(M_i = \tau \) for some \(i\in [1\ldots n]\). The so-stem of a reduced process tree M is the smallest set \({{\,\mathrm{so-stem}\,}}(M)\) with:
, \(n = 2\) and \(M_i = \tau \) for some \(i\in [1\ldots n]\). The so-stem of a reduced process tree M is the smallest set \({{\,\mathrm{so-stem}\,}}(M)\) with:
if M is a so-tree, then \(M \in {{\,\mathrm{so-stem}\,}}(M)\);
for each \(\oplus (M_1,\ldots M_n) \in {{\,\mathrm{so-stem}\,}}(M)\) and each \(M_i, i\in [1\ldots n]\) holds: if \(M_i\) is a so-tree, then \(M_i \in {{\,\mathrm{so-stem}\,}}(M)\)
(For this set, we assume that subtrees can be distinguished.)
For instance, the following tree has an \({{\,\mathrm{so-stem}\,}}\), and \(P_1\), \(P_2\) and \(P_4\) are non-optional non-sequential subtrees:

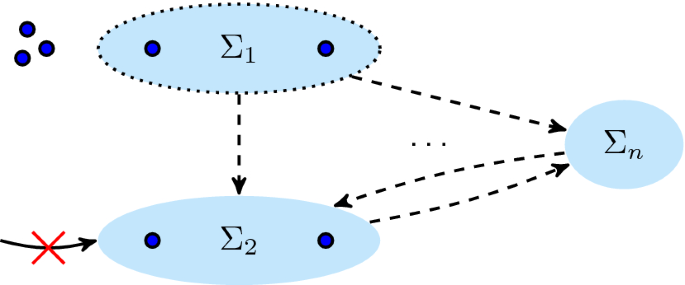
All subtrees shown here are sequential. Some subtrees can be skipped, however dependencies exist: if a subtree is executed, then each “P-sibling” at any higher level is executed as well. For instance, if \(\ldots _3\) is executed, then \(P_2\) is executed, as well as \(P_1\). The challenge in preserving information in the abstraction is to not combine \(P_1\) with \(P_2\) in a partial cut without \(\ldots _3\) and not to combine \(\ldots _3\) and \(P_4\) without \(P_2\).
Lemma B.1
(Partial \(\rightarrow \)-cut for process trees) Let M be a reduced process tree without duplicate activities and with an \({{\,\mathrm{so-stem}\,}}\), and let  . Let S be a partition of \(\Sigma (M)\) such that \(\forall _{i \in [1 \ldots n]}~ \Sigma (M'_i) \in S\) . Then, \((\rightarrow , \Sigma (M'_1), \ldots \Sigma (M'_n))\) is a partial \(\rightarrow \)-cut of \(\alpha _{\text {dfg}}(M)\) over S.
. Let S be a partition of \(\Sigma (M)\) such that \(\forall _{i \in [1 \ldots n]}~ \Sigma (M'_i) \in S\) . Then, \((\rightarrow , \Sigma (M'_1), \ldots \Sigma (M'_n))\) is a partial \(\rightarrow \)-cut of \(\alpha _{\text {dfg}}(M)\) over S.
By the reduction rules, at least one of the children is not optional: \(\exists _{i \in [1 \ldots n]}~ \lnot {\overline{?}}(M_i)\). This child is the pivot. By the reduction rules, a pivot cannot be a sequential node itself. Then, this lemma follows from inspection of semantics of process trees.
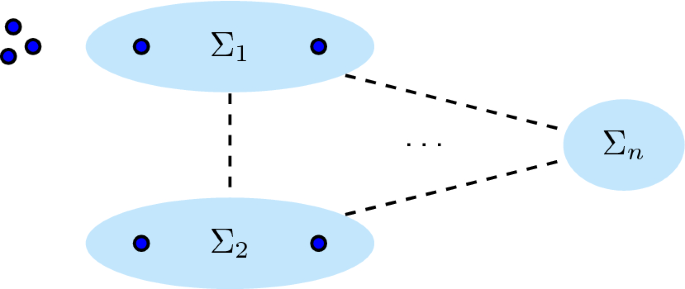
1.4 Concurrent-optional-Or:  (Definition 7.7)
(Definition 7.7)
Let \(\Sigma \) be an alphabet of activities, S a partition of \(\Sigma \), let \(\alpha _{\text {coo}}(S)\) be a coo-graph, let \(\alpha _{\text {dfg}}\) be a directly follows graph, and let  be a partial cut such that \(\forall _{1 \leqslant i \leqslant n}~ \Sigma _i \in S\). Then, C is a partial
be a partial cut such that \(\forall _{1 \leqslant i \leqslant n}~ \Sigma _i \in S\). Then, C is a partial  -cut if in \(\alpha _{\text {coo}}(S)\) and \(\alpha _{\text {dfg}}\):
-cut if in \(\alpha _{\text {coo}}(S)\) and \(\alpha _{\text {dfg}}\):
- o.1:
C is a part of a concurrent cut \((\wedge , X_1, \ldots X_m)\) (Definition 5.2):
\(\forall _{1 \leqslant i \leqslant n}~ \exists _{1 \leqslant j \leqslant m}~ \Sigma _i = X_j\)
- o.2:
all parts are interchangeable in \(\alpha _{\text {coo}}(S)\):

1.5 Concurrent-optional-Or: \(\wedge \) (Definition 7.8)
Let \(\Sigma \) be an alphabet of activities, S a partition of \(\Sigma \), let \(\alpha _{\text {coo}}(S)\) be a coo-graph, let \(\alpha _{\text {dfg}}\) be a directly follows graph, and let \(C = (\wedge , \Sigma _1, \ldots \Sigma _n)\) be a partial cut such that \(\forall _{1 \leqslant i \leqslant n}~ \Sigma _i \in S\). Then, C is a partial \(\wedge \)-cut if in \(\alpha _{\text {coo}}(S)\) and \(\alpha _{\text {dfg}}\):
- c.1:
C is a part of a concurrent cut \((\wedge , X_1, \ldots X_m)\) (Definition 5.2):
\(\forall _{1 \leqslant i \leqslant n}~ \exists _{1 \leqslant j \leqslant m}~ \Sigma _i = X_j\)
Furthermore, in \(\alpha _{\text {coo}}(S)\):
– EITHER –
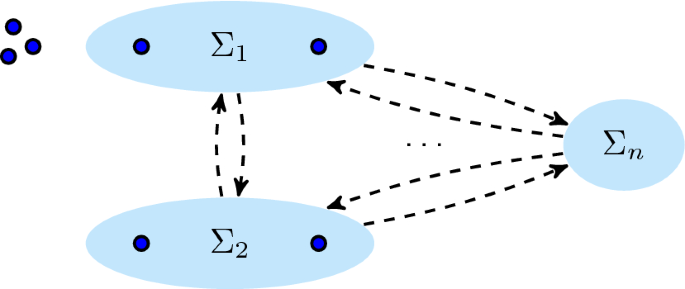
- c.2.1:
all parts bi-imply one another:
\(\forall _{1 \leqslant i < j \leqslant n}~ \Sigma _i\,\overline{\Rightarrow }\,\Sigma _j \wedge \Sigma _j\,\overline{\Rightarrow }\, \Sigma _i\)
– OR –
- c.3.1:
the first part is optional:
\({\overline{?}}{\Sigma _1}\)
- c.3.2:
The first part implies the other parts:
\(\forall _{i \in [2\ldots n]}~ \Sigma _1\,\overline{\Rightarrow }\,\Sigma _i\)
- c.3.3:
All non-first parts bi-imply one another:
\(\forall _{i, j \in [2\ldots n] \wedge i \ne j}~\Sigma _i\,\overline{\Rightarrow }\,\Sigma _j\)
- c.3.4:
No non-first part \(\Sigma _i\) is implied by any part not in C:

end of definition
Similar to so-stems, when considering a process tree M as a graph, the coo-stem of M is the connected subgraph starting at the root of M consisting of \(\wedge \)-,  -, and
-, and  nodes (the latter ones only if they have two children of which one is a \(\tau \)).
nodes (the latter ones only if they have two children of which one is a \(\tau \)).
Definition B.2
(concurrent-optional-or tree and stem) A reduced process tree \(M = \oplus (M_1,\ldots M_n)\) is a coo-tree if and only if  , or if
, or if  , \(n = 2\) and \(M_i = \tau \) for some \(i\in [1\ldots n]\). The coo-stem of a reduced process tree M is the smallest set \({{\,\mathrm{coo-stem}\,}}(M)\) with:
, \(n = 2\) and \(M_i = \tau \) for some \(i\in [1\ldots n]\). The coo-stem of a reduced process tree M is the smallest set \({{\,\mathrm{coo-stem}\,}}(M)\) with:
if M is a coo-tree, then \(M \in {{\,\mathrm{coo-stem}\,}}(M)\);
for each \(\oplus (M_1,\ldots M_n) \in {{\,\mathrm{coo-stem}\,}}(M)\) and each \(M_i, i\in [1\ldots n]\) holds: if \(M_i\) is a coo-tree, then \(M_i \in {{\,\mathrm{coo-stem}\,}}(M)\)
(For this set, we assume that subtrees can be distinguished.)
Lemma B.2
(partial \(\wedge \)- and  -cuts for process trees) Let M be a reduced process tree without duplicate activities and with an \({{\,\mathrm{coo-stem}\,}}\), and let \(M' = \oplus (M'_1, \ldots M'_n) \in {{\,\mathrm{coo-stem}\,}}\), with
-cuts for process trees) Let M be a reduced process tree without duplicate activities and with an \({{\,\mathrm{coo-stem}\,}}\), and let \(M' = \oplus (M'_1, \ldots M'_n) \in {{\,\mathrm{coo-stem}\,}}\), with  . Let S be a partition of \(\Sigma (M)\) such that \(\forall _{i \in [1\ldots n]}~\Sigma (M'_i) \in S\). Then, \((\oplus , \Sigma (M'_1), \ldots \Sigma (M'_n))\) is a partial \(\oplus \)-cut of the coo-graph \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\).
. Let S be a partition of \(\Sigma (M)\) such that \(\forall _{i \in [1\ldots n]}~\Sigma (M'_i) \in S\). Then, \((\oplus , \Sigma (M'_1), \ldots \Sigma (M'_n))\) is a partial \(\oplus \)-cut of the coo-graph \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\).
This lemma follows from inspection of the semantics of process trees.
Class counterexamples
1.1 \(\textsc {C}_{\text {dfg}}\)
An example for the necessity of Requirement \(\hbox {C}_{\mathrm{dfg}}.\hbox {i}.1\): the trees have different languages but equivalent directly follows graphs. These trees differ in their root operator: activity e can be executed before and after all other activities, making the difference between interleaved and concurrent invisible
An example for the necessity of Requirement \(\hbox {C}_{\mathrm{dfg}}.\hbox {i}.2\): four trees having different languages but equivalent directly follows graphs. The difference between these trees is “semi-long-dependencies”, e.g. in \(M_{23}\), a cannot be executed between b and c, and such dependencies cannot be captured by a directly follows relation
Uniqueness for \(\alpha _{\text {dfg}}\)
1.1 Lemma 5.2
Lemma: Take two reduced process trees of \(\textsc {C}_{\text {dfg}}\)\(K = \oplus (K_1, \ldots K_n)\) and \(M = \otimes (M_1, \ldots M_m)\) such that \(\oplus \ne \otimes \). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
Proof
Towards contradiction, assume that \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\). By the reduction rules of Sect. 4, \(n \geqslant 2\) and \(m \geqslant 2\). Perform case distinction on \(\oplus \) to prove that \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
 By semantics of the
By semantics of the  operator and the reduction rules, there exist at least n unconnected parts in \(\alpha _{\text {dfg}}(K)\) (see Lemma 5.1). As
operator and the reduction rules, there exist at least n unconnected parts in \(\alpha _{\text {dfg}}(K)\) (see Lemma 5.1). As  and by the semantics of the other operators, \(\alpha _{\text {dfg}}(M)\) is connected, so \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
and by the semantics of the other operators, \(\alpha _{\text {dfg}}(M)\) is connected, so \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).\(\oplus = \rightarrow \) By semantics of the \(\rightarrow \) operator, \(\alpha _{\text {dfg}}(K)\) is a chain of at least n clusters (see Lemma 5.1). As \(\otimes \ne \rightarrow \) and by the semantics of the other operators, \(\alpha _{\text {dfg}}(M)\) is not a chain (for
 , the graph is not connected while for \(\leftrightarrow \), \(\wedge \) and \(\circlearrowleft \), the graph is a clique), so \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
, the graph is not connected while for \(\leftrightarrow \), \(\wedge \) and \(\circlearrowleft \), the graph is a clique), so \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).\(\oplus = \wedge \) By semantics of the \(\wedge \) operator, \(\alpha _{\text {dfg}}(K)\) consists of at least n fully interconnected clusters (see Lemma 5.1). Perform case distinction on the (due to symmetry) remaining cases of \(\otimes \):
\(\otimes \,=\,\circlearrowleft \) We try to construct a concurrent cut \((\wedge , \Sigma _1, \ldots \Sigma _p)\) for M. Take an activity \(a \in {{\,\mathrm{Start}\,}}(M_1)\). By Requirement \(\hbox {C}_{\mathrm{dfg}}.\hbox {l}.1\), \(a \notin {{\,\mathrm{End}\,}}(M_1)\). Take an activity \(b \in \Sigma (M) \setminus \Sigma (M_1)\). Then, by semantics of \(\circlearrowleft \), \(\lnot \alpha _{\text {dfg}}(a, b)\) and by Requirement c.2, a and b are part of the same \(\Sigma \) in the cut we are constructing, e.g. \(\Sigma _1\). This holds for all a and b, thus \(\Sigma (M) = \Sigma _1\). Hence, there is no non-trivial concurrent cut, and \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
\(\otimes \,=\, \leftrightarrow \) By \(\textsc {C}_{\text {dfg}}\), \(\exists _{1\leqslant i \leqslant n}~ \exists _{a \in \Sigma (M_i)}~ a \notin {{\,\mathrm{Start}\,}}(M_i) \vee a \notin {{\,\mathrm{End}\,}}(M_i)\). Take such an \(M_i\) and a. As either \(a \notin {{\,\mathrm{Start}\,}}(M_i)\) or \(a \notin {{\,\mathrm{End}\,}}(M_i)\), there is no connection to/from a to any other subtree, i.e. \(\forall _{1 \leqslant j \leqslant n, j \ne i}~ \forall _{b \in \Sigma (M_j)}~ \lnot \alpha _{\text {dfg}}(b, a) \vee \lnot \alpha _{\text {dfg}}(a, b)\). If we would construct a concurrent cut \((\wedge , \Sigma _1 \ldots \Sigma _p)\), then both a and all such b’s would be in the same \(\Sigma \), e.g. \(\{a\} \cup (\Sigma (K) \setminus \Sigma (M_j)\}) \subseteq \Sigma _1\). This holds for all activities of \({{\,\mathrm{Start}\,}}(M_i)\) and \({{\,\mathrm{End}\,}}(M_i)\). Hence, if we would construct a concurrent cut, all \({{\,\mathrm{Start}\,}}(K)\) and \({{\,\mathrm{End}\,}}(K)\) activities would be part of the same \(\Sigma \). Therefore, there cannot be a non-trivial concurrent cut for K, and hence, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
\(\oplus \,=\, \circlearrowleft \) Perform case distinction on the remaining case of \(\otimes \):
\(\otimes \,=\, \leftrightarrow \) We try to construct a loop cut \((\circlearrowleft , \Sigma _1, \ldots \Sigma _n)\). Consider a child \(M_i\), and an activity s from the start activities of another child. Moreover, consider a path \(\alpha _{\text {dfg}}(a_1, a_2) \ldots \alpha _{\text {dfg}}(a_{p-1}, a_p)\) such that all activities on the path are in \(\Sigma (M_i)\), and \(a_1 \in {{\,\mathrm{Start}\,}}(M_i)\) and \(a_p \in {{\,\mathrm{End}\,}}(M_i)\). By Lemma 5.1, \(a_1 \in \Sigma _1 \wedge a_p \in \Sigma _1\). Consider activity \(a_2\). If \(a_2 \in {{\,\mathrm{Start}\,}}(M_i)\), then \(a_2 \in \Sigma _1\). If \(a_2 \in {{\,\mathrm{End}\,}}(M_i)\), then \(a_2 \in \Sigma _1\). If \(a_2 \notin {{\,\mathrm{Start}\,}}(M_i) \wedge a_2 \notin {{\,\mathrm{End}\,}}(M_i)\), then by the semantics of \(\leftrightarrow \), \(\lnot \alpha _{\text {dfg}}(s, a_2)\). If \(a_2\) would be in \(\Sigma _2\), as it has a connection \(\alpha _{\text {dfg}}(a_1, a_2)\), by the semantics of \(\circlearrowleft \) there should be a connection \(\alpha _{\text {dfg}}(s, a_2)\). Thus, \(a_2 \in \Sigma _1\). This argument holds for the entire path, and by construction of \(\alpha _{\text {dfg}}(M)\) each activity is on such a path; thus, \(\Sigma (M_i) \subseteq \Sigma _1\). This holds for all children \(M_i\), so there cannot be a non-trivial loop cut. Hence, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
As these arguments are symmetric in \(\oplus \) and \(\otimes \), we conclude that \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\). \(\square \)
1.2 Lemma 5.3
Lemma: Take two reduced process trees of \(\textsc {C}_{\text {dfg}}\)\(K = \oplus (K_1 \ldots K_n)\) and \(M = \oplus (M_1 \ldots M_m)\) such that their activity partition is different: \(\exists _{1 \leqslant w \leqslant \text {min}(n, m)}~ \Sigma (K_w) \ne \Sigma (M_w)\). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
Proof
Without loss of generality, we assume that children of the non-commutative operators (\(\rightarrow \), \(\circlearrowleft \)) have a fixed order. Towards contradiction, assume that \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\). Perform case distinction on \(\oplus \) (the case for K and M swapped is symmetric):
 Take a pair of activities a, b such that \(a \in \Sigma (K_x)\), \(a \in \Sigma (M_y)\), \(b \in \Sigma (K_x)\) and \(b \notin \Sigma (M_y)\) (choose x and y as desired). Obviously, if the activity partitions of K and M are different such a pair exists. By the reduction rules, no child \(K_1 \ldots K_n\) is an exclusive-choice subtree itself, and by semantics of the other operators there is an undirected path in \(\alpha _{\text {dfg}}(K)\), i.e. \(a \leftrightsquigarrow b\) in \(\alpha _{\text {dfg}}(K)\). However, as \(a \in \Sigma (M_y) \wedge b \notin \Sigma (M_y)\),
Take a pair of activities a, b such that \(a \in \Sigma (K_x)\), \(a \in \Sigma (M_y)\), \(b \in \Sigma (K_x)\) and \(b \notin \Sigma (M_y)\) (choose x and y as desired). Obviously, if the activity partitions of K and M are different such a pair exists. By the reduction rules, no child \(K_1 \ldots K_n\) is an exclusive-choice subtree itself, and by semantics of the other operators there is an undirected path in \(\alpha _{\text {dfg}}(K)\), i.e. \(a \leftrightsquigarrow b\) in \(\alpha _{\text {dfg}}(K)\). However, as \(a \in \Sigma (M_y) \wedge b \notin \Sigma (M_y)\), 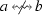 in \(\alpha _{\text {dfg}}(M)\). Hence, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
in \(\alpha _{\text {dfg}}(M)\). Hence, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).\(\oplus = \rightarrow \) Take \(a \in \Sigma (K_i)\) and \(b \in \Sigma (K_j)\) such that \(i < j\). Then by the \(\rightarrow \)-cut, \(\alpha _{\text {dfg}}\!\!^{+}\!(a, b) \wedge \lnot \alpha _{\text {dfg}}\!\!^{+}\!(b, a)\). By the reduction rules, all children of K and M are not \(\rightarrow \)-nodes themselves, thus, by the semantics of the other operators (
 is unconnected, \(\wedge \) and \(\circlearrowleft \) are strongly connected), either \(\lnot \alpha _{\text {dfg}}(a, b)\) or \(\alpha _{\text {dfg}}\!\!^{+}\!(b, a)\). Then, \(a \in \Sigma (M_x) \wedge b \in \Sigma (M_y)\) with \(x < y\). This holds for all such a and b, hence \(\forall _{1 \leqslant i \leqslant n = m}~ \Sigma (K_i) = \Sigma (M_i)\), which contradicts the initial assumption.
is unconnected, \(\wedge \) and \(\circlearrowleft \) are strongly connected), either \(\lnot \alpha _{\text {dfg}}(a, b)\) or \(\alpha _{\text {dfg}}\!\!^{+}\!(b, a)\). Then, \(a \in \Sigma (M_x) \wedge b \in \Sigma (M_y)\) with \(x < y\). This holds for all such a and b, hence \(\forall _{1 \leqslant i \leqslant n = m}~ \Sigma (K_i) = \Sigma (M_i)\), which contradicts the initial assumption.\(\oplus = \wedge \) To prove the equality of the activity partitions, we consider two symmetrical directions: a) if two activities are in the same \(\Sigma _i\) in K, then they are in the same \(\Sigma _i\) in M. b) if two activities are in the same \(\Sigma _i\) in M, then they are in the same \(\Sigma _i\) in K.
Consider a child \(M_x\). Perform case distinction on the structure of \(M_x\):
\(M_x = a\) A single activity cannot be split. Thus, \(\Sigma (K_x) \subseteq \Sigma (M_x)\).
 Take two activities \(a \in \Sigma (M_{x_1})\) and \(b \in \Sigma (M_{x_2})\). By semantics of
Take two activities \(a \in \Sigma (M_{x_1})\) and \(b \in \Sigma (M_{x_2})\). By semantics of  , \(\lnot \alpha _{\text {dfg}}(a, b)\). Thus, in a concurrent cut, a and b should be part of the same \(\Sigma \). This holds for all such activities of all children of \(M_x\); thus, \(\Sigma (K_x) \subseteq \Sigma (M_x)\).
, \(\lnot \alpha _{\text {dfg}}(a, b)\). Thus, in a concurrent cut, a and b should be part of the same \(\Sigma \). This holds for all such activities of all children of \(M_x\); thus, \(\Sigma (K_x) \subseteq \Sigma (M_x)\).\(M_x \,=\,\rightarrow (M_{x_1}, \ldots M_{x_p})\) Similar, using that either \(\lnot \alpha _{\text {dfg}}(a, b)\) or \(\lnot \alpha _{\text {dfg}}(b, a)\).
\(M_x \,=\, \wedge (M_{x_1}, \ldots M_{x_p})\) Excluded by the reduction rules.
\(M_x \,=\, \circlearrowleft (M_{x_1}, \ldots M_{x_p})\) By \(\textsc {C}_{\text {dfg}}\), there is at least one child \(M_{x_i}\) such that \({{\,\mathrm{Start}\,}}(M_{x_i})\)\({}\cap {}\)\({{\,\mathrm{End}\,}}(M_{x_i}) = \emptyset \). Take such a \(M_{x_i}\) and an a from \(\Sigma (M_{x_i})\). Furthermore, take b from any other child. There are three cases for a: \(a \notin {{\,\mathrm{Start}\,}}(M_{x_i})\), \(a \notin {{\,\mathrm{End}\,}}(M_{x_i})\) or both. For all these three cases, \(\lnot \alpha _{\text {dfg}}(a, b) \vee \lnot \alpha _{\text {dfg}}(b, a)\). Thus, by argumentation similar to the
 case, \(\Sigma (K_x) \subseteq \Sigma (M_x)\).
case, \(\Sigma (K_x) \subseteq \Sigma (M_x)\).\(M_x \,=\, \leftrightarrow (M_{x_1}, \ldots M_{x_p})\) Similar to the \(\circlearrowleft \) case.
Hence, \(\Sigma (K_x) \subseteq \Sigma (M_x)\). This holds for all \(\Sigma (M_x)\) and by symmetry for all \(\Sigma (K_x)\). Hence, \(\forall _{1 \leqslant i \leqslant n}~ \Sigma (K_i) = \Sigma (M_i)\), which contradicts the initial assumption.
\(\oplus \,=\, \circlearrowleft \) Consider \(\Sigma (K_i)\) for some \(2 \leqslant i \leqslant n\). By the reduction rules, \(K_i\) is of the form
 . By semantics of the other operators, for all \(a, b \in \Sigma (K_i)\), there exists an undirected path \(a \leftrightsquigarrow b\) in \(\alpha _{\text {dfg}}(K)\), such that all activities on this undirected path are in \(K_i\). Between all the activities on this path, there exists a connection in \(\alpha _{\text {dfg}}(K_i)\), and none of the activities on this path is in \({{\,\mathrm{Start}\,}}(K)\) or \({{\,\mathrm{End}\,}}(K)\). By Lemma 5.1, in a non-trivial loop cut, (without loss of generality) \(\Sigma (K_i) \subseteq \Sigma (M_i)\).
. By semantics of the other operators, for all \(a, b \in \Sigma (K_i)\), there exists an undirected path \(a \leftrightsquigarrow b\) in \(\alpha _{\text {dfg}}(K)\), such that all activities on this undirected path are in \(K_i\). Between all the activities on this path, there exists a connection in \(\alpha _{\text {dfg}}(K_i)\), and none of the activities on this path is in \({{\,\mathrm{Start}\,}}(K)\) or \({{\,\mathrm{End}\,}}(K)\). By Lemma 5.1, in a non-trivial loop cut, (without loss of generality) \(\Sigma (K_i) \subseteq \Sigma (M_i)\).Let \(K_1 \,=\, \otimes (K_{1_1}, \ldots K_{1_p})\). Perform case distinction on \(\otimes \):
 Take a child \(K_{1_i}\). By the reduction rules, this child is not an
Take a child \(K_{1_i}\). By the reduction rules, this child is not an  . For all activities \(a \in {{\,\mathrm{Start}\,}}(K_{1_i}), b \in {{\,\mathrm{End}\,}}(K_{1_i})\), there exist a directed path \(\alpha _{\text {dfg}}\!\!^{+}\!(a, b)\), such that this path is completely in \(\Sigma (K_{1_i})\). Furthermore, take an activity \(c \in {{\,\mathrm{End}\,}}(K_{1_{j \ne i}})\). By semantics of
. For all activities \(a \in {{\,\mathrm{Start}\,}}(K_{1_i}), b \in {{\,\mathrm{End}\,}}(K_{1_i})\), there exist a directed path \(\alpha _{\text {dfg}}\!\!^{+}\!(a, b)\), such that this path is completely in \(\Sigma (K_{1_i})\). Furthermore, take an activity \(c \in {{\,\mathrm{End}\,}}(K_{1_{j \ne i}})\). By semantics of  , c has no directly follows connection to any node on the path. Towards contradiction, assume there is a first node d on the path \(\notin \Sigma (M_1)\). Then, by semantics of \(\circlearrowleft \), there should be a connection \(\alpha _{\text {dfg}}(c, d)\). This holds for all activities d and children i, so \(\Sigma (K_1) \subseteq \Sigma (M_1)\).
, c has no directly follows connection to any node on the path. Towards contradiction, assume there is a first node d on the path \(\notin \Sigma (M_1)\). Then, by semantics of \(\circlearrowleft \), there should be a connection \(\alpha _{\text {dfg}}(c, d)\). This holds for all activities d and children i, so \(\Sigma (K_1) \subseteq \Sigma (M_1)\).\(\otimes \,=\, \rightarrow \) Similar to the
 -case.
-case.\(\otimes \,=\, \wedge \)\({{\,\mathrm{Start}\,}}(K) \cup {{\,\mathrm{End}\,}}(K) \subseteq \Sigma (M_1)\), thus we only need to consider non-start non-end activities. Take such an activity a in child \(K_{1_i}\), and take an activity \(b \in {{\,\mathrm{End}\,}}(K_{1_{j \ne i}})\). By semantics of \(\wedge \), \(\alpha _{\text {dfg}}(a, b)\); by \(\textsc {C}_{\text {dfg}}\), \(b \notin {{\,\mathrm{Start}\,}}(K_1)\); thus by Lemma 5.1, \(a \in \Sigma (M_1)\). This holds for all a, so \(\Sigma (K_1) \subseteq \Sigma (M_1)\).
\(\otimes \,=\, \circlearrowleft \) Excluded by the reduction rules.
\(\otimes \,=\, \leftrightarrow \) Similar to the
 -case.
-case.
\(\oplus \,=\, \leftrightarrow \) Take a w such that \(\Sigma (K_w) \ne \Sigma (M_w)\) and let \(K_w = \otimes (K_{w_1}\ldots K_{w_p})\). Perform case distinction on \(\otimes \):
 By semantics of
By semantics of  , no end activity of \(K_{w_1}\) has a connection to any start activity of any other \(K_{w_j}\). Thus, as M contains an interleaved activity partition, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).
, no end activity of \(K_{w_1}\) has a connection to any start activity of any other \(K_{w_j}\). Thus, as M contains an interleaved activity partition, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).\(\otimes \,=\, \rightarrow \) Similar to the
 case.
case.\(\otimes \,=\, \wedge \) By \(\textsc {C}_{\text {dfg}}\), at least one child of \(K_w\) has disjoint start and end activities. Take such a child \(K_{w_y}\), and consider two activities: \(a \notin {{\,\mathrm{Start}\,}}(K_{w_y})\) and \(b \in \Sigma (K_w) \setminus K_{w_y}\). By semantics of \(\wedge \), \(\alpha _{\text {dfg}}(b, a)\). Then, by Lemma 5.1, \(a \in \Sigma (M_w)\) and \(b \in \Sigma (M_w)\). This holds for all b and by symmetry for \({{\,\mathrm{Start}\,}}(K_{w_y}) \cup {{\,\mathrm{End}\,}}(K_{w_y})\). By semantics of \(\leftrightarrow \), non-start non-end activities only have connections with start/end activities of \(K_w\). Therefore, \(\Sigma (K_w) \setminus ({{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w)) \subseteq \Sigma (M_w)\). Hence, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).
\(\otimes \,=\, \circlearrowleft \) By semantics of \(\leftrightarrow \), non-start non-end activities only have connections with start/end activities of \(K_w\). Therefore, \(\Sigma (K_w) \setminus ({{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w)) \subseteq \Sigma (M_w)\). All activities \(\in {{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w)\) have connections from/to \({{\,\mathrm{End}\,}}(K_{w_2}) \cup {{\,\mathrm{Start}\,}}(K_{w_2})\), thus \({{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w) \subseteq \Sigma (M_w)\). Hence, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).
\(\otimes \,=\, \leftrightarrow \) Excluded by \(\textsc {C}_{\text {dfg}}\).
By contradiction, we conclude \(\alpha _{\text {dfg}}{K} \ne \alpha _{\text {dfg}}{M}\). \(\square \)
Uniqueness for \(\textsc {C}_{\text {msd}}\)
Lemma E.1
(Operators are mutually exclusive) Take two reduced process trees of \(\textsc {C}_{\text {msd}}\)\(K = \oplus (K_1, \ldots K_n)\) and \(M = \otimes (M_1, \ldots M_m)\) such that \(\oplus \ne \otimes \). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {msd}}(K) \ne \alpha _{\text {msd}}(M)\).
This proof of this lemma is similar to the proof of Lemma 5.2: for each combination of \(\oplus \) and \(\otimes \), a difference in \(\alpha _{\text {msd}}\)-graphs is shown. For a detailed proof, please refer to “Appendix E.2”.
Lemma E.2
(Partitions are mutually exclusive) Take two reduced process trees of \(\textsc {C}_{\text {dfg}}\)\(K = \oplus (K_1 \ldots K_n)\) and \(M = \oplus (M_1 \ldots M_m)\) such that their activity partition is different: \(\exists _{1 \leqslant w \leqslant \text {min}(n, m)}~ \Sigma (K_w) \ne \Sigma (M_w)\). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {msd}}(K) \ne \alpha _{\text {msd}}(M)\).
This proof of this lemma is similar to the proof of Lemma 5.3: for each \(\oplus \), it is shown that a difference in partitions must lead to a difference in \(\alpha _{\text {msd}}\)-graphs. For a detailed proof, please refer to “Appendix E.3”.
Lemma E.3
(Abstraction uniqueness for \(\textsc {C}_{\text {msd}}\)) Take two reduced process trees of class \(\textsc {C}_{\text {msd}}\): \(K = \oplus (K_1, \ldots K_n)\) and \(M = \otimes (M_1, \ldots M_m)\). Then, \(K = M\) if and only if \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\) and \(\alpha _{\text {msd}}(K) = \alpha _{\text {msd}}(M)\).
The proof of this lemma is similar to the proof of Lemma 5.4, using Lemmas E.1 and E.2.
Corollary E.1
(Language uniqueness for \(\textsc {C}_{\text {msd}}\)) There are no two different reduced process trees of \(\textsc {C}_{\text {msd}}\) with equal languages. Hence, for trees of class \(\textsc {C}_{\text {msd}}\), the normal form of Sect. 4 is uniquely defined.
1.1 LC-property
The minimum self-distance graph possesses more expressive power than the footprints of Definition 6.3 utilize. That is, there exist pairs of process trees that have different normal forms, languages and \(\alpha _{\text {msd}}\)-graphs, but that the footprints do not distinguish.
For instance, consider the trees

and

These trees have a different language, an equivalent \(\alpha _{\text {dfg}}\)-graph (shown in Fig. 9b) but a different \(\alpha _{\text {msd}}\)-graph (shown in Fig. 9c, d). Thus, they could be distinguished using their \(\alpha _{\text {msd}}\)-graph.
However, the footprint (Definition 6.3) cannot distinguish these trees: both cuts \((\circlearrowleft , \{a, b, c\}, \{d\})\) and \((\circlearrowleft , \{a, c, d\}, \{b\})\) are valid in both \(\alpha _{\text {msd}}\)-graphs, where \((\circlearrowleft , \{a, b, c\}, \{d\})\) corresponds to \(M_{12}\) and \((\circlearrowleft , \{a, c, d\}, \{b\})\) corresponds to \(M_{13}\). This implies that a discovery algorithm that uses only the footprint cannot distinguish these two trees.
This problem occurs in certain nestings of loops and concurrent operators, as indicated in the proof of Lemma E.2. We formalize this remaining problem as a loop-concurrency property (LC-property). An LC-property could distinguish the specific nesting using only the \(\alpha _{\text {msd}}\)-graph.
Definition E.1
(LC-property) Let \(K, M \in \textsc {C}_{\text {msd}}{}\) be process trees in normal form such that


and \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\). Then, an LC-propertyLC is a function that distinguishes the cuts of K and M in their minimum self-distance graphs, i.e. \(LC(\alpha _{\text {msd}}(K)) \wedge LC(\alpha _{\text {msd}}(M))\) if and only if the cut \((\circlearrowleft , \Sigma (K_1), \ldots \Sigma (K_n))\) conforms to both K and M.
Consider \(\textsc {C}_{\text {msd}}{}'\) to be the class of trees \(\textsc {C}_{\text {msd}}{}\) where arbitrary nestings of \(\circlearrowleft \) and \(\wedge \) are allowed, that is, Requirement \(\hbox {C}_{\mathrm{msd}}.\hbox {l}.1\) is dropped. Then, if an LC-property exists, Lemma E.2 applies for \(\textsc {C}_{\text {msd}}{}'\).
We did not find an LC-property, but we also did not prove that it cannot exist. A proof that an LC-property cannot exist would, for instance, be the existence of an example of two process trees of \(\textsc {C}_{\text {msd}}{}'\) in normal form with equivalent \(\alpha _{\text {msd}}\)-graphs. We did not find such examples in an extensive search, so we conjecture that an LC-property exists:
Conjecture E.1
(LC-property) There exists an LC-property (Definition E.1).
1.2 Lemma E.1
Lemma: Take two reduced process trees of \(\textsc {C}_{\text {msd}}\)\(K = \oplus (K_1, \ldots K_n)\) and \(M = \otimes (M_1, \ldots M_m)\) such that \(\oplus \ne \otimes \). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {msd}}(K) \ne \alpha _{\text {msd}}(M)\).
Proof
Towards contradiction, assume \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\) and \(\alpha _{\text {msd}}(K) = \alpha _{\text {msd}}(M)\). We only consider the cases that were not covered in the proof of Lemma 5.2.
\(\oplus = \wedge \) and \(\otimes = \circlearrowleft \). We try to construct a concurrent cut \(\Sigma _1 \ldots \Sigma _q\) for M. By Requirement c.1, every such \(\Sigma _i\) must have a start and an end activity. Thus, we only need to prove that \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1) \subseteq \Sigma _1\). Perform case distinction on \(M_1\):
 Each \(a \in \Sigma (M_{1_i})\) has no \(\alpha _{\text {dfg}}\)-connection to any activity in \(\Sigma (M_{j \ne i})\). Therefore, \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1) \subseteq \Sigma _1\).
Each \(a \in \Sigma (M_{1_i})\) has no \(\alpha _{\text {dfg}}\)-connection to any activity in \(\Sigma (M_{j \ne i})\). Therefore, \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1) \subseteq \Sigma _1\).\(M_1\,=\,\rightarrow (M_{1_1}, \ldots M_{1_p})\) Each \(a \in \Sigma (M_{1_i})\) has no \(\alpha _{\text {dfg}}\)-connection to any activity in \(\Sigma (M_{j < i})\). Therefore, \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1) \subseteq \Sigma _1\).
\(M_1 = \wedge (\ldots )\) Consider three cases:
If any of the \(M_{2 \leqslant i \leqslant p}\) contains a \(\circlearrowleft \), consider an activity a in the redo of that \(\circlearrowleft \). By semantics of \(\circlearrowleft \), there is no \(\alpha _{\text {dfg}}\)-connection between a and any activity in \(\Sigma (M_1)\). Therefore, \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1) \subseteq \Sigma _1\).
If none of the \(M_{2 \leqslant i \leqslant p}\) contains a \(\circlearrowleft \) and \(M_1\) does not contain a \(\circlearrowleft \), then the \(\alpha _{\text {msd}}\)-graph is connected, and therefore, by Requirement ci.1, \(\Sigma (M) \subseteq \Sigma _1\).
If none of the \(M_{2 \leqslant i \leqslant p}\) contains a \(\circlearrowleft \) and \(M_1\) contains a \(\circlearrowleft \), then consider an activity a under a redo of any such \(\circlearrowleft \), and any activity \(b \in \Sigma (M_{2 \leqslant i \leqslant m})\). By semantics of \(\circlearrowleft \), \(\lnot \alpha _{\text {dfg}}(a, b)\) and \(\lnot \alpha _{\text {dfg}}(b, a)\), thus a and b must be in the same \(\Sigma _1\). All activities \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1)\) have at least an \(\alpha _{\text {msd}}\)-connection with at least some activity in the redo of a \(\circlearrowleft \). Thus, by Requirement ci.1, \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1) \subseteq \Sigma _1\).
\(M_1\,=\,\circlearrowleft (\ldots )\) Excluded by \(\textsc {C}_{\text {msd}}\).
\(M_1\,=\, \leftrightarrow (\ldots )\) By \(\textsc {C}_{\text {msd}}\), there exists a child \(M_{1_i}\) such that \({{\,\mathrm{Start}\,}}(M_{1_i}) \cap {{\,\mathrm{End}\,}}(M_{1_i})\,=\,\emptyset \). Thus, all activities in \({{\,\mathrm{End}\,}}(M_{1_{j \ne i}})\) have no \(\alpha _{\text {dfg}}\)-connection to \({{\,\mathrm{End}\,}}(M_{1_i})\), and similarly for the activities of \({{\,\mathrm{Start}\,}}(M_{1_j})\). Therefore, \({{\,\mathrm{Start}\,}}(M_1) \cup {{\,\mathrm{End}\,}}(M_1) \subseteq \Sigma _1\).
Hence, there is no concurrent cut in M, and therefore, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
\(\oplus \,=\,\circlearrowleft \) and \(\otimes \,=\,\leftrightarrow \). No change is necessary. \(\square \)
1.3 Lemma E.2
Lemma: Take two reduced process trees of \(\textsc {C}_{\text {dfg}}\)\(K = \oplus (K_1 \ldots K_n)\) and \(M = \oplus (M_1 \ldots M_m)\) such that their activity partition is different: \(\exists _{1 \leqslant w \leqslant \text {min}(n, m)}~ \Sigma (K_w) \ne \Sigma (M_w)\). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {msd}}(K) \ne \alpha _{\text {msd}}(M)\).
Proof
Towards contradiction, assume that \(\oplus = \otimes \), \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\), \(\alpha _{\text {msd}}(K) = \alpha _{\text {msd}}(M)\) and that there is a w such that \(\Sigma (K_w) \ne \Sigma (M_w)\). We only consider the cases that were not covered in the proof of Lemma 5.2.
\(\oplus = \wedge \) and \(M_x\,=\,\circlearrowleft (M_{x_1},\ldots M_{x_p})\). Try to construct a \(\wedge \)-cut and prove that \(\Sigma (M_x) \subseteq \Sigma _x\). Consider three cases:
If any of the \(M_{x_{2 \leqslant i \leqslant p}}\) contains a \(\circlearrowleft \), consider an activity a in the redo of that \(\circlearrowleft \). By semantics of \(\circlearrowleft \), there is no \(\alpha _{\text {dfg}}\)-connection between a and any activity in \(\Sigma (M_{x_1})\). Therefore, \(\Sigma (M_{x_1}) \subseteq \Sigma _x\). This holds for all such a, thus all such redo activities are in \(\Sigma _x\). Consider all remaining activities, i.e. \(b \in \Sigma (M_{x_{j \ne i}})\) such that b is in no other \(\circlearrowleft \)-redo than \(M_x\). For each of these activities b, there is a \(\alpha _{\text {msd}}\)-relation with an activity in \(\Sigma _{x_1}\) or an activity such as a. Thus, \(\Sigma (M_x) \subseteq \Sigma _x\).
If none of the \(M_{x_{2 \leqslant i \leqslant p}}\) contains a \(\circlearrowleft \) and \(M_{x_1}\) does not contain a \(\circlearrowleft \), then the \(\alpha _{\text {msd}}\)-graph is connected, and therefore, \(\Sigma (M_x) \subseteq \Sigma _x\).
If none of the \(M_{x_{2 \leqslant i \leqslant p}}\) contains a \(\circlearrowleft \) and \(M_{x_1}\) contains a \(\circlearrowleft \), then consider an activity a under a redo of any such \(\circlearrowleft \), and any activity \(b \in \Sigma (M_{x_{2 \leqslant i \leqslant m}})\). By semantics of \(\circlearrowleft \), \(\lnot \alpha _{\text {dfg}}(a, b)\) and \(\lnot \alpha _{\text {dfg}}(b, a)\), thus a and b must be in the same \(\Sigma _x\). All activities in \(\Sigma (M_{x_1})\) have at least an \(\alpha _{\text {msd}}\)-connection with at least some activity in the redo of a \(\circlearrowleft \), Thus, \(\Sigma (M_x) \subseteq \Sigma _x\).
\(\oplus =\, \circlearrowleft \) and \(K_1 = \wedge (K_{1, 1}, \ldots K_{1, p})\). Try to construct a \(\circlearrowleft \)-cut and prove that \(\Sigma (K_1) \subseteq \Sigma _1\). By semantics of \(\circlearrowleft \), \({{\,\mathrm{Start}\,}}(K_1) \cup {{\,\mathrm{End}\,}}(K_1) \subseteq \Sigma _1\). Take an activity \(a \in \Sigma (K_1)\), such that \(a \notin {{\,\mathrm{Start}\,}}(K_1) \cup {{\,\mathrm{End}\,}}(K_1)\), and take another \(b \in \bigcup _{1 \leqslant i \leqslant n} \Sigma (K_i)\) such that \(b \in {{\,\mathrm{Start}\,}}(K_1) \cup {{\,\mathrm{End}\,}}(K_1)\). Then, \(b \in \Sigma _1\). Perform case distinction on b:
\(b \notin {{\,\mathrm{End}\,}}(K_1)\) Then, \(\alpha _{\text {dfg}}(b, a)\) and thus \(a \in \Sigma _1\).
\(b \notin {{\,\mathrm{Start}\,}}(K_1)\) Then, \(\alpha _{\text {dfg}}(a, b)\) and thus \(a \in \Sigma _1\).
\(b \in {{\,\mathrm{Start}\,}}(K_1) \cap {{\,\mathrm{End}\,}}(K_1)\) Excluded by \(\textsc {C}_{\text {msd}}\). (Here, the LC-property (Conjecture E.1) would detect and guarantee \(a \in \Sigma _1\)). \(\square \)
Uniqueness for \(\alpha _{\text {coo}}\)
Given a particular language, several partial cuts might apply. In this section, we prove that each of these partial cuts is “correct”, that is, corresponds to the process tree from which the language was derived. We first formalize this concept, after which we use it to prove uniqueness for so- and coo-stems.
Definition F.1
(partition correspondence, \(\mathbb {M}^{\Sigma }\)) Let M be a reduced process tree without duplicate activities. Then, \(\mathbb {M}^{\Sigma }(M)\) denotes the set of all partitions S that correspond to M. That is, let \(S = \{S_1, \ldots S_n\}\) be a partition of \(\Sigma (M)\), then \(S \in \mathbb {M}^{\Sigma }(M)\) if and only if there exists an \(M'\) such that \(M'\) reduces to M using only the associativity rules ( , \(\textsc {A}_{\rightarrow }{}\), \(\textsc {A}_{\wedge }{}\),
, \(\textsc {A}_{\rightarrow }{}\), \(\textsc {A}_{\wedge }{}\),  , \(\textsc {A}_{\circlearrowleft \textsc {b}}{}\), \(\textsc {A}_{\circlearrowleft \textsc {r}}{}\)); and for every \(S_i \in S\), there is a subtree \(M''\) of \(M'\) such that \(S_i = \Sigma (M'')\).
, \(\textsc {A}_{\circlearrowleft \textsc {b}}{}\), \(\textsc {A}_{\circlearrowleft \textsc {r}}{}\)); and for every \(S_i \in S\), there is a subtree \(M''\) of \(M'\) such that \(S_i = \Sigma (M'')\).
Intuitively, a partition corresponds to a process tree if each set of activities in the partition can be mapped to a node in the process tree (up to the associativity rules). For instance, let

Then,
Each of these partitions corresponds to \(M_{29}\). For instance, consider the partition \(\{\{a, c\}, \{b\}, \{d\}\}\). Each of the sets in this partition can be mapped on a node in the tree

which reduces to \(M_{29}\) using the associativity rules. In this mapping, \(\{d\}\) is mapped on the leaf d, \(\{b\}\) is mapped on the leaf b, and \(\{a, c\}\) is mapped on the node

In contrast, the partition \(\{\{a, b\}, \{c, d\}\}\) does not correspond to \(M_{29}\), as c and d cannot be mapped together without a and b.
1.1 SO-stems
In Lemma B.1, we showed that a tree with an  structure has a partial \(\rightarrow \)-cut. Now, we prove the opposite: there can only be a partial \(\rightarrow \)-cut if the tree has such a structure.
structure has a partial \(\rightarrow \)-cut. Now, we prove the opposite: there can only be a partial \(\rightarrow \)-cut if the tree has such a structure.
Lemma F.1
(Partitions are mutually exclusive for so-stems) Let \(M = \rightarrow (M_1, \ldots M_m)\), \(K = \rightarrow (K_1, \ldots K_n)\) be reduced trees of \(\textsc {C}_{\text {coo}}\) such that their activity partition is different, i.e. there is a \(w \in [1 \ldots n]\) such that \(\Sigma (K_w) \ne \Sigma (M_w)\). Then, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).
Proof
Towards contradiction, assume that \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\), and perform case distinction.
In case no child \(K_i\) has the  structure, \(\alpha _{\text {dfg}}(K)\) is a chain of strongly connected or unconnected clusters, which correspond to \(\Sigma (K_i)\)’s. Notice that \(\alpha _{\text {dfg}}\)-edges can skip clusters, hence \(\alpha _{\text {dfg}}(K)\) contains a maximal \(\rightarrow \) cut. The same holds for \(\alpha _{\text {dfg}}(M)\), and this holds for all such \(\Sigma (K_i)\), so \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).
structure, \(\alpha _{\text {dfg}}(K)\) is a chain of strongly connected or unconnected clusters, which correspond to \(\Sigma (K_i)\)’s. Notice that \(\alpha _{\text {dfg}}\)-edges can skip clusters, hence \(\alpha _{\text {dfg}}(K)\) contains a maximal \(\rightarrow \) cut. The same holds for \(\alpha _{\text {dfg}}(M)\), and this holds for all such \(\Sigma (K_i)\), so \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).
In case at least one child \(K_i\) has a structure  , the corresponding cluster \(\Sigma (K_i)\) is a chain itself. By Rule
, the corresponding cluster \(\Sigma (K_i)\) is a chain itself. By Rule  , at least one child of \(K_i\) (say \(K_{i_p}\)) is a pivot (Definition 7.3). By Lemma B.1, \((\rightarrow , \Sigma (K_{i_1}), \Sigma (K_{i_k}) )\) is a partial \(\rightarrow \)-cut. Due to Requirement s.5, for every pivot, there is one partial \(\rightarrow \)-cut. The same holds for \(\alpha _{\text {dfg}}(M)\), and this holds for all such \(\Sigma (K_i)\), so \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).
, at least one child of \(K_i\) (say \(K_{i_p}\)) is a pivot (Definition 7.3). By Lemma B.1, \((\rightarrow , \Sigma (K_{i_1}), \Sigma (K_{i_k}) )\) is a partial \(\rightarrow \)-cut. Due to Requirement s.5, for every pivot, there is one partial \(\rightarrow \)-cut. The same holds for \(\alpha _{\text {dfg}}(M)\), and this holds for all such \(\Sigma (K_i)\), so \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).
Hence, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\). \(\square \)
1.2 Coo-stems
In Lemma B.2, we showed that a tree with a coo-stem has partial \(\wedge \)- and  -cuts. In this section, we prove the opposite: there can only be a partial \(\wedge \)- and
-cuts. In this section, we prove the opposite: there can only be a partial \(\wedge \)- and  -cuts if the tree has such a corresponding coo-stem.
-cuts if the tree has such a corresponding coo-stem.
The main Lemmas, F.5 and F.6, consider partitions in a repetitive way: starting from a particular partition, a partial cut is considered, after which the sets of activities of the partial are merged in the partition, and a new, smaller, partition is obtained. For instance, the partition \(\{\{a\}, \{b\}, \{c\}\}\) combined with the partial \(\wedge \)-cut \((\wedge , \{a\}, \{b\})\) becomes \(\{\{a, b\}, \{c\}\}\). This reasoning procedure traverses the coo-stem of the process tree.
Invariant in the repetition is that every obtained partition corresponds to the process tree (\(\mathbb {M}^{\Sigma }\)). To keep the invariant, we prove that for any partition in \(\mathbb {M}^{\Sigma }\), partial \(\wedge \)- and  -cuts are always “correct” (Lemmas F.2 and F.3). Second, we prove that every obtained partition using such a partial cut is in \(\mathbb {M}^{\Sigma }\) (Lemma F.4).
-cuts are always “correct” (Lemmas F.2 and F.3). Second, we prove that every obtained partition using such a partial cut is in \(\mathbb {M}^{\Sigma }\) (Lemma F.4).
The repetition starts with the partition of the concurrent cut, which we formalize in Definition F.2. The repetition ends when the partial cut partitions the entire alphabet, and a contradiction is derived.
Definition F.2
(activity sets of non-coo-subtrees) Let M be a reduced process tree without duplicate activities. Then, \({\Sigma ^{\mathcal {C}}}(M)\) denotes the activity sets of the non-coo-subtrees of M:

Notice that \({\Sigma ^{\mathcal {C}}}(M)\) corresponds to a concurrent cut of the directly follows graph (Definition 5.2).
Lemma F.2
(partial  -cut corresponds to
-cut corresponds to  ) Let \(M \in \textsc {C}_{\text {coo}}{}\) be a reduced process tree with a coo-stem, let
) Let \(M \in \textsc {C}_{\text {coo}}{}\) be a reduced process tree with a coo-stem, let  , \(M' \in {{\,\mathrm{coo-stem}\,}}(M)\) be a coo-stem node, let \(M'_i\) be a child of \(M'\), let \(S \in \mathbb {M}^{\Sigma }(M)\) be a partition such that \(\Sigma (M'_i) \in S\), and let \(\alpha _{\text {coo}}(S)\) be a coo-graph. Take any \(A \in S\) such that \(A \ne \Sigma (M'_i)\). Then,
, \(M' \in {{\,\mathrm{coo-stem}\,}}(M)\) be a coo-stem node, let \(M'_i\) be a child of \(M'\), let \(S \in \mathbb {M}^{\Sigma }(M)\) be a partition such that \(\Sigma (M'_i) \in S\), and let \(\alpha _{\text {coo}}(S)\) be a coo-graph. Take any \(A \in S\) such that \(A \ne \Sigma (M'_i)\). Then,  is a partial
is a partial  -cut of \(\alpha _{\text {coo}}(S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\).
-cut of \(\alpha _{\text {coo}}(S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\).
The proof of this lemma considers both directions of the bi-implication separately. Towards contradiction, it is assumed that such an A exists, after which semantics of sub-structures of M are used to derive a contradiction. “Appendix F.4” shows the detailed proof.
Lemma F.3
(partial \(\wedge \)-cut corresponds to \(\wedge \)) Let \(M \in \textsc {C}_{\text {coo}}{}\) be a reduced process tree with a coo-stem, let \(M' = \wedge (M'_1, \ldots M'_m)\), \(M' \in {{\,\mathrm{coo-stem}\,}}(M)\) be a coo-stem node, let \(M'_i\) be a child of \(M'\), let \(S \in \mathbb {M}^{\Sigma }(M)\) a partition such that \(\Sigma (M'_i) \in S\), and let \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\) be a coo-graph. Take any \(A \in S\) such that \(A \ne \Sigma (M'_i)\). Then, \((\wedge , \Sigma (M'_i), A)\) or \((\wedge , A, \Sigma (M'_i))\) is a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\).
The proof of this lemma is similar to the proof of Lemma F.2: the two directions are proven separately and semantics of sub-structures of M are used to derive a contradiction. For a detailed proof, see “Appendix F.5”.
Lemma F.4
(merge sigmaset preservation) Let M be a reduced process tree of \(\textsc {C}_{\text {coo}}\) with a coo-stem. Let \(S \in \mathbb {M}^{\Sigma }(M)\) and let \(C = (\oplus , S_1, \ldots S_n)\) be a partial \(\oplus \)-cut of \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\). Let \(S' = S \setminus \{S_1, \ldots S_n\} \cup \{\cup _{i \in [1 \ldots n]} S_i\}\) be S collapsed with respect to C. Then, \(S' \in \mathbb {M}^{\Sigma }(M)\).
Proof
As \(S \in \mathbb {M}^{\Sigma }(M)\), there must be a tree \(M'\) to which S can be structurally mapped (Definition F.1). By Lemmas F.2 and F.3, for each \(S_i\) there is a node \(M'_i\) in \(M'\) such that \(S_i = \Sigma (M'_i)\). By the associativity rules, \(M'\) can be transformed into \(M''\) such that \(M''\) contains a node \(\oplus (M'_1, \ldots M'_n)\). Then, \(S'\) can be structurally mapped to \(M''\). Hence, \(S' \in \mathbb {M}^{\Sigma }(M)\). \(\square \)
Lemma F.5
(Operators are mutually exclusive for coo-stems) Let \(M = \wedge (M_1, \ldots M_m)\),  be reduced trees of \(\textsc {C}_{\text {coo}}\). Then, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\).
be reduced trees of \(\textsc {C}_{\text {coo}}\). Then, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\).
Proof
Towards contradiction, assume that \(\alpha _{\text {dfg}}(M) = \alpha _{\text {dfg}}(K)\) and \(\alpha _{\text {coo}}(M) = \alpha _{\text {coo}}(K)\). Let \(S = {\Sigma ^{\mathcal {C}}}(M)\) be a partition of \(\Sigma (M)\). As \(\alpha _{\text {dfg}}(M) = \alpha _{\text {dfg}}(K)\), \(S \in {\Sigma ^{\mathcal {C}}}(K)\). Then, \(S \in \mathbb {M}^{\Sigma }(M)\) and \(S \in \mathbb {M}^{\Sigma }(K)\). (repeat from here) Take a partial cut C in \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\). As \(\alpha _{\text {coo}}(M) = \alpha _{\text {coo}}(K)\), C is a partial cut in \(\alpha _{\text {coo}}(\mathcal {L}(K), S)\) as well. Update S by collapsing it using C. Then, by Lemma F.4, still \(S \in \mathbb {M}^{\Sigma }(M)\) and \(S \in \mathbb {M}^{\Sigma }(K)\). Repeat such that \(S = \{\Sigma (M_1), \ldots \Sigma (M_m)\}\). As \(S \in \mathbb {M}^{\Sigma }(K)\), \(\forall _{i \in [1 \ldots n]}~ \Sigma (K_i) \in S\). By Lemmas F.3 and F.2, there is a partial cut \((\wedge , \Sigma (M_1), \ldots \Sigma (M_m))\) and a partial cut  , which cannot happen by Definitions 7.7 and 7.8. Hence, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\). \(\square \)
, which cannot happen by Definitions 7.7 and 7.8. Hence, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\). \(\square \)
Lemma F.6
(Partitions are mutually exclusive for coo-stems) Let \(M = \oplus (M_1, \ldots M_m)\), \(K = \oplus (K_1, \ldots K_n)\) be reduced trees of \(\textsc {C}_{\text {coo}}\) such that their activity partition is different, i.e. there is a \(w \in [1 \ldots n]\) such that \(\Sigma (K_w) \ne \Sigma (M_w)\). Then, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\).
Proof
Towards contradiction, assume that there exists such a w. Similar to the proof of Lemma F.5, obtain a partition \(S = \{\Sigma (M_1), \ldots \Sigma (M_m)\}\) such that \(S \in \mathbb {M}^{\Sigma }(M)\) and \(S \in \mathbb {M}^{\Sigma }(K)\). By Lemmas F.3 and F.2, there is a node \(K_x\) in K that corresponds to \(\Sigma (M_w)\). As we assumed \(\Sigma (K_w) \ne \Sigma (M_w)\), this cannot happen, so \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\). \(\square \)
1.3 Uniqueness
Lemma F.7
(Operators are mutually exclusive for \(\textsc {C}_{\text {coo}}\)) Take two reduced process trees of \(\textsc {C}_{\text {coo}}\)\(K = \oplus (K_1, \ldots K_n)\) and \(M = \otimes (M_1, \ldots M_m)\) such that \(\oplus \ne \otimes \). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {coo}}(K) \ne \alpha _{\text {coo}}(M)\).
We prove this lemma by showing a difference in abstraction for each pair of process tree operators. For a detailed proof, please refer to “Appendix F.6”.
Lemma F.8
(Partitions are mutually exclusive for \(\textsc {C}_{\text {coo}}\)) Take two reduced process trees of \(\textsc {C}_{\text {coo}}\)\(K = \oplus (K_1 \ldots K_n)\) and \(M = \oplus (M_1 \ldots M_m)\) such that their activity partition is different, i.e. there is a \(1 \leqslant w \leqslant n\) such that \(\Sigma (K_w) \ne \Sigma (M_w)\). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {coo}}(K) \ne \alpha _{\text {coo}}(M)\).
This lemma is proven by case distinction on the process tree operators, while for each operator showing a difference in abstraction if the root partition differs. For a detailed proof, see “Appendix F.7”.
Lemma F.9
(Directly follows graph and coo-relation uniqueness for \(\textsc {C}_{\text {coo}}\)) For trees of class \(\textsc {C}_{\text {coo}}\), the abstractions of normal forms of Sect. 4 are uniquely defined: for any two reduced process trees \(K \ne M\) of \(\textsc {C}_{\text {coo}}\), it holds that \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {coo}}(K) \ne \alpha _{\text {coo}}(M)\).
The proof for this lemma is similar to the proof of Lemma 5.4, using Lemmas F.7 and F.8.
1.4 Lemma F.2
Lemma: Let \(M \in \textsc {C}_{\text {coo}}{}\) be a reduced process tree with a coo-stem, let  , \(M' \in {{\,\mathrm{coo-stem}\,}}(M)\) be a coo-stem node, let \(M'_i\) be a child of \(M'\), let \(S \in \mathbb {M}^{\Sigma }(M)\) a partition such that \(\Sigma (M'_i) \in S\), and let \(\alpha _{\text {coo}}(S)\) be a coo-graph. Take any \(A \in S\) such that \(A \ne \Sigma (M'_i)\). Then,
, \(M' \in {{\,\mathrm{coo-stem}\,}}(M)\) be a coo-stem node, let \(M'_i\) be a child of \(M'\), let \(S \in \mathbb {M}^{\Sigma }(M)\) a partition such that \(\Sigma (M'_i) \in S\), and let \(\alpha _{\text {coo}}(S)\) be a coo-graph. Take any \(A \in S\) such that \(A \ne \Sigma (M'_i)\). Then,  is a partial
is a partial  -cut of \(\alpha _{\text {coo}}(S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\).
-cut of \(\alpha _{\text {coo}}(S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\).
Proof
Prove both directions separately:
- \(\Leftarrow \):
Take such an \(M'_j\). By Lemma B.2,
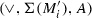 is a partial
is a partial  -cut of \(\alpha _{\text {coo}}(S)\).
-cut of \(\alpha _{\text {coo}}(S)\).- \(\Rightarrow \):
Towards contradiction, assume that there exists a set of activities A such that
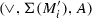 is a partial
is a partial  -cut of \(\alpha _{\text {coo}}(S)\) and \(\forall _{1 \leqslant j \leqslant m}~ A \ne \Sigma (M'_j)\). By Definition F.1, A corresponds to a node in M. Let \(M_A\) be this node. Perform case distinction on whether the lowest common parent of \(M_A\) and \(M'\) is either \(M'\) itself or a parent of \(M'\):
-cut of \(\alpha _{\text {coo}}(S)\) and \(\forall _{1 \leqslant j \leqslant m}~ A \ne \Sigma (M'_j)\). By Definition F.1, A corresponds to a node in M. Let \(M_A\) be this node. Perform case distinction on whether the lowest common parent of \(M_A\) and \(M'\) is either \(M'\) itself or a parent of \(M'\):
The lowest common parent is \(M'\). By the assumptions made, \(M_A\) is not a direct child of \(M'\), so there is a \(\wedge \)-node between \(M'\) and \(M_A\). Without loss of generality, assume that this \(\wedge \)-node is a direct child of \(M'\). Then, M contains the following structure, for certain nodes X and Y (wiggled edges denote possibly indirect children; \(M_A\) may be equal to Y):
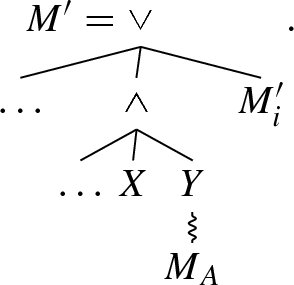
By semantics of
 , execution of \(M'_i\) does not imply execution of either X or \(M_A\). If X is not optional, then execution of \(M_A\) implies execution of X, and therefore, \(M_A\) and \(M'_i\) are not interchangeable (
, execution of \(M'_i\) does not imply execution of either X or \(M_A\). If X is not optional, then execution of \(M_A\) implies execution of X, and therefore, \(M_A\) and \(M'_i\) are not interchangeable ( ).
).If X is optional, then Y cannot be optional (reduction rule
 ) and execution of X implies execution of Y. That is, a coo-graph \(\alpha _{\text {coo}}(S)'\) that contains \(\Sigma (Y)\) and \(\Sigma (X)\) would contain the traces \(\langle \Sigma (X), \Sigma (Y)) \rangle \) and \(\langle \Sigma (X), \Sigma (M'_i), \Sigma (Y) \rangle \) but not \(\langle \Sigma (X), \Sigma (M'_i) \rangle \). Therefore,
) and execution of X implies execution of Y. That is, a coo-graph \(\alpha _{\text {coo}}(S)'\) that contains \(\Sigma (Y)\) and \(\Sigma (X)\) would contain the traces \(\langle \Sigma (X), \Sigma (Y)) \rangle \) and \(\langle \Sigma (X), \Sigma (M'_i), \Sigma (Y) \rangle \) but not \(\langle \Sigma (X), \Sigma (M'_i) \rangle \). Therefore, 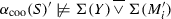 . By definition of the occurrence function (“contains any activity of”),
. By definition of the occurrence function (“contains any activity of”),  .
.The lowest common parent is a parent of \(M'\). Then, M contains either of the following structures, for certain nodes X and Y (wiggled edges denote possibly indirect children; \(M_A\) may be equivalent to Y):
In the first case, X and \(M'\) cannot be both optional (reduction rule  ). Then, by semantics of \(\wedge \), execution of X implies execution of \(M'\) (if \(M'\) is not optional) and/or execution of \(M'\) implies execution of X (if X is not optional). By the reduction rules, there must be an
). Then, by semantics of \(\wedge \), execution of X implies execution of \(M'\) (if \(M'\) is not optional) and/or execution of \(M'\) implies execution of X (if X is not optional). By the reduction rules, there must be an  -node or an
-node or an  construct between \(\oplus \) and \(M'\). Then, execution of neither \(M'\) nor X is implied by execution of \(M_A\), so
construct between \(\oplus \) and \(M'\). Then, execution of neither \(M'\) nor X is implied by execution of \(M_A\), so  .
.
In the second case, a similar argument holds for Y and \(M'\).
Then, by Definition 7.7,  is not a partial
is not a partial  -cut of \(\alpha _{\text {coo}}(S)\).
-cut of \(\alpha _{\text {coo}}(S)\).
Hence,  is a partial
is a partial  -cut of \(\alpha _{\text {coo}}(S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\). \(\square \)
-cut of \(\alpha _{\text {coo}}(S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\). \(\square \)
1.5 Lemma F.3
Lemma: Let \(M \in \textsc {C}_{\text {coo}}{}\) be a reduced process tree with a coo-stem, let \(M' = \wedge (M'_1, \ldots M'_m)\), \(M' \in {{\,\mathrm{coo-stem}\,}}(M)\) be a coo-stem node, let \(M'_i\) be a child of \(M'\), let \(S \in \mathbb {M}^{\Sigma }(M)\) a partition such that \(\Sigma (M'_i) \in S\), and let \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\) be a coo-graph. Take any \(A \in S\) such that \(A \ne \Sigma (M'_i)\). Then, \((\wedge , \Sigma (M'_i), A)\) or \((\wedge , A, \Sigma (M'_i))\) is a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(\mathcal {L}(M), S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\).
Proof
Prove both directions separately:
- \(\Leftarrow \):
Take such an \(M'_j\). By Lemma B.2, \((\wedge , \Sigma (M'_i), A)\) is a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\).
- \(\Rightarrow \):
Towards contradiction, assume that there exists a set of activities A such that \((\wedge , \Sigma (M'_i), A)\) is a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\) and \(\forall _{1 \leqslant j \leqslant m}~ A \ne \Sigma (M'_j)\). By Definition F.1, A corresponds to a node in M. Let \(M_A\) be this node. Perform case distinction on whether the lowest common parent of \(M_A\) and \(M'\) is either \(M'\) itself or a parent of \(M'\):
The lowest common parent is \(M'\). By the assumptions made, \(M_A\) is not a direct child of \(M'\). Then, M contains either of the following structures, for a certain node X (wiggled edges denote possibly indirect children):
In all cases,
 , so \((\wedge , \Sigma (M'_i), A)\) is not a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\) and the partial cut \((\wedge , A, \Sigma (M_i'))\) must adhere to the second option of Definition 7.8.
, so \((\wedge , \Sigma (M'_i), A)\) is not a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\) and the partial cut \((\wedge , A, \Sigma (M_i'))\) must adhere to the second option of Definition 7.8.In the first case, if \(M'_i\) is not optional, then execution of X implies execution of \(M'_i\). Then, for every \(Y \in \mathbb {M}^{\Sigma }(X)\), \(\alpha _{\text {coo}}(S) \models Y \overline{\Rightarrow }\Sigma (M'_i)\), and at least one such Y is in S, which violates Requirement c.3.4. If \(M'_i\) is optional, then
 , which violates Requirement c.3.2. In the second and third cases, by reduction rule
, which violates Requirement c.3.2. In the second and third cases, by reduction rule  , \(M_i'\) cannot be optional, and an argument similar to the first case applies. Hence, \((\wedge , A, \Sigma (M_i'))\) is not a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\).
, \(M_i'\) cannot be optional, and an argument similar to the first case applies. Hence, \((\wedge , A, \Sigma (M_i'))\) is not a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\).The lowest common parent is a parent of \(M'\). Then, M contains either of the following structures, for certain nodes \(X_1, X_2, X_4\) (wiggled edges denote possibly indirect children):

In all these cases,
 , so \((\wedge , A, \Sigma (M'_i))\) is not a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\) and the partial cut \((\wedge , \Sigma (M_i'), A)\) must adhere to the second option of Definition 7.8.
, so \((\wedge , A, \Sigma (M'_i))\) is not a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\) and the partial cut \((\wedge , \Sigma (M_i'), A)\) must adhere to the second option of Definition 7.8.
In the first case, if \(\alpha _{\text {coo}}(S) \models \Sigma (M'_i) \overline{\Rightarrow }A\) then for every \(Y \in \mathbb {M}^{\Sigma }(X_1)\) it holds that \(\alpha _{\text {coo}}(S) \models Y \overline{\Rightarrow }A\), and at least one such Y is in S, which violates Requirement c.3.4.
The second case is similar to the first.
In the third case,
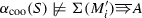 , which violates Requirement c.3.2.
, which violates Requirement c.3.2.In the fourth case, for every \(\alpha _{\text {coo}}(S) \models Y \in \mathbb {M}^{\Sigma }(X_4)\), \(Y \overline{\Rightarrow }A\), and one such Y is in S, which violates Requirement c.3.4.
Then, neither \((\wedge , A, \Sigma (M'_i))\) nor \((\wedge , \Sigma (M'_i), A)\) is a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\).
Hence, \((\wedge , \Sigma (M'_i), A)\) or \((\wedge , A, \Sigma (M'_i))\) is a partial \(\wedge \)-cut of \(\alpha _{\text {coo}}(S)\) if and only if \(\exists _{1 \leqslant j \leqslant m}~ A = \Sigma (M'_j)\). \(\square \)
1.6 Lemma F.7
Lemma: Take two reduced process trees of \(\textsc {C}_{\text {coo}}\)\(K = \oplus (K_1, \ldots K_n)\) and \(M = \otimes (M_1, \ldots M_m)\) such that \(\oplus \ne \otimes \). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {coo}}(K) \ne \alpha _{\text {coo}}(M)\).
Proof
Towards contradiction, assume that \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\) and \(\alpha _{\text {coo}}(K) = \alpha _{\text {coo}}(M)\). Perform case distinction on \(\oplus \):
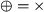 and one child \(K_i\) is a \(\tau \). As described before, the footprint of
and one child \(K_i\) is a \(\tau \). As described before, the footprint of  applies whenever the root is optional. Thus, we need to consider the case in which M is optional, but does not have the
applies whenever the root is optional. Thus, we need to consider the case in which M is optional, but does not have the  construct as root. Let
construct as root. Let  (or
(or  if
if 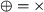 ) and perform case distinction on \(\otimes \):
) and perform case distinction on \(\otimes \): By semantics of
By semantics of  , \(\alpha _{\text {dfg}}(M)\) consists of unconnected clusters. As \(\alpha _{\text {dfg}}(M) = \alpha _{\text {dfg}}(K)\), and by semantics of the operators,
, \(\alpha _{\text {dfg}}(M)\) consists of unconnected clusters. As \(\alpha _{\text {dfg}}(M) = \alpha _{\text {dfg}}(K)\), and by semantics of the operators, 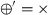 . At least one child (say \(M_j\)) is optional, but does not have the
. At least one child (say \(M_j\)) is optional, but does not have the  construct as root. Let \(K'_i\) be the corresponding child in K. Then, \(\mathcal {L}(K'_i) \cup \{\epsilon \} = M_j\). \(M_j\) cannot be a single activity (cannot be optional without the
construct as root. Let \(K'_i\) be the corresponding child in K. Then, \(\mathcal {L}(K'_i) \cup \{\epsilon \} = M_j\). \(M_j\) cannot be a single activity (cannot be optional without the 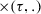 construct), or
construct), or  (by Rule
(by Rule  ). For the other operators, see the other cases (termination of the argument guaranteed as \(K_i\) and \(M_j\) are strictly smaller than M).
). For the other operators, see the other cases (termination of the argument guaranteed as \(K_i\) and \(M_j\) are strictly smaller than M).\(\otimes \,=\,\rightarrow \) By semantics of \(\rightarrow \), \(\alpha _{\text {dfg}}(M)\) consists of a chain of clusters. As \(\alpha _{\text {dfg}}(M) = \alpha _{\text {dfg}}(K)\), and by semantics of the operators, \(\oplus ' = \rightarrow \). By semantics of \(\rightarrow \), all children \(M_j\) are optional. By Rule
 , at least one child (say \(K_i\)) is not optional. Therefore, there is a non-empty trace in \(\mathcal {L}(K)\) in which no activity of \(\Sigma (K_i)\) occurs. There is no such \(M_j\), thus \(\mathcal {L}(K) \ne \mathcal {L}(M)\).
, at least one child (say \(K_i\)) is not optional. Therefore, there is a non-empty trace in \(\mathcal {L}(K)\) in which no activity of \(\Sigma (K_i)\) occurs. There is no such \(M_j\), thus \(\mathcal {L}(K) \ne \mathcal {L}(M)\).\(\otimes \,=\,\wedge \) By semantics of \(\wedge \), all children \(M_j\) must be optional. However, by Rule
 , this situation cannot occur.
, this situation cannot occur. By semantics of
By semantics of  , at least one child \(M_j\) is optional. Consider the options for \(M_j\) exhaustively:
, at least one child \(M_j\) is optional. Consider the options for \(M_j\) exhaustively:  (would be reduced by Rule
(would be reduced by Rule  ),
),  (would be reduced by Rule
(would be reduced by Rule  ), \(\wedge (\ldots )\) with all children optional (would be reduced by Rule
), \(\wedge (\ldots )\) with all children optional (would be reduced by Rule 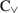 ), a (cannot be optional without
), a (cannot be optional without 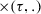 construct), or, hence, an optional non-coo-subtree without
construct), or, hence, an optional non-coo-subtree without  as root. For the other operators, see the other cases (termination of the argument guaranteed as \(K_i\) and \(M_j\) are strictly smaller than M).
as root. For the other operators, see the other cases (termination of the argument guaranteed as \(K_i\) and \(M_j\) are strictly smaller than M).\(\otimes \,=\, \leftrightarrow \) By semantics of the process tree operators, \(\oplus ' \,=\, \leftrightarrow \). By reduction rule
 , at least one child \(K'_i\) is not optional. By Definition 7.9, all children \(M_i\) must be optional.
, at least one child \(K'_i\) is not optional. By Definition 7.9, all children \(M_i\) must be optional.Take a child \(K'_{j \ne i}\). Then, execution of some activity in \(K'_j\) implies execution of some activity in \(K'_i\), while there can be no child \(M_{j \ne i}\) with such a dependency can exist in \(M_i\), as \(\leftrightarrow \) cannot be nested by Definition 7.9. Hence, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
\(\otimes \,=\, \circlearrowleft \) In this case, \(\circlearrowleft \) is optional and this is excluded by Requirement \(\hbox {C}_{\mathrm{coo}}.\hbox {l}.2\).
Hence, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
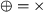 and no child is a \(\tau \). The graph \(\alpha _{\text {dfg}}(M)\) consists of several unconnected components, while as \(\otimes \) is either
and no child is a \(\tau \). The graph \(\alpha _{\text {dfg}}(M)\) consists of several unconnected components, while as \(\otimes \) is either 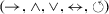 , \(\alpha _{\text {dfg}}(M)\) is connected. Thus, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
, \(\alpha _{\text {dfg}}(M)\) is connected. Thus, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).\(\oplus = \rightarrow \) The graph \(\alpha _{\text {dfg}}(M)\) is a chain, while as \(\otimes \) is either
 , \(\alpha _{\text {dfg}}(M)\) is either unconnected or strongly connected. Thus, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).
, \(\alpha _{\text {dfg}}(M)\) is either unconnected or strongly connected. Thus, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\).\(\oplus \,=\,\wedge \) We consider the remaining cases of \(\otimes \):
 By Lemma F.5, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\).
By Lemma F.5, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\) or \(\alpha _{\text {coo}}(M) \ne \alpha _{\text {coo}}(K)\).\(\otimes \,=\, \leftrightarrow \) As shown in Sect. 7.1, optionality does not influence the footprint of \(\wedge \) or \(\leftrightarrow \). Therefore, Lemma 5.2 applies. Hence, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).
\(\otimes \,=\, \circlearrowleft \) By Definition 7.9, children of \(\circlearrowleft \) are not allowed to be optional. Therefore, Lemma 5.2 applies. Hence, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).

 has the same directly follows footprint as \(\wedge \). Therefore, the arguments given at \(\oplus = \wedge , \otimes \,=\,\leftrightarrow \) and \(\otimes \,=\,\circlearrowleft \) apply.
has the same directly follows footprint as \(\wedge \). Therefore, the arguments given at \(\oplus = \wedge , \otimes \,=\,\leftrightarrow \) and \(\otimes \,=\,\circlearrowleft \) apply.\(\oplus \,=\,\leftrightarrow \) We consider the remaining case of \(\otimes \), being \(\otimes \,=\, \circlearrowleft \).
By Definition 7.9, children of \(\circlearrowleft \) are not allowed to be optional. Therefore, Lemma 5.2 applies. Hence, \(\alpha _{\text {dfg}}(M) \ne \alpha _{\text {dfg}}(K)\).
We conclude that \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {coo}}(K) \ne \alpha _{\text {coo}}(M)\). \(\square \)
1.7 Lemma F.8
Lemma: take two reduced process trees of \(\textsc {C}_{\text {coo}}\)\(K = \oplus (K_1 \ldots K_n)\) and \(M = \oplus (M_1 \ldots M_m)\) such that their activity partition is different, i.e. there is a \(1 \leqslant w \leqslant n\) such that \(\Sigma (K_w) \ne \Sigma (M_w)\). Then, \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {coo}}(K) \ne \alpha _{\text {coo}}(M)\).
Proof
Without loss of generality, we assume a fixed order of subtrees for all operators. Towards contradiction, assume that \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\) and \(\alpha _{\text {coo}}(K) = \alpha _{\text {coo}}(M)\). Perform case distinction on \(\oplus \) (the case for K and M swapped is symmetric).
 If a child \(K_i\) is \(\tau \), see the proof of Lemma F.7.
If a child \(K_i\) is \(\tau \), see the proof of Lemma F.7.As K is reduced, \(\alpha _{\text {dfg}}(K)\) contains n unconnected clusters, corresponding to \(\Sigma (K_i)\)’s. These clusters themselves are connected (by Rule
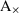 and semantics of the other operators); hence, \(\alpha _{\text {dfg}}(K)\) contains a maximal
and semantics of the other operators); hence, \(\alpha _{\text {dfg}}(K)\) contains a maximal  cut. The same holds for \(\alpha _{\text {dfg}}(M)\), hence \(\Sigma (K_w) = \Sigma (M_w)\).
cut. The same holds for \(\alpha _{\text {dfg}}(M)\), hence \(\Sigma (K_w) = \Sigma (M_w)\).\(\oplus = \rightarrow \) By Lemma F.1, \(\Sigma (K_w) = \Sigma (M_w)\).
\(\oplus = \wedge \) By Lemma F.6, \(\Sigma (K_w) = \Sigma (M_w)\).
\(\oplus = \leftrightarrow \) Let \(K_w = \otimes (K_{w_1}\ldots K_{w_p})\). Perform case distinction on \(\otimes \):
 and a child \(M_i\) is \(\tau \). The \(\leftrightarrow \) operator has a distinct directly follows graph footprint, on which
and a child \(M_i\) is \(\tau \). The \(\leftrightarrow \) operator has a distinct directly follows graph footprint, on which  has no influence. Therefore, refer to the other cases as if \(\otimes \) is the child of
has no influence. Therefore, refer to the other cases as if \(\otimes \) is the child of  , using the requirements of \(\textsc {C}_{\text {coo}}\).
, using the requirements of \(\textsc {C}_{\text {coo}}\).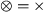 and no child \(M_i\) is \(\tau \). By semantics of
and no child \(M_i\) is \(\tau \). By semantics of  , no end activity of \(K_{w_1}\) has a connection to any start activity of any other \(K_{w_j}\). Thus, as M contains an interleaved activity partition, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).
, no end activity of \(K_{w_1}\) has a connection to any start activity of any other \(K_{w_j}\). Thus, as M contains an interleaved activity partition, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).\(\otimes =\,\rightarrow \) Similar to the
 case.
case.\(\otimes =\,\wedge \) and
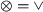 . By Definition 7.9, at least one child of \(K_w\) has disjoint start and end activities. Take such a child \(K_{w_y}\), and consider two activities: \(a \notin {{\,\mathrm{Start}\,}}(K_{w_y})\) and \(b \in \Sigma (K_w){\setminus }K_{w_y}\). By semantics of \(\wedge \) and
. By Definition 7.9, at least one child of \(K_w\) has disjoint start and end activities. Take such a child \(K_{w_y}\), and consider two activities: \(a \notin {{\,\mathrm{Start}\,}}(K_{w_y})\) and \(b \in \Sigma (K_w){\setminus }K_{w_y}\). By semantics of \(\wedge \) and  , \(\alpha _{\text {dfg}}(b, a)\). Then, by Lemma 5.1, \(a \in \Sigma (M_w)\) and \(b \in \Sigma (M_w)\). This holds for all b and by symmetry for \({{\,\mathrm{Start}\,}}(K_{w_y}) \cup {{\,\mathrm{End}\,}}(K_{w_y})\). By semantics of \(\leftrightarrow \), non-start non-end activities only have connections with start/end activities of \(K_w\). Therefore, \(\Sigma (K_w) {\setminus }{}\)\(({{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w))\)\(\subseteq \Sigma (M_w)\). Hence, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).
, \(\alpha _{\text {dfg}}(b, a)\). Then, by Lemma 5.1, \(a \in \Sigma (M_w)\) and \(b \in \Sigma (M_w)\). This holds for all b and by symmetry for \({{\,\mathrm{Start}\,}}(K_{w_y}) \cup {{\,\mathrm{End}\,}}(K_{w_y})\). By semantics of \(\leftrightarrow \), non-start non-end activities only have connections with start/end activities of \(K_w\). Therefore, \(\Sigma (K_w) {\setminus }{}\)\(({{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w))\)\(\subseteq \Sigma (M_w)\). Hence, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).\(\otimes \,=\, \leftrightarrow \) Excluded by Definition 7.9.
\(\otimes \,=\,\circlearrowleft \) By semantics of \(\leftrightarrow \), non-start non-end activities only have connections with start/end activities of \(K_w\). Therefore, \(\Sigma (K_w) \setminus ({{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w)) \subseteq \Sigma (M_w)\). All activities \(\in {{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w)\) have connections from/to \({{\,\mathrm{End}\,}}(K_{w_2}) \cup {{\,\mathrm{Start}\,}}(K_{w_2})\), thus \({{\,\mathrm{Start}\,}}(K_w) \cup {{\,\mathrm{End}\,}}(K_w)\)\({}\subseteq \Sigma (M_w)\). Hence, \(\Sigma (K_w) \subseteq \Sigma (M_w)\).
By symmetry, \(\Sigma (K_w) = \Sigma (M_w)\).
 In K,
In K,  . By Lemma F.2 and as \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\) and \(\alpha _{\text {coo}}(K) = \alpha _{\text {coo}}(M)\), it holds that
. By Lemma F.2 and as \(\alpha _{\text {dfg}}(K) = \alpha _{\text {dfg}}(M)\) and \(\alpha _{\text {coo}}(K) = \alpha _{\text {coo}}(M)\), it holds that 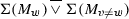 . Hence, \(\Sigma (K_w) = \Sigma (M_w)\).
. Hence, \(\Sigma (K_w) = \Sigma (M_w)\).\(\oplus = \circlearrowleft \) By Definition 7.9, children of \(\circlearrowleft \) are not allowed to be optional. Therefore, Lemma 5.3 applies.
By contradiction, we conclude that \(\alpha _{\text {dfg}}(K) \ne \alpha _{\text {dfg}}(M)\) or \(\alpha _{\text {coo}}(K) \ne \alpha _{\text {coo}}(M)\). \(\square \)
Rights and permissions
About this article
Cite this article
Leemans, S.J.J., Fahland, D. Information-preserving abstractions of event data in process mining. Knowl Inf Syst 62, 1143–1197 (2020). https://doi.org/10.1007/s10115-019-01376-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-019-01376-9




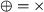 and
and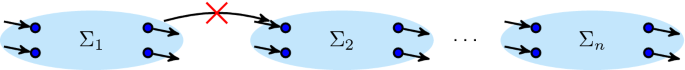




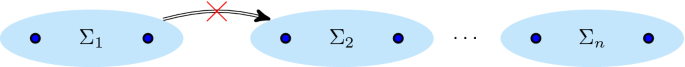


 -constructs: (Definition
-constructs: (Definition 
 (Definition
(Definition 







 (
( By semantics of the
By semantics of the  operator and the reduction rules, there exist at least n unconnected parts in
operator and the reduction rules, there exist at least n unconnected parts in  and by the semantics of the other operators,
and by the semantics of the other operators,  , the graph is not connected while for
, the graph is not connected while for  Take a pair of activities a, b such that
Take a pair of activities a, b such that 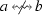 in
in  is unconnected,
is unconnected,  Take two activities
Take two activities  ,
,  case,
case,  . By semantics of the other operators, for all
. By semantics of the other operators, for all  Take a child
Take a child  . For all activities
. For all activities  , c has no directly follows connection to any node on the path. Towards contradiction, assume there is a first node d on the path
, c has no directly follows connection to any node on the path. Towards contradiction, assume there is a first node d on the path  -case.
-case. -case.
-case. By semantics of
By semantics of  , no end activity of
, no end activity of  case.
case. Each
Each 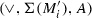 is a partial
is a partial  -cut of
-cut of 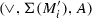 is a partial
is a partial  -cut of
-cut of 
 , execution of
, execution of  ).
). ) and execution of X implies execution of Y. That is, a coo-graph
) and execution of X implies execution of Y. That is, a coo-graph 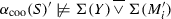 . By definition of the occurrence function (“contains any activity of”),
. By definition of the occurrence function (“contains any activity of”),  .
.

 , so
, so  , which violates Requirement c.3.2. In the second and third cases, by reduction rule
, which violates Requirement c.3.2. In the second and third cases, by reduction rule  ,
, 
 , so
, so 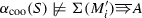 , which violates Requirement c.3.2.
, which violates Requirement c.3.2. and one child
and one child  applies whenever the root is optional. Thus, we need to consider the case in which M is optional, but does not have the
applies whenever the root is optional. Thus, we need to consider the case in which M is optional, but does not have the  construct as root. Let
construct as root. Let  (or
(or  if
if  ) and perform case distinction on
) and perform case distinction on 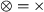 By semantics of
By semantics of  ,
, 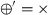 . At least one child (say
. At least one child (say  construct as root. Let
construct as root. Let 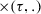 construct), or
construct), or  (by Rule
(by Rule  ). For the other operators, see the other cases (termination of the argument guaranteed as
). For the other operators, see the other cases (termination of the argument guaranteed as  , at least one child (say
, at least one child (say  , this situation cannot occur.
, this situation cannot occur. By semantics of
By semantics of  , at least one child
, at least one child  (would be reduced by Rule
(would be reduced by Rule  ),
),  (would be reduced by Rule
(would be reduced by Rule 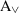 ),
), 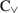 ), a (cannot be optional without
), a (cannot be optional without 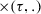 construct), or, hence, an optional non-coo-subtree without
construct), or, hence, an optional non-coo-subtree without  as root. For the other operators, see the other cases (termination of the argument guaranteed as
as root. For the other operators, see the other cases (termination of the argument guaranteed as  , at least one child
, at least one child 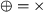 and no child is a
and no child is a 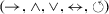 ,
,  ,
,  By Lemma
By Lemma 
 has the same directly follows footprint as
has the same directly follows footprint as  If a child
If a child  and semantics of the other operators); hence,
and semantics of the other operators); hence,  cut. The same holds for
cut. The same holds for  and a child
and a child  has no influence. Therefore, refer to the other cases as if
has no influence. Therefore, refer to the other cases as if  , using the requirements of
, using the requirements of  and no child
and no child  , no end activity of
, no end activity of  case.
case. . By Definition
. By Definition  ,
,  In K,
In K,  . By Lemma
. By Lemma 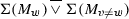 . Hence,
. Hence,