Abstract
We focus on the automatic detection of communities in large networks, a challenging problem in many disciplines (such as sociology, biology, and computer science). Humans tend to associate to form families, villages, and nations. Similarly, the elements of real-world networks naturally tend to form highly connected groups. A popular model to represent such structures is the clique, that is, a set of fully interconnected nodes. However, it has been observed that cliques are too strict to represent communities in practice. The k-plex relaxes the notion of clique, by allowing each node to miss up to k connections. Although k-plexes are more flexible than cliques, finding them is more challenging as their number is greater. In addition, most of them are small and not significant. In this paper we tackle the problem of finding only large k-plexes (i.e., comparable in size to the largest clique) and design a meta-algorithm that can be used on top of known enumeration algorithms to return only significant k-plexes in a fraction of the time. Our approach relies on: (1) methods for strongly reducing the search space and (2) decomposition techniques based on the efficient computation of maximal cliques. We demonstrate experimentally that known enumeration algorithms equipped with our approach can run orders of magnitude faster than full enumeration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the most studied problems for the analysis of fundamental properties of large networks is the automatic detection of communities, that is, groups of highly interconnected nodes [17].
A formal and strict way of defining a community is the clique, a set of nodes in a network connected by all possible edges among them. However, it has been observed that cliques are too rigid to use in practice [22]. A more appropriate notion in many practical cases is the k-plex: a set of nodes such that each of them is linked to all the others, except at most k. For example, for \(k = 1\), k-plexes are cliques as each node misses only the link to itself, for \(k=2\), each node may miss the link to one neighbor (and itself), and so on. Hence, k-plexes are a simple and intuitive generalization of cliques.
The problem of finding k-plexes arises in several application domains, including social network analysis [2] and more in general graph-based data mining [5, 22, 29]. Unfortunately, the detection of all maximal k-plexes in a network is not practical, being hindered by three main problems:
-
maximal k-plexes are even more numerous than maximal cliques;
-
most k-plexes are small and not significant;
-
state-of-the-art algorithms for computing maximal k-plexes (such as [5]) are far more inefficient than the available algorithms to compute cliques (such as [24]).
In this paper we propose a solution to the three problems above. Namely, we show that if we restrict the search to large k-plexes, which are the most meaningful in practice, we can devise efficient algorithms to detect them.
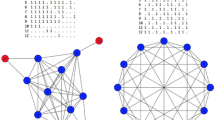
Indeed, computing all maximal k-plexes produces too many insignificant results when the purpose is that of detecting communities. In this respect, it is useful to focus on the relationship between s, the size of a k-plex, and k itself. Starting from \(k=1\), which corresponds to cliques, by increasing the value of k, we obtain progressively sparser communities that are clearly less interesting in practice, as it can be observed in Fig. 1. In addition, there is a dramatic effect on small k-plexes: it is trivial that if \(s \le k\) a k-plex can be composed of isolated nodes, but, as we discuss in Sect. 6, even if \(s < 2k\) the k-plex can be disconnected (Corollary 1). In these cases, small k-plexes do not correspond to communities. In particular, in order to avoid finding the degenerate k-plexes mentioned above, it is natural to impose at least that \(s \ge 2k\). On the other hand, using an enumeration algorithm and then filtering small k-plexes implies long waiting times.
In this context, our strategy for finding large k-plexes relies on two main observations. First, the complexity of the problem can be efficiently reduced in the vast majority of cases on the basis of certain properties of large k-plexes. This allows us to filter out a large portion of the network before starting the search. The second consideration is that we can find all k-plexes of size at least m, where m is a user-defined threshold, by looking just in the neighborhood of cliques of a size that depends on k and m. Hence, it turns out that the knowledge of maximal cliques in a network provides a hint for finding all the significant k-plexes. We note that the state-of-the-art techniques to compute all maximal cliques are able to scale up to millions of nodes [7, 10].
In sum, our contributions are the following.
-
We identify three criteria, which we call cliqueness, coreness and overlappingCliques to filter out portions of the network that cannot contain k-plexes. These criteria, introduced in the conference version of this paper [11], have inspired recent algorithms for enumerating or searching k-plexes in large graphs [15, 18].
-
We propose a decomposition strategy of the network into overlapping blocks that can be processed independently. This decomposition is based on maximal cliques, which can be efficiently computed, and is, to the best of our knowledge, the first decomposition proposed for k-plex detection.
-
Based on the above ingredients, we present a technique to efficiently detect all maximal k-plexes whose size is at least a given threshold.
-
As an application of the detection technique, we devise an algorithm to efficiently find the maximum k-plex of a network.
-
We provide an experimental analysis on real-world networks. In particular: (1) We consider different clique size distributions and show the effectiveness of our filtering criteria; (2) We show the superiority of our filtering technique over a variant in [15]; (3) We study the sensitivity of our approach with respect to the number of k-plexes; (4) We finally compare our technique to the full enumeration approach. It turns out that the techniques introduced in this paper are able to speed up the computation with respect to the state of the art, increasing the size of the networks for which computing maximal k-plexes is a feasible task by several orders of magnitude.
Outline. The rest of this paper is organized as follows. Section 2 contains an overview of our approach and results. Sections 3 to 5 describe in detail our approach to find all largest k-plexes in the network and all the most significant k-plexes, respectively. Section 6 contains the theoretical basis of our algorithms. The efficiency of our algorithms is experimentally measured in Sect. 7. Finally, Sections 8 and 9 contain related work and our concluding remarks.
2 Overview
As mentioned in the introduction, our approach is based on two main ideas: (1) before starting the search for k-plexes, we can filter out a relevant portion of the network in which necessary conditions for the presence of large k-plexes do not hold, and (2) in large networks, cliques can drive the search for k-plexes. While the first point provides an effective way to simplify the problem at hand, the second can lead to an efficient strategy for finding k-plexes.
As we noted in the introduction, an exhaustive search of all k-plexes does not make much sense, since very small k-plexes are not significant, to the point that they may even be disconnected (if their size is less than 2k) or composed by a set of isolated nodes (if their size is less than \(k+1\)).
An example network, where we search for all 2-plexes of size greater than or equal to 5. Nodes \(\{g,h,i,l,m\}\) have coreness = 4 and cliqueness = 5. Nodes \( \{a,b,c,d,e,f\}\) have coreness = 4 and cliqueness = 3. Orange nodes have coreness = 2 and cliqueness=3. Nodes \(\{u,v,z\}\) have coreness = 2 and cliqueness = 3. Hence, they are filtered out based on the coreness criterion. Finally, the two nodes \(\{x,y\}\) in the bottom of the picture are filtered out because of the cliqueness criterion
Global filtering criteria. Consider, for instance, the network in Fig. 2, which we will use as a running example in this section. Let us focus on the problem of finding all k-plexes of size at least \(m=5\), with \(k=2\). Assume that we have computed all the maximal cliques of the network. It turns out that two global filtering criteria can be applied.
-
1.
Coreness Our first intuition follows from the very definition of k-plex: all the nodes of a k-plex of size s must have degree at least \(s-k\). If we search for k-plexes with size at least m, this means that we can iteratively filter out every node that has degree lower than \(m-k\). This corresponds to computing the coreness of all the nodes of the network (Lemma 2), a process that can be executed in linear time [3]. In our example, we can filter out the three nodes \(\{u,v,z\}\) at the top of the picture since they have coreness 2, which is less than \(m-k=5-2=3\). In larger networks we show that this criterion allows us to filter out even \(97\%\) of the nodes.
-
2.
Cliqueness The second intuition is that any node of a k-plex of size s must be included in a clique of a size that depends on s. This is confirmed by Corollary 3, which states that any node of a k-plex larger than or equal to s is included in a clique of size at least \(\lceil s/k \rceil \). Then, if we search for k-plexes of size at least m, we can filter out all nodes that do not belong to any clique of size at least \(\lceil m/k \rceil \). Regarding complexity, this operation requires to compute the cliques of the network, a process that may require exponential time but that can be executed efficiently in real-world networks [6].
In our example, we can filter out all nodes that do not belong to cliques of size at least \(\lceil m/k \rceil = \lceil 5/2 \rceil =3\), that is, the nodes \(\{x,y\}\) in the bottom of the network. We will show in Sect. 7 that in larger instances this criterion can be tested efficiently and is able to cut up even \(80\%\) of the nodes.
Even if some nodes can be filtered out because of both their low cliqueness and low coreness, the network in Fig. 2 shows that the two filtering criteria are indeed independent. When both criteria are used, the size of the network can be reduced by several orders of magnitude and standard techniques for finding k-plexes can be efficiently applied (e.g. full enumeration techniques). These techniques are described in Sect. 3.
Block decomposition and advanced filtering. As mentioned above, our idea is to start from cliques (which are k-plexes but not necessarily maximal) and possibly enlarge them to find maximal k-plexes.
The cliqueness criterion guarantees that each node in a k-plex C of size at least s belongs to a clique K of size at least \(\lceil s/k \rceil \) included in the k-plex. If we set \(m \ge k^2\), we have that \(|K| \ge \lceil s/k \rceil > k\), which implies that any other node of C must be adjacent to at least one node of K (in other words, K is a dominating set of C). Hence, we can search for C restricting to a block including K and all its adjacent nodes. Each block can be separately processed, possibly in a distributed environment.
We also show that a k-plex can be obtained by considering only nodes belonging to a clique K of size at least \(\lceil s/k \rceil \) and to other cliques of size at least \(\lceil s/k \rceil \) intersecting with K (Lemma 5). This gives rise to an advanced filtering technique and an efficient search algorithm that decompose the network into blocks each composed of one clique as the core, and all intersecting cliques as the boundary. These techniques are described in Section 4.
Finding k -plexes. Our filtering and decomposition strategies can be applied on top of any known enumeration algorithm to find all the k-plexes larger than a user-specified threshold m more efficiently. We describe the resulting enumeration meta-algorithms in Section 5.
3 Global filtering criteria
Our target is the enumeration of the large k-plexes of the input graph G, that is, of all k-plexes with size not smaller than a user-chosen threshold m. One ingredient of our approach is that of restricting the search to a suitable sub-graph of G, that we refer to as H. Clearly, the smaller H is with respect to G, the faster solving the problem is. Ideally, H consists exclusively of the nodes of the k-plexes we are looking for. Precisely, we aim at extracting a sub-graph H out of G, that is:
-
1.
Small enough to make the enumeration fast;
-
2.
Large enough to capture all k-plexes of G of size at least m.
We design two different global filtering criteria, dubbed coreness and cliqueness. Our criteria are of the form “all the k-plexes of size at least m consist of nodes with property P”, and fulfill the above desiderata for a choice of m.
We now describe our coreness and cliqueness criteria, and how to use them for extracting the sub-graph H out of G.
Our first criterion is the simplest, and it is based on the intuition that all the nodes of a k-plex C, with \(|C| \ge m\) have degree at least \(m-k\). Clearly, we do not know a priori what are the nodes of C. However, we can recursively filter out any node that has degree lower than \(m-k\). Formally, this is equivalent to searching for the \((m-k)\)-cores of G. We define this concept in the following:
Definition 1
An h-core of G is a maximal connected subgraph of G in which all nodes have degree at least h. A node u has coreness h if it belongs to a h-core, but not to any \((h+1)\)-core.
An h-core is one of the connected components of the sub-graph of G formed by repeatedly deleting all nodes of degree less than h. We are now ready to state our coreness criterion:
Filtering Criterion 1
(Coreness) All the k-plexes of G of size at least m consist of nodes having coreness at least \(m-k\).
Our second criterion is based on the intuition that all the nodes of a k-plex C, with \(|C| \ge m\), form smaller cliques with other nodes of C. Informally speaking, if we try to “draw” a k-plex by adding one edge at a time, we soon realize that there are no ways of placing edges without forming progressively larger cliques here and there. Lemma 3 in Section 6 proves that every node of C participates in a clique of size at least \(\frac{m}{k}\). Therefore, we can filter out any node that only participates in smaller cliques. Formally:
Definition 2
A node u has cliqueness h if it belongs to a clique of size h, but not to any clique of size \(h+1\).
We are now ready to state our cliqueness criterion:
Filtering Criterion 2
(Cliqueness) All the k-plexes of G of size at least m consist of nodes having cliqueness at least \(\frac{m}{k}\).

Computing the sub-graph. Let m be the minimum size of the searched k-plexes specified by the user. The procedure Prune(G, k, m) shown in Algorithm 1, returns the sub-graph H resulting from deleting nodes of G according to the coreness and cliqueness criteria. We first compute the \((m-k)\)-cores (line 2), and then we filter out all the nodes with low cliqueness in the cores (line 3). Note that the two criteria can be applied sequentially, in any order. Since computing coreness is easy [3], we chose to apply coreness first and compute cliqueness on the smaller graph \(G'\) (line 3). At this point, one could re-apply coreness, then cliqueness and so on, until the graph does not change anymore. In practice, however, we observed that this yields marginal to no gain.
We remark that Algorithm 1 corresponds to the filtering criteria used in the preliminary version of this paper [11]. In the next section we describe some additional filtering criteria which allow further pruning.
4 Block decomposition and advanced filtering

As mentioned in Sect. 2, our approach leverages on a decomposition of the network into blocks that can be processed independently, that is, we guarantee that any k-plex is entirely contained in some block of the decomposition.
Our decomposition exploits the cliqueness criterion. Namely, let C be a k-plex of size at least m. Consider any maximal clique \(K \in C\). We know from the cliqueness criterion that \(|K| \ge \frac{m}{k}\), that is, every node of C must participate in a clique at least as large as \(\frac{m}{k}\). Observe that a k-plex is dominated by any set of k nodes of the k-plex, since every other node can miss up to \(k-1\) neighbors. Therefore, if \(m \ge k^2\), then \(|K| \ge \frac{m}{k} = k\) and the clique K dominates C. It follows that, in order to find C, it suffices to search in the neighborhood of K.
For example, suppose you are searching for all maximal 2-plexes of size at least 5 in the network of Fig. 3a. Consider any clique of size at least \(\lceil s/k \rceil = \lceil 5/2 \rceil = 3\), for example the clique \(K=\{a,b,e\}\) (light gray nodes in Fig. 3a). The nodes of any k-plex of size at least 5 containing K are either (1) in K or (2) adjacent to K (circled nodes in Fig. 3a). This allows us to target our search for large k-plexes to the neighborhood of each clique K.
In Algorithm 2 we show the Block(K) method for returning a block of nodes that can be processed independently to find all the k-plexes including a given clique K. The method returns K together with its neighborhood and it can be called multiple times during enumeration, as discussed in the next section (Sect. 5).

Advanced filtering. Consider again the network in Fig. 3, where we search for 2-plexes of size at least \(m=5\), such as \(C=\{a,b,c,d,e,f\}\). Let \(K=\{a,b,e\}\). As shown in Fig. 3b, all the nodes of C not in K participate in cliques overlapping with K, that is, sharing at least one node with K, for instance \(\{a,b,c\}\), \(\{b,c,d\}\) and \(\{a,e,f\}\). Note that, edge (a, g) is included in the neighborhood of K but is not needed to find C nor any other 2-plex larger than m.
This enables us to state a new filtering criterion, that we refer to as overlappingCliques. We state the criterion as follows and provide a proof of its correctness in Lemma 5.
Filtering Criterion 3
(OverlappingCliques) All the k-plexes of G with size \(m \ge k^2\) consist of nodes (and edges) either belonging to a clique K s.t. \(|K| \ge \frac{m}{k}\), or to overlapping cliques \(K'\), s.t. \(|K'| \ge \frac{m}{k}\) and \(K \cap K' \ne \emptyset \).
We implement this criterion via the Filter_Edges(G) method in Algorithm 3, which filters away all the edges that do not participate in at least one clique larger than \(\frac{m}{k}\): indeed any such edge cannot belong to either K, or any of the overlapping cliques. Observe that the method Filter_Edges(G) can be called just once on the input graph, rather than when computing each block.
For example, method Filter_Edges(G) launched on the graph of Fig. 3a yields the graph in Fig. 3b, filtering out the edge (a, g). When calling the method Block(K) on the latter graph, only nodes in overlapping cliques with K are returned (represented as colored circles in Fig. 3b).
Algorithm 3 also shows our final filtering strategy, that we refer to as Filter(). Such strategy providing a more effective approach than the procedure Prune() (Algorithm 1) at a reasonable efficiency cost. In a nutshell, Filter() starts by calling Prune() (line 13) and Filter_Edges() (line 14). Then, it enumerates all the maximal cliques of the resulting sub-graph H (line 16). Such set of cliques (line 16) is used to construct all the blocks with the method Block() in Algorithm 2 (line 17). Since blocks can be processed independently, we can re-apply coreness and cliqueness individually on each block (line 18) without missing any k-plex and we can further reduce the size of H. Specifically, Filter() collects all the nodes and edges surviving the application of Prune() on each block (line 18) and returns their union \(H'\) (line 20) for subsequent processing. Our experiments show that further pruning at line 18 can provide on some instances a substantial reduction of the surviving nodes, with respect to the result of line 13.
5 Finding large k-plexes
In this section, we discuss how to apply our filtering criteria and block decomposition to find all the k-plexes larger than a user-specified threshold m.
5.1 Enumerating all large k-plexes
Algorithm 4 describes our approach for the enumeration of large k-plexes that exploits state-of-the-art algorithms for the exhaustive enumeration of cliques and k-plexes. In particular, the procedure LargePlexes() leverages AllCliques() and AllPlexes(), implemented for instance as in [6, 10] and in [5], respectively. Further, LargePlexes() uses the auxiliary methods Block() and Filter(), that are detailed in Algorithm 2 and Algorithm 3 of Sect. 4, respectively.

Algorithm LargePlexes() first calls the advanced Filter() procedure (line 2) to extract a sub-graph H based on our filtering criteria and on the input threshold m. In fact, it is guaranteed (see Sect. 3) that the removed nodes and edges do not participate in any k-plex of size larger than or equal to m. Second, LargePlexes() enumerates all the maximal cliques of the sub-graph H (line 3). The resulting set \(\mathcal {K}\) only consists of those cliques that are larger than \(\frac{m}{k}\) (because of the constructive process of H) and that can be used as “seeds” from which large k-plexes can be derived. Then, the LargePlexes() algorithm iterates over \(\mathcal {K}\) (lines 4–12) and for each clique constructs a block by adding its neighborhood (line 5). Let B be the current set of nodes returned by Block()Footnote 1. We first enumerate all the maximal k-plexes of the sub-graph of H induced by B, denoted by H[B] (line 6). Observe that the same k-plex C may be found in multiple blocks. Therefore, we rely on a “de-duplication” method to return only one copy of each k-plex of size at least m (lines 7–11).
De-duplication. Let C be any k-plex computed by AllPlexes(H[B], k). We introduce the concept of “parent clique” of C, and return C only when the clique that generated the current block is equal to its parent clique. Specifically, let min(C) be the node u in C with smallest idFootnote 2 and let complete(X, Y) be a method that iteratively adds to the clique X the node in Y that is adjacent to all the nodes in X and has the minimum id, if any exists. The method stops when there is no node left in Y adjacent to all nodes in X. The parent clique of C is defined by construction as follows.
Specifically, we start from the node u in C with smallest id. Then, the process of construction has two phases. We first extend u into a clique inside C, we then keep extending the clique by selecting nodes from the whole H. Both operations are performed by taking nodes in increasing order of id. It is apparent that each k-plex C is contained into at least one block, and in particular we prove that C is contained into the block B built starting from its parent clique P (see Lemma 6 in Section 6). Conversely, there cannot be two blocks for which the procedure IsNotDuplicate returns true. This guarantees that each k-plex is produced by exactly one block.
We remark that the graph H computed at line 2 of Algorithm 4 can be empty if the user specifies a very high threshold m. In this case, LargePlexes() terminates without yielding any k-plex. Also, it may happen that H consists of a single clique. In this case, there is no need to execute lines 3–11: the enumeration procedure returns H and terminates.
5.2 Finding the maximum k-plex

While community detection algorithms typically aim at finding several communities, an important problem is also that of finding the largest, most relevant, one. The techniques of Sect. 5.1 can be used in this direction as well, to produce an algorithm for finding the maximum k-plex.
Let \(\omega \) be the size of the maximum clique in G. Since the maximum clique is also the maximum 1-plex and the size of the maximum k-plex is lower-bounded by the size of the maximum \(k-1\)-plex, \(\omega \) can be though of as a lower-bound for any maximum k-plex of G. This strategy, which we refer to as MaxPlex(), is illustrated in Algorithm 5 and proceeds as follows. We first enumerate all the maximal cliques of G (line 1) and then use \(\omega +1\) as the threshold m for LargePlexes() (lines 2–4). Observe that the set of maximal cliques \(\mathcal {K}\) computed at line 1 can be passed as an optional parameter to LargePlexes(), in order to avoid their computation twice. Finally, we consider all the maximal k-plexes in \(\mathcal {C}\), and return the maximum one (lines 5–10). If there are no k-plexes found, we return \(K_M\) (line 9).Footnote 3
We observe that one might want to apply a binary search approach, by starting from a large threshold, until \(C_M \ne \emptyset \) We observed experimentally that this approach yields better performances than the MaxPlex() in Algorithm 5 approach only when the maximum k-plex is order of magnitudes larger than \(\omega \). However this is rarely the case in real-world graphs. We discuss more in detail the effectiveness of such a binary search algorithm for finding largest k-plex in [11].
In Sect. 7 we experimentally investigate the effectiveness of Algorithm 5.
6 Theoretical basis
In this section we consider a k-plex \(C=(V,E)\) with \(|C| = s\) nodes. For the sake of simplicity C may refer to both the set of nodes it contains and to the induced graph. We recall that if C is a k-plex then each of its nodes is adjacent to all nodes in C except at most k, thus a clique can be thought of as a 1-plex. We also observe that any subset of a k-plex is also a k-plex, and any k-plex is also a \(k+1\)-plex. We now need to prove the correctness of Criteria 1, 2, and 3 dubbed coreness, cliqueness and overlappingCliques, respectively, and described in the previous sections.
6.1 Coreness criterion
Criterion 1 states that all the k-plexes of a graph G of size larger than or equal to m consist of nodes having coreness at least \(m-k\). To prove this claim we need some preliminary results.
Let C be a k-plex of size s. Denote \(\Delta (C)\) the diameter of C, that is, the largest number of edges which must be traversed in order to travel from one node to another. While a clique, or a 1-plex, has diameter equal to 1, k-plexes with \(k > 1\) come in a variety of forms and can have arbitrarily high diameters (which is not a desirable property for a community, as shown in Fig. 1). However, for \(k \le \frac{s}{2}\) – which means that every node is adjacent to more than half of the nodes in C – the diameter is at most 2. This is proven in the following.
Lemma 1
Let C be a k-plex of size s. If \(s \ge 2k\) then \(\Delta (C) \le 2\).
Proof
Assume, by contradiction, that C has diameter larger than 2. Then, there are at least two nodes u and v at distance more than 2. Since u is missing at most k edges, it has at least \(|N(u)|\ge s-k\) neighbors. However, neither u nor its neighbors are connected to v and therefore v is missing at least \(|N(u)\cup \{u\}| \ge s-k+1\) edges. Since \(s \ge 2k\), we have \(s-k+1 \ge k+1\), so v violates the k-plex requirement – a contradiction. \(\square \)
Corollary 1
If \(s \ge 2k\) then C is connected.
We are now ready for proving the coreness criterion.
Lemma 2
(Coreness) Every node of C has coreness at least \(s-k\) in C.
Proof
Let |N(u)| denote the number of nodes of C adjacent to u. By the definition of k-plex every node \(c \in C\) has \(|N(c)| \ge s-k\). Hence, C is unchanged by recursively removing nodes of degree less than \(s-k\), that is, every node in C has coreness \(s-k\) [27]. \(\square \)
Since the coreness does not decrease when considering a supergraph of C, we have the following.
Corollary 2
Every node of C has coreness at least \(s-k\) in G.
Corollary 2 justifies the filtering based on Criterion 1 used in Section 3.
6.2 Other criteria
We give the technical lemma below, that we use for deriving the cliqueness and decomposition criteria, and the advanced filtering principle.
Lemma 3
Every clique \(X \subseteq C\), s.t. \(|X| < \frac{s}{k}\), is included in a larger clique \(X_{big}\), s.t. \(|X_{big}| \ge \frac{s}{k}\).
Proof
Let \(X \subseteq C\) be any clique of C, s.t. \(|X| < \frac{s}{k}\). Let \(N \subseteq C\) be the set of nodes which are not adjacent to all nodes of X, that is, that are adjacent to only h nodes of X, with \(0 \le h \le |X|-1\). It is obvious that by picking any node \(u' \in C {\setminus } (X \cup N)\) (provided such a node \(u'\) exists) we have that \(X'=X \cup \{u'\}\) is a clique of size \(|X|+1\). Since every \(u \in X\) can miss at most k neighbors including itself, \(|N \cup X| \le |X|(k-1) + |X| = k |X|\). This means that at most k|X| nodes are excluded for the selection of \(u'\). Let \(N'\) be the nodes not adjacent to all nodes of \(X'\). We can repeat the process and grow \(X'\), by picking any node \(u'' \in C{\setminus } (X' \cup N')\), until we run out of nodes. Note that the newly-excluded nodes for selecting \(u''\) are \(u'\) and its missing neighbors, which are at most \(k-1\). Such a clique-growing process can be thought of as an iterative process starting from a node and growing a clique – as if X itself were grown after |X| steps of the process – and excluding at most k nodes at a time. Therefore, the process will run at least \(\frac{s}{k}\) steps, after which X has been grown to \(\frac{s}{k}\) nodes. \(\square \)
Note that, in case \(\frac{s}{k}\) is not integer, the proof yields \(|X_{big}| \ge \lceil \frac{s}{k} \rceil \). This directly implies the cliqueness criterion.. Precisely, the corollary below follows from the clique-growing argument given in the proof of Lemma 3, by starting from a single node.
Corollary 3
(cliqueness) Every node in C has cliqueness at least \(\lceil \frac{s}{k} \rceil \).
We now give the lemma below for proving the correctness of our block decomposition strategy.
Lemma 4
Consider a clique \(X \subseteq C\), s.t. \(|X| \ge \frac{s}{k}\). If \(s\ge k^2\), every node in C either belongs to X or has a neighbor in X.
Proof
We know that such a clique always exists from Lemma 3. Since its size is at least k by assumption, then every \(u \in C{\setminus } X\) has to be adjacent to at least one node in X. \(\square \)
Our last criterion is a stricter form of the above lemma, which we formalize as follows and which justifies the Filter_Edges() procedure in Algorithm 3.
Lemma 5
[OverlappingCliques] Consider a clique \(X \subseteq C\), s.t. \(|X| \ge \frac{s}{k}\). If \(s\ge k^2\), every node in C either belongs to X or to an overlapping clique \(X'\), s.t. \(|X'| \ge \frac{s}{k}\) and \(X \cap X' \ne \emptyset \).
Proof
Let u be any node of \(C{\setminus } X\). We know from Lemma 4 that exists a node \(v \in X\) adjacent to u. Since \(\{u,v\}\) is a clique of size 2, we can apply Lemma 3 and conclude that both nodes belong to a clique \(X'\) of size at least \(\frac{s}{k}\). Finally, \(v \in X \cup X'\). \(\square \)
Finally, we demonstrate the correctness of our duplication check for Algorithm 4.
Lemma 6
(Duplication check) Any k-plex C is contained into the block B generated by its parent clique P.
Proof
Let \(P'=C \cap P\) denote the portion of the parent clique that is inside C. By construction, \(P'\) is maximal within C and thus from Lemma 3 it follows that \(|P'| \ge \frac{s}{k}\). Since \(s \ge m \ge k^2\), by Lemma 4 we have that all nodes of C are either in P or neighbors of a node in P. It follows that C is contained into B. \(\square \)
7 Experiments
In this section we experimentally verify the effectiveness and efficiency of the approaches described in the paper.
7.1 Experimental set-up
We now describe our experimental set-up. The code for our experiments is publicly available.Footnote 4
Test environment. Our experiments were performed on a machine with 32 CPU Intel Xeon E5-520 units, running at 2.26GHz, with 8MB of cache and 32GB RAM. The operating system was Linux CentOS 6.7, with kernel version 2.6.32, Java Virtual Machine version 1.8.0_111 (64-Bit) and Python version 2.6.6 (64-Bit). All our executions have a 12 hours timeout, after which they are interrupted. In the tables of this section, the symbol \(*\) denotes that the execution was interrupted due to timeout. All the running times are averaged over 3 runs.
Datasets. As shown in Table 1, we consider six real-world networks from the Stanford Large Network Dataset CollectionFootnote 5 with different sizes and different clique size distribution. The size \(\omega \) of the largest clique for each network is shown in Table 1, while the clique size distributions are shown in Fig. 4. In the experiments, we show that with traditional methods even the smallest networks can incur in timeout. Our algorithms, instead, can process networks up to hundreds of thousands of nodes.
Variants and Baseline. We use the algorithm described in [5], denoted by AllPlexes(), as the k-plex enumeration method in the algorithm described in Sect. 5. We use the algorithm in [24] as the maximal cliques enumeration method, denoted by AllCliques(), in the filtering and search algorithms. We have implemented coreness criterion with the method in [3] for computing k-cores, and the cliqueness criterion with the already mentioned algorithm in [24] for computing cliques. We consider the following variants of our enumeration methods:
-
1.
Filter&BlockEnum, corresponding to running Filter() followed by AllPlexes() over individual blocks of the filtered graph (as in the LargePlexes procedure in Algorithm 4);
-
2.
Filter&Baseline, corresponding to running Filter() followed by AllPlexes() over the filtered graph as a whole;
-
3.
BlockEnum, corresponding to running AllPlexes() over individual blocks of the original (i.e., unfiltered) graph;
-
4.
Baseline, corresponding to running AllPlexes() [5] over the original (unfiltered) graph as a whole, as described in [5].
In the variants Filter&BlockEnum and BlockEnum the enumeration method is executed over each block in parallel. We demonstrate the efficiency and effectiveness of our techniques for different values of k and the threshold size m. For comparison, we also consider the filtering method in [15], that is a variant of our coreness technique described in Sect. 3. We denote this method as KDD18.
7.2 Impact of the filtering techniques
In the following we demonstrate the benefit of our filtering methods, by measuring how many nodes of real-world networks can be filtered out, and comparing them with the technique KDD18 in [15].
Effectiveness. Table 2 shows the impact of the filtering techniques on the largest graphs of our dataset for a threshold equal to 10, 50, and 100. In particular, column Filter() shows the number of nodes of the networks surviving our advanced filtering method (see Algorithm 3) when searching for k-plexes with k equal to 2 and 3 (the two sections of the table). It is apparent that the percentage of nodes filtered out by Filter() if very large, reducing the size of the graphs by orders of magnitude. Increasing the value of m yields less surviving nodes, depending on the distribution of k-plexes in the input graph. We observe that, for values of the threshold that are higher than the maximum k-plex, there might be no surviving node at all, allowing us to immediately recognize that no such k-plex exists. Note also that increasing the value of k decreases the effectiveness of the filtering. These values justify the reduced computation times that we will have on the filtered networks with respect to the original ones.
Columns Coreness and Cliqueness show the impact of the two filtering criteria if they were applied separately. In most of the cases Coreness is more effective than Cliqueness, however, it is not obvious when one technique is preferable to the other. Hence, it is advisable to use both as in Algorithm 1 (while in most of the cases the advantage of using both criteria is limited, in some cases yields a much smaller networks). Although it is not shown in Table 2, we also tested the repeated application of the two criteria multiple times, obtaining a negligible gain. We remark that the Cliqueness criterion is more sensitive to the parameter k than the Coreness one and becomes quickly less effective as k increases. As a frame of comparison, we show in Fig. 4 the clique distribution of the networks in Table 2. The graphs confirm the intuition that when the distribution is skewed (i.e., there are few large cliques and a long tail of smaller ones) the cliqueness criterion is most effective. We remark that having a skewed distribution is a property that can be expected in a scale-free network.
Back to Table 2, column [15] shows the impact of the filtering technique described in [15], that is a variant of our Coreness technique described in Sect. 3. The technique in [15] is comparable to coreness alone. For the sake of completeness we also show the impact of the Prune() method alone, that corresponds to the filtering technique described in [11]. These experiments prove that the filtering criteria described in this paper are extremely effective, which is also confirmed by the fact that, after the introduction of these techniques in a preliminary version of this paper [11], they have inspired several works on the enumeration or on the search of k-plexes in large graphs, such as [15, 18].
Efficiency of the filtering. Table 3 shows the preprocessing overhead. We measured the time needed to apply the two criteria coreness and cliqueness separately. (obviously, the total time of the filtering procedure in Algorithm 1 is equal to the sum of the two times). We also measured the running time of the Filter() procedure, for different values of m and for \(k=2\). We observe that, as expected, coreness is faster to compute than cliqueness, although the order of magnitude is the same. For comparison, we report in the same Table 3 the computation time of the exhaustive enumeration of k-plexes (Algorithm AllPlexes() described in [5]). The difference between the largest time for computing Filter() (24 minutes) and the corresponding enumeration time (more than 12 h) suggests that filtering times are acceptable. Similar observations could be done for larger values of k.
7.3 Enumeration of large k-plexes
In this Section, we demonstrate the efficiency and effectiveness of the techniques in Sect. 5 for finding the larger k-plexes in a fraction of the time required by the method AllPlexes() in [5].
Enumerating all large k -plexes. Table 4 shows the running time of our large k-plexes enumeration strategy on different networks in our dataset, for different values of k and m, and for the variants presented in the experimental set-up section (Sect. 7.1). For this experiment, we set m to different fractions of the largest clique size (\(\omega \)) in order to ensure that the number of large k-plexes found (\(|\mathcal {C}|\)) is at least one. Indeed, values of m larger than \(\omega \) do not yield any k-plex in our experiments while values of m smaller than \(0.5 \omega \) can yield thousands of k-plexes, which is almost analogous to exhaustive enumeration. The time required for enumerating all k-plexes (column AllPlexes) of such networks is always larger than our timeout (12 hours), except for the smallest network and \(k=2\). The table also shows the number of k-plexes returned (column \(|\mathcal {C}|\)). All the networks considered, except for cagrqc, contain less than a hundred k-plexes of size at least \(0.5 \omega \), which can be quickly found by our filtering-based strategies, showing output-semsitive properties. In order to demonstrate the benefit of our block decomposition method, we show the running time of the exhaustive enumeration strategy (that is, without filtering) by processing blocks in parallel (column BlockEnum). Our results show that as long as the network size is small enough to make exhaustive enumeration feasible, block decomposition can decrease running time by orders of magnitude, by completing the task in less than 1 hour, as opposite of more than 12 hours required for the traditional strategy with no decomposition. After filtering, in the networks considered in our experiments, we are left with at most a dozen blocks, except for citationCiteseer, and therefore the impact of block decomposition (column Filter&BlockEnum) is less evident. Nonetheless, with more than 10 blocks, running time can be boosted up to 2.4x.
We conclude discussion of Table 4 by summarizing when to apply the filtering and block decomposition strategies presented in our framework.
-
1.
Filtering (i.e., the Filter() method in Algorithm 3) is always beneficial. Indeed, it typically decreases running time by orders of magnitude, and its overhead is negligible with respect to exhaustive enumeration time (i.e., AllPlexes).
-
2.
The block decomposition strategy is always beneficial when the number of blocks is less than the number of available processors. Indeed, it can decrease running time more than 2.4x, without overhead.
-
3.
The block decomposition strategy can be beneficial even if the number of blocks is more than the number of available processors (e.g., BlockEnum(cagrqc)), but the overhead due to duplicate enumeration (see theory in Sect. 6) can be high (Filter&BlockEnum(citationCiteseer)). In this case, if we have p processors, we can reserve one processor for no blocking and \(p-1\) for blocking.
Finding the maximum k-plex. Finally, table 5 shows the efficiency of the MaxPlex() method in Algorithm 5, for different values of k. We observe that the method is not only faster than AllPlexes() (which only terminated before timeout for cagrqc and \(k=2\)) but it yields similar performances up to \(k=6\), for all the graphs except citationCiteseer.
8 Related works
In the field of network analysis, dense substructures in graphs (aka dense subgraphs) are associated with communities, or more in general sets of closely related elements [17, 22]. The problem of finding these substructures has been extensively studied for decades, and continues to be the object of cutting edge research. The simplest and most rigorous definition of dense subgraph is the clique, i.e., a subgraph in which all nodes are pairwise connected. Many algorithms for finding all maximal cliques have been developed, most of them being inspired to the Bron-Kerbosh algorithm [6], such as [16, 24] or to the more recent paradigm of reverse search [1], such as [9, 14, 20]. The definition of clique may be too strict in some instances, such as in real datasets where data can be noisy and incomplete, so several definitions of pseudo-clique have been produced [22], such as the k-plex [23].
To the best of our knowledge, our work provides the first meta-algorithm for detecting large k-plexes. The closest works to our are full enumeration k-plexes algorithms, such as [5, 8]. The search space reduction mechanisms in [15, 18] are inspired by our filtering criteria (in particular, by coreness), which have been described originally in [11]. These and other related works are discussed next.
We point out that this is an extended version of the paper appeared in [11]. With respect to our earlier work [11, 12], we have: (1) largely improved the filtering algorithm, now referred to as Filter, (2) extensively extended the related works considering more recent literature, (3) presented a more thorough and extensive experiment campaign, including executions on a parallel architecture, and (4) introduced new practical discussion on how to configure the proposed techniques in real-world applications.
Full enumeration. Cohen et al. [8] give a generic framework for enumerating all maximal subgraphs with respect to hereditary and connected hereditary graph properties, i.e., properties that are closed with respect to induced subgraphs and connected induced subgraphs, respectively. Berlowitz et al. [5] apply the framework in [8], together with insights on the k-plex problem, to produce efficient algorithms for the enumeration of maximal k-plexes and maximal connected k-plexes, which are, respectively, hereditary and connected hereditary. An important property of this algorithm is that it is output-sensitive for small values of k, that is, the total running time will be a function of the size of the graph and the number of maximal k-plexes. The algorithm for connected k-plexes in [5] outperformed the current state of the art enumeration algorithms, such as the recursive one by Wu et al. [28], and constitutes our baseline for the experimental evaluation. A noteworthy theoretical result is achieved by Zhou et al. [30], who are the first to present an algorithm with guaranteed total time significantly lower than \(O(2^n)\): their algorithm runs in \(O(n^2(2-\gamma )^n)\) time, for some \(\gamma \) which depends on k but is strictly larger than 0.
Largest k-plex. McClosky [21] performs a thorough study to devise exact algorithms for finding the largest k-plex, and heuristics for finding lower upper bounds on its size, exploiting co-k-plexes (i.e., k-plexes on the complement graph) and graph coloring techniques. The usability of such algorithm is however limited to small networks, as the running time exceeds the hour for graphs with hundreds of nodes. We note that, provided with a lower-bound on the size of largest k-plex, our extraction layer can be also helpful in the extreme scenario where we want to enumerate only k-plexes of maximum size. Indeed, one of the ideas behind the more recent algorithm in [18] consists in finding a lower-bound on the size of the largest k-plex and then use coreness for filtering out nodes that can be proven only participating in k-plexes with smaller size. Such efficient algorithm is more efficient than those provided by McClosky [21] and can run on larger instances. Recently, a heuristic algorithm for the maximum k-plex has been proposed in [19], based on the fact that k-plexes correspond to graphs of degree bounded by \(k-1\) in the complement graph.
Parallel algorithms. Full enumeration can be slow when processing large instances. To this end, Wu et al. [28] propose Pemp, a parallel algorithm for enumerating all the k-plexes, which successfully improves its performance with the usage of multiple cores, which was later improved by Wang et al. [26]. In particular, [15] incorporates a filtering procedure based on degeneracy that can be optionally turned on to skip small k-plexes during enumeration. Such filtering criteria, rather than cutting the highest amount of vertices, aims to have minimal time spent on pruning in order to take advantage as quickly as possible of a distributed environment. the result is a computationally lighter pruning procedure which has the same underlying principle as the coreness criterion, and can provide similar results in practice, as discussed in Section 7. The k-plex computation step in [15] is then handled via a recursive procedure, which does not have the output-sensitive properties of [5], but shows good performance on real networks. Finally, our LargePlexes() algorithm can be implemented effectively in a distributed environment, as discussed in Section 5.
Efficient clique enumeration. Since the number of cliques can be exponential in the worst case [24], a great amount effort was dedicated to find efficient algorithms for clique enumeration [7, 10]. These algorithms can decompose the input graph into smaller sub-graphs that can be processed independently, allowing efficient in-memory computation of very large instances. Our Block() method is inspired to the the blocking idea in [10]. Technically, we leverage a generalization of the principle in [10] that says that every clique is dominated by any of its nodes, by realizing that every k-plex is dominated by any k of its nodes. In terms of memory-efficiency, the recent work in [13] describes a shared-nothing distributed algorithm for the detection of 2-plexes, that is, for the specific case where \(k=2\).
Other quasi-clique models. Finally, let us observe alternative quasi-clique models studied in the literature, together with some pros and cons concerning their usability for the purpose of finding graphs communities.
Uno [25] considers the notion of dense subgraph, defined as a set S of nodes such that G[S] has density over a desired threshold. Dense subgraphs, however, are challenging to enumerate and the proposed algorithm enumerates also non-maximal solutions (which may be exponentially more in number).
A k-club [22] is a set S of nodes such that G[S] has diameter k; this concept relaxes the adjacency requirement in a clique to distance k in G[S], however they do not have the hereditary property (a subset of a k-club may not be a k-club), making their detection elusive, and indeed an efficient enumeration algorithm is yet unknown.
Behar et al. [4] give an enumeration algorithms for s-cliques, a set S of nodes each at distance s or less from all others in G. This relaxes the k-club as distances may depend on connections outside of S, which may result in a less cohesive community, but allows for efficient enumeration.
A variant of the k-plex can be found in Zhai et al. [29], who add further connectivity constraints called CLB.
Finally, more models can be found in the survey by Pattillo et al. [22].
Out of all these quasi-clique models, it appears that k-plexes received a larger interest. This is perhaps due to their structure having strong cohesiveness, despite being more relaxed and thus noise-tolerant than a clique, while at the same time maintaining the hereditary property (a subset of a k-plex is a k-plex) and allowing for efficient detection, and thus making them a suitable model for our study.
9 Conclusions and future works
We have proposed a novel approach for the enumeration of large k-plexes, that are a formal and meaningful way to define interesting communities in real-world networks that generalizes the notion of clique. Our approach can be implemented efficiently in parallel over a distributed environment, which meets our goal of making the problem of computing k-plexes in large real-world networks practically tractable.
Two main clues have driven our solution:
-
a relevant portion of the network can be filtered out before starting the detection of large k-plexes and
-
cliques, which are more restricted but can be computed efficiently, can be used as starting points for the search of k-plexes in the network. The efficiency of the approach over state-of-the-art algorithms has been confirmed by our experiments.
Finally, we demonstrated the effectiveness of our approach in a parallel setting, by processing different blocks of LargePlexes() on different cores with a shared memory.
In the future, we intend to further extend the applicability of our approach and tackle the problem of computing large k-plexes on real-world networks in a shared-nothing infrastructure (for any value of k).
Notes
Observe that, it would be possible, in principle, to launch the Filter() procedure on the sub-graph induced by each block. We measured experimentally that this does not reduce significantly the size of the blocks.
For instance, with respect to the lexicographic ordering.
Note that in the classic “max k-plex” application scenario the goal is to find just one largest k-plex, rather than enumerating all of them.
References
Avis D, Fukuda K (1996) Reverse search for enumeration. Discret Appl Math 65(1–3):21–46
Balasundaram B, Butenko S, Hicks IV (2011) Clique relaxations in social network analysis: the maximum k-plex problem. Oper Res 59(1):133–142. https://doi.org/10.1287/opre.1100.0851
Batagelj V, Zaversnik M (2003) An O(m) algorithm for cores decomposition of networks. CoRR cs.DS/0310049
Behar R, Cohen S (2018) Finding all maximal connected s-cliques in social networks. In: 21th International Conference on Extending Database Technology, EDBT, pp 61–72. https://doi.org/10.5441/002/edbt.2018.07
Berlowitz D, Cohen S, Kimelfeld B (2015) Efficient enumeration of maximal k-plexes. In: Proceedings of the 2015 ACM SIGMOD international conference on management of data, SIGMOD ’15, pp 431–444. ACM, New York, NY, USA
Bron C, Kerbosch J (1973) Finding all cliques of an undirected graph (algorithm 457). Commun ACM 16(9):575–576
Cheng J, Zhu L, Ke Y, Chu S (2012) Fast algorithms for maximal clique enumeration with limited memory. In: KDD, pp 1240–1248
Cohen S, Kimelfeld B, Sagiv Y (2008) Generating all maximal induced subgraphs for hereditary and connected-hereditary graph properties. J Comput Syst Sci 74(7):1147–1159
Comin C, Rizzi R (2018) An improved upper bound on maximal clique listing via rectangular fast matrix multiplication. Algorithmica 80(12):3525–3562
Conte A, De Virgilio R, Maccioni A, Patrignani M, Torlone, R (2016) Finding all maximal cliques in very large social networks. In: Proceedings of the 19th international conference on extending database technology, EDBT 2016, Bordeaux, France, March 15-16, 2016, Bordeaux, France, March 15-16, 2016., pp 173–184
Conte A, Firmani D, Mordente C, Patrignani M, Torlone R (2017) Fast enumeration of large k-plexes. In: Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pp 115–124. ACM
Conte A, Firmani D, Mordente C, Patrignani M, Torlone R (2018) Cliques are too strict for representing communities: finding large k-plexes in real networks. In: Proceedings of the 26th Italian symposium on advanced database systems
Conte A, Firmani D, Patrignani M, Torlone R (2019) Shared-nothing distributed enumeration of 2-plexes. In: Proceedings of the 28th ACM international conference on information and knowledge management, CIKM 2019, Beijing, China, November 3-7, pp 2469–2472 (2019)
Conte A, Grossi R, Marino A, Versari L (2016) Sublinear-space bounded-delay enumeration for massive network analytics: maximal cliques. In: 43rd international colloquium on automata, languages, and programming, ICALP 2016, July 11-15, 2016, Rome, Italy, pp 148:1–148:15
Conte A, Matteis TD, Sensi DD, Grossi R, Marino A, Versari, L (2018) D2K: scalable community detection in massive networks via small-diameter k-plexes. In: Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining, KDD 2018, London, UK, August 19-23, 2018, pp. 1272–1281
Eppstein D, Strash D (2011) Listing all maximal cliques in large sparse real-world graphs. In: SEA, pp 364–375
Fortunato S (2010) Community detection in graphs. Phys Rep 486(3):75–174
Gao J, Chen J, Yin M. Chen R, Wang Y (2018) An exact algorithm for maximum k-plexes in massive graphs. In: IJCAI, pp 1449–1455
Hsieh SY, Kao SS, Lin YS (2019) A swap-based heuristic algorithm for the maximum \( k \)-plex problem. IEEE Access 7:110267–110278
Makino K, Uno T (2004) New algorithms for enumerating all maximal cliques. In: SWAT, pp 260–272
McClosky B, Hicks IV (2012) Combinatorial algorithms for the maximum k-plex problem. J Comb Optim 23(1):29–49
Pattillo J, Youssef N, Butenko S (2012) Clique relaxation models in social network analysis. Springer, New York
Seidman SB, Foster BL (1978) A graph-theoretic generalization of the clique concept. J Math Sociol 6(1):139–154. https://doi.org/10.1080/0022250X.1978.9989883
Tomita E, Tanaka A, Takahashi H (2006) The worst-case time complexity for generating all maximal cliques and computational experiments. Theor Comput Sci 363(1):28–42
Uno T (2010) An efficient algorithm for solving pseudo clique enumeration problem. Algorithmica 56(1):3–16
Wang Z, Chen Q, Hou B, Suo B, Li Z, Pan W, Ives ZG (2017) Parallelizing maximal clique and k-plex enumeration over graph data. J Parallel Distrib Comput 106:79–91
West DB et al (2001) Introduction to graph theory, vol 2. Prentice hall Upper Saddle River, New Jersey
Wu B, Pei X (2007) A parallel algorithm for enumerating all the maximal k-plexes. In: Pacific-Asia conference on knowledge discovery and data mining, pp 476–483. Springer
Zhai H, Haraguchi M, Okubo Y, Tomita E (2016) A fast and complete algorithm for enumerating pseudo-cliques in large graphs. Int J Data Sci Anal 2(3–4):145–158
Zhou Y, Xu J, Guo Z, Xiao M, Jin Y (2020) Enumerating maximal k-plexes with worst-case time guarantee. In: The thirty-fourth AAAI conference on artificial intelligence, AAAI, pp 2442–2449
Acknowledgements
We thank the authors of [5] for providing us with their code, Caterina Mordente for contributing to an earlier version of this work and Simone Rossetti for insightful discussions. We also thank the anonymous reviewers for their helpful comments and suggestions. This research was supported in part by the European Commission Project “PANTHEON” under the grant agreement number 774571, by MIUR Project “AHeAD” under PRIN 20174LF3T8, and by Roma Tre University Azione 4 Project “GeoView”.
Funding
Open access funding provided by Università degli Studi Roma Tre within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Conte, A., Firmani, D., Patrignani, M. et al. A meta-algorithm for finding large k-plexes. Knowl Inf Syst 63, 1745–1769 (2021). https://doi.org/10.1007/s10115-021-01570-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-021-01570-8