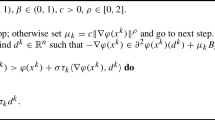Hessian barrier algorithms for non-convex conic optimization

Abstract

A key problem in mathematical imaging, signal processing and computational statistics is the minimization of non-convex objective functions that may be non-differentiable at the relative boundary of the feasible set. This paper proposes a new family of first- and second-order interior-point methods for non-convex optimization problems with linear and conic constraints, combining logarithmically homogeneous barriers with quadratic and cubic regularization respectively. Our approach is based on a potential-reduction mechanism and, under the Lipschitz continuity of the corresponding derivative with respect to the local barrier-induced norm, attains a suitably defined class of approximate first- or second-order KKT points with worst-case iteration complexity $O(\varepsilon ^{-2})$ (first-order) and $O(\varepsilon ^{-3/2})$ (second-order), respectively. Based on these findings, we develop new path-following schemes attaining the same complexity, modulo adjusting constants. These complexity bounds are known to be optimal in the unconstrained case, and our work shows that they are upper bounds in the case with complicated constraints as well. To the best of our knowledge, this work is the first which achieves these worst-case complexity bounds under such weak conditions for general conic constrained non-convex optimization problems.

1 Introduction

Non-convex optimization is an active area of research in optimization with one of the goals being to establish complexity guarantees for finding approximate stationary points, see the review [40] and the references therein. Two large groups of algorithms that allow one to achieve this goal are first-order methods [2, 20, 23, 32, 51] and second-order methods [18, 26, 27, 29,30,31,32, 37, 38, 42, 79]. Higher-order algorithms are also analyzed, e.g., in [17, 28, 33, 74]. One of the challenges in the development and analysis of algorithms for non-convex optimization is dealing with constraints. The class of optimization problems we consider in this paper is described as follows.

Let $\mathbb {E}$ be a finite dimensional vector space with inner product $\langle \cdot ,\cdot \rangle$ and Euclidean norm $\Vert \cdot \Vert$. We are concerned with solving constrained conic optimization problems of the form

$$\begin{aligned} \min _{x} f(x)\quad \text {s.t.: } {\textbf{A}}x=b,\; x\in \bar{\textsf{K}}. \end{aligned}$$

(Opt)

The main working assumption underlying our developments is as follows:

Assumption 1

• 1. $\bar{\textsf{K}}\subset \mathbb {E}$ is a pointed (i.e., $\bar{\textsf{K}}\cap (-\bar{\textsf{K}})=\{0\}$) closed convex cone with nonempty interior $\textsf{K}$;

• 2. ${\textbf{A}}:\mathbb {E}\rightarrow \mathbb {R}^{m}$ is a linear operator assigning each element $x\in \mathbb {E}$ to a vector in $\mathbb {R}^m$ and having full rank., i.e., ${{\,\textrm{im}\,}}({\textbf{A}})=\mathbb {R}^{m}$, $b \in \mathbb {R}^{m}$;

• 3. The feasible set $\bar{\textsf{X}}=\bar{\textsf{K}}\cap \textsf{L}$, where $\textsf{L}=\{x\in \mathbb {E}\vert {\textbf{A}}x=b\}$, is compact and has nonempty relative interior denoted by $\textsf{X}=\textsf{K}\cap \textsf{L}$;

• 4. $f:\mathbb {E}\rightarrow \mathbb {R}$ is possibly non-convex, continuous on $\bar{\textsf{X}}$ and continuously differentiable on $\textsf{X}$;

• 5. Problem (Opt) admits a global solution. We let $f_{\min }(\textsf{X})=\min \{f(x)\vert x\in \bar{\textsf{X}}\}$.

Note that f is not assumed to be globally differentiable, but only over the relative interior of the feasible set. Problem (Opt) contains many important classes of optimization problems as special cases. We summarize the three most important ones below.

Example 1

(NLP with non-negativity constraints) For $\mathbb {E}=\mathbb {R}^n$ and $\bar{\textsf{K}}\equiv \bar{\textsf{K}}_{\text {NN}}=\mathbb {R}^n_{+}$ we recover non-linear programming problems with linear equality constraints and non-negativity constraints: $\bar{\textsf{X}}=\{x\in \mathbb {R}^n\vert {\textbf{A}}x=b,\text { and } x_{i}\ge 0\text { for all }i=1,\ldots ,n\}.$ $\Diamond$

Example 2

(Optimization over the second-order cone) Consider $\mathbb {E}=\mathbb {R}^{n}$ and $\bar{\textsf{K}}\equiv \bar{\textsf{K}}_{\text {SOC}}=\{x=(x_{0},\underline{x})\in {\mathbb {R}\times \mathbb {R}^{n-1}}\vert x_{0}\ge \Vert \underline{x}\Vert _2\}$, the second-order cone (SOC). In this case problem (Opt) becomes a non-linear second-order conic optimization problem. Such problems have a huge number of applications, including energy systems [75], network localization [84], among many others [3]. $\Diamond$

Example 3

(Semi-definite programming) If $\mathbb {E}=\mathbb {S}^{n}$ is the space of real symmetric $n\times n$ matrices and $\bar{\textsf{K}}\equiv \bar{\textsf{K}}_{\text {SDP}}=\mathbb {S}^{n}_{+}$ is the cone of positive semi-definite matrices, we obtain a non-linear semi-definite programming problem. Endow this space with the standard inner product $\langle a,b\rangle ={{\,\textrm{tr}\,}}(ab)$. In this case, the linear operator ${\textbf{A}}$ assigns a matrix $x\in \mathbb {S}^{n}$ to a vector ${\textbf{A}}x = [\langle a_{1},x\rangle , \ldots , \langle a_{m},x\rangle ]^\top$. Such mathematical programs have received enormous attention due to the large number of applications in control theory, combinatorial optimization, and engineering [13, 41, 70]. $\Diamond$

Example 4

(Exponential cone programming) Consider the exponential cone defined as

$$\begin{aligned} \textsf{K}_{\exp }=\{x\in \mathbb {R}^{3}\vert x_{1}\ge x_{2}e^{x_{3}/x_{2}},x_{2}>0\} \end{aligned}$$

with the closure $\bar{\textsf{K}}_{\exp }={{\,\textrm{cl}\,}}(\textsf{K}_{\exp })=\textsf{K}_{\exp }\cup \{(x_{1},0,x_{3})\vert x_{1}\ge 0,x_{3}\le 0\}$. $\textsf{K}_{\exp }$ is an important convex cone that is implemented in standard numerical solution packages like YALMIP, MOSEK, and CVX, as it can be used to represent a lot of interesting convex sets arising in optimization; see [34] and the PhD thesis [35]. $\Diamond$

1.1 Motivating applications

1.1.1 Inverse problems with non-convex regularization

An important instance of (Opt) is the composite optimization problem

$$\begin{aligned} \min _{x}\left\{ f(x)=\ell (x)+\lambda \sum _{i=1}^{n}\varphi (x_{i}^{p})\right\} \quad \text {s.t.: } x\in \bar{\textsf{K}}_{\text {NN}}, \end{aligned}$$

(1)

where $\ell :\mathbb {R}^n\rightarrow \mathbb {R}$ is a smooth data fidelity function, $\varphi :\mathbb {R}\rightarrow \mathbb {R}$ is a convex function, $p\in (0,1)$, and $\lambda >0$ is a regularization parameter. A common use of this problem formulation is the regularized empirical risk-minimization problem in high-dimensional statistics, or the variational regularization technique in inverse problems. Non-negativity constraints can be motivated by some prior knowledge about the observed object which needs to be reconstructed. For example, the true signal may represent an image with positive intensities of the pixels, or one can consider Poisson Inverse Problem as in [59]. Common specifications for the regularizing function are $\varphi (s)=s$, or $\varphi (s)=s^{2/p}$. In the first case, we obtain $\sum _{i=1}^{n}\varphi (x^{p}_{i})=\sum _{i=1}^{n}x_{i}^{p}=\Vert x\Vert ^{p}_{p}$ on $\textsf{K}_{\text {NN}}$, whereas in the second case, we get $\sum _{i=1}^{n}\varphi (x^{p}_{i})=\sum _{i=1}^{n}x_{i}^{2}=\Vert x\Vert ^{2}$. Note that the first case yields the objective f which is non-convex and non-differentiable at the boundary of the feasible set. It has been reported in imaging sciences that the use of such non-convex and non-differentiable regularizer has advantages in the restoration of piecewise constant images. Bian and Chen [15] contains a nice survey of studies supporting this observation. Moreover, in variable selection, the $L_{p}$ penalty function with $p\in (0,1)$ owns the oracle property [44] in statistics, while $L_{1}$ (called the LASSO) does not; problem (1) with $p\in (0,1)$ can be used for variable selection at the group and individual variable levels simultaneously, while the very same problem with $p=1$ can only work for individual variable selection [66]. See [36, 50] for a complexity-theoretic analysis of this problem.

1.1.2 Low rank matrix recovery

On the space of symmetric matrices $\mathbb {E}=\mathbb {S}^{n}$, together with the feasible set $\bar{\textsf{X}}=\{x\in \mathbb {E}\vert {\textbf{A}}x=b,x\in \bar{\textsf{K}}_{\text {SDP}}\}$ we can consider the composite model $f(x)=\ell (x)+r(x)$, with smooth loss function $\ell :\mathbb {E}\rightarrow \mathbb {R}$, and with regularizer $r:\mathbb {E}\rightarrow \mathbb {R}\cup \{+\infty \}$. In applications the regularizer is given in the form of a matrix function $r(x)=\sum _{i}\sigma _{i}(x)^{p}$ on $x\in \textsf{K}_{\text {SDP}}$, where $p\in (0,1)$ and $\sigma _{i}(x)$ is the i-th singular value of the matrix x. The resulting optimization problem is a matrix version of the non-convex regularized problem (1). See [67, 86] for a wealth of optimization problems following this description.

1.2 Challenges and contribution

One of the challenges in approaching problem (Opt) algorithmically is to deal with the feasible set $\textsf{L}\cap \bar{\textsf{K}}$. A projection-based approach faces the computational bottleneck to project onto the intersection of a cone with an affine subspace, which makes the majority of the existing first-order [2, 20, 23, 32, 51, 57, 77] and second-order [18, 26, 27, 31, 32, 37, 38, 42, 79] methods practically less attractive, as they either are designed for unconstrained problems or use proximal steps in the updates. When primal feasibility is not a major concern, augmented Lagrangian algorithms [5, 7, 19, 54] are an alternative, though they do not always come with complexity guarantees. These observations motivate us to focus on primal barrier-penalty methods that allow us to decompose the feasible set and treat $\bar{\textsf{K}}$ and $\textsf{L}$ separately. Barrier methods are classical and powerful for convex optimization in the form of interior-point methods [78]. In the non-convex optimization setting results are in a sense fragmentary, with many different algorithms existing for different particular instantiations of (Opt). In particular, the main focus of barrier methods for non-convex optimization has been on particular cases, such as non-negativity constraints [16, 22, 58, 82, 85, 87] and quadratic programming [47, 73, 87]. In this paper we develop a flexible and unifying algorithmic framework that is able to accommodate first- and second-order interior-point algorithms for (Opt) with potentially non-convex and non-smooth at the relative boundary objective functions, and general, possibly non-symmetric, conic constraints. To the best of our knowledge, our framework is the first one providing complexity results for first- and second-order algorithms to reach points satisfying, respectively, suitably defined approximate first- and second-order necessary optimality conditions, under such weak assumptions and for such a general setting.

1.2.1 Our approach

At the core of our approach is the assumption that the cone $\bar{\textsf{K}}$ admits a logarithmically homogeneous self-concordant barrier (LHSCB) h(x) ([78], cf. Definition 1), for which we can retrieve information about the function value h(x), the gradient $\nabla h(x)$ and the Hessian $H(x)=\nabla ^{2}h(x)$ with relative ease. This is not a very restrictive assumption, since all standard conic restrictions in optimization (i.e., $\bar{\textsf{K}}_{\text {NN}},\bar{\textsf{K}}_{\text {SOC}},\bar{\textsf{K}}_{\text {SDP}}$ and $\bar{\textsf{K}}_{\exp }$) have this property. Using this barrier function, our algorithms are designed to reduce the potential function

$$\begin{aligned} F_{\mu }(x)=f(x)+\mu h(x), \end{aligned}$$

(2)

where $\mu >0$ is a (typically) small penalty parameter. By definition, the domain of the potential function $F_{\mu }$ is the interior of the cone $\bar{\textsf{K}}$. Therefore, any algorithm designed to reduce the potential will automatically respect the conic constraints, and the satisfaction of the linear constraints $\textsf{L}$ can be ensured by choosing search directions from the nullspace of the linear operator ${\textbf{A}}$. Our target is to find points satisfying suitably defined approximate necessary first- and second-order optimality conditions for problem (Opt) expressed in terms of $\varepsilon$-KKT and $(\varepsilon _1,\varepsilon _2)$-2KKT points respectively (cf. Sect. 3 for a precise definition).¹

1.2.2 Finding points satisfying approximate necessary first-order conditions

To produce an $\varepsilon$-KKT point for the model problem (Opt), we construct a novel gradient-based method, which we call the first-order adaptive Hessian barrier algorithm (${{\,\mathrm{\textbf{FAHBA}}\,}}$, Algorithm 1). The main computational steps involved in ${{\,\mathrm{\textbf{FAHBA}}\,}}$ are the identification of a search direction and a step-size policy, guaranteeing feasibility and sufficient decrease in the potential function value. The algorithm starts from an approximate analytic center of the feasible set. To find a search direction, we employ a linear model for $F_{\mu }$, regularized by the squared local norm induced by the Hessian of the barrier function h, which is then minimized over the tangent space of the affine subspace $\textsf{L}$. The step-size is adaptively chosen to ensure feasibility and sufficient decrease in the objective function value f. For a judiciously chosen value of $\mu$, we prove that this gradient-based method enjoys the upper iteration complexity bound $O(\varepsilon ^{-2})$ for reaching an $\varepsilon$-KKT point when a “descent Lemma” holds relative to the local norm induced by the Hessian of h (cf. Assumption 3 and Theorem 1 in Sect. 4). We then move on in proving that ${{\,\mathrm{\textbf{FAHBA}}\,}}$ can be embedded within a path-following scheme that iteratively reduces the value of $\mu$. This renders our first-order interior-point method parameter-free and any-time convergent, with basically the same iteration complexity of $O(\varepsilon ^{-2})$.

1.2.3 Finding points satisfying approximate necessary second-order conditions

To obtain $(\varepsilon _1,\varepsilon _2)$-2KKT points, we construct a second-order adaptive Hessian barrier algorithm (${{\,\mathrm{\textbf{SAHBA}}\,}}$, Algorithm 3). As for ${{\,\mathrm{\textbf{FAHBA}}\,}}$, the search direction subroutine minimizes a local model of the potential function $F_{\mu }$ over the tangent space of the affine subspace $\textsf{L}$. The minimized model is composed of the linear model for $F_{\mu }$, augmented by second-order information on the objective function f and regularized by the cube of the local norm induced by the Hessian of h. The regularization parameter is chosen adaptively to allow for potentially larger steps in the areas of small curvature. For a judiciously chosen value of $\mu$, we establish (cf. Theorem 3) the worst-case upper bound $O(\max \{\varepsilon _1^{-3/2},\varepsilon _2^{-3/2}\})$ on the number of iterations for reaching an $(\varepsilon _1,\varepsilon _2)$-2KKT point, under a weaker version of the assumption that the Hessian of f is Lipschitz relative to the local norm induced by the Hessian of h (cf. Assumption 4 in Sect. 5 for a precise definition). We then propose a path-following version of ${{\,\mathrm{\textbf{SAHBA}}\,}}$ that iteratively reduces the value of $\mu$ making the algorithm parameter-free and any-time convergent, with $O(\max \{\varepsilon _1^{-3/2},\varepsilon _2^{-3/2}\})$ complexity.

1.3 Related work

To the best of our knowledge, ${{\,\mathrm{\textbf{FAHBA}}\,}}$ and ${{\,\mathrm{\textbf{SAHBA}}\,}}$ are the first interior-point algorithms that achieve such complexity bounds for the general non-convex problem template (Opt). Closest to our approach, but within the trust-region framework, are the works [58, 65, 82]. All these papers focus on the special case of non-negativity constraints with $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}$ (Example 1) and fix $\mu$ before the start of the algorithm based on the desired accuracy $\varepsilon$, which may require some hyperparameter tuning in practice and may not work if the desired accuracy is not yet known. Interestingly, for the special case $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}$, our algorithms provide stronger results under weaker assumptions, compared to the first- and second-order methods in [58], the second-order method in [65] specified to our setting of linear constraints, and the first-order implementation of the second-order method in [82]. We make this claim precise in Sects. 4.4 and 5.3.

1.3.1 First-order methods

In the unconstrained setting, when the gradient is Lipschitz continuous, the standard gradient descent achieves the lower iteration complexity bound $O(\varepsilon ^{-2})$ to find a first-order $\varepsilon$-stationary point $\hat{x}$ such that $\Vert \nabla f(\hat{x})\Vert \leqslant \varepsilon$ [24, 25, 76]. The original inspiration for the construction of our methods comes from the paper [22] on Hessian barrier algorithms, which in turn was strongly influenced by continuous-time techniques [4, 21]. We extend the first-order method of [22] to general conic constraints, and develop a unified complexity analysis, which goes far beyond the quadratic optimization case studied in detail in that reference.

1.3.2 Second-order methods

In unconstrained optimization with Lipschitz continuous Hessian, cubic-regularized Newton methods [55, 79] and second-order trust region algorithms [27, 37, 38] achieve the lower iteration complexity bound $O(\max \{\varepsilon _1^{-3/2},\varepsilon _2^{-3/2}\})$ [24, 25] to find a second-order $(\varepsilon _1,\varepsilon _2)$-stationary point, i.e., a point $\hat{x}$ satisfying $\Vert \nabla f(\hat{x})\Vert \le \varepsilon _1$ and $\lambda _{\min } \left( \nabla ^2 f(\hat{x})\right) \ge - \sqrt{\varepsilon _2}$, where $\lambda _{\min }(\cdot )$ denotes the minimal eigenvalue of a matrix.² The existing literature on non-convex problems with non-linear constraints either considers only equality constraints [39], only inequality constraints [65], or both, but require projection [32]. Moreover, they do not consider general conic constraints as as we do in this paper.

1.3.3 Approximate optimality conditions

Bian et al. [16] consider box-constrained minimization of the same objective as in (1) and propose a notion of $\varepsilon$-scaled KKT points. Their definition is tailored to the geometry of the optimization problem, mimicking the complementarity slackness condition of the classical KKT theorem for the non-negative orthant. In particular, their first-order condition consists of feasibility of x along with a scaled gradient condition. Haeser et al. and O’Neill–Wright [58, 82] convincingly argue that, without additional assumptions on the objective function, points that satisfy the scaled gradient condition may not approach KKT points as $\varepsilon$ decreases. Thus, [58, 82], provide alternative notions of approximate first- and second-order KKT conditions for the domain $\textsf{K}_{\text {NN}}$. Inspired by [58], we define the corresponding notions for general cones. Our first-order conditions turn out to be stronger than those of [58, 82] and the second-order condition is equivalent to theirs in the particular case of non-negativity constraints (cf. Sects. 3.3, 4.4, and 5.3). The proof that our algorithms are guaranteed to find such approximate KKT points requires some fine analysis exploiting the structural properties of logarithmically homogeneous barriers associated to the cone $\textsf{K}$, and are not simple extensions of arguments used for $\textsf{K}_{\text {NN}}$.

We remark that after the first release of our preprint on arXiv on October 29, 2021 (https://arxiv.org/abs/2111.00100v1), the paper [61] appeared in July 2022, of which we became aware during the revision of our paper after its submission. They also consider the model problem (Opt) and also build their algorithmic developments on a barrier construction. They propose a Newton-CG based method for finding $(\varepsilon ,\varepsilon )$-second-order approximate KKT points with similar to ours iteration complexity guarantee $O(\varepsilon ^{-3/2})$, yet the dependence of their complexity bound on the barrier parameter is not clear. Their algorithm also runs for a fixed parameter $\mu$, and thus is not parameter-free, unlike our parameter-free versions. Also, unlike them, we propose a first-order algorithm.

1.4 Notation

In what follows, $\mathbb {E}$ denotes a finite-dimensional real vector space, and $\mathbb {E}^{*}$ the dual space, which is formed by all linear functions on $\mathbb {E}$. The value of $s\in \mathbb {E}^{*}$ at $x\in \mathbb {E}$ is denoted by $\langle s,x\rangle$. In the particular case where $\mathbb {E}=\mathbb {R}^n$, we have $\mathbb {E}=\mathbb {E}^{*}$. The gradient vector of a differentiable function $f:\mathbb {E}\rightarrow \mathbb {R}$ is denoted as $\nabla f(x)\in \mathbb {E}^{*}$. For an operator $\textbf{H}:\mathbb {E}\rightarrow \mathbb {E}^{*}$, denote by $\textbf{H}^{*}$ is adjoint operator, defined by the identity

$$\begin{aligned} (\forall u,v\in \mathbb {E}): \qquad \langle \textbf{H}u,v\rangle =\langle u,\textbf{H}^{*}v\rangle . \end{aligned}$$

Thus, $\textbf{H}^{*}:\mathbb {E}\rightarrow \mathbb {E}^{*}$. It is called self-adjoint if $\textbf{H}=\textbf{H}^{*}$. We use $\lambda _{\max }(\textbf{H})\; (\lambda _{\min }(\textbf{H}))$, to denote the maximum (minimum) eigenvalue of such operators. Important examples of such self-adjoint operators are Hessians of twice differentiable functions $f:\mathbb {E}\rightarrow \mathbb {R}$:

$$\begin{aligned} (\forall u,v\in \mathbb {E}):\qquad \langle \nabla ^{2}f(x)u,v\rangle =\langle u,\nabla ^{2}f(x)v\rangle . \end{aligned}$$

Operator $\textbf{H}:\mathbb {E}\rightarrow \mathbb {E}^{*}$ is positive semi-definite if $\langle \textbf{H}u,u\rangle \ge 0$ for all $u\in \mathbb {E}$. If the inequality is always strict for non-zero u, then $\textbf{H}$ is called positive definite. These attributes are denoted as $\textbf{H}\succeq 0$ and $\textbf{H}\succ 0$, respectively. By fixing a positive definite self-adjoint operator $\textbf{H}:\mathbb {E}\rightarrow \mathbb {E}^{*}$, we can define the following Euclidean norms

$$\begin{aligned} \Vert u\Vert =\langle \textbf{H}u,u\rangle ^{1/2},\quad \Vert s\Vert ^{*}=\langle s,\textbf{H}^{-1}s\rangle ^{1/2}\quad u\in \mathbb {E},s\in \mathbb {E}^{*}. \end{aligned}$$

In some cases we use notation $\Vert u\Vert _{\textbf{H}}$ to explicitly indicate the operator used to define the norm. If $\mathbb {E}=\mathbb {R}^n$, then $\textbf{H}$ is usually taken as the identity matrix $\textbf{H}=\textbf{I}$. The $L_{\infty }$-norm of $x \in \mathbb {R}^n$ is denoted as $\Vert x\Vert _{\infty } = \max _{i=1,\ldots ,n} |x_i|$. The directional derivative of function $f:\mathbb {E}\rightarrow \mathbb {R}$ is defined in the usual way:

$$\begin{aligned} Df(x)[v]=\lim _{\varepsilon \rightarrow 0+} \frac{1}{\varepsilon }[f(x+\varepsilon v)-f(x)]. \end{aligned}$$

More generally, for $v_{1},\ldots ,v_{p}\in \mathbb {E}$, we define $D^{p}f(x)[v_{1},\ldots ,v_{p}]$ the p-th directional derivative at x along directions $v_{i}\in \mathbb {E}$. In that way we define $\nabla f(x)\in \mathbb {E}^{*}$ by $Df(x)[u]=\langle \nabla f(x),u\rangle$ and the Hessian $\nabla ^{2}f(x):\mathbb {E}\rightarrow \mathbb {E}^{*}$ by $\langle \nabla ^{2}f(x)u,v\rangle =D^{2}f(x)[u,v]$. We denote by $\textsf{L}_{0}\triangleq \{ v \in \mathbb {E}\vert {\textbf{A}}v = 0\}{\triangleq \ker ({\textbf{A}})}$ the tangent space associated with the affine subspace $\textsf{L}\subset \mathbb {E}$.

2 Preliminaries

2.1 Cones and their self-concordant barriers

Let $\bar{\textsf{K}}\subset \mathbb {E}$ be a regular cone: $\bar{\textsf{K}}$ is closed convex with nonempty interior $\textsf{K}={{\,\textrm{int}\,}}(\bar{\textsf{K}})$, and pointed (i.e. $\bar{\textsf{K}}\cap (-\bar{\textsf{K}})=\{0\}$). Any such cone admits a self-concordant logarithmically homogeneous barrier h(x) with finite parameter value $\theta$ [78].

Definition 1

A function $h:\bar{\textsf{K}}\rightarrow (-\infty ,\infty ]$ with ${{\,\textrm{dom}\,}}h=\textsf{K}$ is called a $\theta$-logarithmically homogeneous self-concordant barrier ($\theta$-LHSCB) for the cone $\bar{\textsf{K}}$ if:

• (a) h is a $\theta$-self-concordant barrier for $\bar{\textsf{K}}$, i.e., for all $x \in \textsf{K}$ and $u\in \mathbb {E}$

  $$\begin{aligned}&|D^{3}h(x)[u,u,u]|\le 2D^{2}h(x)[u,u]^{3/2},\text { and } \\&\sup _{u\in \mathbb {E}}|2 Dh(x)[u]-D^{2}h(x)[u,u]|\le \theta . \end{aligned}$$

• (b) h is logarithmically homogeneous:

  $$\begin{aligned} h(tx)=h(x)-\theta \ln (t)\qquad \forall x\in \textsf{K},t>0. \end{aligned}$$

We denote the set of $\theta$-logarithmically homogeneous barriers by $\mathcal {H}_{\theta }(\textsf{K})$.

The constant $\theta$ is called the parameter of the barrier function. Just like in standard interior point methods, it affects the iteration complexity of our methods. Given $h\in \mathcal {H}_{\theta }(\textsf{K})$, from [76, Thm 5.1.3] we know that for any $\bar{x}\in {{\,\textrm{bd}\,}}(\bar{\textsf{K}})$, any sequence $(x_{k})_{k \ge 0}$ with $x_{k}\in \ \textsf{K}$ and $\lim _{k\rightarrow \infty }x_{k}=\bar{x}$ satisfies $\lim _{k\rightarrow \infty }h(x_{k})=+\infty$. For a pointed cone $\bar{\textsf{K}}$, we have $\theta \ge 1$ and the Hessian $H(x)\triangleq \nabla ^{2}h(x):\mathbb {E}\rightarrow \mathbb {E}^{*}$ is a positive definite linear operator defined by $\langle H(x)u,v\rangle \triangleq D^{2}h(x)[u,v]$ for all $u,v\in \mathbb {E}$, see [76, Thm. 5.1.6]. The Hessian gives rise to a (primal) local norm

$$\begin{aligned} (\forall x\in \textsf{K})(\forall u\in \mathbb {E}):\quad \Vert u\Vert _{x}\triangleq \langle H(x)u,u\rangle ^{1/2}. \end{aligned}$$

We also define a dual local norm on $\mathbb {E}^{*}$ as

$$\begin{aligned} (\forall x\in \textsf{K})(\forall s\in \mathbb {E}^{*}):\quad \Vert s\Vert _{x}^{*}\triangleq \langle [H(x)]^{-1}s,s\rangle ^{1/2}. \end{aligned}$$

The Dikin ellipsoid with center $x\in \textsf{K}$ and radius $r>0$ is defined as the open set $\mathcal {W}(x;r)\triangleq \{u\in \mathbb {E}\vert \;\Vert u-x\Vert _{x}<r\}$. The usage of the local norm adapts the unit ball to the local geometry of the set $\textsf{K}$. Indeed, the following classical results are key to the development of our methods, since they allow us to ensure feasibility of the iterates and sufficient decrease of the potential function in each iteration of our algorithms.

Lemma 1

(Theorem 5.1.5 [76]) For all $x\in \textsf{K}$ we have $\mathcal {W}(x;1)\subseteq \textsf{K}$.

Proposition 1

(Theorem 5.1.9 [76]) Let $h\in \mathcal {H}_{\theta }(\textsf{K})$, $x\in {{\,\textrm{dom}\,}}h$, and a fixed direction $d \in \mathbb {E}$. For all $t \in [0,\frac{1}{\Vert d\Vert _x})$, with the convention that $\frac{1}{\Vert d\Vert _{x}}=+\infty$ if $\Vert d\Vert _x=0$, we have:

$$\begin{aligned} h(x + t d) \le h(x) + t\langle \nabla h(x),d\rangle + t^2 \Vert d\Vert _{x}^2 \omega (t \Vert d\Vert _{x}), \end{aligned}$$

where $\omega (t)=\frac{-t-\ln (1-t)}{t^2}$.

We will also use the following inequality for the function $\omega (t)$ [76, Lemma 5.1.5]:

$$\begin{aligned} \omega (t) \le \frac{1}{2(1-t)}, \; t \in [0,1). \end{aligned}$$

(3)

Appendix A contains some more technical properties of LHSCBs which are used in the proofs. We close this section with important examples of conic domains to which our methods can be directly applied.

Example 5

(Non-negativity constraints) For $\mathbb {E}=\mathbb {R}^n$ and $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}$, we define the log-barrier $h(x)=-\sum _{i=1}^{n}\ln (x_{i})$ for all $x\in \textsf{K}_{\text {NN}}=\mathbb {R}^n_{++}$. It is readily seen that $h\in \mathcal {H}_{n}(\textsf{K})$. $\Diamond$

Example 6

(SOC constraints) Let $\mathbb {E}=\mathbb {R}^{n}$ and $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {SOC}}$, defined in Example 2. For $x=(x_{0},\underline{x})\in \bar{\textsf{K}}_{\text {SOC}}$, we define the barrier $h(x)=-\ln (x_{0}^{2}-\underline{x}^{\top }\underline{x})$. It is well known that $h\in \mathcal {H}_{2}(\textsf{K}_{\text {SOC}})$ [78]. $\Diamond$

Example 7

(SDP constraints) Let $\mathbb {E}=\mathbb {S}^{n}$ and $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {SDP}}$, defined in Example 3. Consider the barrier $h(x)=-\ln \det (x)$. It is well known that $h\in \mathcal {H}_{n}(\textsf{K}_{\text {SDP}})$. $\Diamond$

Example 8

(The exponential cone) Consider the exponential cone $\textsf{K}_{\exp }$ with closure $\bar{\textsf{K}}_{\exp }$ introduced in Example 4. This set admits a 3-LHSB

$$\begin{aligned} h(x_{1},x_{2},x_{3})= -\ln (x_{2}\ln (x_{1}/x_{2})-x_{3})-\ln (x_{1})-\ln (x_{2})\in \mathcal {H}_{3}(\textsf{K}_{\exp }). \end{aligned}$$

We remark that this cone is not self-dual (cf. Definition 2), but

$$\begin{aligned} G\bar{\textsf{K}}_{\exp }=\bar{\textsf{K}}^{*}_{\exp }={{\,\textrm{cl}\,}}\left( \{y\in \mathbb {R}^{3}\vert y_{1}\ge -y_{3}e^{y_{2}/y_{3}-1},y_{1}>0,y_{3}<0\}\right) , \end{aligned}$$

under the linear transformation $G=\left[ \begin{array}{ccc} 1/e &{} 0 &{} 0 \\ 0 &{} 0 &{} -\,1 \\ 0 &{} -\,1 &{} 0 \end{array}\right] .$ There are many convex sets that can be represented using the exponential cone. We list some examples below, but refer to the PhD thesis [35] for further details.

• Exponential: $\{(t,u)\vert t\ge e^{u}\}\iff (t,1,u)\in \bar{\textsf{K}}_{\exp }$;

• Logarithm: $\{(t,u)\vert t\le \ln (u)\}\iff (u,1,t)\in \bar{\textsf{K}}_{\exp }$;

• Entropy: $t\le -u\ln (u)\iff t\le u\ln (1/u)\iff (1,u,t)\in \bar{\textsf{K}}_{\exp }$;

• Relative Entropy: $t\ge u\log (u/w)\iff (w,u,t)\in \bar{\textsf{K}}_{\exp }$;

• Softplus function: $t\ge \ln (1+e^{u})\iff a+b\le 1,(a,1,u-t)\in \bar{\textsf{K}}_{\exp },(b,1,-t)\in \bar{\textsf{K}}_{\exp }$.

$\Diamond$

2.2 Exploiting the structure of symmetric cones

Nesterov and Todd [80] introduced self-scaled barriers, which later were realized as LHSCBs for symmetric cones. Such barriers are nowadays key to define primal–dual interior point methods with potentially larger step-sizes for convex problems. Our methods can also exploit the structure of self-scaled barriers, leading to potentially larger step-sizes and eventual faster convergence in practice. For a given closed convex nonempty cone $\bar{\textsf{K}}$, its dual cone is the closed convex and nonempty cone $\bar{\textsf{K}}^{*}\triangleq \{s\in \mathbb {E}^{*}\vert \langle s,x\rangle \ge 0\;\forall x\in \bar{\textsf{K}}\}$. If $h\in \mathcal {H}_{\theta }(\textsf{K})$, then the dual barrier is defined as $h_{*}(s)\triangleq \sup _{x\in \textsf{K}}\{\langle -s,x\rangle -h(x)\}$ for $s\in \bar{\textsf{K}}^{*}$. Note that $h_{*}\in \mathcal {H}_{\theta }(\textsf{K}^{*})$ [78, Theorem 2.4.4].

Definition 2

An open convex cone is self-dual if $\textsf{K}^{*}=\textsf{K}$. $\textsf{K}$ is homogeneous if for all $x,y\in \textsf{K}$ there exists a linear bijection $G:\mathbb {E}\rightarrow \mathbb {E}$ such that $Gx=y$ and $G\textsf{K}=\textsf{K}$. An open convex cone $\textsf{K}$ is called symmetric if it is self-dual and homogeneous.

The class of symmetric cones can be characterized within the language of Euclidean Jordan algebras [45, 46, 63, 64]. For optimization, the three symmetric cones of most relevance are $\bar{\textsf{K}}_{\text {NN}},\bar{\textsf{K}}_{\text {SOC}}$, and $\bar{\textsf{K}}_{\text {SDP}}$.

Definition 3

([80]) $h\in \mathcal {H}_{\theta }(\textsf{K})$ is a $\theta$-self-scaled barrier ($\theta$-SSB) if for all $x,w\in \textsf{K}$ we have $H(w)x\in \textsf{K}$ and $h_{*}(H(w)x)=h(x)-2h(w)-\theta$. Let $\mathcal {B}_{\theta }(\textsf{K})$ denote the class of $\theta$-SSBs.

Clearly, $\mathcal {B}_{\theta }(\textsf{K})\subset \mathcal {H}_{\theta }(\textsf{K})$. Hauser and Güler [60] showed that every symmetric cone admits a $\theta$-SSB for some $\theta \ge 1$, while a characterization of the barrier parameter $\theta$ has been obtained in [56]. The main advantage of working with SSBs instead of LHSCBs is that we can make potentially longer steps in the interior of the cone $\textsf{K}$ towards the direction of its boundary, and have larger decrease of the potential. Let $x \in \textsf{K}$ and $d \in \mathbb {E}$. Denote

$$\begin{aligned} \sigma _x(d)\triangleq (\sup \{ t: x -t d \in \textsf{K}\})^{-1}. \end{aligned}$$

Since $\mathcal {W}(x;1) \subseteq \textsf{K}$ for all $x\in \textsf{K}$, we have that $\sigma _x(d) \le \Vert d\Vert _{x}$ and $\sigma _{x}(-d)\le \Vert d\Vert _{x}$ for all $d\in \mathbb {E}$. Therefore $[0,\frac{1}{\Vert d\Vert _{x}})\subseteq [0,\frac{1}{\sigma _{x}(d)})$. Hence, if the scalar quantity $\sigma _{x}(d)$ can be computed efficiently, it would allow us to make a larger step without violating feasibility.

Example 9

For $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}$, to guarantee $x-td\in \textsf{K}_{\text {NN}}$, we need $x_{i}-t d_{i}>0$ for all $i\in \{1,\ldots ,n\}$. Hence, if $d_{i}\le 0$, this is satisfied for all $t\ge 0$. If $d_{i}>0$, we obtain the restriction $t\le \frac{x_{i}}{d_{i}}$. Therefore, $\sigma _{x}(-d)=\max \{\frac{d_{i}}{x_{i}}:d_{i}>0\}$. $\Diamond$

Example 10

For $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {SDP}}$, we see that $x-td\succ 0$ if and only if ${{\,\textrm{Id}\,}}\succ t x^{-1/2}dx^{-1/2}$, where ${{\,\textrm{Id}\,}}$ is the identity matrix and $x^{1/2}$ denotes the square root of a matrix $x\in \textsf{K}_{\text {SDP}}$. Hence, if $\lambda _{\max }(x^{-1/2}dx^{-1/2})>0$, then $t<\frac{1}{\lambda _{\max }(x^{-1/2}dx^{-1/2})}$. Thus, $\sigma _{x}(d)=\max \{\lambda _{\max }(x^{-1/2}dx^{-1/2}),0\}$. $\Diamond$

The analogous result to Proposition 1 for barriers $h\in \mathcal {B}_{\theta }(\textsf{K})$ reads as follows:

Proposition 2

(Theorem 4.2 [80]) Let $h\in \mathcal {B}_{\theta }(\textsf{K})$ and $x \in \textsf{K}$. Let $d \in \mathbb {E}$ be such that $\sigma _x(-d)>0$. Then, for all $t \in [0,\frac{1}{\sigma _x(-d)})$, we have:

$$\begin{aligned} h(x + t d) \le h(x) + t \langle \nabla h(x),d\rangle + t^2 \Vert d\Vert _x^2 \omega (t \sigma _x(-d)). \end{aligned}$$

2.3 Unified notation

Our algorithms work on any conic domain on which we can efficiently evaluate a $\theta$-LHSCB.

Assumption 2

$\bar{\textsf{K}}$ is a regular cone admitting an efficient barrier setup $h\in \mathcal {H}_{\theta }(\textsf{K})$. By this we mean that at a given query point $x\in \textsf{K}$, we can construct an oracle that returns to us information about the values $h(x),\nabla h(x)$ and $H(x)=\nabla ^{2}h(x)$, with low computational efforts.

Note that when $h \in \mathcal {B}_{\nu }(\textsf{K})$, we have the flexibility to treat h either as $h \in \mathcal {H}_{\nu }(\textsf{K})$ or as $h \in \mathcal {B}_{\nu }(\textsf{K})$. Given the potential advantages when working on symmetric cones, it is useful to develop a unified notation handling the case $h\in \mathcal {H}_{\theta }(\textsf{K})$ and $h\in \mathcal {B}_{\theta }(\textsf{K})$ at the same time. We therefore introduce the notation

$$\begin{aligned} (\forall (x,d)\in \textsf{X}\times \mathbb {E}):\;\zeta (x,d)\triangleq \left\{ \begin{array}{ll} \Vert d\Vert _{x} &{} \text {if }h\in \mathcal {H}_{\theta }(\textsf{K})\setminus \mathcal {B}_{\theta }(\textsf{K}),\\ \sigma _{x}(-d) &{} \text {if }h\in \mathcal {B}_{\theta }(\textsf{K}). \end{array} \right. \end{aligned}$$

(4)

Note that

$$\begin{aligned}&(\forall (x,d)\in \textsf{X}\times \mathbb {E}):\; \zeta (x,d)\le \Vert d\Vert _{x}, \end{aligned}$$

(5)

$$\begin{aligned}&(\forall (x,d)\in \textsf{X}\times \mathbb {E})\left( \forall t \in \left[ 0,\frac{1}{\zeta (x,d)}\right) \right) :\; x + td \in \textsf{K}. \end{aligned}$$

(6)

Propositions 1 and 2 together with Eq. (4), give us the one-and-for-all Bregman bound

$$\begin{aligned} h(x+t d)-h(x)-\langle \nabla h(x),td\rangle \le t^2 \Vert d\Vert _{x}^2 \omega (t \zeta (x,d)), \end{aligned}$$

(7)

valid for all $(x,d)\in \textsf{X}\times \mathbb {E}$ and $t \in \left[ 0,\frac{1}{\zeta (x,d)}\right)$.

3 Approximate optimality conditions

Consider the non-convex optimization problem (Opt). If $x^{*}$ is a local solution of the optimization problem at which the objective function f is continuously differentiable, then there exists $y^{*}\in \mathbb {R}^{m}$ such that

$$\begin{aligned} \nabla f(x^{*})-{\textbf{A}}^{*}y^{*}\in -{{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(x^{*}). \end{aligned}$$

(8)

This is equivalent to the standard local optimality condition [81]

$$\begin{aligned} \langle \nabla f(x^{*}),x-x^{*}\rangle \ge 0\qquad \forall x\in \bar{\textsf{X}}=\bar{\textsf{K}}\cap \textsf{L}. \end{aligned}$$

(9)

Remark 1

Since $-{{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(x^{*})\subseteq \bar{\textsf{K}}^{*}$, the inclusion (8) implies $s^{*}\triangleq \nabla f(x^{*})-{\textbf{A}}^{\top }y^{*}\in \bar{\textsf{K}}^{*}$.$\Diamond$

3.1 First-order approximate KKT conditions

The next definition specifies our notion of an approximate first-order KKT point for problem (Opt).

Definition 4

Given $\varepsilon {\ge }0$, a point $\bar{x}\in \mathbb {E}$ is an $\varepsilon$-KKT point for problem (Opt) if there exists $\bar{y}\in \mathbb {R}^{m}$ such that

$$\begin{aligned}&{\textbf{A}}\bar{x}=b,\bar{x}\in \textsf{K}, \end{aligned}$$

(10)

$$\begin{aligned}&\bar{s}=\nabla f(\bar{x})-{\textbf{A}}^{*}\bar{y}\in \bar{\textsf{K}}^{*},\end{aligned}$$

(11)

$$\begin{aligned}&\langle \bar{s},\bar{x}\rangle \le \varepsilon . \end{aligned}$$

(12)

Note that by conditions (10) and (11) $\bar{x}\in \textsf{K}$ and $\bar{s}\in \bar{\textsf{K}}^{*}$, i.e., are feasible and $\langle \bar{s},\bar{x}\rangle \ge 0$. Thus, condition (12) is reasonable since it recovers the standard complementary slackness when $\varepsilon \rightarrow 0$. Although our definition explicitly requires strict primal feasibility, similar approximate KKT conditions have been introduced for candidates $\bar{x}$ which may be infeasible. This gains relevance in primal–dual settings and sequential optimality conditions for Lagrangian-based methods. In such setups a projection should be used [7, 9].

Definition 4 can be motivated as an approximate version of the exact first-order KKT condition stated as Theorem 5 in Appendix B. It is also easy to show that the above definition readily implies the standard approximate first-order stationarity condition $\langle \nabla f(\bar{x}), x - \bar{x}\rangle \ge -\varepsilon$, for all $x \in \bar{\textsf{X}}$ (cf. (9)). Indeed, let $x \in \bar{\textsf{X}}$ be arbitrary and $\bar{x}$ satisfy Definition 4. Then,

$$\begin{aligned} \langle \nabla f(\bar{x}), x - \bar{x}\rangle = \langle \bar{s}, x - \bar{x} \rangle + \langle \bar{y}, {\textbf{A}}(x - \bar{x}) \rangle = \langle \bar{s}, x \rangle - \langle \bar{s}, \bar{x} \rangle \ge -\varepsilon , \end{aligned}$$

where we used that ${\textbf{A}}x = {\textbf{A}}\bar{x}=b$, $\langle \bar{s}, x \rangle \ge 0$ since $x \in \bar{\textsf{K}}$ and $\bar{s} \in \bar{\textsf{K}}^{*}$, and $\langle \bar{s}, \bar{x} \rangle \le \varepsilon$.

The next result uses a perturbation argument based on an interior penalty approach, inspired by [58], and shows that our definition of an $\varepsilon$-KKT point is attainable and can be read as an approximate KKT condition.

Proposition 3

Let $x^{*}\in \bar{\textsf{X}}$ be a local solution of problem (Opt) where f is continuously differentiable on $\textsf{X}$. Then, there exist sequences $(x_{k})_{k\ge 1}\subset \textsf{X},(y_{k})_{k\ge 1}\subset \mathbb {R}^{m}$ and $s_{k}=\nabla f(x_{k})-{\textbf{A}}^{*}y_{k}$, $k\ge 1$ satisfying the following:

• (i) $x_{k}\rightarrow x^{*}$.

• (ii) For all $\varepsilon >0$ we have $|\langle s_{k},x_{k}\rangle |\le \varepsilon$ for all k sufficiently large.

• (iii) All accumulation points of the sequence $(s_{k})_{k\ge 1}$ are contained in $-{{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(x^{*})\subseteq \bar{\textsf{K}}^{*}$.

Proof

(i):

Consider the following perturbed version of problem (Opt), for which $x^*$ is the unique global solution if we take $\delta >0$ sufficiently small,

$$\begin{aligned} \min _{x} f(x) + \frac{1}{2}\Vert x-x^*\Vert ^2 \quad \text {s.t.: } {\textbf{A}}x=b, \; x\in \bar{\textsf{K}}, \; \Vert x-x^*\Vert ^2 \le \delta . \end{aligned}$$

(13)

Further, consider the penalty function

$$\begin{aligned} \varphi _{k}(x)\triangleq f(x)+\mu _{k}h(x)+\frac{1}{2}\Vert x-x^{*}\Vert ^{2} \end{aligned}$$

for a sequence $\mu _{k}\rightarrow 0^{+}$ as $k\rightarrow \infty$ and the optimization problem

$$\begin{aligned} \min _{x}\varphi _{k}(x) \quad \text {s.t.: } {\textbf{A}}x=b,\; x\in \textsf{K},\; \Vert x-x^{*}\Vert ^{2}\le \delta . \end{aligned}$$

It is well known [48] that a global solution $x_{k}$ exists for this problem for all $k\ge 1$, and that cluster points of the sequence $(x_{k})_{k\ge 1}$ are global solutions of (13). Since $\Vert x_k-x^*\Vert ^2 \le \delta$, the sequence $x_k$ is bounded and, thus, $x_k \rightarrow x^*$ as $k\rightarrow \infty$.

(ii):

For k large enough, $x_{k}$ is a local solution of

$$\begin{aligned} \min _{x}\varphi _{k}(x) \quad \text {s.t.: } {\textbf{A}}x=b. \end{aligned}$$

The optimality conditions for this problem read as

$$\begin{aligned} \nabla f(x_{k})+(x_{k}-x^{*})+\mu _{k}\nabla h(x_{k})-{\textbf{A}}^{*}y_{k}=0, \end{aligned}$$

where $y_k \in \mathbb {R}^m$ is a Lagrange multiplier. Setting $s_{k}\triangleq \nabla f(x_{k})-{\textbf{A}}^{*}y_{k}$, we can continue with

$$\begin{aligned} |\langle s_{k},x_{k}\rangle |=|\langle x^{*}-x_{k},x_{k}\rangle -\mu _{k}\langle \nabla h(x_{k}),x_{k}\rangle | {\mathop {=}\limits ^{\tiny (81)}} |\langle x^{*}-x_{k},x_{k}\rangle +\mu _{k}\theta |. \end{aligned}$$

As $x_{k}\rightarrow x^{*}$ and $\mu _k \rightarrow 0$, we conclude that $\lim _{k\rightarrow \infty }|\langle s_{k},x_{k}\rangle |=0$.

(iii):

Let $x\in \bar{\textsf{K}}$ be arbitrary. Using part (ii) and the Cauchy–Schwarz inequality, we see that

$$\begin{aligned} \langle s_{k},x\rangle&=\langle s_{k},x-x_{k}\rangle +\langle s_{k},x_{k}\rangle \\&=\langle x^{*}-x_{k},x-x_{k}\rangle +\langle s_{k},x_{k}\rangle -\mu _{k}\langle \nabla h(x_{k}),x-x_{k}\rangle \\&{\mathop {\ge }\limits ^{\tiny (83)}} -\Vert x^{*}-x_{k}\Vert \cdot \Vert x-x_{k}\Vert +\langle s_{k},x_{k}\rangle -\mu _{k}\theta \rightarrow 0. \end{aligned}$$

Hence, $\liminf _{k\rightarrow \infty }\langle s_{k},x\rangle \ge 0$ for all $x\in \bar{\textsf{K}}$, which proves that accumulation points of $(s_{k})_{k\ge 1}$ are contained in the dual cone $\bar{\textsf{K}}^{*}$. Let $x_{k}\rightarrow x^{*}$. Assume first that $x^{*}\in \textsf{X}=\textsf{K}\cap \textsf{L}$. Then the sequence $(s_{k})_{k\ge 1}$ constructed as in part (ii) satisfies $s_{k}=-\mu _{k}\nabla h(x_{k})+(x^{*}-x_{k})$ for all $k\ge 1$. Consequently, $s_{k}\rightarrow 0$ as $k\rightarrow \infty$. Now assume that $x^{*}\in {{\,\textrm{bd}\,}}(\textsf{X})$. Choosing $\mu _{k}\triangleq \frac{1}{\Vert \nabla h(x_{k})\Vert }\rightarrow 0$ as $k\rightarrow \infty$, gives $s_{k}=x^{*}-x_{k}-\frac{1}{\Vert \nabla h(x_{k})\Vert }\nabla h(x_{k})$. Lemma 4 in Appendix A shows that the sequence $\left( \frac{\nabla h(x_{k})}{\Vert \nabla h(x_{k})\Vert }\right) _{k\ge 1}$ is bounded with all its accumulation points contained in ${{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(x^{*})$. This readily implies that accumulation points of the sequence $(s_{k})_{k\ge 1}$ must be contained in $-{{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(x^{*})$.

$\square$

3.2 Second-order approximate KKT conditions

Our definition of an approximate second-order KKT point is motivated by the exact definition in Theorem 6, stated in Appendix B. The natural inexact version of this definition reads as follows.

Definition 5

Given $\varepsilon _1,\varepsilon _2 \ge 0$, a point $\bar{x}\in \mathbb {E}$ is an $(\varepsilon _1,\varepsilon _2)$-2KKT point for problem (Opt) if there exists $\bar{y}\in \mathbb {R}^{m}$ such that for $\bar{s}=\nabla f(\bar{x})-{\textbf{A}}^{*}\bar{y}$ conditions (10) and (11) hold, as well as

$$\begin{aligned}&\langle \bar{s},\bar{x}\rangle \le \varepsilon _1, \end{aligned}$$

(14)

$$\begin{aligned}&\nabla ^2f(\bar{x}) +\sqrt{\varepsilon _{2}} H(\bar{x}) \succeq 0 \;\; \text {on} \;\; \textsf{L}_0. \end{aligned}$$

(15)

Given $x\in \textsf{X}$, define the set of feasible directions as $\mathcal {F}_{x}\triangleq \{v\in \mathbb {E}\vert x+v\in \textsf{X}\}.$ Lemma 1 implies that

$$\begin{aligned} \mathcal {T}_{x}\triangleq \{v\in \mathbb {E}\vert {\textbf{A}}v=0,\Vert v\Vert _{x}<1\}\subseteq \mathcal {F}_{x}. \end{aligned}$$

(16)

Upon defining $d=[H(x)]^{1/2}v$ for $v\in \mathcal {T}_{x}$, we obtain a direction d satisfying ${\textbf{A}}[H(x)]^{-1/2}d=0$ and $\Vert d\Vert =\Vert v\Vert _{x}$. Hence, for $x\in \textsf{K}$, we can equivalently characterize the set $\mathcal {T}_{x}$ as $\mathcal {T}_{x}=\{[H(x)]^{-1/2}d\vert {\textbf{A}}[H(x)]^{-1/2}d=0,\Vert d\Vert <1\}$. In terms of feasible directions contained in the set $\mathcal {T}_{x}$, we observe that condition (15) can be rewritten as follows:

$$\begin{aligned}&\nabla ^2f(\bar{x}) +\sqrt{\varepsilon _{2}} H(\bar{x}) \succeq 0 \;\; \text {on} \;\; \textsf{L}_0 \\&\iff \langle \nabla ^{2}f(x)[H(x)]^{-1/2}u,[H(x)]^{-1/2}u\rangle \ge -\sqrt{\varepsilon _{2}}\\&\quad \Vert u\Vert ^{2}\qquad \forall u\in \ker ({\textbf{A}}[H(x)]^{-1/2})\\&\iff \langle \nabla ^{2}f(x)[H(x)]^{-1/2}u,[H(x)]^{-1/2}u\rangle \ge -\sqrt{\varepsilon _{2}}\\&\quad \forall u\in \ker ({\textbf{A}}[H(x)]^{-1/2})\cap \{u\in \mathbb {E}\vert \Vert u\Vert <1\}\\&\iff \langle \nabla ^{2}f(x)v,v\rangle \ge -\sqrt{\varepsilon _{2}}\qquad \forall v\in \mathcal {T}_{x}. \end{aligned}$$

The last line connects our approximate KKT condition with the exact condition stated in Theorem 6 in Appendix B. The next Proposition gives a justification of Definition 5. We again use a perturbation argument based on an interior penalty approach, inspired by [58].

Proposition 4

Let $x^{*}\in \bar{\textsf{X}}$ be a local solution of problem (Opt), where f is twice continuously differentiable on $\textsf{X}$. Then, there exist sequences $(x_{k})_{k\ge 1}\subset \textsf{X},(y_{k})_{k\ge 1}\subset \mathbb {R}^{m}$ and $s_{k}=\nabla f(x_{k})-{\textbf{A}}^{*}y_{k}$, $k \ge 1$, satisfying the following:

• (i) $x_{k}\rightarrow x^{*}$.

• (ii) For all $\varepsilon _{1}>0$ we have $|\langle s_{k},x_{k}\rangle |\le \varepsilon _{1}$ for all k sufficiently large.

• (iii) All accumulation points of the sequence $(s_{k})_{k\ge 1}$ are contained in $-{{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(x^{*})\subseteq \bar{\textsf{K}}^{*}$.

• (iv) For all sequences $v_{k}\in \mathcal {T}_{x_{k}}$ we have

  $$\begin{aligned} \liminf _{k\rightarrow \infty }\langle \nabla ^{2}f(x_{k})v_{k},v_{k}\rangle \ge 0. \end{aligned}$$

Proof

Consider the penalty function

$$\begin{aligned} \varphi _{k}(x)\triangleq f(x)+\mu _{k}h(x)+\frac{1}{4}\Vert x-x^{*}\Vert ^{4}. \end{aligned}$$

It is easy to see that the proof of Proposition 3 still applies, mutatis mutandis, showing that items (i)–(iii) of the current Proposition hold.

(iv) The point $x_{k}$ satisfies the necessary second-order condition

$$\begin{aligned} \left\langle \left( \nabla ^{2}f(x_{k})+\mu _{k}\nabla ^{2} h(x_{k}) +\Vert x_{k}-x^{*}\Vert ^{2}{{\,\textrm{Id}\,}}_{\mathbb {E}}+2(x_{k}-x^{*})\otimes (x_{k}-x^{*})\right) v,v\right\rangle \ge 0 \end{aligned}$$

for all $v\in \textsf{L}_{0}$. Here ${{\,\textrm{Id}\,}}_{\mathbb {E}}$ is the identity operator on $\mathbb {E}$. This reads as

$$\begin{aligned} \langle \nabla ^{2}f(x_{k})v,v\rangle \ge -\mu _{k}\Vert v\Vert ^{2}_{x_{k}}-\rho _{k}\Vert v\Vert ^{2}, \end{aligned}$$

where $\rho _k$ is the largest eigenvalue of $\Vert x_{k}-x^{*}\Vert ^{2}{{\,\textrm{Id}\,}}_{\mathbb {E}}+2(x_{k}-x^{*})\otimes (x_{k}-x^{*})$. We know that $x_{k}\rightarrow x^{*}$. Let $(v_{k})_{k\ge 1}$ be an arbitrary sequence with $v_{k}\in \mathcal {T}_{x_{k}}$ for all $k\ge 1$. Then, there exists a sequence $(u_{k})_{k\ge 1}$ satisfying $v_{k}=[H(x_{k})]^{-1/2}u_{k}$ and $\Vert u_{k}\Vert <1$. Therefore, $\Vert v_{k}\Vert ^{2}_{x_{k}}=\Vert u_{k}\Vert ^{2}<1$, and $\Vert v_{k}\Vert =\Vert u_{k}\Vert ^{*}_{x_{k}}\le \Vert x_{k}\Vert \texttt{e}_{*}(u_{k})$, where we have used Lemma 5 and the definition $\texttt{e}_{*}(v)\triangleq \sup _{x\in \textsf{K}:\Vert x\Vert =1}\Vert v\Vert _{x}^{*}$. We thus obtain the bound

$$\begin{aligned} \langle \nabla ^{2}f(x_{k})v_{k},v_{k}\rangle \ge -\mu _{k}\Vert u_{k}\Vert ^{2}-\rho _k\Vert x_{k}\Vert ^2\texttt{e}_{*}(u_{k})^{2}. \end{aligned}$$

Since the sequence $(u_{k})_{k\ge 1}$ is bounded, $\mu _{k}\rightarrow 0^{+}$ and $\rho _k\rightarrow 0^{+}$ as $k \rightarrow \infty$, the claim follows.$\square$

3.3 Discussion

3.3.1 Comparison with approximate KKT conditions for interior-point methods

To compare our approximate KKT conditions with the ones previously formulated in the literature we consider the particular case $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}\subset \mathbb {E}=\mathbb {R}^n$ as in [58, 82]. The exact optimality condition for problem (Opt), assuming that f is continuously differentiable at $x^{*}$, reads in this case as the complementarity system for the primal–dual triple $(x^{*},y^{*},s^{*})\in \bar{\textsf{K}}_{\text {NN}}\times \mathbb {R}^m \times \bar{\textsf{K}}_{\text {NN}}$ given by

$$\begin{aligned}&{\textbf{A}}x^{*}=b,\quad s^{*}=\nabla f(x^{*})-{\textbf{A}}^{*}y^{*}\in \bar{\textsf{K}}_{\text {NN}},\\&(\forall i=1,\ldots ,n): x_{i}^{*}s_{i}^{*}=0. \end{aligned}$$

These conditions directly motivate the approximate optimality conditions used in the interior-point method of [58], which are ${\textbf{A}}^{*}\bar{x}=b$, $\bar{x}>0$, and

$$\begin{aligned}&\bar{s} = \nabla f(\bar{x})-{\textbf{A}}^{*}\bar{y}\ge -\varepsilon \textbf{1}_{n}, \end{aligned}$$

(17)

$$\begin{aligned}&\max _{1\le i\le n}|\bar{x}_{i}[\nabla f(\bar{x})-{\textbf{A}}^{*}\bar{y}]_{i}|\le \varepsilon , \end{aligned}$$

(18)

$$\begin{aligned}&d^{\top }\left( {{\,\textrm{diag}\,}}[\bar{x}]\nabla ^{2}f(\bar{x}){{\,\textrm{diag}\,}}[\bar{x}]+\sqrt{\varepsilon }\textbf{I}\right) d\ge 0\qquad \forall d\in \ker ({\textbf{A}}[H(\bar{x})]^{-1/2}), \end{aligned}$$

(19)

where $\textbf{1}_{n} \in \mathbb {R}^n$ is the vector of all ones and $\textbf{I}={{\,\textrm{Id}\,}}_{\mathbb {R}^n}$ is the $n\times n$ identity matrix. Note that, in this particular case, our first-order conditions (10)–(12) are similar but a bit stronger since they imply (17) and (18). Note also that the change of variable $v=[H(\bar{x})]^{-1/2} d = {{\,\textrm{diag}\,}}[\bar{x}] d$ shows the equivalence between our second-order condition (15) and the condition (19). These observations provide additional motivation for our definitions of approximate KKT points since similar in spirit definitions of approximate KKT points were previously used in the literature, i.e., in [58].

As pointed out in [82], conditions (18) and (19) are commonly used approximate optimality conditions for (Opt) [15, 36]. However, these two conditions alone are insufficient to guarantee that a sequence of points that satisfies these conditions as $\varepsilon \rightarrow 0$ converges to a KKT point for f [58]. For this reason the condition (17) is added in [58]. These conditions can be overly stringent for coordinates i in which $\bar{x}_{i}$ is positive and numerically large (which is possible only if the norm of the vectors is not too much restricted in concrete instances, due to our compactness assumption). In this case, the complementarity condition (18) requires the corresponding dual variable $\bar{s}_{i}$ to be very small. Similarly, (19) requires that the Hessian in the subspace spanned by these coordinates can have only minimal negative curvature. Such requirements contrast sharply with the case of unconstrained minimization. In the limiting scenario in which all of the coordinates of $\bar{x}$ are far from the boundary, these approximate first-order conditions are significantly harder to satisfy than in the (equivalent) unconstrained formulation. To remedy this potential problem, O’Neill and Wright [82] proposed scaling in Eqs. (18) and (19) only when $\bar{x}_{i}\in (0,1]$. This operation aims for an interpolation between the bound-constrained case (when $\bar{x}_{i}$ is small) and the unconstrained case (when $\bar{x}_{i}$ is large), while also controlling the norm of the matrix used in their optimality conditions. Since [82] only assume non-negativity constraints without linear equality constraints, and no further upper bounds on the decision variables, this clipping of variables makes a lot of sense. However, since we assume compactness, the coordinates of the approximate solutions can become large, but only up to a pre-defined and known upper bound. Hence, the hardness issue of identifying an approximate KKT point is less pronounced in our work. Moreover, we prove that our algorithms produce approximate KKT points with standard scaling and with a similar iteration complexity as in the setting of [82]. Finally, it is easy to show that the conditions with interpolating scaling of [82] follow in our setting for $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}$ as well since $0 \le \min \{x_i,1\}\le x_i$ in this case.

3.3.2 Complementarity conditions for symmetric cones

If $\bar{\textsf{K}}$ is a symmetric cone, the approximate complementarity conditions (12) and (14) are equivalent to approximate complementarity conditions formulated in terms of the multiplication $\circ$ under which $\textsf{K}$ becomes an Euclidean Jordan algebra. [72, Prop.2.1] shows that $x\circ y=0$ if and only if $\langle x,y\rangle =0$, where $\langle \cdot ,\cdot \rangle$ is the inner product of the space $\mathbb {E}$. Moreover, if $\bar{\textsf{K}}$ is a primitive symmetric cone, then by [45, Prop.III.4.1], there exists a constant $a>0$ such that $a{{\,\textrm{tr}\,}}(x\circ y)=\langle x,y\rangle$ for all $x,y\in \textsf{K}$. In view of this relation, our approximate complementarity conditions can be written in the form of condition $\bar{s}\circ \bar{x}\le \varepsilon$. Hence, our approximate KKT conditions reduce to the ones reported in [6]. In particular, for $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}$ we recover the standard approximate complementary slackness condition $\bar{s}^{k}_{i}\bar{x}^{k}_{i} \le \varepsilon$ for all i, as in this case the Jordan product $\circ$ gives rise to the Hadamard product. See [5] for more details.

3.3.3 On the relation to scaled critical points

In absence of differentiability at the boundary, a popular formulation of necessary optimality conditions involves the definition of scaled critical points. Indeed, at a local minimizer $x^{*}$, the scaled first-order optimality condition $x_{i}^{*}[\nabla f(x^{*})]_{i}=0,1\le i\le n$ holds, where the product is taken to be 0 when the derivative does not exist. Based on this characterization, one may call a point $x\in \textsf{K}_{\text {NN}}$ with $|x_{i}[\nabla f(x)]_{i}|\le \varepsilon$ for all $i=1,\ldots ,n$ an $\varepsilon$-scaled first-order point. Algorithms designed to produce $\varepsilon$-scaled first-order points, with some small $\varepsilon >0$, have been introduced in [15, 16]. As reported in [58], there are several problems associated with this weak definition of a critical point. First, when derivatives are available on $\bar{\textsf{K}}_{\text {NN}}$, the standard definition of a critical point would entail the inequality $\langle \nabla f(x),x'-x\rangle \ge 0$ for all $x'\in \bar{\textsf{K}}_{\text {NN}}.$ Hence, $[\nabla f(x)]_{i}=0$ for $x_{i}>0$ and $[\nabla f(x)]_{i}\ge 0$ for $x_{i}=0$. It follows that $\nabla f(x)\in \bar{\textsf{K}}_{\text {NN}}$, a condition that is absent in the definition of a scaled critical point. Second, scaled critical points come with no measure of strength, as they hold trivially when $x=0$, regardless of the objective function. Third, there is a general gap between local minimizers and limits of $\varepsilon$-scaled first-order points, when $\varepsilon \rightarrow 0^{+}$ (see [58]). Similar remarks apply to the scaled second-order condition, considered in [15]. Our definition of approximate KKT points overcome these issues. In fact, our definitions of approximate first- and second-order KKT points are continuous in $\varepsilon$, and therefore in the limit our approximate KKT conditions coincide with first- and weak second-order necessary conditions for a local minimizer. This is achieved without assuming global differentiability of the objective function or performing an additional smoothing of the problem data as in [14, 15].

3.3.4 Second-order conditions in the literature on interior-point methods compared to standard second-order conditions

As discussed above, our necessary second-order optimality conditions stated in Proposition 4, and their approximate counterpart given in Definition 5, are in alignment with the existing body of work that studies non-convex conic optimization [58, 61, 82]. In particular, condition (15) coincides with those used in [58, 82] for the particular case of non-negativity constraints, and in [61] for general conic constraints. However, the necessary second-order optimality conditions in Proposition 4, [58, Theorem 1], [82, Theorem 3.1], [61, Theorem 4] are weaker than the standard ones that we refer to as strong conditions. This can be easily illustrated with the following example.³

Example 11

(Strong vs. weak necessary second-order optimality conditions) Consider $\mathbb {E}= \mathbb {R}$ and $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}} = \mathbb {R}_{+}$. Also, assume that there are no linear equality constraints. Consider the function $f:\mathbb {R}_{+}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} f(x) =\left\{ \begin{array}{ll} -\frac{1}{2} x^2 &{}\quad \text { if }x \in [0,1],\\ \frac{1}{2} (x-2)^2-1 &{}\quad \text {if }x \in (1,3],\\ x-\frac{7}{2} &{}\quad \text {if }x\in (3,\infty ). \end{array}\right. \end{aligned}$$

This function is continuously differentiable on $\mathbb {R}_{++}$, bounded from below, and has Lipschitz gradient. The minimization problem $\min \{f(x)\vert x\in \mathbb {R}_{+}\}$ has two first-order KKT points $x\in \{0,2\}$, both supported by Lagrange multiplier $s=0$. A strong second-order necessary optimality condition involves the strong critical cone [81, Section12.5], which in the current example reads as

$$\begin{aligned} C^{s}(x)=\{d\in \mathbb {R}\vert d\ge 0 \text { if }x=0\}. \end{aligned}$$

A strong second-order necessary condition is then

$$\begin{aligned} \langle d,\nabla ^{2}f(\bar{x})d\rangle \ge 0 \qquad \forall d\in C^{s}(\bar{x}). \end{aligned}$$

Since $C^{s}(0)=[0,\infty )$, but $\nabla ^{2}f(0)=-1$, it follows that $\bar{x}=0$ does not satisfy the strong second-order necessary condition. However, $C^{s}(2)=\mathbb {R}$, and $\nabla ^{2}f(2)=1$. In fact $(x^*,s^*)=(2,0)$ is the global solution to the problem. When the strong critical cone is replaced by the weak critical cone [52, 53]

$$\begin{aligned} C^{w}(x)=\{d\in \mathbb {R}\vert d=0\text { if }x=0\}, \end{aligned}$$

the weak second-order necessary condition reads as

$$\begin{aligned} \langle d,\nabla ^{2}f(\bar{x})d\rangle \ge 0 \qquad \forall d\in C^{w}(\bar{x}). \end{aligned}$$

(20)

Clearly $\bar{x}=0$ satisfies this weak second-order condition.

At the same time, $\bar{x}=0$ is a second-order stationary point in the sense of Proposition 4 since the necessary conditions (i)–(iv) of that Proposition hold. Indeed, let us consider the sequence $x_k=\frac{1}{k}$, $k\ge 1$ and the corresponding sequence $s_k = \nabla f(x_k) = -x_k = -\frac{1}{k}$. Then, clearly $x_k \rightarrow 0=\bar{x}$ and condition (i) holds. Condition (ii) also holds since $|\langle s_k,x_k\rangle | = \frac{1}{k^2} \le \varepsilon _1$ for sufficiently large k. Since $s_k \rightarrow 0$ as $k \rightarrow \infty$, we have that condition (iii) holds as well. We finally show that (iv) holds. Let us consider arbitrary $v_k \in \mathcal {T}_{x_k}$. Then, by the Definition (16) of $\mathcal {T}_{x_k}$ we have that $1 > \Vert v_k\Vert _{x_k} = \sqrt{\langle H(x_k)v_k,v_k\rangle } = |v_k/x_k| = |k v_k|$, which implies $|v_k| \le \frac{1}{k}$ and $\langle \nabla ^2 f(x_k) v_k, v_k\rangle = - v_k^2 \rightarrow 0$ as $k\rightarrow \infty$, which finishes the proof of (iv). Thus, we proved that $\bar{x}=0$ is a second-order stationary point in the sense of Proposition 4. Importantly, one can show that in this example the point $\bar{x}=0$ satisfies also second-order necessary optimality conditions in [58, Theorem 1], [82, Theorem 3.1], [61, Theorem 4]. Overall, in this example we see that $\bar{x}=0$ is not a strong second-order stationary point, but is a weak second-order stationary point since (20) as well as conditions in Proposition 4, [58, Theorem 1], [82, Theorem 3.1], [61, Theorem 4] hold. $\Diamond$

Our second-order necessary conditions involve the set $\mathcal {T}_{x}$. Theorem 3.2 in [73] demonstrates that the cone generated by $\mathcal {T}_{x}$ coincides with the weak critical cone for conic programming, which is used in weak second-order necessary conditions [8, 52]. At the same time, weak second-order necessary conditions are appropriate notions for barrier algorithms. Indeed, [53] gives an explicit example illustrating that accumulation points of trajectories generated by barrier algorithms will converge to stationary points satisfying the weak second-order necessary condition, but not the strong version. Later, Andreani and Secchin [10] made a small modification in Gould and Toint’s counterexample to come to the same conclusion for augmented Lagrangian-type algorithms. Hence, the most we can expect from our method is that it generates points that approximately satisfy the weak second-order necessary optimality conditions.

4 A first-order Hessian barrier algorithm

In this section we introduce a first-order potential reduction method for solving (Opt) that uses a barrier $h \in \mathcal {H}_{\theta }(\textsf{K})$ and potential function (2). We assume that we are able to compute an approximate analytic center at low computational cost. Specifically, our algorithm relies on the availability of a $\theta$-analytic center, i.e. a point $x^{0}\in \textsf{X}$ such that

$$\begin{aligned} h(x)\ge h(x^{0})-\theta \qquad \forall x\in \textsf{X}. \end{aligned}$$

(21)

To obtain such a point $x^{0}$, one can apply interior point methods to the convex programming problem $\min _{x\in \textsf{X}}h(x)$. Moreover, since $\theta \ge 1$ we do not need to solve it with high precision, making the application of computationally cheap first-order method, such as [43], an appealing choice for this preprocessing step.

4.1 Local properties

Our complexity analysis relies on the ability to control the behavior of the objective function along the set of feasible directions and with respect to the local norm.

Assumption 3

(Local smoothness) $f:\mathbb {E}\rightarrow \mathbb {R}\cup \{+\infty \}$ is continuously differentiable on $\textsf{X}$ and there exists a constant $M>0$ such that for all $x\in \textsf{X}$ and $v\in \mathcal {T}_{x}$, where $\mathcal {T}_{x}$ is defined in (16), we have

$$\begin{aligned} f(x+v) - f(x) - \langle \nabla f(x),v\rangle \le \frac{M}{2}\Vert v\Vert _x^2. \end{aligned}$$

(22)

Remark 2

If the set $\bar{\textsf{X}}$ is bounded, we have $\lambda _{\min }(H(x)) \ge \sigma$ for some $\sigma >0$. In this case, assuming f has an M-Lipschitz continuous gradient, the classical descent lemma [76] implies Assumption 3. Indeed,

$$\begin{aligned} f(x+v) - f(x) - \langle \nabla f(x),v\rangle \le \frac{M}{2}\Vert v\Vert ^2 \le \frac{M}{2\sigma }\Vert v\Vert _x^2. \end{aligned}$$

$\Diamond$

Remark 3

We emphasize that the local Lipschitz smoothness condition (22) does not require global differentiability. Consider the composite non-smooth and non-convex model (1) on $\bar{\textsf{K}}_{\text {NN}}$, with $\varphi (s)=s$ for $s \ge 0$. This means $\sum _{i=1}^{n}\varphi (x_{i}^{p})=\Vert x\Vert _{p}^{p}$ for $p\in (0,1)$ and $x\in \bar{\textsf{K}}_{\text {NN}}$. As a concrete example for the smooth part of the problem let us consider the $L_{2}$-loss $\ell (x)=\frac{1}{2}\Vert \textbf{N}x-\textbf{p}\Vert ^{2}$. This gives rise to the $L_{2}-L_{p}$ minimization problem, an important optimization formulation arising in phase retrieval, mathematical statistics, signal processing and image recovery [36, 49, 50, 71]. Setting $M=\lambda _{\max }(\textbf{N}^{*}\textbf{N})$, the descent lemma yields

$$\begin{aligned} \ell (x^{+})\le \ell (x)+\langle \nabla \ell (x),x^{+}-x\rangle +\frac{M}{2}\Vert x^{+}-x\Vert ^{2}, \end{aligned}$$

for $x,x^{+}\in \textsf{K}_{\text {NN}}$. Since $t\mapsto t^{p}$ is concave for $t>0$ and $p\in (0,1)$, we have, for $x,x^{+}\in \textsf{K}_{\text {NN}}$,

$$\begin{aligned} (x_{i}^{+})^{p}\le x^{p}_{i}+px_{i}^{p-1}(x^{+}_{i}-x_{i})\qquad i=1,\ldots ,n. \end{aligned}$$

Adding these inequalities, we immediately arrive at condition (22) in terms of the Euclidean norm. Over a bounded feasible set $\bar{\textsf{X}}$, this implies Assumption 3 (cf. Remark 2). At the same time, f is not differentiable for $x \in {{\,\textrm{bd}\,}}(\textsf{K}_{\text {NN}})=\{x\in \mathbb {R}^n_{+}\vert x_i=0\text { for some } i\}$. $\Diamond$

We emphasize that in Assumption 3, the Lipschitz modulus M is hardly known exactly in practice, and it is also not an easy task to obtain universal upper bounds that can be efficiently used in the algorithm. Therefore, adaptive techniques should be used to estimate it and are likely to improve the practical performance of the method.

Considering $x\in \textsf{X},v\in \mathcal {T}_{x}$ and combining Eq. (22) with Eq. (7) (with $d=v$ and $t=1< \frac{1}{\Vert v\Vert _x} {\mathop {\le }\limits ^{\tiny (5)}} \frac{1}{\zeta (x,v)}$) reveals a suitable quadratic model, to be used in the design of our first-order algorithm.

Lemma 2

(Quadratic overestimation) For all $x\in \textsf{X},v\in \mathcal {T}_{x}$ and $L\ge M$, we have

$$\begin{aligned} F_{\mu }(x+v)\le F_{\mu }(x)+\langle \nabla F_{\mu }(x),v\rangle +\frac{L}{2}\Vert v\Vert ^{2}_{x}+\mu \Vert v\Vert ^{2}_{x}\omega (\zeta (x,v)). \end{aligned}$$

(23)

4.2 Algorithm description and its complexity

4.2.1 Defining the step direction

Let $x \in \textsf{X}$ be given. Our first-order method employs a quadratic model $Q^{(1)}_{\mu }(x,v)$ to compute a search direction $v_{\mu }(x)$, given by

$$\begin{aligned} v_{\mu }(x) \triangleq \mathop {\textrm{argmin}}\limits _{v\in \mathbb {E}:{\textbf{A}}v=0} \left\{ Q^{(1)}_{\mu }(x,v) \triangleq F_{\mu }(x) + \langle \nabla F_{\mu }(x),v\rangle +\frac{1}{2}\Vert v\Vert _{x}^{2} \right\} . \end{aligned}$$

(24)

For the above problem, we have the following system of optimality conditions involving the dual variable $y_{\mu }(x)\in \mathbb {R}^{m}$:

$$\begin{aligned} \nabla F_{\mu }(x) + H(x)v_{\mu }(x) - {\textbf{A}}^{*} y_{\mu }(x)&= 0, \end{aligned}$$

(25)

$$\begin{aligned} {\textbf{A}}v_{\mu }(x)&=0. \end{aligned}$$

(26)

Since $H(x)\succ 0$ for $x\in \textsf{X}$, any standard solution method [81] can be applied for the above linear system. Moreover, this system can be solved explicitly. Indeed, since $H(x)\succ 0$ for $x\in \textsf{X}$, and ${\textbf{A}}$ has full row rank, the linear operator ${\textbf{A}}[H(x)]^{-1}{\textbf{A}}^{*}$ is invertible. Hence, $v_{\mu }(x)$ is given explicitly as

$$\begin{aligned} v_{\mu }(x){} & {} = - ([H(x)]^{-1}{\textbf{A}}^{*}({\textbf{A}}[H(x)]^{-1}{\textbf{A}}^{*})^{-1}{\textbf{A}}[H(x)]^{-1}\\{} & {} \quad - [H(x)]^{-1} ) \nabla F_{\mu }(x) \triangleq -\textbf{S}_{x}\nabla F_{\mu }(x). \end{aligned}$$

To give some intuition behind this expression, observe that we can give an alternative representation of $\textbf{S}_{x}$ as $\textbf{S}_{x}v = [H(x)]^{-1/2}\Pi _{x}[H(x)]^{-1/2}v$, where

$$\begin{aligned} \Pi _{x}v\triangleq v-[H(x)]^{-1/2}{\textbf{A}}^{*}({\textbf{A}}[H(x)]^{-1}{\textbf{A}}^{*})^{-1}{\textbf{A}}[H(x)]^{-1/2}v. \end{aligned}$$

This shows that $\textbf{S}_{x}$ is just the $\Vert \cdot \Vert _{x}$-orthogonal projection operator onto $\ker ({\textbf{A}}[H(x)]^{-1/2})$.

4.2.2 Defining the step-size

To determine an acceptable step-size, consider a point $x \in \textsf{X}$. The search direction $v_{\mu }(x)$ gives rise to a family of parameterized arcs $x^{+}(t)\triangleq x+tv_{\mu }(x)$, where $t\ge 0$. Our aim is to choose this step-size to ensure feasibility of iterates and decrease of the potential. By (6) and (26), we know that $x^{+}(t)\in \textsf{X}$ for all $t\in I_{x,\mu } \triangleq [0,\frac{1}{\zeta (x,v_{\mu }(x))})$. Multiplying (25) by $v_{\mu }(x)$ and using (26), we obtain $\langle \nabla F_{\mu }(x),v_{\mu }(x)\rangle =-\Vert v_{\mu }(x)\Vert _{x}^{2}$. Choosing $t \in I_{x,\mu }$, we bound

$$\begin{aligned} t^{2}\Vert v_{\mu }(x)\Vert _{x}^{2}\omega (t\zeta (x,v_{\mu }(x))) {\mathop {\le }\limits ^{\tiny (3)}} \frac{t^{2}\Vert v_{\mu }(x)\Vert _{x}^{2}}{2(1-t\zeta (x,v_{\mu }(x)))}. \end{aligned}$$

Therefore, if $t\zeta (x,v_{\mu }(x))\le 1/2$, we readily see from (23) that

$$\begin{aligned} F_{\mu }(x^{+}(t))-F_{\mu }(x)&\le -t\Vert v_{\mu }(x)\Vert _{x}^{2}+\frac{t^{2}M}{2}\Vert v_{\mu }(x)\Vert _{x}^{2}+\mu t^{2}\Vert v_{\mu }(x)\Vert _{x}^{2} \nonumber \\&= -t \Vert v_{\mu }(x)\Vert _{x}^{2}\left( 1-\frac{M+2\mu }{2}t\right) \triangleq -\eta _{x}(t). \end{aligned}$$

(27)

The function $t \mapsto \eta _{x}(t)$ is strictly concave with the unique maximum at $\frac{1}{M+2\mu }$, and two real roots at $t\in \left\{ 0,\frac{2}{M+2\mu }\right\}$. Thus, maximizing the per-iteration decrease $\eta _{x}(t)$ under the restriction $0\le t\le \frac{1}{2\zeta (x,v_{\mu }(x))}$, we choose the step-size

$$\begin{aligned} \texttt{t}_{\mu ,M}(x)\triangleq \min \left\{ \frac{1}{M+2\mu },\frac{1}{2\zeta (x,v_{\mu }(x))}\right\} . \end{aligned}$$

4.2.3 Backtracking on the Lipschitz modulus

The above step-size rule, however, requires knowledge of the parameter M. To boost numerical performance, we employ a backtracking scheme in the spirit of [79] to estimate the constant M at each iteration. This procedure generates a sequence of positive numbers $(L_{k})_{k\ge 0}$ for which the local Lipschitz smoothness condition (22) holds. More specifically, suppose that $x^{k}$ is the current position of the algorithm with the corresponding initial local Lipschitz estimate $L_{k}$ and $v^{k}=v_{\mu }(x^{k})$ is the corresponding search direction. To determine the next iterate $x^{k+1}$, we iteratively try step-sizes $\alpha _k$ of the form $\texttt{t}_{\mu ,2^{i_k}L_k}(x^{k})$ for $i_k\ge 0$ until the local smoothness condition (22) holds with $x=x^{k}$, $v= \alpha _k v^{k}$ and local Lipschitz estimate $M=2^{i_k}L_k$, see (30). This process must terminate in finitely many steps, since when $2^{i_k}L_k \ge M$, inequality (22) with M changed to $2^{i_k}L_k$, i.e., (30), follows from Assumption 3.

4.2.4 First-order algorithm and its complexity result

Combining the search direction finding problem (24) with the just outlined backtracking strategy, yields a First-order Adaptive Hessian Barrier Algorithm (${{\,\mathrm{\textbf{FAHBA}}\,}}$, Algorithm 1).

Algorithm 1

First-order Adaptive Hessian Barrier Algorithm - ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu ,\varepsilon ,L_{0},x^{0})$

Our main result on the iteration complexity of Algorithm 1 is the following Theorem, whose proof is given in Sect. 4.3.

Theorem 1

Let Assumptions 1–3 hold. Fix the error tolerance $\varepsilon >0$, the regularization parameter $\mu =\frac{\varepsilon }{\theta }$, and some initial guess $L_0>0$ for the Lipschitz constant in (22). Let $(x^{k})_{k\ge 0}$ be the trajectory generated by ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu ,\varepsilon ,L_{0},x^{0})$, where $x^{0}$ is a $\theta$-analytic center satisfying (21). Then the algorithm stops in no more than

$$\begin{aligned} \mathbb {K}_{I}(\varepsilon ,x^{0})= \Bigg \lceil 4(f(x^{0}) - f_{\min }(\textsf{X})+ \varepsilon ) \frac{\theta ^{2}(\max \{M,L_0\}+\varepsilon /\theta )}{\varepsilon ^{2}}\Bigg \rceil \end{aligned}$$

(31)

outer iterations, and the number of inner iterations is no more than $2(\mathbb {K}_{I}(\varepsilon ,x^{0})+1)+\max \{\log _{2}(M/L_{0}),0\}$. Moreover, the last iterate obtained from ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu ,\varepsilon ,L_{0},x^{0})$ constitutes a $2\varepsilon$-KKT point for problem (Opt) in the sense of Definition 4.

Remark 4

The line-search process of finding the appropriate $i_k$ is simple since only recalculating $z^k$ is needed, and repeatedly solving problem (28) is not required. Furthermore, the sequence of constants $L_k$ is allowed to decrease along subsequent iterations, which is achieved by the division by the constant factor 2 in the final updating step of each iteration. This potentially leads to longer steps and faster decrease of the potential. $\Diamond$

Remark 5

Since $\theta \ge 1$, $f(x^{0}) - f_{\min }(\textsf{X})$ is expected to be larger than $\varepsilon$, and the constant M is potentially large, we see that the main term in the complexity bound (31) is $O\left( \frac{M\theta ^2(f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^2}\right) =O\left( \frac{\theta ^{2}}{\varepsilon ^{2}}\right)$, i.e., has the same dependence on $\varepsilon$ as the standard complexity bounds [24, 25, 69] of first-order methods for non-convex problems under the standard Lipschitz-gradient assumption, which on bounded sets is subsumed by our Assumption 3. Further, if the function f is linear, Assumption 3 holds with $M=0$ and we can take $L_0=0$. In this case, the complexity bound (31) improves to $O\left( \frac{\theta (f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon }\right)$. $\Diamond$

Remark 6

Just like classical interior-point methods, the iteration complexity of ${{\,\mathrm{\textbf{FAHBA}}\,}}$ depends on the barrier parameter $\theta \ge 1$. For conic domains, the characterization of this barrier parameter has thus been an active research line. [56] demonstrated that for symmetric cones, the barrier parameter is equivalent to algebraic properties of the cone and identified it with the rank of the cone (see [45] for a definition of the rank of a symmetric cone). This deep analysis gives an exact characterization of the optimal barrier parameter for the most important conic domains in optimization. For $\textsf{K}_{\text {NN}}$ and $\textsf{K}_{\text {SDP}}$, it is known that $\theta =n$ is optimal, whereas for $\textsf{K}_{\text {SOC}}$ the optimal barrier parameter is $\theta =2$ (and therefore independent of the dimension n). $\Diamond$

4.2.5 Connection with interior point flows on polytopes

Consider $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}$, and $\textsf{X}=\textsf{K}_{\text {NN}}\cap \textsf{L}$. We are given a function $f:\bar{\textsf{X}}\rightarrow \mathbb {R}$ which is the restriction of a smooth function $f:\mathbb {R}^n\rightarrow \mathbb {R}$. The canonical barrier for this setting is $h(x)=-\sum _{i=1}^{n}\ln (x_{i})$, so that $H(x)={{\,\textrm{diag}\,}}[x_{1}^{-2},\ldots ,x_{n}^{-2}]\triangleq \textbf{X}^{-2}$ for $x\in \textsf{X}$. Applying our first-order method on this domain gives the search direction $v_{\mu }(x)=-\textbf{S}_{x}\nabla F_{\mu }(x)=-\textbf{X}(\textbf{I}-\textbf{X}{\textbf{A}}^{\top }({\textbf{A}}\textbf{X}^{2}{\textbf{A}}^{\top })^{-1}{\textbf{A}}\textbf{X})\textbf{X}\nabla F_{\mu }(x)$. This explicit formula yields various interesting connections between our approach and classical methods. First, for $f(x)=c^{\top }x$ and $\mu =0$, we obtain from this formula the search direction employed in affine scaling methods for linear programming [1, 11, 12]. Second, [22] partly motivated their algorithm as a discretization of the Hessian-Riemannian gradient flows introduced in [4, 21]. Heuristically, we can think of ${{\,\mathrm{\textbf{FAHBA}}\,}}$ as an explicit Euler discretization (with non-monotone adaptive step-size policies) of the gradient-like flow $\dot{x}(t)=-\textbf{S}_{x(t)}\nabla F_{\mu }(x(t))$, which resembles very much the class of dynamical systems introduced in [21]. This gives an immediate connection to a large class of interior point flows on polytopes, heavily studied in control theory [62].

4.3 Proof of Theorem 1

Our proof proceeds in several steps. First, we show that procedure ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu ,\varepsilon ,L_{0},x^{0})$ produces points in $\textsf{X}$, and, thus, is indeed an interior-point method. Next, we show that the line-search process of finding appropriate $L_k$ in each iteration is finite, and estimate the total number of trials in this process. Then we enter the core of our analysis where we prove that if the stopping criterion does not hold at iteration k, i.e., $\Vert v^{k}\Vert _{x^{k}} \ge \tfrac{\varepsilon }{\theta }$, then the objective f is decreased by a quantity $O(\varepsilon ^{2})$, and, since the objective is globally lower bounded, we conclude that the method stops in at most $O(\varepsilon ^{-2})$ iterations. Finally, we show that when the stopping criterion holds, the method has generated an $\varepsilon$-KKT point.

4.3.1 Interior-point property of the iterates

By construction $x^{0}\in \textsf{X}$. Proceeding inductively, let $x^{k}\in \textsf{X}$ be the k-th iterate of the algorithm, delivering the search direction $v^{k}\triangleq v_{\mu }(x^{k})$. By Eq. (29), the step-size $\alpha _k$ satisfies $\alpha _{k}\le \frac{1}{2\zeta (x^{k},v^{k})}$, and, hence, $\alpha _{k}\zeta (x^{k},v^{k})\le 1/2$ for all $k\ge 0$. Thus, by (6) $x^{k+1}=x^{k}+\alpha _{k}v^{k} \in \textsf{K}$. Since, by (28), ${\textbf{A}}v^{k} =0$, we have that $x^{k+1} \in \textsf{L}$. Thus, $x^{k+1}\in \textsf{K}\cap \textsf{L}=\textsf{X}$. By induction, we conclude that $(x^{k})_{k\ge 0}\subset \textsf{X}$.

4.3.2 Bounding the number of backtracking steps

Let us fix iteration k. Since the sequence $2^{i_k} L_k$ is increasing as $i_k$ is increasing, and Assumption 3 holds, we know that when $2^{i_k} L_k \ge \max \{M,L_k\}$, the line-search process for sure stops since inequality (30) holds. Hence, $2^{i_k} L_k \le 2\max \{M,L_k\}$ must be the case, and, consequently, $L_{k+1} = 2^{i_k-1} L_k \le \max \{M,L_k\}$, which, by induction, gives $L_{k+1} \le \bar{M}\triangleq \max \{M,L_0\}$. At the same time, $\log _{2}\left( \frac{L_{k+1}}{L_{k}}\right) = i_{k}-1$, $\forall k\ge 0$. Let N(k) denote the number of inner line-search iterations up to the $k-$th iteration of ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu ,\varepsilon ,L_{0},x^{0})$. Then, using that $L_{k+1} \le \bar{M}=\max \{M,L_0\}$,

$$\begin{aligned} N(k)&=\sum _{j=0}^{k}(i_{j}+1)=\sum _{j=0}^{k} (\log _{2}(L_{j+1}/L_{j})+2 ) \le 2(k+1)+\max \{\log _{2}(M/L_{0}),0\}. \end{aligned}$$

This shows that on average the inner loop ends after two trials.

4.3.3 Per-iteration analysis and a bound for the number of iterations

Let us fix iteration counter k. Since $L_{k+1} = 2^{i_k-1}L_k$, the step-size (29) reads as $\alpha _{k}=\min \left\{ \frac{1}{2L_{k+1} + 2 \mu },\frac{1}{2\zeta (x^k,v^k)} \right\}$. Hence, $\alpha _{k}\zeta (x^{k},v^{k})\le 1/2$, and (27) with the specification $t=\alpha _k = \texttt{t}_{\mu ,2L_{k+1}}(x^{k})$, $M=2L_{k+1}$, $x=x^{k}$, $v_{\mu }(x^{k}) \triangleq v^k$ gives:

$$\begin{aligned} F_{\mu }(x^{k+1})-F_{\mu }(x^{k})\le -\alpha _k \Vert v^k\Vert _{x^k}^{2}\left( 1-(L_{k+1}+\mu )\alpha _k\right) \le -\frac{\alpha _k \Vert v^k\Vert _{x^k}^{2}}{2}, \end{aligned}$$

(32)

where we used that $\alpha _k \le \frac{1}{2(L_{k+1}+\mu )}$ in the last inequality. Substituting into (32) the two possible values of the step-size $\alpha _k$ in (29) gives

$$\begin{aligned} F_{\mu }(x^{k+1})-F_{\mu }(x^{k})\le \left\{ \begin{array}{ll} - \frac{\Vert v^{k}\Vert _{x^{k}}^{2} }{4(L_{k+1}+\mu )} &{} \text {if } \alpha _k=\frac{1}{2(L_{k+1}+\mu )}\\ - \frac{\Vert v^{k}\Vert _{x^{k}}^{2} }{4\zeta (x^k,v^k)} {\mathop {\le }\limits ^{\tiny (5)}} - \frac{\Vert v^{k}\Vert _{x^{k}}}{4} &{} \text {if } \alpha _k=\frac{1}{2\zeta (x^k,v^k)}. \end{array}\right. \end{aligned}$$

(33)

Recalling $L_{k+1} \le \bar{M}$ (see Sect. 4.3.2), we obtain that

$$\begin{aligned} F_{\mu }(x^{k+1}) - F_{\mu }(x^{k}) \le -\frac{\Vert v^{k}\Vert _{x^{k}}}{4} \min \left\{ 1, \frac{\Vert v^{k}\Vert _{x^{k}}}{\bar{M}+\mu }\right\} \triangleq -\delta _{k}. \end{aligned}$$

Rearranging and summing these inequalities for k from 0 to $K-1$ gives

$$\begin{aligned}&K\min _{k=0\ldots ,K-1} \delta _{k} \le \sum _{k=0}^{K-1}\delta _{k}\le F_{\mu }(x^{0})-F_{\mu }(x^{K}) \nonumber \nonumber \\&{\mathop {=}\limits ^{\tiny (2)}} f(x^{0}) - f(x^{K}) + \mu (h(x^{0}) - h(x^{K})) \le f(x^{0}) - f_{\min }(\textsf{X}) + \varepsilon , \end{aligned}$$

(34)

where we used that, by the assumptions of Theorem 1, $x^{0}$ is a $\theta$-analytic center defined in (21) and $\mu = \varepsilon /\theta$, implying that $h(x^{0}) - h(x^{K}) \le \theta = \varepsilon /\mu$. Thus, up to passing to a subsequence, $\delta _{k}\rightarrow 0$, and consequently $\Vert v^{k}\Vert _{x^{k}} \rightarrow 0$ as $k \rightarrow \infty$. This shows that the stopping criterion in Algorithm 1 is achievable.

Assume now that the stopping criterion $\Vert v^k\Vert _{x^k} < \frac{\varepsilon }{ \theta }$ does not hold for K iterations of ${{\,\mathrm{\textbf{FAHBA}}\,}}$. Then, for all $k=0,\ldots ,K-1,$ it holds that $\delta _{k}\ge \min \left\{ \frac{\varepsilon }{4 \theta },\frac{\varepsilon ^{2}}{4 \theta ^{2}(\bar{M}+\mu )}\right\}$. Together with the parameter coupling $\mu =\frac{\varepsilon }{\theta }$, it follows from (34) that

$$\begin{aligned} K\frac{\varepsilon ^{2}}{4 \theta ^{2}(\bar{M}+\varepsilon /\theta )} = K \min \left\{ \frac{\varepsilon }{4 \theta },\frac{\varepsilon ^{2}}{4 \theta ^{2}(\bar{M}+\varepsilon /\theta )}\right\} \le f(x^{0})-f_{\min }(\textsf{X})+\varepsilon . \end{aligned}$$

Hence, recalling that $\bar{M}=\max \{M,L_0\}$, we obtain

$$\begin{aligned} K \le 4(f(x^{0}) - f_{\min }(\textsf{X})+ \varepsilon ) \cdot \frac{\theta ^{2}(\max \{M,L_0\}+\varepsilon /\theta )}{\varepsilon ^{2}}, \end{aligned}$$

i.e., the algorithm stops for sure after no more than this number of iterations. This, combined with the bound for the number of inner steps in Sect. 4.3.2, proves the first statement of Theorem 1.

4.3.4 Generating $\varepsilon$-KKT point

To finish the proof of Theorem 1, we now show that when Algorithm 1 stops for the first time, it returns a $2\varepsilon$-KKT point of (Opt) according to Definition 4.

Let the stopping criterion hold at iteration k. By the optimality condition (25) and the definition of the potential (2), we have

$$\begin{aligned} \nabla f(x^{k})-{\textbf{A}}^{*}y^{k}+\mu \nabla h(x^{k})= & {} -H(x^{k})v^{k}\iff [H(x^{k})]^{-1}\nonumber \\ {}{} & {} \left( \nabla f(x^{k})-{\textbf{A}}^{*}y^{k}+\mu \nabla h(x^{k}) \right) =-v^{k}. \end{aligned}$$

(35)

Denoting $g^{k}\triangleq -\mu \nabla h(x^{k})$, multiplying both equations, and using the stopping criterion $\Vert v^{k}\Vert _{x^{k}} < \frac{\varepsilon }{\theta }$, we conclude

$$\begin{aligned} \Vert \nabla f(x^{k})-{\textbf{A}}^{*}y^{k}-g^{k}\Vert ^{*}_{x^{k}}=\Vert v^{k}\Vert _{x^{k}}<\frac{\varepsilon }{\theta }. \end{aligned}$$

Whence, setting $s^{k}\triangleq \nabla f(x^{k})-{\textbf{A}}^{*}y^{k}\in \mathbb {E}^{*}$, the definition of the dual norm yields

$$\begin{aligned} \frac{\varepsilon }{\theta } > \Vert v^{k}\Vert _{x^{k}}&=\Vert s^{k}-g^{k}\Vert ^{*}_{x^{k}} \nonumber \\&=\Vert s^{k}-g^{k}\Vert _{[H(x^{k})]^{-1}}{\mathop {=}\limits ^{\tiny (79)}}\Vert s^{k}-g^{k}\Vert _{\nabla ^{2}h_{*}(-\nabla h(x^{k}))} \nonumber \\&=\Vert s^{k}-g^{k}\Vert _{\nabla ^{2}h_{*}(\frac{1}{\mu }g^{k})} = \mu \Vert s^{k}-g^{k}\Vert _{\nabla ^{2}h_{*}(g^{k})}, \end{aligned}$$

(36)

where in the last equality we used the fact $h_{*}\in \mathcal {H}_{\theta }(\textsf{K}^{*})$, so that Eq. (80) delivers the identity $\nabla ^{2}h_{*}(\frac{1}{\mu }g^{k})=\mu ^{2}\nabla ^{2}h_{*}(g^{k})$. Since we set $\mu =\frac{\varepsilon }{\theta }$, it follows

$$\begin{aligned} \Vert s^{k}-g^{k}\Vert _{\nabla ^{2}h_{*}(g^{k})} = \frac{\Vert v^{k}\Vert _{x^{k}}}{\mu } < \frac{\varepsilon }{\mu \theta } = 1. \end{aligned}$$

(37)

Thus, since, by (78), $g^{k}=-\mu \nabla h(x^{k})\in {{\,\textrm{int}\,}}(\textsf{K}^{*})$, applying Lemma 1, we can now conclude that $\nabla f(x^{k})-{\textbf{A}}^{*}y^{k}=s^{k}\in {{\,\textrm{int}\,}}(\textsf{K}^{*})$ and therefore (11) holds. By construction, $x^{k}\in \textsf{K}$ and ${\textbf{A}}x^{k} = b$. Thus, (10) holds as well. Finally, since $(x^{k},s^{k})\in \textsf{K}\times \textsf{K}^{*}$, we see

$$\begin{aligned} 0 \le \langle s^{k},x^{k}\rangle&=\langle s^{k}-g^{k},x^{k}\rangle +\langle g^{k},x^{k}\rangle \nonumber \\&\le \Vert s^{k}-g^{k}\Vert _{x^{k}}^{*}\cdot \Vert x^{k}\Vert _{x^{k}}-\mu \langle \nabla h(x^{k}),x^{k}\rangle \nonumber \\&{\mathop {=}\limits ^{\tiny (36),(82), (81)}}\Vert v^{k}\Vert _{x^{k}}\sqrt{\theta }+\mu \theta \nonumber \\&<\sqrt{\theta }\frac{\varepsilon }{\theta }+\varepsilon \le 2\varepsilon , \end{aligned}$$

(38)

where the last inequality uses $\theta \ge 1$. Hence, the complementarity condition (12) holds as well. This finishes the proof of Theorem 1.

4.4 Discussion

4.4.1 Special case of non-negativity constraints

For $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}=\mathbb {R}^n_{+}$, i.e., a particular case covered by our general problem template (Opt), [58] consider a first-order potential reduction method employing the standard log-barrier $h(x)=-\sum _{i=1}^n \ln (x_i)$ and using a trust-region subproblem for obtaining the search direction. For $x\in \textsf{K}_{\text {NN}}$, we have $\nabla h(x)=[-x_{1}^{-1},\ldots ,-x_{n}^{-1}]^{\top }$, $H(x)={{\,\textrm{diag}\,}}[x_{1}^{-2},\ldots ,x_{n}^{-2}]\triangleq \textbf{X}^{-2}$, which makes the problem in a sense simpler since we have a natural coupling between the variable x and the Hessian H(x) expressed as $[H(x^{k})^{-\frac{1}{2}}s^{k}]_i=x_i^{k}s_i^{k}$ and simplifying the derivation of the complementarity condition. More precisely, combining (35), the information $[H(x^{k})]^{-1/2}\nabla h(x^{k})= - \textbf{1}_{n},\;\theta =n$, and the stopping criterion of Algorithm 1 at iteration k, saying that $\Vert v^{k}\Vert _{x^{k}}<\frac{\varepsilon }{\theta }$, we see

$$\begin{aligned} \Vert [H(x^{k})]^{-\frac{1}{2}} (\nabla f(x^{k})-{\textbf{A}}^{*}y^{k}) - \mu \textbf{1}_{n}\Vert _{\infty }&\le \Vert [H(x^{k})]^{-\frac{1}{2}} (\nabla f(x^{k})-{\textbf{A}}^{*}y^{k}) - \mu \textbf{1}_{n} \Vert \\&= \Vert -[H(x^{k})]^{\frac{1}{2}} v^{k}\Vert < \frac{\varepsilon }{n}. \end{aligned}$$

Therefore, since $\mu =\varepsilon /n$ and $s^{k}=\nabla f(x^{k})-{\textbf{A}}^{*}y^{k}$, we have $H(x^{k})^{-\frac{1}{2}}s^{k}= \textbf{X}^{k}s^{k} > 0$ and $x^{k}\in \mathbb {R}^n_{++}$ implies $s^{k} \in \mathbb {R}^n_{++}$. Additionally, from the triangle inequality, we have

$$\begin{aligned} \Vert \textbf{X}^{k}s^{k}\Vert _{\infty }\le \Vert H(x^{k})^{-1/2} s^{k}-\mu \textbf{1}_{n}\Vert _{\infty }+\mu \le \frac{2\varepsilon }{n}. \end{aligned}$$

(39)

By Remark 5, these results are achieved after $O\left( \frac{M n^2(f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^2}\right)$ iterations of ${{\,\mathrm{\textbf{FAHBA}}\,}}$. This bound is by the factor $\frac{1}{n}$ sharper than the complementarity measure employed in [58] who have just $\varepsilon$ in the r.h.s. of relation (39), although they work under an assumption similar to our Assumption 3 and the additional assumption that the level sets of f are bounded. Conversely, in order to attain an approximate KKT point with the same strength as in [58], the above calculations suggest that we can weaken our tolerance from $\varepsilon$ to $\varepsilon \cdot n$, which results in an overall iteration complexity of $O\left( \frac{M (f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^2}\right)$, and a complementarity measure $\Vert \textbf{X}^{k}s^{k}\Vert _{\infty }\le 2\varepsilon$. Thus, in the particular case of non-negativity constraints our general algorithm is able to obtain results similar to [58], but under weaker assumptions. At the same time, our algorithm ensures a stronger measure of complementarity. Indeed, our algorithm guarantees that $x^{k}\in \textsf{K}_{\text {NN}},s^{k}=\nabla f(x^k) -{\textbf{A}}^{*}y^{k}\in \textsf{K}_{\text {NN}}$, i.e., $x^{k},s^{k}> 0$, and approximate complementary $0\le \sum _{i=1}^{n}|x_{i}^{k}s_{i}^{k}|=\sum _{i=1}^{n}x_{i}^{k}s_{i}^{k}\le 2\varepsilon$ after $O\left( \frac{M n^2(f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^2}\right)$ iterations, which is stronger than $\max _{1\le i\le n}|x_{i}^{k}s_{i}^{k}| \le 2\varepsilon$ guaranteed by [58]. Indeed, $\max _{1\le i\le n}|x_{i}^{k}s_{i}^{k}| \le \sum _{i=1}^{n}|x_{i}^{k}s_{i}^{k}| \le n \max _{1\le i\le n}|x_{i}^{k}s_{i}^{k}|$, and both equalities are achievable. Moreover, to match our stronger guarantee, one has to change $\varepsilon \rightarrow \varepsilon /n$ in the complexity bound of [58], which leads to the same $O\left( \frac{M n^2(f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^2}\right)$ complexity bound. Besides these important insights, our algorithm is designed for general cones, rather than only for $\bar{\textsf{K}}_{\text {NN}}$. For more general cones we can not use the identity $[H(x)]^{-\frac{1}{2}} = \textbf{X}$, which was very helpful for the derivation of (39) and for the analysis in [58]. Thus, for general, potentially non-symmetric, cones we have to exploit suitable properties of the barrier class $\mathcal {H}_{\theta }(\textsf{K})$ and develop a new analysis technique. Finally, our method does not rely on the trust-region techniques as in [58] that may slow down the convergence in practice since the radius of the trust region is no greater than $O(\varepsilon )$ leading to short steps.

4.4.2 Exploiting the structure of symmetric cones

In (33) we can clearly observe the benefit of the use of $\theta$-SSB in our algorithm, whenever $\textsf{K}$ is a symmetric cone. Indeed, when $\alpha _k=\frac{1}{2\zeta (x^k,v^k)}$, the per-iteration decrease of the potential is $\frac{\Vert v^{k}\Vert _{x^{k}}^{2} }{4\zeta (x^k,v^k)} \ge \frac{ \varepsilon \Vert v^{k}\Vert _{x^{k}}}{4\theta \zeta (x^k,v^k)}$ which may be large if $\zeta (x^k,v^k)=\sigma _{x^k}(-v^k) \ll \Vert v^{k}\Vert _{x^{k}}$.

4.4.3 The role of the penalty parameter

Next, we discuss more explicitly, how the algorithm and complexity bounds depend on the parameter $\mu$. The first observation is that from (37), to guarantee that $s^{k} \in \textsf{K}^{*}$, we need the stopping criterion to be $\Vert v^{k}\Vert _{x^k} < \mu$, which by (38) leads to the error $2 \mu \theta$ in the complementarity conditions. From the analysis following equation (34), we have that

$$\begin{aligned} K\frac{\mu ^{2}}{4 (\bar{M}+\mu )} = K \min \left\{ \frac{\mu }{4},\frac{\mu ^{2}}{4 \ (\bar{M}+\mu )}\right\} \le f(x^{0})-f_{\min }(\textsf{X})+\mu \theta . \end{aligned}$$

Whence, recalling that $\bar{M}=\max \{M,L_0\}$,

$$\begin{aligned} K \le 4(f(x^{0}) - f_{\min }(\textsf{X})+ \mu \theta ) \cdot \frac{\max \{M,L_0\}+\mu }{\mu ^{2}}. \end{aligned}$$

Thus, we see that after $O(\mu ^{-2})$ iterations the algorithm finds a $(2 \mu \theta )$-KKT point, and if $\mu \rightarrow 0$, we have convergence to a KKT point, but the complexity bound tends to infinity and becomes non-informative. At the same time, as it is seen from (28), when $\mu \rightarrow 0$, the algorithm itself can be interpreted as a preconditioned gradient method with the local preconditioner given by the Hessian H(x).

We also see from the above explicit expressions in terms of $\mu$ that the design of the algorithm requires careful balance between the desired accuracy of the approximate KKT point expressed mainly by the complementarity condition, stopping criterion, and complexity. Moreover, the step-size should be also taken carefully to ensure the feasibility of the iterates, and the standard for first-order methods step-size 1/M may not work.

4.5 Anytime convergence via restarting ${{\,\mathrm{\textbf{FAHBA}}\,}}$

The analysis of Algorithm 1 is based on the a-priori fixed tolerance $\varepsilon >0$ and the parameter coupling $\mu =\varepsilon /\theta$. This coupling allows us to embed Algorithm 1 within a restarting scheme featuring a decreasing sequence $\{\mu _{i}\}_{i\ge 0}$, combined with restarts of ${{\,\mathrm{\textbf{FAHBA}}\,}}$ for each particular $\mu _{i}$. This restarting strategy frees Algorithm 1 from hard-coded parameters and connects it well to traditional barrier methods. Moreover, the complexity of such path-following method is the same as for ${{\,\mathrm{\textbf{FAHBA}}\,}}$, up to a constant factor.

To describe this double-loop algorithm, we fix $\varepsilon _{0}>0$ and select the starting point $x_0^{0}$ as a $\theta$-analytic center of $\textsf{X}$ with respect to $h\in \mathcal {H}_{\theta }(\textsf{K})$. We let $i \ge 0$ denote the counter for the restarting epochs at the start of which the value $\mu _{i}$ is decreased. In epoch i, we generate a sequence $\{x^{k}_{i}\}_{k=0}^{K_{i}}$ by calling ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu _{i},\varepsilon _{i},L_0^{(i)},x^{0}_{i})$ until the stopping condition is reached. This will take at most $\mathbb {K}_{I}(\varepsilon _{i},x^{0}_{i})$ iterations, specified in Eq. (31). We store the last iterate $\hat{x}_{i}=x^{K_{i}}_{i}$ and the last estimate of the Lipschitz constant $\hat{M}_{i}=L_{K_i}^{(i)}$ obtained from procedure ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu _{i},\varepsilon _{i},L_0^{(i)},x^{0}_{i})$ and then restart the algorithm using the “warm start” $x^{0}_{i+1}=\hat{x}_{i}$, $L_{0}^{(i+1)}=\hat{M}_{i}/2$, $\varepsilon _{i+1}=\varepsilon _{i}/2$, $\mu _{i+1}=\varepsilon _{i+1}/\theta$. If $\varepsilon \in (0,\varepsilon _0)$ is the target accuracy of the final solution, it suffices to perform $\lceil \log _{2}(\varepsilon _{0}/\varepsilon )\rceil +1$ restarts since, by construction, $\varepsilon _{i} = \varepsilon _0 \cdot 2^{-i}$.

Algorithm 2

Restarting ${{\,\mathrm{\textbf{FAHBA}}\,}}$

Theorem 2

Let Assumptions 1–3 hold. Then, for any $\varepsilon \in (0,\varepsilon _0)$, Algorithm 2 finds a $2\varepsilon$-KKT point for problem (Opt) in the sense of Definition 4 after no more than $I(\varepsilon )=\lceil \log _{2}(\varepsilon _{0}/\varepsilon )\rceil +1$ restarts and at most

iterations of ${{\,\mathrm{\textbf{FAHBA}}\,}}$.

Proof

Let us consider a restart $i \ge 0$ and repeat the proof of Theorem 1 with the change $\varepsilon \rightarrow \varepsilon _i$, $\mu \rightarrow \mu _i = \varepsilon _i/\theta$, $L_0 \rightarrow L_0^{(i)}=\hat{M}_{i-1}/2$, $\bar{M}=\max \{M,L_0\} \rightarrow \bar{M}_i=\max \{M,L_0^{(i)}\}$, $x^0 \rightarrow x^{0}_{i}=\hat{x}_{i-1}$. Let $K_i$ be the last iteration of ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu _{i},\varepsilon _i,L_0^{(i)},x^{0}_{i})$ meaning that $\Vert v^{K_i}\Vert _{x^{K_i}} < \frac{\varepsilon _i}{\theta }$, $\Vert v^{K_i-1}\Vert _{x^{K_i-1}} \ge \frac{\varepsilon _i}{\theta }$, and the stopping criterion does not hold for $K_i$ iterations $k=0,\ldots ,K_i-1$. From the analysis following Eq. (34), we have that

$$\begin{aligned}&K_i \frac{\varepsilon _i^{2}}{4 \theta ^{2}(\bar{M}_i+\varepsilon _i/\theta )} \le K_i \min _{k=0\ldots ,K_i-1} \delta _{k}^i \le \sum _{k=0}^{K_i-1}\delta _{k}^i\le F_{\mu _i}(x^{0}_i)-F_{\mu _i}(x^{K_i}_i). \end{aligned}$$

(40)

Further, using the fact that $\mu _i$ is a decreasing sequence and (21), it is easy to deduce

$$\begin{aligned} F_{\mu _{i+1}}(x^{0}_{i+1})&=F_{\mu _{i+1}}(x^{K_i}_{i}){\mathop {=}\limits ^{\tiny (2)}}f(x^{K_i}_{i}) + \mu _{i+1} h(x^{K_i}_{i}) {\mathop {=}\limits ^{\tiny (2)}}F_{\mu _{i}}(x^{K_i}_{i})\nonumber \\&\quad + (\mu _{i+1} - \mu _{i}) h(x^{K_i}_{i}) \nonumber \\&{\mathop {\le }\limits ^{\tiny (21)}} F_{\mu _{i}}(x^{K_i}_{i}) + (\mu _{i+1} - \mu _{i}) (h(x_0^0)-\theta )\nonumber \\&{\mathop {\le }\limits ^{\tiny (40)}}F_{\mu _i}(x^{0}_i)-K_i \frac{\varepsilon _i^{2}}{4 \theta ^{2}(\bar{M}_i+\varepsilon _i/\theta )} + (\mu _{i+1} - \mu _{i}) (h(x_0^0)-\theta ). \end{aligned}$$

(41)

Letting $I\equiv I(\varepsilon )=\lceil \log _2 (\frac{\varepsilon _0}{\varepsilon }) \rceil +1$, by Theorem 1 applied to the restart $I-1$, we see that ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu _{I-1},\varepsilon _{I-1},L_0^{(I-1)},x^{0}_{I-1})$ outputs a $2\varepsilon$-KKT point for problem (Opt) in the sense of Definition 4. Summing inequalities (41) for all the performed restarts $i=0,\ldots ,I-1$ and rearranging the terms, we obtain

$$\begin{aligned}&\sum _{i=0}^{I-1} K_i \frac{\varepsilon _i^{2}}{4 \theta ^{2}(\bar{M}_i+\varepsilon _i/\theta )} \le F_{\mu _0}(x^{0}_0) - F_{\mu _{I}}(x^{0}_{I}) + (\mu _{I} - \mu _{0}) (h(x_0^0)-\theta ) \nonumber \\&\qquad {\mathop {=}\limits ^{\tiny (2)}} f(x^{0}_0) + \mu _0 h(x^{0}_0)- f(x^{0}_{I}) - \mu _{I}h(x^{0}_{I}) + (\mu _{I} - \mu _{0}) (h(x_0^0)-\theta ) \nonumber \\&\qquad {\mathop {\le }\limits ^{\tiny (21)}} f(x^{0}_0) - f_{\min }(\textsf{X}) + \mu _0 h(x^{0}_0) - \mu _{I}h(x^{0}_{0}) + \mu _{I} \theta + (\mu _{I} - \mu _{0}) (h(x_0^0)-\theta ) \nonumber \\&\qquad \le f(x^{0}_0) - f_{\min }(\textsf{X}) + \mu _0 \theta = f(x^{0}_0) - f_{\min }(\textsf{X}) + \varepsilon _0. \end{aligned}$$

Moreover, based on our updating choice $L_0^{(i+1)}=\hat{M}_{i}/2$, it holds that

$$\begin{aligned} \bar{M}_i&= \max \{M,L_0^{(i)}\} = \max \{M,\hat{M}_{i-1}/2\}\\&= \max \{M,L_{K_{i-1}}^{(i-1)}/2\} \le \max \{M,\bar{M}_{i-1}\} \le ... \le \max \{M, \bar{M}_{0}\} \le \max \{M,L_0^{(0)}\}. \end{aligned}$$

Hence,

$$\begin{aligned} K_i \le 4(f(x^{0}) - f_{\min }(\textsf{X})+ \varepsilon _0) \cdot \frac{\theta ^{2}(\bar{M}_i+\varepsilon _i/\theta )}{\varepsilon _i^{2}} \le \frac{C}{\varepsilon _i^2}, \end{aligned}$$

where $C\equiv 4(f(x^{0})-f_{\min }(\textsf{X})+\varepsilon _0)\theta ^2(\max \{M,L_0^{(0)}\}+\varepsilon _0/\theta )$. Finally, we obtain that the total number of iterations of procedures ${{\,\mathrm{\textbf{FAHBA}}\,}}(\mu _{i},\varepsilon _{i},L_0^{(i)},x_{i}^{0}),0\le i \le I-1$, to reach accuracy $\varepsilon$ is at most

$$\begin{aligned} \sum _{i=0}^{I-1}K_{i}&\le \sum _{i=0}^{I-1} \frac{C}{\varepsilon _i^2} \le \frac{C}{\varepsilon _0^2} \sum _{i=0}^{I-1} (2^2)^i \le \frac{C}{3\varepsilon _0^2} \cdot \left( 4^{{1}+\log _2\left( \frac{\varepsilon _0}{\varepsilon }\right) }\right) = \frac{{4}C}{3\varepsilon ^2}\\&=\frac{{16}(f(x^{0})-f_{\min }(\textsf{X})+\varepsilon _0)\theta ^2(\max \{M,L_0^{(0)}\}+\varepsilon _0/\theta )}{3\varepsilon ^{2}}. \end{aligned}$$

$\square$

5 A second-order Hessian barrier algorithm

We now present a second-order potential reduction method for (Opt) under the assumption that the second-order Taylor expansion of f on the set of feasible directions $\mathcal {T}_{x}$ defined in (16) is sufficiently accurate in the geometry induced by $h \in \mathcal {H}_{\theta }(\textsf{K})$.

Assumption 4

(Local second-order smoothness) $f:\mathbb {E}\rightarrow \mathbb {R}\cup \{+\infty \}$ is twice continuously differentiable on $\textsf{X}$ and there exists a constant $M>0$ such that, for all $x\in \textsf{X}$ and $v\in \mathcal {T}_{x}$, where $\mathcal {T}_{x}$ is defined in (16), we have

$$\begin{aligned} \Vert \nabla f(x+v)-\nabla f(x)-\nabla ^{2}f(x)v\Vert ^{*}_{x}\le \frac{M}{2}\Vert v\Vert ^{2}_{x}. \end{aligned}$$

(42)

A sufficient condition for (42) is the following local counterpart of the global Lipschitz condition on the Hessian of f:

$$\begin{aligned} (\forall x\in \textsf{X})(\forall u,v\in \mathcal {T}_{x}):\;\Vert \nabla ^{2}f(x+u)-\nabla ^{2}f(x+v)\Vert _{\text {op},x}\le M\Vert u-v\Vert _{x}, \end{aligned}$$

where $\Vert {\textbf{B}}\Vert _{\text {op},x}\triangleq \sup _{u:\Vert u\Vert _{x}\le 1}\left\{ \frac{\Vert {\textbf{B}}u\Vert _{x}^{*}}{\Vert u\Vert _{x}}\right\}$ is the induced operator norm for a linear operator ${\textbf{B}}:\mathbb {E}\rightarrow \mathbb {E}^{*}$. Indeed, this condition implies (42):

$$\begin{aligned}&\Vert \nabla f(x+v)-\nabla f(x)-\nabla ^{2}f(x)v\Vert ^{*}_{x}=\Vert \int _{0}^{1}(\nabla ^{2}f(x+tv)-\nabla ^{2}f(x))v\,dt \Vert ^{*}_{x}\\&\quad \le \int _{0}^{1}\Vert \nabla ^{2}f(x+tv)-\nabla ^{2}f(x)\Vert _{\text {op},x}\cdot \Vert v\Vert _{x}\,dt \le \frac{M}{2}\Vert v\Vert ^{2}_{x}. \end{aligned}$$

Further, Eq. (42) implies

$$\begin{aligned} f(x+v)-\left[ f(x)+\langle \nabla f(x),v\rangle +\frac{1}{2}\langle \nabla ^{2}f(x)v,v\rangle \right] \le \frac{M}{6}\Vert v\Vert ^{3}_{x}. \end{aligned}$$

(43)

To obtain this, observe that for all $x\in \textsf{X}$ and $v\in \mathcal {T}_{x}$, we have

$$\begin{aligned}&|f(x+v)-f(x)-\langle \nabla f(x),v\rangle -\frac{1}{2}\langle \nabla ^{2}f(x)v,v\rangle |\\&\quad =|\int _{0}^{1}\langle \nabla f(x+tv)-\nabla f(x)-\frac{1}{2}\nabla ^{2}f(x)v,v\rangle \,dt|\\&\quad \le \int _{0}^{1}\Vert \nabla f(x+tv)-\nabla f(x)-\frac{1}{2}\nabla ^{2}f(x)v\Vert _{x}^{*}\,dt\cdot \Vert v\Vert _{x} \le \frac{M}{6}\Vert v\Vert ^{3}_{x}. \end{aligned}$$

Remark 7

Assumption 4 subsumes, when $\bar{\textsf{X}}$ is bounded, the standard Lipschitz-Hessian setting. If the Hessian of f is Lipschitz with modulus M with respect to the standard Euclidean norm, we have by [76, Lemma 1.2.4] that

$$\begin{aligned} \Vert \nabla f(x+v)-\nabla f(x)-\nabla ^{2}f(x)v\Vert \le \frac{M}{2}\Vert v\Vert ^{2}. \end{aligned}$$

Since $\bar{\textsf{X}}$ is bounded, one can observe that $\lambda _{\max }([H(x)]^{-1})^{-1}=\lambda _{\min }(H(x)) \ge \sigma$ for some $\sigma >0$, and (42) holds. Indeed, denoting $g=\nabla f(x+v)-\nabla f(x)-\nabla ^{2}f(x)v$, we obtain

$$\begin{aligned} (\Vert g\Vert _x^*)^2 \le \lambda _{\max }([H(x)]^{-1})\Vert g\Vert ^{2} \le \frac{M^2}{4\lambda _{\min }(H(x))}\Vert v\Vert ^{4} \le \frac{M^2}{4\sigma ^{3}}\Vert v\Vert _x^4. \end{aligned}$$

$\Diamond$

Remark 8

The cubic overestimation of the objective function in (43) does not rely on global second order differentiability assumptions. To illustrate this, we revisit the structured composite optimization problem (1), assuming that the data fidelity function $\ell$ is twice continuously differentiable on an open neighborhood containing $\textsf{X}$, with Lipschitz continuous Hessian $\nabla ^{2}\ell$ with modulus $\gamma$ w.r.t. the Euclidean norm. On the domain $\textsf{K}_{\text {NN}}$ we employ the canonical barrier $h(x)=-\sum _{i=1}^{n}\ln (x_{i})$, having $H(x)={{\,\textrm{diag}\,}}[x_{1}^{-2},\ldots ,x_{n}^{-2}]=\textbf{X}^{-2}$. This means, for all $x,x^{+}\in \textsf{X}$, we have

$$\begin{aligned} \ell (x^{+})\le \ell (x)+\langle \nabla \ell (x),x^{+}-x\rangle +\frac{1}{2} \langle \nabla ^{2}\ell (x)(x^{+}-x),x^{+}-x\rangle +\frac{\gamma }{6}\Vert x^{+}-x\Vert ^{3}. \end{aligned}$$

As penalty function, we again consider the $L_{p}$-regularizer with $p\in (0,1)$. For any $t,s>0$, one has

$$\begin{aligned} t^{p}\le s^{p}+ps^{p-1}(t-s)+\frac{p(p-1)}{2} s^{p-2}(t-s)^{2}+\frac{p(p-1)(p-2)}{6}s^{p-3}(t-s)^{3}. \end{aligned}$$

Further, $v\in \mathcal {T}_{x}$ if and only if $v=[H(x)]^{-1/2}d=\textbf{X}d$ for some $d\in \mathbb {R}^{n}$ satisfying ${\textbf{A}}\textbf{X}d=0$ and $\Vert d\Vert <1$. Since $p(1-p)\le 1/4$, it follows that $p(1-p)(2-p)\le 1/2$. Thus, using $x^{+}=x+v=x+\textbf{X}d$, we get

$$\begin{aligned} f(x^{+})&- \left( (f(x)+\langle \nabla f(x),\textbf{X}d\rangle +\frac{1}{2}\langle \nabla ^{2}f(x)\textbf{X}d,\textbf{X}d\rangle \right) \le \frac{\gamma }{6}\Vert \textbf{X}d\Vert ^{3}+\frac{1}{12}\sum _{i=1}^{n}x^{p}_{i}d_{i}^{3}\\&\le \frac{\gamma }{6}\Vert \textbf{X}d\Vert ^{3}+\frac{1}{12}\Vert x\Vert ^{p}_{\infty }\sum _{i=1}^{n}d_{i}^{3} \le \frac{1}{6}\left( \gamma \Vert x\Vert _{\infty }^{3}+\frac{1}{2}\Vert x\Vert ^{p}_{\infty }\right) \Vert d\Vert ^{3}. \end{aligned}$$

Since we assume that $\bar{\textsf{X}}$ is bounded, there exists a universal constant $M>0$ such that $\gamma \Vert x\Vert _{\infty }^{2}+\frac{1}{2}\Vert x\Vert ^{p}_{\infty }\le M$. Combining this with Remark 7, we obtain a cubic overestimation as in Eq. (43). Importantly, f(x) is not differentiable for $x \in {{\,\textrm{bd}\,}}(\textsf{K}_{\text {NN}})=\{x\in \mathbb {R}^n_{+}\vert x_i=0\text { for some } i\}$. $\Diamond$

We emphasize that in Assumption 4, the Lipschitz modulus M is hardly known exactly in practice, and it is also not an easy task to obtain universal upper bounds that can be used in implementations. Therefore, adaptive techniques should be used to estimate it and are likely to improve the practical performance of the method. Assumption 4 also implies, via (43) and (7) (with $d=v$ and $t=1< \frac{1}{\Vert v\Vert _x} {\mathop {\le }\limits ^{\tiny (5)}} \frac{1}{\zeta (x,v)}$), the following upper bound for the potential function $F_{\mu }$.

Lemma 3

(Cubic overestimation) For all $x\in \textsf{X},v\in \mathcal {T}_{x}$ and $L\ge M$, we have

$$\begin{aligned} F_{\mu }(x+v)\le F_{\mu }(x)+\langle \nabla F_{\mu }(x),v\rangle +\frac{1}{2}\langle \nabla ^{2}f(x)v,v\rangle +\frac{L}{6}\Vert v\Vert ^{3}_{x}+\mu \Vert v\Vert ^{2}_{x}\omega (\zeta (x,v)). \end{aligned}$$

5.1 Algorithm description and its complexity

5.1.1 Defining the step direction

Let $x\in \textsf{X}$ be given. In order to find a search direction, we choose a parameter $L>0$, construct a cubic-regularized model of the potential $F_{\mu }$(2, and minimize it on the linear subspace $\textsf{L}_{0}$):

$$\begin{aligned} v_{\mu ,L}(x)\in \mathop {\textrm{Argmin}}\limits _{v\in \mathbb {E}:{\textbf{A}}v=0}\left\{ Q^{(2)}_{\mu ,L}(x,v)\triangleq F_{\mu }(x)+\langle \nabla F_{\mu }(x),v\rangle +\frac{1}{2}\langle \nabla ^{2}f(x)v,v\rangle +\frac{L}{6}\Vert v\Vert _{x}^{3} \right\} ,\nonumber \\ \end{aligned}$$

(44)

where by $\mathop {\textrm{Argmin}}\limits$ we denote the set of global minimizers. The model consists of three parts: linear approximation of h, quadratic approximation of f, and a cubic regularizer with penalty parameter $L>0$. Since this model and our algorithm use the second derivative of f, we call it a second-order method. Our further derivations rely on the first-order optimality conditions for the problem (44), which say that there exists $y_{\mu ,L}(x)\in \mathbb {R}^{m}$ such that $v_{\mu ,L}(x)$ satisfies

$$\begin{aligned} \nabla F_{\mu }(x)+\nabla ^{2}f(x)v_{\mu ,L}(x)+\frac{L}{2}\Vert v_{\mu ,L}(x)\Vert _{x}H(x)v_{\mu ,L}(x) - {\textbf{A}}^{*} y_{\mu ,L}(x)&= 0, \end{aligned}$$

(45)

$$\begin{aligned} - {\textbf{A}}v_{\mu ,L}(x)&=0. \end{aligned}$$

(46)

We also use the following extension of [79, Prop. 1] with the local norm induced by H(x).

Proposition 5

For all $x\in \textsf{X}$ it holds

$$\begin{aligned} \nabla ^{2}f(x)+\frac{L}{2}\Vert v_{\mu ,L}(x)\Vert _{x}H(x)\succeq 0\qquad \text { on }\;\;\textsf{L}_{0}. \end{aligned}$$

(47)

Proof

The proof follows the same strategy as Lemma 3.2 in [29]. Let $\{z_{1},\ldots ,z_{p}\}$ be an orthonormal basis of $\textsf{L}_{0}$ and the linear operator $\textbf{Z}:\mathbb {R}^{p}\rightarrow \textsf{L}_{0}$ be defined by $\textbf{Z}w=\sum _{i=1}^{p}z_{i}w^{i}$ for all $w=[w^{1};\ldots ;w^{p}]^{\top }\in \mathbb {R}^{p}$. With the help of this linear map, we can absorb the nullspace restriction, and formulate the search-direction finding problem (44) using the projected data

$$\begin{aligned} \textbf{g}\triangleq \textbf{Z}^{*}\nabla F_{\mu }(x),\; \textbf{J}\triangleq \textbf{Z}^{*}\nabla ^{2}f(x)\textbf{Z},\;\textbf{H}\triangleq \textbf{Z}^{*}H(x)\textbf{Z}\succ 0. \end{aligned}$$

(48)

We then arrive at the cubic-regularized subproblem to find $u_{L}\in \mathbb {R}^{p}$ s.t.

$$\begin{aligned} u_{L}\in \mathop {\textrm{Argmin}}\limits _{u\in \mathbb {R}^{p}}\left\{ \langle \textbf{g},u\rangle +\frac{1}{2}\langle \textbf{J}u,u\rangle +\frac{L}{6}\Vert u\Vert ^{3}_{\textbf{H}}\right\} , \end{aligned}$$

(49)

where $\Vert \cdot \Vert _{\textbf{H}}$ is the norm induced by the operator $\textbf{H}$. From [79, Thm. 10] we deduce

$$\begin{aligned} \textbf{J}+\frac{L\Vert u_{L}\Vert _{\textbf{H}}}{2}\textbf{H}\succeq 0. \end{aligned}$$

Denoting $v_{\mu ,L}(x) = \textbf{Z}u_{L}$, we see

$$\begin{aligned} \Vert u_{L}\Vert _{\textbf{H}}=\langle \textbf{Z}^{*}H(x)\textbf{Z}u_{L},u_{L}\rangle ^{1/2}=\langle H(x)(\textbf{Z}u_{L}),\textbf{Z}u_{L}\rangle ^{1/2}&=\Vert v_{\mu ,L}(x)\Vert _{x}, \text { and} \\ \textbf{Z}^{*}\left( \nabla ^{2}f(x)+\frac{L}{2}\Vert v_{\mu ,L}(x)\Vert _{x}H(x)\right) \textbf{Z}&\succeq 0, \end{aligned}$$

which implies $\nabla ^{2}f(x)+\frac{L}{2}\Vert v_{\mu ,L}(x)\Vert _{x}H(x)\succ 0$ over the nullspace $\textsf{L}_{0} = \{ v\in \mathbb {E}:{\textbf{A}}v=0\}$. $\square$

The above proposition gives some ideas on how one could numerically solve problem (44) in practice. In a preprocessing step, we once calculate matrix $\textbf{Z}$ and use it during the whole algorithm execution. At each iteration we calculate the new data using (48), leaving us with a standard unconstrained cubic subproblem (49). Nesterov and Polyak [79] show how such problems can be transformed to a convex problem to which fast convex programming methods could in principle be applied. However, we can also solve it via recent efficient methods based on Lanczos’ method [29, 68]. Whatever numerical tool is employed, we can recover our search direction $v_{\mu ,L}(x)$ by the matrix vector product $\textbf{Z}u_{L}$ in which $u_{L}$ denotes the solution obtained from this subroutine.

5.1.2 Defining the step-size

Our next goal is to construct an admissible step-size policy, given the search direction $v_{\mu ,L}(x)$. Let $x\in \textsf{X}$ be the current position of the algorithm. Define the parameterized family of arcs $x^{+}(t)\triangleq x+t v_{\mu ,L}(x)$, where $t\ge 0$ is a step-size. By (6) and since $v_{\mu ,L}(x)\in \textsf{L}_{0}$ by (46), we know that $x^{+}(t)$ is in $\textsf{X}$ provided that $t\in I_{x,\mu ,L}\triangleq [0,\frac{1}{\zeta (x,v_{\mu ,L}(x))})$. For all such t, Lemma 3 yields

$$\begin{aligned} F_{\mu }(x^{+}(t))&\le F_{\mu }(x)+t\langle \nabla F_{\mu }(x),v_{\mu ,L}(x)\rangle + \frac{t^2}{2}\langle \nabla ^{2}f(x)v_{\mu ,L}(x),v_{\mu ,L}(x)\rangle \nonumber \\&\quad + \frac{Mt^3}{6}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} +\mu t^{2}\omega (t\zeta (x,v_{\mu ,L}(x))). \end{aligned}$$

(50)

Since $v_{\mu ,L}(x) \in \textsf{L}_0$, multiplying (47) with $v_{\mu ,L}(x)$ from the left and the right, and multiplying (45) by $v_{\mu ,L}(x)$ and combining with (46), we obtain

$$\begin{aligned}&\langle \nabla ^{2}f(x)v_{\mu ,L}(x),v_{\mu ,L}(x)\rangle \ge -\frac{L}{2}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x}, \end{aligned}$$

(51)

$$\begin{aligned}&\langle \nabla F_{\mu }(x),v_{\mu ,L}(x)\rangle +\langle \nabla ^{2}f(x)v_{\mu ,L}(x),v_{\mu ,L}(x)\rangle +\frac{L}{2}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x}=0. \end{aligned}$$

(52)

Under the additional assumption that $t\le 2$ and $L\ge M$, we obtain

$$\begin{aligned}&t\langle \nabla F_{\mu }(x),v_{\mu ,L}(x)\rangle + \frac{t^2}{2}\langle \nabla ^{2}f(x)v_{\mu ,L}(x),v_{\mu ,L}(x)\rangle + \frac{Mt^3}{6}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x}\\&{\mathop {=}\limits ^{\tiny (52)}} - t \left( \langle \nabla ^{2}f(x)v_{\mu ,L}(x),v_{\mu ,L}(x)\rangle +\frac{L}{2}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x}\right) \\&\qquad +\, \frac{t^2}{2}\langle \nabla ^{2}f(x)v_{\mu ,L}(x),v_{\mu ,L}(x)\rangle + \frac{Mt^3}{6}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \\&\quad = \left( \frac{t^2}{2} - t \right) \langle \nabla ^{2}f(x)v_{\mu ,L}(x),v_{\mu ,L}(x)\rangle - \frac{Lt}{2}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} + \frac{Mt^3}{6}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \\&{\mathop {\le }\limits ^{\tiny (51),t\le 2}} \left( \frac{t^2}{2} - t \right) \left( - \frac{L}{2}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \right) - \frac{Lt}{2}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} + \frac{Mt^3}{6}\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \\&\quad = - \Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \left( \frac{Lt^2}{4} - \frac{Mt^3}{6} \right) {\mathop {\le }\limits ^{L \ge M}} - \Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \frac{Lt^2}{12} \left( 3 - 2t \right) . \end{aligned}$$

Substituting this into (50), we arrive at

$$\begin{aligned} F_{\mu }(x^{+}(t))&\le F_{\mu }(x) - \Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \frac{Lt^2}{12} \left( 3 - 2t \right) +\mu t^{2}\omega (t\zeta (x,v_{\mu ,L}(x)))\\&{\mathop {\le }\limits ^{\tiny (3)}} F_{\mu }(x) - \Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \frac{Lt^2}{12} \left( 3 - 2t \right) +\mu \frac{t^{2}\Vert v_{\mu ,L}(x)\Vert _{x}^{2}}{2(1-t\zeta (x,v_{\mu ,L}(x)))}. \end{aligned}$$

for all $t \in I_{x,\mu ,L}$. Therefore, if $t\zeta (x,v_{\mu ,L}(x))\le 1/2$, we readily see

$$\begin{aligned} F_{\mu }(x^{+}(t))-F_{\mu }(x)&\le - \frac{Lt^2\Vert v_{\mu ,L}(x)\Vert ^{3}_{x} }{12} \left( 3 - 2t \right) +\mu t^{2}\Vert v_{\mu ,L}(x)\Vert _{x}^{2} \nonumber \\&= - \Vert v_{\mu ,L}(x)\Vert ^{3}_{x} \frac{Lt^2}{12}\left( 3 - 2t - \frac{12 \mu }{L\Vert v_{\mu ,L}(x)\Vert _{x}} \right) \triangleq -\eta _{x}(t). \end{aligned}$$

(53)

Maximizing the function $\eta _{x}(t)$ explicitly and carrying the resulting minimizer $t^*$ through the analysis by finding an upper bound for the corresponding per-iteration decrease $-\eta _{x}(t^*)$ is technically quite challenging. Instead, we adopt the following step-size rule

$$\begin{aligned} \texttt{t}_{\mu ,L}(x) \triangleq \frac{1}{\max \{1,2\zeta (x,v_{\mu ,L}(x))\}} = \min \left\{ 1, \frac{1}{2\zeta (x,v_{\mu ,L}(x))} \right\} . \end{aligned}$$

(54)

Note that $\texttt{t}_{\mu ,L}(x) \le 1$ and $\texttt{t}_{\mu ,L}(x)\zeta (x,v_{\mu ,L}(x))\le 1/2$. Thus, this choice of the step-size is feasible to derive (53).

5.1.3 Backtracking on the Lipschitz modulus

Just like Algorithm 1, our second-order method employs a line-search procedure to estimate the Lipschitz constant M in (42), (43) in the spirit of [27, 79]. More specifically, suppose that $x^{k}\in \textsf{X}$ is the current position of the algorithm with the corresponding initial local Lipschitz estimate $M_{k}$. To determine the next iterate $x^{k+1}$, we solve problem (44) with $L= L_k = 2^{i_k}M_{k}$ starting with $i_k =0$, find the corresponding search direction $v^{k}=v_{\mu ,L_{k}}(x^{k})$ and the new point $x^{k+1} = x^{k} + \texttt{t}_{\mu , L_{k}}(x^{k})v^{k}$. Then, we check whether the inequalities (42) and (43) hold with $M=L_{k}$, $x=x^{k}$, $v = \texttt{t}_{\mu , L_{k}}(x^{k})v^{k}$, see (58) and (57). If they hold, we make a step to $x^{k+1}$. Otherwise, we increase $i_k$ by 1 and repeat the procedure. Obviously, when $L_{k} = 2^{i_k}M_k \ge M$, both inequalities (42) and (43) with M changed to $L_k$, i.e., (58) and (57), are satisfied and the line-search procedure ends. For the next iteration we set $M_{k+1} = \max \{2^{i_k-1}M_{k},\underline{L}\}=\max \{L_{k}/2,\underline{L}\}$, so that the estimate for the local Lipschitz constant on the one hand can decrease allowing larger step-sizes, and on the other hand is bounded from below.

5.1.4 Second-order algorithm and its complexity result

The resulting procedure gives rise to a Second-order Adaptive Hessian Barrier Algorithm (${{\,\mathrm{\textbf{SAHBA}}\,}}$, Algorithm 3).

Algorithm 3

Second-order Adaptive Hessian Barrier Algorithm - ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu ,\varepsilon ,M_{0},x^{0})$

Our main result on the iteration complexity of Algorithm 3 is the following Theorem, whose proof is given in Sect. 5.2.

Theorem 3

Let Assumptions 1, 2, and 4 hold. Fix the error tolerance $\varepsilon >0$, the regularization parameter $\mu = \frac{\varepsilon }{4\theta }$, and some initial guess $M_0>144\varepsilon$ for the Lipschitz constant in (42). Let $(x^{k})_{k\ge 0}$ be the trajectory generated by ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu ,\varepsilon ,M_{0},x^{0})$, where $x^{0}$ is a $4\theta$-analytic center satisfying (21). Then the algorithm stops in no more than

$$\begin{aligned} \mathbb {K}_{II}(\varepsilon ,x^{0})= \Bigg \lceil \frac{192 \theta ^{3/2} \sqrt{2\max \{M,M_0\}}(f(x^{0}) -f_{\min }(\textsf{X})+ \varepsilon )}{\varepsilon ^{3/2} }\Bigg \rceil \end{aligned}$$

(59)

outer iterations, and the number of inner iterations is no more than $2(\mathbb {K}_{II}(\varepsilon ,x^{0})+1)+2\max \{\log _{2}(2M/M_{0}),1\}$. Moreover, the output of ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu ,\varepsilon ,M_{0},x^{0})$ constitutes an $(\varepsilon ,\frac{\max \{M,M_0\}\varepsilon }{8\theta })$-2KKT point for problem (Opt) in the sense of Definition 5.

Remark 9

Since $f(x^{0}) - f_{\min }(\textsf{X})$ is expected to be larger than $\varepsilon$, and the constant M is potentially large, we see that the main term in the complexity bound (59) is $O\left( \frac{\theta ^{3/2}\sqrt{M}(f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^{3/2}}\right) =O((\frac{\theta }{\varepsilon })^{3/2})$. Note that the complexity result $O(\max \{\varepsilon _1^{-3/2},\varepsilon _2^{-3/2}\})$ reported in [24, 25] to find an $(\varepsilon _1,\varepsilon _2)$-2KKT point for arbitrary $\varepsilon _1,\varepsilon _2 > 0$, is known to be optimal for unconstrained smooth non-convex optimization by second-order methods under the standard Lipschitz–Hessian assumption, subsumed on bounded sets by our Assumption 4. A similar dependence on arbitrary $\varepsilon _1,\varepsilon _2 > 0$ can be easily obtained from our theorem by setting $\varepsilon =\min \{\varepsilon _1,\varepsilon _2\}$. $\Diamond$

5.2 Proof of Theorem 3

The main steps of the proof are similar to the analysis of Algorithm 1. We start by showing the feasibility of the iterates and correctness of the line-search process. Next, we analyze the per-iteration decrease of $F_{\mu }$ and f and show that if the stopping criterion does not hold at iteration k, then the objective function is decreased by the value $O(\varepsilon ^{3/2})$. From this, since the objective is globally lower bounded, we conclude that the algorithm stops in $O(\varepsilon ^{-3/2})$ iterations. Finally, we show that when the stopping criterion holds, the primal–dual pair $(x^{k}$, $y^{k-1})$ resulting from solving the cubic subproblem (55) yields a dual slack variable $s^{k}$ such that this triple constitutes an approximate second-order KKT point.

5.2.1 Interior point property of the iterates

By construction $x^{0}\in \textsf{X}$. Proceeding inductively, let $x^{k}\in \textsf{X}$ be the k-th iterate of the algorithm, with the search direction $v^{k}\triangleq v_{\mu ,L}(x^{k})$. By Eq. (56), the step-size $\alpha _k$ satisfies $\alpha _{k}\le \frac{1}{2\zeta (x^{k},v^{k})}$. Consequently, $\alpha _{k}\zeta (x^{k},v^{k})\le 1/2$ for all $k\ge 0$, and using (6) as well as ${\textbf{A}}v^{k} =0$ (see Eq. (55)), we have that $x^{k+1}=x^{k}+\alpha _{k}v^{k}\in \textsf{X}$. By induction, it follows that $x^{k}\in \textsf{X}$ for all $k\ge 0$.

5.2.2 Bounding the number of backtracking steps

To bound the number of cycles involved in the line-search process for finding appropriate constants $L_{k}$, we proceed as in Sect. 4.3.2. Let us fix an iteration k. The sequence $L_k = 2^{i_k} M_k$ is increasing as $i_k$ is increasing, and Assumption 4 holds. This implies (43), and thus when $L_k = 2^{i_k} M_k \ge \max \{M,M_k\}$, the line-search process for sure stops since inequalities (57) and (58) hold. Hence, $L_k=2^{i_k} M_k \le 2\max \{M,M_k\}$ must be the case, and, consequently, $M_{k+1}=\max \{L_k/2, \underline{L}\} \le \max \{\max \{M,M_k\}, \underline{L}\} = \max \{M,M_k\}$, which, by induction, gives $M_{k} \le \bar{M} \triangleq \max \{M,M_0\}$ and $L_k \le 2\bar{M}$. At the same time, by construction, $M_{k+1}= \max \{2^{i_k-1}M_{k},\underline{L}\} = \max \{L_k/2,\underline{L}\} \ge L_k/2$. Hence, $L_{k+1} = 2^{i_{k+1}} M_{k+1} \ge 2^{i_{k+1}-1} L_k$ and therefore $\log _{2}\left( \frac{L_{k+1}}{L_{k}}\right) \ge i_{k+1}-1$, $\forall k\ge 0$. At the same time, at iteration 0 we have $L_0=2^{i_0} M_0 \le 2\bar{M}$, whence, $i_0 \le \log _2\left( \frac{2\bar{M}}{M_0}\right)$. Let N(k) denote the number of inner line-search iterations up to iteration k of ${{\,\mathrm{\textbf{SAHBA}}\,}}$. Then,

$$\begin{aligned} N(k)&=\sum _{j=0}^{k}(i_{j}+1)\le i_0+1 + \sum _{j=1}^{k}\left( \log _{2}\left( \frac{L_{j}}{L_{j-1}}\right) +2\right) \\&\le 2(k+1) + 2 \log _2\left( \frac{2\bar{M}}{M_0}\right) , \end{aligned}$$

since $L_{k} \le 2\bar{M}= 2\max \{M,M_0\}$ in the last step. Thus, on average, the inner loop ends after two trials.

5.2.3 Per-iteration analysis and a bound for the number of iterations

Let us fix iteration counter k. The main assumption of this subsection is that the stopping criterion is not satisfied, i.e., either $\Vert v^{k}\Vert _{x^{k}} \ge \Delta _{k}$ or $\Vert v^{k-1}\Vert _{x^{k-1}} \ge \Delta _{k-1}$. Without loss of generality, we assume that the first inequality holds, i.e., $\Vert v^{k}\Vert _{x^{k}} \ge \Delta _{k}$, and consider iteration k. Otherwise, if the second inequality holds, the same derivations can be made considering the iteration $k-1$ and using the second inequality $\Vert v^{k-1}\Vert _{x^{k-1}} \ge \Delta _{k-1}$. Thus, at the end of the k-th iteration

$$\begin{aligned} \Vert v^{k}\Vert _{x^{k}} \ge \Delta _{k}=\sqrt{\frac{\varepsilon }{4L_{k}\theta }}. \end{aligned}$$

(60)

Since the step-size $\alpha _k= \min \{1,\frac{1}{ 2\zeta (x^k,v^k)}\} = \texttt{t}_{\mu ,L_k}(x^{k})$ in (56) satisfies $\alpha _k \le 1$ and $\alpha _k \zeta (x^k,v^k) \le 1/2$ (cf. (54) and a remark after it), we can repeat the derivations of Sect. 5.1, changing (43) to (57). In this way we obtain the following counterpart of (53) with $t=\alpha _k$, $L=L_k$, $x=x^k$, $v_{\mu ,L_k}(x^{k}) \triangleq v^k$:

$$\begin{aligned} F_{\mu }(x^{k+1})-F_{\mu }(x^{k})&\le - \Vert v^{k}\Vert ^{3}_{x^{k}} \frac{L_k\alpha _k^2}{12}\left( 3 - 2\alpha _k - \frac{12 \mu }{L_k\Vert v^{k}\Vert _{x^{k}}} \right) \nonumber \\&\le - \Vert v^{k}\Vert ^{3}_{x^{k}} \frac{L_k\alpha _k^2}{12}\left( 1 - \frac{12 \mu }{L_k\Vert v^{k}\Vert _{x^{k}}} \right) , \end{aligned}$$

(61)

where in the last inequality we used that $\alpha _k \le 1$ by construction. Substituting $\mu = \frac{\varepsilon }{4\theta }$, and using (60), we obtain

$$\begin{aligned} 1 - \frac{12 \mu }{L_k\Vert v^{k}\Vert _{x^{k}}}&= 1 - \frac{12 \varepsilon }{4\theta L_k\Vert v^{k}\Vert _{x^{k}}} {\mathop {\ge }\limits ^{\tiny (60)}} 1 - \frac{3 \varepsilon }{\theta L_k\sqrt{\frac{\varepsilon }{4L_{k}\theta }}} \\&= 1 - \frac{6 \sqrt{\varepsilon }}{ \sqrt{\theta L_k}} \ge 1 - \frac{6 \sqrt{\varepsilon }}{ \sqrt{ 144 \theta \varepsilon }} \ge \frac{1}{2}, \end{aligned}$$

using that, by construction, $L_k =2^{i_k}M_k \ge \underline{L} = 144 \varepsilon$ and that $\theta \ge 1$. Hence, from (61),

$$\begin{aligned} F_{\mu }(x^{k+1})-F_{\mu }(x^{k})\le - \Vert v^{k}\Vert ^{3}_{x^{k}} \frac{L_k\alpha _k^2}{24}. \end{aligned}$$

(62)

Substituting into (62) the two possible values of the step-size $\alpha _k$ in (56) gives

$$\begin{aligned} F_{\mu }(x^{k+1})-F_{\mu }(x^{k})\le \left\{ \begin{array}{ll} - \Vert v^{k}\Vert ^{3}_{x^{k}} \frac{L_k}{24}, &{} \text {if } \alpha _k=1,\\ - \frac{L_k\Vert v^{k}\Vert ^{3}_{x^{k}}}{96 (\zeta (x^k,v^k))^2} {\mathop {\le }\limits ^{\tiny (5)}} - \frac{L_k\Vert v^{k}\Vert _{x^{k}}}{96}&{} \text {if } \alpha _k=\frac{1}{2\zeta (x^k,v^k)}. \end{array}\right. \end{aligned}$$

(63)

This implies

$$\begin{aligned} F_{\mu }(x^{k+1})-F_{\mu }(x^{k}) \le - \frac{L_k\Vert v^{k}\Vert _{x^{k}}}{96} \min \left\{ 1, 4\Vert v^{k}\Vert _{x^{k}}^2 \right\} \triangleq -\delta _{k}. \end{aligned}$$

(64)

Rearranging and summing these inequalities for k from 0 to $K-1$, and using that $L_k \ge \underline{L}$, we obtain

$$\begin{aligned} K\min _{k=0,\ldots ,K-1}&\frac{\underline{L}\Vert v^{k}\Vert _{x^{k}}}{96} \min \left\{ 1, 4\Vert v^{k}\Vert _{x^{k}}^2\right\} \le \sum _{k=0}^{K-1} \delta _k \le F_{\mu }(x^{0})-F_{\mu }(x^{K}) \nonumber \\&{\mathop {=}\limits ^{\tiny (2)}} f(x^{0}) - f(x^{K}) + \mu (h(x^{0}) - h(x^{K})) \le f(x^{0}) - f_{\min }(\textsf{X}) + \varepsilon , \end{aligned}$$

(65)

where we used that, by the assumptions of Theorem 3, $x^{0}$ is a $4\theta$-analytic center defined in (21) and $\mu = \frac{\varepsilon }{4\theta }$, implying that $h(x^{0}) - h(x^{K}) \le 4\theta = \varepsilon /\mu$. Thus, up to passing to a subsequence, we have $\Vert v^{k}\Vert _{x^{k}} \rightarrow 0$ as $k \rightarrow \infty$, which makes the stopping criterion in Algorithm 3 achievable.

Assume now that the stopping criterion does not hold for K iterations of ${{\,\mathrm{\textbf{SAHBA}}\,}}$. Then, for all $k=0,\ldots ,K-1,$ it holds that

$$\begin{aligned} \delta _k&= \frac{L_k}{96} \min \left\{ \Vert v^{k}\Vert _{x^{k}}, 4\Vert v^{k}\Vert _{x^{k}}^3 \right\} {\mathop {\ge }\limits ^{\tiny (60)}} \frac{L_k}{96} \min \left\{ \sqrt{\frac{\varepsilon }{4L_{k}\theta }} , \frac{4 \varepsilon ^{3/2}}{4^{3/2}L_{k}^{3/2}\theta ^{3/2}} \right\} \nonumber \\&{\mathop {\ge }\limits ^{L_k \le 2\bar{M}, \theta \ge 1}} \frac{1}{96} \min \left\{ \frac{L_k \sqrt{\varepsilon }}{\sqrt{8\bar{M}} \theta ^{3/2}} , \frac{ \varepsilon ^{3/2}}{2 L_{k}^{1/2}\theta ^{3/2}} \right\} \nonumber \\&{\mathop {\ge }\limits ^{L_k \le 2\bar{M},L_k \ge 144 \varepsilon }} \frac{1}{96} \min \left\{ \frac{(144 \varepsilon ) \cdot \sqrt{\varepsilon }}{\sqrt{8\bar{M}} \theta ^{3/2}} , \frac{ \varepsilon ^{3/2}}{\sqrt{8\bar{M}}\theta ^{3/2}} \right\} = \frac{\varepsilon ^{3/2}}{192 \theta ^{3/2} \sqrt{2\bar{M}} }. \end{aligned}$$

Thus, from (65)

$$\begin{aligned} K \frac{\varepsilon ^{3/2}}{192 \theta ^{3/2} \sqrt{2\bar{M}} } \le f(x^{0}) - f_{\min }(\textsf{X}) + \varepsilon . \end{aligned}$$

Hence, recalling that $\bar{M}=\max \{M_0,M\}$, we obtain $K \le \frac{192 \theta ^{3/2} \sqrt{2\max \{M_0,M\}}(f(x^{0}) - f_{\min }(\textsf{X})+ \varepsilon )}{\varepsilon ^{3/2} }$, i.e., the algorithm stops for sure after no more than this number of iterations. This, combined with the bound for the number of inner steps in Sect. 5.2.2, proves the first statement of Theorem 3.

5.2.4 Generating $(\varepsilon _{1},\varepsilon _{2})$-2KKT point

In this section, to finish the proof of Theorem 3, we show that if the stopping criterion in Algorithm 3 holds, i.e., $\Vert v^{k-1}\Vert _{x^{k-1}} < \Delta _{k-1}$ and $\Vert v^{k}\Vert _{x^{k}} < \Delta _{k}$, then the algorithm has generated an $(\varepsilon _{1},\varepsilon _{2})$-2KKT point of (Opt) according to Definition 5, with $\varepsilon _{1}=\varepsilon$ and $\varepsilon _{2}=\frac{\max \{M_{0},M\}\varepsilon }{8\theta }$.

Let the stopping criterion hold at iteration k. Using the first-order optimality condition (45) for the subproblem (55) solved at iteration $k-1$, there exists a Lagrange multiplier $y^{k-1}\in \mathbb {R}^{m}$ such that (45) holds. Now, expanding the definition of the potential (2) and adding $\nabla f(x^{k})$ to both sides, we obtain

$$\begin{aligned} \nabla f(x^{k}) - {\textbf{A}}^{*}y^{k-1} + \mu \nabla h(x^{k-1})&=\nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1}\\&\quad - \frac{L_{k-1}}{2}\Vert v^{k-1}\Vert _{x^{k-1}}H(x^{k-1})v^{k-1}. \end{aligned}$$

Setting $s^{k}\triangleq \nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1} \in \mathbb {E}^{*}$ and $g^{k-1}\triangleq -\mu \nabla h(x^{k-1})$, after multiplication by $[H(x^{k-1})]^{-1}$, this is equivalent to

$$\begin{aligned}{}[H(x^{k-1})]^{-1}\left( s^{k}-g^{k-1}\right)&=[H(x^{k-1})]^{-1}\left( \nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1}\right) \\&\quad - \frac{L_{k-1}}{2}\Vert v^{k-1}\Vert _{x^{k-1}}v^{k-1}. \end{aligned}$$

Multiplying both of the above equalities, we arrive at

$$\begin{aligned} \left( \Vert s^{k}\!-\!g^{k-1}\Vert ^{*}_{x^{k-1}}\right) ^{2}\!=\!\left( \left\| \nabla f(x^{k}) \!-\! \nabla f(x^{k-1}) \!-\! \nabla ^2 f(x^{k-1})v^{k-1} \!-\! \frac{L_{k-1}}{2}\Vert v^{k-1}\Vert _{x^{k-1}}H(x^{k-1})v^{k-1} \right\| _{x^{k-1}}^*\!\right) ^{2}\!. \end{aligned}$$

Taking the square root and applying the triangle inequality, we obtain

$$\begin{aligned} \Vert s^{k}-g^{k-1}\Vert ^{*}_{x^{k-1}}&\le \Vert \nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1}\Vert ^{*}_{x^{k-1}}+\frac{L_{k-1}}{2}\Vert v^{k-1}\Vert ^{2}_{x^{k-1}} \nonumber \\&{\mathop {\le }\limits ^{\tiny (58)}} \frac{L_{k-1}}{2}\Vert \alpha _{k-1}v^{k-1}\Vert ^{2}_{x_{k-1}}+\frac{L_{k-1}}{2}\Vert v^{k-1}\Vert ^{2}_{x^{k-1}}. \end{aligned}$$

(66)

Since the stopping criterion holds, at iteration $k-1$ we have

$$\begin{aligned} \hspace{-1em}\zeta (x^{k-1},v^{k-1})&{\mathop {\le }\limits ^{\tiny (5)}} \Vert v^{k-1}\Vert _{x^{k-1}}< \Delta _{k-1} = \sqrt{\frac{\varepsilon }{4L_{k-1}\theta }} \le \sqrt{\frac{\varepsilon }{4 \cdot 144 \varepsilon \theta }} < \frac{1}{2}, \end{aligned}$$

(67)

where we used that, by construction, $L_{k-1} \ge \underline{L} = 144 \varepsilon$ and that $\theta \ge 1$. Hence, by (56), we have that $\alpha _{k-1}=1$ and $x^{k}=x^{k-1}+v^{k-1}$. This, in turn, implies that

$$\begin{aligned} \Vert s^{k}-g^{k-1}\Vert ^{*}_{x^{k-1}} {\mathop {\le }\limits ^{\tiny (66)}} L_{k-1}\Vert v^{k-1}\Vert ^{2}_{x^{k-1}}. \end{aligned}$$

(68)

As in the analysis of the first-order method, we note that $\Vert s^{k}-g^{k-1}\Vert ^{*}_{x^{k-1}}=\mu \Vert s^{k}-g^{k-1}\Vert _{\nabla ^{2}h_{*}(g^{k-1})}$ and $\mu =\frac{\varepsilon }{4\theta }$, which implies

$$\begin{aligned} \Vert s^{k}-g^{k-1}\Vert _{\nabla ^{2}h_{*}(g^{k-1})}\le \frac{L_{k-1}}{\mu }\Vert v^{k-1}\Vert ^{2}_{x^{k-1}}<\frac{L_{k-1}}{\mu }\Delta _{k-1}^{2} = \frac{L_{k-1}}{\frac{\varepsilon }{4\theta }} \cdot \frac{\varepsilon }{4L_{k-1}\theta } = 1. \nonumber \\ \end{aligned}$$

(69)

Thus, since, by (78), $g^{k-1}=-\mu \nabla h(x^{k-1})\in {{\,\textrm{int}\,}}(\textsf{K}^{*})$, applying Lemma 1, we deduce that $\nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1}=s^{k}\in {{\,\textrm{int}\,}}(\textsf{K}^{*})$. By construction, $x^{k}\in \textsf{K}$ and ${\textbf{A}}x^{k} = b$. Therefore, conditions (10) and (11) both hold. We now check for the complementarity condition (14). We have

$$\begin{aligned} \langle s^{k},x^{k}\rangle =\langle s^{k},x^{k-1}+v^{k-1}\rangle =\langle s^{k},x^{k-1}\rangle +\langle s^{k},v^{k-1}\rangle . \end{aligned}$$

We estimate each of the two terms in the r.h.s. separately. First,

$$\begin{aligned} 0 \le \langle s^{k},x^{k-1}\rangle&= \langle s^{k}-g^{k-1},x^{k-1}\rangle + \langle g^{k-1},x^{k-1}\rangle \\&\le \Vert s^{k}-g^{k-1}\Vert ^{*}_{x^{k-1}}\cdot \Vert x^{k-1}\Vert _{x^{k-1}}-\mu \langle \nabla h(x^{k-1}),x^{k-1}\rangle \\&{\mathop {\le }\limits ^{\tiny (68),(82), (81)}} L_{k-1}\Vert v^{k-1}\Vert ^{2}_{x^{k-1}}\sqrt{\theta }+\mu \theta . \end{aligned}$$

Second,

$$\begin{aligned} \langle s^{k},v^{k-1}\rangle&\le \Vert s^{k}\Vert ^{*}_{x^{k-1}}\cdot \Vert v^{k-1}\Vert _{x^{k-1}}\le \left( \Vert s^{k}-g^{k-1}\Vert ^{*}_{x^{k-1}}+\Vert g^{k-1}\Vert ^{*}_{x^{k-1}}\right) \cdot \Vert v^{k-1}\Vert _{x^{k-1}}\\&{\mathop {\le }\limits ^{\tiny (68), (82),(81)}} \left( L_{k-1}\Vert v^{k-1}\Vert ^{2}_{x^{k-1}}+\mu \sqrt{\theta }\right) \Delta _{k-1}. \end{aligned}$$

Summing up, using the stopping criterion $\Vert v^{k-1}\Vert _{x^{k-1}}<\Delta _{k-1}$ and that, by (67), $\Delta _{k-1} \le 1\le \sqrt{\theta }$, we obtain

$$\begin{aligned} 0&\le \langle s^k,x^k\rangle = \langle s^k,x^{k-1}+v^{k-1}\rangle \le 2L_{k-1}\Delta _{k-1}^2 \sqrt{\theta } + 2\mu \theta \nonumber \\&= 2 L_{k-1} \frac{\varepsilon }{4L_{k-1}\theta } \sqrt{\theta } + 2\frac{\varepsilon }{4\theta } \theta \le \varepsilon , \end{aligned}$$

(70)

i.e., (14) holds with $\varepsilon _1=\varepsilon$.

Finally, we show the second-order condition (15). By inequality (47) for subproblem (55) solved at iteration k, we obtain on $\textsf{L}_0$

$$\begin{aligned} \nabla ^2 f(x^{k})&\succeq - \frac{L_{k}\Vert v^{k}\Vert _{x^{k}}}{2} H(x^{k}) \succeq -\frac{L_{k} \Delta _k}{2} H(x^{k}) \nonumber \\&= - \frac{L_{k}}{2}\sqrt{\frac{\varepsilon }{4L_{k}\theta }} H(x^{k}) = - \frac{\sqrt{L_k \varepsilon }}{4\theta ^{1/2}}H(x^{k}) \succeq - \frac{ \sqrt{2\bar{M}\varepsilon }}{4\theta ^{1/2}}H(x^{k}), \end{aligned}$$

(71)

where we used the second part of the stopping criterion, i.e., $\Vert v^{k}\Vert _{x^{k}}< \Delta _k$ and that $L_k \le 2\bar{M}=2\max \{M,M_0\}$ (see Sect. 5.2.2). Thus, (15) holds with $\varepsilon _2=\frac{\max \{M,M_0\}\varepsilon }{8\theta }$, which finishes the proof of Theorem 3.

5.3 Discussion

5.3.1 Special case of non-negativity constraints

As in Sect. 4.4, our aim in this section is to compare our result with those available in the contemporary literature. [58, 82] focus exclusively on the domain $\bar{\textsf{K}}=\bar{\textsf{K}}_{\text {NN}}=\mathbb {R}^n_{+}$, i.e., a particular case covered by our general problem template (Opt). A second-order algorithm and a first-order implementation of a second-order algorithm are proposed respectively. To compare their results with ours, consider the cone $\bar{\textsf{K}}_{\text {NN}}$, endowed with the standard log-barrier $h(x)=-\sum _{i=1}^n \ln (x_i)$. Recall that for this barrier setup we have $\nabla h(x)=[-x_{1}^{-1},\ldots ,-x_{n}^{-1}]^{\top }$ and $H(x)={{\,\textrm{diag}\,}}[x_{1}^{-2},\ldots ,x_{n}^{-2}]=\textbf{X}^{-2}$. Assume that the stopping criterion applies at iteration k. Using the first-order optimality condition (45) for the subproblem (55) solved at iteration $k-1$ and expanding the definition of the potential (2), there exists a dual variable $y^{k-1}\in \mathbb {R}^{m}$ such that (45) holds, i.e.,

$$\begin{aligned}&\nabla f(x^{k-1}) + \mu \nabla h(x^{k-1}) + \nabla ^2 f(x^{k-1})v^{k-1} - {\textbf{A}}^{*}y^{k-1} \\&\quad = - \frac{L_{k-1}}{2}\Vert v^{k-1}\Vert _{x^{k-1}}H(x^{k-1})v^{k-1}. \end{aligned}$$

Multiplying both sides by $[H(x^{k-1})]^{-1/2}=\textbf{X}^{k-1}$, using the stopping criterion $\Vert v^{k-1}\Vert _{x^{k-1}}<\sqrt{\frac{\varepsilon }{4\theta L_{k-1}}}$, since

$\textbf{X}^{k-1} \nabla h(x^{k-1}) = [H(x^{k-1})]^{-1/2}\nabla h(x^{k-1})= - \textbf{1}_{n}$ and $\theta =n$, we obtain

$$\begin{aligned}&\Vert \textbf{X}^{k-1}(\nabla ^2 f(x^{k-1})v^{k-1} + \nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1}) - \mu \textbf{1}_{n}\Vert _{\infty } \nonumber \\&\quad \le \Vert \textbf{X}^{k-1} (\nabla ^2 f(x^{k-1})v^{k-1} + \nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1}) \nonumber \\&\qquad - \mu \textbf{1}_{n} \Vert = \frac{L_{k-1}}{2} \Vert -H(x^{k-1})^{\frac{1}{2}} v^{k-1}\Vert ^2=\frac{L_{k-1}}{2} \Vert v^{k-1}\Vert _{x^{k-1}}^2\nonumber \\&\quad < \frac{\varepsilon }{8n}. \end{aligned}$$

(72)

Whence, since $\mu =\frac{\varepsilon }{4n}$, the above bound (72) combined with the triangle inequality yields

$$\begin{aligned}&\Vert \textbf{X}^{k-1}(\nabla ^2 f(x^{k-1})v^{k-1} +\nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1})\Vert _{\infty } \nonumber \\&\quad \le \Vert \textbf{X}^{k-1} (\nabla ^2 f(x^{k-1})v^{k-1} + \nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1}) - \mu \textbf{1}_{n} \Vert _{\infty } +\Vert \mu \textbf{1}_{n}\Vert _{\infty } < \frac{3\varepsilon }{8n}. \end{aligned}$$

(73)

Let $\textbf{V}^{k-1} = {{\,\textrm{diag}\,}}[v_{1}^{k-1},\ldots ,v_{n}^{k-1}] = {{\,\textrm{diag}\,}}(v^{k-1})$. Using the fact that $x^{k}=x^{k-1}+v^{k-1}$ shown after (67), we obtain

$$\begin{aligned}&\Vert \textbf{X}^{k}(\nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1})\Vert _{\infty } \nonumber \\&\quad = \Vert (\textbf{X}^{k-1}+\textbf{V}^{k-1})(\nabla ^2 f(x^{k-1})v^{k-1} +\nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1} + \nabla f(x^{k}) \\&\qquad - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1})\Vert _{\infty } \\&\quad \le \Vert \textbf{X}^{k-1}(\nabla ^2 f(x^{k-1})v^{k-1} +\nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1} )\Vert _{\infty }\\&\qquad + \Vert \textbf{X}^{k-1} (\nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1})\Vert _{\infty }\\&\qquad + \Vert \textbf{V}^{k-1}(\nabla ^2 f(x^{k-1})v^{k-1} +\nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1} )\Vert _{\infty }\\&\qquad + \Vert \textbf{V}^{k-1}(\nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1})\Vert _{\infty }\\&\quad =I+II+III+IV. \end{aligned}$$

Let us estimate each of the four terms $I-IV$ using two technical facts (87) and (88) proved in Appendix C. We have:

$$\begin{aligned} I&{\mathop {<}\limits ^{\tiny (73)}} \frac{3\varepsilon }{8n}, \\ II&\le \Vert \textbf{X}^{k-1} (\nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1})\Vert \\&= \Vert \nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1}\Vert _{x^{k-1}}^* {\mathop {\le }\limits ^{\tiny (58)}} \frac{L_{k-1}}{2}\Vert v^{k-1}\Vert _{x^{k-1}}^2<\frac{\varepsilon }{8n}, \\ III&{\mathop {\le }\limits ^{\tiny (88)}} \Vert v^{k-1}\Vert _{x^{k-1}} \cdot \Vert \textbf{X}^{k-1} (\nabla ^2 f(x^{k-1})v^{k-1} +\nabla f(x^{k-1})-{\textbf{A}}^{*}y^{k-1} )\Vert _{\infty } {\mathop {<}\limits ^{\tiny (67), (73)}}\frac{3\varepsilon }{8n}, \end{aligned}$$

where we used $x^{k}=z^{k-1}=x^{k-1}+v^{k-1}$ in bounding II, and the last bound for expression III uses $\Vert v^{k-1}\Vert _{x^{k-1}}<1$, which is implied by Eq. (67). Finally, we also obtain

$$\begin{aligned} IV&{\mathop {\le }\limits ^{\tiny (87)}} \Vert v^{k-1}\Vert _{x^{k-1}} \cdot \Vert \nabla f(x^{k}) - \nabla f(x^{k-1}) - \nabla ^2 f(x^{k-1})v^{k-1}\Vert _{x^{k-1}}^{*}\\&{\mathop {\le }\limits ^{\tiny (67),(58)}} \frac{L_{k-1}}{2}\Vert v^{k-1}\Vert _{x^{k-1}}^2 <\frac{\varepsilon }{8n}. \end{aligned}$$

Summarizing, we arrive at

$$\begin{aligned} \Vert \textbf{X}^{k}(\nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1})\Vert _{\infty } \le \frac{\varepsilon }{n}. \end{aligned}$$

(74)

Further, by Theorem 3, we have that $\nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1} = s^k \in {{\,\textrm{int}\,}}(\textsf{K}^{*}_{\text {NN}})=\mathbb {R}^n_{++}$, and

$$\begin{aligned} \nabla ^2f(x^k) + H(x^k) \sqrt{\frac{M\varepsilon }{n}} \succeq 0 \;\; \text {on} \;\; \textsf{L}_0. \end{aligned}$$

By Remark 9, these inequalities are achieved after $O\left( \frac{\sqrt{M} n^{3/2}(f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^{3/2}}\right)$ iterations of ${{\,\mathrm{\textbf{SAHBA}}\,}}$. Assuming that $M\ge 1$, if we change $\varepsilon \rightarrow \tilde{\varepsilon }=\min \{n\varepsilon , n\varepsilon /M\}$, we obtain from these inequalities that in $O\left( \frac{\sqrt{M} n^{3/2}(f(x^{0}) - f_{\min }(\textsf{X}))}{\tilde{\varepsilon }^{3/2}}\right) = O\left( \frac{M^2 (f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^{3/2}}\right)$ iterations ${{\,\mathrm{\textbf{SAHBA}}\,}}$ guarantees

$$\begin{aligned}&x^{k}> 0, \; \nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1} >0 \\&\Vert \textbf{X}^{k}(\nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1})\Vert _{\infty } \le \frac{\tilde{\varepsilon }}{n} \le \varepsilon , \\&\nabla ^2f(x^k) + H(x^k) \sqrt{\varepsilon } \succeq \nabla ^2f(x^k) + H(x^k) \sqrt{\frac{M\tilde{\varepsilon }}{n}} \succeq 0 \;\; \text {on} \;\; \textsf{L}_0. \end{aligned}$$

In contrast, the second-order algorithm of [58] gives a slightly worse guarantee $\nabla f(x^{k})-{\textbf{A}}^{*}y^{k-1} > -\varepsilon$, and requires a larger number of iterations $O\left( \frac{ \max \{M,R\}^{7/2}(f(x^{0}) - f_{\min }(\textsf{X}))}{\varepsilon ^{3/2}}\right)$ (R denoting the $L_{\infty }$ upper bound on the diameter of the level set corresponding to $x^{0}$), albeit making similar assumptions to ours. We also can repeat the remarks from Sect. 4.4, arguing that our measure of complementarity $0\le \langle s^{k},x^{k}\rangle \le \varepsilon$ is stronger than $\max _{1\le i\le n}|x_{i}^{k}s_{i}^{k}|$ used in [58, 82]. Also, the works [65, 82] consider problem (Opt) without linear equality constraints.

Our complexity of $O(\varepsilon ^{-3/2})$ is better than the complexity bound $O(\varepsilon ^{-7/4})$ in [65] when their algorithm is specified to problem with linear constraint $x \in \bar{\textsf{K}}_{\text {NN}}$ instead of nonlinear inequality constraint $a(x)\ge 0$ with an appropriately smooth function $a: \mathbb {R}^n \rightarrow \mathbb {R}^m$. Furthermore, our algorithm is applicable to general cones admitting an efficient barrier setup, rather than only for $\bar{\textsf{K}}_{\text {NN}}$ as in the discussed previous works [58, 65, 82]. For more general cones we can not use the coupling $H(x)^{-\frac{1}{2}} = \textbf{X}$, which was seen to be very helpful in the derivations of the bound (74) above. Thus, to deal with general cones, we had to find and exploit suitable properties of the barrier class $\mathcal {H}_{\theta }(\textsf{K})$ and develop a new analysis technique that works for general, potentially non-symmetric, cones. Finally, our method does not rely on the trust-region techniques as in [58] that may slow down the convergence in practice since the radius of the trust region is no greater than $O(\sqrt{\varepsilon })$ leading to short steps.

5.3.2 Exploiting the structure of symmetric cones

We note that in (63) we can clearly observe the benefit of the use of $\theta$-SSB in our algorithm. When $\alpha _k=\frac{1}{2\zeta (x^k,v^k)}$, the per-iteration decrease of the potential is $\frac{L_k\Vert v^{k}\Vert ^{3}_{x^{k}}}{96 (\zeta (x^k,v^k))^2} \ge \frac{ \sqrt{\varepsilon L_k} \Vert v^{k}\Vert _{x^{k}}^2}{96 \sqrt{4\theta } (\zeta (x^k,v^k))^2}$ which may be large if $\zeta (x^k,v^k)=\sigma _{x^k}(-v^k) \ll \Vert v^{k}\Vert _{x^{k}}$.

5.3.3 The role of the penalty parameter

Next, we discuss more explicitly, how the algorithm and complexity bounds depend on the parameter $\mu$. The first observation is that from (69), to guarantee that $s^{k} \in \textsf{K}^{*}$, we need the stopping criterion to be $\Vert v^{k-1}\Vert _{x^{k-1}} < \Delta _{k-1}= \sqrt{\mu /L_{k-1}}$, which by (70) leads to the error $4 \mu \theta$ in the complementarity conditions and by (71) leads to the error $\sqrt{\mu /\bar{M}}$ in the second-order condition. From the analysis following equation (63), we have that

$$\begin{aligned} K\frac{\mu ^{3/2}}{24 \sqrt{\bar{M}}} \le f(x^{0})-f_{\min }(\textsf{X})+\mu \theta . \end{aligned}$$

Whence, recalling that $\bar{M}=\max \{M,M_0\}$,

$$\begin{aligned} K \le 24(f(x^{0}) - f_{\min }(\textsf{X})+ \mu \theta ) \cdot \frac{\sqrt{2\max \{M,M_0\}}}{\mu ^{3/2}}. \end{aligned}$$

Thus, we see that after $O(\mu ^{-3/2})$ iterations the algorithm finds a $(4 \mu \theta ,\mu /\bar{M})$-2KKT point, and if $\mu \rightarrow 0$, we have convergence to a KKT point, but the complexity bound tends to infinity and becomes non-informative. At the same time, as it is seen from (55), when $\mu \rightarrow 0$, the algorithm resembles a cubic-regularized Newton method, but with the regularization with the cube of the local norm. We also see from the above explicit expressions in terms of $\mu$ that the design of the algorithm requires careful balance between the desired accuracy of the approximate KKT point expressed mainly by the complementarity conditions, stopping criterion, and complexity. Moreover, the step-size must be selected carefully to ensure the feasibility of the iterates. This is also in contrast to the cubic-regularized Newton’s method where one can always take the step-size 1.

5.4 Anytime convergence via restarting ${{\,\mathrm{\textbf{SAHBA}}\,}}$

Similarly to the restarted FAHBA (Algorithm 2), we can obtain anytime convergence with a similar complexity as that of SAHBA by invoking a restarted method that uses SAHBA as an inner procedure. We fix $\varepsilon _{0}>0$ and select the starting point $x_0^{0}$ as a $4\theta$-analytic center of $\textsf{X}$ in the sense of Eq. (21). In epoch $i\ge 0$ we generate a sequence $\{x_{i}^{k}\}_{k=0}^{K_{i}}$ by calling ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu _{i},\varepsilon _{i},M_0^{(i)},x^{0}_{i})$ with $\mu _{i}=\frac{\varepsilon _{i}}{4\theta }$ until the stopping condition is reached. We know that this inner procedure terminates after at most $\mathbb {K}_{II}(\varepsilon _{i},x^{0}_{i})$ iterations. We store the values $x^{K_{i}}_{i}$ and $M_{K_{i}}^{(i)}$, and set $x_{i+1}^{0}\equiv x^{K_{i}}_{i}$, as well as $M_{0}^{(i+1)}\equiv M_{K_{i}}^{(i)}/2$. Updating the parameters to $\mu _{i+1}$ and $\varepsilon _{i+1}$, we restart by calling procedure ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu _{i+1},\varepsilon _{i+1},M_0^{(i+1)},x^{0}_{i+1})$ anew. This is formalized in Algorithm 4.

Algorithm 4

Restarting ${{\,\mathrm{\textbf{SAHBA}}\,}}$

Theorem 4

Let Assumptions 1, 2, 4 hold. Then, for any $\varepsilon \in (0,\varepsilon _0)$, Algorithm 4 finds an $(\varepsilon ,\frac{\max \{M,M_0^{(0)}\}\varepsilon }{8\theta })$-2KKT point for problem (Opt) in the sense of Definition 5 after no more than $I(\varepsilon )=\lceil \log _{2}(\varepsilon _{0}/\varepsilon )\rceil +1$ restarts and at most $\lceil {300}(f(x^{0})-f_{\min }(\textsf{X})+\varepsilon _0)\theta ^{3/2}\varepsilon ^{-3/2}\sqrt{2\max \{M,M_0^{(0)}\}}\rceil$ iterations of ${{\,\mathrm{\textbf{SAHBA}}\,}}$.

Proof

Let us consider a restart $i \ge 0$ and mimic the proof of Theorem 3 with the substitution $\varepsilon \rightarrow \varepsilon _i$, $\mu \rightarrow \mu _i = \varepsilon _i/(4\theta )$, $M_0 \rightarrow M_0^{(i)}=\hat{M}_{i-1}/2$, $\underline{L} = 144 \varepsilon \rightarrow \underline{L}_i = 144 \varepsilon _i$, $\bar{M}=\max \{M,M_0\} \rightarrow \bar{M}_i=\max \{M,M_0^{(i)}\}$, $x^0 \rightarrow x^{0}_{i}=\hat{x}_{i-1}$. Note that $M_0^{(i)} \ge 144 \varepsilon _i=\underline{L}_i$ for $i\ge 0$. We verify this via induction. By construction $M_0^{(0)}\ge 144 \varepsilon _0$. Assume the bound holds for some $i\ge 1$. Then, $M_0^{(i+1)}=M_{K_{i}}^{(i)}/2=\max \{L_{K_{i}-1}^{(i)}/2,\underline{L}_{i}\}/2\ge 144 \varepsilon _{i}/2=144 \varepsilon _{i+1}$, where we used the induction hypothesis and the definition of the sequence $\varepsilon _{i}$.

Let $K_i$ be the last iteration of ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu _{i},\varepsilon _i,M_0^{(i)},x^{0}_{i})$ meaning that the stopping criterion does not hold at the inner $K_i$ iterations $k=0,\ldots ,K_i-1$. From the analysis following Eq. (64), we obtain

$$\begin{aligned} K_i \frac{\varepsilon _i^{3/2}}{192 \theta ^{3/2} \sqrt{2\bar{M}_i}} \le F_{\mu _i}(x^{0}_i)-F_{\mu _i}(x^{K_i}_i). \end{aligned}$$

(75)

Using that $\mu _i$ is a decreasing sequence and $x_{0}^{0}$ is a $4\theta$-analytic center, we see

$$\begin{aligned} F_{\mu _{i+1}}(x^{0}_{i+1})&=F_{\mu _{i+1}}(x^{K_i}_{i})=f(x^{K_i}_{i}) + \mu _{i+1} h(x^{K_i}_{i})=F_{\mu _{i}}(x^{K_i}_{i}) + (\mu _{i+1} - \mu _{i}) h(x^{K_i}_{i}) \nonumber \\&{\mathop {\le }\limits ^{\tiny (21)}} F_{\mu _{i}}(x^{K_i}_{i}) + (\mu _{i+1} - \mu _{i}) (h(x_0^0)-4\theta )\nonumber \\&{\mathop {\le }\limits ^{\tiny (75)}}F_{\mu _i}(x^{0}_i)-K_i \frac{\varepsilon _i^{3/2}}{192 \theta ^{3/2} \sqrt{2\bar{M}_i} } + (\mu _{i+1} - \mu _{i}) (h(x_0^0)-4\theta ). \end{aligned}$$

(76)

Let $I\equiv I(\varepsilon )=\lceil \log _2 \frac{\varepsilon _0}{\varepsilon } \rceil +1$. By Theorem 3 applied to the restart $I-1$, we see that ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu _{I-1},\varepsilon _{I-1},M_0^{(I-1)},x^{0}_{I-1})$ outputs an $(\varepsilon _{I-1},\frac{\bar{M}_{I-1}\varepsilon _{I-1}}{8\theta })$-2KKT point for problem (Opt) in the sense of Definition 5. Since $\varepsilon _{I-1}\le \varepsilon$ and, for all $i\ge 1$,

$$\begin{aligned} \bar{M}_i&= \max \{M,M_0^{(i)}\} = \max \{M,\hat{M}_{i-1}/2\} = \max \{M,M_{K_{i-1}}^{(i-1)}/2\} \nonumber \\&= \max \{M,\max \{L_{K_{i-1}-1}^{(i-1)}/2,\underline{L}_{i-1}\}/2\} \nonumber \\&\le \max \{M,\max \{\bar{M}_{i-1},M_0^{(i-1)}\}/2\} \le \max \{M,\bar{M}_{i-1}\} \nonumber \\&\le ... \le \max \{M,\bar{M}_{0}\} \le \max \{M,M_0^{(0)}\}, \end{aligned}$$

(77)

it follows that actually we generate an $(\varepsilon ,\frac{\max \{M,M_{0}^{(0)}\}\varepsilon }{8\theta })$-2KKT point. Summing inequalities (76) for all the performed restarts $i=0,\ldots ,I-1$ and rearranging the terms, we obtain

$$\begin{aligned}&\sum _{i=0}^{I-1} K_i \frac{\varepsilon _i^{3/2}}{192 \theta ^{3/2} \sqrt{2\bar{M}_i} } \le F_{\mu _0}(x^{0}_0) - F_{\mu _{I}}(x^{0}_{I}) + (\mu _{I} - \mu _{0}) (h(x_0^0)-4\theta )\\&\quad =f(x^{0}_0) + \mu _0 h(x^{0}_0)- f(x^{0}_{I}) - \mu _{I}h(x^{0}_{I}) + (\mu _{I} - \mu _{0}) (h(x_0^0)-4\theta ) \nonumber \\&{\mathop {\le }\limits ^{\tiny (21)}} f(x^{0}_0) - f_{\min }(\textsf{X}) + \mu _0 h(x^{0}_0) - \mu _{I}h(x^{0}_{0}) + 4\mu _{I} \theta + (\mu _{I} - \mu _{0}) (h(x_0^0)-4\theta ) \nonumber \\&\quad \le f(x^{0}_0) - f_{\min }(\textsf{X}) + 4\mu _0 \theta = f(x^{0}_0) - f_{\min }(\textsf{X}) + \varepsilon _0, \end{aligned}$$

where in the last steps we used the coupling $\mu _{0}=\varepsilon _{0}/\theta$. From this inequality, using (77), we obtain

$$\begin{aligned} K_i \le (f(x^{0}) - f_{\min }(\textsf{X})+ \varepsilon _0) \cdot \frac{192\theta ^{3/2}\sqrt{2\bar{M}_i}}{\varepsilon _i^{3/2}} \le \frac{C}{\varepsilon _i^{3/2}}, \end{aligned}$$

where $C \equiv 192(f(x^{0})-f_{\min }(\textsf{X})+\varepsilon _0)\theta ^{3/2}\sqrt{2\max \{M,M_0^{(0)}\}}$. Finally, we obtain that the total number of iterations of procedures ${{\,\mathrm{\textbf{SAHBA}}\,}}(\mu _{i},\varepsilon _{i},M_0^{(i)},x_{i}^{0}),0\le i \le I-1$, to reach accuracy $\varepsilon$ is at most

$$\begin{aligned} \sum _{i=0}^{I-1}K_{i}&\le \sum _{i=0}^{I-1} \frac{C}{\varepsilon _i^{3/2}} \le \frac{C}{\varepsilon _0^{3/2}} \sum _{i=0}^{I-1} (2^{3/2})^i \\&\le \frac{C}{\varepsilon _0^{3/2}} \cdot \frac{2^{3/2\cdot ({1}+\log _2(\frac{\varepsilon _0}{\varepsilon }))}-1}{2^{3/2}-1}\le \frac{{2^{3/2}}C}{(\sqrt{8}-1)\varepsilon ^{3/2}}\\&<\frac{{300}(f(x^{0})-f_{\min }(\textsf{X})+\varepsilon _0)\theta ^{3/2}\sqrt{2\max \{M,M_0^{(0)}\}}}{\varepsilon ^{3/2}}. \end{aligned}$$

$\square$

6 Conclusion

We derived Hessian barrier algorithms based on first- and second-order information on the objective f. We performed a detailed analysis of their worst-case iteration complexity in order to find a suitably defined approximate KKT point. Under weak regularity assumptions and in the presence of general conic constraints, our Hessian barrier algorithms share the best known complexity rates in the literature for first- and second-order approximate KKT points. Our methods are characterized by a decomposition approach of the feasible set which leads to numerically efficient subproblems at each their iteration. Several open questions for the future remain. First, our iterations assume that the subproblems are solved exactly, and for practical reasons, this should be relaxed. Second, we mentioned that ${{\,\mathrm{\textbf{FAHBA}}\,}}$ can be interpreted as a discretization of the Hessian-barrier gradient system [4], but the exact relationship is not explored yet. This, however, could be an important step towards understanding acceleration techniques of ${{\,\mathrm{\textbf{FAHBA}}\,}}$, akin to an accelerated version of the cubic regularized Newton method. Furthermore, the cubic-regularized version has no corresponding continuous-time version yet. It will be very interesting to investigate this question further. Additionally, the question of convergence of the trajectory $(x^{k})_{k\ge 0}$ generated by either scheme is open. Another interesting direction for future research would be to allow for higher-order Taylor expansions in the subproblems in order to boost convergence speed further, similar to [28].

Appendices

Appendix A: More results on self-concordant barriers

In this appendix we collect important auxiliary results about logarithmically homogeneous barriers and their limit properties along primal sequences that converge to the boundary.

We denote by $\mathcal {L}(\mathbb {E},\mathbb {E}^{*})$ the set of linear operators from $\mathbb {E}$ to $\mathbb {E}^{*}$. Given $h\in \mathcal {H}_{\theta }(\textsf{K})$, we define the operator $D^{2}h:\textsf{K}\rightarrow \mathcal {L}(\mathbb {E},\mathbb {E}^{*})$, by the bilinear form $D^{2}h(x)[u,v]$ for all $x\in \textsf{K}$ and for all $(u,v)\in \mathbb {E}.$ Fixing the coordinate system ${\textbf{B}}$, we can define a matrix representation of the operator $D^{2}h(x)$ as follows. First, by the Riesz-Fréchet representation theorem, there exists a unique element in $\mathbb {E}^{*}$, denoted by H(x)u such that $D^{2}h(x)[u,v]=\langle H(x)u,v\rangle$ for all $v\in \mathbb {E}$. H(x) is a linear operator, so that $H(x)u\in \mathbb {E}^{*}$ for all $u\in \mathbb {E}$. Let $u,v\in \mathbb {E}$ with $u={\textbf{B}}\xi$ and $v={\textbf{B}}\alpha$ and $\xi ,\alpha \in \mathbb {R}^{p}$. Then, using the bilinearity, we see that for all $x\in \textsf{K}$

$$\begin{aligned} D^{2}h(x)[u,v]&=D^{2}h(x)[u,\sum _{j=1}^{n}b_{j}\alpha _{j}]=\sum _{j=1}^{n} \alpha _{j}D^{2}h(x)[u,b_{j}]\\&=\sum _{i,j=1}^{n}\xi _{i}\alpha _{j}D^{2}h(x)[b_{i},b_{j}]. \end{aligned}$$

Hence, $\langle H(x)b_{i},b_{j}\rangle =D^{2}h(x)[b_{i},b_{j}]$ for all $i,j=1,\ldots ,p.$ Therefore,

$$\begin{aligned} D^{2}h(x)[u,v]&=\langle H(x)u,v\rangle =\langle H(x){\textbf{B}}\xi ,{\textbf{B}}\alpha \rangle =\langle {\textbf{B}}^{*}H(x){\textbf{B}}\xi ,\alpha \rangle _{\mathbb {R}^{p}}. \end{aligned}$$

This gives $\textbf{H}^{{\textbf{B}}}_{x}\triangleq {\textbf{B}}^{*}H(x){\textbf{B}}:\mathbb {R}^{p}\rightarrow \mathbb {R}^{p}$ as a matrix representation of the linear operator H(x) in terms of the primal basis ${\textbf{B}}$ on $\mathbb {E}$ and the dual basis ${\textbf{B}}^{*}$ on $\mathbb {E}^{*}$. From now on we identify $\mathbb {E}^{*}$ with $\mathbb {E}$ so that $H(x)\in \mathcal {L}(\mathbb {E};\mathbb {E})\triangleq \mathcal {L}(\mathbb {E})$. Since H(x) is a positive definite operator, there exists an inverse $[H(x)]^{-1}:\mathbb {E}\rightarrow \mathbb {E}$ so that $H(x)\circ [H(x)]^{-1}=[H(x)]^{-1}\circ H(x)={{\,\textrm{Id}\,}}_{\mathbb {E}}$. $[H(x)]^{-1}$ is again a positive definite linear operator and thus admits a unique square root $R_{x}:\mathbb {E}\rightarrow \mathbb {E}$ satisfying $[H(x)]^{-1}=R_{x}\circ R_{x}$. We denote this linear operator as $R_{x}=[H(x)]^{-1/2}\in \mathcal {L}(\mathbb {E})$.

The dual cone $\bar{\textsf{K}}^{*}$ is defined as $\bar{\textsf{K}}^{*}\triangleq \{s\in \mathbb {E}^{*}\vert \langle s,x\rangle \ge 0\;\forall x\in \bar{\textsf{K}}\}$, and the dual barrier is defined as $h_{*}(s)\triangleq \sup _{x\in \textsf{K}}\{\langle -s,x\rangle -h(x)\}$ for $s\in \bar{\textsf{K}}^{*}$. From [83, Theorem 3.3.1] we know that if $h\in \mathcal {H}_{\theta }(\textsf{K})$, then $h_{*}\in \mathcal {H}_{\theta }(\textsf{K}^{*})$. Moreover,

$$\begin{aligned}&x \in \textsf{K}\Rightarrow -\nabla h(x) \in {{\,\textrm{int}\,}}(\textsf{K}^{*}), \end{aligned}$$

(78)

$$\begin{aligned}&s=-\nabla h(x)\iff \nabla h_{*}(s)=-x\Rightarrow \nabla ^{2}h_{*}(s)=[\nabla ^{2}h(x)]^{-1}. \end{aligned}$$

(79)

We also use the following properties listed in [76, Lemma 5.4.3, Theorem 5.3.7].

Proposition 6

Let $h\in \mathcal {H}_{\theta }(\textsf{K})$, $x\in \textsf{K}$, $t>0$ and $H(x)=\nabla ^{2}h(x)$. Then,

$$\begin{aligned}&\nabla ^2 h(t x) = t^{-2} \nabla ^2 h(x), \end{aligned}$$

(80)

$$\begin{aligned}&-\langle \nabla h(x),x\rangle = \theta , \end{aligned}$$

(81)

$$\begin{aligned}&\Vert x\Vert _{x}^2 = \langle H(x) x ,x \rangle = \theta , \quad \langle \nabla h(x), [H(x)]^{-1}\nabla h(x) \rangle = \theta . \end{aligned}$$

(82)

$$\begin{aligned}&{\langle \nabla h(x),y-x\rangle <\theta \qquad \forall y\in \textsf{K}} \end{aligned}$$

(83)

The next fact is essentially [4, Lemma 4.2]. We give the simple proof here to be self-contained.

Lemma 4

Let ${h\in \mathcal {H}_{\theta }(\textsf{K})}$. Consider a sequence ${(x_{k})_{k\ge 1}\subset \textsf{K}}$ such that ${x_{k}\rightarrow \bar{x}\in {{\,\textrm{bd}\,}}(\textsf{K})}$. Then all accumulation points of ${\left( \frac{\nabla h(x_{k})}{\Vert \nabla h(x_{k})\Vert }\right) _{k\ge 1}}$ are contained in ${{{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(\bar{x})}$.

Proof

By convexity of h, we have ${\langle \nabla h(x_{k})-\nabla h(x),x_{k}-x\rangle \ge 0}$ for all ${x\in \textsf{K}}$. The sequence ${(\Vert \nabla h(x_{k})\Vert ^{-1}\nabla h(x_{k}))_{k\ge 1}}$ is bounded and thus converging subsequences exist. Let $\xi$ denote an accumulation point. After eventual relabeling, let us assume ${\Vert \nabla h(x_{k})\Vert ^{-1}\nabla h(x_{k})\rightarrow \xi }$. Then, dividing the last inner product by ${\Vert \nabla h(x_{k})\Vert }$ and letting ${k\rightarrow \infty }$, we get ${\langle \xi ,\bar{x}-x\rangle \ge 0}$ for all ${x\in \textsf{K}}$. Hence, ${\xi \in {{\,\mathrm{\textsf{NC}}\,}}_{\bar{\textsf{K}}}(\bar{x})}$. Since ${\xi }$ is an arbitrary accumulation point, the claim follows. $\square$

Lemma 5

Define the mapping $\texttt{e}_{*}:\mathbb {E}\rightarrow [0,\infty ]$ by

$$\begin{aligned} \texttt{e}_{*}(v)\triangleq \sup _{x\in \textsf{K}:{\Vert x\Vert }=1}\Vert v\Vert _{x}^{*}. \end{aligned}$$

Then ${{\,\textrm{dom}\,}}(\texttt{e}_{*})=\mathbb {E}$.

Proof

Let ${x\in \textsf{K}}$ satisfy ${\Vert x\Vert =1}$ and ${y\in \textsf{K}}$ be arbitrary. Denote ${r_{1}\triangleq \Vert x-y\Vert }$. There exists $r_{2}>0$ such that the open ball with center y and radius $r_{2}$ is contained in $\textsf{K}$. By convexity, all points on the line $x+\alpha (y-x)$ are therefore in ${\textsf{K}}$, provided that ${\alpha \in [0,\frac{r_{1}+r_{2}}{r_{1}}]}$. Define the Minkowski functional of ${\bar{\textsf{K}}}$ with pole y as

$$\begin{aligned} \pi _{y}(x)\triangleq \inf \left\{ t\ge 0\vert y+\frac{1}{t}(x-y)\in \bar{\textsf{K}}\right\} . \end{aligned}$$

It follows

$$\begin{aligned} \pi _{x}(y)\le \frac{r_{1}}{r_{1}+r_{2}}\le \frac{1+\Vert y\Vert }{1+\Vert y\Vert +r_{2}}\triangleq \texttt{a}(y). \end{aligned}$$

This, together with [78, Proposition 2.3.2], yields the bound

$$\begin{aligned} \Vert v\Vert _{y}\le \frac{1+3\theta }{1-\pi _{x}(y)}\Vert v\Vert _{x}\le \frac{1+3\theta }{1-\texttt{a}(y)}\Vert v\Vert _{x}. \end{aligned}$$

Hence, $H(x)\left( \frac{1+3\theta }{1-\texttt{a}(y)}\right) ^{2}\succeq H(y)$, and therefore $[H(y)]^{-1}\left( \frac{1+3\theta }{1-\texttt{a}(y)}\right) ^{2}\succeq [H(x)]^{-1}$. We conclude

$$\begin{aligned} \Vert v\Vert ^{*}_{x}\le \frac{1+3\theta }{1-\texttt{a}(y)}\Vert v\Vert ^{*}_{y}\qquad \forall y\in \textsf{K}. \end{aligned}$$

Therefore, fixing some $y\in \textsf{K}$, we have $\texttt{e}_{*}(v)=\sup _{x \in \textsf{K}:\Vert x\Vert =1}\Vert v\Vert ^{*}_{x}<\frac{1+3\theta }{1-\texttt{a}(y)}\Vert v\Vert ^{*}_{y}<\infty$. $\square$

Lemma 6

Let $h\in \mathcal {H}_{\theta }(\textsf{K})$. For all $(x,v)\in \textsf{K}\times \mathbb {E}$ we have

$$\begin{aligned} \Vert v\Vert ^{*}_{x}\le \Vert x\Vert \cdot \texttt{e}_{*}(v). \end{aligned}$$

Proof

If $h\in \mathcal {H}_{\theta }(\textsf{K})$, then by (80)

$$\begin{aligned} t^{2}H(tx)=H(x)\qquad \forall x\in \textsf{K},t>0. \end{aligned}$$

This gives $t^{2}H(tx)\circ H(x)^{-1}=H(x)^{-1}\circ (t^{2}H(tx))={{\,\textrm{Id}\,}}_{\mathbb {E}}$. Hence,

$$\begin{aligned}{}[t^{2}H(tx)]^{-1}=t^{-2}[H(tx)]^{-1}=[H(x)]^{-1}. \end{aligned}$$

Choosing $t=1/\Vert x\Vert$ gives $\Vert x\Vert ^{2}[H(x/\Vert x\Vert )]^{-1}=[H(x)]^{-1}$ for all $x\in \textsf{K}$. Hence, for all $v\in \mathbb {E}$, we get

$$\begin{aligned} \Vert v\Vert ^{*}_{x}=\Vert x\Vert \cdot \Vert v\Vert ^{*}_{x/\Vert x\Vert }\le \Vert x\Vert \sup _{d:\Vert d\Vert =1}\Vert v\Vert ^{*}_{d}\equiv \Vert x\Vert \texttt{e}_{*}(v) \qquad \forall v\in \mathbb {E}. \end{aligned}$$

$\square$

Note that

$$\begin{aligned} \Vert R_{x}v\Vert _{x}^{2}=\langle H(x)R_{x}v,R_{x}v\rangle =\langle v,v\rangle =\Vert v\Vert ^{2}\qquad \forall (x,v)\in \textsf{K}\times \mathbb {E}. \end{aligned}$$

We use the operator $R_{x}$ to define a mapping

$$\begin{aligned} \tau :\textsf{K}\times \mathbb {E}\rightarrow \mathbb {E},(x,v)\mapsto \tau (x,v)\triangleq x-\frac{1}{\Vert v\Vert +1}R_{x}v. \end{aligned}$$

In geometric terms, we can think of $\tau (x,v)$ as a retraction acting on the Riemannian manifold $(\textsf{K},\Vert \cdot \Vert _{x})$. This is the content of the next result.

Lemma 7

For all $(x,v)\in \textsf{K}\times \mathbb {E}$ we have $\tau (x,v)\in \textsf{K}$.

Proof

We use the Dikin ellipsoid condition (Lemma 1) for viability:

$$\begin{aligned} \Vert (x-\frac{1}{\Vert v\Vert +1}R_{x}v)-x\Vert _{x}=\frac{1}{\Vert v\Vert +1}\Vert R_{x}v\Vert _{x}=\frac{\Vert v\Vert }{\Vert v\Vert +1}<1. \end{aligned}$$

$\square$

We next show that the operator $R_{x}$ can be extended to the boundary of the cone $\textsf{K}$. Recall that we identify the dual space $\mathbb {E}^{*}$ with $\mathbb {E}$. Lemma 6 states that $\Vert R_{x}v\Vert \le \Vert x\Vert \cdot \texttt{e}_{*}(v)$ for all $x\in \textsf{K}$ and $v\in \mathbb {E}$. This shows that the mapping $\textsf{K}\ni x\mapsto R_{x}v\in \mathbb {E}$ is locally bounded. This allows us to define an extension of the domain of $x\mapsto R_{x}$ to $\bar{\textsf{K}}=\textsf{K}\cup {{\,\textrm{bd}\,}}(\textsf{K})$ via a limiting procedure. Let $(x_{n})_{n\ge 1}\subset \textsf{K}$ with $x_{n}\rightarrow \bar{x}\in {{\,\textrm{bd}\,}}(\textsf{K})$, and $v\in \mathbb {E}$ arbitrary. Let $\{b_{1},\ldots ,b_{p}\}$ be a basis of $\mathbb {E}$, so that any vector $v\in \mathbb {E}$ admits a unique representation $v=\sum _{i}\alpha _{i}b_{i}$ for some scalars $\alpha _{i}\in \mathbb {R}$. Then, by linearity, we have

$$\begin{aligned} R_{x_{n}}v=\sum _{i=1}^{p}\alpha _{i}R_{x_{n}}b_{i}. \end{aligned}$$

Since $R_{x_{n}}b_{i}\le \Vert x_{n}\Vert \texttt{e}_{*}(b_{i})$ for all i, we can extract a converging subsequence $R_{x_{n_{k}}}b_{i}\rightarrow Rb_{i}$ as $k\rightarrow \infty$. Via a diagonal procedure, we obtain another subsequence $(x_{n_{j}})_{j\ge 1}$ in order to construct a linear operator $R:\mathbb {E}\rightarrow \mathbb {E}$ satisfying

$$\begin{aligned} R_{x_{n_{j}}}v=\sum _{i}\alpha _{i}R_{x_{n_{j}}}b_{i}\rightarrow \sum _{i}\alpha _{i}Rb_{i}=Rv \end{aligned}$$

as $j\rightarrow \infty$ for all $v\in \mathbb {E}$.

Remark 10

If $\textsf{K}$ is a symmetric cone, it is well-known that $\lim _{n\rightarrow \infty }R_{x_{n}}$ exists for $x_{n}\rightarrow \bar{x}\in {{\,\textrm{bd}\,}}(\textsf{K})$ and is a well-defined linear operator [73].

The next result is concerned with the semi-continuity of the multi-valued mapping $x\mapsto \mathcal {T}_{x}$, defined in (16). The discussion following that equation showed that this set can be equivalently represented as $\mathcal {T}_{x}=\{R_{x}u\vert {\textbf{A}}R_{x}u=0,\Vert u\Vert <1\}.$

Proposition 7

Let $h\in \mathcal {H}_{\theta }(\textsf{K})$, $\bar{x}\in {{\,\textrm{bd}\,}}(\textsf{K})$, and ${\textbf{A}}\bar{x}=b$. Let $(x_{n})_{n\ge 1}\subset \textsf{K}$ such that $x_{n}\rightarrow \bar{x}$ and $v_{n}\in \mathcal {T}_{x_{n}}$ be a corresponding sequence of direction vectors. Then, the sequence $p_{n}\triangleq x_{n}+v_{n}$ is contained in $\textsf{K}$ and converges to a limit point $p\in \bar{\textsf{K}}$. Moreover, ${\textbf{A}}p=b$.

Proof

For all $n\ge 1$, we have $v_{n}=R_{x_{n}}u_{n}$ for some sequence $(u_{n})_{n\ge 1}\subset \mathbb {B}_{\mathbb {E}}\triangleq \{u\in \mathbb {E}\vert \Vert u\Vert <1\}$, and ${\textbf{A}}v_{n}=0$ for all $n\ge 1$. Therefore, $\Vert p_{n}-x_{n}\Vert _{x_{n}}=\Vert v_{n}\Vert _{x_{n}}=\Vert u_{n}\Vert <1$, which shows $p_{n}\in \textsf{K}$ for all $n\ge 1$ (cf. Lemma 1). Let $(u_{n_{j}})_{j\ge 1}$ be a converging subsequence and denote $v_{n_{j}}=R_{x_{n_{j}}}u_{n_{j}}$ the corresponding subsequence in $\mathcal {T}_{x_{n_{j}}}$. Since $\Vert v_{n_{j}}\Vert =\Vert R_{x_{n_{j}}}u_{n_{j}}\Vert \le \Vert x_{n_{j}}\Vert \texttt{e}_{*}(u_{n_{j}})$, taking eventually a further subsequence (we omit the relabeling), we can assume that $(v_{n_{j}})_{j\ge 1}$ converges to a limit v. This limit point must obviously satisfy the condition ${\textbf{A}}v=0$ and $\lim _{j\rightarrow \infty }\Vert v_{n_{j}}\Vert _{x_{n_{j}}}=\lim _{j\rightarrow \infty }\Vert u_{n_{j}}\Vert \le 1$. Hence, $\lim _{j\rightarrow \infty }p_{n_{j}}=p\triangleq \bar{x}+v$ has the properties ${\textbf{A}}p={\textbf{A}}\bar{x}=b$ and $p\in \bar{\textsf{K}}$. $\square$

Deriving second-order optimality conditions for (Opt) is based on a perturbation argument. To define admissible perturbations at boundary points $\bar{x}\in {{\,\textrm{bd}\,}}(\textsf{K})$, we can use Proposition 7 that motivates the definition

$$\begin{aligned}{} & {} \mathcal {T}_{\bar{x}}\triangleq \{v\in \mathbb {E}\vert \exists x_{n}{\mathop {\rightarrow }\limits ^{\textsf{X}}}\bar{x},(u_{n})_{n {\ge 1}}\subset \mathbb {B}_{\mathbb {E}}\text { s.t. }v=\lim _{n\rightarrow \infty }R_{x_{n}}u_{n}\text { and }{\textbf{A}}R_{x_{n}}u_{n}\nonumber \\{} & {} \quad = 0\text { for all }n\ge 1\}. \end{aligned}$$

(84)

This definition is a natural extension of the corresponding set already defined at interior points in (16). Indeed, if $\bar{x}\in \textsf{K}\cap \textsf{L}=\textsf{X}$ is taken as the base point in the construction of the variations in $\mathcal {T}_{\bar{x}}$, we can take the constant sequences $x_{n}\equiv {\bar{x}}$ and $u_{n}\equiv u\in \mathbb {B}_{\mathbb {E}}$ in (84), and obtain the definition (16).

Appendix B: Optimality conditions

Suppose $x^{*}$ is a local minimizer of problem (Opt) and f is continuously differentiable at $x^{*}$. Assumption 1 guarantees that there exists a Lagrange multiplier $y^{*}\in \mathbb {R}^{m}$ such that the inclusion (8) holds. The following exact optimality conditions for the model problem (Opt) are proved in [61].

Theorem 5

[61, Theorem 3] Let $x^{*}$ be a local solution of problem (Opt) and let R be a limit operator of the sequence $(R_{x_{n}})_{n {\ge 1}}$ obtained by $x_{n}\rightarrow x^{*}$. Suppose that f is continuously differentiable at $x^{*}$. Then there exists a Lagrangian multiplier $y^{*}\in \mathbb {R}^{m}$ such that

$$\begin{aligned}&\nabla f(x^{*})-{\textbf{A}}^{*}y^{*}\in \bar{\textsf{K}}^{*}, \end{aligned}$$

(85)

$$\begin{aligned}&R(\nabla f(x^{*})-{\textbf{A}}^{*}y^{*})=0 . \end{aligned}$$

(86)

[61, Proposition 1] proves that the conditions in Theorem 5 are equivalent to $\nabla f(x^{*})-{\textbf{A}}^{*}y^{*}\in \bar{\textsf{K}}^{*},\text { and }\langle \nabla f(x^{*})-{\textbf{A}}^{*}y^{*},x^{*}\rangle =0.$

Theorem 6

[61, Theorem 4] Let $x^{*}$ be a local minimizer of problem (Opt) and R be a limit operator of the sequence $(R_{x_{n}})_{n {\ge 1}}$ obtained by $x_{n}\rightarrow x^{*}$. Suppose that f is twice continuously differentiable at $x^{*}$. Then there exists a Lagrangian multiplier $y^{*}\in \mathbb {R}^{m}$ such that (85) and (86) hold and additionally

$$\begin{aligned} \langle \nabla ^{2}f(x^{*})v,v\rangle \ge 0\quad \forall v\in \mathcal {T}_{x^{*}}. \end{aligned}$$

The set $\mathcal {T}_{x^{*}}$ for $x^{*}\in {{\,\textrm{bd}\,}}(\bar{\textsf{X}})$ is defined in (84).

Appendix C: Useful inequalities

Consider the cone $\textsf{K}_{\text {NN}}$ with the standard log-barrier $h(x)=-\sum _{i=1}^n \ln (x_i)$ which has Hessian $H(x)={{\,\textrm{diag}\,}}[x_{1}^{-2},\ldots ,x_{n}^{-2}]=\textbf{X}^{-2}$. Let $\textbf{V}={{\,\textrm{diag}\,}}[v_{1},\ldots ,v_{n}]={{\,\textrm{diag}\,}}(v)$, $z \in \mathbb {R}^n$, and $x\in \textsf{K}_{\text {NN}}$. Then,

$$\begin{aligned}&\Vert \textbf{V}z\Vert _{\infty } \le \Vert \textbf{V}z\Vert \le \Vert v\Vert _{x} \cdot \Vert z\Vert _x^*, \end{aligned}$$

(87)

$$\begin{aligned}&\Vert \textbf{V}z\Vert _{\infty } \le \Vert v\Vert _{x} \cdot \Vert \textbf{X}z\Vert _{\infty }. \end{aligned}$$

(88)

The first inequality in (87) is trivial. Let us prove the second inequality. Indeed, we have

$$\begin{aligned}&\Vert \textbf{V}z\Vert ^2 = \sum _{i=1}^n (v_iz_i)^2 = \sum _{i=1}^n (v_i/x_i)^2\cdot (x_iz_i)^2 \le \left( \sum _{i=1}^n (v_i/x_i)^2 \right) \\&\quad \cdot \left( \sum _{i=1}^n(x_iz_i)^2 \right) = \langle H(x)v,v\rangle \cdot \langle [H(x)]^{-1}z,z\rangle = \Vert v\Vert _{x}^2 \cdot (\Vert z\Vert _x^*)^2, \end{aligned}$$

which finishes the proof of (87). For the inequality (88), we have, denoting by v/x the componentwise division of v by x,

$$\begin{aligned}&\Vert \textbf{V}z\Vert _{\infty } = \Vert \textbf{V}\textbf{X}^{-1}\textbf{X}z\Vert _{\infty } \le \Vert v/x\Vert _{\infty } \cdot \Vert \textbf{X}z\Vert _{\infty } \le \Vert v/x\Vert \\&\quad \cdot \Vert \textbf{X}z\Vert _{\infty }= \Vert \textbf{X}^{-1}v\Vert \cdot \Vert \textbf{X}z\Vert _{\infty } = \Vert H(x)^{1/2}v\Vert \cdot \Vert \textbf{X}z\Vert _{\infty } = \Vert v\Vert _x \cdot \Vert \textbf{X}z\Vert _{\infty }. \end{aligned}$$