Strong substitutes: structural properties, and a new algorithm for competitive equilibrium prices

Abstract

We show the strong substitutes product-mix auction bidding language provides an intuitive and geometric interpretation of strong substitutes as Minkowski differences between sets that are easy to identify. We prove that competitive equilibrium prices for agents with strong substitutes preferences can be computed by minimizing the difference between two linear programs for the positive and the negative bids with suitably relaxed resource constraints. This also leads to a new algorithm for computing competitive equilibrium prices which is competitive with standard steepest descent algorithms in extensive experiments.

1 Introduction

This paper shows that for an important and widely-studied class of problems–those for which agents have strong substitutes valuations over multiple units of multiple differentiated goods–competitive-equilibrium prices can be found by considering two linear programs. Specifically, we relax resource constraints on both programs in the same way, and find the relaxation that minimizes the difference between the objectives of the two programs; the dual prices of one of these relaxed programs are competitive equilibrium prices. We derive this result by using the geometric representation of preferences provided by the Strong Substitutes Product-Mix Auction (SSPMA) bidding language. This then allows us to develop an efficient algorithm to find the competitive equilibrium prices when preferences are represented this way. Since, as we detail below, the SSPMA language is a natural way for agents to express their preferences, our algorithm is a practical way to find competitive equilibrium prices for strong substitutes.

Our paper also provides a novel algorithm to find the prices in an SSPMA, since these are prices that would be competitive equilibrium prices for the given aggregate supply if bidders had bid their actual values.¹ Participants in SSPMAs make bids that express “strong-substitutes” preferences for multiple units of multiple, differentiated, indivisible goods. Strong substitutes preferences are those that would be ordinary substitutes preferences if every unit of every good were treated as a separate good [35]. They are an extension of gross substitutes preferences [25] from single-unit to multi-unit, multi-item markets, and are equivalent to $M^\natural$-concavity [17, 37, 45]. They have many attractive properties. In particular, all agents having strong substitutes preferences is a sufficient condition for the existence of competitive equilibrium prices in markets with indivisible goods.

Furthermore, even though strong substitutes are a small subset of the set of all possible valuation functions of a bidder, they are practically relevant for various applications such as auctions used by the Bank of England [26, 28]. So a significant amount of theoretical literature has been devoted to markets where participants have these valuations [4, 8, 38, 41].

Importantly, valid bids in the SSPMA bidding language permits the specification of precisely the set of preferences that are strong substitutes, and indeed is the only language that is known to do this.² As we will see, it is also parsimonious, or “compact”, in that many valuations can be expressed using only a small number of simple bids.³ Finally, it expresses valuations in a natural way, which can be understood and analyzed geometrically; we show aggregate demand is the Minkowski difference between two easily identified demand sets.

1.1 The strong substitutes product-mix auction (SSPMA)

There is significant literature on computing competitive equilibria with strong substitutes valuations. See, for example, [4, 11, 13, 21, 25, 35, 38, 39, 41, 42].⁴ The interest in strong substitutes is due to the fact that it captures practically relevant valuations for indivisible goods, but the allocation problem can be solved in polynomial time and Walrasian competitive equilibrium prices always exist, which is not the case for general valuations [14].

Prior literature requires either value oracles for exponentially many bundles, or demand oracles. Demand oracles can be understood as indirect or iterative mechanisms, where bidders reveal their demand correspondence for a set of prices specified by the auctioneer. So in a large market with many goods that is organized as a sealed-bid auction, the auctioneer needs to perform an exponential number of value queries for each bidder before the allocation algorithm can be run. Such enumerative (XOR) bid languages are used in spectrum auctions, but can lead to “missing bids” problems, which can significantly affect prices, and also create efficiency losses [12].⁵

The SSPMA was developed by [26] for the Bank of England to provide liquidity to financial institutions by auctioning loans to them. The SSPMA is neither based on a value nor a demand oracle.⁶ A collection of bids specifies a large number of package values, which mitigates the missing bids problem. This type of preference elicitation permits efficient ways to compute Walrasian prices, and allows us to uncover new properties of strong substitutes valuations.

Each bidder makes a set of bids, each of which is a vector ${\mathbf {b}}$, incorporating an integer weight $w({\mathbf {b}})$. Each bidder’s set of bids is interpreted as specifying a quasi-linear utility function over multiple units of each of n goods plus money. A bid in which $w({\mathbf {b}}) > 0$ (a “positive” bid) is simply interpreted as a bid for up to, but not more than, $w({\mathbf {b}})$ units, in total, of the goods $i = 1, \ldots , n$, in which the expressed value of receiving $x_i$ units of good i is $x_i \cdot b_i$.

Example 1

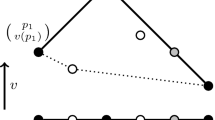
A bidder might be interested in 2 units, and be willing to pay up to price 2 for each unit of good 1, but only up to price 1 for each unit of good 2. These preferences can be implemented by a single bid ${\mathbf {b}} = (2,1)$ with $w({\mathbf {b}}) = 2$. Figure 1 shows how the bid ${\mathbf {b}}$ divides price space into three regions: for example, if the price vector ${\mathbf {p}} = (p_1,p_2)$ lies in the region labeled as “(2, 0) demanded” then, at this price vector, receiving the bundle (2, 0) maximizes the bidder’s utility among all feasible bundles. The black lines mark the borders at which the demanded bundle changes. If prices lie exactly on the boundary of two or more regions, then the set of demanded bundles is given by the discrete convex hull of the bundles demanded in the adjacent regions. For example, if ${\mathbf {p}} = (2,4)$, the bidder demands bundles (0, 0), (1, 0) or (2, 0).

Fig. 1

Example of using a single bid to represent preferences in a Product-Mix auction. The single bid with weight 2 implements the preferences of Example 1. The total demand generated by the bid is indicated in each region of price space

Fig. 2

Example of using positive and negative bids to represent preferences in a Product-Mix auction. The set of bids implements the preferences of Example 2. The sizes of the bids ($millions) are shown next to the black and white circles that represent the positive and negative bids, respectively. The total demand generated by the complete set of bids, ($millions of weak, $millions of strong), is indicated in each region of price space

Bids in which $w({\mathbf {b}}) < 0$ (“negative” bids) are interpreted as “cancellation” bids that cancel part of the demand created by positive bids. But this means that all bids can be treated by the auctioneer in exactly the same way: a bid is accepted whenever at least one of its prices exceeds the corresponding auction price and, if it is accepted, then it is allocated the good on which its price exceeds the corresponding auction price by most.⁷ The following example from [26, 27] demonstrates the potential usefulness of negative bids in the context of the Bank of England’s auctions, in which the different goods were “weak collateral” and “strong collateral”, and the prices were the interest rates that the winning bidders paid:⁸

Example 2

A bidder might be interested in $100 million of weak collateral (good 1) at up to a 7% interest rate, and $80 million of strong collateral (good 2) at up to a 5% interest rate. However, even if prices are high, the bidder wants an absolute minimum of $40 million (see Fig. 2). These preferences can be implemented by making all of the following four bids:

• I $100 million of weak at 7%.

• II $80 million of strong at 5%.

• III $40 million of {weak at maximum permitted bid OR strong at maximum permitted bid less 2%}.

• IV minus $40 million of {weak at 7% OR strong at 5%}.

Note that the bids lead to an arrangement of hyperplanes, at each of which the agent is indifferent among more than one bundle. Bids (I) and (II) together generate the demand shown in the three quadrants to the left of (7, 0) and/or below (0, 5), but would on their own imply zero demand in the top right quadrant. Adding the high positive bid, (III), at $(k, k - 2)$, in which k is the maximum permitted bid on either good (we assume k is large), would add demand of $40 million of weak everywhere above the $45\deg$ diagonal line through (2, 0), and $40 million of strong everywhere below this line; the negative bid, (IV), at (7, 5) then cancels this bid everywhere to the left of, and below, (7, 5).

Preferences of the kind illustrated in Example 2 are very natural for a liquidity-constrained bidder, but cannot be accurately represented without the use of a negative bid.⁹ However, with positive and negative bids, valid bids in the bidding language can precisely represent any “strong substitutes” preferences.¹⁰ Moreover, the way in which positive and negative bids define demand sets has a nice geometric interpretation as Minkowski differences, as we will show. And, importantly, as we discuss below, in practical settings expressing valuations with SSPMA bids is likely to be much more compact than listing valuations explicitly as assumed in [13] or subsequent literature. For all these reasons, the SSPMA is a natural choice for applications.

To make practical use of SSPMAs, however, requires that we can find competitive equilibrium prices among participants using the bid language.¹¹ That is, given the collection of the sets of bids made by all the participants, we need to be able to find a price vector at which any given quantity vector of goods would be exactly demanded if all the bids expressed participants’ actual preferences.

If all the bids are positive, the competitive equilibrium price vectors are just the shadow price vectors in the solution to a simple linear program, more specifically a network flow problem, in which the number of variables is linear in the number of bids and distinct goods. The reason is that competitive equilibrium maximizes social surplus in our setting, so the relevant linear program allocates the bids among participants to maximize the sum of their surpluses, subject to allocating exactly the available supply.¹² With negative bids, however, the allocation problem cannot be modeled with only a single linear program, and the computation of prices is then more challenging.

1.2 Our contribution

We study characteristics of strong substitutes by using the SSPMA language. First, we show that the positive and negative bids in the SSPMA allow us to interpret strong substitutes as Minkowski differences between sets that are easy to identify. This gives new insight into the geometric structure of strong substitutes, a valuation class that is difficult to characterize. We then illustrate the SSPMA language’s expressiveness using [40]’s notorious example of strong substitutes that other languages cannot represent. We also explain that the language is compact for realistic settings, since the bidder need not explicitly give a value for every bundle which it might be allocated.

Our main contribution is an equivalence result for different mathematical formulations of the pricing problem. We show that minimizing the difference between the maximum social surpluses attained by solving certain pairs of allocation problems–each of which is a simple problem–provides the information we need to compute the equilibrium prices. Specifically, the correct quantity of negative bids, s, accepted by the auctioneer minimizes the difference between the objective function of the linear program that would be solved to allocate the available supply increased by s if only the positive bids were available (we call this the “positive program”), and the objective of a corresponding linear program that would be solved to allocate a quantity of s using only the negative bids (the “negative program”). Moreover, the competitive equilibrium price vectors are the shadow price vectors for the positive program for this value of s.¹³ We prove these results by showing that minimizing the difference between the positive and negative programs is dual to minimizing a Lyapunov function $L({\mathbf {p}})$. More precisely, we show that the Toland-Singer dual [33, 47] of $L({\mathbf {p}})$ is the minimum difference between the positive and negative linear programs.

[6] have recently shown that a standard steepest-descent algorithm based on the Lyapunov function (following [38]) can solve the SSPMA pricing problem, but their method takes only limited advantage of the special features of the geometric representation.¹⁴ By taking fuller advantage of the structure of strong substitutes analyzed in this paper, we find an alternative to steepest descent on the Lyapunov function. Our algorithm draws on DC (difference of convex functions) programming.¹⁵ Steepest descent algorithms on the Lyapunov function are known to be very efficient. But we find that the DC algorithm is at least similarly fast in all our experiments. Neither algorithm is consistently faster, and in environments with only a low number of negative bids (which we conjecture are the most likely ones in practice–see Section 2.3), the DC algorithm is the faster one. So, while both algorithms terminate in a few seconds even for large problem instances, the DC algorithm provides an valuable new alternative by taking advantage of the structural properties of strong substitutes.

1.3 Outline

We proceed as follows. Section 2 introduces the SSPMA bidding language. We illustrate its expressiveness, and explain that it is a compact language that expresses all strong substitutes valuations (and no others) as the Minkowski difference of positive and negative bids. Section 3 proves that the pricing problem can be solved by minimizing the difference between the objectives of the two linear programs, by showing that this is dual to minimizing the Lyapunov function. Section 4 takes advantage of this result to use “DC programming” (difference of convex functions programming) to specify an algorithm to solve the problem, and uses numerical experiments to compare our algorithm to a steepest-descent algorithm based on the Lyapunov function. Section 5 concludes. All proofs are in the Appendix.

2 The SSPMA bid language

2.1 Formal description of the SSPMA language

In the SSPMA, each of m bidders $j \in \{1,\ldots ,m\}$ submit an arbitrary number of bids for distinct goods $i\in \{1,\ldots ,n\}$. A bid is a vector ${\mathbf {b}}= (b_1,\dots ,b_n;b_{n+1}) \in {\mathbb {Z}}_{\ge 0}^{n}\times ({\mathbb {Z}}\setminus \{0\})$. Here, for $i=1,\ldots ,n$, coordinate $b_i$ gives the value for good i. The final coordinate $b_{n+1}\in {\mathbb {Z}}\setminus \{0\}$ is the weight of the bid; we write $w({\mathbf {b}})$ for the projection to this final coordinate. We refer to positive and negative bids according to the sign of $w({\mathbf {b}})$. Prices ${\mathbf {p}}=(p_1,\ldots ,p_n)\in {\mathbb {R}}^n$ are linear. Our bundles of indivisible goods will be written ${\mathbf {x}},{\mathbf {y}}\in {\mathbb {Z}}^n_{\ge 0}$. We write ${\mathbf {e}}^i$ for the coordinate vectors $i=1,\ldots ,n$ in ${\mathbb {Z}}^n$.

A positive bid ${\mathbf {b}}$ expresses the willingness of the bidder to pay at most $b_i$ for units of good $i=1,\ldots ,n$, and for up to $w({\mathbf {b}})$ units in total. It defines a valuation $v_{\mathbf {b}}$ on the domain $\varDelta _{w({\mathbf {b}})}$ of bundles of at most $w({\mathbf {b}})$ units, that is, $\varDelta _{w({\mathbf {b}})}=\{{\mathbf {y}}\in {\mathbb {Z}}^n_{\ge 0}:\sum _{i=1}^n y_i\le w({\mathbf {b}})\}$, with $v_{\mathbf {b}}({\mathbf {y}})=\sum _{i=1}^n b_i y_i$. The utility associated with this bid is quasi-linear, $v_{\mathbf {b}}({\mathbf {y}})-\langle {\mathbf {p}},{\mathbf {y}}\rangle$, so the indirect utility associated with such a bid is just

$$\begin{aligned} u_{{\mathbf {b}}}({\mathbf {p}}) = w({\mathbf {b}})\max _{i \in \{1,\dots ,n\}}( b_i-p_i,0), \end{aligned}$$

(1)

where we include 0 because the bid may instead be rejected. Any combination of $w({\mathbf {b}})$ units of utility-maximizing goods is acceptable, as are fewer units when $u_{{\mathbf {b}}}({\mathbf {p}})=0$, so the demand set is

$$\begin{aligned} D_{{\mathbf {b}}}({\mathbf {p}}):=\left\{ {\mathbf {y}}\in \varDelta _{w({\mathbf {b}})}~:~ \sum _{i=1}^n y_i(b_i-p_i)=u_{{\mathbf {b}}}({\mathbf {p}})\right\} . \end{aligned}$$

(2)

This set comprises all integer bundles in the convex polytope in which the bundles $w({\mathbf {b}}){\mathbf {e}}^i$, where i maximizes $b_i-p_i\ge 0$, are vertices, and ${\mathbf {0}}$ is also a vertex if $\max _{i \in \{1,\dots ,n\}}( b_i-p_i,0)= 0$. If $D_{{\mathbf {b}}}({\mathbf {p}})$ contains more than one bundle, we say all goods $i=1,\ldots ,n$ maximizing $b_i-p_i$ are marginal for bid ${\mathbf {b}}$ at ${\mathbf {p}}$. If $\{{\mathbf {0}}\}\subsetneq D_{{\mathbf {b}}}({\mathbf {p}})$ then we say the bid is marginal to be accepted. If $D_{{\mathbf {b}}}({\mathbf {p}})=\{{\mathbf {0}}\}$ we say the bid is rejected.

Now consider a multiset ${\mathcal {B}}$ of positive bids, which could be all those placed by a single bidder, or could, for example, be all bids from all bidders. The aggregate indirect utility $u_{{\mathcal {B}}}({\mathbf {p}})$ is just the sum of indirect utilities: $u_{{\mathcal {B}}}({\mathbf {p}})=\sum _{{\mathbf {b}}\in {\mathcal {B}}}u_{\mathbf {b}}({\mathbf {p}})$, and the aggregate demand set $D_{{\mathcal {B}}}({\mathbf {p}})$ is the Minkowski sum of demand sets $D_{{\mathcal {B}}}({\mathbf {p}})=\sum _{{\mathbf {b}}\in {\mathcal {B}}}D_{{\mathbf {b}}}({\mathbf {p}})$.

However, we also allow negative bids: those for which $w({\mathbf {b}})<0$. These do not represent a meaningful economic valuation on their own, but do so in “valid” combinations with positive bids. Given a collection ${\mathcal {B}}$ of bids, write respectively ${\mathcal {B}}_+$ and ${\mathcal {B}}_-$ for the positive and negative bids in ${\mathcal {B}}$. Write $|{\mathbf {b}}|$ for the bid $(b_1,\ldots ,b_n;|w({\mathbf {b}})|)$, and write $|{\mathcal {B}}_-|$ for the set of bids $|{\mathbf {b}}|$ where ${\mathbf {b}}\in {\mathcal {B}}_-$. Now the aggregate indirect utility is an appropriately signed sum of indirect utilities:

$$\begin{aligned} u_{{\mathcal {B}}}({\mathbf {p}}) := \sum _{{\mathbf {b}}\in {\mathcal {B}}_+} u_{\mathbf {b}}({\mathbf {p}})-\sum _{{\mathbf {b}}\in |{\mathcal {B}}_-|} u_{\mathbf {b}}({\mathbf {p}}). \end{aligned}$$

(3)

We say that the set ${\mathcal {B}}$ is valid when the indirect utility $u_{{\mathcal {B}}}$ is concave. (See Theorem 1 of [6]; further discussion of this notion is given below after Definition 2.)

To define the aggregate demand set with positive and negative bids, first define the demand $D_{{\mathbf {b}}}({\mathbf {p}})$ associated with an individual negative bid ${\mathbf {b}}$ as $D_{\mathbf {b}}({\mathbf {p}})=-D_{|{\mathbf {b}}|}({\mathbf {p}})=\{-{\mathbf {x}}~|~{\mathbf {x}}\in D_{|{\mathbf {b}}|}({\mathbf {p}})\}$. Let ${\mathcal {Q}}$ comprise all price vectors ${\mathbf {q}}$ in a small neighborhood of ${\mathbf {p}}$, and such that $D_{{\mathbf {b}}}({\mathbf {q}})=\{{\mathbf {x}}_{{\mathbf {b}}}({\mathbf {q}})\}$ are singletons for all ${\mathbf {b}}\in {\mathcal {B}}$. Then the aggregate demand set is equal to the discrete convex hull

$$\begin{aligned} D_{{\mathcal {B}}}({\mathbf {p}}) = {{\,\mathrm{conv}\,}}\left\{ \sum _{{\mathbf {b}}\in {\mathcal {B}}} D_{{\mathbf {b}}}({\mathbf {q}}): {\mathbf {q}}\in {\mathcal {Q}}\right\} \cap {\mathbb {Z}}^n. \end{aligned}$$

In particular, if $D_{{\mathbf {b}}}({\mathbf {p}})$ is a singleton for all ${\mathbf {b}}\in {\mathcal {B}}$, then $D_{{\mathcal {B}}}({\mathbf {p}})$ is just $\sum _{{\mathbf {b}}\in {\mathcal {B}}} D_{{\mathbf {b}}}({\mathbf {p}})=\sum _{{\mathbf {b}}\in {\mathcal {B}}_+} D_{{\mathbf {b}}}({\mathbf {p}})-\sum _{{\mathbf {b}}\in |{\mathcal {B}}_-|} D_{{\mathbf {b}}}({\mathbf {p}})$: negative bids are used to “cancel” part of the demand arising from positive bids. We cannot extend this rule to prices at which the demand set is non-unique simply by taking the Minkowski sum of demand sets associated with all bids; negative bids which are marginal between goods must be treated consistently with positive bids marginal on those same goods.¹⁶ However, if the bids ${\mathcal {B}}^j$ of each bidder $j=1,\ldots ,m$ are valid, then the full aggregate demand set $D_{{\mathcal {B}}}({\mathbf {p}})$ defined by ${\mathcal {B}}=\bigcup _{j=1}^m {\mathcal {B}}^j$ is indeed the Minkowski sum: $D_{{\mathcal {B}}}({\mathbf {p}})=\sum _{j=1}^m D_{{\mathcal {B}}^j}({\mathbf {p}})$.

When ${\mathcal {B}}$ contains only positive bids, we can aggregate the simple valuations implied by individual bids, to obtain the aggregate valuation $v_{{\mathcal {B}}}:\varDelta _W\rightarrow {\mathbb {Z}}$, where $W=\sum _{{\mathbf {b}}\in {\mathcal {B}}}w({\mathbf {b}})$:

$$\begin{aligned} v_{{\mathcal {B}}}({\mathbf {y}}) = \max \left\{ \sum _{{\mathbf {b}}\in {\mathcal {B}}}\sum _{i=1}^n x_{i{\mathbf {b}}}b_i:\, \sum _{{\mathbf {b}}\in {\mathcal {B}}} x_{i{\mathbf {b}}} \le y_i \, \forall i\text { and } \sum _{i=1}^n x_{i{\mathbf {b}}} \le w({\mathbf {b}}) \, \forall {\mathbf {b}}\in {\mathcal {B}}\right\} . \end{aligned}$$

(4)

As usual, the relations $u_{{\mathcal {B}}}({\mathbf {p}}) = \max _{{\mathbf {x}}\in {\mathbb {Z}}_{\ge 0}^n} v_{{\mathcal {B}}}({\mathbf {x}})-\langle {\mathbf {p}},{\mathbf {x}}\rangle$ and $v_{{\mathcal {B}}}({\mathbf {x}}) = \min _{{\mathbf {p}}\in {\mathbb {R}}^n} u_{{\mathcal {B}}}({\mathbf {p}}) + \langle {\mathbf {p}},{\mathbf {x}}\rangle$ hold. The latter equation also gives us an indirect way to identify the aggregate valuation if ${\mathcal {B}}$ is a valid set of positive and negative bids. However, one of our main results, which is also the starting point to our equilibrium pricing algorithm, is a purely primal expression for the aggregate valuation in the presence of negative bids (Theorem 1).

The valuation implied by such bids is for strong substitutes:

Definition 1

(Ordinary and strong substitutes, [8] and [35]) A valuation v is ordinary substitutes, if for any price vectors ${\mathbf {p}}' \ge {\mathbf {p}}$ with singleton demand sets $D_v({\mathbf {p}}') = \{{\mathbf {x}}'\}$ and $D_v({\mathbf {p}}) = \{{\mathbf {x}}\}$, we have ${\mathbf {x}}_k' \ge {\mathbf {x}}_k$ for all k with $p_k' = p_k$. A valuation v is strong substitutes, if, when we consider every unit of every good to be a separate good, v is ordinary substitutes.

The SSPMA only expresses preferences of this kind, and can express any strong substitutes valuation [7, 9]¹⁷. It is, to our knowledge, the only bidding language that provably has this feature.

In an SSPMA such as the Bank of England’s, total supply is not pre-determined; the auctioneer represents its preferences as supply schedules, and the auction finds competitive equilibrium given the auctioneer’s and bidders’ expressed preferences. However, the auctioneer can equivalently auction the maximum quantity of each good that it would ever sell at any price vector, and place appropriate bids to buy back quantities at lower prices.¹⁸ So we index the auctioneer as agent 0 and include its bids in the set ${\mathcal {B}}$ of all bids from all bidders. This paper therefore addresses the following problem:

Definition 2

(Equilibrium pricing problem) Given a valid set ${\mathcal {B}}$ of all bids from all bidders (including the auctioneer) and a target supply ${\mathbf {t}}$, find a price vector ${\mathbf {p}}\in {\mathbb {R}}^n$, such that ${\mathbf {t}}$ is demanded at ${\mathbf {p}}$, that is, ${\mathbf {t}}\in D_{{\mathcal {B}}}({\mathbf {p}})$. Such a price vector is called an equilibrium price.¹⁹

It is well-known that a competitive equilibrium does indeed exist, given our assumptions of strong substitutes and a seller who will retain units of any underdemanded good at a price of zero [17, 35]. Indeed, this also implies that equilibrium price in ${\mathbb {R}}^n_{\ge 0}$ exists. The set of equilibrium prices forms a lattice with respect to the Euclidean ordering [21, 36], i.e., for any valuations $v_1, \cdots , v_m$, if ${\mathbf {p}}$ and ${\mathbf {p}}'$ are equilibrium prices for such valuations, then ${\mathbf {p}}\wedge {\mathbf {p}}'$ and ${\mathbf {p}}\vee {\mathbf {p}}'$ are also equilibrium prices. This implies that there exists an unique minimal equilibrium price vector. It is possible to modify the algorithm we will develop to find the minimal equilibrium price vector rather than an arbitrary price vector.

To understand the “validity” of bids in the SSPMA, we briefly outline some geometric ideas from [8]. First, the collection ${\mathcal {B}}$ of bids induces a set of prices at which the aggregate demand is not unique: the “locus of indifference prices” (LIP), notated ${\mathcal {L}}_{{\mathcal {B}}} :=\left\{ {\mathbf {p}}:\, |D_{{\mathcal {B}}}({\mathbf {p}})| > 1 \right\}$. For a price ${\mathbf {p}}$ to be in the LIP, at least one bid must be marginal, so some equality of the form $b_i=p_i$ or $b_i-p_i=b_j-p_j$ must hold, where $i,j\in \{1,\ldots ,n\}$ and $j\ne i$. Therefore, ${\mathcal {L}}_{{\mathcal {B}}}$ consists of a union of pieces of hyperplanes with normals in $\{{\mathbf {e}}^i,{\mathbf {e}}^i-{\mathbf {e}}^j:\, 1 \le i < j \le n\}$. These pieces of hyperplanes are known as facets. To each facet F, we assign a weight w(F), given by the sum of the weights of bids that are marginal at a price in the relative interior of F. Facets always have nonzero weight; if the sum of weights of marginal bids is zero then one may see that demand is in fact unique.

The LIP ${\mathcal {L}}_{{\mathcal {B}}}$ splits price space into multiple unique demand regions (UDRs) at which a unique bundle is demanded. Let ${\mathbf {p}}$ be a price vector in an UDR for which the demand is known (for example, for ${\mathbf {p}}$ large, the demand is 0). If the price ${\mathbf {p}}$ changes along a curve, and crosses a facet F of ${\mathcal {L}}_{{\mathcal {B}}}$, then the demand changes by $w(F) {\mathbf {n}}$, where ${\mathbf {n}}$ is the normal of F pointing into the opposite direction of the path. For an illustration, see Fig. 3. Thus, the LIP fully encodes the aggregate demand at every UDR-price, and so – by taking convex hulls – at every price.

Fig. 3

Finding demand in each UDR of a LIP. The black circles represent positive bids with weight 1, namely (2, 2; 1), (1, 0; 1) and (0, 1; 1); the white circle represents a negative bid, $(1,1;-1)$. Note that all facets emanating from this negative bid are canceled by parts of facets arising from positive bids. A curve which determines demand in every UDR is shown as a dashed line. The curve starts at a high price, where the demand is (0, 0). The vectors where the path intersects the LIP indicate the correctly oriented normals of the facets with respect to the path. For example, inspecting the crossings of facets reveals that the demand at (0.5, 0.5) is $1 \cdot (1,0) + 1 \cdot (-1,1) + 1\cdot (1,0) = (1,1)$

Now, a negative-weighted facet cannot arise from a quasi-linear preference relation: when the price of one good decreases, the demand for that good must not also decrease. So negative bids must be placed in such a way that, in the resulting collection of facets, no facet has a negative weight. This condition is equivalent to concavity of the indirect utility function.²⁰ From now on we assume that our bid collections are always valid. Note that if each individual bidder’s bid set is valid, then so is the set of all bids from all bidders.

The following two subsections discuss geometrical interpretations and properties of this bid language. While they do not contribute directly to our main Theorem 1 and the algorithm, they provide useful background on the role of negative bids in the SSPMA and intuition for the overall approach.

2.2 Interpretation via Minkowski differences

Fig. 4

The Minkowski sum $A+(-B)$ and Minkowski difference $A-B$ of rectangle A and a triangle B. Left: the rectangle A (in gray); four instances of $a+(-B)$, in which $a\in A$ and $-B$ is the triangle (dashed line and its interior); and $A+(-B)$ (black line, including its interior). Right: the same rectangle A (in gray); six instances of $a+B$. For five of these, such as $a=x$, we have $a+B\subseteq A$ and so $a\in A-B$, but $y+B\not \subseteq B$ and so $y\notin A-B$. The full set $A-B$ is given by the black line and its interior

There appears to be a contrast between the intuitive definition of the aggregate demand set when all bids are positive (so the aggregate demand set is just the Minkowski sum of the individual demand sets) and the more involved definition when negative bids are present. Recall from Sect. 2.1 that in this case we defined the aggregate demand set to be the discrete convex hull of bundles which are demanded uniquely when we slightly change the price vector ${\mathbf {p}}$. We cannot simply take Minkowski sums because we must ensure that negative bids are treated in a valid way with their associated positive bids (see the discussion after Definition 2). However, if ${\mathcal {B}}$ is valid, then we can provide a more parsimonious novel definition by using the Minkowski difference operation. We recall that $A-B$ consists of all points ${\mathbf {x}}\in {\mathbb {R}}^n$, such that ${\mathbf {x}}+B \subseteq A$. The geometric effect of this operation is illustrated in Fig. 4. Note in particular that in general $A+(-B) \ne A - B$.

Proposition 1

Let ${\mathcal {B}}$ be a valid collection of bids in an SSPMA. Then for every price vector ${\mathbf {p}}$ the demand set $D_{{\mathcal {B}}}({\mathbf {p}})$ is equal to $D_{{\mathcal {B}}_+}({\mathbf {p}}) - D_{|{\mathcal {B}}_-|}({\mathbf {p}})$.

We prove this result in Appendix A.1.

2.3 Expressiveness and compactness of the SSPMA

To illustrate the expressive power of negative bids, we consider [40]’s notorious example of a valuation, $v_r$, that shows that prior bid languages such as the endowed assignment valuations by [22] are strictly less expressive than the set of gross substitutes (and so also strong substitutes) valuations.²¹ (We discuss the construction of $v_r$ in Appendix A.2.) However,

Proposition 2

The valuation $v_r$ in [40] can be represented by 8 positive and 6 negative SSPMA bids.

This proposition illustrates [9]’s more general result that all strong substitutes valuations can be depicted in the SSPMA. We prove Proposition 2 without relying on this general result by explicitly providing the list of SSPMA bids.

Moreover, an important feature of the SSPMA language is that it is parsimonious: the valuations that are most used in practice can be expressed very simply, using far fewer bids than the number of different bundles valued. Let $W := \sum _{{\mathbf {b}}\in {\mathcal {B}}} w({\mathbf {b}})$. Note that W equals the maximum number of units that a bidder who makes bids ${{\mathbf {b}}\in {\mathcal {B}}}$ is interested in. Then SSPMA bids can assign a “non-trivial” value to $\varOmega (W^n)$ bundles:

Proposition 3

Consider an SSPMA with n goods, and suppose a bidder makes bids ${\mathcal {B}}$.

Let $D := \bigcup \{D_{{\mathcal {B}}}({\mathbf {p}}):\, {\mathbf {p}}\in {\mathbb {R}}^n\}$ and let $W := \sum _{{\mathbf {b}}\in {\mathcal {B}}} w({\mathbf {b}})$. Then $D=\varDelta _W$ and so $|D| = {{n+W}\atopwithdelims (){n}} \ge (1+W/n)^n$.

Moreover, bidders in practical applications are likely to need to make far fewer bids than Proposition 3 suggests: Expressing a demand function for each good independently is trivial–it just requires providing a separate list of bids for each i with, for each i, $b_j=0$ for all $j\ne i$. In many settings these bids will express much of the information about bidders’ valuations.

At a second, higher, level of complexity, any bid which selects the “best value” among any number of goods can be expressed using only positive bids. Observe that W is the maximum number of bids that a bidder who is interested in winning at most W units, and who uses only positive bids, needs to make—and if any of her bids have greater weight than 1, she will need fewer bids. So such a bidder can express her valuations of all possible bundles with only a few bids.

More complex features of preferences require negative bids to express, but these features seem less likely to arise frequently. Example 2 is one example, and there are others,²² but we expect most bidders would be unlikely to have to handle more than a very small number of these special issues. In fact, in the Bank of England’s auctions, bidders showed relatively little interest even in bids of the “second level” of complexity, and they used such bids only rarely–perhaps because they are only very important to banks in times of real crisis.²³ So bidders are unlikely to need many negative bids in most practical auction settings.²⁴ The number of bids needed by a bidder who is interested in winning at most W units, and who needs only a small number of negative bids, cannot much exceed W. Moreover, such a bidder will need to use many fewer than W bids unless most or all of her bids are of weight only 1. So these bidders, too, are likely to be able to express their full valuations with only a few bids.

The number of bundles valued by a set of bids of mixed sign can be much smaller than the lower bound on the number of bundles valued by the same number of bids that are all positive.²⁵ But we expect the SSPMA bidding language will be much more “compact”²⁶ in most practical cases than—say—listing valuations for all bundles explicitly.

So in the settings that we believe are most likely to arise, bidders can probably build up their valuations bit by bit through adding individual bids. We expect most of these bids will be positive; moreover, software can make entering negative bids easier, by checking feasibility and by allowing the bidding of “words,”²⁷, and by checking feasibility.²⁸

At least with human participants, it seems less likely that a valuation function with all exponentially many package values would be available, but in this case the prices can be computed directly, using steepest descent or linear programming algorithms. Alternatively, bidders could use [20]’s algorithm to generate bids from an arbitrary value function.²⁹

3 The SSPMA pricing problem

With only positive bids, our equilibrium pricing problem (Definition 2) can be solved via a simple linear program that maximizes the total welfare given the target bundle ${\mathbf {t}}$. We know that ${\mathbf {t}}\in \varDelta _W$, where W is the total weight of bids placed, by our assumption about the bids of the auctioneer. But recall from Equation (4) that, given the collection ${\mathcal {B}}$ of all bids of all bidders, the aggregate valuation of any bundle ${\mathbf {t}}\in \varDelta _W$ is given - in LP notation - by

$$\begin{aligned} v_{{\mathcal {B}}}({\mathbf {t}}) = \max \sum _{{\mathbf {b}}\in {\mathcal {B}}} \sum _{i \in [n]} b_i x_{{\mathbf {b}}i}&\\ \text {s.t.} \ \sum _{i \in [n]} x_{{\mathbf {b}}i}&\le w({\mathbf {b}})&\forall {\mathbf {b}}&\in {\mathcal {B}}&(\pi _{{\mathbf {b}}})\\ \sum _{{\mathbf {b}}\in {\mathcal {B}}} x_{{\mathbf {b}}i}&= t_i&\forall i&\in [n]&(p_i)\\ x_{{\mathbf {b}}i}&\ge 0&\forall {\mathbf {b}}&\in {\mathcal {B}},\, i \in [n] . \end{aligned}$$

(LP)

Here $\pi _{{\mathbf {b}}}$ and $p_i$ denote the respective dual variables. This program always has an integral optimal solution, as may be seen either by properties of strong substitutes valuations, or by recognizing that it is an instance of the min-cost flow problem. The number of constraints and variables is polynomial in the number of bids and goods, in contrast to the formulation of [13]. The set of equilibrium prices can be computed directly:

Proposition 4

In an SSPMA with only positive bids, the equilibrium prices for the target supply ${\mathbf {t}}$ are the optimal dual variables ${\mathbf {p}}=(p_1,\dots ,p_n)$ of the network linear program (LP) which can be solved in polynomial time in the number of goods and bids.

Proposition 4 simply follows from writing down the complementary slackness conditions of (LP), so we do not provide an explicit proof. If ${\mathcal {B}}$ also contains negative bids, the problem of efficiently computing equilibrium prices is less obvious. One route, taken by [6], is to minimize the Lyapunov function $L:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ [4], defined for target ${\mathbf {t}}$ as

$$\begin{aligned} L({\mathbf {p}}) = u_{{\mathcal {B}}}({\mathbf {p}}) + \langle {\mathbf {p}},{\mathbf {t}}\rangle \end{aligned}$$

where aggregate indirect utility $u_{{\mathcal {B}}}({\mathbf {p}})$ is as defined in Eq. (3). The set of minimizers of L coincides with the set of equilibrium prices, and structural properties of L allow for polynomial-time steepest descent algorithms to find these minima [6, 36, 42]. However, this approach works by invoking a rather generic submodular function minimization algorithm, under the assumption that a demand oracle is available.

By contrast, with only positive bids we can build upon much more specialized algorithms to solve network linear programs. And, as we now show, taking advantage of the economic structure of the problem allows us to incorporate negative bids into this approach:

Recall that the total allocation in an SSPMA is equal to that assigned to positive bids minus that assigned to negative bids. So, to assign ${\mathbf {t}}$ units in total, we must assign ${\mathbf {t}}+{\mathbf {s}}$ units to positive bids and ${\mathbf {s}}$ to negative bids, for some “supplementary” bundle ${\mathbf {s}}$. Recall also that we write ${\mathcal {B}}_+$ for the positive bids in ${\mathcal {B}}$, and $|{\mathcal {B}}_-|$ for the negative bids ${\mathbf {b}}\in {\mathcal {B}}$ endowed with weights $|w({\mathbf {b}})|$. We introduce two additional SSPMAs: that with bids ${\mathcal {B}}_+$ and target ${\mathbf {t}}+{\mathbf {s}}$, which we call the “positive auction”; and that with (positive) bids $|{\mathcal {B}}_-|$ and target ${\mathbf {s}}$, which we call the “negative auction”. Write $W_+$ and $W_-$ for the total weights of bids in these respective auctions, so that $\varDelta _{W_+}$ and $\varDelta _{W_-}$ are the sets of bundles that may be sold by each of them. Note that for each ${\mathbf {t}}\in \varDelta _W$ and ${\mathbf {s}}\in \varDelta _{W_-}$, ${\mathbf {t}}+{\mathbf {s}}$ lies in $\varDelta _{W_+}$ (see Appendix Lemma 4).

If we pick ${\mathbf {s}}$ correctly, then this is equivalent to allocating ${\mathbf {t}}$ units in the auction with bids ${\mathcal {B}}$. Moreover, since both ${\mathcal {B}}_+$ and $|{\mathcal {B}}_-|$ are sets of positive bids, their respective aggregate valuations and equilibrium prices can be evaluated using the linear program above. We now show how to find ${\mathbf {s}}$:

Theorem 1

If ${\mathcal {B}}$ represents all bids from all bidders, then the aggregate valuation at the target supply ${\mathbf {t}}\in \varDelta _W$ can be written as

$$\begin{aligned} v_{{\mathcal {B}}}({\mathbf {t}}) = \min _{{\mathbf {s}}\in \varDelta _{W_-} }\left( v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})-v_{|{\mathcal {B}}_-|}({\mathbf {s}}) \right) . \end{aligned}$$

Moreover, given a minimizer ${\bar{{\mathbf {s}}}}$, each equilibrium price ${\bar{{\mathbf {p}}}}$ of the auction with bids ${\mathcal {B}}_+$ and target supply ${\mathbf {t}}+{\bar{{\mathbf {s}}}}$ is an equilibrium price for the auction with bids $|{\mathcal {B}}_-|$ and target supply ${\bar{{\mathbf {s}}}}$, and also for the complete auction with bids ${\mathcal {B}}$ and target supply ${\mathbf {t}}$.

We prove Theorem 1 in Appendix A.4.

To understand the economic intuition underlying Theorem 1 assume that the set of equilibrium prices is $n$-dimensional and consider a price ${\mathbf {p}}$ in its interior. (Although the SSPMA would choose the minimum of the equilibrium prices, choosing an interior price simplifies the intuition.) Let ${\bar{{\mathbf {s}}}}$ be the vector of negative bids accepted in the equilibrium. Initially set the target ${\mathbf {s}}$ of the negative auction to be ${\bar{{\mathbf {s}}}}$, which means that ${\mathbf {p}}$ is an equilibrium price for both the positive and negative auctions.

Consider the effect of changing ${\mathbf {p}}$ on the weighted sum of bids accepted in these two auctions. Recall that the full set ${\mathcal {B}}$ of positive and negative bids in the original SSPMA is valid. So for any price at which additional negative bids are marginal to be accepted, positive bids with at least as great a weight must also be marginal to be accepted–see the discussion of validity of ${\mathcal {B}}$ at the end of Sect. 2.1. (The converse does not hold: positive bids can be marginal at prices at which no negative bid is marginal.) So, any change in price from ${\mathbf {p}}$ would alter the total weight of bids accepted in the positive auction by weakly more than it would alter the total weight of bids accepted in the negative auction.

Now consider an increase in one coordinate of the supplementary bundle, from ${\bar{{\mathbf {s}}}}$ to ${\mathbf {s}}\ge {\bar{{\mathbf {s}}}}$, in both the positive and negative auctions. The additional bids that will be accepted in the positive auction with target ${\mathbf {t}}+{\mathbf {s}}$ will, because of our observation above, have weakly greater value than the additional bids accepted in the negative auction. That is, $v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})-v_{{\mathcal {B}}_+}({\mathbf {t}}+{\bar{{\mathbf {s}}}})\ge v_{|{\mathcal {B}}_-|}({\mathbf {s}})-v_{|{\mathcal {B}}_-|}({\bar{{\mathbf {s}}}})$. Similarly, if we decrease one coordinate to ${\mathbf {s}}\le {\bar{{\mathbf {s}}}}$, then bids which are now rejected from the positive auction will have weakly lower value than the bids rejected from the negative auction. So, again, $v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})-v_{{\mathcal {B}}_+}({\mathbf {t}}+{\bar{{\mathbf {s}}}})\ge v_{|{\mathcal {B}}_-|}({\mathbf {s}})-v_{|{\mathcal {B}}_-|}({\bar{{\mathbf {s}}}})$. General changes in ${\mathbf {s}}$ may be understood as a sequence of these two operations.

It follows that ${\bar{{\mathbf {s}}}}$ can be identified by minimizing $v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})-v_{|{\mathcal {B}}_-|}({\mathbf {s}})$.

The formal proof of Theorem 1 rests on applying a version of Toland-Singer duality [47] to the valuations in the positive and negative auctions, and relating this to the Lyapunov function $L({\mathbf {p}})$. [33] provide a theoretical treatment of discrete DC-functions, establishing (their Theorem 4.6) Toland-Singer duality in discrete DC-functions.

First recall that, for a function $f:{{\,\mathrm{dom}\,}}f \rightarrow {\mathbb {R}}$, where ${{\,\mathrm{dom}\,}}f\subseteq {\mathbb {R}}^n$, the convex conjugate $f^*:{{\,\mathrm{dom}\,}}f^*\rightarrow {\mathbb {R}}$ is defined by $f^*({\mathbf {p}})=\sup _{{\mathbf {x}}\in {{\,\mathrm{dom}\,}}f}( \langle {\mathbf {p}}, {\mathbf {x}}\rangle - f({\mathbf {x}}) )$, where ${{\,\mathrm{dom}\,}}f^*\subseteq {\mathbb {R}}^n$ comprises those ${\mathbf {p}}$ at which $f^*({\mathbf {p}})$ is finite-valued. The subdifferential of f is the set-valued function

$$\begin{aligned} \partial f({\mathbf {x}})=\{{\mathbf {p}}\in {\mathbb {R}}^n: \langle {\mathbf {p}}, {\mathbf {y}}\rangle - f({\mathbf {y}}) \le \langle {\mathbf {p}},{\mathbf {x}}\rangle - f({\mathbf {x}}) \quad \forall {\mathbf {y}}\in {\mathbb {R}}^n\}. \end{aligned}$$

The domain ${{\,\mathrm{dom}\,}}\partial f$ of the subdifferential consists of all points ${\mathbf {x}}\in {{\,\mathrm{dom}\,}}f$ with $\partial f({\mathbf {x}}) \ne \emptyset$. It turns out that in our application the convex conjugates and subdifferentials have an intuitive economic meaning.

Lemma 1

Let ${\mathcal {B}}$ be a collection of positive bids. Then $-v_{{\mathcal {B}}}$ can be naturally extended to a convex function $f: {{\,\mathrm{dom}\,}}f \rightarrow {\mathbb {R}}$ with the following properties:

• 1. ${{\,\mathrm{dom}\,}}\partial f = {{\,\mathrm{dom}\,}}f = {{\,\mathrm{conv}\,}}\varDelta _W$ and ${{\,\mathrm{dom}\,}}\partial f^* = {{\,\mathrm{dom}\,}}f^* = {\mathbb {R}}^n$

• 2. $f^*({\mathbf {q}}) = u_{{\mathcal {B}}}(-{\mathbf {q}})$ and $\partial f^*({\mathbf {q}}) = {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}(-{\mathbf {q}})$

• 3. $\partial f({\mathbf {x}}) = -\{ {\mathbf {p}}\in {\mathbb {R}}^n \,:\, {\mathbf {x}}\in {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}({\mathbf {p}})\}$.

We will use the following version of Toland-Singer duality, which allows for restricted domains:

Theorem 2

(Toland-Singer duality) Let $f:{{\,\mathrm{dom}\,}}f\rightarrow {\mathbb {R}}$ and $g:{{\,\mathrm{dom}\,}}g\rightarrow {\mathbb {R}}$ be proper convex lower semi-continuous functions with closed and convex domains ${{\,\mathrm{dom}\,}}f \subseteq {{\,\mathrm{dom}\,}}g\subseteq {\mathbb {R}}^n$ and such that ${{\,\mathrm{dom}\,}}g^* \subseteq {{\,\mathrm{dom}\,}}f^*\subseteq {\mathbb {R}}^n$. If one of the differences $f({\mathbf {x}})-g({\mathbf {x}})$ and $g^*({\mathbf {y}})-f^*({\mathbf {y}})$ has a minimum in ${{\,\mathrm{dom}\,}}f$, respectively ${{\,\mathrm{dom}\,}}g^*$, the other difference also has one, and

$$\begin{aligned} \min _{{\mathbf {x}}\in {{\,\mathrm{dom}\,}}f} f({\mathbf {x}})-g({\mathbf {x}}) = \min _{{\mathbf {y}}\in {{\,\mathrm{dom}\,}}g^*} g^*({\mathbf {y}})-f^*({\mathbf {y}}). \end{aligned}$$

Moreover, if ${\bar{{\mathbf {x}}}}$ minimizes $f({\mathbf {x}})-g({\mathbf {x}})$, then any ${\bar{{\mathbf {y}}}} \in \partial g({\bar{{\mathbf {x}}}})$ minimizes $g^*({\mathbf {y}})-f^*({\mathbf {y}})$. Conversely, for any minimizer ${\bar{{\mathbf {y}}}}$ of $g^*({\mathbf {y}})-f^*({\mathbf {y}})$, any ${\bar{{\mathbf {x}}}} \in \partial f^*({\bar{{\mathbf {y}}}})$ minimizes $f({\mathbf {x}})-g({\mathbf {x}})$.

For a proof see [46, Theorem 1]. We will apply Theorem 2 to the convex extensions of $-v_{|{\mathcal {B}}_-|}$ and $-v_{{\mathcal {B}}_+}$ (to the convex hulls of their domains).

4 The pricing algorithm

Using Theorem 1, we can approach the pricing problem by minimizing the difference $v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})-v_{|{\mathcal {B}}_-|}({\mathbf {s}})$. While the valuations $v_{{\mathcal {B}}_+}$ and $v_{|{\mathcal {B}}_-|}$ can be extended to concave functions, and can efficiently be evaluated with linear programs at any given pair of bundles, their difference is in general neither concave nor convex. Moreover, as recently shown by [29], minimizing the difference between two $M^{\natural }$-convex functions is an NP-hard optimization problem. However, there is a class of algorithms on the difference of convex functions (DC algorithms; see [2, 46]), that find at least local minima of such problems and are often very fast in practice.

4.1 A DC auction algorithm

By Theorem 1, we seek ${\bar{{\mathbf {s}}}}$ minimizing $v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})-v_{|{\mathcal {B}}_-|}({\mathbf {s}})$. We will approach this by minimizing $f({\mathbf {s}})-g({\mathbf {s}})$, where $f({\mathbf {s}})$ and $g({\mathbf {s}})$ are the convex extensions of $-v_{|{\mathcal {B}}_-|}({\mathbf {s}})$, respectively $-v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})$, to the convex hulls of their domains. A necessary condition for such ${\bar{{\mathbf {s}}}}$ is that it gives a stationary point, that is, ${\bar{{\mathbf {s}}}} \in {{\,\mathrm{dom}\,}}\partial f$ with $\partial f(\bar{s}) \cap \partial g({\bar{s}}) \ne \emptyset$. To interpret this in our context, if ${\mathbf {q}}\in \partial f({{\bar{{\mathbf {s}}}}}) \cap \partial g({{\bar{{\mathbf {s}}}}})$ then ${\mathbf {p}}=-{\mathbf {q}}$ is a price at which ${\mathbf {t}}+{{\bar{{\mathbf {s}}}}}$ is demanded in the positive auction, and ${{\bar{{\mathbf {s}}}}}$ is demanded in the negative auction (see Lemma 1).

The DC Algorithm 1 finds a stationary point for two convex functions $f: {{\,\mathrm{dom}\,}}f \rightarrow {\mathbb {R}}$ and $g: {{\,\mathrm{dom}\,}}g \rightarrow {\mathbb {R}}$ with ${{\,\mathrm{dom}\,}}\partial f \subseteq {{\,\mathrm{dom}\,}}\partial g$ and ${{\,\mathrm{dom}\,}}\partial g^* \subseteq {{\,\mathrm{dom}\,}}\partial f^*$ [46]. Our functions f and g, defined above, satisfy these conditions: By Appendix Lemma 4, ${{\,\mathrm{dom}\,}}f = {{\,\mathrm{conv}\,}}\varDelta _{W_-} \subseteq {{\,\mathrm{conv}\,}}\{ {\mathbf {s}}\in {\mathbb {Z}}^n \,:\, {\mathbf {t}}+{\mathbf {s}}\in \varDelta _{W_+} \} = {{\,\mathrm{dom}\,}}g$, ${{\,\mathrm{dom}\,}}g^* = {\mathbb {R}}^n = {{\,\mathrm{dom}\,}}f^*$, and by Lemma 1 the domains of the respective functions coincide with the domains of their subdifferentials.

However, ${{\bar{{\mathbf {s}}}}}$ being a stationary point for f and g is not a sufficient condition for ${{\bar{{\mathbf {s}}}}}$ to globally minimize $f-g$. So we check whether a corresponding ${\mathbf {p}}$ is a local – and hence global – minimizer of the Lyapunov function L. If it is, then it is indeed an equilibrium price. If not, we go one step in the direction of steepest descent of the Lyapunov function and then restart the DC-algorithm. This is Algorithm 2 (where lines 1–8 are exactly Algorithm 1 with expressed in their economic interpretation; see Lemma 1 for more details).

The value of $L({\mathbf {p}}^k)$ decreases by at least one in every iteration 2–8 of the algorithm until the termination criterion in Step 5 is satisfied (we refer to Appendix A.5 for details). Whenever the algorithm is restarted in Step 10, L also decreases by at least one. Since there exists a minimizer for L, the algorithm terminates:

Theorem 3

Algorithm 2 always terminates in a Walrasian equilibrium price.

Algorithm 2 does not specify how to choose bundles $\mathbf{{s}}^k$ and prices ${\mathbf {p}}^{k+1}$. Determining bundles $\mathbf{{s}}^k$ is particularly simple when valuations are expressed in the SSPMA - we just allocate each bid with utility maximizing goods. For finding prices ${\mathbf {p}}^{k+1}$, an instance of (LP) must be solved. We use a min-cost flow solver to do so. Appendix A.6 explains our implementation in more detail.

Obtaining sharp worst-case bounds for Algorithm 2 is challenging due to the very generic nature of the DC-Algorithm 1. Note that the class of functions representable as a difference of convex functions is very large - for example, it contains all functions with continuous second derivative [24]. Also recall that [29] shows that minimizing the difference of two general $M^\natural$-convex functions is NP-hard. Intuitively, we expect Algorithm 2 to perform particularly well when the number of negative bids is small. For example, when there are no negative bids at all, the algorithm boils down to solving the min-cost flow problem (LP). For the general case, we provide the following simple bound for Algorithm 2 by the number of negative bids.

First, observe that we may implement Step 3 to choose a bundle ${\mathbf {s}}^k$ which is uniquely demanded at some price–and indeed we do so in our practical implementation, because the vertices of demand sets $D_{|{\mathcal {B}}_-|}({\mathbf {p}}^k)$ have this property. We also assume that prices in Step 4 are chosen deterministically – for the same bundle, the algorithm always returns the same price.

Second, observe that if ${\mathbf {s}}^{k+1} = {\mathbf {s}}^k$, then the chosen prices in Step 4 are also equal, so the termination criterion 5 is satisfied. After a possible restart, the algorithm also can never reach this bundle again – this would contradict the strict monotonicity properties as we explain in the Appendix (Lemma 6). So in the worst case, after each restart of the algorithm, we directly choose bundles ${\mathbf {s}}^0={\mathbf {s}}^1$ in the first two iterations which immediately causes another restart. It follows that every possible bundle uniquely demanded in the negative auction is chosen at most twice in Step 3 of the algorithm.³⁰ If there is only one single negative bid, these are exactly $n+1$ bundles, and so the number of iterations, by which we mean the total number of iterations through the loop from Step 2 to Step 8, of Algorithm 2 is in ${\mathcal {O}}(n)$. Note that after each restart, we iterate at least once through the for loop, so the number of restarts is also in ${\mathcal {O}}(n)$. More generally, Proposition 3 shows that ${{n+|{\mathcal {B}}_-|}\atopwithdelims (){n}}$ bundles are demanded in total in the negative auction if the weights of all negative bids are equal to one. Since the number of uniquely demanded bundles does not change if we increase weights, ${{n+|{\mathcal {B}}_-|}\atopwithdelims (){n}}$ bounds the number of uniquely demanded bundles in general negative auctions. This therefore provides an upper bound on the number of bundles demanded uniquely in this auction, so on the number of iterations of Algorithm 2.

Proposition 5

Algorithm 2 requires at most ${\mathcal {O}}\left( {{n+|{\mathcal {B}}_-|}\atopwithdelims (){n}}\right)$ iterations for solving the equilibrium pricing problem.

This analysis gives a rather pessimistic worst-case bound for the algorithm, but it suggests that the algorithm performs particularly well with a low number of negative bids. In fact, in our experimental evaluation, we find that the DC algorithm is even faster than steepest descent in these environments.

When there are only positive bids, Algorithm 2 boils down to solving a single linear program, which can be formulated as a min-cost flow problem on a graph with $|V| = {\mathcal {O}}(n+|{\mathcal {B}}|)$ vertices and $|E|={\mathcal {O}}(n|{\mathcal {B}}|)$ edges (see Appendix A.6). The enhanced capacity scaling algorithm [1] finds an optimal integral solution in

$$\begin{aligned} {\mathcal {O}}(|E|\log |V| (|E|+|V|\log |V|)) \end{aligned}$$

iterations, which implies that the pricing problem can be solved in time

$$\begin{aligned} {\mathcal {O}}(n^2|{\mathcal {B}}|^2\log ^2(n+|{\mathcal {B}}|)) = \tilde{ {\mathcal {O}}}(n^2|{\mathcal {B}}|^2) \end{aligned}$$

this way. On the other hand, [6] provide the worst-case bound ${\mathcal {O}}(n^2|{\mathcal {B}}|^2\log M + n|{\mathcal {B}}|T(n))$ for the steepest descent algorithm, where $M = \max _{{\mathbf {b}} \in {\mathcal {B}}} \Vert {\mathbf {b}} \Vert _{\infty }$ is the maximal price of a bid vector and T(n) is the complexity of minimizing an n-dimensional submodular function. Note that the total asymptotic runtime of the network flow formulation coincides with the first summand $n^2|{\mathcal {B}}|^2\log M$ of the steepest descent formulation up to a logarithmic factor. However, we may expect the second summand $n|{\mathcal {B}}|T(n)$ to dominate the runtime. To the best of our knowledge, the best known weakly polynomial worst case bound for minimizing a general integral submodular function is ${\mathcal {O}}(n^2 \log (nU) \cdot EO + n^3\log ^{{\mathcal {O}}(1)} (nU))$, where U is an upper bound for the maximal value of the submodular function [16, 30]. Thus, the worst-case bound for $n|{\mathcal {B}}|T(n)$ cannot be better than ${\mathcal {O}}(n^4|{\mathcal {B}}|\log (nU))$ using known methods. Hence, in particular when the number of goods increases, we may expect the min-cost flow formulation to outperform the steepest descent formulation in the absence of negative bids.³¹

[42] present a polynomial time algorithm for computing competitive equilibrium prices for bidders with general preferences and provide a specialization of their algorithm for gross substitutes valuations, which is the fastest algorithm for this setting currently known. They provide the worst-case bound

$$\begin{aligned}&mn\cdot T_V + {\mathcal {O}}(mn\log m + n^3\log (mnM) + n^3 \log ^{{\mathcal {O}}(1)}(mnM)) \\&\quad = \tilde{{\mathcal {O}}}(mn\cdot T_V + n^3) \end{aligned}$$

for the runtime of their algorithm, where n is the number of goods, m is the number of bids, M is the maximum value a bid has for a bundle and $T_V$ is the runtime of the value oracle. So the worst-case runtime of [42]’s algorithm grows linearly in the number of bidders, while the worst-case runtime of our algorithm (when all its bids are positive) grows quadratically.³² However, our algorithm performs much better than [42]’s as we increase the number of units available without changing the number of goods (when all the SSPMA bids are positive), because its worst case is unaffected, whilst [42]’s worst case is cubic in the number of units because they must treat each additional unit as an additional good.³³ Moreover, even when there are only small numbers of units available of each distinct good, we expect the use cases for the two algorithms to be different: in a setting where fast direct access to bidders’ valuations is possible, we expect applying [42]’s algorithm would be preferable to first computing the corresponding SSPMA bids for every bidder and then applying our algorithm. On the other hand, when preferences are provided by bidders in the SSPMA bid language, we expect it is faster to use our algorithm directly, rather than translating the SSPMA bids into value oracles first and then using [42].

4.2 Experimental evaluation

We implemented both the DC auction algorithm and a steepest descent algorithm based on the Lyapunov function. The Lyapunov approach and the restart step in the DC algorithm require the minimization of a submodular function. As in [6], we use the Fujishige-Wolfe algorithm [15], which in practice often outperforms other submodular minimization algorithms.

In our experimental evaluation we solved problems with 10-50 goods, 1020/1200/1500/3020/3500 positive and 20/200/500 negative bids. We drew on a specialization of the algorithm by [5] to randomly generate valid groups of bids, each group consisting of 3 positive and 1 negative bids. Algorithm 3 in Appendix A.7 describes this procedure, and Table 2 in Appendix A.8 gives our results.

The DC algorithm appears to be faster if there are not too many negative bids (less than 200, in our experiments). Table 1 shows a selection of our results for the case of 20 negative bids. So if the number of negative bids is small, which we consider the most likely scenario (see Sect. 2.3), our DC algorithm is a particularly good choice.

Table 1 Runtimes of the DC and the steepest descent (SD)-algorithm for instances where the number of negative bids is low

However, the main conclusion from Table 2 is that both algorithms are very fast, solving even the largest problems in our experiments in less than 3 seconds. Experiments with up to 50 goods and 10,000 bids can also be solved in a few seconds only.³⁴

5 Conclusion

Strong substitutes valuations are of central importance for both theory and practical applications. We have developed a new algorithm for computing competitive equilibrium prices when agents’ preferences are expressed using the Strong Substitutes Product-Mix Auction bidding language, a compact language that permits the expression of all strong substitutes valuations (and no other valuations). By contrast with a previous approach of using a standard steepest-descent algorithm that tests candidate solutions in turn, we began from the economics of the problem. We used the fact that the shadow prices of two separate linear programs that maximize value for “positive” and “negative” bids, respectively, must be equal, and proved that our model formulation is dual to the Lyapunov function. We also used the bidding language to provide new insight into the geometric structure of strong substitutes valuations.

Appendix: Additional proofs

1.1 Proof of Proposition 1

We need the following simple Lemmas.

Lemma 2

(See, e.g. [44] Lemma 3.1.11) Let $A,B \subseteq {\mathbb {R}}^n$ be convex. Then $(A+B)-B=A$.

Lemma 3

Suppose $({{\,\mathrm{conv}\,}}A)\cap {\mathbb {Z}}^n=A$ and $({{\,\mathrm{conv}\,}}B)\cap {\mathbb {Z}}^n=B$. Then $({{\,\mathrm{conv}\,}}A-{{\,\mathrm{conv}\,}}B)\cap {\mathbb {Z}}^n=A-B$.

Proof

If ${\mathbf {x}}\in ({{\,\mathrm{conv}\,}}A-{{\,\mathrm{conv}\,}}B)\cap {\mathbb {Z}}^n$ then ${\mathbf {x}}\in {\mathbb {Z}}^n$ and ${\mathbf {x}}+{{\,\mathrm{conv}\,}}B\subseteq {{\,\mathrm{conv}\,}}A$, so ${\mathbf {x}}+({{\,\mathrm{conv}\,}}B)\cap {\mathbb {Z}}^n\subseteq ({{\,\mathrm{conv}\,}}A)\cap {\mathbb {Z}}^n$, and therefore ${\mathbf {x}}+B\subseteq A$. So ${\mathbf {x}}\in A-B$. Conversely, if ${\mathbf {x}}\in A-B$ then ${\mathbf {x}}\in \mathbb {Z}^n$, and ${\mathbf {x}}+B\subseteq A$ implies ${{\,\mathrm{conv}\,}}({\mathbf {x}}+B)={\mathbf {x}}+{{\,\mathrm{conv}\,}}B\subseteq {{\,\mathrm{conv}\,}}A$. $\square$

Proof of Proposition 1

By the strong substitutes property, the sets $D_{{\mathcal {B}}_+}({\mathbf {p}})$ and $D_{|{\mathcal {B}}_-|}({\mathbf {p}})$ are equal to the set of integer points of their respective convex hull, as by definition is $D_{{\mathcal {B}}}({\mathbf {p}})$. So if we can show that ${{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}({\mathbf {p}}) + {{\,\mathrm{conv}\,}}D_{|{\mathcal {B}}_-|}({\mathbf {p}}) = {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}_+}({\mathbf {p}})$, this implies by Lemma 2 that ${{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}({\mathbf {p}}) = {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}_+}({\mathbf {p}}) - {{\,\mathrm{conv}\,}}D_{|{\mathcal {B}}_-|}({\mathbf {p}})$ and by Lemma 3 consequently that $D_{{\mathcal {B}}}({\mathbf {p}}) = D_{{\mathcal {B}}_+}({\mathbf {p}}) - D_{|{\mathcal {B}}_-|}({\mathbf {p}})$.

But, as ${\mathcal {B}}$ is a valid set of bids, we know by [6] Theorem 2.3 that $u_{{\mathcal {B}}}$ is the indirect utility of a strong substitutes valuation v such that $D_v({\mathbf {p}})=D_{{\mathcal {B}}}({\mathbf {p}})$ for all ${\mathbf {p}}\in {\mathbb {R}}^n$. It follows that each vertex ${\mathbf {x}}$ of $D_{{\mathcal {B}}}({\mathbf {p}})$ is the unique element of $D_{{\mathcal {B}}}({\mathbf {q}})$ for a price ${\mathbf {q}}$ close to ${\mathbf {p}}$ and such that ${\mathbf {x}}$ minimizes $({\mathbf {q}}-{\mathbf {p}})\cdot {\mathbf {x}}'$ for ${\mathbf {x}}'\in D_{{\mathcal {B}}}({\mathbf {p}})$. But similarly the minimizers of $({\mathbf {q}}-{\mathbf {p}})\cdot {\mathbf {x}}'$ for ${\mathbf {x}}'\in D_{{\mathcal {B}}_+}({\mathbf {p}})$ and ${\mathbf {x}}'\in D_{|{\mathcal {B}}_-|}({\mathbf {p}})$ are, respectively, the unique elements of $D_{{\mathcal {B}}_+}({\mathbf {q}})$ and $D_{|{\mathcal {B}}_-|}({\mathbf {q}})$. By definition, we have $D_{{\mathcal {B}}}({\mathbf {q}}) = D_{{\mathcal {B}}_+}({\mathbf {q}})-D_{|{\mathcal {B}}_-|}({\mathbf {q}})$, so $D_{{\mathcal {B}}}({\mathbf {q}}) + D_{|{\mathcal {B}}_-|}({\mathbf {q}}) = D_{B_+}({\mathbf {q}})$. As this holds for all extreme points of $D_{{\mathcal {B}}}({\mathbf {p}})$, it follows that ${{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}({\mathbf {p}}) + {{\,\mathrm{conv}\,}}D_{|{\mathcal {B}}_-|}({\mathbf {p}}) = {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}_+}({\mathbf {p}})$, as required. $\square$

1.2 The valuation $v_r$ from [40]

We now explain the construction of $v_r$ from [40]. Let $G = (V,E)$ be an undirected graph with 4 vertices and 6 edges $E = \{1,\dots ,6\}$, such that every vertex is connected to every other vertex by an edge (see Figure 5).

Fig. 5

Graph used to construct the valuation $v_r$ from [40]

A subset H of E is called independent if it contains no cycles. For any $H \subseteq E$, the rank of H is the maximal cardinality of an independent subset contained in H:

$$\begin{aligned} {{\,\mathrm{rank}\,}}\left( H\right) = \max \left\{ |H'|:\, H' \subseteq H \text { is independent}\right\} . \end{aligned}$$

The rank function induces the valuation $v_r:\{0,1\}^6\rightarrow {\mathbb {Z}}$ given by $v_r({\mathbf {x}})= {{\,\mathrm{rank}\,}}\left( \left\{ i :\, x_i =1 \right\} \right)$. As [40] show, $v_r$ is strong substitutes. However, it does not satisfy the property of strong exchangeability which, as [40] show, is a characteristic of every endowed assignment valuation. Consequently, it is not possible to express $v_r$ by endowed assignment messages. We demonstrate, however, that it can be expressed using the SSPMA. Note that valuations induced by SSPMA bids are always defined on a scaled simplex $\varDelta _W$ for some total weight $W \in {\mathbb {Z}}_{\ge 0}$. We thus naturally extend $v_r$ to $\varDelta _6 \supseteq \{0,1\}^6$ by assuming free disposal: $v_r({\mathbf {x}}) = {{\,\mathrm{rank}\,}}(\{i: x_i \ge 1\})$.

Proof of Proposition 2

Given $H\subseteq E$, we write ${\mathbf {b}}^H: = \sum _{i \in H} {\mathbf {e}}_i$. We make the following bids:

• 0. Place a bid ${\mathbf {b}}^{\emptyset }$ with $w({\mathbf {b}}^{\emptyset }) = 3$.

• 1. For all $H\subseteq E$ with $|H|=3$ and $H^c$ is a cycle in G, make a bid ${\mathbf {b}}^H$ with $w({\mathbf {b}}^H) = 1$.

• 2. For all $H\subseteq E$ constituting a cycle of length 4, make a bid ${\mathbf {b}}^H$ with $w({\mathbf {b}}^H) = 1$.

• 3. For all $H\subseteq E$ with $|H|=5$ make a bid ${\mathbf {b}}^H$ with $w({\mathbf {b}}^H)=-1$.

• 4. Make a bid ${\mathbf {b}}^E$ with $w({\mathbf {b}}^E) = 2$.

Denote by $v_r({\mathbf {x}}) = {{\,\mathrm{rank}\,}}(\{i:\, x_i \ge 1\})$ for ${\mathbf {x}}\in \varDelta _6$ the valuation induced by the rank function, and by $v_{{\mathcal {B}}}({\mathbf {x}})$ the valuation induced by the above bids. Our goal is to show $v_{{\mathcal {B}}}=v_r$. Note that bid 0 only ensures that the domains of $v_r$ and $v_{{\mathcal {B}}}$ are equal, and does not “contribute” to the valuations apart from this. So let us check that indeed ${{\,\mathrm{dom}\,}}v_{{\mathcal {B}}} = \varDelta _6$. There is 1 bid of type 0, 4 bids of type 1, 3 bids of type 2, and 1 bid of type 4. So summing up the weights of these bids gives $W_+ = 12$. On the other hand, there are 6 bids of type 3, so $W_- = 6$, and consequently ${{\,\mathrm{dom}\,}}v_{{\mathcal {B}}} = \varDelta _{12-6} = \varDelta _6$.

We have $u_{r}({\mathbf {p}}) = \max _{{\mathbf {x}}\in \varDelta _6} v_{r}({\mathbf {x}})-\langle {\mathbf {p}}, {\mathbf {x}}\rangle$ and $u_{{\mathcal {B}}}$ is defined by Equation (3). Recall from Section 2.1 that, for $i\in \{r,{\mathcal {B}}\}$, we have $v_{i}({\mathbf {x}}) = \min _{{\mathbf {p}}\in {\mathbb {R}}^6} u_{i}({\mathbf {p}}) + \langle {\mathbf {p}},{\mathbf {x}}\rangle$, where one can check that ${\mathbf {p}}\mapsto u_{i}({\mathbf {p}}) + \langle {\mathbf {p}}, {\mathbf {x}}\rangle$ always possesses a non-negative minimizer ${\mathbf {p}}$ for ${\mathbf {x}}\in \varDelta _6$. So in order to prove Proposition 2, it suffices to show that $u_{r}({\mathbf {p}}) = u_{{\mathcal {B}}}({\mathbf {p}})$ for all ${\mathbf {p}}\in {\mathbb {R}}^6_{\ge 0}$. By $\mathrm {L}^\natural$-convexity of $u_r$ and $u_{{\mathcal {B}}}$ [36], both are determined uniquely on ${\mathbb {R}}^6_{\ge 0}$ by the values $u_{r}({\mathbf {p}})$ and, respectively, $u_{{\mathcal {B}}}({\mathbf {p}})$ for ${\mathbf {p}}\in {\mathbb {Z}}_{\ge 0}^6$. Moreover, given ${\mathbf {p}}\in {\mathbb {Z}}_{\ge 0}^6$, define ${\tilde{{\mathbf {p}}}}$ by ${\tilde{p}}_i = p_i$ if $p_i \le 1$ and ${\tilde{p}}_i = 1$, otherwise. Since the marginal value of any good is at most 1 for $v_r$, and no bid in ${\mathcal {B}}$ has any value greater than 1, allocating a good i with ${\tilde{p}}_i =1$ can never increase utilities, so we have $u_{r}({\mathbf {p}}) = u_{r}({{\tilde{{\mathbf {p}}}}})$ and $u_{{\mathcal {B}}}({\mathbf {p}}) = u_{{\mathcal {B}}}({{\tilde{{\mathbf {p}}}}})$. So our problem reduces to showing that $u_r({\mathbf {p}}) = u_{{\mathcal {B}}}({\mathbf {p}})$ for all ${\mathbf {p}}\in \{0,1\}^6$. For $H \subseteq \{1,\dots ,6\}$, denote by ${\mathbf {p}}^H \in \{0,1\}^6$ the price vector with $p_i^H = 1$ if and only if $i \in H$. We will show that $u_r({\mathbf {p}}^H) = u_{{\mathcal {B}}}({\mathbf {p}}^H)$ for all $H \subseteq \{1,\dots ,6\}$.

We claim that $u_r({\mathbf {p}}^H) = {{\,\mathrm{rank}\,}}(H^c)$. To see this, let ${\mathbf {x}}$ be a bundle with $u_r({\mathbf {p}}^H) = v_r({\mathbf {x}})-\langle {\mathbf {p}}^H, {\mathbf {x}}\rangle = v_r({\mathbf {x}}) - \sum _{i \in H} {\mathbf {x}}_i$. Let $P = \{i:\, x_i \ge 1\}$. Then

$$\begin{aligned} u_r({\mathbf {p}}^H) = {{\,\mathrm{rank}\,}}(P)-|P \cap H|&\le {{\,\mathrm{rank}\,}}(P \cap H^c) + {{\,\mathrm{rank}\,}}(P \cap H) - |P \cap H| \\&\le {{\,\mathrm{rank}\,}}(P \cap H^c) + |P \cap H| - |P \cap H| \\&\le {{\,\mathrm{rank}\,}}(H^c) = v_r\left( \sum _{i \in H^c}{\mathbf {e}}_i\right) -0 \le u_r({\mathbf {p}}^H) \end{aligned}$$

by properties of matroid rank functions. Consequently, equality must hold everywhere, so $u_r({\mathbf {p}}^H) = {{\,\mathrm{rank}\,}}(H^c)$.

Regarding the indirect utility of our bids, we observe that at prices ${\mathbf {p}}^H$, the bid ${\mathbf {b}}^{\tilde{H}}$ generates a utility of $w({\mathbf {b}}^{\tilde{H}})$ if and only if $\tilde{H} \cap H^c \ne \emptyset$, i.e., if and only if ${\mathbf {b}}^{\tilde{H}}$ has positive value for at least one good not in H. Otherwise it generates utility 0.

We now consider all subsets $H \subseteq \{1,\dots ,6\}$ and show that in each case, $u_r({\mathbf {p}}^H) = u_{{\mathcal {B}}}({\mathbf {p}}^H)$.

First, for price vectors ${\mathbf {p}}^H$ with $|H| < 3$, all bids are accepted, since every placed bid has positive values for at least 3 goods. There are 4 bids of type 1, 3 bids of type 2, 6 bids of type 3 and 1 bid of type 4. In total, we get

$$\begin{aligned} u_b({\mathbf {p}}^H) = 4\cdot 1 + 3 \cdot 1 + 6 \cdot (-1) + 1 \cdot 2 = 3. \end{aligned}$$

On the other hand, one can see from Fig. 5 that every subset containing at least 4 edges contains a cycle-free subset of cardinality 3, and there is no cycle-free subset with more than 3 elements. Consequently, $u_r({\mathbf {p}}^H) = {{\,\mathrm{rank}\,}}(H^c) = 3$.

Now consider ${\mathbf {p}}^H$ with $|H| = 3$. Obviously, all bids on more than 3 edges get accepted. A bid ${\mathbf {b}}^{\tilde{H}}$ with $\tilde{H} = 3$ is rejected, if and only if $H=\tilde{H}$. In this case, $H^c$ is a cycle of length 3, so $u_r({\mathbf {p}}^H) = {{\,\mathrm{rank}\,}}(H^c) = 2$. We then also clearly have $u_{{\mathcal {B}}}({\mathbf {p}}^H) = 2$, since exactly one bid is rejected, and all others are accepted.

On the other hand, if $|H|=3$ and no bid is rejected, $H^c$ is cycle free, so $u_r({\mathbf {p}}^H) = {{\,\mathrm{rank}\,}}(H^c) = 3 = u_{{\mathcal {B}}}({\mathbf {p}}^H)$.

Next, suppose $|H| = 4$, so $u_r({\mathbf {p}}^H) = {{\,\mathrm{rank}\,}}(H^c) = 2$, because 2 edges cannot form a cycle. Regarding the bids, if H is a cycle of length 4, one bid of type 2 is rejected. In this case, $H^c$ consists of two non adjacent edges. Consequently, there is no $i \in H$ such that $\{i\} \cup H^c$ is a cycle. Equivalently, for no $\tilde{H} \subseteq H$ with $|\tilde{H}| = 3$ we have that $\tilde{H}^c$ is a cycle, so no bid of type 1 is rejected, and $u_{{\mathcal {B}}}({\mathbf {p}}^H) = 2$.

If, otherwise, H has no cycle of length 4, $H^c$ consists of two adjacent edges. Thus, there is a unique $e \in H$ with $\{i\} \cup H^c$ being a cycle, so a single bid of type 1 is rejected, which means that again $u_{{\mathcal {B}}}({\mathbf {p}}^H) = 2$.

Concerning $|H|=5$, since the graph is complete, we can assume by symmetry that $H = \{1,2,3,4,5\}$. Then the bids ${\mathbf {b}}^{\tilde{H}}$ with

$$\begin{aligned} \tilde{H} \in \left\{ \{1,2,5\},\{3,4,5\}, \{1,2,3,4\}, \{1,2,3,4,5\} \right\} \end{aligned}$$

are rejected, and $u_{{\mathcal {B}}}({\mathbf {p}}^H) = 2 \cdot 1 + 2 \cdot 1 + 5 \cdot (-1) + 1 \cdot 2 = 1 = {{\,\mathrm{rank}\,}}(H^c) = u_r({\mathbf {p}}^H)$.

Finally, for $H = E$, all bids are rejected, so $u_{{\mathcal {B}}}({\mathbf {p}}^H) = u_r({\mathbf {p}}^H) = 0$.

We have shown that for all $p \in \{0,1\}^6$, $u_{{\mathcal {B}}}({\mathbf {p}}) = u_r({\mathbf {p}})$, which proves our statement. $\square$

1.3 Proof of Proposition 3

Proof of Proposition 3

We will show that $D = \varDelta _W={\mathbb {Z}}^n \cap W \varDelta$, where $\varDelta$ is the standard simplex in dimension n, spanned by ${\mathbf {0}}$ and the standard unit vectors ${\mathbf {e}}_i$. Since $W \varDelta$ contains exactly ${n+W}\atopwithdelims (){n}$ integer points [10, Theorem 2.2], the remaining results follow.

By the strong substitutes property, $D=({{\,\mathrm{conv}\,}}D) \cap {\mathbb {Z}}^n$, so it suffices to show that ${{\,\mathrm{conv}\,}}D = W \varDelta$. To that goal we note that if we set $p_i = -1$ and $p_j$ very large for $j \ne i$, then $D({\mathbf {p}}) = \{W{\mathbf {e}}_i\}$, since every bid ${\mathbf {b}}$ is allocated with $w({\mathbf {b}})$ items of good i and the total weight of all bids is W. Also, for a very large price (in every coordinate) ${\mathbf {p}}$, we have $D_{{\mathcal {B}}}({\mathbf {p}}) = \{{\mathbf {0}}\}$. Consequently, ${{\,\mathrm{conv}\,}}D \supseteq W\varDelta$. To see the reverse inclusion, note that any demanded bundle cannot contain strictly more than W items, as some bid would have to be allocated with more than $w({\mathbf {b}})$ items otherwise. The lower bounds come from the basic inequality ${m \atopwithdelims ()k} \ge (m/k)^k$. $\square$

1.4 Proof of Theorem 1

Proof of Lemma 1

The linear program (LP) of Sect. 3 is clearly defined for any ${\mathbf {x}}={\mathbf {t}}\in {{\,\mathrm{conv}\,}}\varDelta _W$, and we can use this to assign a real value to ${\tilde{v}}_{{\mathcal {B}}}({\mathbf {x}})$ for ${\mathbf {x}}\in {{\,\mathrm{conv}\,}}\varDelta _W$ and set $f = -{\tilde{v}}_{{\mathcal {B}}}$. Since f is a polyhedral convex function according to [43, p. 172], its subdifferential is nonempty at every point of ${{\,\mathrm{dom}\,}}f$ [43, Theorem 23.10], so ${{\,\mathrm{dom}\,}}\partial f = {{\,\mathrm{dom}\,}}f = {{\,\mathrm{conv}\,}}\varDelta _W$. Let us consider the convex conjugate $f^*$ of $f({\mathbf {x}}) = -{\tilde{v}}_{{\mathcal {B}}}({\mathbf {x}})$. By definition, $f^*({\mathbf {q}}) = \max _{{\mathbf {x}}\in {{\,\mathrm{conv}\,}}\varDelta _W} \langle {\mathbf {q}}, {\mathbf {x}}\rangle + {\tilde{v}}_{{\mathcal {B}}}({\mathbf {x}})$, or in LP-form:

$$\begin{aligned}&\begin{array}{llll} f^*({\mathbf {q}}) = \max \sum _{{\mathbf {b}}\in {\mathcal {B}}} \sum _{i \in [n]} (b_i+q_i) y_{{\mathbf {b}}i} &{}&{}\\ &{}\text {s.t.} \ x_i = \sum _{{\mathbf {b}}\in {\mathcal {B}}} y_{{\mathbf {b}}i} \forall i \in [n] &{}\\ &{}\sum _{i \in [n]} y_{{\mathbf {b}}i} \le w({\mathbf {b}}) \forall {\mathbf {b}}\in {\mathcal {B}}&{} \\ &{}y_{{\mathbf {b}}i} \ge 0 \forall {\mathbf {b}}\in {\mathcal {B}},\, i \in [n].&{} \end{array} \end{aligned}$$

Note that since the set of feasible solutions ${\mathbf {x}}$ is compact, $f^*({\mathbf {q}})$ attains a finite value for all ${\mathbf {q}}\in {\mathbb {R}}^n$, so ${{\,\mathrm{dom}\,}}\partial f^* = {{\,\mathrm{dom}\,}}f^* = {\mathbb {R}}^n$, since $f^*$ is also polyhedral convex. Let us now derive the expressions for $\partial f$ and $\partial f^*$. To that goal, note that ${\mathbf {x}}$ maximizes the above linear program if and only if ${\mathbf {x}}\in \partial f^*({\mathbf {q}})$, which is in turn equivalent to ${\mathbf {q}}\in \partial f({\mathbf {x}})$ [43, Theorem 23.5]. It is not hard to see from Equations (1) and (2) that the variables $y_{{\mathbf {b}}i}$ constitute an optimal solution for the above linear program, if and only if for every fixed ${\mathbf {b}}$ the vector $(y_{{\mathbf {b}}i})_{i=1}^n$ lies in ${{\,\mathrm{conv}\,}}D_{{\mathbf {b}}}(-{\mathbf {q}})$, which can be seen to be equivalent to ${\mathbf {x}}\in {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}(-{\mathbf {q}})$ (recall that in the case of only positive bids, the aggregate demand set is just the Minkowski sum of the individual demand sets). It now directly follows that $\partial f^*({\mathbf {q}}) = {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}(-{\mathbf {q}})$ and $\partial f({\mathbf {x}}) = -\{{\mathbf {p}}\,:\, {\mathbf {x}}\in {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}({\mathbf {p}}) \}$. $\square$

Lemma 4

Let ${\mathcal {B}}$ be a valid collection of bids. Let ${\mathbf {t}}\in \varDelta _W$ and ${\mathbf {s}}\in \varDelta _{W_-}$. Then ${\mathbf {t}}+{\mathbf {s}}\in \varDelta _{W_+}$. Consequently, for the convex extensions f of ${\mathbf {s}}\mapsto -v_{|{\mathcal {B}}_-|}({\mathbf {s}})$ and g of ${\mathbf {s}}\mapsto -v_{{\mathcal {B}}_+}({\mathbf {t}}+ {\mathbf {s}})$ we have that ${{\,\mathrm{dom}\,}}f = {{\,\mathrm{conv}\,}}\varDelta _{W_-} \subseteq {{\,\mathrm{conv}\,}}\{{\mathbf {s}}\in {\mathbb {Z}}^n\,:\, {\mathbf {t}}+ {\mathbf {s}}\in \varDelta _{W_+}\} = {{\,\mathrm{dom}\,}}g$.

Proof

As ${\mathbf {t}}\in \varDelta _{W}$, we have $\sum _{i=1}^n t_i \le W$. Similarly, $\sum _{i=1}^n s_i \le W_-$. Since $W = W_+-W_-$ it follows that $\sum _{i=1}^n (t_i+s_i) \le W_+$, so ${\mathbf {t}}+ {\mathbf {s}}\in \varDelta _{W_+}$. This directly implies the second part of the Lemma. $\square$

Proof of Theorem 1

Let f be the convex extension of ${\mathbf {s}}\mapsto -v_{|{\mathcal {B}}_-|}({\mathbf {s}})$ and g the convex extension of ${\mathbf {s}}\mapsto -v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})$. Then ${{\,\mathrm{dom}\,}}f = {{\,\mathrm{conv}\,}}\varDelta _{W_-} \subseteq {{\,\mathrm{dom}\,}}g$ and ${{\,\mathrm{dom}\,}}g^* = {\mathbb {R}}^n = f^*$ by Lemmas 1 and 4. From Lemma 1 we know that $f^*({\mathbf {q}}) = u_{|{\mathcal {B}}_-|}(-{\mathbf {q}})$. Similarly, $g^*({\mathbf {q}}) = u_{{\mathcal {B}}_+}(-{\mathbf {q}}) - \langle {\mathbf {q}}, {\mathbf {t}}\rangle$. So we can apply Theorem 2 to $f-g$ and get

$$\begin{aligned} \min _{{\mathbf {s}}\in {{\,\mathrm{conv}\,}}\varDelta _{W_-}} {\tilde{v}}_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}}) - {\tilde{v}}_{|{\mathcal {B}}_-|}({\mathbf {s}}) = \min _{{\mathbf {q}}\in {\mathbb {R}}^n} u_{{\mathcal {B}}_+}(-{\mathbf {q}}) - u_{|{\mathcal {B}}_-|}(-{\mathbf {q}}) - \langle {\mathbf {q}}, {\mathbf {t}}\rangle , \end{aligned}$$

if any of the two problems has a solution. By substituting ${\mathbf {p}}= -{\mathbf {q}}$, we can rewrite the problem on the right as

$$\begin{aligned} \min _{{\mathbf {p}}\in {\mathbb {R}}^n} u_{{\mathcal {B}}_+}({\mathbf {p}}) - u_{|{\mathcal {B}}_-|}({\mathbf {p}}) + \langle {\mathbf {p}}, {\mathbf {t}}\rangle = \min _{{\mathbf {p}}\in {\mathbb {R}}^n} u_{{\mathcal {B}}}({\mathbf {p}}) + \langle {\mathbf {p}}, {\mathbf {t}}\rangle . \end{aligned}$$

The expression $u_{{\mathcal {B}}}({\mathbf {p}}) + \langle {\mathbf {p}}, {\mathbf {t}}\rangle$ is exactly the Lyapunov function $L({\mathbf {p}})$ introduced in Section 3. For strong substitutes valuations, the Lyapunov function always attains a minimum, and the set of minimizers is equal to the set of equilibrium prices for the target ${\mathbf {t}}$ [3]. Consequently, the problem $\min _{{\mathbf {s}}\in {{\,\mathrm{conv}\,}}\varDelta _{W_-}} {\tilde{v}}_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}}) - {\tilde{v}}_{|{\mathcal {B}}_-|}({\mathbf {s}})$ also has a solution ${\mathbf {s}}\in {{\,\mathrm{conv}\,}}\varDelta _{W_-}$, and the values of both minimization problems are equal. There exists at least one integral solution ${{\bar{{\mathbf {s}}}}} \in \varDelta _{W}$ to this problem: Let ${\mathbf {p}}$ be a minimizer of the Lyapunov function. By Theorem 2, each ${\mathbf {s}}\in \partial f^*(-{\mathbf {p}}) = {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}}({\mathbf {p}})$ minimizes ${\tilde{v}}_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}})-{\tilde{v}}_{|{\mathcal {B}}_-|}({\mathbf {s}})$, so in particular each ${{\bar{{\mathbf {s}}}}} \in D_{{\mathcal {B}}}({\mathbf {p}}) \ne \emptyset$ does so. Since the valuations $v_{{\mathcal {B}}_+}$ and $v_{|{\mathcal {B}}_-|}$ coincide on integral bundles with ${\tilde{v}}_{{\mathcal {B}}_+}$ and ${\tilde{v}}_{|{\mathcal {B}}_-|}$ by construction,

$$\begin{aligned} \min _{{\mathbf {s}}\in \varDelta _{W_-}} v_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}}) - v_{|{\mathcal {B}}_-|}({\mathbf {s}}) = \min _{{\mathbf {s}}\in {{\,\mathrm{conv}\,}}\varDelta _{W_-}} {\tilde{v}}_{{\mathcal {B}}_+}({\mathbf {t}}+{\mathbf {s}}) - v_{|{\mathcal {B}}_-|}({\mathbf {s}}) = \min _{{\mathbf {p}}\in {\mathbb {R}}^n} L({\mathbf {p}}). \end{aligned}$$

Finally, again by Theorem 2, if ${{\bar{{\mathbf {s}}}}} \in \varDelta _{W_-}$ is a minimizer, each ${\mathbf {p}}$ with $-{{\bar{{\mathbf {p}}}}} \in \partial g({\mathbf {t}}+{\mathbf {s}}) = -\{{\mathbf {p}}\in {\mathbb {R}}^n\,:\, {\mathbf {t}}+{{\bar{{\mathbf {s}}}}} \in {{\,\mathrm{conv}\,}}D_{{\mathcal {B}}_+}({\mathbf {p}}) \}$ minimizes L. In other words, each equilibrium price for ${\mathbf {t}}+ {\mathbf {s}}$ for the positive auction is an equilibrium price for the complete auction as well. $\square$

1.5 Proof of Theorem 3

We now prove Theorem 3 which states that our DC-algorithm always terminates in a global minimum. First, we collect some properties of the DC-algorithm.

Proposition 6

Algorithm 1 has the following properties:

• 1. The sequences $f({\mathbf {s}}^k)-g({\mathbf {s}}^k)$ and $g^*({\mathbf {q}}^k) - f^*({\mathbf {q}}^k)$ are decreasing. Furthermore, $f({\mathbf {s}}^k) - g({\mathbf {s}}^k) \le g^*({\mathbf {q}}^k)-f^*({\mathbf {q}}^k)$ and $g^*({\mathbf {q}}^{k+1})-f^*({\mathbf {q}}^{k+1}) \le f({\mathbf {s}}^k) - g({\mathbf {s}}^k)$. The sequence $g^*({\mathbf {q}}^k)-f^*({\mathbf {q}}^k)$ is strictly decreasing until the termination criterion is met.

• 2. If the algorithm terminates with $({\mathbf {s}}^k, {\mathbf {q}}^k)$, then ${\mathbf {s}}^k \in \partial f^*({\mathbf {q}}^k) \cap \partial g^*({\mathbf {q}}^k)$ and ${\mathbf {q}}^k \in \partial f({\mathbf {s}}^k) \cap {\partial g({\mathbf {s}}^k)}$. Furthermore, $f({\mathbf {s}}^k)-g({\mathbf {s}}^k) = g^*({\mathbf {q}}^k)-f^*({\mathbf {q}}^k)$.

Proof

A proof can be found in [46, Theorem 3]. The sequence $g^*({\mathbf {q}}^k)-f^*({\mathbf {q}}^k)$ is strictly decreasing because the algorithm terminates as soon as $g^*({\mathbf {q}}^k)-f^*({\mathbf {q}}^k) = g^*({\mathbf {q}}^{k+1})-f^*({\mathbf {q}}^{k+1})$. $\square$

Next, we show that we can always restart the DC algorithm from a computed stationary point.

Lemma 5

Suppose that in Algorithm 2 the termination criterion in line 5 is met with supply ${\mathbf {s}}$ and price vector ${\mathbf {p}}$. If ${\mathbf {p}}$ is no equilibrium price, then there exists a descent direction ${\mathbf {e}}\in \pm \{0,1\}^n$ of the Lyapunov function at ${\mathbf {p}}$. If we restart the algorithm with ${\tilde{{\mathbf {p}}}}^0 := {\mathbf {p}}+ {\mathbf {e}}$, we have for all elements $({\tilde{{\mathbf {p}}}}^k,{\tilde{{\mathbf {s}}}}^k)$ of the new sequence that $L({\tilde{{\mathbf {p}}}}^k) \le L({\mathbf {p}}) - 1$.

Proof

If the returned price ${\mathbf {p}}$ is no equilibrium price, then it is no minimizer of the Lyapunov function [4]. It follows by $\mathrm{L}^\natural$-convexity of L that there exists ${\mathbf {e}}\in \pm \{0,1\}^n$ with $L({\mathbf {p}}+{\mathbf {e}}) \le L({\mathbf {p}})-1$ [36]. By Property 1 in Proposition 6 we have that $L({{\tilde{{\mathbf {p}}}}}^k) \le L({\mathbf {p}})-1$ for the sequence of prices generated after the restart with initial price ${{\tilde{{\mathbf {p}}}}}^0 = {\mathbf {p}}+ {\mathbf {e}}$. Since L possesses a minimizer [4] and after each restart the value of the Lyapunov function decreases by at least 1, the algorithm terminates with an equilibrium price. $\square$

This completes the proof of Theorem 3: In each step of the main loop, the value of $L({\mathbf {p}}^{k})$ strictly decreases by an integer amount, and if we leave the main loop, we either restart with a price vector of a strictly smaller value, or we terminate, if we are at a global minimum already.

Lemma 6

Suppose that the prices ${\mathbf {p}}^{k+1}$ in Step 4 of Algorithm 2 are chosen deterministically. Let $R \in {\mathbb {Z}}_{\ge 0}$ be the number of restarts of the algorithm and let $S_r = ({\mathbf {s}}^0_r,{\mathbf {s}}^1_r,\dots ,{\mathbf {s}}^{|S_r|}_r)$ denote the sequence of iterates generated in Step 3 after the r-th restart for $r=0,\dots ,R$ ($S_0$ is the sequence before the first restart). Then for $r_1 \ne r_2$, $S_{r_1}$ and $S_{r_2}$ do not contain any common bundle. Moreover, for each r the bundles ${\mathbf {s}}^0_r,\dots ,\mathbf {s}_r^{|{S}_r|-1}$ are pairwise distinct.

Proof

Suppose that ${\mathbf {s}}^k_{r_1} = {\mathbf {s}}^l_{r_2}$ for some $r_1 \le r_2$ and k, l. Then we have for the computed prices in Step 4 that ${\mathbf {p}}^{k+1}_{r_1} = {\mathbf {p}}^{l+1}_{r_2}$, so $L({\mathbf {p}}^{k+1}_{r_1}) = L({\mathbf {p}}^{l+1}_{r_2})$. This can only happen if $r_1 = r_2$, since otherwise $L({\mathbf {p}}^{l+1}_{r_2}) \le L({\mathbf {p}}^{k+1}_{r_1})-1$ by Lemma 5. Now suppose that $r_1=r_2=r$ and $k \le l$. Then again $L({\mathbf {p}}^{k+1}_r) = L({\mathbf {p}}^{l+1}_r)$. By Property 1 of Proposition 6, it follows that $k=l-1$ and the termination criterion is satisfied in iteration l, so $l = |S_r|$ and the bundles ${\mathbf {s}}^0_r,\dots ,{\mathbf {s}}^{|{S}_r|-1}_r$ are pairwise distinct. $\square$

1.6 DC algorithm

Fig. 6

A flow graph modeling (LP)

For the DC algorithm, reformulating the (LP) as a min-cost flow problem comes with a significant computational advantage as compared to solving it with a generic LP-solver. We briefly describe the general min-cost flow problem. For more details, we refer to [1]. Given a directed graph, an arc is a tuple $({\mathbf {v}},{\mathbf {w}})$ where ${\mathbf {v}}$ and ${\mathbf {w}}$ are nodes of the graph. We denote by $u({\mathbf {v}},{\mathbf {w}}) \ge 0$ the maximum capacity of this arc and by $c({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}$ the cost per unit flow along $({\mathbf {v}},{\mathbf {w}})$. For a node ${\mathbf {v}}$, we denote by $\beta ({\mathbf {v}}) \in {\mathbb {R}}$ the supply at node ${\mathbf {v}}$. Depending on the sign of $\beta ({\mathbf {v}})$, a total flow of $|\beta ({\mathbf {v}})|$ must leave (positive sign) or enter (negative sign) ${\mathbf {v}}$. If the supply is 0, the inflow must equal the outflow. A flow f assigns a value $f({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}$ to each arc, the amount of flow from ${\mathbf {v}}$ to ${\mathbf {w}}$. It is feasible, if $0 \le f({\mathbf {v}},{\mathbf {w}}) \le u({\mathbf {v}},{\mathbf {w}})$ for each arc $({\mathbf {v}},{\mathbf {w}})$ in the network, and $\sum _{{\mathbf {w}}} f({\mathbf {v}},{\mathbf {w}}) - \sum _{{\mathbf {w}}} f({\mathbf {w}},{\mathbf {v}}) = \beta ({\mathbf {v}})$ for all nodes ${\mathbf {v}}$, where the sums run over all ${\mathbf {w}}$ such that $({\mathbf {v}},{\mathbf {w}})$, respectively $({\mathbf {w}},{\mathbf {v}})$ is an arc in the network. The cost of the flow is equal to $\sum _{({\mathbf {v}},{\mathbf {w}})} c({\mathbf {v}},{\mathbf {w}})f({\mathbf {v}},{\mathbf {w}})$. The objective of the min-cost flow problem is to find a feasible flow with minimal cost.

The linear program (LP) is used to solve Step 4 in Algorithm 2 where we need to compute a price vector ${\mathbf {p}}^{k+1}$ at which the bundle $\mathbf{t }+{\mathbf {s}}^k$ is demanded. A straightforward network flow model for (LP) is illustrated in Fig. 6. For each good $i \in \{1,\dots ,n\}$ there is a node ${\mathbf {g}}^i$, and for each of the $m=|{\mathcal {B}}_+|$ positive bids indexed by $j\in \{1,\dots ,m\}$ there is a node ${\mathbf {b}}^j$. Finally, there is a destination node ${\mathbf {d}}$. In our flow network, there is an arc $({\mathbf {g}}^i,{\mathbf {b}}^j)$ from each good i to each bid j with unlimited capacity $u({\mathbf {g}}^i,{\mathbf {b}}^j) = \infty$ and cost $c({\mathbf {g}}^j,{\mathbf {b}}^i) = -b^j_i$, i.e., the negative value of bid j for good i. The arcs $({\mathbf {b}}^j,{\mathbf {d}})$ from the bids to the destination node have capacity $u({\mathbf {b}}^j,{\mathbf {d}}) = w({\mathbf {b}}^j)$ and cost $c({\mathbf {b}}^j,{\mathbf {d}}) = 0$. In Step 4 of Algorithm 2, a supply of ${\mathbf {t}}+{\mathbf {s}}^k$ must be distributed among the bids. We set the supply of node ${\mathbf {g}}^i$ to $\beta ({\mathbf {g}}^i) = t_i+s^k_i$ and the supply of node ${\mathbf {d}}$ to $\beta ({\mathbf {d}}) = -\sum _{i=1}^n t_i+s^k_i$. Finally, the supply of node ${\mathbf {b}}^j$ is set to $\beta ({\mathbf {b}}^j) = 0$. Since ${\mathbf {t}}+{\mathbf {s}}^k \in \varDelta _{W_+}$ (Appendix Lemma 4), $\sum _{i=1}^n {\mathbf {t}}_i + {\mathbf {s}}^k_i \le \sum _{j=1}^m w({\mathbf {b}}^j)$, so a feasible flow f exists. Moreover, since the capacities and supplies are all integral, an integral optimal flow exists. Note that the proposed flow network contains arcs with negative cost. If required by a specific solver, it can however easily be transformed into a network with only non-negative costs [1, p. 40].

We assume that the applied min-cost flow solver provides us with an integral optimal flow f, as well as with an integral optimal dual solution, consisting of node potentials $\pi ({\mathbf {v}}) \in {\mathbb {R}}$ for each node ${\mathbf {v}}$ in the network. These satisfy the following complementary slackness conditions [1, Theorem 9.4].

• 1. If $c({\mathbf {v}},{\mathbf {w}}) + \pi ({\mathbf {v}}) - \pi ({\mathbf {w}}) > 0$, then $f({\mathbf {v}},{\mathbf {w}}) = 0$.

• 2. If $0< f({\mathbf {v}},{\mathbf {w}}) < u({\mathbf {v}},{\mathbf {w}})$, then $c({\mathbf {v}},{\mathbf {w}}) + \pi ({\mathbf {v}}) - \pi ({\mathbf {w}}) = 0$.

• 3. If $c({\mathbf {v}},{\mathbf {w}}) + \pi ({\mathbf {v}}) - \pi ({\mathbf {w}}) <0$, then $f({\mathbf {v}},{\mathbf {w}}) = u({\mathbf {v}},{\mathbf {w}})$.

From the complementary slackness conditions it is not hard to deduce that ${\mathbf {p}}$ defined by $p_i = \pi ({\mathbf {g}}^i)-\pi ({\mathbf {d}})$ is an equilibrium price vector for the supply ${\mathbf {t}}+ {\mathbf {s}}^k$, so we can choose ${\mathbf {p}}^{k+1} = {\mathbf {p}}$ in Step 4 of the algorithm.

Let us finally consider Step 3 of Algorithm 2, where a bundle ${\mathbf {s}}^k$ must be chosen that is demanded at price ${\mathbf {p}}^k \in {\mathbb {Z}}^n$ in the negative auction. This is particularly easy to do in the Product-Mix Auction (see also [6]): For each bid ${\mathbf {b}}$ in the negative auction, choose a bundle ${\mathbf {s}}({\mathbf {b}}) \in D_{{\mathbf {b}}}({\mathbf {p}})$. By Equs. (1) and (2), this can be done in linear time in the number of different goods. Then set ${\mathbf {s}}^{k} = \sum _{{\mathbf {b}}\in |{\mathcal {B}}_-|} {\mathbf {s}}({\mathbf {b}})$. In our implementation, we choose a bundle ${\mathbf {s}}^k$ which is a vertex of $D_{|{\mathcal {B}}_-|}({\mathbf {p}})$. This can be achieved by suitably perturbing ${\mathbf {p}}$: Let ${\mathbf {q}}= {\mathbf {p}}+ \varDelta$ be a price such that $D_{|{\mathcal {B}}_-|}({\mathbf {q}}) \cap D_{|{\mathcal {B}}_-|}({\mathbf {p}}) \ne \emptyset$ and $|D_{|{\mathcal {B}}_-|}({\mathbf {q}})|=1$. For example, $\varDelta = (\varepsilon ,2\varepsilon ,\dots ,n\varepsilon )$ works for $\varepsilon > 0$ small enough. Then simply choose the unique ${\mathbf {s}}({\mathbf {b}}) \in D_{|{\mathcal {B}}_-|}({\mathbf {q}})$ and construct ${\mathbf {s}}^k$ as above.

1.7 Generating valid bid groups

1.8 Experimental results

See Table 2.

Table 2 Runtimes of the DC- and the steepest descent (SD)-algorithm. For each experimental setting, we generated 15 sample auctions. The indicated runtimes are the averages over the respective 15 samples