Packing under convex quadratic constraints

Abstract

We consider a general class of binary packing problems with a convex quadratic knapsack constraint. We prove that these problems are $\mathsf {APX}$-hard to approximate and present constant-factor approximation algorithms based upon two different algorithmic techniques: a rounding technique tailored to a convex relaxation in conjunction with a non-convex relaxation, and a greedy strategy. We further show that a combination of these techniques can be used to yield a monotone algorithm leading to a strategyproof mechanism for a game-theoretic variant of the problem. Finally, we present a computational study of the empirical approximation of these algorithms for problem instances arising in the context of real-world gas transport networks.

1 Introduction

We consider packing problems with a convex quadratic knapsack constraint of the form

where $W \in \mathbb {Q}_{\ge 0}^{n \times n}$ is a symmetric positive semi-definite (psd) matrix with non-negative entries, $p \in \mathbb {Q}_{\ge 0}^n$ is a non-negative profit vector, and $c \in \mathbb {Q}_{\ge 0}$ is a non-negative budget. Such convex and quadratically constrained packing problems are clearly ${\mathsf {NP}}$-complete since they contain the classical (linearly constrained) ${\mathsf {NP}}$-complete knapsack problem (cf. Karp [14]) as a special case when $W$ is a diagonal matrix. In this paper, we therefore focus on the development of approximation algorithms. For some $\rho \in [0,1]$, an algorithm is a $\rho$-approximation algorithm if its runtime is polynomial in the input size and for every instance, it computes a solution with objective value at least $\rho$ times that of an optimum solution. The value $\rho$ is then called the approximation ratio of the algorithm. We note that for general matrices W no sensible approximation is possible, e.g., when W is the adjacency matrix of an undirected graph and $c = 0$, (P) encodes the problem of finding an independent set of maximal weight, which is ${\mathsf {NP}}$-hard to approximate within a factor better than $n^{-(1-\epsilon )}$ for any $\epsilon > 0$, even in the unweighted case; see Håstad [10].

The packing problems that we consider also have a natural interpretation in terms of mechanism design. Consider a situation where a set of n selfish agents demands a service, and the subsets of agents that can be served simultaneously are modeled by a convex quadratic packing constraint. Each agent j has private information $p_j$ about its willingness to pay for receiving the service. In this context, a (direct revelation) mechanism takes as input the matrix $W$ and the budget c. It then elicits the private value $p_j$ from agent j. Each agent j may misreport a value $p'_j$ instead of its true value $p_j$ if this is to its benefit. The mechanism then computes a solution $x \in \{0,1\}^n$ to (P) as well as a payment vector $g \in \mathbb {Q}_{\ge 0}^n$. A mechanism is strategyproof if no agent has an incentive in misreporting $p_j$, no matter what the other agents report.

Before we present our results on approximation ratios and mechanisms for non-negative, convex, and quadratically constrained packing problems, we give two real-world examples that fall into this category.

Example 1

(Welfare maximization in gas supply networks) Consider a gas pipeline network modeled by a directed graph $G = (V,E)$ with different entry and exit nodes. There is a set of n transportation requests $(s_j,t_j,q_j,p_j)$ for $j \in [n] \,{:}{=}\,\{1, \dots , n\}$, each specifying an entry node $s_j \in V$, an exit node $t_j \in V$, the amount of gas to be transported $q_j \in \mathbb {Q}_{\ge 0}$, and an economic value $p_j \in \mathbb {Q}_{\ge 0}$. Gas flows in pipe networks are modeled by the Weymouth equations [29] of the form $\beta _e\, q_e\, |{q_e}| = \pi _u - \pi _v$ for all $e = (u,v) \in E$. Here, the parameter $\beta _e \in \mathbb {Q}_{>0}$ is a pipe specific value that depends on physical properties of the pipe segment, such as length, diameter, and roughness. Positive flow values $q_e > 0$ denote flow from u to v, while a negative $q_e$ indicates flow in the opposite direction. The value $\pi _u$ denotes the square of the pressure at node $u \in V$. In real-life gas networks, there is typically a bound $c \in \mathbb {Q}_{\ge 0}$ on the maximal difference of the squared pressures in the network. For the operation of gas networks, it is a natural problem to find the welfare-maximal subset of transportation requests that can be satisfied simultaneously while satisfying the pressure constraint.

To obtain the connection to our problem (P) we now restrict the setting to a path topology and assume that for each request the entry node is left of the exit node; see Fig. 1 for an example. Thus, the pressure in the network is decreasing from left to right. For $j \in [n]$, let $E_j \subseteq E$ denote the set of edges on the unique $(s_j,t_j)$-path in G. Indexing the vertices $v_0,\dots ,v_k$ and edges $e_1, \dots , e_k$ from left to right, the maximal squared pressure difference in the network is given by

$$\begin{aligned} \pi _0 - \pi _k&= \sum _{i=1}^k \bigl ( \pi _{i-1} - \pi _i \bigr ) = \sum _{i=1}^{k}\beta _{e_i} \Bigl (\sum _{j \in [n] : e_i \in E_j} q_j\, x_j\Bigr )^{\!2}, \end{aligned}$$

where $x_j\in \{0,1\}$ indicates whether transportation request $j \in [n]$ is being served. For the matrix $W = (w_{ij})_{i,j \in [n]}$ defined by $w_{ij} = \sum _{e \in E_i \cap E_j} \beta _e\, q_i\,q_j$, the pressure constraint can be formulated as $\smash {x ^{\top } W x \le c}$. To see that the matrix $W$ is positive semi-definite, we write $W = \sum _{e \in E} \beta _e\, q^e\, (q^e)^{\top }$, where $q^e \in \mathbb {Q}_{\ge 0}^n$ is defined as $q^e_i = q_i$ if $e \in E_i$, and $q^e_i = 0$, otherwise.

Gas networks are particularly interesting from a mechanism design perspective, since several countries employ or plan to employ auctions to allocate gas network capacities (cf. Newbery [22]), but theoretical and experimental work uses only linear flow models thus ignoring the physics of the gas flow; see, e.g., McCabe et al. [19] and Rassenti et al. [25].

Fig. 1

Gas network with feed-in and feed-out nodes

Example 2

(Processor speed scaling) Consider a mobile device with battery capacity c and k compute cores. Further, there is a set of n tasks $(q^j, p_j)$, each specifying a load $q^j \in \mathbb {Q}_{\ge 0}^k$ for the k cores and a profit $p_j$. The computations start at time 0 and all computations have to be finished at time 1. In order to adapt to varying workloads, the compute cores can run at different speeds. In the speed scaling literature, it is a common assumption that energy consumption of core i when running at speed s is equal to $\beta _i\, s^2$, where $\beta _i \in \mathbb {Q}_{>0}$ is a core-specific parameter; see, e.g., Bansal et al. [3] Irani and Pruhs [13] and Wierman et al. [30].¹ The goal is to select a profit-maximal subset of tasks that can be scheduled in the available time with the available battery capacity. Given a subset of tasks, it is without loss of generality to assume that each core runs at the minimal speed such that the core finishes at time 1, i.e., every core i runs at speed $\sum _{j \in [n]} x_j\, q^j_i$ so that the total energy consumption is $\smash {\sum _{i=1}^k \beta _{i} (\sum _{j \in [n]} x_j\, q^j_i)^2}$. The energy constraint can thus be formulated as a convex quadratic constraint.

Mechanism design problems for processor speed scaling are interesting when the tasks are controlled by selfish agents and access to computation on the energy-constrained device is determined via an auction.

1.1 Our results

In Sect. 3 we derive a $\phi$-approximation algorithm for packing problems with convex quadratic constraints where $\phi = (\sqrt{5}-1)/2 \approx 0.618$ is the inverse golden ratio. The algorithm first solves a convex relaxation and scales the solution by $\phi$, which turns it into a feasible solution to a second non-convex relaxation. The latter relaxation has the property that any solution can be transformed into a solution with at most one fractional component without decreasing the objective value. In the end, the algorithm returns the integral part of the transformed solution. Combining this procedure with a partial enumeration scheme yields a $\phi$-approximation; see Theorem 1. In Sect. 4 we prove that the Greedy Algorithm, when combined with partial enumeration, is a constant-factor approximation algorithm with an approximation ratio between $(1 - \sqrt{3}/e)\approx 0.363$ and $\phi$; see Theorems 2 and 3. In Sect. 5, we show that a combination of the results from the previous sections allows to derive a strategyproof mechanism with constant approximation ratio. In Sect. 6 we show that packing problems with convex quadratic constraints of type (P) are $\mathsf {APX}$-hard; see Theorem 5. Finally, in Sect. 7, we apply the three algorithms devised in the paper to several instances of the problem type described in Example 1 based on real-world data from the GasLib library [27].

1.2 Related work

When $W$ is a non-negative diagonal matrix, the quadratic constraint in (P) becomes linear and the problem is then equivalent to the 0-1-knapsack problem which admits a fully polynomial-time approximation scheme (FPTAS); see Ibarra and Kim [12]. Another interesting special case is when $W$ is completely-positive, i.e., it can then be written as $W = U U^{\top }$ for some matrix $U \in \mathbb {Q}_{\ge 0}^{n \times k}$ with non-negative entries. The minimal k for which $W$ can be expressed in this way is called the cp-rank of $W$; see Berman and Shaked-Monderer [4] for an overview on completely positive matrices. The quadratic constraint in (P) can then be expressed as $\Vert {U^{\top } x}\Vert _2 \le \sqrt{c}$. For the case that $U \in \mathbb {Q}_{\ge 0}^{n \times 2}$, this problem is known as the 2-weighted knapsack problem for which Woeginger [31] showed that it does not admit an FPTAS, unless $\mathsf {P} = {\mathsf {NP}}$. Chau et al. [6] settled the complexity of this problem showing that it admits a polynomial-time approximation scheme (PTAS). Elbassioni et al. [7] generalized this result to matrices with constant cp-rank. It is worth noting that the welfare maximization problem for gas networks discussed in Example 1 has only constant cp-rank in general if the number of edges in the gas network is constant, so that these results do not apply here. Similarly, the speed scaling problem discussed in Example 2 has only constant cp-rank for a constant number of processors in general. Exchanging constraints and objective in (P) leads to knapsack problems with quadratic objective function and a linear constraint first studied by Gallo [8]. These problems have a natural graph-theoretic interpretation where nodes and edges have profits, the nodes have weights, and the task is to choose a subset of nodes so as to maximize the total profit of the induced subgraph. Rader and Woeginger [24] give an FPTAS when the graph is edge series-parallel. Pferschy and Schauer [23] generalize this result to graphs of bounded treewidth. They also give a PTAS for graphs not including a forbidden minor which includes planar graphs.

Mechanism design problems with a knapsack constraint are contained as a special case when W is a diagonal matrix. For this special case, Mu’alem and Nisan [20] give a mechanism that is strategyproof and yields a 1/2-approximation. Briest et al. [5] give a general framework that allows to construct a mechanism that is an FPTAS for the objective function. Aggarwal and Hartline [2] study knapsack auctions with the objective to maximize the sum of the payments to the mechanism. Chau et al. [6] develop truthful mechanisms for knapsack problems with complex demand.

In a technical report, we also develop an approximation algorithm for the more general problem with multiple quadratic constraints [15].

2 Preliminaries

For ease of exposition, we assume that all matrices and vectors are integer. The general problem with rational input can be reduced to this problem by scaling. Let $[n] \,{:}{=}\,\{1,\dots , n\}$ and $W = (w_{ij})_{i,j \in [n]}\in \mathbb {N}^{n\times n}$ be a symmetric psd matrix. Furthermore, let $p\in \mathbb {N}^n$ be a profit vector and let $c \in \mathbb {N}$ be a budget. We consider problems of the form (P), i.e., $\max \,\{p^\top x : x^\top W x \le c,\; x \in \{0,1\}^n\}$. Throughout the paper, we denote the characteristic vector of a subset $S \subseteq [n]$ by $\chi _S \in \{0,1\}^n$, i.e., $\chi _S = (\chi _{S,1},\dots ,\chi _{S,n})^\top$ where for $i \in [n]$ we have $\chi _{S,i} = 1$ if $i \in S$ and $\chi _{S,i} = 0$, otherwise.

We first state the intuitive result that after fixing $x_i = 1$ for $i \in N_1 \subseteq [n]$ and fixing $x_i = 0$ for $i \in N_0 \subseteq [n]$ (with $N_0 \cap N_1 = \emptyset$), we again obtain a packing problem with a convex and quadratic packing constraint.

Lemma 1

Let $\smash {W \in \mathbb {N}^{n \times n}}$ be symmetric psd, $\smash {p \in \mathbb {N}^n}$, and $\smash {c \in \mathbb {N}}$. Further, let $N_0$, $N_1 \subseteq [n]$ with $N_0 \cap N_1 = \emptyset$ and $N_0 \cup N_1 \subsetneq [n]$ be arbitrary. Then, there exist ${\tilde{n}} \in \mathbb {N}$, $\tilde{W} \in \mathbb {N}^{{\tilde{n}} \times {\tilde{n}}}$ symmetric psd, $\tilde{p} \in \mathbb {N}^{{\tilde{n}}}$, and ${\tilde{c}} \in \mathbb {N}$ such that

$$\begin{aligned}&\max \,\bigl \{ p^\top x \,:\, x^\top W x \le c,\; x \in \{0,1\}^n,\; x_i = 0 \;\forall i \in N_0,\; x_i = 1 \;\forall i \in N_1\bigr \}\\&\quad = p^\top \chi _{N_1} + \max \, \bigl \{ \tilde{p}^{\top }\tilde{x} \,:\, \tilde{x}^\top \tilde{W} \tilde{x} \le {\tilde{c}},\; \tilde{x} \in \{0,1\}^{{\tilde{n}}}\bigr \}. \end{aligned}$$

Proof

Let $n_0 = |{N_0}|$, $n_1 = |{N_1}|$, and ${\tilde{n}} \,{:}{=}\,n - n_0 - n_1$. Without loss of generality we can assume that $[{{\tilde{n}}}] = [n]{\setminus }(N_0\cup N_1)$. Consider the matrix $\tilde{W} = ({\tilde{w}}_{ij}) \in \mathbb {N}^{{\tilde{n}} \times {\tilde{n}}}$ defined as

$$\begin{aligned} {\tilde{w}}_{ij} = {\left\{ \begin{array}{ll} w_{ij} &{}\text { if }i \ne j,\\ w_{ij} + 2\sum _{k \in N_1} w_{ik}&{}\text { if }i = j, \end{array}\right. } \qquad i,\,j\in [{{\tilde{n}}}]. \end{aligned}$$

Note that $\tilde{W}$ is obtained by taking a principal submatrix of $W$ and adding a diagonal matrix with non-negative entries so that $\tilde{W}$ is positive semi-definite. Let . With a slight abuse of notation, for a set $S \subseteq [{\tilde{n}}]$, let $\tilde{\chi }_S$ denote its characteristic vector in $\{0,1\}^{{\tilde{n}}}$ and $\chi _S$ its characteristic vector in $\{0,1\}^n$. We then obtain for all $S \subseteq [{\tilde{n}}]$ the equality

Thus, we have if and only if . Defining ${\tilde{p}} \in \mathbb {N}^{{\tilde{n}}}$ with ${\tilde{p}}_i = p_i$ for all $i \in [{\tilde{n}}]$ then establishes the claimed result. $\square$

Using Lemma 1, we show that the following assumptions are without loss of generality.

Lemma 2

It is without loss of generality to assume that $0 < w_{ii} \le c$ and $p_i > 0$ for all $i \in [n]$.

Proof

If $w_{ii} > c$ for some $i \in [n]$, then $x_i = 0$ in every feasible solution $x$. If $w_{ii} = 0$, then the positive semi-definiteness of $W$ implies $w_{ij} = w_{ji} = 0$ for every $j \in [n]$. Hence, the value of $x_i$ does not influence the value of $x^{\top }W x$ and it is without loss of generality to assume that $x_i = 1$. Furthermore, if $p_i = 0$ then the value of $x_i$ does not influence the value of $p^{\top }x$ and it is without loss of generality to assume that $x_i = 0$. In all cases, Lemma 1 yields the result. $\square$

3 Approximation via two relaxations

In this section, we derive a $\phi$-approximation algorithm for packing problems with convex quadratic constraints of type (P) where $\phi = (\sqrt{5}-1)/2 \approx 0.618$ is the inverse golden ratio. To this end, we first solve a convex relaxation of the problem. We then use the resulting solution to compute a feasible solution to a non-convex relaxation of the problem. The second relaxation has the property that any solution can be transformed so that it has at most one fractional value, and the transformation does not decrease the objective value. Together with a partial enumeration scheme in the spirit of Sahni [26], this yields a $\phi$-approximation.

Denote by $d \in \mathbb {N}^n$ the diagonal of $W\in \mathbb {N}^{n \times n}$ and let $\smash {D\,{:}{=}\,{{\,\mathrm{diag}\,}}(d)\in \mathbb {N}^{n\times n}}$ be the corresponding diagonal matrix. For a vector $x\in \{0,1\}^n$ we have $x_i^2 = x_i$ for all $i \in [n]$ and, thus, we obtain $x^{\top } W x \ge x^{\top } D x = d^{\top }x$ for all $x \in \{0,1\}^n$. We arrive at the following relaxation of (P):

The following lemma shows that an exact optimal solution to ($R_1$) is computable in polynomial time.

Lemma 3

The relaxation ($R_1$) can be solved exactly in polynomial time.

Proof

For every $x \in [0,1]^n$, we have $\lfloor {p^\top x}\rfloor \in P \,{:}{=}\,\{0,\dots ,\sum _{i\in [n]} p_i\}$. For fixed $q \in P$, consider the mathematical program

with optimal value c(q). Since ($D_q$) is quadratic and convex with linear constraints, it can be solved exactly in polynomial time; see Kozlov et al. [18]. If $c(q) > c$, we conclude that the maximal value of ($R_1$) is strictly smaller than q. If $c(q) \le c$, the corresponding solution $x$ solves ($R_1$) with an objective value of q. With binary search over P, we compute the maximal value $q^* \in P$ such that ($D_q$) has a solution of at most c. The thus computed value $q^*$ is the maximal objective of ($R_1$) and the corresponding optimal solution $x$ of ($D_q$) is an optimal solution of ($R_1$). $\square$

We proceed to propose a second relaxation of (P). To this end, note that for every $x\in \{0,1\}^n$ we have

$$\begin{aligned} x^{\top }W x = x^{\top }(W-D) x + x^{\top }D x = x^{\top }(W-D) x + d^{\top } x. \end{aligned}$$

Relaxing the integrality condition yields the following relaxation of (P):

Note that since the diagonal of $W - D$ is zero, $W - D$ is not positive semi-definite, unless $W$ is a diagonal matrix. Therefore, relaxation ($R_2$) is in general not convex.

Applying a rounding technique resembling “pipage rounding" introduced by Ageev et al. [1], we show that every feasible solution to ($R_2$) can be transformed into another solution with at most one fractional variable without decreasing the objective value. For $x\in \mathbb {R}^n$, let $N_0(x) \,{:}{=}\,\{i\in [n] : x_i = 0\}$, $N_1(x) \,{:}{=}\,\{i\in [n] : x_i = 1\}$, and $N_f(x) \,{:}{=}\,[n] \setminus (N_1(x) \cup N_0(x))$.

Lemma 4

For any feasible solution $x$ of ($R_2$), a feasible solution $\bar{x}$ with $|{N_f(\bar{x})}| \le 1$ and $p^{\top } \bar{x} \ge p^\top x$ can be constructed in linear time.

Proof

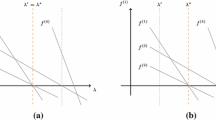
Let $x$ be a feasible solution of ($R_2$). Assume $|{N_f(x)}| \ge 2$, and consider i, $j\in N_f( x)$ with $i\ne j$, in particular, $x_i$, $x_j \in (0,1)$. We proceed to construct a feasible solution $\bar{x}$ with $|N_f(\bar{x})| \le |N_f(x)| -1$ and $p^\top \bar{x} \ge p^\top x$; see Fig. 2 for an illustration.

Fig. 2

Any feasible solution x of ($R_2$) with $|N_f(x)|\ge 2$ can be transformed into a feasible solution ${\bar{x}}$ with $|N_f({\bar{x}})|\le |N_f(x)|-1$ without decreasing the objective value

Denote $v(x) \,{:}{=}\, x^{\top }(W-D)x + d^{\top }x$, and for $k \in \{i,j\}$ let

$$\begin{aligned} \nu _k(x) \,{:}{=}\, \frac{\partial {}}{\partial {x_k}} v(x) = \sum _{l \in [n]{\setminus }\{k\}} 2\,w_{kl}\,x_l + w_{kk},\qquad r_k(x) \,{:}{=}\, \frac{p_k}{\nu _k(x)}. \end{aligned}$$

By Lemma 2 it is without loss of generality to assume that $w_{kk}>0$ and thus $\nu _k(x) > 0$. Note that $\nu _k(x)$ does not depend on $x_k$ and therefore, for all $x\in \mathbb {R}^n$ and $t \in \mathbb {R}$, we have that

$$\begin{aligned} v(x + t \chi _k) = v(x) + t\, \nu _k(x), \end{aligned}$$

(1)

where $\chi _k\in \{0,1\}^n$ denotes the k-th unit vector. Without loss of generality, assume that $r_i(x) \ge r_j(x)$ and define

$$\begin{aligned} {\bar{\varepsilon }}&\,{:}{=}\, \frac{\nu _i(x)}{\nu _j(x)}(1 - x_i),&\varepsilon&\,{:}{=}\, \min (x_j, {\bar{\varepsilon }}),&\delta&\,{:}{=}\, \frac{\nu _j(x)}{\nu _i(x)} \varepsilon . \end{aligned}$$

Consider the vector $\bar{x} = x - \varepsilon \chi _j + \delta \chi _i$. By the definition of $\varepsilon$, we have ${\bar{x}}_j = x_j - \varepsilon \ge 0$. We further obtain

$$\begin{aligned} {\bar{x}}_i&= x_i + \delta = x_i + \frac{\nu _j(x)}{\nu _i(x)}\varepsilon \le x_i + \frac{\nu _j(x)}{\nu _i(x)} {\bar{\varepsilon }} = 1. \end{aligned}$$

Note that $\bar{x}_j = 0$ if $\varepsilon = x_j$ and $\bar{x}_i = 1$ if $\varepsilon = \bar{\varepsilon }$ so that at least one of the inequalities $\bar{x}_j \ge 0$ and $\bar{x}_i \le 1$ is tight. We conclude that $\bar{x} \in [0,1]^n$ and $|N_f(\bar{x})| \le |N_f(x)| -1$. Furthermore, applying Equation (1), we obtain

$$\begin{aligned} v({\bar{x}})&= v(x - \varepsilon \chi _j + \delta \chi _i) = v(x - \varepsilon \chi _j) + \delta \nu _i(x - \varepsilon \chi _j) \\&= v(x) - \varepsilon \nu _j(x) + \delta \nu _i(x - \varepsilon \chi _j) \le v(x) -\varepsilon \nu _j(x) + \delta \nu _i(x) = v(x). \end{aligned}$$

Thus, $\bar{x}$ is a feasible solution of ($R_2$). Moreover, we have

$$\begin{aligned} p^\top \bar{x}&= p^{\top } x - \varepsilon p_j + \delta p_i = p^{\top }x - \varepsilon p_j + \varepsilon \nu _j(x)\frac{p_i}{\nu _i(x)} = p^{\top } x - \varepsilon p_j + \varepsilon \nu _j(x)r_i(x) \\&\ge p^{\top } x - \varepsilon p_j + \varepsilon \nu _j(x) r_j(x) = p^\top x - \varepsilon p_j + \varepsilon p_j = p^\top x. \end{aligned}$$

Applying this construction iteratively (at most) $|N_f(x)|-1 \le n - 1$ times yields the required result. $\square$

Remark 1

The algorithm in the proof of Lemma 4 can be improved by setting

$$\begin{aligned} {\bar{\varepsilon }} \,{:}{=}\, \frac{(1-x_i)\,\nu _i(x)}{\nu _j(x)+2\,w_{ij}\,(1-x_i)}, \qquad \varepsilon \,{:}{=}\, \min (x_j, {\bar{\varepsilon }}), \qquad \delta \,{:}{=}\, \frac{\varepsilon \, \nu _j(x)}{\nu _i(x)-2\,w_{ij}\,x_j\,\varepsilon }. \end{aligned}$$

In this way, we obtain $v({\bar{x}}) = v(x)$ and increase the objective value at least as much as in the proof of Lemma 4 while still ensuring that $\bar{x}$ is feasible for ($R_2$) and $|N_f(\bar{x})| \le |N_f(x)| - 1$.

We proceed to devise a $\phi$-approximation algorithm. The algorithm iterates over all sets $H{\subseteq }[n]$ with $|H| \le 3$. For each set H it computes an optimal solution $y^H$ to the convex relaxation ($R_1$) with the additional constraints

$$\begin{aligned} x_i&= 1 \quad \text { for all }i \in H,\text { and }\\ x_i&= 0 \quad \text { for all }i \in \{j \in [n]{\setminus } H : p_j > \min \nolimits _{h \in H} p_h\}. \end{aligned}$$

Then, we scale down $y^H$ by a factor of $\phi$ and show that $\phi y^H$ is a feasible solution to the non-convex relaxation ($R_2$). By Lemma 4, we can transform this solution into another solution $z^H$ with at most one fractional variable. The integral part of $z^H$ is our candidate solution for the starting set H. In the end, we return the best thus computed candidate over all possible sets H; see Algorithm 1.

Theorem 1

Algorithm 1 computes a $\phi$-approximation for (P).

Proof

Fix an optimal solution $x^*$ of (P) and define $S^* \,{:}{=}\, \{i \in [n] : x_i^* = 1\}$. Since the algorithm iterates over all solutions of size at least three, it is without loss of generality for our following arguments to assume that $|S^*| \ge 4$. Let $H^* \subset S^*$ with $|H^*| = 3$ be chosen such that $p_i \le \min _{h \in H^*} p_h$ for all $i \in S^*$, and consider the run of the algorithm when starting with $H^*$. Let

$$\begin{aligned} \bar{H} \,{:}{=}\,\{i \in [n]\setminus H^* : p_i > \min _{h \in H^*} p_h\} \end{aligned}$$

and $k \,{:}{=}\,|{\bar{H}}|$. It is without loss of generality to assume that $[n] {\setminus } (H^* \cup {\bar{H}}) = [n-k-3]$. Consider the packing problem where as additional constraints we have $x_i = 1$ for all $i \in H^*$ and $x_i = 0$ for all $i \in \bar{H}$. By Lemma 1, this packing problem can be written as

where $\tilde{W}$ is a symmetric and positive semi-definite matrix. We then have $p^\top x^* = \sum _{h \in H^*} p_i + \tilde{p}^{\top } \tilde{x}^*$ for an optimal solution $\tilde{x}^*$ of (${\tilde{P}}$).

Let $y$ be an optimal solution to the convex relaxation ($R_1$) of (${\tilde{P}}$). Since ($R_1$) is a relaxation of (${\tilde{P}}$), we have ${{\tilde{p}}}^\top y \ge {\tilde{p}}^\top \tilde{x}^*$. We proceed to show that $\phi y$ is feasible for the non-convex relaxation ($R_2$) of (${\tilde{P}}$). To this end, we calculate

$$\begin{aligned} (\phi y)^\top (\tilde{W} - \tilde{D}) (\phi y) + \phi \, \tilde{d}^\top y = \phi ^2 y^\top (\tilde{W} - \tilde{D}) y + \phi \, \tilde{d}^\top y \le \phi ^2 {\tilde{c}} + \phi {\tilde{c}} = {\tilde{c}}, \end{aligned}$$

where for the inequality we used that $y$ is feasible for the convex relaxation and, thus, $y^\top \tilde{W} y \le {\tilde{c}}$ and $\tilde{d}^\top y \le {\tilde{c}}$. By Lemma 4, we can transform $\phi y$ into a solution $z$ such that $\tilde{p}^\top z \ge \phi \tilde{p}^{\top } y$ and $z$ has at most one fractional value $z_{\ell }$ with $\ell \in [n-k-3]$.

Let $S = H^* \cup \{i \in [n-k-3] : z_i = 1\}$ and consider the solution $\chi _S$. We have that

so that $\chi _S$ is feasible for (P). Moreover, we obtain

$$\begin{aligned} p^\top \chi _S&= \sum _{h \in H^*} p_h + \tilde{p}^\top z - p_{\ell } z_{\ell } \ge \sum _{h \in H^*} p_h + \phi \tilde{p}^\top y - p_{\ell } \ge \sum _{h \in H^*} p_h + \phi \tilde{p}^\top \tilde{x}^* - p_{\ell }\\&= \phi p^\top x^* + (1-\phi ) \sum _{h \in H^*} p_h - p_{\ell } \ge \phi p^\top x^* + (3(1-\phi )-1)\min _{h \in H^*} p_h \ge \phi p^\top x^*, \end{aligned}$$

establishing the claimed result. $\square$

As a result of Theorem 1, we can derive an upper bound on the optimal value of ($R_1$). This will turn out to be useful when constructing a monotone greedy algorithm in Sect. 5.

Corollary 1

Let $x^*$ and $y^*$ be optimal solutions to (P) and ($R_1$), respectively. Then $p^{\top }y^* \le \frac{2}{\phi }p^{\top } x^*$.

Proof

Since $y^*$ is feasible for ($R_1$), we have

$$\begin{aligned} (\phi y^*)^{\top }(W-D)(\phi y^*) + d^{\top }(\phi y^*) \le \phi ^2 (y^*)^TWy^* + \phi d^{\top }y^* \le (\phi ^2 + \phi )c = c. \end{aligned}$$

Therefore, $\phi y^*$ is feasible for ($R_2$). By Lemma 4, we can transform $\phi y^*$ into a vector z with $p^{\top } z \ge p^{\top }(\phi y^*) = \phi p^{\top } y^*$ and $|{N_f(z)}| \le 1$. The integral part $\lfloor {z}\rfloor$ of z is feasible for (P), and thus, $p^{\top } z \le p^{\top } \lfloor {z}\rfloor + \max _{i\in [n]} p_i \le 2p^{\top } x^*$. We conclude that $p^{\top }y^* \le \frac{1}{\phi }p^{\top }z \le \frac{2}{\phi }p^{\top }x^*$. $\square$

4 The Greedy algorithm

In this section we analyze the Greedy Algorithm and show that, when combined with a partial enumeration scheme in the spirit of Sahni [26], it is at least a $(1 - \sqrt{3}/e)$-approximation for packing problems with quadratic constraints of type (P). We further show that its approximation ratio can be bounded from above by the inverse golden ratio $\phi = (\sqrt{5}-1)/2$. Even though this approximation ratio is thus not better than the one guaranteed by the Golden Ratio Algorithm (Theorem 1), it is worth analyzing it for several reasons. Firstly, it is simple to understand as well as to implement and turns out to have a much better running time in practice than the Golden Ratio Algorithm developed in Sect. 3; see the computational results in Sect. 7. And, secondly, the Greedy Algorithm serves as a main building block to devise a strategyproof mechanism with constant welfare guarantee; see Sect. 5.

For a set $S\subseteq [n]$, we write . The core idea of the Greedy Algorithm is as follows. Assume that we have an initial solution $S \subset [n]$. Amongst all remaining items in $[n]{\setminus }S$, we pick an item i that maximizes the ratio between profit gain and weight gain, i.e.,

$$\begin{aligned} i \in \mathop {{\hbox {argmax}}}\limits _{j\in [n]\setminus S}\; \frac{p_j}{w(S\cup \{j\}) - w(S)}. \end{aligned}$$

If adding i to the solution set would make it infeasible, i.e., $w(S \cup \{i\}) > c$, then we delete i from [n]. Otherwise, we add i to S. We repeat this process until $[n]{\setminus }S$ is empty.

It is known from the knapsack problem that, when starting the Greedy Algorithm as described above with the empty set as initial set, then the produced solution can be arbitrarily bad compared to an optimal solution. However, the Greedy Algorithm can be turned into a constant-factor approximation by using partial enumeration: For all feasible subsets $U\subseteq [n]$ with $|U| \le 2$, we run the Greedy Algorithm starting with U as initial set. In the end we return the best solution set found in this process; see Algorithm 2.

The analysis of the algorithm is similar to the one of Sviridenko [28] for the Greedy Algorithm for maximizing a submodular function under a linear knapsack constraint. Roughly speaking (and ignoring the issue of partial enumeration of solutions), Sviridenko considers the sequence of densities $\theta _1, \theta _2,\dots ,\theta _m$ of the items of the greedy solution in the order they appear in it. This allows to express the profit of the greedy solution as $\sum _{i=1}^{m} \theta _i(w_{i}- w_{i-1})$ where $w_i$ is the total weight after the insertion of i items, and m is the number of items inserted. On the other hand, one can show that the profit of the optimal solution is bounded from above by $\min _{t \in \{0,\dots ,m-1\}} \sum _{i=1}^{t} \theta _i(w_i - w_{i-1}) + c\, \theta _{t+1}$. Intuitively, this means that the optimal solution cannot be better than following a prefix of t items of the greedy solution, and then filling the whole knapsack capacity with the next highest density. An inequality due to Wolsey [32] shows that the worst case ratio of

$$\begin{aligned} \frac{\sum _{i=1}^{m} \theta _i(w_{i}-w_{i-1})}{\min _{t \in \{0,\dots ,m-1\}} \sum _{i=1}^{t} \theta _i(w_i - w_{i-1}) + c\, \theta _{t+1}} \end{aligned}$$

is $1 - 1/e$, which yields the result of Sviridenko. A main challenge when applying this analysis to the case of non-linear constraints is the following. For maximizing a submodular function subject to a linear constraint, it is not harmful for the Greedy Algorithm to include items that are not contained in the optimal solution except for the lost capacity. However, when the constraint is quadratic, including an item not included in the optimal solution may be harmful since it increases the weight of future items in a nonlinear way. To deal with this issue, we bound this effect by introducing an additional correction term. In the end, we bound the profit of the optimal solution by $\sum _{i=1}^{t} \theta _i(w_{i}-w_{i-1}) + \theta _{t+1}(c + 2\sqrt{w_t c})$ for all $t \in \{0,\dots ,m-1\}$. For this expression, we cannot apply the result of Wolsey and, thus, we need to provide a worst-case bound on the ratio

$$\begin{aligned} \frac{\sum _{i=1}^{m} \theta _i(w_{i}- w_{i-1})}{\min _{t \in \{0,\dots ,m-1\}} \sum _{i=1}^{t} \theta _i(w_{i}-w_{i-1}) + \theta _{t+1}(c + 2\sqrt{w_t c})}. \end{aligned}$$

The lower bound that we will finally obtain is $1 - \sqrt{3}/e$. Before we prove this result, we need the following technical lemma.

Lemma 5

Let $m\in \mathbb {N}$ and consider the sequence $(\theta _t)_{t\in \mathbb {N}}$ defined by the recursive formula $\theta _1 = \frac{1}{m}$ and $1 - \big (m + 2\sqrt{tm} \big )\theta _{t+1} =\sum _{i=1}^t\theta _i$ for all $t \ge 1$. Then $\sum _{t=1}^m \theta _t \ge 1 - \frac{\sqrt{3}}{e}$.

Proof

Consider the initial value problem

$$\begin{aligned} \psi '(x) = \frac{1 - \psi (x)}{1 + 2\sqrt{x}}, \quad x\in [0,1],\quad \psi (0) = 0. \end{aligned}$$

Since the function $f:[0,1] \times \mathbb {R}\rightarrow \mathbb {R}$, $(x,s) \mapsto \frac{1-s}{1 + 2\sqrt{x}}$ is Lipschitz-continuous in s, by the Picard-Lindelöf Theorem, this problem has a unique solution, which is given by

$$\begin{aligned} \psi (x) = 1 - e^{-\sqrt{x}}\sqrt{1 + 2\sqrt{x}}, \quad x\in [0,1]. \end{aligned}$$

Since its first derivative

$$\begin{aligned} \psi '(x) = \frac{e^{-\sqrt{x}}}{\sqrt{1 + 2\sqrt{x}}}, \quad x\in [0,1], \end{aligned}$$

is monotonically decreasing, it follows that $\psi$ is concave.

Define $z_t \,{:}{=}\,\sum _{i=1}^t\theta _i$, $t\in \{0, \dots , m\}$. We claim that for every $t \in \{0, \dots , m\}$

$$\begin{aligned} z_t \ge \psi \big (\tfrac{t}{m}\big ) \end{aligned}$$

(2)

holds. Note that (2) implies the result using $\sum _{t=1}^m \theta _t = z_{m}\ge \psi (1) = 1 - \frac{\sqrt{3}}{e}$. We proceed to prove (2) by induction. We have $z_0 = 0 = \psi (0)$. Now assume that (2) holds for some arbitrary but fixed $t\in \{0,\dots ,m-1\}$. By the recursive definition of $(\theta _t)_{t\in \mathbb {N}}$ and the concavity of $\psi$, it then follows that

$$\begin{aligned} z_{t+1}&= z_t + \theta _{t+1} = z_t + \frac{1 - z_t}{m + 2\sqrt{tm}} \\&= z_t \left( 1 - \frac{1}{m + 2\sqrt{tm}} \right) + \frac{1}{m + 2\sqrt{tm}} \\&\ge \psi \big (\tfrac{t}{m}\big )\left( 1 - \frac{1}{m + 2\sqrt{tm}} \right) + \frac{1}{m + 2\sqrt{tm}} \\&= \psi \big (\tfrac{t}{m}\big ) + \frac{1 - \psi (\frac{t}{m})}{m + 2\sqrt{tm}} \\&= \psi \big (\tfrac{t}{m}\big ) + \tfrac{1}{m} \psi '\big (\tfrac{t}{m}\big ) \\&\ge \psi \big ( \tfrac{t+1}{m} \big ), \end{aligned}$$

completing the proof. $\square$

The following lemma will be used to bound the ratio of the profit of the optimal solution and the solution of the Greedy Algorithm.

Lemma 6

Let $w_0,\dots , w_m \!\in \! \mathbb {N}$ with $0 \!=\! w_0 \!<\! w_1 \!<\! \dots \!<\! w_m$, and $\theta _i \!\ge \! 0$, $i \!\in \! [m]$. Then,

$$\begin{aligned} \sum _{i=1}^m \!\theta _i (w_i \!-\! w_{i-1}) \ge \biggl (1 \!-\! \frac{\sqrt{3}}{e} \biggr ) \min _{t=0,\dots ,m\!-\!1} \sum _{i=1}^t \!\theta _i(w_i \!-\!w_{i-1}) + \theta _{t+1}(w_m \!+\! 2\sqrt{w_tw_m}). \end{aligned}$$

Proof

We first show the statement for sequences $0 = w_0< w_1< \dots < w_m$ with the additional property that $w_i - w_{i-1} = 1$ for all $i \in [m]$. For this case, we need that $\sum _{i=1}^m \theta _i \ge ( 1 - \frac{\sqrt{3}}{e} ) \min _{t=0,\dots ,m-1} \sum _{i=1}^t \theta _i + \theta _{t+1} (m + 2\sqrt{tm})$. It suffices to show that the optimal value of the following optimization problem is at least $1 - \sqrt{3}/e$.

$$\begin{aligned} \begin{aligned} \text {minimize} \qquad&\sum _{i=1}^m \theta _i\\ \text {subject to} \qquad&\sum _{i=1}^t \theta _i + \theta _{t+1}(m + 2\sqrt{tm}) \ge 1 \quad \text {for all }t=0,\dots , m-1, \\&\theta _i \ge 0 , \qquad \text {for all }i =1,\dots , m. \end{aligned} \end{aligned}$$

(3)

We claim that every optimal solution to (3) satisfies all inequalities with equality. For a contradiction, fix an optimal solution $\theta ^*_1,\dots ,\theta _m^*$ and suppose there is $s \in \{0,\dots ,m-1\}$ such that $\sum _{i=1}^s \theta _i^* + \theta _{s+1}^*(m + 2\sqrt{sm}) > 1$. Choosing the minimal s with this property, we have $\theta _{s+1}^* > 0$. Let

$$\begin{aligned} \delta =\min \left\{ \theta _{s+1}^* , \frac{\sum _{i=1}^s \theta _i^* + \theta _{s+1}^*(m + 2\sqrt{sm}) - 1}{m+2\sqrt{sm}} \right\} , \end{aligned}$$

and consider the solution $\theta _1',\dots ,\theta _m'$ defined as

$$\begin{aligned} \theta _i' = {\left\{ \begin{array}{ll} \theta _i^* &{} \text { if } i < s+1,\\ \theta _i^* - \delta &{} \text { if } i = s+1,\\ \theta _i^* + \frac{\delta }{m+2\sqrt{(i-1)m}} &{} \text { if } i > s+1.\\ \end{array}\right. } \end{aligned}$$

We first check that the solution $\theta _1',\dots ,\theta _m'$ is feasible. For the inequalities for $t=0,\dots ,s-1$, there is nothing to show since the involved variables are not altered. For $t=s$, the inequality is satisfied by the choice of $\delta$. For $t > s$, we obtain

$$\begin{aligned} \sum _{i=1}^t \theta _i' \!+\! \theta '_{t+1}(m \!+\! 2\sqrt{tm}) \ge \sum _{i=1}^t \theta _i^* \!-\! \delta \!+\! \biggl (\theta ^*_{t+1} \!+\! \frac{\delta }{m \!+\! 2 \sqrt{tm}}\biggr )(m \!+\! 2\sqrt{tm}) \ge 1, \end{aligned}$$

where for the second inequality we used that $\theta _1^*,\dots ,\theta _m^*$ is feasible. Finally, we note that

$$\begin{aligned} \sum _{i=1}^m \theta _i^* - \sum _{i=1}^m \theta _i' = \delta - \sum _{i=s+2}^m \frac{\delta }{m+2\sqrt{(i-1)m}} \ge \delta \biggl (1 - \frac{m-1}{m}\biggr ) > 0, \end{aligned}$$

contradicting the optimality of $\theta ^*_1,\dots ,\theta ^*_m$. We conclude that every optimal solution of (3) satisfies all inequalities with equality. The result then follows from Lemma 5.

It is left to show that the statement holds for arbitrary finite sequences $0 = w_0< w_1< \dots < w_m$. Fix such a sequence, let $m' \,{:}{=}\,w_m$, and let $\theta _1',\dots , \theta _{m'}$ be such that there are first $w_1 - w_0$ copies of $\theta _1$, then $w_2 - w_1$ copies of $\theta _2$, and so on. We thus obtain

$$\begin{aligned}&\sum _{i=1}^m \theta _i(w_i - w_{i-1}) = \sum _{i=1}^{m'} \theta _i' \\&\quad \ge \biggl (1 - \frac{\sqrt{3}}{e} \biggr )\min _{t=0,\dots ,m'-1}\sum _{i=1}^{t} \theta _i' + \theta '_{t+1}(m' + 2\sqrt{t m'}) \\&\quad = \biggl (1 - \frac{\sqrt{3}}{e} \biggr )\min _{t=w_0,\dots ,w_{m-1}}\sum _{i=1}^{t} \theta _i' + \theta '_{t+1}(m' + 2\sqrt{t m'}) \\&\quad = \biggl (1 - \frac{\sqrt{3}}{e} \biggr )\min _{t=0,\dots ,m-1}\sum _{i=1}^{t} (w_i - w_{i-1})\theta _i + \theta _{t+1}(w_m + 2\sqrt{t w_m}), \end{aligned}$$

yielding the result. $\square$

We are now in position to prove the approximation ratio of the Greedy Algorithm.

Theorem 2

The Greedy Algorithm with partial enumeration (Algorithm 2) is an approximation algorithm with approximation ratio $\smash {1 - \frac{\sqrt{3}}{e}}$ for (P).

Proof

Let $x^*$ be an optimal solution of (P) and set $S^* \,{:}{=}\,\{i\in [n]: x^*_i = 1\}$. Number the items of $S^* = \{i_1^*,i_2^*,\dots , i_k^*\}$ such that $p_{i_1^*} \ge p_{i_2^*} \ge \dots \ge p_{i_k^*}$. Since the algorithm enumerates all solutions with at most two items, it is without loss of generality to assume that $|S^*|\ge 3$. Consider the run of the Greedy Algorithm with $U = \{i_1^*,i_2^*\}$. Without loss of generality, we assume that $i_1^* = n-1$ and $i_2^* = n$. Set $S^0\,{:}{=}\,U$, and for $t = 1,2,\dots$, denote by $S^t$ and $i_t$ the values of S and i after the t-th pass of the while loop. Furthermore, define

$$\begin{aligned} \theta _{t}\,{:}{=}\,\frac{p_{i_{t}}}{w(S^{t-1}\cup \{i_{t}\}) - w(S^{t-1})}. \end{aligned}$$

By Lemma 1, we can treat the problem after fixing $x_{i_1^*} = x_{i_2^*}= 1$ as a new problem of the same form with matrix $\smash {\tilde{W} \in \mathbb {N}^{(n-2) \times (n-2)}}$, profit vector $\smash {\tilde{p}}$, and budget $\smash {{\tilde{c}}}$. In the following, for a set $S \subseteq [n]{\setminus }U$ we write . Note that ${{\tilde{w}}}$ is supermodular, i.e., for any two sets S, $S' \subseteq [n]\setminus U$ we have

$$\begin{aligned} \sum _{i\in S'\setminus S} {{\tilde{w}}}(S\cup \{i\}) - {{\tilde{w}}}(S) \le {{\tilde{w}}}(S\cup S') - {{\tilde{w}}}(S). \end{aligned}$$

By Lemma 2, it is without loss of generality to assume ${{\tilde{w}}}(S\cup \{i\}) - {{\tilde{w}}}(S) > 0$. Let T be the first step of the Greedy Algorithm for which $i_{T} \in S^*$ but the algorithm does not add $i_{T}$ to its solution set. It is without loss of generality to assume that in all previous iterations $t \in \{1,\dots ,T-1\}$ we had $S^{t} = S^{t-1} \cup \{i_t\}$ as otherwise item $i_t$ would be neither contained in the optimal solution nor the solution computed by the Greedy Algorithm; thus, removing it from the instance would not change the analysis. Since $i_{T}$ is not included in the solution, we have ${\tilde{w}}(S^{T-1}\cup \{i_{T}\}{\setminus }U) > {\tilde{c}}$. In the following, we write $S^{T} \,{:}{=}\,S^{T-1} \cup \{i_{T}\}$, ${\tilde{S}}^* \,{:}{=}\,S^* \setminus U$, and for $t \in \{0,\dots ,T\}$, we write ${\tilde{S}}^t \,{:}{=}\,S^t{\setminus }U$.

For all $t \in \{0,\dots ,T-1\}$, we obtain

$$\begin{aligned} \sum _{i \in {\tilde{S}}^*} p_i&\le \sum _{i \in {\tilde{S}}^t} p_i + \sum _{i \in {\tilde{S}}^*\setminus {\tilde{S}}^t} p_i\\&= \sum _{i \in {\tilde{S}}^t} p_i + \sum _{i \in {\tilde{S}}^*\setminus {\tilde{S}}^t} \frac{p_i}{{\tilde{w}}({\tilde{S}}^{t} \cup \{i\}) - {\tilde{w}}({\tilde{S}}^{t})}\big ({\tilde{w}}({\tilde{S}}^{t} \cup \{i\}) - {\tilde{w}}({\tilde{S}}^{t})\big )\\&\le \sum _{i \in {\tilde{S}}^t} p_i + \theta _{t+1} \sum _{i \in {\tilde{S}}^*\setminus {\tilde{S}}^t} \big ({\tilde{w}}({\tilde{S}}^{t} \cup \{i\}) - {\tilde{w}}({\tilde{S}}^{t})\big )\\&\le \sum _{i \in {\tilde{S}}^t} p_i + \theta _{t+1} \big ({\tilde{w}}({\tilde{S}}^{t} \cup {\tilde{S}}^*) - {\tilde{w}}({\tilde{S}}^{t})\big ), \end{aligned}$$

where we used the supermodularity of ${\tilde{w}}$. By the Cauchy-Schwarz inequality it holds that

$$\begin{aligned} {\tilde{w}}({\tilde{S}}^{t} \cup {\tilde{S}}^*) - {\tilde{w}}({\tilde{S}}^{t})&= (\chi _{{\tilde{S}}^t} + \chi _{{\tilde{S}}^*{\setminus }S^t})^\top {\tilde{W}} (\chi _{{\tilde{S}}^t} + \chi _{{\tilde{S}}^*{\setminus }{\tilde{S}}^t}) - w({\tilde{S}}^t)\\&\le {\tilde{w}}({\tilde{S}}^*{\setminus }{\tilde{S}}^t) +2 \sqrt{{\tilde{w}}({\tilde{S}}^t) {\tilde{w}}({\tilde{S}}^*\setminus {\tilde{S}}^t)}\\&\le {\tilde{c}} + 2\sqrt{{\tilde{w}}({\tilde{S}}^t){\tilde{c}}}. \end{aligned}$$

Thus, we get

$$\begin{aligned} \sum _{i \in {\tilde{S}}^*} p_i&\le \sum _{i \in {\tilde{S}}^t} p_i + \theta _{t+1}\Bigl ( {\tilde{c}} + 2\sqrt{{\tilde{w}}({\tilde{S}}^t){\tilde{c}}} \Bigr ) \quad \text {for all } t \in \{0,\dots ,T-1\}. \end{aligned}$$

Since ${{\tilde{c}}} < {{\tilde{w}}}({{\tilde{S}}}^{T})$, it follows that

$$\begin{aligned} \sum _{i \in {\tilde{S}}^*} p_i&\le \min _{t = 0,\dots ,T-1}\sum _{i \in {\tilde{S}}^t} p_i + \theta _{t+1}\Big ({{\tilde{w}}}({{\tilde{S}}}^{T}) + 2\sqrt{{{\tilde{w}}}({{\tilde{S}}}^{T}){{\tilde{w}}}({{\tilde{S}}}^t})\Big )\\&= \min _{t = 0,\dots ,T-1}\sum _{i = 1}^t \theta _i\Big ({{\tilde{w}}}({{\tilde{S}}}^i) \!-\! {{\tilde{w}}}({{\tilde{S}}}^{i-1}) \Big ) + \theta _{t+1}\Big ({{\tilde{w}}}({{\tilde{S}}}^{T}) \!+\! 2\sqrt{{{\tilde{w}}}({{\tilde{S}}}^{T}){{\tilde{w}}}({{\tilde{S}}}^t})\Big ). \end{aligned}$$

Furthermore,

$$\begin{aligned} \sum _{i \in {\tilde{S}}^{T}} p_i = \sum _{i = 1}^{T}\theta _i\Big ({{\tilde{w}}}({{\tilde{S}}}^i) - {{\tilde{w}}}({{\tilde{S}}}^{i-1}) \Big ) \end{aligned}$$

and thus, by Lemma 6,

$$\begin{aligned} \sum _{i \in {\tilde{S}}^{T}} p_i \ge \bigg ( 1 - \frac{\sqrt{3}}{e} \bigg ) \sum _{i \in {\tilde{S}}^*} p_i. \end{aligned}$$

Finally, this leads to

$$\begin{aligned} \sum _{i \in S^{T-1}} p_i&= \sum _{i \in U} p_i + \sum _{i \in {\tilde{S}}^{T-1} } p_i\\&= \sum _{i \in U} p_i + \sum _{i \in {{\tilde{S}}}^{T}} p_i - p_{i_{T}} \\&\ge \sum _{i \in U} p_i + \biggl (1- \frac{\sqrt{3}}{e}\biggr )\sum _{i \in {\tilde{S}}^*} p_i -p_{i_{T}} \\&\ge \sum _{i \in U} p_i + \biggl (1- \frac{\sqrt{3}}{e}\biggr )\sum _{i \in {\tilde{S}}^*} p_i -\frac{1}{2}\sum _{i \in U} p_i\\&\ge \biggl (1- \frac{\sqrt{3}}{e}\biggr )\sum _{i \in S^*} p_i. \end{aligned}$$

Since the Greedy Algorithm with starting solution U obtains a profit of at least $\sum _{i \in S^{T-1}} p_i$, this implies the claimed result. $\square$

We proceed to show that the approximation ratio of the Greedy Algorithm can be bounded from above by the inverse golden ratio.

Theorem 3

The approximation ratio of the Greedy Algorithm with partial enumeration is at most $\phi = (\sqrt{5} -1)/2$, even if we allow partial enumeration over an arbitrary but fixed number of items.

Proof

Consider the following instance. Let m, $\ell$, $k\in \mathbb {N}$ with $\ell < k$ and denote by $\chi _i$ the i-th unit vector in $\mathbb {R}^m$. Let there be two types of items: m items of type 1 with profit $p^{(1)} = 1$ and weight vector $y^{(1)}_i = k\chi _i$, $i\in [m]$, and $m\ell$ type 2 items with profit $p^{(2)} = \frac{1+2\ell }{k^2+2k\ell }$ and weight vector $y^{(2)}_i = \chi _{\lceil \frac{i}{\ell } \rceil }$, $i\in [m\ell ]$; see Fig. 3 for an illustration.

Fig. 3

A partial greedy solution $S = (S_1,S_2)$ with initial set $S^0 = (S^0_1,S^0_2)$, where $S^0_1 = \{1,2\}$ and $S^0_2 = \emptyset$. The long bars represent type 1 items whereas the short bars represent type 2 items

We wish to solve

$$\begin{aligned} \text {maximize} \qquad&p(S_1,S_2) \,{:}{=}\,|S_1|\, p^{(1)} +|S_2|\,p^{(2)} \\ \text {subject to} \qquad&w(S_1,S_2) \,{:}{=}\,\Big \Vert \sum _{i\in S_1}y_i^{(1)} + \sum _{i\in S_2}y_i^{(2)} \Big \Vert ^2_2 \le mk^2, \\&S_1\subseteq [m], \; S_2\subseteq [m\ell ]. \end{aligned}$$

Setting $Y \,{:}{=}\,[y_1^{(1)},\dots , y_m^{(1)},y_1^{(2)},\dots ,y_{m\ell }^{(2)}]$, this optimization problem can be reformulated as in (P) with weight matrix $W = Y^{\top }Y$, which is clearly nonnegative and positive semidefinite.

We first derive the solution produced by the Greedy Algorithm. Partition $[m\ell ] = \bigcup _{i=1}^{m}T_i$, where $T_i = \{j\in [m\ell ]: \lceil \frac{j}{\ell }\rceil = i\}$. Consider a partial greedy solution $S = (S_1,S_2)$ and assume that $i\notin S_1$ and $j \notin S_2$ for some type 1 item $i\in [m]$ and type 2 item $j\in T_i$. Let $h := |S_2\cap T_i| < \ell$. Then we have $w(S_1,S_2\cup \{j\}) - w(S_1,S_2)$ = $(h+1)^2 - h^2 = 1 + 2h$, and thus

$$\begin{aligned}&\frac{p^{(2)}}{w(S_1,S_2\cup \{j\}) - w(S_1,S_2)} = \frac{1+2\ell }{(k^2+2k\ell )(1+2h)} \\&\quad > \frac{1+2\ell }{(k^2+2kh)(1+2\ell )} = \frac{1}{k^2 + 2kh} = \frac{p^{(1)}}{w(S_1\cup \{i\},S_2) - w(S_1,S_2)}. \end{aligned}$$

Hence, the Greedy Algorithm will always include type 2 item $j\in T_i$ before type 1 item i in its solution.

Assume that for a partial solution $S = (S_1,S_2)$ we have $i\in S_1$, $i'\notin S_1$, and $j\notin S_2$ for some type 1 items i, $i'\in [m]$ and a type 2 item $j\in T_i$. Since $|S_2 \cap T_{i'}| \le \ell$, we have

$$\begin{aligned}&\frac{p^{(1)}}{w(S_1\cup \{i'\},S_2) - w(S_1,S_2)} \ge \frac{1}{k^2 + 2k\ell } \\&\quad > \frac{1+2\ell }{(1+2k)(k^2+2k\ell )} \ge \frac{p^{(2)}}{w(S_1,S_2\cup \{j\})-w(S_1,S_2)}. \end{aligned}$$

Consequently, the Greedy Algorithm always adds type 1 item $i'$ before type 2 item $j\in T_i$ to its solution given that type 1 item i is already included.

Thus, the Greedy Algorithm starts with some initial solution $S^0 = (S_1^0,S_2^0)$. Afterwards, it includes all type 2 items in $[m\ell ] \setminus \bigcup _{i\in S_1^0} T_i$ (Step 1). Finally, it adds type 1 items until the capacity bound of $mk^2$ is reached (Step 2). Let $s \,{:}{=}\,|S_1^0|$. The weight of the partial solution after Step 1 is given by $sk^2 + (m-s)\ell ^2$. Adding any type 1 item in Step 2 increases the weight of the solution by $k^2 + 2k\ell$. Hence, in Step 2,

$$\begin{aligned} r:= \frac{mk^2 - sk^2 - (m-s)\ell ^2}{k^2 + 2k\ell } = \frac{(m-s)(k^2 - \ell ^2)}{k^2 + 2k\ell } \end{aligned}$$

type 1 items are added until the capacity is reached. (It is without loss of generality to assume that $r\in \mathbb {Z}$ since otherwise after adding $\lfloor {r}\rfloor$ type 1 items, the remaining capacity would be filled with type 2 items and the resulting approximation ratio would be even lower.) Thus, the profit of the solution ${\hat{S}}$ produced by the Greedy Algorithm is given by

$$\begin{aligned} p({\hat{S}})&= (s+r)p^{(1)} + (m-s)\ell p^{(2)} \\&= s + \frac{(m-s)(k^2 - \ell ^2)}{k^2 + 2k\ell } + \frac{(m-s)\ell (1+2\ell )}{k^2+2k\ell } \\&= s + \frac{(m-s)(k^2 + \ell ^2 + \ell )}{k^2+2k\ell } \\&= m\left[ \frac{s}{m} + \frac{ (1 - \frac{s}{m})(1 + \frac{\ell ^2}{k^2} + \frac{\ell }{k^2})}{1 + 2\frac{\ell }{k}} \right] \\&= m\left[ \frac{s}{m} + \frac{(1 - \frac{s}{m}) (1+ q^2 + \frac{q}{k})}{1 + 2q} \right] , \end{aligned}$$

where $q:= \frac{\ell }{k}$.

On the other hand, consider the solution $S^* = (S_1^*,S_2^*)$ with $S_1^* = [m]$ and $S_2^* = \emptyset$. It fulfills $p(S) = m$ and $w(S) = mk^2$. Thus, we have

$$\begin{aligned} \rho (q):= \lim _{k,m\rightarrow \infty } \frac{p({\hat{S}})}{p(S^*)} = \frac{1 + q^2}{1 + 2q}. \end{aligned}$$

Under the constraint $q\in (0,1)$, the ratio $\rho (q)$ attains its minimum at $q = \phi$ with value $q(\phi ) = \phi$, where $\phi = \frac{\sqrt{5}-1}{2}$ is the inverse golden ratio. $\square$

5 Monotone algorithms

To illustrate the need for monotone algorithms, reconsider the situation described in Example 1 with a set of n selfish agents requesting permission to send gas through a pipeline. Each agent j has a private value $p_j$ expressing the monetary gain from being allowed to send the gas. A natural objective of a system provider is to maximize social welfare, i.e., to solve (P). Since the true value $p_j$ is the private information of agent j, the system designer has to employ a mechanism that incentivizes the agents to report their true values $p_j$.² It is without loss of generality to assume the following form of a direct revelation mechanism; see Gibbard [9] and Myerson [21]. The mechanism elicits a (potentially misrepresented) bid $p_j'$ from each agent j and computes a solution $x(p') \in \{0,1\}^n$ to (P) based on these values. Further, the mechanism computes a payment $g_j$ for each agent j. The utility of agent j, when its true valuation is $p_j$ and the agents report $p'$, is then $p_j x_j(p') - g_j(p')$. The mechanism is strategyproof if truthtelling is a dominant strategy of each agent j in the underlying game where each agent chooses a value to report.

Myerson [21] shows that an algorithm ${\mathcal {A}}$ can be turned into a strategyproof mechanism if and only if it is monotone in the following sense. Let $x(p')$ denote the feasible solution to (P) computed by ${\mathcal {A}}$ as a function of the reported valuations. Then ${\mathcal {A}}$ is monotone if for all agents j the function $x_j(p')$ is nondecreasing in $p'_j$ for all fixed values $p_i'$ with $i \ne j$. For a monotone algorithm, charging every agent j with $x_j(p') = 1$ the critical bid $\inf \, \{z \in \mathbb {R}_{\ge 0} : x_j(z,p'_{-j}) = 1\}$ and charging all other agents nothing yields a strategyproof mechanism. Here, $x_j(z,p_{-j}')$ denotes the binary variable $x_j$ as a function of the bid of agent j, when the bids $p'_{-j}$ of the other agents are fixed.

We note that the algorithms designed in Sects. 3 and 4 are unlikely to be monotone, since the partial enumeration schemes in both of them are not monotone. On the other hand, without the enumeration scheme, they do not provide a constant approximation, even when W is a diagonal matrix. However, by combining ideas from both algorithms, we derive a monotone algorithm with constant approximation guarantee; see Algorithm 3.

Theorem 4

Algorithm 3 is a monotone $\alpha$-approximation algorithm for (P), where $\alpha = \smash {\bigl (1 - \frac{\sqrt{3}}{e} \bigr ) / \bigl (1 + \frac{4}{\sqrt{5}-1} \bigr ) \approx 0.086}$. The corresponding critical payments can be computed in polynomial time.

Proof

We first prove the approximation ratio. For $\phi \,{:}{=}\,\frac{\sqrt{5}-1}{2}$ and $\rho \,{:}{=}\,1 - \frac{\sqrt{3}}{e}$, we have $\alpha = \nicefrac {\rho }{1+\frac{2}{\phi }}$. Let $p^*$ and $q^*$ be the optimal values of Problems (P) and ($R_1$), respectively. Since ($R_1$) is a relaxation of (P) we have that $q^* \ge p^*$. If $p_i\ge \alpha q^*$ for some $i\in [n]$ it follows that $p^{\top }\chi _i \ge \alpha p^*$.

Assume that $p_i < \alpha q^*$ for all $i\in [n]$, and let x be the solution computed by the Greedy Algorithm (without partial enumeration). Following the proof of Theorem 2 we see that $p^{\top }x \ge \rho p^* - p_j$ for some item $j\in [n]$. Since $p_j < \alpha q^*$, and by Corollary 1 we have $q^* \le \frac{2}{\phi }p^*$, we obtain $p^{\top } x \ge (\rho - \frac{2\alpha }{\phi })p^* = \alpha p^*$.

Next, we prove the monotonicity of the algorithm. To this end, let p, ${\hat{p}}\in \mathbb {N}^n$ be two declared profit vectors such that there is $i \in [n]$ with ${\hat{p}}_i = p_i + 1$ and ${\hat{p}}_j = p_j$ for all $j \ne i$. Let x and ${\hat{x}}$ be the corresponding solutions computed by Algorithm 3 and assume that $x_i = 1$. It is to show that ${\hat{x}}_i = 1$. Let $q^*$ and ${\hat{q}}^*$ be the optimal values of ($R_1$) with respect to p and ${\hat{p}}$. Then $q^* \le {\hat{q}}^* \le q^* +1$. Let $H:= \{j\in [n] : p_j \ge \alpha q^*\}$ and ${\hat{H}}:= \{j\in [n] : {\hat{p}}_j \ge \alpha {\hat{q}}^*\}$.

First, assume that $H\ne \emptyset$. Since by assumption $x_i = 1$, it follows that $p_i \ge \alpha q^*$ and $p_i = \max _{j\in [n]}p_j$. Therefore,

$$\begin{aligned} {\hat{p}}_i = p_i + 1 \ge \alpha q^* + 1 \ge \alpha (q^* +1) \ge \alpha {\hat{q}}^*, \end{aligned}$$

and thus ${\hat{H}} \ne \emptyset$. Furthermore, i is the only item in $\mathop {{\hbox {argmax}}}\limits _{j\in [n]}{\hat{p}}_j$ and hence ${\hat{x}}_i = 1$.

Next, assume that $H = \emptyset$. Then either ${\hat{H}} = \{i\}$ and thus ${\hat{x}}_i = 1$, or ${\hat{H}} = \emptyset$. In the latter case, Algorithm 3 executes the Greedy Algorithm for both p and ${\hat{p}}$. But since for every $S\subseteq [n]{\setminus } \{i\}$

$$\begin{aligned} \frac{{\hat{p}}_i}{w(S\cup \{i\})-w(S)} > \frac{p_i}{w(S\cup \{i\})-w(S)} \end{aligned}$$

and for every $j\in [n]\setminus \{i\}$ and every $S\subseteq [n] \setminus \{j\}$

$$\begin{aligned} \frac{{\hat{p}}_j}{w(S\cup \{j\})-w(S)} = \frac{p_j}{w(S\cup \{j\})-w(S)}, \end{aligned}$$

when the Greedy Algorithm adds item i to its solution after k iterations for p, then it also adds i to its solution after at most k iterations for ${\hat{p}}$. The critical payments can be computed with binary search. $\square$

6 Approximation hardness

In this section, we show that packing problems with convex quadratic constraints of type (P) are $\mathsf {APX}$-hard.

Theorem 5

It is ${\mathsf {NP}}$-hard to approximate packing problems with convex quadratic constraints by a factor of $\frac{91}{92} + \varepsilon$, for any $\varepsilon > 0$.

Proof

We reduce from the 6-set packing problem which is ${\mathsf {NP}}$-hard to approximate by a factor of $\frac{22}{23} + \varepsilon$ for all $\varepsilon > 0$; see Hazan et al. [11]. An instance of a 6-set packing is given by a ground set [m] and a family ${\mathcal {S}} \subseteq 2^{[m]}$ of subsets of [m] such that $|S| = 6$ for all $S \in {\mathcal {S}}$. A subfamily ${\mathcal {S}}^* \subseteq {\mathcal {S}}$ is a feasible solution to the 6-set packing problem if $S \cap T = \emptyset$ for all $S,T \in {\mathcal {S}}^*$ with $S\ne T$. For a given instance of 6-set packing, and a value $k \in \mathbb {N}$ the gap problem is the decision problem to decide whether:

$\mathsf {Yes}$::

there is a solution to the 6-set packing problem of size at least k, or

${\mathsf {No}}$::

every solution has size strictly smaller than $\frac{22}{23}k$.

For optimal sizes in the interval $[\frac{22}{23}k,k)$ any answer is admissible. The approximation hardness of 6-set packing implies that the gap problem is an ${\mathsf {NP}}$-hard decision problem.

Let $n \,{:}{=}\,|{\mathcal {S}}|$ and number the sets ${\mathcal {S}} = \{S_1,S_2,\dots ,S_n\}$. Define the matrix $A = (a_{ij})_{i,j}\in \{0,1\}^{m \times n}$ by $a_{ij} = 1$ if and only if $i \in S_j$, and let $W = A^{\top } A$. Consider the problem

where ${\mathbf {1}}= (1,\dots ,1)^\top$ is the all-ones vector. We calculate

$$\begin{aligned} x^{\top } W x = \Vert {A x}\Vert _2^2 = \sum _{i=1}^m \bigg (\sum _{j=1}^n a_{ij}\, x_j\bigg )^{\!2} = \sum _{i=1}^m \biggl ( \sum _{j \in [n] : i \in S_j} x_{j}\biggr )^2. \end{aligned}$$

(4)

Suppose, we have a $\mathsf {Yes}$-instance for the gap problem and let ${\mathcal {S}}^*$ be a subset of pairwise disjoint sets of cardinality k. Then a feasible solution for (SP) is given by $x^*$ defined as $x^*_j = 1$ if $S_j \in {\mathcal {S}}^*$, and $x^*_j = 0$, otherwise. Since every set $S_j$, $j \in [n]$, contributes exactly 6 to the left hand side of the knapsack constraint (4), this solution is also optimal for (SP) and has an objective value of k.

Next, consider a ${\mathsf {No}}$-instance for the gap problem, let $x^*$ be a corresponding optimal solution of (SP), and let $k'$ be its objective value. Since for a ${\mathsf {No}}$-instance every solution of the 6-set packing problem has size strictly less than $\frac{22}{23}k$, every set that is picked beyond the first $\lfloor \frac{22}{23}k \rfloor$ sets, intersects at least once with at least one of the first $\lfloor \frac{22}{23}k \rfloor$ sets. Thus, the first $\lfloor \frac{22}{23}k \rfloor$ sets each contribute at least 6 to (4), and each of the further $k' - \lfloor \frac{22}{23}k \rfloor$ sets each contributes at least $5 + 4 -1 = 8$ to (4). We obtain

$$\begin{aligned} 6k&\ge (x^*)^{\top } W x^* \ge 6 \bigg \lfloor \frac{22}{23}k\bigg \rfloor + 8\biggl (k' - \bigg \lfloor \frac{22}{23}k\bigg \rfloor \biggr ) \ge 8k' - \frac{44}{23}k \end{aligned}$$

implying $k' \le \frac{91}{92}k$. We conclude that for a $\mathsf {Yes}$-instance the objective value of (SP) is at least k while for a ${\mathsf {No}}$-instance it is strictly less than $\frac{91}{92}k$. Therefore, the problem is ${\mathsf {NP}}$-hard to approximate by a factor of $\frac{91}{92} + \varepsilon$ for any $\varepsilon > 0$. $\square$

Fig. 4

The Gaslib-134 instance. Sources are shown as pentagons, sinks as circles

7 Computational results

We apply our algorithms to gas transportation as described in Example 1, using the GasLib-134 instance [27]; see Fig. 4. The instance contains upper and lower pressure bounds for every node $v\in V$ as well as all physical properties to compute the pipe resistances $\beta _e$, $e\in E$. Sources and sinks are denoted by S and T, respectively. Every sink $t\in T$ has a demand of $q_t$ units of gas. To ensure network robustness in the sense of [16], we assume that all sinks between $s_1$ and $s_2$ are supplied by $s_1$, all sinks between $s_3$ and $t_{45}$ by $s_3$, and all other sinks by $s_2$. Denote by $T_i$ the set of sinks supplied by $s_i$, $i=1,2,3$. For simplicity, we assume that the economic welfare is proportional to the amount of transported gas, i.e., there is a constant $\theta > 0$ such that for every sink $t\in T$, the economic welfare $p_t$ of transporting $q_t$ units of gas to t equals $\theta q_t$.

The goal is to choose a welfare-maximal subset of transportations that can be routed simultaneously, while the pressures at all nodes are within their feasible interval. Since our algorithms are only applicable to path topologies, we solve a relaxation of the problem by only requiring that the pressures of all nodes on the path between the first sink $s_1$ and the last source $t_{45}$ are feasible. Let ${\bar{E}}$ denote the path from $s_1$ to $t_{45}$, and for every $t\in T_i$ denote by $E_t$ the path from $s_i$ to t, $i=1,2,3$. Let $p = (p_t)_{t\in T}$, $W = (w_{t,t'})_{t,t'\in T}$, with $w_{t,t'} = \sum _{e\in {\bar{E}} \cap E_t\cap E_{t'}}\beta _e\, q_t\, q_{t'}$, and let , where ${\bar{\pi }}_v$ and denote the upper and lower bound on the squared pressure at node v, respectively. Finally, let $x = (x_t)_{t\in T} \in \{0,1\}^T$, where $x_t = 1$ if and only if sink t is supplied. This results in a formulation as (P); see Example 1.

The GasLib-134 instance contains different scenarios, where each scenario provides demands ${\hat{q}}_t$ for every sink $t\in T$. In order to make the optimization problem non-trivial, we increase the node demands by setting $q_t = \gamma \, \hat{q}_t$, for $\gamma \in \Gamma {:}{=}\{5,10,50,100\}$. We apply the Golden Ratio Algorithm devised in Sect. 3, the Greedy Algorithm devised in Sect. 4, and the Monotone Greedy Algorithm devised in Sect. 5 to the first 100 scenarios, using each $\gamma \in \Gamma$. The first two algorithms are executed using k initial elements in partial enumeration for each $k \in \{0,1,2,3\}$. The Monotone Greedy Algorithm is only executed without partial enumeration in order to guarantee its monotonicity.

For the Golden Ratio Algorithm, instead of scaling the optimal solution y of ($R_1$) by $\phi$, we scale it by the largest number $\lambda \in [\phi ,1]$ such that $\lambda \, y$ is feasible for ($R_2$), using binary search. The result of each algorithm is compared to an optimal solution computed with Gurobi 9.0 applied to the following mixed-integer program

$$\begin{aligned} \text {maximize} \qquad&p^\top x\\ \text {subject to} \qquad&\sum _{i=1}^n z_i \le c,\\&z_i \ge \max \biggl \{0,\sum _{j=1}^n w_{ij}(x_i+x_j-1)\biggr \} \quad \text {for all } i\in [n], \\&x \in \{0,1\}^n, \end{aligned}$$

which can be shown to be equivalent to (P). The computations were executed on a 4-core Intel Core i5-2520M processor with 2.5 GHz. The code is implemented in Python 3.6 and we use the SLSQP algorithm of the SciPy optimize package to solve ($R_1$). The results are shown in Table 1 and as box plots in Fig. 5.

Table 1 Mean and standard deviation (SD) of the approximation ratio of the Golden Ratio Algorithm (GO), the Greedy Algorithm (GR), and the Monotone Greedy Algorithm (MO) with partial enumeration of $k \in \{0,1,2,3\}$ elements

Fig. 5

Approximation ratios and runtimes for the Golden Ratio Algorithm (GO), the Greedy Algorithm (GR), both with partial enumeration of $k \in \{0,1,2,3\}$ elements, the Monotone Greedy Algorithm (MO), and the optimal solution (OPT) computed with Gurobi 9.0. Boxes are from lower quartile to upper quartile, median is thick, lower whisker is smallest data point larger than lower quartile minus 150% of interquartile range, upper whisker equivalently, and data points outside whiskers are shown as dots

The Greedy Algorithm achieves the best approximation ratios on average and is, when executed without partial enumeration, around 200 times faster than computing the optimal solution with Gurobi 9.0 and around 20 times faster than the Golden Ratio Algorithm and the Monotone Greedy Algorithm, because the latter rely on solving the convex relaxation ($R_1$) first. As expected, combining the algorithms with partial enumeration drastically increases their running times.

The approximation ratios of all three algorithms are on average much higher than their proven worst case lower bounds, even when executed without partial enumeration. However, the quality of the solutions produced by the Golden Ratio Algorithm is subject to strong fluctuations. By running the algorithm with partial enumeration with $k = 3$ initial elements, the ratio is at least $\phi$ for every instance, as guaranteed by Theorem 1. Among the tested algorithms, only the Greedy Algorithm without partial enumeration and the Monotone Greedy Algorithm are known to be monotone. Although the approximation ratio of the Greedy Algorithm without partial enumeration may be arbitrarily low, we see that it performs much better in practice and outperforms the Monotone Greedy Algorithm.