Convergence analysis of a Lasserre hierarchy of upper bounds for polynomial minimization on the sphere

Abstract

We study the convergence rate of a hierarchy of upper bounds for polynomial minimization problems, proposed by Lasserre (SIAM J Optim 21(3):864–885, 2011), for the special case when the feasible set is the unit (hyper)sphere. The upper bound at level $r \in {\mathbb {N}}$ of the hierarchy is defined as the minimal expected value of the polynomial over all probability distributions on the sphere, when the probability density function is a sum-of-squares polynomial of degree at most 2r with respect to the surface measure. We show that the rate of convergence is $O(1/r^2)$ and we give a class of polynomials of any positive degree for which this rate is tight. In addition, we explore the implications for the related rate of convergence for the generalized problem of moments on the sphere.

1 Introduction

We consider the problem of minimizing an n-variate polynomial $f:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$ over a compact set $K\subseteq {{\mathbb {R}}}^n$, i.e., the problem of computing the parameter:

$$\begin{aligned} f_{\min ,K}:= \min _{x\in K}f(x). \end{aligned}$$

(1)

In this paper we will focus on the case when K is the unit sphere: $K={\mathbb {S}}^{n-1}=\{x\in {{\mathbb {R}}}^n:\Vert x\Vert =1\}$. Here and throughout, $\Vert x\Vert$ denotes the Euclidean norm for real vectors. When considering $K={\mathbb {S}}^{n-1}$, we will omit the subscript K and simply write $f_{\min }=\min _{x\in {\mathbb {S}}^{n-1}} f(x).$

Problem (1) is in general a computationally hard problem, already for simple sets K like the hypercube, the standard simplex, and the unit ball or sphere. For instance, the problem of finding the maximum cardinality $\alpha (G)$ of a stable set in a graph $G=([n],E)$ can be expressed as optimizing a quadratic polynomial over the standard simplex [18], or a degree 3 polynomial over the unit sphere [19]:

$$\begin{aligned} {1\over \alpha (G)}= & {} \min _{x\in {{\mathbb {R}}}^n} \Bigg \{x^T(I+A_G)x: x\ge 0, \sum _{i=1}^nx_i=1\Bigg \} \\= & {} \min _{y \in {\mathbb {S}}^{n-1}} \left( \sum _{i\ne j: \{i,j\} \in E} y_i^2y_j^2 + \sum _{i \in [n]} y_i^4\right) , \\ {\sqrt{2}\over 3\sqrt{3}} \sqrt{ 1-{1\over \alpha (G)}}= & {} \max _{(y,z)\in {\mathbb {S}}^{n+ m -1}} \sum _{ij \in {\overline{E}}} y_iy_jz_{ij}, \end{aligned}$$

where $A_G$ is the adjacency matrix of G, ${\overline{E}}$ is the set of non-edges of G and $m=|{\overline{E}}|$. Other applications of polynomial optimization over the unit sphere include deciding whether homogeneous polynomials are positive semidefinite. Indeed, a homogeneous polynomial f is defined as positive semidefinite precisely if

$$\begin{aligned} f_{\min }= \min _{x\in {\mathbb {S}}^{n-1}} f(x) \ge 0, \end{aligned}$$

and positive definite if the inequality is strict; see e.g. [22]. As special case, one may decide if a symmetric matrix $A = (a_{ij}) \in {\mathbb {R}}^{n\times n}$ is copositive, by deciding if the associated form $f(x) = \sum _{i,j \in [n]} a_{ij}x_i^2x_j^2$ is positive semidefinite; see, e.g. [20].

Another special case is to decide the convexity of a homogeneous polynomial f, by considering the parameter

$$\begin{aligned} \min _{(x,y)\in {\mathbb {S}}^{2n-1}} y^T\nabla f(x)y, \end{aligned}$$

which is nonnegative if and only if f is convex. This decision problem is known to be NP-hard, already for degree 4 forms [1].

As shown by Lasserre [16], the parameter (1) can be reformulated via the infinite dimensional program

$$\begin{aligned} f_{\min ,{K}}=\inf _{h\in {\varSigma }[x]}\int _{K}h(x)f(x)d\mu (x) \ \ \text{ s.t. } \int _{{K}}h(x)d\mu (x)=1\text{, } \end{aligned}$$

(2)

where ${\varSigma }[x]$ denotes the set of sums of squares of polynomials, and $\mu$ is a given Borel measure supported on K. Given an integer $r\in {{\mathbb {N}}}$, by bounding the degree of the polynomial $h\in {\varSigma }[x]$ by 2r, Lasserre [16] defined the parameter:

$$\begin{aligned} {\overline{f}}^{(r)}_K:=\min _{h\in {\varSigma }[x]_r}\int _{{K}}h(x)f(x)d\mu (x) \ \ \text{ s.t. } \, \int _{{K}}h(x)d\mu (x)=1, \end{aligned}$$

(3)

where ${\varSigma }[x]_r$ consists of the polynomials in ${\varSigma }[x]$ with degree at most 2r. Here we use the ‘overline’ symbol to indicate that the parameters provide upper bounds for $f_{\min ,K}$, in contrast to the parameters ${\underline{f}}^{(r)}$ in (9) below, which provide lower bounds for it.

Since sums of squares of polynomials can be formulated using semidefinite programming, the parameter (3) can be expressed via a semidefinite program. In fact, since this program has only one affine constraint, it even admits an eigenvalue reformulation [16], which will be mentioned in (12) in Sect. 2.2 below. Of course, in order to be able to compute the parameter (3) in practice, one needs to know explicitly (or via some computational procedure) the moments of the reference measure $\mu$ on K. These moments are known for simple sets like the simplex, the box, the sphere, the ball and some simple transforms of them (they can be found, e.g., in Table 1 in [9]).

As a direct consequence of the formulation (2), the bounds ${\overline{f}}^{(r)}_K$ converge asymptotically to the global minimum $f_{\min ,K}$ when $r\rightarrow \infty$. How fast the bounds converge to the global minimum in terms of the degree r has been investigated in the papers [7, 8, 11], which show, respectively, a convergence rate in $O(1/\sqrt{r})$ for general compact K (satisfying a minor geometric condition, implying a nonempty interior), a convergence rate in O(1/r) when K is a convex body, and a convergence rate in $O(1/r^2)$ when K is the box $[-1,1]^n$. In these works the reference measure $\mu$ is the Lebesgue measure, except for the box $[-1,1]^n$ where more general measures are considered (see Theorem 3 below for details).

The convergence rates in [7, 11] are established by constructing an explicit sum of squares $h\in {\varSigma }[x]_r$, obtained by approximating the Dirac delta at a global minimizer a of f in K by a suitable density function and considering a truncation of its Taylor expansion. Roughly speaking, a Gaussian density of the form $\exp (-\Vert x-a\Vert ^2/\sigma ^2)$ (with $\sigma \sim 1/r$) is used in [11], and a Boltzman density of the form $\exp (-f(x)/T)$ (with $T\sim 1/r$) is used in [7] (and relying on a result of [14] about simulated annealing for convex bodies). For the box $K=[-1,1]^n$, the stronger analysis in [8] relies on an eigenvalue reformulation of the bounds and exploiting links to the roots of orthogonal polynomials (for the selected measure), as will be briefly recalled in Sect. 2.2 below. These results do not apply to the sphere, which has an empty interior and is not a convex body. Nevertheless, as we will see in this paper, one may still derive information for the sphere from the analysis for the interval $[-1,1]$.

In this paper we are interested in analyzing the worst-case convergence of the bounds (3) in the case of the unit sphere $K={\mathbb {S}}^{n-1}$, when selecting as reference measure the surface (Haar) measure $d\sigma (x)$ on ${\mathbb {S}}^{n-1}$. We let $\sigma _{n-1}$ denote the surface measure of ${\mathbb {S}}^{n-1}$, so that $d\sigma (x) /\sigma _{n-1}$ is a probability measure on ${\mathbb {S}}^{n-1}$, with

$$\begin{aligned} \sigma _{n-1}:= \int _{{\mathbb {S}}^{n-1}} d\sigma (x)= {2\pi ^{n\over 2}\over {\varGamma }\left( {n\over 2}\right) }. \end{aligned}$$

(4)

(See, e.g., [6, relation (2.2.3)].) To simplify notation we will throughout omit the subscript $K={\mathbb {S}}^{n-1}$ in the parameters (1) and (3), which we simply denote as

$$\begin{aligned} f_{\min }= & {} \min _{x\in {\mathbb {S}}^{n-1}}f(x), \ \ \nonumber \\ {\overline{f}}^{(r)}= & {} \inf _{h\in {\varSigma }[x]_r}\Bigg \{\int _{{\mathbb {S}}^{n-1}} h(x)f(x)d\sigma (x) : \int _{{\mathbb {S}}^{n-1}} h(x)d\sigma (x)=1\Bigg \}. \end{aligned}$$

(5)

Example 1

Consider the minimization of the Motzkin form

$$\begin{aligned} f(x_1,x_2,x_3) = x_3^6+x_1^4x_2^2+x_1^2x_2^4-3x_1^2x_2^2x_3^2 \end{aligned}$$

on ${\mathbb {S}}_2$. This form has 12 minimizers on the sphere, namely $\frac{1}{\sqrt{3}}(\pm 1, \pm 1, \pm 1)$ as well as $(\pm 1,0,0)$ and $(0, \pm 1,0)$, and one has $f_{\min } = 0$.

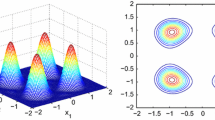
In Table 1 we give the bounds ${\overline{f}}^{(r)}$ for the Motzkin form for $r \le 9$. In Fig. 1 we show contour plots of the optimal density function for $r=3$, $r=6$, and $r=9$. In the figure, the red end of the spectrum denotes higher function values.

When $r = 3$ and $r=6$, the modes of the optimal density are at the global minimizers $(\pm 1,0,0)$ and $(0, \pm 1,0)$ (one may see the contours of two of these modes in one hemisphere). On the other hand, when $r=9$, the mass of the distribution is concentrated at the 8 global minimizers $\frac{1}{\sqrt{3}}(\pm 1, \pm 1, \pm 1)$ (one may see 4 of these in one hemisphere), and there are no modes at the global minimizers $(\pm 1,0,0)$ and $(0, \pm 1,0)$.

Table 1 Upper bounds for the Motzkin form

Fig. 1

Contour plots of the optimal density for $r=3$, $r=6$, and $r=9$

Fig. 2

Plots of the optimal density for $r=3$ (top left), $r=6$ (top right), and $r=9$ (bottom), in spherical coordinates

It is also illustrative to do the same plots using spherical coordinates:

$$\begin{aligned} x_1= & {} \sin \theta \sin \phi \\ x_2= & {} \sin \theta \cos \phi \\ x_3= & {} \cos \theta \\ \theta\in & {} [0,\pi ]\\ \phi\in & {} [0,2\pi ]. \end{aligned}$$

In Fig. 2 we plot the optimal density function that corresponds to $r=3$ (top right), $r=6$ (bottom left), and $r=9$ (bottom right). For example, when $r=9$ one can see the 8 modes (peaks) of the density that correspond to the 8 global minimizers $\frac{1}{\sqrt{3}}(\pm 1, \pm 1, \pm 1)$. (Note that the peaks at $\phi = 0$ and $\phi = 2\pi$ correspond to the same mode of the density, due to periodicity.) Likewise when $r=3$ and $r=6$ one may see 4 modes corresponding to $(\pm 1,0,0)$ and $(0, \pm 1,0)$.

The convergence rate of the bounds ${\overline{f}}^{(r)}$ was investigated by Doherty and Wehner [4], who showed

$$\begin{aligned} {\overline{f}}^{(r)}-f_{\min }=O\left( {1\over r}\right) \end{aligned}$$

(6)

when f is a homogeneous polynomial. As we will briefly recap in Sect. 2.1, their result follows in fact as a byproduct of their analysis of another Lasserre hierarchy of bounds for $f_{\min }$, namely the lower bounds (9) below.

Our main contribution in this paper is to show that the convergence rate of the bounds ${\overline{f}}^{(r)}$ is $O(1/r^2)$ for any polynomial f and, moreover, that this analysis is tight for any (nonzero) linear polynomial f (and some powers). This is summarized in the following theorem, where we use the usual Landau notation: for two functions $f_1,f_2:{\mathbb {N}} \rightarrow {\mathbb {R}}_+$, then

$$\begin{aligned} f_1 = {\varOmega }(f_2) \Longleftrightarrow \liminf _{r \rightarrow \infty } \frac{f_1(r)}{f_2(r)} > 0. \end{aligned}$$

Theorem 1

• (i) For any polynomial f we have

  $$\begin{aligned} {\overline{f}}^{(r)}-f_{\min }=O\left( {1\over r^2}\right) . \end{aligned}$$

  (7)

• (ii) For any polynomial $f(x)=(-1)^{d-1}(c^Tx)^d$, where $c\in {{\mathbb {R}}}^n\setminus \{0\}$ and $d\in {{\mathbb {N}}}$, $d\ge 1$, we have

  $$\begin{aligned} {\overline{f}}^{(r)}-f_{\min }={\varOmega }\left( {1\over r^2}\right) . \end{aligned}$$

  (8)

Let us say a few words about the proof technique. For the first part (i), our analysis relies on the following two basic steps: first, we observe that it suffices to consider the case when f is linear (which follows using Taylor’s theorem), and then we show how to reduce to the case of minimizing a linear univariate polynomial over the interval $[-1,1]$, where we can rely on the analysis completed in [8]. For the second part (ii), by exploiting a connection recently mentioned in [17] between the bounds (3) and cubature rules, we can rely on known results for cubature rules on the unit sphere to show tightness of the bounds.

Organization of the paper In Sect. 2 we recall some previously known results that are most relevant to this paper. First we give in Sect. 2.1 a brief recap of the approach of Doherty and Wehner [4] for analysing bounds for polynomial optimization over the unit sphere. After that, we recall our earlier results about the quality of the bounds (3) in the case of the interval $K=[-1,1]$. Section 3 contains our main results about the convergence analysis of the bounds (3) for the unit sphere: after showing in Sect. 3.1 that the convergence rate is in $O(1/r^2)$ we prove in Sect. 3.2 that the analysis is tight for nonzero linear polynomials (and their powers).

2 Preliminaries

2.1 The approach of Doherty and Wehner for the sphere

Here we briefly sketch the approach followed by Doherty and Wehner [4] for showing the convergence rate O(1/r) mentioned above in (6). Their approach applies to the case when f is a homogeneous polynomial, which enables using the tensor analysis framework. A first and nontrivial observation, made in [4, Lemma B.2], is that we may restrict to the case when f has even degree, because if f is homogeneous with odd degree d then we have

$$\begin{aligned} \max _{x\in {\mathbb {S}}^{n-1}} f(x) ={d^{d/2}\over (d+1)^{(d+1)/2}} \max _{(x,x_{n+1})\in {\mathbb {S}}^n} x_{n+1}f(x). \end{aligned}$$

So we now assume that f is homogeneous with even degree $d=2a$.

The approach in [4] in fact also permits to analyze the following hierarchy of lower bounds on $f_{\min }$:

$$\begin{aligned} {\underline{f}}^{(r)}:= \sup _{\lambda \in {{\mathbb {R}}}}\lambda \ \text { s.t. } \ f(x)-\lambda \in {\varSigma }[x]_r + (1-\Vert x\Vert ^2){{\mathbb {R}}}[x], \end{aligned}$$

(9)

which are the usual sums-of-squares bounds for polynomial optimization (as introduced in [15, 21]).

One can verify that (9) can be reformulated as

$$\begin{aligned} \begin{aligned} {\underline{f}}^{(r)}&= \displaystyle \sup _{\lambda \in {{\mathbb {R}}}} \lambda \ \text { s.t. }\ (f(x)-\lambda \Vert x\Vert ^{2a})\Vert x\Vert ^{2r-2a} \in {\varSigma }[x]_r + (1-\Vert x\Vert ^2){{\mathbb {R}}}[x]\\&= \displaystyle \sup _{\lambda \in {{\mathbb {R}}}} \lambda \ \text { s.t. } \ f(x)\Vert x\Vert ^{2r-2a} -\lambda \Vert x\Vert ^{2r} \in {\varSigma }[x] \end{aligned} \end{aligned}$$

(10)

(see [10]). For any integer $r\in {{\mathbb {N}}}$ we have

$$\begin{aligned} {\underline{f}}^{(r)}\le f_{\min }\le {\overline{f}}^{(r)}. \end{aligned}$$

The following error estimate is shown on the range ${\overline{f}}^{(r)}-{\underline{f}}^{(r)}$ in [4].

Theorem 2

[4] Assume $n\ge 3$ and f is a homogeneous polynomial of degree 2a. There exists a constant $C_{n,a}$ (depending only on n and a) such that, for any integer $r\ge a(2a^2+n-2)-n/2$, we have

$$\begin{aligned} {\overline{f}}^{(r)}-{\underline{f}}^{(r)} \le {C_{n,a} \over r} (f_{\max }-f_{\min }), \end{aligned}$$

where $f_{\max }$ is the maximum value of f taken over ${\mathbb {S}}^{n-1}$.

The starting point in the approach in [4] is reformulating the problem in terms of tensors. For this we need the following notion of ‘maximally symmetric matrix’. Given a real symmetric matrix $M=(M_{{\underline{i}},{\underline{j}}})$ indexed by sequences ${\underline{i}}\in [n]^a$, where $[n] := \{1,\ldots ,n\}$, M is called maximally symmetric if it is invariant under action of the permutation group $\text {Sym}(2a)$ after viewing M as a 2a-tensor acting on ${{\mathbb {R}}}^n$. This notion is the analogue of the ‘moment matrix’ property, when expressed in the tensor setting. To see this, for a sequence ${\underline{i}}=(i_1,\ldots ,i_a)\in [n]^a$, define $\alpha ({\underline{i}})=(\alpha _1,\ldots ,\alpha _n)\in {{\mathbb {N}}}^n$ by letting $\alpha _\ell$ denote the number of occurrences of $\ell$ within the multi-set $\{i_1,\ldots ,i_a\}$ for each $\ell \in [n]$, so that $a=|\alpha |=\sum _{i=1}^n \alpha _i$. Then, the matrix M is maximally symmetric if and only if each entry $M_{{\underline{i}},{\underline{j}}}$ depends only on the n-tuple $\alpha ({\underline{i}})+\alpha ({\underline{j}})$. Following [4] we let $\text {MSym}(({{{\mathbb {R}}}}^n)^{\otimes a})$ denote the set of maximally symmetric matrices acting on $({{\mathbb {R}}}^n)^{\otimes a}$.

It is not difficult to see that any degree 2a homogeneous polynomial f can be represented in a unique way as

$$\begin{aligned} f(x)=(x^{\otimes a})^T Z_f x^{\otimes a}, \end{aligned}$$

where the matrix $Z_f$ is maximally symmetric.

Given an integer $r\ge a$, define the polynomial $f_r(x)=f(x)\Vert x\Vert ^{2r-2a}$, thus homogeneous with degree 2r. The parameter (10) can now be reformulated as

$$\begin{aligned} {\underline{f}}^{(r)}= \sup \{\langle Z_{f_r},M\rangle : M\in \text {MSym}(({{{\mathbb {R}}}}^n)^{\otimes r}),\ M\succeq 0,\ \text {Tr}(M)=1\}. \end{aligned}$$

(11)

The approach in [4] can be sketched as follows. Let M be an optimal solution to the program (11) (which exists since the feasible region is a compact set). Then the polynomial $Q_M(x):= (x^{\otimes r})^T M x^{\otimes r}$ is a sum of squares since $M\succeq 0$. After scaling, we obtain the polynomial

$$\begin{aligned} h(x)=Q_M(x)/\int _{{\mathbb {S}}^{n-1}} Q_M(x)d\sigma (x) \in {\varSigma }[x]_r, \end{aligned}$$

which defines a probability density function on ${\mathbb {S}}^{n-1}$, i.e., $\int _{{\mathbb {S}}^{n-1}} h(x)d\sigma (x)=1$. In this way h provides a feasible solution for the program defining the upper bound ${\overline{f}}^{(r)}$. This thus implies the chain of inequalities

$$\begin{aligned} \langle Z_{f_r},M\rangle ={\underline{f}}^{(r)}\le f_{\min }\le {\overline{f}}^{(r)}\le \int _{{\mathbb {S}}^{n-1}} f(x)h(x)d\sigma (x). \end{aligned}$$

The main contribution in [4] is their analysis for bounding the range between the two extreme values in the above chain and showing Theorem 2, which is done by using, in particular, Fourier analysis on the unit sphere.

Using different techniques we will show below a rate of convergence in $O(1/r^2)$ for the upper bounds ${\overline{f}}^{(r)}$, thus stronger than the rate O(1/r) in Theorem 2 above and applying to any polynomial (not necessarily homogeneous). On the other hand, while the constant involved in Theorem 2 depends only on the degree of f and the dimension n, the constant in our result depends also on other characteristics of f (its first and second order derivatives). A key ingredient in our analysis will be to reduce to the univariate case, namely to the optimization of a linear polynomial over the interval $[-1,1]$. Thus we next recall the relevant known results that we will need in our treatment.

2.2 Convergence analysis for the interval $[-\,1,1]$

We start with recalling the following eigenvalue reformulation for the bound (3), which holds for general K compact and plays a key role in the analysis for the case $K=[-1,1]$. For this consider the following inner product

$$\begin{aligned} (f,g)\mapsto \int _K f(x)g(x)d\mu (x) \end{aligned}$$

on the space of polynomials on K and let $\{b_\alpha (x):\alpha \in {{\mathbb {N}}}^n\}$ denote a basis of this polynomial space that is orthonormal with respect to the above inner product; that is, $\int _K b_\alpha (x)b_{\beta }(x)d\mu (x)=\delta _{\alpha ,\beta }.$ Then the bound (2) can be equivalently rewritten as

$$\begin{aligned} {\overline{f}}^{(r)}= \lambda _{\min }(A_f), \quad \text { where } A_f=\left( \int _K f(x)b_\alpha (x)b_{\beta }(x)d\mu (x) \right) _{\begin{array}{c} \alpha ,\beta \in {{\mathbb {N}}}^n \\ |\alpha |,|\beta |\le r \end{array}} \end{aligned}$$

(12)

(see [8, 16]). Using this reformulation we could show in [8] that the bounds (3) have a convergence rate in $O(1/r^2)$ for the case of the interval $K=[-1,1]$ (and as an application also for the n-dimensional box $[-1,1]^n$).

This result holds for a large class of measures on $[-1,1]$, namely those which admit a weight function $w(x)=(1-x)^a(1+x)^b$ (with $a,b>-1$) with respect to the Lebesgue measure. The corresponding orthogonal polynomials are known as the Jacobi polynomials $P^{a,b}_d(x)$ where $d\ge 0$ is their degree. The case $a=b=-1/2$ (resp., $a=b=0$) corresponds to the Chebychev polynomials (resp., the Legendre polynomials), and when $a=b=\lambda -1/2$, the corresponding polynomials are the Gegenbauer polynomials $C_d^{\lambda }(x)$ where d is their degree. See, e.g., [6, Chapter 1] for a general reference about orthogonal polynomials.

The key fact is that, in the case of the univariate polynomial $f(x)=x$, the matrix $A_f$ in (12) has a tri-diagonal shape, which follows from the 3-term recurrence relationship satisfied by the orthogonal polynomials. In fact, $A_f$ coincides with the so-called Jacobi matrix of the orthogonal polynomials in the theory of orthogonal polynomials and its eigenvalues are given by the roots of the degree $r+1$ orthogonal polynomial (see, e.g. [6, Chapter 1]). This fact is key to the following result.

Theorem 3

[8] Consider the measure $d\mu (x)=(1-x)^a(1+x)^bdx$ on the interval $[-1,1]$, where $a,b>-1$. For the univariate polynomial $f(x)=x$, the parameter ${\overline{f}}^{(r)}$ is equal to the smallest root of the Jacobi polynomial $P^{a,b}_{r+1}$ (with degree $r+1$). In particular, ${\overline{f}}^{(r)} =-\cos \Big ({\pi \over 2r+2}\Big )$ when $a=b=-1/2$. For any $a,b>-1$ we have

$$\begin{aligned} {\overline{f}}^{(r)} -f_{\min } = {\overline{f}}^{(r)}+1={\varTheta }\Big ({1\over r^2}\Big ). \end{aligned}$$

3 Convergence analysis for the unit sphere

In this section we analyze the quality of the bounds ${\overline{f}}^{(r)}$ when minimizing a polynomial f over the unit sphere ${\mathbb {S}}^{n-1}$. In Sect. 3.1 we show that the range ${\overline{f}}^{(r)} -f_{\min }$ is in $O(1/r^2)$ and in Sect. 3.2 we show that the analysis is tight for linear polynomials.

3.1 The bound $O(1/r^2)$

We first deal with the n-variate linear (coordinate) polynomial $f(x)=x_1$ and after that we will indicate how the general case can be reduced to this special case. The key idea is to get back to the analysis in Sect. 2.2, for the interval $[-1,1]$ with an appropriate weight function. We begin with introducing some notation we need.

To simplify notation we set $d=n-1$ (which also matches the notation customary in the theory of orthogonal polynomials where d usually is the number of variables). We let ${\mathbb {B}}^d=\{x\in {{\mathbb {R}}}^d: \Vert x\Vert \le 1\}$ denote the unit ball in ${{\mathbb {R}}}^d$. Given a scalar $\lambda >-1/2$, define the d-variate weight function

$$\begin{aligned} w_{d,\lambda }(x)=(1-\Vert x\Vert ^2)^{\lambda -1/2} \end{aligned}$$

(13)

(well-defined when $\Vert x\Vert <1$) and set

$$\begin{aligned} C_{d,\lambda }:= \int _{{\mathbb {B}}^d} w_{d,\lambda }(x_1,\ldots ,x_d)dx_1\cdots dx_d = {\pi ^{d/2}{\varGamma }\Big (\lambda +{1\over 2}\Big )\over {\varGamma }\Big (\lambda +{d+1\over 2}\Big )} \end{aligned}$$

(14)

so that $C_{d,\lambda }^{-1}w_{d,\lambda }(x_1,\ldots ,x_d)dx_1\cdots dx_d$ is a probability measure over the unit ball ${\mathbb {B}}^d$. See, e.g., [6, Section 2.3.2] or [2, Section 11].

We will use the following simple lemma, which indicates how to integrate the d-variate weight function $w_{d,\lambda }$ along $d-1$ variables.

Lemma 1

Fix $x_1\in [-1,1]$ and let $d\ge 2$. Then we have:

$$\begin{aligned} \int _{\{(x_2,\ldots ,x_d):x_2^2+\cdots +x_d^2\le 1-x_1^2\}} w_{d,\lambda }(x_1,\ldots ,x_d)dx_2\cdots dx_d = C_{d-1,\lambda }(1-x_1^2)^{\lambda +{d-2\over 2}}, \end{aligned}$$

which is thus equal to $C_{d-1,\lambda }w_{1,\lambda +(d-1)/2}(x_1)$.

Proof

Change variables and set $u_j= {x_j/ \sqrt{1-x_1^2}}$ for $2\le j\le d$. Then we have $w_{d,\lambda }(x)=(1-x_1^2 -x_2^2+\cdots -x_d^2)^{\lambda -{1\over 2}}= (1-x_1^2)^{\lambda -{1\over 2}}(1-u_2^2-\cdots -u_d^2)^{\lambda -{1\over 2}}$ and $dx_2\cdots dx_d= (1-x_1^2)^{d-1\over 2} du_2\cdots du_d.$ Putting things together and using relation (14) we obtain the desired result. $\square$

We also need the following lemma, which relates integration over the unit sphere ${\mathbb {S}}^d\subseteq {{\mathbb {R}}}^{d+1}$ and integration over the unit ball ${\mathbb {B}}^d\subseteq {{\mathbb {R}}}^{d}$ and can be found, e.g., in [6, Lemma 3.8.1] and [2, Lemma 11.7.1].

Lemma 2

Let g be a $(d+1)$-variate integrable function defined on $S^d$ and $d\ge 1$. Then we have:

$$\begin{aligned} \int _{{\mathbb {S}}^d} g(x)d\sigma (x)= \int _{{\mathbb {B}}^d} \left( g(x,\sqrt{1-\Vert x\Vert ^2})+ g(x,-\sqrt{1-\Vert x\Vert ^2})\right) {dx_1\cdots dx_d\over \sqrt{1-\Vert x\Vert ^2}}. \end{aligned}$$

By combining these two lemmas we obtain the following result.

Lemma 3

Let $g(x_1)$ be a univariate polynomial and $d\ge 1$. Then we have:

$$\begin{aligned} \sigma _d^{-1} \int _{{\mathbb {S}}^d}g(x_1) d\sigma (x_1,\ldots ,x_{d+1})= C_{1,\nu }^{-1} \int _{-1}^1 g(x_1) w_{1,\nu }(x_1) dx_1, \end{aligned}$$

where we set $\nu = {d-1\over 2}.$

Proof

Applying Lemma 2 to the function $x\in {{\mathbb {R}}}^{d+1}\mapsto g(x_1)$ we get

$$\begin{aligned} \sigma _d^{-1} \int _{{\mathbb {S}}^d}g(x_1) d\sigma (x_1,\ldots ,x_{d+1})= 2\sigma _d^{-1} \int _{{\mathbb {B}}^d} g(x_1) w_{d,0}(x)dx_1\cdots dx_d. \end{aligned}$$

(15)

If $d=1$ then $\nu =0$ and the right hand side term in (15) is equal to

$$\begin{aligned} 2\sigma _1^{-1} \int _{-1}^1 g(x_1) w_{1,0}(x_1) dx_1= C_{1,0}^{-1} \int _{-1}^1 g(x_1) w_{1,0}(x_1) dx_1, \end{aligned}$$

as desired, since $2\sigma _1^{-1}C_{1,0}=1$ using $\sigma _1=2\pi$ and $C_{1,0}= \pi$ (by (14) and ${\varGamma }(1/2)=\sqrt{\pi }$). Assume now $d\ge 2$. Then the right hand side in (15) is equal to

$$\begin{aligned}&2\sigma _d^{-1}\int _{-1}^1 g(x_1)\left( \int _{x_2^2+\cdots +x_d^2\le 1-x_1^2} w_{d,0}(x_1,\ldots ,x_d) dx_2\cdots dx_d\right) dx_1 \\&\quad =2\sigma _d^{-1}C_{d-1,0}\int _{-1}^1g(x_1) (1-x_1^2)^{(d-2)/2} dx_1 \\&\quad = 2\sigma _d^{-1}C_{d-1,0}\int _{-1}^1 g(x_1) w_{1,\nu }(x_1) dx_1, \end{aligned}$$

where we have used Lemma 1 for the first equality. Finally we verify that the constant $2\sigma _d^{-1}C_{d-1,0} C_{1,\nu }$ is equal to 1:

$$\begin{aligned} 2\sigma _d^{-1}C_{d-1,0}C_{1,\nu } = 2 {{\varGamma }\left( {d+1\over 2}\right) \over 2\pi ^{d+1\over 2}} {\pi ^{d-1\over 2}{\varGamma }\left( {1\over 2}\right) \over {\varGamma }\left( {d\over 2}\right) } {\pi ^{1\over 2} {\varGamma }\left( {d\over 2}\right) \over {\varGamma }\left( {d+1\over 2}\right) }=1 \end{aligned}$$

[using relations (4) and (14)], and thus we arrive at the desired identity. $\square$

We can now complete the convergence analysis for the minimization of $x_1$ on the unit sphere.

Lemma 4

For the minimization of the polynomial $f(x)=x_1$ over ${\mathbb {S}}^d$ with $d\ge 1$, the order r upper bound (3) satisfies

$$\begin{aligned} {\overline{f}}^{(r)}= -1 +O\left( {1\over r^2}\right) . \end{aligned}$$

Proof

Let $h(x_1)$ be an optimal univariate sum-of-squares polynomial of degree 2r for the order r upper bound corresponding to the minimization of $x_1$ over $[-1,1]$, when using as reference measure on $[-1,1]$ the measure with weight function $w_{1,\nu }(x_1)C_{1,\nu }^{-1}$ and $\nu =(d-1)/2$ (thus $\nu >-1$). Applying Lemma 3 to the univariate polynomials $h(x_1)$ and $x_1h(x_1)$, we obtain

$$\begin{aligned} \sigma _d^{-1}\int _{{\mathbb {S}}^d} h(x_1) d\sigma (x)=C_{1,\nu }^{-1}\int _{-1}^1 h(x_1)w_{1,\nu }(x_1)dx_1 =1 \end{aligned}$$

and

$$\begin{aligned} {\overline{f}}^{(r)}\le \sigma _d^{-1}\int _{{\mathbb {S}}^d}x_1h(x_1) d\sigma (x)= C_{1,\nu }^{-1}\int _{-1}^1 x_1h(x_1) w_{1,\nu }(x_1)dx_1. \end{aligned}$$

Since the function $x_1$ has the same global minimum $-1$ over $[-1,1]$ and over the sphere ${\mathbb {S}}^d$, we can apply Theorem 3 to conclude that

$$\begin{aligned} {\overline{f}}^{(r)}+1\le 1+ C_{1,\nu }^{-1}\int _{-1}^1 x_1h(x_1) w_{1,\nu }(x_1)dx_1 =O\Big ({1\over r^2}\Big ). \end{aligned}$$

$\square$

We now indicate how the analysis for an arbitrary polynomial f reduces to the case of the linear coordinate polynomial $x_1$. To see this, suppose $a\in {\mathbb {S}}^{n-1}$ is a global minimizer of f over ${\mathbb {S}}^{n-1}$. Then, using Taylor’s theorem, we can upper estimate f as follows:

$$\begin{aligned} \begin{array}{llll} &{}f(x) \le f(a) +\nabla f(a)^T (x-a)+{1\over 2}C_f\Vert x-a\Vert ^2 \quad \quad \qquad \forall x\in {\mathbb {S}}^{n-1} \\ &{}\quad \quad \quad = f(a) +\nabla f(a)^T (x-a)+C_f (1-a^Tx)=: g(x) \quad \forall x\in {\mathbb {S}}^{n-1}, \end{array} \end{aligned}$$

(16)

where $C_f=\max _{x\in {\mathbb {S}}^{n-1}} \Vert \nabla ^2f(x)\Vert _2$, and we have used the identity

$$\begin{aligned} \Vert x - a\Vert ^2 = \Vert x\Vert ^2 + \Vert a\Vert ^2 - 2 a^T x = 2 - 2 a^T x \quad \text{ for } a,x\in {\mathbb {S}}^{n-1}. \end{aligned}$$

Note that the upper estimate g(x) is a linear polynomial, which has the same minimum value as f(x) on ${\mathbb {S}}^{n-1}$, namely $f(a)=f_{\min }=g_{\min }$. From this it follows that ${\overline{f}}^{(r)}-f_{\min }\le {\overline{g}}^{(r)}-g_{\min }$ and thus we may restrict to analyzing the bounds for a linear polynomial.

Next, assume f is a linear polynomial, of the form $f(x)=c^Tx$ with (up to scaling) $\Vert c\Vert =1$. We can then apply a change of variables to bring f(x) into the form $x_1$. Namely, let U be an orthogonal $n\times n$ matrix such that $Uc=e_1$, where $e_1$ denotes the first standard unit vector in ${\mathbb {R}}^n$. Then the polynomial $g(x):=f(U^Tx)= x_1$ has the desired form and it has the same minimum value $-1$ over ${\mathbb {S}}^{n-1}$ as f(x). As the sphere is invariant under any orthogonal transformation it follows that ${\overline{f}}^{(r)}={\overline{g}}^{(r)}= -1+O(1/r^2)$ (applying Lemma 4 to $g(x)=x_1$).

Summarizing, we have shown the following.

Theorem 4

For the minimization of any polynomial f(x) over ${\mathbb {S}}^{n-1}$ with $n\ge 2$, the order r upper bound (3) satisfies

$$\begin{aligned} {\overline{f}}^{(r)}-f_{\min }= O\left( {1\over r^2}\right) . \end{aligned}$$

Note the difference to Theorem 2 where the constant depends only on the degree of f and the number n of variables; here the constant in $O(1/r^2)$ does also depend on the polynomial f, namely it depends on the norm of $\nabla f(a)$ at a global minimizer a of f in ${\mathbb {S}}^{n-1}$ and on $C_f=\max _{x\in {\mathbb {S}}^{n-1}}\Vert \nabla ^2 f(x)\Vert _2$.

3.2 The analysis is tight for some powers of linear polynomials

In this section we show—through a class of examples—that the convergence rate cannot be better than ${\varOmega }\left( 1/r^2\right)$ for general polynomials. The class of examples is simply minimizing some powers of linear functions over the sphere ${\mathbb {S}}^{n-1}$. The key tool we use is a link between the bounds ${\overline{f}}^{(r)}$ and properties of some known cubature rules on the unit sphere. This connection, recently mentioned in [17], holds for any compact set K. It goes as follows.

Theorem 5

[17] Assume that the points $x^{(1)},\ldots ,x^{(N)}\in K$ and the weights $w_1,\ldots ,w_N>0$ provide a (positive) cubature rule for K for a given measure $\mu$, which is exact up to degree $d+2r$, that is,

$$\begin{aligned} \int _K g(x) d\mu (x)=\sum _{i=1}^N w_i g(x^{(i)}) \end{aligned}$$

for all polynomials g with degree at most $d+2r$. Then, for any polynomial f with degree at most d, we have

$$\begin{aligned} {\overline{f}}^{(r)} \ge \min _{1 \le i \le N} f(x^{(i)}). \end{aligned}$$

The argument is simple: if $h\in {\varSigma }[x]_r$ is an optimal sum-of-squares density for the parameter ${\overline{f}}^{(r)}$, then we have

$$\begin{aligned} 1= & {} \int _K h(x)d\mu (x)= \sum _{i=1}^N w_i h(x^{(i)}), \\ {\overline{f}}^{(r)}= & {} \int _K f(x)h(x)d\mu (x)=\sum _{i=1}^N w_i f(x^{(i)})h(x^{(i)}) \ge \min _{1 \le i \le N} f(x^{(i)}). \end{aligned}$$

As a warm-up we first consider the case $n=2$, where we can use the cubature rule in Theorem 6 below for the unit circle. We use spherical coordinates $(x_1,x_2)=(\cos \theta ,\sin \theta )$ to express a polynomial f in $x_1,x_2$ as a polynomial g in $\cos \theta ,\sin \theta$.

Theorem 6

[2, Proposition 6.5.1] For each $d \in {{\mathbb {N}}}$, the cubature formula

$$\begin{aligned} \frac{1}{2\pi }\int _0^{2\pi } g(\theta ) d\theta = \frac{1}{d} \sum _{j=0}^{d-1}g\left( \frac{2\pi j}{d}\right) \end{aligned}$$

is exact for all $g \in \text{ span }\{1,\cos \theta ,\sin \theta ,\ldots ,\cos (d\theta ), \sin (d\theta )\}$, i.e. for all polynomials of degree at most d, restricted to the unit circle.

Using this cubature rule on ${\mathbb {S}}^1$ we can lower bound the parameters ${\overline{f}}^{(r)}$ for the minimization of the coordinate polynomial $f(x)=x_1$ over ${\mathbb {S}}^1$. Namely, by setting $x_1=\cos \theta$, we derive directly from Theorems  5 and 6 that

$$\begin{aligned} {\overline{f}}^{(r)} \ge \min _{0\le j\le 2r} \cos \Big ({2\pi j\over 2r+1}\Big )= \cos \Big ( {2\pi r\over 2r+1}\Big ) = -1 + {\varOmega }\Big ({1\over r^2}\Big ). \end{aligned}$$

This reasoning extends to any dimension $n\ge 2$, by using product-type cubature formulas on the sphere ${\mathbb {S}}^{n-1}$. In particular we will use the cubature rule described in [2, Theorem 6.2.3], see Theorem 8 below.

We will need the generalized spherical coordinates given by

$$\begin{aligned} \left. \begin{array}{rcl} x_1 &{}=&{} r\sin \theta _{n-1}\cdots \sin \theta _3 \sin \theta _2\sin \theta _1 \\ x_2 &{}=&{} r\sin \theta _{n-1}\cdots \sin \theta _3\sin \theta _2 \cos \theta _1 \\ x_3 &{}=&{} r\sin \theta _{n-1}\cdots \sin \theta _3 \cos \theta _2 \\ &{}\vdots &{} \\ x_{n} &{}=&{} r\cos \theta _{n-1}, \end{array} \right\} \end{aligned}$$

(17)

where $r \ge 0$ ($r=1$ on ${\mathbb {S}}^{n-1}$), $0 \le \theta _1 \le 2 \pi$, and $0 \le \theta _i \le \pi$ ($i=2,\ldots ,n-1$).

To define the nodes of the cubature rule on ${\mathbb {S}}^{n-1}$ we need the Gegenbauer polynomials $C^\lambda _d(x)$, where $\lambda > -1/2$. Recall that these are the orthogonal polynomials with respect to the weight function

$$\begin{aligned} w_{1,\lambda }(x) = (1-x^2)^{\lambda - 1/2}, \quad x \in (-1,1) \end{aligned}$$

on $[-1,1]$. We will not need the explicit expressions for the polynomials $C^\lambda _d(x)$, we only need the following information about their extremal roots, shown in [7] (for general Jacobi polynomials, using results of [3, 5]). It is well known that each $C_d^{\lambda }(x)$ has d distinct roots, lying in $(-1,1)$.

Theorem 7

Denote the roots of the polynomial $C^\lambda _d(x)$ by $t^{(\lambda )}_{1,d}< \cdots < t^{(\lambda )}_{d,d}$. Then, $t^{(\lambda )}_{1,d} +1 = {\varTheta }(1/d^2)$ and $1-t^{\lambda }_{d,d}={\varTheta }(1/d^2)$.

The cubature rule we will use may now be stated.

Theorem 8

[2, Theorem 6.2.3] Let $f:{\mathbb {S}}^{n-1} \rightarrow {\mathbb {R}}$ be a polynomial of degree at most $2k-1$, and let

$$\begin{aligned} g(\theta _1,\ldots ,\theta _{n-1}) := f(x_1,\ldots ,x_n), \end{aligned}$$

be the expression of f in the generalized spherical coordinates (17). Then

$$\begin{aligned}&\int _{{\mathbb {S}}^{n-1}} f(x)d\sigma (x) \nonumber \\&\quad = \frac{\pi }{k} \sum _{j_1=0}^{2k-1} \sum _{j_2 = 1}^k\cdots \sum _{j_{n-1} = 1}^k \prod _{i=2}^{n-1} {\mu ^{((i-1)/2)}_{i,k}} g\left( \frac{\pi j_1}{k},\theta ^{(1/2)}_{j_2,k}, \ldots ,\theta ^{(({n}-2)/2)}_{j_{n-1},k}\right) ,\nonumber \\ \end{aligned}$$

(18)

where $\cos \left( \theta ^{(\lambda )}_{j,k}\right) := t^{(\lambda )}_{j,k}$ and the parameters $\mu ^{((i-1)/2)}_{i,k}$ are positive scalars as in relation (6.2.3) of [2].

We can now show the tightness of the convergence rate ${\varOmega }(1/r^2)$ for the minimization of a coordinate polynomial on ${\mathbb {S}}^{n-1}$.

Theorem 9

Consider the problem of minimizing the coordinate polynomial $f(x)=x_n$ on the unit sphere ${\mathbb {S}}^{n-1}$ with $n\ge 2$. The convergence rate for the parameters (3) satisfies

$$\begin{aligned} {\overline{f}}^{(r)}- f_{\min } ={\overline{f}}^{(r)}+1= {\varOmega }\left( \frac{1}{r^2}\right) . \end{aligned}$$

Proof

We have $f(x_1,\ldots ,x_n) = x_n$, so that $g(\theta _1,\ldots ,\theta _{n-1}) = \cos \theta _{n-1}$. Using Theorem 5 combined with Theorem 8 (applied with $2k-1=2r+1$, i.e., $k=r+1$) we obtain that

$$\begin{aligned} {\overline{f}}^{(r)}\ge \min _{1\le j\le r+1} \cos \theta ^{((n-2)/2)}_{j,r+1} =\min _{1\le j\le r+1} t^{((n-2)/2)}_{j,r+1} = t^{((n-2)/2)}_{1,r+1}= -1 + {\varOmega }\Big ({1\over r^2}\Big ), \end{aligned}$$

where we use the fact that $t^{(\lambda )}_{1,r+1} +1 = {\varTheta }(1/r^2)$ (Theorem 7). $\square$

This reasoning extends to some powers of linear forms.

Theorem 10

Given an integer $d\ge 1$ and a nonzero $c\in {{\mathbb {R}}}^n$, the following holds for the polynomial $f(x)=(-1)^{d-1}(c^Tx)^d$:

$$\begin{aligned} {\overline{f}}^{(r)}- f_{\min } = {\varOmega }\left( \frac{1}{r^2}\right) . \end{aligned}$$

Proof

Up to scaling we may assume $\Vert c\Vert =1$ and, up to applying an orthogonal transformation, we may assume that $f(x)=(-1)^{d-1}x_n^d$, so that $f_{\min }=-1$. Again we use Theorem 5, as well as Theorem 8, now with $2k-1= 2r+d$, i.e., $k= r + (d+1)/2$, and we obtain

$$\begin{aligned} {\overline{f}}^{(r)}\ge \min _{1\le j\le k} (-1)^{d-1}\cos ^d \theta ^{((n-2)/2)}_{j,k} =\min _{1\le j\le k} (-1)^{d-1}(t^{((n-2)/2)}_{j,k})^d. \end{aligned}$$

We can now conclude using Theorem 7. For d odd, the right hand side is equal to $(t^{((n-2)/2)}_{1,k})^d= -1 + {\varTheta }({1\over r^2})$ and, for d even, the right hand side is equal to $- (t^{((n-2)/2)}_{k,k})^d= -1 + {\varTheta }({1\over r^2})$. $\square$

4 Some extensions

Here we mention some possible extensions of our results. First we consider the general problem of moments and its application to the problem of minimizing a rational function. Thereafter we mention that the rate of convergence in $O(1/r^2)$ extends to some other measures on the unit sphere.

4.1 Implications for the generalized problem of moments

In this section, we describe the implications of our results for the generalized problem of moments (GPM), defined as follows for a compact set $K \subset {\mathbb {R}}^n$:

$$\begin{aligned} val := \inf _{\nu \in {\mathcal {M}}(K)_+} \left\{ \int _K f_0(x)d\nu (x) \; : \; \int _K f_i(x)d\nu (x) = b_i \quad \forall i \in [m]\right\} , \end{aligned}$$

(19)

where

• the functions $f_i$ $(i=0,\ldots ,m)$ are continuous on K;

• ${\mathcal {M}}(K)_+$ denotes the convex cone of probability measures supported on the set K;

• the scalars $b_i\in {{\mathbb {R}}}$ ($i \in [m]$) are given.

As before, we are interested in the special case where $K = {\mathbb {S}}^{n-1}$. This special case is already of independent interest, since it contains the problem of finding cubature schemes for numerical integration on the sphere, see e.g. [9] and the references therein. Our main result in Theorem 4 has the following implication for the GPM on the sphere, as a corollary of the following result in [12] (which applies to any compact K, see also [9] for a sketch of the proof in the setting described here).

Theorem 11

(De Klerk-Postek-Kuhn [12]) Assume that $f_0,\ldots ,f_m$ are polynomials, K is compact, $\mu$ is a Borel measure supported on K, and the GPM (19) has an optimal solution. Given $r \in {\mathbb {N}}$, define the parameter

$$\begin{aligned} {\varDelta }(r)= \min _{h\in {\varSigma }_r} \max _{i\in \{0,1,\ldots ,m\}} \big | \int _K f_i(x)h(x)d\mu (x) -b_i\big |, \end{aligned}$$

setting $b_0=val$. Assume $\varepsilon :{\mathbb {N}}\rightarrow {\mathbb {R}}_+$ is such that $\lim _{r \rightarrow \infty } \varepsilon (r) = 0$, and that, for any polynomial f, we have

$$\begin{aligned} {\overline{f}}^{(r)}_K - f_{\min } = O(\varepsilon (r)). \end{aligned}$$

Then the parameters ${\varDelta }(r)$ satisfy: ${\varDelta }(r) = O(\sqrt{\varepsilon (r)})$.

As a consequence of our main result in Theorem 4, combined with Theorem 11, we immediately obtain the following corollary.

Corollary 1

Assume that $f_0,\ldots ,f_m$ are polynomials, $K = {\mathbb {S}}^{n-1}$, and the GPM (19) has an optimal solution. Then, for any integer $r\in {{\mathbb {N}}}$, there exists a polynomial $h_r \in {\varSigma }_{r}$ such that

$$\begin{aligned} \left| \int _{{\mathbb {S}}^{n-1}} f_0(x) h_r(x) d\sigma (x) - val \right|= & {} O(1/r), \\ \; \left| \int _{{\mathbb {S}}^{n-1}} f_i(x) h_r(x) d\sigma (x) - b_i \right|= & {} O(1/r) \quad \forall i \in [m]. \end{aligned}$$

Minimization of a rational function on K is a special case of the GPM where we may prove a better rate of convergence. In particular, we now consider the global optimization problem:

$$\begin{aligned} val = \min _{x \in K} \frac{p(x)}{q(x)}, \end{aligned}$$

(20)

where p, q are polynomials such that $q(x) > 0$ $\forall$ $x \in K$, and $K \subseteq {\mathbb {R}}^n$ is compact.

It is well-known that one may reformulate this problem as the GPM with $m=1$ and $f_0 = p$, $f_1 = q$, and $b_1 =1$, i.e.:

$$\begin{aligned} val = \min _{\nu \in {\mathcal {M}}(K)_+} \left\{ \int _K p(x)d\nu (x) \; : \; \int _K q(x)d\nu (x) = 1\right\} . \end{aligned}$$

Analogously to (3), we now define the hierarchy of upper bounds on val as follows:

$$\begin{aligned} \overline{p/q}^{(r)}_K:=\min _{h\in {\varSigma }[x]_r}\int _{{K}}p(x)h(x)d\mu (x) \ \ \text{ s.t. } \int _{{K}}q(x)h(x)d\mu (x)=1\text{, } \end{aligned}$$

(21)

where $\mu$ is a Borel measure supported on K.

Theorem 12

Consider the rational optimization problem (20). Assume $\varepsilon :{\mathbb {N}}\rightarrow {\mathbb {R}}_+$ is such that $\lim _{r \rightarrow \infty } \varepsilon (r) = 0$, and that, for any polynomial f, we have

$$\begin{aligned} {\overline{f}}^{(r)}_K - f_{\min } = O(\varepsilon (r)). \end{aligned}$$

Then one also has $\overline{p/q}^{(r)}_K - val = O(\varepsilon (r))$. In particular, if $K = {\mathbb {S}}^{n-1}$, then $\overline{p/q}^{(r)}_K - val = O(1/r^2)$.

Proof

Consider the polynomial

$$\begin{aligned} f(x) = p(x) - val \cdot q(x). \end{aligned}$$

Then $f(x) \ge 0$ for all $x \in K$, and $f_{\min ,K} = 0$, with global minimizer given by the minimizer of problem (20).

Now, for given $r \in \mathbb {{N}}$, let $h \in {\varSigma }_r$ be such that ${\overline{f}}^{(r)}_K = \int _K f(x)h(x)d\mu (x)$, and $\int _K h(x)d\mu (x) = 1$, where $\mu$ is the reference measure for K. Setting

$$\begin{aligned} h^* = \frac{1}{\int _K h(x)q(x)d\mu (x)}h, \end{aligned}$$

one has $h^* \in {\varSigma }_r$ and $\int _K h^*(x)q(x)d\mu (x) = 1$. Thus $h^*$ is feasible for problem (21). Moreover, by construction,

$$\begin{aligned} \int _K p(x)h^*(x)d\mu (x) - val= & {} \frac{ {\overline{f}}^{(r)}_K}{\int _K h(x)q(x)d\mu (x)} \\\le & {} \frac{ {\overline{f}}^{(r)}_K}{\min _{x \in K} q(x)} = O(\varepsilon (r)). \end{aligned}$$

The final result for the special case $K = {\mathbb {S}}^{n-1}$ and $\mu = \sigma$ (surface measure) now follows from our main result in Theorem 4. $\square$

4.2 Extension to other measures

Here we indicate how to extend the convergence analysis to a larger class of measures on the unit sphere ${\mathbb {S}}^{n-1}$ of the form $d\mu (x)=w(x)d\sigma (x)$, where w(x) is a positive bounded weight function on ${\mathbb {S}}^{n-1}$, i.e., w(x) satisfies the condition:

$$\begin{aligned} \text {There exist } \ m,M>0 \ \text { such that } m\le w(x)\le M \ \text { for all } x\in {\mathbb {S}}^{n-1}. \end{aligned}$$

(22)

Given a polynomial f we let ${\overline{f}}^{(r)} _\mu$ denote the bound obtained by using the measure $\mu$ instead of the Haar measure $\sigma$ on ${\mathbb {S}}^{n-1}$. We will show that under the condition (22) the bounds ${\overline{f}}^{(r)}_\mu$ converge to $f_{\min }$ with the same convergence rate $O(1/r^2)$. These results follow the same line of arguments as in the recent paper [23]. We start with dealing with the case of linear polynomials.

Lemma 5

Consider an affine polynomial g of the form $g(x)=1-c^Tx$, where $c\in {\mathbb {S}}^{n-1}$. If $d\mu (x)=w(x)d\sigma (x)$ and w satisfies (22) then we have:

$$\begin{aligned} {\overline{g}}^{(r)}_\mu \le {\overline{g}}^{(r)} {M\over m}. \end{aligned}$$

Proof

Let $H\in {\varSigma }_r$ be an optimal sum of squares density for the Haar measure $\sigma$, i.e., such that

$$\begin{aligned} \int _{{\mathbb {S}}^{n-1}} H(x)d\sigma (x)=1 \quad \text { and } \quad \int _{{\mathbb {S}}^{n-1}} g(x)H(x)d\sigma (x)= {\overline{g}}^{(r)}. \end{aligned}$$

Define the polynomial

$$\begin{aligned} h= {H\over \int _{{\mathbb {S}}^{n-1}} H(x)w(x)d\sigma (x)}\in {\varSigma }_r, \end{aligned}$$

which defines a density for the measure $\mu$ on ${\mathbb {S}}^{n-1}$, so that we have

$$\begin{aligned} {\overline{g}}^{(r)}_\mu \le \int _{{\mathbb {S}}^{n-1}} g(x) h(x)d\mu (x)= {\int _{{\mathbb {S}}^{n-1}} g(x)H(x)w(x)d\sigma (x)\over \int _{{\mathbb {S}}^{n-1}} H(x) w(x) d\sigma (x)}. \end{aligned}$$

Since $m\le w(x)\le M$ on ${\mathbb {S}}^{n-1}$ the numerator is at most $M {\overline{g}}^{(r)}$ and the denominator is at least m, which concludes the proof. $\square$

Theorem 13

Consider a weight function w(x) on ${\mathbb {S}}^{n-1}$ that satisfies the condition (22), and the corresponding measure $d\mu (x)=w(x)d\sigma (x)$ on the unit sphere ${\mathbb {S}}^{n-1}$. Then, for any polynomial f, we have

$$\begin{aligned} {\overline{f}}^{(r)}_\mu -f_{\min }=O\Big ({1\over r^2}\Big ). \end{aligned}$$

Proof

Let $a\in {\mathbb {S}}^{n-1}$ be a global minimizer of f in the unit sphere. We may assume that $f_{\min }=f(a)=0$ (else replace f by $f-f(a)$). As observed in relation (16), we have

$$\begin{aligned} f(x)\le \nabla f(a)^T (x-a) +C_f(1-a^Tx)=:g(x) \ \ \text { for all } x\in {\mathbb {S}}^{n-1}. \end{aligned}$$

Note that g is affine linear with $g_{\min }=g(a)=0$. Hence we may apply Lemma 5 which, combined with Theorem 4 (applied to g), implies that ${\overline{g}}^{(r)}_\mu =O(1/r^2)$. As $f\le g$ on ${\mathbb {S}}^{n-1}$ it follows that ${\overline{f}}^{(r)}_\mu \le {\overline{g}}^{(r)}_\mu$ and thus ${\overline{f}}^{(r)}_\mu =O(1/r^2)$ as desired. $\square$

5 Concluding remarks

In this paper we have improved on the O(1/r) convergence result of Doherty and Wehner [4] for the Lasserre hierarchy of upper bounds (3) for (homogeneous) polynomial optimization on the sphere. Having said that, Doherty and Wehner also showed that the hierarchy of lower bounds (9) of Lasserre satisfies the same rate of convergence, due to Theorem 2. In view of the fact that we could show the improved $O(1/r^2)$ rate for the upper bounds, and the fact that the lower bounds hierarchy empirically converges much faster in practice, one would expect that the lower bounds (9) also converge at a rate no worse than $O(1/r^2)$. This has been recently confirmed in the paper [13].

Another open problem is the exact rate of convergence of the bounds in Theorem 11 for the generalized problem of moments (GPM). In our analysis of the GPM on the sphere in Corollary 1, we could only obtain O(1/r) convergence, which is a square root worse than the special cases for polynomial and rational function minimization. We do not know at the moment if this is a weakness of the analysis or inherent to the GPM.

As we showed in Theorem 13, if we pick another reference measure $d\mu (x)=w(x)d\sigma (x)$, where w is upper and lower bounded by strictly positive constants on the sphere, then the convergences rates with respect to both measures $\sigma$ and $\mu$ have the same behaviour. It would be interesting to understand the convergence rate for more general reference measures.