New polyhedral and algorithmic results on greedoids

Abstract

We present various new results on greedoids. We prove a theorem that generalizes an equivalent formulation of Edmonds’ classic matroid polytope theorem to local forest greedoids—a class of greedoids that contains matroids as well as branching greedoids. We also describe an application of this theorem in the field of measuring the reliability of networks by game-theoretical tools. Finally, we prove new results on the optimality of the greedy algorithm on greedoids and correct some mistakes that have been present in the literature for almost 3 decades.

1 Introduction

Greedoids were introduced by Korte and Lovász at the beginning of the 1980s as a generalization of matroids. The motivation behind the concept was the observation that in the proofs of various results on matroids subclusiveness (that is, the property that all subsets of independent sets are also independent) is not needed. Besides matroids, the class of greedoids includes some further very important combinatorial objects such as the edge sets of subtrees of a graph rooted at a given node.

Although the research of greedoids was very active until the mid-1990s, the topic seems to have faded away since then. Most of the known results on greedoids are already included in the comprehensive book of Korte et al. [8] published in 1991. The fact that greedoids have not gained as much importance within combinatorial optimization as matroids is probably due to the fact that the class of greedoids is much more diverse than that of matroids and classic concepts and results on matroids do not seem to generalize easily to greedoids.

The motivations behind the results of this paper are threefold. Firstly, we identify a class of greedoids, local forest greedoids, that includes both matroids and branching greedoids and that admits a generalization of a fundamental polyhedral result on matroids: Edmonds’ classic theorem on the polytope spanned by incidence vectors of independent sets of a matroid. In particular, we prove a generalization of an eqivalent formulation of this theorem to local forest greedoids. To the best of our knowledge, no generalization of (any form of) the matroid polytope theorem to greedoids has been known. We do this partly in the (perhaps vain) hope that further fundamental results on matroids will turn out to be generalizable to this class of greedoids.

Secondly, we aim at generalizing some results obtained in [13]. There we considered some attacker–defender games played on graphs with the aim of defining new security metrics of graphs and better understanding others that had been known in the literature. For this purpose, we defined a general framework involving matroids: the Matroid Base Game is a two-player, zero sum game in which the Attacker aims at hitting a base chosen by the Defender. In particular, the Attacker chooses an element of the ground set of a given matroid and the Defender chooses a base of the same matroid; then the payoff depends on both of their choices in such a way that it is favorable for the Attacker if his chosen element belongs to the base chosen by the Defender. The results of [13] on the Matroid Base Game served as a common generalization of some results that had been known in the literature on measuring the security of networks via game-theoretical means. In particular, the Nash-equilibrium payoff of the Matroid Base Game was determined and it was proved that it is a common generalization of some known graph reliability metrics. However, there are other known metrics of a very similar nature which did not fit into the framework provided by the Matroid Base Game. In this paper we further generalize the definition of the Matroid Base Game by replacing matroids with local forest greedoids and we prove that some of the results of [13] generalize to this case too. We also show that this more general framework is capable of handling and generalizing some further graph reliability metrics known from the literature beyond the ones already contained in the framework provided by the matroid base game.

The third motivation behind the results of this paper is to better understand the conditions under which the greedy algorithm is optimal on greedoids. This question is a central topic in the literature of greedoids, the name greedoid itself comes from “a synthetic blending of the words greedy and matroid” [8] which indicates that one of the basic motivations of the notion was to extend the theoretical background behind greedy algorithms beyond the well-known results on matroids. Accordingly, Korte and Lovász proved some fundamental results on the optimality of the greedy algorithm on greedoids in [6, 7] which were also presented and further extended in [8]. Most surprisingly however, they seem to have overlooked a detail which led them to some false claims. These mistakes, which seem to have remained hidden in the literature of greedoids for almost 3 decades, will be pointed out and corrections will be proposed and proved.

It should be emphasized though that, although the optimality of the greedy algorithm in a certain special case (see Theorem 3) will be a crucial tool for proving the above mentioned polyhedral result, the results of the present paper on the optimality of the greedy algorithm are not needed for this proof, it is only Theorem 3 proved in [2] that is relied on.

This paper is structured as follows. In Sects. 2 and 3 all the necessary background on greedoids and the greedy algorithm on greedoids, respectively, is given. In Sect. 4 the above mentioned polyhedral result is clamied and proved and in Sect. 5 we briefly outline an application of this result concerning the measurement of the reliability of networks. Finally, Sect. 6 is dedicated to some results on the optimality of the greedy algorithm on greedoids.

2 Preliminaries on greedoids

All the definitions and claims in this section are taken from [8].

A greedoid $G=(S,{\mathcal {F}})$ is a pair consisting of a finite ground set S and a collection of its subsets ${\mathcal {F}}\subseteq 2^S$ such that the following properties are fulfilled:

• (2.1) $\emptyset \in {\mathcal {F}}$

• (2.2) If $X,Y\in {\mathcal {F}}$ and $|X|<|Y|$ then there exists a $y\in Y-X$ such that $X+y\in {\mathcal {F}}$.

When we apply  (2.2) on the sets $X,Y\in {\mathcal {F}}$ with $|X|<|Y|$, we say that we augment X from Y. Members of ${\mathcal {F}}$ are called feasible sets. Obviously, the definition of greedoids is obtained from that of matroids by relaxing subclusiveness, that is, subsets of feasible sets are not required to be feasible any more. On the other hand, (2.2) immediately implies that every $X\in {\mathcal {F}}$ has a feasible ordering: $(x_1,x_2,\ldots ,x_k)$ is a feasible ordering of X if $X=\{x_1,x_2,\ldots ,x_k\}$ and $\{x_1,x_2,\ldots ,x_i\}\in {\mathcal {F}}$ holds for every $1\le i\le k$. The existence of a feasible ordering, in turn, implies the accessible property of greedoids: for every $\emptyset \ne X\in {\mathcal {F}}$ there exists an $x\in X$ such that $X-x\in {\mathcal {F}}$.

In this paper, the following notations will be (and have been) used: for a subset $X\subseteq S$ and an element $x\in S$ we will write $X+x$ and $X-x$ instead of $X\cup \{x\}$ and $X-\{x\}$, respectively. Furthermore, given any function $c:S\rightarrow {\mathbb {R}}$ and a subset $X\subseteq S$, c(X) will stand for $\sum \{c(x):x\in X\}$.

Some of the well-known terminology on matroids can be applied to greedoids without any modification. In particular, the rank r(A) of a set $A\subseteq S$ is $r(A)=\max \{|X|:X\subseteq A, X\in {\mathcal {F}}\}$. Given a subset $A\subseteq S$, a base of A is a subset $X\subseteq A$, $X\in {\mathcal {F}}$ of maximum size. This, by property (2.2) is equivalent to saying that $X+y\notin {\mathcal {F}}$ for every $y\in A-X$. A base of S is called a base of the greedoid $G=(S,{\mathcal {F}})$. The set of bases of G will be denoted by ${\mathcal {B}}$.

Minors of greedoids can also be defined almost identically to those of matroids. If $G=(S,{\mathcal {F}})$ is a greedoid and $X\subseteq S$ is an arbitrary subset then the deletion of X yields the greedoid $G{\setminus } X=(S-X,{\mathcal {F}}{\setminus } X)$, where ${\mathcal {F}}{\setminus } X=\{Y\subseteq S-X:Y\in {\mathcal {F}}\}$. If $X\in {\mathcal {F}}$ is a feasible set then the contraction of X yields the greedoid $G/X=(S-X,{\mathcal {F}}/X)$, where ${\mathcal {F}}/X=\{ Y\subseteq S-X: Y\cup X\in {\mathcal {F}}\}$. Then a minor of G is obtained by applying these two operations on G. It is straightforward to check that minors are indeed greedoids. (Note, however, that G / X was only defined here in the $X\in {\mathcal {F}}$ case. The definition could be extended to a wider class of subsets, but unless some further structural properties are imposed on the greedoid, not to arbitrary ones. See [8, Chapter V.] for the details.)

In this paper the following terminology will also be used: $X\subseteq S$ will be called subfeasible if there exists a $Y\in {\mathcal {F}}$ such that $X\subseteq Y$. The set of subfeasible sets will be denoted by ${\mathcal {F}}^{\vee }$.

There are many known examples of greedoids beyond matroids and they arise in diverse areas of mathematics, see [8] for an extensive list. For the purposes of this paper, branching greedoids will be of importance. Let $H=(V,E_u,E_d)$ be a mixed graph (that is, it can contain both directed and undirected edges) with V, $E_u$ and $E_d$ being its set of nodes, undirected edges and directed edges, respectively. Furthermore, let $r\in V$ be a given root node. The ground set of the branching greedoid on H is $E_u\cup E_d$ and ${\mathcal {F}}$ consists of all subsets $A\subseteq E_u\cup E_d$ such that disregarding the directions of the arcs in $A\cap E_d$, A is the edge set of a tree containing r and for every path P in A starting in r all edges of $P\cap E_d$ are directed away from r. It is straightforward to check that $G=(E_u\cup E_d,{\mathcal {F}})$ is indeed a greedoid. G is called an undirected branching greedoid or a directed branching greedoid if H is an undirected graph (that is, $E_d=\emptyset$) or a directed graph (that is, $E_u=\emptyset$), respectively.

Most of the known results on greedoids are about special classes of greedoids, that is, further structural properties are assumed. Among these, the following will be of relevance in this paper:

• (2.3) Local Union Property:

  if $A,B\in {\mathcal {F}}$ and $A\cup B\in {\mathcal {F}}^{\vee }$ then $A\cup B\in {\mathcal {F}}$

• (2.4) Local Intersection Property:

  if $A,B\in {\mathcal {F}}$ and $A\cup B\in {\mathcal {F}}^{\vee }$ then $A\cap B\in {\mathcal {F}}$

• (2.5) Local Forest Property:

  if $A, A+x, A+y, A\cup \{x,y\}, A\cup \{x,y,z\}\in {\mathcal {F}}$ then either $A\cup \{x,z\}\in {\mathcal {F}}$ or $A\cup \{y,z\}\in {\mathcal {F}}$

A greedoid $G=(S,{\mathcal {F}})$ is called an interval greedoid if it fulfills property (2.3); G is a local poset greedoid if it fulfills  (2.3) and (2.4); finally, G is a local forest greedoid if it fulfills (2.3), (2.4) and (2.5).

Obviously, all matroids are local forest greedoids and it is easy to check that so are branching greedoids. However, there are further examples that do not belong to either of these classes: for example, the direct sum of the uniform matroid $U_{3,2}$ and a branching greedoid that is not a matroid is also a local forest greedoid but it is neither a matroid nor a branching greedoid (since all these classes are closed under taking minors and $U_{3,2}$ is clearly not a branching greedoid). Another type of example can be obtained from any local forest greedoid (even a matroid): let $G=(S,{\mathcal {F}})$ be a local forest greedoid, $X\in {\mathcal {F}}$ a feasible set and $(x_1,x_2,\ldots ,x_k)$ an arbitrary (not necessarily feasible) ordering of X; then

$$\begin{aligned} {\mathcal {F}}^{(x_1,\ldots ,x_k)}=\{Y\in {\mathcal {F}}: X\subseteq Y\} \cup \left\{ \{x_1,x_2,\ldots ,x_i\}:i=1,\ldots ,k\right\} \cup \{\emptyset \} \end{aligned}$$

is also a local forest greedoid on S.

Observe that in interval greedoids (2.3) implies that every $X\in {\mathcal {F}}^{\vee }$ has a unique base; indeed, it is the union of all feasible sets in X. In this paper, this unique base will be denoted by $\varDelta (X)$. Analogously, (2.4) implies that if $X\subseteq A$ and $A\in {\mathcal {F}}$ then there is a unique minimum size feasible set containing X in A. This gives rise to the definition of paths: if $G=(S,{\mathcal {F}})$ is a local poset greedoid, $A\in {\mathcal {F}}$ and $x\in A$ then the x-path in A, denoted by $P_x^A$ (or simply $P_x$ if this is unambiguous) is the unique feasible set in A containing x such that no proper feasible subset of $P_x^A$ contains x. Clearly, in case of branching greedoids this notion translates to paths starting in the root node r that are directed in the sense that all directed edges in the path are directed away from r. The following theorem was proved in [11]; we also give a simple proof here for the sake of self-containedness.

Theorem 1

(Schmidt [11, 8, Theorem VII.4.4]) Let $G=(S,{\mathcal {F}})$ be a local poset greedoid. Then the following are equivalent:

• (i) G is a local forest greedoid (that is, it fulfills (2.5));

• (ii) every path in G has a unique feasible ordering;

• (iii) if $(a_1,a_2,\ldots ,a_k)$ is the feasible ordering of a path then $\{a_1,a_2,\ldots ,a_i\}$ is also a path for every $1\le i\le k$.

Proof

Assume by way of contradiction that (i) is fulfilled but (ii) is not and choose a path $P_z$ of minimum cardinality that has two different feasible orderings: $(a_1,\ldots ,a_k,x,z)$ and $(b_1,\ldots ,b_k,y,z)$. We first show that $x\ne y$ can be assumed without loss of generality. Indeed, if $x=y$ then $\{a_1,\ldots ,a_k,x\}$ is not a path by the minimality of $|P_z|$, but since it is feasible, it contains an x-path $P_x$ as a proper subset. Then augmenting a feasible ordering of $P_x$ from $P_z$ by (2.2) we get a feasible ordering of $P_z$ the second to last element of which is not y. So assume $x\ne y$ and let $A=P_z-\{x,y,z\}$. Then clearly $A+x\in {\mathcal {F}}$ and $A+y\in {\mathcal {F}}$ hold by the feasibility of the two orderings and $A\cup \{x,y,z\}=P_z\in {\mathcal {F}}$. Hence by (2.3) and (2.4) we have $A\cup \{x,y\}\in {\mathcal {F}}$ and $A\in {\mathcal {F}}$ too. Therefore (2.5) implies $A\cup \{x,z\}\in {\mathcal {F}}$ or $A\cup \{y,z\}\in {\mathcal {F}}$. In both cases we get a smaller feasible set containing z than $P_z$ contradicting the definition of $P_z$.

Proving (iii) from (ii) is almost immediate: if $\{a_1,a_2,\ldots ,a_i\}$ were not a path then it would contain an $a_i$-path by definition which could be augmented by (2.2) from $P=\{a_1,\ldots ,a_k\}$ to obtain a different feasible ordering of P.

Finally, we show (i) from (iii). Let A and x, y, z be given according to (2.5) and let $B=A\cup \{x,y,z\}$. Clearly, if $A\cap \{x,y,z\}\ne \emptyset$ or $|\{x,y,z\}|<3$ then (2.5) is automatically fulfilled, so we can assume that neither of these is the case. Since $A+x\in {\mathcal {F}}$, we have $P_x^B\subseteq A+x$ and hence $y\notin P_x^B$. Similarly, $x\notin P_y^B$. This, by (iii), implies that $P_z^B$ contains at most one of x and y; indeed, if it contained both and, for example, x preceded y in a feasible ordering of $P_z^B$ then since the prefix of this ordering up to y would be a path by (iii), we would get $x\in P_y^B$. So assume $y\notin P_z^B$ without loss of generality. Then applying (2.3) on $A+x$ and $P_z^B$, both of which are subsets of $B\in {\mathcal {F}}$, we get $A\cup \{x,z\}\in {\mathcal {F}}$ as claimed.$\square$

3 Preliminaries on the greedy algorithm in greedoids

As mentioned in the Introduction, the notion of greedoids was motivated by the fact that they provide the underlying structure for a simple greedy algorithm.

Let $G=(S,{\mathcal {F}})$ be an arbitrary greedoid and $w:{\mathcal {F}}\rightarrow {\mathbb {R}}$ an objective function. Assume that we are interested in finding a base $B\in {\mathcal {B}}$ that maximizes w(B) across all bases of G. For every $A\in {\mathcal {F}}$ the set of continuations of A is defined as $\varGamma (A)=\{x\in S-A: A+x\in {\mathcal {F}}\}$. Then the greedy algorithm for the above problem can be described as follows [6, 8]:

• Step 1. Set $A=\emptyset$.

• Step 2. If $\varGamma (A)=\emptyset$ then stop and output A.

• Step 3. Choose an $x\in \varGamma (A)$ such that $w(A+x)\ge w(A+y)$ for every $y\in \varGamma (A)$.

• Step 4. Replace A by $A+x$ and continue at Step 2.

Obviously, if one is interested in minimizing w(B) across all bases then, since this is equivalent to maximizing $-w(B)$, the only modification needed in the algorithm is to require $w(A+x)\le w(A+y)$ for every $y\in \varGamma (A)$ in Step 3.

Many of the well-known, elementary algorithms in graph theory fall under this framework as shown by the following examples.

Example 1

If M is a matroid and w is linear (meaning that $w(A)=c(A)$ for some weight function $c:S\rightarrow {\mathbb {R}}$) then the above greedy algorithm is nothing but the well-known greedy algorithm on matroids. In particular, we get Kruskal’s algorithm for finding a maximum weight spanning tree in case of the cycle matroid.

Example 2

Let G be the branching greedoid of the undirected graph H and w a linear objective function. Then the greedy algorithm translates to Prim’s well-known algorithm for finding a maximum weight spanning tree. (Note that this algorithm cannot be interpreted in a matroid-theoretical context).

Example 3

Let G be the branching greedoid of the mixed graph $H=(V,E_u,E_d)$ with root node r and let $c:E_u\cup E_d\rightarrow {\mathbb {R}}^+$ be a non-negative valued weight function. Then let $w(A)=\sum \{c(P_e^A):e\in A\}$ for every $A\in {\mathcal {F}}$. Korte and Lovász observed [6] that in this case the greedy algorithm for minimizing w(B) translates to Dijkstra’s well-known shortest path algorithm. Indeed, Dijkstra’s algorithm constructs a spanning tree on the set of nodes reachable from r such that the unique path from r to every other node in this tree is a shortest path and hence it clearly minimizes w.

Although the greedy algorithm finds an optimum base in the above examples, it is obviously not to be expected that this is true in general. The first sufficient condition for the optimality of the greedy algorithm was given by Korte and Lovász in [6]. There they introduced an even broader framework: they considered objective functions defined on all feasible orderings of feasible sets. Given a greedoid $G=(S,{\mathcal {F}})$, let ${\mathcal {L}}({\mathcal {F}})$ denote the set of all feasible orderings of all feasible sets. Extending the greedy algorithm to the case of an objective function $w:{\mathcal {L}}({\mathcal {F}})\rightarrow {\mathbb {R}}$ is obvious: instead of augmenting a feasible set $A\in {\mathcal {F}}$, it keeps maintaining and updating a feasible ordering of A that is always augmented by the best possible choice x.

Theorem 2

(Korte and Lovász [6, 8, Theorem XI.1.3]) Let $G=(S,{\mathcal {F}})$ be an arbitrary greedoid and $w:{\mathcal {L}}({\mathcal {F}})\rightarrow {\mathbb {R}}$ an objective function. Assume that whenever $(a_1,\ldots ,a_i,x)$ is a feasible ordering of a set $A+x\in {\mathcal {F}}$ (where $i=0$ is possible) such that $w\left( (a_1,\ldots ,a_i,x)\right) \ge w\left( (a_1,\ldots ,a_i,y)\right)$ for every $y\in \varGamma (A)$ then the following conditions hold:

• (3.1) $w\left( (a_1,\ldots ,a_i,b_1,\ldots ,b_j,x,c_1,\ldots ,c_k)\right) \ge w\left( (a_1,\ldots ,a_i,b_1,\ldots ,b_j,z,c_1, \ldots ,c_k)\right)$

  if both of these strings are in ${\mathcal {L}}({\mathcal {F}})$ (and $j=0$ or $k=0$ is possible).

• (3.2) $w\left( (a_1,\ldots ,a_i,x,b_1,\ldots ,b_j,z,c_1,\ldots ,c_k)\right) \ge w\left( (a_1,\ldots ,a_i,z,b_1,\ldots ,b_j,x, c_1,\ldots ,c_k)\right)$

  if both of these strings are in ${\mathcal {L}}({\mathcal {F}})$ (and $j=0$ or $k=0$ is possible).

Then the greedy algorithm finds a maximum base with respect to w.

Since in most applications the objective function only depends on the feasible sets themselves and not on their orderings, one would want to formulate the corresponding corollary of Theorem 2. Obviously, (3.2) is automatically fulfilled in these cases, however, it is not at all straightforward to specialize (3.1) to such objective functions. Both in [6] and [8, Chapter XI, condition (1.4)] it is claimed that for objective functions $w:{\mathcal {F}}\rightarrow {\mathbb {R}}$ (3.1) is equivalent to the following:

• (3.3) If $A,B,A+x,B+x\in {\mathcal {F}}$ hold for some sets $A\subseteq B$ and $x\in S-B$, and $w(A+x)\ge w(A+y)$ for every $y\in \varGamma (A)$ then $w(B+x)\ge w(B+z)$ for every $z\in \varGamma (B)$.

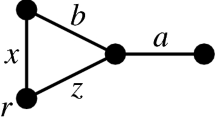
This reformulation, however, clearly disregards the fact that $\{a_1,\ldots ,a_i,$ $b_1,\ldots ,$ $b_j,c_1,\ldots ,c_k\}$ need not be a feasible set. In actual fact, (3.3) does not guarantee the optimality of the greedy algorithm as shown by the trivial example of Fig. 1: consider the undirected branching greedoid of the graph on the left hand side and let the objective function be defined as in the table on the right hand side. It is easy to check that (3.3) is fulfilled, however, the greedy algorithm gives $\{a,c\}$ instead of $\{b,c\}$. On the other hand, (3.1) is clearly violated: a is the best continuation of $\emptyset$ but $w((a,c))<w((b,c))$.

Fig. 1

Property (3.3) does not imply property (3.1) for order-independent objective functions, nor does it guarantee the optimality of the greedy algorithm

Unfortunately, as innocuous as the above mistake might look, it led the authors of [8] to the following false claim (see [8, page 156]): if $G=(S,{\mathcal {F}})$ is a local poset greedoid and $w:{\mathcal {F}}\rightarrow {\mathbb {R}}$ is defined as $w(A)=\sum \{c(P_x^A):x\in A\}$ for a $c:S\rightarrow {\mathbb {R}}^+$ analogously to Example 3, then the greedy algorithm finds a minimum base with respect to w. To disprove this, let $S=\{x,y,z,u\}$, ${\mathcal {F}}=\left\{ \emptyset , \{x\}, \{y\}, \{x,y\}, \{x,u\}, \{x,y,z\}, \{x,z,u\}\right\}$ and $c(x)=3$, $c(y)=2$, $c(z)=c(u)=0$. Then it is easy to check that $(S,{\mathcal {F}})$ is a local poset greedoid, but since the greedy algorithm starts with choosing y, it terminates with $\{x,y,z\}$ which is not minimum as $w(\{x,y,z\})=10$ and $w(\{x,z,u\})=9$.

Moreover, it is worth noting that while the optimality of Dijkstra’s algorithm does follow from Theorem 2 for directed graphs, it does not follow in the undirected case as shown by the example of Fig. 2: although x is the best continuation of the empty set, $11=w((x,b,a))>w((z,b,a))=10$, hence $(-w)$ violates (3.1).

Fig. 2

The optimality of Dijkstra’s algorithm does not follow from Theorem 2 for undirected graphs

On the other hand, the following was shown in [2].

Theorem 3

(Boyd [2]) Let $G=(S,{\mathcal {F}})$ be a local forest greedoid, $c:S\rightarrow {\mathbb {R}}^+$ a non-negative valued weight function and $w(A)=\sum \{c(P_x^A):x\in A\}$ for every feasible set $A\in {\mathcal {F}}$. Then the greedy algorithm finds a minimum base with respect to w.

Since both undirected and directed branching greedoids are local forest greedoids, the above theorem implies the optimality of Dijkstra’s algorithm both for undirected and directed graphs. A generalization of Theorem 3 will be given in Sect. 6 (see Theorem 16) the proof of which will also be shorter than the rather technical one given in [2].

Although the optimality of the greedy algorithm is a central topic in the theory of greedois, most results regarding this question are about linear objective functions. In [7] Korte and Lovász proved that on an arbitrary greedoid $G=(S,{\mathcal {F}})$ the greedy algorithm is optimal for all linear objective functions if and only if the following strong exchange axiom is fulfilled: for every $A\subseteq B$, $A\in {\mathcal {F}}$, $A+x\in {\mathcal {F}}$, $B\in {\mathcal {B}}$ and $x\in S-B$ there exists a $y\in B-A$ such that $B-y+x\in {\mathcal {B}}$ and $A+y\in {\mathcal {F}}$. A generalization of this result to arbitrary objective functions will be given in Sect. 6 (see Theorem 13). In [5] another generalization of the above result of Korte and Lovász [7] was given: a necessary and sufficient condition for the optimality of the greedy algorithm for linear objective functions on accessible set systems. In [10] a variant of the greedy algorithm on interval greedoids that “looks two step ahead” is defined and a necessary and sufficient condition for its optimality on linear objective functions is derived. As for general (that is, not necessarily linear) and possibly order-dependent objective functions a generalization of Theorem 2 was most recently given in [15] that, among other applications, completely covers Example 3 (also for undirected graphs).

4 A polyhedral result

In this section we prove a generalization of Edmonds’ classic matroid polytope theorem to local forest greedoids.

Theorem 4

(Edmonds [4]) Let $M=(S,{\mathcal {F}})$ be a matroid with rank function r and let $P_{\text {ind}}(M)$ denote the polytope spanned by the incidence vectors of all independent sets of M. Then

$$\begin{aligned} \displaystyle P_{\text {ind}}(M)=\left\{ x\in {\mathbb {R}}^S: x(U)\le r(U) \text{ for } \text{ all } U\subseteq S, x(s)\ge 0 \text{ for } \text{ all } s\in S\right\} . \end{aligned}$$

The theorem has some equivalent formulations, the one of relevance for the purposes of this paper is the following. The up-hull of a polyhedron $P\subseteq {\mathbb {R}}^n$, denoted by $P^{\uparrow }$, is defined as $P^{\uparrow }=\{x\in {\mathbb {R}}^n:\exists z\in P, z\le x\}$; in other words, $P^{\uparrow }$ is the Minkowski-sum of P and the non-negative orthant of ${\mathbb {R}}^n$ (and as such, it is also a polyhedron).

Theorem 5

Let $M=(S,{\mathcal {F}})$ be a matroid with rank function r and let $P_{\text {base}}(M)$ denote the polytope spanned by the incidence vectors of all bases of M. Then

$$\begin{aligned} \displaystyle P_{\text {base}}^{\uparrow }(M)=\left\{ x\in {\mathbb {R}}^S: x(U)\ge r(S)-r(S-U) \text{ for } \text{ all } U\subseteq S\right\} . \end{aligned}$$

As claimed above, this theorem is just a reformulation of Theorem 4. Indeed, by applying Theorem 4 to the dual of a matroid one gets a description of the polytope spanned by the incidence vectors of all spanning sets (that is, sets containing a base of M); then it is easy to check that this polytope is nothing but the intersection of $P_{\text {base}}^{\uparrow }(M)$ and the hypercube $[0,1]^S$. The details are given in [12, Chapter 40.2].

Definition 1

Given a greedoid $G=(S,{\mathcal {F}})$, a feasible set $A\in {\mathcal {F}}$ and an $x\in S$, the shadow of x on A is $sh_A(x)=|A|-r(A-x)$. The shadow vector of A is the vector $sh_A\in {\mathbb {R}}^S$ for which $sh_A(x)$ is the shadow of x on A for every $x\in S$. The shadow polytope $P_{\text {shadow}}(G)$ of G is defined as the polytope spanned by the shadow vectors of all bases of G.

For example, if $G=(E,{\mathcal {F}})$ is the undirected branching greedoid of a graph H with root node r, $A\in {\mathcal {F}}$ is the edge set of a subtree $T=(V_T,A)$ of H such that $r\in V_T$ and $x\in E$ is arbitrary then it is easy to check that $sh_A(x)$ is the number of nodes in $V_T$ that are unreachable via a path from r in $(V_T, A-x)$. Obviously, in every greedoid $sh_A(x)=0$ if and only if $x\notin A$. Furthermore, if M is a matroid then ${sh_A(x)=1}$ is obvious for every $x\in A$ and hence $sh_A$ is nothing but the incidence vector of A. Consequently, $P_{\text {shadow}}(M)=P_{\text {base}}(M)$ holds for every matroid M.

The significance of the notion of the shadow vector for local poset greedoids is indicated by the following lemma: it shows that for every weight function $c:S\rightarrow {\mathbb {R}}$ on the ground set, the value of the objective function already seen in Example 3 is the dot product of the shadow vector and c. This observation, together with Theorem 3, implies that for local forest greedoids the greedy algorithm minimizes non-negative, linear objective functions over the shadow polytope. This fact will greatly be relied on in the proof of Theorem 6.

Recall that $\varDelta (X)$ denotes the unique base of a subfeasible set $X\in {\mathcal {F}}^{\vee }$ in interval greedoids.

Lemma 1

Let $G=(S,{\mathcal {F}})$ be a local poset greedoid, $A\in {\mathcal {F}}$ and $c:S\rightarrow {\mathbb {R}}$ a weight function. Then $\sum _{x\in A}c(x)\cdot sh_A(x)=\sum _{x\in A}c(P_x^A)$.

Proof

We claim that $y\in P_x^A$ if and only if $x\in A-\varDelta (A-y)$ for every $x,y\in A$. Indeed, $x\in \varDelta (A-y)$ implies $P_x^A\subseteq \varDelta (A-y)$ by $\varDelta (A-y)\in {\mathcal {F}}$, hence $x\in A-\varDelta (A-y)$ follows from $y\in P_x^A$. The converse follows from the local union property: since $P_x^A,\varDelta (A-y)\in {\mathcal {F}}$, $P_x^A,\varDelta (A-y)\subseteq A$, $P_x^A\cup \varDelta (A-y)\in {\mathcal {F}}$ holds and thus $y\in P_x^A$ by the definition of $\varDelta (A-y)$.

Then the lemma follows by

$$\begin{aligned} \sum _{x\in A}c(P^A_x)=\sum _{y\in A}|A-\varDelta (A-y)|\cdot c(y) =\sum _{y\in A}sh_A(y)\cdot c(y). \end{aligned}$$

$\square$

We mentioned above that for matroids the shadow polytope and the base polytope coincide. Therefore the following theorem, which is the main result of this section, is indeed a direct generalization of Theorem 5.

Theorem 6

Let $G=(S,{\mathcal {F}})$ be a local forest greedoid with rank function r. Then

$$\begin{aligned} P_{\text {shadow}}^{\uparrow }(G)=\left\{ x\in {\mathbb {R}}^S: x(U)\ge r(S)-r(S-U) \text{ for } \text{ all } U\subseteq S\right\} . \end{aligned}$$

To prepare the proof of Theorem 6, we need the following lemmas.

Lemma 2

(Local Supermodularity Property) If $G=(S,{\mathcal {F}})$ is a local poset greedoid then $r(A)+r(B)\le r(A\cup B)+r(A\cap B)$ holds for $A,B\subseteq S$ if $A\cup B\in {\mathcal {F}}^{\vee }$.

Proof

Let $X=\varDelta (A)$ and $Y=\varDelta (B)$. Then $X\cap Y\in {\mathcal {F}}$ by the local intersection property. Furthermore, since for every feasible set $Z\subseteq A\cap B$, $Z\cup X\in {\mathcal {F}}$ and $Z\cup Y\in {\mathcal {F}}$ by the local union property, $Z\subseteq X\cap Y$ must hold by the definition of $\varDelta (A)$ and $\varDelta (B)$. Therefore $X\cap Y=\varDelta (A\cap B)$. Finally, since $X\cup Y\in {\mathcal {F}}$ is also true by the local union property, we have $r(A)+r(B)=|X|+|Y|=|X\cup Y|+|X\cap Y|\le r(A\cup B)+r(A\cap B)$ as claimed.$\square$

Note that the above local supermodularity property also characterizes local poset greedoids among all greedoids since it implies both the local intersection and the local union properties if applied to feasible sets.

Lemma 3

If $G=(S,{\mathcal {F}})$ is a local poset greedoid, $B\in {\mathcal {F}}^{\vee }$ is a subfeasible set and $\emptyset \ne A\subseteq B$ then

$$\begin{aligned} \sum _{x\in A}r(B-x)\le r(B-A)+(|A|-1)\cdot r(B). \end{aligned}$$

Proof

We proceed by induction on |A|. The claim is trivial for $|A|=1$, so let $|A|\ge 2$ and $A'=A-z$ for an arbitrary $z\in A$. Then

$$\begin{aligned} \sum _{x\in A}r(B-x)= & {} \sum _{x\in A'}r(B-x)+r(B-z)\le r(B-A')+(|A|-2)\cdot r(B)+r(B-z)\\\le & {} r(B-A)+r(B)+(|A|-2)\cdot r(B)=r(B-A)+(|A|-1)\cdot r(B), \end{aligned}$$

where the first inequality follows by induction and the second by Lemma 2.$\square$

Proposition 7

Let $G=(S,{\mathcal {F}})$ be a local poset greedoid, $P_{\text {shadow}}(G)$ its shadow polytope and $Q=\left\{ x\in {\mathbb {R}}^S:x(U)\ge r(S)-r(S-U) \text{ for } \text{ all } U\subseteq S\right\}$. Then $P_{\text {shadow}}^{\uparrow }(G) \subseteq Q$.

Proof

Let B be a base of G, $sh_B$ its shadow vector and $U\subseteq S$. Then using Lemma 3 we have

$$\begin{aligned} sh_B(U)= & {} \sum _{x\in U\cap B}\left( |B|-r(B-x)\right) =|U\cap B|\cdot r(S)- \sum _{x\in U\cap B}r(B-x)\\\ge & {} |U\cap B|\cdot r(S)-r(B-U)-(|U\cap B|-1)\cdot r(S)\\= & {} r(S)-r(B-U)\ge r(S)-r(S-U). \end{aligned}$$

Therefore all vertices of $P_{\text {shadow}}(G)$ are in Q which implies $P_{\text {shadow}}(G)\subseteq Q$. Consequently, $P_{\text {shadow}}^{\uparrow }(G)\subseteq Q^{\uparrow }=Q$.$\square$

It can happen that $P_{\text {shadow}}^{\uparrow }(G)$ is a proper subset of Q in the above proposition as shown by the example already seen in Sect. 3: let $S=\{a,b,c,d\}$ and ${\mathcal {F}}=\left\{ \emptyset , \{a\}, \{b\}, \{a,b\}, \{a,d\}, \{a,b,c\}, \{a,c,d\}\right\}$. Then $G=(S,{\mathcal {F}})$ is a local poset greedoid, the shadow vectors of its two bases are (2, 2, 1, 0) and (3, 0, 1, 2) (if the elements are arranged in alphabetical order), both of which fulfill $2x_a+x_b\ge 6$, hence this inequality is fulfilled by every member of $P_{\text {shadow}}^{\uparrow }(G)$. However, $(2,1,1,1)\in Q$ is easy to check which shows that $Q-P_{\text {shadow}}^{\uparrow }(G)\ne \emptyset$.

The claim of Theorem 6 is that $\subseteq$ can be replaced by $=$ in Proposition 7 in case of local forest greedoids. The proof will follow the argument of Edmonds’ original proof of Theorem 4: the greedy algorithm will be used to construct an optimum dual solution. However, it should be noted that the construction we give below is not an extension of that of Edmonds: even if applied to matroids it gives a different optimum dual solution. In particular, Edmonds’ construction (even if adapted to prove Theorem 5, which can easily be done) yields a chain of subsets of the ground set which is not true for the construction given below.

Theorem 8

Let $G=(S,{\mathcal {F}})$ be a local forest greedoid, $|S|=n$, $c:S\rightarrow {\mathbb {R}}^+$ a non-negative valued weight function, $w(A)=\sum \{c(P_x^A):x\in A\}$ for every $A\in {\mathcal {F}}$ and $B_m$ a minimum base with respect to w. Then there exist the subsets $U_1,U_2,\ldots ,U_n\subseteq S$ and corresponding values $y(U_1),y(U_2),\ldots ,y(U_n)$ such that $y(U_i)\ge 0$ for all $1\le i\le n$, $\sum \{y(U_i):x\in U_i\}=c(x)$ holds for every $x\in S$ and $\sum _{i=1}^n\left( r(S)-r(S-U_i)\right) \cdot y(U_i)=w(B_m)$.

Proof

Assume that a running of the greedy algorithm gives the base $B=\{s_1,s_2,\ldots ,s_r\}$ choosing the elements in this order and let $B_1=\emptyset$ and $B_i=\{s_1,s_2,\ldots ,s_{i-1}\}$ for every $2\le i\le r$. Let $S-B=\{s_{r+1},\ldots ,s_n\}$ with the elements ordered arbitrarily. Finally, denote $P_0=\emptyset$ and $P_i=P_{s_i}^{B}$ for every $1\le i\le r$. Then let

$$\begin{aligned} \begin{array}{r@{}c@{}l@{\quad }l} U_i\,\,&{}=&{}\,\left\{ \begin{array}{ll} \varGamma (B_i),&{}\text {if }1\le i\le r,\\ \{s_i\},&{}\text {if }r<i\le n\\ \end{array}\right. &{}\text {and}\\ y(U_i)\,\,&{}=&{}\,\left\{ \begin{array}{ll} c(P_i)-c(P_{i-1}),&{}\text {if }1\le i\le r,\\ c(s_i)-\sum \{y(U_j):j\le r, s_i\in U_j\},&{}\text {if }r<i\le n.\\ \end{array}\right. \end{array} \end{aligned}$$

We prove that the above choice of $U_i$ and $y(U_i)$ fulfills all requirements of the theorem through a series of claims.

Claim 1

Let $x\in \bigcup _{i=1}^rU_i$ and $j=\min \{i:x\in U_i\}$. Then $P_x^{B_j+x}=P_{j-1}+x$.

Proof

If $j=1$ then $P_x^{B_j+x}=\{x\}$ and thus the claim is obvious, so assume $j\ge 2$ and hence $|P_x^{B_j+x}|\ge 2$. Since $x\in U_j-U_{j-1}$, we have $B_j+x\in {\mathcal {F}}$ and $B_{j-1}+x\notin {\mathcal {F}}$. Since $B_{j-1},P_x^{B_j+x},B_j+x\in {\mathcal {F}}$, $B_{j-1}\cup P_x^{B_j+x}\in {\mathcal {F}}$ follows from the local union property. This implies $s_{j-1}\in P_x^{B_j+x}$ by $B_{j-1}+x\notin {\mathcal {F}}$.

Since $P_x^{B_j+x}-x\in {\mathcal {F}}$ and $s_{j-1}\in P_x^{B_j+x}-x\subseteq B_j$, $P_{j-1}\subseteq P_x^{B_j+x}-x$ and therefore $P_{j-1}+x\subseteq P_x^{B_j+x}$ follows from the definition of a path. The second to last element in the unique ordering of $P_x^{B_j+x}$ is obviously $s_{j-1}$ otherwise $s_{j-1}\in P_t\subseteq B_{t+1}$ would follow from Theorem 1 for some $t<j-1$, a contradiction. Therefore $P_x^{B_j+x}=P_{j-1}+x$ as claimed. $\square$

Claim 2

Let $x\in \bigcup _{i=1}^rU_i$, $j=\min \{i:x\in U_i\}$, $k=\max \{i:x\in U_i,i\le r\}$. Then $x\in U_i$ holds for every $j\le i\le k$ and $\sum \{y(U_i):x\in U_i,i\le r\}=c(P_k)-c(P_{j-1})$.

Proof

From $x\in U_j\cap U_k$ we have $B_j+x\in {\mathcal {F}}$ and $B_k+x\in {\mathcal {F}}$ which, by the local union property, imply $B_i+x\in {\mathcal {F}}$ and therefore $x\in U_i$ for every $j\le i\le k$ as claimed. Consequently,

$$\begin{aligned} \sum \{y(U_i):x\in U_i,i\le r\}=\sum _{i=j}^k\left( c(P_i)-c(P_{i-1})\right) =c(P_k)-c(P_{j-1}). \end{aligned}$$

$\square$

Claim 3

$c(P_1)\le c(P_2)\le \ldots \le c(P_r)$.

Proof

If $s_i\in U_{i-1}$ for some $2\le i\le r$ then $c(P_{i-1})\le c(P_i)$ is implied by the fact that the greedy algorithm could have chosen $s_i$ instead of $s_{i-1}$. If, on the other hand, $s_i\notin U_{i-1}$ then $P_i=P_{i-1}+s_i$ follows from Claims 1 and 2. Hence $c(P_i)=c(P_{i-1})+c(s_i)$ which proves the claim.$\square$

Claim 4

$y(U_i)\ge 0$ for all $1\le i\le n$ and $\sum \{y(U_i):x\in U_i\}=c(x)$ for all $x\in S$.

Proof

Let first $x=s_t$ for some $1\le t\le r$. Then $y(U_t)\ge 0$ is immediate from Claim 3. Define j and k as in Claim 3. Then $k=t$ is obvious and Claim 1 gives $P_t=P_{j-1}+s_t$. Therefore from Claim 2 we have $\sum \{y(U_i):s_i\in U_i\}=c(P_t)-c(P_{j-1})=c(s_t)$ as claimed.

Now let $x=s_t$ for some $r<t\le n$. If $s_t\notin \bigcup _{i=1}^rU_i$ then $\sum \{y(U_i):s_t\in U_i\}=y(U_t)=c(s_t)\ge 0$ is clear. If, on the other hand, $s_t\in \bigcup _{i=1}^rU_i$ then again define j and k as in Claim 3. Since the greedy algorithm could have chosen x instead of $s_k$ by $x=s_t\in U_k$, we have $c(P_x^{B_k+x})\ge c(P_k)$. Furthermore, $B_j+x\subseteq B_k+x$ implies $P_x^{B_j+x}=P_x^{B_k+x}$. These, together with Claims 1 and 2 imply

$$\begin{aligned} c(x)=c(P_x^{B_k+x})-c(P_{j-1})\ge c(P_k)-c(P_{j-1})= \sum \{y(U_i):x\in U_i,i\le r\}, \end{aligned}$$

hence we have the claim by the definitions of $U_i$ and $y(U_i)$.$\square$

Claim 5

$$\begin{aligned} r(S-U_i)=\left\{ \begin{array}{ll} i-1,&{}\quad \text {if }1\le i\le r,\\ r(S),&{}\quad \text {if }r<i\le n\\ \end{array}\right. \end{aligned}$$

Proof

If $r<i$ then $B\subseteq S-U_i$ so $r(S-U_i)=r(S)$ is obvious. For $1\le i\le r$ we show that $B_i$ is a base of $S-U_i$ which will settle the claim by $|B_i|=i-1$. $B_i\subseteq S-U_i$ and $B_i\in {\mathcal {F}}$ are obvious. Furthermore, if $|B_i|<|X|$ and $X\in {\mathcal {F}}$ then $B_i+x\in {\mathcal {F}}$ for some $x\in X-B_i$ by (2.2) and hence $x\in U_i$, which proves that $B_i$ is indeed a base of $S-U_i$.$\square$

Finally, it remains to show that $\sum _{i=1}^n\left( r(S)-r(S-U_i)\right) \cdot y(U_i)=w(B_m)$ holds. Using Claim 5 we get

$$\begin{aligned}&\sum _{i=1}^n\left( r(S)-r(S-U_i)\right) \cdot y(U_i)= \sum _{i=1}^r\left( r(S)-i+1\right) \cdot y(U_i)\\&\quad =\sum _{i=1}^r\left( r-i+1\right) \cdot \left( c(P_i)-c(P_{i-1})\right) = \sum _{i=1}^r c(P_i)=w(B)=w(B_m), \end{aligned}$$

where the last equation follows from Theorem 3.$\square$

Now we are ready for the

Proof of Theorem 6

Let $P=P_{\text {shadow}}^{\uparrow }(G)$ for short. By Proposition 7 we have $P\subseteq Q$, where $Q=\left\{ x\in {\mathbb {R}}^S:x(U)\ge r(S)-r(S-U) \text{ for } \text{ all } U\subseteq S\right\}$. To show equality it suffices to prove that $\min \{cx:x\in P\}=\min \{cx:x\in Q\}$ holds for every $c\in {\mathbb {R}}^S$, $c\ge 0$. (Indeed, since $P^{\uparrow }=P$ holds, P can be written in the form $P=\{x:Ax\ge b\}$ for some matrix $A\ge 0$. If a $z\in Q-P$ existed then z would violate a constraint $cx\ge \delta$ of $Ax\ge b$ and hence $\min \{cx:x\in P\}>\min \{cx:x\in Q\}$ would follow.)

So let a $c\in {\mathbb {R}}^S$, $c\ge 0$ be fixed, let $w(A)=\sum \{c(P_x^A):x\in A\}$ for every $A\in {\mathcal {F}}$ and $B_m$ a minimum base with respect to w. Using Lemma 1 and since $\min \{cx:x\in P_{\text {shadow}}(G)\}$ is attained on a vertex of $P_{\text {shadow}}(G)$ and $P_{\text {shadow}}(G)\subseteq P\subseteq Q$, we get

$$\begin{aligned} w(B_m)= & {} \min \left\{ \sum _{s\in B}c(P_s^B):B\in {\mathcal {B}}\right\} = \min \left\{ \sum _{s\in B}c(s)\cdot sh_B(s):B\in {\mathcal {B}}\right\} \nonumber \\= & {} \min \{cx:x\in P_{\text {shadow}}(G)\}\ge \min \{cx:x\in P\}\ge \min \{cx:x\in Q\}.\nonumber \\ \end{aligned}$$

(1)

From the duality theorem of linear programming we get

$$\begin{aligned} \min \{cx:x\in Q\}= & {} \max \Big \{\sum y(U)(r(S)-r(S-U)):\\&\sum \{y(U):s\in U\}=c(s) \text { for all }s\in S,y(U)\ge 0\text { for all }U\subseteq S\Big \}. \end{aligned}$$

Theorem 8 implies that this maximum is at least $w(B_m)$, which in turn implies that every inequality in (1) is fulfilled with equation and hence concludes the proof.$\square$

Corollary 9

If $G=(S,{\mathcal {F}})$ is a local forest greedoid and $c:S\rightarrow {\mathbb {Z}}^+$ is a non-negative integer valued weight function then the linear programming problem

$$\begin{aligned} \min \big \{cx:x(U)\ge r(S)-r(S-U) \text{ for } \text{ all } U\subseteq S\big \} \end{aligned}$$

and its dual

$$\begin{aligned}&\max \Big \{\sum y(U)(r(S)-r(S-U)):\sum \{y(U):s\in U\}=c(s) \text { for all }s\in S,\\&\quad y(U)\ge 0\text { for all }U\subseteq S\Big \} \end{aligned}$$

have integer optimum solutions.

Proof

It follows from the proof Theorem 6 that the minimum of the primal problem is attained on the shadow vector of a base of G which is obviously integer. Furthermore, the construction of the proof of Theorem 8 yields an integer optimum solution of the dual problem if c is integer.$\square$

Corollary 10

If $G=(S,{\mathcal {F}})$ is a local forest greedoid then the system

$$\begin{aligned} x(U)\ge r(S)-r(S-U) \text{ for } \text{ all } U\subseteq S \end{aligned}$$

is totally dual integral.

Proof

Immediately from Corollary 9 after observing that the minimum of the primal program clearly does not exist if c contains a negative component.$\square$

We remark that no similar description of $P_{\text {shadow}}(G)$ is to be hoped for, not even for branching greedoids. Indeed, it follows from Lemma 1 that maximizing a linear objective function over $P_{\text {shadow}}(G)$ translates to maximizing $\sum _{e\in E(H)}c(P_e)$ which is, as it was pointed out in [8, Chapter XI.], NP-hard as it contains the Hamilton path problem. Therefore the existence of such a description of $P_{\text {shadow}}(G)$ would imply that, for example, the Hamilton path problem is in co-NP, which is highly unlikely.

5 An application: reliability of networks via game theory

The problem of measuring the robustness or reliability of a graph arises in many applications. The most widely applied reliability metrics are obviously the connectivity based ones, however, these are unsuitable in many cases—for example because in many applications the network is almost completely functional if removing some nodes or links results in the loss of only a small number of nodes that are in some sense insignificant or peripheral.

Applying game-theoretical tools for measuring the reliability of a graph has become very common. The basic idea is very natural: define a game between two virtual players, the Attacker and the Defender, such that the rules of the game capture the circumstances under which reliability is to be measured. Then analyzing the game might give rise to an appropriate security metric: the better the Attacker can do in the game, the lower the level of reliability is. This kind of analysis can give rise to new graph reliability metrics and in some cases it can shed a new light on some well-known ones.

To illustrate this, consider the following Spanning Tree Game: a connected, undirected graph G, a positive valued damage function $d:E(G)\rightarrow {\mathbb {R}}^+$ and a cost function $c:E(G)\rightarrow {\mathbb {R}}$ are given. For each edge, d(e) represents the “damage” caused by the loss of e (or in other words, the “importance” of e) and c(e) represents the cost of attacking e. The Attacker chooses (or “attacks and destroys”) an edge e of G and the Defender (without knowing the Attacker’s choice) chooses a spanning tree T of G (that she intends to use as some kind of “communication infrastructure”). Regardless of the Defender’s choice, the Attacker has to pay the cost of attack c(e) to the Defender. There is no further payoff if $e\notin T$. If, on the other hand, $e\in T$ then the Defender pays the Attacker the damage value d(e). Since this game is a two-player, zero-sum game, it has a unique Nash-equilibrium payoff (or, in simpler terms, game value) V by Neumann’s classic Minimax Theorem. Since V is the highest expected gain the Attacker can guarantee himself by an appropriately chosen mixed strategy (that is, probability distribution on the set of edges), it makes sense to say that $\frac{1}{V}$ is a valid reliability metric.

After some preliminary results on some special cases in the literature (see [14] for the details), the Spanning Tree Game was solved in the above defined general form in [13]. In fact, it was considered there in a more general, matroidal setting: the Matroid Base Game was defined analogously to the Spanning Tree Game with the only difference being that the Attacker chooses an element of the ground set of a matroid $M=(S,{\mathcal {F}})$ and the Defender chooses a base B of M. Then the following result was proved.

Theorem 11

([13]) For every input of the Matroid Base Game the game value is

$$\begin{aligned} \max _{\emptyset \ne U\subseteq S} \frac{r(S)-r(S-U)-q(U)}{p(U)}, \end{aligned}$$

where $p(s)=\frac{1}{d(s)}$ and $q(s)=\frac{c(s)}{d(s)}$ for all $s\in S$. Furthermore, if M is given by an independence testing oracle then there exists a strongly polynomial algorithm that computes the game value of the Matroid Base Game and an optimum mixed strategy for both players.

The running time of the algorithm given in [13] was later substantially improved in [1].

If specialized to the Spanning Tree Game and to the $c\equiv 0$ case, the above theorem implies that the game value is the reciprocal of a well-known graph reliability metric: the strength of a graph is defined as

$$\begin{aligned} \sigma _p(G)=\min \left\{ \frac{p(U)}{\mathrm{comp}(G-U)-1}: U\subseteq E(G),\mathrm{comp}(G-U)>1\right\} , \end{aligned}$$

where ${\mathrm{comp}(G-U)}$ is the number of components of the graph obtained from G by deleting U and $p:E(G)\rightarrow {\mathbb {R}}^+$ is a weight function. This notion was defined in the weighted case and its computability in strongly polynomial time was proved in [3].

While the Matroid Base Game has further relevant applications beyond the Spanning Tree Game (see [13]), there are other types of games of a similar nature which do not fit into this framework. The following Rooted Spanning Tree Game was considered in [9]: a (mixed) graph H with a “headquarters” node r is given such that every node is reachable from r. (The role of r can be that all other nodes need to communicate with r only, for example to transmit some collected data to r.) Furthermore assume that a cost function $c:E(H)\rightarrow {\mathbb {R}}$ is also given. Again, the Attacker chooses an edge e, the Defender chooses a spanning tree T and the cost of attack c(e) is payed by the Attacker to the Defender in all cases and there is no further payoff if $e\notin T$. However, if $e\in T$ then the payoff from the Defender to the Attacker is the number of nodes that become unreachable from r in T after removing e.

Since this number is nothing but the shadow $sh_T(e)$ in case of the branching greedoid, the definition of the Local Forest Greedoid Base Game presents itself: given a local forest greedoid $G=(S,{\mathcal {F}})$ and weight functions $d,c\in {\mathbb {R}}^S$ with $d>0$, the Attacker chooses an element $s\in S$, the Defender chooses a base B of G and then the payoff from the Defender to the Attacker is $d(s)\cdot sh_B(s)-c(s)$. Clearly, this game is a direct generalization of the Matroid Base Game mentioned above. Then, using Theorem 6 and following the proof of [13, Theorem 5] we can prove the following.

Theorem 12

For every input of the Local Forest Greedoid Base Game the game value is

$$\begin{aligned} \max _{\emptyset \ne U\subseteq S} \frac{r(S)-r(S-U)-q(U)}{p(U)}, \end{aligned}$$

where $p(s)=\frac{1}{d(s)}$ and $q(s)=\frac{c(s)}{d(s)}$ for all $s\in S$.

Proof

Denote the game value by V and assume that a mixed strategy of the Defender $\{\delta (B):B\in {\mathcal {B}}\}$ (that is, a probability distribution $\delta$ on ${\mathcal {B}}$) is given. Then assuming that the Attacker chooses a given fixed element $s\in S$ in the game, the Defender’s expected loss is

$$\begin{aligned} \sum _{B\in {\mathcal {B}}}\delta (B)\cdot \big (d(s)\cdot sh_B(s)-c(s)\big )= d(s)\cdot \left( \sum _{B\in {\mathcal {B}}}\delta (B)\cdot sh_B(s)\right) -c(s). \end{aligned}$$

(2)

Let $x(s)=\sum \{\delta (B)\cdot sh_B(s):B\in {\mathcal {B}}\}$ for all $s\in S$. Then the vector $x\in {\mathbb {R}}^S$ is nothing but an element of $P_{\text {shadow}}(G)$ by definition (since the values $\delta (B)$ form the set of coefficients of a convex combination). Since, by definition, the Defender’s objective is to minimize the maximum expected loss she has to suffer, her task amounts to the following by (2):

$$\begin{aligned} \min \big \{\mu : \exists x\in P_{\text {shadow}}(G), d(s)\cdot x(s)-c(s)\le \mu \text{ for } \text{ all } s\in S\big \}. \end{aligned}$$

(3)

In other words, the minimum in (3) is equal to V by Neumann’s Minimax Theorem. Rearranging (3):

$$\begin{aligned} V=\min \big \{\mu : \exists x\in P_{\text {shadow}}(G), x\le \mu \cdot p+q\}. \end{aligned}$$

Using the definition of $P_{\text {shadow}}^{\uparrow }(G)$ this is further equivalent to the following:

$$\begin{aligned} V=\min \big \{\mu : \mu \cdot p+q\in P_{\text {shadow}}^{\uparrow }(G)\}. \end{aligned}$$

(4)

By Theorem 6$\mu \cdot p+q\in P_{\text {shadow}}^{\uparrow }(G)$ is true if and only if

$$\begin{aligned} \mu \cdot p(U)+q(U)\ge r(S)-r(S-U) \end{aligned}$$

holds for all $U\subseteq S$. Then simple rearranging (and observing that this inequality is trivial for $U=\emptyset$) immediately gives that $\mu \cdot p+q\in P_{\text {shadow}}^{\uparrow }(G)$ is true if and only if

$$\begin{aligned} \mu \ge \max _{\emptyset \ne U\subseteq S} \frac{r(S)-r(S-U)-q(U)}{p(U)}. \end{aligned}$$

Hence V, the minimum of all such $\mu$’s is exactly this maximum.$\square$

If specialized to the branching greedoid and to the $c\equiv 0$ case it follows that the value of the Rooted Spanning Tree Game is the reciprocal of another known graph reliability metric, also defined in [3]. Interested readers are referred to [14] for the details. Furthermore, the above theorem also generalizes the first statement of Theorem 11. However, generalizing the algorithmic statement of Theorem 11 to the Local Forest Greedoid Base Game is left as an open problem.

6 Optimality of the greedy algorithm in greedoids

We start with the following theorem which seems to be new, but its proof is just an adaptation of that of the result of Korte and Lovász [7, 8, Theorem XI.2.2] mentioned at the end of Sect. 3 on the optimality of the greedy algorithm in case of linear objective functions.

Theorem 13

Let $G=(S,{\mathcal {F}})$ be an arbitrary greedoid and $w:{\mathcal {F}}\rightarrow {\mathbb {R}}$ an objective function that fulfills the following property:

• (6.1) If for some $A\subseteq B$, $A\in {\mathcal {F}}$, $A+x\in {\mathcal {F}}$, $B\in {\mathcal {B}}$ and $x\in S-B$ it holds that $w(A+x)\ge w(A+u)$ for every $u\in \varGamma (A)$ then there exists a $y\in B-A$ such that $B-y+x\in {\mathcal {B}}$ and $w(B-y+x)\ge w(B)$.

Then the greedy algorithm gives a maximum base with respect to w.

Proof

Assume by way of contradiction that the greedy algorithm gives the base $B_g=\{a_1,a_2,\ldots ,a_r\}$ choosing the elements in this order, but $B_g$ is not maximum with respect to w. Choose a maximum base $B_m$ with respect to w such that $\max \{i:a_1,\ldots ,a_i\in B_m\}$ is maximum possible, let this maximum be k and $A=\{a_1,\ldots ,a_k\}$. Then $A\in {\mathcal {F}}$, $A\subseteq B_m$, $a_{k+1}\notin B_m$ and $w(A+a_{k+1})\ge w(A+u)$ for every $u\in \varGamma (A)$ by the operation of the greedy algorithm. Therefore, by (6.1), there exists a $y\in B_m-A$ such that $B_m-y+a_{k+1}\in {\mathcal {B}}$ and $w(B_m-y+a_{k+1})\ge w(B_m)$. Therefore $B_m-y+a_{k+1}$ is also a maximum base with respect to w, but $\{a_1,\ldots ,a_k,a_{k+1}\}\subseteq B_m-y+a_{k+1}$ contradicts the choice of $B_m$.$\square$

It is worth noting that, in spite of its simplicity, the above theorem implies the optimality of the greedy algorithm in all three examples listed in Sect. 3. This is easy to check in case of Examples 1 and 2 and in case of Example 3 it will follow from the results below. Furthermore, it is not too hard to show that Theorem 13 also implies Theorem 2 in case of objective functions $w:{\mathcal {F}}\rightarrow {\mathbb {R}}$ that are independent of the ordering. (This could be proved by an argument similar to that of Theorem 15 below, we omit the details here.)

Moreover, Theorem 13 is in a sense best possible as shown by the following theorem. To claim the theorem, we need to extend the definition of minors of greedoids given in Sect. 2 to incorporate modifying the objective function $w_G:{\mathcal {F}}\rightarrow {\mathbb {R}}$ in an obvious way: in case of a deletion $G{\setminus } X$ $w_G$ is simply restricted to $S-X$, while in case of a contraction G / X the modified objective function becomes $w_{G/X}(A)=w_G(A\cup X)$.

Theorem 14

Assume that the objective function $w_G:{\mathcal {F}}\rightarrow {\mathbb {R}}$ violates condition (6.1) for a greedoid $G=(S,{\mathcal {F}})$. Then there exists a minor H of G such that a legal running of the greedy algorithm on H gives a base that is not maximum with respect to $w_H$.

Proof

Assume that (6.1) is violated by an $A\in {\mathcal {F}}$, $B\in {\mathcal {B}}$ and $x\in S-B$. Let $Y=S-B-x$ and $H=(G{\setminus } Y)/A$. Then the greedy algorithm run on H with respect to $w_H$ can start with x since $w_H(\{x\})\ge w_H(\{u\})$ for every $u\in \varGamma (\emptyset )$ holds in H by (6.1). Therefore this running of the greedy algorithm terminates with a base $B_g$ of H such that $x\in B_g$. Since the ground set of H is $S_H=B-A+x$ and $B-A$ is a base of H, $S_H-B_g=\{y\}$ for some $y\in B-A$. Since (6.1) is violated by A, B and x, we have $w(B-y+x)<w(B)$. Consequently, $w_H(B_g)=w(B-y+x)<w(B)=w_H(B-A)$ which proves that $B_g$ is not maximum with respect to $w_H$.$\square$

The following theorem will be weaker than Theorem 13—not only because it applies to interval greedoids only, but also because it will not cover Example 2 given in Sect. 3 (or the case of linear objective functions in general). However, it can also be regarded as a corrected version of the faulty condition (3.3) mentioned in Sect. 3 and it will be easier to work with later on.

Theorem 15

Let $G=(S,{\mathcal {F}})$ be an interval greedoid and $w:{\mathcal {F}}\rightarrow {\mathbb {R}}$ an objective function that fulfills the following property:

• (6.2) If for some $A\subseteq B$, $A\in {\mathcal {F}}$, $A+x\in {\mathcal {F}}$, $x,z\in S-B$ and $B+x\in {\mathcal {B}}$, $B+z\in {\mathcal {B}}$ such that $\varDelta (B)\cup \{x,z\}\notin {\mathcal {F}}$ it holds that $w(A+x)\ge w(A+u)$ for every $u\in \varGamma (A)$ then $w(B+x)\ge w(B+z)$.

Then the greedy algorithm gives a maximum base with respect to w.

Proof

We will show that (6.2) implies (6.1) which will obviously settle the proof by Theorem 13. So let A, B and x be given such that $A\subseteq B$, $A,A+x\in {\mathcal {F}}$, $B\in {\mathcal {B}}$ and $w(A+x)\ge w(A+u)$ for every $u\in \varGamma (A)$. We need to show the existence of a $y\in B-A$ according to (6.1).

Let $(b_1,\ldots ,b_k)$ be a feasible ordering of A and, using (2.2), augment this repeatedly to get a feasible ordering $(b_1,\ldots ,b_k,b_{k+1},\ldots ,b_r)$ of B. Denote $B_0=\emptyset$ and $B_i=\{b_1,\ldots ,b_i\}$ for every $1\le i\le r$. Let $t\in \{1,\ldots ,r\}$ be the largest index such that $B_{t-1}+x\in {\mathcal {F}}$. Obviously, t exists and $t\ge k+1$ since $B_k+x=A+x\in {\mathcal {F}}$. Now set $y=b_t$; we claim that this is a suitable choice for (6.1).

Trivially, $y\in B-A$ by $t\ge k+1$. To show $B-y+x\in {\mathcal {F}}$, augment $B_{t-1}+x$ from $B_{t+1}$; then augment the obtained feasible set from $B_{t+2}$ and continue like this until a base is obtained. Then $b_t$ can never occur as an augmenting element during this process by the choice of t which implies $B-y+x\in {\mathcal {F}}$ as claimed.

Let $C=B-y$. We claim that $\varDelta (C)\cup \{x,y\}\notin {\mathcal {F}}$, so assume the opposite towards a contradiction. Since $B_{t-1}\in {\mathcal {F}}$ and $B_{t-1}\subseteq C$, we have $B_{t-1}\subseteq \varDelta (C)$. Furthermore, $B_{t-1}+x\in {\mathcal {F}}$ by the choice of t and $B_{t-1}+y=B_t\in {\mathcal {F}}$ is also true. Since $B_{t-1}+x,B_{t-1}+y\subseteq \varDelta (C)\cup \{x,y\}$, $B_{t-1}\cup \{x,y\}=B_t+x\in {\mathcal {F}}$ follows by the local union property (2.3). This either contradicts the choice of t if $t<r$ or the fact that B is a base if $t=r$.

Consequently, since we have $C+y=B\in {\mathcal {B}}$, $C+x=B-y+x\in {\mathcal {B}}$ and $w(A+x)\ge w(A+u)$ for every $u\in \varGamma (A)$, we get $w(C+x)\ge w(C+y)$ from (6.2), which concludes the proof by $C+x=B-y+x$ and $C+y=B$.$\square$

The next theorem gives a generalization of Theorem 3.

Theorem 16

Let $G=(S,{\mathcal {F}})$ be a local forest greedoid, ${\mathcal {P}}$ its set of paths and $f:{\mathcal {P}}\rightarrow {\mathbb {R}}$ a function that satisfies the following monotonicity constraints:

• (i) if $A,B\in {\mathcal {P}}$ and $A\subseteq B$ then $f(A)\le f(B)$;

• (ii) if $A,B,A\cup C,B\cup C\in {\mathcal {P}}$ and $f(A)\le f(B)$ then $f(A\cup C)\le f(B\cup C)$.

Finally, let $w(A)=\sum \{f(P_x):x\in A\}$ for every $A\in {\mathcal {F}}$. Then the greedy algorithm gives a minimum base with respect to w.

We will need the following lemma for proving the above theorem.

Lemma 4

Let $G=(S,{\mathcal {F}})$ be a local poset greedoid, $B\subseteq S$ and $x,z\in S-B$ such that $B+x\in {\mathcal {F}}$, $B+z\in {\mathcal {F}}$ and $\varDelta (B)\cup \{x,z\}\notin {\mathcal {F}}$. Then $P_e^{B+x}\cap (B-\varDelta (B))=P_e^{B+z}\cap (B-\varDelta (B))$ holds for every $e\in B-\varDelta (B)$.

Proof

Since no feasible set in B can contain e by $e\in B-\varDelta (B)$ and the local union property (2.3), we have $x\in P_e^{B+x}$ and $z\in P_e^{B+z}$. Let $D_i=P_e^{B+i}\cap \varDelta (B)$ and $H_i=P_e^{B+i}\cap (B-\varDelta (B))$ for $i\in \{x,z\}$. We need to show $H_x=H_z$.

Since $P_e^{B+x},\varDelta (B),B+x\in {\mathcal {F}}$ and $P_e^{B+x},\varDelta (B)\subseteq B+x$, the local union property implies $\varDelta (B)\cup H_x+x\in {\mathcal {F}}$.

We claim that $\varDelta (B)\cup H_x+z\in {\mathcal {F}}$. To show this, first observe that augmenting $\varDelta (B)$ from $B+x$ and $B+z$ implies $\varDelta (B)+x,\varDelta (B)+z\in {\mathcal {F}}$ by the definition of $\varDelta (B)$. Therefore $\varDelta (B)\cup \{x,z\}\notin {\mathcal {F}}$ also implies $\varDelta (B)\cup \{x,z\}\notin {\mathcal {F}}^{\vee }$ by the local union property. Consequently, repeatedly augmenting $\varDelta (B)+z$ from $\varDelta (B)\cup H_x+x$ yields $\varDelta (B)\cup H_x+z\in {\mathcal {F}}$ as claimed since x can not augment.

Then since $P_e^{B+z},\varDelta (B)\cup H_x+z,B+z\in {\mathcal {F}}$ and $P_e^{B+z},\varDelta (B)\cup H_x+z\subseteq B+z$, the local intersection property (2.4) implies $D_z\cup (H_x\cap H_z)+z\in {\mathcal {F}}$. Since $P_e^{B+z}=D_z\cup H_z+z$, $H_z\subseteq H_x$ must hold by the definition of a path. By symmetry we also have $H_x\subseteq H_z$, which completes the proof.$\square$

Now we are ready for proving Theorem 16. The proof follows the argument of [8, page 156] where they showed that property (3.3) is fulfilled by a similarly defined objective function w in local poset greedoids. As mentioned in Sect. 3, that was insufficient for guaranteeing the optimality of the greedy algorithm, however, a similar argument will work well with Theorem 15.

Proof of Theorem 16

We will show that (6.2) is fulfilled by $(-w)$. So let A, B, x and z given such that $A,A+x\in {\mathcal {F}}$, $x,z\in S-B$, $B+x,B+z\in {\mathcal {B}}$, $\varDelta (B)\cup \{x,z\}\notin {\mathcal {F}}$ and $w(A+x)\le w(A+u)$ for every $u\in \varGamma (A)$ hold. We need to show $w(B+x)\le w(B+z)$.

Since $\varDelta (B)\in {\mathcal {F}}$, we have

$$\begin{aligned} w(B+i)=w(\varDelta (B))+f(P_i^{B+i})+\sum _{e\in B-\varDelta (B)}f(P_e^{B+i}) \end{aligned}$$

(6)

for $i\in \{x,z\}$. Let $(b_1,\ldots ,b_k=z)$ be the unique feasible ordering of $P_z^{B+z}$ according to Theorem 1 and let $j\in \{1,\ldots ,k\}$ be the smallest index such that $b_j\notin A$ and denote $u=b_j$. Then since $\{b_1,\ldots ,b_j\},A,P_z^{B+z}\in {\mathcal {F}}$ and $\{b_1,\ldots ,b_j\},A\subseteq P_z^{B+z}$, we have $A+u\in {\mathcal {F}}$ by the local union property. Therefore $w(A+x)\le w(A+u)$, which implies $f(P_x^{A+x})\le f(P_u^{A+u})$ by $w(A+i)=w(A)+f(P_i^{A+i})$ for $i\in \{x,u\}$. Furthermore, $P_u^{B+z}=\{b_1,\ldots ,b_j\}$ by Theorem 1, which implies $f(P_u^{B+z})\le f(P_z^{B+z})$ by property (i). Noting that $P_x^{A+x}=P_x^{B+x}$ and $P_u^{A+u}=P_u^{B+z}$ are obvious by $A+x,A+u\in {\mathcal {F}}$, these together imply $f(P_x^{B+x})\le f(P_z^{B+z})$.

First assume $B\in {\mathcal {F}}$. Then $B=\varDelta (B)$ and hence $w(B+i)=w(\varDelta (B))+f(P_i^{B+i})$ follows from (6) for $i\in \{x,z\}$. Therefore $w(B+x)\le w(B+z)$ follows immediately from $f(P_x^{B+x})\le f(P_z^{B+z})$.

Now assume $B\notin {\mathcal {F}}$. Then by Lemma 4 we have $P_e^{B+x}\cap (B-\varDelta (B))=P_e^{B+z}\cap (B-\varDelta (B))$ for every $e\in B-\varDelta (B)$, denote this common set by $H_e$. Fix an $e\in B-\varDelta (B)$ and an $i\in \{x,z\}$ and let the unique ordering of $P_e^{B+i}$ be $(a_1,a_2,\ldots ,a_k)$ according to Theorem 1. Then $i\in P_e^{B+i}$ is again obvious by the definition of $\varDelta (B)$, so let $i=a_j$ for some $1\le j\le k$. Then $\{a_1,\ldots ,a_j\}=P_i^{B+i}$ by Theorem 1. Since $\varDelta (B)+i\in {\mathcal {F}}$ is again true as in the proof of Lemma 4, $P_i^{B+i}\subseteq \varDelta (B)+i$ by the definition of a path. Furthermore, if $y=a_t$ for some $j<t\le k$ then $i\in P_y^{B+i}$ by Theorem 1 and hence $y\in \varDelta (B)$ is impossible because that would imply $i\in P_y^{B+i}\subseteq \varDelta (B)$ by $\varDelta (B)\in {\mathcal {F}}$. All these together imply $P_e^{B+i}=P_i^{B+i}\cup H_e$. Since $f(P_x^{B+x})\le f(P_z^{B+z})$ was shown above, this implies $f(P_e^{B+x})\le f(P_e^{B+z})$ by property (ii) for every $e\in B-\varDelta (B)$. This completes the proof by (6).$\square$

Since $f(P)=c(P)$ obviously fulfills the monotonicity constraints (i) and (ii) for all non-negative valued weight functions $c:S\rightarrow {\mathbb {R}}^+$, Theorem 16 is indeed a generalization Theorem 3. Another application of Theorem 16 is to set $f(P)=\max \{c(x):x\in P\}$ for a weight function $c:S\rightarrow {\mathbb {R}}$, which again obviously fulfills conditions (i) and (ii). Theorem 16 implies the fact, which was also proved in [2], that in local forest greedoids the greedy algorithm finds a minimum base with respect to w in this case. If applied to the branching greedoid (and for maximizing $(-w)$), this implies the well-known fact that the corresponding modification of Dijkstra’s algorithm solves the widest path problem (also known as the bottleneck shortest path problem) in graphs.