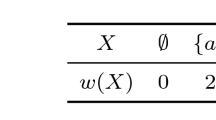Sufficient conditions for the optimality of the greedy algorithm in greedoids

Abstract

Greedy algorithms are among the most elementary ones in theoretical computer science and understanding the conditions under which they yield an optimum solution is a widely studied problem. Greedoids were introduced by Korte and Lovász at the beginning of the 1980s as a generalization of matroids. One of the basic motivations of the notion was to extend the theoretical background behind greedy algorithms beyond the well-known results on matroids. Indeed, many well-known algorithms of a greedy nature that cannot be interpreted in a matroid-theoretical context are special cases of the greedy algorithm on greedoids. Although this algorithm turns out to be optimal in surprisingly many cases, no general theorem is known that explains this phenomenon in all these cases. Furthermore, certain claims regarding this question that were made in the original works of Korte and Lovász turned out to be false only most recently. The aim of this paper is to revisit and straighten out this question: we summarize recent progress and we also prove new results in this field. In particular, we generalize a result of Korte and Lovász and thus we obtain a sufficient condition for the optimality of the greedy algorithm that covers a much wider range of known applications than the original one.

1 Introduction

“Greed is a sin against God, just as all mortal sins, in as much as man condemns things eternal for the sake of temporal things”, wrote Thomas Aquinas in the 13th century. However, when it comes to algorithm design, being greedy is not necessarily a mortal sin: treasuring temporal things by always choosing a locally best option might lead to an eternal value, a globally optimal solution. The first one to observe this was probably Borůvka, who discovered a variant of Kruskal’s algorithm for finding a minimum weight spanning tree as early as 1926.

Later on the theory of matroids evolved which provided a general framework for certain greedy algorithms and the classic result of Edmonds and Rado asserted that these algorithms are always optimal if the objective function is linear. However, at the beginning of the 1980s Korte and Lovász observed that in the proofs of various results on matroids subclusiveness (that is, the property that all subsets of independent sets are also independent) is not needed; hence they defined greedoids by relaxing this condition (see Definition 1).

The term greedoid comes from “a synthetic blending of the words greedy and matroid” (Korte et al. 1991) which indicates that one of the basic motivations of Korte and Lovász when introducing this notion was to extend the theoretical background behind greedy algorithms beyond the well-known results on matroids. Although many well-known algorithms of a greedy nature are special cases of the greedy algorithm defined on greedoids (see Sect. 3), no general result is known that would imply the optimality of all these algorithms. Instead, various sufficient conditions on the optimality of the greedy algorithm are known that together cover some of these applications and individual proofs exist for the rest of the cases. Even more surprisingly, it turned out that Korte and Lovász overlooked a detail in Korte and Lovász (1984a) and Korte et al. (1991) that led them to some false claims concerning this question (see Sect. 3 for the details). To the best of our knowledge, these mistakes remained hidden for more than three decades until they were pointed out and corrections were proposed in Szeszlér (2021).

In this paper we survey some old and new results in this field and we point out faulty claims that have been present in the literature. (However, all the previous results mentioned in the present paper that are claimed as numbered and cited theorems are obviously valid and true results.) We also give new sufficient conditions on the optimality of the greedy algorithm in greedoids that generalize a result of Korte and Lovász (1984a); see Theorems 6 and 7. For showing these, we will refine and extend some techniques introduced in Korte and Lovász (1984a); see Lemma 2. The sufficient conditions presented in the paper will be strong enough to cover important examples beyond the ones covered by previously known results.

This paper is meant to be self-contained in the sense that no preliminary knowledge on greedoids is assumed. The structure of this paper is as follows. We summarize the necessary background on greedoids in Sect. 2. In Sect. 3 the greedy algorithm on greedoids is defined, a number of known examples are shown where it is optimal and results on its optimality are summarized. Finally, Section 4 is dedicated to the case where the value of the objective function may depend on the order of the elements chosen and new results regarding this case are presented. This section contains all the new results of the paper that are positive results.

A preliminary version of this paper appeared as an extended abstract of the 11th Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications (Szeszlér 2019). Here we give a more in-depth treatment of the topic, we provide some more new results and we fill in the gaps of the proof sketches of Szeszlér (2019).

Since the optimality of the greedy algorithm is one of the central motivations behind the theory of greedoids, straightening out this question by pointing out long-hidden mistakes and limitations of previous results and providing more powerful ones is also meant to pump new steam into this field.

2 Preliminaries on greedoids

All the definitions and claims in this section are taken from Korte et al. (1991).

Definition 1

A greedoid $G=(S,{\mathscr {F}})$ is a pair consisting of a finite ground set S and a collection of its subsets ${\mathscr {F}}\subseteq 2^S$ such that the following properties are fulfilled:

• (2.1) $\emptyset \in {\mathscr {F}}$

• (2.2) If $X,Y\in {\mathscr {F}}$ and $|X|<|Y|$ then there exists a $y\in Y-X$ such that $X+y\in {\mathscr {F}}$.

Members of ${\mathscr {F}}$ are called feasible sets.

Property (2.2) immediately implies that every $X\in {\mathscr {F}}$ has a feasible ordering: the sequence $x_1 x_2\ldots x_k$ is a feasible ordering of X if $\{x_1,x_2,\ldots ,x_i\} \in {\mathscr {F}}$ holds for every $1\le i\le k$ and $X=\{x_1,x_2,\ldots ,x_k\}$. The existence of a feasible ordering, in turn, implies the accessible property of greedoids: for every $\emptyset \ne X\in {\mathscr {F}}$ there exists an $x\in X$ such that $X-x\in {\mathscr {F}}$.

In this paper, the following notations will be (and have been) used: for a subset $X\subseteq S$ and an element $x\in S$ we will write $X+x$ and $X-x$ instead of $X\cup \{x\}$ and $X-\{x\}$, respectively. Furthermore, given any function $c:S\rightarrow {\mathbb {R}}$ and a subset $X\subseteq S$, c(X) will stand for $\sum \{c(x):x\in X\}$.

There are many known examples of greedoids beyond matroids and they arise in diverse areas of mathematics, see Korte et al. (1991) for an extensive list. For the purposes of this paper, branching greedoids will be of importance. Let $H=(V,E_u,E_d)$ be a mixed graph (that is, it can contain both directed and undirected edges) with V, $E_u$ and $E_d$ being its set of nodes, undirected edges and directed edges, respectively. Furthermore, let $r\in V$ be a given root node. The ground set of the branching greedoid on H is $E_u\cup E_d$ and ${\mathscr {F}}$ consists of all subsets $A\subseteq E_u\cup E_d$ such that disregarding the directions of the arcs in $A\cap E_d$, A is the edge set of a tree containing r and for every path P in A starting in r all edges of $P\cap E_d$ are directed away from r (meaning that the tail of such a directed edge is closer to r along P than its head). It is straightforward to check that $G=(E_u\cup E_d,{\mathscr {F}})$ is indeed a greedoid. G is called an undirected branching greedoid or a directed branching greedoid if H is an undirected graph (that is, $E_d=\emptyset$) or a directed graph (that is, $E_u=\emptyset$), respectively.

Another simple example is the poset greedoid. Let $P=(S,\le )$ be a partially ordered set. An ideal of P is a subset $I\subseteq S$ such that $x,y\in S$, $x\le y$ and $y\in I$ imply $x\in I$. Then it is easy to to check that if ${\mathscr {F}}$ consists of all the ideals of P then $G=(S,{\mathscr {F}})$ is a greedoid. The same can also be expressed in a graph-theoretical setting: if $H=(S,D)$ is an acyclic digraph and ${\mathscr {F}}$ consists of all subsets of S with in-degree zero then $G=(S,{\mathscr {F}})$ is the poset greedoid induced by the poset in which $x\le y$ holds if and only if y is reachable from x via a directed path.

Most of the known results on greedoids are about special classes of greedoids, that is, further structural properties are assumed. Among these, the following will be of relevance in this paper:

• (2.3) Local Union Property:

  if $A,B,C\in {\mathscr {F}}$ and $A\cup B\subseteq C$ then $A\cup B\in {\mathscr {F}}$

• (2.4) Local Intersection Property:

  if $A,B,C\in {\mathscr {F}}$ and $A\cup B\subseteq C$ then $A\cap B\in {\mathscr {F}}$

• (2.5) Local Forest Property:

  if $A, A+x, A+y, A\cup \{x,y\}, A\cup \{x,y,z\}\in {\mathscr {F}}$ then either $A\cup \{x,z\}\in {\mathscr {F}}$ or $A\cup \{y,z\}\in {\mathscr {F}}$

A greedoid $G=(S,{\mathscr {F}})$ is called an interval greedoid if it fulfills property (2.3); G is a local poset greedoid if it fulfills (2.3) and (2.4); finally, G is a local forest greedoid if it fulfills (2.3), (2.4) and (2.5).

Obviously, all matroids are local forest greedoids and it is easy to check that so are branching greedoids. Poset greedoids are local poset greedoids (in fact, they have the much stronger property that $A,B\in {\mathscr {F}}$ implies $A\cup B\in {\mathscr {F}}$ and $A\cap B\in {\mathscr {F}}$), but they are not necessarily local forest greedoids; for example, the poset greedoid on $S=\{x,y,z\}$ induced by the digraph with edges (x, z) and (y, z) clearly violates (2.5) with $A=\emptyset$.

There is an alternative way to define greedoids in terms of languages which is of utmost importance. Denote by $S^*$ the set of all finite sequences $x_1x_2\ldots x_k$ of the finite ground set S. Elements of S and $S^*$ are referred to as letters and words, respectively and a set ${\mathscr {L}}\subseteq S^*$ is referred to as a language. The empty word is denoted by $\emptyset$. The set of letters of a word $\alpha$ is denoted by $\tilde{\alpha }$ and the length of a word $\alpha$ is denoted by $|\alpha |$. ${\mathscr {L}}$ is a simple language if no letter of S appears more than once in any word of ${\mathscr {L}}$. The concatenation of two words $\alpha ,\beta \in S^*$ is simply denoted by $\alpha \beta$ and $\alpha$ is called a prefix of $\alpha \beta$. Single letter words are identified with the corresponding element of S (and hence $\alpha x$ denotes the word $\alpha$ followed by the letter x).

Definition 2

Let S be a finite ground set and ${\mathscr {L}}$ a simple language on S. Then $G=(S,{\mathscr {L}})$ is a greedoid language if the following properties hold:

• (2.6) $\emptyset \in {\mathscr {L}}$

• (2.7) $\alpha \beta \in {\mathscr {L}}$ implies $\alpha \in {\mathscr {L}}$

• (2.8) If $\alpha ,\beta \in {\mathscr {L}}$ and $|\alpha |>|\beta |$ then there exists an $x\in \tilde{\alpha }$ such that $\beta x\in {\mathscr {L}}$.

Obviously, the above definition can be viewed as a language equivalent of the definition of matroids. On the other hand, there is a one-to-one correspondence between greedoids and greedoid languages. For a greedoid $G=(S,{\mathscr {F}})$ let the language ${\mathscr {L}}({\mathscr {F}})$ consist of all feasible orderings of all feasible sets of ${\mathscr {F}}$. Conversely, for a greedoid language $G=(S,{\mathscr {L}})$ let ${\mathscr {F}}({\mathscr {L}}) =\{\tilde{\alpha }:\alpha \in {\mathscr {L}}\}$. Then it is easy to show (see (Korte et al. 1991, Theorem IV.1.2)) that for every greedoid $(S,{\mathscr {F}})$, $(S,{\mathscr {L}}({\mathscr {F}}))$ is a greedoid language and conversely, for every greedoid language $(S,{\mathscr {L}})$, $(S,{\mathscr {F}}({\mathscr {L}}))$ is a greedoid; moreover, in both cases we get the unique greedoid language and greedoid, respectively, for which ${\mathscr {F}}({\mathscr {L}}({\mathscr {F}}))={\mathscr {F}}$ and ${\mathscr {L}}({\mathscr {F}}({\mathscr {L}}))={\mathscr {L}}$ holds. This relation between greedoids and greedoid languages justifies the above claim that greedoid languages can be thought of as an alternative way to define greedoids.

Some of the well-known terminology on matroids can be applied to greedoids without any modification. In particular, a base of a greedoid $G=(S,{\mathscr {F}})$ is a feasible set $X\in {\mathscr {F}}$ of maximum size. This, by property (2.2), is equivalent to saying that $X+y\notin {\mathscr {F}}$ for every $y\in S-X$. Analogously, a basic word of a greedoid language $G=(S,{\mathscr {L}})$ is a word $\alpha \in {\mathscr {L}}$ of maximum length; or, equivalently by property (2.8), a word $\alpha \in {\mathscr {L}}$ for which $\alpha x\notin {\mathscr {L}}$ for every $x\in S-\tilde{\alpha }$. Analogously to the case of matroids, all bases or basic words in every greedoid or greedoid language, respectively, are obviously of equal size. Both the set of bases and the set of basic words will be denoted by ${\mathscr {B}}$.

Minors of greedoids can also be defined almost identically to those of matroids. If $G=(S,{\mathscr {F}})$ is a greedoid and $X\subseteq S$ is an arbitrary subset then the deletion of X yields the greedoid $G\setminus X=(S-X,{\mathscr {F}}\setminus X)$, where ${\mathscr {F}}\setminus X=\{Y\subseteq S-X:Y\in {\mathscr {F}}\}$. If $X\in {\mathscr {F}}$ is a feasible set then the contraction of X yields the greedoid $G/X=(S-X,{\mathscr {F}}/X)$, where ${\mathscr {F}}/X=\{ Y\subseteq S-X: Y\cup X\in {\mathscr {F}}\}$. Then a minor of G is obtained by applying these two operations on G. It is straightforward to check that minors are indeed greedoids. (Note, however, that G/X was only defined here in the $X\in {\mathscr {F}}$ case. The definition could be extended to a wider class of subsets, but unless some further structural properties are imposed on the greedoid, not to arbitrary ones. See (Korte et al. 1991, Chapter V.) for the details.)

3 The greedy algorithm on greedoids

Let $G=(S,{\mathscr {L}})$ be a greedoid language and $w:{\mathscr {L}}\rightarrow {\mathbb {R}}$ an objective function. Assume that we are interested in finding a basic word $\beta \in {\mathscr {B}}$ that minimizes $w(\beta )$ across all basic words of G.

For every $\alpha \in {\mathscr {L}}$ the set of continuations of $\alpha$ is defined as $\Gamma (\alpha )=\{x\in S-\tilde{\alpha }: \alpha x\in {\mathscr {L}}\}$. Then the greedoid greedy algorithm for the above problem can be described as follows Korte and Lovász (1984a); Korte et al. (1991):

Step 1.:

Set $\alpha =\emptyset$.

Step 2.:

If $\Gamma (\alpha )=\emptyset$ then stop and output $\alpha$.

Step 3.:

Choose an $x\in \Gamma (\alpha )$ such that $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$.

Step 4.:

Replace $\alpha$ by $\alpha x$ and continue at Step 2.

Obviously, if the task is to maximize $w(\beta )$ across all basic words then, since this is equivalent to minimizing $-w(\beta )$, $w(\alpha x)\ge w(\alpha y)$ is to be required for every $y\in \Gamma (\alpha )$ in Step 3.

3.1 Examples of the greedoid greedy algorithm

Many of the well-known, elementary algorithms in graph theory fall under the above framework. In this subsection, we list all the known examples from the literature.

Example 1

(Matroid greedy algorithm) If M is a matroid and w is linear (meaning that $w(A)=c(A)$ for some weight function $c:S\rightarrow {\mathbb {R}}$) then the greedoid greedy algorithm is nothing but the well-known greedy algorithm on matroids. In particular, we get Kruskal’s algorithm for finding a minimum weight spanning tree in case of the cycle matroid.

Example 2

(Prim’s algorithm) Let G be the branching greedoid of the undirected, connected graph H and w a linear objective function. Then the greedoid greedy algorithm translates to Prim’s well-known algorithm for finding a minimum weight spanning tree. (Note that this algorithm cannot be interpreted in a matroid-theoretical context.)

Example 3

(Dijkstra’s shortest path algorithm) Let G be the branching greedoid of the mixed graph $H=(V,E_u,E_d)$ with root node r and let $c:E_u\cup E_d\rightarrow {\mathbb {R}}^+$ be a non-negative valued weight function. For every feasible set A and $e\in A$ let $P_e^A$ denote the unique path in A starting at r and ending in e. Then let $w(A)=\sum \{c(P_e^A):e\in A\}$ for every $A\in {\mathscr {F}}$. It was observed in Korte and Lovász (1984a) that in this case the greedoid greedy algorithm for minimizing w(B) translates to Dijkstra’s well-known shortest path algorithm. Indeed, Dijkstra’s algorithm constructs a spanning tree on the set of nodes reachable from r such that the unique path from r to every other node in this tree is a shortest path and hence it clearly minimizes w.

Example 4

(Dijkstra’s widest path algorithm) Given a graph with weights on its edges, the widest path problem is the problem of finding a path between two given vertices that maximizes the weight of the minimum-weight edge on the path. It is well-known (and it seems to belong to graph theory folklore) that a trivial modification of Dijkstra’s shortest path algorithm solves this problem too. This is again a special case of the greedoid greedy algorithm: let $c:E_u\cup E_d\rightarrow {\mathbb {R}}$ be a (real valued) weight function on the edge set of the mixed graph $H=(V,E_u,E_d)$ with root node r, let $\mu (P_e^A)=\min \{c(z):z\in P_e^A\}$ for every path of H starting at r and let $w(A)=\sum \{\mu (P_e^A):e\in A\}$ for every feasible set A of the branching greedoid of H. Then, analogously to the above example, the greedoid greedy algorithm for maximizing w(B) translates to the above mentioned modified version of Dijkstra’s algorithm (and hence it is optimal) and it constructs a spanning tree on the set of nodes reachable from r such that the unique path from r to every other node in this tree is a widest path.

Example 5

(Lawler’s single machine scheduling algorithm) Let $D=(V,A)$ be an acyclic digraph whose vertices represent jobs to be scheduled on a single machine (with no interruptions) and arcs of D represent precedence constraints to be respected by the schedule. Furthermore, a processing time $a(v)\in {\mathbb {N}}$ is also given for every job $v\in V$. Finally, a monotone non-decreasing cost function $c_v:\{0,\ldots ,N\} \rightarrow {\mathbb {R}}$ is also given for every job $v\in V$, where $N=\sum _{v\in V}a(v)$ such that $c_v(t)$ represents the cost incurred by job v if it is completed at time t. The problem is to find a schedule (that is, a topological ordering of the jobs with respect to D) such that the maximum of the costs incurred is minimized. Lawler (1973) gave a simple greedy algorithm for this problem: it builds up the schedule in a reverse order always choosing out of the currently possible jobs one with the lowest cost at the current completion time. As it was pointed out in Korte and Lovász (1984a), this algorithm is also a special case of the greedoid greedy algorithm if the underlying greedoid is the poset greedoid induced by the digraph obtained from D by reversing all its arcs. (More precisely: each legal running of Lawler’s algorithm is a legal running of the greedoid greedy algorithm, but not vice versa. However, the optimality of both is easily proved by the method of Lawler (1973).)

3.2 Korte and Lovász’s theorem

Although the greedy algorithm is optimal in the above examples, it is obviously not to be expected that this is true in general. The first sufficient condition on the optimality of the greedy algorithm was given in Korte and Lovász (1984a).

Theorem 1

(Korte and Lovász 1984a, (Korte et al. 1991, Theorem XI.1.3)) Let $G=(S,{\mathscr {L}})$ be a greedoid language and $w:{\mathscr {L}}\rightarrow {\mathbb {R}}$ an objective function. Assume that for every $\alpha x\in {\mathscr {L}}$ such that $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$ the following conditions hold:

• (3.1) $w(\alpha \beta x\gamma )\le w(\alpha \beta z\gamma )$, if $\alpha \beta x\gamma ,\alpha \beta z\gamma \in {\mathscr {L}}$;

• (3.2) $w(\alpha x\beta z\gamma )\le w(\alpha z\beta x\gamma )$, if $\alpha x\beta z\gamma ,\alpha z\beta x\gamma \in {\mathscr {L}}$.

Then the greedoid greedy algorithm finds a basic word of minimum weight with respect to w.

Both properties required by the above theorem can be as regarded intuitive. (3.1) says that if x is an optimal choice at a certain iteration then it will be an optimal choice at any later iteration, regardless of how the process is completed. Similarly, (3.2) says that if x is optimal at a certain point then it cannot be worse to choose x at this point and another letter z later than vice versa. Obviously, if the objective function w is order-independent (meaning that $w(\alpha )=w(\beta )$ whenever $\tilde{\alpha }=\tilde{\beta }$) then (3.2) is trivially fulfilled; this holds for Examples 1-4 above, but not for Example 5.

Unfortunately, out of the above listed Examples 1-5 it is only Example 1 that Theorem 1 completely covers (in the sense that it implies the optimality of the greedy algorithm). Indeed, it is easy to verify that the conditions of Theorem 1 are fulfilled by linear objective functions on matroids and hence Theorem 1 implies the Edmonds-Rado theorem. However, this verification strongly relies on the subclusiveness property of matroids and therefore it is not a surprise that (3.1) is violated in case of Example 2 (as shown by trivial examples).

In case of Examples 3 and 4 it is easy to verify that the conditions of Theorem 1 are fulfilled if the underlying graph is directed (that is, the greedoid is a directed branching greedoid). However, although the same is also claimed for Example 3 in the undirected case in (Korte et al. 1991, page 156), condition (3.1) is not necessarily fulfilled either for Example 3 or for 4 in case of undirected graphs (that is, undirected branching greedoids) as shown by the following simple examples. In case of Example 3, consider the graph of Figure 1 with the following edge weights: $c(x)=1$, $c(z)=2$, $c(a)=0$ and $c(b)=4$. Then although x is the “best continuation” of $\emptyset$ (that is, the assumption of Theorem 1 holds for $\alpha =\emptyset$ and the edge x), $11=w(xba)>w(zba)=10$ hence w violates (3.1) with $\alpha =\beta =\emptyset$ and $\gamma =ba$. (Indeed, $w(xba)=c(P^A_x)+c(P^A_b)+c(P^A_a)=1+(1+4)+(1+4+0)=11$, where $A=\{x,b,a\}$ and calculating w(zba) is analogous.) Similarly, in case of Example 4 consider the following edge weights on the same graph: $c(x)=4$, $c(z)=3$, $c(a)=3$ and $c(b)=1$. Then $(-w)$ violates (3.1) since again x is the best continuation of $\emptyset$, but $6=w(xba)<w(zba)=7$.

Fig. 1

The optimality of Dijkstra’s shortest path and widest past algorithms does not follow from Theorem 1 for undirected graphs

Finally, regarding Example 5 the following was written in Korte and Lovász (1984a): “For this problem Lawler [1973] developed a greedy algorithm with a special optimality proof. It is a direct corollary of theorem 4.1.” (Here “theorem 4.1” refers to Theorem 1.) As opposed to this, while conditions (3.1) and (3.2) are fulfilled in the special case where all processing times a(v) are equal (and hence the cost incurred by a job only depends on its position in the seqence and not on the processing times of previously completed jobs), the same is not true in the general case. Therefore it is only this special case that Theorem 1 covers. To simplify the description of a counterexample to show that the general case is not covered by Theorem 1, we define the “reverse-Lawler scheduling problem”: it is identical to the one described in Example 5 with the difference being that the cost functions $c_v$ are monotone non-increasing and $c_v(t)$ represents the cost incurred by job v if it is started at time t. Obviously, this problem is equivalent to the original one by reversing all possible schedules, however, in this version the basic words of the corresponding poset greedoid are identical to the possible schedules (and not the reverses of those). Then consider the following example: let $S=\{x,y,z\}$, let D be the empty graph (meaning that there are no precedence constraints), let $a(x)=a(y)=1$ and $a(z)=2$, and finally let the cost functions $c_v$ be as in the table below.

t	0	1	2	3	4
$c_x(t)$	0	0	0	0	0
$c_y(t)$	2	2	1	0	0
$c_z(t)$	1	0	0	0	0

Then x is the best continuation of $\emptyset$, but $w(xy)=\max \{0,2\}=2$ and $w(zy)=\max \{1,1\}=1$ which shows that (3.1) is violated with $\alpha =\beta =\emptyset$ and $\gamma =y$.

3.3 A Long-hidden mistake

As it was the case in Examples 1–4, in many applications the objective function only depends on the feasible sets themselves and not on their orderings; in other words, it is a greedoid $G=(S,{\mathscr {F}})$ that the objective function $w:{\mathscr {F}}\rightarrow {\mathbb {R}}$ is defined on. Therefore one would want to formulate the corresponding corollary of Theorem 1. As it was mentioned above, (3.2) is automatically fulfilled in these cases, however, it is not at all straightforward to specialize (3.1) to order-independent objective functions. Both in Korte and Lovász (1984a) and (Korte et al. 1991, Chapter XI) it is claimed that (3.1) is equivalent to the following for objective functions $w:{\mathscr {F}}\rightarrow {\mathbb {R}}$:

• (3.3) If $A,B,A+x,B+x\in {\mathscr {F}}$ hold for some sets $A\subseteq B$ and $x\in S-B$, and $w(A+x)\le w(A+y)$ for every $y\in \Gamma (A)$ then $w(B+x)\le w(B+z)$ for every $z\in \Gamma (B)$.

However, as it was pointed out recently in Szeszlér (2021), this reformulation clearly disregards the fact that the set $\tilde{\alpha }\cup \tilde{\beta }\cup \tilde{\gamma }$, that should correspond from (3.1) to B in (3.3), need not be a feasible set. In actual fact, (3.3) does not imply (3.1), nor does it guarantee the optimality of the greedy algorithm as shown by the following trivial example: consider the undirected branching greedoid of the graph of Figure 2 with the following objective function w.

X	$\emptyset$	$\{a\}$	$\{b\}$	$\{a,c\}$	$\{b,c\}$
w(X)	0	3	4	2	1

It is easy to check that (3.3) is fulfilled, however, the greedy algorithm gives $\{a,c\}$ instead of $\{b,c\}$. On the other hand, (3.1) is clearly violated with $\alpha =\beta =\emptyset$, $\gamma =c$, $x=a$ and $z=b$: a is the best continuation of $\emptyset$ but $w(ac)>w(bc)$.

Fig. 2

Property (3.3) does not imply property (3.1) for order-independent objective functions, nor does it guarantee the optimality of the greedy algorithm

Most surprisingly, the above mistake was already present in the very first publication of Korte and Lovász on greedoids, a five-page-long proceedings paper from 1981 (Korte and Lovász 1981).

We mention that although it might look tempting to correct (3.3) by removing ${B\in {\mathscr {F}}}$ from its assumptions, that would not work either: although the obtained property would imply (3.1), but not vice versa. Furthermore, although this modification of (3.3) would obviously imply the optimality of the greedy algorithm (since it implies (3.1)), but it would be useless in all the above listed examples.

Unfortunately, as innocuous as this mistake might look, it led the authors of Korte et al. (1991) to a further false claim regarding Example 3. One can generalize the objective functions of Examples 3 and 4 to local poset greedoids by appropriately defining paths: if $G=(S,{\mathscr {F}})$ is a local poset greedoid, $A\in {\mathscr {F}}$ and $x\in A$ then the x-path in A, denoted by $P_x^A$, is the unique feasible set in A containing x such that no proper feasible subset of $P_x^A$ contains x. Uniqueness of $P_x^A$ follows directly from property (2.4): $P_x^A$ is the intersection of all feasible sets in A containing x. Clearly, in case of branching greedoids this notion translates to paths starting in the root node r that are directed in the sense that all directed edges in the path are directed away from r. Then, given a local poset greedoid $G=(S,{\mathscr {F}})$ and a non-negative weighting $c:S\rightarrow {\mathbb {R}}^+$ on its ground set, the objective functions of Examples 3 and 4 become meaningful. It is claimed in (Korte et al. 1991, page 156) that the greedy algorithm finds a minimum base with respect to the objective function corresponding to Example 3 in all local poset greedoids. The following simple counterexample to this claim was given in Szeszlér (2021): let $S=\{x,y,z,u\}$, ${\mathscr {F}}=\left\{ \emptyset , \{x\}, \{y\}, \{x,y\}, \{x,u\}, \{x,y,z\}, \{x,z,u\}\right\}$ and $c(x)=3$, $c(y)=2$, $c(z)=c(u)=0$. Then it is easy to check that $(S,{\mathscr {F}})$ is a local poset greedoid, but since the greedy algorithm starts with choosing y, it terminates with $\{x,y,z\}$ which is not minimum as $w(\{x,y,z\})=10$ and $w(\{x,z,u\})=9$.

3.4 Further results on the greedoid greedy algorithm

Although the above mentioned claim is not true for local poset greedoids, it is true for local forest greedoids as shown in Boyd (1988).

Theorem 2

(Boyd (1988)) Let $G=(S,{\mathscr {F}})$ be a local forest greedoid and $c:S\rightarrow {\mathbb {R}}^+$ a non-negative valued weight function. Then the greedy algorithm finds an optimum base with respect to the objective functions corresponding to Examples 3 and 4.

Since both undirected and directed branching greedoids are local forest greedoids, the above theorem implies the optimality of Dijkstra’s shortest path and widest path algorithms both for undirected and directed graphs (and even mixed graphs). The claim of the above theorem regarding the objective function corresponding to Example 3 played a central role in the proof of a recent result given in Szeszlér (2021) that generalized an equivalent formulation of Edmonds’ classic matroid polytope theorem to local forest greedoids. The following generalization of Theorem 2 was also given in Szeszlér (2021) (with a much shorter proof than the rather technical one of Boyd (1988)).

Theorem 3

(Szeszlér 2021) Let $G=(S,{\mathscr {F}})$ be a local forest greedoid, ${\mathscr {P}}$ its set of paths and $f:{\mathscr {P}}\rightarrow {\mathbb {R}}$ a function that satisfies the following monotonicity constraints:

• (i) if $A,B\in {\mathscr {P}}$ and $A\subseteq B$ then $f(A)\le f(B)$;

• (ii) if $A,B,A\cup C,B\cup C\in {\mathscr {P}}$ and $f(A)\le f(B)$ then $f(A\cup C)\le f(B\cup C)$.

Finally, let $w(A)=\sum \{f(P_x):x\in A\}$ for every $A\in {\mathscr {F}}$. Then the greedy algorithm gives a minimum base with respect to w.

It is trivial to verify that the objective functions corresponding to Examples 3 and 4 fulfill properties (i) and (ii) and hence this theorem indeed generalizes Theorem 2.

Optimality of the greedy algorithm for linear objective functions is a naturally arising question. While optimality holds for undirected branching greedoids (cf. Example 2), it does not hold for directed ones. The following result of Korte and Lovász provides a theoretical background for this phenomenon.

Theorem 4

(Korte and Lovász 1984b, (Korte et al. 1991, Theorem XI.2.2)) Let $G=(S,{\mathscr {F}})$ be a greedoid. Then the greedoid greedy algorithm finds a minimum weight base for every linear objective function $c:S\rightarrow {\mathbb {R}}$ if and only if the following condition holds:

• (3.4) If $A,A+x\in {\mathscr {F}}$, $B\in {\mathscr {B}}$ hold for some sets $A\subseteq B$ and $x\in S-B$ then there exists a $y\in B-A$ such that $A+y\in {\mathscr {F}}$ and $B-y+x\in {\mathscr {B}}$.

It is easy to verify that (3.4) is fulfilled by undirected branching greedoids and hence Theorem 4 implies the optimality of the greedy algorithm for Example 2 above. The following generalization of the sufficiency of (3.4) to arbitrary order-independent objective functions was given in Szeszlér (2021) (by adapting the proof of Theorem 4).

Theorem 5

(Szeszlér 2021) Let $G=(S,{\mathscr {F}})$ be a greedoid and $w:{\mathscr {F}}\rightarrow {\mathbb {R}}$ an objective function that fulfills the following property:

• (3.5) If for some $A\subseteq B$, $A,A+x\in {\mathscr {F}}$, $B\in {\mathscr {B}}$ and $x\in S-B$ it holds that $w(A+x)\le w(A+u)$ for every $u\in \Gamma (A)$ then there exists a $y\in B-A$ such that $B-y+x\in {\mathscr {B}}$ and $w(B-y+x)\le w(B)$.

Then the greedy algorithm gives a minimum base with respect to w.

The above theorem will follow from Theorem 6 below. A certain necessity of (3.5) was also proved in Szeszlér (2021): if (3.5) is violated then the greedy algorithm can give a suboptimal base in a minor of the greedoid; see Szeszlér (2021) for the details. It can also be easily verified that Theorem 5 implies the optimality of the greedy algorithm in all Examples 1-4 above. Furthermore, Theorem 5 also implies Theorem 3 in the sense that the latter was proved in Szeszlér (2021) by relying on the former one; however, proving (3.5) from the conditions of Theorem 3 is non-trivial.

4 Order-dependent objective functions

In this section, we aim at generalizing Theorem 1: we will give sufficient conditions on the optimality of the greedoid greedy algorithm for (possibly) order-dependent objective functions that are weaker than requiring (3.1) and (3.2) and which, besides other examples, will completely cover Example 5 above. We start with the following theorem.

Theorem 6

Let $G=(S,{\mathscr {L}})$ be a greedoid language and $w:{\mathscr {L}}\rightarrow {\mathbb {R}}$ an objective function. Assume that the following condition holds:

• (4.1) If $\alpha x\in {\mathscr {L}}$ such that $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$ and $\gamma =\alpha z\beta \in {\mathscr {B}}$ is a basic word then there exists a basic word $\delta =\alpha x\epsilon \in {\mathscr {B}}$ such that $w(\delta )\le w(\gamma )$.

Then the greedoid greedy algorithm finds a basic word of minimum weight with respect to w.

Proof

Assume by way of contradiction that the greedy algorithm gives the basic word $\omega \in {\mathscr {B}}$ that is not optimal with respect to w. Let $\gamma \in {\mathscr {B}}$ be a minimum weight basic word with respect to w and choose $\gamma$ such that its common prefix with $\omega$ is the longest possible among all optimal basic words. Let this common prefix be $\alpha$ and let $\omega =\alpha x\omega '$ and $\gamma =\alpha z\beta$. Then $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$ follows from the operation of the greedy algorithm. Therefore by (4.1) there exists the basic word $\delta =\alpha x\epsilon \in {\mathscr {B}}$ such that $w(\delta )\le w(\gamma )$. Hence $\delta$ is also a minimum weight basic word with respect to w, but it has a longer common prefix with $\omega$ than $\gamma$ contradicting the choice of $\gamma$. $\square$

It is straightforward to see that Theorem 6 implies Theorem 5; indeed, if (3.5) holds then, after applying it on $A=\tilde{\alpha }$ and $B=\tilde{\beta }$, $\alpha x$ can be repeatedly augmented to get a feasible ordering of $B-y+x$ thus providing the basic word $\delta$ required by (4.1). Therefore Theorem 6 covers Examples 1-4 and it will follow from the results below that it also covers Example 5 and it generalizes Theorem 1. On the other hand, an important question presents itself regarding Theorem 6: is the problem of deciding if property (4.1) holds in co-NP? To avoid meaningless or “unfair” theorems it would feel natural to require that the answer is yes – as it is obviously the case for Theorems 1, 4 and 5. However, upon first looking at property (4.1) it might seem that checking the non-existence of a suitable $\delta$ according to (4.1) for a given $\alpha x$ and $\gamma$ might require checking all basic words that start with $\alpha x$ which could be impossible in polynomial time. The following proposition shows that in actual fact the opposite is true.

Proposition 1

Assume that a greedoid language $G=(S,{\mathscr {L}})$ together with an objective function $w:{\mathscr {L}}\rightarrow {\mathbb {R}}$ are given by a polynomial time oracle that decides if $\alpha \in {\mathscr {L}}$ holds for every word $\alpha \in S^*$ and if it does then it gives the value of $w(\alpha )$. Then deciding if property (4.1) holds is in co-NP.

Proof

If $\alpha x\in {\mathscr {L}}$ and $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$ then we say (in accordance with the above) that x is a best continuation of $\alpha$. Let $x\in \tilde{\alpha }$ for a word $\alpha \in {\mathscr {L}}$; call $\alpha$ a greedy word from x if x and every letter y of $\alpha$ following x is a best continuation of the prefix of $\alpha$ up to y.

We claim that property (4.1) is violated if and only if

• (4.2) there exist the basic words $\alpha x\epsilon , \alpha z\beta \in {\mathscr {B}}$ such that $\alpha x\epsilon$ is a greedy word from x and $w(\alpha x\epsilon )>w(\alpha z\beta )$.

This claim will obviously settle the proof since a pair of bases $(\alpha x\epsilon ,\alpha z\beta )$ corresponding to (4.2) will be a suitable certificate for showing that (4.1) is violated. Indeed, checking if a word $\delta$ is a base is possible by running the oracle on $\delta$ and all words of the form $\delta y$. Furthermore, checking if $\alpha x\epsilon$ is a greedy word from x is obviously possible by at most $|S|^2$ runnings of the oracle.

The only if direction of the above claim is obvious: if (4.1) is violated by an $\alpha x\in {\mathscr {L}}$ and a $\gamma =\alpha z\beta \in {\mathscr {B}}$ then $\alpha x$ can be extended to a basic word $\alpha x\epsilon \in {\mathscr {B}}$ that is greedy from x (by running the greedy algorithm starting from $\alpha x$); then, since (4.1) is violated, $w(\alpha x\epsilon )>w(\alpha z\beta )$ and hence (4.2) is fulfilled. To show the opposite direction, consider the contracted greedoid $G/\tilde{\alpha }$ with the objective function $\overline{w}(\beta )=w(\alpha \beta )$. Then both $x\epsilon$ and $z\beta$ are bases of $G/\tilde{\alpha }$, $x\epsilon$ is a possible output of the greedy algorithm with respect to $\overline{w}$, but it is not optimal since $\overline{w}(x\epsilon )>\overline{w} (z\beta )$. This, by Theorem 6, implies that property (4.1) is violated in $G/\tilde{\alpha }$ with respect to $\overline{w}$. This immediately implies that (4.1) is also violated in G with respect to w (by words starting with $\alpha$). $\square$

The claim shown in the above proof also implies a certain necessity of property (4.1): if it is violated then the greedy algorithm might give a suboptimal base in a minor of the greedoid.

Corollary 1

If property (4.1) is violated in the greedoid language $G=(S,{\mathscr {L}})$ with respect to the objective function $w:{\mathscr {L}}\rightarrow {\mathbb {R}}$ then there exists an $\alpha \in {\mathscr {L}}$ such that a legal running of the greedy algorithm in the minor $G/\tilde{\alpha }$ gives a basic word that is not of minimum weight with respect to the objective function $\overline{w}(\beta )=w(\alpha \beta )$.

Proof

Immediate from the above proved claim that (4.1) is violated if and only if (4.2) holds. $\square$

Although Proposition 1 and Corollary 1 both justify the relevance of Theorem 6, its usefulness in applications can still be questioned. Indeed, proving the existence of a $\delta =\alpha x\epsilon$ corresponding to property (4.1) could be non-trivial. For example, showing that Theorem 6 covers Example 5 or that it implies Theorem 1 (both of which will be proved below) is not at all straightforward. Moreover, Theorem 6 can be viewed as an order-dependent version of Theorem 5; however, while the applicability of the latter is aided greatly by the fact that it requires a minimal modification in the base B to obtain a better one (that is, $B-y+x$), the same does not hold for Theorem 6 where the basic word $\alpha x\epsilon$ can be far from $\alpha z\beta$. In what follows, we aim at claiming a theorem that will follow from Theorem 6 by replacing the basic word $\delta =\alpha x\beta$ by a specific nominee for its role. Therefore this theorem will be weaker than Theorem 6, but it will still have notable virtues: firstly, it will be strong enough to imply Theorem 1 and to cover all the examples listed in Sect. 3 except for Example 2; secondly, it will be easier to utilize in applications; and thirdly, it will be closer in spirit to Theorem 5 since the size of the symmetric difference of the set of letters of the two basic words it refers to will again be two. Claiming this theorem will take some preparation.

Definition 3

Let $G=(S,{\mathscr {L}})$ be a greedoid language, $\alpha \in {\mathscr {L}}$, $x\in S$, $y\in \tilde{\alpha }$ and $\alpha =\alpha _0y\alpha _1$. Then y is said to be an entry point of x in $\alpha$ if $\alpha _0x\in {\mathscr {L}}$.

Note that $x\in \tilde{\alpha }$ is possible and in that case x is an entry point of itself in $\alpha$ by (2.7) (but not necessarily the only one).

Definition 4

Let $G=(S,{\mathscr {L}})$ be a greedoid language, $\alpha \in {\mathscr {L}}$ and $x\in S$ that has at least one entry point in $\alpha$. Assume that $y_1,y_2,\ldots ,y_r\in \tilde{\alpha }$ is the list of all entry points of x in $\alpha$ appearing in this order and for every $1\le i\le r$ let $\alpha _x^{y_i}$ denote the word obtained from $\alpha$ by replacing $y_i$ with x and $y_j$ with $y_{j-1}$ for every $i<j\le r$. That is, if $\alpha =\alpha _0y_1\alpha _1y_2\alpha _2\ldots y_r\alpha _r$ then

$$\begin{aligned} \alpha _x^{y_i}=\alpha _0y_1\alpha _1\ldots y_{i-1}\alpha _{i-1}x \alpha _iy_i\alpha _{i+1}y_{i+1}\ldots y_{r-1}\alpha _r. \end{aligned}$$

Obviously, if $x\in \tilde{\alpha }$ then $x=y_r$ is the last entry point of itself in $\alpha$ and $\alpha _x^x=\alpha$. To demonstrate the above notion via an example, assume that $G=(S,{\mathscr {F}})$ is the undirected branching greedoid of the connected, simple graph H with root node r, $\alpha \in {\mathscr {B}}$ is a basic word and $e\notin \tilde{\alpha }$ is an edge of H. Then $\tilde{\alpha }$ is the edge set of a spanning tree of H and each prefix of $\alpha$ is the edge set of a subtree of H containing r. Assume that x and y are the two edges incident to e in the unique cycle contained in $\tilde{\alpha }+e$ and x precedes y in $\alpha$. Then the entry points of e in $\alpha$ are all the letters of $\alpha$ occuring after x and no later than y. Furthermore, if $z\in \tilde{\alpha }$, $z\ne y$ is an entry point of e and $\alpha =\alpha _0 x\alpha _1 z \alpha _2 y\alpha _3$ then $\alpha _e^z=\alpha _0 x\alpha _1 ez \alpha _2\alpha _3$; moreover, $\alpha _e^y$ is obtained from $\alpha$ simply by replacing y with e.

The following lemma shows that it is not by chance that the entry points of e in $\alpha$ happened to be consecutive in the above example: this is implied by the fact that undirected branching greedoids are interval greedoids.

Lemma 1

Assume that $G=(S,{\mathscr {L}})$ is a greedoid language corresponding to the interval greedoid $(S,{\mathscr {F}}({\mathscr {L}}))$. Then for every $\alpha \in {\mathscr {L}}$ and $e\in S$ the entry points of e in $\alpha$ are consecutive (if they exist).

Proof

Let x and y be the first and last entry points of e in $\alpha$, respectively. If $x=y$ or x and y are adjacent letters of $\alpha$ then there is nothing to prove, so assume the opposite and let $\alpha =\alpha _0 x\alpha _1 z \alpha _2 y\alpha _3$ (as in the above example). Then $\beta =\alpha _0 x\alpha _1\in {\mathscr {L}}$ by (2.7) and $\gamma =\alpha _0 e\in {\mathscr {L}}$ and $\delta =\alpha _0 x\alpha _1 z \alpha _2 e\in {\mathscr {L}}$ since x and y are entry points of e in $\alpha$. Furthermore, since $\tilde{\beta } \cup \tilde{\gamma }\subseteq \tilde{\delta }$, (2.3) implies $\tilde{\alpha _0}\cup \tilde{\alpha _1}\cup \{x,e\} \in {\mathscr {F}}({\mathscr {L}})$ and hence $\alpha _0 x\alpha _1 e\in {\mathscr {L}}$ by $\alpha _0 x\alpha _1\in {\mathscr {L}}$. Therefore z is also an entry point of e in $\alpha$. Since this holds for every letter z between x and y in $\alpha$, this concludes the proof. $\square$

The following lemma is a generalization of a lemma proved in Korte and Lovász (1984a); its proof is also a refinement of the one given in Korte and Lovász (1984a), but it is simpler than that.

Lemma 2

Assume that $G=(S,{\mathscr {L}})$ is a greedoid language, $\alpha \in {\mathscr {L}}$, $x\in S$ and $y\in \tilde{\alpha }$ is an entry point of x in $\alpha$. Then $\alpha _x^y\in {\mathscr {L}}$.

Proof

We proceed by induction on $|\alpha |$. If $|\alpha |=1$ then the claim is trivial, so assume $|\alpha |>1$. Let the last letter of $\alpha$ be z, $\alpha =\gamma z$ and let u denote the last entry point of x in $\gamma$ if it exists.

Assume first that z is an entry point of x in $\alpha$. Then $\alpha _x^z=\gamma x$, so $\alpha _x^z\in {\mathscr {L}}$ (since z is an entry point). For all other entry points $y\ne z$ of x in $\alpha$, $\alpha _x^y=\gamma _x^yu$. We have $\gamma _x^y \in {\mathscr {L}}$ by induction. Then applying (2.8) on $\gamma _x^y$ and $\gamma x$ we get $\alpha _x^y =\gamma _x^yu\in {\mathscr {L}}$ as claimed.

So assume now that z is not an entry point of x, that is, $\gamma x\notin {\mathscr {L}}$. We again have $\gamma _x^y$ by induction. Applying (2.8) on $\gamma _x^y$ and $\alpha$ we get that either $\gamma _x^yz\in {\mathscr {L}}$ or $\gamma _x^yu \in {\mathscr {L}}$. If $x\in \tilde{\alpha }$ then the latter is clearly impossible (since $u=x$ must hold). However, even in the $x\notin \tilde{\alpha }$ case if $\gamma _x^yu\in {\mathscr {L}}$ were true then applying (2.8) on $\gamma$ and $\gamma _x^yu$ would imply $\gamma x\in {\mathscr {L}}$ contradicting our assumption. Therefore $\alpha _x^y=\gamma _x^yz\in {\mathscr {L}}$ as claimed. $\square$

Now we are ready for the above promised generalization of Theorem 1.

Theorem 7

Let $G=(S,{\mathscr {L}})$ be a greedoid language and $w:{\mathscr {L}}\rightarrow {\mathbb {R}}$ an objective function. Assume that the following condition holds:

• (4.3) If $\alpha x\in {\mathscr {L}}$ such that $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$ and $\gamma =\alpha z\beta \in {\mathscr {B}}$ is a basic word then $w(\gamma _x^z)\le w(\gamma )$.

Then the greedoid greedy algorithm finds a basic word of minimum weight with respect to w.

Proof

The theorem follows directly from Theorem 6 and Lemma 2 since $\delta =\gamma _x^z$ is a suitable choice for (4.1) if (4.3) holds. $\square$

The following proposition shows that Theorem 7 is strong enough to imply Theorem 1; this, in turn, will prove that Theorem 6 also implies Theorem 1 as claimed above.

Proposition 2

Conditions (3.1) and (3.2) together imply condition (4.3).

Proof

Let $\gamma =\alpha z\beta \in {\mathscr {B}}$ be a basic word and $\alpha x\in {\mathscr {L}}$ such that $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$. Let the entry points of x in $\gamma$ that do not belong to $\tilde{\alpha }$ be $z=y_1,y_2,\ldots ,y_r$ in this order. Then (3.1) implies $w(\gamma )\ge w(\gamma _x^{y_r})$. Furthermore, applying the combination of (3.1) and (3.2) consecutively $r-1$ times we get $w(\gamma _x^{y_r})\ge w(\gamma _x^{y_{r-1}})\ge \ldots \ge w(\gamma _x^{y_2})\ge w(\gamma _x^z)$. Indeed, (3.1) guarantees that x is a best continuation of the prefix of $\gamma _x^{y_j}$ up to $y_j$ for every $2\le j\le r$. From this, $w(\gamma _x^{y_j})\ge w(\gamma _x^{y_{j-1}})$ follows by (3.2) for every $2\le j\le r$. All these together give $w(\gamma )\ge w(\gamma _x^z)$ as claimed. $\square$

We mentioned in Sect, 3 that Example 5 is only covered by Theorem 1 in the special case where all processing times are equal. The following proposition (the proof of which is based on the one given in Lawler (1973)) shows that Theorem 7 is already strong enough to completely cover Example 5.

Proposition 3

Condition (4.3) is fulfilled by the objective function of Example 5 (and therefore the optimality of Lawler’s scheduling algorithm follows from Theorem 7).

Proof

For the sake of simplicity, we will give the proof for the equivalent “reverse-Lawler” problem described in Sect. 3. So assume that the set of jobs V with the precedence digraph $D=(V,A)$, processing times $a(v)\in {\mathbb {N}}$ and non-increasing cost functions $c_v$ are given.

Assume that $\gamma =\alpha z\beta \in {\mathscr {B}}$ is a basic word of the poset greedoid $(V,{\mathscr {L}})$, that is, a topological ordering of all the jobs. Assume further that x is the best continuation of $\alpha$ (that is, $w(\alpha x)\le w(\alpha y)$ for every $y\in \Gamma (\alpha )$). If $x=z$ then there is nothing to prove by $\gamma _x^x=\gamma$, so assume the opposite. Then $x\in \tilde{\beta }$ (since $\gamma$ lists all the jobs) so let $\beta =\beta _1 x\beta _2$. Then, since poset greedoids are interval greedoids, every $v\in \tilde{\beta }_1$ is an entry point of x in $\gamma$ by Lemma 1 and hence $\gamma _x^z=\alpha xz\beta _1\beta _2$. This shows that for every job $v\ne x$ the starting time of v in $\gamma _x^z$ is at least as big as in $\gamma$ and hence the cost incurred by v in $\gamma _x^z$ is at most the one as in $\gamma$. Let $t=\sum _{v\in \tilde{\alpha }} a(v)$. Then $w(\alpha x)\le w(\alpha z)$ implies that either $c_x(t)\le c_z(t)$ or there is a job $v\in \tilde{\alpha }$ such that the cost incurred by v in $\gamma$ is at least as big as $c_x(t)$. In both cases we get that $c_x(t)\le w(\gamma )$ and hence $w(\gamma _x^z)\le w(\gamma )$ as claimed. $\square$

It is also worth noting that, besides Example 5, Theorem 7 implies the optimality of the greedy algorithm in all the examples listed in Sect. 3 except for Example 2.