Derivative-free robust optimization by outer approximations

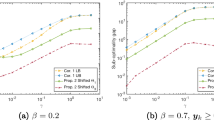
Abstract

We develop an algorithm for minimax problems that arise in robust optimization in the absence of objective function derivatives. The algorithm utilizes an extension of methods for inexact outer approximation in sampling a potentially infinite-cardinality uncertainty set. Clarke stationarity of the algorithm output is established alongside desirable features of the model-based trust-region subproblems encountered. We demonstrate the practical benefits of the algorithm on a new class of test problems.

Appendices

Appendix A: optimality measure properties

Here we collect proofs for Section 2.

1.1 A.1 Proof of Proposition 2

For fixed $\hat{x}\in \mathbb {R}^n$, we have that $\theta (\hat{x},h)$ from (3) can be written as

$$\begin{aligned} \theta (\hat{x},h)= & {} \displaystyle \max _{(\xi _0,\xi )\in \mathcal {E}(\hat{x})} (-\xi _0 + \varPsi (\hat{x})) + \langle \xi ,h\rangle + \displaystyle \frac{1}{2}\Vert h\Vert ^2 - \varPsi (\hat{x})\\= & {} \displaystyle \max _{(\xi _0,\xi )\in \mathcal {E}(\hat{x})} -\xi _0 + \langle \xi ,h\rangle + \displaystyle \frac{1}{2}\Vert h\Vert ^2, \end{aligned}$$

which is a maximization of a linear function over

$$\begin{aligned} \mathcal {E}(\hat{x}) \triangleq \displaystyle \cup _{u\in \mathcal {U}} \left[ \begin{array}{c} \varPsi (\hat{x}) - f(\hat{x},u)\\ \nabla _x f(\hat{x},u) \end{array}\right] \subseteq \mathbf {co}\mathcal {E}(\hat{x}) = \mathcal {D}_{f,\mathcal {U}}(\hat{x})\subseteq \mathbb {R}^{n+1}. \end{aligned}$$

Thus, its optimal value is equal to the optimal value of

$$\begin{aligned} \displaystyle \max _{(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})} -\xi _0 + \langle \xi ,\hat{h}\rangle + \displaystyle \frac{1}{2}\Vert \hat{h}\Vert ^2 \end{aligned}$$

(30)

since an extreme point of $\mathcal {D}_{f,\mathcal {U}}(\hat{x})$, which is necessarily in $\mathcal {E}(\hat{x})$ by definition of the convex hull, is an optimal solution of (30). Thus, we have established that

$$\begin{aligned} \varTheta (\hat{x}) = \displaystyle \min _{h\in \mathbb {R}^n}\displaystyle \max _{(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})} -\xi _0 + \langle \xi ,h\rangle + \displaystyle \frac{1}{2}\Vert h\Vert ^2. \end{aligned}$$

(31)

Letting $b(h,(\xi _0,\xi )) \triangleq -\xi _0 + \langle \xi ,h\rangle + \displaystyle \frac{1}{2}\Vert h\Vert ^2$, the function involved in the minimax expression of (31), we note that

• $b(h,(\xi _0,\xi ))$ is continuous on $\mathbb {R}^{n}\times \mathbb {R}^{n+1}$;

• $b(h,(\hat{\xi }_0,\hat{\xi }))$ is strictly convex in h for any $(\hat{\xi }_0,\hat{\xi })\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$;

• $b(\hat{h},(\xi _0,\xi ))$ is concave in $(\xi _0,\xi )$ for any $\hat{h}\in \mathbb {R}^n$;

• $\mathcal {D}_{f,\mathcal {U}}(\hat{x})$ is, by definition, a convex set; and

• $b(h,(\xi _0,\xi ))\rightarrow \infty$ as $\Vert h\Vert \rightarrow \infty$ uniformly in $(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$.

Thus, the conditions of von Neumann’s theorem apply, and so we conclude that (31) is equivalent to

$$\begin{aligned} \varTheta (\hat{x}) = \displaystyle \max _{(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})}\displaystyle \min _{h\in \mathbb {R}^n} -\xi _0 + \langle \xi ,h\rangle + \displaystyle \frac{1}{2}\Vert h\Vert ^2. \end{aligned}$$

(32)

Now, for a fixed $(\hat{\xi }_0,\hat{\xi })\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$, the solution to the unconstrained convex inner minimization problem of (32) satisfies (by sufficient and necessary first-order conditions) $h = -\hat{\xi }$. Thus, the inner minimization in (32) can be replaced with $-\hat{\xi }_0 - \displaystyle \frac{\Vert \hat{\xi }\Vert ^2}{2}$, yielding the desired result

$$\begin{aligned} \varTheta (\hat{x}) = \displaystyle \max _{(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})} -\xi _0 - \displaystyle \frac{1}{2}\Vert \xi \Vert ^2. \end{aligned}$$

$\square$

1.2 A.2 Proof of Proposition 3

Clearly, $\xi _0 = \varPsi (\hat{x}) - f(\hat{x},u) \ge 0$ for all $(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$. Combined with the nonnegativity of norms, it follows immediately from the definition of $\varTheta (\hat{x})$ in (5) that $\varTheta (\hat{x})=0$ if and only if $\mathbf {0}\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$. Thus, it suffices to show that $\mathbf {0}\in \partial \varPsi (\hat{x})$ if and only if $\mathbf {0}\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$.

Suppose that $\mathbf {0}\in \partial \varPsi (\hat{x})$. Let $u^*(\hat{x})\in \mathcal {U}^*(\hat{x})$, where we have defined

$$\begin{aligned} \mathcal {U}^*(\hat{x})\triangleq \displaystyle {{\mathrm{argmax}}}_{u\in \mathcal {U}} f(\hat{x},u). \end{aligned}$$

Then, for any such $u^*(\hat{x})$, $\varPsi (\hat{x}) - f(\hat{x},u^*(\hat{x}))=0$. It follows that the set

$$\begin{aligned} D^*(\hat{x}) \triangleq \left\{ (\xi _0,\xi ): \xi _0=0, \xi \in \partial \varPsi (\hat{x})\right\} \end{aligned}$$

satisfies $D^*(\hat{x})\subseteq \mathcal {E}(\hat{x})\subseteq \mathcal {D}_{f,\mathcal {U}}(\hat{x})$. Thus, $\mathbf {0}\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$.

Now suppose that $\mathbf {0}\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$. By Carathéodory’s theorem and the convex hull definition of $\mathcal {D}_{f,\mathcal {U}}(\hat{x})$ in (4), there exist $q\le n+2$; $u^1,\dots ,u^q\in \mathcal {U}$; and $\{\lambda \in \mathbb {R}^{q}_{+}: \lambda _1 + \dots + \lambda _q = 1\}$ such that

$$\begin{aligned} \mathbf {0} = \displaystyle \sum _{j=1}^q \lambda _j \left[ \begin{array}{c} \varPsi (\hat{x})-f(\hat{x},u^j)\\ \nabla _x f(\hat{x},u^j) \end{array}\right] . \end{aligned}$$

(33)

Clearly, $\varPsi (\hat{x})-f(\hat{x},\hat{u}) = \displaystyle {{\mathrm{argmax}}}_{u\in \mathcal {U}}f(\hat{x},u)-f(\hat{x},\hat{u})\ge 0$ for all $\hat{u}\in \mathcal {U}$. Thus, projecting the convex combination (33) into its first coordinate, we must have that all q vectors satisfy $\varPsi (\hat{x})-f(\hat{x},u^j)=0$; that is,

$$\begin{aligned} u^j\in {{\mathrm{argmax}}}_{u\in \mathcal {U}} f(\hat{x},u) \quad \text {for} \quad j=1,\dots ,q. \end{aligned}$$

(34)

Likewise, projecting (33) into its last n coordinates,

$$\begin{aligned} \mathbf {0} = \displaystyle \sum _{j=1}^q \lambda _j\nabla _x f(\hat{x},u^j). \end{aligned}$$

(35)

Together, (34) and (35) imply that $\mathbf {0}\in \partial \varPsi (\hat{x})$. $\square$

1.3 A.3 Proof of Proposition 4

For completeness, we state the definition of a continuous set-valued mapping.

Definition 1

Consider a sequence of sets $\{S_j\}_{j=0}^\infty \subset \mathbb {R}^{n}$.

• 1. The point $x^*\in \mathbb {R}^n$ is a limit point of$\{S_j\}$ provided $dist(x^*,S_j)\rightarrow 0$.

• 2. The point $x^*\in \mathbb {R}^n$ is a cluster point of$\{S_j\}$ if there exists a subsequence $\mathcal {K}$ such that $dist(x^*,S_j)\rightarrow _\mathcal {K}0$.

• 3. We denote the set of limit points of $\{S_j\}$ by $\liminf S_j$ and refer to it as the inner limit.

• 4. We denote the set of cluster points of $\{S_j\}$ by $\limsup S_j$ and refer to it as the outer limit.

Definition 2

We say that a set-valued mapping $\varGamma : \mathbb {R}^{n}\rightarrow 2^{\mathbb {R}^{m}}$ is

• 1. outer semicontinuous (o.s.c.) at$\hat{x}$ provided for all sequences $\{x^j\}\rightarrow \hat{x}$, $\displaystyle \limsup \varGamma (x^j) \subseteq \varGamma (\hat{x})$,

• 2. inner semicontinuous (i.s.c.) at$\hat{x}$ provided for all sequences $\{x^j\}\rightarrow \hat{x}$, $\displaystyle \liminf \varGamma (x^j) \supseteq \varGamma (\hat{x})$, and

• 3. continuous at$\hat{x}$ provided $\varGamma$ is o.s.c. and i.s.c. at $\hat{x}$.

Without proof, we state Corollary 5.3.9 from [36].

Proposition 7

Suppose that $g:\mathbb {R}^{n}\times \mathbb {R}^{m}\rightarrow \mathbb {R}^{p}$ is continuous and that $\varGamma : \mathbb {R}^{n}\rightarrow 2^{\mathbb {R}^{m}}$ is a continuous set-valued mapping. Then, the set-valued mapping $G: \mathbb {R}^{n}\rightarrow 2^{\mathbb {R}^{p}}$ defined by

$$\begin{aligned} G(x) \triangleq \mathbf {co}\left\{ g(x,u) : \, u\in \varGamma (x)\right\} \end{aligned}$$

(36)

is continuous.

By using Proposition 7, we get the following intermediate result needed to prove continuity of $\varTheta$.

Proposition 8

Let Assumption 1 hold; then, the set-valued mapping $\mathcal {D}_{f,\mathcal {U}}(\cdot ):\mathbb {R}^n\rightarrow 2^{\mathbb {R}^{n+1}}$ is continuous.

Proof

We look to (36) in Proposition 7 as a template. In the definition of $\mathcal {D}_{f,\mathcal {U}}(\cdot )$, $\varGamma (x) = \mathcal {U}$ for all $x\in \mathbb {R}^n$, and as such, $\mathcal {U}$ is trivially a continuous set-valued mapping. We have only to show that $D:\mathbb {R}^{n}\times \mathbb {R}^m\rightarrow \mathbb {R}^{n+1}$ defined by

$$\begin{aligned} D(x,u) \triangleq \left[ \begin{array}{c} \varPsi (x) - f(x,u)\\ \nabla _x f(x,u) \end{array}\right] \end{aligned}$$

is continuous. Continuity follows since, by Assumption 1, $\varPsi (x)-f(x,u)$ is a continuous function on $\mathbb {R}^n\times \mathcal {U}$, and $\nabla _x f(x,u):\mathbb {R}^{n}\times \mathcal {U}\rightarrow \mathbb {R}^n$ is a Lipschitz continuous function on $\mathbb {R}^n\times \mathcal {U}$. $\square$

We can now prove Proposition 4:

Proof

Consider the equivalent form of $\varTheta$ from Proposition 2 in (5),

$$\begin{aligned} \varTheta (\hat{x}) = \displaystyle \max _{(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})} q(\xi _0,\xi ), \end{aligned}$$

where we have defined the concave quadratic $q(\xi _0,\xi )\triangleq -\xi _0 - \displaystyle \frac{1}{2}\Vert \xi \Vert ^2.$

Let $\hat{x}$ be arbitrary, and let $\{x^j\}_{j=0}^\infty$ be an arbitrary sequence satisfying $x^j\rightarrow \hat{x}$. For $j=0,1,\dots$, let $(\xi ^j_0,\xi ^j)$ be any $(\xi ^j_0,\xi ^j)\in \mathcal {D}_{f,\mathcal {U}}(x^j)$ such that $\varTheta (x^j) = -\xi _0^j - \displaystyle \frac{1}{2}\Vert \xi ^j\Vert ^2.$

The sequence $\{x^j\}_{j=0}^\infty$ is bounded (it is convergent by assumption); we can also show that despite the arbitrary selection, there exists $M\ge 0$ such that $\Vert (\xi ^j_0,\xi ^j)\Vert \le M$ uniformly for $j=0,1,\dots$. To see this, suppose instead that $\Vert (\xi ^j_0,\xi ^j)\Vert \rightarrow \infty$. Then, since $\mathcal {D}_{f,\mathcal {U}}(\hat{x})$ is a compact set, there exists $M\ge 0$ such that $\displaystyle \max \nolimits _{(\xi _0,\xi )\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})} \Vert (\xi _0,\xi )\Vert = M$. By our contradiction hypothesis, there exists $\underline{j}$ sufficiently large so that $\Vert (\xi ^j_0,\xi ^j)\Vert >2M$ for all $j\ge \underline{j}$. From Proposition 8, $\mathcal {D}_{f,\mathcal {U}}(\cdot )$ is a continuous set-valued mapping. Thus, for any $\epsilon >0$, there exists $\underline{j}(\epsilon )\ge \underline{j}$ sufficiently large so that $\mathbf {dist} \left( (\xi ^j_0,\xi ^j), \mathcal {D}_{f,\mathcal {U}}(\hat{x})\right) < \epsilon$ for all $j > \underline{j}(\epsilon )$; this means that $\Vert (\xi ^j_0,\xi ^j)\Vert \le M + \epsilon$. This is impossible for all $\epsilon \in [0,M]$, yielding a contradiction.

Thus, since $\Vert (\xi ^j_0,\xi ^j)\Vert \le M$ for $j=0,1,\dots$ and because $q(\cdot )$ is a continuous function of $(\xi _0,\xi )$, $\displaystyle \limsup \nolimits _{j\rightarrow \infty } q(\xi ^j_0,\xi ^j)$ exists by the Bolzano–Weierstrass theorem. Let $\mathcal {K}$ denote a subsequence witnessing

$$\begin{aligned} \displaystyle \lim _{j\in \mathcal {K}} q(\xi ^j_0,\xi ^j) = \displaystyle \limsup _{j\rightarrow \infty } q(\xi ^j_0,\xi ^j), \end{aligned}$$

and let $(\hat{\xi }_0,\hat{\xi }) = \displaystyle \lim \nolimits _{j\in \mathcal {K}} (\xi ^j_0,\xi ^j)$ denote the corresponding accumulation point. Again using the fact that $\mathcal {D}_{f,\mathcal {U}}(\cdot )$ is o.s.c., we conclude that $(\hat{\xi }_0,\hat{\xi })\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$. Using the definition of $\varTheta (\hat{x})$, we have

$$\begin{aligned} \varTheta (\hat{x})\ge q(\hat{\xi }_0,\hat{\xi }) = \displaystyle \lim _{j\in \mathcal {K}} q(\xi ^j_0,\xi ^j) = \displaystyle \limsup _{j\rightarrow \infty } q(\xi ^j_0,\xi ^j) = \displaystyle \limsup _{j\rightarrow \infty } \varTheta (x^j). \end{aligned}$$

(37)

As written, (37) means that $\varTheta (\cdot )$ is upper semicontinuous. We now demonstrate that $\varTheta (\cdot )$ is also lower semicontinuous, which will complete the proof of the continuity of $\varTheta (\cdot )$. To establish a contradiction, we suppose that there exist $\hat{x}\in \mathbb {R}^n$ and a sequence $\{x^j\}_{j=0}^\infty$ satisfying $x^j\rightarrow \hat{x}$ such that $\varTheta (x^j)$ exists for all j and

$$\begin{aligned} \displaystyle \lim _{j\rightarrow \infty } \varTheta (x^j) < \varTheta (\hat{x}). \end{aligned}$$

(38)

Let $(\hat{\xi }_0,\hat{\xi })\in \mathcal {D}_{f,\mathcal {U}}(\hat{x})$ satisfy $\varTheta (\hat{x})=q(\hat{\xi }_0,\hat{\xi })$. Since $\mathcal {D}_{f,\mathcal {U}}(\hat{x})$ is a continuous set-valued mapping by Proposition 8, there exists a $(\xi ^j_0,\xi ^j)\in \mathcal {D}_{f,\mathcal {U}}(x^j)$ satisfying $\varTheta (x^j)=q(\xi ^j_0,\xi ^j)$ for all $j=0,1,\dots$ such that $(\xi ^j_0,\xi ^j)\rightarrow (\hat{\xi }_0,\hat{\xi })$. Since $q(\cdot )$ is a continuous function in $(\xi _0,\xi )$, $\displaystyle \lim \nolimits _{j\rightarrow \infty } q(\xi ^j_0,\xi ^j) = q(\hat{\xi }_0,\hat{\xi })$. Thus, by using the contradiction hypothesis (38), we have

$$\begin{aligned} q(\hat{\xi }_0,\hat{\xi }) = \displaystyle \lim _{j\rightarrow \infty } q(\xi ^j_0,\xi ^j) = \displaystyle \lim _{j\rightarrow \infty } \varTheta (x^j) < \varTheta (\hat{x}) = q(\hat{\xi }_0,\hat{\xi }), \end{aligned}$$

the desired contradiction. $\square$

Appendix B: Convergence of inexact method of outer approximation

We now establish intermediate results needed to prove Theorem 1.

For brevity of notation, we use the following shorthand for the quadratic objective that appears in the definition of the optimality measure (7):

$$\begin{aligned} q_{\hat{\mathcal {U}}}(x,h) \triangleq \displaystyle \max _{u} \left\{ f(x,u) + \langle \nabla _x f(x,u),h\rangle + \displaystyle \frac{1}{2}\Vert h\Vert ^2 : \, u\in \hat{\mathcal {U}} \right\} . \end{aligned}$$

(39)

Consistent with our previous notation, we write q(x, h) in (39) in the case where $\hat{\mathcal {U}}=\mathcal {U}$.

Lemma 6

Let $\mathcal {S}\subset \mathbb {R}^{n}$ be a bounded subset. Suppose Assumptions 1 and 2 hold, and let $L\in [0,\infty )$ be a Lipschitz constant valid for $f(\cdot ,\cdot )$ and $\nabla _x f(\cdot ,\cdot )$ on $\mathcal {S}\times \mathcal {U}$. Then, there exists $\kappa _1<\infty$ such that for all $x\in \mathcal {S}$ and for all $k=0,1,\dots$,

$$\begin{aligned} {|}\varPsi _{\varOmega ^k} (x) - \varPsi (x)|\le \kappa _1\delta (k). \end{aligned}$$

Moreover, for the $\delta :\mathbb {N}\rightarrow \mathbb {R}$ from Assumption 2, there exists $\kappa _2 \in (\kappa _1,\infty )$ such that

$$\begin{aligned} |\varTheta _{\varOmega ^k}(x)-\varTheta (x)|\le \kappa _2\delta (k). \end{aligned}$$

Proof

Since $\varOmega ^k\subseteq \mathcal {U}$, we have that $\varPsi _{\varOmega ^k}(\hat{x})\le \varPsi (\hat{x})$ for all $\hat{x}\in \mathcal {S}$ and all $k=0,1,\dots .$

Fix $\hat{x}\in \mathcal {S}$ and $u^*(\hat{x})\in \mathcal {U}^*(\hat{x})$. Then, by definition of $\varPsi$, $\varPsi (\hat{x})=f(\hat{x},u^*(\hat{x})).$ By Assumption 2, for all k, there exists $[u^*(\hat{x})]'\in \varOmega ^k$ and $\kappa _0>0$ such that $\Vert u^*(\hat{x})-[u^*(\hat{x})]'\Vert \le \kappa _0\delta (k)$. Thus,

$$\begin{aligned} \varPsi _{\varOmega ^k}(\hat{x}) \ge f(\hat{x},[u^*(\hat{x})]') \ge f\left( \hat{x},u^*(\hat{x})\right) - L \kappa _0 \delta (k) = \varPsi (\hat{x}) - L \kappa _0 \delta (k), \end{aligned}$$

(40)

proving the first part of the lemma, with $\kappa _1=L \kappa _0$.

For the second part, let $\hat{x}\in \mathcal {S}$ and $\hat{h}\in \mathbb {R}^n$ be arbitrary. By the definition of q in (39),

$$\begin{aligned} \displaystyle \min _{h\in \mathbb {R}^n} q_{\varOmega ^k}(\hat{x},h) \le q_{\varOmega ^k}(\hat{x},\hat{h}) \le q(\hat{x},\hat{h}) \end{aligned}$$

for any $k=0,1,\ldots$. Since $\hat{h}$ was arbitrary, we can replace it with a minimizer of the convex $q(\hat{x},\cdot )$; that is,

$$\begin{aligned} \displaystyle \min _{h\in \mathbb {R}^n} q_{\varOmega ^k}(\hat{x},h) \le \displaystyle \min _{h'\in \mathbb {R}^n} q(\hat{x},h'). \end{aligned}$$

(41)

Observing that $\varTheta$ in (2) and $\varTheta _{\varOmega ^k}$ in (7) can be written, respectively, as

$$\begin{aligned} \varTheta (\hat{x})= & {} \displaystyle \min _{h\in \mathbb {R}^n} q(\hat{x},h)-\varPsi (\hat{x}) \\ \varTheta _{\varOmega ^k}(\hat{x})= & {} \displaystyle \min _{h\in \mathbb {R}^n} q_{\varOmega ^k}(\hat{x},h)-\varPsi _{\varOmega ^k}(\hat{x}), \end{aligned}$$

we conclude from (40) and (41) that

$$\begin{aligned} \varTheta _{\varOmega ^k}(\hat{x})= & {} \displaystyle \min _{h\in \mathbb {R}^n} q_{\varOmega ^k}(\hat{x},h) - \varPsi _{\varOmega ^k}(\hat{x})\nonumber \\\le & {} \displaystyle \min _{h\in \mathbb {R}^n} q(\hat{x},h) - \varPsi _{\varOmega ^k}(\hat{x})\nonumber \\= & {} \varTheta (\hat{x}) + \varPsi (\hat{x}) - \varPsi _{\varOmega ^k}(\hat{x})\nonumber \\\le & {} \varTheta (\hat{x}) + L \kappa _0 \delta (k). \end{aligned}$$

(42)

Denote the minimizer of $\varTheta _{\varOmega ^k}(\hat{x})$ by

$$\begin{aligned} h_k(\hat{x}) \triangleq \displaystyle {{\mathrm{argmin}}}_{h\in \mathbb {R}^n} q_{\varOmega ^k}(\hat{x},h)-\varPsi _{\varOmega ^k}(\hat{x}). \end{aligned}$$

Then, from the dual characterization of $\varTheta _{\varOmega ^k}(\hat{x})$ in Proposition 2, we have

$$\begin{aligned} h_k(\hat{x}) \in \left\{ -\xi : (\xi _0,\xi )\in \mathcal {D}_{f,\varOmega ^k}(\hat{x})\right\} = \left\{ -\nabla f(\hat{x},u): u\in \varOmega ^k\right\} . \end{aligned}$$

(43)

By Assumption 1 and since we supposed $\mathcal {S}$ and $\varOmega ^k$ are bounded, $\nabla _x f(\cdot ,u)$ is continuous over $\mathcal {S}$ for each $u\in \varOmega ^k$; furthermore, by (43), there exists $M\in [0,\infty )$ such that $\Vert h_k(x)\Vert \le M$ for all $x\in \mathcal {S}$. Let $u^*(\hat{x})\in \mathcal {U}$ be a maximizer in the definition of $q\left( \hat{x},h_k(\hat{x})\right)$ in (39) such that

$$\begin{aligned} q\left( \hat{x},h_k(\hat{x})\right) = f\left( \hat{x},u^*(\hat{x})\right) + \left\langle \nabla _x f\left( \hat{x},u^*(\hat{x})\right) , h_k(\hat{x})\right\rangle + \displaystyle \frac{1}{2}\Vert h_k(\hat{x})\Vert ^2. \end{aligned}$$

(44)

By Assumption 2, for all k, there exists $[u^*(\hat{x})]'\in \varOmega ^k$ such that $\Vert u^*(\hat{x}) -[u^*(\hat{x})]'\Vert \le \kappa _0\delta (k)$. Combining that with the Lipschitz continuity of Assumption 1, we obtain both

$$\begin{aligned} \left| f\left( \hat{x},u^*(\hat{x})\right) -f\left( \hat{x},[u^*(\hat{x})] '\right) \right| \le L \kappa _0 \delta (k) \end{aligned}$$

and

$$\begin{aligned}&\left| \left\langle \nabla _x f\left( \hat{x},u^*(\hat{x})\right) -\nabla _x f(\hat{x},[u^*(\hat{x})]'), h_k(\hat{x})\right\rangle \right| \\&\quad \le \left\| \nabla _x f\left( \hat{x},u^*(\hat{x})\right) - \nabla _x f(\hat{x},[u^*(\hat{x})]')\right\| \Vert h_k(\hat{x})\Vert \\&\quad \le MLc\delta (k). \end{aligned}$$

Combining these Lipschitz bounds with (44), we obtain

$$\begin{aligned} q_{\varOmega ^k}(\hat{x},h_k(\hat{x}))\ge & {} f(\hat{x},[u^*(\hat{x})]') + \langle \nabla _x f(\hat{x},[u^*(\hat{x})]'), h_k(\hat{x})\rangle + \displaystyle \frac{1}{2}\Vert h_k(\hat{x})\Vert ^2\nonumber \\\ge & {} q(\hat{x},h_k(\hat{x})) - (M+1)L \kappa _0 \delta (k). \end{aligned}$$

(45)

Using the definition of $\varTheta _{\varOmega ^k}(\hat{x})$, we can rewrite (45) as

$$\begin{aligned} \varTheta _{\varOmega ^k}(\hat{x}) + \varPsi _{\varOmega ^k}(\hat{x}) \ge q(\hat{x},h_k(\hat{x})) - (M+1)L \kappa _0 \delta (k). \end{aligned}$$

(46)

Likewise, by using the fact that $\varTheta (\hat{x}) = \displaystyle {{\mathrm{argmin}}}_{h\in \mathbb {R}^n} q(\hat{x},h) - \varPsi (\hat{x}) \le q(\hat{x},h_k(\hat{x})) - \varPsi (\hat{x})$, (46) is equivalent to

$$\begin{aligned} \varTheta _{\varOmega ^k}(\hat{x}) \ge \varTheta (\hat{x}) + \varPsi (\hat{x}) - \varPsi _{\varOmega ^k}(\hat{x}) - (M+1)L \kappa _0 \delta (k). \end{aligned}$$

(47)

Inserting the bound from (40) into (47), we obtain

$$\begin{aligned} \varTheta _{\varOmega ^k}(\hat{x}) \ge \varTheta (\hat{x}) - (M+2)L \kappa _0 \delta (k). \end{aligned}$$

(48)

Combining the bounds in (42) and (48), we have proved the second part of the lemma, with $\kappa _2=(M+2)L \kappa _0$, since $\kappa _2 > \kappa _1 = L \kappa _0$. $\square$

The next lemma demonstrates that, under our assumptions, the accumulation points $x^*$ of a sequence $\{x^k\}$ generated by Algorithm 1 satisfy (on the same subsequence K defining the accumulation) $\varPsi _{\mathfrak {U}^{k}}(x^k) \rightarrow _K \varPsi (x^*)$.

Lemma 7

Suppose that Assumptions 1 and 2 hold and that both

• 1. $\{x^k\}_{k=0}^\infty \subset \mathbb {R}^n$ and

• 2. $\mathfrak {U}^{k}\subseteq \varOmega ^k$ are constructed recursively with $\mathfrak {U}^{0} \ne \emptyset$, $\mathfrak {U}^{0}\subseteq \mathcal {U}$, and $\mathfrak {U}^{k+1} = \mathfrak {U}^{k}\cup \{u{'}\}$, where $u{'}\in (\varOmega ^{k+1})^*(x^{k+1})$.

If $x^*$ is an accumulation point of $\{x^k\}_{k=0}^\infty$ (i.e., for some infinite subset $\mathcal {K}\subset \mathbb {N}$, $x^k\rightarrow _\mathcal {K}x^*$), then $\varPsi _{\mathfrak {U}^{k}}(x^k)\rightarrow _\mathcal {K}\varPsi (x^*)$.

Proof

For any $k\in \{1,2,\dots \}$, let $\underline{k} \triangleq \max \{k'\in \mathcal {K}: k' \le k\}$. Then, by our recursive construction, for any k, $u^{\underline{k}}\in \mathfrak {U}^{k}$. Since $\mathfrak {U}^{k}\subseteq \mathcal {U}$ for $k=0,1,\dots$,

$$\begin{aligned} \varPsi (x^k) \ge \varPsi _{\mathfrak {U}^{k}}(x^k) \ge f(x^k,u^{\underline{k}}). \end{aligned}$$

(49)

By the triangle inequality,

$$\begin{aligned} |\varPsi _{\varOmega ^{\underline{k}}}(x^{\underline{k}}) - \varPsi (x^*)| \le |\varPsi _{\varOmega ^{\underline{k}}}(x^{\underline{k}}) - \varPsi (x^{\underline{k}})| +|\varPsi (x^{\underline{k}}) - \varPsi (x^*)|. \end{aligned}$$

(50)

Because $x^k\rightarrow _\mathcal {K}x^*$ and because $\varPsi (\cdot )$ is a continuous function as a result of Assumption 1, the second summand in (50) satisfies $|\varPsi (x^{\underline{k}}) - \varPsi (x^*)|\rightarrow 0$. By Lemma 6 and the continuity of $\varPsi (\cdot )$, we also conclude that the first summand in (50) satisfies $|\varPsi _{\varOmega ^{\underline{k}}} (x^{\underline{k}}) - \varPsi (x^{\underline{k}})|\rightarrow 0$. Thus,

$$\begin{aligned} \varPsi _{\varOmega ^{\underline{k}}}(x^{\underline{k}})\rightarrow \varPsi (x^*). \end{aligned}$$

(51)

Since from Assumption 1, $f(\hat{x},u)$ is a uniformly continuous function in u over a compact set, and since $\Vert x^k-x^{\underline{k}}\Vert \rightarrow 0$ (by accumulation), we have

$$\begin{aligned} {|}f(x^k,u^{\underline{k}}) - f(x^{\underline{k}},u^{\underline{k}})|\rightarrow 0. \end{aligned}$$

By definition, $\varPsi _{\varOmega ^{\underline{k}}}(x^{\underline{k}}) = f(x^{\underline{k}},u^{\underline{k}})$, and so the above can be written as

$$\begin{aligned} |f(x^k,u^{\underline{k}}) - \varPsi _{\varOmega ^{\underline{k}}}(x^{\underline{k}})|\rightarrow 0. \end{aligned}$$

(52)

It follows immediately from (51) and (52) that $f(x^k,u^{\underline{k}})\rightarrow \varPsi (x^*)$. So, by (49) and an application of the sandwich theorem, we conclude $\varPsi _{\mathfrak {U}^{k}}(x^k)\rightarrow _\mathcal {K}\varPsi (x^*)$, as we intended to show. $\square$

By using Lemma 7, we can now give a proof of Theorem 1.

Proof of Theorem 1

Recalling the definition of $q_{\hat{\mathcal {U}}}$ in (39), and since $\mathfrak {U}^{k}\subseteq \mathcal {U}$ for $k=0,1,\dots$, we have that for all k and for all $\hat{h}\in \mathbb {R}^n$, $q_{\mathfrak {U}^{k}}(x^k,\hat{h})\le q(x^k,\hat{h})$. Then, by the definition of $\varTheta _{\mathfrak {U}^{k}}$ in (7), we have that

$$\begin{aligned} \varTheta _{\mathfrak {U}^{k}}(x^k)= & {} \displaystyle \min _{h\in \mathbb {R}^n} q_{\mathfrak {U}^{k}}(x^k,h) - \varPsi _{\mathfrak {U}^{k}}(x^k)\nonumber \\\le & {} \displaystyle \min _{h\in \mathbb {R}^n} q(x^k,h) - \varPsi _{\mathfrak {U}^{k}}(x^k)\nonumber \\= & {} \varTheta (x^k) + \varPsi (x^k) - \varPsi _{\mathfrak {U}^{k}}(x^k). \end{aligned}$$

(53)

By using the criteria imposed on $\varTheta _{\mathfrak {U}^{k}}(x^{k+1})$ in Line 5 of Algorithm 1 and (53), we have that for $k=0,1,\dots$,

$$\begin{aligned} -\epsilon _k \le \varTheta _{\mathfrak {U}^{k}}(x^{k+1}) \le \varTheta (x^{k+1}) + \varPsi (x^{k+1}) - \varPsi _{\mathfrak {U}^{k+1}}(x^{k+1}). \end{aligned}$$

(54)

Let $\mathcal {K}$ be a subsequence defining the accumulation $\{x^k\}\rightarrow _\mathcal {K}x^*$. Taking the limit with respect to $\mathcal {K}$ in (54), we obtain

By the continuity of $\varTheta$ from Proposition 4, the result follows from the sandwich theorem. $\square$

C Availability of a generalized cauchy point

We refer the reader to [13, Chapter 12.2] for a detailed discussion of generalized Cauchy decrease in trust-region subproblems with convex (here, linear) constraints, but we provide some necessary details here, beginning with

Definition 3

Let $p(r):\mathbb {R}\rightarrow \mathbb {R}^{n+1}$ denote the projection $\mathcal {P}_{\mathcal {C}}([-r;\mathbf {0}])$, where

$$\begin{aligned} \mathcal {C}= \left\{ [z;d]: G^{t\top } d -z\mathbf {e} \le \varPsi _{\mathfrak {U}^{k}}(y^t)\mathbf {e} - F^t\right\} . \end{aligned}$$

Use the notation $p(r) = [p_z(r); p_d(r)]$ to indicate the separation of p(r) into the scalar z component and the n-dimensional d component. Then, the generalized Cauchy point for (P) is defined as $p(r^*)$, where

$$\begin{aligned} r^* = \displaystyle {{\mathrm{argmin}}}_{r} \left\{ p_z(r) + \displaystyle \frac{1}{2}p_d(r)^\top B^t p_d(r) : 0\le r \le \varDelta _t \right\} . \end{aligned}$$

The generalized Cauchy point is the global minimizer of the objective in (P) restricted to an arc described by the projected steepest descent direction at $(z,d) = (0,\mathbf {0})$. Algorithm 3 (see [13, Algorithm 12.2.2]) computes an approximate generalized Cauchy point for (P) via a Goldstein-type line search. The notation $\mathcal {T}_{\mathcal {C}}(y)$ denotes the tangent cone to a convex set $\mathcal {C}$ at a point y (and we remark that, given a linear polytope $\mathcal {C}$, this set is easily computable).

We further remark that the computation of p(r) for a given r involves the solution of the convex quadratic program

$$\begin{aligned} \displaystyle \min _{s_z,s_d} \left\{ (r + s_z)^2 + \Vert s_d\Vert ^2 : G^{t\top } s_d - s_z\mathbf {e} \le \varPsi _{\mathfrak {U}^{k}}(y^t)\mathbf {e} - F^t\right\} . \end{aligned}$$

Although we anticipate that Algorithm 3 has benefits in many real-world settings, here it is merely of theoretical convenience, and we do not use it in the implementation tested.

D Global maximization of (28)

First, we remark that the objective function of (28) is separable with respect to the variables L and b. Thus, it is evident that the optimal value of b is given by

$$\begin{aligned} b_i^* = \left\{ \begin{array}{ll} \hat{b}_i - \alpha , &{} \text { if}\ x_i < 0 \\ \hat{b}_i + \alpha , &{} \text { otherwise}\\ \end{array}\right. \qquad i =1, \ldots , n. \end{aligned}$$

We now consider the optimal value of L. After deleting rows and columns of $I_n \otimes xx^\top$ corresponding to the entries $L_{ij}$ where $L_{ij}=0$, we are left with a matrix of the form

$$\begin{aligned} \left[ \begin{array}{ccccc} x_{\bar{1}}x_{\bar{1}}\top &{} \mathbf {0} &{} \cdots &{} &{} \mathbf {0}\\ \mathbf {0} &{} x_{\bar{2}}x_{\bar{2}}^\top &{} \mathbf {0} &{} \cdots &{} \mathbf {0} \\ \vdots &{} \mathbf {0} &{} \ddots &{} &{} \vdots \\ &{} \vdots &{} &{} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} &{} \cdots &{}\mathbf {0} &{} x_{\bar{n}}x_{\bar{n}}^\top \end{array}\right] , \end{aligned}$$

where $x_{\bar{i}}$ denotes the truncated vector $[x_1,\dots ,x_i]$. Exploiting this block structure, the maximization of the quadratic decomposes into n bound-constrained quadratic maximization problems of the form

$$\begin{aligned} \displaystyle \max _{\ell \in \mathbb {R}^{i}} \left\{ \frac{1}{2}\ell ^\top \left( x_{\bar{i}} x_{\bar{i}}^\top \right) \ell : \; |\ell _j - \hat{\ell }_j| \le \alpha , \; j = 1,\ldots ,i\right\} \end{aligned}$$

(55)

for $i=1,\dots ,n$. In turn, solving (55) is equivalent to solving the problem

$$\begin{aligned} \displaystyle \max _{\ell \in \mathbb {R}^{i}} \left\{ |x_{\bar{i}}^\top \ell | : \; {|}\ell _j - \hat{\ell }_j| \le \alpha , \; j = 1,\dots ,i \right\} , \end{aligned}$$

(56)

which can be cast as a mixed-integer linear program with exactly one binary variable; that is, solving (56) to global optimality entails the solution of two linear programs with $\mathcal {O}(i)$ variables and $\mathcal {O}(i)$ constraints each. Thus, the total cost of solving (28) to global optimality through this reformulation is bounded by the cost of solving 2n linear programs, the largest of which has $\mathcal {O}(n)$ variables and constraints, and the smallest of which has $\mathcal {O}(1)$ variables and constraints.