Robust convex optimization: A new perspective that unifies and extends

Abstract

Robust convex constraints are difficult to handle, since finding the worst-case scenario is equivalent to maximizing a convex function. In this paper, we propose a new approach to deal with such constraints that unifies most approaches known in the literature and extends them in a significant way. The extension is either obtaining better solutions than the ones proposed in the literature, or obtaining solutions for classes of problems unaddressed by previous approaches. Our solution is based on an extension of the Reformulation-Linearization-Technique, and can be applied to general convex inequalities and general convex uncertainty sets. It generates a sequence of conservative approximations which can be used to obtain both upper- and lower- bounds for the optimal objective value. We illustrate the numerical benefit of our approach on a robust control and robust geometric optimization example.

1 Introduction

In this paper, we consider a general hard robust constraint

$$\begin{aligned} h\left( {\varvec{A}} ( {\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}}) \right) \le 0, \qquad \qquad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

(1)

where $h : {\mathbb {R}}^{m} \mapsto [-\infty , +\infty ]$ is a proper, closed and convex function, ${\varvec{A}} : {\mathbb {R}}^{n_x} \mapsto {\mathbb {R}}^{m \times L}$, ${\varvec{b}}: {\mathbb {R}}^{n_x} \mapsto {\mathbb {R}}^{L}$ are affine, and ${\varvec{{\mathcal {Z}}}}$ is a nonempty convex subset of ${\mathbb {R}}^{L}$. Unlike inequalities that are concave in the uncertain parameters [4], a tractable equivalent reformulation for the robust constraint (1) is out of reach in general.

When $h(\cdot )$ is (conic) quadratic, several exact reformulations have been proposed for specific uncertainty sets. We refer to [3, Chapter 6] for an overview of these methods. In the general case, generic approximate methods have been proposed for safely approximating (1). For homogeneous convex functions $h(\cdot )$ and symmetric norm-based uncertainty sets ${\varvec{ {\mathcal {Z}}}}$, Bertsimas and Sim [8] propose a computationally tractable safe approximation together with probabilistic guarantees. Zhen et al. [21] develop safe approximations for conic quadratic and SDP problems with polyhedral uncertainty sets. They first reformulate the robust inequality into an equivalent set of linear adaptive robust constraints, which can then be approximated by, e.g., static or affine decision rules. Roos et al. [18] extend their approach with affine decision rules to general convex functions $h(\cdot )$ but still with polyhedral uncertainty sets. For general convex uncertainty sets, they propose a similar approach, yet using static decision rules only.

In this paper, we propose a new general safe approximation procedure for robust convex constraint (1). Our approach is ‘general’ in the sense that it can be applied to a generic convex function $h(\cdot )$ and convex uncertainty set ${\varvec{{\mathcal {Z}}}}$. Using the Reformulation-Perspectification-Technique (RPT) as a unifying lens [20], our approach not only unifies many previous work from the literature but also extends them in a significant way. First, it is superior on special cases with homogeneous functions $h(\cdot )$ and/or polyhedral uncertainty sets. Second, it is applicable to any convex function $h(\cdot )$ and convex uncertainty set ${\varvec{{\mathcal {Z}}}}$ under mild assumptions, namely that one can explicitly describe the uncertainty set and the domain of the conjugate of h (see definition in Sect. 1.2) via convex inequalities.

We develop our main approximation for a generic class of uncertainty sets, described as the intersection of a polyhedron and a convex set. We first prove that the original uncertain convex inequality (1) is equivalent to an uncertain linear constraint with a non-convex uncertainty set. In other words, we reformulate (1) as a linear robust constraint where the new uncertainty set ${\varvec{\varTheta }}$ is non-convex due to the presence of bilinear equality constraints. We then use the recently developed Reformulation-Perspectification-Technique (RPT) [20] to obtain a hierarchy of safe approximations, i.e, we construct convex sets ${\varvec{\varTheta }}_i$, $i=0,1,\dots ,3$, such that ${\varvec{\varTheta }} \subseteq {\varvec{\varTheta }}_3 \subseteq {\varvec{\varTheta }}_2 \subseteq {\varvec{\varTheta }}_1 \subseteq {\varvec{\varTheta }}_0$. We show that this approach unifies a variety of methods known in the literature, and extends them in a significant way. When the uncertainty set lies in the non-negative orthant, we show that the first-level approximation ${\varvec{\varTheta }}_1$ coincides with the perspectification approach, a generalization of the approach of Bertsimas and Sim [8] for which we also provide probabilistic guarantees. Consequently, our approach connects and generalizes further the work of Bertsimas and Sim [8] and Roos et al. [18] to a broader class of uncertainty sets, and improves them by proposing tighter approximations, ${\varvec{\varTheta }}_2$ and ${\varvec{\varTheta }}_3$. For polyhedral uncertainty sets, our RPT-based approach with ${\varvec{\varTheta }}_1$ coincides with the approximation from Roos et al. [18] with linear decision rules [18, Theorem 2].

The paper is structured as follows: In Sect. 2, we present our RPT-based hierarchy of safe approximations. We connect it with existing results from the literature in Sect. 3. In particular, for uncertainty sets lying in the non-negative orthant, we show in Appendix A that our first-level approximation with ${\varvec{\varTheta }}_1$ can be alternatively derived using a ‘perspectification’ technique and provide probabilistic guarantees in this case. When applied to a minimization problem, our safe approximations provide a valid upper bound on the objective value. Our approach can also be adapted to derive lower bounds, as described in Sect. 4. Finally, we assess the numerical performance of our technique in Sect. 5, and conclude our findings in Sect. 6.

1.1 Examples

In this section, we present a few examples of the robust convex constraint (1) often encountered in the literature and summarize them in Table 1.

Quadratic Optimization (QO) We consider the general quadratic constraint

$$\begin{aligned} {\varvec{z}}^\top {\varvec{F}}({\varvec{x}})^\top {\varvec{F}}({\varvec{x}}) {\varvec{z}} + {\varvec{f}}({\varvec{x}})^\top {\varvec{z}} \le g({\varvec{x}}), \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

where ${\varvec{F}} : {\mathbb {R}}^{n_x} \mapsto {\mathbb {R}}^{m \times L}$, ${\varvec{f}} : {\mathbb {R}}^{n_x} \mapsto {\mathbb {R}}^{L}$ and $g : {\mathbb {R}}^{n_x} \mapsto {\mathbb {R}}$ are affine in ${\varvec{x}}$. The constraint is of the form (1) with

$$\begin{aligned} h\left( \begin{bmatrix} {\varvec{y}} \\ {\bar{y}} \end{bmatrix} \right) := {\varvec{y}}^\top {\varvec{y}} + {\bar{y}}, \quad {\varvec{A}}({\varvec{x}}) := \begin{bmatrix} {\varvec{F}}({\varvec{x}}) \\ {\varvec{f}}({\varvec{x}})^\top \end{bmatrix}, \quad \text {and } {\varvec{b}}({\varvec{x}}) := \begin{bmatrix} {\varvec{0}} \\ g({\varvec{x}}) \end{bmatrix}. \end{aligned}$$

Alternatively, the constraint can be represented as a second-order cone constraint

$$\begin{aligned} \left\| \begin{matrix} {\varvec{F}}({\varvec{x}}) {\varvec{z}} \\ (1+ {\varvec{f}} ({\varvec{x}})^\top {\varvec{z}} - g({\varvec{x}}))/2\\ \end{matrix} \right\| _2 \le (1 - {\varvec{f}}({\varvec{x}})^\top {\varvec{z}} + g({\varvec{x}})), \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

which is also of the form (1) for

$$\begin{aligned} h\left( \begin{bmatrix} {\varvec{y}} \\ \tilde{y} \\ {\bar{y}} \end{bmatrix} \right) := \sqrt{{\varvec{y}}^\top {\varvec{y}} + \tilde{y}^2} + {\bar{y}}, \, {\varvec{A}}({\varvec{x}}) := \begin{bmatrix} {\varvec{F}}({\varvec{x}}) \\ \tfrac{1}{2} {\varvec{f}}({\varvec{x}})^\top \\ \tfrac{1}{2} {\varvec{f}}({\varvec{x}})^\top \end{bmatrix}, \text { and } {\varvec{b}}({\varvec{x}}) := \begin{bmatrix} {\varvec{0}} \\ \tfrac{{1} - g({\varvec{x}})}{2} \\ -\tfrac{{1}+g({\varvec{x}})}{2} \end{bmatrix}. \end{aligned}$$

Piecewise linear constraints (PWL) We consider the piece-wise linear convex constraint

$$\begin{aligned} \max _{k \in [m]} \, \left\{ {\varvec{a}}_k ( {\varvec{x}})^\top {\varvec{z}} + b_k ( {\varvec{x}}) \right\} \le 0, \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

where ${\varvec{a}}_k: {\mathbb {R}}^{n_x} \mapsto {\mathbb {R}}^{L}$ and $b_k : {\mathbb {R}}^{n_x} \mapsto {\mathbb {R}}$ are affine functions of ${\varvec{x}}$. Such a constraint is a special case of (1) with

$$\begin{aligned} h( {\varvec{y}}) := \max _{k \in [m]} y_k, \quad {\varvec{A}}({\varvec{x}}) := [{\varvec{a}}_{k}({\varvec{x}})^\top ]_k, \quad \text {and } \quad {\varvec{b}}({\varvec{x}}) := [b_k ({\varvec{x}})]_k. \end{aligned}$$

Sum-of-max of linear constraints (SML) The sum-of-max of linear constraints is defined as $h({\varvec{y}}) := \sum _{k}\max _{i\in I_k} y_i$, for any ${\varvec{y}} \in {\mathbb {R}}^{n_y}$.

Geometric optimization (GO) In geometric optimization, the function h in (1) is the log-sum-exp function defined by $h({\varvec{y}}) := \log \left( e^{y_1} + \dots + e^{y_{n_y}} \right)$ for any ${\varvec{y}} \in {\mathbb {R}}^{n_y}$.

Sum-of-convex constraints (SC) The sum of general convex functions is defined as $h({\varvec{y}}) := \sum _{i \in [I]} h_i({\varvec{y}})$, where $h_i : {\mathbb {R}}^{m} \mapsto [-\infty , +\infty ]$, $i \in [I]$, are proper, closed and convex with $\cap _{i\in [I]} \mathrm{ri} (\mathrm{dom} h_i) \ne \emptyset$.

Table 1 Example of functions $h(\cdot )$ and their corresponding conjugate, defined as $h^*({\varvec{w}}) := \sup _{{\varvec{y}} \in {\text {dom}} h} \, \{ {\varvec{y}}^\top {\varvec{w}} - h({\varvec{y}}) \}$

In this paper, we study robust convex constraints, and not only robust conic constraints, on purpose. It is generally believed that most convex problems can be modeled in terms of the five basic cones: linear, quadratic, semi-definite, power, and exponential cones. Still, we do not restrict our attention to robust conic optimization for the following reason: Although conic optimization is a powerful modeling framework, the uncertainty is often split over multiple constraints, and the robust version of the conic representation is not equivalent to the original one. For example, while the sum-of-max of linear functions is linear-cone representable, its robust counterpart is not necessarily equivalent with the robust version of the original constraint. The conclusion is that the right order is to first develop the robust counterpart of the nonlinear inequality and then reformulate it into a conic representation, instead of the other way around.

1.2 Notations

We use nonbold face characters (x) to denote scalars, lowercase bold faced characters (${\varvec{x}}$) to denote vectors, uppercase bold faced characters (${\varvec{X}}$) to denote matrices, and bold calligraphic characters such as ${\varvec{{\mathcal {X}}}}$ to denote sets. We denote by ${\varvec{e}}_i$ the unit vector with 1 at the ith coordinate and zero elsewhere, with dimension implied by the context.

We use [n] to denote the finite index set $[n]= \{1,\dots , n\}$ with cardinality $\vert [n]\vert =n$. Whenever the domain of an optimization variable is omitted, it is understood to be the entire space (whose definition will be clear from the context).

The function $\delta ^*( {\varvec{x}} \vert {\varvec{{\mathcal {S}}}})$ denotes the support function of the set ${\varvec{{\mathcal {S}}}}$ evaluated at ${\varvec{x}}$, i.e., $\delta ^*( {\varvec{x}} \vert {\varvec{{\mathcal {S}}}}) = \sup _{{\varvec{y}} \in {\varvec{{\mathcal {S}}}}} \, {\varvec{y}}^\top {\varvec{x}}.$

A function $f:{\mathbb {R}}^{n_y} \mapsto [-\infty , +\infty ]$ is said to be proper if there exists at least one vector ${\varvec{y}}$ such that $f({\varvec{y}}) < + \infty$ and for any ${\varvec{y}} \in {\mathbb {R}}^{n_y}$, $f({\varvec{y}}) > - \infty$. For a proper, closed and convex function f, we define its conjugate as $f^*({\varvec{w}}) = \sup _{{\varvec{y}} \in {\text {dom}} f} \, \left\{ {\varvec{w}}^\top {\varvec{y}} - f({\varvec{y}}) \right\}$. When f is closed and convex, $f^{**} = f$. If the function $f:{\mathbb {R}}^{n_y} \mapsto [-\infty , +\infty ]$ is proper, closed and convex, the perspective function of f is defined for all ${\varvec{y}} \in {\mathbb {R}}^{n_y}$ and $t \in {\mathbb {R}}_+$ as

$$\begin{aligned} {\text {persp}}_f \, : \, ({\varvec{y}},t) \mapsto {\left\{ \begin{array}{ll} t f({\varvec{y}} /t), &{} \text{ if } t > 0, \\ f_\infty ({\varvec{y}}), &{} \text{ if } t = 0. \end{array}\right. } \end{aligned}$$

The function $f_\infty :{\mathbb {R}}^{n_y} \times {\mathbb {R}}_+ \mapsto [-\infty , +\infty ]$ is the recession function, which can be equivalently defined as

$$\begin{aligned} f_\infty ({\varvec{y}}) = \lim _{t\rightarrow 0} t f({\varvec{y}} /t) = \delta ^*({\varvec{y}} \vert {\text {dom}} f^*). \end{aligned}$$

Among others, the perspective and conjugate functions of f satisfy the relationship

$$\begin{aligned} t f \left( \dfrac{{\varvec{y}}}{t} \right) = \sup _{{\varvec{w}} \in {\text {dom}} f^*} \, \left\{ {\varvec{y}}^\top {\varvec{w}} - t f^*({\varvec{w}}) \right\} \quad \text {for } t > 0. \end{aligned}$$

For ease of exposition, we use $tf({\varvec{y}} /t)$ to denote the perspective function f.

2 The reformulation-perspectification approach

In this section, we describe our main approach, which is based on an extension of the Reformulation-Linearization-Technique, that is, Reformulation-Perspectification-Technique [20].

Our approach comprises three steps:

• Step 1. Reformulate the robust convex constraint (1) into a robust linear optimization problem with bilinear equalities in the uncertainty set.

• Step 2. Apply the Reformulation-Perspectification-Technique to get a safe approximation of the robust convex inequality that is linear in the uncertain parameters.

• Step 3. Construct a computationally tractable robust counterpart of the approximation obtained in Step 2 by using the approach described in Ben-Tal et al. [4].

2.1 Step 1: Bilinear reformulation

We first describe Step 1 in more detail. The following proposition shows that the robust convex constraint (1) is equivalent to a robust linear constraint with bilinear equality constraints in the uncertainty set.

Proposition 1

(Bilinear Reformulation) The robust convex constraint (1) is equivalent to

$$\begin{aligned} \sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }} } \quad \left\{ \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{V}} ) + {\varvec{b}}( {\varvec{x}})^\top {\varvec{w}} - {w_0} \right\} \le 0, \end{aligned}$$

(2)

where

$$\begin{aligned} {\varvec{\varTheta }}\!=\! \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \; {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \, {\varvec{w}} \in {\text {dom}} h^*, \, h^*({\varvec{w}}) \le w_0 , \, {\varvec{V}} \!=\! {\varvec{w}} {\varvec{z}}^\top , {\varvec{v}}_0 \!=\! w_0 {\varvec{z}} \right. \right\} . \end{aligned}$$

Proof

Because h is closed and convex we have

$$\begin{aligned} h({\varvec{s}}) = h^{**} ({\varvec{s}}) = \sup _{{\varvec{w}} \in {\text {dom}} h^*} \left\{ {\varvec{s}}^\top {\varvec{w}} - h^*({\varvec{w}})\right\} , \end{aligned}$$

and thus

$$\begin{aligned} \sup _{ {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} \, h\left( {\varvec{A}}({\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}}) \right)&= \, \sup _{{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} \, \sup _{{\varvec{w}} \in {\text {dom}} h^*} \, {\varvec{z}}^\top {\varvec{A}}({\varvec{x}})^\top {\varvec{w}} + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - h^*({\varvec{w}}) \nonumber \\&= \, \sup _{ \begin{array}{c} {\varvec{z}} \in {\varvec{{\mathcal {Z}}}} \\ {\varvec{w}} \in {\text {dom}} h^* \\ h^*({\varvec{w}}) \le w_0 \end{array}} \, \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{w}}{\varvec{z}}^\top ) + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - {w_0} \nonumber \\&= \, \sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }} } \, \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{V}}) + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - {w_0} , \end{aligned}$$

(3)

for the properly defined set ${\varvec{\varTheta }}$. $\square$

The complication in (2) is that the extended uncertainty set ${\varvec{\varTheta }}$ is not convex due to the bilinear constraint ${\varvec{V}} = {\varvec{w}} {\varvec{z}}^\top$. Therefore, in Step 2 we propose a safe approximation of ${\varvec{\varTheta }}$ based on the Reformulation-Perspectification-Technique [20]. Formally, we provide tractable approximations of the robust convex constraint in (1) by exhibiting convex sets ${\varvec{\varPhi }}$ such that ${\varvec{\varTheta }} \subseteq {\varvec{\varPhi }}$. Indeed, if ${\varvec{\varTheta }} \subseteq {\varvec{\varPhi }}$, then

$$\begin{aligned} \sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varPhi }} } \, \left\{ \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{V}}) + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - {w_0} \right\} \le 0 \end{aligned}$$

constitutes a safe approximation of (1). In addition, this safe approximation is linear in the uncertain parameter $({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0)$ and convex in the decision variable ${\varvec{x}}$. Hence, provided that the new uncertainty sets ${\varvec{\varPhi }}$ is convex, its robust counterpart can be derived in a tractable manner using techniques from Ben-Tal et al. [4] (Step 3). Observe that since the objective function is linear, we can replace ${\varvec{\varTheta }}$ by ${\text {conv}}({\varvec{\varTheta }})$ in (2) without loss of optimality. So we effectively need to construct sets ${\varvec{\varPhi }}$ that approximate ${\text {conv}}({\varvec{\varTheta }})$ as closely as possible.

2.2 Step 2: Hierarchy of safe approximations

To develop a hierarchy of safe approximations (Step 2) for the robust non-convex constraint (2), we assume that the uncertainty set ${\varvec{{\mathcal {Z}}}}$ is described through $K_0$ linear and $K_1$ convex inequalities.

Assumption 1

The uncertainty set ${\varvec{{\mathcal {Z}}}} = \{ {\varvec{z}} \in {\mathbb {R}}^{L} \ \vert {\varvec{D}} {\varvec{z}} \le {\varvec{d}},\ c_k ({\varvec{z}}) \le 0, \ k \in [K_1] \}$, where ${\varvec{D}} \in {\mathbb {R}}^{K_0 \times L}$, ${\varvec{d}} \in {\mathbb {R}}^{K_0}$, and $c_k:{\mathbb {R}}^{L} \mapsto [-\infty , +\infty ]$ is proper, closed and, convex for each $k \in [K_1]$.

Note that the decomposition of ${\varvec{{\mathcal {Z}}}}$ into linear and convex constraints in Assumption 1 is not unique. Indeed, affine functions are also convex so one could assume $K_0=0$ without loss of generality. However, the presence of linear constraints in the definition of ${\varvec{{\mathcal {Z}}}}$ will be instrumental in deriving good approximations. Consequently, from a practical standpoint, we encourage to include as many linear constraints as possible in the linear system of inequalities ${\varvec{D}} {\varvec{z}} \le {\varvec{d}}$. We illustrate this modeling choice on a simple example.

Example 1

Consider the polytope ${\varvec{{\mathcal {Z}}}} = \{ {\varvec{z}} \in {\mathbb {R}}^L_+ \vert \sum _{\ell =1}^L z_\ell \le 1, \ell \in [L]\}$. ${\varvec{{\mathcal {Z}}}}$ satisfies Assumption 3 with $K=1$ and $c_1({\varvec{z}}) = \sum _{\ell } z_\ell - 1$. Therefore, ${\varvec{{\mathcal {Z}}}}$ also satisfies Assumption 1 with ${\varvec{D}} = - {\varvec{I}}_L$, ${\varvec{d}} = {\varvec{0}}_L$, and $c_1({\varvec{z}}) = \sum _{\ell } z_\ell - 1$, hence $K_0=L$ and $K_1=1$. Alternatively, ${\varvec{{\mathcal {Z}}}}$ satisfies Assumption 1 with $K_0=L+1$ and $K_1=0$ with

$$\begin{aligned} {\varvec{D}} = \begin{bmatrix} - {\varvec{I}}_L \\ {\varvec{e}}^\top \end{bmatrix}, \text{ and } {\varvec{d}} = \begin{bmatrix} {\varvec{0}}_L \\ 1 \end{bmatrix}. \end{aligned}$$

Similarly, we assume that ${\text {dom}} h^*$ can be described with $J_0$ linear and $J_1$ convex inequalities.

Assumption 2

The set ${\text {dom}} h^* = \{{\varvec{w}} \; \vert \; {\varvec{F}} {\varvec{w}} \le {\varvec{f}}, \; g_j ({\varvec{w}}) \le 0, \ j \in [J_1] \}$ has $J_0$ linear inequalities defined by ${\varvec{F}}$ and ${\varvec{f}}$, and $J_1$ nonlinear inequalities defined by $g_j$, $j \in [J_1]$, where $g_j$ is proper, closed, and convex for each $j \in [J_1]$.

Under Assumptions 1 and 2 , the non-convex uncertainty set ${\varvec{\varTheta }}$ can be represented as

$$\begin{aligned} {\varvec{\varTheta }} = \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} {\varvec{D}} {\varvec{z}} \le {\varvec{d}},\; c_k({\varvec{z}}) \le 0,\ k \in [K_1] &{}({\varvec{z}} \in {\varvec{{\mathcal {Z}}}}) \\ {\varvec{F}} {\varvec{w}} \le {\varvec{f}}, \; g_j ({\varvec{w}}) \le 0, \ i \in [J_1] &{} ({\varvec{w}} \in {\text {dom}} h^*) \\ h^*({\varvec{w}}) \le w_0 &{} (\text {epigraph})\\ {\varvec{V}} = {\varvec{w}} {\varvec{z}}^\top \\ {\varvec{v}}_0 = w_0 {\varvec{z}} \end{array} \right. \right\} . \end{aligned}$$

Proposition 2

(Convex Relaxation via RPT) For any $({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}$, we have

• a) $\displaystyle \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}} \in {\text {dom}} h^*,$ for all $k \in [K_0]$,

• b) $\displaystyle \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \in {\varvec{{\mathcal {Z}}}}$, for all $j \in [J_0]$.

Each of these two set memberships can be expressed through constraints that are convex in $({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0)$. As a result, the three sets

$$\begin{aligned} {\varvec{\varTheta }}_{0}&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \\ {\varvec{w}} \in {\text {dom}} h^*, \\ h^*({\varvec{w}}) \le w_0 \end{array} \right. \right\} , \\ \\ {\varvec{\varTheta }}_{1}&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}_0, \\ \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}} \in {\text {dom}} h^*,\ k \in [K_0] \end{array} \right. \right\} , \\ \\ {\varvec{\varTheta }}_2&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}_1, \\ \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \in {\varvec{{\mathcal {Z}}}},\ j \in [J_0] \end{array} \right. \right\} \end{aligned}$$

are convex and satisfy ${\varvec{\varTheta }} \subseteq {\varvec{\varTheta }}_2 \subseteq {\varvec{\varTheta }}_1 \subseteq {\varvec{\varTheta }}_0$.

Proof

• a) Consider a linear constraint on ${\varvec{z}}$, ${\varvec{e}}_k^\top \left( {\varvec{d}} - {\varvec{D}} {\varvec{z}} \right) \ge 0$ for some $k \in [K_0]$. If $d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}} > 0$, algebraic manipulations yield

  $$\begin{aligned} {\varvec{w}} = \dfrac{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}} }{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}} } {\varvec{w}} = \dfrac{d_k {\varvec{w}} - ( {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}} ) {\varvec{w}}}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}} } = \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}}, \end{aligned}$$

  where the last equality follows from the fact that ${\varvec{V}} = {\varvec{w}} {\varvec{z}}^\top$. Since ${\varvec{w}} \in {\text {dom}} h^*$, we must have $\displaystyle \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}} \in {\text {dom}} h^*$. We then derive convex constraints in $({\varvec{w}},w_0,{\varvec{z}},{\varvec{V}},{\varvec{v}}_0)$ that enforces this set membership. By multiplying both sides of a generic convex constraint on ${\varvec{w}}$, $g({\varvec{w}}) \le 0$, by the non-negative scalar $d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}$, we obtain

  $$\begin{aligned} ( d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}} ) g({\varvec{w}}) = (d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}) g \left( \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}} \right) \le 0, \end{aligned}$$

  (4)

  which is convex in $\left( d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}, d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k \right)$, since the constraint function is the perspective of the convex function g. Hence, it is convex in $({\varvec{w}},{\varvec{z}},{\varvec{V}})$. Note that if $d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}$ is not strictly positive, constraint (4) should still hold by a limit argument. We apply this methodology to:

  • Linear constraints on ${\varvec{w}}$, ${\varvec{g}}({\varvec{w}}) = {\varvec{F}} {\varvec{w}} - {\varvec{f}} \le {\varvec{0}}$. In this case, (4) leads to

    $$\begin{aligned} (d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}) \left[ {\varvec{F}} \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}} - {\varvec{f}} \right]&\le {\varvec{0}}, \end{aligned}$$

    and can be expressed as a linear constraint in $({\varvec{w}},{\varvec{z}}, {\varvec{V}})$:

    $$\begin{aligned} {\varvec{F}} \left[ d_k {\varvec{w}} - {\varvec{VD}}^\top {\varvec{e}}_k \right]&\le (d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}) \, {\varvec{f}}. \end{aligned}$$

    (5)

  • $g({\varvec{w}}) = g_j({\varvec{w}})$, $j \in [J_1]$, i.e,

    $$\begin{aligned} (d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}) g_j \left( \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}} \right) \le 0, \quad \forall j \in [J_1], \end{aligned}$$

    (6)

  • and the epigraph constraint, $h^*({\varvec{w}}) \le w_0$, yielding

    

    (7)

    where the equivalence follows from ${\varvec{v}}_0 = w_0 {\varvec{z}}$.

  Together, these constraints (5)–(6)–(7) enforce that

  $$\begin{aligned} \dfrac{d_k {\varvec{w}} - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k}{d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}} \in {\text {dom}} h^*. \end{aligned}$$

• b) Similarly, we can consider a linear constraint in ${\varvec{w}}$, ${f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}} \ge 0$, for some $j\in [J_0]$. We have

  $$\begin{aligned} {\varvec{z}} = \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \text{ so } \text{ that } \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \in {\mathcal {Z}}. \end{aligned}$$

  Given a generic convex constraint in ${\varvec{z}}$, $c({\varvec{z}}) \le 0$, we obtain a new convex constraint

  $$\begin{aligned} ({f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}) c \left( \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \right) \le 0. \end{aligned}$$

  Applying these manipulations to the linear constraints ${\varvec{D}}{\varvec{z}} \le {\varvec{d}}$ yields

  $$\begin{aligned} {\varvec{D}} \left[ f_j {\varvec{z}} - {\varvec{FV}} {\varvec{e}}_j \right]&\le (f_j - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}) \, {\varvec{d}}. \end{aligned}$$

  (8)

  Taking $c({\varvec{z}}) = c_k ({\varvec{z}})$, $k \in [K_1]$ we get

  $$\begin{aligned} ({f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}) c_k \left( \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \right) \le 0, \quad \forall k \in [K_1]. \end{aligned}$$

  (9)

  Eventually, we obtain constraints (8)-(9), enforcing that

  $$\begin{aligned} \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \in {\varvec{{\mathcal {Z}}}}. \end{aligned}$$

$\square$

Proposition 2 exhibits a hierarchy of approximations to convexify the non-convex set ${\varvec{\varTheta }}$. A safe approximation is then obtained by considering the robust linear constraint

$$\begin{aligned} \sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varPhi }} } \, \left\{ \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{V}}) + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - {w_0} \right\} \le 0, \end{aligned}$$

(10)

with ${\varvec{\varPhi }} = {\varvec{\varTheta }}_i$, $i=0,1,2$. Observe that for ${\varvec{\varTheta }}_0$, the robust counterpart of the safe approximation is

$$\begin{aligned} {\varvec{A}}({\varvec{x}}) = {\varvec{0}},\quad h({\varvec{b}}({\varvec{x}})) \le 0. \end{aligned}$$

Accordingly, it is fair to admit that ${\varvec{\varTheta }}_0$ offers a poor approximation and that relevant safe approximations are to be found at higher orders of the hierarchy. A higher order in the hierarchy, however, does not necessarily imply a tighter safe approximation, as discussed in Sect. 2.5.

So far, we obtained convex constraints on $({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0)$ by multiplying a linear constraint on ${\varvec{z}}$ (resp. ${\varvec{w}})$ with a convex constraint on ${\varvec{w}}$ (resp. ${\varvec{z}}$). However, in many cases multiplying two general convex constraints, e.g., multiplying $c_k({\varvec{z}}) \le 0$ with $g_j({\varvec{w}}) \le 0$, also yields valuable convex constraints. The resulting set, which we denote ${\varvec{\varTheta }}_3$ and concisely define as

$$\begin{aligned} {\varvec{\varTheta }}_3&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}_2, \\ c_k({\varvec{z}}) \times g_j({\varvec{w}}) \le 0,\ k \in [K_1],\ j \in [J_1] \end{array} \right. \right\} \end{aligned}$$

provides an even tighter safe approximation of (2). In the definition above, “$c_k({\varvec{z}}) \times g_j({\varvec{w}}) \le 0$” denotes valid convex inequalities obtained when multiplying “$c_k({\varvec{z}}) \le 0$” with “$g_j({\varvec{w}}) \le 0$”. In the following example, we illustrate this approach when $c_k$ and $g_j$ are two conic quadratic functions, which typically occurs with ellipsoidal uncertainty sets and a conic quadratic function h. We refer to Zhen et al. [20] for a thorough analysis of all 15 possible multiplications of any two of the five basic convex cones (linear, conic quadratic, power, exponential, semi-definite).

Example 2

Consider two conic quadratic inequalities

$$\begin{aligned}&\left\{ \begin{array}{l} b_1 -{\varvec{a}}_1^\top {\varvec{w}} \ge \Vert {{\varvec{D}}_1 {\varvec{w}} + {\varvec{p}}_1}\Vert \\ b_2 - {\varvec{a}}_2^\top {\varvec{z}} \ge \Vert {{\varvec{D}}_2 {\varvec{z}} + {\varvec{p}}_2}\Vert , \end{array} \right. \end{aligned}$$

the first one coming from the description of ${\text {dom}} h^*$, and the second is one of the constraints that define ${\varvec{{\mathcal {Z}}}}$. We now apply RPT to these inequalities, i.e., we multiply the LHS and RHS of the two constraints, and we multiply the LHS of the first constraint with the second constraint, and multiply the LHS of the second constraint with the first constraint. We obtain:

$$\begin{aligned}&\left\{ \begin{array}{l} (b_1 -{\varvec{a}}_1^\top {\varvec{w}} ) (b_2 - {\varvec{a}}_2^\top {\varvec{z}} ) \ge \Vert {{\varvec{D}}_1 {\varvec{w}} + {\varvec{p}}_1}\Vert \Vert {{\varvec{D}}_2 {\varvec{z}} + {\varvec{p}}_2}\Vert \\ (b_1 -{\varvec{a}}_1^\top {\varvec{w}} ) (b_2 - {\varvec{a}}_2^\top {\varvec{z}} ) \ge (b_1 -{\varvec{a}}_1^\top {\varvec{w}} ) \Vert {{\varvec{D}}_2 {\varvec{z}} + {\varvec{p}}_2}\Vert \\ (b_1 -{\varvec{a}}_1^\top {\varvec{w}} ) (b_2 - {\varvec{a}}_2^\top {\varvec{z}} ) \ge (b_2 - {\varvec{a}}_2^\top {\varvec{z}} ) \Vert {{\varvec{D}}_1 {\varvec{w}} + {\varvec{p}}_1}\Vert \end{array} \right. \\ \Leftrightarrow&\left\{ \begin{array}{l} b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{x}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{w}} {\varvec{z}}^\top {\varvec{a}}_2 \ge \Vert {({\varvec{D}}_1 {\varvec{w}} + {\varvec{p}}_1) ({\varvec{D}}_2 {\varvec{z}} + {\varvec{p}}_2)^\top }\Vert _2 \\ b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{w}} {\varvec{z}}^\top {\varvec{a}}_2 \ge \Vert {b_1 {\varvec{D}}_2 {\varvec{z}} + b_1 {\varvec{p}}_2 - {\varvec{D}}_2 {\varvec{w}} {\varvec{z}}^\top {\varvec{a}}_1 - {\varvec{a}}_1^\top {\varvec{w}} {\varvec{p}}_2 }\Vert \\ b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{w}} {\varvec{z}}^\top {\varvec{a}}_2 \ge \Vert {b_2 {\varvec{D}}_1 {\varvec{w}} + b_2 {\varvec{p}}_1 - {\varvec{D}}_1 {\varvec{w}} {\varvec{z}}^\top {\varvec{a}}_2 - {\varvec{a}}_2^\top {\varvec{z}} {\varvec{p}}_1 }\Vert \end{array} \right. \\ \Leftrightarrow&\left\{ \begin{array}{l} b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{V}} {\varvec{a}}_2 \ge \Vert { {\varvec{D}}_1 {\varvec{V}} {\varvec{D}}_2^\top + {\varvec{p}}_1 {\varvec{z}}^\top {\varvec{D}}_2^\top + {\varvec{D}}_1 {\varvec{w}} {\varvec{p}}_2^\top + {\varvec{p}}_1 {\varvec{p}}_2^\top }\Vert _2 \\ b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{V}} {\varvec{a}}_2 \ge \Vert {b_1 {\varvec{D}}_2 {\varvec{z}} + b_1 {\varvec{p}}_2 - {\varvec{D}}_2 {\varvec{V}} {\varvec{a}}_1 - {\varvec{a}}_1^\top {\varvec{w}} {\varvec{p}}_2 }\Vert \\ b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{V}} {\varvec{a}}_2 \ge \Vert {b_2 {\varvec{D}}_1 {\varvec{w}} + b_2 {\varvec{p}}_1 - {\varvec{D}}_1 {\varvec{V}} {\varvec{a}}_2 - {\varvec{a}}_2^\top {\varvec{z}} {\varvec{p}}_1 }\Vert , \end{array} \right. \end{aligned}$$

since ${\varvec{V}} = {\varvec{w}} {\varvec{z}}^\top$. Here, $\Vert \cdot \Vert _2$ denotes the 2-norm of a matrix defined as its largest singular value, i.e., $\Vert {\varvec{M}} \Vert _2 := \sigma _{\max }({\varvec{M}}) = \sqrt{\lambda _{\max }({\varvec{M}} {\varvec{M}}^\top )}$. In particular, we used the fact that for rank-1 matrices ${\varvec{M}} = {\varvec{u}} {\varvec{v}}^\top$, $\Vert {\varvec{M}} \Vert _2 = \Vert {\varvec{u}} \Vert \Vert {\varvec{v}} \Vert$. In practice, constraints of the form $\Vert {\varvec{M}} \Vert _2 \le \lambda$ can be modeled as semidefinite constraints using Schur complement. To improve scalability, however, one can replace the 2-norm in the first constraint by the Frobenius norm of the matrix. Indeed, $\Vert {\varvec{M}} \Vert _2 \le \Vert {\varvec{M}} \Vert _F$, and the equality holds for rank-1 and zero matrices, so

$$\begin{aligned}&\left\{ \begin{array}{l} b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{V}} {\varvec{a}}_2 \ge \Vert { {\varvec{D}}_1 {\varvec{V}} {\varvec{D}}_2^\top + {\varvec{p}}_1 {\varvec{z}}^\top {\varvec{D}}_2^\top + {\varvec{D}}_1 {\varvec{w}} {\varvec{p}}_2^\top + {\varvec{p}}_1 {\varvec{p}}_2^\top }\Vert _F \\ b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{V}} {\varvec{a}}_2 \ge \Vert {b_1 {\varvec{D}}_2 {\varvec{z}} + b_1 {\varvec{p}}_2 - {\varvec{D}}_2 {\varvec{V}} {\varvec{a}}_1 - {\varvec{a}}_1^\top {\varvec{w}} {\varvec{p}}_2 }\Vert \\ b_1 b_2 - b_1 {\varvec{a}}_2^\top {\varvec{z}} - b_2 {\varvec{a}}_1^\top {\varvec{w}} + {\varvec{a}}_1^\top {\varvec{V}} {\varvec{a}}_2 \ge \Vert {b_2 {\varvec{D}}_1 {\varvec{w}} + b_2 {\varvec{p}}_1 - {\varvec{D}}_1 {\varvec{V}} {\varvec{a}}_2 - {\varvec{a}}_2^\top {\varvec{z}} {\varvec{p}}_1 }\Vert \end{array} \right. \end{aligned}$$

are valid, yet looser, constraints.

We could even further tighten our approximations by applying RPT to ${\varvec{z}}$ and to ${\varvec{w}}$ separately. More specifically, we could multiply the linear and nonlinear constraints that define ${{\varvec{{\mathcal {Z}}}}}$ with each other and express them in terms of ${\varvec{z}}$, an additional variable defined as ${\varvec{Z}} = {\varvec{z}} {\varvec{z}}^\top$. The same could be done for the constraints in ${\text {dom}} h^*$, and define ${\varvec{W}} = {\varvec{w}} {\varvec{w}}^\top$. By doing so, all the nonlinear substitutions are concisely defined as

$$\begin{aligned} \begin{pmatrix} {\varvec{W}} &{}\quad {\varvec{V}} \\ {\varvec{V}}^\top &{}\quad {\varvec{z}} \end{pmatrix} = \begin{pmatrix} {\varvec{w}} \\ {\varvec{z}} \end{pmatrix} \begin{pmatrix} {\varvec{w}} \\ {\varvec{z}} \end{pmatrix}^\top . \end{aligned}$$

In a relaxation, the equality $=$ is replaced by $\succeq$ and, by using Schur complements, yields the semidefinite constraint:

$$\begin{aligned} \begin{pmatrix} {\varvec{W}} &{}\quad {\varvec{V}} &{}\quad {\varvec{w}} \\ {\varvec{V}}^\top &{}\quad {\varvec{z}} &{}\quad {\varvec{z}} \\ {\varvec{w}}^\top &{}\quad {\varvec{z}}^\top &{}\quad 1 \end{pmatrix} \succeq 0. \end{aligned}$$

(11)

Hence, we can add this LMI to any of the safe approximations obtained by RPT ${\varvec{\varTheta }}_i$ and the resulting uncertainty set, ${\varvec{\varTheta }}_{LMI, i}$, would provide a safe approximation at least as good as the one obtained from ${\varvec{\varTheta }}_i$. However, whether the extra computational burden outweighs the improvement of the approximation remains an open question, whose answer might depend on the specific problem. On a geometric optimization example in Sect. 5.2, for instance, we observed no numerical improvement from adding this LMI.

2.3 Step 3: Tractable robust counterpart

Finally, the safe approximation (10) is a robust constraint, linear in the uncertain parameters $({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0)$, and with a convex uncertainty set ${\varvec{\varPhi }} = {\varvec{\varTheta }}_i$, $i=0,1,2,3$. Hence, following the approach of Ben-Tal et al. [4], one can derive its robust counterpart by computing the support function of ${\varvec{\varPhi }}$, $\delta ^*( \cdot | {\varvec{\varPhi }})$. In particular, (10) is equivalent to

$$\begin{aligned} \delta ^* \left( \left. ({\varvec{b}}({\varvec{x}}), -1, {\varvec{0}}, {\varvec{A}}({\varvec{x}}), {\varvec{0}} ) \right| {\varvec{\varPhi }} \right) \le 0. \end{aligned}$$

In our hierarchy, note that ${\varvec{\varTheta }}_{i+1}$ is obtained by imposing additional constraints to ${\varvec{\varTheta }}_i$, hence is of the form ${\varvec{\varTheta }}_{i+1} = {\varvec{\varTheta }}_{i} \cap {\varvec{\varPhi }}_{i+1}$ for some convex set ${\varvec{\varPhi }}_{i+1}$. Consequently, the support function of ${\varvec{\varTheta }}_{i+1}$ can be expressed as a function of the support functions of ${\varvec{\varTheta }}_i$ and ${\varvec{\varPhi }}_{i+1}$ [see [4, Lemma 6.4]].

2.4 Description of the approach for conic constraints

In this section, we describe our Reformulation-Perspectification-Technique for conic inequalities. We consider an uncertain conic constraint of the type

$$\begin{aligned} {\varvec{A}}({\varvec{x}}){\varvec{z}} + {\varvec{b}}({\varvec{x}}) \preceq _{\mathcal {K}} {\varvec{0}}, \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

(12)

where ${\mathcal {K}} \in \Re ^m$ is a closed convex cone with nonempty relative interior. Examples of these cones are the linear cone, the second-order cone, the semi-definite cone, the power cone, and the exponential cone. We refer the reader to MOSEK [16] for an extensive treatment of these five cones. The dual cone, referred to as ${\mathcal {K}}^*$ of ${\mathcal {K}}$ is defined as

$$\begin{aligned} {\mathcal {K}}^* = \left\{ {\varvec{w}} \in \Re ^m\ :\ {\varvec{w}}^\top {\varvec{u}} \ge 0, \ \forall {\varvec{u}} \in {\mathcal {K}} \right\} , \end{aligned}$$

and is again a convex cone. Furthermore, we have ${\mathcal {K}} = \left( {\mathcal {K}}^{*}\right) ^*$, because the cone is closed and convex. Using these properties, we derive for (12)

We can now directly apply our RPT approach to the last inequality that is bilinear in the uncertain parameters ${\varvec{w}}$ and ${\varvec{z}}$. Note that this conic case is a special case of (2) where we have $h^*({\varvec{w}})=0$, and ${\text {dom}} h^* = \mathcal {K^*}$.

2.5 Trade-off between approximation accuracy and computational complexity

Our RPT approach exhibits a hierarchy of increasingly tighter safe approximations. In this section, we discuss the trade-off between the quality of a safe approximation and its computational tractability.

In terms of computational tractability, Table 2 reports the number of linear and convex inequalities involved in each set of our hierarchy, ${\varvec{\varTheta }}_i, i=0,1,2$. Observe that imposing constraints (8) for all $j \in [J_0]$ is redundant with imposing (5) for all $k \in [K_0]$. Hence, ${\varvec{\varTheta }}_2$ requires no additional linear constraints compared with ${\varvec{\varTheta }}_1$. Moving one level higher in the hierarchy requires adding a quadratic number of linear/convex constraints compared with the number of constraints defining ${\varvec{{\mathcal {Z}}}}$ and ${\text {dom}}h^*$. Furthermore, our approach involves the perspective functions and conjugates of the functions defining ${\varvec{{\mathcal {Z}}}}$ and ${\text {dom}}h^*$. If a function is conic representable in a cone ${\mathcal {K}}$, then its perspective (resp. conjugate) is conic representable in the same cone ${\mathcal {K}}$ (resp. the dual cone ${\mathcal {K}}^*$). On this aspect, our approach does not increase the computational complexity.

Table 2 Number of constraints defining the uncertainty sets of our hierarchy, ${\varvec{\varTheta }}_i, i=0,1,2$

Regarding approximation guarantees, we note that if the description of ${\varvec{{\mathcal {Z}}}}$ involves no linear constraints ($K_0 = 0$), then ${\varvec{\varTheta }}_0 = {\varvec{\varTheta }}_1$, and ${\varvec{\varTheta }}_2$ would provide a substantial benefit. Alternatively, when ${\varvec{{\mathcal {Z}}}}$ is polyhedral ($J_0 = 0$), ${\varvec{\varTheta }}_1 = {\varvec{\varTheta }}_2$ and ${\varvec{\varTheta }}_1$ provides all the benefit. Consequently, we intuit that the relative benefit of ${\varvec{\varTheta }}_2$ over ${\varvec{\varTheta }}_1$ depends on how binding the convex constraints in ${\varvec{{\mathcal {Z}}}}$ are. For instance, if the description of ${\mathcal {Z}}$ contains one convex constraint $c({\varvec{z}}) \le 0$ that is redundant with the linear constraints ${\varvec{D}}{\varvec{z}} \le {\varvec{d}}$, then the constraints

$$\begin{aligned} ({f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}) c \left( \dfrac{{f_j}{\varvec{z}} - {\varvec{F}} {\varvec{V}} {\varvec{e}}_j}{{f_j} - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}} \right) \le 0, \ \forall j \in [J_0] \end{aligned}$$

(13)

in ${\varvec{\varTheta }}_2$ are redundant with linear constraints in ${\varvec{\varTheta }}_1$.

Proof

As previously observed, imposing constraints (5) for all $k \in [K_0]$ in ${\varvec{\varTheta }}_1$ is equivalent to imposing (8) for all $j \in [J_0]$. Hence, for any $j \in [J_0]$, for any $({\varvec{w}},w_0,{\varvec{z}},{\varvec{V}},{\varvec{v}}_0) \in {\varvec{\varTheta }}_1$, if $f_j - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}>0$, ${\varvec{y}} := (f_j {\varvec{z}} - {\varvec{F}}{\varvec{V}}{\varvec{e}}_j) / (f_j - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}})$ satisfies ${\varvec{D}} {\varvec{y}} \le {\varvec{d}}$. Hence, $c({\varvec{y}}) \le 0$ and constraints (13) are satisfied. Note that the result holds if $f_j - {\varvec{e}}_j^\top {\varvec{F}} {\varvec{w}}=0$, by continuity. $\square$

When ${\varvec{{\mathcal {Z}}}}$ is polyhedral, we will show in Sect. 3.2 that RPT with ${\varvec{\varTheta }}_1$ can be viewed as approximating an adaptive robust optimization problem (with uncertainty set ${\text {dom}}h^*$) with linear decision rules [as in [18, Theorem 2]]. In addition, if h is piecewise linear, then ${\text {dom}}h^*$ is a simplex. Since linear decision rules are optimal for simplex uncertainty sets, as proved by Bertsimas and Goyal [7, Theorem 1] and generalized in Ben-Ameur et al. [1, Corollary 1], ${\varvec{\varTheta }}_1$ provides an exact reformulation of (1). In general, for polyhedral ${\varvec{{\mathcal {Z}}}}$, the quality of the approximation with ${\varvec{\varTheta }}_1$ will thus depend on the geometry of ${\text {dom}}h^*$, in particular its symmetry and “simplex dilation factor” [5]; see El Housni and Goyal [12, 13] and references therein for some average- and worst-case performance results of linear decision rules. Theoretical results to precisely quantify the benefit, in terms of approximation guarantee, of each level of the hierarchy constitutes an interesting future direction.

From a practical standpoint, when using our approach with the uncertainty set ${\varvec{\varTheta }}_1$, one can check whether the additional constraints in ${\varvec{\varTheta }}_2$ are satisfied by the worst-case scenario for the current solution. If so, the current solution remains robust feasible for ${\varvec{\varTheta }}_2$ and ${\varvec{\varTheta }}_2$ will not provide any improvement. Alternatively, our approach provides both an upper and lower bound (see Sect. 4). Combined, they can be used to measure the approximation gap and decide whether to use ${\varvec{\varTheta }}_{2}$ instead.

3 Connection with previous approaches from the literature

In this section, we show that our RPT approach unifies many existing robust convex optimization techniques, and extends them in a significant way.

3.1 Case when the uncertainty set lies in the non-negative orthant

First, we restrict our analysis to cases where the linear inequalities describing ${\varvec{{\mathcal {Z}}}}$ in Assumption 1 are non-negativity constraints only. Formally, we make the following assumption:

Assumption 3

The uncertainty set ${\varvec{{\mathcal {Z}}}} = \left\{ {\varvec{z}}\, \vert \, {\varvec{z}} \ge {\varvec{0}},\ c_k({\varvec{z}}) \le {\varvec{0}}, k \in [K] \right\}$ is full dimensional and bounded, where $c_k:{\mathbb {R}}^{L} \mapsto [-\infty , +\infty ]$ is proper, closed and convex for each $k \in [K]$.

Note that the non-negativity assumption of ${\varvec{{\mathcal {Z}}}}$ can always be satisfied by properly lifting or shifting the uncertainty set (see the detailed discussion in Sect. 5.1 and Appendix A). Under this more specialized assumption, we reformulate our RPT-based safe approximation with ${\varvec{\varTheta }}_1$ (Corollary 1) and discuss its connection with the approaches from Bertsimas and Sim [8] and Roos et al. [18]. We will later refer to Corollary 1 as the perspectification approach because it can also be derived without invoking the RPT but a perspectification lemma instead (as we do in Appendix A).

Corollary 1

For ${\varvec{{\mathcal {Z}}}}$ satisfying Assumption 3, the safe approximation obtained with RPT and ${\varvec{\varTheta }}_1$ is equivalent to

$$\begin{aligned} \sum _{\ell \in [L]} z_\ell h_\infty \left( {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right) + h\left( {{\varvec{b}}({\varvec{x}})} \right) \le 0, \quad \forall {{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}}. \end{aligned}$$

(14)

Proof

We need the following identity, for any $u \ge 0$,

$$\begin{aligned} u \ h\left( \frac{{\varvec{y}}}{u}\right)&= \sup _{\begin{array}{c} {\varvec{w}} \in {\text {dom}} h^* \end{array}} \quad \left\{ {\varvec{y}}^\top {\varvec{w}} - u h^*({\varvec{w}}) \right\} . \end{aligned}$$

Denoting between brackets the dual variables associated with constraints in the definition of ${\varvec{\varTheta }}_1$,

$$\begin{aligned} {\varvec{\varTheta }}_{1}&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \\ {\varvec{w}} \in {\text {dom}} h^*, h^*({\varvec{w}}) \le w_0, &{}[u]\\ {{\varvec{V}} {\varvec{e}}_\ell }/{{z}_\ell } \in {\text {dom}} h^*, {z}_\ell h^* \left( \dfrac{{\varvec{V}} {\varvec{e}}_\ell }{{z}_\ell } \right) \le {{\varvec{v}}_{0\ell }}, \ \ell \in [L], &{} [u_\ell ] \end{array} \right. \right\} , \end{aligned}$$

we have

$$\begin{aligned}&\sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}_1 } \left\{ \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{V}} ) + {\varvec{b}}( {\varvec{x}})^\top {\varvec{w}} - {w_0} \right\} \\ =&\sup _{ \begin{array}{c} {\varvec{z}} \in {\varvec{{\mathcal {Z}}}} \\ w_0, {\varvec{v}}_{0} \end{array}} \, \sup _{ \begin{array}{c} {\varvec{w}} \in {\text {dom}} h^*\\ {\varvec{V}}{\varvec{e}}_\ell /z_\ell \in {\text {dom}} h^* \end{array} } \, \inf _{ {u, {\varvec{u}} \ge 0} } \quad \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{V}} ) + {\varvec{b}}( {\varvec{x}})^\top {\varvec{w}} - {w_0} - u( h^*({\varvec{w}}) - w_0) \\&\quad - \sum _{\ell \in [L]} u_\ell \left( z_\ell h^*\left( \frac{{\varvec{V}} {\varvec{e}}_\ell }{ z_\ell }\right) - v_{0 \ell }\right) . \end{aligned}$$

Let us observe that

$$\begin{aligned} \sup _{{\varvec{w}} \in {\text {dom}}h^*} \, {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - u h^*({\varvec{w}}) = u h\left( \dfrac{{\varvec{b}}({\varvec{x}})}{u}\right) , \end{aligned}$$

and similarly for the terms involving ${\varvec{V}}{\varvec{e}}_\ell / z_\ell$, $\ell \in [L]$, so that

$$\begin{aligned}&\sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}_1 } \left\{ \mathrm {Tr}( {\varvec{A}}({\varvec{x}})^\top {\varvec{V}} ) + {\varvec{b}}( {\varvec{x}})^\top {\varvec{w}} - {w_0} \right\} \\ =&\sup _{ {{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} } \inf _{ {u, {\varvec{u}} \ge 0} } \sup _{w_0, {\varvec{v}}_0} \sum _{\ell } u_\ell z_\ell h\left( \dfrac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{u_\ell } \right) + u h\left( \dfrac{{\varvec{b}}({\varvec{x}})}{u}\right) + \, {\varvec{u}}^\top {\varvec{v}}_0 + (u-1)w_0 \\ =&\sup _{ {{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} } \, \sum _{\ell \in [L]} z_\ell h_\infty \left( {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right) + h\left( {{\varvec{b}}({\varvec{x}})} \right) , \end{aligned}$$

where the last equality holds because ${\varvec{u}}= {\varvec{0}}$ and $u = 1$. $\square$

Remark 1

Corollary 1 might be uninformative if the recession function of h is unbounded (e.g., if h is strongly convex). In this case, we propose an alternative to Corollary 1 with the additional requirement that $h({\varvec{0}})=0$. Indeed, $h({\varvec{0}}) = 0$ implies $w_0 \ge h^*({\varvec{w}}) \ge 0$. In this case, we should define

$$\begin{aligned} {\varvec{\varTheta }}_{0}&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \\ {\varvec{w}} \in {\text {dom}} h^*, \\ w_0 \ge 0, h^*({\varvec{w}}) \le w_0, \\ {\varvec{v}}_0 / w_0 \in {\varvec{{\mathcal {Z}}}} \end{array} \right. \right\} , \end{aligned}$$

in Proposition 2, where the membership ${\varvec{v}}_0 / w_0 \in {\varvec{{\mathcal {Z}}}}$ is enforced by multiplying each constraint in the definition of ${\varvec{{\mathcal {Z}}}}$ by $w_0 \ge 0$. The resulting safe approximation is:

$$\begin{aligned} \exists ({\varvec{u}}, u )\in {\mathbb {R}}^{L+1}_+, \ \text{ s.t. }&\sum _{\ell \in [L]} z_\ell u_\ell h\left( \frac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{u_\ell }\right) + u \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{u}\right) \le 0,&\forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \\&{\varvec{z}}^\top {\varvec{u}} + u \le 1,&\forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}. \end{aligned}$$

The key benefit from Corollary 1 is that it preserves the uncertainty set. Namely, it safely approximates the robust convex constraint (1) by a robust constraint that is linear in the same uncertain parameter ${\varvec{z}}$. Consequently, one can also derive probabilistic guarantees for this safe approximation, after positing a generative distributional model for ${\varvec{z}}$. We derive such guarantees in Appendix A.

We now compare this formulation with the approaches from Bertsimas and Sim [8] and Roos et al. [18].

For positively homogeneous functions h, we show that Corollary 1recovers the approach of Bertsimas and Sim [8].

Indeed, Bertsimas and Sim [8] construct a safe approximation for the robust constraint (1) in the special case where the function $h(\cdot )$ is positively homogeneous, i.e., $h(\lambda {\varvec{y}}) = \lambda h({\varvec{y}})$ for any $\lambda > 0$ and ${\varvec{y}}$. In this case,

$$\begin{aligned} h_\infty ({\varvec{y}}) = \lim _{t \rightarrow 0} t h({\varvec{y}} / t) = h({\varvec{y}}), \end{aligned}$$

so Corollary 1 is equivalent to

$$\begin{aligned} \sum _{\ell \in [L]} z_\ell h\left( {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right) + h\left( {\varvec{b}}({\varvec{x}})\right) \le 0, \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

which coincides with the approximation proposed by Bertsimas and Sim [8]. Accordingly, the RPT approach extends the one in Bertsimas and Sim [8] in multiple significant ways. First, Bertsimas and Sim [8] require h to be convex and homogeneous, hence sub-additive. They use sub-additivity to derive their safe approximation. In contrast, Corollary 1 applies to any convex function. In Appendix A, we show how Corollary 1 can also be obtained independently from the RPT approach, by using a generalization of sub-additivity to general convex functions called the perspectification lemma (Lemma 1). Second, the RPT approach can lead to tighter approximations when (a) some of the generic convex constraints $c_k({\varvec{z}}) \le 0$ are also linear and can be used to define a smaller set ${\varvec{\varTheta }}_1$, or when (b) a higher set in the hierarchy of approximations is used. Finally, besides the safe approximation, Bertsimas and Sim [8] also propose a non-convex lifting procedure to transform any norm-based set into a lifted uncertainty set that lies in the non-negative orthant and satisfies Assumption 3. On that regard, our proposal is agnostic of the procedure used in practice to ensure Assumption 3 holds.

We now show that Corollary 1coincides with the safe approximation of (1) from Roos et al. [18] with static policies.

Roos et al. [18] propose to first reformulate (1) as an adaptive robust nonlinear constraint, which they then approximate with static decision rules:

Proposition 3

([18], Theorem 7) Under Assumption 3, the robust convex constraint (1) can be safely approximated by the constraints

$$\begin{aligned} \begin{array}{ll} \exists {\varvec{\lambda }}\ge {\varvec{0}}, \{{\varvec{u}}^k\}_k , \text{ s.t. } ,\ &{} \displaystyle \sum _{k=1}^K \lambda _k c_k^* \left( {\varvec{u}}^k / \lambda _k \right) + h({\varvec{b}}({\varvec{x}})) \le 0, \\ &{} \displaystyle h_\infty ( {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell )\le \sum _{k=1}^K {\varvec{u}}^k_\ell , \forall \ell \in [L]. \end{array} \end{aligned}$$

Proposition 3 is equivalent to Corollary 1 after observing that, for any ${\varvec{y}}$,

$$\begin{aligned} \sup _{{\varvec{z}} \ge 0 : c_k ({\varvec{z}}) \le 0, k \in [K]} \, {\varvec{y}}^\top {\varvec{z}} = \inf _{\begin{array}{c} {\varvec{u}}^k, k \in [K] \\ \lambda _k \ge 0, k \in [K] \end{array}} \, \sum _{k} \lambda _k c^*\left( \dfrac{{\varvec{u}}^k}{\lambda _k}\right) \text{ s.t. } {\varvec{y}} \le \sum _{k\in [K]} {\varvec{u}}^k. \end{aligned}$$

Consequently, our RPT approach extends Roos et al. [18, Theorem 7] by providing tighter approximations when additional linear constraints are present or when using a higher set in the hierarchy.

3.2 Case when the uncertainty set is a polyhedron

In this subsection, we show that the safe approximation obtained from ${\varvec{\varTheta }}_1$ for (1) with ${\varvec{{\mathcal {Z}}}} = \left\{ {\varvec{z}}\, \vert \, {\varvec{D}} {\varvec{z}} \le {\varvec{d}} \right\}$, where ${\varvec{D}} \in {\mathbb {R}}^{K_0 \times L}$, ${\varvec{d}} \in {\mathbb {R}}^{K_0}$, coincides with that of Theorem 2 in Roos et al. [18].

It follows from Proposition 2 that the convex robust constraint (1) can be safely approximated by

$$\begin{aligned} \sup _{({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}_{1}} \left\{ \mathrm {Tr}\{{\varvec{A}}({\varvec{x}})^\top {\varvec{V}}\} + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - w_0 \right\} \le 0, \end{aligned}$$

where ${\varvec{\varTheta }}_{1}$ is equal to

$$\begin{aligned} \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} {\varvec{D}} {\varvec{z}} \le {\varvec{d}}, \\ h^*({\varvec{w}}) \le w_0, \\ (d_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}) h^*\left( \frac{{\varvec{w}} d_k - {\varvec{V}} {\varvec{D}}^\top {\varvec{e}}_k }{p_k - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{z}}}\right) \le d_k w_0 - {\varvec{e}}_k^\top {\varvec{D}} {\varvec{v}}_0 , k \in [K_0] \end{array} \right. \right\} . \end{aligned}$$

The corresponding tractable robust counterpart constitutes a safe approximation of (1), which coincides with the safe approximation of (1) proposed in Roos et al. [18, Theorem 2].

3.3 Connection to result for robust quadratic with an ellipsoid

It is well-known that robust quadratic inequalities with an ellipsoidal uncertainty set admit an exact SDP reformulation via the S-lemma [see [3]]. Alternatively, we show that the same reformulation can be obtained via RPT. To this end, consider the following robust quadratic inequality, which is a special case of the bilinear reformulation in Proposition 1 with ${\varvec{w}} = {\varvec{z}}$,

$$\begin{aligned} {\varvec{z}}^\top {\varvec{A}}({\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}})^\top {\varvec{z}} \le g({\varvec{x}}) \quad \forall {\varvec{z}} \in \{ {\varvec{z}} \in {\mathbb {R}}^{L} : {\varvec{z}}^\top {\varvec{D}} {\varvec{z}} + {\varvec{d}}^\top {\varvec{z}} \le c \}, \end{aligned}$$

(15)

which is equivalent to

$$\begin{aligned} \max _{ ({\varvec{z}} , {{\varvec{Z}}}) \in {\varvec{\varTheta }}_{ell}} \left\{ \mathrm {Tr} ({\varvec{A}}({\varvec{x}}) {{\varvec{Z}}}) + {\varvec{b}}({\varvec{x}})^\top {\varvec{z}} \right\} \le g({\varvec{x}}), \end{aligned}$$

where ${\varvec{\varTheta }}_{ell} = \left\{ ({\varvec{z}} , {{\varvec{Z}}}) \in {\mathbb {R}}^{L} \times {\mathbb {S}}^{L} \ \vert \ \mathrm{Tr} ({\varvec{D}} {{\varvec{Z}}}) + {\varvec{d}}^\top {\varvec{z}} \le c, \ {{\varvec{Z}}} = {\varvec{z}} {\varvec{z}}^\top \right\}$. The set ${\varvec{\varTheta }}_{ell}$ is non-convex because of the nonlinear equality ${{\varvec{Z}}} = {\varvec{z}} {\varvec{z}}^\top$, and the outer approximations of ${\varvec{\varTheta }}_{ell}$ proposed in Proposition 2 satisfy ${\varvec{\varTheta }}_{ell} \subseteq {\varvec{\varTheta }}_{{ell},0} = {\varvec{\varTheta }}_{{ell},1} = {\varvec{\varTheta }}_{{ell},2}$. By relaxing the non-convex constraint ${{\varvec{Z}}} = {\varvec{z}} {\varvec{z}}^\top$ to ${{\varvec{Z}}} \succeq {\varvec{z}} {\varvec{z}}^\top$, and then using Schur complement we obtain:

$$\begin{aligned} {\varvec{\varTheta }}_{{ell},3} = \left\{ ({\varvec{z}} , {{\varvec{Z}}}) \in {\mathbb {R}}^{L} \times {\mathbb {S}}^{L} \ \left| \ \mathrm{Tr} ({\varvec{D}} {{\varvec{Z}}}) + {\varvec{d}}^\top {\varvec{z}} \le c, \begin{pmatrix} {{\varvec{Z}}} &{} {\varvec{z}} \\ {\varvec{z}}^\top &{} 1 \end{pmatrix} \succeq 0 \right. \right\} . \end{aligned}$$

The tractable robust counterpart of

$$\begin{aligned} \max _{ ({\varvec{z}} , {{\varvec{Z}}}) \in {\varvec{\varTheta }}_{ell,3}} \left\{ \mathrm {Tr} ({\varvec{A}}({\varvec{x}}) {{\varvec{Z}}}) + {\varvec{b}}({\varvec{x}})^\top {\varvec{z}} \right\} \le g({\varvec{x}}) \end{aligned}$$

coincides with the tractable robust counterpart of (15) obtained from using the S-lemma. Moreover, if the uncertainty set constitutes an intersection of ellipsoids, the obtained safe approximation for the robust quadratic inequality via RPT coincides with that from the approximate S-lemma [2]. In Zhen et al. [20], a similar relationship between the (approximate) S-lemma and RPT is established for quadratically constrainted quadratic optimization.

4 Obtaining lower bounds

One simple way of relaxing constraint (1) is to consider a finite subset of scenarios $\overline{{\varvec{{\mathcal {Z}}}}}$ sampled from the uncertainty set ${\varvec{{\mathcal {Z}}}}$, and the sampled version of (1) constitutes a finite set of convex inequalities:

(16)

where $\{{\varvec{z}}^{(1)}, \cdots , {\varvec{z}}^{(I)} \} = \overline{{\varvec{{\mathcal {Z}}}}} \subseteq {\varvec{{\mathcal {Z}}}}$. Here, the point-wise maximum of convex functions in the sampled inequality can be reformulated into a finite set of convex inequalities (16), and provides a naive progressive approximation of (1).

The question that remains is how to choose the finite set of scenarios. One simple way to do this would be to consider all extreme points of ${\varvec{{\mathcal {Z}}}}$, and the sampled version (16) is then optimal. However, the number of extreme points of ${\varvec{{\mathcal {Z}}}}$ could be large in general. Hadjiyiannis et al. [14] propose a way to obtain a small but effective finite set of scenarios for two-stage robust linear problems, which takes scenarios that are binding for the model solved with affine policies.

Alternatively, we can also adopt a dual perspective and sample scenarios from ${\text {dom}} h^*$. Consider the following form of the bilinear reformulation (2) with a fixed ${\varvec{x}}$:

$$\begin{aligned} \sup _{\begin{array}{c} {\varvec{z}} \in {\varvec{{\mathcal {Z}}}} \\ {\varvec{w}} \in {\text {dom}} h^* \end{array}} \left\{ {\varvec{w}}^\top {\varvec{A}}({\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - h^*({\varvec{w}}) \right\} . \end{aligned}$$

(17)

The embedded maximization problem in (17) can be interpreted as a disjoint bilinear problem, that is, fixing either ${\varvec{z}}$ or ${\varvec{w}}$, the embedded problem becomes a convex optimization problem. Hence, given a finite set $\overline{{\varvec{{\mathcal {W}}}}} \subseteq {\text {dom}} h^*$, the constraints

$$\begin{aligned} \sup _{{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} \left\{ {\varvec{w}}^\top {\varvec{A}}({\varvec{x}}') {\varvec{z}} + {\varvec{b}}({\varvec{x}}')^\top {\varvec{w}} - h^*({\varvec{w}}) \right\} \le 0,\ \forall {\varvec{w}} \in \overline{{\varvec{{\mathcal {W}}}}} \end{aligned}$$

(18)

provide a progressive approximation of (1) as well.

Hence, we propose a hybrid approach to obtain valid lower bounds where we replace both ${\varvec{{\mathcal {Z}}}}$ and ${\text {dom}} h^*$ in (17) by finite subsets $\overline{{\varvec{{\mathcal {Z}}}}}$ and $\overline{{\varvec{{\mathcal {W}}}}}$ respectively. The idea here is adopted from Zhen et al. [21].

For a fixed ${\varvec{x}}$, we observe that the embedded problem in (17) becomes a convex optimization problem whenever ${\varvec{z}}$ or ${\varvec{w}}$ is fixed. By exploiting this observation, for any given ${\varvec{z}}' \in \overline{{\varvec{{\mathcal {Z}}}}} \subseteq {\varvec{{\mathcal {Z}}}}$, the maximizer

$$\begin{aligned} {\varvec{w}}' = {{\,\mathrm{arg\,max}\,}}_{{\varvec{w}} \in \mathrm{dom} \ h^*} {\varvec{w}}^\top {\varvec{A}}({\varvec{x}}) {\varvec{z}}' + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - h^*({\varvec{w}}) \end{aligned}$$

is a violating scenario if the corresponding optimal value is larger than 0, and ${\varvec{w}}'$ can be used to update $\overline{{\varvec{{\mathcal {W}}}}}$, that is, $\overline{{\varvec{{\mathcal {W}}}}} \leftarrow \overline{{\varvec{{\mathcal {W}}}}}\cup \{{\varvec{w}}'\}$. Subsequently, fixing the obtained ${\varvec{w}}'$ in (17), the maximizer

$$\begin{aligned} {\varvec{z}}' = {{\,\mathrm{arg\,max}\,}}_{{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} {{\varvec{w}}'}^\top {\varvec{A}}({\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}}' - h^*({\varvec{w}}) \end{aligned}$$

(19)

is a violating scenario if the corresponding optimal value is larger than 0, and ${\varvec{z}}'$ can be used to update $\overline{{\varvec{{\mathcal {Z}}}}}$, that is, $\overline{{\varvec{{\mathcal {Z}}}}} \leftarrow \overline{{\varvec{{\mathcal {Z}}}}}\cup \{{\varvec{z}}'\}$. We can repeat this iterative procedure till no improvement on the lower bound for (17) can be achieved. The enriched sets $\overline{{\varvec{{\mathcal {Z}}}}}$ and $\overline{{\varvec{{\mathcal {W}}}}}$ can then be used to improve ${\varvec{x}}$ by solving the optimization problem with both (16) with $\overline{{\varvec{{\mathcal {Z}}}}}$ and (18) with $\overline{{\varvec{{\mathcal {W}}}}}$. The procedure can be repeated till no improvement can be achieved or the prescribed computational limit is met.

Remark 2

One can improve the efficiency of the iterative procedure if ${\varvec{A}}({\varvec{x}}) = {\varvec{A}}$ in (1), that is, ${\varvec{A}}$ is independent of ${\varvec{x}}$. In this case, for a given ${\varvec{w}}'$, de Ruiter et al. [19] have shown that the maximizer ${\varvec{z}}'$ in (19) dominates ${\varvec{w}}'$, that is, the feasible region of ${\varvec{x}}$ in (16) with $\overline{{\varvec{{\mathcal {Z}}}}}' = \{ {\varvec{z}}' \}$ is larger or equal to the one in (18) with $\overline{{\varvec{{\mathcal {W}}}}}' = \{{\varvec{w}}'\}$. Therefore, the inequalities involving ${\varvec{w}}'$ is redundant, and can be omitted throughout the procedure to improve the efficiency of this iterative procedure.

5 Computational results

In this section, we assess the numerical benefit from our RPT hierarchy on two examples, a robust control and geometric optimization setting, respectively.

5.1 Constrained linear-quadratic control

In this section, we consider an example from stochastic linear-quadratic control as in Bertsimas and Brown [6]. They consider a discrete-time stochastic system of the form:

$$\begin{aligned} {\varvec{y}}_{k+1} = {\varvec{A}}_k {\varvec{y}}_k + {\varvec{B}}_k {\varvec{u}}_k + {\varvec{C}}_k {\varvec{z}}_k, \quad k = 0,\dots ,N-1, \end{aligned}$$

where ${\varvec{y}}_k$, ${\varvec{u}}_k$, and ${\varvec{z}}_k$ are the state, control, and disturbance vectors respectively. The objective is to control the system (find control vectors ${\varvec{u}}_k$) in order to minimize the cost function

$$\begin{aligned} J({\varvec{y}}_0, {\varvec{u}}, {\varvec{z}}) = \sum _{k=1}^N ({\varvec{y}}_k^\top {\varvec{Q}}_k {\varvec{y}}_k + 2 {\varvec{q}}_k^\top {\varvec{y}}_k) + \sum _{k=0}^{N-1} ({\varvec{u}}_k^\top {\varvec{R}}_k {\varvec{u}}_k + 2 {\varvec{r}}_k^\top {\varvec{u}}_k), \end{aligned}$$

under some uncertainty on the disturbance vectors ${\varvec{z}}_k$. After algebraic manipulations and given a robust description of the uncertainty, the problem can be cast into

$$\begin{aligned} \min _{{\varvec{x}}, t} \, t \, \text{ s.t. } \Vert {\varvec{x}} \Vert _2^2 + 2 ({\varvec{F}}^\top {\varvec{x}} + {\varvec{h}})^\top {\varvec{z}} + {\varvec{z}}^\top {\varvec{C}} {\varvec{z}} \le t, \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

where ${\varvec{{\mathcal {Z}}}} = \{ {\varvec{z}} \, : \, \Vert {\varvec{z}} \Vert _2 \le \gamma \}$, and properly define vector ${\varvec{h}}$ and matrices ${\varvec{F}}$, ${\varvec{C}}$ (${\varvec{C}} \succeq {\varvec{0}}$). Note that ${\varvec{x}}$ can be subject to other deterministic constraints. For instance, imposing ${\varvec{u}}_k \ge {\varvec{0}}$ yields linear constraints on ${\varvec{x}}$. We refer the reader to Bertsimas and Brown [6] and references therein for problem motivation and details on the derivations.

Hence, we focus our attention to the robust convex constraint

$$\begin{aligned} 2 ({\varvec{F}}^\top {\varvec{x}} + {\varvec{h}})^\top {\varvec{z}} + {\varvec{z}}^\top {\varvec{C}} {\varvec{z}} \le t - \Vert {\varvec{x}} \Vert _2^2, \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}. \end{aligned}$$

(20)

Note that ${\varvec{{\mathcal {Z}}}}$ is described using a single quadratic constraint. However, our approximations partly rely on the presence of linear constraints in the definition of the uncertainty set. Hence, one could consider a shifted uncertainty set instead, obtained by introducing redundant linear inequalities such as with $\bar{{\varvec{z}}} = \gamma {\varvec{e}}$ and , or a non-convex lifting of ${\varvec{{\mathcal {Z}}}}$ as in Bertsimas and Sim [8]. In this section, we compare these modeling alternatives with three objectives in mind: (a) illustrate the benefit of our general RPT approach outlined in Sect. 2 over the perspectification approach from Sect. 3.1 (and Appendix A), which requires more stringent assumptions on the uncertainty set, (b) measure the relative benefit from shifting or lifting the uncertainty set, and (c) compare and assess the overall strength of our proposed safe approximations.

It is well-known that the robust constraint (20) is equivalent to a semidefinite constraint, which we will use as a benchmark to measure the suboptimality of our approach. In our numerical experiments, as in Bertsimas and Brown [6], we take ${\varvec{y}}_0=-1$, ${\varvec{A}}_k = {\varvec{B}}_k = {\varvec{C}}_k = 1$, ${\varvec{Q}}_k = {\varvec{R}}_k = \beta ^k$ with $\beta \in (0,1)$, and ${\varvec{q}}_k = {\varvec{r}}_k = 0$.

5.1.1 Benefit from RPT over Perspectification

As we derived in Sect. 3.1, applying RPT up to ${\varvec{\varTheta }}_1$ in Proposition 2 leads to the safe approximation presented in Corollary 1. In addition, here, there are no linear constraints in the description of ${\text {dom}} h^*$, so ${\varvec{\varTheta }}_1 = {\varvec{\varTheta }}_2$ and the benefit from using RPT (Proposition 2) over perspectification (Corollary 1) might be unclear. Yet, as discussed in Sect. 2.2, RPT is more flexible and can allow for an arbitrary number of linear constraints, while perspectification can only account for non-negativity constraints on ${\varvec{z}}$. We illustrate this point on the present example.

To derive meaningful safe approximations, we need to enrich the definition of ${\varvec{{\mathcal {Z}}}}$ with linear constraints. A generic method for doing so is shifting the uncertainty set. For instance, any ${\varvec{z}} : \Vert {\varvec{z}} \Vert _2 \le \gamma$ satisfies $-\gamma {\varvec{e}} \le {\varvec{z}} \le \gamma {\varvec{e}}$. Accordingly, we can:

• Consider the shifted uncertain vector $\tilde{{\varvec{z}}} = \gamma {\varvec{e}} + {\varvec{z}}$, ${\varvec{z}} \in {\varvec{{\mathcal {Z}}}}$, so that $\tilde{{\varvec{z}}} \ge {\varvec{0}}$ and apply Corollary 1. We will refer to this method as [Cor. 1 LB];

• Consider the shifted uncertainty set $\gamma {\varvec{e}} - {\varvec{{\mathcal {Z}}}} \subseteq {\mathbb {R}}_+^I$ and apply Corollary 1 [Cor. 1 UB];

• Add the 2L linear inequalities $-\gamma {\varvec{e}} \le {\varvec{z}} \le \gamma {\varvec{e}}$ to the definition of ${\varvec{{\mathcal {Z}}}}$ and apply RPT with ${\varvec{\varTheta }}_1$ [Prop. 2, Shifted $\varTheta _1$].

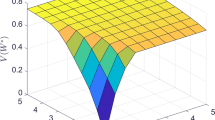
Derivations of the resulting three safe approximations are provided in Appendix B. Figure 1 displays the sub-optimality gap of each alternative, compared with the exact SDP reformulation, as $\gamma$ increases. [Prop. 2, Lifted $\varTheta _1$] provides a substantial improvement over both [Cor. 1 LB] and [Cor. 1 UB], hence illustrating the benefit from accounting for both lower and upper bounds on ${\varvec{z}}$ when safely approximating the robust constraint. Corollary 1, however, is unable to leverage such information, for it requires exactly and only L non-negativity constraints. In addition, applying RPT opens the door to a hierarchy of approximations. For instance, by multiplying the two norm constraints in the definition of ${\varvec{{\mathcal {Z}}}}$ and ${\text {dom}} h^*$ respectively, one can consider the third level of approximation ${\varvec{\varTheta }}_3$ which further reduces the optimality gap (see performance of [Prop. 2, Lifted $\varTheta _3$] in Fig. 1).

Fig. 1

Computational results on constrained linear-quadratic control. Evolution of the sub-optimality gap of the safe approximation as $\gamma$ increases for a constrained linear-quadratic control examples with $N=20$ periods and shifted uncertainty sets

5.1.2 Benefit from lifting over shifting

Another option to add linear constraints into the definition of the uncertainty set is to decompose ${\varvec{z}}$ into ${\varvec{z}} = {\varvec{z}}^+ - {\varvec{z}}^-$ and consider the lifted uncertainty set $\{ ({\varvec{z}}^+, {\varvec{z}}^-) \, : \, {\varvec{z}}^+,{\varvec{z}}^- \ge {\varvec{0}},\ \Vert {\varvec{z}}^+ + {\varvec{z}}^-\Vert _2 \le \gamma \}$. Observe that this kind of non-convex lifting cannot be applied to any uncertainty set, for the constraint $\Vert {\varvec{z}} \Vert _2 \le \gamma$ is replaced by $\Vert {\varvec{z}}^+ + {\varvec{z}}^-\Vert _2 \le \gamma$ - instead of $\Vert {\varvec{z}}^+ - {\varvec{z}}^-\Vert _2 \le \gamma$ - and constitutes a valid lifting of ${\varvec{{\mathcal {Z}}}}$ for norm-sets only [8]. Yet, as demonstrated on Fig. 2, such non-convex lifting of the uncertainty set can lead to tighter safe approximations (see [Prop. 2, Lifted $\varTheta _1$] and [Prop. 2, Lifted $\varTheta _3$]) than shifting, especially for low to moderate values of $\gamma$. We remark that the first level of approximation with the lifted uncertainty set [Prop. 2, Lifted $\varTheta _1$] - which is equivalent to the approach outlined in Bertsimas and Sim [8] - competes and even surpasses the third level of approximation on the shifted one. However, we observe that the difference between shifting and lifting shrinks as $\gamma$ increases. Also, we should emphasize the fact that shifting is a very generic procedure that can be applied to any bounded uncertainty set, without further assumption on its structure.

Fig. 2

Computational results on constrained linear-quadratic control. Relative performance of shifting vs. lifting the uncertainty set as $\gamma$ increases for constrained linear-quadratic control examples with $N=20$ periods. Performance is measured in terms of sub-optimality gap with respect to the SDP reformulation

5.1.3 Overall performance

Figure 3 compares the performance of the SDP reformulation with safe approximations obtained from ${\varvec{\varTheta }}_3$ in Proposition 2, with the original uncertainty set $\{ {\varvec{z}} : \Vert {\varvec{z}} \Vert _2 \le \gamma \}$, its shifted and lifted versions respectively. In short, we observe that our approach successfully provides near-optimal solution to (within $5\%$ optimality) at a fraction of the cost of solving the exact SDP reformulation.

Fig. 3

Computational results on constrained linear-quadratic control. Numerical behavior of three level-3 safe approximations derived with RPT (Proposition 2) as the number of time periods N increases, compared with the exact SDP reformulation of the robust constraint. For this experiment, we set $\beta = 1.0$ and impose ${\varvec{y}}_k \ge {\varvec{0}}$

5.2 Robust geometric optimization

We evaluate the performance of our proposed approach on geometric optimization instances that are randomly as in  Hsiung et al. [15]. In particular, we consider geometric optimization problems with a linear objective, and a system of two-term log-sum-exp robust inequalities

$$\begin{aligned} \min _{{\varvec{x}}}&\quad {\varvec{c}}^\top {\varvec{x}} \nonumber \\ \text {s.t.}&\log \left( e^{ \left( -{\mathbf {1}} + {\varvec{B}}^{(1)}_i {\varvec{z}} \right) ^\top {\varvec{x}}} + e^{\left( -{\mathbf {1}} + {\varvec{B}}^{(2)}_i {\varvec{z}} \right) ^\top {\varvec{x}}} \right) \le 0, \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \; i\in [I], \end{aligned}$$

(21)

where ${\varvec{c}} = {\mathbf {1}} \in {\mathbb {R}}^{n_x}$ is the all ones vector, and ${\varvec{B}}^{(1)}_i, \, {\varvec{B}}^{(2)}_i \in {\mathbb {R}}^{n_x \times L}$ are randomly generated sparse matrices with sparsity density 0.1 whose nonzero elements are uniformly distributed on the interval $\left[ -1, 1\right]$. The uncertainty set is assumed to be an intersection of a hypercube and a ball, that is,

$$\begin{aligned}&{\varvec{{\mathcal {Z}}}} = \left\{ {\varvec{z}} \in {\mathbb {R}}^L \ \vert \ \Vert {\varvec{z}} \Vert _\infty \le 1, \ \Vert {\varvec{z}} \Vert _2 \le \gamma \right\} . \end{aligned}$$

We consider a set of instances with $n_x = I = 100$ and $L \in \{6, 8, \cdots , 20\}$. We select a $\gamma = \root L \of {\frac{2^L\varGamma (n/2+1)}{\pi ^{L/2}}}$, where $\varGamma$ denotes the gamma function, that ensures the volume of the ball $\{{\varvec{z}} \ \vert \ \Vert {\varvec{z}} \Vert _2 \le \gamma \}$ coincides with the volume of the hypercube $\{{\varvec{z}} \ \vert \ \Vert {\varvec{z}} \Vert _\infty \le 1 \}$. All the reported numerical results are from the average of 10 randomly generated instances.

Consider the bilinear reformulation of the i-th constraint of (21)

$$\begin{aligned} \sup _{ ({\varvec{w}}, {\varvec{z}}, {\varvec{v}}_1, {\varvec{v}}_2, {\varvec{v}}_0) \in {\varvec{\varTheta }}} \, \left\{ \left( -{\mathbf {1}}w_1 + {\varvec{B}}^{(1)}_i {\varvec{v}}_1 \right) ^\top {\varvec{x}} + \left( -{\mathbf {1}} w_2 + {\varvec{B}}^{(2)}_i {\varvec{v}}_2 \right) ^\top {\varvec{x}} - w_0 \right\} \end{aligned}$$

with the non-convex uncertainty set

$$\begin{aligned} {\varvec{\varTheta }} = \left\{ ({\varvec{w}}, {\varvec{z}}, {\varvec{v}}_1, {\varvec{v}}_2, {\varvec{v}}_0) \; \left| \begin{array}{ll} \Vert {\varvec{z}} \Vert _\infty \le 1, \ \Vert {\varvec{z}} \Vert _2 \le \gamma , &{} ({\varvec{z}} \in {\varvec{{\mathcal {Z}}}}) \\ w_1, w_2 \ge 0, \ w_1 + w_2 = 1, &{} ({\varvec{w}} \in {\text {dom}} h^*)\\ w_1 \log w_1 + w_2 \log w_2 \le w_0, &{} (\text {epigraph}) \\ {\varvec{v}}_1 = w_1 {\varvec{z}}, \ {\varvec{v}}_2 = w_2 {\varvec{z}}, \\ {\varvec{v}}_0 = w_0 {\varvec{z}}, \\ \end{array} \right. \right\} , \end{aligned}$$

which is safely approximated by four convex sets that satisfy ${\varvec{\varTheta }}\subseteq {\varvec{\varTheta }}_{LMI, 2}\subseteq {\varvec{\varTheta }}_2 \subseteq {\varvec{\varTheta }}_1 \subseteq {\varvec{\varTheta }}_{1'}$, where ${\varvec{\varTheta }}_1$ and ${\varvec{\varTheta }}_2$ are obtained from applying Proposition 2 to ${\varvec{\varTheta }}$, while ${\varvec{\varTheta }}_{LMI, 2}$ is obtained by enriching ${\varvec{\varTheta }}_2$ with the LMI in (11). In addition, we also compare the safe approximations from ${\varvec{\varTheta }}_1$, ${\varvec{\varTheta }}_2$ and ${\varvec{\varTheta }}_{LMI, 2}$ with ${\varvec{\varTheta }}_{1'}$, where ${\varvec{\varTheta }}_{1'}$ is the corresponding ${\varvec{\varTheta }}_1$ if ${\varvec{{\mathcal {Z}}}}_{box} = \{{\varvec{z}} \ \vert \ \Vert {\varvec{z}} \Vert _\infty \le 1 \}$ is considered instead of ${\varvec{{\mathcal {Z}}}}$. Note that the obtained safe approximation from ${\varvec{\varTheta }}_{1'}$ coincides with that of Roos et al. [18] as discussed in Sect. 3.2. We refer to Appendix C.1 for a detailed representation of ${\varvec{\varTheta }}_1$, ${\varvec{\varTheta }}_{1'}$, ${\varvec{\varTheta }}_2$ and ${\varvec{\varTheta }}_{LMI, 2}$. We resort to comparing our solutions’ objective value to a lower bound. To this end, we compute a lower bound by using the optimal solution to the tightest obtained safe approximation to find potentially critical scenarios in the uncertainty set. The lower bound is then constructed by solving a model that only safeguards for this finite set of critical scenarios; see more detail in Sect. 4.

Fig. 4

Computational results on robust geometric optimization. Numerical behavior of the safe approximations from ${\varvec{\varTheta }}_{1'}$, ${\varvec{\varTheta }}_1$ and ${\varvec{\varTheta }}_2$ as the size of the instance, that is, $L \in \{6, 8, \cdots , 20\}$, increases

5.2.1 Numerical performance

From Fig. 4 we observe that, while our proposed safe approximations from ${\varvec{\varTheta }}_1$ and ${\varvec{\varTheta }}_2$ requires similar computational effort as that from ${\varvec{\varTheta }}_{1'}$, the average optimality gaps from considering ${\varvec{\varTheta }}_1$ and ${\varvec{\varTheta }}_2$ are consistently smaller than that from considering ${\varvec{\varTheta }}_{1'}$. For all considered instances, we observe that despite the significant additional computational effort, the optimality gaps obtained from considering ${\varvec{\varTheta }}_{LMI, 2}$ coincide with the optimality gaps from considering ${\varvec{\varTheta }}_2$. Therefore, we do not report the computation time for the safe approximations from ${\varvec{\varTheta }}_{LMI, 2}$. Moreover, we also consider the shifted uncertainty set, and observe that the obtained optimality gaps coincide with the optimality gaps when the original uncertainty set is considered.

5.2.2 Benefit from lifting

Alternatively, we consider the following lifted uncertainty set of ${\varvec{{\mathcal {Z}}}}$.

$$\begin{aligned} {\varvec{{\mathcal {Z}}}}^+ = \left\{ ({\varvec{z}}^+ , {\varvec{z}}^-) \in {\mathbb {R}}^L_+ \times {\mathbb {R}}^L_+ \ \vert \ \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _\infty \le 1, \ \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _2 \le \gamma \right\} . \end{aligned}$$

This non-convex projection is first proposed in Bertsimas and Sim [8] and then extended to solve adaptive robust linear problems in Chen and Zhang [11]. By substituting ${\varvec{z}}$ with ${\varvec{z}}^+ - {\varvec{z}}^-$, the bilinear reformulation becomes

$$\begin{aligned} \sup _{ \left( {{\varvec{w}}, {\varvec{z}}^\pm , {\varvec{v}}_i^\pm } \right) \in {\varvec{\varTheta }}^+} (-w_1 {\mathbf {1}} + {\varvec{B}}^{(1)}_i [{\varvec{v}}_1^+ - {\varvec{v}}_1^-] )^\top {\varvec{x}} + (-w_2 {\mathbf {1}} + {\varvec{B}}^{(2)}_i [{\varvec{v}}_2^+ - {\varvec{v}}_2^-] )^\top {\varvec{x}} - w_0 \end{aligned}$$

with the lifted non-convex uncertainty set

$$\begin{aligned} {\varvec{\varTheta }}^+ = \left\{ \left( \begin{array}{ll}{\varvec{w}}, {\varvec{z}}^+, {\varvec{z}}^-, {\varvec{v}}_1^+, {\varvec{v}}_1^- &{}\\ {\varvec{v}}_2^+, {\varvec{v}}_2^-, {\varvec{v}}_0^+, {\varvec{v}}_0^- &{} \end{array}\right) \; \left| \begin{array}{ll} \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _\infty \le 1, \\ \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _2 \le \gamma , &{} ( ({\varvec{z}}^+ , {\varvec{z}}^-) \in {\varvec{{\mathcal {Z}}}}^+ ) \\ {\varvec{z}}^+, {\varvec{z}}^- \in {\mathbb {R}}^{L}_+ \\ w_1, w_2 \ge 0, \ w_1 + w_2 = 1, &{} ({\varvec{w}} \in \mathrm {dom } h^*) \\ w_1 \log w_1 + w_2 \log w_2 \le w_0, &{} (\text {epigraph})\\ {\varvec{v}}_1^+ = w_1 {\varvec{z}}^+, \ {\varvec{v}}_1^- = w_1 {\varvec{z}}^-, \\ {\varvec{v}}_2^+ = w_2 {\varvec{z}}^+, \ {\varvec{v}}_2^- = w_2 {\varvec{z}}^-,\\ {\varvec{v}}_0^+ = w_0 {\varvec{z}}^+, \ {\varvec{v}}_0^- = w_0 {\varvec{z}}^-, \end{array} \right. \right\} , \end{aligned}$$

which is safely approximated by four convex sets that satisfy ${\varvec{\varTheta }}^+ \subseteq {\varvec{\varTheta }}_2^+ \subseteq {\varvec{\varTheta }}_1^+ \subseteq {\varvec{\varTheta }}_{1'}^+$ and ${\varvec{\varTheta }}^+ \subseteq {\varvec{\varTheta }}_2^+ \subseteq {\varvec{\varTheta }}_1^+ \subseteq {\varvec{\varTheta }}_{\mathrm{BS}}$, where ${\varvec{\varTheta }}_1^+$ and ${\varvec{\varTheta }}_2^+$ obtained from applying Proposition 2 to ${\varvec{\varTheta }}^+$, and ${\varvec{\varTheta }}_{1'}^+$ is the corresponding ${\varvec{\varTheta }}_1^+$ if ${\varvec{{\mathcal {Z}}}}_{box}^+ = \{({\varvec{z}}^+ , {\varvec{z}}^-) \in {\mathbb {R}}^L_+ \times {\mathbb {R}}^L_+ \ \vert \ \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _\infty \le 1 \}$ is considered instead of ${\varvec{{\mathcal {Z}}}}^+$. We define ${\varvec{\varTheta }}_{\mathrm{BS}}$ in such a way that the obtained safe approximation coincides with that of the extended approach of Bertsimas and Sim [8]; see Sects. 3.1 and Appendix A. We refer to Appendix C.2 for a detailed representation of ${\varvec{\varTheta }}_{\mathrm{BS}}$, ${\varvec{\varTheta }}_1^+$, ${\varvec{\varTheta }}_{1'}^+$ and ${\varvec{\varTheta }}_2^+$. We do not consider ${\varvec{\varTheta }}_{LMI, 2}^+$, that is, ${\varvec{\varTheta }}_2^+$ with addition LMI similarly as in (11), because we already observe that ${\varvec{\varTheta }}_{LMI, 2}$ does not improve the approximation from ${\varvec{\varTheta }}_2$ for the problem we consider here.

5.2.3 Numerical performance with lifting

From Fig. 5 we observe that, while our proposed safe approximations from ${\varvec{\varTheta }}_1^+$ and ${\varvec{\varTheta }}_2^+$ require similar computational effort as that from ${\varvec{\varTheta }}_{\mathrm{BS}}$, the average optimality gaps from considering ${\varvec{\varTheta }}_1^+$ and ${\varvec{\varTheta }}_2^+$ are consistently smaller than that from considering ${\varvec{\varTheta }}_{\mathrm{BS}}$. For all considered instances, we observe that the optimality gaps obtained from considering ${\varvec{\varTheta }}_{1'}^+$ coincide with the optimality gaps from considering ${\varvec{\varTheta }}_1$ (i.e., without lifting). Therefore, we do not report the computation time for the safe approximations from ${\varvec{\varTheta }}_{1'}^+$.

Fig. 5

Computational results on robust geometric optimization. Numerical behavior of the safe approximations from ${\varvec{\varTheta }}^+_{1'}$, ${\varvec{\varTheta }}^+_1$ and ${\varvec{\varTheta }}^+_2$ as the size of the instance, that is, $L \in \{6, 8, \cdots , 20\}$, increases

5.2.4 Overall performance

Firstly, the average optimality gaps from ${\varvec{\varTheta }}_{1'}$ (which has the same performance as Roos et al. [18]; see Sect. 3.2) and ${\varvec{\varTheta }}_{\mathrm{BS}}$ (which has the same performance as the extended approach of Bertsimas and Sim [8]; see Sects. 3.1 and Appendix A) are very close to each other, while the computational effort required for computing the safe approximation from ${\varvec{\varTheta }}_{\mathrm{BS}}$ is almost twice as much as that from ${\varvec{\varTheta }}_{1'}$. Our proposed safe approximations from ${\varvec{\varTheta }}_1$, ${\varvec{\varTheta }}_2$, ${\varvec{\varTheta }}_1^+$ and ${\varvec{\varTheta }}_2^+$ consistently outperform that from considering ${\varvec{\varTheta }}_{1'}$ and ${\varvec{\varTheta }}_{\mathrm{BS}}$. Although the computational effort required for computing the safe approximations from ${\varvec{\varTheta }}_1^+$ and ${\varvec{\varTheta }}_2^+$ is more than twice of that from ${\varvec{\varTheta }}_{1'}$ and ${\varvec{\varTheta }}_{\mathrm{BS}}$, the average optimality gaps from ${\varvec{\varTheta }}_1^+$ and ${\varvec{\varTheta }}_2^+$ are half of the ones from ${\varvec{\varTheta }}_{1'}$ and ${\varvec{\varTheta }}_{\mathrm{BS}}$.

6 Conclusion

We propose a hierarchical safe approximation scheme for (1). Via numerical experiments, we demonstrate that our approach either coincides with or improves upon the existing approaches of Bertsimas and Sim [8] and Roos et al. [18]. Furthermore, our approach not only provides a trade-off between the solution quality and the computational effort, but also allows a direct integration with existing safe approximation schemes, e.g., the lifting technique proposed in Bertsimas and Sim [8] and Chen and Zhang [11], which is used to further improve the obtained safe approximations.

Appendices

The perspectification approach

In this section, we propose an extension of the approach proposed by Bertsimas and Sim [8] for general convex constraints and general convex uncertainty sets. Although this approach is dominated by our main RPT-based approach in Sect. 2, it has the advantage that probability guarantees can be derived for the solutions obtained. While Bertsimas and Sim [8] requires the function h to be sub-additive, our generalization is based on the ‘perspectification’ of the function $h(\cdot )$.

As in Bertsimas and Sim [8], we make the additional assumption that the uncertainty set lies in the non-negative orthant, as stated in Assumption 3. The non-negativity assumption of ${\varvec{{\mathcal {Z}}}}$ holds without loss of generality and can always be satisfied by properly lifting or shifting the uncertainty set. Indeed, if ${\varvec{{\mathcal {Z}}}} \nsubseteq {\mathbb {R}}_+^{L}$, one can decompose ${\varvec{z}}$ into ${\varvec{z}} = {\varvec{z}}^+ - {\varvec{z}}^-$ with ${\varvec{z}}^+$, ${\varvec{z}}^- \ge {\varvec{0}}$. Then,

$$\begin{aligned} {\varvec{A}}( {\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}}) = {\varvec{A}}({\varvec{x}}) {\varvec{z}}^+ - {\varvec{A}}({\varvec{x}}) {\varvec{z}}^- + {\varvec{b}}( {\varvec{x}}) = \tilde{{\varvec{A}}}({\varvec{x}}) \begin{bmatrix} {\varvec{z}}^+ \\ {\varvec{z}}^- \end{bmatrix} + {\varvec{b}}({\varvec{x}}), \end{aligned}$$

where $\tilde{{\varvec{A}}}({\varvec{x}}) = \begin{bmatrix} {\varvec{A}}({\varvec{x}}), \; -{\varvec{A}}({\varvec{x}}) \end{bmatrix}$ is linear in ${\varvec{x}}$ and our analysis applies to the lifted uncertainty set

$$\begin{aligned} {\varvec{{\mathcal {Z}}}}' = \left\{ ( {\varvec{z}}^+ , {\varvec{z}}^-) \in {\mathbb {R}}_+^{L} \times {\mathbb {R}}_+^{L} \, : \, ({\varvec{z}}^+ - {\varvec{z}}^-) \in {\varvec{{\mathcal {Z}}}} \right\} . \end{aligned}$$

However, the lifted uncertainty set ${\varvec{{\mathcal {Z}}}}'$ defined above might be unbounded. As a result, Bertsimas and Sim [8] and Chen and Zhang [11] propose to incorporate a non-convex lifting for norm-based uncertainty sets. For instance, if $\bar{{\varvec{{\mathcal {Z}}}}} = \left\{ {\varvec{z}} \in {\mathbb {R}}^{L} \, : \, {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \, \Vert {\varvec{z}}\Vert _\infty \le 1, \, \Vert {\varvec{z}}\Vert _2 \le \gamma \right\}$, Bertsimas and Sim [8] consider the following lifted uncertainty set:

$$\begin{aligned} {\varvec{{\mathcal {Z}}}}^+ = \left\{ ( {\varvec{z}}^+ , {\varvec{z}}^-) \in {\mathbb {R}}_+^{L} \times {\mathbb {R}}_+^{L} \, : \, \begin{array}{l} \Vert {\varvec{z}}^+ + {\varvec{z}}^-\Vert _\infty \le 1, \\ \Vert {\varvec{z}}^+ + {\varvec{z}}^-\Vert _2 \le \gamma \end{array} \right\} . \end{aligned}$$

Alternatively, we can shift the uncertainty set by some constant factor ${\varvec{z}}_0$ such that ${\varvec{z}} + {\varvec{z}}_0 \in {\varvec{z}}_0 + {\varvec{{\mathcal {Z}}}} \subseteq {\mathbb {R}}_+^L$. Hence,

$$\begin{aligned} {\varvec{A}}( {\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}}) = {\varvec{A}}({\varvec{x}}) ({\varvec{z}} + {\varvec{z}}_0) \underbrace{- {\varvec{A}}({\varvec{x}}) {\varvec{z}}_0 + {\varvec{b}}( {\varvec{x}})}_{=: \, \tilde{{\varvec{b}}}({\varvec{x}}) \text { affine in } {\varvec{x}} }. \end{aligned}$$

We numerically discussed the implications of these two alternatives on the numerical behavior of our proposed approximations in Sect. 5.1.

As previously discussed in Sect. 3.1, the perspectification lemma we present in this section offers an alternative derivation of Corollary 1, i.e., the RPT-based approximation with ${\varvec{\varTheta }}_1$ under Assumption 3. In addition, for this approach, we derive probabilistic guarantees, i.e., bounds on the probability of constraint violation, under the assumption that the uncertain parameter has sub-Gaussian tails.

1.1 Safe approximations via perspectification

The perspectification approach is based on the following perspectification lemma [19]:

Lemma 1

(Perspectification of Convex Functions) If the function $g:{\mathbb {R}}^{m} \mapsto [-\infty , +\infty ]$ is proper, closed and convex, then for any ${\varvec{y}}_1,\dots ,{\varvec{y}}_m \in {\mathbb {R}}^{m}$ and non-negative weights $\alpha _1, \dots , \alpha _{m} \ge 0$, we have:

$$\begin{aligned} g\left( \sum _{i=1}^{m} \alpha _i {\varvec{y}}_i \right) \le \sum _{i=1}^{m} \alpha _i t_i g\left( \frac{{\varvec{y}}_i}{t_i}\right) , \end{aligned}$$

(22)

for any ${\varvec{t}} \ge {\varvec{0}}$ satisfying $\sum _{i=1}^{m} \alpha _i t_i = 1$.

Remark 3

If g is positively homogeneous, i.e., for any vector ${\varvec{y}} \in {\mathbb {R}}^{m}$ and any positive scalar $\lambda > 0$, $g(\lambda {\varvec{y}}) = \lambda g({\varvec{y}})$, then (22) reduces to

$$\begin{aligned} g\left( \sum _{i=1}^{m}\alpha _i {\varvec{y}}_i\right) \le \sum _{i=1}^{m} \alpha _i g\left( {\varvec{y}}_i\right) , \end{aligned}$$

and the additional variables $t_i$ in (22) need not to be introduced. In this case, Lemma 1 simply states that g is sub-additive.

Remark 4

The terms in the right-hand side of Lemma 1 should be interpreted as $\alpha _i$ times the perspective function of g at $(t_i,{\varvec{y}}_i)$. In particular, it is defined when $t_i=0$ and equal to $\alpha _i g_\infty ({\varvec{y}}_i)$ in this case.

We use this lemma to develop a safe approximation of (1), i.e., a sufficient condition for ${\varvec{x}}$ to satisfy (1).

Proposition 4

(Safe Approximation via Perspectification) Under Assumption 3, a safe approximation of (1) is:

$$\begin{aligned} \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \ \exists ({\varvec{u}}, u )\in {\mathbb {R}}^{L+1}_+, \text{ s.t. }&\sum _{\ell \in [L]} z_\ell u_\ell h\left( \frac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{u_\ell }\right) + u \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{u}\right) \le 0, \end{aligned}$$

(23a)

$$\begin{aligned}&\sum _{i=1}^{L} z_i u_i + u = 1, \end{aligned}$$

(23b)

where ${\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell$ selects the $\ell$-th column of the matrix ${\varvec{A}}({\varvec{x}})$ for each $\ell \in [L]$.

Proof

Consider ${\varvec{z}} \in {\varvec{{\mathcal {Z}}}}$. If there exists a vector $({\varvec{u}}, u)\in {\mathbb {R}}^{L+1}_+$ satisfying (23a)–(23b), $({\varvec{u}}, u)$ satisfies the assumption of Lemma 1, (23b). Hence,

$$\begin{aligned} h({\varvec{A}}({\varvec{x}}){\varvec{z}} + {\varvec{b}}({\varvec{x}}))&= \quad h\left( \sum _{\ell \in [L]} z_\ell {\varvec{A}}(x) {\varvec{e}}_\ell + {\varvec{b}}({\varvec{x}}) \right) \\&\le \quad \sum _{\ell \in [L]} z_\ell u_\ell h\left( \frac{{\varvec{A}}(x) {\varvec{e}}_\ell }{u_\ell }\right) + u \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{u}\right) . \end{aligned}$$

Finally, the right-hand side is lower than 0 from (23a) so (1) holds. $\square$

Following Remark 4, the terms $u_\ell h ( {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell / u_l )$ in (23a) should be interpreted as ${\text {persp}}_h(u_\ell , {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell )$. In particular, for $u_\ell = 0$, $u_\ell h ( {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell / u_l) = h_\infty ( {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell )$. Proposition 4 approximates the robust convex constraint (1) via a set of adaptive robust constraints that depend linearly in the uncertainty ${\varvec{z}}$. Note, however, that even in the fully adaptive case where $({\varvec{u}},u)$ can depend arbitrarily on the uncertain parameter ${\varvec{z}}$, Proposition 4 is only a valid approximation of the robust constraint (1), not an equivalent reformulation.

Remark 5

The safe approximation in Proposition 4 can be concisely written as

$$\begin{aligned} \sup _{{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} \quad \inf _{\begin{array}{c} ({\varvec{u}}, u )\in {\mathbb {R}}^{L+1}_+ \\ {\varvec{z}}^\top {\varvec{u}} + u = 1 \end{array}} \quad \sum _{\ell \in [L]} z_\ell u_\ell h\left( \frac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{u_\ell }\right) + u \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{u}\right) \le 0. \end{aligned}$$

Expressing $h(\cdot )$ as the conjugate of its conjugate, we have

$$\begin{aligned} z_\ell u_\ell h\left( \frac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{u_\ell }\right)&= \sup _{\begin{array}{c} {\varvec{v}}_\ell :{\varvec{v}}_\ell / z_\ell \in {\text {dom}} h^* \end{array} } \quad \left\{ {\varvec{e}}_\ell ^\top {\varvec{A}}({\varvec{x}})^\top {\varvec{v}}_\ell - z_\ell u_\ell h^* \left( \frac{{\varvec{v}}_\ell }{z_\ell }\right) \right\} , \\ u \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{u}\right)&= \sup _{\begin{array}{c} {\varvec{w}} \in {\text {dom}} h^* \end{array}} \quad \left\{ {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - u h^*({\varvec{w}}) \right\} . \end{aligned}$$

Finally, for a fixed ${\varvec{z}} \in {\varvec{{\mathcal {Z}}}}$, we can interchange the $\inf$ and $\sup$ operators, take the dual with respect to $({\varvec{u}}, u)$, and reformulate Proposition 4 as

$$\begin{aligned} \sup _{{\varvec{z}} \in {\varvec{{\mathcal {Z}}}}} \quad \sup _{ \begin{array}{c} {\varvec{w}} \in {\text {dom}} h^* \\ \frac{{\varvec{v}}_\ell }{z_\ell } \in {\text {dom}} h^* \end{array}} \quad \sup _{\begin{array}{c} w_0 : \, h^*({\varvec{w}}) \le w_0 \\ \quad z_\ell h^*(\frac{{\varvec{v}}_\ell }{z_\ell }) \le z_\ell w_0 \end{array}} \sum _{\ell \in [L]} {\varvec{e}}_\ell ^\top {\varvec{A}}({\varvec{x}})^\top {\varvec{v}}_\ell \quad + {\varvec{b}}({\varvec{x}})^\top {\varvec{w}} - w_0, \end{aligned}$$

where $w_0$ is the dual variable associated with the linear constraint ${\varvec{z}}^\top {\varvec{u}} + u = 1$. However, the maximization problem above is not convex in $({\varvec{z}}, \{{\varvec{v}}_\ell \}_\ell , {\varvec{w}}, w_0)$ due to the product of variable $z_\ell w_0$ in the constraint $z_\ell h\left( \tfrac{{\varvec{v}}_\ell }{z_\ell } \right) \le z_\ell w_0$ for every $\ell = 1,\dots , L$.

Since the safe approximation in Proposition 4 is an adaptive robust linear constraint, we can then derive tractable reformulations by restricting our attention to specific adaptive policies. For instance, if we consider only static policies, we obtain the following safe approximations of the inequalities (23b) and (23a) which are equivalent to Corollary 1:

Corollary 2

Under Assumption 3, a safe approximation of (1) is:

$$\begin{aligned} \sum _{\ell \in [L]} {\varvec{z}}_\ell h_\infty ({\varvec{A}}({\varvec{x}}){\varvec{e}}_\ell ) + h\left( {{\varvec{b}}({\varvec{x}})}\right) \le 0, \quad \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}. \end{aligned}$$

Proof

$$\begin{aligned} \exists ({\varvec{u}}, u )\in {\mathbb {R}}^{L+1}_+, \ \text{ s.t. }&\sum _{\ell \in [L]} z_\ell u_\ell h\left( \frac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{u_\ell }\right) + u \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{u}\right) \le 0,&\forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \\&{\varvec{z}}^\top {\varvec{u}} + u = 1,&\forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}. \end{aligned}$$

Since ${\varvec{{\mathcal {Z}}}}$ is full dimensional by Assumption 3, the equality constraint implies ${\varvec{u}}={\varvec{0}}$ and $u=1$. $\square$

Remark 6

For the safe approximation (14) to be meaningful, we need the recession function of h, $h_\infty (\cdot )$ to be finite. If this is not the case - if h is quadratic for instance - then, by decomposing ${\varvec{A}}({\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}})$ into $\sum _\ell z_\ell {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell + {\varvec{b}}({\varvec{x}}) + {\varvec{0}}$ and applying the same line of reasoning as for Proposition 4, we can show that

$$\begin{aligned} \exists ({\varvec{u}}, u )\in {\mathbb {R}}^{L+1}_+, \ \text{ s.t. }&\sum _{\ell \in [L]} z_\ell u_\ell h\left( \frac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{u_\ell }\right) + u \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{u}\right) \le 0,&\forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \\&{\varvec{z}}^\top {\varvec{u}} + u \le 1,&\forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

also constitutes a safe approximation of (1) under the additional assumption that $h({\varvec{0}}) = 0$. However, now, the inequality constraint does not force ${\varvec{u}}=0$ so it does not involve the recession function of h.

1.2 Probabilistic guarantees

The main advantage of the safe approximation obtained with Corollary 1-2 is that the resulting constraint is a robust constraint with the same uncertainty set ${\varvec{{\mathcal {Z}}}}$ for which probabilistic guarantees can be derived. In order to provide such guarantees, distributional assumptions on the “true” uncertain parameter are needed. However, Assumption 3 requires the uncertainty set ${\varvec{{\mathcal {Z}}}}$ to lie in the non-negative orthant, an assumption which is often satisfied in practice once the original uncertain parameter is shifted or lifted. Accordingly, we derive probabilistic guarantees for these two cases.

For clarity, we will refer to this original uncertain vector as ${\varvec{u}}$ and identify random variables with tildes ($\tilde{\cdot }$).

1.2.1 Shifted uncertainty set

We first consider the case where the uncertainty set is shifted and make the following assumption:

Assumption 4

We assume that

• (i) the uncertainty set ${\varvec{{\mathcal {Z}}}} \subseteq {\mathbb {R}}_+^{L}$ can be decomposed into ${\varvec{{\mathcal {Z}}}} = {\varvec{z}}_0 + {\varvec{{\mathcal {U}}}}$, where ${\varvec{{\mathcal {U}}}}$ is full dimensional and contains ${\varvec{0}}$ in its interior;

• (ii) the random vector $\tilde{{\varvec{z}}}$ can be decomposed into $\tilde{{\varvec{z}}} = {\varvec{z}}_0 + \tilde{{\varvec{u}}}$, where ${\varvec{z}}_0$ is a deterministic vector and $\tilde{{\varvec{u}}}$ is a random vector whose coordinates are L independent sub-Gaussian random variables with parameter 1 (see Definition 1 ).

In practice, the uncertain parameter ${\varvec{z}}$ is often decomposed into ${\varvec{z}} = \hat{{\varvec{z}}} + {\varvec{u}}$, where $\hat{{\varvec{z}}}$ is the nominal value and ${\varvec{u}}$ the (uncertain) deviation from the nominal. Then, an uncertainty set for ${\varvec{u}}$ is built, ${\varvec{{\mathcal {U}}}}$, and ${\varvec{z}}$ is taken in the uncertainty set $\hat{{\varvec{z}}} + {\varvec{{\mathcal {U}}}}$. Assumption 4 mirrors this modelling process with the additional caveat that the uncertainty set is further shifted by ${\varvec{z}}_0 - \hat{{\varvec{z}}}$ in order to guarantee that ${\varvec{{\mathcal {Z}}}} \subseteq {\mathbb {R}}_+^{L}$.

From a probability distribution standpoint, Assumption 4 requires the coordinates of $\tilde{{\varvec{u}}}$ to be sub-Gaussian, i.e.,

Definition 1

[17, Definition 1.2 in] A random variable $\tilde{u} \in {\mathbb {R}}$ is said to be sub-Gaussian with parameter $\sigma ^2$, denoted $\tilde{u} \sim \text {subG}(\sigma ^2)$, if $\tilde{u}$ is centered, i.e., ${\mathbb {E}}[\tilde{u} ] = 0$, and for all $s \in {\mathbb {R}}$,

$$\begin{aligned} {\mathbb {E}}\left[ e^{s\tilde{u} } \right]&\le e^{\tfrac{s^2 \sigma ^2}{2}}. \end{aligned}$$

Requiring $\tilde{{\varvec{u}}}$ to be sub-Gaussian or, equivalently, to have Gaussian-type tail probabilities, is a fairly general assumption. In particular, standard Gaussian random variables or random variables with mean 0 and bounded between $-1$ and 1 are special cases of sub-Gaussian random variables with parameter 1 ; see [17, Lemma 1.8]. From a bound on the moment generating function, one can derive large deviation bounds. More precisely, if $\tilde{u} \sim \text {subG}(\sigma ^2)$, then for any $t>0$, ${\mathbb {P}}( \tilde{u} > t ) \le \exp (-t^2/(2\sigma ^2))$  [17, Lemma 1.3].

Under this set of assumptions, we derive the following probabilistic guarantees.

Proposition 5

Under Assumption 3 and 4 , if ${\varvec{x}}$ satisfies

$$\begin{aligned} {\varvec{z}}^\top {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) + h({\varvec{b}}({\varvec{x}})) \le 0,\ \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

with ${\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) = \left( {h}_\infty ({\varvec{A}}({\varvec{x}}){\varvec{e}}_{1}), \dots , {h}_\infty ({\varvec{A}}({\varvec{x}}){\varvec{e}}_{L}) \right) ^\top$, then

$$\begin{aligned} {\mathbb {P}} \left( h\left( {\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) \right) > 0 \right)&\le \exp \left( - \dfrac{\delta ^*\left( {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) \vert {\varvec{{\mathcal {U}}}}\right) ^2}{2 \Vert {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) \Vert _2^2} \right) + p_0 \\&\le \exp \left( -\tfrac{1}{2} \rho ({\varvec{{\mathcal {U}}}})^2 \right) + p_0, \end{aligned}$$

where

• a) $\displaystyle \delta ^*({\varvec{y}} \vert {\varvec{{\mathcal {U}}}}) := \max \nolimits _{{\varvec{u}} \in {\varvec{{\mathcal {U}}}}} \, {\varvec{y}}^\top {\varvec{u}}$ is the support function of the set ${\varvec{{\mathcal {U}}}}$,

• b) $\displaystyle \rho ({\varvec{{\mathcal {U}}}}) := \min \nolimits _{{\varvec{y}} : \Vert {\varvec{y}} \Vert _2 =1} \delta ^*({\varvec{y}}\vert {\varvec{{\mathcal {U}}}})$ denotes its robust complexity [10],

• c) and $p_0 \ge {\mathbb {P}}( \tilde{{\varvec{z}}} \ngeq 0)$.

Proposition 5 displays a posteriori and a priori probabilistic guarantees, i.e., a bound that depends on a specific robust solution ${\varvec{x}}$ and one that only depends on the uncertainty set ${\varvec{{\mathcal {U}}}}$. In both cases, it involves $p_0 \ge {\mathbb {P}}( \tilde{{\varvec{z}}} \ngeq 0) = {\mathbb {P}}( \tilde{{\varvec{u}}} \ngeq - {\varvec{z}}_0)$, i.e., the probability that a random uncertain parameter $\tilde{{\varvec{z}}}$ does not belong to the non-negative orthant. In cases where $\tilde{{\varvec{z}}}$ is known or assumed to have bounded support –for instance $\tilde{{\varvec{z}}} \in [-1,1]^{L}$ almost surely– then ${\varvec{z}}_0$ can be chosen large enough so that ${\mathbb {P}}( \tilde{{\varvec{z}}} \ngeq 0) = 0$. Otherwise, for a general ${\varvec{z}}_0 \ge 0$, a union bound inequality yields

$$\begin{aligned} {\mathbb {P}}( \tilde{{\varvec{z}}} \ngeq 0) = {\mathbb {P}}( \tilde{{\varvec{u}}} \ngeq -{\varvec{z}}_0) \le \sum _{i=1}^{L} {\mathbb {P}}( \tilde{u}_i \ngeq - z_{0i}) \le \sum _{i=1}^{L} \exp (- z_{0i}^2/2), \end{aligned}$$

where the last inequality follows from the fact that $\tilde{u_i} \sim \text {subG}(1)$. Hence, $p_0$ is a valid upper bound on ${\mathbb {P}}( \tilde{{\varvec{z}}} \ngeq 0)$ and can be as low as 0 and in general depends on the shifting vector ${\varvec{z}}_0$.

The a priori guarantees in Proposition 5 depend on the uncertainty set through its robust complexity, $\rho ({\varvec{{\mathcal {U}}}})$, introduced by Bertsimas et al. [10]. We report closed-form expressions of $\rho ({\varvec{{\mathcal {U}}}})$, or at least a lower bound, for commonly used uncertainty set in Table 3.

Table 3 Valid lower bound on robust complexity of ${\varvec{{\mathcal {U}}}}$, defined as $\rho ({\varvec{{\mathcal {U}}}}) := \min _{{\varvec{y}} : \Vert {\varvec{y}} \Vert _2 =1} \max _{{\varvec{u}} \in {\varvec{{\mathcal {Z}}}}} {\varvec{y}}^\top {\varvec{u}}$, for some common uncertainty sets. Instances denoted by a * are valid under the assumption that the true uncertain parameter $\tilde{{\varvec{u}}}$ satisfies $\Vert \tilde{{\varvec{u}}}\Vert _\infty \le 1$. Results are taken from Table 2 in Bertsimas et al. [10]

Proof

We consider a robust solution ${\varvec{x}}$. With support function notations, ${\varvec{x}}$ satisfies

$$\begin{aligned} \delta ^* \left( \left. {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) \right| {\varvec{{\mathcal {Z}}}} \right) + h({\varvec{b}}({\varvec{x}})) \le 0. \end{aligned}$$

We denote ${\mathcal {A}}$ the event that $\tilde{{\varvec{z}}} \ge {\varvec{0}}$. Hence, ${\mathbb {P}} \left( {\mathcal {A}}^c \right) = {\mathbb {P}} \left( \tilde{{\varvec{z}}} \ngeq 0 \right) \le p_0$, by definition of $p_0$. Conditioned on ${\mathcal {A}}$, the assumptions of Lemma 1 are satisfied, leading to

$$\begin{aligned} h({\varvec{A}}({\varvec{x}})\tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}))&\le \tilde{{\varvec{z}}}^\top {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) + h({\varvec{b}}({\varvec{x}})), \end{aligned}$$

and

$$\begin{aligned} {\mathbb {P}} \big ( \left. h({\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) )> 0 \, \right| {\mathcal {A}} \, \big )&\le {\mathbb {P}} \left( \tilde{{\varvec{z}}}^\top {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}}))> \delta ^* \left( \left. {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) \right| {\varvec{{\mathcal {Z}}}} \right) \, \right) \\&= {\mathbb {P}} \left( \tilde{{\varvec{u}}}^\top {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) > \delta ^* \left( \left. {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) \right| {\varvec{{\mathcal {U}}}} \right) \, \right) \\&\le \exp \left( - \dfrac{\delta ^*\left( {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) \vert {\varvec{{\mathcal {U}}}}\right) ^2}{2 \Vert {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}})) \Vert _2^2} \right) , \end{aligned}$$

where the last inequality follows from the fact that, by affine transformation of sub-Gaussian random variables, $\tilde{{\varvec{u}}}^\top {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}}))$ is itself sub-Gaussian with parameter $\Vert {\varvec{h}}_\infty ({\varvec{A}}({\varvec{x}}))\Vert _2^2$. By definition of the robust complexity, for any vector ${\varvec{v}}$,

$$\begin{aligned} \frac{ \delta ^*( {\varvec{v}}\vert {\varvec{{\mathcal {U}}}} )}{\Vert {\varvec{v}}\Vert _2} \ge \min _{{\varvec{v}} : \Vert {\varvec{v}} \Vert _2 =1} \, \delta ^*\left( \left. {\varvec{v}} \right| {\varvec{{\mathcal {U}}}} \right) = \rho ({\varvec{{\mathcal {U}}}}), \end{aligned}$$

so that we obtain

$$\begin{aligned} {\mathbb {P}} \big ( \left. h({\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) ) > 0 \, \right| {\mathcal {A}} \, \big ) \le \exp \left( - \tfrac{1}{2} \rho ({\varvec{{\mathcal {U}}}})^2 \right) . \end{aligned}$$

All things considered,

$$\begin{aligned} {\mathbb {P}} \left( h({\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) )> 0 \right)&= {\mathbb {P}} \left( h({\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) )> 0 \vert {\mathcal {A}} \right) {\mathbb {P}} \left( {\mathcal {A}} \right) \\&\qquad + {\mathbb {P}} \left( h({\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) )> 0 \vert {\mathcal {A}}^c \right) {\mathbb {P}} \left( {\mathcal {A}}^c \right) \\&\le {\mathbb {P}} \left( h({\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) ) > 0 \vert {\mathcal {A}} \right) + {\mathbb {P}} \left( {\mathcal {A}}^c \right) , \end{aligned}$$

and the result follows. $\square$

Remark 7

As previously suggested, if the recession function of h is not finite, we can further assume that $h({\varvec{0}}) = 0$ and show that

$$\begin{aligned} \exists ({\varvec{v}}, v )\in {\mathbb {R}}^{L+1}_+, \ \text{ s.t. }&\sum _{\ell \in [L]} z_\ell v_\ell h\left( \frac{{\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell }{v_\ell }\right) + v \ h\left( \frac{{\varvec{b}}({\varvec{x}})}{v}\right) \le 0, \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \\&{\varvec{z}}^\top {\varvec{v}} + v \le 1, \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

constitutes a valid safe approximation of (1). If ${\varvec{x}}$ satisfies such a safe approximation, then a similar line of reasoning yields (proof omitted)

$$\begin{aligned} {\mathbb {P}} \left( h\left( {\varvec{A}}({\varvec{x}}) \tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) \right) > 0 \right)&\le \exp \left( - \dfrac{\delta ^*({\varvec{g}} ({\varvec{x}}, {\varvec{v}}) \vert {\varvec{{\mathcal {U}}}})^2}{2 \Vert {\varvec{g}} ({\varvec{x}},{\varvec{v}}) \Vert _2^2} \right) + \exp \left( - \frac{\delta ^*({\varvec{v}} \vert {\varvec{{\mathcal {U}}}})^2 }{2 \Vert {\varvec{v}} \Vert _2^2} \right) + p_0 \\&\le 2 \exp \left( -\tfrac{1}{2} \rho ({\varvec{{\mathcal {U}}}})^2 \right) + p_0, \end{aligned}$$

with ${\varvec{g}}({\varvec{x}}, {\varvec{v}})^\top {\varvec{e}}_\ell = v_\ell h \left( \dfrac{{\varvec{A}}({\varvec{x}}){\varvec{e}}_\ell }{v_\ell } \right)$.

1.2.2 Lifted uncertainty set

We now consider the case where ${\varvec{{\mathcal {Z}}}}$ is a lifted version of an original uncertainty set. Accordingly, we assume the following:

Assumption 5

We assume that

• (i) the uncertainty set ${\varvec{{\mathcal {Z}}}} \subseteq {\mathbb {R}}_+^{2L}$ is of the form ${\varvec{{\mathcal {Z}}}} = \{ ({\varvec{z}}^+ , {\varvec{z}}^-) \in {\mathbb {R}}_+^{L} \times {\mathbb {R}}_+^{L} \, \vert \, \exists {\varvec{u}} \in {\varvec{{\mathcal {U}}}} \text{: } {\varvec{z}}^+ = \max ( {\varvec{u}},{\varvec{0}}), \ {\varvec{z}}^- = \max ( -{\varvec{u}}, {\varvec{0}}) \}$, where ${\varvec{{\mathcal {U}}}}$ is full dimensional and contains ${\varvec{0}}$ in its interior;

• (ii) the random vector $\tilde{{\varvec{z}}}$ can be decomposed into $\tilde{{\varvec{z}}} = (\max (\tilde{{\varvec{u}}}, {\varvec{0}}), \max (-\tilde{{\varvec{u}}}, {\varvec{0}})) \in {\mathbb {R}}_+^{2 L}$, where the coordinates of $\tilde{{\varvec{u}}} \in {\mathbb {R}}^L$ are L independent sub-Gaussian random variables with parameter 1.

Under this assumption, we can write Corollary 1–2 as:

$$\begin{aligned} ({\varvec{z}}^+)^\top {\varvec{h}}_\infty \left( {\varvec{A}}({\varvec{x}}) \right) + ({\varvec{z}}^-)^\top {\varvec{h}}_\infty \left( -{\varvec{A}}({\varvec{x}}) \right) + h\left( {{\varvec{b}}({\varvec{x}})}\right) \le 0, \, \forall ({\varvec{z}}^+, {\varvec{z}}^-) \in {\varvec{{\mathcal {Z}}}}. \end{aligned}$$

Since ${\varvec{z}}^+$ and ${\varvec{z}}^-$ cannot be simultaneously positive, the constraint above is equivalent to

$$\begin{aligned} \sum _\ell \vert u_\ell \vert \max \left[ {h}_\infty \left( \pm {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right) \right] + h\left( {{\varvec{b}}({\varvec{x}})}\right) \le 0, \, \forall {\varvec{u}} \in {\varvec{{\mathcal {U}}}}. \end{aligned}$$

Despite additional technicalities due to the fact that the coordinates of ${\varvec{z}}^\pm$ are defined as the positive (resp. negative) parts of sub-Gaussian random variables, we obtain similar guarantees.

Proposition 6

Define $\vert {\varvec{{\mathcal {U}}}} \vert := \{ \vert {\varvec{u}} \vert : {\varvec{u}} \in {\varvec{{\mathcal {U}}}} \}$, ${\varvec{g}}({\varvec{A}},{\varvec{x}}) := [ \max h_\infty (\pm {\varvec{A}}({\varvec{x}}){\varvec{e}}_\ell ) ]_{\ell =1,\dots ,L}$ and $\alpha = \sqrt{L}$. Consider a vector ${\varvec{x}}$ satisfying

• 1. If $\displaystyle t := \dfrac{\delta ^*\left( \left. {\varvec{g}}({\varvec{A}},{\varvec{x}}) \right| \vert {\varvec{{\mathcal {U}}}} \vert \right) }{ \alpha \Vert {\varvec{g}}({\varvec{A}},{\varvec{x}}) \Vert _2} > 1,$ and under Assumption 5, then

  $$\begin{aligned} {\mathbb {P}} \left( h \left( {\varvec{A}}({\varvec{x}})\tilde{{\varvec{u}}} + {\varvec{b}}({\varvec{x}}) \right) > 0 \right)&\le \sqrt{e} t \exp \left( - \frac{t^2}{2} \right) . \end{aligned}$$

• 2. If $\rho (\vert {\varvec{{\mathcal {U}}}}\vert ) > \alpha$ and under Assumption 5, then

  $$\begin{aligned} {\mathbb {P}} \left( h \left( {\varvec{A}}({\varvec{x}})\tilde{{\varvec{u}}} + {\varvec{b}}({\varvec{x}}) \right) > 0 \right)&\le \dfrac{\sqrt{e}}{\alpha } \rho (\vert {\varvec{{\mathcal {U}}}}\vert ) \exp \left( -\dfrac{1}{2\alpha ^2} \rho (\vert {\varvec{{\mathcal {U}}}}\vert ) ^2 \right) . \end{aligned}$$

Proposition 6 recovers exactly Theorem 2 from Bertsimas et al. [9], under the weaker assumption that ${\varvec{u}}_j$’s are independent sub-Gaussian random variables (instead of independent Gaussian random variables) and for any uncertainty set ${\varvec{{\mathcal {U}}}}$. In particular, our proof relies on a novel generalization of the Hanson-Wright inequality to sub-Gaussian random variables, which is of independent interest (see the Online Supplement, Theorem OS.2 and Corollary OS.4). However, the constant $\alpha$ in Proposition 6 is weaker than the ones obtained by Bertsimas et al. [9]. Indeed, while our bound is generic, they provide h-specific values for $\alpha$, which we could use to tighten our bound as well.

Before proving Proposition 6, we establish a technical lemma.

Lemma 2

For any ${\varvec{x}}$ and ${\varvec{z}}$, we have

$$\begin{aligned} \max \left( h_\infty \left( \pm {\varvec{A}}({\varvec{x}}) {\varvec{z}}\right) \right) \le \alpha \Vert {\varvec{H}}({\varvec{A}},{\varvec{x}}) {\varvec{z}} \Vert _2. \end{aligned}$$

for $\alpha = \sqrt{L}$ and ${\varvec{H}}({\varvec{A}},{\varvec{x}})$ the $L \times L$ diagonal matrix whose diagonal coefficients are $\max \left[ h_\infty \left( \pm {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right) \right]$.

Proof

Since $h_\infty$ is positively homogeneous with $h_\infty ({\varvec{0}}) = 0$, it is sub-additive and

$$\begin{aligned} h_\infty \left( {\varvec{A}}({\varvec{x}}) {\varvec{z}}\right)&\le \sum _\ell h_\infty \left( z_\ell {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right)&\text {(Sub-additivity)} \\&\le \sum _{j=1}^L \vert z_j\vert h_\infty \left( \epsilon _\ell {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right)&\text { with } \epsilon _\ell = \text {sign}(z_\ell ) \\&\le \sum _{j=1}^L \vert z_j\vert \max \left[ h_\infty \left( \pm {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right) \right] \\&\le \sqrt{L} \sqrt{ \sum _{j=1}^L \max \left[ h_\infty \left( \pm {\varvec{A}}({\varvec{x}}) {\varvec{e}}_\ell \right) \right] ^2 z_j^2 }&\text {(Cauchy-Schwarz)}. \end{aligned}$$

$\square$

Finally, let us prove the Proposition 6.

Proof

• 1. Using the safe approximation

  $$\begin{aligned} h \left( {\varvec{A}}({\varvec{x}})\tilde{{\varvec{u}}} + {\varvec{b}}({\varvec{x}}) \right)&\le h_\infty \left( {\varvec{A}}({\varvec{x}})\tilde{{\varvec{u}}}\right) + h\left( {\varvec{b}}({\varvec{x}}) \right) \le \max \left[ h_\infty \left( \pm {\varvec{A}}({\varvec{x}})\tilde{{\varvec{u}}}\right) \right] + h\left( {\varvec{b}}({\varvec{x}}) \right) , \end{aligned}$$

  together with

  $$\begin{aligned} \delta ^* \left( \left. {\varvec{g}}({\varvec{A}},{\varvec{x}}) \right| \vert {\varvec{{\mathcal {U}}}}\vert \right) + \, h\left( {{\varvec{b}}({\varvec{x}})}\right) \le 0, \end{aligned}$$

  we have

  $$\begin{aligned} {\mathbb {P}} \left( h \left( {\varvec{A}}({\varvec{x}})\tilde{{\varvec{u}}} + {\varvec{b}}({\varvec{x}}) \right)> 0 \right)&\le {\mathbb {P}}\left( \max \left[ h_\infty \left( \pm {\varvec{A}}({\varvec{x}})\tilde{{\varvec{u}}}\right) \right] > \delta ^* \left( \left. {\varvec{g}}({\varvec{A}},{\varvec{x}}) \right| \vert {\varvec{{\mathcal {U}}}}\vert \right) \right) . \end{aligned}$$

  Applying Lemma 2, we eventually get

  $$\begin{aligned} {\mathbb {P}} \left( h \left( {\varvec{A}}({\varvec{x}})\tilde{{\varvec{z}}} + {\varvec{b}}({\varvec{x}}) \right)> 0 \right)&\le {\mathbb {P}}\left( \alpha \Vert {\varvec{H}}({\varvec{A}}, {\varvec{x}}) \tilde{{\varvec{u}}} \Vert _2 > \delta ^* \left( \left. {\varvec{g}}({\varvec{A}},{\varvec{x}}) \right| \vert {\varvec{{\mathcal {U}}}}\vert \right) \right) . \end{aligned}$$

  Both sides of the inequality being positive, we compare their squares and the result follows from the generalized Hanson-Wright inequality (Corollary OS.4) with $t = {\delta ^* \left( \left. {\varvec{g}}({\varvec{A}},{\varvec{x}}) \right| \vert {\varvec{{\mathcal {U}}}}\vert \right) ^2}/{\alpha ^2}$.

• 2. The function $t \mapsto \sqrt{e} t \exp (-{t^2}/{2})$ is monotonically decreasing over $[1,\infty )$. Denoting $t({\varvec{x}}) = \tfrac{\delta ^*( {\varvec{g}}({\varvec{A}}, {\varvec{x}}) \vert \vert {\varvec{{\mathcal {U}}}}\vert )}{\alpha \Vert {\varvec{g}} ({\varvec{A}}, {\varvec{x}}) \Vert _2}$, we have $t({\varvec{x}}) \ge \rho (\vert {\varvec{{\mathcal {U}}}}\vert )/\alpha$.

$\square$

Remark 8

A tighter, yet more overwhelming, bound can be obtained by invoking the generalized Hanson-Wright inequality stated in Theorem OS.2 instead of Corollary OS.4.

Remark 9

We recover exactly Theorem 2 of Bertsimas et al. [9], under the weaker assumption that ${\varvec{u}}_j$’s are independent sub-Gaussian random variables (instead of independent Gaussian random variables) and for any uncertainty set ${\mathcal {U}}$. However, the generic constant $\alpha$ we obtain is weaker. Indeed, Bertsimas et al. [9] provide an h-specific proof of Lemma 2 and are able to derive tighter values of $\alpha$ in these special cases, which could in turn be used to tighten our bound as well.

Derivations for the robust control example

Constraint (20) is of the form

$$\begin{aligned} h\left( {\varvec{A}}({\varvec{x}}) {\varvec{z}} + {\varvec{b}}({\varvec{x}}) \right) \le t - \Vert {\varvec{x}} \Vert _2^2,\ \forall {\varvec{z}} \in {\varvec{{\mathcal {Z}}}}, \end{aligned}$$

with

$$\begin{aligned} h\left( \begin{bmatrix} {\varvec{u}} \\ {\bar{u}} \end{bmatrix} \right) = {\varvec{u}}^\top {\varvec{u}} + {\bar{u}}, \quad {\varvec{A}}({\varvec{x}}) = \begin{bmatrix} {\varvec{C}}^{1/2} \\ 2 {\varvec{x}}^\top {\varvec{F}} + 2 {\varvec{h}}^\top \end{bmatrix}, \quad {\varvec{b}}({\varvec{x}}) = \begin{bmatrix} {\varvec{0}} \\ 0 \end{bmatrix}. \end{aligned}$$

In this case, since there are no linear constraints in the definition of ${\text {dom}} h^*$, ${\varvec{\varTheta }}_1 = {\varvec{\varTheta }}_2$ in the hierarchy of safe approximations presented in Proposition 2.

1.1 Ellipsoidal uncertainty set

We first consider the raw description of the uncertainty set ${\varvec{{\mathcal {Z}}}} = \{ {\varvec{z}} : \Vert {\varvec{z}}\Vert _2 \le \gamma \}$ and consider the bilinear reformulation (2)

$$\begin{aligned} \sup _{ ({\varvec{w}}, {\bar{w}}, w_0, {\varvec{z}}, {\varvec{V}}, \bar{{\varvec{v}}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}} \left[ \, \mathrm {Tr} ({\varvec{C}}^{1/2} {\varvec{V}} ) + 2{\varvec{x}}^\top {\varvec{F}} \bar{{\varvec{v}}} + 2 {\varvec{h}}^\top \bar{{\varvec{v}}} - w_0 \right] \le t - \Vert {\varvec{x}} \Vert _2^2, \end{aligned}$$

with

$$\begin{aligned} {\varvec{\varTheta }} = \left\{ ({\varvec{w}}, {\bar{w}}, w_0, {\varvec{z}}, {\varvec{V}}, \bar{{\varvec{v}}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} \Vert {\varvec{z}} \Vert _2 \le \gamma , &{}({\varvec{z}} \in {\varvec{{\mathcal {Z}}}}) \\ {\bar{w}} = 1, &{} ( ({\varvec{w}},{\bar{w}}) \in {\text {dom}} h^*) \\ 0 \le w_0,\ \tfrac{1}{4} \Vert {\varvec{w}}\Vert _2^2 \le w_0, &{} (h^*({\varvec{w}},{\bar{w}}) \le w_0) \\ {\varvec{V}} = {\varvec{w}} {\varvec{z}}^\top , \\ \bar{{\varvec{v}}} = {\bar{w}} {\varvec{z}}, \\ {\varvec{v}}_0 = w_0 {\varvec{z}} \end{array} \right. \right\} . \end{aligned}$$

After careful inspection, we can eliminate the variables ${\bar{w}}(=1)$ and $\bar{{\varvec{v}}}(={\varvec{z}})$ and consider instead

$$\begin{aligned} \sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}} \left[ \, \mathrm {Tr} ({\varvec{C}}^{1/2} {\varvec{V}} ) + 2{\varvec{x}}^\top {\varvec{F}} {\varvec{z}} + 2 {\varvec{h}}^\top {\varvec{z}} - w_0 \right] \le t - \Vert {\varvec{x}} \Vert _2^2, \end{aligned}$$

with

$$\begin{aligned} {\varvec{\varTheta }} = \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} \Vert {\varvec{z}} \Vert _2 \le \gamma , \\ 0 \le w_0,\ \tfrac{1}{4} \Vert {\varvec{w}}\Vert _2^2 \le w_0, \\ {\varvec{V}} = {\varvec{w}} {\varvec{z}}^\top , \\ {\varvec{v}}_0 = w_0 {\varvec{z}} \end{array} \right. \right\} . \end{aligned}$$

However, in the absence of linear inequalities in the description of ${\varvec{{\mathcal {Z}}}}$ and ${\text {dom}} h^*$, we have ${\varvec{\varTheta }}_0 = {\varvec{\varTheta }}_1 = {\varvec{\varTheta }}_2$ and the resulting safe approximations are uninformative. Yet, we can apply the third level of approximation,

$$\begin{aligned} {\varvec{\varTheta }}_3 = \left\{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \; \left| \begin{array}{ll} \Vert {\varvec{z}} \Vert _2 \le \gamma , \\ 0 \le w_0,\ \tfrac{1}{4} \Vert {\varvec{w}}\Vert _2^2 \le w_0, \\ \tfrac{1}{4} \Vert {\varvec{V}} \Vert _2^2 \le \gamma ^2 w_0, \\ \Vert {\varvec{v}}_0 \Vert _2 \le \gamma w_0 \end{array} \right. \right\} , \end{aligned}$$

and eventually get the following robust counterpart

$$\begin{aligned} 2 \gamma \Vert {\varvec{F}}^\top {\varvec{x}} + {\varvec{h}} \Vert _2 + \gamma ^2 \Vert {\varvec{C}} \Vert _2 \le t - \Vert {\varvec{x}} \Vert _2^2. \end{aligned}$$

This is equivalent to upper-bounding the strongly convex part in the original constraint by $\gamma ^2 \Vert {\varvec{C}}\Vert _2$ and take the robust counterpart of the robust linear constraint. This is the approach chosen by Bertsimas and Brown [6], although with different derivations.

1.2 Shifted uncertainty set

We enrich the definition of ${\varvec{{\mathcal {Z}}}}$ with redundant linear constraints, i.e., we consider

with $\bar{{\varvec{z}}} = \gamma {\varvec{e}}$ and . As a result, and we can apply Corollary 1 for the shifted uncertainty . Namely, we introduce additional decision variables ${\varvec{u}}, u \ge 0$ such that , i.e., , and such that

Alternatively, $\bar{{\varvec{z}}} - {{\varvec{z}}} \ge {\varvec{0}}$ and we can apply Corollary 1 for the shifted uncertainty $\bar{{\varvec{z}}} - {\varvec{{\mathcal {Z}}}} \subseteq {\mathbb {R}}_+^I$. Namely, we introduce additional decision variables ${\varvec{u}}, u \ge 0$ such that ${\varvec{u}}^\top (\bar{{\varvec{z}}} - {{\varvec{z}}}) + u \le 1,\ \forall {\varvec{z}}$, i.e., ${\varvec{u}}^\top \bar{{\varvec{z}}} + \gamma \Vert {\varvec{u}}\Vert _2 + u \le 1$, and such that

Finally, we can also employ the bilinear reformulation (2):

$$\begin{aligned} \sup _{ ({\varvec{w}}, w_0, {\varvec{z}}, {\varvec{V}}, {\varvec{v}}_0) \in {\varvec{\varTheta }}} \left[ \, \mathrm {Tr} ({\varvec{C}}^{1/2} {\varvec{V}} ) + 2{\varvec{x}}^\top {\varvec{F}} {\varvec{z}} + 2 {\varvec{h}}^\top {\varvec{z}} - w_0 \right] \le t - \Vert {\varvec{x}} \Vert _2^2, \end{aligned}$$

with

and derive the corresponding hierarchy (Proposition 2):

1.3 Lifted uncertainty set

Another way to introduce meaningful constraints is to lift the uncertainty set into positive and negative part, i.e., consider $\{ ({\varvec{z}}^+, {\varvec{z}}^-) \in {\mathbb {R}}^{2L}_+ \ \vert \ \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _2 \le \gamma \}$. In this case, we can apply Corollary 1 for the lifted uncertainty set and introduce additional decision variables ${\varvec{u}}^+, {\varvec{u}}^-, u^+, u^- \ge 0$ such that

$$\begin{aligned}&\gamma \Vert \max ({\varvec{u}}^+, {\varvec{u}}^- ) \Vert _2 + u^+ + u^- \le 1, \\&\gamma \left\| \max \left( \left[ \tfrac{C_{ii}}{u_{+i}} \ \right] _i + 2 {\varvec{F}}^\top {\varvec{x}} + 2 {\varvec{h}}, \left[ \tfrac{C_{ii}}{u_{-i}} \ \right] _i - 2 {\varvec{F}}^\top {\varvec{x}} - 2 {\varvec{h}} \right) \right\| _2 \le t - \Vert {\varvec{x}} \Vert _2^2. \end{aligned}$$

We can also apply the bilinear formulation and enforce

$$\begin{aligned} \sup _{ ({\varvec{w}}, w_0, {\varvec{z}}^\pm ,{\varvec{V}}^\pm , {\varvec{v}}_0) \in {\varvec{\varTheta }}} \left[ \, \mathrm {Tr} ({\varvec{C}}^{1/2} {\varvec{V}}^+ ) - \mathrm {Tr} ({\varvec{C}}^{1/2} {\varvec{V}}^- ) + 2({\varvec{F}}^\top {\varvec{x}} + {\varvec{h}})^\top ({{\varvec{z}}}^+ - {{\varvec{z}}}^-) - w_0 \right] \end{aligned}$$

to be less than $t - \Vert {\varvec{x}} \Vert _2^2$, with

$$\begin{aligned} {\varvec{\varTheta }} = \left\{ ({\varvec{w}}, {\bar{w}}, w_0, {\varvec{z}}^\pm , {\varvec{V}}^\pm , {\varvec{v}}_{0}^\pm ) \; \left| \begin{array}{ll} {\varvec{0}} \le {\varvec{z}}^\pm , \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _2 \le \gamma , &{}(({\varvec{z}}^+, {\varvec{z}}^-) \in {\varvec{{\mathcal {Z}}}}) \\ 0 \le w_0,\ \tfrac{1}{4} \Vert {\varvec{w}}\Vert _2^2 \le w_0, &{} (h^*({\varvec{w}},{\bar{w}}) \le w_0) \\ {\varvec{V}}^\pm = {\varvec{w}} {{\varvec{z}}^\pm }^\top , \\ {\varvec{v}}_{0}^\pm = w_0 {\varvec{z}}^\pm \end{array} \right. \right\} , \end{aligned}$$

and the corresponding hierarchy is

$$\begin{aligned} {\varvec{\varTheta }}_0&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}^\pm , {\varvec{V}}^\pm , {\varvec{v}}_{0}^\pm ) \; \left| \begin{array}{ll} {\varvec{0}} \le {\varvec{z}}^\pm , \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _2 \le \gamma , &{}(({\varvec{z}}^+, {\varvec{z}}^-) \in {\varvec{{\mathcal {Z}}}}) \\ 0 \le w_0,\ \tfrac{1}{4} \Vert {\varvec{w}}\Vert _2^2 \le w_0, &{} (h^*({\varvec{w}},{\bar{w}}) \le w_0) \\ {\varvec{v}}_{0}^\pm \ge {\varvec{0}}, \Vert {\varvec{v}}_{0}^+ + {\varvec{v}}_{0}^- \Vert _2 \le \gamma w_0 \end{array} \right. \right\} , \\ {\varvec{\varTheta }}_1&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}^\pm , {\varvec{V}}^\pm , {\varvec{v}}_{0}^\pm ) \; \left| \begin{array}{ll} ({\varvec{w}}, w_0, {\varvec{z}}^\pm , {\varvec{V}}^\pm , {\varvec{v}}_{0}^\pm ) \in {\varvec{\varTheta }}_0 \\ \dfrac{z_{k}^\pm }{4} \left\| \dfrac{1}{z_{k}^\pm } {\varvec{V}}^\pm {\varvec{e}}_k \right\| _2^2 \le v_{0,k}^\pm \end{array} \right. \right\} , \\ {\varvec{\varTheta }}_2&= {\varvec{\varTheta }}_1, \\ {\varvec{\varTheta }}_3&= \left\{ ({\varvec{w}}, w_0, {\varvec{z}}^\pm , {\varvec{V}}^\pm , {\varvec{v}}_{0}^\pm ) \; \left| \begin{array}{ll} ({\varvec{w}}, w_0, {\varvec{z}}^\pm , {\varvec{V}}^\pm , {\varvec{v}}_{0}^\pm ) \in {\varvec{\varTheta }}_2 \\ \dfrac{1}{4} \left\| {\varvec{V}}^+ + {\varvec{V}}^- \right\| _F^2 \le \gamma ^2 w_0 \end{array} \right. \right\} . \end{aligned}$$

Derivations for the robust geometric optimization example

1.1 Original formulation

The safe approximation at Level 1 with ${\varvec{{\mathcal {Z}}}}_{box} = \{{\varvec{z}} \ \vert \ \Vert {\varvec{z}} \Vert _\infty \le 1 \}$ (instead of ${\varvec{z}}$) is:

$$\begin{aligned} {\varvec{\varTheta }}_{1'} = \left\{ ({\varvec{w}}, {\varvec{z}}, {\varvec{v}}_1, {\varvec{v}}_2, {\varvec{v}}_0) \; \left| \begin{array}{ll} \Vert {\varvec{z}} \Vert _\infty \le 1 \\ w_1, w_2 \ge 0, \ w_1 + w_2 = 1 \\ w_1 \log w_1 + w_2 \log w_2 \le w_0 \\ \Vert {\varvec{v}}_1 \Vert _\infty \le w_1, \ \Vert {\varvec{v}}_2 \Vert _\infty \le w_2 \\ {\varvec{v}}_1 + {\varvec{v}}_2 = {\varvec{z}} \\ (w_1 - v_{1\ell }) \log \frac{w_1 - v_{1\ell }}{1- z_\ell } + (w_2 - v_{2\ell }) \log \frac{w_2 - v_{2\ell }}{1- z_\ell } \\ \qquad \qquad \qquad \qquad \quad \ \le w_0 - v_{0\ell }, \; \ell \in [L]\\ (w_1 + v_{1\ell }) \log \frac{w_1 + v_{1\ell }}{1 + z_\ell }b + (w_2 + v_{2\ell }) \log \frac{w_2 + v_{2\ell }}{1 + z_\ell } \\ \qquad \qquad \qquad \qquad \quad \ \ \le w_0 + v_{0\ell }, \; \ell \in [L] \end{array} \right. \right\} . \end{aligned}$$

The safe approximation at Level 1 is:

$$\begin{aligned} {\varvec{\varTheta }}_1 = \left\{ ({\varvec{w}}, {\varvec{z}}, {\varvec{v}}_1, {\varvec{v}}_2, {\varvec{v}}_0) \in {\varvec{\varTheta }}_{1'} \; \left| \begin{array}{ll} \Vert {\varvec{z}} \Vert _2 \le \gamma \end{array} \right. \right\} . \end{aligned}$$

The safe approximation at Level 2 is:

$$\begin{aligned} {\varvec{\varTheta }}_2 = \left\{ ({\varvec{w}}, {\varvec{z}}, {\varvec{v}}_1, {\varvec{v}}_2, {\varvec{v}}_0) \in {\varvec{\varTheta }}_1 \; \left| \begin{array}{ll} \Vert {\varvec{v}}_1 \Vert _2 \le w_1\gamma , \ \Vert {\varvec{v}}_2 \Vert _2 \le w_2\gamma \end{array} \right. \right\} . \end{aligned}$$

The safe approximation at Level 3 is:

$$\begin{aligned} {\varvec{\varTheta }}_{LMI, 2} = \left\{ ({\varvec{w}}, {\varvec{z}}, {\varvec{v}}_1, {\varvec{v}}_2, {\varvec{v}}_0) \in {\varvec{\varTheta }}_2 \; \left| \begin{array}{ll} \exists {\varvec{z}}, {\varvec{W}}: \begin{pmatrix} {\varvec{W}} &{} {\varvec{V}} &{} {\varvec{w}} \\ {\varvec{V}}^\top &{} {\varvec{z}} &{} {\varvec{z}} \\ {\varvec{w}}^\top &{} {\varvec{z}}^\top &{} 1 \end{pmatrix} \succeq 0 \end{array} \right. \right\} , \end{aligned}$$

where ${\varvec{W}} \in {\mathbb {R}}^{3\times 3}$, ${\varvec{V}} = [{\varvec{v}}_0 \ {\varvec{v}}_1 \ {\varvec{v}}_2]^\top \in {\mathbb {R}}^{3\times L}$, ${\varvec{z}} \in {\mathbb {R}}^{L\times L}$ and ${\varvec{w}} = [ w_0 \ w_1 \ w_2]^\top$.

1.2 Lifted formulation

The safe approximation of the extended approach of Bertsimas and Sim [8] is:

$$\begin{aligned} {\varvec{\varTheta }}_{\mathrm{BS}} = \left\{ \left( \begin{array}{ll}{\varvec{w}}, {\varvec{z}}^+, {\varvec{z}}^-, {\varvec{v}}_1^+ , {\varvec{v}}_1^- &{}\\ {\varvec{v}}_2^+, {\varvec{v}}_2^-, {\varvec{v}}_0^+, {\varvec{v}}_0^- &{} \end{array}\right) \; \left| \begin{array}{ll} \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _\infty \le 1, \ \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _2 \le \gamma \\ w_1, w_2 \ge 0, \ w_1 + w_2 = 1 \\ w_1 \log w_1 + w_2 \log w_2 \le w_0 \\ \Vert {\varvec{v}}_1^+ + {\varvec{v}}_1^- \Vert _\infty \le w_1, \ \Vert {\varvec{v}}_2^+ + {\varvec{v}}_2^- \Vert _\infty \le w_2\\ {\varvec{v}}_1^+ + {\varvec{v}}_2^+ = {\varvec{z}}^+, \ {\varvec{v}}_1^- + {\varvec{v}}_2^- = {\varvec{z}}^- \\ v_{1\ell }^+ \log (v_{1\ell }^+/z_\ell ^+) + v_{2\ell }^+ \log (v_{2\ell }^+/z_\ell ^+ ) \le v_{0\ell }^+ &{} \ell \in [L]\\ v_{1\ell }^- \log (v_{1\ell }^-/z_\ell ^-) + v_{2\ell }^- \log (v_{2\ell }^-/z_\ell ^- ) \le v_{0\ell }^- &{} \ell \in [L] \\ {\varvec{z}}^+, {\varvec{z}}^-, {\varvec{v}}_1^+, {\varvec{v}}_1^-, {\varvec{v}}_2^+, {\varvec{v}}_2^- \in {\mathbb {R}}^{L}_+ \end{array} \right. \right\} . \end{aligned}$$

The safe approximation at Level 1 with ${\varvec{{\mathcal {Z}}}}^+_{box} = \left\{ ({\varvec{z}}^+ , {\varvec{z}}^-) \in {\mathbb {R}}^L_+ \times {\mathbb {R}}^L_+ \ \vert \ \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _\infty \le 1 \right\}$ is:

$$\begin{aligned} {\varvec{\varTheta }}_{1'}^+ = \left\{ \left( \begin{array}{ll}{\varvec{w}}, {\varvec{z}}^+, {\varvec{z}}^-, {\varvec{v}}_1^+ , {\varvec{v}}_1^- &{}\\ {\varvec{v}}_2^+, {\varvec{v}}_2^-, {\varvec{v}}_0^+, {\varvec{v}}_0^-&{}\end{array} \right) \; \left| \begin{array}{ll} \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _\infty \le 1 \\ w_1, w_2 \ge 0, \ w_1 + w_2 = 1 \\ w_1 \log w_1 + w_2 \log w_2 \le w_0 \\ \Vert {\varvec{v}}_1^+ + {\varvec{v}}_1^- \Vert _\infty \le w_1, \ \Vert {\varvec{v}}_2^+ + {\varvec{v}}_2^- \Vert _\infty \le w_2\\ {\varvec{v}}_1^+ + {\varvec{v}}_2^+ = {\varvec{z}}^+, \ {\varvec{v}}_1^- + {\varvec{v}}_2^- = {\varvec{z}}^- \\ v_{1\ell }^+ \log (v_{1\ell }^+/z_\ell ^+) + v_{2\ell }^+ \log (v_{2\ell }^+/z_\ell ^+ ) \le v_{0\ell }^+ &{} \ell \in [L]\\ v_{1\ell }^- \log (v_{1\ell }^-/z_\ell ^-) + v_{2\ell }^- \log (v_{2\ell }^-/z_\ell ^- ) \le v_{0\ell }^- &{} \ell \in [L] \\ (w_1 - v_{1\ell }^+ - v_{1\ell }^-) \log \frac{w_1 - v_{1\ell }^+ - v_{1\ell }^-}{1 - z_\ell ^+ - z_\ell ^-} + \\ (w_2 - v_{2\ell }^+ - v_{2\ell }^-) \log \frac{w_2 - v_{2\ell }^+ - v_{2\ell }^-}{1 - z_\ell ^+ - z_\ell ^-} ... \\ \qquad \le w_0 - v_{0\ell }^+ - v_{0\ell }^-, \; \ell \in [L]\\ {\varvec{z}}^+, {\varvec{z}}^-, {\varvec{v}}_1^+, {\varvec{v}}_1^-, {\varvec{v}}_2^+, {\varvec{v}}_2^- \in {\mathbb {R}}^{L}_+ \end{array} \right. \right\} . \end{aligned}$$

The safe approximation at Level 1 is:

$$\begin{aligned} {\varvec{\varTheta }}_1^+ = \left\{ \left( \begin{array}{ll}{\varvec{w}}, {\varvec{z}}^+, {\varvec{z}}^-, {\varvec{v}}_1^+ , {\varvec{v}}_1^-&{} \\ {\varvec{v}}_2^+, {\varvec{v}}_2^-, {\varvec{v}}_0^+, {\varvec{v}}_0^-&{}\end{array} \right) \in {\varvec{\varTheta }}_{1'}^+ \; \left| \Vert {\varvec{z}}^+ + {\varvec{z}}^- \Vert _2 \le \gamma \right. \right\} . \end{aligned}$$

The safe approximation at Level 2 is:

$$\begin{aligned} {\varvec{\varTheta }}_2^+ = \left\{ \left( \begin{array}{ll}{\varvec{w}}, {\varvec{z}}^+, {\varvec{z}}^-, {\varvec{v}}_1^+ , {\varvec{v}}_1^- &{}\\ {\varvec{v}}_2^+, {\varvec{v}}_2^-, {\varvec{v}}_0^+, {\varvec{v}}_0^-&{}\end{array} \right) \in {\varvec{\varTheta }}_1^+ \; \left| \Vert {\varvec{v}}_1^+ \!+\! {\varvec{v}}_1^- \Vert _2 \le w_1 \gamma , \ \Vert {\varvec{v}}_2^+ + {\varvec{v}}_2^- \Vert _2 \!\le \! w_2 \gamma \right. \right\} . \end{aligned}$$