Abstract
According to the standard Arrhenius relation, tissue damage is linearly dependent on the duration of exposure to elevated temperatures and exponentially dependent on the temperature itself. However, recently published measurements of damage threshold temperatures at extremely short exposure times (commonly present during laser treatments) exhibit a shift to temperatures that are higher than what would normally be expected from a single-process Arrhenius model. A novel variable heat shock (VHS) response model was developed that takes into account the observed deviation from the single-process Arrhenius relation, by assuming that the cell viability can be described as the combined effect of two biochemical processes that dominate cell survival characteristics at very short and very long exposure times. The potential implications of the VHS model are explored theoretically through an example of non-ablative laser resurfacing. The VHS model shows that under the appropriate conditions, very high temperature heat shocks can be generated within the superficial epithelium tissue layer without causing irreversible tissue damage. A mechanism of action for tissue regeneration by means of non-ablative resurfacing with the Er:YAG laser is proposed, which involves indirect triggering of tissue regeneration through intense heat shock to the epithelia, in addition to the tissue regeneration mechanism by means of direct thermal injury to deeper lying connective tissues.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Medical laser procedures typically involve the exposure of tissues to elevated temperatures. For example, in selective photo-thermolysis procedures [1], the goal is to heat the target chromophore, such as hemoglobin in blood vessels [2] or melanin in hair follicles [3], to a higher temperature than the surrounding tissue.
In order to minimize the influence of heat diffusion from the heated target into the surrounding tissue, it was proposed to use laser pulse durations shorter than the thermal relaxation time (TRT) of the target [1,2,3]. The TRT was defined as the time during which the target temperature decreases by 50% as a result of heat diffusion. The relaxation time of a target is proportional to the square of the diameter of the target, and therefore, according to the TRT concept, smaller targets require shorter laser pulse durations. However, it is not only the temperature but also the time of exposure that is important [4]. In laser procedures, the physical process of thermodynamically heating the target is typically accompanied by the chemical process of protein denaturation as a result of the heat-induced shock, i.e., the cellular exposure to the increased temperature (T) for the exposure time (texp) [5]. The cell damage induced by the heat shock is described by the Arrhenius damage integral [4, 6, 7], with the damage being exponentially dependent on T and linearly dependent on texp. Therefore, the recommended pulse durations according to the TRT concept may be too short to achieve controlled and predictable damage to the targeted structure [8].
A commonly used metric for tissue damage (Ω) is the ratio of the concentration of native (undamaged) tissue before thermal exposure (C0) to the concentration of native tissue at the end of the exposure time (Cf). The tissue damage is then calculated using the Arrhenius damage integral calculated over the time of the thermal exposure [7, 9]:
Here, A is the frequency factor, i.e., the damage rate (in s−1), E is the activation energy (in J/kmol), and R is the gas constant (R = 8.31 103 J/kmol K).
In the standard model originally proposed by Henriques and Moritz [4, 6], based on measurements for texp > 1 s, it is assumed that a single chemical process representing the kinetics of protein denaturation is involved and, therefore, the Arrhenius coefficients E and A are fixed and independent of the exposure time [10,11,12,13,14,15]. However, with more recent studies performed at extremely short exposure times (texp < 10 ms), the obtained activation energies were significantly smaller and the damage threshold temperatures were significantly higher than what would be expected from the standard single-process Arrhenius model [16,17,18,19]. This finding is of particular significance in the context of medical laser procedures, where extremely short exposures are very common.
In this paper, we propose a VHS (variable heat shock) response model where the damage integral coefficients and, therefore, the heat shock response vary with exposure time. The model is based on an assumption that the heat shock response can be modeled with two interacting biochemical processes, with different time–temperature correlations and activation energies, defining the cell viability at very long and very short exposure times [16, 17]. Additionally, an original “VHS” numerical method for calculating the damage integral is introduced, which takes into account that Arrhenius coefficients are not constant during the non-square-shaped heat shock pulses that are commonly present at short laser-induced exposures.
The proposed VHS model is particularly relevant for laser procedures involving targets with short thermal relaxation times, such as thin hair follicles or blood vessels, where the VHS model predicts much higher damage threshold temperatures than the values that would be expected from the standard Arrhenius model.
Another example of a target with a short thermal relaxation time is encountered during tissue rejuvenation procedures, such as skin [20, 21] or mucous tissue resurfacing [22,23,24]. In this type of procedure, it is the bulk tissue water which plays the role of the absorbing chromophore, and the temperature elevation is not limited to a particular tissue structure but to the superficially irradiated tissue layer with its thickness determined by the laser’s optical penetration depth (δ) and subsequent thermal diffusion [20, 25, 26]. In this paper, we demonstrate the potential implications of the VHS model for understanding the mechanism of action during non-ablative resurfacing of vaginal and oral tissues with mid-IR (λ = 2940 nm) Er:YAG lasers [22,23,24].
Materials and methods
Variable heat shock model
In the standard Arrhenius model of a chemical process, the tissue damage kinetics is commonly characterized by a critical (i.e., damage threshold) temperature (Tcrit) which is, assuming a square-shaped temperature pulse with a constant temperature during the thermal exposure time (texp), defined by [7, 9]:
and represents the temperature at which the concentration of the undamaged tissue is reduced by a factor of e (i.e., when Ω = 1).
Transient heating of tissues leading to protein denaturation and, consequently, to cellular stress or death is very common in medicine and biology, and it has been extensively studied, especially for exposure times longer than approximately 1 s [4,5,6, 10,11,12,13,14,15]. Studies of cellular survival during shorter exposures to higher temperatures, for example, in a millisecond domain, which is very common during laser exposures, are less abundant and have been published more recently [16,17,18,19]. The published Arrhenius coefficients vary considerably, especially when comparing the results obtained at very short and very long exposures. This can be seen in Fig. 1, which shows the dependence of Tcrit on texp as calculated for a number of published Arrhenius coefficients [4, 5, 10,11,12,13,14,15,16,17,18].
Arrhenius curves according to published Arrhenius coefficients (full lines) [4, 5, 10,11,12,13,14,15,16, 18], together with imaginary Arrhenius curves representing the limiting damage processes at very short and very long exposure times (dotted lines), and the imaginary temperature versus exposure time curve (slashed line) representing the combined effect of both limiting processes. The publication references for the shown Arrhenius curves are in the legend listed from top to bottom corresponding to the curves starting from the steepest to the least steep Arrhenius curve. The steepness of a curve is defined as the absolute value of the curve’s slope, ΔTcrit/Δtexp
Although some of the variability in the published Arrhenius coefficients can be attributed to the difference in studied tissue types and/or to different criteria for accessing cell damage, Fig. 1 suggests that the large variability of the reported Arrhenius coefficients can be, at least to a certain extent, attributed to the difference in the studied exposure times. This is supported by the observation that the plotted Arrhenius curves (represented by full lines in Fig. 1) appear to approximately follow the local Tcrit versus texp slope of an imaginary curve (represented by the dashed line in Fig. 1) representing the combined effect of two damage processes (represented by two dotted lines) dominating at the limiting very long and very short exposure times.
Even though the observed shift to higher Tcrit at shorter exposure times is not completely understood [16], we shall in what follows assume that the cell viability depends on a combination of two biochemical processes with different time–temperature correlations and activation energies, defining the cell viability at very long (process 1 with A1 and E1) and very short (process 2 with A2 and E2) exposure times, as has been suggested already elsewhere [16, 19]. The two limiting biochemical processes may describe a situation where the activation energy for protein denaturation shifts to a lower value when the temperature is increased above a certain temperature [16]. Alternatively, the short exposure process 2 may represent the primary protein denaturation dynamics, and the long exposure process 1 describes a combined effect of the primary process together with the slower cellular repair mechanism [11, 16, 19, 27].
We further assume, based on the similarity with parallel resistor circuits, that the effective VHS (variable heat shock) damage integral ΩVHS can be calculated for any exposure time texp from the combined effect of the damage integrals Ω1 (texp) and Ω2 (texp) belonging correspondingly to processes 1 and 2, as follows:
where p is the transition coefficient that determines the transition between the two limiting processes. For example, the dashed line in Fig. 1 represents an imaginary VHS critical temperature curve for a transition coefficient of p = 0.15.
The effective critical temperature (Tcrit) of the combined processes is then determined by the following VHS relation:
The effective damage rate AVHS and the effective activation energy EVHS, representing the VHS coefficients for the combined effect of the two processes for a thermal exposure time texp can then be obtained from:
Physical model of tissue resurfacing
Mid-IR lasers, such as carbon dioxide (10,640 nm) and Er:YAG (2940 nm), are selectively highly absorbed by tissue water, with optical penetration depths (δ) in the range of 1–30 μm, and are thus the most effective for non-ablative or ablative heating of superficial tissues in a very precise fashion [20, 28]. In our study, we applied a numerical model of the physical process of tissue resurfacing as originally developed to study thermo-mechanical ablation with mid-IR lasers. The details of the model are described in [25] and will not be repeated here.
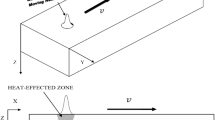
In the model, a single wavelength (λ) pulsed laser radiation is delivered to the surface of the treated tissue with a total pulse fluence F (in J/cm2). Since we were interested in mucous tissue resurfacing, we modeled the tissue as a water-containing homogeneous media characterized by a single absorption coefficient of k = 1/δ, for the delivered laser wavelength λ. For simplicity, a square-shaped laser pulse with a duration, tin, was assumed. Since the main focus of our study was on laser wavelengths with short penetration depths, the effects of the scattering of the laser light within the tissue were not included. Similarly, it was taken that the laser spot size is much larger than the penetration depth (δ), and therefore, the diffusion of dissipated heat was treated in one dimension using a finite-difference scheme.
The model enabled calculation of the temporal evolution of the superficial tissue temperature during and following laser irradiation for different depths, z, within the tissue. As an example, Fig. 2 shows a simulated temporal temperature profile at the tissue surface for a CO2 laser radiation (λ = 10,640 nm) with a pulse duration of tin = 1 ms. For comparison, an experimentally measured temporal temperature profile is also shown, as obtained in a study of the viability of mammalian fibroblast cells exposed to heat shocks under similar conditions ([16], Fig. 7). For the monolayer cell culture used in the experiment, we assumed a CO2 laser penetration depth of δ = 17 μm [16]. In all our calculations, we used the physical parameters of the irradiated media as published in [25].
As can be seen from Fig. 2, for short laser pulse durations and penetration depths, the temperature pulse shape resembles more a quasi “triangular” shape than a square shape. The heat shock pulse consists of the temperature ramp-up heating phase during which the temperature reaches its maximal value (Tmax) and of the temperature ramp-down cooling phase during which the temperature returns back to its initial temperature T0. The heating phase lasts approximately for the duration of the laser intensity pulse (tin), while the cooling phase is determined predominantly by the rate of the heat flow away from the heated tissue volume. We shall define the maximal value Tmax of such a pulse during which the cell damage characterized by Ω = 1 occurs, as the damage threshold temperature Tthr.
Since we were interested in the coagulation dynamics for fluences below and above the threshold for ablation, the model also included the microscopic physical model of the micro-explosion process, which combines the thermodynamic behavior of tissue water with the elastic response of the solid tissue components [25]. As an example, Fig. 3 presents the dependence of the maximal temperature Tmax on the delivered laser fluence F for the CO2 laser wavelength and pulse duration tin = 1 ms.
As shown in Fig. 3, the maximal temperature Tmax grows approximately linearly with fluence until the ablation temperature Tabl for confined tissue boiling is reached at the ablation threshold fluence Fabl, above which the ablation of the superficial tissue layers by means of micro-explosions keeps the surface temperature at Tabl. The calculated ablation temperature is equal to Tabl = 256 °C, in good agreement with other reports [25, 28, 29]. The ablation threshold fluence is higher for larger δ and longer tin. On the other hand, Tabl depends only on the tissue’s physical properties and is therefore the same for all predominantly water-absorbed lasers, providing that no tissue desiccation occurs during irradiation [30].
VHS damage integration method
It is important to note that Eqs. (1)–(5) describe damage characteristics for square-shaped temperature pulses. For long exposure times, approximately square-shaped temperature pulses are relatively easy to achieve. However, this becomes exceedingly more difficult for exposure pulse durations shorter than approximately 1 s, as can be seen from Fig. 2.
A standard approach for calculating the damage caused by a non-square-shaped thermal exposure pulse has been to numerically calculate the integral of Eq. (1) over the duration of the pulse, by dividing the pulse into equidistant time segments ∆t, and by adding the contribution of each temporal segment i to the overall damage using the experimentally measured time-dependent values of temperature (Ti), and by assuming A and E to be constant [16, 17]:
However, as can be concluded from Eqs. (3)–(5), a “triangularly”-shaped pulse cannot be characterized by a fixed set of Arrhenius coefficients. The exposure time to low temperatures present at the base of a heat shock pulse is relatively long, while the exposure time to higher temperatures is increasingly shorter towards the peak of the “triangularly”-shaped temperature pulse. Therefore, the integration over time (Eq. (6)) is not adequate for calculating damages under variable heat shock response conditions. For this reason, we introduced an alternative “VHS” integration algorithm that is based on the integration over temperature instead of over time.
In the VHS damage integration method (depicted in Fig. 4), it is assumed that a single-peak temperature (Tmax) pulse, consisting of a monotonically increasing heating phase and a monotonically decreasing cooling phase, can be considered as consisting of a set of N = Tmax/∆T square-shaped temperature pulses, with their peak temperatures separated by equidistant temperatures ∆T. Each of such rectangular pulses (j) is characterized by the pulse temperature Tj, where Tj = Tj − 1 + ∆T, and the exposure time (texpj) spanning between two identical temperature values (Tj), one belonging to the heating phase and the other to the cooling phase (see Fig. 4). Taking into account that the Arrhenius coefficients Aj and Ej are not fixed but are functions of texpj, the tissue damage caused by a heat shock pulse can be calculated from
It should be noted that within the standard single-process Arrhenius model, where coefficients A and E are independent of texp, the two integration methods, represented by Eqs. (6) and (7), can be considered equivalent since they yield identical damage integral values, regardless of whether the integration is made over time (Eq. (6)) or over temperature (Eq. (7)). The only difference is that the VHS integration algorithm is more time-consuming since it requires a numerical determination of texpj for each of the constituting rectangular pulses j. However, within the VHS model, where coefficients A and E are functions of texp, the integration over time fails, and it is the VHS integration algorithm that is at an advantage since it takes into account that A and E are not constant during a heat shock pulse.
Clinical test
The influence of larger penetration depths and, consequently, of longer thermal exposure times on the damage threshold was preliminarily tested on a case of skin resurfacing. The clinical effect on the dorsal skin located between the thumb and the index finger of one of the authors was observed following a single pulse with 2940 nm Er:YAG laser (δ ≈ 3 μm) (Dynamis, Fotona d.o.o., Slovenia) or with 1340 nm Nd:YAP laser (Dualis, Fotona d.o.o., Slovenia) (δ ≈ 400–800 μm; [31]), both with the laser spotsize on the skin of approximately 1 mm. The single-pulse fluence was adjusted to be just below the ablation threshold, resulting in the maximal skin surface temperature during irradiation of Tmax ≈ 250 °C for both laser types. Photographs of the irradiated skin area were taken using an optical microscope immediately and one day after the irradiation. The irradiation procedure used in this test is cleared for use and thus regularly applied to treat patients. Informed consent was obtained from the volunteer, and the procedure was performed according to the Declaration of Helsinki.
Results
Variable heat shock model coefficients
In order to obtain the parameters for the variable heat shock response (Eq. (4)), we used threshold temperatures Tthr for the measured heat shock temporal profiles T(t), as published by Simanovskii et al. [16, 17]. Simanovskii et al. studied the viability of mammalian fibroblast cells exposed to heat shocks generated with a CO2 laser with laser pulse durations in the range of tin = 0.3–100 ms. An example of the published temporal temperature profile was already shown in Fig. 2 for tin = 1 ms. The measured threshold temperature for this particular heat shock profile was Tthr ≈ 121 °C [16].
For longer exposure times, we used the published threshold temperatures from Moritz and Henriques [4], assuming square-shaped temperature profiles.
Using the VHS model and the VHS damage integration algorithm (Eq. (7)), we calculated damage integrals for the published temperature temporal profiles (Fig. 7 in [16] and Fig. 3 in [17]), characterized by Tmax = Tthr. By varying A1, E1, A2, E2, and p and using the least squares method, we searched for the optimal coupling coefficient p and the Arrhenius coefficients defining the two limiting processes, for which the calculated damage integrals for all temperature profiles deviated the least from ΩVHS = 1. The resulting VHS relation for Tcrit versus texp is represented by the VHS model line in Fig. 5. The fitted transition coefficient is equal to p = 0.161 ± 0.02. The short pulse and long pulse Arrhenius lines represent the dependence of the critical temperatures on the exposure time for the long exposure process 1, characterized by A1 = (4.7 ± 1.4) × 1089 s−1 and E1 = (5.67 ± 0.11) × 107 J kmol−1, and for the short exposure process 2 characterized by A2 = (1.45 ± 0.15) × 104 s−1 and E2 = (1.03 ± 0.03) × 107 J kmol−1.
The VHS model’s critical temperature as a function of the exposure time. According to the VHS model, the critical temperature represents a combined effect of two limiting Arrhenius processes, defining cell viability at extremely long and short exposure times. The symbols represent the effective exposure times as calculated for the measured temperature pulse shapes and corresponding critical temperatures from [4, 16,17,18]
To compare the Tcrit versus texp relation according to the VHS model, with the published data on the viability of cells [16,17,18], we followed a similar procedure as in [16]. The “effective exposure time” for the “triangularly”-shaped heat shock pulse was defined as the duration of an imaginary rectangular temperature pulse of a constant temperature Tcrit, which produces the same amount of damage (ΩVHS) as calculated for the actually measured “triangularly”-shaped temperature pulse with maximal temperature Tmax:
Here, texp is calculated from Eq. (4) and ΩVHS is calculated using Eq. (7), taking Tcrit = Tmax. The obtained calculated effective times for the published measured heat shock temperature profiles and corresponding measured critical temperatures are in Fig. 5 depicted by squares [16] and triangles [17] for short exposures and by circles for long exposures [4]. Additionally, although not used for the fit, a published thermal damage data point for the endodontic pathogen Enterococcus faecalis bacteria exposed to a tin = 25 ms laser pulse is also shown (represented by the diamond) [18, 32].
VHS model of laser resurfacing
In the following, we modeled the temporal and spatial temperature evolution and the resulting damage integral Ω during non-ablative laser resurfacing of an optically and physically homogeneous water-containing tissue, approximately representing a mucous vaginal or oral tissue.
Figure 6 shows the temperature evolution at the tissue surface as simulated for a case of irradiation with a tin = 100 μs energy pulse for three energy penetration depths within the tissue, approximately representing Er:YAG (δ = 3.3 μm [25], further in the text denoted by δ = 3 μm), CO2 (δ = 17 μm), and near IR lasers in the range of 1.2–1.6 μm (δ ≈ 400 μm) [31, 33, 34]. An example of a laser with δ ≈ 400 μm is a 1.47 μm diode laser [34]; however, this penetration depth can also be considered to approximately represent tissue resurfacing with radiofrequency (RF) [35] or ultrasound [36] energy-based devices that are typically characterized by even deeper energy penetration depths. The laser pulse fluence was set to slightly below the threshold value as calculated for each of the three penetration depths.
As can be seen from Fig. 6, the duration of the cooling phase of a heat shock pulse depends strongly on the laser penetration depth. The conductive cooling of the interaction layer is more effective for smaller penetration depths characterized by larger temperature gradients. Consequently, for smaller penetration depths, the duration of the cooling phase is shorter, resulting in shorter effective exposure times and therefore also higher threshold temperatures. Similarly, the duration of the energy pulse (tin) influences the duration of the heating phase, with shorter energy pulse durations resulting in higher Tthr.
The dependence of Tthr at the tissue surface on penetration depth and energy pulse duration can be seen from Fig. 7, which shows damage threshold temperatures (Tthr) as calculated using the VHS response model and simulated temporal temperature evolutions for different values of δ and tin.
Dependence of the damage threshold temperature Tthr of the epithelial surface on the energy penetration depth δ, for different energy delivery times tin. The optimal efficacy and safety window (denoted by the vertical line) lie within the range of parameters for an energy-based device, characterized by Tthr < Tabl
As can be concluded from Fig. 7, there exists a range of “safe” fluences within which the maximal temperature does not exceed the threshold temperature. This range of safe fluences is defined by the energy device’s penetration depth (δ) and pulse duration (tin). As an example, Fig. 8 shows the dependence of Tmax on laser fluence for tin = 100 μs, and three penetration depths (δ = 3, 17, and 400 μm), together with corresponding threshold temperatures. The safe fluence range lies below 0.15 Fabl for δ = 400 μm (diode laser) and below 0.47 Fabl for δ = 17 μm (CO2 laser). On the other hand, for the Er:YAG laser (δ = 3.3 μm), the maximal temperature never exceeds the threshold temperature, since Tthr > Tabl, and the maximal temperature stops growing once the ablation threshold temperature has been reached.
The damage caused by a heat shock pulse depends on whether the maximal temperature reached during a heat shock pulse is below or above the threshold temperature. The calculated damage ΩVHS as a function of the depth z within the tissue for different laser pulse fluences is for δ = 3 μm (representing Er:YAG) and δ = 17 μm (representing CO2) depicted in Fig. 9a, b, respectively.
As expected, the tissue damage is much higher for the δ = 17 μm penetration depth, where exposure times are longer. For the shorter penetration depth of δ = 3 μm, the damage never exceeds ΩVHS ≈ 0.8. Therefore, under appropriate energy source conditions characterized by Tthr < Tabl, the safe fluence window extends up to and above the ablation threshold fluence, providing extremely safe operating conditions for tissue resurfacing.
Clinical test
Figure 10 shows the clinical effect on human skin following a single pulse with 2940 nm Er:YAG laser or with 1340 nm Nd:YAP laser. In spite of the same maximal temperature, the longer exposure time generated by the Nd:YAP laser resulted in a significantly higher damage to the tissue.
Discussion
It is not clear whether the two processes of the VHS model (Fig. 5) describe the actual situation or whether they represent only a useful tool for calculating the damage integral under different exposure conditions. An extrapolation of the imaginary Arrhenius curve 2 of the short exposure process 2 to longer exposure times reveals that the curve already intersects 37 °C at exposure times longer than approximately 6 ms (see Fig. 5), which is obviously not what is observed in nature. One explanation could be that at lower temperatures the activation energy shifts to higher values [16]. However, it is also possible that the observed cellular viability characteristics at short pulse durations represent the primary process of thermal damage, while the data at longer pulse durations represent a combined effect of the primary process together with the slower cellular repair mechanism becoming increasingly more effective at longer exposure times [16, 19]. This hypothesis appears to be supported by the observation that exposing cells to pre-conditioning heat shock pulses induces thermo-tolerance [11, 27], which could be explained by the cellular repair mechanism taking place during and following a heat shock pulse.
By taking into account the relatively high critical temperatures at extremely short exposure times, the VHS damage response model is potentially relevant for many laser medical procedures. For example, when attempting to damage a thin hair or a thin vessel with short laser pulses corresponding to the short tissue relaxation (TRT) time of these targets, the temperatures and/or exposure times required to achieve their protein denaturation are even higher than what would be expected by taking into account the standard Arrhenius relation [8].
When applied to the case of laser resurfacing, the VHS model demonstrates that under appropriate conditions, very intense (i.e., short-duration, high-temperature) heat shock pulses can be safely delivered to the epithelia without causing irreversible tissue damage. Based on this observation, we propose below an additional mechanism of action which may be responsible for the reported clinical regeneration effects of non-ablative Er:YAG resurfacing [22, 23, 37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. This additional mechanism involves indirect triggering of tissue regeneration through intense heat shock to the superficial epithelia, in addition to the slower direct thermal injury to the connective tissues [20, 21, 47, 61, 62].
Non-ablative laser rejuvenation procedures typically focus on regenerating connective tissues, such as dermis or lamina propria, which are responsible for holding the skin, vagina, and other organs together. The regeneration mechanism is based on direct thermal injury (“coagulation”) to the connective tissue in order to cause a reactive inflammatory response resulting in the increase of the biosynthetic capacity of fibroblasts and other cells, inducing the reconstruction of an optimal physiological environment, the enhancement of cell activity, hydration, and the synthesis of collagen and elastin [63]. When using an energy-based medical device, such as a laser, radiofrequency [35], or an ultrasound device [36], to create a thermal exposure pulse within the connective tissue, the duration and the shape of the resulting thermal exposure pulse typically do not follow the duration and the shape of the delivered energy. This is because the volume of the heated connective tissue is typically relatively large, and the major mechanism by which this large volume can be cooled down is through the relatively slow diffusion of the deposited heat into the surrounding unheated tissues [25]. It is therefore the thermal diffusion rather than the temporal pulse length (tin) of the delivered energy that sets the lower limit to the achievable duration of the exposure time. Typical cooling times of the connective tissues are on the order of seconds or longer. This limits the treatment temperatures for direct connective tissue regeneration to about 45–70 °C (see Fig. 5).
The technique employed to achieve direct heating of the deeper lying connective tissue using an Er:YAG laser involves delivering laser energy in one or several 0.1–1-s-long “SMOOTH” mode sequences, each consisting of several consecutive sub-ablative sub-millisecond Er:YAG laser pulses [20, 47, 61, 62]. Using this technique, the laser-generated heat is effectively “pumped” by means of heat diffusion away from the epithelia, several hundred microns deep into the connective tissue [47, 61, 62].
Since the Er:YAG laser wavelength is limited to its very shallow optical penetration depth, it has been hypothesized that instead of having to rely on the SMOOTH mode heat pumping technique, devices with a deeper penetration depth may represent a more suitable means for deep thermal remodeling [64]. However, the excellent clinical results obtained with the Er:YAG laser wavelength, with a small number of reported complications, warrant further investigation of the potential mechanisms of action that make this laser so effective not only for ablative but also for non-ablative resurfacing. The Er:YAG laser has been, for example, very successfully used for non-ablative resurfacing of vaginal [22, 38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] and oral tissues [23]. Histological studies have demonstrated neo-collagenesis and elastogenesis, foci of neo-angiogenesis, reduction of epithelial degeneration and atrophy, and an increase of the fibroblast population [38,39,40,41]. The rejuvenation of the mucous tissue following Er:YAG non-ablative vaginal resurfacing has been shown to alleviate symptoms of atrophy [42,43,44,45,46,47], stress urinary incontinence [48,49,50,51,52,53,54,55], and vaginal relaxation syndrome [56,57,58,59,60,61]. Similarly, non-ablative resurfacing of soft palate, uvula, and tonsillary regions has been reported to significantly reduce symptoms of chronic snoring-related sleep disorders [23].
It should be noted that it represents a considerable challenge to heat up the deeper lying connective tissue to appropriately high temperatures. This is because in order to reach the fibroblasts, the delivered energy must first traverse the epithelial layer located above the basement membrane. This means that the delivered energy may be predominantly absorbed by the superficial epithelium layers. Accordingly, the maximally allowed temperatures which apply to the epithelial layer limit the temperatures that can be generated within the connective tissue. In many cases, the physician is thus faced with a trade-off between using enough energy for effective therapy, while staying within the thresholds to prevent damage to the superficial tissue. In this regard, delivering laser energy in short laser pulses, and only to the thin superficial layer of epithelia, is an advantage according to the VHS model since it allows much higher epithelial temperatures than what would be considered safe if the energy was delivered over longer times and into a larger tissue volume.
As shown in Fig. 7, the damage threshold temperatures are much higher than the normally assumed safe temperatures of up to 65–70 °C [48], providing that the energy penetration depth (δ) and the duration of energy delivery (tin) are sufficiently short. The influence of larger penetration depths and, consequently, of longer thermal exposure times on the damage threshold was observed also during skin resurfacing. In spite of the same maximal temperature, the longer exposure time generated by the Nd:YAP laser resulted in a significantly higher damage to the tissue (see Fig. 10). It should be noted, however, that this is just one example which cannot be considered to be statistically significant.
We propose that intense heat shocks that can be safely delivered to the epithelium tissue using energy devices with short penetration depths, with shorter penetration depths allowing higher superficial temperature heat shocks, may represent an additional mechanism of action for the reported clinical effects of Er:YAG laser resurfacing. Our hypothesis is based on the understanding that it is not only fibroblasts but also the superficially located keratinocytes that are involved in the wound healing process. It is known that keratinocytes recruit, stimulate, and coordinate the actions of multiple cell types involved in healing [65,66,67]. In particular, keratinocytes and fibroblasts communicate with each other via double paracrine signaling loops, known as cross-talk or dynamic reciprocity, that coordinate their actions to restore normal tissue homeostasis after wounding [67]. In response to paracrine signaling from keratinocytes and inflammatory cells, fibroblasts synthesize collagen and promote cross-linking to form an extracellular matrix. We therefore propose an additional, indirect tissue regeneration mechanism, which is complementary to the direct stimulation of fibroblasts and other cells, to respond to wound healing scenarios caused by relatively slow thermal pulsing of the connective tissue. The mechanism is based on stimulating signal transduction processes for transcription factor activation, gene expression, and fibroblast growth, thus leading to new collagen and extracellular matrix formation. A spatially localized, laser-generated supra-physiological level of heat is able to induce a transient heat shock response (HSR), characterized by the production of a family of proteins, termed the heat shock proteins (HSP), which are presumed to initiate temporary changes in cellular metabolism, resulting in the release and production of growth factors and thus in the increase of the rate of cell proliferation [27, 68, 69]. In addition, a controlled generation of reactive oxygen species (ROS) at very high local temperatures occurs within the shallow penetration depth of the Er:YAG laser, which was proposed to explain the healing effects exerted by the Er:YAG laser during rejuvenation treatments [70, 71]. Namely, low amounts of ROS have been found to stimulate wound healing via increased proliferation of keratinocytes and fibroblasts, which in turn generate collagen [72,73,74,75,76]. Furthermore, the generation of ROS during resurfacing procedures has been found to be enhanced by the unique 2940 nm Er:YAG laser wavelength, which matches the exact vibrational oxygen-hydrogen (OH) stretch frequency of water, resulting in a resonant splitting of water molecules at high local temperatures [71].
Furthermore, for laser wavelengths with extremely short penetration depths, such as the 2940 nm wavelength of the Er:YAG laser, a safety window of laser pulse durations characterized by Tabl < Tthr, exists within which the damage threshold temperature cannot be exceeded regardless of the laser pulse fluence delivered to the tissue. This characteristic potentially makes this type of device extremely safe for tissue resurfacing since once the epithelia temperature reaches Tabl, the onset of minimally invasive, micron layer-by-layer ablation automatically prevents the epithelium surface temperature from getting heated above Tabl < Tthr. Figure 10 demonstrates that the longest penetration depth of an energy-based device for which the safety window exists is about δ ≤ 6 μm. This applies for extremely short energy delivery times (tin ≤ 10 μs). For more realistic energy delivery times (tin ≤ 150 μs), the requirement for the penetration depth is δ ≤ 3.5 μm. This is important, for example, when treating body cavities, such as the vagina, where the internal surface may not be regularly shaped, and therefore the delivered fluence and consequently the generated heat may vary from one location to another. Also, the energy source may not always be kept at the optimal distance or optimal angle with regard to the tissue surface, again resulting in non-uniform heat pulse generation. Finally, human error can also occur. In all these cases, the laser ablation mechanism protects the patient from any irreversible injury and keeps the treatment within the safe resurfacing limits.
It should be noted here that our calculation of the VHS model coefficients was based on the available published experimental data for the fibroblast cell culture. Therefore, the results of the model should be considered to describe only the basic qualitative features of the variable heat shock response, with the exact quantitative features depending on the damage response characteristics of a particular type of the affected tissue. Also, in the model, it was assumed that the treated tissue is optically and physically homogeneous, which more closely applies to moist mucous tissues than to skin, where the water content has been found to vary considerably within the first approximately 50 μm of the epidermis [77].
It is interesting to note that the VHS model requirements limit the range of energy-based devices that are potential candidates for the proposed hypothetical indirect superficial triggering of tissue regeneration to short pulsed lasers with appropriately short penetration depth within the tissue. Other types of energy-based devices [78], such as radiofrequency or ultrasound devices, have too long energy delivery times and extremely deep penetration depths, and are therefore not suitable for epithelial heat shock signaling. The requirement for the penetration depth to be below about 6 μm further narrows the choice of energy devices primarily to lasers with a wavelength positioned close to or preferably at the water absorption peak at 2940 nm. The Er:YAG laser therefore appears to hold a unique position within the group of resurfacing lasers. We believe that this explains the extreme safety of Er:YAG lasers when used for ablative or non-ablative resurfacing.
The proposed superficial signaling mechanism resembles the effects of the micro-needling technique, which aims to not injure keratinocytes but to stimulate them with superficial punctures and without any injury to fibroblasts [79, 80]. Similarly to laser resurfacing, the mechanism of action of micro-needling appears to involve not only a direct inflammatory response to the localized “ablation,” but also indirectly induced cell proliferation by electrical signals [80]. Since with micro-needling only a relatively small percentage of the skin is being affected, the treatment outcome is expected to be accordingly limited. On the other hand, the Er:YAG laser-induced thermal triggering mechanism can be viewed as non-ablative thermal “needling” (i.e., triggering) of the total treated skin surface, with the action of the spatially sharp needles being replaced by the action of temporarily “sharp” but spatially extended heat shock pulses.
Conclusions
Published critical temperatures over a broad range of thermal exposure times indicate that tissue denaturation under elevated temperatures cannot be adequately described by a single biochemical process with fixed Arrhenius coefficients. In this paper, we propose a different, variable heat shock (VHS) response model that describes the tissue response as a combined effect of two limiting processes defining cell viability at very long and very short thermal exposure times. Based on the VHS model, the activation energy E and the damage rate A are not constant parameters but are functions of the thermal exposure time. In order to be able to calculate damage integrals for non-square-shaped temperature pulses under VHS conditions, a novel numerical algorithm for calculating the damage integral was developed. Instead of integrating the damage over time, the new algorithm is based on the integration of damage over temperature, which enables taking into account that Arrhenius coefficients are not constant during a heat shock pulse.
The proposed VHS model is potentially particularly relevant for understanding laser procedures involving targets with short thermal relaxation times, such as thin superficially heated tissue layers during tissue resurfacing, or thin hair follicles or blood vessels, where the VHS model predicts much higher damage threshold temperatures than what would be expected from the standard single-process Arrhenius model.
Our analysis of tissue resurfacing using the VHS damage model demonstrates that under appropriate conditions, intense heat shocks can be safely generated within the superficial epithelium tissue layer. A mechanism of action for tissue regeneration with Er:YAG lasers involving indirect triggering of tissue regeneration through intense heat shocking of epithelia is proposed. This mechanism of action is in addition to the commonly accepted mechanism of tissue regeneration by means of direct thermal injury to deeper lying connective tissues. Further research is needed to verify this hypothesis.
References
Anderson RR, Parrish JA (1983) Selective photothermolysis: precise microsurgery by selective absorption of pulsed radiation. Science 220:524–527
Anderson RR, Parrish JA (1981) Microvasculature can be selectively damaged using dye laser: a basic theory and experimental evidence in human skin. Lasers Surg Med 1(3):263–276
Altshuler GB, Anderson RR, Manstein D, Zenzie HH, Smirnov MZ (2001) Extended theory of selective photothermolysis. Lasers Surg Med 29:416–432
Moritz AR, Henriques FC (1947) Studies of thermal injury, 2. The relative importance of time and surface temperature in the causation of burns. Am J Pathol 23:695–720
Chen B et al (2008) Histological and modeling study of skin thermal injury to 2.0 μm laser irradiation. Lasers Surg Med 40:358–370
Henriques FC, Moritz AR (1947) Studies of thermal injury, 1. The conduction of heat to and through skin and the temperature attained therein. A theoretical and an experimental investigation. Am J Pathol 23:531–549
Johnson FH, Eyring H, Stover BJ (1974) The theory of rate processes in biology and medicine. Wiley, New York
Murphy MJ, Torstensson PA (2014) Thermal relaxation times: an outdated concept in photothermal treatments. Lasers Med Sci 29:973–978
Wright NT (2003) On a relationship between the Arrhenius parameters from thermal damage studies. J Biomech Eng 125(2):300–304
Weaver JA, Stoll AM (1967) NADC memo report 6708. United Stated Naval Air Development Center, Johnsville
Beckham JT (2008) The role of heat shock protein 70 in laser irradiation and thermal preconditioning. PhD thesis, Faculty of the Graduate School of Vanderbilt University
Takata AN (1974) Development of criterion for skin burns. Aerosp Med 45:634–637
Wu YC (1982) A modified criterion for predicting thermal injury. Nat Bur Stand. In: Washington, District of Columbia
Fugitt CE (1995) A rate process of thermal injury. Armed Forces special weapons project no. AFSWP-606
Gaylor DC (1989) Physical mechanism of cellular injury in electrical trauma. Ph.D. thesis. Massachusetts Institute of Technology
Simanovskii DM, Mackanos MA, Irani AR, O’Connell-Rodwell CE, Contag CH, Schwettman HA, Palanker DV (2006) Cellular tolerance to pulsed hyperthermia. Phys Rev E 74:011915. https://doi.org/10.1103/PhysRevE.74.011915
Simanovskii D, Sarkar M, Irani A, O’Connell-Rodwell C, Contag C, Schwettman A, Palanker D (2005) Cellular tolerance to pulsed heating. Proc SPIE 5695:254–259. https://doi.org/10.1117/12.601774
Pirnat S, Lukac M, Ihan A (2011) Thermal tolerance of E. faecalis to pulsed heating in the millisecond range. Lasers Med Sci 26:229–237
Kampmeier J, Radt B, Birngruber R, Brinkman R (2000) Thermal and biomechanical parameters of porcine cornea. Cornea 19:355–363
Lukac M, Perhavec T, Nemes K, Ahcan A (2010) Ablation and thermal depths in VSP Er:YAG laser skin resurfacing. J LA&HA, J Laser and Health Academy 2010(1):56–71
Alexiades-Armenakas MR, Dover JS, Arndt KA (2008) The spectrum of laser skin resurfacing: nonablative, fractional, and ablative laser resurfacing. J Am Acad Dermatol 58(5):719–737
Vizintin Z, Lukac M, Kazic M, Tettamanti M (2015) Erbium laser in gynecology. Climacteric 18(1):4–8
Storchi IF, Parker S, Bovis F, Benedicenti S, Amaroli A (2018) Outpatient erbium:YAG (2940 nm) laser treatment for snoring: a prospective study on 40 patients. Lasers Med Sci, published online Jan 15, 2018.
Zerbinati N et al (2015) Microscopic and ultrastructural modifications of postmenopausal atrophic vaginal mucosa after fractional carbon dioxide laser treatment. Lasers Med Sci 30(1):429–436
Majaron B, Plestenjak P, Lukac M (1999) Thermo-mechanical laser ablation of soft biological tissue: modeling the micro-explosions. Appl Phys B Lasers Opt 69:71–80
Majaron B, Sustercic D, Lukac M, Skaleric U, Funduk N (1998) Heat diffusion and debris screening in Er:YAG laser ablation of hard biological tissues. Appl Phys B Lasers Opt 66:479–487
Bowman PD (1997) Survival of human epidermal keratinocytes after short-duration high temperature: synthesis of HSP70 and IL-8. Am J Phys 272(6 Pt 1):C1988–C1994
Zweig AD, Frenz M, Romano V, Weber HP (1988) A comparative study of laser tissue interaction at 2.94 μm and 10.6 μm. Appl Phys B Lasers Opt 47:259–265
LeCarpentier GL, Motamedi M, McMath LP, Rastegar S, Welch AJ (1993) Continuous wave laser ablation of tissue: analysis of thermal and mechanical events. IEEE Trans Biomed Eng 40:188–200
Lukac N, Suhovrsnik T, Lukac M, Jezersek M (2016) Ablation characteristics of quantum square pulse mode dental erbium laser. J Biomed Opt 21(1):1–10
Milanic M, Majaron B (2012) Energy deposition profile in human skin upon irradiation with a 1,342 nm Nd:YAP laser. Lasers Surg Med 45:8–14
Lukac M, Private communication related to experimental details of ref [18].
Mordon S et al (2000) In vivo experimental evaluation of skin remodeling by using an Er:glass laser with contact cooling. Lasers Surg Med 27:1–9
Dodero D et al (2018) Solid state vaginal laser for the treatment of genitourinary syndrome of menopause: a preliminary report. Open J Obstet Gynecol 8:113–1210
Millheiser LS, Pauls RN, Herbst SJ, Chen BH (2010) Radiofrequency treatment of vaginal laxity after vaginal delivery: nonsurgical vaginal tightening. J Sex Med 7(9):3088–3095
Meyer-Rogge D, Rösken F, Holzschuh P, D’hont B, Kruglikov I (2012) Facial skin rejuvenation with high frequency ultrasound: multicentre study of dual-frequency ultrasound. J Cosmet Dermatol Sci Appl 2:68–73
Lapii GA, Yakovleva AY, Neimark AI (2017) Structural reorganization of the vaginal mucosa in stress urinary incontinence under conditions of Er:YAG laser treatment. Bull Exp Biol Med 162(10):510–514
Gaspar A, Brandi H, Gomez V, Luque D (2016) Efficacy of erbium:YAG laser treatment compared to topical estriol treatment for symptoms of genitourinary syndrome of menopause. Laser Surg Med 49(2):160–168. https://doi.org/10.1002/lsm.22569
Bezmenko AA et al (2014) Morphological substantiation of applying the Er:YAG laser for the treatment of stress urinary incontinence in women. J Obstet Women Dis 63(3):21–25
Kulikov IA, Spokoinyi LB, Gorbunova EA, Apolikhina IA (2017) A method for photothermal tissue reconstruction using ErYAG laser Fotona in modern gynecology. Akush Ginekol/Obstet Gynecol 11:160–167
Bojanini B JF, Mejía C AM (2014) Laser treatment of vaginal atrophy in post-menopause and post-gynecological cancer patients. J Laser Health Acad 1:65–71
Gambacciani M et al (2015) Short term effect of vaginal erbium laser on the genitourinary syndrome of menopause. Minerva Ginecol 67(2):97–102
Gambacciani M, Levancini M (2015) Vaginal erbium laser: the second generation thermotherapy for the genitourinary syndrome of menopause (GSM) in breast cancer survivors. A preliminary report of a pilot study. Ital J Gynecol Obstet 27(N1):9–11
Gambacciani M, Levancini M, Cervini M (2015) Vaginal erbium laser: the second-generation thermotherapy for the genitourinary syndrome of menopause. Climacteric 18:1–7
Gambacciani M, Levancini M (2017) Vaginal erbium laser as second-generation thermotherapy for the genitourinary syndrome of menopause: a pilot study in breast cancer survivors. Menopause 24(3):316–319
Gambacciani M, Palacios S (2017) Laser therapy for the restoration of vaginal function. Maturitas 99:10–15
Fistonic N, Fistonic I, Findri Gustek S, Sorta Bilajac Turina I, Franic D, Vizintin Z, Kazic M, Hreljac I, Perhavec T, Lukac M (2016) Minimally invasive, non-ablative Er:YAG laser treatment of stress urinary incontinence in women—a pilot study. Lasers Med Sci 31:635–643
Gaspar A, Brandi H (2017) Non-ablative erbium YAG laser for the treatment of type III stress urinary incontinence (intrinsic sphincter deficiency). Laser Med Sci 32(3):685–691
Gambacciani M et al (2015) Rationale and design for the Vaginal Erbium Laser Academy Study (VELAS): an international multicenter observational study on genitourinary syndrome of menopause and stress urinary incontinence. Climacteric 18(sup1):43–48
Fistonic N, Fistonic I, Lukanovic A, Findri-Gustek S, Sorta Bilajac Turina I, Franic D (2015) First assessment of short term efficacy of Er:YAG laser treatment on stress urinary incontinence in women: prospective cohort study. Climacteric 18(sup1):37–42
Khalafalla MM, Elbiaa AM, Abdelazim IA, Hussain M (2015) Minimal invasive laser treatment for female stress urinary incontinence. Obstet Gynecol Int J (2015) 2(2):00035
Ogrinc UB, Sencar S, Lenasi H (2015) Novel minimally invasive laser treatment of urinary incontinence in women. Lasers Surg Med 47(9):689–697
Pardo J, Sola V, Morales A (2016) Treatment of female stress urinary incontinence with erbium YAG laser in non-ablative mode. Eur J Obstet Gynecol Reprod Biol 204(1–4)
Tien YW, Hsiao SM, Lee CN, Lin HH (2017) Effects of laser procedure for female urodynamic stress incontinence on pad weight, urodynamics, and sexual function. Int Urogynecol J 28(3):469–476
Barber MA, Eguiluz I (2016) Patient satisfaction with vaginal erbium laser treatment of stress urinary incontinence, vaginal relaxation syndrome and genito-urinary syndrome of menopause. J Laser Health Acad, J LA&HA; 2016(1):18–23
Pardo JI, Dalenz VS (2016) Laser vaginal tightening with non-ablative Er:YAG for vaginal relaxation syndrome. Evaluation of patient satisfaction. J Laser Health Acad; J LA&HA 2016(1):12–17
Gaviria J, Korosec B, Fernandez J, Montero G (2016) Up to 3-year follow-up of patients with vaginal relaxation syndrome participating in laser vaginal tightening. J Laser Health Acad; J LA&HA 2016(1):6–11
Ogrinc UB, Sencar S (2017) Non-ablative vaginal erbium YAG laser for the treatment of cystocele. Ital J Gynecol Obstet 29:N1
Okui N (2017) Comparison of erbium-YAG laser treatment with TVT and TOT in Asian women with SUI. Geriatr Med 55(4):421–423
Yu E, Dobrokhotova I, Yu I, Venedkitova MG, Morozova KV, Suvorova VA, Zalesskaya SA (2017) ErYAG laser treatment for genitourinary disorders. Akush Ginekol/Obstet Gynecol 2017(10):84–91
Drnovsek Olup B, Beltram M, Pizem J (2004) Repetitive Er:YAG laser irradiation of human skin: a histological evaluation. Lasers Surg Med 35:146–151
Majaron B, Srinivas SM, Huang HL, Nelson JS (2000) Deep coagulation of dermal collagen with repetitive Er:YAG laser irradiation. Lasers Surg Med 26:215–222
Ganceviciene R et al (2012) Skin anti-aging strategies. Dermatoendocrinology 4(3):308–319
Hardy LA et al (2016) Laser treatment of female stress urinary incontinence: optical, thermal, and tissue damage simulations. Proceedings volume 9689, photonic therapeutics and diagnostics XII; 96891R
Bourke CD et al (2015) Epidermal keratinocytes initiate wound healing and pro-inflammatory immune responses following percutaneous schistosome infection. Int J Parasitol 45:215–224
Pastar I et al (2014) Epithelialization in wound healing: a comprehensive review. Adv Wound Care 3(7):445–464
Wojtowicz AM et al (2014) The importance of both fibroblasts and keratinocytes in a bilayered living cellular construct used in wound healing. Wound Repair Regen 22:246–255
Capon A, Mordon S (2003) Can thermal lasers promote skin wound healing? Am J Clin Dermatol 4(1):1–12
Mackanosa MA, Contag CH (2011) Pulse duration determines levels of Hsp70 induction in tissues following laser irradiation. J Biomed Opt 16(7) 078002 (July 2011)
Lubart R, Friedmann H, Lavie R, Baruchin A (2011) A novel explanation for the healing effect of the Er:YAG laser during skin rejuvenation. J Cosmet Laser Ther 13:33–34
Lubart R, Kesler G, Lavie R, Friedmann H (2005) Er:YAG laser promotes gingival wound repair by photo-dissociating water molecules. Photomed Laser Surg 23(4):369–372
Gordillo GM, Sen CK (2003) Revisiting the essential role of oxygen in wound healing. Am J Surg 186:259–263
Rojkind M, Dominguez-Rosales JA, Nieto N, Green P (2002) Role of hydrogen peroxide and oxidative stress in healing responses. Cell Mol Life Sci 59:1872–1891
Burdon RH (1995) Superoxide and hydrogen peroxide in relation to mammalian cell proliferation. Free Radic Biol Med 18:775–794
Gill V (1995) Hydrogen peroxide and the proliferation of BHK-21 cells. Free Radic Res 23:471–486
Carrasco E, Calvo MI, Blázquez-Castro A, Vecchio D, Zamarrón A, Dias de Almeida IJ, Stockert JC, Hamblin MR, Juarranz Á, Espada J (2015) Photoactivation of ROS production in situ transiently activates cell proliferation in mouse skin and in the hair follicle stem cell niche promoting hair growth and wound healing. J Investig Dermatol 135:2611–2622
Noriaki Nakagawa N, Matsumoto M, Sakai S (2010) In vivo measurement of the water content in the dermis by confocal Raman spectroscopy. Skin Res Technol 16:137–141
Tadir Y et al (2017) Light and energy based therapeutics for genitourinary syndrome of menopause: consensus and controversies. Lasers Surg Med 49(2):137–159
Zhu H (2014) Acupoints initiate the healing process. Med Acupunct 26(5):264–270
Liebla H, Kloth LC (2013) Skin cell proliferation stimulated by microneedles. J Am Coll Clin Wound Spec 4(1):2–6
Funding
The authors acknowledge the financial support from the state budget of the Ministry of Education, Science and Sport of Slovenia and the European Regional Development Fund (Project GOSTOP).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The clinical example is from a study which was approved by the Slovenian national ethics committee (KME 120-365/2017-9).
Conflict of interest
Three of the authors (ML, TP, FB) are currently affiliated also with Fotona d.o.o.
Informed consent
The skin resurfacing was performed on a volunteer who is one of the authors (ML). Informed consent was obtained from the volunteer, and the procedure was performed according to the Declaration of Helsinki.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lukač, M., Lozar, A., Perhavec, T. et al. Variable heat shock response model for medical laser procedures. Lasers Med Sci 34, 1147–1158 (2019). https://doi.org/10.1007/s10103-018-02704-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10103-018-02704-1