Abstract
Penetration depth of ultraviolet, visible light and infrared radiation in biological tissue has not previously been adequately measured. Risk assessment of typical intense pulsed light and laser intensities, spectral characteristics and the subsequent chemical, physiological and psychological effects of such outputs on vital organs as consequence of inappropriate output use are examined. This technical note focuses on wavelength, illumination geometry and skin tone and their effect on the energy density (fluence) distribution within tissue. Monte Carlo modelling is one of the most widely used stochastic methods for the modelling of light transport in turbid biological media such as human skin. Using custom Monte Carlo simulation software of a multi-layered skin model, fluence distributions are produced for various non-ionising radiation combinations. Fluence distributions were analysed using Matlab mathematical software. Penetration depth increases with increasing wavelength with a maximum penetration depth of 5378 μm calculated. The calculations show that a 10-mm beam width produces a fluence level at target depths of 1–3 mm equal to 73–88% (depending on depth) of the fluence level at the same depths produced by an infinitely wide beam of equal incident fluence. Meaning little additional penetration is achieved with larger spot sizes. Fluence distribution within tissue and thus the treatment efficacy depends upon the illumination geometry and wavelength. To optimise therapeutic techniques, light-tissue interactions must be thoroughly understood and can be greatly supported by the use of mathematical modelling techniques.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Human skin is the interface between man and his environment. One of the environmental factors it has to deal with is ultraviolet (UV) radiation. Ultraviolet radiation may cause negative effects such as erythema, skin ageing and skin cancer. The upper layer of skin, the epidermis, acts as a natural UV filter and may thicken or develop a stronger pigmentation as an adaption to excess UV exposure. On the other hand, UV radiation induces photo production of previtamin D3 in the skin and thus provides the major natural source for vitamin D3 for humans. Thus, it seems reasonable that skin has not evolved as a mere sun block but as a sun screen.
Red light penetrates deeper than blue light [1]. The reason is that skin consists of a range of chromophores which have scattering and absorption coefficients which are highly wavelength dependent [1,2,3,4,5,6]. The scattering properties of tissue are due to attenuation properties intrinsic to the chromophore and also to the size of the particles within the tissue which also governs the type of scattering that occurs, namely Mie or Rayleigh scattering [7]. Scattering leads to light dispersion in the tissue and the eventual reduction in the energy density with increasing depth [8]. Zhao and Fairchild looked at the transmission of laser light through tissues over a range of skin types and for laser wavelengths in the range 532–1064 nm and showed that 1064-nm light penetrated deepest into tissue [9] (Fig. 1).
Light penetration into skin illustrating the depth to which wavelengths penetrate human skin. Red light is extinguished some 4–5 mm beneath the surface of the skin whereas ultraviolet hardly penetrates at all and blue barely 1 mm into tissue [8]
Intense pulsed light (IPL) systems emit light in the wavelength range 400–1200 nm [10]. For wavelengths greater than 1000 nm, there is not a great amount of information regarding the penetration depth, and there is also little information regarding the photobiological effects at wavelengths greater than 1000 nm.
The wavelength of a therapeutic source therefore has a double importance, namely to ensure absorption of the incident photons in the target chromophores and to be able to do so at the depths at which these chromophores exist. The waveband in which the wavelength of the incident photons is located determines not only which part of the cell is the target but also the primary photo action. Wavelength is thus probably the single most important consideration in phototherapy, because without absorption, there can be no reaction.
For normally incident radiation, this regular reflectance is on the order of 4–7% [11]. The remaining 93–96% of the radiation entering the skin is either scattered or absorbed. The type of scattering is an elastic interaction between a photon and matter in which only the direction of propagation of the photon is altered. Elastic scattering results from inhomogeneity’s in the skin’s index of refraction corresponding to the physical boundaries of anatomical features, such as collagen fibres, and is characterised by the wavelength-dependent scattering coefficient, μ s (λ) (cm−1). Once absorbed, the radiation is predominantly converted non-radiatively (i.e. without luminescence) into heat by the absorbing chromophore molecules. When there are pigmented tissue structures present that are more strongly absorbing at the laser wavelength than the surrounding tissue, e.g. hair shafts, the photons propagating randomly within the tissue will tend to be absorbed selectively by the pigmented structures. Thus, given enough deposited energy, selective photothermolysis of the pigmented structures will occur. Absorption by the pigmented structures or the surrounding tissue is characterised by their respective wavelength-dependent absorption coefficients, μ a (λ) (cm−1).
A question that often appears throughout the literature asks: To what depth does optical light penetrate in skin tissue? This question is of importance when targeting treatment areas, optimising treatments, reducing risks and ensuring that the optical radiation does not reach vital organs and the foetus during pregnancy which may lead to complications. This computational investigation shows the effect of incident wavelength and beam width on penetration of human skin.
Materials and method
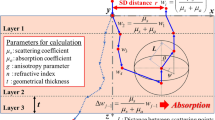
The 2-D mathematical simulation described here was previously utilised for a study modelling blood vessels [12], but was modified to simulate the 2-D penetration of photos into a homogeneous tissue matrix [13]. The authors of this study modelled the tissue matrix using a 5-μm cell size as a Cartesian coordinate, an 80-μm melanin rich epidermis with 5% melanin concentration and a melanin free dermis, as depicted in Fig. 2. The simulation is comprised of two interacting subroutines, a Monte Carlo photon distribution and a heat diffusion calculation to typical pulse structures as produced by an IPL system as shown in Fig. 2. The model was calibrated against thermography measurements of human skin exposed to IPL exposure. These measurements used various skin tones (Caucasian, Indian and Afro Caribbean) with ranging IPL exposure (2–20 J/cm2) at a known distance from skin. For this investigation, only the Monte Carlo section of photon distribution is used.
The calculation of the energy distribution was achieved by using a Monte Carlo process. This computer simulation allows observation of comparative data that cannot be performed in skin. The Monte Carlo simulation of photons is a numerical calculation repeated random sampling to obtain numerical results by probability distribution to compute the radiative transport in scattering and absorbing media.
In the computations of photon pathways, the absorption coefficients (μ a) provide energy conversion of the photon to the cell, the scattering coefficient (μ s) provides the angle of deflection between tissue cell interaction and the whole anisotropy factor (g) of each material at the specific wavelength is considered whereby light is forward scattered in tissue. These respective values were taken from the literature [14,15,16,17,18,19], and the respective absorption coefficients at these wavelengths are tabulated in Table 1 and shown in Fig. 3.
Absorption coefficients of melanin, oxyhaemoglobin and water. The IPL emission spectrum used for this evaluation is overlaid for reference [3]
The wavelength dependency of the optical parameters of the IPL spectrum complicates mathematical modelling of light-tissue interaction for IPL, as compared to monochromatic lasers [20]. For comparison of system design and efficiency, the total radiant exposure of the 1 × 109 photons that constitute the spectrum shown in Fig. 3 equals 10 J/cm2. When filtered broadband IPL is delivered to the subject’s skin, a fraction of the optical energy is reflected from the skin’s surface while the rest is scattered beneath the skin’s surface and is then absorbed in biological cells. Such absorption causes the hair shaft and hair bulb to heat up resulting in damage to the follicle, shedding of the hair and prevention of future regrowth.
A custom Monte Carlo simulation package was created by the School of Applied Computing, University of Wales Trinity Saint David, UK, and implemented on a personal computer. Within this Monte Carlo simulation, the absorption coefficient of melanin (μ a) is computed. The scattering coefficient (μ s) is measured from experimental techniques originating from Mie scattering due to collagen fibres and from Rayleigh scattering due to small tissue structures, respectively [21]. Scattering in tissue by photons is characterised by the Henyey-Greenstein scattering phase function [17, 22, 23] which is mathematically expressed in the form…
The longitudinal angle of scattering, (θ), is characterised by the Henyey-Greenstein phase function, and since this phase function is forwardly biased, θ will be randomly influenced to reflect this characteristic. Applying the probability density function for the random number R to the above equation and solving for cos(θ) lead the following expression (Fig. 4).
The azimuthal angle, φ, is uniformly distributed within the interval [0, 2π]. Its probability density function is constant and equals \( \frac{1}{2\pi } \). Hence, φ takes the form:
A predefined number of photons are directed onto a skin model. These photons are given a weight (W), which is equal to 1. A photon starts at a boundary position with the tissue interface with a step size, anisotropy angle of rotation and a deflection angle. At each interaction, the photon delivers a portion of its energy, pre-set to values determined of tissue optical properties. The loss in energy at each of the on-going interaction sites is determined by the weight that the photon deposits. The change in weight is defined by the following equation [24,25,26].
The photons are terminated when the value of ΔW is below a threshold. In this simulation, the photons are terminated when one hundredth of the original weight remained after multiple interactions. Then after this photon is deposited in its final position, a new photon is released and the process is repeated. A sufficient number of photons are required to generate an absorption energy density matrix for the defined tissue configuration for absorption of the IPL power output [24, 25, 27]. This energy density matrix is used with a factor of total energy output within this defined area [24, 25]. The absorbed energy at each Cartesian cell can be used as a heat source for thermal diffusion approximation. The time-dependant heat flow equation is reduced to its 2-D form and subsequently evaluated over the discretised domain using the Alternating Direction Implicit (ADI) method.
Where H is the volumetric distribution of energy calculated in the Monte Carlo simulation and stored in number array, y and z are the radial and axial coordinates, respectively.
Effect of wavelength
In order to obtain a relationship between the penetration depth and wavelength, Monte Carlo simulations were carried out for wavelengths in the range 300–750 nm in 50 nm increments. The default beam width of 30 mm was also used. Photon distributions were then extracted from the Monte Carlo model and input into a custom Matlab programme for data manipulation and more effective data analysis.
Effect of beam width
In order to obtain a relationship between the penetration depth of light and the beam width of the treatment device used, Monte Carlo simulations were carried out for beam widths in the range of 1 to 40 mm. The simulations used 1 × 109 photons with an epidermal melanin concentration of 4.3% (skin type 2) [28] on the top layer and a total dermis depth of 5560 μm.
For each of the beam widths used, a default IPL spectra was used (Fig. 3). Photon distributions were then extracted from the Monte Carlo model and input into a custom Matlab programme which provides a visual representation of the penetration depth of the light on a contour plot and also calculates the depth of penetration for and 1% values from the data matrices produced which then allowed beam width penetration depth relationships to be graphically represented.
Simulations were carried out for a range of beam widths in the range 1 to 40 mm, shown in Fig. 7. The results show that as the beam width is increased there is an increase in the depth of penetration, which can clearly be seen by the use of intensity contours, each representing a 1% fraction of the maximum intensity. The 1% fraction contours were chosen after experimentation with other values for penetration such as 1/e and 1/e 2 for a clear and clean graphical representation of the photo-distribution matrix. The figures also show the beam divergence as the light passes through the skin model.
Results—effect of wavelength
Monte Carlo simulations were carried out for the whole spectral range offered by the TODDY package; 300–750 nm in increments of 50 nm. Figure 5 clearly illustrates that on increasing the wavelength of light used in skin therapy, there is a corresponding increase in the penetration depth, of the 1% contour lines (which is the line which penetrates the deepest in Fig. 5). Each of the contours represents a 1% fraction of the maximum intensity.
It can be seen that for increasing wavelengths, the 1% contour line penetrates deeper into the tissue as expected. In the penetration depth of 1%, the intensity is reached at 5378 μm (5.4 mm) with a wavelength of 750 nm. This is in agreement with literature which states the penetration of optical light systems reaching to a depth of 4–6 mm [8, 28]. However, it will again be noted that there is a lack of information regarding the definition of penetration depth for light therapy.
Figure 6 provides a more detailed representation of the wavelength-dependent penetration within the epidermis and the epidermal-dermal boundary. The lower amount of 550 nm absorption is perhaps visualised more clearly here as it passes the epidermal-dermal boundary.
Figure 6 shows that there is greater absorption of shorter wavelength light at the front end of the epidermis (box a) which tails off rapidly towards the boundary layer (b). The increase in intensity of higher wavelengths at b is due to the backscatter from the boundary and the dermal layer into the epidermis which is then absorbed in this region. The backscatter or reflection at the boundary layer is increased by the refractive indices of the epidermis, and the dermis are different and the photons travel from the epidermis to the dermis and back again. Once the light has passed through the boundary layer, its absorption rapidly reduces by greater than 50% for all wavelengths. Again, following the 300 nm curve, this illustrates the highly photoprotective nature of melanin which reduces the blue light absorption by greater than 90% as it passes through into the dermis (c) where the protection from blue light is required most. As can be seen from box c, there is a rapid decrease in the attenuation which then dips and then rises again until a depth of 110 μm is reached. The reason for this behaviour might be explained by the significantly increased mean free path in the dermis relative to the epidermis. It is not known how thick the boundary is, if the boundary consists of a reduced fraction of melanin or if the boundary is simply an abrupt change in attenuation coefficient in the matrix.
Results—effect of beam width on penetration depth
A key contributor to the penetration depth is the treatment area or spot size employed by the device. Spot size has important clinical implications due to its effect on penetration and light dispersion in tissue. With increasing spot size, there is a reduction in the amount of lateral scattering; this results in greater penetration for larger spot sizes. As a result, lower energy densities can be applied when using larger spot sizes to achieve the same penetration depth for treatment. Variation in spot size is also important depending on the condition being treated, if the treatment region is over a large area then a larger spot size is used and for isolated small lesions in blood vessels for instance, a smaller spot size would be recommended resulting in increased intensity at the target. A beam width of 4–6 mm is usually used to penetrate to the mid-dermal and deeper layers of skin where the hair follicles and blood vessels are situated. It has also been found that although the penetration depth increases, there is a point at which the beam width has no further effect on the penetration depth and this is expected to be in the region of 5–12 mm in beam width [8, 28, 29]. It should also be noted that there is a distinct lack of information regarding the penetration depth for IPL systems with most of the work being carried out on laser treatment devices.
There is a noticeable increase in the penetration depth when the beam width is increased from 1 up to 5 mm before maintaining a constant penetration depth of approximately 10 mm when the intensity is reduced to 1% regardless of the increase in beam width (Fig. 7).
The trend shows that a critical point is reached for a beam width of 10 mm at which a further increase in the beam width of the treatment device used does not affect the penetration of the light in tissue. A smaller beam width is associated with increased scattering, and as the beam width is increased, the photon propagation becomes increasingly forward projected up to that critical point where the scattering in the medium saturates. This can be graphically shown in Fig. 8.
It was found in the literature that the critical point appears between 5 and 12 mm [29]. There is also a distinct lack of information regarding the therapeutic depth of penetration where papers simply state the penetration depth of light, and it is assumed that by this, it is referring to the maximum depth of penetration, since the criteria used have been found in literature which is not focussed on biological interactions of lasers but simply the theoretical basis of penetration depth.
Beam widths for IPL treatment devices are usually quoted as spot sizes in the range 6 to 4.8 mm [10], where the spot sizes are not always square and thus not always symmetrical, e.g. 20 × 30 mm spot size is employed by the Silk’n system.
Based simply on this 2-D model and the assuming that spot sizes are symmetrical, the fluence levels need not be adjusted for beam widths greater than 10 mm when attempting to reach a specific depth in tissue, and hence, spot sizes for various devices greater than this only have the added benefits of greater area for irradiance and so a reduction in surface heating and also the benefit of a greater beam width to treat a larger volume in the skin.
The Monte Carlo model used is a 2-D model and as such the spot size can only be adjusted in terms of a beam width. Of course, this 2-D model does not give the complete picture of light penetration into the tissue since a typical device may utilise a spatial profile which is not ‘homogeneous’, although it is hoped that the spatial profile remain consistent throughout the medium and does not follow the Gaussian intensity distribution which is employed by laser systems [30,33,33].
Discussion
In summary, it has been found from Monte Carlo simulations that an increase in penetration depth can be achieved using longer wavelengths of light and using a spot size which is of at least 10 mm in width. Maximum penetration depths using the IPL system were found to be 5 mm using the 1% criterion and 0.37 mm using the 13.5% criterion. Although from this data and the lack of literature referring to the penetration depth, it is not possible to identify a therapeutic depth of penetration. It can however be suggested that if a maximum penetration depth of 5 mm is achieved using the IPL (for skin type 2) with a reduction in the intensity to the extreme of 1% maximum intensity, then it is safe to assume that the IPL does not have much of an effect at depth greater than 5 mm and so there would be remote risk of damage to tissues beneath the skin and indeed no damage to organs or a foetus which rests beneath the skin, adipose and muscular tissue. However, this model just looks at the penetration depth of light and not at the heat it produces on interacting with the tissue. Thus, it would be useful to produce a spatial heat diffusion model to identify the temperature at the maximum penetration depth and also to identify the temperature rise at therapy associated locations such as the hair follicle and blood vessels.
It should be noted that the intensities reported in this section are not as a percentage of the incident intensity but as a percentage of the maximum deposited photon energy; the radiation which has escaped the sample is not included in this intensity. It would thus be useful for future investigations to identify the percentage of light which has escaped the sample and from this, deduce the absorption intensities as a fraction of the intensity produced by the device and not just as a fraction of that maximum amount which is absorbed in the skin. Therefore, the actual penetration depths would be less than those found.
Other further investigation could include identifying the relationship between wavelength and penetration depth for wavelengths greater than 750 nm, since the Monte Carlo simulation package only looks at wavelengths in the range 300–750 nm. Use of smaller increments would also allow more accurate representation of the wavelength-dependent attenuation profiles of the chromophores to be identified.
It should be acknowledged also that this model does not take into account the compression of skin when the device is placed on it. This would reduce the thickness of skin but at the same time the attenuation coefficients change [1]. However, this may be of irrelevance due to the slight pressure applied when using the device and also the fact that a coupling gel is applied between the device and the skin, though it would be interesting to identify the effect of this compression on penetration depth. Compressing the skin squeezes the blood, a competing chromophore, out of the treatment area and forces the hair follicles to lie down bringing the roots closer to the surface. As a result, the effective penetration of the beam is improved up to 15%.
Conclusion
This work addresses the risk assessment of laser and IPL devices that at these wavelengths and radiant exposures, photons are unable to reach vital organs as these results show a maximum penetration depth of 5 mm of 1% incident light. Therefore, these devices do not pose a photothermal or photochemical health risk to vital internal organs or foetus’s.
Fluence distribution within tissue and thus the treatment efficacy depends upon the illumination geometry and wavelength. To optimise therapeutic techniques, light-tissue interactions must be thoroughly understood and can be greatly supported by the use of mathematical modelling techniques. The TODDY simulation provides the relationship of photon distribution with wavelength of epidermis-dermis-epidermis backscatter in our model.
This study illustrates that on increasing the wavelength of light used in skin therapy, there is a corresponding increase in the penetration depth. Simulation of various beam widths has presented the increase in the penetration depth when the beam width is increased from 1 up to 5 mm before maintaining a constant penetration depth of approximately 10 mm when the intensity is reduced to 1% intensity regardless of the increase in beam width.
References
Kwon K, Son T, Lee K, Jung B (2009) Enhancement of light prop depth in skin: cross-validation of mathematical modelling methods. Lasers Med Sci 24(4):605–615
Meredith P, Sarna T (2006) The physical and chemical properties of Eumelanin. Pigment Cell Res 19:572–594
Ash C (2009) Optimising output dosimetry of a broadband pulsed light source for the removal of unwanted hair, PhD Thesis. (Unpublished)
Anderson R, Parrish J (1981) The optics of human skin. J Invest Dermatol 77(1):13–19
Brenning M, Hearing V (2008) The protective role of melanin against UV damage in human skin. Photochem Photobiol 84(3):539–549
Young A (1997) Chromophores in human skin. Phys Med Biol 42:789–802
Flewelling R, Noninvasive optical monitoring. In J.D. Bronzino, editor, The biomedical engineering handbook, Section 86, pages 1–11, Boca Raton, 1981. IEEE Press
Clement M, Daniel G, Trelles M (2005) Optimising the design of a broad band light source for the treatment of skin. J Cosmetic Laser Ther 7:177–189
Zhao Z, Fairchild P (1998) Dependence of light transmission through human skin on incident beam diameter at different wavelengths. SPIE Proceedings of Laser-Tissue Interaction IX 3254:354–360
Thayson-Peterson D, Bjerring P, Dierickx C, Nash J, Town G, Haedershal M (2012) A systematic review of light based home use devices for hair removal and considerations on human safety. Eur Acad Dermatol Venereol 26(5):545–553
Randall V, Lanigan S, Hamzavi I, Chamberlain J (2006) New dimensions in hirsutism. Lasers Med Sci 21(3):126–133
Saladin K (2007) Human anatomy, 1st edn. McGraw-Hill, Quezon City
Ash C, Donne K, Daniel G, Town G, Clement M, Valentine R (2012) Mathematical modelling of the optimum pulse structure for safe and effective photo epilation using broadband pulsed light. J Appl Clin Med Phys 13(5):3702. https://doi.org/10.1120/jacmp.v13i5.3702..
Lister T, Wright PA, Chappell PH (2012) Optical properties of human skin. J Biomed Opt 17(9):90901–90901. https://doi.org/10.1117/1.JBO.17.9.090901
Jacques S (2013) Optical properties of biological tissues: a review. Phys Med Biol 58:R37–R61
Bashkatov AN, Genina EA, Tuchin VV (2011) Optical properties of skin, subcutaneous, and muscle tissues: a review. J Innov Opt Health Sci 4(1):9–38
Barnes C A (2011) Review of optical and physical coefficients for modelling light tissue interaction, MSc Thesis. (Unpublished)
Baranoski G, Krishnaswamy A (2010) Light and skin interactions: simulations for computer graphics applications, 1st edn. USA, Elsevier Inc
Bonnett R (1995) Photosensitizers of the porphyrin and phthalocyanine series for photodynamic therapy. Chem Soc Rev 24:19–33
Gemert M, Jacques S, Sterenborg H, Star W (1989) Skin optics. IEEE Trans Biomed Eng 36(12):1146–1154
Weber R, Taylor B, Engelman D (2011) Laser induced tissue reactions and dermatology. Curr Probl Dermatol 42:24–34
Lakowizc J, Principles of fluorescence spectroscopy, volume 1. 3rd ed. New York. Springer; 2010.
Chen J, Wang D, Xi J, Au L, Siekkinen A, Warsen A, Li Z, Zhang H, Xia Y, Li X (2008) Immuno gold nanocages with tailored optical properties for targeted photothermal destruction of cancer cells. Nano Lett 7(5):1318–1322
Crochet JJ, Gnyawali SC, Chen Y, Lemley EC, Wang LV, Chen WR (2006) Temperature distribution in selective laser-tissue interaction. J Biomed Opt 11:34031
van Gemert M, Jacques S, Sterenborg HJ, Star WM (1989) Skin optics. IEEETrans Biomed Eng 36(12):1146–1154
Welch AJ, van Gemert MJ (1995) Optical-thermal response of laser-irradiated tissue. Plenum Press, New York
Welch AJ, Gardner CM (1997) Monte Carlo model for determination of the role of heat generation in laser-irradiated tissue. J Biomech Eng 119(4):489–495
Fitzpatrick TB (1988) The validity and practicality of sun-reactive skin types I through VI. Arch Dermatol 124(6):869–871
Nouri K (2011) Lasers in dermatology and medicine, 1st edn. Springer, London
Goldberg D (2011) Laser dermatology: pearls and problems. 1st ed. John Wiley and Sons, New Jersey
Gorjan M (2008) Modelling and measurements of laser-skin thermal interaction. University of Ljubljana graduate seminar
Thomas G (2010) Investigation and development of measurement techniques for the spatial energy distribution of intense pulsed light (IPL) systems, MSc Thesis. (Unpublished)
Brenning MAHV (2008) The protective role of melanin against UV damage in human skin. Photochem Photobiol 84(3):539–549
Acknowledgements
We would like to pay thanks to Richard Hugtenburg for his support of Michael Dubec MSc studies. Many thanks to Rebecca Whittall and Kevin Herbert for their review of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ash, C., Dubec, M., Donne, K. et al. Effect of wavelength and beam width on penetration in light-tissue interaction using computational methods. Lasers Med Sci 32, 1909–1918 (2017). https://doi.org/10.1007/s10103-017-2317-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10103-017-2317-4