Altruistic preferences in global emission games

Abstract

This paper analyses the impact of altruism on the individual country goverments’ incentives to reduce global polluting emissions. The game theory perspective provides insights into the strategic decision-making processes of the governments regarding the problem of climate change. We propose a model of strategic interactions among countries in which each government is concerned with its own benefit, as well as with the benefits of all the other countries.The model is a vector-valued non-cooperative game that permits the representation of situations in which the preferences of the governments are incomplete and there is imprecision about the degrees of altruism. The focus is on the identification of the potential equilibria that will eventually be reached when the governments show different attitudes towards other countries or groups of countries. As a result, we show that the incorporation of altruism into the model produces equilibria with a positive effect on the reduction of emissions.

1 Introduction

Emissions of pollutant gases from countries around the world have sharply risen over the past decades. Since these emissions are considered a significant determinant in global warming and climate change, multiple efforts have been made to analyse the possibility of reducing them. Governments of countries from different parts of the world have expressed their concern and responsibility with respect to the mitigation of climate change, especially regarding the reduction of pollutant gases emitted into the atmosphere. However, the mitigation of global climate change is a particularly difficult challenge to address, as it requires the concerted action from a large number of countries, which hinders an effective response due to strong free-riding incentives. Hence, the results of the international treaties to control climate change have so far been rather disappointing.

Most of the economic models developed so far to represent the strategic behavior of the country governments rely on the assumption that, when the governments decide their level of emissions, they are solely motivated by self-interest. However, some behavioral studies have tested that agents are often willing to mitigate emissions guided by an altruistic attitude. The aim of our paper is to propose a framework where to explore the effects of altruistic behavior of governments of countries in their strategic decisions.

Strategic aspects are particularly important in international pollution control, since there is no world government that could enforce the agreements. The analysis of emisions control as a game was originally introduced by Mäller (1989). He proposed the acid rain game as a non-cooperative game and provided different cooperative solutions to reach an agreement on emissions reductions involving European countries. Interesting reviews on the application of cooperative and non-cooperative game models to the International Environmental Agreements are Finus (2008), Wood (2011) and Finus and Caparrós (2015). A more general overview of the application possibilities of game theory to climate change is Kutasi (2012).

To understand why cooperation fails, these collective-action problems can be addressed from the perspective of social dilemmas, which represent cases of important conflict between individual self-interest and collective interest. In this respect, DeCanio and Fremstad (2013), after an exhaustive examination of climate-relevant dilemma games, concluded that emission reductions predicted by these models depend on several aspects, such as the payoff structure of the game, the solution concept considered, the power assigned to the countries, and their preferences over their payoffs. Madani (2013) pointed out some limitations of the models analysed by DeCanio and Fremstad, and he discussed alternative assumptions and solution methods in order to provide useful policy advice.

Other game theory models have also been used to explore the countries strategic behavior with respect to the process of mitigating gas emissions. Verma and Kauskal (2016) presented cooperative and non-cooperative approaches to analyse the economics of climate change. They showed that a reduction in the emission of gases is possible only when all countries work together under incentives. More recently, Molina et al. (2020) proposed a matching-commitment agreement in which countries can change each other’s incentives by committing to conditional emissions reductions, before countries decide on their unconditional reductions. They establish that this type of agreement can result in increased abatement and welfare for the countries involved.

In addition, governments can show altruistic behaviors with respect other countries given that certain global problems, such as climate change, require shared responsibility and collective action to address. There are several reasons that support these attitudes. For instance, interconnectedness since environmental issues have transboundary effects that require focusing on the coordinated effort of governments. Promoting global stability is another argument that can encourage non-selfish behavior, because by working towards environmental sustainability, governments can help favour peace and stability both within and between nations. Furthermore, to take into account environmental issues in other countries can also bring strategic benefits, such as improving diplomatic relations, enhancing national security, and encouraging economic development. In general, an altruistic interest to environmental issues can benefit not only other countries but also the global community as a whole. As a consequence, altruistic behavior of governments can demonstrate a commitment to working together with other nations to find solutions to these challenges.

Moreover, there is another issue that may influence the actions that governments may take in response to climate change: the individual perception of the country’s citizens. In order to determine the reasons that motivate individual pro-environmental behavior, Fleiß et al. (2020) carried out a laboratory experiment to evaluate the degree to which people’s social value orientation is related to environmental concerns. Their results showed that humanitarian and environmental value orientations are strongly interrelated, since the negative consequences of the global warming for humans are considered more important than the non-human consequences of climate change, that is, for the environment in general, flora and fauna. Likewise, some recent reports (see, for instance, Pew Research Center 2021 and Eurobarometer Survey 2021) show that citizens are increasingly sensitive to the problems derived from climate change, not only because of the consequences in their own country, but also because of the effects on a global level. This awareness of the population could lead the government to move away from a strictly self-maximizing behavior to the inclusion of altruistic criteria.

The present paper proposes a static model that permits a theoretical analysis of possible non-self oriented behavior of the country governments. The global emission game (Finus 2001) is extended to a non-cooperative game with vector-valued utilities that permits the representation of altruistic attitudes. We assume that an altruistic government is one that cares about the others, and, therefore, takes into account not only its own payoff, but also the payoffs of the other countries. A related concept of altruism is considered in van der Pol et al. (2012). These authors modified a two-stage game for the analysis of the international environmental agreements to consider altruistic preferences in the decision of the countries. They assumed that, when government decides whether or not to participate in an international climate agreement, it exhibits a concern for other countries by considering the aggregated net benefits of other countries with a positive weight in its payoff function. They show that altruistic preferences play an important role on group formation and on its stability.

In the non-cooperative static game introduced in the present paper, which we name the altruistic emission game, the payoff function of each country is a vector-valued function whose components are the net benefits obtained from emissions of all the countries. This general approach permits the representation of the incomplete preferences, and enables the analysis of situations in which the degree of altruism of the countries is imprecise.

Several types of countries are established by considering the attitude that their governments show regarding the benefits of the other countries. In particular, according to the classification provided by Mármol et al. (2020), we distinguish between pro-self countries, who care at least as much about their own net benefit as they do about the net benefits of the others, and pro-social countries, that consider the net benefits of other countries at least as important as their own benefits. We characterize the subsets of equilibria which are likely to be attained depending on the types of countries involved. This allows us to analyse interesting cases as, for instance, a scenario where the countries are gathered into groups that mutually consider the net benefit of the countries within the same group, but not the net benefit of the countries belonging to other groups.

Thus, the theoretical model developed in this paper provides an appropriate framework to analyse the strategic decisions of the country governments on gas emissions when they deviate from their own profit-maximizing behavior and are heterogenous regarding the attitude adopted towards other countries. The differentiated feature with respect to existing models is that the vector-valued generalisation permits the introduction of imprecise information on the degrees of altruism of the countries, enabling the identification of the set of foreseeable equilibria as a result of the different attitudes of the countries. A conclusion is that, even when all the governments show a pro-self attitude, there is still a range of potential equilibria in which the aggregated global emissions are less than when they are self-interested.

The rest of the paper is organized as follows. In Sect. 2, we describe the standard emission game, we set up our model of altruistic game and derive its set of equilibria. Section 3 is devoted to the analysis of the weighted emission games obtained when the preferences of the agents are represented by additive value functions. The effect of the different attitudes of the countries on the set of foreseeable equilibria is studied in Sect. 4. Finally, concluding remarks of this research are included in Sect. 5 and the Appendix contains the proofs.

2 Emission games

We study situations in which two or more countries emit polluting gases to the environment, such that the damages from the pollutant on each country depend on the total amount of pollution emitted by all of them. These decision-making problems are analysed as strategic games with a continuous strategy space in which each player chooses how much pollution to emit, rather than whether to pollute or not.

We consider a set of n agents (country governments), $N= \{1,\ldots ,n\}$, and $E_i$ the set of strategies that agent $i \in N$ can adopt. The strategy profile, denoted by $e= (e_{1},\ldots ,e_{n})$ with $e_i \in E_i$, can be written as $e=(e_i, e_{-i})$, where $e_i$ represents the quantity of gases emitted by country i, as a consequence of its production capacity and $e_{-i}=( e_{1},\ldots ,e_{i-1}, e_{i+1},\ldots ,e_{n})$ stands for the strategy combination of all countries except for country i. An upper bound for the emissions of each country exists, $e_i^0$, and therefore $E_i=[0, e_i^0]$. We can assume that the upper bound for each country consists of a sufficiently high quantity of emissions that does not limit the results of interaction.

The net benefit function of country i is modeled as:

$$\begin{aligned} \pi _i(e)=\beta _i(e_i)-\phi _i\left( \sum _{j=1}^n e_j\right) , \forall i \in N \end{aligned}$$

where $\beta _i$ is the benefit derived from the own emission and $\phi _i$ represents the damage for country i derived from the aggregated emissions. We assume that both functions are continuous with $\beta _i'(e_i) \ge 0$, $\beta _i''(e_i) \le 0$, for all $e_i \in E_i$, and $\phi ' _i(\sum _{j=1}^n e_j) \ge 0$, $\phi '' _i(\sum _{j=1}^n e_j) >0$, for all $\sum _{j=1}^n e_j \ge 0$. Under these assumptions, the benefit of country i, $\beta _i$, increases at a strictly decreasing rate, and the damage for country i derived from the global emission, $\phi _i$, increases at an increasing rate. Moreover, since $\beta _i''(e_i) < \phi _i''(\sum _{j=1}^n e_j)$ for $e_i \in E_i$, $\pi _i$ is strictly concave in its own action.

2.1 The standard emission game

The standard emission game in normal-form, as described in Finus (2001), is denoted as $SG=\{(E_i, \pi _i)_{i\in N}\}$. This game models a situation in which, when choosing their strategies, each country only cares about its net benefit function.

We denote by $r_{i}$ the best response correspondence of country i to the strategies of all remaining countries. The best response function of country i is determined by the first-order optimality conditions, that is, for a given $e_{-i}$:

$$\begin{aligned} e_i\ge 0, \, e_i\left( \beta _i' (e_i)-\phi _i'\left( \sum _{j=1}^n e_j\right) \right) =0,\, \text{ and } \beta _i' (e_i)\le \phi _i'\left( \sum _{j=1}^n e_j\right) . \end{aligned}$$

Note that for those $e_{-i}$, such that the equation $\beta _i' (e_i)-\phi _i'(\sum _{j=1}^n e_j)=0$ determines a negative value of $e_i$, $r_i(e_{-i})=0$. As a consequence, the best response of a country is a continuous piecewise function. It is also differentiable except at the points where the function first reaches value zero.

The features of the profiles of strategies that are stable in a non-cooperative game are captured by the concept of Nash equilibrium (Nash 1951).

A strategy profile $e^*$ is a Nash equilibrium of the game $SG=\{(E_i, \pi _i)_{i\in N}\}$ if for all $e_i\in E_i$, $\pi _i(e_i, e_{-i}^*) \le \pi _i(e_i^*, e_{-i}^*)$.

It follows from the first-order optimality conditions that in an interior equilibrium ($e_i^*>0$ for all $i\in N$), marginal benefits from emissions equal marginal damages in each country. For extreme equilibria this condition may hold for some countries while the emissions of other countries are null.

Under the above assumptions on the benefit and damage functions, and on the sets of strategies of the countries, the existence and uniqueness of a Nash equilibrium in this model is guaranteed (see, for instance, Rosen 1965). The equilibrium of this standard model is denoted by $e^{NE}$ and the aggregated emissions of the countries at the equilibrium is $\sum _{ i\in N} e_i^{NE}$.

Example 2.1

(adapted from Finus 2001) Consider n countries with the following net benefit functions:

$$\begin{aligned} \pi _i(e)=b_i\left( de_i-\frac{1}{2}e_i^2\right) -\frac{c_i}{2}\left( \sum _{j=1}^n e_j\right) ^2, \end{aligned}$$

where $b_i, c_i, d>0$.

With this functional form, the ratio $\frac{b_i}{c_i}$ represents the benefit-damage ratio of the emissions for country i. The net benefit function, $\pi _i$, is strictly concave since $\beta _i'' (e_i)<\phi _i''(\sum _{j=1}^n e_j)$, and consequently, the uniqueness of the optimum with respect to the own action is assured.

Moreover, the best response correspondence for country i is

$$\begin{aligned} r_i(e_{-i})= max \left\{ 0, \frac{b_id-c_i\sum _{j\ne i}e_j}{b_i+c_i}\right\} . \end{aligned}$$

In order to describe the Nash equilibrium of this game, consider the quantities at equilibria obtained when the non-negativity constraint is relaxed:

$$\begin{aligned} {{\hat{e}}}_i=\left( 1-\frac{n}{\frac{b_i}{c_i} \left( 1+\sum _{j\in N}\frac{c_j}{b_j}\right) }\right) d. \end{aligned}$$

Denote by $N'$ the set of countries for which ${{\hat{e}}}_i>0$. The components of the corresponding Nash equilibrium are $e^{NE}_i=\left( 1-\frac{| N' |}{\frac{b_i}{c_i} (1+\sum _{j\in N'}\frac{c_j}{b_j})}\,\right) d$, for $i\in N'$,¹ and $e_i^{NE}=0$ for $i\notin N'$. $\square$

2.2 The emission game with altruistic preferences

We now propose an extension of the standard emission game that is adequate to model the strategic interaction among countries that do not only care about their own payoff function but also about the payoff function of all the other countries. We assume that the preferences of the governments are altruistic in the sense that they prefer (or weakly prefer) greater net benefits for all the countries. That is, given two profiles of strategies $e, {{\bar{e}}}\in \times _{i\in N} E_i$, such that $\pi _j({{\bar{e}}})\ge \pi _j(e)$ for all $j\in N$, ${{\bar{e}}}$ would be at least as preferred as e by all the countries, and if in addition $\pi _k({{\bar{e}}})> \pi _k(e)$ for some $k\in N$, then all the countries would strictly prefer ${{\bar{e}}}$ to e.

These situations can be modeled as a vector-valued game, $G=\{(E_i, \pi )_{i\in N}\}$, where the components of vector-valued function $\pi : \times _{i\in N}E_i \rightarrow \mathbb {R}^{n}$, $\pi :=(\pi _1, \ldots ,\pi _n)$, represent the payoff functions for all the agents. That is, every governments considers its own net benefit, together with the net benefits of the other countries with monotonous preferences as described above. We call this vector-valued game the altruistic emission game.

In this setting the well-known extensions of the notion of Nash equilibrium are²:

Definition 2.2

A strategy profile $e^*$ is an equilibrium for the vector-valued game $G=\{(E_i, \pi )_{i\in N}\}$ if $\,\,\,/\!\!\!\exists \,i\in N$ with $e_i\in E_i$ such that $\pi (e_i, e_{-i}^*)\ge \pi (e_i^*, e_{-i}^*)$.

The set of equilibria of G is denoted as ${{{\mathcal {E}}}}(G)$.

Definition 2.3

A strategy profile $e^*$ is a weak equilibrium for the vector-valued game $G=\{(E_i, \pi )_{i\in N}\}$ if $\,\,\,/\!\!\!\exists \,i\in N$ with $e_i\in E_i$ such that $\pi (e_i, e_{-i}^*)> \pi (e_i^*, e_{-i}^*)$.

The set of weak equilibria of G is denoted as ${\tilde{{\mathcal {E}}}}(G)$.

The set of equilibria and the set of weak equilibria in a vector-valued game often do not differ significantly. In fact, under our original assumptions on the benefit and damage functions both sets coincide, and under certain concavity assumptions, the whole set of equilibria for a vector-valued game can be characterized in terms of the best response of the agents in relation to the components of the vector-valued function:

Theorem 2.4

(Mármol et al. 2017) Let $G=\{(E_i, u_i)_{i\in N}\}$ be a game with vector-valued utilities, where for all $i\in N$, $E^i\subset \mathbb {R}$ is non-empty convex and compact, $u_i:\times _{i\in N}E_i \rightarrow \mathbb {R}^{J_i}$, $u_i:=(u_i^j)_{j \in J_i}$, and $u_i^j$ is strictly concave in its own action for each $j\in J_i$. The set of equilibria of the game G is

$$\begin{aligned} {{{{\mathcal {E}}}}}(G)=\{(e_1, \ldots , e_n)\in \times _{i\in N}E_i: {\underline{r}}_i(e_{-i})\le e_i\le {{\bar{r}}}_i(e_{-i}), \, i\in N\}, \end{aligned}$$

where ${\underline{r}}_i(e_{-i})= min_{j\in J_i} \,r^{j}_i (e_{-i})$, ${\bar{r}}_i(e_{-i})= max_{j \in J_i} \,r^{j}_i (e_{-i})$, and $r^{j}_i$ stands for the best response correspondence of agent i to the strategies of all remaining agents for $u_i^j$.

In this result, the hypothesis of strict concavity of the functions $u_i^j$ can be relaxed to concavity, providing a similar result which characterizes the set of weak equilibria in terms of the minimum and of the maximum values of the best responses, for those ${\underline{r}}_i(e_{-i})$ and ${\bar{r}}_i(e_{-i})$ that are not singletons.

In our model, the altruistic preferences of the agents are incorporated into their utility functions leading to a vector-valued utility game. In this respect, the methodology applied in this paper differs from those usually employed to analyse the emission games. Therefore, the components of the vector-utility of each country correspond to the net benefits of all the countries, and since for each $i\in N$, $\pi _i$ and $\pi _j$ are strictly concave in $e_i$ then the assumptions in Theorem 2.4 hold. Since $\pi _j$ is decreasing on the action $e_i$ for all $j \ne i$, the maximum of $\pi _j(e_i)$ is attained when $e_i=0$, hence $r^{i}_j (e_{-i})=0$ for all $j \ne i$, and therefore ${\underline{r}}_i(e_{-i})=0$. In addition, ${\bar{r}}_i(e_{-i})=r^{i}_i (e_{-i})={r}_i(e_{-i})$. Thus, the whole set of equilibria for the emission game with altruistic preferences is described in the following result.

Proposition 2.5

The set of equilibria of the altruistic emission game $G=\{(E_i, \pi )_{i\in N}\}$, is

$$\begin{aligned} {{{{\mathcal {E}}}}}(G)=\{(e_1, \ldots , e_n)\in \times _{i\in N}E_i: 0\le e_i\le r_i(e_{-i}), \, i\in N\}. \end{aligned}$$

In this game, since the emissions of each country affect other countries only in the form of costs, the altruistic preferences of the countries create incentives for less emissions. Therefore, a first consequence is that the aggregated emissions at any equilibria of the vector-valued game is less than the aggregated emissions at the Nash equilibrium of the standard game.

Example 2.6

The altruistic emission game for the example is $G=\{(E_i, \pi )_{i\in N}\}$, with

$$\begin{aligned} \pi _i(e)=b_i(de_i-\frac{1}{2}e_i^2)-\frac{c_i}{2}\left( \sum _{j=1}^n e_j\right) ^2. \end{aligned}$$

Since $\pi _i$ is continuous and strictly concave in $e_j$ for each $j \in N$, the whole set of equilibria for this game is

$$\begin{aligned} {{{{\mathcal {E}}}}}(G)=\left\{ (e_1,\ldots , e_n)\in \times _{i=1}^n E_i: 0\le e_i\le max\left\{ 0, \frac{b_id-c_i\sum _{j\ne i}e_j}{b_i+c_i} \right\} \right\} . \end{aligned}$$

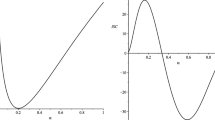
To clearly illustrate this result, in Fig. 1 we show a graphical representation of the particular case of two countries with identical net benefit functions. $\square$

Fig. 1

Nash equilibrium of the standard game and the set of equilibria of the altruistic game

3 Weighted emission games

The literature on vector-valued games has mainly focused on the case where the preferences of the agents are represented by additive value functions. In this section, we follow this approach and assume that the preferences of the governments can be represented by a weighted sum of the individual net benefit functions. This assumption entails that the countries consider that trade-off rates exist such that the net benefits of the different countries could be compensable.

Formally, let $\lambda ^i \in \Delta ^{n}=\{ \lambda ^i\in \mathbb {R}^{n}:\sum _{j=1}^{n} \lambda ^i_j=1, \lambda ^i_j\ge 0\}$ be a vector of weights corresponding to country i. For $\lambda ^i \in \Delta ^n$, the preference of agent i is given by

$$\begin{aligned} v_{\lambda ^i}(e)=\lambda ^i\cdot \pi ^t(e)= \sum _{j=1}^n\lambda ^i_j\pi _j(e)=\sum _{j=1}^n\lambda ^i_j \left( \beta _j(e_j)-\phi _j\left( \sum _{k=1}^n e_k\right) \right) , \end{aligned}$$

where $\pi ^t$ is the transpose of $\pi$, $\lambda ^i= (\lambda ^i_j)_{j \in N}$, and $\lambda ^i_j$ represents the relative importance that agent i assigns to the net benefit of the agent j.

For $\lambda \in \Delta =\times _{i=1}^n \Delta ^{n}$, we consider the scalar weighted game $G_\lambda =\{(E_i,v_{\lambda ^i})_{i\in N}\}$. Let $E(G_{\lambda })$ denote the set of equilibria of $G_\lambda$.

The links between the equilibria of a vector-valued game and the equilibria of the corresponding weighted games have already been established in the literature. Shapley (1959) characterized the set of equilibria and the set of weak equilibria, for two-player zero-sum vector games, in terms of the Nash equilibrium of scalar games with weighted-sum payoffs. Subsequently, for convex sets of strategies and concave payoff functions, Bade (2005) established the relationship between the set of equilibria of a vector-valued game and the set of equilibria of weighted games with positive weights and with non-negative weights showing that:

$$\begin{aligned} \cup \{ E(G_{\lambda }): \lambda \in \Delta ^+ \} \subseteq {{{{\mathcal {E}}}}(G)} \subseteq \cup \{ E(G_{\lambda }): \lambda \in \Delta \}. \end{aligned}$$

where $\Delta ^+= \{\lambda \in \Delta : \lambda _j^i>0, \text{ for } i,j \in N\}$.

In Mármol et al. (2017) it is proven that the equilibria of weighted games with non-negative weights are weak equilibria of vector-valued games, that is, $\cup \{ E(G_{\lambda }): \lambda \in \Delta \} \subseteq {{\tilde{{\mathcal {E}}}}(G)}$. Moreover, under concavity assumptions (the sets of strategies of each agent are nonempty convex subsets of a finite dimensional space and for each agent the components of the vector-valued utilities are concave in its own action), both sets coincide: $\cup \{ E(G_{\lambda }): \lambda \in \Delta \} ={{\tilde{{\mathcal {E}}}}}(G)$. In addition, when the components of the vector-valued utilities are strictly concave, the set of weak equilibria coincides with the set of equilibria.

In our model each net benefit function is strictly concave in the action of any of the countries. Therefore, the whole set of equilibria can be identified as the union of the equilibria of the weighted games, that is:

$$\begin{aligned} {{{{\mathcal {E}}}}(G)} = \cup \{ E(G_{\lambda }): \lambda \in \Delta \}. \end{aligned}$$

In order to determine the equilibria of the scalar weighted game, $G_\lambda$, we establish the best response correspondence of each country. Denote by $r_{\lambda ^i}$ the best response correspondence of country i to the strategies of the other countries in the weighted game $G_{\lambda }$. Since the value function of the weighted games inherit the concavity properties of the original net benefit functions, the best response of country i is obtained from the first-order conditions:

$$\begin{aligned} e_i\ge 0, e_i \left( \lambda ^i_i \beta _i'(e_i)-\sum _{j=1}^n \lambda ^i_j \phi _j'\left( \sum _{k=1}^n e_k\right) \right) =0, \text{ and } \lambda ^i_i \beta _i'(e_i)\le \sum _{j=1}^n \lambda ^i_j \phi _j'\left( \sum _{k=1}^n e_k\right) . \end{aligned}$$

It should be pointed out that if $\lambda ^i_i=1$, then $\lambda ^i_j=0$ for all $j \ne i$ and the best response is the response in the standard game, $r_{i}$, and if $\lambda _i^ i =0,$ then $r_{\lambda ^i}(e_{-i}) =0$ for all $e_{-i}$ since the weighted function considered, $\sum _{j \ne i} \lambda _j^i \pi _j(e) =- \sum _{j \ne i} \lambda _j^i \phi _j(\sum _{k=1}^n e_k),$ is decreasing with respect to $e_i$.

In addition, it follows that for all $\lambda ^i \in \Delta ^n$, $r_{\lambda ^i}(e_{-i})\le r_{i}(e_{-i} )$ holds. Therefore, since the standard game has a unique Nash equilibrium, the uniqueness of the equilibria for all the weighted games is assured.

A special case is when all the agents attach the same weight to the net benefit functions of the other agents, including its own net benefit. In this case the weights for all countries are $\lambda ^i=(\frac{1}{n},\ldots ,\frac{1}{n})$. This weighted game has a unique Nash equilibrium which coincides with the social optimum that is, the equilibrium when the joint net benefit is maximized. This profile of strategies can be regarded as the level of emissions recommended by an external arbitrator who seeks to maximize the aggregated net benefit. For the best responses in this case, denoted as $r_{i}^S$, $r_{i}^S (e_{-i})\le r_{i}(e_{-i})$ also holds.

Now consider the case in which a government is only concerned about the net benefits of a subset of countries $H \subseteq N$ attaching the same weight to all of them and ignoring the rest of the agents. The corresponding vector of weights is then $\lambda _j^i=\frac{1}{|H|}$ for $j \in H$, and $\lambda _j^i=0$ for $j \notin H$. The value function of the scalar weighted game is $\frac{\sum _{j \in H} \pi _j(e)}{|H|}$, and we denote by $r_{i}^{S_H}$ the corresponding best response. We show that when a country takes into account additional countries, then its level of emissions at its best response does not increase.

Proposition 3.1

For all $e_{-i} \in \times _{j\ne i}{E_j}$ and for all $H, I \subseteq N$ such that $i \in H\subseteq I$, $r_{i}^{S_I}(e_{-i})\le r_{i}^{S_H}(e_{-i})$ holds.

In particular, the level of emissions at the best response in the standard emission game is not lower than the level of emissions at the best response when considering the sum of the net benefits of some countries including the own net benefit, that is, $r_{i}^{S_I}(e_{-i})\le r_{i}(e_{-i}),$ for all I such that $i \in I \subseteq N.$ Moreover, $r_{i}^S(e_{-i})\le r_{i}^{S_I}(e_{-i}),$ for all $I \subseteq N.$

Example 3.2

(continued) For the emission game considered in the previous example, the additive value function is

$$\begin{aligned} v_{\lambda ^i}(e)=\sum _{j=1}^n\lambda ^i_j\pi _j(e)=\sum _{j=1}^n\lambda ^i_j \left( b_j\left( de_j-\frac{1}{2}e_j^2\right) -\frac{c_j}{2}\left( \sum _{k=1}^n e_k\right) ^2\right) , \end{aligned}$$

with $\lambda ^i$ the vector of weights that country i assigns to its own net benefit ($\lambda ^i_i$) and to the other countries’ net benefit ($\lambda ^i_j, j \ne i$).

The best response correspondence for the weighted game $G_\lambda =\{(E_i,v_{\lambda ^i})_{i\in N}\}$ is

$$\begin{aligned} r_{\lambda ^i}(e_{-i}) = max \left\{ 0, \frac{\rho _i d-\sum _{j\ne i} e_j}{\rho _i+1}\right\} , \end{aligned}$$

where $\rho _i=\frac{\lambda _i^i b_i}{\sum _{k=1}^n \lambda _k^i c_k}$. The quantity $\rho _i$ represents the evaluation of the benefit-damage ratio with the weights provided by country i. The Nash equilibrium of the corresponding weighted game can be obtained analogously as for the standard game. By computing the quantities

$$\begin{aligned} ({{\hat{e}}}_{\lambda })_i=\left( 1- \frac{n}{\rho _i \left( 1+ \sum _{j=1}^n \frac{1}{\rho _j}\right) }\right) d, \end{aligned}$$

the components of the Nash equilibrium of the weighted game are $(e^{NE}_{\lambda })_i= (1- \frac{|N'|}{\rho _i (1+ \sum _{j\in N'}\frac{1}{\rho _j}) })d$, for $i\in N'$ and $(e^{NE}_{\lambda })_i=0$ for $i\notin N'$, where $N'$ denotes the set of countries for which $({{\hat{e}}}_{\lambda })_i>0$.

Note that at equilibrium the level of emissions of each country depends not only on its evaluation of the benefit-damage ratio but also on the other countries’ evaluation of their ratio. The level of emissions of country i increases with $\rho _i$ and decreases with $\rho _j$ for $j\ne i$.

To illustrate the variation of the best response correspondence of country i in the weighted game $G_\lambda$ for different vector of weights, we consider the particular case of two countries with identical net benefit functions:

$$\begin{aligned} \pi _i(e)=b\left( de_i-\frac{1}{2}e_i^2\right) -\frac{c}{2}\left( \sum _{j=1}^n e_j\right) ^2, \end{aligned}$$

for $i=1,2$ where $b, c, d>0$.

Given $\lambda \in \Delta$, the best response correspondences of country i in the weighted game $G_\lambda$ is

$$\begin{aligned} r_{\lambda ^i}(e_{j})= max \left\{ 0, \frac{\lambda ^i_i bd-ce_j}{\lambda ^i_ib+c} \right\} \end{aligned}$$

Figure 2 shows the best responses for different vector of weights $\lambda ^1$ ($\lambda _1^1=0, \frac{1}{3},\frac{1}{2},\frac{2}{3}$ and 1). The value of the best response of country 1 is increasing with respect to the value of $\lambda _1^1$. In particular $r_1^S(e_2)\le r_1(e_2).$ $\square$

Fig. 2

Best responses, $r_{\lambda ^1}$, for different values of $\lambda _1^1$

4 Attitudes of the country governments in the altruistic emission game

In what follows we present an analysis of the equilibria of the altruistic emission game in terms of the attitudes of the different country governments towards the others. The attitude of a government can be represented by the weights that it attaches to its own net benefit function and to the other countries net benefits, and will finally determine its behavior in the strategic game. When the attitudes of all the country governments are completely determined, their vector of weights are fixed and the predicted result is the equilibria of the corresponding weighted game. On the other hand, if no information about the attitudes is available, then any vector of weights is considered admissible for each country and the prediction of the model consists of the whole set of equilibria of the vector-valued game. However, the information about the governments’ attitudes is usually in-between these two extreme situations in a way that there is imprecision on the weights that the countries will be willing to adopt, but they can still establish that the weights belong to a certain subset of admissible weights.

An easily understandable way to represent imprecision about importance weights is to provide a subset of admissible weights described by linear relations. For $i=1,\ldots , n$, consider the polyhedron of admissible weights of agent i, $\Gamma ^i\subseteq \Delta ^n$. Let $p _i$ denote the number of its extreme points and let $B^i$ be the $p_i\times n$ matrix whose rows are the extreme points of $\Gamma ^i$. For each $i\in N$, define a function, $v_{\Gamma ^i}$, with values in $\mathbb {R}^{p_i}$, given by $v_{\Gamma ^i}=B^i\cdot \pi ^t.$ This function has ${p_i}$ components, each of them is a weighted sum of the original payoff functions. Let $\Gamma =\times _{i=1}^n\Gamma ^i$.

The result in Theorem 3.3 proved by Mármol et al. (2017) provides a procedure to incorporate preference information in a vector-valued game and permits the identification of the equilibria that are compatible with the information provided as the equilibria of a transformed game. For the model in the current paper, this result can be written as follows:

Proposition 4.1

Let $G=\{(E_i, \pi )_{i\in N}\}$ be an altruistic emission game such that each $E_i$ is a nonempty convex subset of $\mathbb {R}$, and for each $i\in N$, $\pi _i$ is strictly concave in $e_i.$ The set of equilibria of the game with preference information $\Gamma$ coincides with the set of equilibria of the transformed vector-valued game $G_{\Gamma }=\{(E_i, v_{\Gamma ^i})_{i\in N}\}$.

We will first address the case in which the set of countries is split into separate groups, so that the countries belonging to a group take into account the utilities of all its members, although possibly with imprecise intensity. We assume that, within a group, each government considers the utility of any other country at most as important as its own, but still the corresponding weights are not completely determined. In addition, the attitude of the members of a group with respect to the countries outside the group is a selfish attitude and they do not take their utilities into account. It is worth noting that in this setting we are not modeling attitudes of countries that seek to harm others, they simply do not take their interests into account.

Given a group of countries, $C\subset N$, the set of information weights for any country $i \in C$ is:

$$\begin{aligned} \Gamma ^i=\{\lambda ^i \in \Delta ^n: \lambda _i^i \ge \lambda _j^i \text{ for } j \in C,\, j\ne i,\, \lambda _j^i=0, \, \text{ for }\, j \notin C\}. \end{aligned}$$

We next analyse the effect of these attitudes on the foreseeable equilibria of the game. Note that the transformed games, as defined in Proposition  4.1, inherit the concavity properties of the original vector-valued game, and therefore, the result in Theorem 2.4 can be applied to the transformed game in order to identify its equilibria in terms of the maximum and of the minimum of the best responses in the corresponding transformed game.

The following result provides the description of the sets of equilibria of the altruistic emission game in the situation in which the set of countries is split into separate groups, that is, $N=\cup _{k=1,\ldots ,r} C_k$ with $C_j\cap C_h=\emptyset$, when $j\ne h$.

Let $r_i^{S_{C_k}}$ be the best response of government $i\in C_k$ to the action of the other countries, when this government attaches the same importance to the utilities of all the countries in the group, that is, the scalar weighted game considered by i consists of the aggregated utilities of the countries belonging to the group, $\sum _{j \in C_k} \pi _j(e)$.

Proposition 4.2

Let $G=\{(E_i, \pi )_{i\in N}\}$ be an altruistic emission game. $N=\cup _{k=1,\ldots ,r} C_k$ with $C_j\cap C_h=\emptyset$, when $j\ne h$. For $k=1,\ldots , r$ and for each $i\in C_k$, $\Gamma ^i=\{\lambda ^i \in \Delta ^n: \lambda _i^i \ge \lambda _j^i \text{ for } j\ne i, j \in {C_k}, \, \lambda _j^i=0, \, \text{ for }\, j \notin {C_k}\}$. The set of equilibria of the game with preference information $\Gamma = \times _{i \in N} \Gamma ^i$ is

$$\begin{aligned} {{{\mathcal {E}}}}_{\Gamma }(G) =\{e \in \times _{i\in N}E_i: \, r_i^{S_{C_k}}(e_{-i}) \le e_i\le r_i(e_{-i})\, \text{ for } \text{ all }\,\,\,\, i\in {C_k},\,\,k=1,\ldots , r\}. \end{aligned}$$

Example 4.3

Consider the emission game in the previous example when $N=C_1\cup C_2$, with $C_1\cap C_2=\emptyset$, that is, each country belongs to one of two groups $C_1$ or $C_2$. Hence the set of equilibria of the game with this preference information $\Gamma = \times _{i \in N} \Gamma _i$ is the following

$$\begin{aligned} {{{\mathcal {E}}}}_{\Gamma }(G)= & {} \left\{ e \in \times _{i\in N}E_i:max\left\{ 0,\frac{b_id- \left( \sum _{j\in {C_k} }c_j\right) \sum _{ j\ne i}e_j}{b_i+\sum _{j\in { C_k}}c_j}\right\} \le e_i \right. \\\le & {} \left. max\left\{ 0,\frac{b_id- c_i\sum _{j\ne i}e_j}{b_i+c_i}\right\} \, \text{ for } i \in {C_k},\, k=1,2 \right\} . \end{aligned}$$

$\square$

In a more general setting, we can consider that a given government, i, can exhibit a different attitude towards the utilities of other countries, classifying them into four categories: those whose utilities are considered at most as important as its own, $M^i$; those whose utilities are considered at least as important as its own, $K^i$; those that are considered of equal importance, $R^i$, and those whose utilities are not taken into account, $T^i$.

Formally, the set of weights for country $i\in N$ is described as

$$\begin{aligned} \Gamma ^i= & {} \{\lambda ^i \in \Delta ^n: \, \lambda _i^i \ge \lambda _j^i \text{ for } j \in M^i, \lambda _i^i \le \lambda _j^i \text{ for } j \in K^i,\,\lambda _j^i=\lambda _i^i\\{} & {} \quad \text{ for } j\in R^i,\,\lambda _j^i=0, \, \text{ for }\, j \in T^i \}. \end{aligned}$$

Note that the case previously analysed in which each country belongs to a unique group is a particular case of this more general setting, where for each $i \in C_k$, $K^i=\emptyset$, $R^i=\emptyset$, $M^i=C_k{\setminus } i$, and $T^i=N{\setminus } C_k$.

With an analogous reasoning to that of Proposition 4.2, the set of equilibria when the attitudes of the governments can be represented by these sets of weights, is identified in terms of the maximum and of the minimum of the best responses in the transformed game. Denote by ${\hat{r}}_i^j$ $j=1,\ldots ,p_i$, the best response correspondences of country i to the strategies of the other countries in the transformed game corresponding to the sets of weights $\Gamma ^i$. The identification of the equilibria for this more general case (established in Proposition 4.5) relies on the following Lemma.

Lemma 4.4

Let $G=\{(E_i, \pi )_{i\in N}\}$ be an altruistic emission game. For the set of information weights, $\Gamma ^i=\{\lambda ^i \in \Delta ^n: \lambda _i^i \ge \lambda _j^i \text{ for } j \in M^i, \lambda _i^i \le \lambda _j^i \text{ for } j \in K^i,\,\lambda _j^i=\lambda _i^i \text{ for } j\in R^i,\,\lambda _j^i=0, \, \text{ for }\, j \in T^i \},$

$$\begin{aligned}{} & {} min_{j=1,\ldots ,p_i} {\hat{r}}_j^i(e_{-i})= \left\{ \begin{array}{ll} 0&{}\quad \text {if } K^i\ne \emptyset \\ r_i^{S_{N\setminus T^i }}(e_{-i})&{} \quad \text {if } K^i=\emptyset , \end{array} \right. \quad max_{j=1,\ldots ,p_i} {\hat{r}}_j^i(e_{-i})= r_i^{S_{N\setminus (T^i\cup M^i) }}(e_{-i}). \end{aligned}$$

Proposition 4.5

Let $G=\{(E_i, \pi )_{i\in N}\}$ be an altruistic emission game. For $i\in N$, $\Gamma ^i=\{\lambda ^i \in \Delta ^n: \, \lambda _i^i \ge \lambda _j^i \text{ for } j \in M^i, \lambda _i^i \le \lambda _j^i \text{ for } j \in K^i,\,\lambda _j^i=\lambda _i^i\, \text{ for } j\in R^i,\,\lambda _j^i=0, \, \text{ for }\, j \in T^i \}.$ The set of equilibria of the game with preference information $\Gamma = \times _{i \in N} \Gamma ^i$ is

$$\begin{aligned} {{{\mathcal {E}}}}_{\Gamma }(G)= & {} \{e \in \times _{i\in N}E_i: \,0 \le e_i\le r_i^{S_{N\setminus (T^i\cup M^i) }}(e_{-i})\, \text{ for } \text{ all } \text{ i } \text{ such } \text{ that }\,\,\,\, K^i\ne \emptyset ,\\{} & {} \quad r_i^{S_{N\setminus T^i }}(e_{-i}) \le e_i\le r_i^{S_{N\setminus (T^i\cup M^i) }}(e_{-i})\, \text{ for } \text{ all } \text{ i } \text{ such } \text{ that }\,\,\,\, K^i=\emptyset \}. \end{aligned}$$

Example 4.6

Consider the case of two countries with identical net benefit functions in the emission game of the previous example. In addition to an egoistic or to an equanimous behavior, countries can show a pro-self or a pro-social behavior towards the rest of the countries. We say that a country is pro-self if the weights of importance that it attaches to its own net benefit is not less than the weight of importance that it attaches to the net benefits of the others. A country is pro-social if it considers that the net benefit of the other countries are at least as important as its own net benefit.

If both countries are egoistic, that is, they only take into account their own net benefits, then the corresponding equilibrium is the Nash equilibrium of the standard emission game

$$\begin{aligned} e^{NE} =\left( \frac{bd}{b+2c},\frac{bd}{b+2c}\right) , \end{aligned}$$

with net benefits for each country $\pi _i(e^{NE} )= \frac{b^3d^2}{2(b+2c)^2}$.

If the countries are equanimous in the altruistic game, then the equilibrium coincides with the social optimum:

$$\begin{aligned} e^S=\left( \frac{bd}{b+4c},\frac{bd}{b+4c}\right) , \end{aligned}$$

with net benefits for each country $\pi _i(e^S)= \frac{b^2d^2}{2(b+4c)}$. These benefits are above the benefits in the case of egoistic countries, that is, $e^S_i<e^{NE} _i$ and $\pi _i(e^S)> \pi _i(e^{NE} ).$

An interesting situation is when the two countries behave symmetrically in the sense that the importance that both countries assign to their own net benefit coincides ($\lambda ^1_1=\lambda ^2_2=\lambda$), and thus the importances that each country assign to the other country also coincides. In this case, the Nash equilibrium depends on the common weight attached to $\lambda$:

$$\begin{aligned} e^*_\lambda =\left( \frac{\lambda bd}{\lambda b+2c}, \frac{\lambda bd}{\lambda b+2c}\right) . \end{aligned}$$

Net benefits at this equilibrium for each agent i are $\pi _i(e^*_\lambda )= \frac{\lambda ^2b^3d^2+4\lambda (1-\lambda )b^2c d^2 }{2(\lambda b+2c)^2}.$

Note that in this case, when both countries are pro-self, at the equilibria each country’s level of emissions is higher than that at the social optimum, and lower than the level of emissions at the egoistic case. On the other hand, if both countries are pro-social, the situation is the opposite: the emission for each country is lower than that of the social equilibrium. Moreover, the aggregated net benefit is always below the aggregated benefit at the equilibrium when countries are equanimous. In fact, since the derivative of the aggregated benefit $\frac{\partial \pi }{\partial \lambda }(e^*_\lambda )= \frac{8-16\lambda }{2(\lambda b+2c)^3}$ equals 0 if and only if $\lambda =\frac{1}{2}$, and the second derivative is positive, a maximum is attained at $\lambda = \frac{1}{2}$ (which coincides with the case in which the countries are equanimous).

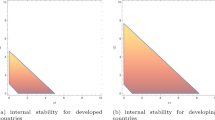
In the general case for two countries, it is possible to establish a partition of the set of equilibria in terms of the pro-self or pro-social attitudes of each of the countries. This partition is shown in Fig. 3 for the values of the parameters $b=5,c=1,d=10.$

Fig. 3

Partition of the set of equilibria for $b=5,c=1,d=10$

The different sets of equilibria depending on the attitudes of the countries are described as:

• Both countries are pro-self:

  ${{{\mathcal {E}}}}_{\Gamma _{self}}(G)=\{e\in E_1 \times E_2: \max \{0, \frac{50- 2 e_j}{7}\} \le e_i \le \max \{0, \frac{50-e_j}{6}\} \}.$

• Both countries are pro-social:

  ${{{\mathcal {E}}}}_{\Gamma _{soc}}(G)= \{e\in E_1 \times E_2: 0\le e_i \le \max \{0, \frac{50- 2e_j}{7}\} \}.$

• Country i is pro-social, country j is pro-self:

  ${{{\mathcal {E}}}}_{\Gamma _{cro}}(G)=E(G_{\Gamma _{cro}})=\{e\in E_1 \times E_2: 0\le e_i \le \max \{0, \frac{50-2e_j}{7}\}, \max \{0, \frac{50-2e_i}{7}\} \le e_j \le \max \{0, \frac{50-e_i}{6}\} \}.$

It is worth remarking that the situation illustrated here for two countries can be generalized to the case of n countries with different net benefit functions. That is to say, the whole set of equilibria can be partitioned into subsets, each one corresponding to different combined sets of weights, as described in Lemma 4.4.

In Table 1 we observe the influence of the weights assigned to the own net benefit function on the corresponding equilibria of the altruistic emission game. The first four cases correspond to countries that behave symmetrically. As can be observed, when $\lambda ^i_i$ starts to decrease from 1 (egoistic countries), net benefit increases up to its maximum, reached at the social equilibrium, i.e., when countries are equanimous. If $\lambda ^i_i$ continues to decrease, net benefits also decrease until they reach their minimum at zero when countries are fully social ($\lambda ^i_i$=0).

Table 1 Equilibria for different vectors of weights for $b=5,c=1,d=10$

5 Concluding remarks

In the current context of awareness about climate change, there may be relevant incentives for the governments to move away from strictly self-interest maximizing criteria, and include altruistic considerations in their strategic decisions regarding the mitigation of gas emissions. In this respect, this paper provides a theoretical framework that permits an analysis of the implications derived from the inclusion of altruistic preferences in these strategic decisions.

A main issue is that very often there is no complete information about the attitudes of the country governments with respect to the other countries, this hampers the prediction of the equilibria which countries will eventually attain. In this vein, we have provided results that permit us to deal with situations in which only imprecise information on these attitudes is available. In fact, the results obtained allow us to describe the sets of equilibria of the altruistic emission game for the various combinations of attitudes that the countries may show: cases in which each country shows a homogeneous attitude with respect to the others and/or situations where the attitude of the countries are heterogeneous with regard to the others. For instance, governments may show a more altruistic attitude towards politically and/or socially close countries, as compared to those who are perceived as distant in terms of political or social affinity, or may show different attitudes depending on the level of development of the countries involved.

An interesting conclusion is that, even when all the countries show a pro-self attitude, there is still a range of potential equilibria in which the aggregated global emissions are less than when the countries are self-interested. We also find that the whole set of the equilibria of the altruistic game is the union of the sets of equilibria obtained by the different combination of pro-self and pro-social attitudes that the countries can adopt.

The theoretical framework provided in this paper significantly contributes to the analysis of the strategic interactions of the countries with respect to the decisions on the greenhouse gas emissions. The approach may lead to more realistic predictions of the level of emissions at equilibria when different attitudes of the country governments are considered.

Appendix

Proof Proposition 3.1

Consider $H, I \subseteq N$ such that $i \in H \subseteq I$. For those $e_{-i}\in \times _{j\ne i}E_j$ such that $r_i^{S_I}(e_{-i})=0$, the result follows.

For those $e_{-i}\in \times _{j\ne i}E_j$ such that $r_i^{S_I}(e_{-i})\ne 0$, denote ${{\bar{e}}}_i^I=r_i^{S_I}(e_{-i})$ and ${{\bar{e}}}_i^H=r_i^{S_H}(e_{-i})$. Note that $\frac{1}{|I|}\beta _i'({{\bar{e}}}_i^I)=\frac{1}{|I|}\sum _{j\in I} \phi _j'({{\bar{e}}}_i^I+e_{-i})$ and $\frac{1}{|H|} \beta _i'({{\bar{e}}}_i^H)\le \frac{1}{|H|} \sum _{j\in H}\phi _j'({{\bar{e}}}_i^H+e_{-i})$ holds. Suppose, on the contrary, that ${{\bar{e}}}_i^I>{{\bar{e}}}_i^H$. Since $\phi _i'' (\sum _{k=1}^n e_k)>0$ for all e, then $\beta _i'({{\bar{e}}}_i^I)= \sum _{j\in I} \phi _j'({{\bar{e}}}_i^I+e_{-i})=\sum _{j\in H} \phi _j'({{\bar{e}}}_i^I+e_{-i})+\sum _{j\in I\backslash H} \phi _j'({{\bar{e}}}_i^{I}+e_{-i}) \ge \sum _{j\in H} \phi _j'({{\bar{e}}}_i^I+e_{-i})> \sum _{j\in H} \phi _j'({{\bar{e}}}_i^H+e_{-i})$ and $\sum _{j\in H} \phi _j'({{\bar{e}}}_i^H+e_{-i})\ge \beta _i'({{\bar{e}}}_i^H)$. Thus, $\beta _i'(e_i^I)>\beta _i'(e_i^H)$. This contradicts the fact that $\beta _i'$ is decreasing ($\beta _i'' \le 0$), and the result follows. $\square$

Proof Proposition 4.2

Without loss of generality we assume that $i=1$ and $C_k{\setminus } \{1\}=2,\ldots ,|C_k|$.

From Proposition 2 in Mármol et al. (2002), it follows that the polyhedron $\Gamma ^1$ has the extreme points:

• $(1,0,\ldots ,0).$

• $(\frac{1}{2},0,\ldots , 0,\frac{1}{2}^{j_1)},0,\ldots ,0)$ for all $j_1=2,\ldots ,|C_k|.$

• $(\frac{1}{3},0,\ldots , 0,\frac{1}{3}^{j_1)},0,\ldots , 0,\frac{1}{3}^{j_2)},0,\ldots ,0)$ for all $j_1,j_2=2,\ldots ,|C_k|$.

  ...

• $(\frac{1}{|C_k|},\ldots ,\frac{1}{|C_k|},0,\ldots ,0).$

By applying Proposition 4.1, the equilibria of the altruistic game with this information are obtained as the equilibria of the transformed game. The components of the transformed vector-valued function are:

$$\begin{aligned} \pi _1; \dfrac{\pi _1+\pi _{j_1}}{2}, j_1=2,\ldots ,|C_k|; \, \dfrac{\pi _1+\pi _{j_1}+\pi _{j_2}}{3} \, j_1,j_2=2,\ldots ,|C_k|; \ldots ; \dfrac{ \sum _{j\in C_k}\pi _j}{|C_k|}. \end{aligned}$$

The best responses of country 1 to the actions of the other countries are, respectively,

$$\begin{aligned} r_1, \, r_1^{S_{\{1, j_1\}}}, j_1=2,\ldots ,|C_k|,\,\, r_1^{S_{\{1, j_1, j_2\}}}, j_1, j_2 =2,\ldots ,|C_k|,\,\, \ldots , r_1^{S_{C_k}}. \end{aligned}$$

Since by Proposition 3.1,

$$\begin{aligned} r_1^{S_{C_k}} (e_{-1}) \le r_1^{S_I} (e_{-1})\le r_1^{S_{\{1\}}} (e_{-1})= r_1(e_{-1}), \end{aligned}$$

for all I, such that $1\in I\subseteq C_k$, then the result follows. $\square$

Proof Lemma 4.4

Without loss of generality we assume $i=1$, $R^1=2,\ldots ,1+|R^1|$, and $T^1=n-| T^1|,\ldots ,n$. Two cases can be considered: $K^1= \emptyset$ and $K^1\ne \emptyset$.

a) If $K^1= \emptyset$, from Proposition 2 in Mármol et al. (2002), it follows that the polyhedron $\Gamma ^1$ has the following extreme points:

• $(\frac{1}{1+|R^1|},\ldots ,\frac{1}{1+|R^1|},0,\ldots ,0).$

• $(\frac{1}{2+|R^1|},\ldots ,\frac{1}{2+|R^1|},0,\ldots , 0,\frac{1}{2+|R^1|}^{j_1)},0,\ldots ,0)$ for all $j_1\in M^1.$

• $(\frac{1}{3+|R^1|},\ldots ,\frac{1}{3+|R^1|},0,\ldots , 0,\frac{1}{3+|R^1|}^{j_1)},0,\ldots , 0,\frac{1}{3+|R^1|}^{j_2)},0,\ldots ,0)$ for all $j_1,j_2 \in M^1.$

  ...

• $(\frac{1}{1+|R^1|+|M^1|},\ldots ,\frac{1}{1+|R^1|+|M^1|}, 0,\ldots ,0).$

With an analogous reasoning as in Proposition 4.2, by applying Proposition 4.1, the equilibria of the altruistic game with this information are obtained as the equilibria of the transformed game. The components of the transformed vector-valued function are:

$$\begin{aligned}{} & {} \dfrac{ \pi _1+\sum _{j\in R^1}\pi _j}{1+|R^1|}\\{} & {} \dfrac{\pi _1+\sum _{j\in R^1}\pi _j+\pi _{j_1}}{2+|R^1|}, j_1\in M^1,\\{} & {} \dfrac{\pi _1+\sum _{j\in R^1}\pi _j+\pi _{j_1}+\pi _{j_2}}{3+|R^1|}, \, j_1,j_2 \in M^1,\\{} & {} \quad \vdots \\{} & {} \dfrac{ \sum _{j \in \{1\}\cup M^1\cup R^i}\pi _j}{1+|R^1|+|M^1|}.\\ \end{aligned}$$

The corresponding best responses of country 1 to the actions of the other countries are, respectively,

$$\begin{aligned} r_1^{S_{\{1\}\cup R^1}}, r_1^{S_{\{1, j_1\}\cup R^1}}, j_1\in M^1, r_1^{S_{\{1, j_1, j_2\}\cup R^1}}, j_1, j_2 \in M^1, \ldots , r_1^{S_{\{1\}\cup M^1\cup R^1}}. \end{aligned}$$

Since by Proposition 3.1,

$$\begin{aligned} r_1^{S_{\{1\}\cup M^1\cup R^1}} (e_{-1}) \le r_1^{S_I} (e_{-1})\le r_1^{S_{\{1\}\cup R^1}} (e_{-1}), \end{aligned}$$

for all I, such that $\{1\}\cup R^1\subset I\subseteq {\{1\}\cup M^1\cup R^1}$, and $\{1\}\cup M^1\cup R^1=N{\setminus } T^1$ and $\{1\}\cup R^1=N\setminus (T^1 \cup M^1)$, then the result follows.

b) If $K^1\ne \emptyset$, assume $R^1=2,\ldots , 1+|R^1|$, if $K^1=2+|R^1|,\ldots ,1+|R^1|+|K^1|$, and $T^1=n-| T^1|,\ldots ,n$. The extreme points of $\Gamma ^1$ are:

• $(0,\ldots ,0,1^{j)},0,\ldots ,0)$ for all $j =2+|R^1|,\ldots ,1+|R^1|+|K^1|$.

• $(\frac{1}{1+|R^1|+|K^1|},\ldots ,\frac{1}{1+|R^1|+|K^1|}, 0,\ldots ,0).$

• $(\frac{1}{2+|R^1|+|K^1|},\ldots ,\frac{1}{2+|R^1|+|K^1|},0,\ldots , 0,\frac{1}{2+|R^1|+|K^1|}^{j_1)},0,\ldots ,0)$ for all $j_1 \in M^1.$

• $(\frac{1}{3+|R^1|+|K^1|},\ldots ,\frac{1}{3+|R^1|+|K^1|},0,\ldots , 0,\frac{1}{3+|R^1|+|K^1|}^{j_1)},0,\ldots , 0,\frac{1}{3+|R^1|+|K^1|}^{j_2)},0,\ldots ,0)$ for all $j_1, j_2 \in M^1.$

  $\vdots$

• $(\frac{1}{1+|R^1|+|K^1|+|M^1|},\ldots ,\frac{1}{1+|R^1|+|K^1|+|M^1|},0,\ldots ,0).$

The components of the transformed vector-valued function are:

• $\pi _{2+|R^1|},\ldots , \pi _{1+|R^1|+|K^1|},$

• $\dfrac{ \sum _{j=1}^{1+|R^1|+|K^1|}\pi _j}{1+|R^1|+|K^1|},$

• $\dfrac{ \pi _{j_1}+\sum _{j=1}^{1+|R^1|+|K^1|} \pi _j}{2+|R^1|+|K^1|}, j_1\in M^1,$

• $\dfrac{ \pi _{j_1}+\pi _{j_2}+\sum _{j=1}^{1+|R^1|+|K^1|} \pi _j}{3+|R^1|+|K^1|}, j_1, j_2\in M^1,$

• $\quad \quad \quad \vdots$

• $\dfrac{ \sum _{j=1}^{1+|R^1|+|K^1|+|M^1|}\pi _j}{1+|R^1|+|K^1|+|M^1|}.$

The corresponding best responses of country 1 to the actions of the other countries are, respectively,

$$\begin{aligned}{} & {} r_1^{2+|R^1|},\ldots , r_1^{{1+|R^1|+|K^1|}}, r_1^{S_{R^1 \cup K^1\cup \{ 1\}}}, r_1^{S_{R^1\cup K^1\cup \{1, j_1\}}}, j_1\in M^1,\\{} & {} r_1^{S_{R^1\cup K^1\cup \{1,j_1, j_2\}}}, j_1, j_2 \in M^1, \ldots , r_1^{S_{R^1 \cup K^1\cup \{ 1\}\cup M^ 1}}. \end{aligned}$$

Since $r_1^j(e_{-1})=0$ for all $j\ne 1$, and by Proposition 3.1,

$$\begin{aligned} 0\le r_1^{S_{R^1 \cup K^1\cup \{ 1\}\cup M^ 1}} (e_{-1}) \le r_1^{S_I} (e_{-1})\le r_1^{S_{R^1 \cup K^1\cup \{ 1\}}} (e_{-1}), \end{aligned}$$

for all I, such that $R^1 \cup K^1\cup \{ 1\} \subseteq I\subseteq R^1 \cup K^1\cup \{ 1\}\cup M^ 1$, and $R^1 \cup K^1\cup \{ 1\}=N{\setminus } (T^1 \cup M^1)$, then the result follows. $\square$