Abstract
Logistics providers have to utilize available capacities efficiently in order to cope with increasing competition and desired quality of service. One possibility to reduce idle capacity is to build coalitions with other players on the market. While the willingness to enter such coalitions does exist in the logistics industry, the success of collaborations strongly depends on mutual trust and behavior of participants. Hence, a proper mechanism design, where carriers do not have incentives to deviate from jointly established rules, is needed. We propose to use a combinatorial auction system, for which several properties are already well researched but little is known about the auction’s first phase, where carriers have to decide on the set of requests offered to the auction. Profitable selection strategies, aiming at maximization of total collaboration gains, do exist. However, the impact on individual outcomes, if one or more players deviate from jointly agreed selection rules is yet to be researched. We analyze whether participants in an auction-based transport collaboration face a Prisoners’ Dilemma. While it is possible to construct such a setting, our computational study reveals that carriers do not profit from declining the cooperative strategy. This is an important and insightful finding, since it further strengthens the practical applicability of auction-based trading mechanisms in collaborative transportation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In a world full of disruptions and scarce resources, the concept of the Sharing Economy is on the rise. Logistics providers are seen as critical infrastructure. In order to keep freights moving, available capacities have to be used efficiently. During a global pandemic crisis, this is crucial. However, even in normal times, the logistics industry is known to suffer from inefficiencies. Hence, collaborative consumption of transportation capacities is one of the hot topics in transportation and logistics (Speranza 2018). This is due to the growth of the e-commerce sector, which boosts competition and brings down prices. Customers have small order sizes but expect same-day delivery with a maximum level of flexibility and customer service. The transport sector is one of the main contributors to \(CO_2\) emissions. In the European Union, the share of road transportation has ranged around 75% in recent years (Eurostat 2018). However, acting in an economically and ecologically efficient manner becomes increasingly challenging.
One possibility of sharing transportation resources is collaborative vehicle routing, where it is assumed that carriers are willing to exchange transportation requests with competitors (Gansterer and Hartl 2018b). Such exchanges can be done on a bilateral basis. However, if more players are involved, it is recommended to make use of collaboration platforms. These platforms can be centrally or decentrally organized. If a central fully-informed authority exists, it is considered a centralized collaboration, while in the absence of such a decision maker, it is denoted as decentrally planned collaboration.
In this study we analyze a special form of decentralized collaborations: auction-based systems. The great advantage of auctions is that carriers can communicate preferences to their competitors without having to reveal critical information. This is extremely important, since forced data disclosure and lack of trust are known to be a major obstacle for collaborations (Bratton et al. 2000; Cruijssen 2006; Cruijssen et al. 2007a; Lydeka and Adomavičius 2007; Pan et al. 2019). If trading items are not only offered individually, but can also be acquired in packages, combinatorial auctions are the appropriate auction mechanism. Typically, the value of such a package or bundle has lower costs or higher value than the sum of the individual items. This is denoted as sub- or superadditivity, respectively. From standard auction theory, we know that desirable properties of exchange mechanisms are: (i) efficiency, (ii) incentive compatibility, (iii) individual rationality, and (iv) budget balance. Efficiency in our context indicates that each transportation request is allocated to the player that values it highest. An incentive compatible mechanism prevents players from deviating from the actions established by the group. Individual rationality is fulfilled if participants do not have an incentive to leave the cooperation. Finally, budget balance refers to the requirement that the auctioneer does not incur a deficit or loss.
The typical procedure of combinatorial auctions runs over 5 phases (Berger and Bierwirth 2010; Gansterer et al. 2020a):
-
1.
Request selection: Each player has to select the set of requests that should be offered to other carriers.
-
2.
Bundling: Either the central auctioneer or the carriers build packages for bidding.
-
3.
Bidding: Carriers provide their bids for each bundle they are willing to acquire.
-
4.
Winner determination: The requests are distributed among bidders, such that the total profit for the coalition is maximized.
-
5.
Profit sharing: Collaboration profits are distributed among the carriers.
In our study, we focus on the first phase, where carriers have to decide which requests they are willing to offer. In Gansterer and Hartl (2016), several selection strategies for pickup and delivery carriers are compared. The authors show that there is a significant increase in total collaboration profit if all carriers apply a cooperative selection strategy. Such a cooperative strategy assumes that carriers are interested in offering requests that have a high probability of being valuable for other players. This is in contrast to traditional selection strategies, where players aim at getting rid of low value requests, not taking competitors’ preferences into account. It should be noted that such selections have to be performed under incomplete information since we assume that carriers are not willing to reveal critical information to their competitors.
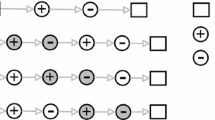
In the remainder of our study, we will assume that carriers have the choice to be either cooperative by applying the jointly agreed selection rule, or decline this recommended strategy and act in a selfish manner. It should be noted that the dominant strategy is not obvious. In acting selfishly, carriers risk that the collaboration profit is decreased considerably and thus their individual profits are less than in the cooperative solution. Hence, this raises the question whether carriers face a Prisoners’ Dilemma. This would be the case, if, whatever strategy the competitors choose, a carrier is better-off by choosing to decline. An example of a Prisoners’ Dilemma in a 2 player game of pickup and delivery carriers is illustrated in Fig. 1. Each carrier (A and B) has 2 pickup and delivery requests (A1, A2, B1, B2). Let us assume that the carriers are interested in exchanging requests in order to increase their profits. If a carrier cooperates, the request closer to the competitor is offered (i.e., A2 and B1). However, if the carrier declines, the other request is offered (A1 and B2). The illustration shows that whatever carrier B decides to do, carrier A’s individual solution is better, if she decides to decline. The same applies to carrier B. Hence, the carriers are facing a Prisoners’ Dilemma.
It should be noted that the example presented in Fig. 1 only holds under some very specific assumptions. These include that (i) only one request per carrier is traded, (ii) request have equal revenues, and (iii) no profit sharing mechanism is applied.
In Fig. 2 we show an example, where no Prisoners’ Dilemma occurs. Obviously, whatever request is offered by carrier A, carrier B profits from following the cooperative strategy, that is selecting request B2 for trading.
In our study, we analyze whether carriers profit from declining the cooperative strategy. For this purpose, we perform a broad computational study, where carriers trade requests using a combinatorial auction mechanism. They can either follow the cooperative strategy by submitting requests that are expected to be of value for other carriers, or decline, which implies that they submit unprofitable requests. The question whether a Prisoners’ Dilemma occurs or not is an important issue, since it shows whether a carrier’s profitable strategy depends on the behavior of other carriers. Hence, we are investigating a special case of incentive compatibility, which does not refer to the reporting true values but to submitting requests according to the jointly established strategy.
The remainder of our study is structured as follows. In Sect. 2, we discuss related literature. The underlying problem and the auction mechanism are provided in Sects. 3 and 4, respectively. We present the computational study and discuss results in Sect. 5, while Sect. 6 concludes our study.
2 Literature
Krajewska and Kopfer (2006) and Cruijssen et al. (2007b) were the first to examine the potential benefits of collaborative vehicle routing. Empirical studies were conducted by, e.g., Cruijssen et al. (2007a), Lydeka and Adomavičius (2007), Pateman et al. (2016). These studies investigate drivers and obstacles facing companies when entering logistics partnerships.
Recent surveys are provided by Allen et al. (2017), Gansterer and Hartl (2018b), Cleophas et al. (2019), Pan et al. (2019), and Basso et al. (2019). Gansterer and Hartl (2020) reveal that collaborative vehicle routing is intensively discussed, but a huge majority focuses on centralized planning approaches. Examples are Dai and Chen 2012, who analyze online platforms providing services for collaborative decision making or Sprenger and Mönch (2012), research a real-world scenario found in the German food industry, for which they can show that the cooperative strategy clearly outperforms the non-cooperative algorithms in a dynamic and stochastic logistics system. Several studies focus on ecological rather an economic goals. Pérez-Bernabeu et al. (2015), for instance, emphasize that cooperations can contribute to a noticeable reduction of expected travel costs as well as of greenhouse gas emissions. Exact solution approaches for centralized carrier collaborations are examined in Gansterer et al. (2018a), while Gansterer et al. (2020c) show that these solutions might lead to unevenly distributed workloads. This bears the risk to reduce acceptance in practice. The authors propose to impose assignment constraints, in order to redistribute the workload in a fair manner. Rationality constraints for LTL carriers serving e-commerce customers are discussed by Zhang et al. (2017).
The dominance of centralized approaches is surprising since generally decentralized approaches are considered more realistic from a practical point of view. Gansterer and Hartl (2020) reveal that relatively little progress has been made in this field, though. This might come from the inherent complexity in distributed decision making. While centralized problems typically can be broken down to a standard single- or multi-objective optimization problem, decentralized decision making leads to challenging mechanism design problems (Bichler 2020).
Early studies on auction-based horizontal transportation collaboration are presented by Krajewska and Kopfer (2006), Ackermann et al. (2011), and Berger and Bierwirth (2010). Gansterer et al. (2020a) emphasize the potential of combinatorial auctions in this field. Dai and Chen (2011) and Li et al. (2015) assess single item per carrier submissions and Xu et al. (2017) show effective auction mechanisms for the truckload carrier collaboration problem with bilateral lane exchange. A combinatorial clock-proxy exchange is proposed by Chen (2016).
Group decisions can also be approached using negotiations (Vetschera 2013). Population-based negotiations of contract clauses and transportation request assignments are discussed in Jacob and Buer (2016). Decision processes under incomplete preference information within members of groups are analyzed by Vetschera et al. (2014). Multi-agent systems in decentralized full truckload carrier and shipper collaborations are considered by Mes et al. (2013). A review on coordination mechanisms with mathematical programming models for decentralized decision making is provided by Rius-Sorolla et al. (2020).
Incentives in transport collaborations are rarely investigated. Jacob and Buer (2018) investigate the impact of non-truthful bidding on transport coalition profits. Incentive compatibility and other desired properties of carrier collaboration auctions are discussed in Gansterer et al. (2018b). The authors show that incentive compatibility can be ensured at the cost of individual rationality. However, Gansterer and Hartl (2018a) analyze strategic behavior of carriers in auction bidding phases. Numerical results indicate that—even if truthfulness is not explicitly enforced by the auction design—profitable cheating strategies are not obvious. This is due to the problem’s inherent complexity. Different selection strategies and their impact on total collaboration profits are investigated by Gansterer and Hartl (2016). Cost allocation or profit sharing as a means to create incentives for collaboration among transport companies is analyzed by Dahlberg et al. (2019) and Gansterer et al. (2020a).
To the best of our knowledge, the question whether carriers have incentives to deviate from jointly agreed selections rules has not been researched so far.
3 Problem description
We assume carriers to serve less than truckload paired pickup and delivery requests, which means that each request is associated with a given origin and destination. Less than truckload transportation is known to be particularly suitable for collaborative transportation, since loads destined for several customers can be packed into the same vehicle. This enables carriers to share their capacities and integrate transportation requests of collaboration partners into their own routes.
In our study, we assume that carriers own several vehicles, which start their tours at a depot, visit a given set of pickup and delivery nodes and return to the same depot. Each vehicle is capable of transporting a limited load. Also, the duration of vehicle tours is limited. This problem belongs to the class of Vehicle Routing Problems with Precedence Constraints which is an \({\mathcal {N}}{\mathcal {P}}\)-hard optimization problem. Parragh et al. (2008) refer to this problem as the single vehicle case of the Vehicle Routing Problem with Pickups and Deliveries (SPDP). Berbeglia et al. (2007) classify it as one-to-one pickup and delivery problem. Initially, each carrier is in charge of serving a specific set of requests. All carriers are willing to enter a collaboration, where requests are offered to competitors; new requests are acquired using an auction mechanism (see Sect. 4).
Each carrier’s objective is to maximize profit. This includes (i) the sum of revenues gained by serving customers, and (ii) the share of jointly gathered collaboration profits. Obviously, there is only limited influence on this share since it depends on collaborative behavior under incomplete information and on the established profit sharing mechanism (see Sect. 4).
The request selection phase of collaborative auction mechanisms has a strong impact for each participant. This impact has four aspects:
-
1.
Lost revenue: Requests that are offered for trading might be lost to competitors. Hence, it seems profitable to keep high value requests. However, this lost revenues might be compensated by the following three dimensions.
-
2.
Increased total collaboration profit: In Gansterer and Hartl (2016) it is shown that the total collaboration profit is significantly increased if carriers offer valuable requests to their collaboration partners. Thus, the share of an individual carrier might increase if she submits valuable requests to the auction pool. On the other hand, if only requests with low value are submitted, the auction might fail, since no profitable exchanges can be performed.
-
3.
Mechanism design: Desired properties of auction mechanisms include amongst others individual rationality and incentive compatibility. It is well known that desired properties bear a trade-off in the sense that they are conflicting. Vickrey-Clarke-Groves (VCG) auctions, for instance, are proven to be incentive compatible but cannot be realized such that all other desired properties can be ensured (Gansterer et al. 2018b). The impact of the first auction phase clearly depends on such design decisions; in particular how a surplus or a loss of the collaboration is shared among players.
-
4.
Profit Sharing: In the literature several profit sharing mechanisms are presented. The interested reader is pointed to an extensive survey by Guajardo and Rönnqvist (2016). However, the prevalent mechanism in various fields of application is the well-known Shapley Value (e.g., Kimms and Kozeletskyi 2016). Shapley Value takes players’ individual contributions to the collaboration’s success into account. Hence, if profits are shared based on this (or a related) scheme, the contribution, (i.e., the selected requests), of a carrier have an impact on the post-auction share of total collaboration profits. It should be noted that the classical Shapley Value cannot be applied in the setting of this study. This is due to the complexity of the underlying \({\mathcal {N}}{\mathcal {P}}\)-hard routing problems. In order to apply Shapley Value, the contribution of each carrier has to be determined by comparing the outcome of several different settings, where a huge number of routing problems have to be solved (see Sect. 4). This is computationally intractable. Therefore, related but simpler profit sharing mechanisms, which still rely on players’ individual contributions, have been proposed (e.g., Gansterer et al. 2020a).
In our study, we apply a Shapley Value-based mechanism proposed by Gansterer et al. (2020a), where individual contributions to the total collaboration profits impact the share of each carrier. Hence, the selection strategy is a crucial issue for each participant. The profit sharing method proposed by Gansterer et al. (2020a) (i) guarantees group and individual rationality, (ii) is computationally tractable, (iii) allows for incomplete information such that collaboration gains but no initial or ex-post profits have to be revealed, (iv) takes carriers’ contributions to the success of the collaboration into account. The required information is extracted from bids submitted by the carriers (see Sect. 4.5).
In Gansterer et al. (2018b) it is shown that the VCG concepts can be applied to two-sided transport markets, but only at the cost of individual rationality. The authors recommend to give up on incentive compatibility since in Gansterer and Hartl (2018a) it is shown that due to the system’s complexity, cheating is not straightforward. We follow this recommendation and do not apply the adapted VCG mechanism presented in Gansterer et al. (2018b), but ensure individual rationality (see Sect. 4). It should be noted that individual rationality has so far only been discussed for the bidding phase, while the selection phase might also bear incentives to deviate from the commonly established strategy. Hence, even if an incentive compatible bidding mechanism is imposed, the overall mechanism might not be incentive compatible. To the best of our knowledge, we are the first to investigate strategic behavior and incentive compatibility of carriers apart from the bidding phase.
4 Auction mechanism
Combinatorial auctions typically follow a 5-phase procedure (see Sect. 1): (1) request selection, (2) bundling, (3) bidding, (4) winner determination, (5) profit sharing. In the following we provide details on the design of each phase as they have been implemented in our computational study.
4.1 Request selection
On the one hand, carriers have to decide which requests they are willing to offer to other carriers and also which requests offered by other carriers they want to acquire. Hence, carriers act as both buyers and sellers on two-sided markets. The decision which requests to offer, is strongly related to the decision which requests to acquire, since the outcomes of both of these decisions determine which requests have to be served by which carrier (see Sect. 3). In our study, we use a selection strategy proposed by Gansterer and Hartl (2016) and adapted by Gansterer et al. (2020b). This strategy is based on the finding that total collaboration profit increases considerably, if carriers select requests, which they assume to be of high value for their collaboration partners. Since carriers might be reluctant to share information on existing customers, the identification of requests that are attractive for other carriers is not straightforward. Gansterer et al. (2020b) propose to share aggregated information by superimposing a grid over the area covered by the requests and providing counts on the number of request origins and destinations in a grid cell. An example is depicted in Fig. 3.
Example of a grid superimposed over an area covered by three carriers (red, blue, green) to allow the carriers to calculate and share aggregate (geographical) information about their set of requests. The right part of the figure shows the aggregate information each carrier reveals (Gansterer et al. 2020b)
Carriers select requests based on the aggregate information on their coalition partners’ distribution of requests, which they approximate from the numbers provided in the grid. A simple scheme incorporates aggregate information about the requests of other carriers when selecting requests to submit to the request pool. Specifically, it is assumed that a carrier assigns a score \(s_r\) to each request r, sorts her requests in order of non-increasing scores, and selects the \(\lceil f n \rceil \) requests with the highest scores to submit to the request pool, where n is the carrier’s total number of requests and \(0< f < 1\). The score \(s_r\) is composed of the number of origins and destinations of requests from other carriers located in the grid cells with the origin and destination of request r and \(m_r\) being the marginal profit of r. That is, the method seeks to submit requests with a high (potential) attractiveness to other carriers and a low marginal profit to the request pool. More details on this approach can be found in Gansterer et al. (2020b).
We declare this selection rule, in the following denoted as grid, as the cooperative strategy. Carriers who decline to play cooperatively select request based on marginal profits. This implies that for each request the individual profit with and without serving this request is calculated. The set of requests with the lowest marginal profit is offered to the auction. This non-cooperative strategy is denoted as marginal profit.
4.2 Bundling
We assume that bundling is performed by the auctioneer based on the method proposed by Gansterer et al. (2020a). It builds on the assumption that no information on the transportation requests of a carrier that have not been submitted to the request pool, is made available. The auctioneer uses a Genetic Algorithm-based framework, where the fitness function is a proxy of: (i) isolation, which is the distance to other bundles, (ii) density, which is the ratio of the area covered by the requests and the number of requests, and (iii) tour length of bundles. The Genetic Algorithm evaluates a set of disjoint bundles B using the following formula:
where \(i_b\), \(d_b\), and \(t_b\) are the isolation, the density, and the tour length of bundle \(b \in B\). It further identifies a specified number of attractive bundles, which are then offered to the carriers. The interested reader is referred to Gansterer et al. (2020a) for details on this approach.
4.3 Bidding
Bids on offered bundles are generated based on marginal profits, which are the differences between the profit realized when serving requests including and excluding those in the bundle. It should be noted that for these evaluations several \({\mathcal {N}}{\mathcal {P}}-hard\) optimization problems have to be solved. Hence, it is crucial to apply effective bundling approaches as indicated in Gansterer and Hartl (2018a). We assume that carriers only bid on bundles that meet with their capacity restrictions (i.e., their maximum tour lengths).
4.4 Winner determination
Based on the bids, the auctioneer has to perform the allocation of bundles to bidders such that the total collaboration profit is maximized. This is generally denoted as the winner determination problem. We formulate this problem as a set partitioning problem. Alternative approaches would be to assume set packing (Pekeč and Rothkopf 2003) or set covering (Buer and Pankratz 2010) formulations. The mathematical model used in our framework is formulated in Gansterer et al. (2020b) and is solved to optimality after collection of all bids.
4.5 Profit sharing
In order to share the total collaboration profit among participants, we apply the approach proposed in Gansterer et al. (2020a). This method is based on the Shapley Value concept in the sense that it weights the share according to individual contributions. However, these contributions are derived from bids revealed during the auction process. It should be noted that the exchange of requests is only performed if it yields a positive collaboration profit. Further details can be found in Gansterer et al. (2020a).
5 Computational study
In our computational study, we use publicly available instances presented in Gansterer et al. (2020a).Footnote 1 In these instances, we consider different degrees of carrier competition (high, medium, low) as suggested by Berger and Bierwirth (2010). For this purpose, different radii of customer distribution related to carrier depots are reflected. There are 3 types of instances depending on the degree of customer area overlaps (O1_xx, O2_xx, O3_xx). Note that competition depends on the overlap of customer regions. In scenarios, where customers regions are strongly overlapping, carriers can easily integrate customers (initially served by other carriers) into existing tours. Thus, the level of competition is known to be high. If customer regions are disjunct, however, integration of other player’s customers might be costly. For each instance, we generate equidistant carrier depots with a distance of 200. Requests are randomly generated within a radius of 150 (O1), 200 (O2), and 300 (O3). Each carrier initially holds 15 requests. We present 20 instances for each scenario. All experiments are coded in C++ and executed single threaded on an Intel Core i5-3570 3.4GHz computer.
We use these test instances to numerically analyze the impact of carriers’ behavior in the first phase of the auction mechanism described in Sect. 4. For this purpose, we select one of the carriers, the carrier of interest (C1), and analyze her individual situation depending on the behavior of the set of remaining carriers (CR). Both C1 and CR can either cooperate (c), that is to offer requests based on the jointly established selection method grid, or decline (d), which they do by offering only unprofitable requests for trading, selected by applying rule marginal profit. All combinations (cc, dc, dc, dd) are depicted in Fig. 4.
In our computational study we analyze whether the profit gain of C1 is positively or negatively affected by the behavior of CR. It should be noted that we exclude scenario dd, where all players decline, since this reflects a situation where all requests are selected based on marginal profits only. It has already been shown in Gansterer and Hartl (2016) that such a situation reduces total collaboration profits considerably. Hence, it is obvious that all players would be negatively affected in this setting. Results for scenarios cc, dc, and cd are presented in Table 1. We provide individual collaboration profits of C1 (\(\omega _{C1}\)) and CR (\(\omega _{CR}\)), which are the sum of post-auction profits of all carriers compared to the sum of profits before entering the collaboration. However, even more relevant for our analysis is C1’s share of the total collaboration profit \(\varOmega \), denoted as \(S^{C1}\) and calculated as
where \(\omega _{C1}\) gives the difference in C1’s profit before and after the auctioning process.
The results show that, generally, collaboration profits increase with the degree of competition. Recall that O1 contains all instances with a low level of competition (i.e., only loosely overlapping customer areas), while O3 indicates that customer areas are strongly overlapping and therefore competition is high. O2 reflects an in-between situation. This finding, however, is not surprising and supports results already reported in Gansterer and Hartl (2018a).
Comparing \(S^{C1}\) provides very interesting results. We observe that C1’s share of \(\varOmega \) is reduced by up to 5.22% if she deviates from the jointly established selection rule, while the other carriers (CR) play cooperatively (scenario dc). This effect is particularly high, in instance set O1 and decreases with increasing competition. This can be explained by the fact that in situations with a low degree of competition, deviating from selection grid leads with high probability to offered requests that are unattractive to collaboration partners. In situations with a high degree of competition, however, even requests selected by rule marginal profit might be rather attractive for competitors. This is illustrated in Fig. 5.
Additionally, we observe that C1 profits from staying with selection rule grid in case all other players change to marginal profit, that is C1 cooperates while CR declines (scenario cd). It is surprising to see that in this case C1 yields an even higher share (\(S^{C1}\)) than in the scenario where all player cooperate (scenario cc). This effect is maximized in case of low competition (8.44% increase if \(S^{C1}\)) and decreases with a decrease of competition (5.41% and 4.98% for O2 and O3, respectively).
Again, this can be explained by the fact that the effect of offering unattractive requests is particularly strong if customer areas are not strongly overlapping. These findings are supported by the numbers reported in column \(\omega _{C1}\). In order to maximize \(\omega _{C1}\) in scenarios O1 and O2, carrier C1 should not deviate from the cooperative strategy. However, in scenario O3, the best strategy is less obvious. While the share of the total collaboration profit \(\varDelta S^{C1}\) decreases if carrier C1 deviates, the absolute individual profit increases \(\omega _{C1}\). This can be explained by the fact that in the high competition scenario O3, requests selected by marginal profits might still be valuable for other players.
In conclusion, the results show very clearly that carriers do not face a Prisoners’ Dilemma. Independently from CR’s decision, C1 profits from playing cooperatively and selecting requests according to the jointly established rule grid. Surprisingly, we observe that C1’s share \(S^{C1}\) is maximized if CR deviates, while C1 stays with the commonly established rule. This is an important and insightful finding, since it further strengthens the practical applicability of auction-based trading mechanisms in collaborative transportation. While mutual trust seems to be one of the major obstacles to establish collaborations, Gansterer and Hartl (2018a) showed that carriers do not necessarily profit from untruthfulness in the auction’s bidding phase. The present study extends this finding by showing that even in the selection phase, carriers do not increase individual profit shares by deviating from agreements.
6 Conclusion
We investigated the selection phase in auction-based transport collaborations. While the literature has focused on incentive compatibility of such systems, little is known about whether carriers entering such collaborations have incentives to deviate from commonly agreed rules in early phases of the auction.
We used a combinatorial auction-based mechanism in order to investigate whether collaboration partners are facing a Prisoners’ Dilemma. While we could show that a Prisoners’ Dilemma can be constructed, our computational study revealed the opposite. We could show that independently from coalition partners’ behavior, participants reduce their share of gained collaboration profits if they deviate from the jointly agreed selection rule. This is an important and insightful finding, since it further strengthens the practical applicability of auction-based trading mechanisms in collaborative transportation.
Obviously, this finding depends on the applied profit sharing mechanism. If profits are not shared based on carriers’ individual contribution to the overall collaboration profit, the effect might be reduced. Also, the number of participating carriers might play a crucial role. If several carriers apply a cooperative selection rule and by this generate a considerable total collaboration gain, a smaller subset of participants might benefit from deviating from the common agreement. These dependencies on profit sharing mechanisms and coalition sizes raise several relevant research question worth investigating.
References
Ackermann H, Ewe H, Kopfer H, Küfer K (2011) Combinatorial auctions in freight logistics. In: Böse J, Hu H, Carlos C, Shi X, Stahlbock R, Voss S (eds) Computational logistics, Lecture notes in computer science, vol 6971. Springer, Berlin, pp 1–17
Allen J, Bektaş T, Cherrett T, Friday A, McLeod F, Piecyk M, Piotrowska M, Austwick MZ (2017) Enabling a freight traffic controller for collaborative multidrop urban logistics: practical and theoretical challenges. Transp Res Rec 2609(1):77–84
Basso F, D’Amours S, Rönnqvist M, Weintraub A (2019) A survey on obstacles and difficulties of practical implementation of horizontal collaboration in logistics. Int Trans Oper Res 26(3):775–793
Berbeglia G, Cordeau JF, Gribkovskaia I, Laporte G (2007) Static pickup and delivery problems: a classification scheme and survey. TOP 15(1):1–31
Berger S, Bierwirth C (2010) Solutions to the request reassignment problem in collaborative carrier networks. Transp Res Part E Logist Transp Rev 46:627–638
Bichler M (2020) Comments on: shared resources in collaborative vehicle routing. TOP 28:21–24
Bratton TW, Mentzer JT, Foggin JH, Quinn F, Golicic S (2000) Supply chain collaboration: the enablers, impediments, and benefits. In: Council of logistics management, Fall Meeting, pp 11–23
Buer T, Pankratz G (2010) Grasp with hybrid path relinking for bi-objective winner determination in combinatorial transportation auctions. Bus Res 3(2):192–213
Chen H (2016) Combinatorial clock-proxy exchange for carrier collaboration in less than truck load transportation. Transp Res Part E Logist Transp Rev 91:152–172
Cleophas C, Cottrill C, Ehmke JF, Tierney K (2019) Collaborative urban transportation: recent advances in theory and practice. Eur J Oper Res 273(3):801–816
Cruijssen F (2006) Horizontal cooperation in transport and logistics. PhD thesis, Tilburg University
Cruijssen F, Cools M, Dullaert W (2007a) Horizontal cooperation in logistics: opportunities and impediments. Transp Res Part E Logist Transp Rev 43(2):129–142
Cruijssen F, Dullaert W, Fleuren H (2007b) Horizontal cooperation in transport and logistics: a literature review. Transp J 46:22–39
Dahlberg J, Engevall S, Göthe-Lundgren M, Jörnsten K, Rönnqvist M (2019) Incitements for transportation collaboration by cost allocation. Cent Eur J Oper Res 27:1009–1032
Dai B, Chen H (2011) A multi-agent and auction-based framework and approach for carrier collaboration. Logist Res 3(2–3):101–120
Dai B, Chen H (2012) Mathematical model and solution approach for carriers’ collaborative transportation planning in less than truckload transportation. Int J Adv Oper Manag 4:62–84
Eurostat (2018) Energy, transport and environment indicators. European Commission, Brussels
Gansterer M, Hartl RF (2016) Request evaluation strategies for carriers in auction-based collaborations. OR Spectr 38(1):3–23
Gansterer M, Hartl RF (2018a) Centralized bundle generation in auction-based collaborative transportation. OR Spectr 40(3):613–635
Gansterer M, Hartl RF (2018b) Collaborative vehicle routing: a survey. Eur J Oper Res 268(1):1–12
Gansterer M, Hartl RF (2020) Shared resources in collaborative vehicle routing. TOP 28:1–20
Gansterer M, Hartl RF, Salzmann PEH (2018a) Exact solutions for the collaborative pickup and delivery problem. Cent Eur J Oper Res 26(2):357–371
Gansterer M, Hartl RF, Vetschera R (2018b) The cost of incentive compatibility in auction-based mechanisms for carrier collaboration. Networks 73:490–514
Gansterer M, Hartl R, Sörensen K (2020a) Pushing frontiers in auction-based transport collaborations. Omega 94:102042
Gansterer M, Hartl RF, Savelsbergh M (2020b) The value of information in auction-based carrier collaborations. Int J Prod Econ 221:107485
Gansterer M, Hartl RF, Wieser S (2020) Assignment constraints in shared transportation services. Ann Oper Res. https://doi.org/10.1007/s10479-020-03522-x
Guajardo M, Rönnqvist M (2016) A review on cost allocation methods in collaborative transportation. Int Trans Oper Res 23(3):371–392
Jacob J, Buer T (2016) Population-based negotiation of contract clauses and transportation request assignments. IFAC-PapersOnLine 49(12):1862–1867
Jacob J, Buer T (2018) Impact of non-truthful bidding on transport coalition profits. In: Fink A, Fügenschuh A, Geiger MJ (eds) Operations Research Proceedings 2016. Springer, Cham, pp 203–208
Kimms A, Kozeletskyi I (2016) Shapley value-based cost allocation in the cooperative traveling salesman problem under rolling horizon planning. EURO J Transp Logist 5(4):371–392
Krajewska M, Kopfer H (2006) Collaborating freight forwarding enterprises. OR Spectr 28(3):301–317
Li J, Rong G, Feng Y (2015) Request selection and exchange approach for carrier collaboration based on auction of a single request. Transp Res Part E Logist Transp Rev 84:23–39
Lydeka Z, Adomavičius B (2007) Cooperation among the competitors in international cargo transportation sector: key factors to success. Eng Econ 51(1):80–90
Mes M, van der Heijden M, Schuur P (2013) Interaction between intelligent agent strategies for real-time transportation planning. Cent Eur J Oper Res 21:337–358
Pan S, Trentesaux D, Ballot E, Huang GQ (2019) Horizontal collaborative transport: survey of solutions and practical implementation issues. Int J Prod Res 57(15–16):5340–5361
Parragh S, Dörner K, Hartl R (2008) A survey on pickup and delivery problems. Part II: transportation between pickup and delivery locations. J für Betriebswirtschaft 58:21–51
Pateman H, Cahoon S, Chen SL (2016) The role and value of collaboration in the logistics industry: an empirical study in Australia. Asian J Shipp Logist 32(1):33–40
Pekeč A, Rothkopf M (2003) Combinatorial auction design. Manag Sci 49(11):1485–1503
Pérez-Bernabeu E, Juan AA, Faulin J, Barrios BB (2015) Horizontal cooperation in road transportation: a case illustrating savings in distances and greenhouse gas emissions. Int Trans Oper Res 22(3):585–606
Rius-Sorolla G, Maheut J, Estellés-Miguel S (2020) Coordination mechanisms with mathematical programming models for decentralized decision-making: a literature review. Cent Eur J Oper Res 61:61–104
Speranza MG (2018) Trends in transportation and logistics. Eur J Oper Res 264(3):830–836
Sprenger R, Mönch L (2012) A methodology to solve large-scale cooperative transportation planning problems. Eur J Oper Res 223:626–636
Vetschera R (2013) Negotiation processes: an integrated perspective. EURO J Decis Process 1:135–164
Vetschera R, Sarabando P, Dias L (2014) Levels of incomplete information in group decision models—a comprehensive simulation study. Comput Oper Res 51:160–171
Xu SX, Huang GQ, Cheng M (2017) Truthful, budget-balanced bundle double auctions for carrier collaboration. Transp Sci 51(4):1365–1386
Zhang M, Pratap S, Huang GQ, Zhao Z (2017) Optimal collaborative transportation service trading in b2b e-commerce logistics. Int J Prod Res 55(18):5485–5501
Funding
Open access funding provided by University of Klagenfurt.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gansterer, M., Hartl, R.F. The Prisoners’ Dilemma in collaborative carriers’ request selection. Cent Eur J Oper Res 29, 73–87 (2021). https://doi.org/10.1007/s10100-020-00717-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10100-020-00717-2