1 Introduction

In recent years, online shopping has significantly expanded, gaining traction due to various factors (Chetioui et al., 2021). While confirming the economic weight of e-commerce, such a growth has raised several issues related to the last mile deliveries, sustainability and environmental protection. Indeed, the number of parcel delivery services and express shipments has increased, resulting in greater pollution deriving from the road transport (Siragusa et al., 2022).

On the other hand, one of the key challenges for carriers in the transportation industry is to minimize costs while improving their service quality. Inefficient utilization of resources, such as transporting goods while empty, can significantly impact their bottom line.

To tackle this challenge, carriers have found a solution consisting in engaging in horizontal collaboration. Horizontal collaboration involves multiple carriers cooperating at the same level but belonging to different supply chains (Pan et al., 2019). This form of collaboration has proven effective in addressing several major industry challenges. For example, it has been shown to reduce transport costs, decrease carbon emissions, and enhance the quality of distribution services (Bae et al., 2022). Due to these benefits, this type of collaboration is currently the subject of active research and is a fundamental element of emerging trends, particularly in the sharing economy. The sharing economy in transportation is a strategy that helps businesses reduce costs, minimize environmental impacts, and optimize resource usage by sharing equipment, storage space, and logistics services. Such concepts are typically organized through digital platforms that facilitate efficient exchange of goods or services (Daglis, 2022; Gansterer et al., 2022).

In this context, we will focus on a particular type of collaboration that is based on managing a set of shared customers. Shared customers are customers who agree to subcontract their transport services, which means that they are ready to be delivered by any carrier participating in the collaboration (Fernández et al., 2018).

The concept of shared customers has been previously explored in earlier research, as shown in the study conducted by Cruijssen et al., (2007). They discuss a situation where three Dutch frozen product companies had a significant overlap in their customer base, sharing about 68% of their clients. Another case described in Sprenger and Mönch (2012) pertains to the German food industry. In this scenario, various manufacturers serving the same customers with complementary products collaborated to transport goods using shared vehicle fleets. More recently, several studies, including those by Padmanabhan et al. (2022) and Mrad et al. (2023), have utilized the concept of shared customers to reduce transportation costs. These examples illustrate how shared customer collaboration can be applied across various sectors, including daily deliveries to bars and restaurants, parcel shipping, and the transportation of other goods, resulting in increased efficiency and cost savings for the businesses involved (Fernandez et al. 2018).

Therefore, this paper specifically addresses the pre-auction phase and presents a novel strategy for managing shared customers through the exchange mechanism of a coalition pool in decentralized context.

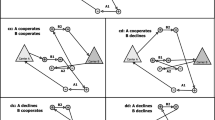
This study is analyzed from the perspective of a carrier who has with a set of customers that can be divided into private and shared ones. The private customers must be delivered by their own carrier, whereas the shared ones can even be outsourced to peers that belong to a common coalition. The key criteria on which the decision of serving or outsourcing a shared contact is based on the profitability of each customer. In other words, the carrier will attempt to surrender the service of any of his shared customer that results to be unprofitable for his economics (for example, because geographically isolated). In this context, an efficient management of the carrier’s customers portfolio is crucial. The approach that we propose here for exchanging shared customers among the cooperating carriers is based on the concept of auction. As highlighted in Fig. 1, every carrier can select a subset of shared customers to push to the pool and can, at the same time, bid to gain new business to be won through the auction. In some cases, the carrier may initially add a certain customers to the pool, but then he includes some of them in their bids in future rounds. This is because the customer is only profitable when combined with other customers pushed by different carriers to the pool. From this point of view, the coalition pool represents, for each carrier, an opportunity to ensure a higher economy of scope in his/her transportation network (Caplice & Sheffi, 2006).

Fig. 1
figure 1

The selection mechanism

Full size image

The auction we are considering here is a first-price two-sided exchange mechanism that runs continuously in multiple sessions over each day to allow carriers to opportunely update their customers portfolio. According to Guastaroba et al. (2009) the auction is composed of three different phases. The first is the pre-auction phase in which the carrier will select the subset of shared customers to be pushed to the pool and the subset that he/she is willing to pull from the pool. Subsequently, there are to bidding phase and the auction clearing phase. Each auction phase “bears a complex and at least partly unsolved decision problem in itself”, as claimed by Gansterer and Hartl (2018) in their recently review. Clearly, this work is concerned with the pre-auction stage which is the phase that has received the least attention in the scientific literature compared to its bidding and clearing counterparts.

As highlighted by Gansterer et al. (2022), collaboration approaches based on the employment of the auction mechanism had a very limited attention with respect to other collaborative approaches. Consequently, the originality of this paper lies in the development of an auction-based mechanism for the horizontal collaboration among a group of coalited carriers for the management of shared customers. To the best of our knowledge, this is the first study that integrates the above features within the same optimization framework. More specifically, our contributions can be outlined as follows:

  • An innovative selection mechanism is proposed to enhance carrier profit operations within a decentralized collaborative context.

  • Carriers' customer portfolios are managed by employing an auction mechanism to handle shared customers.

  • Optimal delivery schedules for carrier fleets are generated, while the required time window is respected.

  • Simulation-Based Optimization (SBO) approach is developed for solving the proposed problem, incorporating a stochastic bimodal distribution to realistically model travel times.

  • Validation of our approach is conducted through computational experiments with a real-life case related to the parcel delivery industry.

The paper is organised as follows: next section will provide an overview of the literature review related to this study. Section 3 will present the problem description and model formulation. Section 4 will be devoted to for the description of our solution approach, then a real-life case for parcel delivery will be described and solved in Sect. 5. Finally, Sect. 6 will conclude the work and provide some managerial insights and future developments.

2 Literature review

The contributions of this paper find their roots in three main streams of research, namely the shared customers management as a tool of collaboration, the simulation-based optimization approach and customer selection in pre-auction phase.

2.1 Collaboration through customers sharing

Collaboration through shared customers generates economic benefits and contributes to sustainable logistics. Here are some studies conducted in this context:

Fernández et al. (2018) proposed a study in which they presented a new model of horizontal cooperation based on the concept of shared customer collaboration within a vehicle routing problem (VRP) framework. Given a shared customer who expects to receive his/her deliveries from several carriers, the proposed model decides whether it is more convenient to deliver each request as expected by the designed carrier or it can be consolidated through inter-carrier collaboration and delivered together with other requests by one of the coaliting carriers. This model is designed to reduce the total operational cost of serving the shared customers by all the carriers in a collaborative setting. Shared customers are explicitly defined as those characterized by a high level of flexibility with respect to the transport service provider, i.e., those who accept to be served by any carrier involved in the collaboration scheme.

Afterwards, only a few further works appeared in the literature adopting such a collaborative approach as proposed by Fernández et al. (2018). Specifically, Rekik et al. (2018) considered the horizontal cooperative VRP with flexible time windows. Two types of customers are taken into account: shared and exclusive. The problem aims to minimize the total operational cost while ensuring a collaborative delivery plan to meet all customers’ demands. The authors developed efficient hybrid heuristic approaches to solve the collaborative logistics problem. Within the same context, Jaoua et al. (2020) proposed two different modelling approaches to solve a VRP model with soft time windows within a shared customers’ collaboration schemes under both uninterrupted and more complex interrupted traffic flow. Accordingly, a Mixed Integer Linear Programing (MILP) formulation was developed to solve the deterministic case and a SBO model was proposed to solve its stochastic counterpart.

Terros-Ramos et al. (2018) expanded the study of Fernández et al. (2018) to address the issue of managing the shared customers collaboration through a cluster-first-route-second approach. The clustering step assigns each customer's request to the fleet of vehicles able to meet that request’s requirements, whereas the routing step defines the order of visits for each vehicle. Paul et al. (2019) investigated the customer consolidated routing problem in omni-channel retail distribution. Their strategy of consolidation allows one carrier to use the extra capacity of another carrier to minimize the total transportation costs and reduce the number of delivery stops. They considered a set of shared customers across multiple carriers.

Later, Himstedt and Meisel (2021) proposed three different extensions to the Fernández et al.’s approach: firstly, cost constraints are included in case the decision to collaborate would lead to a more unfavourable situation for the carrier compared to his non-collaborative state. Second, time windows are added. Third, an inter-depot freight transfer is considered to face the scenario of receiving requests (expected from different carriers) in one visit by a single carrier. Padmanabhan et al. (2022) investigate how collaboration among LTL carriers can improve pickup and delivery tasks. They examine a common strategy where a central authority assigns shared customers, referred to as shared jobs in this study, to minimize transportation costs. To tackle this challenge, the authors propose a mathematical model and a solution based on the large neighborhood search approach. Mrad et al. (2023) address the integration of location, allocation, and routing within a pooled transportation system. Businesses with shared customers consider pooling resources for efficiency. Two collaborative methods are introduced and solved using a genetic algorithm. A comparison shows that collaborative scenarios always outperform non-collaborative scenarios, resulting in annual reductions in transport costs.

In addition, Antit et al. (2021) introduced a decentralized cooperative approach for shared customer delivery management, utilizing a coalition pool to optimize profits. This study extends their work by incorporating an auction-based mechanism to manage for shared customers. While Antit et al. focused on outsourcing unprofitable customers, this research expands to include selecting profitable auctioned customers, aiming to attract new business for carriers.

From the above literature review, it results clear that despite the several extensions proposed to the work of Fernández et al. (2018) none of the above studies considered the auction mechanism as a tool for the exchange of the shared customers, as suggested in this paper.

2.2 The simulation-based optimization approach

Simulation-based optimisation has emerged as a robust solution to complex decision-making problems with stochastic behaviors and mathematical intractability.

This approach, also known as black-box optimization, involves coupling a simulation model with an optimization tool. The simulation model acts as an evaluator for configurations sent by the optimizer. Subsequently, a solution cost is returned to the optimizer to facilitate the search for improved solutions. This iterative search aims to identify a set of input values with the most significant contribution to the key performance indicators (Glover et al., 2003; Mazzuco et al., 2017).

Numerous research studies have explored SBO in the field of industrial engineering and logistics. De Sousa Junior et al. (2019) provide an extensive review of discrete simulation-based optimization practices in industrial engineering, highlighting ongoing projects and outlining future directions. Addressing routing and distribution logistics issues, Perboli et al. (2021) used SBO to tackle dynamic and stochastic vehicle routing with time windows, incorporating crowd drivers and cargo bikes to embrace urban synchromodality. Their method encompasses Monte Carlo simulation and a neighborhood search heuristic. An illustrative case study showed the advantages of crowd drivers and cargo bikes in parcel delivery, improving operational efficiency. Snoeck and Winkenbach (2022) applied SBO to design last-mile delivery networks to meet the growing demand for fast online and omnichannel deliveries. Tests have shown that their approach outperforms current methods by creating better delivery networks. Calabrò et al. (2020) introduced an ant colony SBO for inbound logistics planning, exemplified by a case study involving a freight transport company. This method optimizes product routing, ultimately reducing costs and improving scheduling. Boru İpek (2023) applied SBO to address the pollution routing problem, incorporating time constraints and limited vehicle capacities. The approach minimizes delays and fuel consumption, utilizing Simio simulation software and the Non-dominated Sorting Genetic Algorithm II. Rabe et al. (2021) used SBO to tackle multi-period facility location issues in last-mile logistics, emphasizing urban automated parcel locker systems. Their approach integrates system dynamics simulation with a multi-period capacitated facility location problem. A case study illustrates the model's effectiveness as a decision support tool for implementing Automated Parcel Lockers in last-mile distribution.

The proposed strategy for managing shared customers will be implemented and solved using the Simulation-Based Optimization approach, which takes into account the stochastic nature of travel times.

2.3 Customers selection in the pre-auction phase

As described in the Introduction, the auctioning process is composed by three phases that are executed consecutively one after the other: the pre-auction, the auctioning and the post-auction phases (Caplice & Sheffi, 2006). Each stage involves several complex optimization and decision-making problems. Figure 2 depicts for each phase the actor involved in the decision process as well as the specific problem to be solved. It is worth noting that, unlike the traditional reverse auction in which the shipper has the responsibility of solving the contract/customer selection problem (Guastaroba et al., 2009), within this two-sided auction design, the carrier is the active actor even during the pre-auction phase.

Fig. 2
figure 2

The auction process, actors and problems to be solved

Full size image

In the auction stage, the pool operator will advertise the shared customers put to auction among the coalited carriers so they can make their own assessments to define their own bidding strategies. The outcomes of this bid generation problem would be a set of bids, that obey to the auctioning rules, to be submitted to the pool. Each bid consists of a subset of auctioned shared customers and the corresponding price suggested by the bidding carrier (Hammami et al., 2020; Yan et al., 2020). On the other hand, the winner determination problem, related to the post-auction phase, is the most studied topic in the literature on transportation procurement through auctions. Here, the auctioneer (or pool operator in our specific case) intervenes to clear the auction and to decide on the allocation of customers to the bidding carriers (Rüther & Rieck, 2022; Badiee et al., 2022).

In the pre-auction phase the carrier should select, among his transportation commitments, which shared customers should be served by his own fleet and those to be offered to the auctioned pool. The objective consists in maximizing the carrier’s profit subject to the constraint of serving all the committed customers either directly or through outsourcing. To the best of our knowledge, there are only few papers that have dealt with this problem in the context of transportation auctions. Most of such studies deal with the reverse one-buyer-multiple-sellers and refer to the commitment to be served to as a lane (Ghiani et al., 2008). The first work is due to Guastaroba et al. (2009) who proposed two routing-based models and solved them by using a general-purpose optimization software. In the second work, Gansterer and Hartl (2016) developed a set of evaluation criteria that allows to identify the most appropriate lanes to be offered to the auction. They find that geographical-based strategies outperform profit-based policies. Subsequently, Triki et al. (2017) suggested an integer programming formulation that extends the time horizon to cover a multi-period planning horizon. They also developed three metaheuristic approaches that are able to efficiently solve large-scale problems.

Recently, Yang et al. (2023) solved the lane selection problem and considered time windows on each lane. The problem is formulated such as it minimizes both the delivery cost and the setup cost. A 2-steps solution approach is developed followed by an improvement procedure that enhances the quality of the solution through the use of an iterative process. Finally, even though developed for a completely different context related to the coordination of the production–distribution planning from the viewpoint of a manufacturer-shipper, it is worthwhile mentioning here the study of Triki et al. (2021). The authors introduced a new variant of the lane selection problem that integrates the production scheduling with the design of the distribution routes. The study proposes an auction-based selection model, in which the available occasional drivers submit bids in order to win the shipments. A complex optimization model is developed and two heuristic methods are proposed to solve even large-scale instances.

This paper is focussed on the pre-auction phase and develops a new strategy for managing shared customers based on the coalition pool exchange mechanism. On the basis of the above review of the scientific literature, it is clear that this study provides novel contributions that have never addressed in an integrated way in precedence.

3 Problem description and model formulation

The carrier's customer portfolio consists, as shown in Fig. 1, of two types of customers: pre-existing private customers who must be served by their contracted carrier and shared clients who allow their own carrier to subcontract their service through a coalition pool. To maximize profitability, unprofitable shared customers are outsourced to the coalition pool, whereas profitable auctioned customers are selected through bidding in an auction mechanism. This involves first outsourcing all unprofitable shared customers, and then insourcing all profitable auctioned customers.

3.1 Problem description

As shown in Fig. 3, the selection mechanism provides the retention of all private clients, favors maintaining those shared clients that result to be profitable and attracts some of the auctioned customers who represent a new profitable deal. Conversely, rejected customers include all shared customers identified as unprofitable (which are pushed to the coalition pool for sale) and those available through the auction but are not attractive for the carrier’s network.

Fig. 3
figure 3

Example of carrier’s network before and after participating in an auction-based collaboration for the management of f shared customers

Full size image

This customers selection study is formulated based on the variant of capacitated vehicle routing problem with soft time windows under the following assumptions: (i) single carrier with single depot equipped with a capacitated fleet of vehicles operating under the less than truckload scheme (ii) the depot is characterized by a specific time window corresponding to its working time (iii) each customer has a specific time window, and in case of delay a penalty will be applied (iv) customers’ demand is not fractionable, i.e. the demand of each customer should be served during one single visit of one of the trucks.

3.2 Model formulation

The problem can be defined mathematically on a full-connected directed graph G = (V,A) where V is the set of vertices representing all possible cities, including the depot, and A is the set of edges, modeling all possible roads between cities. Our notation can be summarized as follows:

3.3 Sets

  • Keset of private customers.

  • Ksset of the shared customers.

  • Knset of customers that can be gained from auctions.

  • Nset of all possible customers, indexed by j, N = Ke ∪ Kn ∪ Ks.

  • DOne single depot, indexed by w.

  • Lset of available trucks, indexed by l.

  • VN ∪ D, indexed by i.

3.4 Parameters

  • cijcost of traversing arc (i,j) ∈ A.

  • \(d_{j}\) demand of the customer j ∈ N.

  • Q preset of the truck capacity.

  • Pe jprice associated with each private customer j, j \(\in {\text{k}}_{{\text{e}}}\).

  • Pn jprice associated with each auctioned customer j, j \(\in {\text{k}}_{{\text{n}}}\).

  • Ps jprice associated with the shared customer j, j \(\in {\text{k}}_{{\text{s}}}\).

  • P’s jprice associated with pushing the shared customer j, j \(\in {\text{k}}_{{\text{s}}}\) to the pool.

  • TWjmax/ TWjmin feasible latest and earliest time windows of node j, j ∈ N.

  • TTijthe total travel time for traversing (i, j) ∈ A.

  • bpenalty cost applied when delivery happens outside time windows.

3.5 Decision variables

  • \({\text{x}}_{{{\text{ij}}}}^{{\text{l}}}\): binary decision variable that takes value 1 if carrier’s vehicle \({\text{l}}\), \({\text{l}} \in {\text{L}}\) is moving from city i to city j, 0 otherwise.

  • \({\text{f}}_{{\text{j}}}\): binary decision variable equals to 1 if the vehicle’s arrival time to node j, \({\text{j}} \in {\text{N}}\) is outside its time window, 0 otherwise.

  • \({\text{t}}_{{\text{j}}}^{{\text{l}}}\): continuous non-negative variable which reflects the arrival time of vehicle l, l \(\in {\text{L}}\) to node \({\text{j}}\), \({\text{j}} \in {\text{N}}\).

  • \({\text{Y}}_{j}\): binary decision variable equals to 1 if the auctioned customer \({\text{j}} \in {\text{K}}_{{\text{n }}}\) is selected to be included in the carrier’s bid as a new business, 0 otherwise.

  • \({\text{Z}}_{j}\): binary decision variable equals to 1 if shared customer j \(\in {\text{K}}_{{\text{s}}}\) is not served (pushed to the pool), 0 otherwise.

3.6 Mathematical model

Using the notations, our MILP formulation can be stated as follows:

$$ {\text{Max }}\left( {\left( {\mathop \sum \limits_{{{\text{j}} \in {\text{K}}_{{\text{e}}} }} {\text{P}}_{{{\text{ej}}}} + \mathop \sum \limits_{{{\text{j}} \in {\text{K}}_{{\text{n}}} }} {\text{Y}}_{{\text{j}}} \cdot {\text{P}}_{{{\text{nj}}}} + \mathop \sum \limits_{{{\text{j}} \in {\text{K}}_{{\text{s}}} }} {\text{P}}_{{{\text{sj}}}} } \right) - \left( {\mathop \sum \limits_{{{\text{j}} \in {\text{K}}_{{\text{s}}} }} {\text{Z}}_{{\text{j}}} \cdot {\text{P}}_{{{\text{sj}}}}^{\prime } + \mathop \sum \limits_{{{\text{l}} \in {\text{L}}}} \mathop \sum \limits_{{\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}}}} {\text{c}}_{{{\text{ij}}}} {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} + \mathop \sum \limits_{{{\text{j}} \in {\text{N}}}} {\text{b f}}_{{\text{j}}} } \right)} \right) $$
(1)

The objective function (1) aims to maximize profits, calculated as the difference between revenues and costs. Revenues comprise, respectively, the sum of the purchase prices of private customers, auctioned customers and shared customers. Costs include, respectively, the total cost of outsourcing unprofitable shared customers, routing costs and penalties for late deliveries.

Subject to:

$$ \mathop \sum \limits_{{{\text{l}} \in {\text{L}}}} {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} = 1,\quad \forall {\text{i}} \in {\text{V}};{ }\forall {\text{j}} \in {\text{K}}_{{\text{e}}} ;\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(2)

Constraints (2) ensure that all private customers are served exactly once.

$$ \mathop \sum \limits_{{{\text{l}} \in {\text{L}}}} {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} = {\text{Y}}_{{\text{j}}} ,\quad \forall {\text{i}} \in {\text{V}};{ }\forall {\text{j}} \in {\text{K}}_{{\text{n}}} ;\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(3)

Constraints (3) ensure that if selected, the auctioned customers must be included in one of the trucks’ tours. These constraints also establish the logical linkage between xlij and Yj.

$$ \mathop \sum \limits_{{{\text{l}} \in {\text{L}}}} {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} = 1 - {\text{Z}}_{{\text{j}}} ,\quad \forall {\text{i}} \in {\text{V}};{ }\forall {\text{j}} \in {\text{K}}_{{\text{s}}} ;\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(4)

Constraints (4) ensure that every shared customer must be served by the carrier’s fleet or, otherwise, should be pushed to the pool.

$$ {\text{Y}}_{{\text{j}}} \ge {\text{f}}_{{\text{j}}} \quad \forall {\text{j}} \in {\text{K}}_{{\text{n}}} $$
(5)

Constraints (5) establish the linkage between fj and Yj to ensure that the penalty will apply only for the auctioned customers that are selected within the carrier’s bid.

$$ 1 - {\text{Z}}_{{\text{j}}} \ge {\text{f}}_{{\text{j}}} \quad \forall {\text{j}} \in {\text{K}}_{{\text{s}}} $$
(6)

Likewise, constraints (6) ensure that the penalty will not apply for those shared customers that are pushed to the pool.

$$ \mathop \sum \limits_{{{\text{j}} \in {\text{V}}}} {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} - \mathop \sum \limits_{{{\text{j}} \in {\text{V}}}} {\text{x}}_{{{\text{ji}}}}^{{\text{l}}} = 0,\quad \forall {\text{i}} \in {\text{V}},{\text{ l}} \in {\text{L}};\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(7)

Constraints (7) represent the flow balance equations for each node and each vehicle.

$$ \mathop \sum \limits_{{{\text{i}} \in {\text{V}}}} \mathop \sum \limits_{{{\text{j}} \in {\text{N}}}} {\text{d}}_{{\text{j}}} {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} \le {\text{Q}},\quad \forall {\text{ l}} \in {\text{L}};\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(8)

Constraints (8) guarantee that the capacity of each vehicle is not exceeded.

$$ \mathop \sum \limits_{{w \in {\text{D}}}} \mathop \sum \limits_{{{\text{j}} \in {\text{N}}}} {\text{x}}_{{{\text{wj}}}}^{{\text{l}}} \le 1,\quad \forall {\text{l}} \in {\text{L}};\left( {{\text{w}},{\text{j}}} \right) \in {\text{A }} $$
(9)

Constraints (9) ensure that each vehicle completes at most a single tour.

$$ {\text{t}}_{{\text{w}}}^{{\text{l}}} \ge {\text{TW}}_{{\text{w}}}^{{\text{min }}} {\text{x}}_{{{\text{wj}}}}^{{\text{l}}} \quad {\text{w}} \in {\text{D}};{ }\forall {\text{j}} \in {\text{N}};{ }\forall {\text{ l}} \in {\text{L}};\left( {{\text{w}},{\text{j}}} \right) \in {\text{A}} $$
(10)

Constraints (10) indicate the departure time of the truck from the depot if it will be put into service.

$$ {\text{t}}_{{\text{j}}}^{{\text{l}}} \ge {\text{t}}_{{\text{i}}}^{{\text{l}}} + {\text{TT}}_{{{\text{ij}}}} - {\text{M}}(1 - {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} ),\quad \forall {\text{i}} \in {\text{N}};{\text{j}} \in {\text{V}};{\text{ l}} \in {\text{L}};\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(11)

Denoting by \(M\) a prefixed parameter which is a big positive value compared to the input data values, Constraints (11) express the arrival time to each node and ensure the elimination of sub-tours.

$$ {\text{t}}_{{\text{j}}}^{{\text{l}}} \ge {\text{TW}}_{{\text{j}}}^{{{\text{min}}}} {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} - {\text{M f}}_{{\text{j}}} ,\quad \forall {\text{i}} \in {\text{V}};\forall {\text{j}} \in {\text{V}};{\text{ l }} \in {\text{L}};\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(12)
$$ {\text{t}}_{{\text{j}}}^{{\text{l}}} \le {\text{TW}}_{{\text{j}}}^{{{\text{max}}}} + {\text{Mf}}_{{\text{j}}} ,\quad \forall {\text{j}} \in {\text{V}} $$
(13)

Similarly, Constraints (12)-(13) applies the penalty whenever the earliest (latest) time of a customer’s visit or the depot is not respected.

$$ {\text{t}}_{{\text{j}}} \ge 0,\quad \forall {\text{j}} \in {\text{V}} $$
(14)
$$ {\text{x}}_{{{\text{ij}}}}^{{\text{l}}} \in \left\{ {0,1} \right\},\quad \forall {\text{l}} \in {\text{L}};{ }\forall {\text{w}} \in {\text{D}};\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}} $$
(15)
$$ {\text{f}}_{{\text{j}}} \in \left\{ {0,1} \right\},\quad \forall {\text{j}} \in {\text{V}} $$
(16)
$$ {\text{Y}}_{{\text{j}}} \in \left\{ {0,1} \right\},\quad \forall {\text{j}} \in {\text{K}}_{{\text{n}}} $$
(17)
$$ {\text{Z}}_{{\text{j}}} \in \left\{ {0,1} \right\},\quad \forall {\text{j}} \in {\text{K}}_{{\text{s}}} $$
(18)

Finally, constraints (14) define the non-negativity nature of the \(t\) variables and constraints (15)–(18) are the domain definitions for the \(x\), f, Y and Z variables.

The developed model results to be a mixed integer program whose size increases with the number of private and shared customers, number of trucks and also with the number of customers put to the auction in the coalition pool.

3.7 Model validation

Here we will present some experiments to validate the model and to gain insights on the most influencing parameters through a sensitivity analysis study.

3.7.1 Illustrative test problem

We start with a test problem that involves a carrier tasked with serving five customers, one of which is a private customer (N1) and the other four (N2, N3, N4, N5) are shared that can either be served by the same carrier or pushed to a coalition pool. If any of these four shared customers is selected to be outsourced through the pool auction then the hope is that another coalited carrier will be interested to serve it/them. Moreover, we assume that the pool includes already three customers (N6, N7, N8) that are put to auction and the carrier can decide to either bid on to gain a new business or to ignore. The deliveries are made from a single depot using a fleet of three trucks with a capacity of 100 units each (Q = 100). The travel times are randomly generated within the interval [1–4], and the travel costs are calculated based on the generated distances, as shown in Table A1 in Appendix A. Each customer has a pre-specified time window for the delivery, and failure to deliver within this window incurs a penalty cost of $50.

Table A2 in Appendix A, provides detailed data on the demanded amounts, the time availabilities of customers, the prices related to each contract, as well as the ask prices of the contracts if they are pushed to the pool (i.e. the price above which other carriers can bid on). Our model (1)-(18) was used to solve the problem, and the results were obtained using version 12.9 of the state-of-the-art solver IBM ILOG CPLEX software package.

Table 1 displays the solution results, including the overall profit and the arrival time of each vehicle to each selected client. The filled cells indicate the arrival time of each vehicle to each selected client, while blank cells represent unprofitable customers that should not be served by the carrier. For instance, customer N4 is not selected and will be offered through the coalition pool, whereas auctioned customers N6 and N7 are selected as profitable and will be included into the carrier’s bid that he will submit to the auction. The overall profits of the carrier in this scenario amount to $1019.

Table 1 Solution results
Full size table

3.7.2 Sensitivity analysis

In the context of optimizing the selection of shared customers it is important to investigate the behaviour of the carrier’s profits with the variation of the transportation and outsourcing costs, as well as auctioned prices and the check their effects on the selection of shared and auctioned customers. Specifically, we explore various scenarios such as determining when shared customers are profitable and do not require outsourcing, identifying situations where the number of selected auctioned customers increases or decreases, and identifying when outsourcing shared customers becomes necessary.

In Appendix B, additional results of the sensitivity study are presented for other parameters such as capacity, number of vehicles, time windows, and penalty cost.

3.7.3 Transportation costs

Transportation costs of the carrier’s fleet can have a significant impact on profits and customers selection. High transportation costs can make outsourcing of shared customers more favourable, whereas low transportation costs can lead to being more aggressive in attracting more auctioned customers to maximize profits. Indeed, as indicated in Table 2, a decrease of transportation costs of 90%, it becomes advantageous to select all auctioned customers. Conversely, a 300% increase in costs may lead to the exclusion of all auctioned customers and the rejection of 75% of the shared the customers (i.e. pushing them to the pool).

Table 2 Impact of transport costs changes on profit and contracts selection
Full size table

3.8 The sales prices of shared customers

The fluctuations in ask prices of shared customers not only affect the decision of customers selection, but also have a significant impact on the generated profit. This is clearly shown in Table 3 where an increase in the ask prices results in a decrease in profits, making outsourcing and bidding on auctioned customers unattractive. In fact, a 30% increase in ask prices would lead to the retention of all shared customers while rejecting 33% of auctioned customers.

Table 3 Impact of selling prices on profit and contracts selection
Full size table

3.9 Purchase price of the auctioned customer

Changes in the prices of auctioned customers can have a significant impact on both customer selection and resulting profits. Indeed, Table 4 shows that when the price of auctioned customers increases, it benefits the carrier by increasing profits through the selection of most of the auctioned customers and outsourcing shared ones. On the other hand, decreasing the price of auctioned customers leads to the retention of shared customers and the rejection of the auctioned ones. For example, a 50% increase in the price of auctioned customers leads to the selection of all auctioned customers and the outsourcing of 66% of shared ones, while a 50% decrease results in the retention of all shared customers and the rejection of auctioned ones.

Table 4 Impact of auctioned customers prices variation on profit and contracts selection
Full size table

3.9.1 Linear regression analysis

In this sub-section, we conduct a linear regression analysis to examine the relationship between profit and the various relevant factors. These factors include the transport costs (TC), penalty cost (PC), subcontracting costs (SC), as well as the purchase prices of private customers (PP), auctioned customers (AP), and shared customers (SP). The model statics and parameter statics were established using a spreadsheet to validate and analyze our regression models. The confidence interval was set at 95%, and the p-value threshold was set at p < 0.05. For more details on linear regression analysis interested readers are referred to the book of Seber and Lee (2012).

We conducted six regression models to investigate the relationship between the profits and each explanatory variable (TC, PC, SC, PP, AP, and SP). The results of the regression statistics and parameter statistics are shown in Tables 5 and 6, respectively. As can be noted, the regression parameters are significant in sign and magnitude, and for all of them, zero does not belong to any of the respective confidence intervals, which means that if the sample changes, these coefficients are not likely to be null. Thus, all models are validated.

Table 5 Regression statics
Full size table
Table 6 Parameters statics
Full size table

Our analysis revealed that all explanatory variables have an influence on profits, and the adjusted R2 was good for all models. The purchase prices of private, auctioned, and shared customers were positively correlated with profits, whereas transport costs, penalty costs and outsourcing costs were negatively correlated with profit. The adjusted R2 of the purchase price of private customers was found to be 1, which makes sense since they are the ones that must be served, and their purchase price directly impacts the profits. The adjusted R2 of the purchase price of shared customers was slightly lower than 1, which is reasonable since some of them may not be profitable and will be put up for sale. The purchase price of auctioned customers was found to be less influential than the other two purchase prices.

From the cost viewpoint, the adjusted R2 value was good, but transport costs and penalty costs were found to explain profits better than the subcontracting costs of shared customers. The slope of each of these variables was negative, indicating that a decrease in these costs would lead to an increase in profits and conversely.

3.10 Analysis of pooling decisions

The decisions concerning the coalition pool are based on the analyses conducted in the Sect. 3.3. All the results in Table 7 are obtained considering positive variations. It's important to note that negative variations yield opposite results.

Table 7 Analysis of pooling decisions
Full size table

The changes in shared customer sales prices and auctioned customer purchase prices have opposite effects on the results. Higher selling prices for shared customers do not incentivize either outsourcing this customer category or acquiring new customers through auctions. Conversely, a higher purchase value for auctioned customers encourages both outsourcing shared customers and acquiring customers through auctions. Moreover, an increase in transport costs, a primary factor influencing profits, leads solely to the outsourcing of shared customers and does not promote the acquisition of auctioned customers for delivery.

In conclusion, we can make the following observations regarding decisions to push shared customers into the pool and to pull auctioned customers from the pool: Pushing shared customers into the pool is advantageous when the proposed price for auctioned customers is high, transportation costs are high, or subcontracting costs for shared customers are low. However, pushing shared customers into the pool becomes less favorable when the proposed selling price for these customers is high. Pulling auctioned customers out of the pool is beneficial when the price of auctioned customers is high, selling costs for shared customers are low, or transportation costs are low. Nevertheless, pulling auctioned customers out of the pool becomes less advantageous when the price of these customers is very low.

4 The simulation-based optimization approach

In order to conduct the optimization function in our Arena-based SBO model, we used Optquest. The search algorithm embedded by Optquest is a combination of three metaheuristics: tabu search, neural networks, and scatter search (Glover et al., 2003). The arena model (i.e., the.doe file) is available upon request. To describe the conceptual model, a standard UML activity diagram (Fig. 4) was used, which ensures the simulation model's reusability. The Optquest tool is used to evaluate the proposed routes.

Fig. 4
figure 4

Standard UML activity diagram

Full size image

Firstly, as the configuration is received from the Optquest tool, the process of evaluating the proposed routes is triggered. If the proposed configuration is correct, the revenues from shared and private customers are calculated. Else, if the configuration is unfeasible, a value of zero will be assigned to the profit. In this case, the calculation process will stop and send the results to Optquest. The next activity involves the identification of the first customer to be served on the route. In fact, the identification of the selected customers, and consequently the routes to be followed, is achieved through a matrix of variables defined at the model and declared as a set of binary controls in the Optquest. For example, suppose carrier X has a single depot and 23 customers, this means that 576 controls must be declared as binary in Optquest. If M85 equals to 1, with M being the name of the matrix (i.e. row 8 which refers to customer 8 and column 5 refers to customer 5) this means that customers 5 and 8 are selected and customer 5 should be served immediately after customer 8. Once the customer has been identified, the first activity to be carried out is to check that the transport capacity of the truck is respected. If the total demand of the selected clients' is less than the capacity, the configuration will be kept, otherwise a value of zero will be assigned to the benefit in order to stop the calculation process. The next activity consists of calculating the arrival time of the delivery person at the selected customer. If the arrival time is outside the customer's time slot, a penalty will be applied to the carrier. Subsequently, a customer type identification step will be triggered in order to calculate the revenue and/or costs associated with the selected customer. If the customer is a private or shared one, only the transportation costs will be calculated and added to the total costs. If the customer is an auctioned one, in addition to the calculation of the routing costs, the auction prices will be added to the collected revenue. The search for the next destination (selected customers or depot) will be triggered once the total cost and the total revenue collected are updated. If the next destination is a client, a loop will be launched to reactivate all activities from the capacity control. Else, if the next destination is identified as a return to the depot, an activity consisting of checking the existence of another tour will be triggered. If another tour is detected, a loop will be launched to reactivate all the activities starting from the identification of the selected clients. The opposite case means that all selected clients are identified. Thus, an outsourcing customer search activity will be activated in order to calculate the selling cost. This cost will be added to the total cost.

The final activity consists in calculating the profit and finally sending it to the Optquest. For the implementation of the described model with the Arena language, we used the modules CREATE, ASSIGN, ATTRIBUTE, VARIABLE, and DECIDE. These modules allow to reproduce the same evaluation process. For more details on Arena models, interested readers are referred to the work of Kelton et al. (2007).

The optimizer, from its side, will receive the results and decide to continue or stop the SBO process depending on the quality of responses. The configuration generation, performance evaluation of results and decision making are based on the Optquest search process. The simulation model checks and evaluates the responses of the sent configurations. The SBO approach is used in this study to manage the selection of destinations. The most profitable customers will be selected for delivery. All variables used in the SBO process are defined in the simulation model, and automatically sent to the Optquest during coupling. The inputs are called controls, and the outputs are called responses. The selection of the controls (decision variables) and the definition of their nature (binary, continuous, integer) is carried out in the Optquest optimization module. The optimization process cannot start unless the objective function is defined and the constraints are properly formulated. The constraints allow the proposed solution to be restricted to the various required conditions, namely:

  1. 1

    All private customers must be served,

  2. 2

    The shared and auctioned customers can be served, but without obligation,

  3. 3

    Each customer is served just once with a single vehicle,

  4. 4

    Each truck must return to the depot after the delivery round is completed,

  5. 5

    Each truck must leave the delivered customer for the following destination.

Finally, it is worth noting that the validation of the developed SBO model is a critical step to ensure its reliability. To this end, we have implemented and solved the problem test outlined in Sect. 3 and the simulation results confirm the validity of our model, as they match the expected outcomes. Moving forward, we will conduct numerical experiments in the next section, which involve a real-life case study of parcel delivery in a stochastic environment. Our model will be leveraged to address this scenario and provide a practical solution.

5 Numerical experiments under a real-life case study for parcel delivery

Numerical experiments were conducted as part of a real-life case study related to the parcels delivery. The case study perfectly aligns with the assumptions of our study, even though it involves three actors, namely the sender, the carrier, and the receiver.

In this case study, the carrier's customers are the senders of the parcels, whereas the recipients of the parcels are the senders' customers. Each parcel is assigned a type based on the sending customer, such as private, shared, or auctioned. For example, if the sending customer is a private individual, the package will also be classified as private.

The case study is conducted in a parcel delivery company called FLASH EXPRESS TUN (FET), located in the governorate of Nabeul-Tunisia, as shown in Fig. 5. The company employs delivery drivers who use their own partner vehicles for deliveries, limited to the region. FET assumes responsibility for the fuel cost for these vehicles. Each partner vehicle has a boot volume of 664 dm3. Any shipments outside Nabeul governorate are automatically outsourced. The delivery operation begins at 8 a.m. and typically ends in the afternoon. The senders of parcels can be individuals, commercial or industrial companies, or collaborating transport companies. (“LaZ” is one of the Tunisian transport companies that collaborates with FET and is considered as private client).

Fig. 5
figure 5

Governorate of Nabeul-Tunisia

Full size image

FET aims to deliver its parcels as quickly as possible, with a delivery time of up to 24 h for parcels directed to Nabeul governorate, and between 48 to 72 h for parcels outside the region. To maximize the carrier's profits and avoid empty trips, this work proposes a set of parcels to be listed on an auction platform. The senders of these parcels set a predefined price and time window for each delivery, as shown in Table 8. The distance between the parcel senders and the carrier's warehouse is considered negligible, so no additional costs are incurred for picking up the parcels.

Table 8 The case study’s data
Full size table

There are a number of packages to be delivered for each city in Nabeul. Each delivery person will select the parcels of two or three adjacent cities, depending on the volume of the parcels and the vehicle's capacity, and go directly to deliver the parcels. To give an overview of the management outcomes and better visualize the results of the selection, for each city we will choose randomly one or two packages to deliver with the same vehicle. The volume of the latter represents about 68% of the volume of the partner's boot. Each parcel must be delivered within the required period. If there is a delay, a penalty of 10% will be deducted from the delivery price. The price for delivery of a parcel of any size is 8 TND (Tunisian Dinars). If FET decides to subcontract a parcel, the revenue is shared, with FET receiving 2.5 TND and the subcontracting company receiving 5.5 TND. The same rule applies to the collaborative company.

Table 8 presents a detailed overview of all the parcels under consideration, including private, shared, and auctioned parcels, along with their dispatch locations, volumes, time windows, purchase prices, and proposed selling prices for shared customers. In addition, Tables C1 and C2 in Appendix C provide the travel times between different destinations and the corresponding transportation costs, respectively. The transportation cost is computed based on the diesel consumed per distance traveled multiplied by the cost of diesel per litre, which is 2.08 TND. A partner vehicle typically consumes 5.4 L per 100 km.

To evaluate the potential benefits of a shared customer auction-based collaboration at FET carrier, two management strategies are compared. The first strategy, referred to as MS1, which is the FET's existing approach requiring the delivery of all parcels with a destination in Nabeul, regardless of whether they are of a shared type. Only parcels with a destination outside Nabeul and of a shared type are outsourced. The second strategy, referred to as MS2, is the one proposed in this paper, that aims to maximize the carrier's profits by selecting the profitable auctioned customers and utilizing a coalition pool to subcontract unprofitable shared customers.

5.1 Implementation and simulation results

To identify all profitable parcels, the SBO approach designed in this study was implemented in the software Arena. To reflect the real context of the case study, the travel time was assumed to be stochastic. It is important to highlight that each path in our case study has a particular travel time distribution, including lognormal, gamma, bimodal lognormal, and bimodal gamma distributions. However, for the purpose of our analysis, we assume that all travel times follow a common distribution, namely the bimodal gamma distribution as defined by Layeb et al. (2018):

$$ {\text{TT}}_{{{\text{ij}}}} \sim {\text{p}}_{{1}} {\text{Gamma}}\left( {\alpha {1},{\text{ij }},\beta {1},{\text{ij }}} \right) + {\text{ p}}_{{2}} {\text{Gamma }}\left( {\alpha {2},{\text{ij }}, \, \beta {2},{\text{ij}}} \right), $$
(19)

where p1 is the probability of encountering the first mode, αk,ij is the shape parameter, and βk,ij is the scale parameter of the corresponding Gamma (αk,ij, βk,ij) mode, k = 1,2, (i,j) ∈ A. These parameters are respectively expressed as:

$$ {\upalpha }_{{{\text{k}},{\text{ij }}}} = \frac{{E[TT_{k,ij} ]^{2} }}{{{\text{Var }}\left[ {TT_{k,ij} } \right]}},\quad {\text{k}} = { 1},{2}, \, \left( {{\text{i}},{\text{j}}} \right) \in {\text{A}}, $$
(20)
$$ {\upbeta }_{{{\text{k}},{\text{ij }}}} = \frac{{{\text{Var }}\left[ {TT_{k,ij} } \right]}}{{E[TT_{k,ij} ]}},\quad {\text{k}} = { 1},{2},\left( {{\text{i}},{\text{j}}} \right) \in {\text{A}}, $$
(21)

with \({\text{Var }}\left[ {TT_{k,ij} } \right]\) = (CV × \({ }E[TT_{k,ij} ])^{2}\), k = 1,2, (i,j) ∈ A. Parameters αk,ij and βk,ij are estimated using the method of moment.

To accurately capture the stochastic nature of travel times in our case study, we assume that 30% of the time, flows are congested, while 70% of the time, they are free flowing. It is also assumed that the average travel time for congested flows is 20% higher than for free flows. Additionally, the coefficient of variation is set to 50% to reflect the variability in travel times. The performance of travel time is estimated as the sample average over n independent replications. We set n so that, for a confidence level of 95%, the half-width of the confidence interval is less than 0.05.

To compare the performance of the two management strategies, we present our results in Tables 9, 10, and Fig. 6. Table 9 displays the selection results for each parcel type. Table 10 presents the results for each management strategy, including the profit generated, income from auctioned parcels, delay penalties, costs of outsourcing unprofitable parcels, and transport costs. Figure 6 shows the sub-optimal scheduling of deliveries for each strategic management. Note that the results obtained for the first management strategy were derived from simulations of our SBO model when considering that all clients sending parcels are private customers.

Table 9 The selection results
Full size table
Table 10 Comparison of management strategies: profit, income, and costs
Full size table
Fig. 6
figure 6

The sub-optimal scheduling of deliveries

Full size image

5.2 Discussion

The results demonstrate the effectiveness of the proposed MS2 in increasing profits and reducing transportation costs of the delivery service. Specifically, MS2 led to a 22.65% increase in profits compared to the profit resulting from MS1, achieved by managing the selection of shared customers through the auction.

The analysis of the parcels reveals that outsourcing unprofitable parcels (8, 9, 11, 15) resulted in a cost of 18.29 TND, while the selection of profitable parcels (19, 21, 22, 23) produced an income of 29 TND. MS2 retained the same number of packages as MS1, i.e. 15 packages, but transportation costs were lower due to the short distance traveled by the selected parcels. As shown in Fig. 6, the arrival times of the selected auctioned parcels were close to the private and selected shared ones, indicating that these parcels can contribute to increasing profits and decreasing transport costs.

The results also highlight the effectiveness of being open to studying the profitability of parcels offered by the auction and destined for other regions. For instance, package number 22 was selected for delivery even though its destination (BouFicha) is outside of the considered governorate. In contrast to FET's strategy of delivering only parcels destined for Nabeul and subcontracting the rest, MS2 demonstrated that considering parcels from other regions can lead to increased profits.Finally, the results highlight that proximity is not the only factor in the decision-making process. The rejected parcels in the coalition pool were all directed for Nabeul, indicating that proximity alone does not guarantee profitability. As demonstrated in Sect. 3.2.2, the analysis of various factors such as transport costs, subcontracting and purchasing costs of shared customers, pricing for auctioned and private customers, and penalty rates are all critical in determining the profitability of a parcel.

6 Conclusion & managerial insights

This article presents an innovative management strategy designed for transport companies involved in last-mile delivery to effectively manage shared customers, with the primary aim of enhancing profitability within a decentralized collaboration framework. The proposed strategy utilizes the auction mechanism as a tool to manage the selection of these customers, with unprofitable customers being pushed to the coalition pool and profitable ones being selected for delivery.

It is important to highlight that within the transport sector, carriers frequently engage in collaborations by online platforms. Notably, the auction mechanism, which constitutes a central component of our proposed strategy, is commonly employed in these real-world collaborations among carriers. For example, in Europe, Timocom is a known provider of a digital marketplace for shipping. It works like an auctioneer, charging fees to users who can either offer their available cargo for transport or bid on shipments that need moving (Gansterer et al., 2022).

This research article specifically focuses on the pre-auction phase of the process, without addressing issues related to bid generation or winner determination. First, a MILP model is derived to solve the problem in the deterministic framework. Then, the proposed strategy has been implemented in a more realistic environment by utilizing a developed SBO model that takes into account the stochastic nature of the traveling time. This real-world implementation has resulted in a validation of the proposed strategy through a case study related to a parcel delivery system, conclusively demonstrating a significant increase in profits. The results of the study show that the proposed strategy can be an effective approach for managing the shared customers and for increasing profitability. The strategy also contributes to minimizing transport costs and identifies even neighboring regions that can likely present better business opportunities.

Several important managerial insights are derived from the applied test problems and case-study conducted within this work. The sensitivity analysis provides valuable findings regarding the impact of key factors on profitability. Firstly, the analysis reveals that fluctuations in the ask prices of shared customers not only affect customer selection decisions but also have a significant impact on generated profits. An increase in ask prices results in decreased profits, making outsourcing and bidding on auctioned customers less attractive. Secondly, changes in the prices of auctioned customers have a substantial impact on both customer selection and resulting profits. Increasing the price of auctioned customers benefits carriers by increasing profits through the selection of most auctioned customers and outsourcing shared ones. Conversely, decreasing the price of auctioned customers leads to the retention of shared customers and the rejection of the auctioned ones. Thirdly, high transportation costs make outsourcing of shared customers more favorable, while low transportation costs encourage carriers to be more aggressive in attracting more auctioned customers to maximize profits.

Furthermore, the linear regression analysis indicates that the purchase price of auctioned customers has less influence on profits compared to the purchase prices of private and shared customers. From a cost perspective, transport costs and penalty costs provide better explanations for profits than subcontracting costs for shared customers. These insights provide valuable guidance for managers in making informed decisions regarding pricing strategies, customer selection, and cost management. By considering these factors and adjusting them strategically, companies can enhance their profitability and overall financial performance.

To further investigate the proposed management strategy for companies dealing with shared customers, several avenues for future research could be explored. One potential area of investigation could be the impact of incorporating service level as a condition for subcontracting shared customers. This would allow collaborating carriers to select profitable customers while also maintaining a certain level of service quality. Additionally, it may be beneficial to consider adding a probability of rejecting unprofitable shared customers pushed into the coalition pool when they are not of real interest to the carriers.

An important next step could be to move from the pre-auction phase to the actual auctioning phase. While the proposed strategy focuses on managing the selection of shared customers through a coalition pool, an auction mechanism would allow for a more direct and efficient approach to customer selection. By enabling carriers to bid for customers based on their individual profit margins and business objectives, the bidding phase could lead to a more efficient allocation of shared customers. Moreover, developing a specialized winner determination model will ensure an efficient allocation of the shared customers to the different bidding carriers.