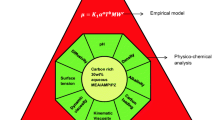
Abstract
The carbon dioxide concentration in the atmosphere has reached extremely high levels, generating environmental concerns. Unfortunately, despite the climate change, CO2 is not included nowadays as a key environmental issue in Best Available Technique (BAT) reference documents (BREF). Industrially, the widespread industrial technology to capture CO2 is the chemical absorption using aqueous monoethanolamine (MEA) at 30%wt, which is the basis of comparison for novel alternative techniques in the literature and seems a suitable candidate to be proposed as Best Available Technique. Nevertheless, there is an intense research to find alternative solvents that decrease the energy consumption for carbon capture and many solvents are claimed in the literature to outperform MEA. A novel empirical surrogate model and exergy balances are used to confirm that MEA is still the best candidate to be proposed as Best Available Technique. The surrogate model proposed in this study properly regresses the CO2 gas liquid equilibrium data. The regressed parameters of the model are tabulated in this study for many aqueous alkanolamines and their mixtures, being the basis for computationally inexpensive chemical absorption column design. The surrogate model parameter considering the temperature is related with the chemical absorption energy and the consumed energy for solvent recovery. The obtained results show that none of the considered alkanolamine outperforms MEA in all the considered aspects, i.e. energy and solvent flowrate. MEA minimum flowrate is 15.62 mol solvent/mol gas and its heat of absorption regression parameter is − 27,745 J/mol. The proposed mathematical method is useful as a fast assessment for other novel alternatives that will be proposed in the future, providing energetically more efficient and cleaner technologies for CO2 capture.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Techniques for CO 2 capture
At present, greenhouse effect is a big environmental problem. The CO2 concentration in atmosphere has increased exponentially to global warming. This includes several forecasted changes such as sea level rise, physical and health impacts, changes in seasons. (European commission 2020). Currently, the concentration of CO2 in the atmosphere is at its highest level according to available records in the past 800,000 years: before the industrial revolution, the CO2 atmospheric concentration did not exceed 300 ppm, but at present exceeds 400 ppm (Ritchie and Roser 2020). Yadav et al (2020) claim that carbon should not be used as a source of fuel or energy but be valorised to other products. As currently a large proportion of the energy produced comes from combustion, some other authors propose the biofixation of CO2 from the exhaust gases, e.g. Hashemi et al (2020), or electricity production by reactive gas electro-sorption (Alaba et al. 2020). Coal-fired power plants are the largest source of carbon dioxide (CO2) emissions into the atmosphere and net CO2 emissions achieve negative values when carbon is captured from the biomass co-firing plants (Cebrucean et al. 2020) and stored in safe geological sites (Aviso et al. 2019) or saline aquifers (Mahmoodpour et al. 2018). Carbon emission Pinch Analysis is a useful tool for planning the electricity generation mix (Salman et al. 2019). Besides of burning biomass to produce energy, negative values are also achievable by biomass pyrolysis to produce biochar as a stable form of carbon storable under the soil, improving its characteristics (Ong et al. 2020) or by biomass torrefaction to produce artificial biochar mines (Thengane and Bandyopadhyay 2020). However, there is some scepticism about keeping valuable products buried underground. Under the Paris agreement of limiting the global average temperature rise to 2 degrees Celsius, special focus is paid to CO2 capture techniques. It is expected that cost-effective carbon capture would contribute significantly to most CO2 decrease scenarios according to the European Commission (2018).
There are several techniques to collect concentrated CO2 from thermal plants: post-combustion, pre-combustion and oxy-combustion. Some techniques can be highlighted such as ultra-supercritical pulverised coal (USC PC) and natural gas combined cycle (NGCC) power plants with CO2 capture. Focusing on post-combustion processes, there are various techniques like membrane separation (Brunetti et al. 2010), adsorption (Gautam 2020), calcium or chemical looping (Cormos 2020), precipitation (Moioli et al. 2019), cryogenic separation, absorption and combinations of those. Nevertheless, the most used technology to capture CO2 at industrial level, which is the basis of comparison for any novel alternative technique, is the absorption: 90% of the carbon captured in large-carbon capture facilities in operation corresponds to absorption. Around the world, the main alternative for large-carbon capture facilities is the chemical absorption using aqueous alkanolamines, such as MDEA, PZ/MDEA for high partial pressure CO2 meanwhile for low partial pressure of CO2 MEA or proprietary aqueous amine solutions such as Cansolv, KS-1, etc. (Yamada 2021) are used. Mendez-Alvarez et al. (2016) pointed out that MEA and MDEA have a large operation window compared to other alkanolamines (Fig. 1).
Operation window for some alkanolamines, calculated with OLI® (Mendez-Alvarez et al. 2016)
Nevertheless, in USA the physical absorption is the most relevant technique, using propylene carbonate or proprietary solvents such as Selexol, Rectisol. (Yamada 2021). Physical absorption avoids the energy consumption related to the reaction enthalpy during solvent regeneration, but the required solvent flow rate becomes impractical for low CO2 partial pressures such as for power plants’ flue gas (Fig. 2). According to Burnard (2020a), two main barriers must be overcome to spread the use of carbon capture: the high capital expenditure and lack of revenue generation for the low commercial value of CO2. Policy incentives and regulatory actions must be put in place urgently to overcome these two barriers.
Minimum solvent flow rate for chemical and physical CO2 absorption at 20 °C (Sala et al. 2014)
The implementation and improvement of any industrial process requires a reference process considered as the Best Available Technique and in fact the chemical absorption with aqueous MEA has been taking this role for low partial pressure CO2 capture for the last half century. European Best Practice Guidelines for CO2 Capture Technologies indicate that the 30% wt MEA solvent scrubbing post-combustion CO2-capture process used in a number of industrial applications is considered the benchmark technology (CESAR 2018). However, despite climate change, CO2 pollution is currently not included as a key environmental issue in the BREF documents (European Commission 2017).
The chemical absorption consists of capturing the gas by cycles of chemical absorption–desorption. Unfortunately, this process comes with a high recycling solvent flowrate and energy demand. Many reports point out that a MEA alkanolamine system to capture 90% CO2 from a power plant flue gas can consume 30% of the power produced, which is translated into a CO2 capture cost of 40–100 €/t CO2 (Merkel et al. 2010). A more favourable scenario is obtained with an energy return of 85% when combined heat and power plants are retrofitted with post-combustion carbon capture (Morales-Mora et al. 2019) or the carbon capture unit also produces electricity (Li et al. 2018). An option to avoid the solvent recovery costs is to use the collected ammonia as fertilizer, e.g. Bonet-Ruiz et al. (2015) or He et al. (2017). Despite the drawbacks and improvements proposed, chemical absorption with alkanolamines has the greatest potential to reduce emissions (Figueroa et al. 2008).
Alternative aqueous alkanolamines to MEA
Alkanolamines are compounds that have both hydroxyl (-OH) and amino (-NH2) groups. The basicity of the amino group allows the chemical capture of CO2 due to its acidic character. Alkanolamines are the most common chemical absorbers for CO2 capture. MEA chemical absorption is the dominant technology to industrially capture CO2 from power plants exhaust gases up to now, but novel amine absorbents are expected to provide more efficient processes. There is an intense research to find alternative solvents that decrease the energy consumption of aqueous MEA solvent recovery and being less prone to degradation, e.g. Alaba et al. (2017). Besides of alternative aqueous alkanolamines, there are many other alternatives assessed in the literature such as alkanolamines in non-aqueous solvents, ionic liquids, amine functionalized deep eutectic solvents, enhanced with solid catalysts. Salting out effect suggests that physical absorption is not the only mechanism through which CO2 is absorbed after full theoretical amine loading (Wanderley et al. 2018). However, the enhanced processes compare their advantages versus the aqueous alkanolamines, which are the most mature for treating flue gas. As the literature available is very extensive, this study focuses only on the aqueous alkanolamines because these are the basis of comparison for any other solvent used, and other alternatives will be assessed in future work.
There are many experimental CO2 equilibrium data available for aqueous alkanolamines (Table 1) and some of their mixtures (Table 2). These data are not only useful to know the load of CO2 on the alkanolamine but also to estimate the enthalpy of absorption using the simplified Gibbs–Helmholtz equation (Mathias 2016). Substituting the CO2 fugacity by its partial pressure and assuming a low CO2 fraction in the gas phase, then the enthalpy of absorption is estimated based on the variation of the CO2 partial pressure with the inverse of the temperature (Eq. 1). A desorption parameter related with the desorption column heat duty is particularly useful for the ranking of alternative alkanolamines (Zhang et al. 2020a, b).
In the literature, there are many studies that claim certain aqueous alkanolamines are better than MEA. Besides the commercially available alkanolamines, the computer-aided molecular design is a powerful tool to propose novel solvents suitable for CO2 capture (Papadopoulos et al. 2016). There is a large number of proposed solvents for CO2 capture in the literature, for many of them there is some experimental gas liquid equilibrium or calorimetric data, for some of them there are pilot plant experiments but very few have been tested at larger capacity units and lengthier campaigns. Pilot plant and industrial operating data are not always published in the available literature although many studies are available.
Morgan et al. (2018) perform a study for a 10 t CO2/h pilot plant, and Feron et al. (2017) run a pilot plant for 1000 h, and both provide a review of previous studies about MEA pilot plants. In pilot plant experiments, Akram et al. (2020) determined that using 40% MEA, the reboiler duty drops by up to 14% compared to the commonly used 30% MEA concentration. Enhanced packings, e.g. (Flechsig et al. 2018), and flexible operation of MEA columns, e.g. (Cormos et al. 2019), are also under study. In the literature, DEA (secondary amine) or MDEA (tertiary amine) are claimed to have a higher absorption capacity, higher resistance to corrosion and lower exergy lost than MEA (Chowdhury et al. 2013). The corrosion resistance and degradation to harmful compounds, e.g. nitrosamines (Mazari et al. 2019), are out the scope of the present study.
Although most of the attention at pilot scale is devoted to MEA, there are also some promising pilot plant studies about DEA/PZ for CO2 rich gases, e.g. Dubois et al. (2017) or Laribi et al. (2019), or about MEA/DEA at ratio 4:1, Idem et al. (2006). Śpiewak et al. (2015) claim the use of AMP/Pz based on process development unit runs; later on, pilot plant runs were performed with MEA solutions as a recognized baseline solvent suitable for future comparative purposes (Stec et al. 2016) and nowadays the pilot plant study focuses on the methanation of the amine-absorbed CO2 (Chwoła et al. 2020). Nwaoha et al. (2019) successfully substituted the toxic PZ by 1,5-diamino-2-methylpentane (DA2MP) in pilot plant experiments for the industrially used MDEA/PZ mixture.
Many other aqueous alkanolamines have been proposed based on laboratory experiments. For example, Barzagli et al (2019) determine experimentally, using pure CO2, that AMP and its mixtures reach higher loads than MEA and the enthalpy of absorption is smaller according to simplified Gibbs–Helmholtz equation. Many studies identify alkanolamines with a lower absorption enthalpy than MEA, e.g. for DEEA and DMEA are − 47.0 and − 48.6 kJ/mol, respectively (Xiao et al. 2016) and for 1DMA2P and MEA are − 31.7 and − 84.3 kJ/mol, respectively (Liu et al. 2017). It is also possible to combine several types of alkanolamines, the purpose of the combination being to take advantage of each compound, e.g. (Xiao et al. 2021). Gómez-Diaz et al. (2021) prove that DMEA/MEA mixture load does not depend on its ratio and DMEA has a faster reaction rate. Therefore, although the MEA is recognized as a proven suitable solvent for CO2 capture at large scale, many promising alternatives are claimed in the literature.
Process optimization and modification based on rigorous simulations show that the energy consumption of a reference MEA chemical absorption of CO2 can be decreased; both for MEA or aqueous alkanolamines mixtures are attained similar regeneration reductions between 5 and 40% (Hosseini-Ardali et al. 2020). There are many simulation results that point out some aqueous alkanolamine mixtures outperforming MEA, not only from the energy point of view but also due to their higher stability, e.g. MDEA/PZ. Among the aqueous alkanolamines, some of them present the advantage to produce a phase split of the rich solvent stream (Papadopoulos et al. 2019). The phase poor in CO2 is recycled directly to the absorption column, decreasing the flow rate of rich CO2 phase fed to the distillation column. Examples of solvents with phase change behaviour are N,N-dimethylcyclohexylamine (DMCA), methylcyclohexylamine (MCA) and 2-amino-2-methyl-1-propanol (AMP) (Tzirakis et al. 2019), or mixtures such as MAPA/DEEA (3-(methylamino)propylamine/2-(diethylamino)ethanol). The computer-aided molecular design allows the screening and proposal of novel solvents suitable for CO2 absorption (Papadopoulos et al. 2020a). A novel very promising solvent proposed by computer-aided molecular design is the S1N (N1-cyclohexylpropane-1,3-diamine), for which laboratory experiments corroborate its suitability when mixed with other alkanolamines, e.g. DMCA, (Papadopoulos et al. 2020b). The phase split solvent is proved to be advisable from economic (Zarogiannis et al. 2020a), environmental (Shavalieva et al. 2021) and operational (resilient to disturbances) (Zarogiannis et al. 2020b) points of view.
This study proposes a fast method that, based solely on experimental data of vapour–liquid equilibrium of CO2 gas, compares alternatives with MEA in terms of required flowrate and energy consumption. This method has been applied to several alkanolamines whose experimental gas liquid equilibrium data are available in the literature (DEA, TEA, DIPA, MDEA, DGA, AEEA, PZ, AMP, NH3) and some of their mixtures (Table 1). Table 1 compiles the operating conditions of temperature, CO2 partial pressure, amine concentration and CO2 load in which each experimental study has been performed. Some aqueous alkanolamines have been extensively studied in the literature by many authors and for some others there is only a single study. The aqueous alkanolamines for which there are not enough experimental points according to the number of model parameters to be properly regressed have not been considered. Although an exhaustive literature review retrieving a vast number of experimental data points has been performed in this study, some interesting alkanolamines may have been missed. However, the proposed method is fast and simple enough to be applied to them in further studies.
Method
Standard model equations for alkanolamines gas liquid equilibrium
Assessment of alkanolamine absorbents capture performance is crucial to decrease the carbon footprint of many processes. There are several activity coefficients models useful for electrolyte mixtures such as Pitzer or ElectNRTL that are implemented in commercial simulation software, e.g. Aspen Plus®. Aspen Plus® allows also to use the MSE or Aqueous models based on Debye–Hückel model from the software specific for electrolytes OLI®. MSE model implemented in OLI® allows very accurate calculations for electrolyte systems but is not easy to generate a novel alkanolamine at user level. The activity models such as ElectNRTL require to determine many tens of unknown parameters before modelling. Figure 3 shows that the absorption operation window without solids or vapours using the parameters readily implemented in ElectNRTL of Aspen Plus® appreciably differs from the operation window calculated using MSE of OLI® (Mendez-Alvarez et al. 2016). The activity coefficients complex models are not suitable when limited experimental data are available, then the regressed parameters have little physical relevance, then this drawback is overcome using simplified shortcut methods including the simplified Gibbs–Helmholtz equation (Jiang et al. 2018). OLI® software is used in the present study to solve the exergy balances.
The present study proposes a simple and effective surrogated model that with a small number of parameters and based solely on few CO2 gas liquid equilibrium experimental data are able to estimate an energy parameter and minimum solvent flow rate required for each solvent. The proposed method is intended to simplify the assessment of CO2 capture performance, but the regressed CO2 vapour liquid equilibrium model also is useful for the absorption column design.
Surrogate model equations for gas liquid equilibrium
Plesu et al. (2018) proposed an equation able to accurately represent the CO2 gas-liquid equilibrium on aqueous MEA available in the literature, in the CO2 load range between 0.2 and 0.4 (Eq. 2). The equation neglects the alkanolamine mass percentage and a value close to the calorimetric determined enthalpy of absorption for MEA for the temperature dependent term is obtained, i.e. − 88 kJ/mol vs − 84 kJ/mol. The equation has a poor regression of the experimental data at high temperatures and loads, i.e. when the CO2 partial pressure is higher and deviates from ideality.
This empirical correlation that relates the molar composition and the temperature with the CO2 partial pressure is computationally inexpensive due to its simplicity, but the main drawback is its low dimensionality which translates into its limited validity range (Carranza-Abaid et al. 2020). In this study, the dimensionality and validity range of the equation is extended. The extension of the previous equation to further alkanolamines including mixtures implies the addition of two parameters to the previous equation, which depend on the alkanolamine mass percentage (Eq. 3). A broad range of CO2 gas liquid equilibrium data is regressed. The model assumes that the dependence of the CO2 partial pressure on the inverse of the temperature does not depend on the composition. This rough approach is applied for sake of simplicity. The absorption energy term of the equation loses its physical meaning and does not correspond to the experimental calorimetric absorption energy. Nevertheless, it is expected to be an averaged value of the enthalpy of absorption providing an insight of the energy consumption for the rich solvent recovery.
In this proposed model equation, the partial pressure of CO2 (PCO2) is expressed in Pa, the heat absorption in J/mol (\(\Delta H_{{{\text{abs}}}}\)), the gas constant (R) is 8.314 m3·Pa/(K·mol), temperature (T) is measured in Kelvin, Xi are the regressed parameters of the surrogate model, %wt Alkanolamine is the amine mass percentage and “α” is the CO2 load (expressed as the ratio of mols CO2 absorbed divided by mols alkanolamines necessary for the absorption). The equation is not only providing insights on the energy consumption according to the ∆Habs term but also on the solvent required according to the load term (Eq. 6).
Mass and exergy balances
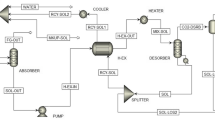
CO2 absorption process scheme is composed mainly of two main sections: the CO2 absorption and the solvent recovery (Fig. 4). The main unit of the process is the absorption column where the spontaneous absorption of CO2 towards the equilibrium takes place. Therefore, in this section there is no appreciable energy consumption and usually operates at a rather low temperature around 40 °C to promote the CO2 absorption. The energy is mainly consumed in the solvent recovery section. The solvent recovery is not spontaneous, and the main energy of the process is consumed at a distillation column reboiler to reverse the CO2 absorption. The flowsheet is completed with other unit operations such as heat exchangers for heat recovery and a decanter in case of phase split. Nevertheless, for sake of simplicity, the present study focuses only on the minimum flow rate of solvent to the absorption column.
The main streams considered in the mass balances are pointed up in accordance with Fig. 4. The carbon is captured from the exhaust gases (stream 1) collecting a treated gas stream (stream 2) at the top of the absorption column. An aqueous stream containing the alkanolamine is fed at the top of the absorption column, generating a stream of solvent enriched in CO2 (stream 5). The CO2-rich solvent is fed to a distillation column whose purpose is to separate pure CO2 collected by the distillate (stream 6) and the CO2 lean solvent stream (stream 4) collected at the bottoms and recycled to the absorption column. The input exhaust gas stream generated from the combustion with an air excess is composed in volume by 79% N2, x % CO2 and (21-x) % O2, where in this study a x = 10% vol CO2 is assumed.
The minimum solvent flow rate is calculated according to the method proposed by Sala et al (2014) assuming an infinite number of stages. Assuming infinite number of equilibrium stages for the absorption column, at absorption column top, CO2 concentration in the treated exhaust gases output (stream 3) is in equilibrium with the CO2 concentration present in the lean solvent output stream from the distillation column (stream 4). On the other hand, at absorption column bottoms, the feed exhaust gas to the absorption column is in equilibrium with the concentration of CO2 present in CO2 rich solvent. Contrary to Sala et al (2014) where the equilibrium was retrieved from a model, in this study, both CO2 equilibrium information is retrieved from literature experimental equilibrium data. N2 and O2 are not absorbed, and therefore, their flow rates at the input (stream 1) and output (stream 2) gas streams are the same.
For a given concentration of solvent in water, all flow rates and compositions of the streams are calculated according to the mass balances described in more detail in the following section. The entropy and enthalpy of these streams required to calculate the exergy balances are determined with OLI ® software.
Mass balances
The mass balances are solved assuming a calculation basis of 100 mol/s for the exhaust gas feed to the system with a 5 to 25% in volume CO2 and a recovery of 70% of CO2. Most of the studies use a recovery of 90%, but this is an artificial cap (Burnard 2020b). The process is operated at 1 atm, and all the streams are at this pressure.
According to the Dalton Law, the partial pressure of CO2 at the exhaust gas is calculated. The CO2 load (relationship between the composition of CO2 in a determined stream and total alkanolamine—Eq. 7) in the liquid stream (stream 5) in equilibrium with the input exhaust gas is retrieved from experimental equilibrium data.
A similar procedure is applied to the top of the absorption column. Establishing a CO2 recovery of 70%, the amount of CO2 that leaves the system can be assessed. The air is not absorbed. According to the Dalton Law, the CO2 partial pressure at the gas phase at the top of the column is also calculated. According to the experimental data of CO2 equilibrium, the load in the liquid phase at the top of the column is determined (Eq. 8).
The alkanolamine flow rate in the lean and rich solvent streams is the same and therefore with the previous CO2 load expressions and the CO2 mass balance, the molar minimum flowrate of alkanolamine is calculated (Eq. 9). Notice that the minimum alkanolamine flowrate depends on the difference of load values between the top and bottom of the adsorption column. The mass percentage of alkanolamine in the aqueous solution provides the water flow rate (Eq. 10). The available experimental data with a mass fraction of solvent closer to 30% have been chosen (Table 2), nevertheless for DGA the available experimental data are at 60% and for TEA is at 18%. The absorption column exergy balance is performed for all the compounds at 40 °C except for the di-isopropanolamine (DIPA) whose experimental data are only available at 50 °C. The mass balance is solved directly on experimental data instead of using the regressed values due to the uncertainties associated with the regression parameters.
Results
Many of the main aqueous alkanolamines studied in the literature for CO2 absorption are critically compared and ranked according to the minimum solvent flow rate required and an energetic parameter provided by the proposed model regression. The literature review indicates that the benchmark process used in the literature to compare any novel exhaust gases CO2 capture technology is the chemical absorption with MEA. It is expected that the present study results help to decide if the MEA absorption is a proper candidate to be proposed as the Best Available Technique (BAT). When a process is proposed as BAT in the BREFs does not imply that there are no other more efficient or advantageous techniques. The BAT process defines a base line of comparison for any novel technique implemented that should be at least better than the BAT. It is expected that the present results provide some light on the carbon capture and help to include the CO2 as contaminant in the BREFs.
Surrogated model
The surrogate model proposed (Eq. 3) correlates the CO2 gas liquid experimental data in general with good correlation coefficients (Tables 3, 4 and 5). However, in some cases such as for TEA or MEA + DAP the correlation is worse. Table 4 presents the regressed parameters for single aqueous alkanolamines and Tables 5 and 6 for binary and ternary mixtures. For some alkanolamines mixtures, there are not enough experimental data at different conditions to fit all the model parameters. The Pareto diagram is presented in Fig. 5, showing a random scatter of points at both sides of the diagonal, proving that the model is able to regress properly the gas liquid equilibrium experimental data for all the alkanolamines. Although more parameters would be included in the model, small deviations from the model are unavoidable due to experimental errors.
Regeneration stream flow rate
The minimum solvent stream flow rate determines the pumping energy and cost related to the equipment and piping diameters. According to the minimum solvent flow rate results, MEA is on a top position together with ammonia (Table 6). DGA is also at a top position, but it is important to notice that no experimental data for 30% alkanolamine were available for DGA and a 60% mass fraction is used in this case (Table 3). NH3 was also industrially used, but its volatility discouraged its use. Therefore, MEA is a suitable alkanolamine from the required flow rate point of view for diluted exhaust gases absorption. There are some alkanolamines that are able to reach a higher CO2 load than MEA but in this case what is important is the CO2 load difference corresponding to the gas liquid equilibrium when the partial pressure of CO2 varies. The obtained results depend on the CO2 gas concentration and recovery and thus, higher CO2 gas concentrations or recoveries affect the calculated minimum flow rate and the alkanolamines ranking. The minimum flow rate of 30% MEA aqueous solution to capture the CO2 from an exhaust gas with 25% vol CO2 is lower than the flowrate of any other assessed alkanolamines to capture a 5% vol CO2.The exception is the volatile NH3 and the DGA, whose experimental data are only available for 60% DGA aqueous solution.
It is expected that a lower minimum solvent flowrate is attainable when the parameters associated with the load of the surrogated model become higher. Figure 6 shows that for 30% alkanolamine and higher concentrations, the lowest minimum solvent flowrate corresponds to the use of MEA. Although being the worst choice according to Table 6, TEA seems also a good option for solvents with high alkanolamine concentrations but due to its low correlation coefficient further experimental research of gas liquid equilibrium is required. The results show that PZ performs better when its mass percentage is low but notice also that PZ regressed parameters provide negative slope values for high % Alkanolamines, which is physically unfeasible.
Energy consumption
Two different approaches are applied in this section for exhaust gases with 10% CO2 content to identify solvent alternatives outperforming MEA:
-
the first approach is based on an exergy balance of the absorption column at 30 °C based on the previous mass balance results and the thermodynamic parameters retrieved from OLI® software;
-
the second approach is based on the regression parameters of the proposed surrogate model.
The energy consumption of the carbon capture process by chemical absorption is expected to be related with the exergy lost in the absorption column. The previously mass balances solved for a minimum solvent flow rate are used to perform the exergy balance. The exergy balance on the absorption column depicts some alkanolamines showing better behaviour than MEA (Table 7), for instance the DEA. In case of DPTA, using the experimental equilibrium data where the process takes places spontaneously, the value of the exergy is positive which is not in agreement with the fact that the process should be spontaneous. Therefore, thermodynamic parameters implemented in commercial simulation software must be used with caution. Nevertheless, again MEA is in a rather favourable result l.
Another approach to determine some energy favourable alkanolamines is based on the regressed surrogated model. According to the surrogated model, for the energy the focus is placed on the temperature-dependent parameters as it is expected to provide some hints about the energy consumption, although its value does not correspond to the absorption enthalpy. For instance, MEA energy regressed parameter has a value of − 28 kJ/mol versus the − 84 kJ/mol enthalpy of absorption (Table 8). The energy regressed parameters are ranked in Table 9, showing that MEA has a lower more favourable value than the other alkanolamines, which is in agreement with the industrial practice. Only the PZ + AMP mixture would have a more favourable parameter. The Pareto diagram between the regressed and the experimental CO2 gas liquid equilibrium for PZ + AMP mixture is shown in Fig. 7, indicating reasonable agreement between the experimental data with the regressed equation (Eqs. 11, 12 and 13).
Although AMP and PZ solvents show worse results at the level of exergy of absorption, when mixed together, they show the best results.
For this mixture, if we assume a total solvent concentration of 30% (23% AMP and 7% PZ), the regeneration flow is 40.15 mol solvent/mol gaseous input, a value much higher as for MEA solvent of 15.62 mol solvent/mol gaseous input (Table 6). Therefore, despite its low value at heat absorption levels, its minimum solvent flowrate is quite high.
The surrogated model including the S1 and S2 parameters has a great influence on the value of the energy regressed parameter, and therefore, the regressions are repeated using only the S1 parameter for single aqueous alkanolamines (Table 9). Without the S2 parameter then the regression correlation of alkanolamines mixtures is rather poor and therefore not performed. The model is not able to regress all the data, and therefore, the regression is performed only in the linearized range of experimental points that is indicated in the table. Although the regressed energy parameter for MEA is still far away from its heat of absorption, the ranking is still showing that MEA is very favourable. In the case of DGA, using S1 and S2 in the surrogated model leads to unfavourable results, when only S1 is considered then its energy and load regression parameters are more favourable than MEA. Therefore, further experimental gas liquid equilibrium studies on DGA would be interesting to find in which operating conditions DGA could be more advantageous than MEA.
The surrogate model provides a very good regression of experimental CO2 gas liquid equilibrium, but the energy parameter has only physical meaning for systems at constant composition. However, the lower relative values for MEA in all the regressions indicate that MEA is a good choice, which is in agreement with its nowadays industrial use. Several regressions at different compositions are required for a more precise energy assessment.
Hence, considering both the exergy assessment and the surrogate model parameters, the obtained results indicate that MEA is a suitable choice as benchmark from the energy point of view, although some alkanolamines could outperform MEA.
Alkanolamines screening
Table 10 indicates that MEA is a good choice to propose it as a BAT, which is in agreement with its nowadays industrial use. Although DGA could require a lower solvent flow rate, a higher energy consumption is expected. However; further, research is required on DGA to find the operating conditions in which this compound could be advantageous. On the other hand, although PZ + AMP mixture would provide an energetically favourable process, its high solvent flow rate discourages its use. Finally, simulation results pointing out that some alkanolamines can have a good performance, e.g. MDEA or DEA, should be taken with caution due to the uncertainties in the thermodynamic data implemented in the commercial simulation software. It is possible that some alternative solvents to MEA are advantageous, therefore further research on this field is required and nowadays MEA is suitable to be proposed as the best available technique.
Alkanolamine losses in exhaust gas
A final important point is that some alkanolamine amount can be lost in the exhaust gas phase. Unfortunately, the experimental data available for this situation are very scarce and mainly available for ammonia. This section shows that the previous expression is not only valid for CO2 gas liquid equilibrium but also for the alkanolamine gas liquid equilibrium. It provides the basis for the application of this model to perform calculations of absorption columns design.
The design of a physical absorption column for low concentration of absorbed compound (e.g. < 10% vol as for CO2 in exhaust gas combustions) can be easily performed assuming a constant gas flow rate (linear operating line, Eq. 14) and the Henry’s law to define the equilibrium line (Eq. 15). NRTL and UNIQUAC thermodynamic models without dissociation are also suitable to describe the physical equilibrium but not the chemical one (Rosa et al. 2021). Solving the integral of Eq. 16 between the mass fraction of the absorbed/desorbed compound at the exhaust gas input and output streams provides the number of transfer units (NTU) of the absorption column (Eq. 16).
where Yi is the mass fraction of compound i in the gas phase, Xi is the mass fraction of compound i in the liquid phase, L/G is the ratio of liquid and gas mass flow rates, Yi1 is the mass fraction of compound i in gas output and Xi0 is the mass fraction of compound i in liquid input, Yi* mass fraction of compound i in the gas phase in gas liquid equilibrium with Xi, H is the Henry’s constant characteristic for each compound at a fixed temperature.
The chemical absorption is performed in an equivalent way, but using an expression derived from the proposed regression model instead of Henry’s law. For a fixed alkanolamine mass percentage and temperature, Eq. 3 leads to an exponential relation between the liquid and gas equilibrium fractions according to Eq. 17, where A and B are the parameters derived from the proposed model.
The pilot plant at Munmorah power station (test serie 5) is used as illustrative example for chemical absorption column design (Yu et al. 2011). The first step is to retrieve the CO2 and NH3 gas liquid experimental data available in the literature and regress the proposed equilibrium model for CO2 (Eq. 18) and NH3 (Eq. 19). The data for CO2 correlation are retrieved from Qi et al. (2015), Jilvero et al (2015), Kurz et al (1995), Otsuka et al (1960) and Verbrugge (1973); the NH3 gas liquid equilibrium is only available in the last two references. The correlation coefficients obtained for the regressed models are of 0.92 and 0.89 for CO2 and NH3, respectively.
The operating conditions assumed, based on the pilot plant data, are the following:
-
Adiabatic absorption, operated at atmospheric pressure and constant temperature of 17.5 °C (pilot plant operates between 101–105 kPa and 15–20 °C)
-
Gas inlet: 760 kg/h flow rate with 8.5% vol CO2 (37.74% CO2 removal)
-
Gas outlet: assumed exhaust gas molar composition of 8.5% CO2, 10% O2, 78% N2 and 3.5% H2O and free of NH3 (pilot plant composition ranges between 8.5–12% CO2, 6.5–10% O2, 76–78% N2, 3–6% H2O, 190–280 ppm SO2, 200–330 ppm NO, < 10 pp NO2).
-
Liquid inlet (rich solvent): 8,040 kg/h flow rate with 4.5% wt NH3 (pilot plant operates between 2–5% wt NH3)
-
Liquid outlet (lean solvent): 4.5% wt NH3 and 0.3 CO2 load (pilot plant operates between 0.2–0.5 load)
Eqs. 18 and 19, for T = 290.15 K and % NH3 = 4.5% wt NH3 in liquid phase, depend only on the load (α) which, due to the constant % NH3, provides the mass fraction of CO2 in the liquid phase. These equations lead to Eqs. 20 and 21, where the gas molar fraction is calculated by applying Dalton law:
The number of transfer units of the absorption column is calculated based on the CO2 data, i.e. using the XCO2 in the exhaust gas inlet and outlet (this last calculated from the CO2 recovery) and the previous equations (Eqs. 14, 16 and 20). Assuming a gas inlet free of ammonia and with the number of transfer units of the column already calculated, the procedure is repeated to calculate the mass fraction of NH3 at the gas outlet (Eqs. 14, 16 and 21). The calculated amount of NH3 lost is of 3.67 kg/h which is in good agreement with the experimental value determined in the pilot plant that was around 3 kg/h.
Conclusions
A novel shortcut model that regresses a surrogate equation and requires a limited amount of gas liquid CO2 experimental data is proven to be useful to compare and screening of alkanolamines. The minimum solvent flow rate is calculated by applying the CO2 mass balance and assuming the liquid CO2 gas liquid equilibrium is reached at both ends of the absorption column. Therefore, the load and the energy parameter of a novel surrogate model are used as key performance indicators related with the minimum solvent flowrate and energy consumption, whose values are compared to the aqueous MEA which is used as reference. MEA minimum flowrate is 15.62 mol solvent/mol gas and its heat of absorption regression parameter is − 27,745 J/mol. Some alkanolamines perform better than MEA in some respects, for example DGA requires less solvent flow rate or PZ + AMP mixture has a more favourable energy parameter but requires higher solvent flow rate. MEA-based CO2 capture processes are the leading technology for the CO2 capture from fossil fuel combustion power plants. The literature review and regression results prove that MEA chemical absorption is a suitable benchmark for other solvents, sustaining its inclusion in BREF documents as best available technique and CO2 should be included as a contaminant in BREF documents. As future work, the method should be applied to a larger number of solvents and identify alternative solvents to MEA, whose operating conditions of use are more advantageous.
Change history
02 November 2021
Open access funding note is included.
Abbreviations
- MEA:
-
Monoethanolamine
- AMP:
-
2-Amino-2-methyl-1-propanol
- DEA:
-
Diethanolamine
- AEEA:
-
2-(2-Aminoethylamine) etanol
- DAP:
-
1–3-Diaminopropane
- DGA:
-
Diglycolamine
- DPTA:
-
Dipropylenetriamine
- DIPA:
-
Diisopropanolamine
- MDEA:
-
Methyldietanolamine
- TEA:
-
Triethanolamine
- PZ:
-
Piperazine
- 1DMA2P:
-
1-Dimethylamino-2-propanol
- DA2MP:
-
1,5-Diamino-2-methylpentane
- DMCA:
-
N,N-Dimethylcyclohexylamine
- MCA:
-
Methylcyclohexylamine
- MAPA:
-
3-(Methylamino)propylamine
- DEEA:
-
Diethylmonoethanolamine
- DMEA:
-
Dimethylmonoethanolamine
- S1N:
-
N1-cyclohexylpropane-1,3-diamine
- α :
-
Relationship between the composition of CO2 in a determined stream and total alkanolamine
- w :
-
Flow rate
- Mw:
-
Molar weight
References
Akram M, Milkowski K, Gibbins J, Pourkashanian M (2020) Comparative energy and environmental performance of 40 % and 30 % monoethanolamine at PACT pilot plant. Int J Greenh Gas Control 95:102946. https://doi.org/10.1016/j.ijggc.2019.102946
Alaba PA, Sani YM, Olupinla SF, Daud WWW, Isah YM, Enweremadu CC, Ayodele OO (2017) Toward N-nitrosamines free water: formation, prevention, and removal. Crit Rev Environ Sci Technol 47(24):2448–2489. https://doi.org/10.1080/10643389.2018.1430438
Alaba PA, Mazari SA, Farouk HU, Sanni SE, Agboola O, Lee CS, Abnisa F, Aroua MK, Daud WMAW (2020) Harvesting electricity from CO2 emission: opportunities. Int J Pr Eng Man-GT In Press, Challenges and Future Prospects. https://doi.org/10.1007/s40684-020-00250-2
Austgen DM, Rochelle GT, Chen CC (1991) Model of vapor–liquid equilibria for aqueous acid gas-alkanolamine systems. 2. Representation of H2S and CO2 solubility in aqueous MDEA and C02 solubility in aqueous mixtures of MDEA with MEA or DEA. Ind Eng Chem Res 30(3):543–555. https://doi.org/10.1021/ie00051a016
Aviso KB, Janairo JIB, Promentilla MAB, Tan RR (2019) Prediction of CO2 storage site integrity with rough set-based machine learning. Clean Technol Environ Policy 21(8):1655–1664. https://doi.org/10.1007/s10098-019-01732-x
Barreau A, Blanchon le Bouhelec E, Habchi Tounsi KN, Mougin P, Lecomte F (2006) Absorption of H2S and CO2 in alkanolamine aqueous solution: experimental data and modelling with the electrolyte-NRTL model. Oil Gas Sci Technol 61(3):345–361. https://doi.org/10.2516/ogst:2006038a
Barzagli F, Giorgi C, Mani F, Peruzzini M (2019) Comparative study of CO2 capture by aqueous and nonaqueous 2-amino-2-methyl-1-propanol based absorbents carried out by 13C NMR and enthalpy analysis. Ind Eng Chem Res 58(11):4364–4373. https://doi.org/10.1021/acs.iecr.9b00552
Bishnoi S, Rochelle GT (2000) Absorption of carbon dioxide into aqueous piperazine: reaction kinetics, mass transfer and solubility. Chem Eng Sci 55(22):5531–5543. https://doi.org/10.1016/S0009-2509(00)00182-2
Bishnoi S, Rochelle GT (2002) Thermodynamics of piperazine/methyldiethanolamine/water/carbon dioxide. Ind Eng Chem Res 41(3):604–612. https://doi.org/10.1021/ie0103106
Bonet-Ruiz A-E, Plesu V, Bonet J, Iancu P, Llorens J (2015) Preliminary technical feasibility analysis of carbon dioxide absorption by ecological residual solvents rich in ammonia to be used in fertigation. Clean Technol Environ Policy 17(5):1313–1321. https://doi.org/10.1007/s10098-015-0950-9
Brunetti A, Scura F, Barbieri G, Drioli E (2010) Membrane technologies for CO2 separation. J Membr Sci 359(1–2):115–125. https://doi.org/10.1016/j.memsci.2009.11.040
Burnard K (2020a) IEGHG Technical Report 2020–08: Future Role of CCS Technologies in the Power Sector. International Energy Agency (IEA) Greenhouse Gas R&D Programme. https://ieaghg.org/ccs-resources/blog/new-ieaghg-report-global-future-role-of-power-ccs-technologies Accessed 7 January 2021
Burnard K (2020b) IEGHG Technical Report 2020–07: Update Techno-Economic Benchmarks for Fossil Fuel-Fired Power Plants with CO2 Capture. International Energy Agency (IEA) Greenhouse Gas R&D Programme. https://ieaghg.org/publications/technical-reports/reports-list/9-technical-reports/1041-2020-07-update-techno-economic-benchmarks-for-fossil-fuel-fired-power-plants-with-co2-capture Accessed 7 January 2021
Carranza-Abaid A, Svendsen HF, Jakobsen JP (2020) Surrogate modelling of VLE: integrating machine learning with thermodynamic constraints. Chem Eng Sci X 8:100080. https://doi.org/10.1016/j.cesx.2020.100080
Cebrucean D, Cebrucean V, Ionel I (2020) Modeling and performance analysis of subcritical and supercritical coal-fired power plants with biomass co-firing and CO2 capture. Clean Technol Environ Policy 22(1):153–169. https://doi.org/10.1007/s10098-019-01774-1
CESAR (2018) 2011-D2.4.3-APPROVED- project 7th FrameWork Programme. Collaborative Project-GA No. 213569. European Best Practice Guidelines for CO2 Capture Technologies—EBTF -2011.03.08.doc https://zenodo.org/record/1312801#.YBRA_hYo-Uk Accessed 7 January 2021 https://doi.org/10.5281/zenodo.1312801
Chen X, Closmann F, Rochelle GT (2011) Accurate screening of amines by the Wetted Wall Column. Energy Procedia 4:101–108. https://doi.org/10.1016/j.egypro.2011.01.029
Chowdhury FA, Yamada H, Higashii T, Goto K, Onoda M (2013) CO2 capture by tertiary amine absorbents: a performance comparison study. Ind Eng Chem Res 52(24):8323–8331. https://doi.org/10.1021/ie400825u
Chung PY, Soriano AN, Leron RB, Li MH (2010) Equilibrium solubility of carbon dioxide in the amine solvent system of (triethanolamine + piperazine + water). J Chem Thermodyn 42(6):802–807. https://doi.org/10.1016/j.jct.2010.02.005
Chwoła T, Spietz T, Więcław-Solny L, Tatarczuk A, Krótki A, Dobras S, Wilka A, Tchórz J, Stec M, Zdeb J (2020) Pilot plant initial results for the methanation process using CO2 from amine scrubbing at the Łaziska power plant in Poland. Fuel 263:116804. https://doi.org/10.1016/j.fuel.2019.116804
Cormos CC (2020) Energy and cost efficient manganese chemical looping air separation cycle for decarbonized power generation based on oxy-fuel combustion and gasification. Energy 191:116579. https://doi.org/10.1016/j.energy.2019.116579
Cormos AM, Burca M, Ilea F, Cristea MV (2019) Process control strategy of amine-based post-combustion CO2 capture systems. Chem Eng Trans 76:757–762. https://doi.org/10.3303/CET1976127
Dash SK, Samanta AN, Bandyopadhyay SS (2011) (Vapour + liquid) equilibria (VLE) of CO2 in aqueous solutions of 2-amino-2-methyl-1-propanol: New data and modelling using eNRTL-equation. J Chem Thermodyn 43(8):1278–1285. https://doi.org/10.1016/j.jct.2011.03.016
Dicko M, Coquelet C, Jarne C, Northrop S, Richon D (2010) Acid gases partial pressures above a 50 wt% aqueous methyldiethanolamine solution: experimental work and modelling. Fluid Phase Equilib 289(2):99–109. https://doi.org/10.1016/j.fluid.2009.11.012
Dubois L, Laribi S, Mouhoubi S, De Weireld G, Thomas D (2017) Study of the post-combustion CO2 capture applied to conventional and partial oxy-fuel cement plants. Energy Procedia 114:6181–6196. https://doi.org/10.1016/j.egypro.2017.03.1756
European Commission (2017) Kick-off meeting for the drawing up of the best available techniques (bat) reference document for common waste gas treatment in the chemical sector. https://eippcb.jrc.ec.europa.eu/sites/default/files/2019-11/WGC_BREF_KoM%20IM%20Report%20May18_1.pdf Accessed 10 December 2020
European Commission (2018) Communication from the commission to the European parliament, the European council, the council, the European economic and social committee, the committee of the regions and the European Investment Bank. A Clean Planet for all A European strategic long-term vision for a prosperous, modern, competitive and climate neutral economy. COM/2018/773 final. https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A52018DC0773 Accessed January 2021
European commission (2020) Climate change. https://ec.europa.eu/clima/change/consequences_en Accessed 10 December 2020
Feron PHM, Cousins A, Gao S, Liu L, Wang J, Niu H, Yu H, Li K, Cottrell A (2017) Experimental performance assessment of a mono-ethanolamine-based post-combustion CO2-capture at a coal-fired power station in China. Greenh Gases 7(3):486–499. https://doi.org/10.1002/ghg.1654
Figueroa JD, Fout T, Plasynski S, McIlvried H, Srivastava RD (2008) Advances in CO2 capture technology—the U.S. Department of Energy’s Carbon Sequestration Program. Int J Greenh Gas Control 2:9–20. https://doi.org/10.1016/S1750-5836(07)00094-1
Flechsig S, Sohr J, Schubert M, Hampel U, Kenig EY (2018) Rate-based modelling of CO2 absorption with sandwich packings. Chem Eng Trans 69:169–174. https://doi.org/10.3303/CET1869029
Gautam SS (2020) Effects of geometric and heat transfer parameters on adsorption–desorption characteristics of CO2-activated carbon pair. Article in Press, Clean Techn Environ Policy. https://doi.org/10.1007/s10098-020-01866-3
Ghalib L, Ali BS, Ashri WM, Mazari S, Saeed IM (2017) Modeling the effect of piperazine on CO2 loading in MDEA/PZ mixture. Fluid Phase Equilib 434:233–243. https://doi.org/10.1016/j.fluid.2016.10.022
Gómez-Díaz D, Muñiz-Mouro A, Navaza JM, Rumbo A (2021) Diamine versus amines blend for CO2 chemical absorption. AIChE J 67(1):e17071. https://doi.org/10.1002/aic.17071
Guo C, Chen S, Zhang Y (2013) Solubility of carbon dioxide in aqueous 2-(2- aminoethylamine)ethanol (AEEA) solution and its mixtures with N- methyldiethanolamine/2-amino-2-methyl-1- propanol. J Chem Eng Data 58(2):460–466. https://doi.org/10.1021/je301174v
Haghtalab A, Talavaki MBZ (2017) Measurement of carbon dioxide solubility in aqueous diisopropanolamine solutions blended by N-(2-aminoethyl) ethanolamine + piperazine and density measurement of solutions. J Nat Gas Sci Eng 46:242–250. https://doi.org/10.1016/j.jngse.2017.07.023
Haghtalab A, Eghbali H, Shojaeian A (2014) Experiment and modeling solubility of CO2 in aqueous solutions of Diisopropanolamine + 2-amino-2-methyl-1- propanol + Piperazine at high pressures. J Chem Thermodyn 71:71–83. https://doi.org/10.1016/j.jct.2013.11.025
Hashemi A, Pajoum Shariati F, Sohani E, Azizi S, Hosseinifar SZ, Delavari Amrei H (2020) CO2 biofixation by Synechococcus elongatus from the power plant flue gas under various light–dark cycles. Clean Technol Environ Policy 22(8):1735–1743. https://doi.org/10.1007/s10098-020-01912-0
He Q, Yu G, Tu T, Yan S, Zhang Y, Zhao S (2017) Closing CO2 loop in biogas production: recycling ammonia as fertilizer. Environ Sci Technol 51(15):8841–8850. https://doi.org/10.1021/acs.est.7b00751
Hosseini-Ardali SM, Hazrati-Kalbibaki M, Fattahi M, Lezsovits F (2020) Multi-objective optimization of post combustion CO2 capture using methyldiethanolamine (MDEA) and piperazine (PZ) bi-solvent. Energy 211:119035. https://doi.org/10.1016/j.energy.2020.119035
Idem R, Wilson M, Tontiwachwuthikul P, Chakma A, Veawab A, Aroonwilas A, Gelowitz D (2006) Pilot plant studies of the CO2 capture performance of aqueous MEA and mixed MEA/MDEA solvents at the University of Regina CO2 capture technology development plant and the boundary dam CO2 capture demonstration plant. Ind Eng Chem Res 45(8):2414–2420. https://doi.org/10.1021/ie050569e
Isaacs EE, Otto FD, Mather AE (1977) Solubility of Hydrogen sulfide and carbon dioxide in an aqueous diisopropanolamine solution. J Chem Eng Data 22(1):71–73. https://doi.org/10.1021/je60072a004
Jahangiri A, Hassankiadeh MN (2019) Effects of piperazine concentration and operating conditions on the solubility of CO2 in AMP solution at low CO2 partial pressure. Sep Sci Technol 54(6):1067–1078. https://doi.org/10.1080/01496395.2018.1524907
Jiang K, Li K, Puxty G, Yu H, Feron PHM (2018) Information derivation from vapour–liquid equilibria data: a simple shortcut to evaluate the energy performance in an amine-based postcombustion CO2 capture. Environ Sci Technol 52(18):10893–10901. https://doi.org/10.1021/acs.est.8b03512
Jilvero H, Jens KJ, Normann F, Andersson K, Halstansen M, Eimer D, Johnsson F (2015) Equilibrium measurements of the NH3-CO2-H2O system—measurement and evaluation of vapour–liquid equilibrium data at low temperatures. Fluid Phase Equilib 385:237–247. https://doi.org/10.1016/j.fluid.2014.11.006
Jong IL, Otto FD, Mather AE (1972) Solubility of carbon dioxide in aqueous diethanolamine solutions at high pressures. J Chem Eng Data 17(4):465–468. https://doi.org/10.1021/je60055a015
Khodadadi MJ, Abbasi M, Riahi S, Shokrollahzadeh H (2019) Investigation on kinetics of carbon dioxide absorption in aqueous solutions of monoethanolamine + 1, 3-diaminopropane. Sep Sci Technol 54(17):2800–2808. https://doi.org/10.1080/01496395.2018.1553984
Kumar G, Kundu M (2012) Vapour-liquid equilibrium of CO2 in aqueous solutions of N-methyl-2-ethanolamine. Can J Chem Eng 90(3):627–630. https://doi.org/10.1002/cjce.20598
Kurz F, Rumpf B, Maurer G (1995) Vapor–liquid–solid equilibria in the system NH3CO2H2O from around 310 to 470 K: new experimental data and modelling. Fluid Phase Equilib 104(C):261–275. https://doi.org/10.1016/0378-3812(94)02653-I
Laribi S, Dubois L, De Weireld G, Thomas D (2019) Study of the post-combustion CO2 capture process by absorption-regeneration using amine solvents applied to cement plant flue gases with high CO2 contents. Int J Greenh Gas Control 90:102799. https://doi.org/10.1016/j.ijggc.2019.102799
Lawson JD, Garst AW (1976) Gas Sweetening data: equilibrium solubility of hydrogen sulfide and carbon dioxide in aqueous monoethanolamine and aqueous diethanolamine solutions. J Chem Eng Data 21(1):20–30. https://doi.org/10.1021/je60068a010
Lemoine B, Li YG, Cadours R, Bouallou C, Richon D (2000) Partial vapor pressure of CO2 and H2S over aqueous methyldiethanolamine solutions. Fluid Phase Equilib 172(2):261–277. https://doi.org/10.1016/S0378-3812(00)00383-6
Li MH, Shan KP (1992) Densities and solubilities of solutions of carbon dioxide in water + monoethanolamine + N-methyldiethanolamine. J Chem Eng Data 37(3):288–290. https://doi.org/10.1021/je00007a002
Li K, Feron PHM, Jiang K, Jones TW, Bennett RD, Hollenkamp AF, Pearson P (2018) Reaction enthalpy conversion in amine based PostCombustion CO2 capture. Chem Eng Trans 69:139–144. https://doi.org/10.3303/CET1869024
Liu H, Gao H, Idem R, Tontiwachwuthikul P, Liang Z (2017) Analysis of CO2 solubility and absorption heat into 1-dimethylamino-2-propanol solution. Chem Eng Sci 170:3–15. https://doi.org/10.1016/j.ces.2017.02.032
Lu R, Li K, Chen J, Yu H, Tade M (2017) CO2 capture using piperazine-promoted, aqueous ammonia solution: rate-based modelling and process simulation. Int J Greenh Gas Control 65:65–75. https://doi.org/10.1016/j.ijggc.2017.08.018
Mahmoodpour S, Rostami B, Emami-Meybodi H (2018) Onset of convection controlled by N2 impurity during CO2 storage in saline aquifers. Int J Greenh Gas Control 79:234–247. https://doi.org/10.1016/j.ijggc.2018.10.012
Martin J, Otto F, Mather A (1978) Solubility of hydrogen sulfide and carbon dioxide in a diglycolamine solution. J Chem Eng Data 23(2):163–164. https://doi.org/10.1021/je60077a001
Mathias PM (2016) The Gibbs−Helmholtz equation in chemical process technology. Ind Eng Chem Res 55(4):1076–1087. https://doi.org/10.1021/acs.iecr.5b03405
Mazari SA, Alaba P, Saeed IM (2019) Formation and elimination of nitrosamines and nitramines in freshwaters involved in post-combustion carbon capture process. J Environ Chem Eng 7(3):103111. https://doi.org/10.1016/j.jece.2019.103111
Mendez-Alvarez C, Plesu V, Bonet Ruiz AE, Bonet Ruiz J, Iancu P, Llorens J (2016) Distillation energy assessment for solvent recovery from carbon dioxide absorption. Comput Aided Chem Eng 38:1917–1922. https://doi.org/10.1016/B978-0-444-63428-3.50324-6
Merkel TC, Lin H, Wei X, Baker R (2010) Power plant post-combustion carbon dioxide capture: an opportunity for membranes. J Membr Sci 359(1–2):126–139. https://doi.org/10.1016/j.memsci.2009.10.041
Moioli S, Ho MT, Pellegrini LA, Wiley DE (2019) Application of absorption by potassium taurate solutions to post-combustion CO2 removal from flue gases with different compositions and flowrates. Chem Eng Trans 74:823–828. https://doi.org/10.3303/CET1974138
Morales-Mora MA, Pretelìn-Vergara CF, Martínez-Delgadillo SA, Iuga C, Nolasco-Hipolito C (2019) Environmental assessment of a combined heat and power plant configuration proposal with post-combustion CO2 capture for the Mexican oil and gas industry. Clean Technol Environ Policy 21(1):213–226. https://doi.org/10.1007/s10098-018-1630-3
Morgan JC, Soares Chinen A, Omell B, Bhattacharyya D, Tong C, Miller DC, Buschle B, Lucquiaud M (2018) Development of a rigorous modeling framework for solvent-based CO2 capture. Part 2: steady-state validation and uncertainty quantification with pilot plant data. Ind Eng Chem Res 57(31):10464–10481. https://doi.org/10.1021/acs.iecr.8b01472
Murrieta-Guevara F, Rebolledo-Libreros ME, Romero-Martınez A, Trejo A (1998) Solubility of CO2 in aqueous mixtures of diethanolamine with methyldiethanolamine and 2-amino-2-methyl-1-propanol. Fluid Phase Equilib 150–151:721–729. https://doi.org/10.1016/S0378-3812(98)00352-5
Nguyen T, Hilliard M, Rochelle GT (2010) Amine volatility in CO2 capture. Int J Greenh Gas Control 4(5):707–715. https://doi.org/10.1016/j.ijggc.2010.06.003
Nwaoha C, Tontiwachwuthikul P, Benamor A (2019) CO2 capture from water-gas shift process plant: comparative bench-scale pilot plant investigation of MDEA-PZ blend vs novel MDEA activated by 1,5-diamino-2-methylpentane. Int J Greenh Gas Control 82:218–228. https://doi.org/10.1016/j.ijggc.2019.01.009
Ong SH, Tan RR, Andiappan V (2020) Optimisation of biochar-based supply chains for negative emissions and resource savings in carbon management networks. Clean Technol Environ Policy. https://doi.org/10.1007/s10098-020-01990-0
Otsuka E, Yoshimura S, Yakabe M, Inoue S (1960) Equilibrium of the NH3–CO2–H2O system. Kogyo Kagaku Zasshi 62:1214–1218
Pacheco M, Kaganoi S, Rochelle GT (2000) CO2 absorption into aqueous mixtures of diglycolamine® and methyldiethanolamine. Chem Eng Sci 55(21):5125–5140. https://doi.org/10.1016/S0009-2509(00)00104-4
Papadopoulos AI, Badr S, Chremos A, Forte E, Zarogiannis T, Seferlis P, Papadokonstantakis S, Adjiman CS, Galindo A, Jackson G (2016) Computer-aided molecular design and selection of CO2 capture solvents considering thermodynamics. Mol Syst Des Eng 1:313–334. https://doi.org/10.1039/C6ME00049E
Papadopoulos AI, Tzirakis F, Tsivintzelis I, Seferlis P (2019) Phase-change solvents and processes for postcombustion CO2 capture: a detailed review. Ind Eng Chem Res 58(13):5088–5111. https://doi.org/10.1021/acs.iecr.8b06279
Papadopoulos AI, Shavalieva G, Papadokonstantakis S, Seferlis P, Perdomo FA, Galindo A, Jackson G, Adjiman CS (2020b) An approach for simultaneous computer-aided molecular design with holistic sustainability assessment: application to phase-change CO2 capture solvents. Comput Chem Eng 135:106769. https://doi.org/10.1016/j.compchemeng.2020.106769
Papadopoulos AI, Perdomo FA, Tzirakis F, Shavalieva G, Tsivintzelis I, Kazepidis P, Nessi E, Papadokonstantakis S, Seferlis P, Galindo A, Jackson G, Adjiman CS (2020a) Molecular engineering of sustainable phase-change solvents: from digital design to scaling-up for CO2 capture. Chem Eng J. https://doi.org/10.1016/j.cej.2020.127624
Park MK, Sandall OC (2001) Solubility of carbon dioxide and nitrous oxide in 50 mass % methyldiethanolamine. J Chem Eng Data 46(1):166–168. https://doi.org/10.1021/je000190t
Plesu V, Bonet J, Bonet-Ruiz AE, Chavarria A, Iancu P, Llorens J (2018) Surrogate model for carbon dioxide equilibrium absorption using aqueous monoethanolamine. Chem Eng Trans 70:919–924. https://doi.org/10.3303/CET1870154
Qi G, Wang S, Lu W, Yu J, Chen C (2015) Vapor–liquid equilibrium of CO2 in NH3–CO2–SO2–H2O system. Fluid Phase Equilib 386:47–55. https://doi.org/10.1016/j.fluid.2014.11.015
Ritchie H, Roser M (2020) CO2 and greenhouse gas emissions. Our World in Data https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Accessed 10 December 2020
Roberts BE, Mather AE (1988) Solubility of CO2 and H2S in a hindered amine solution. Chem Eng Commun 64(1):105–111. https://doi.org/10.1080/00986448808940230
Rosa LPS, Cruz N, Costa GMN, Pontes KV (2021) A comparative study of thermodynamic models to describe the VLE of the ternary electrolytic mixture H2O–NH3–CO2. In Press, Chem Prod Process Model. https://doi.org/10.1515/cppm-2020-0101
Sala M, Bonet J, Plesu V, Bonet-Ruiz AE, Iancu P, Llorens J (2014) Minimum gas/liquid flow rate for absorption columns. Chem Eng Trans 39:241–246. https://doi.org/10.3303/CET143904
Salman B, Nomanbhay S, Foo DCY (2019) Carbon emissions pinch analysis (CEPA) for energy sector planning in Nigeria. Clean Technol Environ Policy 21(1):93–108. https://doi.org/10.1007/s10098-018-1620-5
Seo DJ, Hong WH (1996) Solubilities of carbon dioxide in aqueous mixtures of diethanolamine and 2-amino-2-methyl-1-propanol. J Chem Eng Data 41(2):258–260. https://doi.org/10.1021/je950197o
Shavalieva G, Kazepidis P, Papadopoulos AI, Seferlis P, Papadokonstantakis S (2021) Environmental, health and safety assessment of post-combustion CO2 capture processes with phase-change solvents. Sustain Prod Consum 25:60–76. https://doi.org/10.1016/j.spc.2020.07.015
Sidi-Boumedine R, Horstmann S, Fischer K, Provost E, Fürst W, Gmehling J (2004) Experimental determination of carbon dioxide solubility data in aqueous alkanolamine solutions. Fluid Phase Equilib 218(1):85–94. https://doi.org/10.1016/j.fluid.2003.11.014
Śpiewak D, Krótki A, Spietz T, Stec M, Więcław-Solny L, Tatarczuk A, Wilk A (2015) PDU-scale experimental results of CO2 removal with Amp/Pz solvent. Chem Process Eng 36:39–48. https://doi.org/10.1515/cpe-2015-0003
Stec M, Tatarczuk A, Więcław-Solny L, Krótki A, Spietz T, Wilk A, Śpiewak D (2016) Demonstration of a post-combustion carbon capture pilot plant using amine-based solvents at the Łaziska power plant in Poland. Clean Technol Environ Policy 18(1):151–160. https://doi.org/10.1007/s10098-015-1001-2
Teng TT, Mather AE (1990) Solubility of CO2in an AMP solution. J Chem Eng Data 35(4):410–411. https://doi.org/10.1021/je00062a010
Thengane SK, Bandyopadhyay S (2020) Biochar mines: Panacea to climate change and energy crisis? Clean Technol Environ Policy 22(1):5–10. https://doi.org/10.1007/s10098-019-01790-1
Tong D, Trusler JPM, Maitland GC, Gibbins J, Fennell PS (2012) Solubility of carbon dioxide in aqueous solution of monoethanolamine or 2-amino-2-methyl-1-propanol: experimental measurements and modelling. Int J Greenh Gas Control 6:37–47. https://doi.org/10.1016/j.ijggc.2011.11.005
Tontiwachwuthikul P, Meisen A, Lim CJ (1991) Solubility of carbon dioxide in 2-amino-2-methyl-1-propanol solutions. J Chem Eng Data 36:130–133. https://doi.org/10.1021/je00001a038
Tzirakis F, Tsivintzelis I, Papadopoulos AI, Seferlis P (2019) Experimental measurement and assessment of equilibrium behaviour for phase change solvents used in CO2 capture. Chem Eng Sci 199:20–27. https://doi.org/10.1016/j.ces.2018.12.045
Verbrugge P (1973) Vapour–liquid equilibria of the ammonia–carbon dioxide–water system. Ph.D. Dissertation, Delft University
Wanderley RR, Evjen S, Pinto DDD, Knuutila HK (2018) The salting-out effect in some physical absorbents for CO2 capture. Chem Eng Trans 69:97–102. https://doi.org/10.3303/CET1869017
Xiao M, Liu H, Idem R, Tontiwachwuthiku P, Liang Z (2016) A study of structure–activity relationships of commercial tertiary amines for post-combustion CO2 capture. Appl Energy 184:219–229. https://doi.org/10.1016/j.apenergy.2016.10.006
Xiao M, Cui D, Yang Q, Liang Z, Puxty G, Yu H, Li L, Conway W, Feron P (2021) Role of mono- and diamines as kinetic promoters in mixed aqueous amine solution for CO2 capture. Chem Eng Sci 229:116009. https://doi.org/10.1016/j.ces.2020.116009
Xu Q, Rochelle GT (2011) Total pressure and CO2 solubility at high temperature in aqueous amines. Energy Procedia 4:117–124. https://doi.org/10.1016/j.egypro.2011.01.031
Yadav VG, Yadav GD, Patankar SC (2020) The production of fuels and chemicals in the new world: critical analysis of the choice between crude oil and biomass vis-à-vis sustainability and the environment. Clean Technol Environ Policy 22(9):1757–1774. https://doi.org/10.1007/s10098-020-01945-5
Yamada H (2021) Amine-based capture of CO2 for utilization and storage. Polym J 53(1):93–102. https://doi.org/10.1038/s41428-020-00400-y
Yang ZY, Soriano AN, Caparanga AR, Li MH (2010) Equilibrium solubility of carbon dioxide in (2-amino-2-methyl-1-propanol + piperazine + water). J Chem Thermodyn 42(5):659–665. https://doi.org/10.1016/j.jct.2009.12.006
Yu H, Morgan S, Allport A, Cottrell A, Do T, McGregor J, Wardhaugh L, Feron P (2011) Results from trialling aqueous NH3 based post-combustion capture in a pilot plant at Munmorah power station: absorption. Chem Eng Res Des 89:1204–1215. https://doi.org/10.1016/j.cherd.2011.02.036
Zarogiannis T, Papadopoulos AI, Seferlis P (2020a) Efficient selection of conventional and phase-change CO2 capture solvents and mixtures based on process economic and operating criteria. J Clean Prod 272:122764. https://doi.org/10.1016/j.jclepro.2020.122764
Zarogiannis T, Papadopoulos AI, Seferlis P (2020b) Off-design operation of conventional and phase-change CO2 capture solvents and mixtures: a systematic assessment approach. Appl Sci 10(15):5316. https://doi.org/10.3390/app10155316
Zhang P, Li M, Lv C, Zhang Y, Wang L, Fu D (2020a) Effect of partial pressure on CO2 absorption performance in piperazine promoted 2-diethylaminoethanol and 1-dimethylamino-2-propanol aqueous solutions. J Chem Thermodyn 150:106198. https://doi.org/10.1016/j.jct.2020.106198
Zhang R, Zhang Y, Cheng Y, Yu Q, Luo X, Li C, Li J, Zeng Z, Liu Y, Jiang X, Hu XE (2020b) New approach with universal applicability for evaluating the heat requirements in the solvent regeneration process for postcombustion CO2 capture. Ind Eng Chem Res 59(7):3261–3268. https://doi.org/10.1021/acs.iecr.9b05247
Acknowledgements
Author Alexandra Elena Plesu Popescu is a Serra Húnter fellow. The authors acknowledge the valuable contribution of master students Alan Chavarria, Diana Medina, Enric Selfa, Toni Peiró and Jesús García from University of Barcelona (Master of Environmental Engineering) for their support to the bibliographic review, data mining and surrogate model development during their master thesis research.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Plesu Popescu, A.E., González, À., Llorens, J. et al. Investigating best available technique for CO2 chemical absorption: solvent selection based on empirical surrogate model and exergy loss. Clean Techn Environ Policy 24, 333–350 (2022). https://doi.org/10.1007/s10098-021-02143-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10098-021-02143-7