Abstract
We study the convergence of a family of numerical integration methods where the numerical integration is formulated as a finite matrix approximation to a multiplication operator. For bounded functions, convergence has already been established using the theory of strong operator convergence. In this article, we consider unbounded functions and domains which pose several difficulties compared to the bounded case. A natural choice of method for this study is the theory of strong resolvent convergence which has previously been mostly applied to study the convergence of approximations of differential operators. The existing theory already includes convergence theorems that can be used as proofs as such for a limited class of functions and extended for a wider class of functions in terms of function growth or discontinuity. The extended results apply to all self-adjoint operators, not just multiplication operators. We also show how Jensen’s operator inequality can be used to analyse the convergence of an improper numerical integral of a function bounded by an operator convex function.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article, the aim is to theoretically analyse a class of numerical integration methods for approximate computation of integrals of the form
\(\Omega \subset {\mathbb {R}}^d,\) \(w: \Omega \rightarrow [0,\infty ),\) \(g: \Omega \rightarrow {\mathbb {R}},\) and \(f: {\mathbb {R}} \rightarrow {\mathbb {R}}.\) Without loss of generality, we assume that \(\int _{\Omega } w({\varvec{x}})\,d{\varvec{x}}=1.\) As we have recently shown in [1], numerical integration of (1) can be formulated as a finite matrix approximation of the multiplication operator as follows (see also [2,3,4,5]).
Let \(\langle \cdot ,\cdot \rangle \) be the inner product \(\langle \phi ,\psi \rangle = \int _{\Omega }\overline{\phi ({\varvec{x}})}\,\psi ({\varvec{x}})\, w({\varvec{x}})\,d{\varvec{x}} \) which defines the norm \(\Vert \phi \Vert =\sqrt{\langle \phi , \phi \rangle }\) so that \(\textsf {L}^2_w(\Omega )=\{\phi : \Vert \phi \Vert <\infty \}\) is a complete Hilbert space. Let \(\textsf {M} [g]\) be the multiplication operator of multiplying with the real function g, that is, \(\textsf {M} [g]\,\phi =g\,\phi \) almost everywhere for all \(\phi \in \textsf {D}(\textsf {M} [g])=\{\phi : \Vert g\,\phi \Vert <\infty \}.\) It then turns out that we can define the operator function \(f(\textsf {M} [g])\) which allows us to express the integral (1) as follows:
Let us then consider a finite-dimensional subspace of \(\textsf {L}^2_w(\Omega )\) spanned by orthonormal functions \(1=\phi _0,\phi _1,\phi _2,\ldots ,\phi _n\) and find the projection of the multiplication operator on this subspace (please note that the indexing starts from zero)
The operator function \(f(\textsf {M} [g])\) appearing in (2) can then be approximated via matrix function \(f({\varvec{M}}_n[g])\) which leads to the approximation
As shown in [1], when the inside function is \(g(x)=x\) and the basis functions are polynomials, we get the classical Gaussian quadratures.
In [1], convergence was considered only for bounded outside function f and a bounded inside function g. In this article, our goal is to extend the convergence results to unbounded functions. This allows us to consider improper integrals of functions that attain infinity at either or both endpoints of the integration interval. Our primary interest is in integrals, where infinity is attained at an infinite endpoint or at both endpoints \(\pm \infty .\) Proof of convergence for this type of integral is often considerably more complicated than for bounded functions on bounded intervals. See [6,7,8,9,10,11] for examples of proofs of convergence on unbounded intervals for Gaussian quadratures and Gaussian quadratures generalised on rational functions. Similar results have been proved also purely operator theoretically for Gaussian quadratures on unbounded intervals for polynomially bounded functions [3, Sections 1.8 and 1.13]. We generalise this operator theoretic approach on a larger family of inside functions g and basis functions and under some conditions to faster than polynomially growing outside functions f. We also consider improper integrals, where infinity is attained at a finite endpoint.
As a starting point, we take the strong resolvent convergence (or generalised strong convergence) [12,13,14,15,16] that gives well-known convergence results for continuous functions and characteristic functions. We extend these results to Riemann–Stieltjes integrable functions that are, by definition, bounded but can have infinitely many discontinuities. We also prove convergence results for a class of linearly bounded functions, that is, functions that are less than \(a+b\,|x|\) for some \(a,b>0.\) These results apply to general self-adjoint operators, not just multiplication operators and therefore also apply for more exotic integrals that it is possible to formulate as a function of a self-adjoint operator [17].
For Gaussian quadratures, the convergence proofs are often based on an inequality of the following type (e.g. [6, 7, 11, 8, Chapter IV], [9, Chapter 3, Lemma 1.5]):
that is, a Gaussian quadrature approximation with weights \(w_k\) and nodes \(x_k\) never exceeds the true value of the integral for even monomials \(x^{2\, m}.\) We do not have this type of inequality in general but in special cases when all matrix elements are positive. We give examples of such cases. In those cases, we can still prove convergence for certain fast-growing classes of functions such as exponentially bounded functions.
A similar inequality to (6) also arises from Jensen’s operator inequality when the outside function f is an operator convex function. We use this type of inequality to prove convergence of improper integrals, where infinity of the integrand is attained at a finite endpoint of the integration interval. This type of singularity has been studied in, for example, [18].
The main contributions of this article are:
-
1.
We use the theory of strong resolvent convergence for analysing the convergence of matrix method of numerical integration when the inside function is unbounded.
-
2.
We extend the theory of convergence for functions of self-adjoint operators in a converging sequence from continuous and bounded functions to wider classes of discontinuous and unbounded functions.
-
3.
We show theoretically and by a numerical example that convergence holds for a wider class of unbounded functions when the matrix elements are nonnegative.
-
4.
We also show the convergence of improper integrals on a finite endpoint for functions bounded by an operator convex function by using Jensen’s operator inequality.
The structure of the article is as follows: the key concepts are introduced in Sect. 2, the main results are presented in Sect. 3, numerical examples are presented in Sect. 4, and the conclusions are drawn in Sect. 5.
2 Preliminaries
A self-adjoint operator is such operator that \(\textsf {A} =\textsf {A} ^*.\) When a function g is a measurable real function, the maximal multiplication operator \(\textsf {M} [g],\) that is, the multiplication operator with domain \(\textsf {D}(\textsf {M} [g])=\{\phi : \Vert g\,\phi \Vert <\infty \},\) is self-adjoint.
We denote strong convergence as \(\textsf {A} _n\xrightarrow {s}\textsf {A} .\) Strong resolvent convergence of a sequence of self-adjoint operators \(\textsf {A} _n\) to a self-adjoint operator \(\textsf {A} ,\) means that \((\textsf {A} _n - z)^{-1}\xrightarrow {s}(\textsf {A} -z)^{-1}\) for some nonreal z, which we denote as \(\textsf {A} _n\xrightarrow {srs}\textsf {A} \) [12,13,14,15,16]. For a function of a self-adjoint operator, we have the following useful theorem about the convergence of functions of operators.
Theorem 1
If a sequence of self-adjoint operators \(\textsf {A} _n\) converges in strong resolvent sense to a self-adjoint operator \(\textsf {A} ,\) and f is a bounded continuous function defined on \({\mathbb {R}},\) then \(f(\textsf {A} _n)\) converges strongly to \(f(\textsf {A} ).\)
Proof
See [13, Theorem VIII.20 (b)], [15, Theorem 9.17] or [14, Theorem 11.4]. \(\square \)
The spectral representation of a self-adjoint operator is \( \textsf {A} = \int _{\sigma (\textsf {A} )}t\,d\textsf {E} (t), \) where \(\sigma (\textsf {A} )\) is the spectrum, and \(\textsf {E} (t)\) is the spectral family of the operator \(\textsf {A} \) [12,13,14,15,16, 19,20,21,22,23,24]. For any function which is measurable with respect to the spectral family, we have
The spectral family can be defined as left or right continuous for the parameter t in strong convergence sense [12, Chapter VI, Section 5.1]. We adopt the usual convention of defining it as right continuous. Only points of discontinuity of \(\textsf {E} (t)\) are the eigenvalues of \(\textsf {A} \) [15, Theorem 7.23]. An eigenvalue of an operator is a value \(\lambda \in {\mathbb {C}}\) that satisfies \( \lambda \,\phi =\textsf {A} \,\phi . \) Function \(\phi \) is called an eigenfunction or an eigenvector.
An eigenvalue \(\lambda \) of a multiplication operator \(\textsf {M} [g]\) has to satisfy [15, p. 103, Example 1]
for some set \(S\subset \{{\varvec{x}}\in \Omega : \lambda =g({\varvec{x}})\}\) and an eigenfunction has to be a scalar multiple of a characteristic function \(\chi _S({\varvec{x}}).\) The spectrum of the multiplication operator \(\sigma (\textsf {M} [g])\) for a real function g is the essential range of the function g [22, Problem 67], [13, Chapter VIII.3, Proposition 1], [15, p. 103, Example 1], that is,
For the convergence of the spectral families, we have the following theorem.
Theorem 2
Let \(\textsf {A} _n\) and \(\textsf {A} \) be self-adjoint operators with spectral families \(\textsf {E} _n(t)\) and \(\textsf {E} (t),\) respectively. If \(\textsf {A} _n\xrightarrow {srs}\textsf {A} ,\) then we have the following equivalent results :
-
1.
\(\textsf {E} _n(t)\xrightarrow {s}\textsf {E} (t)\) when t is not an eigenvalue of \(\textsf {A} .\)
-
2.
For characteristic functions, we have \(\chi _{[a,b]}(\textsf {A} _n)\xrightarrow {s}\chi _{[a,b]}(\textsf {A} )\) when a and b are not eigenvalues of \(\textsf {A} .\)
Proof
For 1, see [12, Chapter VIII, Theorem 1.15] or [15, Theorem 9.19]. For 2, see [13, Theorem VIII.24 (b)], [14, Theorem 11.4 e], or [16, Chapter 7.2, problem 5]. \(\square \)
A self-adjoint operator has an infinite matrix representation with matrix elements (3) if and only if the vectors of the orthonormal basis \(\phi _0,\phi _1,\ldots \) are dense in the underlying Hilbert space, and
for all \(i=0,1,\ldots \) (see [19, Theorem 3.4] or [21, Section 47]). For a multiplication operator \(\textsf {M} [g],\) this is equivalent to
for all \(i=0,1,\ldots .\)
If \(\textsf {A} \) is a self-adjoint operator with an infinite matrix representation \({\varvec{A}}_{\infty },\) then also \({\varvec{A}}_{\infty }\) is a self-adjoint operator on \(\ell ^2,\) the space of absolutely square-summable sequences. The domain of \({\varvec{A}}_{\infty }\) is \( \textsf {D}({\varvec{A}}_{\infty })= \left\{ {\varvec{v}}: \Vert {\varvec{A}}_{\infty }\,{\varvec{v}}\Vert <\infty \right\} \) which is isomorphic with \(\textsf {D}(\textsf {A} ).\)
Vectors \({\varvec{e}}_i\) have 1 in component i and 0 in other components. We use the same notation for \({\varvec{e}}_i\) in \({\mathbb {R}}^n\) or \(\ell ^2.\) Vector space \(\ell ^2_0\) is the space of finite linear combinations of \({\varvec{e}}_i\in \ell ^2.\) Matrix \({\varvec{I}}_n\) is an identity matrix in \({\mathbb {R}}^{n+1}\) and \({\varvec{I}}_{\infty }\) in \(\ell ^2.\) Infinite matrix of zeros is \({\varvec{0}}_{\infty },\) and \({\varvec{0}}_{n\times m}\) are \(n\times m\) matrices of zeros where n or m can be \(\infty .\)
2.1 Matrices with nonnegative elements
We define an elementwise partial order of matrices as \({\varvec{A}}\le {\varvec{B}},\) that is, \({\varvec{A}}\le {\varvec{B}}\) if \([{\varvec{A}}]_{i,j}\le [{\varvec{B}}]_{i,j}\) for all i, j. For functions of finite matrices with nonnegative elements, we introduce two classes of special interest [25, 26].
Definition 1
Let \(f:I\mapsto {\mathbb {R}}\) be a real function defined on an interval \(I\subset {\mathbb {R}}.\)
-
1.
f is m-positive if \(0\in I\) and \(f({\varvec{A}})\ge {\varvec{0}}\) for every symmetric \(n\times n\) matrix \({\varvec{A}}\ge {\varvec{0}}\) with spectrum contained in I, and every \(n\in {\mathbb {N}}.\)
-
2.
f is m-monotone if \({\varvec{A}}\le {\varvec{B}}\Rightarrow f({\varvec{A}})\le f({\varvec{B}}),\) for all symmetric \(n\times n\) matrices that satisfy \({\varvec{A}},{\varvec{B}}\ge {\varvec{0}}\) with spectra in I, and every \(n\in {\mathbb {N}}.\)
Under favorable conditions, the concepts of m-positive and m-monotone functions are equal as is shown by the following theorem.
Theorem 3
Let \(f:I\mapsto {\mathbb {R}}\) be a real function defined on an interval \(I\subset {\mathbb {R}}\) such that \(0\in I\) and \(f(0)\ge 0.\) Then f is m-positive if and only if it is m-monotone.
Proof
See [25, Theorem 2.1 (1)]. \(\square \)
On \([0,\infty )\) and \((-\infty ,\infty )\) intervals, all m-positive and hence m-monotone functions are absolutely monotone functions, that is, functions that have a converging power series expansion \(f(x)=\sum _{n=0}^\infty c_n\,x^n\) for \(n=0,1,2,\ldots \) and \(c_n\ge 0\) for all n [25,26,27].
2.2 Jensen’s operator inequality
For bounded operators, we say that a self-adjoint operator \(\textsf {A} \) is positive if \( 0 \le \langle \phi , \textsf {A} \,\phi \rangle \) for all \(\phi \) in the Hilbert space. We mark this as \(\textsf {A} \succeq 0.\) For bounded operators, we can use definition \(\textsf {A} \preceq \textsf {B} \) if \(0 \preceq \textsf {B} -\textsf {A} \) [12, 13, 28, 29]. For unbounded self-adjoint operators, we define \(\textsf {A} \preceq \textsf {B} \) if \(\langle {\text {sgn}}(\textsf {A} )\,\sqrt{|\textsf {A} |}\,\phi , \sqrt{|\textsf {A} |}\,\phi \rangle \le \langle {\text {sgn}}(\textsf {B} )\,\sqrt{|\textsf {B} |}\,\phi , \sqrt{|\textsf {B} |}\,\phi \rangle \) for all \(\phi \in \textsf {D}(\sqrt{|\textsf {B} |})\subset \textsf {D}(\sqrt{|\textsf {A} |})\) where \({\text {sgn}}(\cdot )\) is the sign function.
A real function f defined on an interval I is said to be operator convex for bounded operators if for all self-adjoint bounded operators \(\textsf {A} ,\textsf {B} \) with spectrum in I, for each \(\lambda \in [0,1],\) we have \( f(\lambda \,\textsf {A} +(1-\lambda )\,\textsf {B} )\preceq \lambda \, f(\textsf {A} )+(1-\lambda )\,f(\textsf {B} ) \) [28,29,30].
Operators \(f(\textsf {A} )\) and \(f(\textsf {B} )\) are bounded because operator convex functions are continuous.
The set of operator convex functions does not contain all convex functions. For example, for bounded operators on interval \(I=(0,\infty ),\) \(f(x)=x^p\) is operator convex for \(-1\le p\le 0\) and \(1\le p \le 2\) but not for \(p<-1,\) \(0< p < 1\) or \(2<p\) [29, Theorem 2.6].
For the proof of convergence of the matrix approximation for some integrals, we can use the following version of Jensen’s operator inequality [30, Theorem 2.1 (i) and (iv)]. For an operator convex function f defined on an interval I
for every orthogonal projection operator \(\textsf {P} \) and every bounded self-adjoint operator \(\textsf {A} \) defined on an infinite-dimensional Hilbert space with spectrum in I and every \(s\in I.\)
Another relevant concept is operator monotone functions [28, 29]. A real function f defined on interval I is operator monotone, if for all self-adjoint operators \(\textsf {A} ,\textsf {B} \) with spectrum on I, we have \( \textsf {A} \preceq \textsf {B} \Rightarrow f(\textsf {A} )\preceq f(\textsf {B} ). \)
For example, \(f(x)=-x^p\) is operator monotone for \(-1\le p \le 0\) on interval \(x\in (0,\infty )\) [29, Theorem 2.6]. The definition of operator monotone functions is the same for unbounded operators. Also, functions that are operator monotone for bounded operators on interval \((0,\infty )\) are operator monotone for unbounded positive self-adjoint operators [31, Theorem 5].
3 Convergence
We establish convergence for a growing class of outside functions f. We start by first proving the strong resolvent convergence that then immediately covers the bounded continuous outside functions in Sect. 3.1. Our first extension to this basic result is the class of discontinuous functions in Sect. 3.2.
Then we extend the results to unbounded functions. First, we discuss the topic of general unbounded outside functions in Sect. 3.3 and notice that it is a too wide class of functions to prove convergence in general. Then we find proof for a growing class of unbounded functions as the inside function g and basis functions \(\phi _i\) are polynomials. In Sect. 3.4, we prove convergence for quadratically bounded outside functions without restrictions to the inside function and polynomially bounded outside functions when the inside function and the basis functions are polynomials. In Sect. 3.5, we prove convergence for inside functions that have matrix representations with nonnegative coefficients. The outside functions do not even have to meet the criteria of being functions of operators that have infinite matrix representation.
Finally, we consider convergence for outside functions that are singular on a finite endpoint of an integration interval in Sect. 3.6.
3.1 Proof of the strong resolvent convergence
It can be difficult to prove directly that a sequence of self-adjoint operators converges in the strong resolvent sense. Therefore, we will introduce a concept of core that we can use to give proof of strong resolvent convergence.
Definition 2
A core \(\textsf {D}_0\) of an operator \(\textsf {A} \) is a subspace of the domain of the operator such that \( (\textsf {A} \vert _{\textsf {D}_0})^{**}=\textsf {A} . \)
Usually, the core is defined in terms of the closure of the operator [12, 13, 15, 16] but we note that for densely defined and closable operators, the closure is equivalent to the second adjoint [12, Chapter III, Theorem 5.29], [15, Theorem 5.3 (b)], [13, Theorem VIII.1 (b)] or [16, Theorem 7.1.1 (c)]. With a suitable core, the strong resolvent convergence can be proved by the following theorem.
Theorem 4
Let \(\textsf {D}_0\) be a core of self-adjoint operators \(\textsf {A} _n\) and \(\textsf {A} \) where \(n = 0,1,\ldots .\) If for each \(\phi \in \textsf {D}_0,\)
then \(\textsf {A} _n\xrightarrow {srs}\textsf {A} .\)
Proof
See [13, Theorem VIII.25 (a)] for proof, or [12, Chapter VIII, Corollary 1.6], [15, Theorem 9.16 (i)], or [16, Theorem 7.2.11] for proofs of similar but slightly more general theorems. \(\square \)
After finding a suitable core, we can prove the strong resolvent convergence. The space of absolutely square-summable sequences or infinite-dimensional vectors is \(\ell ^2.\) Its subspace \(\ell ^2_0\) is a space where vectors have only finitely many non-zero elements. It now turns out that \(\ell ^2_0\) is, in general, a core for any self-adjoint infinite matrix. Similar ideas related to infinite band matrices have been discussed in [32, 33]. A space which is isomorphic with \(\ell ^2_0\) has been used as a core without a proof that it is a core in [34]. A space that contains a space that is isomorphic with \(\ell ^2_0\) has also been used as a core in [35]. A proof that a vector space is a core for a certain operator can sometimes be very specialized [36, Lemma 4.4], but we present a very general proof that \(\ell ^2_0\) is a core for self-adjoint infinite matrices or equivalently a space that is isomorphic with \(\ell ^2_0\) is a core for a self-adjoint operator with infinite matrix representation.
Theorem 5
Let \(\textsf {A} \) be a self-adjoint operator with an infinite matrix representation \({\varvec{A}}_{\infty }.\) Then \(\ell ^2_0\) is a core for \({\varvec{A}}_{\infty }.\)
Proof
Our proof is an adaptation of proof of [15, Theorem 6.20]. We use the following property of the adjoint:
-
Let \(\textsf {A} \) and \(\textsf {B} \) be densely defined operators, then \(\textsf {D}(\textsf {A} )\subset \textsf {D}(\textsf {B} )\) and \(\textsf {A} =\textsf {B} \vert _{\textsf {D}(\textsf {A} )}\) \(\Rightarrow \) \(\textsf {D}(\textsf {B} ^*)\subset \textsf {D}(\textsf {A} ^*)\) and \(\textsf {B} ^*=\textsf {A} ^*\vert _{\textsf {D}(\textsf {B} ^*)},\) that is,
$$\begin{aligned} \textsf {A} \subset \textsf {B} \Rightarrow \textsf {B} ^*\subset \textsf {A} ^*. \end{aligned}$$(13)
Let operator \(\textsf {A} _0={\varvec{A}}_{\infty }\vert _{\ell ^2_0}.\) The natural basis vectors of \(\ell ^2\) are vectors \({\varvec{e}}_i.\) Vectors of \(\ell ^2_0\) are finite linear combinations of basis vectors \({\varvec{e}}_i.\) Because all basis vectors \({\varvec{e}}_i\in \textsf {D}({\varvec{A}}_{\infty }),\) we also have \(\ell ^2_0\subset \textsf {D}({\varvec{A}}_{\infty }).\) Therefore, we have \(\textsf {A} _0\subset {\varvec{A}}_{\infty }.\) By (13), we have \({\varvec{A}}_{\infty }^*\subset \textsf {A} _0^*.\) Because \({\varvec{A}}_{\infty }\) is self-adjoint, we have \({\varvec{A}}_{\infty }={\varvec{A}}_{\infty }^*\subset \textsf {A} _0^*.\) We show that also \(\textsf {A} _0^*\subset {\varvec{A}}_{\infty },\) that is, \( \textsf {D}(\textsf {A} _0^*) \subset \textsf {D}({\varvec{A}}_{\infty }) = \{{\varvec{u}}: \Vert {\varvec{A}}_{\infty }\,{\varvec{u}}\Vert ^2<\infty \} \) and \(\textsf {A} _0^*={\varvec{A}}_{\infty }\vert _{\textsf {D}(\textsf {A} _0^*)}.\) Let \({\varvec{u}}\in \textsf {D}(\textsf {A} _0^*)\) and thus \(\Vert \textsf {A} _0^*\,{\varvec{u}}\Vert ^2<\infty .\) Because \({\varvec{e}}_k\in \textsf {D}(\textsf {A} _0),\) we have for all \(k=0,1,\ldots \)
We square and sum over k
that is, \({\varvec{u}}\in \textsf {D}(\textsf {A} _0^*)\Rightarrow {\varvec{u}}\in \textsf {D}({\varvec{A}}_{\infty }).\) By (14) we also have for any \({\varvec{u}}\in \textsf {D}(\textsf {A} _0^*)\)
that is, \(\textsf {A} _0^*={\varvec{A}}_{\infty }\vert _{\textsf {D}(\textsf {A} _0^*)}.\) Because we have \({\varvec{A}}_{\infty }\subset \textsf {A} _0^*\) and \(\textsf {A} _0^*\subset {\varvec{A}}_{\infty },\) we have \(\textsf {A} _0^*={\varvec{A}}_{\infty }.\) Therefore, we also have \(\textsf {A} _0^{**}={\varvec{A}}_{\infty }^*={\varvec{A}}_{\infty }.\) \(\square \)
After discovering the core, it is straightforward to prove the strong resolvent convergence.
Theorem 6
Let \(\textsf {A} \) be a self-adjoint operator with an infinite matrix representation \({\varvec{A}}_{\infty }.\) Let finite matrices \({\varvec{A}}_n\) be the leading principal \((n+1)\times (n+1)\) submatrices of \({\varvec{A}}_{\infty }.\) Then for any \({\varvec{v}}\in \ell ^2_0,\)
because \({\varvec{\tilde{A}}}_n\,{\varvec{v}}\rightarrow {\varvec{A}}_{\infty }\,{\varvec{v}}\) as \(n\rightarrow \infty .\)
Proof
We define an orthonormal projection
With this projection, we can write \({\varvec{\tilde{A}}}_n={\varvec{P}}_n\,{\varvec{A}}_{\infty }\,{\varvec{P}}_n.\) We take an arbitrary vector in the core \({\varvec{v}}\in \ell ^2_0.\) Let m be the last index where components of \({\varvec{v}}\) are non-zero, that is, \(v_i=0\) for all \(i>m.\) For all \(n>m,\) we have \({\varvec{P}}_n\,{\varvec{v}}={\varvec{v}},\) and thus \(({\varvec{\tilde{A}}}_n-{\varvec{A}}_{\infty })\,{\varvec{v}}=({\varvec{P}}_n-{\varvec{I}}_{\infty })\,{\varvec{A}}_{\infty }\,{\varvec{v}}.\) Vector \({\varvec{u}}={\varvec{A}}_{\infty }\,{\varvec{v}}\in \ell ^2,\) and therefore we have \(({\varvec{P}}_n-{\varvec{I}}_{\infty })\,{\varvec{u}}\rightarrow {\varvec{0}}\) as \(n\rightarrow \infty .\) The strong resolvent convergence in (15) follows from Theorem 5. \(\square \)
From this, we already have convergence for bounded and continuous functions.
Theorem 7
Let orthonormal functions \(\phi _0=1,\phi _1,\phi _2,\ldots \) be dense in \(\textsf {L}^2_w(\Omega ).\) Also, let function g satisfy (11) and matrices \({\varvec{M}}_n[g]\) have elements as in (3). Then for bounded and continuous f
and, as \(n\rightarrow \infty ,\)
Proof
By Theorem 6, we have \({\varvec{P}}_n\,{\varvec{M}}_{\infty }[g]\,{\varvec{P}}_n\xrightarrow {srs}{\varvec{M}}_{\infty }[g]\) where \({\varvec{P}}_n\) is as in (16). The convergence of (17) follows from Theorem 1. The convergence of the quadratic form \({\varvec{e}}_o^\top \,f({\varvec{M}}_n[g])\,{\varvec{e}}_0\rightarrow {\varvec{e}}_0^\top \,f({\varvec{M}}_{\infty }[g])\,{\varvec{e}}_0\) is a special case of the weak convergence that follows from the strong convergence (17). \(\square \)
This result already extends the previous result [1, Theorem 3] for inside functions from bounded functions g to unbounded functions g. However, our aim is to further extend the results to discontinuous and unbounded outside functions f as well.
3.2 Convergence for discontinuous functions
First, we consider convergence when the integrand function f in (4) is bounded but discontinuous. The largest space of discontinuous functions that are possible to integrate numerically are the Riemann–Stieltjes integrable functions. It does not seem to be possible to obtain convergence results for a larger set of functions like, for example, Lebesgue–Stieltjes integrable functions [37, Chapter 1.8]. Similar arguments rule out convergence for Borel or Baire measurable functions that are not Riemann–Stieltjes integrable. When the starting point is a Borel measure, the largest set of discontinuous functions that the convergence theorem covers seem to be functions that are discontinuous on a set that is contained in a closed set which has zero measure with respect to the spectral family of the operator [38, Theorem 2.6], [39, 40, Theorem 3] or [1, Theorem 3]. These convergence theorems do not then cover, for example, Thomae’s function [41, Example 7.1.6] which is discontinuous on rational numbers but is Riemann–Stieltjes integrable. The definition of the Riemann- and the related Darboux–Stieltjes integrals are given in Appendix A.
The spectral integral is usually defined as a Borel or a Baire measure. One example of spectral integral as a Riemann–Stieltjes integral can be found in [24, Chapter 4.1]. However, the Riemann–Stieltjes integral is defined there in norm operator topology, and we will rather make the definition in strong operator topology because the finite matrix approximations can converge in norm only if the operator is compact [22, Problem 175], [42, Theorem 1.2] and the function space defined in the norm operator topology can only be a subset of the space defined in the strong operator topology. We define the spectral integral as Darboux–Stieltjes integral in the same manner as it is defined as Lebesgue–Stieltjes integral in [20, Section 126]. The Riemann–Stieltjes integral is then the same as the Darboux–Stieltjes integral except limited to functions that are continuous at the discontinuities of the spectral family. We can define a non-decreasing function \(\rho (t)\) through the spectral family as \(\rho (t)=\Vert \textsf {E} (t)\,\phi \Vert ^2\) for any \(\phi \) in the Hilbert space. Because operators \(\textsf {E} (t)\) are projections, \(\Vert \textsf {E} (t)\,\phi \Vert ^2=\langle \phi ,\textsf {E} (t)\,\phi \rangle .\) Thus, we can define
as a Darboux–Stieltjes integral. We say that a function f is Darboux–Stieltjes integrable with respect to \(\Vert \textsf {E} (t)\,\phi \Vert ^2\) if the Darboux–Stieltjes integral exists.
We can use polarization identity [20, Section 126]
to define Darboux–Stieltjes integral with respect to \(\rho (t)=\langle \phi ,\textsf {E} (t)\,\psi \rangle \) as a linear combination of four Darboux–Stieltjes integrals. Finally, if f is Darboux–Stieltjes integrable with respect to \(\Vert \textsf {E} (t)\,\phi \Vert ^2\) for all \(\phi \) in the Hilbert space, then we say that f is Darboux–Stieltjes integrable with respect to \(\textsf {E} (t).\)
We aim to extend the convergence of Theorem 1 for continuous functions to Darboux– or Riemann–Stieltjes integrable functions. We start by proving the equivalent of Theorem 1 for step functions.
Lemma 8
Let \(\textsf {A} _n\) and \(\textsf {A} \) be self-adjoint operators with spectral families \(\textsf {E} _n(t)\) and \(\textsf {E} (t),\) respectively, for \(n=0,1,2,\ldots .\) If \(\textsf {A} _n\xrightarrow {srs}\textsf {A} ,\) then for a step function \(f(\textsf {A} _n)\xrightarrow {s}f(\textsf {A} )\) provided that discontinuity points of f are not eigenvalues of \(\textsf {A} .\)
Proof
A step function can be represented as a finite linear combination of characteristic functions. By Theorem 2, the convergence is strong for each characteristic function. A finite linear combination of operators that converge strongly also converges strongly [23, Chapter 4.9, Problem 2]. \(\square \)
Next, we extend convergence from step functions to Darboux–Stieltjes integrable functions.
Theorem 9
Let \(\textsf {A} _n\) and \(\textsf {A} \) be self-adjoint operators with spectral families \(\textsf {E} _n(t)\) and \(\textsf {E} (t),\) respectively, for \(n=0,1,2,\ldots .\) Let function f be continuous on eigenvalues of \(\textsf {A} .\) Let \(\textsf {A} _n\xrightarrow {srs}\textsf {A} .\) Then the following statements hold :
-
1.
If f(t) is Darboux–Stieltjes integrable with respect to \(\rho (t)=\Vert \textsf {E} (t)\,\phi \Vert ^2,\) then
$$\begin{aligned} \lim _{n\rightarrow \infty }\langle \phi , f(\textsf {A} _n)\,\phi \rangle =\langle \phi , f(\textsf {A} )\,\phi \rangle . \end{aligned}$$ -
2.
If f(t) is Darboux–Stieltjes integrable with respect to \(\rho (t)=\langle \psi ,\textsf {E} (t)\,\phi \rangle ,\) then
$$\begin{aligned} \lim _{n\rightarrow \infty }\langle \psi , f(\textsf {A} _n)\,\phi \rangle =\langle \psi , f(\textsf {A} )\,\phi \rangle . \end{aligned}$$ -
3.
If f(t) is Darboux–Stieltjes integrable with respect to \(\textsf {E} (t),\) then \( f(\textsf {A} _n)\xrightarrow {s}f(\textsf {A} ). \)
Proof
For the proof of statement 1, we take the idea from [37, Chapter 2.7.8]. We assume that f is Darboux–Stieltjes integrable with respect to \(\rho (t)=\Vert \textsf {E} (t)\,\phi \Vert ^2.\) We define step functions \(f_l\) and \(f_u\) as in Lemma 31. By Lemma 31, we can also select \(f_l\) and \(f_u\) so that they are continuous at eigenvalues of \(\textsf {A} .\) By Lemma 8, we have \( f_l(\textsf {A} _n)\xrightarrow {s}f_l(\textsf {A} )\) and \( f_u(\textsf {A} _n)\xrightarrow {s}f_u(\textsf {A} ).\) Because strong convergence implies weak convergence, we have also
We see from the definition of \(f_l\) and \(f_u\) in Lemma 31 that because, for example,
we have
and
as well. By Lemma 31 we also have \(\langle \phi , (f_u(\textsf {A} )-f_l(\textsf {A} ))\,\phi \rangle <\epsilon ,\) and thus, we get the following inequalities:
By [43, Theorem 3.17 (b)], there is N so that for all \(n\ge N\),
and hence \( \langle \phi , f(\textsf {A} _n)\,\phi \rangle \rightarrow \langle \phi , f(\textsf {A} )\,\phi \rangle \) as \(n\rightarrow \infty .\)
The proof of statement 2 follows from 1 by the polarization identity (18). For the proof of statement 3, we take an arbitrary \(\phi ,\) and set \(\psi =f(\textsf {A} )\,\phi .\) Then
as \(n\rightarrow \infty \) because \(f^2\) is Darboux–Stieltjes integrable when f is [43, Theorem 6.13]. \(\square \)
By this theorem, we can extend the convergence of (17) to functions f that are discontinuous but Darboux–Stieltjes integrable with respect to \(\textsf {E} (t).\) As noted in [1, Theorem 4], because we have strong convergence, we also have convergence for numerical integrals of products of functions (5) when all the functions are Darboux–Stieltjes integrable.
It is good to note that the eigenvalues of \(\textsf {A} \) are the only points of discontinuity of the family \(\textsf {E} (t),\) and points of continuity \(t_0\) of \(\textsf {E} (t)\) are also the points of continuity for \(\rho (t)=\langle \phi ,\textsf {E} (t)\,\psi \rangle .\) The reason for this is because, by definition, \(\textsf {E} (t)\xrightarrow {s}\textsf {E} (t_0)\) when \(t\rightarrow t_0.\) Strong convergence implies weak convergence [12, 13, 15, 16, 20, 21, 23], which means that \(\langle \phi ,\textsf {E} (t)\,\psi \rangle \rightarrow \langle \phi ,\textsf {E} (t_0)\,\psi \rangle \) for all \(\phi ,\psi \) in the Hilbert space. It is still possible that for some \(\phi \) and \(\psi ,\) \(\langle \phi , \textsf {E} (t)\,\psi \rangle \) is continuous at some points that are eigenvalues of \(\textsf {A} \) and hence where \(\textsf {E} (t)\) is not continuous.
If a function f is Riemann–Stieltjes integrable with respect to \(\rho (t)=\Vert \textsf {E} (t)\,\phi \Vert \) for all \(\phi ,\) then f must be continuous on all eigenvalues of \(\textsf {A} \) [44, p. 251]. Then we can say that f is Riemann–Stieltjes integrable with respect to \(\textsf {E} (t)\) or with respect to \(\textsf {A} .\) By Theorem 9 statement 3, we always have convergence for Riemann–Stieltjes integrable functions. Therefore, we notice that Riemann–Stieltjes integrability is a suitable criterion for convergence in terms of discontinuity of the function. In order to have a discontinuity criterion for unbounded functions alike, we extend the definition of Riemann–Stieltjes integrability in the following manner.
Definition 3
Function f is Riemann–Stieltjes integrable with respect to self-adjoint operator \(\textsf {A} \) if f is Riemann–Stieltjes integrable with respect to the spectral family of \(\textsf {A} \) over any finite interval with endpoints that are not eigenvalues of \(\textsf {A} .\)
If an unbounded function f is Riemann–Stieltjes integrable with respect to self-adjoint operator \(\textsf {A} ,\) then for all \(\phi \in \textsf {D}(\textsf {A} ),\) there exists \(f(\textsf {A} )\,\phi =\int _{-\infty }^\infty f(t)\,d\textsf {E} (t)\,\phi \) as an improper integral that is a limit of Riemann–Stieltjes integrals over a finite interval.
3.3 Strong resolvent convergence for unbounded functions
We can now show that an unbounded function of an operator converges in the strong resolvent sense. However, as discussed below the result of this theorem looks more useful than it actually is.
Theorem 10
Let \(\textsf {A} _n\) and \(\textsf {A} \) be self-adjoint operators, and let f be such a continuous real function defined on \({\mathbb {R}}\) that \(f(\textsf {A} _n)\) and \(f(\textsf {A} )\) are densely defined. Then
Proof
Operators \(\textsf {B} _n=f(\textsf {A} _n)\) and \(\textsf {B} =f(\textsf {A} )\) are self-adjoint. Function \( \tilde{f}(x)=(f(x)-z)^{-1} \) is bounded and continuous for nonreal z. By Theorem 1, \(\tilde{f}(\textsf {A} _n)\xrightarrow {s}\tilde{f}(\textsf {A} ),\) and we have \( (\textsf {B} _n-z)^{-1}=\tilde{f}(\textsf {A} _n) \xrightarrow {s}\tilde{f}(\textsf {A} )=(\textsf {B} -z)^{-1}, \) which means by definition of the strong resolvent convergence that \(f(\textsf {A} _n)=\textsf {B} _n\xrightarrow {srs}\textsf {B} = f(\textsf {A} ).\) \(\square \)
It is now important to note that although the above theorem ensures strong resolvent convergence, it does not guarantee convergence of the inner product \(\langle \phi , f(\textsf {A} _n)\,\phi \rangle ,\) which is what we want. It only guarantees the existence of a sequence \(\phi _n\rightarrow \phi ,\) for which \(\langle \phi , f(\textsf {A} _n)\,\phi _n\rangle \) converges, as is shown by the following theorem.
Theorem 11
Let self-adjoint operators \(\textsf {A} _n\) and \(\textsf {A} \) be such that \(\textsf {A} _n\xrightarrow {srs}\textsf {A} .\) Then for each \(\phi \in \textsf {D}(\textsf {A} ),\) there is a sequence \(\phi _n\in \textsf {D}(\textsf {A} _n)\) such that \( \Vert \phi _n-\phi \Vert +\Vert \textsf {A} _n\,\phi _n-\textsf {A} \,\phi \Vert \rightarrow 0 \) as \(n\rightarrow \infty . \)
Proof
See [45, Satz (14)]. \(\square \)
An example sequence of \(\phi _n\) is \(\phi _n=(\textsf {A} _n-z)^{-1}\,(\textsf {A} -z)\,\phi ,\) where z is any nonreal number. For nonreal z, the sequence \(\phi _n\) is not real-valued. However, it is often possible to find a real vector sequence \((\phi _n)\) based on a dominating function \(h^2\ge |f|\) such that \(\langle \phi _n,f(\textsf {A} _n)\,\phi _n\rangle \rightarrow \langle \phi ,\textsf {A} \,\phi \rangle .\) In the case of numerical integration, this changes the construction of the weights of the quadrature rule so that they are based on the function sequence \((\phi _n)\) instead of a fixed function \(\phi ,\) but the convergence of such quadrature can be proved as is shown by the following theorem.
Theorem 12
Let self-adjoint operators \(\textsf {A} _n\) and \(\textsf {A} \) be such that \(\textsf {A} _n\xrightarrow {srs}\textsf {A} .\) Let f and h be Riemann–Stieltjes integrable functions with respect to \(\textsf {A} \) so that \(|f({\varvec{x}})|\le h^2({\varvec{x}}),\) and \(h^2({\varvec{x}})\ge c > 0\) for all \(x\in \sigma (\textsf {A} )\cap \sigma (\textsf {A} _n).\) For \(\phi \in \textsf {D}(h(\textsf {A} )),\) as \(n\rightarrow \infty ,\)
and hence
Proof
Function \(q({\varvec{x}})=\frac{f({\varvec{x}})}{h^2({\varvec{x}})}\) is bounded so that \(|q({\varvec{x}})|\le 1.\) Function q is Riemann–Stieltjes integrable [43, Theorems 6.11 and 6.13]. Therefore, the operators \(\textsf {B} _n=(h(\textsf {A} _n))^{-1}\,f(\textsf {A} _n)\, (h(\textsf {A} _n))^{-1}\) are bounded, operator norm \(\Vert \textsf {B} _n\Vert \le 1\) and
Because \(\phi \in \textsf {D}(h(\textsf {A} )),\) the result follows. \(\square \)
Remark 1
This theorem suggests us a new form of convergent quadrature rule. If we can compute the Fourier coefficients \(\tilde{v}_i=\langle \phi _i, h\rangle ,\) using the above theorem, we can construct a sequence of convergent quadrature rules
where vector \({\varvec{\tilde{v}}}_n=(h({\varvec{M}}_n[g]))^{-1}\,{\varvec{\tilde{v}}},\) and components of vector \({\varvec{\tilde{v}}}\) are \(\tilde{v}_i\) respectively. The nodes are then the eigenvalues \(\lambda _j\) of each finite matrix approximation \({\varvec{M}}_n[g]\) and the weights are
where \({\varvec{\tilde{u}}}_j\) are the unit length eigenvectors of \({\varvec{M}}_n[g]\) corresponding to the eigenvalues \(\lambda _j\) respectively. The numerical integral of (4) is a special case of this approach with \(h=1.\) We give a numerical example of the effects of this theorem in practice in Sect. 4.
3.4 Convergence for quadratically bounded functions
For convergence without an approximating sequence for vectors \(\phi \in \textsf {D}(f(\textsf {A} )),\) we can prove a limited form of convergence for a limited class of unbounded functions.
The following theorem shows that if we can show convergence for one function, it will follow for all smaller functions.
Theorem 13
Let \(\textsf {A} _n\) and \(\textsf {A} \) be self-adjoint operators such that \(\textsf {A} _n\xrightarrow {srs}\textsf {A} .\) Let f and h be such unbounded functions that they are Riemann–Stieltjes integrable with respect to \(\textsf {A} ,\) \(|f(x)|\le |h(x)|\) for all \(x\in {\mathbb {R}}\) and f and h are continuous at eigenvalues of \(\textsf {A} .\) Then for any \(\phi \in \textsf {D}(h(\textsf {A} ))\)
Proof
This follows from [7, Théorème 3]. \(\square \)
The following lemma makes it possible to show not only the convergence of the norms of the vectors but the vectors themselves as well.
Lemma 14
Let self-adjoint operators \(\textsf {A} _n\) converge in the strong resolvent sense to self-adjoint operator \(\textsf {A} .\) Let function \(h:~{\mathbb {R}}\mapsto {\mathbb {C}}\) and vector \(\phi \in \textsf {D}(h(\textsf {A} )) \cap _{n=0}^\infty \textsf {D}(h(\textsf {A} _n)).\) If \(\Vert h(\textsf {A} _n)\,\phi \Vert \rightarrow \Vert h(\textsf {A} )\,\phi \Vert ,\) then also \(h(\textsf {A} _n)\,\phi \rightarrow h(\textsf {A} )\,\phi \) as \(n\rightarrow \infty .\)
Proof
Let \(\textsf {E} (t)\) and \(\textsf {E} _n(t)\) be the spectral families of \(\textsf {A} \) and \(\textsf {A} _n,\) respectively. We can select an interval I with endpoints that are not eigenvalues of \(\textsf {A} \) such that
Because \(\textsf {A} _n\xrightarrow {srs}\textsf {A} ,\) for all \(\epsilon > 0,\) there is an \(N_1\) such that for all \(k>N_1,\) we have
and
The convergence of \(\Vert h(\textsf {A} _n)\,\phi \Vert \rightarrow \Vert h(\textsf {A} )\,\phi \Vert \) means that for all \(\epsilon > 0,\) there is an \(N_2\) such that for all \(k>N_2,\) we have
which means by (20) and (21) that
for all \(k>M=\max (N_1,N_2).\) By (20), (22), and (23) we have
for all \(k>M.\) \(\square \)
Theorem 15
Let \(\textsf {A} _n\) and \(\textsf {A} \) be self-adjoint operators such that \(\textsf {A} _n\xrightarrow {srs}\textsf {A} .\) Let f and h be such unbounded functions that they are Riemann–Stieltjes integrable with respect to \(\textsf {A} ,\) \(|f(x)|\le |h(x)|\) for all \(x\in {\mathbb {R}}\) and f and h are continuous at eigenvalues of \(\textsf {A} .\) Then for any \(\phi \in \textsf {D}(h(\textsf {A} ))\)
Proof
This follows from Theorem 13 and Lemma 14 by using identity \(\Vert f(\textsf {A} )\,\phi \Vert ^2= \langle \phi , |f(\textsf {A} )|^2\,\phi \rangle \) for functions f and h. \(\square \)
For example, we can apply this theorem to linearly bounded functions.
Theorem 16
Let operator \(\textsf {A} \) be self-adjoint with an infinite matrix representation \({\varvec{A}}_{\infty }\) and vector \({\varvec{v}}\in \ell ^2_0.\) Let finite approximations be \( \left[ {\varvec{A}}_n \right] _{i,j} = \left[ {\varvec{A}}_{\infty } \right] _{i,j}\) and \( [{\varvec{v}}_n]_i = [{\varvec{v}}]_i\) for \(i,j=0,1,\ldots ,n.\) Let function f be Riemann–Stieltjes integrable with respect to \(\textsf {A} \) and linearly bounded, that is, for all \(x\in {\mathbb {R}},\) \(|f(x)|\le a + b\,|x|\) for some positive a and b. Then, as \(n\rightarrow \infty ,\)
Proof
By Theorem 6, convergence holds for function \(h(x) = x,\) and by Theorem 15, for function \(h(x)=|x|.\) Convergence then holds also for function \(h(x) = b\,|x|,\) for \(h(x) = a+b\,|x|,\) and again by Theorem 15, for f(x). \(\square \)
We can apply this theorem to a product of two linearly bounded functions.
Theorem 17
Let self-adjoint operators \(\textsf {A} \) and \(\textsf {B} \) have infinite matrix representations \({\varvec{A}}_{\infty }\) and \({\varvec{B}}_{\infty }.\) Furthermore, let vectors \({\varvec{u}},{\varvec{v}}\in \ell ^2_0\) and finite approximations have the elements
for \(i,j=0,1,\ldots ,n.\) Then for linearly bounded \(f_1,f_2\) that are Riemann–Stieltjes integrable with respect to \(\textsf {A} \) and \(\textsf {B} \) respectively, as \(n\rightarrow \infty ,\) we have
Proof
This follows from Theorem 16 and the property that in a Hilbert space, if \({\varvec{x}}_n\rightarrow {\varvec{x}}\) and \({\varvec{y}}_n\rightarrow {\varvec{y}}\) then \(\langle {\varvec{x}}_n,{\varvec{y}}_n\rangle \rightarrow \langle {\varvec{x}},{\varvec{y}}\rangle \) [20, p. 199] or [23, Lemma 3.2-2]. \(\square \)
We can now apply this theorem to quadratically bounded functions.
Theorem 18
Let self-adjoint operator \(\textsf {A} \) have infinite matrix representation \({\varvec{A}}_{\infty }.\) Let vectors \({\varvec{u}},{\varvec{v}}\in \ell ^2_0,\) and let finite approximations have the elements
for \(i,j=0,1,\ldots ,n.\) Let function f be Riemann–Stieltjes integrable with respect to \(\textsf {A} \) and quadratically bounded, that is, for all \(x\in {\mathbb {R}},\) \(|f(x)|\le a + b\,x^2,\) for some positive a and b. Then \( {\varvec{u}}_n^*\, f\left( {\varvec{A}}_n \right) \, {\varvec{v}}_n \rightarrow {\varvec{u}}^*\,f({\varvec{A}}_{\infty })\,{\varvec{v}} \) as \(n\rightarrow \infty .\)
Proof
This follows from Theorem 17 by selecting \(\textsf {A} =\textsf {B} ,\) \(f_1={\text {sgn}}(f)\,\sqrt{|f|}\) and \(f_2=\sqrt{|f|}.\) The product function \(f_1\,f_2\) is Riemann–Stieltjes integrable by [43, Theorem 6.11 and 6.13]. \(\square \)
For the convergence of the numerical approximation of integrals as in (4) and (5), we then have the following theorem.
Theorem 19
Let orthonormal functions \(\phi _0=1,\phi _1,\phi _2,\ldots \) be dense in \(\textsf {L}^2_w(\Omega ).\) Let function g satisfy (11) and let matrices \({\varvec{M}}_n[g]\) have elements as in (3). Further, let quadratically bounded function f be Riemann–Stieltjes integrable with respect to \(\textsf {M} [g].\) Then
Similarly, for functions \(g_1\) and \(g_2\) satisfying (11) and linearly bounded \(f_1\) and \(f_2,\) we have
Proof
The result follows from Theorems 17 and 18. \(\square \)
We can extend this result to polynomially bounded functions in the special case that the inside function g and the basis functions are polynomials. We define the total degree of a multivariate monomial \(\prod _{i=0}^d x_i^{n_i}\) as \(\sum _{i=0}^d n_i.\) Then for a polynomial, that is, a finite linear combination of monomials, its total degree is the total degree of the highest monomial. If polynomials are dense in a Hilbert space, they can be partially ordered according to the total degree of the polynomials, for example, in graded lexicographic order [46, Chapter 3.1].
Theorem 20
Let the orthonormal polynomials \(\phi _0,\phi _1,\phi _2,\ldots \) be partially ordered by their total degree and dense in \(\textsf {L}^2_w(\Omega ).\) Let the function g be polynomial and let the matrices \({\varvec{M}}_n[g]\) have elements as in (3). Let a function f be polynomially bounded that is, \(f(x)\le a + b\,|x|^m\) for some positive a, b and \(m\in {\mathbb {N}},\) then
if f is Riemann–Stieltjes integrable with respect to \(\textsf {M} [g].\)
Proof
Because polynomials are dense in \(\textsf {L}^2_w(\Omega ),\) the function \(a+b\,|g({\varvec{x}})|^m\) is integrable, and g satisfies (11). Let the total degree of polynomial g be k. Let the projection operator \(\textsf {P} _n\) be defined by \( \textsf {P} _n\,\psi =\sum _{i=0}^n\langle \phi _i,\psi \rangle \,\phi _i.\)
For a polynomial \(\phi _j\) of total degree p, we can select n so that the linear combination of \(\{\phi _i\}_{i=0}^n\) covers all polynomials of total degree \(k\,m + p\) and then we have the following equalities
By Theorem 15, we have
from where it follows that
\(\square \)
Remark 2
The same arguments hold also more generally for the convergence of \({\varvec{e}}_i^\top \,f({\varvec{A}}_n)\,{\varvec{e}}_j\rightarrow {\varvec{e}}_i^\top \,f({\varvec{A}}_{\infty })\,{\varvec{e}}_j\) when \({\varvec{A}}_{\infty }\) is a self-adjoint infinite sparse matrix, that is, an infinite matrix with only a finite number of non-zero components in each column and row.
Remark 3
In the special case when the inside function is \(g(x)={\text {id}}(x)=x,\) we have essentially the same proof as in [3, Sections 1.8 and 1.13] for the convergence of Gaussian quadrature on polynomially bounded functions.
We can use the following lemma to prove convergence beyond polynomially bounded functions.
Lemma 21
Let self-adjoint operators \(\textsf {A} _n\) converge to a self-adjoint operator \(\textsf {A} \) in the strong resolvent sense. Let a function \(f:~{\mathbb {R}}\mapsto [0,\infty )\) and a vector \(\phi \) be such that \(\langle \phi ,f(\textsf {A} )\,\phi \rangle <\infty .\) If \(\langle \phi , f(\textsf {A} _n)\,\phi \rangle \) is bounded by \(\langle \phi ,f(\textsf {A} )\,\phi \rangle ,\) then \(\langle \phi , f(\textsf {A} _n)\,\phi \rangle \rightarrow \langle \phi , f(\textsf {A} )\,\phi \rangle \) as \(n\rightarrow \infty .\)
Proof
Let the spectral families of \(\textsf {A} _n\) and \(\textsf {A} \) be \(\textsf {E} _n(t)\) and \(\textsf {E} (t),\) respectively. Because f is nonnegative, for an \(\epsilon > 0,\) we can select a finite interval I with endpoints that are not eigenvalues of \(\textsf {A} ,\) so that
Due to the strong resolvent convergence, there is \(N\in {\mathbb {N}},\) so that for all \(k>N,\) we have
Because f is nonnegative, these inequalities mean that for all \(k>N,\) we have
\(\square \)
In [8, Chapter IV, Section 8–10] and [9, Chapter 3, Theorem 1.6], the proof of convergence for Gaussian quadratures is based on the inequality
when all even derivatives of h are nonnegative for all \(x\in \Omega ,\) which implies (6) that was used in the proof of convergence in [6, 7, 11]. This kind of inequality makes it possible to prove convergence for functions that are bounded by functions that can have negative odd derivatives. When the basis functions are polynomials, in terms of the infinite matrices and the leading principal submatrices, (24) can be expressed as
where function \({\text {id}}(x)=x\) but it does not hold for arbitrary inside functions \(g\ne {\text {id}}\) when the basis functions are not polynomials or for other matrix elements except the 0, 0 element. Therefore, we can consider functions with nonnegative even derivatives at zero as the highest possible bound for which we have convergence if we can generalise (25) for other elements than just 0, 0 element and arbitrary basis functions and inside function g.
3.5 Nonnegative matrix coefficients
We can further expand the space of numerically integrable functions when the matrix coefficients are all nonnegative. This can seem like a hard restriction but, for example, the Jacobi matrix side diagonal elements are always positive, only the diagonal elements can be negative [47, Theorem 1.27 and Definition 1.30]. Examples of such cases are Jacobi matrices for Chebyshev polynomials of the fourth kind and the Jacobi and the Meixner–Pollaczek polynomials with parameter values on certain ranges [47, Table 1.1]. In some cases, it is also possible to extend the results for matrices with nonnegative coefficients to matrices with positive and negative real coefficients by considering the positive and negative parts separately.
We extend the concept of m-positive and m-monotone functions so that matrix entries are allowed to be \(\infty ,\) and the inequality for a matrix element a is defined so that \(a\le \infty \) for \(a<\infty ,\) but \(\infty \le \infty \) is not true.
Definition 4
Let \(f:I\mapsto {\mathbb {R}}\) be a real function defined on an interval \(I\subset {\mathbb {R}}.\)
-
1.
f is unbounded m-positive if \(0\in I\) and \(f({\varvec{A}})\ge {\varvec{0}}_{\infty }\) for every symmetric infinite matrix \({\varvec{A}}\ge {\varvec{0}}_{\infty }\) with spectrum in I. \({\varvec{A}}\) and \(f({\varvec{A}})\) are not required to satisfy (10). Elements of \(f({\varvec{A}})\) are allowed to be \(\infty .\)
-
2.
f is unbounded m-monotone if \({\varvec{A}}\le {\varvec{B}} \Rightarrow f({\varvec{A}})\le f({\varvec{B}}),\) for all symmetric infinite matrices \({\varvec{A}},{\varvec{B}}\ge {\varvec{0}}_{\infty }\) with spectra in I. \({\varvec{A}},\) \({\varvec{B}},\) \(f({\varvec{A}}),\) and \(f({\varvec{B}})\) are not required to satisfy (10). Elements of \(f({\varvec{B}})\) are allowed to be \(\infty .\)
For example, monomials and nonnegative linear combinations of monomials are unbounded m-positive functions. We can extend Theorem 3 to unbounded m-positive and unbounded m-monotone functions.
Theorem 22
Let \(f:I\mapsto {\mathbb {R}}\) be a real function defined on an interval \(I\subset {\mathbb {R}}\) such that \(0\in I\) and \(f({\varvec{0}}_{\infty })\ge {\varvec{0}}_{\infty }.\) Then f is unbounded m-positive if and only if it is unbounded m-monotone.
Proof
We adapt the proof of [25, Theorem 2.1] for symmetric arbitrary sized \(n\times n\) matrices to unbounded symmetric infinite matrices and check that the same steps are valid. First, we prove that if f is unbounded m-monotone, it is also unbounded m-positive. We set \({\varvec{A}}={\varvec{0}}_{\infty }\) to obtain \({\varvec{0}}_{\infty }\le f({\varvec{0}}_{\infty })\le f({\varvec{B}})\) for all symmetric infinite matrices.
To prove that unbounded m-positive f is also unbounded m-monotone, we consider symmetric infinite matrices \({\varvec{A}},{\varvec{B}}\ge {\varvec{0}}\) with the spectra in I. We construct a \(2\times 2\) block infinite matrix
We can extend the \(\le \) relation for the block matrix simply as blockwise. The spectrum of \({\varvec{X}}\) is also contained in I. We define a \(2\times 2\) unitary infinite block matrix
We calculate
and notice that the spectrum of \({\varvec{U}}^*\,{\varvec{X}}\,{\varvec{U}}\) is contained in I and that \({\varvec{U}}^*\,{\varvec{X}}\,{\varvec{U}}\ge {\varvec{0}}_{\infty }\) if \({\varvec{A}}\le {\varvec{B}}.\) If f is unbounded m-positive, then
which implies that \(f({\varvec{A}}) \le f({\varvec{B}}).\) Here we multiply only \(f({\varvec{A}}),\) which has finite elements, with \(-{\varvec{I}}_{\infty }\) and define \(\infty -a=\infty \) for all \(a\in [0,\infty ).\) \(\square \)
Absolutely monotone functions, that is, functions that have power series expansion \(h(x)=\sum _{n=0}^\infty c_n\,x^n\) where \(c_n\ge 0,\) are unbounded m-positive and therefore also unbounded m-monotone. These functions are also very fast-growing, so if we have convergence for such functions, we also have convergence for a large family of functions that grow slower. Examples of functions that have power series representation with nonnegative coefficients are \(\exp (x),\) \(\cosh (\sqrt{x}),\) which were used in [6], and more generally, the Mittag–Leffler functions \( E_\gamma (x)=\sum _{k=0}^\infty \frac{x^k}{\Gamma (\gamma \,k+1)}\) where \(0<\gamma \le 2\) and \(x\in [0,\infty )\) [11, eq. (3.3)].
For functions bounded by unbounded m-positive functions, we have the following theorem.
Theorem 23
Let a self-adjoint infinite matrix \({\varvec{A}}_{\infty }\ge {\varvec{0}}_{\infty }\) satisfy (10). Let function f be bounded by a positive and unbounded m-positive function h, that is, \(|f(x)|\le h(x)\) for \(x\in \sigma ({\varvec{A}}_{\infty }).\) Let finite matrix approximations \({\varvec{A}}_n\) be the leading principal submatrices of \({\varvec{A}}_{\infty }.\) Then, as \(n\rightarrow \infty ,\) \([f({\varvec{A}}_n)]_{k,k}\rightarrow [f({\varvec{A}}_{\infty })]_{k,k}\) for all \(k=0,1,2,\ldots \) for which \([h({\varvec{A}})]_{k,k}<\infty .\)
Proof
Let self-adjoint infinite matrices
Because \({\varvec{B}}_n\le {\varvec{A}},\) by Theorem 22, the sequence \([h({\varvec{B}}_n)]_{k,k}\) is bounded by \([h({\varvec{A}})]_{k,k},\) which means by Lemma 21 that it must converge to \([h({\varvec{A}})]_{k,k}.\) Because for \(n\ge k,\) we have \([h({\varvec{A}}_n)]_{k,k}=[h({\varvec{B}}_n)]_{k,k},\) we also have \([h({\varvec{A}}_n)]_{k,k}\rightarrow [h({\varvec{A}})]_{k,k}.\) Due to Theorem 13, we have convergence for f bounded by h. \(\square \)
In terms of restrictions for the bounds of the outside function h, we can reach the most generic level of convergence, that is, convergence for functions that have nonnegative even derivatives, like in [8, Chapter IV, Section 8–10], on the interval \((-\infty ,\infty )\) when w is an even function, basis functions are even or odd, and g is odd. In more general cases, we have to use a stricter condition that the bounding function h is absolutely monotone, that is, has all derivatives positive.
Theorem 24
Let the orthonormal functions \(\phi _0,\phi _1,\phi _2,\ldots \) be dense in \(\textsf {L}^2_w(\Omega ).\) Let the function g satisfy (11) and let the matrices \({\varvec{M}}_n[g]\) have elements as in (3) that are nonnegative. Furthermore, let a function f be Riemann–Stieltjes integrable with respect to multiplication operator \(\textsf {M} [g]\) and bounded by a function h so that \(|f(x)|\le h(x)\) and
Then
if one of the following additional conditions holds :
-
1.
Function h has the form \( h(x) = \sum _{k=0}^\infty a_k\,x^k\) where \(a_k\ge 0\) for all \(k=0,1,\ldots .\)
-
2.
Function \(g({\varvec{x}})\) satisfies
$$\begin{aligned} \int _{\Omega } g({\varvec{x}})^{2\,k+1}\,|\phi _i({\varvec{x}})|^2\,w({\varvec{x}})\,d{\varvec{x}} =[{\varvec{M}}_n[g]^{2\,k+1}]_{i,i}=0 \end{aligned}$$for all \(k=0,1,2,\ldots \) and all even coefficients of \( h(x)=\sum _{k=0}^\infty a_k\,x^k\) are nonnegative : \(a_{2k}\ge 0.\)
Proof
The proof follows from Theorem 23. Under the second condition, the odd \(a_{2k+1}\) coefficients can also be negative. \(\square \)
We give a numerical example demonstrating the difference in convergence for matrices with purely nonnegative elements and matrices with mixed sign elements in Sect. 4.
In some cases, it is also possible to prove convergence when matrix coefficients have mixed signs by considering the negative and positive parts separately. We decompose a self-adjoint real infinite matrix \({\varvec{A}}\) into positive \({\varvec{P}}\) and negative \({\varvec{N}}\) parts with
so that \({\varvec{P}}={\varvec{A}}^+\) and \({\varvec{N}}=(-{\varvec{A}})^+.\) Then \({\varvec{A}}={\varvec{P}} - {\varvec{N}}.\) We construct a \(2\times 2\) block infinite matrix with nonnegative elements
We can express any matrix element of a function of a self-adjoint real infinite matrix as a function of a \(2\times 2\) block infinite matrix with nonnegative coefficients as
For example, we consider an unbounded function \(g(x)=x\,\cos (\sqrt{x}),\) a weight function \(w(x)=e^{-x}\) on interval \([0,\infty )\) and polynomials as orthogonal functions. The infinite matrix \({\varvec{M}}_{\infty }[g]\) is unbounded because function g is an unbounded function on the interval \([0,\infty ).\) The elements of \({\varvec{M}}_{\infty }[g]\) are given by

where \({\text {erf}}(x)=\frac{2}{\sqrt{\pi }}\int _0^x e^{-t^2}dt.\) Some of the elements are negative, and some are positive. The pattern for the signs of the matrix elements is

However, it is possible to prove convergence for polynomially bounded functions, as is shown in the following theorem.
Theorem 25
Let \(w(x)=e^{-x}\) on interval \([0,\infty ),\) the orthogonal basis functions \(\phi _i\) polynomials and \(g(x)=x\,\cos (\sqrt{x}).\) Let \({\varvec{M}}_n[g]\) have elements as in (3). Then
when f is bounded by some polynomial.
Proof
The orthogonal polynomials \(\phi _i\) are known as the Laguerre polynomials. Elements of the Jacobi matrix, the infinite matrix representation for the function \({\text {id}}(x)=x,\) are nonnegative. We can see this by looking at the exact formula for the recurrence coefficients of the Jacobi matrix for the Laguerre polynomials [47, Table 1.1 and Definition 1.30]. The main diagonal elements are the odd positive numbers, and the off-diagonal elements are the natural numbers all in a growing order and thus nonnegative as is also visible in the few first matrix coefficients
For a function \(h(x)=x\,\cosh (\sqrt{x}),\) the elements of an infinite matrix \({\varvec{M}}_{\infty }[h]\) are also nonnegative because h has a Taylor series expansion \( h(x)=x\,\cosh (\sqrt{x})=\sum _{k=0}^\infty \frac{1}{(2\,k)!}\,x^{k+1} \) with only nonnegative coefficients, and that converges for all \(x\in [0,\infty ).\) The infinite matrix representation of the multiplication operator of function h has a series representation for the elements as
The function g has almost the same Taylor series expansion as the function h except some coefficients are negative \( g(x)=x\,\cos (\sqrt{x})=\sum _{k=0}^\infty \frac{(-1)^k}{(2\,k)!}\,x^{k+1}. \) However, the negative coefficients are bounded by the coefficients of the Taylor series of the function h.
We decompose \({\varvec{M}}_{\infty }[g]\) into the positive and negative parts as \({\varvec{M}}_{\infty }[g]={\varvec{P}}-{\varvec{N}}\) and form a \(2\times 2\) block infinite matrix \({\varvec{T}}\) as in (26). The elements of both the positive \({\varvec{P}}\) and the negative \({\varvec{N}}\) part are bounded by the elements of the infinite matrix representation of the multiplication operator for the function h as
that is, \({\varvec{P}},{\varvec{N}}\le {\varvec{M}}_{\infty }[h].\) By Theorem 22,
Because \({\varvec{M}}_{\infty }[h]^m\) satisfies (10) for all \(m\in {\mathbb {N}},\) then also \({\varvec{T}}^m\) satisfies (10) for all \(m\in {\mathbb {N}}.\) By Theorem 23, we have convergence for the diagonal elements of the \(2\,m\) powers. By Lemma 14, we have
as \(n\rightarrow \infty .\) Convergence for polynomially bounded functions follows from Theorem 15. \(\square \)
3.6 Improper integrals on finite endpoints of an interval
In this section, we analyse convergence for integrals that are singular on a finite endpoint. A minimum requirement for convergence is that a singular endpoint of the function is not a node of the numerical integration rule. We already know that the nodes of numerical integration, that is, the eigenvalues of \({\varvec{M}}_n[g],\) lie in the closed interval \([{\text {ess}}\,{\text {inf}} g,{\text {ess}}\,{\text {sup}} g]\) [1, Theorem 1]. The essential infimum \({\text {ess}}\,{\text {inf}} g\) and the essential supremum \({\text {ess}}\,{\text {sup}} g\) are the endpoints of the convex hull of the essential range \(\mathcal {R}(g)\) (9).
In the case of an improper integral, where the integrand is singular at an endpoint of integration, we do not want the endpoint to be an evaluation point for the numerical integration, that is, if the outside function f is singular at \({\text {ess}}\,{\text {inf}} g\) or \({\text {ess}}\,{\text {sup}} g,\) we do not want \({\text {ess}}\,{\text {inf}} g\) or \({\text {ess}}\,{\text {sup}} g\) to be an eigenvalue of \({\varvec{M}}_n[g].\) Fortunately, we have the following theorem.
Theorem 26
For a measurable real function g, \({\text {ess}}\,{\text {inf}} g\) (or \({\text {ess}}\,{\text {sup}} g\)) cannot be an eigenvalue of the matrix \({\varvec{M}}_n[g]\) unless
-
1.
\({\text {ess}}\,{\text {inf}} g\) (or \({\text {ess}}\,{\text {sup}} g\)) is an eigenvalue of \({\textsf{M}}[g]\) and
-
2.
the corresponding eigenfunction is \(\phi =\sum _{i=0}^n c_i\,\phi _i.\)
Proof
We define a function \(\tilde{g}=g-{\text {ess}}\,{\inf } g.\) Now \({\text {ess}}\,{\inf } \tilde{g}=0.\) If 0 is an eigenvalue of \({\varvec{M}}_n[\tilde{g}],\) then for some non-zero \({\varvec{c}}\in {\mathbb {C}}^{n+1},\) we have \( 0={\varvec{c}}^*\,{\varvec{M}}_n[\tilde{g}]\,{\varvec{c}} .\) This is possible only if
which is possible only if 0 is an eigenvalue of \({\textsf{M}}[\tilde{g}]\) and \(\phi =\sum _{i=0}^n c_i\,\phi _i\) is the corresponding eigenfunction. In that case, \({\text {ess}}\,{\inf } g\) is an eigenvalue of \({\textsf{M}}[g]\) and \(\phi =\sum _{i=0}^n c_i\,\phi _i\) the corresponding eigenfunction. The proof for \({\text {ess}}\,{\text {sup}} g\) is similar to that for a function \(\tilde{g}={\text {ess}}\,{\text {sup}} g - g.\) \(\square \)
For example, by (8), a sufficient condition for \({\text {ess}}\,{\text {inf}} g\) not being an eigenvalue is that
or that none of the basis functions is a characteristic function. For another example, when \(g(x)=x\) and the basis functions are polynomials, we have the well-known property of Gaussian quadrature that the endpoints are not nodes of the Gaussian quadrature rule [47, Theorem 1.46]. For a Gaussian quadrature rule, this property follows from two facts: multiplication operator \(\textsf {M} [g]\) does not have eigenvalues for \(g(x)=x,\) and a finite-order polynomial cannot be a characteristic function.
Once we have shown that the integrand of an improper integral cannot have singularities at the eigenvalues of \({\varvec{M}}_n[g],\) we can use Jensen’s operator inequality to show the monotone growth of the approximations.
Lemma 27
Let \(\textsf {A} \) be a self-adjoint operator with an infinite matrix representation \({\varvec{A}}_{\infty }.\) Let \({\varvec{A}}_{\infty }\) and \({\varvec{v}}\in \ell ^2_0\) have finite approximations with elements \( [{\varvec{A}}_n]_{i,j}=[{\varvec{A}}_{\infty }]_{i,j}\) and \( [{\varvec{v}}_n]_i=[{\varvec{v}}]_i \) for \(i,j=0,1,\ldots ,n.\) Let f be an operator convex function on the interval I that contains the spectrum of \({\varvec{A}}_{\infty }.\) Then for n more than the non-zero elements of \({\varvec{v}},\) we have
Proof
We define projection operators \({\varvec{P}}_n\) as in (16). First, we use Jensen’s operator inequality (12) with \(s\in I\) for operator
We notice that \(\textsf {B} \) is a bounded operator in infinite dimensional Hilbert space and \(\sigma (\textsf {B} )\subset I.\) Therefore, Jensen’s operator inequality (12) applies. We also notice that
and hence obtain
which implies \({\varvec{v}}_n^*\,f({\varvec{A}}_n)\,{\varvec{v}}_n\le {\varvec{v}}_{n+1}^*\,f({\varvec{A}}_{n+1})\,{\varvec{v}}_{n+1}.\) \(\square \)
With an unbounded version of Jensen’s operator inequality (12), we could also establish \({\varvec{v}}^*_n\,f({\varvec{A}}_n)\,{\varvec{v}}_n\le {\varvec{v}}^*\,f({\varvec{A}}_{\infty })\,{\varvec{v}}.\) We do know that operator convex functions of positive bounded operators, like \(f(x)=x^{-1},\) are operator convex for positive unbounded operators as well [48, Theorem 4.3].
For further use of Lemma 27, without an unbounded version of (12), we notice that function \(f(x)=(x+s)^{-p}\) is operator convex for any \(p\in [0,1]\) and \(s\ge 0\) because operator \(\textsf {B} +s\) is also a bounded operator for any bounded operator \(\textsf {B} \) and \(\sigma (\textsf {B} +s)\in (0,\infty )\) if \(\sigma (B)\in (0,\infty ).\) We need also some extension for the class of operator monotone functions.
Lemma 28
Function \(h(x)=-(x+s)^{-p}\) is operator monotone for positive unbounded self-adjoint operators for all \(s\in (0,\infty )\) and \(p\in [0,1].\)
Proof
Function \(h(x)=-(x+s)^{-p}\) is operator monotone on interval \([0,\infty )\) for any positive bounded operator \(\textsf {B} \) because operator \(s+\textsf {B} \) is a positive bounded operator on interval \([s,\infty )\subset (0,\infty )\) and \(\tilde{h}(x)=-x^{-p}\) is operator monotone on interval \((0,\infty ).\) Function h is then operator monotone also for all positive self-adjoint operators.
For extending this result to the unbounded case, see the proof in [31, Theorem 5], which does not depend on the operator algebraic concepts of von Neumann algebra and affiliated operators mentioned in the statement of the theorem. \(\square \)
This allows us to prove convergence for functions bounded by \(x^{-p}\) for the following theorem.
Theorem 29
Let \(p\in [0,1].\) Let self-adjoint operator \(\textsf {A} \) have an infinite matrix representation \({\varvec{A}}_{\infty }.\) Let \({\varvec{u}}, {\varvec{v}}\in \ell ^2_0\) be such that \(|{\varvec{u}}^*\) \(({\varvec{A}}_{\infty } - c\,{\varvec{I}}_{\infty })^{-p}\,{\varvec{v}}| <\infty .\) Let function f have a singularity at endpoint c of the spectrum of \({\varvec{A}}_{\infty }\) such that \(|f(x)|\le a + \frac{b}{|x-c|^p}\) and \({\varvec{A}}_{\infty }\) has no eigenvalue and eigenvector pair such that the endpoint c is the eigenvalue and the corresponding eigenvector is in \(\ell ^2_0.\) Let finite approximations be \( [{\varvec{A}}_n]_{i,j}=[{\varvec{A}}_{\infty }]_{i,j},\) \([{\varvec{u}}_n]_i = [{\varvec{u}}]_i,\) \([{\varvec{v}}_n]_i = [{\varvec{v}}]_i\) for \(i,j=0,1,\ldots ,n.\) Then \( {\varvec{u}}_n^*\,f({\varvec{A}}_n)\,{\varvec{v}}_n\rightarrow {\varvec{u}}^*\,f({\varvec{A}}_{\infty })\,{\varvec{v}} \) as \(n\rightarrow \infty .\)
Proof
It is enough to consider convergence for \( {\varvec{v}}_n^*\,f({\varvec{A}}_n)\,{\varvec{v}}_n\rightarrow {\varvec{v}}^*\,f({\varvec{A}}_{\infty })\,{\varvec{v}}\) when \({\varvec{v}}\in \ell ^2_0.\) The more general convergence follows from the polar decomposition
If \({\varvec{u}},{\varvec{v}}\in \ell ^2_0\cap \textsf {D}(\sqrt{|f({\varvec{A}}_{\infty })|}),\) then also \({\varvec{u}}+{\varvec{v}},{\varvec{u}}-{\varvec{v}},{\varvec{u}}+i\,{\varvec{v}}, {\varvec{u}}-i\,{\varvec{v}}\in \ell ^2_0\cap \textsf {D}(\sqrt{|f({\varvec{A}}_{\infty })|}).\)
It is also enough to show convergence when the lower endpoint of \(\sigma ({\varvec{A}}_{\infty })\) is 0, and \({\varvec{A}}_{\infty }\) has no eigenvalue at 0 such that the corresponding eigenvector is in \(\ell ^2_0.\) Then we can select \(h(x)=x^{-p},\) which is operator convex function on \((0,\infty )\) and \(-h(x)\) is operator monotone on \((0,\infty ).\) Convergence for more general \(\tilde{h}(x)=a+\frac{b}{|x-c|^p}\) follows by simple transformations.
We define a sequence of functions for \(s> 0\) as
Functions \(a_n(s)\) are bounded for all values of \(n<\infty \) and \(s> 0.\) By Lemma 27, sequence \(a_n(s)\) is monotone increasing when n is greater than the number of non-zero elements in \({\varvec{v}}.\) Functions \(a_n(s)\) are monotone decreasing as functions of s because \(-h(x+s)\) is operator monotone on \([0,\infty )\) also for unbounded positive self-adjoint infinite matrices and
when \(s\le r.\) We further define a double sequence \(a_{n,m}=a_n(m^{-1})\) which is monotone increasing in both n and m. By [49, Theorem 4.2], we can change the order of the limits for n and m and have
because \(h({\varvec{A}}_{\infty }+m^{-1})\) is a bounded operator. Convergence for \(|f(x)|\le \tilde{h}(x)=a+\frac{b}{|x-c|^p}\) follows in a similar way as the proof of Theorem 15. \(\square \)
For an improper numerical integral on a finite endpoint, we can present the following theorem.
Theorem 30
Let orthonormal functions \(\phi _0=1,\phi _1,\phi _2,\ldots \) be dense in \(\textsf {L}_w^2(\Omega ).\) Let a function g satisfy (11) and let matrices \({\varvec{M}}_n[g]\) have elements as in (3). Let c be such \({\text {ess}}\,{\text {sup}} g\) or \({\text {ess}}\,{\text {inf}} g\) that it is not an eigenvalue of \({\varvec{M}}_n[g],\) that is, c is not an eigenvalue of \(\textsf {M} [g],\) or if it is, then the corresponding eigenfunction is not a finite linear combination of the basis functions \(\phi _i.\) Let a function f be Riemann–Stieltjes integrable with respect to the spectral family of \(\textsf {M} [g]\) on any finite interval not containing c. Let f be bounded so that \(|f(x)|\le a+\frac{b}{|x-c|^p}\) for some \(a,b\ge 0\) and \(0\le p\le 1\) that satisfy
Then
Proof
This follows from Theorem 29. \(\square \)
4 Numerical examples
As an example of convergence, we consider integration on the interval \([0,\infty )\) with exponential weight function \(w(x)=e^{-x}\) and orthonormal polynomials (Laguerre polynomials) as the orthonormal basis functions. As an example, we use inside functions \(g_1(x)=\sqrt{x},\) \(g_2(x)=x,\) \(g_3(x)=x^{3/2}\) and \(g_4(x)=x^2.\)
The inside function \(g_2\) corresponds to Gauss–Laguerre quadrature and has the well-known good convergence properties of Gaussian quadrature [6,7,8,9, 11]. The inside functions \(g_1,g_2,g_3,g_4\) satisfy condition (11). Matrix \({\varvec{M}}_{\infty }[g_2]\) is the tridiagonal Jacobi matrix for the Laguerre polynomials. Its elements are all nonnegative. We can see this by looking at the exact formula for the recurrence coefficients [47, Table 1.1 and Definition 1.30] as well as in the first few matrix coefficients (27). Also, \({\varvec{M}}_{\infty }[g_4]\) has nonnegative elements because it is a square of a matrix \({\varvec{M}}_{\infty }[g_2]\) that has only nonnegative elements. On the contrary, matrices \({\varvec{M}}_{\infty }[g_1]\) and \({\varvec{M}}_{\infty }[g_3]\) have both positive and negative elements, as we can see from the first few matrix coefficients
We test convergence with two test functions \(f_1(x)=\sin (\sqrt{x})\) and \(f_2(x)=\frac{\exp (x)}{1+x^2}.\) The first one is bounded, and the second one is a very fast-growing function.
For comparison, we formulate the numerical integral as
where \(g_j^{-1}\) exists for all \(g_1,g_2,g_3,g_4.\) This way, we get four different quadrature rules for approximating the integral. We compute the finite matrix approximation of the multiplication operator symbolically as described in [1, Remark 1] and the eigenvalue decomposition numerically with 64-bit IEEE 754 floating point numbers. The reason for using symbolic computation until the eigenvalue decomposition is that we also have the Jacobi matrix for the Gauss–Laguerre quadrature in closed-form. This allows us to compare quadratures up to way more than 30 nodes. With purely 64-bit floating point computation, the method would work for up to only 10 to 15 nodes. This is significantly improved up to 15 to 20 nodes if centralised moments are used instead of the raw ones.
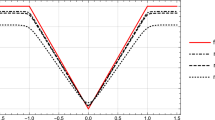
The results of the numerical approximation are presented in Figs. 1a, 2, and 4. The example for a bounded function in Fig. 1a demonstrates convergence for all the inside functions as expected by Theorem 18.
Convergence is not very fast in Fig. 1a. For understanding the reason better, we can take a look at the location of the nodes and how much each node contributes to the numerical integral. In Fig. 1b, we see each node located on the horizontal axis. On the vertical axis, we show the value \(f_1(x_k)\,w_k\) which tells how much the term contributes to the total sum \(\sum _{k=0}^{30} f_1(x_k)\,w_k.\) For comparison, also the function graph is shown weighted by w(x). The graph and the weights are not directly comparable so that it would be a better fit when the points \(f_1(x_k)\,w_k\) are located on the graph. When nodes are further away from each other, the weight should be higher compared to a situation where nodes are close to each other. Notice also that the x-axis is on a logarithmic scale to show the interesting area of the function more clearly. This further distorts the effect that values \(f_1(x_k)\,w_k\) seem far off from the curve \(f_1(x)\,w(x).\) However, the curve of \(f_1(x)\,w(x)\) does show the area where the \(f_1(x_k)\,w_k\) points should be higher assuming that the distance between the nodes does not vary very much.
Figure 1b shows that only 7 or 8 nodes are located in the area where \(f_1(x)\,w(x)\) is high. The rest of the 31 nodes are located in low area. This is quite natural because the support of the integral is \([0,\infty ).\) Because the nodes have the interleaving property [1, Theorem 2], increasing the number of nodes from 31 to 32 is going to add at most one more node in the interesting area. The majority of the nodes are going to have a very small contribution to the numerical integral.
For the fast-growing outside function in Fig. 2a, we have different results. For \(g_1\) and \(g_3,\) we have divergence starting before 15 nodes. This is in line with the fact that we do not have a proof of convergence for \(g_1\) and \(g_3,\) unlike for \(g_2\) and \(g_4.\) The absence of proof, of course, does not mean that the numerical integral is automatically divergent. We do not have a proof that this is diverging either. In principle, it could be convergent in the end but just having the error growing very large for a large number of nodes until convergence would happen. This temporary large error might become too large for the floating point representation.
The only theorem that we have been able to prove which applies to \(g_1\) and \(g_3\) is Theorem 19, which says that for \(g_1(x)=\sqrt{x},\) f would have to be linearly bounded, and for \(g_3(x)=x^{\frac{3}{2}},\) the bound would have to be \(|f(x)|\le a+x^3\) for some \(a>0.\) The true bound where convergence starts to fail is probably somewhere between these quite slowly growing functions and the example function that is almost too fast-growing function to be integrable at all.
Another possible explanation for the divergence could be numerical instability. In order to test this hypothesis, we computed the eigenvalue decomposition and the numerical integral with variable precision for \(g_1\) on 11 nodes where the divergence has already started, and the approximation error is 0.2323. The difference between the floating point and the variable precision calculation is \(1.7170\cdot 10^{-16}\) for both 32- and 64-digit variable precision.
Convergence for \(g_2\) follows from the well-known results [6,7,8,9, 11]. Convergence for \(g_4\) follows from Theorem 24 because
We can make a quadrature rule based on the inside function \(g_1\) or \(g_3\) convergent for the outside function \(f_2\) by Theorem 12. We select a function h of Theorem 12 as \(h_2(x)=\frac{\exp (x/2)}{(1+x^2)^{3/8}}.\) The function \(r(x)=\frac{f_2(x)}{h_2^2(x)}\) is bounded, and we can formulate the integral as
where \({\varvec{v}}\in \ell ^2\) has components \( [{\varvec{v}}]_i=\langle h_2,\phi _i\rangle = \int _0^\infty h_2(x)\,\phi _i(x)\,w(x)\,dx ,\) and \({\varvec{v}}_n\) is a truncation of \({\varvec{v}}\) up to component n. The approximation in (28) is also a special case of this more general approach with function h selected as \(h_1=1.\) Functions \(h_1\) and \(h_2\) do not affect the placement of the nodes but only the weights of the numerical integration as given in (19). Figure 2b shows that with weight function \(h_2,\) this approach is convergent also for the inside functions \(g_1\) and \(g_3.\)
We can again look at the location of the nodes and corresponding values of \(f_2(x_k)\,w(x_k)\) in Fig. 3, which shows that the weights for large values of \(x_k\) are very high for \(g_1\) and \(g_3.\) The location of the nodes is not very different for all of the quadratures.
Finally, we note that using \(h_2\) instead of \(h_1\) does not universally improve convergence as shown in Fig. 4a. The results for inside functions \(g_3,g_4\) are similar to that for \(g_2.\)
Approximation error for bounded outside functions \(f_1(x)=\sin (\sqrt{x})\) and Thomae’s function (29)
As an example of a discontinuous function, we use Thomae’s function
The true value of the integral for Thomae’s function is 0 [41, Example 7.1.6]. The results are shown in Fig. 4b.
Convergence is very fast, although the function value at every node is nonzero. The true value of the node could be an irrational number, which would make convergence even faster. However, we define the node to be an approximation to the eigenvalue in floating point representation which is always a rational number. Even in that case, the nonzero values are so small that the integral quickly converges close to 0.
As an example of a multidimensional integral, we consider the following integral
where the weight function is Gaussian \(w({\varvec{x}})=\pi ^{-\frac{3}{2}}\,e^{-\Vert {\varvec{x}}\Vert ^2}.\) We select functions f and g in (1) as \(f(x)=\frac{1}{x}\) and \(g({\varvec{x}})=\Vert {\varvec{x}}\Vert ^2.\) This turns the integration problem into a linear algebra problem. The approximation for (30) is given by \(I\approx {\varvec{e}}_0^\top \,{\varvec{M}}_n[g]^{-1}\,{\varvec{e}}_0.\) Function f is singular at 0 and the whole integrand at \({\varvec{0}}.\) We expect convergence based on Theorem 30, and convergence should be monotone based on Lemma 27.
We get the matrix elements for the function of the multi-dimensional variable from the elements of a matrix for a one-dimensional variable. We start with the Jacobi matrix for the Hermite system, that is, the orthogonal system with weight function \(w(x)=e^{-x^2}.\)
The Jacobi matrix is symmetric and tridiagonal. We can write a general symmetric tridiagonal infinite matrix as
For the Hermite system, the Jacobi matrix coefficients in (31) are given by \(u_k=0\) and \(v_k=\sqrt{\frac{1}{2}\,(k+1)}\) for \(k=0,1,\ldots \) [47, Table 1.1 and Definition 1.30]. Thus, these are the coefficients of infinite matrix \({\varvec{M}}_{\infty }[{\text {id}}]\) for function \({\text {id}}(x)=x\) in one dimension.
A second power of \({\varvec{M}}_{\infty }[{\text {id}}]\) is a 5-diagonal infinite matrix with 2 side diagonals
where \(a_k = v_{k-1}^2+v_k^2=k+\frac{1}{2},\) \(b_k = 0,\) and \(c_k = v_k\,v_{k+1}=\frac{1}{2}\,\sqrt{(k+1)\,(k+2)}.\)
In the following notation, we use multi-indices as matrix indices. In computation, we use these multi-indices in graded lexicographic order [46, Chapter 3.1]. The monomials of a multidimensional variable are \({\varvec{x}}^{{\varvec{\alpha }}}=\prod _{i=0}^{d-1} x_i^{\alpha _i}\) for \({\varvec{x}}\in {\mathbb {R}}^d\) and \({\varvec{\alpha }}\in {\mathbb {N}}_0^d.\) Similarly, we can index the orthonormal polynomials with multi-indices as \(\phi _{{\varvec{\alpha }}}({\varvec{x}}) =\prod _{i=0}^{d-1}\phi _{\alpha _i}(x_i),\) where \(\phi _i\) are the one-dimensional orthonormal polynomials. For matrix elements, the definition is \({\varvec{M}}_{\infty }[g]_{{\varvec{\alpha }},{\varvec{\beta }}}=\langle \phi _{{\varvec{\alpha }}},g\,\phi _{{\varvec{\beta }}}\rangle .\)
For \(g({\varvec{x}})=\Vert {\varvec{x}}\Vert ^2,\) we get a matrix which has one main diagonal of elements on \(({\varvec{\alpha }},{\varvec{\alpha }})\) and several side diagonal like sets of elements on \(({\varvec{\alpha }},{\varvec{\alpha }}+2\,{\varvec{e}}_i)\) for \(i=0,1,2.\) These sets are symmetric, that is, \({\varvec{M}}_{\infty }[g]_{{\varvec{\alpha }},{\varvec{\alpha }}+2\,{\varvec{e}}_i}={\varvec{M}}_{\infty }[g]_{{\varvec{\alpha }}+2\,{\varvec{e}}_i,{\varvec{\alpha }}}.\) The diagonal matrix elements are
The side diagonal elements are given for \(i=0,1,2\) as
Otherwise, the elements are 0.
For numerical comparison, we compute the numerical integral \({\varvec{e}}_0^\top \,{\varvec{M}}_n[g]^{-1}\,{\varvec{e}}_0\) with different values of the total order of the polynomials \(|{\varvec{\alpha }}|=\sum _{i=0}^{d-1}\alpha _i=1,2,\ldots ,80.\) The size of the matrix \({\varvec{M}}_n[g]\) depends on the total order as \(\left( {\begin{array}{c}|{\varvec{\alpha }}|+3\\ 3\end{array}}\right) \) [46, Chapter 3.1]. At maximum, we make the computation for a matrix of size \(\left( {\begin{array}{c}80+3\\ 3\end{array}}\right) =91881.\) We can compare this to the true value of (30) that we can find in the spherical coordinates as \(I=\frac{4}{\sqrt{\pi }}\,\int _0^\infty e^{-r^2}\,dr=2.\)
Figure 5a shows the values of the approximation for different values of the order of the polynomial approximation as well as the true value.
We see that convergence is monotone as expected but very slow.
The nodes, which we get from \({\varvec{M}}_n[g],\) are not very efficient because of multiple eigenvalues. Moreover, the weights of the nodes corresponding to the multiple eigenvalues are 0. For example, in Table 1, we list the eigenvalues and weights for \({\varvec{M}}_{55}[g]\) in a case where \(|{\varvec{\alpha }}|\le 5.\) The size of the matrix is \(\left( {\begin{array}{c}5+3\\ 3\end{array}}\right) =56.\)
We see that only eigenvalues with multiplicity 1 have non-zero weight and there are only 3 of them in the total 56 eigenvalues.
Figure 6 shows 11 non-zero weights and the corresponding nodes for \(|{\varvec{\alpha }}|\le 20,\) where the size of the matrix is 1771.
We see that some of the weights are very small. However, these small weights are still relevant for fast-growing functions like \(f_1(x)=e^{\frac{1}{2}\,x^2},\) as is shown in Fig. 5b. With the 11-point quadrature in Fig. 6 corresponding to polynomial order of 20, for \(f_1,\) the 2 biggest contributions come from the 2 nodes with the 2 smallest weights.
We further test the convergence of the same \({\varvec{M}}_n[g]\) for 4 different outside functions, that is, for integral
where \(f_1(x)=e^{\frac{1}{2}\,x^2},\) \(f_2(x)=\sqrt{x},\) \(f_3(x)=\sin (\sqrt{x}),\) \(f_4(x)=\sin (x),\) \(g({\varvec{x}})=\Vert {\varvec{x}}\Vert ^2,\) and w is as in (30). Again, we can find the true values of the integrals in the spherical coordinates as
where \({\text {Im}}(x+y\,i)=y.\) Figure 5b shows some rate of convergence for all outside functions.
Convergence follows from Theorem 24 because \({\varvec{M}}_{\infty }[g]\) has only nonnegative elements, and all the functions are bounded by \(f_1(x)=e^{\frac{1}{2}\,x^2}=\sum _{k=0}^\infty \frac{1}{2^k\,k!}\,x^{2\,k}.\)
5 Conclusions
We have proved several theorems on the convergence of the finite matrix approximations of multiplication operators for numerical integration. The theorems also apply generally to self-adjoint operators.
For integration on an unbounded interval, we have shown several theorems for strong resolvent convergence. We have proved strong resolvent convergence of finite matrix truncations of self-adjoint operators with infinite matrix representation. We have proved that the strong resolvent convergence for a sequence of self-adjoint operators implies strong convergence for Riemann–Stieltjes integrable functions and strong resolvent convergence for unbounded functions of the operators. We have proved that the strong resolvent convergence for a sequence of self-adjoint operators implies the convergence of quadratically bounded functions of the operators for certain quadratic forms that can be used in numerical integration. We have proved that for multiplication operators of polynomials or self-adjoint operators with nonnegative coefficients, convergence results can be extended to higher-order functions than quadratically bounded functions. We have also numerically demonstrated how convergence can fail for very fast-growing functions if some matrix coefficients are negative. We have shown a way to improve convergence by using weights that are derived from a bounding function of the integrand.
We have also proved theorems for improper integrals with finite endpoints. We have shown that endpoints of integration are not eigenvalues of the finite matrix approximation of the multiplication operator and, therefore, not nodes of the matrix method of integration which is also a property of Gaussian quadrature. We have shown that numerical integrals converge for improper integrals if the integrand function is bounded by an operator convex function.
References
Sarmavuori, J., Särkkä, S.: Numerical integration as a finite matrix approximation to multiplication operator. J. Comput. Appl. Math. 353, 283–291 (2019)
Gragg, W.B.: Positive definite Toeplitz matrices, the Arnoldi process for isometric operators, and Gaussian quadrature on the unit circle. J. Comput. Appl. Math. 46(1–2), 183–198 (1993)
Simon, B.: Orthogonal Polynomials on the Unit Circle: Part 1: Classical Theory. Colloquium Publications Series, American Mathematical Society, Providence (2009)
Velázquez, L.: Spectral methods for orthogonal rational functions. J. Funct. Anal. 254(4), 954–986 (2008)
Bultheel, A., Cantero, M.J., Cruz-Barroso, R.: Matrix methods for quadrature formulas on the unit circle. A survey. J. Comput. Appl. Math. 284, 78–100 (2015)
Uspensky, J.V.: On the convergence of quadrature formulas related to an infinite interval. Trans. Am. Math. Soc. 30(3), 542–559 (1928)
Jouravsky, A.: Sur la convergence des formules des quadratures mécaniques dans un intervalle infini. J. Soc. Phys. Math. Léningrade 2, 31–52 (1928)
Shohat, J.A., Tamarkin, J.D.: The Problem of Moments. Mathematical Surveys. American Mathematical Society, Providence (1963)
Freud, G.: Orthogonal Polynomials. Pergamon Press, London (1971)
Bultheel, A., Díaz-Mendoza, C., González-Vera, P., Orive, R.: Quadrature on the half line and two-point Padé approximants to Stieltjes functions. Part III. The unbounded case. J. Comput. Appl. Math. 87(1), 95–117 (1997)
Bultheel, A., Díaz-Mendoza, C., González-Vera, P., Orive, R.: On the convergence of certain Gauss-type quadrature formulas for unbounded intervals. Math. Comput. 69(230), 721–747 (2000)
Kato, T.: Perturbation Theory for Linear Operators. Classics in Mathematics, 2nd edn. Springer, Berlin (1995)
Reed, M., Simon, B.: I: Functional Analysis, Revised and enlarged edn. Methods of Modern Mathematical Physics. Academic Press, New York (1981)
Segal, I.E., Kunze, R.A.: Integrals and Operators. Grundlehren der mathematischen Wissenschaften, 2nd edn. Springer, Berlin (1978)
Weidmann, J.: Linear Operators in Hilbert Spaces. Graduate Texts in Mathematics, Springer, New York (1980)
Simon, B.: Operator Theory: A Comprehensive Course in Analysis, Part 4. American Mathematical Society, Providence (2015)
Segal, I.: Algebraic integration theory. Bull. Am. Math. Soc. 71, 419–489 (1965)
Atkinson, K., Chien, D., Hansen, O.: Multivariate quadrature of a singular integrand. Adv. Comput. Math. 47(3), 44 (2021)
Stone, M.H.: Linear Transformations in Hilbert Space and Their Applications to Analysis. American Mathematical Society, Providence (1932)
Riesz, F., Szőkefalvi-Nagy, B.: Functional Analysis. Frederik Ungar Publishing Company, New York (1955)
Akhiezer, N.I., Glazman, I.M.: Theory of Linear Operators in Hilbert Space. Dover Books on Mathematics, Dover Publications, New York (1993)
Halmos, P.R.: A Hilbert Space Problem Book. Graduate Texts in Mathematics, 2nd edn. Springer, New York (1982)
Kreyszig, E.: Introductory Functional Analysis with Applications. Wiley Classics Library, Wiley, New York (1989)
Schmüdgen, K.: Unbounded Self-Adjoint Operators on Hilbert Space. Graduate Texts in Mathematics, vol. 265. Springer, Dordrecht (2012)
Hansen, F.: Functions of matrices with nonnegative entries. Linear Algebra Appl. 166, 29–43 (1992)
Hansen, F.: Operator inequalities associated with Jensen’s inequality. In: Rassias, T.M. (ed.) Survey on Classical Inequalities, pp. 67–98. Springer, Dordrecht (2000)
Micchelli, C.A., Willoughby, R.A.: On functions which preserve the class of Stieltjes matrices. Linear Algebra Appl. 23, 141–156 (1979)
Bhatia, R.: Matrix Analysis. Graduate Texts in Mathematics, Springer, New York (1997)
Carlen, E.: Trace inequalities and quantum entropy: an introductory course. In: Sims, R., Ueltschi, D. (eds.) Entropy and the Quantum. Contemporary Mathematics, vol. 529, pp. 73–140. American Mathematical Society, Providence (2010)
Hansen, F., Pedersen, G.K.: Jensen’s operator inequality. Bull. Lond. Math. Soc. 35(4), 553–564 (2003)
Dinh, T.H., Tikhonov, O.E.: To the theory of operator monotone and operator convex functions. Russ. Math. 54, 7–11 (2010)
Barrios, D., López-Lagomasino, G., Martínez-Finkelshtein, A., Torrano, E.: Finite-dimensional approximations of the resolvent of an infinite band matrix and continued fractions. Sb.: Math. 190(4), 501–519 (1999)
Dombrowski, J.: Orthogonal polynomials and functional analysis. In: Nevai, P. (ed.) Orthogonal Polynomials: Theory and Practice. NATO Science Series C, pp. 147–161. Springer, Dordrecht (1990)
Arai, A.: A general class of infinite dimensional Dirac operators and path integral representation of their index. J. Funct. Anal. 105(2), 342–408 (1992)
Hansen, A.C.: On the approximation of spectra of linear operators on Hilbert spaces. J. Funct. Anal. 254(8), 2092–2126 (2008)
Rösler, F.: On the solvability complexity index for unbounded selfadjoint and Schrödinger operators. Integral Equ. Oper. Theory 91, 54 (2019)
Davis, P.J., Rabinowitz, P.: Methods of Numerical Integration. Computer Science and Applied Mathematics, 2nd edn. Academic Press, San Diego (1984)
Bade, W.G.: Weak and strong limits of spectral operators. Pac. J. Math. 4(3), 393–413 (1954)
Foguel, S.R.: A perturbation theorem for scalar operators. Commun. Pure Appl. Math. 11(3), 293–295 (1958)
Simpson, J.E.: On limits of scalar operators. Trans. Am. Math. Soc. 122(1), 163–176 (1966)
Bartle, R.G., Sherbert, D.R.: Introduction to Real Analysis. Wiley, Hoboken (2011)
Morrison, K.E.: Spectral approximation of multiplication operators. N. Y. J. Math 1, 75–96 (1995)
Rudin, W.: Principles of Mathematical Analysis. International Series in Pure and Applied Mathematics, 3rd edn. International series in pure and applied mathematics. McGraw-Hill, New York (1976)
Kestelman, H.: Modern Theories of Integration, 2nd revised edn. Dover Books on Advanced Mathematics. Dover Publications, New York (1960)
Stummel, F.: Diskrete Konvergenz linearer Operatoren III. In: Butzer, P.L., Kahane, J.-P., Szökefalvi-Nagy, B. (eds.) Linear Operators and Approximation / Lineare Operatoren und Approximation: Proceedings of the Conference Held at the Oberwolfach Mathematical Research Institute, Black Forest, August 14–22, 1971 / Abhandlungen zur Tagung Im Mathematischen Forschungsinstitut Oberwolfach, Schwarzwald, Vom 14. Bis 22. August 1971, pp. 196–216. Birkhäuser Basel, Basel (1972)
Dunkl, C.F., Xu, Y.: Orthogonal Polynomials of Several Variables. Encyclopedia of Mathematics and Its Applications, 2nd edn. Cambridge University Press, Cambridge (2014)
Gautschi, W.: Orthogonal Polynomials: Computation and Approximation. Numerical Mathematics and Scientific Computation, Oxford University Press, Oxford (2004)
Dinh, T.H., Tikhonov, O.E., Veselova, L.V.: Inequalities for the extended positive part of a von Neumann algebra related to operator-monotone and operator-convex functions. Ann. Funct. Anal. 10(3), 425–432 (2019)
Habil, E.: Double sequences and double series. Islam. Univ. J. Ser. Nat. Stud. Eng. 14, 223–254 (2006)
Apostol, T.M.: Mathematical Analysis, 2nd edn. World Student Series Edition. Addison-Wesley, Reading (1974)
Acknowledgements
We thank the anonymous reviewers for their valuable comments. The work was supported by Academy of Finland (Grant no. 321891).
Funding
Open Access funding provided by Aalto University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Riemann–Stieltjes and Darboux–Stieltjes integrable functions
Appendix A: Riemann–Stieltjes and Darboux–Stieltjes integrable functions
The Riemann–Stieltjes integral has been defined in literature in two slightly different ways. We shall adopt a practice of using two different names for the two different definitions. First, we give the definition of the Riemann–Stieltjes integral and then the definition of the Darboux–Stieltjes integral.
A Riemann–Stieltjes integral over an interval [a, b] of a function f with respect to a monotonically non-decreasing function \(\rho \) is the following [37, 44]: Let a partition of the interval [a, b] be \(a=t_0<t_1<t_2<\cdots <t_n=b.\) The norm of the partition is \( \Delta =\max _k t_k-t_{k-1}. \) The Riemann–Stieltjes sum is \( S_n=\sum _{k=1}^n f(\xi _k)\,(\rho (t_k)-\rho (t_{k-1})). \) If the sequence \(S_n\) converges for all partitions for which \(\Delta \rightarrow 0\) and for any \(\xi _k\in [t_{k-1},t_k],\) then the function f is Riemann–Stieltjes integrable with respect to the function \(\rho .\)
The Riemann–Stieltjes integral is often defined so that the partitions are restricted to be refined [50, Definition 7.1]. That kind of change in the definition is equivalent [50, Theorem 7.19] to our second definition, the Darboux–Stieltjes integral [44, p. 250], which is also sometimes termed Riemann–Stieltjes integral [43, Definition 6.2]. A Darboux–Stieltjes integral over an interval [a, b] of a function f with respect to monotonically non-decreasing function \(\rho \) is the following: Let a partition of the interval [a, b] be \(a=t_0<t_1<t_2<\cdots <t_n=b.\) We define
Function f is Darboux–Stieltjes integrable with respect to function \(\rho ,\) if \( \inf U = \sup L \) when \(\inf \) and \(\sup \) are taken over all partitions.
The Darboux–Stieltjes integral is more general than the Riemann–Stieltjes integral [44, p. 250]. If f is Riemann–Stieltjes integrable with respect to \(\rho ,\) then f and \(\rho \) are nowhere simultaneously discontinuous [44, Theorem 317]. Darboux–Stieltjes integral does not have this limitation. If f is continuous whenever \(\rho \) is discontinuous, then the two definitions are equal [44, p. 251]. For the Riemann- and most of the Darboux–Stieltjes integrable functions, we have the following lemma.
Lemma 31
Let \(\rho (t)\) be a right continuous bounded non-decreasing function on interval [a, b]. Let f be a Riemann–Stieltjes integrable function with respect to \(\rho \) (or Darboux–Stieltjes integrable and continuous on the discontinuities of \(\rho ).\) Then for every \(\epsilon >0,\) there is a partition \(a=t_0<t_1<\cdots <t_n=b\) such that we can define step functions
and
so that
The points \(t_k\) can be chosen so that they are not discontinuity points of \(\rho .\)
Proof
The lemma is a straightforward consequence of a well-known result [43, Theorem 6.6] except for the last sentence. The last sentence follows because, due to the continuity, there is a \(\delta \) such that it is possible to move all the points \(t_k\) right by an arbitrary value on the interval \([0,\delta ].\) It is also possible to choose the new points on the intervals \([t_k,t_k+\delta ]\) so that they are not discontinuities of \(\rho .\)
We assume that the theorem holds without the last sentence for points \(\tilde{t}_k\) where \(\rho \) may possibly be discontinuous. Let functions \(\tilde{f}_u,\tilde{f}_l\) be determined like \(f_u,f_l\) in the statement of the theorem, except for the points \(\tilde{t}_k\) instead of points \(t_k.\) By the theorem without the last sentence, we have
If \(\rho \) is continuous at \(\tilde{t}_k,\) we set \(t_k=\tilde{t}_k.\) If not, we use the right continuity of \(\rho \) and f at point \(\tilde{t}_k.\) We select
Due to the right continuity of f and \(\rho ,\) there is a \(\delta >0\) so that for all \(t_k\)
It is also important to select the new \(t_k\) so that it is not a discontinuity point of \(\rho .\) This is possible because \(\rho \) is a non-decreasing function and such a function has at most countable number of discontinuities [43, Theorem 4.30]. Therefore, an interval \([\tilde{t}_k,\tilde{t}_k+\delta ]\) must have an infinite number of such points \(t_k\) where \(\rho \) is continuous. Additionally, for all \(k=1,2,\ldots m,\) we choose \(t_k\) so that \(t_{k-1}<\tilde{t}_k.\)
Next, we look at how \(f_u\) and \(f_l\) change compared to \(\tilde{f}_u\) and \(\tilde{f}_l,\) respectively. We break interval \([\tilde{t}_{k-1},t_k]\) into three parts at \(t_{k-1}\) and \(\tilde{t}_k.\) We notice that \( [\tilde{t}_{k-1},\tilde{t}_k]\supset [t_{k-1},\tilde{t}_k]\subset [t_{k-1},t_k]. \) Due to the continuity of f at points \(\tilde{t}_{k-1}\) and \(\tilde{t}_k,\) we have
which we sum to get
Similarly, \(|\tilde{f}_l(\tilde{t}_k)-f_l(t_k)|<\frac{\nu }{2}\) and thus \( |\tilde{f}_u(\tilde{t}_k)-\tilde{f}_l(\tilde{t}_k)-(f_u(t_k)-f_l(t_k))|<\nu . \) We mark now
for which we have inequalities \( |\tilde{r}_k-r_k|<\nu ,\) \(|\tilde{\Delta }_k-\Delta _k|<\nu ,\) \(|\tilde{r}_k| \le 2\sup |f|,\) and \(|\Delta _k|\le 2\,\sup |\rho |. \) By the triangle inequality, we have
Because both \(r_k\,\Delta _k\) and \(\tilde{r}_k\,\tilde{\Delta }_k\) are positive, this means that \( r_k\,\Delta _k\le \tilde{r}_k\,\tilde{\Delta }_k+\frac{\epsilon }{2\,n}. \) By (A1), we have \(\sum _{k=1}^n\tilde{r}_k\,\tilde{\Delta }_k<\frac{\epsilon }{2}, \) and therefore
where none of the \(t_k\) is a discontinuity point of \(\rho .\) \(\square \)
In the above proof, we used only the right continuity of f. However, f must be left continuous at points where \(\rho \) is not left continuous [50, Theorem 7.29].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sarmavuori, J., Särkkä, S. On the convergence of numerical integration as a finite matrix approximation to multiplication operator. Calcolo 60, 22 (2023). https://doi.org/10.1007/s10092-023-00518-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10092-023-00518-4