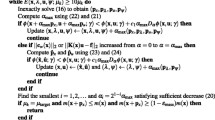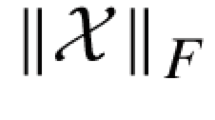Abstract
We propose an algorithm for computing the projection of a symmetric second-order tensor onto the cone of negative semidefinite symmetric tensors with respect to the inner product defined by an assigned positive definite symmetric fourth-order tensor \({\mathcal {C}}\). The projection problem is written as a semidefinite programming problem and an algorithm based on a primal-dual path-following interior point method coupled with a Mehrotra’s predictor-corrector approach is proposed. Implementations based on well-known symmetrization schemes and on direct methods are theoretically and numerically investigated taking into account tensors \({\mathcal {C}}\) arising in the modelling of masonry-like materials. For these special cases, indications on the preferable symmetrization scheme that take into account the conditioning of the arising linear systems are given.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Matrix nearness problems are introduced in [14] where for a fixed matrix A, the problem of finding the nearest member of some given class of matrices is addressed, where distance is measured in a matrix norm. The problem of approximating a matrix with a positive semidefinite symmetric matrix is ubiquitous in scientific computing, see e.g. [13,14,15,16]. In particular, in [15], numerical methods are proposed to calculate the minimum distance between a matrix A and a positive definite symmetric matrix X, considering the Frobenius norm and the 2-norm. Motivated by relevant applications in finance industry, more recent contributions [2, 13, 16, 23, 27] deal with the computation of the projection of a symmetric matrix onto the set of correlation matrices, namely positive semidefinite symmetric matrices with ones on the diagonal.
In this paper, we are concerned with the computation of the projection of a symmetric second-order tensor onto the cone of negative semidefinite symmetric tensors with respect to the inner product defined by an assigned positive definite symmetric fourth-order tensor \({\mathcal {C}}\). In particular, for a given symmetric tensor \(\mathbf {D}\), we want to minimize the distance \(\phi (\mathbf {Y})=\parallel {\mathbf {D}-\mathbf {Y}}\parallel _{{\mathcal {C}}}^{2}\) between \(\mathbf {D}\) and \(\mathbf {Y}\), with \(\mathbf {Y}\) belonging to the cone \(Sym^{-}\) of negative semidefinite symmetric tensors. Problems similar to the minimization of \(\phi (\mathbf {Y})\) in \(Sym^{-}\) have been addressed in [13], where numerical methods for conic projection problems are presented. In particular, in [13], the problem of minimizing the standard Frobenius distance between a given matrix C and a symmetric positive semidefinite matrix X and satisfying a further equality linear constraint is introduced. Then, in [13] (Eq. (7)) the focus is on the more general problem of finding the projection of a vector c onto the intersection of a convex closed set and a convex polyhedron defined by affine inequalities, with respect to \(\parallel x\parallel _{Q}^{2}=x\cdot Qx\), the norm associated to a positive definite matrix Q. In particular, Eq. (7) in [13] is the vector counterpart of our tensor problem in the cone \(Sym^{-}\).
The relevance of the projection problem proposed in the present paper is twofold. Firstly, it is a generalization of the problem dealt with in [15], as in the place of the Frobenius norm, we consider a norm induced by a scalar product defined by an assigned fourth-order tensor \({\mathcal {C}}\). Secondly, its solution allows to model masonry-like materials [7, 22]. In fact, the stress tensor for materials that do not withstand tension can be obtained by suitably projecting the strain tensor onto the cone of negative semidefinite symmetric tensors. Solving such a projection problem has a crucial role in solid mechanics and civil engineering applications, as it allows to calculate a solution to the equilibrium problem of masonry constructions. Fourth-order tensor \({\mathcal {C}}\) contains the mechanical properties of the masonry material and can take different forms depending on the anisotropy of the material [22]. Apart from the isotropic case, for which the explicit solution to the projection problem is available, in the general anisotropic case numerical methods are necessary to calculate the approximate solution. Rather than designing efficient algorithms for large scale problems as done in most of the literature [2, 13, 23], the focus of this work is providing an accurate and cost-effective numerical procedure for small size projection, as done in [17], where an algorithm to compute the polar decomposition of a \(3\times 3\) matrix is proposed. This framework is strongly motivated by the application in the field of solids mechanics and, in particular, on masonry-like materials, where the dimension of the addressed problem is very low. Indeed the considered second-order tensors are linear functions from a three-dimensional vector space into itself. Moreover, the accurate solution of a projection problem is required for each Gauss points of each element constituting the finite element discretization of the masonry structure under examination. Thus, similarly to [17], our algorithm must solve a large number of small size problems accurately.
Inspired by the works [2, 31, 32] for the large-scale setting, we propose to solve the projection problem by using a SemiDefinite Programming (SDP) approach and developing an interior point algorithm that exploits the peculiarities of the problem under consideration. Interior point methods stand out as reliable algorithms which enjoy enviable convergence properties and usually provide accurate solutions within reasonable time. Several proposals are available in the literature for both general and application oriented SDPs, see e.g. [4, 5, 12, 20, 29, 32] and references therein.
In this work we first show that our projection problem can be reformulated as a special monotone semidefinite linear complementarity problem (SDLCP) and observe that it is equivalent to a convex Quadratic SemiDefinteProgramming (QSDP) problem where there are no linear equality constraints. Then we describe a primal-dual path-following interior point that uses Mehrotra’s predictor-corrector steps [31, 32, 34] and adapted it to our QSDP. In particular, we considered two of the most used symmetrization schemes, that is the Nesterov-Todd (NT) direction and the Alizadeh-Haeberly-Overton (AHO) one [28], and focused on the solution of the linear system by direct methods. As a major contribution of this work we show that, when a very accurate solution is required, the use of the popular NT direction yields highly ill-conditioned Schur complement linear systems that may prevent the computation of an accurate solution. On the other hand, we provide a formulation of the Newton’s equation with a much favourable condition number when the AHO direction is used and the \({\mathcal {C}}\) has a special form of interest in solid mechanics. For this case, a theoretical insight of this behaviour is given. The addressed theoretical issues are validated on a number of application oriented numerical tests.
As an outcome of the obtained good numerical results, the proposed algorithm will be implemented in the finite element code NOSA-ITACA [24] developed at ISTI-CNR for the structural analysis of masonry constructions. The implementation and the application of the code to a case study will be the subject of future work.
This paper is organized as follows. In Sect. 2, we list several notions and definitions to be used in the paper that attempt to merge standard notation used in solid mechanics and in SDPs. Section 3 describes the projection problem in the space of symmetric tensors equipped with the scalar product associated with a positive definite symmetric fourth-order tensor \({\mathcal {C}}\). Some results deriving from the minimum norm theorem are proved, including the possibility of expressing the projection problem as a complementarity problem. In Sect. 4, some special forms of \({\mathcal {C}}\) of interest in solid mechanics are presented, focusing on isotropic and transversely isotropic \({\mathcal {C}}\). In particular, the explicit expression of the projection for isotropic \({\mathcal {C}}\) is provided. The transversely isotropic case can not be solved explicitly, and the projection is calculated only for a restricted class of tensors \(\mathbf {D}\). Section 5 contains the description of the primal-dual path-following interior point algorithm adopted for the efficient and accurate solution of the complementarity problem associated with the projection problem. Issues about the conditioning of the arising Newton’s equations depending on the symmetrization scheme are discussed in Sect. 5.1. Section 6 is devoted to the description of the numerical experience. First the implementation of the proposed algorithm is described. Then the data sets are introduced and numerical results are discussed. Conclusions are drawn in Sect. 7.
2 Notations and preliminaries
Let \(\mathcal {V}\) be a real vector space of dimension 3 with the inner product \(\cdot\). Let Lin be the set of all second-order tensors (a second-order tensor, or more simply a tensor, is a linear application from \(\mathcal {V}\) to itself) with the inner product \(\mathbf {A}\bullet \mathbf {B}=tr(\mathbf {A}^{T}\mathbf {B})\) for any \(\mathbf {A}, \mathbf {B}\in\) Lin, with \(\mathbf {A}^{T}\) the transpose of \(\mathbf {A}\) and let \(\parallel \mathbf {A} \parallel = \sqrt{\mathbf {A} \bullet \mathbf {A}}\) be the associated Frobenius norm.
For Sym the subspace of symmetric tensors, \(Sym^{-}\), \(Sym^{+}\) and \(Sym^{++}\) are the sets of all negative semidefinite, positive semidefinite and positive definite elements of Sym, respectively. Orth denotes the group of all orthogonal tensors.
Given the tensors \(\mathbf {A}\) and \(\mathbf {B}\), the tensor product \(\mathbf {A}\odot \mathbf {B}\) of \(\mathbf {A}\) and \(\mathbf {B}\) is the fourth-order tensor (a fourth-order tensor is a linear application from Lin to itself) defined by
\(\mathbf {A}\otimes \mathbf {B}\) is the fourth-order tensor defined by
and we denote by \({\mathbb {I}}_{Sym}\) the fourth-order identity tensor on Sym. For \(\mathbf {a}\) and \(\mathbf {b}\) vectors, the tensor product \(\mathbf {a} \odot \mathbf {b}\) of \(\mathbf {a}\) and \(\mathbf {b}\) is defined by \(\mathbf {a}\odot \mathbf {bh}=(\mathbf {b} \cdot \mathbf {h})\mathbf {a},\) for any vector \(\mathbf {h}\)Footnote 1.
Let \({\mathcal {C}}\) be a fourth-order tensor from Sym to Sym. Let us assume that \({\mathcal {C}}\) is symmetric, i.e.
and positive definite on Sym, i.e.
Because of (2) and (1) \({\mathcal {C}}\) is invertible and its inverse \({\mathcal {C}}^{-1}\) is symmetric and positive definite. Moreover, properties (2) and (1) allow defining the following inner product \(\circ\) on Sym,
and the associated squared \({\mathcal {C}}\)-norm
Let \({\mathsf {P}}= (\mathbf {p}_{1},\mathbf {p}_{2},\mathbf {p}_{3})\) be an orthonormal basis of \(\mathcal {V}\). For \(\mathbf {D}\in Sym\) and \({\mathcal {C}}\) symmetric and positive definite, the components \(D_{ij}\) of \(\mathbf {D}\), \({\mathcal {C}}_{ijkl}\) of \({\mathcal {C}}\) and \({\mathcal {C}}_{ijkl}^{-1}\) of \({\mathcal {C}}^{-1}\) with respect to \({\mathsf {P}}\) are
These components are reported in the Appendix for the special forms of \({\mathcal {C}}\) described in Section 4.
Because \({\mathcal {C}}\) and \({\mathcal {C}}^{-1}\) are symmetric fourth-order tensors from Sym to Sym, their components satisfy the following equalities
With these notations, for a given symmetric tensor \(\mathbf {A}\), the symmetric tensor
has components
It may be convenient to adopt a vector notation in the place of the tensor notation described above. Thus, a symmetric tensor \(\mathbf {A}\) is replaced by the vector \(\mathbf {a}\) with the six components
such that \(\mathbf {a}\cdot \mathbf {a}=\mathbf {A}\bullet \mathbf {A}=tr(\mathbf {A}^2)\). Then, for \(\mathbf {b}\) the vector associated to \(\mathbf {B}\), from (6) we get
where the matrix of the components of \(\mathbf {{\widetilde{C}}}\) is
Finally, we denote by \(\lambda _{\min }(\mathbf {A})\), and \(\lambda _{\max }(\mathbf {A})\) the minimum and maximum eigenvalue of a tensor \(\mathbf {A}\), respectively. Analogous notation is adopted for a fourth-order tensor \(\mathcal {A}\).
3 The projection problem
Given \(\mathbf {D}\in Sym\), we address the problem of minimizing the following functional
over the set of negative semidefinite symmetric tensors \(Sym^{-}\). Since \(Sym^{-}\) is a closed convex cone of Sym, in view of the minimum norm theorem [6], there exists a unique minimum point \({\mathbf {Y}}^*\in Sym^{-}\) for the functional (7). Moreover, \({\mathbf {Y}}^*\) is the minimum point of (7) if and only if it satisfies the variational inequality
which, expressed in terms of the inner product \(\bullet\), reads
The following proposition gives a characterization of the minimizer of the functional \(\phi\) in (7) over \(Sym^{-}\).
Proposition 1
For \(\mathbf {D}\in Sym\), there exists a unique \({\mathbf {Y}}^* \in Sym^{-}\) satisfying the following three equivalent statements
-
(i)
\({\mathbf {Y}}^*\) minimizes functional \(\phi\) in (7)
$$\begin{aligned} \phi ({\mathbf {Y}}^*)\le \phi (\mathbf {Y}) , \, \text{ for } \text{ each } \,\mathbf {Y}\in Sym^{-}. \end{aligned}$$ -
(ii)
\({\mathbf {Y}}^*\) satisfies the following complementarity problem
$$\begin{aligned}&{\mathcal {C}}(\mathbf {D}-{\mathbf {Y}}^*)\in Sym^{+}, \end{aligned}$$(9)$$\begin{aligned}&{\mathbf {Y}}^*\bullet {\mathcal {C}}(\mathbf {D}-{\mathbf {Y}}^*)=0. \end{aligned}$$(10) -
(iii)
\({\mathbf {Y}}^*\) satisfies the variational inequality (8).
Proof
Equivalence of (i) and (iii) follows from the minimum norm theorem [6]. It is an easy matter to show that (ii) implies (iii). The proof that (iii) implies (ii) is based on the fact that \(Sym^{-}\) is a cone, in fact from (8), for \(\mathbf {Y}=\mathbf {0}\) and for \(\mathbf {Y}=2{\mathbf {Y}}^*\), we get (10); condition (9) follows from (8) putting \(\mathbf {Y}={\mathbf {Y}}^*+\mathbf {Y}^\#\), with \(\mathbf {Y}^\#\in Sym^{-}\). \(\square\)
The minimum point \({\mathbf {Y}}^*\) of the functional (7) is the projection of \(\mathbf {D}\) onto \(Sym^{-}\) with respect to the inner product \(\circ\) in Sym. Letting \(P_{{\mathcal {C}},Sym^{-}}: Sym \rightarrow Sym^{-}\) be the nonlinear function which associates to each symmetric tensor its projection onto \(Sym^{-}\) with respect to the inner product (3), we have, therefore that
The projection \(P_{{\mathcal {C}}, Sym^{-}}\) is monotone, Lipschitz continuous, and homogeneous of degree 1, i.e.
and satisfies
Moreover, it is infinitely often Fréchet differentiable on an open dense subset of Sym [25].
From (9) and (10), it follows that if \({\mathcal {C}}(\mathbf {D}) \in Sym^+\), then \({\mathbf {Y}}^*=\mathbf {0}\), and if \(\mathbf {D} \in Sym^-\), then \({\mathbf {Y}}^*=\mathbf {D}\). Moreover, it is easy to prove that when tensors \({\mathbf {Y}}^*\) and \({\mathcal {C}}(\mathbf {D}-{\mathbf {Y}}^*)\) satisfy (9) and (10), then they commute [7, 22],
Thus \({\mathbf {Y}}^*\) and \({\mathcal {C}}(\mathbf {D}-{\mathbf {Y}}^*)\) are coaxial [7, 22], that is there exists an orthonormal basis of \(\mathcal {V}\) constituted by eigenvectors of both \({\mathbf {Y}}^*\) and \({\mathcal {C}}(\mathbf {D}-{\mathbf {Y}}^*)\). From Proposition 1, it follows that each tensor \(\mathbf {D} \in Sym\) can be expressed as the following sum
where \({\mathbf {Y}}^*\) belongs to \(Sym^{-}\) and \(\mathbf {D}-{\mathbf {Y}}^*\) belongs to \({\mathcal {C}}^{-1}Sym^{+}\), with
4 Fourth-order tensors \({\mathcal {C}}\) in solid mechanics
We now describe some possible choices of the symmetric and positive definite tensor \({\mathcal {C}}\) giving details of tensors arising when modelling masonry-like materials that motivated this work.
When the tensor \({\mathcal {C}}\) coincides with the identity tensor, i.e.
then the \({\mathcal {C}}\)-norm coincides with the Frobenius norm. Given \(\mathbf {C}\in Sym\) positive definite, the fourth-order tensor defined by
is symmetric and positive definite and define the weighted Frobenius norm
This norm was introduced in [16], where the problem of finding the nearest correlation matrix is addressed, [14, 15].
Other expressions for \({\mathcal {C}}\) can be chosen within the framework of solids mechanics. In particular, minimizing functional (7) has interesting applications in modelling the mechanical behaviour of masonry constructions. If one adopts the constitutive equation of masonry-like materials [7, 22] to model masonry materials, it is possible to prove that the stress \({\mathbf {Y}}^*\) associated with the infinitesimal strain \(\mathbf {D}\) is the projection of \({\mathcal {C}}(\mathbf {D})\) onto \(Sym^{-}\) with respect to the inner product defined in (3), with \({\mathcal {C}}^{-1}\) in place of \({\mathcal {C}}\). Here \({\mathcal {C}}\) represents the elasticity tensor of the material and can have several expressions depending on its different degrees of anisotropy. In order to recall some of these expressions [10, 11, 26] the following definition has to be introduced. Let \(\varGamma\) be a subset of Orth, we say that \({\mathcal {C}}\) is invariant under \(\varGamma\) if
It is an easy matter to show that if \({\mathcal {C}}\) is invariant under \(\varGamma\), the same holds for \({\mathcal {C}}^{-1}\).
4.1 The isotropic case
If \({\mathcal {C}}\) satisfies the condition (13) with \(\varGamma =Orth\), then there exist two real numbers E and \(\nu\) such that \({\mathcal {C}}\) has the representation
where \(\mathbf {I}\in Sym\) is the identity tensor [10]. In this case, tensor \({\mathcal {C}}\) is called isotropic and is the elasticity tensor of an isotropic elastic material with Young’s modulus E and the Poisson’s ratio \(\nu\) [11]. Because of (2), E and \(\nu\) satisfy the conditions
We point out that if \(E=1\) and \(\nu =0\), tensor in (14) is the identity tensor. When \({\mathcal {C}}\) has the expression in (14), its inverse is
Let us now limit ourselves to consider the isotropic fourth-order tensor \({\mathcal {C}}\) in (14). In this case, from the coaxiality of tensors \({\mathbf {Y}}^*\) and \({\mathcal {C}}(\mathbf {D}-{\mathbf {Y}}^*)\), it follows that \(\mathbf {D}\) and \({\mathbf {Y}}^*\) are coaxial as well. This property makes it easy to calculate for each choice of \(\mathbf {D}\) the minimum point of \(\phi\) explicitly, and then compare the explicit solution to the numerical one. By virtue of Proposition 1 the minimum point of \(\phi\) coincides with the solution of (9)–(10), which, since the involved tensors are coaxial, is a classical linear complementarity problem in \({\mathbb {R}}^3\), the unknowns being the eigenvalues of \({\mathbf {Y}}^*\). For the sake of comparison, the explicit solution \({\mathbf {Y}}^*\) is summarized in the following (see e.g. [22]).
For \(\mathbf {D}\in Sym,\) let \(d_{1}\le d_{2}\le d_{3}\) be its ordered eigenvalues and \(\mathbf {q}_{1},\) \(\mathbf {q}_{2},\mathbf {q}_{3}\) be the corresponding eigenvectors. We introduce the following tensors of Sym
Given \(\mathbf {D}\), the corresponding minimum point \({\mathbf {Y}}^*\) of the functional \(\phi\) in (7) is
When \(\nu =0\), tensor \({\mathcal {C}}\) is equal to \(E {\mathbb {I}}_{Sym}\) and the projection of \(\mathbf {D}\) onto \(Sym^{-}\) with respect to the inner product associated with \({\mathcal {C}}\), is
where the square root \(\sqrt{\mathbf {A}}\) of the positive semidefinite symmetric tensor \(\mathbf {A}\) is the unique positive semidefinite symmetric tensor \(\mathbf {B}\), such that \(\mathbf {B}^2=\mathbf {A}\).
4.2 The transversely isotropic case
If \(\varGamma\) is a proper subset of Orth, then \({\mathcal {C}}\) satisfying (13) is said anisotropic. In this paper, we limit our attention to only one kind of anisotropic tensors, corresponding to the transverse isotropic materials, described in the following.
A fourth-order tensor \({\mathcal {C}}\) is said transversely isotropic if there exists a unit vector \(\mathbf {f}_3\) (the preferred direction of transverse isotropy) such that \({\mathcal {C}}\) is invariant under the subgroup \(\varGamma _{TI} \subset Orth\) constituted by all the rotations about \(\mathbf {f}_3\),
Let \({\mathsf {F}}= (\mathbf {f}_{1},\mathbf {f}_{2},\mathbf {f}_{3})\) be an orthonormal basis of \(\mathcal {V}\). If tensor \({\mathcal {C}}\) is transversely isotropic with respect to the direction \(\mathbf {f}_{3}\), then \({\mathcal {C}}\) has the following representation [26]
where
with \(\mathbf {R}=\mathbf {f}_3 \odot \mathbf {f}_3\) and \(\mathbf {Q}=\mathbf {I}-\mathbf {R}\). The real numbers \(\alpha _i\) satisfy the conditions
which guarantee the positive definiteness of \({\mathcal {C}}\) in (22). Tensor \({\mathcal {C}}\) in (22) describes the mechanical behaviour of a transversely isotropic elastic material [10, 26]. For \(\alpha _3=2 \alpha _2-\alpha _1\) and \(\alpha _4=\alpha _5=\alpha _1-\alpha _2\) the fourth-order tensor in (22) becomes isotropic,
with
In the anisotropic case \(\mathbf {D}\) and \({\mathbf {Y}}^*\) are not coaxial and the the minimum point of functional \(\phi\) can be calculated explicitly only for a few choices of \(\mathbf {D}\). In particular, when \(\mathbf {D}\) has the eigenvector \(\mathbf {f}_3\), then \(\mathbf {D}\), \({\mathbf {Y}}^*\) and \({\mathcal {C}}(\mathbf {D}-{\mathbf {Y}}^*)\) are coaxial and the minimum point \({\mathbf {Y}}^*\) of \(\phi\) can be calculated adopting the same procedure as in the isotropic case. Its explicit expression is provided in the following.
Given \(\mathbf {D}\in Sym,\) let \(d_{1}\le d_{2}\le d_{3}\) be its ordered eigenvalues and \(\mathbf {q}_{1},\) \(\mathbf {q}_{2},\mathbf {f}_{3}\) be the corresponding eigenvectors. For \(\mathbf {O}_{11}\) and \(\mathbf {O}_{22}\) defined in (17), the solution \({\mathbf {Y}}^*\) has the following expressions.
In general, suitable numerical strategies should be adopted to calculate the minimum point of \(\phi\), as proposed in the next section.
5 A primal-dual path following interior-point method
The numerical computation of the minimum point of functional (7) can be efficiently performed by exploiting the characterization of the solutions described in (9) and (10). Indeed, setting \({\mathbf {X}}=-{\mathbf {Y}}\) these conditions describe the following monotone semidefinite linear complementarity problem (SDLCP) in the space of symmetric tensors
where the affine subspace \({\varLambda }\subseteq Sym \times Sym\) is given by
The subspace \({\varLambda }\) has dimension 6 and is monotone as
for all \(({\mathbf {X}}',{\mathbf {S}}')\) and \(({\mathbf {X}},{\mathbf {S}}) \in {\varLambda }\).
We now describe an interior point algorithm for the efficient and accurate solution of (29) that exploits the form of the tensors \({\mathcal {C}}\) presented in the previous section. In [18,19,20], the general theoretical framework of the algorithm is given for SDLCPs with affine subspaces \({\varLambda }\) of a general form but our practical implementation is based on that of interior-point approaches in [31, 32] for a somehow related problem, that is the solution of convex Quadratic SemiDefinte Programming (QSDP) problems.
Problem (29), and equivalently (9) and (10) with \({\mathbf {Y}}=-{\mathbf {X}}\), are in fact the first-order optimality conditions of the following QSDP problem
This problem differs with respect to the standard formulation of QSDPs as only positive semidefiniteness constraints are present while the usual linear constraints are not included, see e.g. [32]. Clearly, the functionals \(p({\mathbf {X}})\) and \(\phi ({\mathbf {Y}})\) defined in (7) and (30) respectively, have the same minimizers (up to the sign).
Several methods have been proposed in the literature for standard QSDPs ranging from interior point methods [31, 32] to semismooth Newton approaches [21], passing through reformulations as a standard semidefinite-quadratic-linear program [2]. Most of these works focus on the design and analysis of efficient algorithms for the case where the matrix dimensions and/or the number of linear constraints are large, and it may be impossible to explicitly store or compute the matrix representation of \({\mathcal {C}}\). Conversely, here we are interested in the accurate solution of problem (30) in the small case setting and propose to use a primal-dual path-following interior point method in the spirit of [31, 32].
We now describe the main steps of an interior point method based on the primal-dual path-following method given in [31, 32] for the solution of (30) coupled with its dual form:
The algorithm, named IPM-Proj, uses Mehrotra’s predictor-corrector steps and practical details are postponed to Sect. 6.1. IPM-Proj is based on approximating a sequence of points on the central path. The central path is defined as the set of solutions \(({\mathbf {X}}_{\mu }, {\mathbf {S}}_{\mu })\) to the central path equations
where \(\sigma \in [0,1]\) is the centering parameter and \(\mu\) is the duality measure defined by
Equations (32) can be also interpreted as the perturbed first-order optimality conditions for problems (30)–(31). Fixed \(\sigma\) and assuming that there exists \(({\mathbf {X}},{\mathbf {S}}) \in {\varLambda }\) with \({\mathbf {X}}\in Sym^{++}\) and \({\mathbf {S}}\in Sym^{++}\), then [20, Theorem 3.1] ensures that for every \(\mu > 0\), there exists a unique \(({\mathbf {X}}_\mu ,{\mathbf {S}}_\mu )\) that lies on the central path, that is that solves (32).
Note that the first block equation in \(F_{\mu }\) above is affine linear, while the second is mildly nonlinear. Hence a Newton step seems a natural idea for an iterative algorithm. Unfortunately, the residual map \(F_\mu\) takes an iterate \(({\mathbf {X}}, {\mathbf {S}}) \in Sym \times Sym\) to a point in \(Sym\times Lin\) (since \({\mathbf {X}}{\mathbf {S}}- \mu \mathbf {I}\) is in general not symmetric), which is a space of higher dimension, and so Newton’s method cannot be applied directly. To apply Newton-type algorithms it is previously necessary to symmetrize the term \({\mathbf {X}}{\mathbf {S}}\) so that the resulting equivalent nonlinear system gives a function that maps \(Sym \times Sym\). A popular and effective technique to overcome this issue is introducing general symmetrization scheme based on the fourth-order tensor \({\mathcal {H}}_{\mathbf {P}} : Lin \rightarrow Sym\) defined as
where \({\mathbf {P}}\) is some nonsingular tensor, see [28] and references therein.
It has been shown that for any nonsingular tensor \({\mathbf {P}}\), the system \(F_{\mu }({\mathbf {X}},{\mathbf {S}})= \mathbf{0}\) in (32) is equivalent to the system
to which a Newton-type method can be applied, see e.g. [30]. Having fixed \(\mu\) and given the current iteration \(({\mathbf {X}}, {\mathbf {S}})\), let \((\varDelta {\mathbf {X}}, \varDelta {\mathbf {S}})\in Sym \times Sym\) denote a Newton direction. Then it satisfies
where the fourth-order tensors \({\mathcal {E}}={\mathcal {E}}({\mathbf {X}},{\mathbf {S}})\) and \({\mathcal {F}}={\mathcal {F}}({\mathbf {X}},{\mathbf {S}})\) are the derivative of \({\mathcal {H}}_{\mathbf {P}}\) with respect to \({\mathbf {X}}\) and \({\mathbf {S}}\) respectively, evaluated at the current iterate, i.e.
and \({\mathbf {R}}_d\) and \({\mathbf {R}}_c\) are the current dual residual and complementarity gap given by
We remark that a crucial role in the the theory and implementation of interior-point methods is played by centrality, that is the solution of the equation \({\mathbf {X}}{\mathbf {S}}= \sigma \mu {\mathbf {I}}\) (or its symmetrization) that takes into account the fulfillment of the complementarity conditions [8] . The main idea of the Mehrotra’s predictor-corrector approach takes inspirations from the predictor-corrector algorithms in ordinary differential equations and consists in splitting the computation of the solution of the system (34)–(35) into two steps. The first step, named the “predictor step”, attempts to reach complementarity and optimality in just one shot by ignoring the perturbation \(\mu\) in the system and then solves (35) by setting \(\sigma =0\). In fact, the predictor step ignores centrality and predicts how much progress in reducing the complementarity gap and infeasibilities may be achieved. Let \((\delta {\mathbf {X}},\delta {\mathbf {S}})\) denote the predictor step. If a full step in this direction was made then the new complementarity product would be
as \({\mathcal {H}}_{\mathbf {P}}({\mathbf {X}}\, \delta {\mathbf {S}}+\delta {\mathbf {X}}\, {\mathbf {S}}) = \mathbf {0}\) from (35) with \(\sigma =0\). Therefore, the “corrector step" solves (34)–(35) with the “corrected" right-hand-side
see also [31] (see further algorithmic details of the predictor-corrector approach in Section 6.1).
Depending on the choice of \(\mathbf {P}\), the tensors \({\mathcal {E}}\) and \({\mathcal {F}}\) have a different form and therefore different forms for the equations (34)--(35) can be derived. Several choices for \(\mathbf {P}\) are available in the literature [28]. One of the most popular choice yields the so-called Nesterov-Todd (NT) direction [30] and is obtained by choosing \({\mathbf {P}} = {\mathbf {W}}^{-1/2}\) with \({\mathbf {W}}\) being the geometric mean of \({\mathbf {X}}\) and \({\mathbf {S}}^{-1}\), i.e.
(\({\mathbf {W}}{\mathbf {S}}{\mathbf {W}}={\mathbf {X}}\)). The corresponding forms of \({\mathcal {E}}\) and \({\mathcal {F}}\) and \({\mathbf {R}}_c\) are:
The popularity of the NT direction is motivated by the fact that methods based on NT are shown to be fast and robust. Also, the NT direction is implemented in SDTP3 [34] that is widely considered as the state-of-art software for solving SDPs. Moreover, system (34)–(35) has a unique solution under mild assumptions, e.g. [30, Theorem 3.1]. Indeed, assuming that \({\mathcal {E}}\) is nonsingular, system (34)–(35) has a unique solution if and only if the Schur complement
is positive definite [30]. This condition holds when \({\mathbf {X}}, {\mathbf {S}}\) and \({\mathcal {H}}_{\mathbf {P}}({\mathbf {X}}{\mathbf {S}})\) are positive semidefinite. In particular, \({\mathcal {H}}_{\mathbf {P}}\) is positive definite whenever \(\mathbf {P}\) is an invertible tensor that satisfies \(\mathbf {P}^T \mathbf {P} = {\mathbf {W}}^{-1}\) where \({\mathbf {W}}\) is such that \({\mathbf {W}}{\mathbf {S}}{\mathbf {W}}= {\mathbf {S}}\), as for the NT direction, see [30].
The application of the method in [31, 32] to problems (30)–(31) yields the following procedure for the solution of the Newton system (34)–(35): solve the Schur complement system
and compute \(\varDelta {\mathbf {X}}= {\mathcal {C}}^{-1}({\mathbf {R}}_d- \varDelta {\mathbf {S}})\).
For the NT direction, the Schur complement tensor takes the form
where \({\mathbf {W}}\) is given in (38) and we recall that \({\mathcal {C}}\) is nonsingular on Sym and that the inverse \({\mathcal {C}}^{-1}\) is explicitly available in the applications considered in this work.
In the next section we will show that the solution of (39) with \({\mathcal {S}}_{NT}\) may yield an inaccurate solution of the original problem (29) due to the fast increasing of the condition number of \({\mathcal {S}}_{NT}\) as \(\mu\) goes to zero.
In order to provide an accurate solution of problem (29), we propose to use an alternative choice of the tensor \({\mathbf {P}}\) that was firstly proposed in [1] and yields the so-called Alizadeh–Haeberly–Overton (AHO) direction. The AHO direction corresponds to set \({\mathbf {P}} = {\mathbf {I}}\) that gives
We observe that with this choice of \({\mathbf {P}}\), the Newton system (34)–(35) admits a unique solution when \({\mathbf {X}},{\mathbf {S}}\) are positive semidefinite and \({\mathbf {X}}{\mathbf {S}}+ {\mathbf {S}}{\mathbf {X}}\) is positive definite [20, Corollary 3.2].
As alternative to the linear system with the Schur complement in (39), in this work we propose to solve a different linear system that for the AHO direction possesses optimal conditioning properties when the tensor \({\mathcal {C}}\) is of the form (14) or (22)–(24) discussed in Sect. 4. Indeed, a solution of (34)–(35) can be obtained also by computing \(\varDelta {\mathbf {X}}\) from
where
and then retrieving \(\varDelta {\mathbf {S}}\) form (34). In fact, for the AHO direction, the above tensor \({\mathcal {M}}\) has the following special form
We observe that while the Schur complement \({\mathcal {S}}\) is symmetric the tensor \({\mathcal {M}}\) is in general nonsymmetric. The conditioning properties of \({\mathcal {S}}_{NT}\) and \({\mathcal {M}}_{AHO}\) are discussed in the next section.
5.1 Conditioning issues
Let \({\mu ^{(k)}}\) be a monotonically decreasing sequence such that \(\lim _{k\rightarrow \infty } \mu ^{(k)} =0\) and let \(({\mathbf {X}}^{(k)}, {\mathbf {S}}^{(k)})\) be a point on the central path corresponding to \(\mu ^{(k)}\), that is \(({\mathbf {X}}^{(k)}, {\mathbf {S}}^{(k)})\) satisfies (32). Moreover, let \({\mathcal {S}}_{NT}^{(k)}\) and \({\mathcal {M}}_{AHO}^{(k)}\) be the corresponding tensors of the Newton systems given in (40) and (42), respectively.
Assume that the sequence \(({\mathbf {X}}^{(k)}, {\mathbf {S}}^{(k)})\) converges to the optimal solution \(({\mathbf {X}}^*, {\mathbf {S}}^*)\) as \(\mu ^{(k)}\) tends to zero and that the ranks of \({\mathbf {X}}^*\) and \({\mathbf {S}}^*\) sum up to 3.
We will now show that under these conditions, the condition number of \({\mathcal {S}}^{(k)}_{NT}\) may not be bounded for \(\mu ^{(k)} \rightarrow 0\) while the condition number of \({\mathcal {M}}^{(k)}_{AHO}\) is uniformly bounded for \(\mu ^{(k)} \rightarrow 0\) when \({\mathcal {C}}\) is the isotropic tensor in (14). Moreover we conjecture that the condition number of \({\mathcal {M}}^{(k)}_{AHO}\) is still bounded in the transversely isotropic case in (22).
Let \(\lambda _1^{(k)}, \lambda _2^{(k)}, \lambda _3^{(k)}\) and \(\xi _1^{(k)}, \xi _2^{(k)}, \xi _3^{(k)}\) be the eigenvalues of \({\mathbf {X}}^{(k)}\) and \({\mathbf {S}}^{(k)}\), respectively. We observe that \({\mathbf {X}}^{(k)}\) and \({\mathbf {S}}^{(k)}\) commute and we denote by \((\mathbf {q}_1^{(k)}, \mathbf {q}_2^{(k)}, \mathbf {q}_3^{(k)})\) a basis of common eigenvectors, moreover it holds
Let \(\lambda _1^{*}, \lambda _2^{*}, \lambda _3^{*}\) and \(\xi _1^{*}, \xi _2^{*}, \xi _3^{*}\) be the eigenvalues of \({\mathbf {X}}^*\) and \({\mathbf {S}}^*\), respectively. They satisfy \(\lambda _i^*\xi _i^* = 0\) and since \(rank({\mathbf {X}}^*)+rank({\mathbf {S}}^*) = 3\), only the following 4 cases can occur:
-
case 1: \(\xi _1^*, \xi _2^*,\xi _3^* >0\), \(\lambda _1^*=\lambda _2^*=\lambda _3^*=0\);
-
case 2: \(\xi _1^*, \xi _2^* >0\) and \(\xi ^*_3=0\), \(\lambda _1^*=\lambda _2^*=0\) and \(\lambda _3^*>0\);
-
case 3: \(\xi _1^* >0\) and \(\xi _2^*=\xi ^*_3=0\), \(\lambda _1^*=0\) and \(\lambda _2^*, \lambda _3^*>0\);
-
case 4: \(\xi _1^*=\xi _2^*=\xi _3^*=0\), \(\lambda _1^*,\lambda _2^*,\lambda _3^*>0\).
We now compute the eigenvalues of \({\mathbf {W}}^{(k)} \otimes {\mathbf {W}}^{(k)}\). Since \({\mathbf {S}}^{(k)}\) and \({\mathbf {X}}^{(k)}\) lie on the central path, by the definition of \({\mathbf {W}}^{(k)}\) in (38) we have that the eigenvalues of \({\mathbf {W}}^{(k)}\) are \(\sqrt{\lambda _i^{(k)}}/\sqrt{\xi _i^{(k)}}\) for \(i = 1,2,3\).
Therefore, the eigenvalues of \({\mathbf {W}}^{(k)} \otimes {\mathbf {W}}^{(k)}\) are \(\frac{\sqrt{\lambda _i^{(k)} \lambda _j^{(k)}}}{\sqrt{\xi _i^{(k)} \xi _j^{(k)}}}\) for \(i,j=1,2,3\), \(i \le j\); thus, taking into account (43) the following cases can occur:
-
case 1: \({\mathbf {S}}^{(k)}\) has eigenvalues \(\xi _1^{(k)}\), \(\xi _2^{(k)}\), \(\xi _3^{(k)}\) and \({\mathbf {X}}^{(k)}\) has eigenvalues \(\frac{\sigma \mu ^{(k)}}{\xi _1^{(k)}}\), \(\frac{\sigma \mu ^{(k)}}{\xi _2^{(k)}}\), \(\frac{\sigma \mu ^{(k)}}{\xi _3^{(k)}}\), then the eigenvalues of \({\mathbf {W}}^{(k)} \otimes {\mathbf {W}}^{(k)}\) are
$$\begin{aligned} \frac{\sigma \mu ^{(k)}}{\xi _i^{(k)} \xi _j^{(k)}},\,\,\, i, j=1,2,3, \,\,\, i \le j. \end{aligned}$$ -
case 2: \({\mathbf {S}}^{(k)}\) has eigenvalues \(\xi _1^{(k)}\), \(\xi _2^{(k)}\), \(\frac{\sigma \mu ^{(k)}}{\lambda _3^{(k)}}\) and \({\mathbf {X}}^{(k)}\) has eigenvalues \(\frac{\sigma \mu ^{(k)}}{\xi _1^{(k)}}\), \(\frac{\sigma \mu ^{(k)}}{\xi _2^{(k)}}\), \(\lambda _3^{(k)}\), then the eigenvalues of \({\mathbf {W}}^{(k)} \otimes {\mathbf {W}}^{(k)}\) are
$$\begin{aligned} \frac{\sigma \mu ^{(k)}}{(\xi _1^{(k)})^2},\,\,\, \frac{\sigma \mu ^{(k)}}{(\xi _2^{(k)})^2}, \,\,\, \frac{\sigma \mu ^{(k)}}{\xi _1^{(k)}\xi _2^{(k)}}, \frac{(\lambda _3^{(k)})^2}{\sigma \mu ^{(k)}},\,\,\,\frac{\lambda _3^{(k)}}{\xi _1^{(k)}}, \,\,\,\frac{\lambda _3^{(k)}}{\xi _2^{(k)}}. \end{aligned}$$ -
case 3: \({\mathbf {S}}^{(k)}\) has eigenvalues \(\xi _1^{(k)}\), \(\frac{\sigma \mu ^{(k)}}{\lambda _2^{(k)}}\), \(\frac{\sigma \mu ^{(k)}}{\lambda _3^{(k)}}\) and \({\mathbf {X}}^{(k)}\) has eigenvalues \(\frac{\sigma \mu ^{(k)}}{\xi _1^{(k)}}\), \(\lambda _2^{(k)}\), \(\lambda _3^{(k)}\), then the eigenvalues of \({\mathbf {W}}^{(k)} \otimes {\mathbf {W}}^{(k)}\) are
$$\begin{aligned} \frac{\sigma \mu ^{(k)}}{(\xi _1^{(k)})^2},\,\,\, \frac{(\lambda _2^{(k)})^2}{\sigma \mu ^{(k)}},\,\,\,\frac{(\lambda _3^{(k)})^2}{\sigma \mu ^{(k)}}, \,\,\, \frac{\lambda _2^{(k)}}{\xi _1^{(k)}},\,\,\,\frac{\lambda _3^{(k)}}{\xi _1^{(k)}},\,\,\, \frac{\lambda _1^{(k)} \lambda _2^{(k)}}{\sigma \mu ^{(k)}}. \end{aligned}$$ -
case 4: \({\mathbf {S}}^{(k)}\) has eigenvalues \(\frac{\sigma \mu ^{(k)}}{\lambda _1^{(k)}}\), \(\frac{\sigma \mu ^{(k)}}{\lambda _2^{(k)}}\), \(\frac{\sigma \mu ^{(k)}}{\lambda _3^{(k)}}\) and \({\mathbf {X}}^{(k)}\) has eigenvalues \(\lambda _1^{(k)}\), \(\lambda _2^{(k)}\), \(\lambda _3^{(k)}\), then the eigenvalues of \({\mathbf {W}}^{(k)} \otimes {\mathbf {W}}^{(k)}\) are
$$\begin{aligned} \frac{(\lambda _1^{(k)})^2}{\sigma \mu ^{(k)}},\,\,\,\frac{(\lambda _2^{(k)})^2}{\sigma \mu ^{(k)}},\,\,\,\frac{(\lambda _3^{(k)})^2}{\sigma \mu ^{(k)}},\,\,\, \frac{\lambda _1^{(k)} \lambda _2^{(k)}}{\sigma \mu ^{(k)}}, \,\,\,\ \frac{\lambda _1^{(k)} \lambda _3^{(k)}}{\sigma \mu ^{(k)}}, \,\,\ \frac{\lambda _2^{(k)} \lambda _3^{(k)}}{\sigma \mu ^{(k)}}. \end{aligned}$$
From the Courant–Fisher–Weyl min-max principle [3, Corollary 3.13]Footnote 2 we get:
and
and the condition number \(\kappa ({\mathcal {S}}^{(k)}_{NT})\) of \({\mathcal {S}}^{(k)}_{NT}\) satisfies the inequality:
Therefore in cases 1 and 4 \(\kappa ({\mathcal {S}}^{(k)}_{NT})\) is bounded, while in cases 2 and 3 we have that \(\kappa ({\mathcal {S}}^{(k)}_{NT}) = O((\mu ^{(k)})^{-1})\).
Let us now consider the nonsymmetric fourth-order tensor \({\mathcal {M}}_{AHO}^{(k)}\) defined in (42) with \({\mathbf {S}}^{(k)}\) and \({\mathbf {X}}^{(k)}\) in the place of \({\mathbf {S}}\) and \({\mathbf {X}}\). In order to analyze its condition number, we consider the positive definite symmetric fourth-order tensor
which has the form
and calculate its eigenvalues focusing on the case in which \({\mathcal {C}}\) is isotropic with expression (14). By introducing the Lamé moduli
from (44) we get for \(\mathbf {H} \in Sym\)
By straightforward calculations we get that the following three positive real numbers
are eigenvalues of \({\mathcal {L}}^{(k)}\) with eigentensors
The remaining eigentensors belong to the subspace of Sym spanned by \(\mathbf {q}_1^{(k)}\odot \mathbf {q}_1^{(k)}\), \(\mathbf {q}_2^{(k)}\odot \mathbf {q}_2^{(k)}\) and \(\mathbf {q}_3^{(k)}\odot \mathbf {q}_3^{(k)}\).
Thus, we look for real numbers m and triples \((\chi _1, \chi _2, \chi _3) \ne (0, 0, 0)\) such that, putting
we have
From (45) we get
and, taking into account the linear independence of tensors \(\mathbf {q}_i^{(k)}\odot \mathbf {q}_i^{(k)}\), \(i=1,2,3\), we can conclude that nonzero triples \((\chi _1, \chi _2, \chi _3)\) exist provided that m is a root of the following third-degree polynomial
which is the determinant of the shifted system derived from (51). The coefficients of \(\tilde{p}_k(m)\) are
and
with
and
From the symmetry and positive definiteness of \({\mathcal {L}}^{(k)}\) it follows that the polynomial (52) has three positive real roots \(m_4^{(k)}\), \(m_5^{(k)}\) and \(m_6^{(k)}\), which are the sought eigenvalues of \({\mathcal {L}}^{(k)}\).
Taking into account the complementarity condition (43) and considering the four cases for the forms of \(\lambda _i^{(k)}\) and \(\xi _i^{(k)}\) as done in the analysis of \(\kappa ({\mathcal {S}}_{NT})\), we get that in all cases \(a_k\), \(b_k\) and \(c_k\) are polynomials of the variable \(\mu _k\) of degree 2, 4 and 6, respectively. Thus the roots of \(\tilde{p}_k(m)\) have the expressions
for some scalars \(e_i^{(k)}\), \(f_i^{(k)}\) and \(g_i^{(k)}\).
We point out that the eigenvalues of \({\mathcal {L}}^{(k)}\) given in (46)–(48) are of the type (53) with \(e_i^{(k)}\ne 0\) for \(i=1,2,3\) in the four possible cases. Assuming \(e_i^{(k)}\ne 0\) for all k and \(i=4, 5, 6\), we can conclude that the condition number of \({\mathcal {M}}_{AHO}^{(k)}\) does not depend on \(\mu ^{(k)}\). We are aware that the assumption on \(e_i^{(k)}\) in (53) is rather strong but we remark that it is fulfilled in all the performed experiments.
In addition, the independence of the condition number of \({\mathcal {M}}_{AHO}^{(k)}\) on \(\mu ^{(k)}\) is corroborated by the analysis of the case \({\mathcal {C}}={\mathbb {I}}_{Sym}\). For this choice of \({\mathcal {C}}\), tensor \({\mathcal {M}}_{AHO}^{(k)}\) is symmetric and its eigenvalues are
with eigentensors in (49) and (50), and
with eigentensors \(\mathbf {q}_1^{(k)}\odot \mathbf {q}_1^{(k)}\), \(\mathbf {q}_2^{(k)}\odot \mathbf {q}_2^{(k)}\) and \(\mathbf {q}_3^{(k)}\odot \mathbf {q}_3^{(k)}\), respectively. Once again, taking into account the complementarity condition (43) and considering the four cases for the forms of \(\lambda _i^{(k)}\) and \(\xi _i^{(k)}\), we get that \(h_i^{(k)}\) have the expression in (53), with \(g_i^{(k)}=0\) and \(e_i^{(k)}\ne 0\) and the desired result follows.
The calculation of the eigenvalues of \({\mathcal {L}}^{(k)}\) for \({\mathcal {C}}\) transversely isotropic is not easy and their explicit expressions are not available. Nevertheless, the numerical experiments reported in Section 6 show that, as in the isotropic case, the condition number of \({\mathcal {M}}_{AHO}^{(k)}\) is uniformly bounded for \(\mu ^{(k)} \rightarrow 0\).
6 Numerical experiments
This section is devoted to numerical experiments; our purpose here is validating the proposed interior point approach for minimizing functional (7) and showing that it provides accurate solutions. Moreover, we show that it is suitable for being implemented in the finite element code NOSA-ITACA [24] for the structural analysis of masonry constructions as it is able to solve problems where \({\mathbf {D}}\) is the infinitesimal strain tensor calculated within NOSA-ITACA for each Gauss point (see the third data set in Sect. 6.2).
We first describe the details of the implemented methods and then discuss the testing sets and the numerical results.
We remark that in the following sections we focus on the problem formulation (30) in the description of both the algorithm and the experiments. Clearly, analogous considerations can be retrieved focusing on the minimization of (7) changing the variable \({\mathbf {Y}}=-{\mathbf {X}}\).
6.1 The IPM-Proj algorithm and implementation details
We report in Algorithm 1 a pseudo-code for the IPM-Proj method that is in fact an adaptation of the Mehrotra-type predictor corrector primal-dual algorithm [31, 32] applied to problem (30). This algorithm is very-well-known and is currently implemented in general purpose software for general QSDPs [33]. It is a generalization of the method used in SDTP3 and cvx for linear semidefinite programming problems [9, 34].
In the description of the algorithm, let the current and the next iterate be \(({\mathbf {X}},{\mathbf {S}})\) and \(({\mathbf {X}}^+,{\mathbf {S}}^+)\), respectively. Also, let the current and the next step-length parameter be denoted by \(\tau\) and \(\tau ^+\), respectively.

The step-length \(\alpha\) is defined at Line 18 as \(\alpha = \min \{\alpha _{\mathbf {X}}, \alpha _{\mathbf {S}}\}\) with
and
At Line 32, \(\alpha\) is defined analogously replacing \(\delta {\mathbf {X}}\) and \(\delta {\mathbf {S}}\) with \(\varDelta {\mathbf {X}}\) and \(\varDelta {\mathbf {S}}\), respectively.
We implemented IPM-Proj in Matlab. In particular, regarding the NT direction, we closely followed the detailed implementation description in [30], where the complexity of each iteration of the algorithm using either the NT or the AHO direction is also given, see [30, Table 2].
The computation of the predictor and the corrector steps involves the computation and factorization either of the Schur complement \({\mathcal {S}}_{NT}\) (if flag = NT) or of the tensor \({\mathcal {M}}_{AHO}\) (if flag = AHO). We used the Cholesky factorization for \({\mathcal {S}}_{NT}\) and the LU factorization with partial pivoting for \({\mathcal {M}}_{AHO}\). Moreover, in computing \(\alpha _{{\mathbf {X}}}\) we computed the minimum eigenvalue of the symmetric tensor \({\mathbf {L}}^{-1}\delta {\mathbf {X}}{\mathbf {L}}^{-T}\) where \({\mathbf {X}}= {\mathbf {L}}{\mathbf {L}}^T\) is the Cholesky factorization of \({\mathbf {X}}\); analogously for \(\alpha _{{\mathbf {S}}}\) (in both Lines 18 and 32).
In all the experiments, we used \(({\mathbf {X}}, {\mathbf {S}}) = 2 ({\mathbf {I}}, {\mathbf {I}})\) as a starting guess. Moreover, we set the accuracy level \(\epsilon\) to the tight value \(\epsilon = 10^{-15}\). Finally, a maximum number of 200 interior point iterations is allowed. The execution of the algorithm is also prematurely interrupted in case an error occurs in the Cholesky factorization of \({\mathbf {X}}\), \({\mathbf {S}}\) or \({\mathcal {S}}_{NT}\) meaning that these tensors are numerically loosing the positive definiteness.
Finally, we mention that IPM-Proj has been implemented using the vector formalism described in Sect. 2 as done in [33, 34].
6.2 Data sets
The performance of the IPM-Proj algorithm is tested on three data sets designed to highlight the features of the projection problem and show the good behaviour of the algorithm for different choices of \({\mathcal {C}}\). In what follows, we denote by \({\mathcal {C}_{I}}\) the isotropic tensor defined in (14) and by \({\mathcal {C}_{TI}}\) the transversely isotropic tensor in (22).
First data set: random \({\mathbf {D}}\) We generated \(10^5\) random symmetric tensors \({\mathbf {D}}\) with random eigenvalues in the interval \([-l,l]\) and removed from the set tensors such that \({\mathbf {D}}\in Sym^-\) or such that \({\mathcal {C}}({\mathbf {D}}) \in Sym^+\) as in these cases the solution is trivial. Overall, we get sets of 74839, 70529 and 83373 tensors for \({\mathcal {C}}= {\mathbb {I}}_{Sym}\), for \({\mathcal {C}_{I}}\) and for \({\mathcal {C}_{TI}}\) with parameters given in Table 1, respectively.
Second data set: Temple \({\mathbf {D}}\) The goal of this data set is to test our algorithm with a view toward applications. To show the algorithm’s efficiency without implementing it into the code NOSA-ITACA, we resort to an artificial case study constituted by the domed temple discretized into 31052 8-nodes hexahedral elements shown in Fig. 1. First, the temple is subjected to its weight, and the strain field is calculated via a static analysis conducted with the NOSA-ITACA code.
Then, tensors \({\mathbf {D}}\) of the data set are the strain tensors calculated by NOSA-ITACA at each of 248216 Gauss points of the mesh. As for the random case, we removed from the set the tensors that gave trivial solutions. In particular, we tested tensors \({\mathcal {C}_{I}}\) and for \({\mathcal {C}_{TI}}\) with values of \(\nu\), E and \(\alpha\)’s given in Table 1 which are driven by physical considerations. Since in our tests the magnitude of these parameters in \({\mathcal {C}}\) greatly differed from the the magnitude of the elements of \({\mathbf {D}}\) generated by NOSA-ITACA, we found numerically convenient to normalize both \({\mathbf {D}}\) and \({\mathcal {C}}\), taking into account the properties of homogeneity (11) and invariance (12) of the projection introduced in Sect. 3. Taking into account the normalization, overall we get 89492 and 21747 tensors \({\mathbf {D}}\) using \({\mathcal {C}_{I}}\) and \({\mathcal {C}_{TI}}\), respectively.
Third data set: parametric \({\mathbf {D}}\) As pointed out in Sect. 4.2, unlike the isotropic case, in the transversely isotropic case, the data \({\mathbf {D}}\) and the exact solution \({\mathbf {Y}}^*\) (and then \({\mathbf {X}}^*\)) are in general not coaxial, and this lack of coaxiality seems to affect the performance of the IPM-Proj algorithm. Thus, the third data set is aimed at showing that the AHO direction behaves better than the NT direction when \({\mathbf {D}}\) is not coaxial with \({\mathbf {S}}\) and \({\mathbf {X}}\). To this purpose, let \((\mathbf {f}_{1},\mathbf {f}_{2},\mathbf {f}_{3})\) be an orthonormal basis of \(\mathcal {V}\), with \(\mathbf {f}_3\) the direction of transverse isotropy and let us consider the orthonormal vectors
and the tensors
for \(\theta _1\) and \(\theta _2 \in [0,2\pi ]\). We then construct tensors \(\mathbf {D}\in Sym\) of the type
For \(\theta _2=0, \pi , 2\pi\) we have \(\mathbf {q}_3(\theta _1, 0)=\mathbf {f}_3\), thus tensors \({\mathbf {D}}\) and the solution \({\mathbf {Y}}^*\) are coaxial and the explicit solution is provided in (25)–(28); for any other choice of \(\theta _2\), \({\mathbf {D}}\) and \({\mathbf {Y}}^*\) deviates from coaxiality.
6.3 Numerical results
All results given in this section were obtained on an a Intel Core i7-9700K PC running at 3.60 GHz x 8 with 16 GB of RAM, 64-bit and using Matlab R2019b.
We first discuss the performance of the proposed algorithm and the effectiveness of the symmetrization schemes described in Sect. 5 on the first two data sets. As a measure of performance we use the complementarity gap defined as \(gap = {\mathbf {X}}\bullet {\mathbf {S}}\) and when an analytic solution \({\mathbf {X}}^*\) is available, i.e. when \({\mathcal {C}}= {\mathbb {I}}_{Sym}\) or with \({\mathcal {C}_{I}}\), the absolute error computed as \(error = \Vert {\mathbf {X}}-{\mathbf {X}}^*\Vert\). We observe that the gap can be interpreted as coaxiality measure, being \({\mathbf {X}}^*\bullet {\mathbf {S}}^* = {\mathbf {Y}}^* \bullet {\mathcal {C}}({\mathbf {D}}-{\mathbf {Y}}^*)\).
We report in Table 2 the average number of interior point iterations \(iter_{Av}\), the average complementarity gap \(gap_{Av}\), the average absolute error \(error_{Av}\) and the total CPU time \(cpu_{tot}\). The symbol ‘-’ means that that \(error_{Av}\) is not available (transversely isotropic case). We observe that both the accuracy measures error and gap are in favour of the IPM-Proj implementing the AHO direction as, in fact, using the NT direction yields from 3 to 6 less order of accuracy. Moreover, the use of the NT direction implies, on average, a larger number of iterations when \({\mathcal {C}_{TI}}\) is used. Both issues are related to the fact that the Schur complement \({\mathcal {S}}_{NT}\) becomes very-ill conditioned for small \(\mu\) yielding poor interior point directions and, in several cases, runs are prematurely stopped due to an error in the Cholesky factorization. Conversely, the nice condition number of \({\mathcal {M}}_{AHO}\) as \(\mu \rightarrow 0\) allows to compute very accurate solutions. Finally, although aware that evaluating the cpu time of Matlab codes is not always meaningful, especially when built-in functions are employed, we note that IPM-Proj with the AHO direction is faster than with the NT one.
In order to deepen the analysis on the condition number of \({\mathcal {S}}_{NT}\) and \({\mathcal {M}}_{AHO}\), we randomly drew one tensor \({\mathbf {D}}\) from the random data set and one from the temple one. For both tensors, we plotted in Figs. 2 and 3 the values of \(\kappa ({\mathcal {S}}_{NT})\) and \(\kappa ({\mathcal {M}}_{AHO})\) along the interior point iterations (IPM iterations), for both \({\mathcal {C}_{I}}\) and \({\mathcal {C}_{TI}}\), together with the value of \(1/\mu\) for a matter of comparison. As expected \(\kappa ({\mathcal {S}}_{NT})\) grows as \(1/\mu\), while \(\kappa ({\mathcal {M}}_{AHO})\) is constant both for \({\mathcal {C}_{I}}\) and \({\mathcal {C}_{TI}}\) as discussed in Sect. 5.1.
In order to interpret the results discussed above with a further tool, we report in Fig. 4 the boxplots of the runs performed for the Temple \({\mathbf {D}}\) related to the \(\log _{10}(gap)\) computed using the AHO and the NT directions for both \({\mathcal {C}_{I}}\) and \({\mathcal {C}_{TI}}\). The plots show that the maximum, i.e. the highest data point in the data set excluding any outliers, is larger using NT than using AHO. Moreover, the use of NT yields a large number of outliers with values above the maximum. We remark that these outliers correspond to runs prematurely stopped for a failure in the Cholesky factorization due to the ill-conditioning of the Schur complement \({\mathcal {S}}_{NT}\).
Concerning the third data set, Fig. 5 reports the plot of the complementarity gap versus the angle \(\theta _2\), for \(\theta _1=\pi /4\), and \((d_1,d_2,d_3)\) randomly chosen in \([-1,1]\), when \({\mathcal {C}_{TI}}\) is employed. The trend of the complementarity gap clearly shows how the deviation from coaxiality of \({\mathbf {D}}\) and \({\mathbf {X}}\) influences the coaxiality of \({\mathbf {X}}\) and \({\mathbf {S}}\) and then the accuracy of the numerical solution. The use of the AHO direction seems to mitigate this effect. The solutions calculated using the AHO and NT direction coincide for \(\theta _2=0, \pi , 2\pi\).
Parametric \({\mathbf {D}}\): value of the complementarity gap at the computed solution varying \(\theta _2\) in the definition of \({\mathbf {D}}\) in (54)
7 Conclusions
In this paper, we addressed a projection problem consisting in determining the projection of a symmetric second-order tensor onto the cone of negative semidefinite symmetric tensors with respect to the inner product defined by an assigned positive definite symmetric fourth-order tensor \({\mathcal {C}}\). Applications of interests in solid mechanics strongly motivated this work supplying special forms for the tensors \({\mathcal {C}}\) which require the numerical solution of the projection problem. To this purpose, we considered an interior point method for a semidefinite programming reformulation of the problem and discuss reliable implementations based on direct solvers for the linear algebra. Several numerical tests are performed to validate the proposed method showing that the use of the AHO direction might be preferable to get accurate solutions.
The implementation of the algorithm in the finite element code NOSA-ITACA [24] developed at ISTI-CNR for the structural analysis of masonry constructions will be the subject of future work together with the analysis of a real-world case study of engineering interest.
Notes
In solid mechanics the tensor product between tensors and between vectors is usually denoted by the symbol \(\otimes\), which, instead, in linear algebra is used to denote the Kronecker product (or the symmetrized Kronecker product). In this work we adopt the notation used in numerical linear algebra for the symmetric Kronecker product and we introduce the symbol \(\odot\) to denote the tensor product of solid mechanics.
We recall that by the Courant-Fisher-Weyl min-max principle [3, Corollary 3.13], for any symmetric tensor \(\mathbf {A}\) and \(\mathbf {B}\), we have that \(\lambda _i(\mathbf {A})+\lambda _{\min }(\mathbf {B})\le \lambda _i(\mathbf {A}+\mathbf {B})\le \lambda _i(\mathbf {A}) +\lambda _{\max }(\mathbf {B})\), where \(\lambda _i(\cdot )\) denotes the ith eigenvalue ordered in increasing order.
References
Alizadeh, F., Haeberly, J.P.A., Overton, M.L.: Primal-dual interior-point methods for semidefinite programming: convergence rates, stability and numerical results. SIAM J. Opt. 8(3), 746–768 (1998)
Anjos, M.F., Higham, N.J., Takouda, P.L., Wolkowicz, H.: A semidefinite programming approach for the nearest correlation matrix problem. Research Report, Department of Combinatorics and Optimization, University of Waterloo (2003)
Axelsson, O.: Iterative solution methods. Cambridge University Press (1996)
Bellavia, S., Gondzio, J., Porcelli, M.: An inexact dual logarithmic barrier method for solving sparse semidefinite programs. Mathe. Programm. 178(1), 109–143 (2019)
Bellavia, S., Gondzio, J., Porcelli, M.: A relaxed interior point method for low-rank semidefinite programming problems with applications to matrix completion. J. Sci. Comput. 89(2), 1–36 (2021)
Brezis, H.: Analyse fonctionnelle—Theorie et applications. Masson Editeur, Paris (1983)
Del Piero, G.: Constitutive equations and compatibility of external loads for linear elastic masonry-like materials. Meccanica 24, 150–162 (1989)
Gondzio, J.: Interior point methods 25 years later. Euro. J. Oper. Res. 218(3), 587–601 (2012)
Grant, M., Boyd, S.: CVX: Matlab software for disciplined convex programming, version 2.0 beta. http://cvxr.com/cvx, (September 2013)
Gurtin, M.E.: The linear theory of elasticity. Encyclopedia of Physics, Vol. VIa/2, Mechanics of Solids II (1972). Truesdell C. (Ed). Springer-Verlag
Gurtin, M.E., Fried, E., Anand, L.: The Mechanics and Thermodynamics of Continua. Cambridge University Press (2010)
Habibi, S., Kavand, A., Kocvara, M., Stingl, M.: Barrier and penalty methods for low-rank semidefinite programming with application to truss topology design. arXiv preprint arXiv:2105.08529 (2021)
Henrion, D., Malick, J.: Projection Methods in Conic Optimization. Handbook on Semidefinite, Conic and Polynomial Optimization. In: Anjos, M., Lasserre, J. (eds.) International Series in Operations Research and Management Science, vol. 166. Springer, Boston, MA (2012)
Higham, N.J.: Matrix nearness problems and applications. University of Manchester, Department of Mathematics (1988)
Higham, N.J.: Computing a nearest symmetric positive semidefinite matrix. Linear algebra and its applications 103, 103–118 (1988)
Higham, N.J.: Computing the nearest correlation matrix-a problem from finance. IMA J. Numer. Anal. 22(3), 329–343 (2002)
Higham, N.J., Noferini, V.: An algorithm to compute the polar decomposition of a 3x3 matrix. Numer. Algorithms 73(2), 349–369 (2016)
Kojima, M., Shida, M., Shindoh, S.: A predictor-corrector interior-point algorithm for the semidefinite linear complementarity problem using the Alizadeh–Haeberly–Overton search direction. SIAM J. Opt. 9(2), 444–465 (1992)
Kojima, M., Shida, M., Shindoh, S.: Search directions in the SDP and the monotone SDLCP: generalization and inexact computation. Mathe. Programm. 85(1), 51–80 (1999)
Kojima, M., Shindoh, S., Hara, S.: Interior-point methods for the monotone semidefinite linear complementarity problem in symmetric matrices. SIAM J. Opt. 7(1), 86–125 (1997)
Li, X., Sun, D., Toh, K.C.: QSDPNAL: A two-phase augmented Lagrangian method for convex quadratic semidefinite programming. Mathe. Programm. Comput. 10(4), 703–743 (2018)
Lucchesi, M., Padovani, C., Pasquinelli, G., Zani, N.: Masonry constructions: mechanical models and numerical applications (2008); Lecture Notes in Applied and Computational Mechanics. Springer–Verlag
Malick, J.: A dual approach to semidefinite least-squares problems. SIAM J Matrix Anal. Appl. 26(1), 272–284 (2004)
Padovani, C., Silhavy, M.: On the derivative of the stress-strain relation in a no-tension material. Mathematics and Mechanics of Solids (2015), Online First 27 February 2015, Sage Publications Inc
Podio-Guidugli, P., Virga, E.: Transversely isotropic elasticity tensors. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 1987, 411, 85–93 (1840)
Qi, H., Sun, D.: A quadratically convergent Newton method for computing the nearest correlation matrix. SIAM J. Matrix Anal. Appl. 28(2), 360–385 (2006)
Todd, M.J.: A study of search directions in primal-dual interior-point methods for semidefinite programming. Opt. Methods Softw. 11(1–4), 1–46 (1999)
Todd, M.J.: Semidefinite optimization. Acta Numerica 10, 515–560 (2001)
Todd, M.J., Toh, K.C., Tütüncü, R.H.: On the Nesterov-Todd Direction in Semidefinite Programming. SIAM J. Opt. 8(3), 769–796 (1998)
Todd, M.J., Toh, K.C., Tütüncü, R.H.: Inexact primal-dual path-following algorithms for a special class of convex quadratic SDP and related problems. Pacific Journal of Optimization, 3, 135–164, (2007)
Toh, K.-C.: An inexact primal-dual path following algorithm for convex quadratic SDP. Math. Programm. 112(1), 221–254 (2008)
Toh, K.- C.: User guide for QSDP-0-a MATLAB software package for convex quadratic semidefinite programming. Technical report 2010, Department of Mathematics, National University of Singapore, Singapore
Toh, K.-C., Todd, M.J., Tütüncü, R.H.: SDPT3-a MATLAB software package for semidefinite programming, version 1.3. Opt. Methods Softw. 11(1–4), 545–581 (1999)
Acknowledgements
The second author is a member of the Gruppo Nazionale per il Calcolo Scientifico (GNCS) of the Istituto Nazionale di Alta Matematica (INdAM) and this work was partially supported by INdAM-GNCS under Progetti di Ricerca 2020 and Progetto di Ricerca GNCS-INdAM CUP_E55F22000270001.
Funding
Open access funding provided by Alma Mater Studiorum - Università di Bologna within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Components of tensor \({\mathcal {C}}\)
Components of tensor \({\mathcal {C}}\)
The components \({\mathcal {C}}_{ijkl}\) of \({\mathcal {C}}\) and \({\mathcal {C}}_{ijkl}^{-1}\) of \({\mathcal {C}}^{-1}\) with respect to an orthonormal basis \({\mathsf {P}}= (\mathbf {p}_{1},\mathbf {p}_{2},\mathbf {p}_{3})\) of \(\mathcal {V}\) are introduced in Sect. 1. These components are reported in the following for the fourth-order tensors \({\mathcal {C}}\) used in the numerical experiments.
In the isotropic case we have
The other components, if not zero, are given by relations (4) and (5).
In the transversely isotropic case, if \(\mathbf {p}_{3}\) is the direction of transverse isotropy, then we have
with
and the remaining components are defined by (4) and (5) or are equal to zero.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Padovani, C., Porcelli, M. A semidefinite programming approach for the projection onto the cone of negative semidefinite symmetric tensors with applications to solid mechanics. Calcolo 59, 33 (2022). https://doi.org/10.1007/s10092-022-00478-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10092-022-00478-1
Keywords
- Conic projection
- Negative semidefinite tensors
- Quadratic semidefinite programming
- Interior point methods