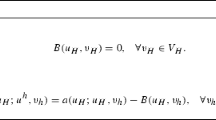1 Introduction

Discontinuous Galerkin (dG) methods are a popular family of non-conforming finite element-type approximation schemes for partial differential equations (PDEs) involving discontinuous approximation spaces. In the context of elliptic problems their inception can be traced back to the 1970s [5, 21]; see also [1] for an accessible overview and history of these methods for second order problems. For higher order problems, for example the (nonlinear) biharmonic problem, dG methods are a useful alternative to using \({\text {C}} ^{1}\)-conforming elements whose derivation and implementation can become very complicated [5, 13, 23].

Inf-sup conditions form one part of the Banach–Nečas–Babuška condition which guarantees the well-posedness of a given variational problem. In this note, we shall describe an analytical framework to examine the stability of dG approximations for \({\text {L}} _{2}\) and \({\text {H}} ^{2}\)-like mesh-dependent norms. This is in keeping with the spirit of [3, 4], where for continuous finite element methods the authors prove equivalent results for second and fourth order problems respectively. The present approach, however, is quite different and results in inf-sup stability for both \({\text {L}} _{2}\)- and \({\text {H}} ^{2}\)-like mesh-dependent norms under the assumption that the underlying mesh is quasi-uniform.

The analysis presented utilises a new \({\text {H}} ^{2}\)-conforming reconstruction operator, based on Hsieh–Clough–Tocher-type \({\text {C}} ^{1}\) reconstructions. Such reconstructions, based on nodal averaging, are used for the proof of a posteriori bounds for non-conforming methods for elliptic [7, 13, 18, 24] and hyperbolic problems [12, 16]. The new reconstruction operators presented below enjoys certain orthogonality properties; in particular, they are adjoint orthogonal to the underlying Hsieh–Clough–Tocher space and maintain the same stability bounds as the \({\text {H}} ^{2}\)-conforming reconstruction from [13].

The argument is quite general and allows the derivation of inf-sup stability results whenever the numerical scheme has a well posed discrete adjoint (dual) problem over an appropriately constructed non-conforming finite element space. This is contrary to the Aubin–Nitsche \({\text {L}} _{2}\) duality argument whereby it is the underlying partial differential operator itself that requires the well posedness of the adjoint continuous problem.

The use of these recovery operators is not limited to an a posteriori setting, indeed, they have been used to quantify inconsistencies appearing in standard interior penalty methods when the exact solution is not \({\text {H}} ^{2}(\Omega )\) [17]. This allows for quasi optimal a priori bounds for elliptic problems under minimal regularity up to data oscillation. Fundamentally the assumption in this analysis is that the singularity arises from the geometry of the domain rather than through the problem data itself. Our analysis allows us to show quasi-optimal \({\text {L}} _{2}\) convergence to problems that have rough problem data. To showcase the result we study the convergence of a method posed for an elliptic problem whose source term is not \({\text {H}} ^{-1}\) in both 1 and 2 spatial dimensions. In this case the Aubin–Nitsche, and indeed the standard treatment of Galerkin methods, are not applicable.

The note is set out as follows: In Sect. 2 we introduce the problem and present the analysis cumulating in inf-sup stability for problems with smooth data. In Sect. 3 we examine a particular problem with rough data and prove quasi-optimal convergence in this case. In addition we give some numerical validation of the method.

2 Problem set up and discretisation

To highlight the main steps of the present developments in this area, we consider the Poisson problem with homogeneous Dirichlet boundary conditions. Let \(\Omega \subset {\mathbb R} ^d\) be an open convex domain and consider the problem: given \(f\in {\text {L}} _{2}(\Omega )\) find \(u\in {\text {H}} ^{2}(\Omega )\cap {\text {H}} ^{1}_0(\Omega )\), such that

$$\begin{aligned} \int _\Omega \nabla u \cdot \nabla v \,\mathrm{d}x= \int _\Omega f \ v \,\mathrm{d}x\quad \,\forall \,v\in {\text {H}} ^{1}_0(\Omega ). \end{aligned}$$
(1)

We consider \({\mathscr {T}} ^{}\) to be a conforming triangulation of \(\Omega \), namely, \({\mathscr {T}} ^{}\) is a finite family of sets such that

  1. (1)

    \(K\in {\mathscr {T}} ^{}\) implies K is an open simplex (segment for \(d=1\), triangle for \(d=2\), tetrahedron for \(d=3\)),

  2. (2)

    for any \(K,J\in {\mathscr {T}} ^{}\) we have that \(\overline{K}\cap \overline{J}\) is a full lower-dimensional simplex (i.e., it is either \(\emptyset \), a vertex, an edge, a face, or the whole of \(\overline{K}\) and \(\overline{J}\)) of both \(\overline{K}\) and \(\overline{J}\) and

  3. (3)

    \(\bigcup _{K\in {\mathscr {T}} ^{}}\overline{K}=\overline{\Omega }\).

The shape regularity constant of \({\mathscr {T}} ^{}\) is defined as the number

$$\begin{aligned} \mu ({\mathscr {T}} ^{}) := \inf _{K\in {\mathscr {T}} ^{}} \frac{\rho _K}{h_K}, \end{aligned}$$
(2)

where \(\rho _K\) is the radius of the largest ball contained inside K and \(h_K\) is the diameter of K. An indexed family of triangulations \(\left\{ {{\mathscr {T}} ^{n}}\right\} _n\) is called shape regular if

$$\begin{aligned} \mu :=\inf _n\mu ({\mathscr {T}} ^{n})>0. \end{aligned}$$
(3)

Further, we define \(h:\Omega \rightarrow {\mathbb R} \) to be the piecewise constant meshsize function of \({\mathscr {T}} ^{}\) given by

$$\begin{aligned} h(\mathbf {x}):=\max _{\overline{K}\ni \mathbf {x}}h_K. \end{aligned}$$

In addition if

$$\begin{aligned} \frac{\max _{K\in {\mathscr {T}} ^{}} h_K}{\min _{K\in {\mathscr {T}} ^{}} h_K} \le C_{qu}, \end{aligned}$$
(4)

we call \({\mathscr {T}} ^{}\) quasiuniform. If an entire indexed family of triangulations satisfy (4), we call it a quasiuniform family. In what follows we shall assume that all triangulations are shape-regular and quasiuniform.

We let \({\mathscr {E}} {}\) be the skeleton (set of common interfaces) of the triangulation \({\mathscr {T}} ^{}\) and say \(e\in {\mathscr {E}} \) if e is on the interior of \(\Omega \) and \(e\in \partial \Omega \) if e lies on the boundary \(\partial \Omega \) and set \(h_e\) to be the diameter of e. We also define the “broken” gradient \(\nabla _h\), Laplacian \(\Delta _h\) and Hessian \(\mathrm {D}^2_h\) to be defined element-wise by \(\nabla _h w|_K = \nabla w\), \(\Delta _h w|_K = \Delta w\), \(\mathrm {D}^2_h w|_K = \mathrm {D}^2w\) for all \(K\in {\mathscr {T}} ^{}\), respectively, for respectively smooth functions on the interior of K,

We let \({\mathbb P} ^{k}({\mathscr {T}} ^{})\) denote the space of piecewise polynomials of degree k over the triangulation \({\mathscr {T}} ^{}\), and introduce the finite element space \(\mathbb {V}:= {\mathbb P} ^{k}({\mathscr {T}} ^{})\) to be the usual space of discontinuous piecewise polynomial functions of degree k. We define average operators for arbitrary scalar functions v and vectors \(\mathbf {v}\) over an edge e shared by elements \(K_1\) and \(K_2\) as \(\{\!\{ v \}\!\} = {\tfrac{1}{2}\!\left( {v|_{K_1} + v|_{K_2}}\right) }\), \(\{\!\{ \mathbf {v} \}\!\} = {\tfrac{1}{2}\!\left( {\mathbf {v}|_{K_1} + \mathbf {v}|_{K_2}}\right) }\) and jump operators as , . Note that on the boundary of the domain \(\partial \Omega \) the jump and average operators are defined as \(\{\!\{ v \}\!\} \Big \vert _{\partial \Omega } := v\), \(\{\!\{ \varvec{v} \}\!\} \Big \vert _{\partial \Omega } := \varvec{v}\), , ,

Definition 2.1

(Mesh dependent norms) We introduce the mesh dependent \({\text {L}} _{2}-\), \({\text {H}} ^{1}\)-and \({\text {H}} ^{2}\)-norms to be

(5)

Note for \(w_h \in \mathbb {V}\) in view of scaling each mesh dependent norm is equaivalent to the continuous counterpart, that is \(\Vert {{w_h}} \Vert _{0,h} \sim \Vert {w_h}\Vert _{{\text {L}} _{2}(\Omega )}\) for example.

Consider the interior penalty (IP) discretisation of (1), to find \(u_h \in \mathbb {V}\) such that

$$\begin{aligned} {\mathscr {A}} _h\!\left( {u_h,v_h}\right) = \left\langle {f,v_h}\right\rangle \quad \,\forall \,v_h \in \mathbb {V}, \end{aligned}$$
(6)

where

(7)

where \(\sigma _0 >0, \sigma _1 \ge 0\) represent penalty parameters. Note that a standard choice is to take \(\sigma _1 = 0\). The choice \(\sigma _1 \ne 0\) results in a class of stabilised dG methods [8].

Proposition 2.2

(Continuity and coercivity of \({\mathscr {A}} _h\!\left( {\cdot ,\cdot }\right) \) [1, 11, c.f.]) For \(\sigma _1 \ge 0\) and \(\sigma _0\) large enough and any \(u_h,v_h\in \mathbb {V}\) the bilinear form \({\mathscr {A}} _h\!\left( {\cdot ,\cdot }\right) \) satisfies

$$\begin{aligned}&{\mathscr {A}} _h\!\left( {u_h,u_h}\right) \ge C \Vert {{u_h}} \Vert _{1,h}^2 \end{aligned}$$
(8)
$$\begin{aligned}&{\mathscr {A}} _h\!\left( {u_h,v_h}\right) \le C \Vert {{u_h}} \Vert _{1,h} \Vert {{v_h}} \Vert _{1,h}. \end{aligned}$$
(9)

Lax-Milgram Theorem guarantees a unique solution to the problem (7). Also, since \(u\in {\text {H}} ^{2}(\Omega )\), the bilinear form is consistent, hence, Strang’s Lemma yields quasioptimal convergence of the method in the \(\Vert {{\cdot }} \Vert _{1,h}\) norm:

$$\begin{aligned} \Vert {{u - u_h}} \Vert _{1,h} \le C \inf _{w_h\in \mathbb {V}} \Vert {{u - w_h}} \Vert _{1,h}. \end{aligned}$$
(10)

Conforming reconstruction operators The key tool in the proof of the inf-sup condition is the notion of reconstruction operators. It is commonplace in the a posteriori analysis of nonconforming schemes to make use of such operators. A simple, quite general methodology for the construction of reconstruction operators is to use an averaging interpolation operator into an \({\text {H}} ^{2}\)-conforming finite element space. For example a \({\text {C}} ^{1}\) Hsieh–Clough–Tocher (HCT) macro-element conforming space for \({\text {H}} ^{2}\) conformity [6, 13, 25, c.f.]. Another option is the use of Argyris-type reconstructions [6].

Example 2.3

(Construction of the HCT(4) space for \(d=2\)) Since the HCT spaces are an integral part of our analysis, we will illustrate the construction of the HCT(4) space for \(d=2\), over triangles, noting that for \(d=1\), we can simply consider families of cubic splines, while for \(d=3\) corresponding constructions are possible [19, Ch. 18]. Consider a triangle K that is partitioned in 3 subtriangles, \(\{K_i \}_{i=1}^3\) by connecting each of the vertices to the barycentre as illustrated in Fig. 1. We then take

$$\begin{aligned} \text {HCT}(4):= \left\{ \phi \in {\text {C}} ^{1}(K):\;u|_{K_i} \in {\mathbb P} ^{4}(K_i) \text { for } i =1,2,3 \right\} . \end{aligned}$$
(11)

The dimension of \({\mathbb P} ^{4}(K_i)\) is 15. It can then be verified that, upon enforcing continuity of functions and their derivatives across the subtriangulation edges for the degrees of freedom depicted in Fig. 1, the dimension of the HCT(4) space is 21 and those degrees of freedom and unisolvent.

Fig. 1
figure 1

The \({\mathbb P} ^{4}\) Hsieh–Clough–Tocher-type macro-element, as a \({\text {H}} ^{2}(\Omega )\)-conforming reconstruction to the quadratic Lagrange element. Here the large, blue circles represent degrees of freedom associated to a function evaluation, the small, red circles represent those associated to full derivative evaluation and the arrows a normal derivative evaluation

Full size image

For the general construction of the macro-element HCT(r) space for simplicial and box-type elements, we refer to [10, 19, 22].

Definition 2.4

(\({\text {H}} ^{2}(\Omega )\) -reconstructions) An example of \({\text {H}} ^{2}(\Omega )\) reconstruction operator \(E^2(u_h)\) of k-th order Lagrange elements is defined as follows. Let \(\mathbf {x}\) be a degree of freedom of the \(H^2\)-conforming space \(\text {HCT}(k+2)\) consisting of HCT-type macro-elements of degree \(k+2\), and let \(\widehat{K_{\mathbf {x}}}\) be the set of all elements sharing the degree of freedom \(\mathbf {x}\). Then, the reconstruction at that specific degree of freedom is given by

$$\begin{aligned} E^2(u_h)(\mathbf {x}) = \frac{1}{{\mathrm{card}}(\widehat{K_{\mathbf {x}}})}\sum _{K \in \widehat{K_{\mathbf {x}}}} u_h\vert _K(\mathbf {x}). \end{aligned}$$
(12)

For the case \(k=2\), the associated degrees of freedom are illustrated in Fig. 1. Notice that the degrees of freedom of the reconstruction are a superset of those of the original finite element. This is due to the lack of existence of a conforming \({\text {H}} ^{2}(\Omega )\) subspace in \(\mathbb {V}\) for low k; for instance, the existence of an \({\text {H}} ^{2}(\Omega )\)-conforming space requires \(k\ge 5\) in two dimensions (Argyris space). Corresponding reconstructions for higher polynomial degrees have been considered in [6, 13], for instance.

Even though the \(\text {HCT}(k+2)\) space contains functions that are not polynomial, it does include \({\mathbb P} ^{k+2}(K)\) and hence the \(\text {HCT}(k+2)\) interpolant preserves \({\mathbb P} ^{k+2}(K)\) functions, hence by Bramble-Hilbert the \(\text {HCT}(k+2)\) space has quasi-optimal approximability.

We refer also to the discussion in [13], regarding reconstructions of box-type k-th order Lagrange elements into \({ HCT}(k+2)\).

Lemma 2.5

(Reconstruction bounds [13, Lem 3.1]) For \(d=1,2\), the \(\text {HCT}(k+2)\) reconstruction operator \(E^2 : \mathbb {V}\rightarrow {\text {H}} ^{2}(\Omega )\) satisifies the following bound for all \(u_h\in \mathbb {V}\):

(13)

with the constant \(C>0\) independent of \(u_h\) and of h.

Remark 2.6

Lemma 2.5 is proven in [13] for \(d=2\). For \(d=1\), we can recover into cubic or quartic splines and the proof is completely analogous. The proof for \(d=3\) using one of the trivariate \(C^1\)-elements with nodal and normal derivative degrees of freedom presented in [19] is conjectured to follow along the same lines to the proof of [13, Lem 3.1].

Using this \(\text {HCT}(k+2)\)-reconstruction, we can construct a further \(\text {HCT}(k+2)\)-reconstruction admitting the same bounds, but also satisfying an adjoint orthogonality property.

Definition 2.7

(\(HCT(k+2)\) -Ritz reconstruction) We define the Hsieh–Clough–Tocher \({\text {H}} ^{2}(\Omega )\)-conforming Ritz reconstruction operator \(E^{{\mathscr {R}}}: \mathbb {V}\rightarrow \text {HCT}(k+2)\) such that

(14)

Lemma 2.8

(Properties of \(E^{{\mathscr {R}}}\)) The \(\text {HCT}(k+2)\)-Ritz reconstruction is well-defined and satisfies the orthogonality condition:

$$\begin{aligned} \int _\Omega \!\left( {u_h - E^{{\mathscr {R}}}(u_h)}\right) \Delta \widetilde{v}= 0 \quad \,\forall \,\widetilde{v}\in \text {HCT}(k+2). \end{aligned}$$
(15)

In addition, for \(\alpha =0,1,2\), we have

(16)

for \(C>0\) constants, independent of \(u_h\) and of h.

Proof

Fixing \(u_h\in \mathbb {V}\), \(E^{{\mathscr {R}}}(u_h)\) is well-defined. Indeed, setting \(\widetilde{v}=E^{{\mathscr {R}}}(u_h)\) in (14), along with a standard inverse estimate, we deduce

$$\begin{aligned} \Vert {\nabla E^{{\mathscr {R}}}(u_h)}\Vert _{{\text {L}} _{2}(\Omega )}\le C\Vert {{u_h}} \Vert _{1,h}, \end{aligned}$$

for \(C>0\) independent of \(u_h\). The orthogonality condition follows from integrating both sides of (14) by parts.

To see (16) we note that

$$\begin{aligned} \Vert {{{E^{{\mathscr {R}}}(u_h) - u_h}}} \Vert _{1,h}^2\le & {} C{\mathscr {A}} _h\!\left( {E^{{\mathscr {R}}}(u_h) - u_h,E^{{\mathscr {R}}}(u_h) - u_h}\right) \nonumber \\= & {} C{\mathscr {A}} _h\!\left( {E^{{\mathscr {R}}}(u_h) - u_h,E^2(u_h) - u_h}\right) \nonumber \\\le & {} C\Vert {{E^{{\mathscr {R}}}(u_h) - u_h}} \Vert _{1,h} \Vert {{E^2(u_h) - u_h}} \Vert _{1,h}. \end{aligned}$$
(17)

Notice that in order to invoke coercivity of \({\mathscr {A}} _h\) over W(h) we must choose \(\sigma _0\) larger than if we merely required coercivity over \(\mathbb {V}\) since, as already mentioned in Example 2.4, W(h) contains piecewise polynomials two degrees higher than \(\mathbb {V}\). Using the properties of \(E^2(u_h)\) from Lemma 2.5 shows the claim for \(\alpha =1\). The result for \(\alpha = 2\) follows by an inverse inequality.

For \(\alpha = 0\) we use a duality argument. Take \(z\in {\text {H}} ^{2}(\Omega )\cap {\text {H}} ^{1}_0(\Omega )\) as the solution of the dual problem

$$\begin{aligned} -\Delta z = E^{{\mathscr {R}}}(u_h) - u_h; \end{aligned}$$
(18)

then

$$\begin{aligned} \Vert {E^{{\mathscr {R}}}(u_h) - u_h}\Vert _{{\text {L}} _{2}(\Omega )}^2= & {} \int _\Omega -\Delta z \!\left( {E^{{\mathscr {R}}}(u_h) - u_h}\right) \,\mathrm{d}x\nonumber \\= & {} \int _\Omega -\!\left( {\Delta z-\Delta \widetilde{z}}\right) \!\left( {E^{{\mathscr {R}}}(u_h) - u_h}\right) \,\mathrm{d}s\quad \,\forall \,\widetilde{z} \in \text {HCT}(k+2),\nonumber \\ \end{aligned}$$
(19)

in view of the orthogonality property (15). Integrating by parts we see

(20)

The result follows using the approximability of the \(\text {HCT}(k+2)\) space [9] that can be inferred through the dimensional analysis in Definition 2.3 and the regularity of the dual problem, specifically

$$\begin{aligned} \Vert {h^{-1}(\nabla z-\nabla \widetilde{z})}\Vert _{{\text {L}} _{2}(\Omega )} + \Vert {h^{-1/2}\{\!\{ \nabla z - \nabla \widetilde{z} \}\!\}}\Vert _{{\text {L}} _{2}({\mathscr {E}})}\le & {} C \left| z\right| _{{\text {H}} ^{2}(\Omega )}\nonumber \\\le & {} C \Vert {E^{{\mathscr {R}}}(u_h) - u_h}\Vert _{{\text {L}} _{2}(\Omega )},\nonumber \\ \end{aligned}$$
(21)

thereby concluding the proof. \(\square \)

Theorem 2.9

(inf–sup stability over W(h)) For polynomial degree \(k \ge 2\) there exists a \(\gamma _h>0\), depending on the quasiuniformity constant \(C_{qu}\), such that, when \(\sigma _0, \sigma _1\) are chosen large enough, we have for all \(w_h\in \mathbb {V}\)

$$\begin{aligned} \sup _{\widetilde{v}\in W(h)} \frac{{\mathscr {A}} _h\!\left( {w_h,\widetilde{v}}\right) }{\Vert {{\widetilde{v}}} \Vert _{0,h}} \ge \gamma _h \Vert {{w_h}} \Vert _{2,h}, \end{aligned}$$
(22)

where \(W(h):= \mathbb {V}+\text {HCT}(k+2)\).

Proof

The proof consists of two steps. We first show for a given \(w_h\in \mathbb {V}\) that there exists a \(\widetilde{v}\in W(h)\) such that

$$\begin{aligned} {\mathscr {A}} _h\!\left( {w_h,\widetilde{v}}\right) \ge C (\min _{x\in \Omega }h)^2 \Vert {{w_h}} \Vert _{2,h}^2 \end{aligned}$$
(23)

and that

$$\begin{aligned} \Vert {\widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \le C(\max _{x\in \Omega }h)^2 \Vert {{w_h}} \Vert _{2,h}, \end{aligned}$$
(24)

which, along with the quasi-uniformity assumption on the mesh, yields the inf-sup condition (22).

Firstly note that, after an integration by parts, the IP method (7) can be written as

(25)

Upon setting \(\widetilde{v}= w_h - E^{{\mathscr {R}}}(w_h) - \alpha h^2 \Delta _h w_h\), for some parameter \(\alpha \in {\mathbb R} \) to be chosen below, we compute

(26)

The orthogonality property of the \(\text {HCT}(k+2)\)-Ritz reconstruction (15) yields

$$\begin{aligned} \int _\Omega -\Delta _h w_h \!\left( {w_h - E^{{\mathscr {R}}}(w_h)}\right) \,\mathrm{d}x= \int _\Omega \!\left( {\Delta E^{{\mathscr {R}}}(w_h) -\Delta _h w_h}\right) \!\left( {w_h - E^{{\mathscr {R}}}(w_h)}\right) \,\mathrm{d}x. \end{aligned}$$
(27)

Repeated use of the Cauchy–Schwarz inequality, therefore, gives

(28)

We proceed to bound each of the terms \({\mathscr {I}} _i\) individually. Note that in view of scaling and inverse inequalities we have for any \(w_h\in \mathbb {V}\):

$$\begin{aligned} \Vert {\{\!\{ w_h \}\!\}}\Vert _{{\text {L}} _{2}(e)}\le & {} C_1 \Vert {h^{-1/2}w_h}\Vert _{{\text {L}} _{2}(\bar{K}_1\cup \bar{K}_2)} \end{aligned}$$
(29)
$$\begin{aligned} \Vert {\{\!\{ \nabla w_h \}\!\}}\Vert _{{\text {L}} _{2}(e)}\le & {} C_2 \Vert { h^{-3/2} w_h}\Vert _{{\text {L}} _{2}(\bar{K}_1\cup \bar{K}_2)} \end{aligned}$$
(30)

for any edge/face \(e:=\bar{K}_1\cap \bar{K}_2\in {\mathscr {E}} \), and elements \(K_1, K_2\in {\mathscr {T}} ^{}\), with \(C_1,C_2\) depending only on the mesh-regularity and shape-regularity constants.

For \({\mathscr {I}} _1\), in view of Lemma 2.8, we have

(31)

with constant \(C_3>0\) being the maximum of all constants in (16) for all \(\alpha \).

For \({\mathscr {I}} _2\), (29) and Lemma 2.8 yield

(32)

For \({\mathscr {I}} _3\), (30) and Lemma 2.8 yield

(33)

For \({\mathscr {I}} _4\), we have

(34)

for any \(\epsilon _4>0\), while for \({\mathscr {I}} _5\), we get

(35)

for any \(\epsilon _5>0\); similarly for \({\mathscr {I}} _6\) and for any \(\epsilon _6>0\), we have

(36)

Finally, the last term \({\mathscr {I}} _7\) can be bounded as follows:

(37)

for any \(\epsilon _7>0\).

Collecting the results (31)–(37) and substituting this into (28) we deduce

(38)

To arrive to (23), we can choose \(\epsilon _4 = \epsilon _5 =\epsilon _6 = \epsilon _7 = \frac{1}{5}\), \(\alpha =(\max \!\left( {\sigma _0^2,\sigma _1^2}\right) )^{-1}\) and \(\sigma _0\) and \(\sigma _1\) large enough.

For (24), we use Lemma 2.8 to see that

$$\begin{aligned} \Vert {\widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \le \Vert {w_h - E^{{\mathscr {R}}}(w_h)}\Vert _{{\text {L}} _{2}(\Omega )} + \Vert {\alpha h^2 \Delta _hw_h}\Vert _{{\text {L}} _{2}(\Omega )} \le C \Vert {{h^2 w_h}} \Vert _{2,h}, \end{aligned}$$
(39)

which, together with the quasiuniformity of the meshes, completes the proof. \(\square \)

Lemma 2.10

(Stability of the Ritz projection) Let \(R:W(h) \rightarrow \mathbb {V}\) denote the \({\mathscr {A}} _h\!\left( {\cdot ,\cdot }\right) \) orthogonal projector into \(\mathbb {V}\). Then, for \(\widetilde{w}\in W(h)\), there exists a \(C>0\), independent of h but possibly dependent on the quasiuniformity constant, \(C_{qu}\), such that

$$\begin{aligned} \Vert {R \widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} \le C \!\left( {{\max _{x\in \Omega } h} \Vert {\nabla \widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} + \Vert {\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} }\right) \le C \Vert {\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )}. \end{aligned}$$
(40)

Proof

Let \(\widetilde{g}\in W(h)\) be the solution to the discrete dual problem such that

$$\begin{aligned} {\mathscr {A}} _h\!\left( {\widetilde{v},\widetilde{g}}\right) = \left\langle {R \widetilde{w},\widetilde{v}}\right\rangle \quad \,\forall \,\widetilde{v}\in W(h). \end{aligned}$$
(41)

Note that this is well posed owing to coercivity as long as the penalty parameters are tuned to account for the fact that W(h) contains piecewise polynomials over the subpartition two degrees higher than \(\mathbb {V}\) itself. Then, we have

$$\begin{aligned} \Vert {R \widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )}^2= & {} \left\langle {R\widetilde{w}- \widetilde{w},R\widetilde{w}}\right\rangle + \left\langle {\widetilde{w},R\widetilde{w}}\right\rangle \nonumber \\= & {} {\mathscr {A}} _h\!\left( {R \widetilde{w}- \widetilde{w},\widetilde{g}}\right) + \left\langle {\widetilde{w},R\widetilde{w}}\right\rangle . \end{aligned}$$
(42)

Let \(\Pi : {\text {H}} ^{1}(\Omega )\rightarrow \mathbb {V}\cap {\text {H}} ^{1}_0(\Omega )\) a suitable projection with optimal approximation properties. Then

$$\begin{aligned} \Vert {R \widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )}^2= & {} {\mathscr {A}} _h\!\left( {R \widetilde{w}- \widetilde{w},\widetilde{g}- \Pi \widetilde{g}}\right) + \left\langle {\widetilde{w},R\widetilde{w}}\right\rangle \nonumber \\\le & {} \Vert {{h (R\widetilde{w}-\widetilde{w})}} \Vert _{1,h} \Vert {{h^{-1}(\widetilde{g}-\Pi \widetilde{g})}} \Vert _{1,h} + \Vert {\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} \Vert {R\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )},\qquad \end{aligned}$$
(43)

through the continuity of \({\mathscr {A}} _h\!\left( {\cdot ,\cdot }\right) \). From the optimal approximation properties of the projection/interpolant \(\Pi \), we have

$$\begin{aligned} \Vert {{h^{-1}\!\left( { \widetilde{g}- \Pi \widetilde{g}}\right) }} \Vert _{1,h}^2 \le { C_{qu} }\tilde{C}\Vert {{\widetilde{g}}} \Vert _{2,h}^2, \end{aligned}$$
(44)

and, using the discrete regularity of \(\widetilde{g}\) induced by the inf-sup condition in Theorem 2.9

$$\begin{aligned} \gamma _h\Vert {{\widetilde{g}}} \Vert _{2,h} \le \sup _{\widetilde{v}\in W(h)} \frac{{\mathscr {A}} _h\!\left( {\widetilde{g},\widetilde{v}}\right) }{\Vert {{\widetilde{v}}} \Vert _{0,h}} = \sup _{\widetilde{v}\in W(h)} \frac{\left\langle {R \widetilde{w},\widetilde{v}}\right\rangle }{\Vert {{\widetilde{v}}} \Vert _{0,h}} \le C \Vert {R\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )}. \end{aligned}$$
(45)

Hence we see that

$$\begin{aligned} \Vert {R \widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )}^2\le & {} C\!\left( { \Vert {{h (R\widetilde{w}-\widetilde{w})}} \Vert _{1,h} \Vert {R\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} + \Vert {\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} \Vert {R\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} }\right) \nonumber \\\le & {} C\!\left( {\Vert {{h\widetilde{w}}} \Vert _{1,h} \Vert {R\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} + \Vert {\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )} \Vert {R\widetilde{w}}\Vert _{{\text {L}} _{2}(\Omega )}}\right) , \end{aligned}$$
(46)

in view of the quasi-best approximation in \(\Vert {{\cdot }} \Vert _{1,h}\) from (10). The conclusion follows from standard inverse inequalities. \(\square \)

Theorem 2.11

(inf–sup stability over \(\mathbb {V}\)) For polynomial degree \(k \ge 2\) there exists a \(\gamma _h>0\), independent of h, but dependent on \(C_{qu}\) such that, when \(\sigma _0, \sigma _1 \ge 1\) are chosen as in Theorem 2.9, we have for all \(w_h \in \mathbb {V}\)

$$\begin{aligned} \sup _{v_h\in \mathbb {V}} \frac{{\mathscr {A}} _h\!\left( {w_h,v_h}\right) }{\Vert {{v_h}} \Vert _{2,h}} \ge \gamma _h \Vert {{w_h}} \Vert _{0,h}. \end{aligned}$$
(47)

Proof

To show (47) we fix \(w_h\) and let \(\Phi \in \mathbb {V}\) be the solution of the dual problem

$$\begin{aligned} {\mathscr {A}} _h\!\left( {\Psi ,\Phi }\right) = \int _\Omega w_h \Psi \,\mathrm{d}x\quad \,\forall \,\Psi \in \mathbb {V}. \end{aligned}$$
(48)

Following the same arguments as in the proof of Theorem 2.9, it is clear that there exists a \(C>0\) such that

$$\begin{aligned} Ch^2 \Vert {{\Phi }} \Vert _{2,h}^2 \le {\mathscr {A}} _h\!\left( {\Phi ,\widetilde{v}}\right) , \end{aligned}$$
(49)

where \(\widetilde{v}:= \Phi - E^{{\mathscr {R}}}(\Phi ) - \alpha h^2 \Delta _h \Phi \). Now it is clear that

$$\begin{aligned} \Vert {\widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \Vert {{\Phi }} \Vert _{2,h} \le Ch^2 \Vert {{\Phi }} \Vert _{2,h}^2 \le C {\mathscr {A}} _h\!\left( {\Phi ,\widetilde{v}}\right) , \end{aligned}$$
(50)

and hence in view of Lemma 2.10 we have, with R denoting the \({\mathscr {A}} _h\) orthogonal projector into \(\mathbb {V}\), that

$$\begin{aligned} \Vert {R \widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \le C { \max _{x\in \Omega } h}\!\left( {\Vert { \nabla \widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} + \Vert {\widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )}}\right) \le C \Vert {\widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )}, \end{aligned}$$
(51)

through inverse inequalities. Hence

$$\begin{aligned} \Vert {R \widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \Vert {{\Phi }} \Vert _{2,h} \le C\Vert {\widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \Vert {{\Phi }} \Vert _{2,h}. \end{aligned}$$
(52)

Now arguing as in the Proof of Theorem 2.9, and noting the constant will now depend on \(C_{qu}\), we may show that

$$\begin{aligned} \Vert {\widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \le C \Vert {{h^2\Phi }} \Vert _{2,h}. \end{aligned}$$
(53)

Combining the previous two inequalities yields

$$\begin{aligned} \Vert {R \widetilde{v}}\Vert _{{\text {L}} _{2}(\Omega )} \Vert {{\Phi }} \Vert _{2,h} \le C\Vert {{h\Phi }} \Vert _{2,h}^2 \le C{\mathscr {A}} _h\!\left( {\Phi ,\widetilde{v}}\right) = C{\mathscr {A}} _h\!\left( {\Phi ,R \widetilde{v}}\right) , \end{aligned}$$
(54)

concluding the proof. \(\square \)

Corollary 2.12

(Convergence) Let u solve (1) and \(u_h \in \mathbb {V}\) be the interior penalty approximation from (7), then, under the assumptions of Theorem 2.11,

$$\begin{aligned} \Vert {{u - u_h}} \Vert _{0,h} \le \!\left( {1+\frac{C_B}{\gamma _h}}\right) \inf _{w_h\in \mathbb {V}} \Vert {{u - w_h}} \Vert _{0,h} + \frac{1}{\gamma _h} \sup _{v_h\in \mathbb {V}} \frac{{\mathscr {A}} _h\!\left( {u_h - u,v_h}\right) }{\Vert {{v_h}} \Vert _{2,h}} , \end{aligned}$$
(55)

where \(\gamma _h\) is the discrete inf-sup constant and \(C_B\) is the continuity constant. If \(u\in {\text {H}} ^{k+1}(\Omega )\) for \(k \ge 2\) the following a priori bound holds:

$$\begin{aligned} \Vert {{u-u_h}} \Vert _{0,h} + \Vert {{h\!\left( {u-u_h}\right) }} \Vert _{1,h} + \Vert {{h^2\!\left( {u - u_h}\right) }} \Vert _{2,h} \le C h^{k+1} \left| u\right| _{k+1}. \end{aligned}$$
(56)

Proof

Using the inf-sup condition from Theorem 2.11 we see for all

(57)

Now using the natural continuity bound

$$\begin{aligned} {\mathscr {A}} _h\!\left( {u-w_h,v_h}\right) \le C_B \Vert {{u-w_h}} \Vert _{0,h} \Vert {{v_h}} \Vert _{2,h} \end{aligned}$$
(58)

we see

$$\begin{aligned} \Vert {{w_h - u_h}} \Vert _{0,h} \le \frac{C_B}{\gamma _h} \Vert {{u-w_h}} \Vert _{0,h} + \frac{1}{\gamma _h} \sup _{v_h\in \mathbb {V}} \frac{{\mathscr {A}} _h\!\left( {u - u_h,v_h}\right) }{\Vert {{v_h}} \Vert _{2,h}}. \end{aligned}$$
(59)

Hence, in view of the triangle inequality

$$\begin{aligned} \Vert {{u - u_h}} \Vert _{0,h} \le \!\left( {1 + \frac{C_B}{\gamma _h}}\right) \Vert {{u-w_h}} \Vert _{0,h} + \frac{1}{\gamma _h} \sup _{v_h\in \mathbb {V}} \frac{{\mathscr {A}} _h\!\left( {u - u_h,v_h}\right) }{\Vert {{v_h}} \Vert _{2,h}}. \end{aligned}$$
(60)

The bound (55) follows since \(w_h\) was arbitrary and (56) follows from the best approximation of \(\mathbb {V}\). \(\square \)

3 Applications to problems with rough data

In this section we examine some problems of the form

$$\begin{aligned} -\Delta u&= f \text { in } \Omega \nonumber \\ u&= 0 \text { on } \partial \Omega \end{aligned}$$
(61)

where f may be as rough as \({\text {H}} ^{-2}(\Omega ) \backslash {\text {H}} ^{-1}(\Omega )\) and so, \(u\in {\text {L}} _{2}(\Omega ) \backslash {\text {H}} ^{1}(\Omega )\). This means that the problem (75) cannot be characterised through a weak formulation, rather an ultra weak formulation, whereby we seek \(u\in {\text {L}} _{2}(\Omega )\) such that

(62)

and the right hand side of (62) is understood as a duality pairing. In this setting standard tools pertaining to the analysis of Galerkin methods may not apply, for example the Aubin–Nitsche duality argument.

However, the stabilised IP method is still well defined and the inf-sup condition still holds. Indeed, we define the modified IP method: seek \(u_h\in \mathbb {V}\) such that

$$\begin{aligned} {\mathscr {A}} _h\!\left( {u_h,v_h}\right) = \left\langle f\,\vert \,E^\mathscr {R}_0(v_h)\right\rangle _{{\text {H}} ^{-2}(\Omega )\times {\text {H}} ^{2}_0(\Omega )} \quad \,\forall \,v_h\in \mathbb {V}, \end{aligned}$$
(63)

where \(E^2_0:\mathbb {V}\rightarrow H^2_0(\Omega )\) is the modification of \(E^2\) recovering onto \(H^2_0(\Omega )\) which is constructed by setting to zero all the degrees of freedom on \(\partial \Omega \). We note that Lemma 2.5 still holds verbatim when \(E^2\) is replaced by \(E^2_0\). The nonstandard definition of the right-hand side allows us to make sense of extremely rough source terms [15] by interpreting the right-hand side a a duality pairing. Correspondingly, we also denote by \(E^{{\mathscr {R}}}_0\) the recovery given by Definition 2.7 when \(E^2\) is replaced by \(E^2_0\). Also, we note that Lemma 2.8 holds for \(E^{{\mathscr {R}}}_0\) also.

Since the inf-sup condition given in Theorem 2.11 is a condition only on the operator itself, the best approximation result given in Corollary 2.12 holds true. The only uncertainty with the bound is the behaviour of the inconsistency term. The control of this term is the main motivation in the nonstandard definition of the right hand side of (63).

Theorem 3.1

(quasi-optimal error control for problems with rough data) Let \(u\in {\text {L}} _{2}(\Omega )\) solve (62) and \(u_h\in \mathbb {V}\) be the approximation defined through (63), then

(64)

Proof

The proof takes some inspiration from that of [17], where inconsistency terms arise from the fact that the solution of an elliptic problem may only lie in \({\text {H}} ^{1}(\Omega )\), for which the operator \({\mathscr {A}} _h\!\left( {u,v_h}\right) \) may not be well defined. Here, the situation is more involved, since the solution \(u\in {\text {L}} _{2}(\Omega )\backslash {\text {H}} ^{1}(\Omega )\).

Using the inf-sup condition from Theorem 2.11 we have

$$\begin{aligned} \gamma _h \Vert {{w_h - u_h}} \Vert _{0,h} \le \sup _{v_h\in \mathbb {V}} \frac{{\mathscr {A}} _h\!\left( {w_h - u_h,v_h}\right) }{\Vert {{v_h}} \Vert _{2,h}}. \end{aligned}$$
(65)

Now, by adding and subtracting appropriate terms and using (62) and (63), we see

$$\begin{aligned} {\mathscr {A}} _h\!\left( {w_h {-} u_h,v_h}\right)= & {} {\mathscr {A}} _h\!\left( {w_h,E^{\mathscr {R}} _0(v_h)}\right) {+} \int _\Omega u \Delta E^{\mathscr {R}} _0(v_h) \,\mathrm{d}x{+} {\mathscr {A}} _h\!\left( {w_h,v_h - E^{\mathscr {R}} _0(v_h)}\right) \nonumber \\= & {} {\mathscr {A}} _h\!\left( {w_h,E^{\mathscr {R}} _0(v_h)}\right) + \int _\Omega u \Delta E^{\mathscr {R}} _0(v_h) \,\mathrm{d}x\nonumber \\&+\, {\mathscr {A}} _h\!\left( {w_h - E^2_0(v_h),v_h - E^{\mathscr {R}} _0(v_h)}\right) \end{aligned}$$
(66)

by the orthogonality properties of \(E^{{\mathscr {R}}}_0(w_h)\) given in (14). Now we may use that

(67)

through the stability of \(E^{{\mathscr {R}}}(v_h)\).

Finally, using the approximation properties of \(E^{{\mathscr {R}}}_0(\cdot )\) and \(E^2_0(\cdot )\) we see

(68)

Substituting (67) and (68) into (66) we have

(69)

and hence

(70)

as required. \(\square \)

3.1 Numerical experiments

The implementation of all the numerical experiments was performed in \(\textsf {Matlab}^{\textregistered }\) on a laptop computer with a 2.3GHz Intel i7 processor and 16 GB of RAM. All computations took less than 2 min on this machine.

3.1.1 Test 1: an one-dimensional example

We begin by assessing the method (63) for \(d=1\). We set \(\Omega = (0,1)\) and consider the problem of finding u such that

$$\begin{aligned} - u''= & {} \delta _{\bar{x}}' \quad \text { in } \Omega \nonumber \\ u= & {} 0 \quad \text { on } \partial \Omega , \end{aligned}$$
(71)

where \(\delta _{\bar{x}}'\) denotes the distributional derivative of the Dirac distribution at a point \(\bar{x} \in \Omega \). This one-dimensional problem was a motivating example in the classical work of Babuška and Osborn [3]; this computation is included here as a tribute to that inspiring work.

For this problem we can even characterise a distributional solution, indeed we have that

$$\begin{aligned} u(x) = {\left\{ \begin{array}{ll} -x &{}\quad \text {when } x < \bar{x} \\ 1-x &{} \quad \text {when } x > \bar{x}, \end{array}\right. } \end{aligned}$$
(72)

solves (75). If we assume that \(\bar{x}\) does not lie on the skeleton of the triangulation we can define our approximation as seeking \(u_h\in \mathbb {V}\) such that

$$\begin{aligned} {\mathscr {A}} _h\!\left( {u_h,v_h}\right) = E^{\mathscr {R}} _0(v_h)'(\bar{x}) \quad \,\forall \,v_h\in \mathbb {V}. \end{aligned}$$
(73)

Using Theorem 3.1 we are able to show this approximation satisfies the a priori bound

$$\begin{aligned} \Vert {u-u_h}\Vert _{{\text {L}} _{2}(\Omega )} \le C h^{1/2-\epsilon } \quad \,\forall \,\epsilon > 0, \end{aligned}$$
(74)

since \(\delta _{\bar{x}} \in {\text {H}} ^{-s}(\Omega )\) for all \(s > 1/2\).

We fix \(k=2\) and solve (73) over a sequence of uniform meshes in 1d with \(h = 1/2, 1/4, \dots , 1/1024\). We take \(\bar{x} = 1/2 + \sqrt{2}/100000\) as to not align it with the nodes of the mesh. In Fig. 2 we show the numerical approximation over the finest mesh along with the experimental order of convergence.

Fig. 2
figure 2

In this experiment we test the \({\text {L}} _{2}\) convergence of the interior penality method to approximate the distributional solution (72). Notice the error converges approximately like \({\text {O}}(h^{1/2})\). a The IP approximation. b Error and the experimental order of convergence

Full size image

3.1.2 Test 2: \(d=2\) with a Dirac source term at a point

We now take \(\Omega = B(0,1)\), the open ball of radius 1 centred at the origin, and consider the problem of finding u such that

$$\begin{aligned} -\Delta u&= \delta _{\mathbf {0}}\quad \text { in } \Omega \nonumber \\ u&= 0 \quad \text { on } \partial \Omega . \end{aligned}$$
(75)

The exact solution u is the fundamental solution of Laplace’s problem

$$\begin{aligned} u(\mathbf {x}) = -\frac{1}{2\pi }\log (\left| \mathbf {x}\right| ), \end{aligned}$$
(76)

for which we have \(u\in {\text {L}} _{2}(\Omega ) \backslash {\text {H}} ^{1}(\Omega )\).

We define our approximation as seeking \(u_h \in \mathbb {V}\) such that

$$\begin{aligned} {\mathscr {A}} _h\!\left( {u_h,v_h}\right) = E^{\mathscr {R}} _0(v_h)(\bar{x}) \quad \,\forall \,v_h\in \mathbb {V}, \end{aligned}$$
(77)

and, under the assumptions of Theorem 3.1, we are able to show that this approximation satifies the a priori bound

$$\begin{aligned} \Vert {u-u_h}\Vert _{{\text {L}} _{2}(\Omega )} \le C h^{1-\epsilon } \quad \,\forall \,\epsilon > 0. \end{aligned}$$
(78)

This is in agreement with the results of [2] for conforming finite elements applied to this problem.

We fix \(k=2\) and solve (80) over a sequence of unstructured, quasiuniform triangulations of B(0, 1). For the coarsest mesh we have \(h \approx 0.13\) and for the most fine \(h \approx 0.0019\). In Fig. 3, we show the numerical approximation over the finest mesh along with the error measured in the \({\text {L}} _{2}\)-norm and its convergence history. We remark, that the boundary approximation by straight-faced elements is not detrimental to the convergence rate in this case as the error is measured in the \({\text {L}} _{2}\)-norm.

Fig. 3
figure 3

We test the \({\text {L}} _{2}\)-norm convergence of the method (80) to approximate the fundamental solution of Laplace’s problem (76). The error converges approximately like \({\text {O}}(h)\). a The IP approximation. b Error and the experimental order of convergence

Full size image

3.2 Test 3: \(d=2\), rough source terms defined over an one-dimensional manifold

We now test the proposed method on a more complicated problem, whereby, we set \(\Omega = (0,1)^2\) and consider the problem of finding u such that

$$\begin{aligned} -\Delta u= & {} \alpha \delta _{{\mathscr {M}}} + \!\left( {1-\alpha }\right) \partial _x \delta _{{\mathscr {M}}}\quad \text { in } \Omega \nonumber \\ u= & {} 0 \quad \text { on } \partial \Omega , \end{aligned}$$
(79)

where \(\alpha \in \{0,1\}\) and \({\mathscr {M}}:= \{ (x,y) : \left| x-1/2\right|< 1/4 \text { and } y = 1/2 \text { or } x = 1/2 \text { and } \left| y-1/2\right| < 1/4\}\) is an one-dimensional manifold. When \(\alpha = 1\), we have \(u\in {\text {H}} ^{1}(\Omega )\), whereas when \(\alpha = 0\), we have \(u\in {\text {L}} _{2}(\Omega )\backslash {\text {H}} ^{1}(\Omega )\).

We seek \(u_h \in \mathbb {V}\) such that

$$\begin{aligned} {\mathscr {A}} _h\!\left( {u_h,v_h}\right) = \alpha E^{\mathscr {R}} _0(v_h)(\bar{x}) + \!\left( {1-\alpha }\right) \partial _x E^{\mathscr {R}} _0(v_h)(\bar{x}) \quad \,\forall \,v_h\in \mathbb {V}, \bar{x}\in {\mathscr {M}}. \end{aligned}$$
(80)

We fix \(k=2\) and solve (80) over a uniform, criss-cross triangulation of \(\Omega \) with \(h \approx 0.015\). In Fig. 4 we show the numerical approximation over this mesh for both values of \(\alpha \).

Fig. 4
figure 4

The approximations to the solution of (79) produced by (80) for two different values of \(\alpha \). The two dark regions on the right plot depict jump discontinuity. a \(\alpha = 1\). b \(\alpha = 0\)

Full size image

We conclude this exposition by noticing that, since the singularity in all tests were isolated, adaptive approximations should be able to recover best approximation. This motivates the extension of this analysis from the quite restrictive quasiuniform meshes to those that allow for some grading. Note the recent work [14] where, using a posteriori localisation techniques, analagous inf-sup results for the classical interior penalty dG scheme have been proven over meshes satisfying a mesh variation condition.