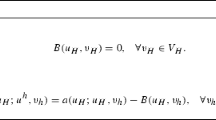1 Introduction

In this article, we consider the a posteriori error analysis, in a natural mesh-dependent energy norm, for a class of interior-penalty hp-version discontinuous Galerkin finite element methods (DGFEMs) for the numerical solution of the following quasilinear elliptic boundary value problem:

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(1)

Here, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is a bounded polygon with a Lipschitz continuous boundary Γ, and f ∈L2(Ω), where for an open set D ⊆ Ω, we signify by L2(D) the space of all square integrable functions on D. Additionally, we assume that the nonlinearity μ satisfies the following assumptions: (A1) \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \); (A2) there exist positive constants m μ and M μ such that m μ(t − s) ≤ μ(x, t)t − μ(x, s)s ≤ M μ(t − s), t ≥ s ≥ 0, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). We remark that, if μ satisfies (A2), there exist constants β ≥ α > 0, such that for all vectors \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), and all \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \),

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(2)

see [14, Lemma 2.1]. For ease of notation, in the sequel, we will simply write μ(s) instead of μ(x, s), thereby suppressing the explicit dependence of μ on x ∈ Ω.

The weak formulation of (1) is to find \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) such that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(3)

where, given \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we define the bilinear form A(w;u, v) =∫Ω μ(|∇w|)∇u ⋅∇v d x, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), as well as the L2(Ω)-inner product \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), v, w ∈L2(Ω). Here, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is the standard Sobolev space of first order, with zero trace along Γ, equipped with the norm \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). Under the assumptions (A1)–(A2) above, it is elementary to show that the form A is strongly monotone and Lipschitz continuous in the sense that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(4)

and

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

respectively. From these properties, classical monotone operator theory implies existence and uniqueness of a solution of (3); see, e.g., [17, Theorem 3.3.23].

The exploitation of automatic adaptive hp-refinement algorithms has the potential to compute numerical solutions to partial differential equations (PDEs) in a highly efficient manner, often leading to exponential rates of convergence as the underlying finite element space is enriched; see, e.g., [11, 16]. The key tool required to design such strategies is the derivation of a posteriori estimates for the Galerkin discretization errors; in recent years such bounds have been extended to the context of linearization and/or linear solver errors, cf. [1, 2, 4, 5, 7, 9]. In the present article we consider the derivation of an hp-version a posteriori error bound for the DGFEM approximation of the second-order quasilinear elliptic PDE problem stated in (1). To this end, we employ the interior penalty DGFEM proposed in [10], cf. also [12], together with a discrete Kačanov iterative linearization scheme, cf. [6]. Based on the analysis undertaken in [12], together with the use of a suitable reconstruction operator, cf. [13, 15], we derive a fully computable bound for the error, measured in terms of a suitable DGFEM energy norm, which separately accounts for the three main sources of error: discretization, linearization, and linear solver errors. On the basis of this a posteriori bound, we design and implement an hp-adaptive refinement algorithm which automatically controls each of these error contributions as the underlying finite element space is enriched. Numerical experiments highlighting the practical performance of the proposed adaptive strategy are presented.

2 Iterative Discontinuous Galerkin Methods

2.1 Discrete hp-Discontinuous Galerkin Spaces

Let \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) be a partition of Ω into disjoint open and shape-regular elements κ such that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). We assume that each \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is an affine image of a given master element \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), which is either the open triangle {(x, y): −1 < x < 1, −1 < y < −x}) or the open square (−1, 1)2 in \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). By h κ we denote the element diameter of \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), and n κ signifies the unit outward normal vector to κ. We allow \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) to be 1-irregular, i.e., each edge of any one element \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) contains at most one hanging node (which, for simplicity, we assume to be the midpoint of the corresponding edge). In this context, we suppose that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is regularly reducible (cf. [18, Section 7.1] and [12]), i.e., there exists a shape-regular conforming (regular) mesh \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) (consisting of triangles and parallelograms) such that the closure of each element in \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is a union of closures of elements of \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), and that there exists a constant C > 0, independent of the element sizes, such that for any two elements \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) we have \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). Note that these assumptions imply that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is of bounded local variation, i.e., there exists a constant ρ 1 ≥ 1, independent of the element sizes, such that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), for any pair of elements \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) which share a common edge e = ∂κ ♯ ∩ ∂κ ♭. Moreover, let us consider the set \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) of all one-dimensional open edges of all elements \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). Further, we denote by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) the set of all edges \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) that are contained in the open domain Ω (interior edges). Additionally, we introduce \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) to be the set of boundary edges consisting of all \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) that are contained in Γ.

For any integer \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we denote by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) the set of polynomials of total degree p on κ. Similarly, when κ is a quadrilateral, we also consider \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), the set of all tensor-product polynomials on κ of degree p in each coordinate direction. To each \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) we assign a polynomial degree p κ (local approximation order). We collect the local polynomial degrees in a vector \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), and then introduce the hp-DGFEM space

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) being either \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) or \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). We shall suppose that the polynomial degree vector p, with p κ ≥ 1 for each \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), has bounded local variation, i.e., there exists a constant ρ 2 ≥ 1, independent of the local element sizes and p, such that, for any pair of neighbouring elements \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we have \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \).

We also define the L2-projection \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) by

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

Evidently, since functions in \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) do not need to be continuous, we have that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), where, for \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we let \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) be the L2-projection onto \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \).

2.2 Nonlinear hp-DGFEM Formulation

Let κ ♯ and κ ♭ be two adjacent elements of \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), and x an arbitrary point on the interior edge \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) given by e = (∂κ ♯ ∩ ∂κ ♭)∘. Furthermore, let v and q be scalar- and vector-valued functions, respectively, that are sufficiently smooth inside each element κ ♯, κ ♭. Then, the averages of v and q at x ∈ e are given by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), respectively. Similarly, the jumps of v and q at x ∈ e are given by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), respectively. On a boundary edge \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we set 〈 〈v〉 〉 = v, 〈 〈q〉 〉 = q and [ [v] ] = v n, with n denoting the unit outward normal vector on the boundary Γ.

Furthermore, we introduce the edge functions \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), which, for an edge \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), are given by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), with h e denoting the length of e. In addition, we define the discontinuity penalisation function \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) given by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) where γ ≥ 1 is a (sufficiently large) constant. Then, we equip the DGFEM space \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) with the DGFEM norm \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), where \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is the element-wise gradient operator.

With this notation, following [10], we introduce the interior penalty DGFEM discretization of (3) by: find \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) such that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(5)

where, for given \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we define the DGFEM bilinear form

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

where θ ∈ [−1, 1] is a method parameter. Referring to [10, Theorem 2.5], provided that γ ≥ 1 is chosen sufficiently large (independent of the local element sizes and of the polynomial degree distribution), the existence and uniqueness of the DGFEM solution \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) satisfying (5) is guaranteed.

Assumption 1

In the sequel, we suppose that there exists a computable a posteriori error estimate of the form \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) , where \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is the solution of (1), and u DG is its hp-DGFEM approximation defined in (5).

Remark 1

In the article [12, Theorem 3.2] it has been proved that such a bound does indeed exist. More precisely, we have that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(6)

where, the local error indicators η κ, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), are defined by

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(7)

and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is a data oscillation term. For \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we have \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) where I denotes a generic identity operator. Here, we write \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). Additionally, we denote by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) the L2-projector onto \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), where we let \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), e = ∂κ ♯ ∩ ∂κ ♭. Moreover, C > 0 in (6) is a constant that is independent of the local element sizes, the polynomial degree vector p, and the parameters γ and θ.

2.3 Iterative DGFEM

In order to provide a practical solution scheme for the nonlinear hp-DGFEM system (5) we propose a linearization approach based on a discrete Kačanov fixed point iteration, see, e.g., [6]. To this end, we begin by selecting an initial guess \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). Then, for n ≥ 1, given \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), we solve the linear hp-DGFEM formulation, defined by

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(8)

for \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). We emphasize that, in actual computations, the linear system (8) may be solved by an iterative algorithm, thereby generating an approximate numerical solution \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), with \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). This means that, in practice, instead of computing the sequence \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) obtained from the iteration (8), an inexact sequence \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is generated such that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(9)

From a mathematical view point, this (inexact) iterative linearization DGFEM approach gives rise to three different sources of error:

  1. 1.

    Discretization error, which is expressed by the residual

    $$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
    (10)
  2. 2.

    Linearization error, which is given in terms of the residual \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \):

    $$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
    (11)

    We observe that, if (1) is linear, then we immediately obtain \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \).

  3. 3.

    Linear solver error, which is described by a residual \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \):

    $$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
    (12)

    Note that, if (8) is solved exactly, then we have \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), and it follows that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \).

Remark 2

Since \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) may not need to be continuous along element interfaces, the linearization and linear solver residuals \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), respectively, can be computed elementwise, i.e., in parallel, and, hence, at a low computational cost.

The aim of the analysis in the following section is to investigate the above residuals, and then to provide a computable a posteriori error estimate for the error \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) between the solution u of (1) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \).

2.4 A Posteriori Error Estimation

In order to bound the residual \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) in (10), we apply an elliptic reconstruction technique along the lines of the works [13, 15], see also [7]. Specifically, we define an auxiliary function \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) to be the unique solution of the weak formulation

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

where \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) are the linearization and linear solver residuals from (11) and (12), respectively. Upon adding (11) and (12), we notice that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

In particular, we observe that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is the DGFEM approximation of \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) based on employing the (nonlinear) DGFEM scheme defined in (5). In particular, we may exploit the a posteriori error estimate in Assumption 1 to infer the computable bound

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(13)

We now turn to bounding the elliptic reconstruction error \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \); to this end, we first observe that \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). Then, employing the strong monotonicity property (4), and recalling the weak formulation (3), we obtain

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

Employing the Cauchy-Schwarz inequality, together with the Poincaré-Friedrichs inequality, \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) for all \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), where C PF > 0 is a constant, we deduce that

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$
(14)

where the linearization and linear solver residuals are given, respectively, by

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

Summarizing the above analysis leads to the following result.

Theorem 1

Suppose that Assumption 1 is satisfied. Then, given a sequence of (possibly inexact) DGFEM approximations \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) , cf. (9), for n ≥ 1, the following a posteriori error bound holds:

$$\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} $$

Here, u is the analytical solution of (1), \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) are the residuals defined in (11) and (12), respectively, and α > 0 is the constant occurring in (2) and (4).

Proof

The result follows immediately upon application of the triangle inequality, i.e., \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), and inserting the bounds (13) and (14).

Remark 3

We note that the above analysis naturally applies to other finite element schemes, provided that Assumption 1 is satisfied.

2.5 Adaptive Iterative hp-DGFEM Procedure

In this section we introduce an automatic hp-refinement algorithm which ensures that each of the three components of the error, namely discretization, linearization, and linear solver, are controlled in a suitable fashion. To this end, we propose the following strategy, cf. [9].

Algorithm 1

Given a (coarse) starting mesh \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) , with an associated (low-order) polynomial degree distribution p , and an initial guess \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) . Set n ← 1.

In Step 2 of Algorithm 1, if (??) is fulfilled then the space \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is adaptively hp-refined based on first marking elements for refinement according to the size of the local element indicators η κ, cf. (7). To this end, we exploit the maximal strategy whereby elements are marked for refinement which satisfy the condition \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) Secondly, once an element \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) has been marked for refinement, we undertake either local mesh subdivision or local polynomial enrichment based on employing the hp-refinement criterion developed within the article [8]. Finally, when (??) is not fulfilled, rather than determining which source of error, i.e., the (computable) quantities \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) or \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) from (11) and (12), respectively, is dominant, we choose to always undertake a further linearization step, and hence a further linear solver step is also computed, since this ensures that the most up to date approximation \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is employed at all times.

3 Application to Quasilinear Elliptic PDEs

In this section we present numerical experiments to highlight the performance of the proposed iterative hp-refinement procedure outlined in Algorithm 1. To this end, we set the interior penalty parameter constant γ to 10 and the steering parameter Υ to 1∕4. The solution of the resulting set of linear equations is computed using an ILU(0) preconditioned GMRES algorithm.

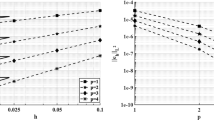
For the first numerical experiment, we let Ω = (0, 1)2 and define the nonlinear coefficient as μ(|∇u|) = 2 + (1 + |∇u|)−1. The right-hand forcing function f is selected so that the analytical solution to (1) is given by \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). In Fig. 1 we present a comparison of the actual error measured in terms of the energy norm versus the square root of the number of degrees of freedom in \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \). From Fig. 1a we clearly observe that exponential convergence of the proposed hp-refinement strategy as \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) in enriched. Furthermore, in Fig. 1b we plot the individual residual error indicators; for this smooth problem, we observe that the discretization indicator (denoted as η n in the figure) is always dominant, while the linearization and linear solver residuals (denoted as Ψ n and λ n, respectively) are roughly of the same magnitude.

Fig. 1
figure 1

Example 1. (a) Comparison of the DGFEM norm of the error and the a posteriori bound, with respect to the square root of the number of degrees of freedom; (b) individual error estimators

Full size image
Fig. 2
figure 2

Example 2. (a) Comparison of the DGFEM norm of the error and the a posteriori bound, with respect to the third root of the number of degrees of freedom; (b) individual error estimators

Full size image

Secondly, we let Ω denote the L-shaped domain \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) and select \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) By writing (r, φ) to denote the system of polar coordinates, we choose the forcing function f and an inhomogeneous boundary condition such that the analytical solution to (1) is \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \), cf. [3]. In Fig. 2 we now present a comparison of the actual error measured in terms of the energy norm versus the third root of the number of degrees of freedom in \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \); as before we again attain exponential convergence of the proposed hp-refinement strategy as \(\displaystyle \begin{aligned} \begin{aligned} u_t + f(u)_x &= 0, & (x,t) \in \mathbb{R}\times \mathbb{R}_{+},\\ u(0) &= u_0, \end{aligned} {} \end{aligned} \) is adaptively refined, though convergence of the a posteriori error estimator is no longer monotonic. Indeed, from Fig. 2b, we observe that once an hp-mesh refinement has been undertaken, then several linearization/solver steps may be required to ensure that the numerical solution has been computed to a sufficient accuracy before future refinements may be undertaken.

4 Conclusions

In this article we have derived a computable hp-version a posteriori error bound for the DGFEM approximation of a second-order quasilinear elliptic PDE problem, whereby a discrete Kačanov iterative linearization scheme is employed. The resulting computable upper bound directly takes into account discretization error, as well as the errors stemming from linearization and the underlying linear solver. Numerical experiments highlighting the performance of this bound within an automatic hp-refinement algorithm are presented.