Introduction

Calorimetric studies reveal information about the dependence of the thermal behavior of a material on molecular mobility, which affects the microstructure and chemical reactions of the material. Differential scanning calorimetry (DSC) measures the thermal behavior and transitions of polymers during heating and cooling. It is especially important for measuring and controlling the glass transition temperatures of industrial polymers in the conditions in which they are used. This is significant because most polymeric materials have amorphous structures and their microstructures gradually change below the glass transition temperature due to enthalpy and volume relaxations. These changes to their microstructures affect their physical and mechanical properties.

Since wood contains amorphous cellulose, hemicellulose and lignin matrices, many studies have used thermal analysis and calorimetry to investigate the relationship between glass transitions and softening of woods and its components [1–9]. Thermomechanical measurements that involve applying a static or dynamic stress detect temperatures at which sudden changes occur in the displacement or the elastic properties. Such temperatures are referred to as softening or glass transition temperatures. Many softening measurements have used water-saturated wood samples to ensure that their moisture conditions remain constant during the tests. The mechanical properties of wood are highly sensitive to the moisture content in the microstructure since water acts as a plasticizer. Consequently, a reduction in the moisture content of a wood sample reduces the molecular mobility (i.e., it increases the glass transition temperature). Since wood is basically used below the fiber saturated moisture content in practical applications, it is important to know the softening and glass transition temperatures of wood at moderate humidity conditions. However, it is difficult to maintain a constant moisture content in a non-saturated wood sample during softening measurements due to water evaporating during heating. In calorimetric methods such as DSC, the heat flow is determined from changes in the heat capacity and kinetic reactions of a sample are measured in a hermetic environment using metallic pans. Previous DSC studies of wood containing moisture found a small endothermic peak in the first heating run; the temperature of this peak increased from 60 °C to over 100 °C when the moisture content was reduced from 30 to 5 % [8, 9]. Since this moisture content dependence of the peak temperature is very similar to the relationship between the softening temperature and the moisture content of wood measured by thermomechanical methods [2, 3], the peak temperature is considered to be the glass transition temperature of moist wood. However, the glass transition phenomenon of polymers produces a step change in the heat flow, which is determined from the change in the heat capacity due to polymer changing from the glassy to the rubbery state. Therefore, the previously reported endothermic peaks must involve some other phenomenon in addition to the glass transition, probably an enthalpy relaxation.

Temperature-modulated DSC is a type of DSC attached with the alternate current (AC) calorimetry where two types of heat flows are coinstantaneously obtained from not only constant heating/cooling temperature programs but also perturbation temperature programs with small amplitude and periods. By superimposing temperature oscillations on a constant heating/cooling rate, temperature-modulated DSC enables the heat flow to be divided into different components associated with the heat capacity and other kinetic processes [10–12]. This technique can be used to obtain a lot of information about glass transition phenomena and other kinetic processes in wood for temperatures that are applicable to practical applications.

In this study, temperature-modulated DSC was used to investigate the thermal behavior and transitions of wood conditioned at various humidity levels and temperatures (including room temperature). In addition to the total heat flow (THF), which is equivalent to the heat flow measured by conventional DSC, the reversing heat flow (RHF) derived from the modulation was measured. The glass transition temperature, which is manifested by a step change in the heat flow, and other kinetic phenomena are discussed.

Materials and methods

Sample preparation

Air-dried hinoki (Chamaecyparis obtusa) wood was used for calorimetry measurements. Thin slices that were up to 2 mm long in the longitudinal direction were cut from this wood. In addition, a ground sample was made by ball milling sliced air-dried samples for 20 min at room temperature and passing through a 32-μm-mesh sieve. Both sliced and ground samples were conditioned for 3 months in a thermo-hygrostat containing desiccators, which were controlled to have relative humidity levels (Rhs) of about 0, 11, 22, 33, 54, 60, and 75 % using silica gel and saturated salt solutions at 20 °C; these Rhs correspond to moisture contents of about 3, 5, 7, 9, 10, 11, and 25 %, as determined using thermogravimetry by drying at 105 °C for 60 min.

In the DSC measurements, 3–8 mg of a wood sample was placed in a hermetic aluminum pan having about 4.5 mm inside diameter, which remains in contact with the sample throughout the heating and cooling runs. Thickness of the samples were about 1 mm in the longitudinal direction for the solid wood and about <0.3 mm for the ground wood in the hermetic pan, and during the DSC measurements, temperature distribution came from heat conduction in a sample was not assumed.

DSC measurements

A heat-flux differential scanning calorimeter (DSC Q100, TA Instruments) equipped with a system for modulating temperature was used.

The modulation temperature program in heating is written as

$$ T(t) = T_{0} + \beta_{0} t + T_{\text{a}} \sin (\omega t) $$
(1)

where t, T 0, \( \beta_{0} \), T a and \( \omega \) are time, an initial temperature, an average heating rate, an amplitude and an angular frequency in the modulation, respectively. From this temperature schedule, the apparent heating rate \( \beta \) is given by

$$ \beta (t) = \frac{{{\text{d}}T(t)}}{{{\text{d}}t}} = \beta_{0} + \omega T_{\text{a}} \cos (\omega t) $$
(2)

Detected heat flow (HF) from the temperature schedule can be shown as

$$ {\text{HF}}(t) = C_{\text{p}} \beta (t) = C_{{{\text{p}}_{1} }} \beta_{0} + C_{{{\text{p}}_{ 2} }} \omega T_{\text{a}} \cos (\omega t) = {\text{THF}} + {\text{RHF}} $$
(3)

where \( C_{{{\text{p}}_{ 1} }} \beta_{0} \) is equivalent to the heat flow measured by the conventional DSC defined as the THF which actually containing the heat capacity at a constant pressure and other kinetic components. On the other hand, the heat flow measured from the modulation detects heat capacity components only depending on the modulation amplitude and the frequency in a conditions of the reversing, in which little phase lag generates between heating rate T(t) and heat flow \( \beta \). In such modulation conditions, reversing C p is equivalent to \( C_{{{\text{p}}_{2} }} \), and then

$$ {\text{Reversing }}C_{\text{p}} = \frac{\text{RHF}}{{\omega T_{\text{a}} \cos (\omega t)}} = C_{{{\text{p}}_{2} }} $$
(4)

Therefore when there is no heat flow associate with kinetics, the THF and RHF are originally same values derived from heat capacity components. However, since there exist non-reversing components for a material from the phase lag, non-reversing heat flow (NRHF) is recognized as

$$ {\text{NRHF = THF - RHF}} $$
(5)

For further information about temperature modulation DSC, Schawe et al. [12] and Lacey et al. [13] have given theoretical descriptions.

From these measurements, the THF which consists of the RHF and NRHF was obtained. The THF is the heat flow measured by conventional DSC. The RHF depends on the heating rate, whereas the NRHF depends only on the absolute temperature [10]. The relative contributions of the RHF and NRHF vary depending on the transition being evaluated. Heating rate-dependent transitions tend to be larger when evaluated using higher heating rates and are reversing (i.e., the transition can be cycled by alternating heating and cooling). In contrast, transitions that depend only on the absolute temperature cannot be reversed by cyclic heating/cooling once they have been initiated and they are considered to be non-reversing.

It should be, however, noted that the reversing C p obtained by temperature-modulated DSC of a sample containing much moisture using a hermetic sample pan is not equivalent to the heat capacity at a constant pressure, because a gradual increase in the surrounding pressure of the sample is induced during heating. In this study, the RHF derived from the reversing C p was dealt with as a heat flow from an apparent heat capacity when discussing the thermal behaviors of the wood samples with much water, although the inner pressure of the pan would not reach so high at lower temperatures below 100 °C.

In the measurements, a sinusoidal modulation was applied with a period of 30 s and with amplitudes ranging from 0.23 to 1.58 °C to generate heating/cooling only conditions with heating rates of 3 to 20 °C/min, respectively [14], at a constant sampling time of 0.2 s. Heating and cooling runs were performed twice between −80 and 100 °C with holding times of 5 min at both these temperatures. A wood sample enclosed in an aluminum pan was placed in the calorimeter at 30 °C and the first cooling run was performed at a constant rate of −10 °C/min from a starting temperature of −80 °C. For reference, measurements were performed using empty pans.

Results and discussion

Total heat flow

Figure 1a and b, respectively, shows how the THFs of the ground and solid hinoki samples conditioned at different Rhs vary during heating in the first (solid lines) and second runs (dashed lines). The thermal behaviors of both the ground and solid samples containing moisture could be detected using hermetic pans with no large endothermic baseline shift at elevated temperatures due to water evaporation. The first and the second runs have similar baselines, which indicate that the samples lost little weight due to water evaporation. Comparison of the results for the first and second runs reveals different thermal behaviors at different Rhs in the high temperature region (indicated by the white triangles). In these regions, both ground and solid samples conditioned above 22 % Rh exhibited endothermic behaviors with small peaks in the first runs. At temperatures near those at which the endothermic peaks occur, the samples exhibited more exothermic behavior in the first run than in the second run. In contrast, no specific peaks were observed in the heat flow variation of the second run. This thermal behavior was reproducible and the dispersion of the first peak temperature remained within 2 °C for both ground and solid samples conditioned at the same humidity condition. The endothermic peak temperature decreased with increasing humidity up to 60 % Rh. The solid samples had slightly higher peak temperatures than the ground samples. The peaks shifted very little when the humidity was increased to 75 % Rh, while a large endothermic peak appeared below 0 °C in the first and second runs for the ground sample.

Fig. 1
figure 1

Thermal behaviors and transitions during heating detected in the THF

Full size image

Several DSC studies have claimed that the endothermic peak temperature is the glass transition temperature or the softening temperature of moist wood [8, 9]. However, when using DSC techniques to analyze glassy polymers, a glass transition should cause a step change in the heat capacity, which is manifested as a step change in the heat flow. Since the endothermic peak temperature tends to decrease with increasing humidity at similar moisture contents at which softening phenomena occur in mechanical methods [2, 3], other phenomena must occur to give the observed endothermic behavior. Most polymers exhibit enthalpy relaxation or volume relaxation at temperatures below their glass transition temperatures when they are cooled from relatively high temperatures close to their melting points at a high cooling rate of about 10 °C/min and are then quenched. For quenched polymers possessing excess potential energy, enthalpy relaxation is considered to occur gradually by releasing the excess energy when the ambient temperature is below the glass transition temperature. The wood samples used in the present study were moisture conditioned at 20 °C for at least 3 months after they had been cut or ground and before they were subjected to the first heating run. Since enthalpy relaxation occurs in the amorphous regions of wood during conditioning, endothermic behaviors were observed only in the first heating run. No transitions were observed during the second run, because the sample had been rapidly cooled before the second heating so that there was insufficient time for enthalpy relaxation to occur. In addition, the heat capacity change at the glass transition was too small to observe (i.e., the glass transition was very weak). Another reason why the endothermic peaks were not observed in the second run may be because the moisture content of the sample changed in the closed pan. Increasing the moisture content of wood samples seems to increase the molecular mobility and this reduces the endothermic peak temperature. In contrast, wood with a lower moisture content exhibits a very weak endothermic peak at high temperatures, as seen in the 0 and 11 % Rh samples. Breaking the wood histology down from a solid to a powder consisting of particles <32 μm, it was confirmed by an electron microscope observation that most wood cells were destroyed. Therefore, the molecular mobility in the ground samples would also be increased, because restrictions such as bonding with other molecules are reduced; in other words, intra and intermolecular interactions are reduced. Similar tendency can be seen in industrial polymers, and the decrease in the molecule mass leads to a drop in the glass transition temperatures. By pulverizing wood, a lot of defects are introduced in the fine structure, and much free volume would generate. Such processes result in a decrease in the cellulose crystallinity [15]. Thus, the ground sample showed endothermic peaks at lower temperatures than the solid sample conditioned at the same humidity.

The exothermic behavior in the high-temperature region above the endothermic peaks in the first run probably indicates that structural changes arise such as a packing which decreases heat capacity so as to attain the release of potential energy to a lower level. Consequently, the first run tends to have a higher enthalpy than the second run at higher temperatures. Comparing this behavior for the samples at lower humidity conditions, the exothermic behavior in the ground samples seemed to get larger because of ease in the molecular mobility. It is deduced that the larger exothermic heat brings the more packing of the fine structure, and that the fine structure of the ground samples conditioned at even lower humidity can easily changed during heating. However, such the structural change and the difference in the solid and ground samples estimated from the exothermic heat will decrease and diminish at higher humidity conditions due to the moisture in the wood functioning as a plasticizer at all measuring temperatures. In addition, it would get difficult to detect thermal behavior of wood in much water, whose heat capacity reaches about four times as large as wood. For the ground sample conditioned at a high humidity, a large endothermic peak was detected below 0 °C in both the first and second runs. It is considered to be caused by water melting from a restricted state known as freezing bound water. Ground wood is predicted to increase both the surface area and the number of adsorption sites relative to that of the solid one, and this also support the assumption that the free volume is increased by powdering. Furthermore, heating history would affect such fine structure from the fact that the melting point of the freezing bound water shifts to the higher temperature side in the second run. It is important to emphasize that the thermal behavior of wood is greatly affected by the conditions prior to measurement; in particular, the thermal properties of wood depend on its temperature and humidity histories. For the utility of most industrial materials such as polymers and metals, taking heat histories into consideration is a fundamental process to clarify the effects of the production conditions on their physical and mechanical properties. For wood consisted by natural polymers, the effects of temperature and humidity histories on the physical/mechanical properties should be elucidated, since variations in the thermal properties of wood by the histories would affect the physical property, as is seen in the industrial polymers.

Reversing heat flow and non-reversing heat flow determined by temperature modulation

Figure 2a and b shows, respectively, the variations in the RHF and NRHF of ground hinoki obtained using the temperature modulation method, which simultaneously measured the THF shown in Fig. 1. A step change occurs in the RHF during the first heating run in the high-temperature region for samples conditioned at over 22 % Rh. The temperatures of the step changes indicated by the gray triangles are almost the same as the peak temperatures in the first run of the THF. This temperature has a similar humidity dependence as the endothermic peak in THF; namely, the temperature of the step change decreased with increasing humidity level in the first run and the step change disappeared in the second run. The thermal behavior of samples at Rhs of approximately 0 and 11 % are almost the same. The endothermic peaks in the NRHF have a similar humidity dependence as the endothermic peaks in the RHF (indicated by the white triangles). Exothermic behavior was observed at temperatures above the endothermic peaks. This exothermic behavior was highly pronounced for the sample conditioned at a humidity of 60 % Rh.

Fig. 2
figure 2

Changes in the RHF and the NRHF after deconvoluting the THF

Full size image

The RHF, which is the heat flow component due to the heat capacity caused by relatively fast molecular motion, exhibited a step change in the first run. A glass transition could occur in this temperature region. Based on the RHF measurements, the glass transition of moist wood could be detected by a sudden change in the heat capacity, which is the conventional method for determining the glass transition temperature. However, the change in the RHF is not only a step change but also it has a gradient change; thus, unlike other industrial polymers, the heat capacity changes gradually with temperature. Cellulose and lignin have been reported to have similar thermal behaviors. These differences in the RHF variations during heating of wood, cellulose, and lignin will be investigated in a future study, because they may reveal other important information about structural changes resulting from molecular motion. The heat quantity of the step changes in the RHF differed in the first and second runs and it tended to increase when the humidity level was increased up to 60 % Rh. The reversing C p change was calculated from the step changes in the RHF to be 0.08 J/g/°C (60 % Rh), which is significantly smaller than those of other polymers [16]. Therefore, the glass transition of moist wood is considered to be relatively weak in the first run and almost no glass transition occurred in the second run. This change in the heat capacity is much smaller than that of solid woods due to poorer molecule mobility as mentioned in the THF results. On the other hand, the value of the reversing C p change in this glass transition reached almost ten times larger than that in drying process [17].

The NRHF corresponds to components of heat flow besides the heat capacity. It is caused by slow molecular motions or relatively large structural changes such as enthalpy relaxation. The endothermic behavior observed in the vicinity of the glass transition temperature during heating is due to enthalpy relaxation; the heat quantity involving enthalpy relaxation increases during conditioning, as has been reported for lignin [18, 19]. Thus, enthalpy relaxation readily occurred for wood containing a lot of moisture. The subsequent exothermic behavior indicates a structural change associated with energy released by molecular motion occurring above the glass transition. Below 60 % Rh, the potential energy of the molecular structure decreases above the glass transition temperature such as packing structure. Such structural changes were rarely observed at higher Rhs because they occurred near the glass transition region due to the high moisture content. These thermal behaviors are similar to those of solid wood, although even solid wood conditioned at an Rh of 75 % exhibited exothermic behavior. The transition below 0 °C for the ground sample conditioned at 75 % Rh (indicated by the black triangle in Fig. 2a) is not well resolved into the RHF and the NRHF, and thus the modulation conditions need to be modified for much moisture conditions. Furthermore, a method for evaluating the thermal behavior of the NRHF could be a powerful and effective technique in order to discuss “unstable wood [20]”.

Relationship between transition temperature and moisture content

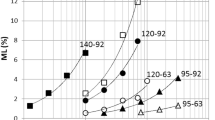
The endothermic peak temperatures T p in the THF and the NRHF and the glass transition temperature T m in the RHF (indicated by the white and gray triangles in Figs. 1 and 2) are plotted in Fig. 3, which shows the moisture contents of both the solid and the ground samples. The glass transition temperature T m is defined as the midpoint of the step change in the RHF. Figure 3 shows that the temperatures of the THF (solid and ground), NRHF (solid and ground), and RHF (ground only) increased drastically when the moisture content is reduced to below 10 %. The T p in the THF and NRHF has quite similar moisture dependencies (as indicated by the black lines). Very similar results have been reported for an endothermic peak observed in the initial heating stage of differential thermal analysis (DTA) and DSC runs [8, 9], so that our missing data between 11 and 25 % of the moisture content anticipated to be followed their results. However, the RHF of solid samples (indicated by the dashed line in Fig. 3) exhibited a different behavior: T m decreased linearly with decreasing moisture content. T m tended to be less affected by the moisture content than T p in the THF and the NRHF of solid wood.

Fig. 3
figure 3

Relationships among transition temperatures detected in THF, RHF, and NRHF of wood samples with various moisture content

Full size image

The similar peak temperature shifts with varying moisture content is considered because the NRHF greatly affects the thermal behaviors of moist ground wood in the same manner as the RHF does, which implies that enthalpy relaxation always occurs below glass transition. However, the glass transition of solid wood defined by the RHF is suppressed at low moisture contents because of the limited interaction among molecules and water in wood. Heat response in the solid samples against the modulation conditions seems to be faster than that of ground ones due to smaller internal loss, such as a discontinuity and an irregular arrangement of the wood fibers. Instead, enthalpy relaxation occurs readily. This is deduced that solid wood containing cell–cell interfaces forms a rigid fine structure compared with ground wood which does not have such interfaces, whereas such structure is built so that the relaxation behavior is similar and the molecular size is large. Further study using other methods such as X-ray diffraction [21] as well as infrared spectrometry [22] is necessary to determine the fine structural changes that occur in wood during the glass transition and the enthalpy relaxation phenomena.

Kinetics of the transitions

Since T p and T m tend to increase with increasing heating rate, these transitions are thought to originate from time-dependent events that depend on molecular dynamics. To investigate the kinetics of the transitions obtained by the temperature-modulated DSC, the apparent activation energies of T p and T m were calculated based on the non-isothermal kinetics. The kinetics assumed to follow the Arrhenius type equation expressed by

$$ \frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = A\exp \left( { - \frac{{E_{\text{a}} }}{RT}} \right)f(a) $$
(6)

where α, A, R, T, E a and \( f(a) \) are a reaction rate, a frequency factor, the gas constant, temperature, an activation energy and a kinetic model-function, respectively.

By differentiating the Eq. (1) with time t, following equation was obtained.

$$ \frac{{{\text{d}}^{2} \alpha }}{{{\text{d}}t^{2} }} = \frac{{{\text{d}}\alpha }}{{{\text{d}}t}}\left[ {\frac{{{\text{d}}f(a)}}{{{\text{d}}\alpha }}A\exp \left( { - \frac{{E_{\text{a}} }}{RT}} \right) + \frac{{\beta E_{\text{a}} }}{{RT^{2} }}} \right] $$
(7)

Assuming the reaction rate reaches the maximum at the temperature (T p) where DSC curve displays the peak,

$$ \left( {\frac{{{\text{d}}^{2} \alpha }}{{{\text{d}}t^{2} }}} \right)_{{T_{\text{p}} }} = 0 $$
(8)

Therefore, Eq. (7) results in

$$ \frac{{{\text{d}}f(a)}}{{{\text{d}}\alpha }}A\exp \left( { - \frac{{E_{\text{a}} }}{RT}} \right) + \frac{{\beta E_{\text{a}} }}{{RT^{2} }} = 0 $$
(9)

By transforming Eq. (9) and taking logarithm of both sides of the equation, the Kissinger’s equation (10) is obtained.

$$ ln\frac{\beta }{{T_{\text{p}}^{2} }} = ln\left[ { - \frac{{{\text{d}}f(a)}}{{{\text{d}}\alpha }}\frac{AR}{{E_{\text{a}} }}} \right] - \frac{{E_{\text{a}} }}{{RT_{\text{p}} }} $$
(10)

For a set of DSC curves with different heating rates, the quantity of ln(β/T 2p ) against 1/T p is plotted to obtain the Kissinger plot. From the slope of the Kissinger plot, the activation energy E a in turn is obtained.

Figure 4 shows Kissinger plots of T p for the THF and the NRHF and of T m for the RHF for the solid and the ground samples conditioned at 60 % Rh. The logarithm of the ratio of the heating rate to the peak temperature squared T 2 varies linearly with the reciprocal of T, which corresponds to T p and T m for both the solid and the ground woods. The apparent activation energies (see Table 1) were obtained from these slopes (indicated by the solid, dashed and thick solid lines). The apparent activation energy ranged from about 200 to 400 kJ/mol, whereas that for T m in the RHF of the solid wood reached 600 kJ/mol. The activation energies for the glass transition and the enthalpy relaxation of wood had not been previously obtained by DSC or DTA. However, in thermal softening studies of water-saturated woods based on mechanical measurements such as dynamic mechanical analysis (DMA) [6], the glass transition and the relaxation process have been calculated to have apparent activation energies in the range of approximately 400–500 kJ/mol. The values obtained in the present experiment are reasonable for relaxation processes such as glass transitions and enthalpy relaxation, although they seem to have considerably smaller moisture contents. Especially the activation energy from the RHF for the solid wood is acceptable for the glass transition considering the moisture content below saturation point about 25 %.

Fig. 4
figure 4

Kissinger plots of the peak temperatures and heating rate-related factors

Full size image
Table 1 Apparent activation energies for glass transition and relaxation process of wood samples conditioned at 60 % Rh
Full size table

Breaking wood into a powder with particles smaller than 32 μm will cause the glass transition (measured from the RHF behavior) to occur more readily. However, other kinetics derived from the NRHF behavior will require a lot of energy. This is deemed to derive from a difference in the enthalpy relaxation quantity during the conditioning of the samples before the DSC measurements. The much relaxation would generate from much molecular mobility in the ground samples compared with the solid samples conditioned at 60 % Rh. This is resulted in the more activation energy required for enthalpy relaxation of the ground sample. Due to the contribution of the energy to the transitions derived from RHF and NRHF behaviors, the apparent transition of the ground samples detected in the THF is thought to require a lot of energy.

Conclusion

Unlike conventional DSCs and DTA, temperature-modulated DSC was able to clearly detect glass transitions in moist solid and ground wood samples as a sudden change in the heat capacity resulting from a step change in the RHF. Other relaxations (such as enthalpy relaxation) occurred simultaneously with the glass transition due to endothermic THF and NRHF behaviors. The transition temperatures depend on the moisture content, which is similar to the behavior of the softening temperature observed in mechanical measurements. Further studies using thermal analysis and calorimetry are required to investigate the relationship between the glass transition and enthalpy relaxation in wood at different moisture conditions.