The perks of being in the smaller team: incentives in overlapping contests

Abstract

We investigate overlapping contests in multi-divisional organizations in which an individual’s effort simultaneously determines the outcome of several contests on different hierarchical levels. We show that individuals in smaller units are advantaged in the grand (organization-wide) contest for two reasons: First, the incentive to free-ride is smaller in inter-divisional contests. Second, competition in the intra-divisional contest is less fierce. Both effects induce a higher marginal utility of effort provision. We test the model in a laboratory experiment and confirm its main predictions. Our results have important consequences for the provision of incentives in organizations and the design of sports competitions.

1 Introduction

Contests are situations in which individuals compete for a prize by spending non-refundable effort which increases the likelihood of winning but does not guarantee victory (see e.g. Konrad 2009). In this sense, many everyday situations may be described as a contest. Indeed, individuals are usually involved in several contests at once. Some of these contests may overlap meaning that they take place on different levels of a given hierarchy and the same effort is relevant (to some extent) for the outcome of each of these contests.

Take sports as a classical example. In the Olympic games, in addition to individual victories, media attention is frequently drawn to the medal table which counts the success of the different nations. Similarly, the Tour de France honors the best team in addition to the best cyclists. In these situations, athletes simultaneously face a grand contest and an inter-team contest between teams partitioning the field. In addition, an athlete’s success relative to the other athletes of the same nation may determine her chances of receiving funding in the next season or taking part in a subsequent competition.¹

Similar situations arise at the workplace where workers may not only struggle to be promoted within the organization, but may simultaneously fight for relative standing within their own division or standing and funding of the division within the entire organization. It is then not always possible to distinguish tasks most relevant for the organization-wide contest from tasks more relevant for the inter- or intra-divisional contests.

In this paper, we investigate overlapping contests in which an individual’s effort simultaneously determines the outcome of several contests taking place at different levels of a given hierarchy. We address the following question: how is the individual chance of winning an organization-wide (grand) contest affected by the presence of an inter-divisional (inter-team) contest or an intra-divisional (intra-team) contest or both? We show that individuals in larger divisions have a disadvantage in the organization-wide contest. This result is driven by two well-known effects: First, larger divisions induce larger incentives to free-ride in inter-divisional contests (see e.g. Konrad 2009). Second, the intra-divisional contest is fiercer the larger the division. Both effects lower the marginal utility of effort provision.

Though these predictions follow straightforwardly from contest theory, their behavioral relevance is not clear. First, overbidding is increasing in the group size in intra-group contests (see Sheremeta 2013). The difference in individual efforts between members of small and large teams is thus often smaller than predicted in the absence of an additional grand contest, and may become negligible when the latter is added. Second, experiments on contests between groups (or teams) show that members of larger groups overbid more relative to Nash equilibrium than members of smaller groups (Sheremeta 2018). As a consequence, the prediction that smaller groups are more likely to win in inter-group contests than larger groups because of less free-riding (see e.g. Katz and Tokatlidu 1996; Baik and Lee 1997), also referred to as “group size paradox” (Olsen 1965; Esteban and Ray 2001), often does not materialize in the laboratory. Whether and how this extends to overlapping contests is an open question. Third, the literature has identified various behavioral forces which affect behavior in individual and group contests (see Sheremeta 2013, 2018). These include, inter alia, risk and loss aversion, noisy decision-making, utility of winning, biases in probabilistic reasoning, and other-regarding preferences.² How these behavioral forces play out in overlapping contests, how this depends on contest design, and how it affects the conclusions regarding effort provision and relative performance of contestants in small and large teams are open questions which motivate the second part of our paper.

To investigate the behavioral relevance of the model, we conduct a first laboratory experiment. In our experimental setup, subjects are assigned to groups of six players and divided in two teams of two and four players, respectively. In each round each subject simultaneously competes in a group-wide (grand) Tullock contest and either an inter-team contest with winnings divided equally among the members of the winning team, or an intra-team contest. While groups are randomly formed in each repetition, subjects are consistently assigned either to the small or to the large team. Given the prizes we choose for the contests, our model predicts that subjects in the smaller team invest twice (1.25 times) as much as subjects in the larger team and are thus twice (1.25 times) as likely to win, if they simultaneously face a grand contest and an inter-team (intra-team) contest. Moreover, adding an inter-team contest to a grand contest is predicted to lead to a lower overall effort and a larger difference between efforts of small and large team members than adding an intra-team effort. Our results can be summarized as follows: First, like many other studies, we find that subjects substantially overinvest. Second, members of the small team invest 42% (23%) more than members of the large team, if simultaneously facing the grand and the inter-team (intra-team) contest, and they also earn more in both treatments. Third, we find no significant differences between the two treatments, neither for total contest expenditures nor for the average effort margin of small team members over large team members.

Our results have important implications for contest design: First, a designer of the complete overlapping contest interested in effort provision should devote all resources to the organization-wide contest. Second, consider how the head of a division should invest resources to further motivate the employees in her division, given an organization-wide contest she cannot alter. Assume that she has money available to introduce a (team) contest between her subdivisions, or (individual) contests within those divisions. Both options will enhance total effort of the division, given that more prize money is spent, and they may also introduce asymmetries between employees, if the subdivisions are of unequal size. Yet, they may induce these effects with different efficacy. While theory predicts that an inter-team contest is less successful in stimulating effort and introduces a greater asymmetry between players, our experimental results suggest that total effort and the distribution of efforts are rather similar in both cases. Third, we may ask how the designer of an intra-team contest intended to maintain similar chances in the organization-wide contest should optimally set prizes. Our results show that this requires the prize in the intra-divisional contest to rise in the size of the division, and larger divisions may be forced to spend more per capita than smaller divisions. Finally, our finding that members of smaller units are advantaged may also highlight a – so far disregarded – aspect of a manager’s decision about the size of her team: While classical insurance concerns (against the weakness or failure of single team members) argue for a larger team, our analysis suggests that a relatively small team may be beneficial to provide individual incentives (besides saving labor costs).

The paper relates to a wide and growing theoretical literature starting with Tullock (1980). Nitzan (1991) was the first to study contests between teams and highlight the free-riding problem. Several other papers have extended this literature by investigating the combination of an inter-team contest with the corresponding intra-team contest which ensues in the winning team over the realized winnings. Most papers study the sequential version of this problem (see e.g. Katz and Tokatlidu 1996; Wärneryd 1998; Inderst et al. 2007). Recently, Münster (2007) and Münster and Staal (2012), among others, have started investigating the simultaneous inter- and intra-team contest for a given prize where subjects choose how to distribute their effort between the inter- and the intra-team contest and a production task. In contrast, the focus of this paper is on simultaneous contests with separate prizes whose outcomes are determined by a single effort choice for each player.³ Moreover, we focus on the combination of a grand contest with inter- and intra-team contests.

The paper also contributes to a large and growing experimental literature on contests between individuals (see Dechenaux et al. 2015; Sheremeta 2013, for recent surveys) and between teams (see Sheremeta 2018). In particular, Ke et al. (2013) and Ke et al. (2015) study the interaction of a team contest and a subsequent individual contest within the winning team, but consider two separate effort choices for the two contests. More closely related, Majerczyk et al. (2019) consider an inter-team contest that overlaps with an intra-team contest, in which the same effort simultaneously determines the outcome of both. They show that the presence of the intra-team contest is effective in mitigating free riding behavior as well as sustaining effort over time. On top of that, we add a grand contest and investigate how its presence affects individual and team efforts in the inter-team contest, the intra-team contest, or both.

Finally, our results may contribute to the literature on internal labor markets and promotion determinants (see Lazear 1999, 2018).

The paper is organized as follows: The general model is presented in Sect. 2 and analyzed in Sect. 3. Section 4 reports on the experiment. Section 5 contains a discussion and conclusion. The appendix contains the proofs. Complementary statistical results and the experimental instructions are provided in the online appendix.

2 Model

We consider a winner-take-all contest between n players divided into 2 teams $g \in \{1,2\}$. Team g comprises $m_g$ players where $m_2 = n-m_1$ and we assume that $m_2 > m_1 \ge 2$. All players compete in a grand contest for the prize $A>0$. In addition, players may compete in an inter-team contest for prize $B \ge 0$ and in intra-team contests for prizes $C_1 \ge 0$ and $C_2 \ge 0$, respectively.

The outcome of all contests is assumed to be simultaneously determined by a single effort choice of each player. Each player has a sufficiently large initial wealth endowment $e \in {\mathbb {R}}_{+}$. Let $x_{gi} \ge 0$ denote the effort chosen by player i in team g and let ${\varvec{x}}_{-gi}$ denote the vector of efforts of all other players. To keep the analysis tractable, we assume that chances of winning are given by the contest-success function (CSF) proposed by Tullock (1980),⁴ effort costs are linear, and players are risk-neutral. Accordingly, the expected payoff of player i in team g is given by

$$\begin{aligned} E\pi _{gi}\left( x_{gi},{\varvec{x}}_{-gi}\right):= & {} \frac{x_{gi}}{\sum _h \sum _j x_{hj}}\;A \,+\, \frac{\sum _j x_{gj}}{\sum _h \sum _j x_{hj}}\;f\left( m_g\right) \;B\,\nonumber \\{} & {} +\,\frac{x_{gi}}{\sum _j x_{gj}}\; C_g \,-\, x_{gi} \text {,} \end{aligned}$$

(1)

where the first fraction is assumed to equal 1/n, the second 1/2, and the third $1/m_g$, if all efforts in the respective denominator are zero. The function $f: \mathbb {N}\rightarrow [0,1]$ captures the fraction $f\left( m_g\right)$ of the prize B in the inter-team contest that each member of the successful team g receives. This depends on the nature of the prize and the team’s sharing rule. For example, $f\left( m_g\right) \equiv 1$ if B is a public good such as fame. In contrast, $f\left( m_g\right) = 1/m_g$, if B is a private good and shared equally among the team members. Finally, the example $f\left( m_g\right) = 1/m_g^2$ may apply if B is a private good and subject to conflict within the winning team.⁵ As rivalry and competition are usually fiercer in larger teams, we assume f to be non-increasing. We refer to the above game as the joint contest.

3 Theoretical predictions

Let $X=\sum _h \sum _j x_{hj}$ and $X_g = \sum _j x_{gj}$ for each $g \in \{1,2\}$. Maximizing (1) with respect to $x_{gi}$ yields the FOC

$$\begin{aligned} \frac{X\,-\,x_{gi}}{X^2}\;A\,+\,\frac{X\,-\,X_g}{X^2}\;f\left( m_g\right) \;B\,+\,\frac{X_g\,-\,x_{gi}}{X_g^2}\;C_g \,=\, 1\text {.} \end{aligned}$$

(2)

Due to symmetry, players of the same team provide identical equilibrium efforts $x_{gi}^* = X_g^*/m_g$ for each $i \in T_g$ and each $g \in \{1,2\}$ where $T_g$ denotes the set of the members of team $g \in \{1,2\}$. Equilibrium conditions for the team efforts are then given by

$$\begin{aligned} \left[ \frac{A}{m_g}\,+\,f\left( m_g\right) \,B\right] \;X_g\,-\,f\left( m_g\right) \; B\;X\,-\,\frac{m_g-1}{m_g}\;C_g\;\frac{X^2}{X_g}\,=\,X\;A\,-\,X^2 \end{aligned}$$

(3)

for each $g \in \{1,2\}$. Combining the two equations yields

$$\begin{aligned} \frac{A}{m_1}\;X_1\,-\,B_1\;X_2\,-\,{\hat{C}}_1\;\frac{\left( X_1+X_2\right) ^2}{X_1} \,=\, \frac{A}{m_2}\;X_2\,-\,B_2\;X_1\,-\,{\hat{C}}_2\;\frac{\left( X_1+X_2\right) ^2}{X_2} \end{aligned}$$

(4)

where $B_g = f\left( m_g\right) \cdot B$ and ${\hat{C}}_g = \left[ \left( m_g-1\right) /m_g\right] \cdot C_g$ for $g\in \{1,2\}$.

We first consider equilibria where $X_g^* > 0$ for each $g \in \{1,2\}$. By multiplying (4) with $X_1$ and $X_2$ and rearranging terms, we obtain

$$\begin{aligned} 0 \,= & {} \, X_1^3\,\left\{ {\hat{C}}_1\;z^3\,+\, \left[ \frac{A}{m_2}\,+\,B_1\,+\,2\;{\hat{C}}_1\,-\,{\hat{C}}_2\right] \;z^2 \,\right. \nonumber \\{} & {} \left. - \,\left[ \frac{A}{m_1}\,+\,B_2\,+\,2\;{\hat{C}}_2\, -\,{\hat{C}}_1\right] \;z\,-\,{\hat{C}}_2\right\} \end{aligned}$$

(5)

where $z = X_2/X_1$. In the appendix we show that the polynomial has a strictly positive root, if and only if either $C_g > 0$ for each $g \in \{1,2\}$, or $C_g = 0$ and ${\hat{C}}_h < \left( A/m_h\right) \,+\,B_g$ for $g,h \in \{1,2\}$ and $g \ne h$. Furthermore, the root is unique in these cases and we denote it henceforth by $z^* \equiv z^{*}\left( A,B,C_1,C_2,m_1,m_2; f\right)$ (we omit the arguments for the sake of readability).⁶ Given $z^*$, the equilibrium is straightforwardly derived.

Assume next that $X_g^* = 0$ for some team $g \in \{1,2\}$. Obviously, this is possible only if $C_g = 0$ since otherwise each player in team g has an incentive to marginally increase her effort to obtain the intra-team prize. Moreover, $X_h > 0$ for team $h \ne g$ by a similar argument regarding the grand (or inter-team) contest. Given $X_g = 0$, the FOC for player i of team $h \ne g$ is given by

$$\begin{aligned} \frac{X_h\,-\,x_{hi}}{X_h^2}\;A\,+\,\frac{X_h\,-\,x_{hi}}{X_h^2}\;C_h \,=\, 1 \text {.} \end{aligned}$$

Applying symmetry and rearranging terms yields $X_h^* = \frac{m_h-1}{m_h}\;\left( A+C_h\right)$. Yet, this may only be an equilibrium if no player in team g has an incentive to exert any effort, i.e., if the marginal utility of player $i \in T_g$ at $x_{gi}=0$ given $X_h^*$ and $x_{gj} = 0$ for each $j \in T_g {\setminus } \{i\}$ is non-positive. Using (2) and rearranging terms we find the necessary condition

$$\begin{aligned} A\,+\,f\left( m_g\right) \;B \le X_h^* = \frac{m_h-1}{m_h}\;\left( A+C_h\right) \text {.} \end{aligned}$$

(6)

In summary, we obtain the following solution of the game:

Lemma 1

The joint contest has a unique symmetric-within-teams Nash equilibrium where $x_{gi}^* = X_g^*/m_g$ for each $g \in \{1,2\}$ and each $i \in T_g$ and equilibrium team efforts are given as follows:

• (a) Interior Equilibrium: If (i) $C_g>0$ for each $g \in \{1,2\}$ or (ii) $\frac{m_g-1}{m_g}\;C_g < \frac{A}{m_g}\,+\,f\left( m_h\right) \;B$ for each $g \in \{1,2\}$, where $h = 3-g$, equilibrium team efforts are given by

  $$\begin{aligned} X_1^* \,=\, \frac{\frac{m_1-1}{m_1}\,+\,z^*}{\left( 1+z^*\right) ^2}\;A \,+\, \frac{z^*}{\left( 1+z^*\right) ^2}\;f\left( m_1\right) \;B \,+\, \frac{m_1-1}{m_1}\,C_1 \end{aligned}$$

  (7)

  and $X_2^* \;=\; z^*\cdot X_1^*$;

• (b) Single Team Equilibrium: If $C_g = 0$ for some $g \in \{1,2\}$ and $\frac{m_h-1}{m_h}\;C_h \ge \frac{A}{m_h}\;+\;B_g$ for $h = 3-g$, equilibrium team efforts are given by $X_g^* = 0$ and $X_h^* = \frac{m_h-1}{m_h}\;\left( A+C_h\right)$.

The proof is relegated to the appendix. To interpret this result, we first discuss the cases in which there is (i) no intra-team contest ($B > 0$, $C_1=C_2=0$) and (ii) no inter-team contest ($B=0$, $C_1, C_2 >0$), respectively, before returning to the joint contest.

3.1 The impact of inter-team competition

Assume that $C_g = 0$ for each g to focus on the impact of simultaneous inter-team competition on the grand contest. Plugging this into (5) and solving for $z^*$ yields the equilibrium condition for relative team efforts

$$\begin{aligned} z^* \,=\, \frac{X_2^*}{X_1^*} \,=\, \frac{m_2}{m_1}\,\cdot \,\frac{A\,+\,m_1\;f\left( m_2\right) \;B}{A\,+\,m_2\;f\left( m_1\right) \;B} \text {.} \end{aligned}$$

(8)

Accordingly, the larger team provides the larger team effort, if and only if

$$\begin{aligned} \left[ \frac{1}{m_1}-\frac{1}{m_2}\right] \;A \,>\, \left[ f\left( m_1\right) -f\left( m_2\right) \right] \;B \text {.} \end{aligned}$$

To provide some examples, this holds, if (i) B is a public good ($f\left( m_g\right) \equiv 1$), or (ii) B is a private good and the grand contest is sufficiently important. Concretely, the condition is $A>B$, if private good B is shared equally within the winning team ($f\left( m_g\right) =1/m_g$), and $A/B>\left( m_1+m_2\right) /\left( m_1\,m_2\right)$, if winnings are contested within the winning team ($f\left( m_g\right) =1/m_g^2$).

Second, as f is non-increasing, (8) also implies that each member of the smaller team provides the higher effort and thus has the better chance of winning in the grand contest (i.e. $X_2/m_2 < X_1/m_1$). To summarize:

Proposition 1

In the symmetric-within-teams Nash equilibrium of the joint contest without intra-team conflict:

• (a) Members from the smaller team have the higher chance of winning in the grand contest.⁷

• (b) The smaller team provides the larger team effort, if and only if (i) $f\left( m_1\right) > f\left( m_2\right)$ and (ii) the prize in the inter-team contest is sufficiently larger than the prize in the grand contest.

The intuition for these results is simple. The free-riding problem in the inter-team contest is more severe in larger teams since more players may potentially contribute to the team effort. Given that the same effort determines chances in the grand contest, incentives to free-ride spill over to the grand contest and lower a large team member’s chances of winning.

As the following examples illustrate, the consequences may be substantial and depend also on the rule f according to which the team prize B is shared. Assume $A = B$ and compare a two-player team ($m_1=2$) with a team of eight players ($m_2=8$). Compared to a player from the large team, a player in a two-player team is three times as likely to win the grand contest, if B is a public good ($f\left( m_g\right) \equiv 1$), and she is four times as likely to win if B is a private good and shared equally within the winning team ($f\left( m_g\right) = 1/m_g$). Hence, the need to share the team winnings among a larger number of players exacerbates the disadvantage of members of the larger team. On the other hand, the player in the two-player team is only 2.9 times as likely to win as a player in the eight-player team, if B is a private good that is contested in the winning team ($f\left( m_g\right) = 1/m^2_g$). Accordingly, fighting over team winnings may help members of the larger team.⁸

We finally turn to the incentives of a contest designer who is able to set the prizes for the grand and the inter-team contest subject to the constraint $A+B \le R$. It is immediate that the designer maximizes total effort by putting all resources into the grand contest. Similarly, a contest designer interested in a close grand contest will not combine it with an inter-team contest, i.e. select $B=0$. On the other hand, a close inter-team contest generally requires to combine the two contests. A balanced inter-team contest may be an important feature in order to generate suspense and attract viewers and sponsors for, e.g., competitions in sports, music, or arts. We summarize our results on contest design in the following corollary.

Corollary 1

A contest designer with budget $R>0$ who maximizes

• (a) total equilibrium effort $X^* = \sum _g \sum _i x_{gi}^*$, will select $A=R$ and $B=0$;

• (b) closeness of the grand contest $C_{GC}:= - \max _{g,i} \left| x_{gi}^*/X^* - 1/n\right|$, will select $A=R$ and $B=0$;

• (c) closeness of the inter-team contest $C_{TC}:= - \left| X_1^* - X_2^*\right|$, will select

  $$\begin{aligned} A \,=\, \frac{f\left( m_1\right) -f\left( m_2\right) }{f\left( m_1\right) -f\left( m_2\right) \,+\,\left( 1/m_1\right) -\left( 1/m_2\right) } \;\cdot \; R \end{aligned}$$

  and $B=R-A$.

Part (a) of the corollary shows that the grand contest provides better incentives to elicit individual efforts than the team contest.⁹ Furthermore, combining the grand contest with an inter-team contest (Part (b)) introduces a discrimination mechanism into an otherwise fully symmetric environment. On the other hand, as shown in Part (c) of the corollary, introducing a grand contest in a setting of inter-team competition can outweigh the disadvantage of larger groups that results from stronger free riding. Conversely, inter-team competition improves the likelihood of smaller teams to have any member win in the grand contest. In general, for a contest designer interested in the closeness of the inter-team contest (or equivalently, of the two teams’ performances), there is an optimal distribution of the budget which depends on the team sizes, the nature of the prize B in the inter-team contest, and the sharing function $f(\cdot )$. If B is a public good, the inter-team contest is maximally close ($X_1^* = X_2^*$) and adding a grand contest only favors the larger team. If B is a private good and shared equally within the winning team ($f\left( m_g\right) = 1/m_g$), the optimal allocation of the budget is given by $A = B = R/2$. Finally, less resources must be allocated to the grand contest ($A< R/2 < B)$, if B is a private good and contested within the winning team ($f\left( m_g\right) = 1/m_g^2$).

3.2 The impact of intra-team competition

We assume next that $B=0$ and analyze the impact of simultaneous intra-team competition on the grand contest. It follows that $z^*$ is the unique positive root of the cubic polynomial

$$\begin{aligned} {\hat{C}}_1\;z^3\,+\,\left[ \frac{A}{m_2}\,+\,2\;{\hat{C}}_1\,-\,{\hat{C}}_2\right] \;z^2\, -\,\left[ \frac{A}{m_1}\,+\,2\;{\hat{C}}_2\,-\,{\hat{C}}_1\right] \;z\,-\,{\hat{C}}_2 \text {,} \end{aligned}$$

where ${\hat{C}}_g = \left[ \left( m_g-1\right) /m_g\right] \;C_g$ for $g \in \{1,2\}$. The properties of $z^*$ yield the following results:

Proposition 2

In the symmetric-within-teams Nash equilibrium of the joint contest without inter-team conflict:

• (a) Members from the smaller team have the higher chance of winning in the grand contest if and only if $C_1/C_2 > \left( \frac{m_1}{m_2}\right) ^2\;\frac{m_2-1}{m_1-1}$ or equivalently if $C_1/m_1 > \frac{m_1}{m_2}\;\frac{m_2-1}{m_1-1}\;\left( C_2/m_2\right)$. Accordingly, ceteris paribus, the prize $C_2$ in the intra-team contest required to maintain parity in the grand contest increases (asymptotically linearly) in the team size $m_2$.

• (b) The smaller team provides the larger team effort, if and only if $C_1 \,>\,\frac{m_1}{m_2}\;\frac{m_2-1}{m_1-1}\;C_2\,+\,\frac{m_2\;-\;m_1}{m_2\;\left( m_1-1\right) }\;\frac{A}{4}$.

Again, the intuition for the results is simple. The intra-team contest is more severe in larger teams and expected winnings for each dollar of prize money are lower.¹⁰ As before, these incentives spill over to the grand contest, lowering the chances of winning for members of the larger team. In this case, however, it is likely that the prize money for the intra-team contest (intra-team prize henceforth) is determined independently by each team. Each team (or the corresponding contest designer) may therefore increase the intra-team prize sufficiently to avoid the disadvantage for its members. The proposition makes these conditions explicit. We discuss them in turn below.

Consider first the players’ chances of winning the grand contest. As shown in the first part of Proposition 2, a member of the small team has a higher chance of winning the grand contest than a member of the large team, if the intra-team prize in the small team is sufficiently large compared to the intra-team prize in the large team. Reassuringly, the small team must spend less than the large team to maintain parity. However, the necessary intra-team prize per capita is larger in the small than in the large team, where the difference is the smaller, the larger is the small team and the smaller is the large team. For example, a team of two players ($m_1=2$) must spend (approximately) twice as much per capita when competing against a very large team. With $m_1 = 11$, it suffices to spend ten percent more per capita than the other team regardless of its size.

Turning to team efforts in equilibrium, notice that the team effort directly translates into the chance that any member from the team wins the grand contest, and may therefore be an important objective for the designer of the intra-team contest. For example, the coach of a sports team (an instructor) may receive larger monetary rewards or have better prospects of personal growth if one of her athletes (apprentices) is successful. Absent the intra-team contests, the smaller team provides a lower team effort simply due to its size. Accordingly, the smaller team needs to set the intra-team prize sufficiently high to overcome this disadvantage: The lower bound for $C_1$ is strictly positive even if $C_2 = 0$. Furthermore, the lower bound is decreasing in the smaller team’s size, increasing in the larger team’s size, and approaches a limit equal to $A/\left[ 4\cdot (m_1-1)\right]$ as $m_2$ grows large. Hence, regardless of the team sizes, setting up an additional intra-team contest with a prize of at least one quarter of the grand prize is sufficient to outweigh the initial disadvantage of the smaller team.

As a consequence, even to achieve a higher equilibrium team effort than the small team, the large team must set up an intra-team contest and offer an intra-team prize comparable to the intra-team prize of the small team. This holds especially if both teams are large. For instance, for two teams with 50 and 100 players, respectively, the large team must offer at least 98 percent of the small team’s intra-team prize in its own intra-team contest. The smaller (larger) the size of the small (large) team, the lower this prize money may be. Regardless of the team sizes, the large team must offer at least $C_1/2-A/8$.

3.3 The joint impact of inter- and intra-team competition

The above sections show that a simultaneous inter- or intra-team competition each lowers the chances of winning in the grand contest for members of the larger team. A combination of all three contests is thus least favorable for the large team. Indeed, we obtain that the larger team may need to spend more prize money per capita in the intra-team contest to guarantee parity for its members in the grand contest.

Proposition 3

In the symmetric-within-teams Nash equilibrium of the joint contest:

• (a) Members from the smaller team have the higher chance of winning in the grand contest if and only if the prizes per capita in the intra-group contest satisfy

  $$\begin{aligned} \frac{C_1}{m_1} \,>\, \frac{m_1}{m_2}\;\frac{m_2-1}{m_1-1}\;\frac{C_2}{m_2} \,-\, \frac{m_1}{m_1-1}\;\frac{m_2\;f\left( m_1\right) \;-\;m_1\;f\left( m_2\right) }{\left( m_1\;+\;m_2\right) ^2}\;B \text {.} \end{aligned}$$

  Accordingly, the larger team must offer a higher prize per capita in the intra-team contest than the small team to guarantee its members equal chances of winning in the grand contest, if

  $$\begin{aligned} \frac{C_1}{m_1} \,<\, \frac{m_1\;m_2}{\left( m_1\;+\;m_2\right) ^2}\;\frac{m_2\;f\left( m_1\right) \;- \;m_1\;f\left( m_2\right) }{m_2\;-\;m_1}\;B. \end{aligned}$$

  (9)

• (b) The smaller team provides the larger team effort, if and only if

  $$\begin{aligned} C_1 > \frac{m_1}{m_2}\;\frac{m_2-1}{m_1-1}\;C_2\,+\,\frac{m_2-m_1}{\left( m_1-1\right) \;m_2}\; \frac{A}{4}\,-\,\left[ f\left( m_1\right) \;-\;f\left( m_2\right) \right] \;B. \end{aligned}$$

The proposition illustrates how the combination of the grand contest with an inter- and an intra-team contest puts the large team at a drastic disadvantage, and makes it very costly for the designer of the large team’s intra-team contest to achieve parity for its members. The results hold whenever the prize in the small team’s intra-team contest is not too large. The upper bound, given in equation (9), is increasing in the prize for the inter-team contest (B), and it increases, as the difference between $f\left( m_1\right)$ and $f\left( m_2\right)$ gets larger. Hence, the more important the inter-team contest and the more severe the conflict which ensues over winnings in the inter-team contest, the more the large team needs to offer in the intra-team contest to maintain its members’ chances in the grand contest. In addition, we also find that the upper bound on $C_1/m_1$ increases (decreases) in the size of the small (large) team for the examples $f(m)=1$, $f(m) = 1/m$, and $f(m) = 1/m^2$.

Finally, Lemma 1 also shows how the intra-team prize may be used to fully deter competition from an opposing team who does not induce an intra-team contest itself. Concretely, by selecting a sufficiently large intra-team prize, team $g \in \{1,2\}$ induces a degree of competition by its own members which is so large – even in the absence of competition from the other team – that the marginal utility of effort is negative for each member of the opposing team $h = 3-g$. Hence, members of team h prefer to abstain from the competition altogether. Notice that such a deterrence is possible for every team regardless of its size. Yet, larger teams must invest less to induce this equilibrium as the lower bound on the intra-team prize is decreasing in the team size.

4 A first experimental test

We here present a first experiment to test the theoretical predictions derived in Sect. 3. As argued in the introduction, various factors not accounted for in the model may affect behavior and thus counteract the effects identified above. An experiment enables us to test the rich predictions of the model and the impact of unaccounted behavioral factors in a controlled environment. Our treatments constitute a first step in this direction. Specifically, we focus on two basic questions:

First, we investigate whether combining a grand contest with an inter- or an intra-team contest induces the small team advantage when this is predicted by theory. Our main concern is therefore the difference in individual efforts of subjects in the small and the large team, and the consequences for winning probabilities, payoffs, and team effort. Various behavioral forces may counteract the theoretical predictions in this regard. In particular, free-riding is typically less pronounced in the lab which is why the group size paradox rarely materializes in experiments. As a consequence, the small team advantage may be smaller than predicted, or even absent in treatment BETWEEN. Moreover, overbidding – which is typically larger in larger groups – may counteract the small team advantage in both treatments.

Second, we are interested in the relative impact of the two potential spill-overs our model identifies (free-riding in the inter-team contest and fierce competition in the intra-team contest, respectively), where we measure impact with respect to (the asymmetry of) the winning probabilities and the total effort. To measure this relative impact as cleanly as possible, we fix the grand contest including the corresponding prize money as well as the overall prize money across treatments, and we vary the nature of the overlapping contest. The behavioral forces described above may also counter the predicted superiority of treatment WITHIN. In particular, if free-riding is less pronounced than predicted in treatment BETWEEN, the treatment may be less disadvantageous in terms of total effort and at the same time enhance the equality of teams. The experimental results may then better inform the problem of designing contests within subunits in the presence of a given grand contest.

Obviously, the model provides a much greater scope for experimental tests. We leave this for future work. Below, we first describe the design and the procedures of the experiment. We then derive our hypotheses and present the experimental results.

4.1 General features

Our experiment consists of two treatments and six sessions. In each session, subjects play 20 repetitions (henceforth rounds) of a six-player Tullock contest overlapping with either an inter-team contest (treatment BETWEEN) or an intra-team contest (treatment WITHIN).¹¹ The two teams constituting the group comprise two and four subjects, respectively. Throughout rounds, we fix whether a subject is assigned to the small or the large team. In contrast, we randomly assign the subjects to the groups in each round to avoid repeated-game effects.

In each round, each subject makes a single effort choice which simultaneously determines her chances of winning in the grand contest and either the inter- or the intra-team contest. To do so, each subject is endowed with $E=400$ points in each round.¹² The prizes for the contests are selected such that the predicted efforts for members of the small and the large team are sufficiently different. Concretely, all subjects compete for a prize of size $A = 600$ points in the grand contest. Subjects in treatment BETWEEN additionally compete in an inter-team contest for a prize of size $B = 600$ points which is split equally among the members of the winning team. Each subject in treatment WITHIN additionally competes with her team members in an intra-team contest for a prize of size $C_t = 300$ points where $t \in \{1, 2\}$, $m_1 = 2$, and $m_2 = 4$.

The experiment enables us to control for factors potentially influencing subjects’ effort choices. In particular, we measure risk preferences at the beginning of the experiment following the multiple price list format of, e.g., Holt and Laury (2002). In addition, we collect several demographics (age, gender, academic major, and mother tongue) as well as self-assessments of certain characteristics with the help of a questionnaire at the end of each session.¹³

4.2 Procedures

Three sessions were conducted for each treatment. The sessions took place at the experimental laboratory of the University of Bamberg in July and November 2018. Students from the University of Bamberg were invited using the ORSEE recruitment system (Greiner 2015). 18 subjects participated in each session. The experiment was programmed in zTree (Fischbacher 2007).

Each experimental session was partitioned into two parts. Upon arrival at the lab, subjects were randomly assigned to cubicles that did not allow for any visual communication between them. Subjects were immediately asked to read the basic instructions provided in their cubicle which informed them about the general rules for behaviour in the laboratory, and the division of the experiment into two parts each starting with the distribution of more specific instructions.¹⁴

In the first part, we elicited subjects risk preferences. Subjects received paper instructions and were given time to read them at their own pace. Instructions were then read aloud and subjects were permitted to ask questions. Afterwards, each subject was presented with a list of ten decisions between a safe amount and a lottery on the computer screen and asked to submit her choices via the computer.

After all subjects had completed the first part, we distributed paper instructions for part 2, following the same procedure as described above. This was followed by a short quiz to check subjects’ understanding. The experimenters controlled subjects’ answers and explained mistakes in private if necessary. Upon completion of the quiz, the 20 contest rounds were run. Subjects submitted their efforts using the computer. The computer interface also allowed each subject to enter fictitious efforts for herself and the other contestants to check the consequences of a decision before submitting it. After all subjects submitted their efforts in a given round, each subject was informed about the efforts chosen by all six members of her group (including herself), clearly separated into efforts by members of the small and the large team, and which of these efforts resulted in a win of the grand contest and the inter- or intra-team contest.

Upon completion of the second part, payments were made. We paid one randomly selected decision from the first part, and two randomly selected rounds from the second part, one each from the first and the last ten rounds. This was clearly communicated to subjects at the beginning of the two parts. To determine payoffs, one of the subjects was selected to role a ten-sided dice four times after the second part. The first and second throw determined, respectively, the payoff-relevant decision and the payoff of the corresponding risky lottery in part 1. The third and fourth throw determined the payoff-relevant rounds in the second part of the experiment. Subjects then filled out the questionnaire, retrieved their earnings in private and left.

Sessions lasted 90 min on average. Points were converted into cash at the rate 1 point = €0.01 and added to a show-up fee of €4.00. The average payment was €15.02 in treatment BETWEEN, and €14.95 in treatment WITHIN. Overall, we collected 2,160 effort choices submitted by 108 subjects.

4.3 Hypotheses

The left part of Table 1 presents predicted efforts, winning probabilities, and expected payoffs by team size for the two games played, respectively, in treatment BETWEEN and WITHIN. From these predictions, we derive our two main hypotheses. The first hypothesis focuses on the comparison of individual efforts between the small and the large team in both treatments:

Hypothesis 1

In both treatments, members of the smaller team invest more than members of the larger team.

We also test the consequences of this prediction. In particular, members of the smaller team are predicted to have a better chance of winning the grand contest and achieve a higher payoff than members of the larger team in both treatments. Moreover, the team effort is predicted to be smaller for the smaller than for the larger team in treatment WITHIN, but not in treatment BETWEEN.

The second hypothesis focuses on the comparison of the two treatments with respect to the sum of individual efforts and the size of the small team advantage:

Hypothesis 2

The sum of individual efforts is larger and the average effort difference between the small and the large team is smaller in treatment WITHIN than in treatment BETWEEN.

The question underlying this hypothesis might be of particular interest to managers. Consider, for instance, the head of a division willing to invest resources to further motivate the employees in her division. Arguably, she will not be able to alter the organization-wide contest. Assume instead that she has money available to introduce a (team) contest between her subdivisions, or (individual) contests within those divisions. Clearly, both options will enhance total effort of the division, given that more prize money is spent. Moreover, both options may introduce asymmetries between employees, if the subdivisions are of unequal size. This raises the question, which of the two options is more effective in stimulating (additional) effort, and at the same time less costly in terms of the (additional) asymmetries it induces. The hypothesis derives from our model in the context of our experimental setup.

4.4 Experimental results

The right part of Table 1 presents an overview of our experimental results. The table suggests that (i) there is considerable overbidding in treatment WITHIN and slight overbidding in treatment BETWEEN, (ii) the small team advantage materializes in individual efforts, winning probabilities, and payoffs in both treatments, and it is slightly larger in treatment WITHIN, and (iii) both treatments are equally effective in stimulating total effort. We test and elaborate on these three findings below.

Table 1 Experimental predictions and results

4.4.1 Overbidding and dynamics

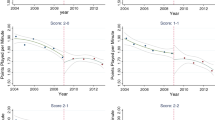
Figure 1 plots average individual efforts across rounds where the left (right) panel contains the results for treatment BETWEEN (WITHIN), and in each panel, the solid blue (orange) line depicts results for members of the small (large) team.¹⁵ We also include dashed lines (of corresponding color) to highlight the theoretical predictions.

Fig. 1

Average efforts across rounds by treatment and role

We find serious overbidding in treatment BETWEEN. Across all (the last ten) rounds, members of the small team invest on average 42 (46) points more than the equilibrium prediction ($p<0.001$).¹⁶ Similarly, members of the large team invest on average 61 (49) points more than the equilibrium prediction across all (the last ten) rounds ($p<0.001$). In contrast, we find no significant deviation from equilibrium predictions in treatment WITHIN. Our preliminary explanation is threefold:¹⁷ First, we show below that a substantial fraction of subjects seem to dislike competition and thus underbid compared to the equilibrium prediction in treatment WITHIN when assigned to the small team. Second, the predicted effort for the large team is much smaller in treatment BETWEEN which is why an anchoring-and-adjustment-heuristic around the natural benchmark of 150 points¹⁸ leads to much more substantial overbidding for large team members in treatment BETWEEN. Finally, overbidding has been found to be the larger, the larger is the endowment (Price and Sheremeta 2011). As the endowment is larger relative to equilibrium predictions in treatment BETWEEN, this may also explain the treatment difference in overbidding. Note, however, that we find almost the same number of cases in which a subject invested her entire endowment in both treatments.

In summary, we (only) partially confirm the recurrent finding in the literature that subjects overbid in contest experiments. In addition, we find little evidence for changes of individual efforts across rounds. The sole exception is a slight reduction of large team members’ efforts in treatment BETWEEN. Our subsequent analysis therefore relies on all rounds. The online appendix contains robustness checks in which the first and the last ten rounds are distinguished, and we mention the differences where necessary.

4.4.2 Small team advantage and its implications

To statistically test Hypothesis 1, we estimate random-effect Tobit models of effort choices with a dummy for the large team as the sole explanatory variable.¹⁹ In further specifications, we also control for the number of safe choices in the first part of the experiment as well as demographics and self-assessments elicited through the questionnaire. The results are presented in Table 2 (results including the complete set of coefficients are presented in the online appendix).

Table 2 Random-effects Tobit models for individual effort choices

The results for treatment BETWEEN clearly show that members of the large team invest significantly less than members of the small team. In contrast, the difference is not significant in treatment WITHIN. Additional findings (presented in the online appendix) reveal that the lack of a significant difference in treatment WITHIN is mainly driven by certain subgroups of subjects. In particular, the difference in efforts between small and large team members becomes significantly positive, if we exclude students of the social sciences and humanities (SSH). Indeed, our estimations suggest that SSH students in large teams invest more than SSH students in small teams. Compared to other subjects, SSH students invest less (more) in the small (large) team. Based on their demographic differences from other subjects,²⁰ SSH students may be classified less competitive, and the predicted fierrcer competition within the larger team may thus have less bite in this group.

We summarize our findings on Hypothesis 1 as follows:

Result 1

In line with the theoretical predictions, members of the small team invest significantly more than members of the large team in treatment BETWEEN. In contrast, efforts of small and large team members are not significantly different in treatment WITHIN, if all subjects are considered. The predicted difference is significant for subgroups of subjects that are arguably more competitive.

Individual efforts straightforwardly induce team efforts, winning probabilities, and payoffs. We discuss these in turn. The corresponding statistical analysis is presented in the online appendix.

First, Table 1 shows that the average team effort is substantially smaller for the small than for the large team in both treatments. OLS regression results provide evidence for the significance of this difference in both treatments. Accordingly, the small team advantage does not translate to the team level. The finding is fully in line with the theoretical prediction in treatment WITHIN, and it confirms the recurrent absence of the group size paradox in the lab.

Second, Table 1 suggests that members of the small team are more likely to win the grand contest. This naturally holds for the winning probabilities calculated from the chosen efforts using the Tullock CSF, but it also holds for the empirical winning frequencies: In treatment BETWEEN (WITHIN), the grand contest was won 82 (75) times by a member of the small team and 98 (105) times by a member of the large team. Dividing these numbers by the total number of contests and the team size yields the entries in row “Pr(Win): Grand Contest” of Table 1. Estimating random-effects logit models of the propensity to win the grand contest shows that (i) members of the small team win the contest significantly more frequently than members of the large team in treatment BETWEEN, (ii) this holds especially in the last ten rounds, i.e. the small team advantage strengthens across rounds, and (iii) members of the small and the large team are (statistically) equally likely to win the grand contest in treatment WITHIN.

Third, Table 1 shows that subjects assigned to a small team earn about one euro more than subjects assigned to a large team in both treatments. Estimation results for random-effects linear models of subjects’ payoffs in each round confirm that small team members have significantly larger payoffs than large team members, if we focus on the last ten rounds (in treatment WITHIN, this also holds across all rounds). In addition, payoffs increase from the first to the second half of the experiment for small (large) team members in treatment BETWEEN (WITHIN), whereas they decrease for the other two groups. Thus, the payoff difference between small and large team members widens in treatment BETWEEN and shrinks in treatment WITHIN.

4.4.3 Treatment comparison: on the efficacy of additional incentives

Regarding our second hypothesis, we find that the total effort invested in the contest is on average 927 (888) points across all (the last ten) rounds in treatment BETWEEN, and 930 (911) points in treatment WITHIN. The left part of Table 3 reports the results from an OLS regression of the total contest expenditure on a constant and a dummy for treatment WITHIN (accordingly, we have one observation per group and round). The results show that the total contest expenditure is not significantly different across treatment, neither across all rounds, nor across the first ten or last ten rounds. Both treatments are thus equally effective in stimulating effort. Apparently, the much stronger overbidding in treatment BETWEEN fully compensates for the predicted gap in contest expenditures.

Table 3 OLS regressions of treatment differences

Does one of the treatments induce a greater asymmetry between small and large team members? We find that the difference between the average individual efforts in the small and the large team equals 56 and 33 points, respectively, in treatment BETWEEN and WITHIN. Moreover, the gap between the two treatments strengthens across rounds (the differences equal 72 and 37 points across the last ten rounds). To test for significance, we calculate the difference between the average efforts of small and large team members for each group and round, and we regress these differences on a constant and a dummy for treatment WITHIN. The right part of Table 3 presents the results and reveals no significant different between treatments, regardless of the sample.

Hence, our experimental results suggest that adding an inter- or an intra-team contest to a grand contest has similar consequences on total effort and effort inequality. To summarize:

Result 2

Total contest expenditures are not significantly different in the two treatments. And although the difference between small and large team members’ efforts is, on average, 70 percent larger in treatment BETWEEN than in treatment WITHIN, we cannot reject equality of these differences.

5 Discussion and conclusion

In many everyday situations such as at the workplace or in sports competitions, subjects are simultaneously involved in multiple contests whose outcome depends on the same effort choice of an individual. This paper shows that such overlapping contests adversely affect the chances of winning in the grand contest for members of larger teams. First, the free-riding problem is more severe in an additional contest between teams. Second, competition in an additional intra-team contest is tougher in larger teams. Both effects spill over to the grand contest with the given interdependent incentive structure.

The results of the paper have important consequences for the design of overlapping contests, and also hierarchies. In particular, if an intra-team contest is desired but not supposed to affect chances of winning in the grand contest, prizes in each team should be set proportional to the team size. Moreover, we find that complementing an organization-wide contest with either a contest between teams of different sizes or contests within those teams–while holding the total additional costs constant – has similar consequences for total effort and inequality of efforts, contrary to the predicted better performance of intra-team contests. Besides these consequences for contest design, the finding that members of smaller units are advantaged may also be relevant for a team manager’s decision about the size of her unit. In team sports, for instance, a frequently asked question is the one about the optimal size of a squad.²¹ Here, issues of insurance (against the risk of single team members being injured or out of shape) provide a classical argument for large squads. By contrast, our analysis suggests that a relatively small squad may be beneficial to provide individual incentives (besides reducing the wage bill).

There are many avenues for future research. Indeed, the overlapping contests setting offers considerable scope to study why and how inter- or intra-team competition may restrict (or enhance) individuals’ overall competitiveness. In this sense, our experimental results only offer a first step in this direction. For example, it would be worthwhile to investigate, if and why the combination of a grand and an intra-team contest consistently lowers overbidding. Moreover, investigating the joint impact of all three contests may also be an interesting next step. On a different level, one may ask whether, in the presence of intra-team contests, larger teams anticipate the potential disadvantage and set the prize for the intra-team contest sufficiently high to maintain the chances of their members. Ultimately, this yields a meta-game between teams in which each team attempts to maximize the chances of its members by choosing the optimal prize for the intra-team contest. It would be interesting to study the outcome of this game both theoretically and experimentally.

In addition, our findings also raise empirical questions to be answered in the field. In particular, one may ask whether, controlling for all other factors, employees in smaller units of firms have a better chance of being promoted.

Appendix. Proofs

Proof of Lemma 1

We start by determining the roots of the cubic polynomial

$$\begin{aligned} Q(z) \,=\, {\hat{C}}_1\;z^3\,+\,\left[ \frac{A}{m_2}\,+\,B_1\,+\,2\;{\hat{C}}_1\,-\,{\hat{C}}_2\right] \;z^2 \,-\,\left[ \frac{A}{m_1}\,+\,B_2\,+\,2\;{\hat{C}}_2\,-\,{\hat{C}}_1\right] \;z\,-\,{\hat{C}}_2 \end{aligned}$$

in equation (5). Consider first the case $C_g > 0$ for each $g \in \{1,2\}$. It is easily seen that $Q(0) = -{\hat{C}}_2 < 0$, and $Q(z) \rightarrow \pm \infty$ as $z \rightarrow \pm \infty$. Furthermore, from the first derivative

$$\begin{aligned} Q'(z) \,=\, 3\;{\hat{C}}_1\;z^2\,+\,2\;\left[ \frac{A}{m_2}\,+\,B_1\,+\,2\;{\hat{C}}_1\,-\,{\hat{C}}_2\right] \;z \,-\,\left[ \frac{A}{m_1}\,+\,B_2\,+\,2\;{\hat{C}}_2\,-\,{\hat{C}}_1\right] \end{aligned}$$

we obtain that Q(z) either reaches a maximum at $z_{max} < 0$ or is strictly increasing everywhere. Hence, there is a unique strictly positive root $z^*>0$.

Second, let $C_1 = 0$. The polynomial then becomes quadratic and there are three cases: If $C_2 = 0$, the roots are given by $z_1 = 0$ and $z_2 = z^* = \left( \frac{A}{m_2}\,+\,B_1\right) /\left( \frac{A}{m_1}\,+\,B_2\right) > 0$. Notice that $z_1$ cannot support an equilibrium because of the necessary condition (6) derived in the text. If $0< {\hat{C}}_2 < \left( A/m_2\right) \,+\,B_1$, the quadratic polynomial satisfies $Q(0) < 0$ and $Q(z) \rightarrow \infty$ as $z \rightarrow \pm \infty$ and therefore has a unique strictly positive root $z^* > 0$. Finally, if ${\hat{C}}_2 \ge \left( A/m_2\right) \,+\,B_1$, then $Q(z) < 0$ for each $z \ge 0$.

Third, let $C_2 = 0$ and $C_1 > 0$. Then

$$\begin{aligned} Q(z) \,=\, z\;\cdot \;\left\{ {\hat{C}}_1\;z^2\,+\,\left[ \left( A/m_2\right) \, +\,B_1\,+\,2\;{\hat{C}}_1\right] \;z \,-\,\left[ \left( A/m_1\right) \,+\,B_2\,-\,{\hat{C}}_1\right] \right\} \end{aligned}$$

with roots $z_1 = 0$, and

$$\begin{aligned} z_{2,3} \,= & {} \,\frac{1}{{\hat{C}}_1}\;\left[ -\left( \frac{A}{m_2}\,+\,B_1\, +\,2\;{\hat{C}}_1\right) \, \right. \\{} & {} \left. \pm \,\sqrt{\left( \frac{A}{m_2}\,+\,B_1\,+\,2\; {\hat{C}}_1\right) ^2\,+\,{\hat{C}}_1^2\;\left( \frac{A}{m_1}\,+\,B_2\,-\,{\hat{C}}_1\right) }\quad \right] \text {.} \end{aligned}$$

There are two cases: If ${\hat{C}}_1 < \frac{A}{m_1}\,+\,B_2$, then $z_2< 0 < z_3 = z^*$. In contrast, if ${\hat{C}}_1 \ge \frac{A}{m_1}\,+\,B_2$, then $z_2 < z_3 \le 0$.

Assume now that a strictly positive root $z^*>0$ of Q(z) exists. Plugging $X_2 = z^*\cdot X_1$ into (2) for $g=1$ yields

$$\begin{aligned} \frac{\left( 1+z^*\right) \;X_1\,-\,\frac{1}{m_1}\;X_1}{\left( 1+z^*\right) ^2\;X_1^2}\;A\, +\,\frac{z^*\;X_1}{\left( 1+z^*\right) ^2\;X_1^2}\;f\left( m_1\right) \;B\,+\,\frac{m_1-1}{m_1}\; \frac{X_1}{X_1^2}\;C_1\,=\,1 \end{aligned}$$

and thus immediately the equilibrium team efforts. Notice that $X_g^* > 0$ for each $g \in \{1,2\}$. To prove that these team efforts constitute an equilibrium, we show that they induce a strictly positive expected payoff for each player in each team which rules out that players could do better by abstaining from the joint contest. Accordingly, the expected payoff of player i in team $g=1$ is given by

$$\begin{aligned} E\pi _{1i}\left( X_1^*/m_1,X_2^*/m_2\right) \,=\, \frac{X_1^*/m_1}{\left( 1+z^*\right) \,X_1^*}\;A\,+\,\frac{1}{1+z^*}\;f\left( m_1\right) \;B\,+\,\frac{C_1}{m_1}\,-\,\frac{X_1^*}{m_1} \end{aligned}$$

which is strictly positive, if and only if

$$\begin{aligned}&\frac{1}{1+z^*}\;\frac{A}{m_1}\,+\,\frac{1}{1+z^*}\;f\left( m_1\right) \;B\,+\,\,+\,\frac{C_1}{m_1} \\ >\,&\frac{X_1^*}{m_1} \,=\, \frac{\frac{m_1-1}{m_1}\;+\;z^*}{\left( 1+z^*\right) ^2}\;\frac{A}{m_1}\,+\,\frac{z^*}{\left( 1+z^*\right) ^2}\;\frac{f\left( m_1\right) \;B}{m_1}\,+\,\frac{m_1-1}{m_1}\,\frac{C_1}{m_1} \text {.} \end{aligned}$$

This follows from $\left( m_1-1\right) /m_1<1$ and $z^* < 1+z^*$. The proof for $g=2$ is similar using $v^* = 1/z^*$ and thus omitted.

Finally, the arguments given in the main text show that (i) there is no other equilibrium, if a strictly positive root of Q(z) exists, and (ii) there exists a unique equilibrium satisfying $X_g^* = 0$ for some $g \in \{1,2\}$, if Q(z) does not possess a strictly positive root. $\square$

Proof

Ad (i): Plugging $C_1 = 0$ and $z^* = \frac{m_2}{m_1}\,\cdot \,\frac{A\,+\,m_1\;f\left( m_2\right) \;B}{A\,+\,m_2\;f\left( m_1\right) \;B}$ into eq. (7) and rearranging, we obtain

$$\begin{aligned} X_1^* \,=\, \frac{m_1\;A\,+\,m_1\;m_2\;B_1}{\left( m_1+m_2\right) \;A\,+\,m_1\;m_2\;\left( B_1+B_2\right) }\,\left[ A\,+\,\frac{m_1\;m_2\;B_1\;B_2\,-\,A^2}{\left( m_1+m_2\right) \;A\,+\,m_1\;m_2\;\left( B_1+B_2\right) }\right] \text {.} \end{aligned}$$

It follows that the total equilibrium effort is given by

$$\begin{aligned} X^* = A\,+\,\frac{m_1\;m_2\;B_1\;B_2\,-\,A^2}{\left( m_1+m_2\right) \;A\,+\,m_1\;m_2\;\left( B_1+B_2\right) }\text {.} \end{aligned}$$

Selecting $A = (1-\theta )\cdot R$ and $B = \theta \cdot R$ for $0 \le \theta \le 1$ and rewriting yields

$$\begin{aligned} X^* = \frac{m_1\;m_2\;f_1\;f_2\;\theta ^2\,+\,\left( m_1+m_2-1\right) \;\left( 1-\theta \right) ^2\, +\,m_1\;m_2\;\left( f_1+f_2\right) \;\theta \;(1-\theta )}{m_1\;m_2\; \left( f_1+f_2\right) \;\theta \,+\,\left( m_1+m_2\right) \;(1-\theta )} \end{aligned}$$

where $f_g = f\left( m_g\right)$. The results follows because the expression is strictly decreasing in $\theta$. To see this, differentiate with respect to $\theta$ and note that the resulting denominator is positive everywhere whereas the numerator is a quadratic function in $\theta$ which has a positive squared term and is negative at $\theta =0$ and $\theta =1$.

Ad (ii): Obviously, $B=0$ yields $x_{gi}^* = \frac{n-1}{n^2}\,A$ and thus $x_{gi}^*/X^* = 1/n$ for each g and i. On the other hand, equation (8) implies that $x_{2i}^*/x_{1j}^* < 1$ and thus $x_{2i}^*/X^* < 1/n$ for each player i in team 2.

Ad (iii): Equation (8) implies that $X_2^* = X_1^*$, if and only if $f\left( m_1\right) > f\left( m_2\right)$ and $\left( m_2-m_1\right) \;A \,=\, m_1\;m_2\;\left[ f\left( m_1\right) -f\left( m_2\right) \right] \;B$. If $f\left( m_1\right) = f\left( m_2\right)$, the RHS of equation (8) is strictly larger than one and decreasing in B. Hence, the optimal contest satisfies $A=0$ and $B>0$. $\square$

Proof of Proposition 2

Ad. (i): A member from the smaller team has a better chance of winning in the grand contest than a member from the larger team, if she provides the larger effort. In equilibrium, this happens, if $X_1^*/m_1 > X_2^*/m_2$, i.e. if $z^* < m_2/m_1$. This is equivalent to requiring that the polynomial on the RHS of equation (5) with $B = 0$ is strictly positive at $z = m_2/m_1$. The result follows by re-arranging terms.

Ad. (ii): The small team provides a larger equilibrium team effort than the large team, if $X_1^* > X_2^*$ which is equivalent to requiring that $z^* < 1$, or that the polynomial on the RHS of equation (5) with $B=0$ is strictly positive at $z = 1$. Re-arranging terms yields the result. $\square$

Proof of Proposition 3

The proof is similar to the proof of Propostion 2. In particular, the first (respectively second) part follows from the requirement that the polynomial on the RHS of equation (5) is strictly positive at $z = m_2/m_1$ (resp. $z=1$). $\square$