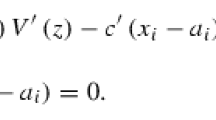Entry regulations and optimal prize allocation in parallel contests

Abstract

In parallel contests, the contest organizer controls the entry of heterogeneous contestants by regulating access to the contests and determining the prize allocation across contests. The organizer can prevent a contestant from entering more than one contest. I show that the organizer allows entry to multiple contests and uniquely sets identical prizes across contests to maximize aggregate effort in all contests. Independent of the entry regulation, I find no sorting effects. Thus, a contest with a relatively high prize does not necessarily attract contestants with higher abilities. Furthermore, I discover interesting spillover effects of prizes between contests in the case of restricted entry regulations. For instance, the individual (aggregate) effort increases (decreases) in a contest if the prize in another contest increases. The endogeneity of contestants’ participation drives many of these results.

1 Introduction

In parallel contests, numerous contestants simultaneously compete in different contests while each contest offers an individual contest prize. Parallel contests are omnipresent in the real world. For instance, job candidates simultaneously apply for different vacancies in the job market. Scientists apply for several research grants. Political candidates run for a seat in the senate as well as in the representative house in bicameral systems. Firms submit various proposals in parallel public tenders. Consultancies compete with each other to win several mandates from private firms. Soccer players simultaneously play in national leagues as well as in international competitions (e.g., the UEFA Champions League and the FIFA World Cup). Boxers fight in parallel tournaments (e.g., WBA, IBF) at the same time. In all these examples, contestants must decide for each individual contest whether they want to enter the contest and, if so, how much effort they want to put forth in each contest. Two important factors affect these decisions: entry regulations and the distribution of prizes across contests.

In this article, I assume that a global contest organizer controls these two factors and thereby influences the parallel contests in order to maximize aggregate effort in all contests. First, this organizer regulates entry to the contests as follows: either each contestant can enter all the contests or each contestant is allowed to participate in no more than one contest. Second, the organizer determines the allocation of prize money across contests subject to a budget constraint.

Regarding the first factor, the limitation of participation can have various causes in the real world. On the one hand, specific regulations can prevent participation in multiple contests. For example, political candidates running simultaneously for a seat in the senate and a seat in the representative house usually must choose one of the two seats if both candidacies are successful. Similarly, a research-funding organization can limit the number of issued grants assigned to a particular researcher. On the other hand, the (physical or financial) resources of contestants and/or the scheduling prevent participation in parallel contests. For example, two ATP¹ 500 tennis tournaments in Tokyo and Beijing took place between September 30 and October 6, 2019. Due to this scheduling, players could only participate in one of the two tournaments. Subsequent to these two tournaments, the ATP 1000 tournament in Shanghai started on October 6, 2019. Even if players could take part in two consecutive tournaments, for instance in Tokyo and Shanghai, they would probably skip one tournament due to exhaustion, travel costs, or insufficient time for preparation.²

1.1 Global contest organizer versus local contest organizer

Considering the real world examples, there are global and local organizers in parallel contests. The global organizer is usually responsible for the overall organization of the parallel contests. For instance, the global organizer determines the allocation of the prize money across the parallel contests under consideration of a budget constraint.³ Moreover, the global organizer influences entry to the contests by introducing access regulations. The local organizer is responsible only for a specific contest, but has no direct influence on the parallel contests. For illustration, I present three examples. In the first two examples, the global organizer plays an important role. The third example shows that not all types of parallel contests are under the supervision of a global organizer.

Example 1

As a global organizer of numerous tennis tournaments, the ATP regulates the prize money distribution for the different categories of tournaments,⁴ controls the calendar of tournaments and regulates the participation of players in these tournaments⁵ according to the “2021 ATP official rulebook”.⁶

Example 2

Governmental institutions financially support and promote scientific research as a global organizer of parallel contests. These institutions must decide how to allocate their available budget to different research areas.⁷ Researchers then compete with each other to acquire research funds in various contests.

Example 3

Consultancies compete with each other in separate contests to obtain individual mandates from private firms. Each private firm offers a prize (i.e., a mandate) and, therefore, acts as a local organizer of a particular contest. In this example, a global organizer does not exist.

The three examples show that the existence of a global organizer and/or a local organizer as well as the scope of action of these organizers depend on the context. In this paper, I focus exclusively on the global organizer’s role. This implies that the local organizer has a passive role, i.e., I assume that the local organizer simply exhausts the budget allocated by the global organizer. However, even if a global organizer does not exist, the model still provides interesting insights. Namely, it allows to analyze the spillover effects of an exogenous prize shock. In particular, I discuss whether different prizes in the parallel contests can explain the composition of the participating contestants, i.e., the proportion of low and high ability contestants.⁸

1.2 Main results

I show that the global contest organizer does not implement a restricted entry regulation and uniquely allocates the prize money identically across contests in order to maximize aggregate effort in all contests. Identical prizes across contests are optimal due to the following reason. For illustration, suppose that there are only two contests 1 and 2 with identical prizes. Introducing asymmetry between the two contests by increasing the prize in contest 1 by one unit and simultaneously decreasing the prize in contest 2 by one unit reduces aggregate effort, as the higher effort incentives in contest 1 do not compensate the lower effort incentives in contest 2. The global organizer’s unrestricted entry regulation has two side-effects on the local organizer’s contest. First, the individual effort of a contestant is lower under the implemented unrestricted entry regime than under a restricted entry regime. Second, the aggregate effort in a specific contest is greater under an unrestricted entry regime than under a restricted entry regime (for a given prize allocation).

One could expect that relative prizes between contests also induce sorting effects of different types of contestants. I show, however, that a contest with a high prize does not necessarily attract high ability contestants. In the case of unrestricted entry regulations, the reason for this result is obvious: all contestants enter all contests such that relative prizes do not generate sorting effects. In the case of restricted entry regulations, multiple equilibria exist. In this case, the composition of the field of participants, i.e., the proportion of high ability contestants and low ability contestants, depends on the realized type of equilibrium.

Under a restricted entry regime, I additionally show that spillover effects of prizes between contests exist: individual (aggregate) effort increases (decreases) in a particular contest if the prize in another contest increases. The reason for this result is that contestants leave the low-prize contest and join the high-prize contest increasing the individual effort incentives in the abandoned contest. However, the outflow of the contestants dominates such that aggregate effort decreases in the abandoned contest.

1.3 Literature review

To some extent, the model in this paper is connected to contests with multiple prizes (see, e.g., Barut and Kovenock 1998; Clark and Riis 1998; Moldovanu and Sela 2001; Eriksen et al. 2011).⁹ In multiple prize contests, the contest organizer offers $n>1$ prizes. The contestants choose their bids, and the n highest bidders win the prizes. However, the models usually consider only one contest and neglect the entry decisions of contestants. Some papers analyze the entry decisions in a single contest. Appelbaum and Katz (1986, 1987); Fu and Lu (2010), and Morgan et al. (2012) discuss contests either with outside options or with entry fees. A higher value of outside option or a lower entry fee increases the number of participating contestants.¹⁰

Contestants’ choice to enter one of two parallel contests is discussed by the following papers. In a field experiment, Leuven et al. (2011) disentangle the sorting and incentive effects of different prizes in tournaments. They find that larger prizes induce a higher productivity of contestants. Interestingly, sorting effects (and not incentive effects) are responsible for the higher productivity. Morgan et al. (2015) show that contestants with higher abilities are less likely to enter the contest that offers the larger prize. Moreover, the introduction of a show-up fee can attract the low and high ability types, while repelling the middle types. Büyükboyacı (2016) compares the performance in a single-prize tournament with the performance in two parallel tournaments. In her paper, two heterogeneous contestants choose between two possible effort levels. If the degree of heterogeneity between contestants is large, the parallel tournaments perform better, i.e., the designer’s profit is higher, than the single-prize tournament. Azmat and Möller (2018) as well as Azmat and Möller (2009) consider the contestants’ decision to enter one out of two types of contests. Azmat and Möller (2018) find a complete sorting of high ability types to high-prize contests if high ability types represent a small proportion in the population.¹¹ Azmat and Möller (2009) analyze the effect of the prize structure on participation.¹² Each contest awards multiple prizes to a large number of heterogeneous contestants. The authors conclude that more contestants participate in a contest, if multiple prizes (instead of a winner-takes-all prize) are awarded in a contest as long as the contest success function is sufficiently sensitive with respect to effort.¹³ Konrad and Kovenock (2012) and DiPalantino and Vojnović (2009) analyze a two-stage contest with a large number of contestants. At stage one, each contestant chooses to enter one contest. At stage two, contestants compete for one or multiple prizes offered in the contest. Konrad and Kovenock discuss the coordination problem of the contestants as situations might result at stage two with many participants but few prizes (and vice versa).¹⁴ The authors derive that a contest organizer can increase welfare if the number of contests is increased. DiPalantino and Vojnović theoretically analyze a contest in the context of crowdsourcing. In recent years, more and more crowdsourcing platforms have emerged. On a crowdsourcing platform, tasks are described with a time limit and rewards. Afterwards, the platform users can make submissions, whereby the best submissions are compensated with the rewards. DiPalantino and Vojnović show that the participation rate increases logarithmically with the contest reward. Thus, higher rewards increase the participation, but the increase is diminishing.¹⁵$^{,}$¹⁶

Vojnović (2015) provides a comprehensive survey of simultaneous contests. The author extensively analyzes the single participation case in the presence of multiple all-pay contests, differentiating between complete and incomplete information (see chapter 5). For contests with a proportional allocation of prizes and fixed budgets, Vojnović concludes that a pure-strategy Nash Equilibrium may not exist. He provides conditions that guarantee the existence of pure-strategy Nash equilibrium. In equilibrium, contestants split their effort budgets over all contests in proportion to their prize valuations, if the utility functions are linear and the valuations are symmetric.¹⁷

In Colonel Blotto games, contestants simultaneously compete in different battlefields. The contestant’s overall payoff depends on the proportion of wins on the individual battlefields.¹⁸ Konrad and Kovenock (2009) discuss multi-battle contests, in which contestants win a final prize if they win a certain number of sequential subgames. Konrad and Kovenock show that intermediate prizes offered in the subgames can make the overall competition more intense as contestants lagging behind can still catch up.¹⁹ In contrast to my model, the winner of each battlefield (subgame) is usually determined by an all-pay auction in Colonel Blotto games as well as in multi-battle games. Moreover, these games neglect the influence of an organizer who controls entry to the contests.

Snyder (1989) analyzes a two-party contest for legislative seats, in which the winner of a seat in a district is determined by a non-discriminatory contest. The author concentrates on the effect of the different goals of the two parties. Either a party maximizes the expected number of seats or maximizes the probability of winning a majority of the seats. In the former case, parties spend more resources on districts in which the race is close. In the latter case, the analysis is more complex since incentives are additionally affected by the probability that a specific seat is decisive. In contrast to my model, Snyder neglects entry regulations as well as entry decisions.

1.4 Outline

The subsequent Sect. 2 starts with the notation and the assumptions of the model. In Sect. 3.1, I derive contestants’ effort in equilibrium, if contestants are allowed to participate in several (or even in all) contests. In Sect. 3.2, I present the equilibrium if the entry to contests is limited. Spillover effects are discussed in Sect. 3.3. In Sect. 4, I derive the optimal entry regulation and prize allocation of the global organizer. As an extension, I consider alternative cost functions in Sect. 5. Section 6 concludes.

2 Notation and assumptions

Two different types $t\in \{H,L\}$ of contestants exist. A measure 1 of high types H (with high abilities) and a measure 1 of low types L (with low abilities) exist.²⁰ Contestants can participate in $K\in \mathbb {N} ^{+}\backslash \left\{ 1\right\}$ contests. Each contest offers a prize to the winner. The prize in contest k is denoted by $V_{k}>0$ for $k\in \{1,\ldots ,K\}$. If a participant enters a contest, he/she exerts effort to increase the probability of winning the contest. The effort in contest $k\in \{1,\ldots ,K\}$ is only valid in contest k and does not affect the contestant’s success in other contests. The representative i of the high types exerts effort $x_{i,k}^{H}$ and the representative j of the low types exerts effort $x_{j,k}^{L}$ in contest k for $k\in \{1,\ldots ,K\}$, $i\in [0,1]$ and $j\in [0,1]$. The effort cost of type t in contest k is denoted by $C^{t}(x_{\ell ,k}^{t})=\frac{1}{\mu }c^{t}\left( x_{\ell ,k}^{t}\right) ^{\mu }$ for $t\in \{H,L\}$ and $\ell \in \{i,j\}$ with $0<c^{H}=c<1=c^{L}$. Thus, high types with high abilities have a lower cost parameter than low types with low abilities. I set parameter $\mu =2$. However, the analyses in this paper also hold for $\mu \in \{ \mathbb {R} \mid \mu >1\}.$ In the main part of this paper, I ignore any fixed costs, i.e. costs to enter contests, and I exclude the case of constant marginal costs.²¹ In the model, total costs $\mathop {\sum }\nolimits _{k=1}^{K}C^{t}(x_{\ell ,k}^{t})=\mathop {\sum }\nolimits _{k=1}^{K}\frac{1}{2 }c^{t}\left( x_{\ell ,k}^{t}\right) ^{2}$ are additive separable for each contestant. This assumption is only adequate in some real world examples of parallel contests. In the extension of this paper, I therefore relax some of the above mentioned assumptions. I check the robustness of the model addressing the case of constant marginal costs, discussing the effects of entry costs and considering a total cost function with interdependence between contests. For the latter case, I will analyze the model with a type t’s total cost function $\tilde{C}^{t}(x_{\ell ,1}^{t},\ldots ,x_{\ell ,K}^{t})= \frac{1}{\mu }c^{t}\left( \mathop {\sum }\nolimits _{k=1}^{K}x_{\ell ,k}^{t}\right) ^{\mu }$. According to this cost function, total effort costs of a contestant depend on aggregate efforts. Contestants do not face any strict resource constraints, but a large value of $\mu$ approximates this situation fairly closely.²²

I differentiate between two types of entry regimes by the global organizer: (i) unrestricted entry regulations and (ii) restricted entry regulations. In scenario (i), each contestant can enter each contest, as illustrated in Fig. 1. In scenario (ii), a contestant is allowed to enter at most one contest, as shown in Fig. 2. In both Figs. 1 and 2, only three contestants of each type are explicitly displayed.

Fig. 1

Multiple participation in parallel contests

Fig. 2

Single participation in parallel contests

The variable $n_{k}^{H}$ $(n_{k}^{L})$ with $n_{k}^{H}\in [0,1]$ $(n_{k}^{L}\in [0,1])$ represents the share of high (low) types that enter contest k. The aggregate effort of the high type i (low type j) in all the contests is defined as $X_{i}^{H}=\mathop {\sum } \nolimits _{k=1}^{K}x_{i,k}^{H}$ $(X_{j}^{L}=\mathop {\sum }\nolimits _{k=1}^{K}x_{j,k}^{L})$. The aggregate effort in contest k is $X_{k}=\mathop {\int } \limits _{i=0}^{1}x_{i,k}^{H}di+\mathop {\int }\limits _{j=0}^{1}x_{j,k}^{L}dj$ and the aggregate effort of all the contestants over all the contests is denoted by $X=\mathop {\sum }\nolimits _{k=1}^{K}X_{k}$. The winning probability of a high type i and a low type j in contest k is determined according to the Tullock contest success function (CSF)²³

$$\begin{aligned} p_{i,k}^{H}=\frac{x_{i,k}^{H}}{X_{k}}\text { and }p_{j,k}^{L}=\frac{ x_{j,k}^{L}}{X_{k}} \end{aligned}$$

with $0\leqslant p_{i,k}^{H}\leqslant 1$ and $0\leqslant p_{j,k}^{L}\leqslant 1$. Due to the continuum of the two types, the contest success function actually represents a density function. In equilibrium, this density function determines the distribution of the contest prize over the continuum.²⁴

The expected profit function of a high type i and a low type j in contest k is defined as follows:²⁵

$$\begin{aligned} \pi _{i,k}^{H}=p_{i,k}^{H}V_{k}-\frac{1}{2}c\left( x_{i,k}^{H}\right) ^{2} \,\text { and }\,\pi _{j,k}^{L}=p_{j,k}^{L}V_{k}-\frac{1}{2}\left( x_{j,k}^{L}\right) ^{2} \end{aligned}$$

The expected total profits of a high type i and a low type j are $\pi _{i}^{H}=\mathop {\sum }\nolimits _{k=1}^{K}\pi _{i,k}^{H}$ and $\pi _{j}^{L}=\mathop {\sum }\nolimits _{k=1}^{K}\pi _{j,k}^{L}.$ Each aggregation (of the individual profits) is based on the assumption that costs are additively separable in the model. I assume that contestants maximize their expected profits.

2.1 Aggregate-taking behavior

I assume aggregate-taking behavior (ATB) of contestants. ATB was introduced into the literature by Alós-Ferrer and Ania (2005).²⁶ Aggregate-taking behavior means that the contestants take the aggregate effort in a contest as given when maximizing their expected profits. Even if contestants take the aggregate as given with ATB, the aggregate is determined endogenously in equilibrium.²⁷ Hefti and Grossmann (2015) and Grossmann and Dietl (2015) discuss the advantages of the ATB approach. They argue that ATB can be more realistic if a contestant does not know the competitor’s type in detail but rather has a general estimate of the aggregate behavior. This holds true especially when the number of competitors is large in a contest. Moreover, the ATB equilibrium converges to the Nash equilibrium for a large number of contestants. In my model, the ATB assumption allows me to derive closed solutions. Closed solutions are desirable because they are easier to interpret than implicit solutions. The cost of the ATB assumption is that I omit one effect: contestants ignore their own impact on the aggregate. But, as already mentioned, this effect is infinitesimally small if the number of contestants is large.²⁸

2.2 Objective function of the global contest organizer

The global organizer allocates the total prize money V across the contests considering the budget constraint $\mathop {\sum }\nolimits _{k=1}^{K}V_{k}\leqslant V$. I assume that the global organizer aims to maximize aggregate effort in all contests.²⁹ In equilibrium, the entire budget is obviously exhausted by the global organizer. As explained in the Introduction, I do not model any scope of action of local organizers within the individual contests. Moldovanu and Sela (2006) argue that in some types of contests, an organizer of a single contest can be interested in maximizing the individual effort of a contestant instead of aggregate effort.³⁰ Therefore, I also analyze the side-effects of the global organizer’s optimal entry regulation on the individual effort of a contestant in a particular contest that could be of interest to a local organizer.

3 Equilibrium

The global organizer determines whether competitors are allowed to participate in only a single contest or in multiple contests. Depending on this decision, different outcomes result, which are discussed in the following two subsections. Based on these outcomes, I discuss spillover effects and analyze the global organizer’s decisions to maximize aggregate effort afterwards.

3.1 Unrestricted entry regime

In this subsection, I assume that contestants are allowed to participate in all contests, as illustrated in Fig. 1. Therefore, there is no participation constraint. The representative contestant i (j) maximizes $\pi _{i}^{H}$ $(\pi _{j}^{L})$ with respect to $x_{i,k}^{H}$ $(x_{j,k}^{L})$ for all $k=1,\ldots ,K$. As the contestants take the aggregate $X_{k}$ in the Tullock contest success function as given (due to ATB), the first-order conditions of representatives i and j are as follows:

$$\begin{aligned} \frac{\partial \pi _{i}^{H}}{\partial x_{i,k}^{H}}= & {} \frac{V_{k}}{X_{k}} -cx_{i,k}^{H}=0\quad \forall ~k=1,\ldots ,K \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \pi _{j}^{L}}{\partial x_{j,k}^{L}}= & {} \frac{V_{k}}{X_{k}} -x_{j,k}^{L}=0 \quad \forall ~k=1,\ldots ,K \end{aligned}$$

(2)

Note that the first-order conditions in (1) hold $\forall ~i\in [0,1]~$and the first-order conditions in (2) hold $\forall ~j\in [0,1]$. Combining the first-order conditions of the two representatives i and j in contest k, I obtain:

$$\begin{aligned} x_{i,k}^{H}=\frac{1}{c}x_{j,k}^{L} \end{aligned}$$

(3)

Assuming symmetry within types in equilibrium, i.e., $x_{i,k}^{H}=x_{k}^{H}$ and $x_{j,k}^{L}=x_{k}^{L}$ with $i\in [0,1]$ and $j\in [0,1]$ , I obtain the following lemma:

Lemma 1

Under an unrestricted entry regime,

• (i) each contestant participates in all the contests,

• (ii) the individual efforts of a high type i and a low type j in contest k are $x_{k}^{H,M}=\frac{\sqrt{V_{k}}}{\sqrt{c\left( 1+c\right) }}$ and $x_{k}^{L,M}=\frac{\sqrt{c}}{\sqrt{1+c}}\sqrt{V_{k}},$

• (iii) the aggregate effort of a high type i equals $X_{i}^{H,M}=\frac{1}{ \sqrt{c\left( 1+c\right) }}\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}$ and the aggregate effort of a low type j equals $X_{j}^{L,M}=\frac{\sqrt{c}}{\sqrt{ 1+c}}\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}},$

• (iv) the aggregate effort in contest k is $X_{k}^{M}=\frac{\sqrt{1+c}}{ \sqrt{c}}\sqrt{V_{k}},$

• (v) and the aggregate effort in all the contests is $X^{M}=\frac{\sqrt{1+c}}{ \sqrt{c}}\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}$ for $k\in \{1,\ldots ,K\}$, $i\in [0,1]$ and $j\in [0,1]$ in an ATB equilibrium.³¹

Proof

See “Appendix”. $\square$

The contestants enter each contest because the marginal cost equals zero and the marginal revenue is strictly positive at $x=0$ in each contest. Therefore, the incentives for effort provision are positive in each contest for each type of contestant. It is very intuitive that the high type i contributes more effort than the low type j to each contest due to the lower marginal cost of effort.

3.2 Restricted entry regime

In contrast to the previous subsection, I now assume that contestants are only allowed to participate in a single contest, as previously illustrated in Fig. 2. I find equilibria in which both types of contestant are present in a single contest. This situation is shown in Fig. 3 in detail. The contestants are arranged in groups on the line with measure 1 associated with the contest that they enter. For each type, only three of the K groups, that is, $n_{1},n_{k},$ and $n_{K}$, are explicitly displayed. However, I derive that $n_{k}^{H}=0$ or $n_{k}^{L}=0$ is possible in equilibrium, too. Therefore, equilibria exist in which high or low types participate only in some of the K contests.

Fig. 3

Participation of different types in each contest

Since the contestants are constrained with respect to their participation, entry depends on contestants’ beliefs regarding the behavior of the other participants. In equilibrium, the expected profits must be equal within types in all contests. The reason for this result is as follows: if the expected profits were different, the contestant with a lower expected profit would have an incentive to switch to another contest. This argument holds because the contestants are infinitesimal and the shares $n_{k}^{H}$ and $n_{k}^{L}$ are arbitrarily divisible for all $k\in \{1,\ldots ,K\}$. I define the set $G_{k}\equiv \{i,j:i$ and j participate in contest $k\}$. Therefore, $G_{k}$ represents the set of all the contestants who enter contest k (see Fig. 3).

Suppose that contestant i and contestant j enter contest k. The profit function of a high type in contest k and therefore his/her total profit is given as follows:

$$\begin{aligned} \pi _{i,k}^{H}=\frac{x_{i,k}^{H}}{X_{k}}V_{k}-\frac{1}{2}c\left( x_{i,k}^{H}\right) ^{2}=\frac{x_{i,k}^{H}}{\mathop {\int }\limits _{i\in G_{k}}x_{i,k}^{H}di+\mathop {\int }\limits _{j\in G_{k}}x_{j,k}^{L}dj}V_{k}-\frac{1}{2} c\left( x_{i,k}^{H}\right) ^{2} \end{aligned}$$

The profit function of a low type j in contest k and therefore his/her total profit is given as follows:

$$\begin{aligned} \pi _{j,k}^{L}=\frac{x_{j,k}^{L}}{X_{k}}V_{k}-\frac{1}{2}\left( x_{j,k}^{L}\right) ^{2}=\frac{x_{j,k}^{L}}{\mathop \int \limits _{i\in G_{k}}x_{i,k}^{H}di+\mathop {\int }\limits _{j\in G_{k}}x_{j,k}^{L}dj}V_{k}-\frac{1}{2} \left( x_{j,k}^{L}\right) ^{2} \end{aligned}$$

Using ATB, the first-order conditions for a high type i and a low type j are as follows:

$$\begin{aligned} \frac{\partial \pi _{i,k}^{H}}{\partial x_{i,k}^{H}}= & {} \frac{V_{k}}{X_{k}} -cx_{i,k}^{H}=0 \end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial \pi _{j,k}^{L}}{\partial x_{j,k}^{L}}= & {} \frac{V_{k}}{X_{k}} -x_{j,k}^{L}=0 \end{aligned}$$

(5)

The difference of the first-order conditions (4) and (5) from the conditions in Sect. 3.1 is the way in which the aggregate $X_{k}$ is determined in equilibrium. The aggregate effort in conditions (4) and (5) depends on the endogenous shares $n_{k}^{H}$ and $n_{k}^{L}$ in contest k. Combining the first-order conditions, I obtain

$$\begin{aligned} x_{i,k}^{H}=\frac{1}{c}x_{j,k}^{L} \end{aligned}$$

(6)

Assuming symmetry within types in equilibrium, i.e., $x_{i,k}^{H}=x_{k}^{H}$ and $x_{j,k}^{L}=x_{k}^{L}$ with $i\in [0,1]$ and $j\in [0,1]$ , it is easy to derive the following Lemma:

Lemma 2

Under a restricted entry regime,

• (i) each contestant enters one contest, but an infinite number of equilibria exists in which the number of low and high types in contest k is implicitly defined by the relation $n_{k}^{H}=\frac{V_{k}}{V}\left( 1+c\right) -cn_{k}^{L}$ with $n_{k}^{H}\geqslant 0,$ $n_{k}^{L}\geqslant 0,$ $\mathop {\sum }\nolimits _{k=1}^{K}n_{k}^{H}=1$ and $\mathop {\sum }\nolimits _{k=1}^{K}n_{k}^{L}=1,$

• (ii) the individual efforts of high type i and low type j in contest k are $x_{k}^{H,S}=\frac{\sqrt{V}}{\sqrt{c\left( 1+c\right) }}$ and $x_{k}^{L,S}=\sqrt{\frac{c}{1+c}}\sqrt{V},$

• (iii) the aggregate effort in contest k is given by $X_{k}^{S}=\frac{V_{k} }{\sqrt{V}}\sqrt{\frac{1+c}{c}},$ and

• (iv) the aggregate effort in all the contests is given by $X^{S}=\sqrt{V} \sqrt{\frac{1+c}{c}}$ for $k\in \{1,\ldots ,K\}$, $i\in [0,1]$ and $j\in [0,1]$ in an ATB equilibrium.³²

Proof

See “Appendix”. $\square$

According to Lemma 2(i), it is possible that both types enter a particular contest. In this case, the high type i’s effort is larger than the low type j’s effort in that contest due to the lower marginal effort costs of the high type. In addition, Lemma 2(i) also shows that multiple equilibria exist. The composition of the field of participants, i.e., the share of high types and low types, in contest k depends on the realized equilibrium according to the condition $n_{k}^{H}=\frac{V_{k}}{V}\left( 1+c\right) -cn_{k}^{L}$. Thus, a high-prize contest does not attract high types from low-prize contests.³³ In some types of equilibria, Lemma 2(i) also suggests that one type is possibly not present in contest k, namely, if $n_{k}^{H}=0$ or $n_{k}^{L}=0$. Suppose that $n_{k}^{H}=n_{k}^{L}\equiv n_{k}$ holds in contest k in a particular equilibrium. In this case, the shares of high and low types in contest k equal the relative contest prize, viz., $n_{k}=V_{k}/V.$ Then, a larger relative prize $V_{k}/V$ in contest k implies more participating contestants.³⁴

3.3 Spillover effects

Based on Lemmas 1 and 2, I examine spillover effects of prizes between contests in this subsection.

Corollary 1

Under an unrestricted entry regime: the individual effort of a contestant in contest k as well as the aggregate efforts in contest k do not depend on the prizes offered in the other contests such that no spillover exists between contests.

Proof

Follows directly from Lemma 1. $\square$

Spillovers between contests do not exist under an unrestricted entry regime, because the contestants’ participation does not depend on prizes. Since each contestant is present in all the contests and costs are additively separable, only the specific contest prize affects contestants’ effort provision in this contest.

Corollary 2

Under a restricted entry regime:

• (i) Suppose that the total prize money V is constant. Then,

• (ia) the distribution of the total prize money V across the contests does not affect the individual effort, and

• (ib) the aggregate effort in a particular contest k increases for a higher relative prize $V_{k}/\sqrt{V}.$

• (ii) Suppose that the total prize money V increases due to an exogenous prize shock and the additional money is added completely to the prize in contest q with $q=1,\ldots ,K$ and $q\ne k$. Then,

• (iia) the individual effort of a contestant increases in contest k, and

• (iib) the aggregate effort in contest k decreases.

Proof

Follows directly from Lemma 2. $\square$

This corollary shows that the endogeneity of contestants’ participation has a decisive impact on contestants’ effort provision. Result (ia) shows that the individual effort in contest k only depends on the aggregate prize money V under a restricted entry regime. Surprisingly, neither the distribution of the prize money across the contests nor the specific prize $V_{k}$ in contest k have an impact on individual effort in contest k. The reason for this result is that an increase in $V_{k}$ and an equivalent decrease in $V_{q}$ such that $\Delta V=\Delta V_{k}+\Delta V_{q}=0$ with $q\ne k$ induces two offsetting effects. In contest k (q), marginal revenue of effort increases due to the higher (lower) prize. But, at the same time, more (less) contestants enter contest k (q) such that marginal revenue decreases (increases). Both effects cancel each other out such that individual effort in both contests k and q do not change. According to result (ib), the aggregate effort in contest k depends on the relative prize $V_{k}/\sqrt{V}.$ A larger relative prize increases aggregate effort since more contestants enter contest k while the individual effort of a contestant in contest k does not change for a fixed prize money V.

Result (iia) shows that there are spillover effects between contests if the total prize money V,  i.e., the global organizer’s budget, increases due to an exogenous prize shock. A unilateral prize increase in contest q (ceteris paribus) then implies that the individual effort of a contestant in contest k with $k\ne q$ increases. The reason for these spillover effects is that a larger prize in contest q attracts contestants and therefore the marginal revenue of individual effort increases in the abandoned contest k.³⁵ According to result (iib), the deserting of contestants also explains the decrease of aggregate effort in contest k if V increases due to a prize increase in contest $q\ne k$, i.e., $\Delta V_{q}>0$ and $\Delta V_{k}=0$ such that $\Delta V>0.$

4 Prize allocation and entry regulation

In the following two subsections, I consider the global organizer’s optimal prize allocation and access regulation.

4.1 Prize allocation

According to Lemma 1, the total effort in all the contests depends on the term $\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}$ under an unrestricted entry regime. Under a restricted entry regime, total effort in all the contests depends on the budget V (see Lemma 2). Thus, I derive the following proposition.

Proposition 1

• (i) Under an unrestricted entry regime: the global contest organizer sets identical prizes across contests, that is, $\bar{V}\equiv \frac{V}{K} =V_{1}=\cdots =V_{k}=\cdots =V_{K}$ to maximize the aggregate effort in all the contests.

• (ii) Under a restricted entry regime: the global organizer’s prize allocation across contests does not influence the aggregate effort in all the contests.

Proof

See “Appendix”. $\square$

Under both regimes, the global organizer exhausts its budget since aggregate effort in all the contests increases for higher prizes.

• (i) Under an unrestricted entry regime, identical prizes across contests are optimal for the global organizer for the following reason. In equilibrium, marginal revenue of effort $(MR_{k})$ equals marginal cost of effort $(MC_{k})$ in contest k according to the first-order condition $MR_{k}=V_{k}/X_{k}=cx_{k}^{H}=MC_{k}.$ A higher prize in contest k increases $MR_{k}$. For a fixed value $X_{k}$, contestants’ effort would therefore increase in contest k due to the convexity of effort costs. However, more individual effort increases aggregate effort $X_{k}$ in contest k. Higher aggregate effort in contest k mitigates the increase in marginal revenue. This explains the concave relationship between individual effort $x_{k}^{t,M}$ and the prize $V_{k}$ in contest k for both types $(t=H,L)$ according to Lemma 1(ii). This concavity carries over to the aggregate effort in all the contests $X^{M}=\frac{\sqrt{1+c}}{\sqrt{c} }\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}$ according to Lemma 1(v). Thus, the convexity of costs and the mitigating effect through the aggregate on marginal revenue are responsible for the global organizer’s smoothing of prizes across the contests under an unrestricted entry regime.

• (ii) Under a restricted entry regime, the prize distribution across contests does not affect aggregate effort in all contests. The mechanism for this result is as follows. Aggregate effort only depends on the total prize money V since a prize increase in contest k and (a symmetric prize decrease in contest q with $q\ne k)$ increases (decreases) effort incentive in contest k (q). However, contestants switch from contest q to contest k such that MR of effort decreases (increases) in contest k (q) offsetting the two effects. Thus, the distribution of the prize money V across contests has no impact on aggregate effort in all contests under a restricted entry regime.

4.2 Entry regulations

The global organizer anticipates the contestants’ effort provision that depends on the entry regulation as well as on the optimal prize allocation derived in Proposition 1. Thus, I obtain the following proposition by backward induction.

Proposition 2

The global contest organizer chooses an unrestricted entry regime and uniquely sets identical prizes across contests to maximize aggregate efforts in all contests.

Proof

See “Appendix”. $\square$

This proposition is based on the results of Proposition 1. The organizer should not implement a restricted entry regime, since an unrestricted entry regime is always superior with respect to aggregate effort in all contests compared to a restricted entry regime independent of the prize distribution across contests. In addition, the global organizer sets identical prizes since identical prizes elicit the highest aggregate effort in all contests.

The global organizer’s optimal entry regulation, i.e., an unrestricted entry regime, has side-effects for the local organizers. These effects are presented in the following corollary.

Corollary 3

The global organizer’s decision for an unrestricted entry regime implies that

• (i) the individual effort of each type is lower in each contest k, i.e., $x_{k}^{H,M}<x_{k}^{H,S}$ and $x_{k}^{L,M}<x_{k}^{L,S},$

• (ii) but the aggregate effort in contest k is larger, i.e., $X_{k}^{M}>X_{k}^{S},$ than it would be under a restricted entry regime.

Proof

Directly follows from Lemmas 1 and 2. $\square$

On the one hand, result (i) of this corollary means that the unrestricted entry regime partly destroys contestants’ effort incentive in a contest due to the large number of participating contestants. If a (passive) local organizer is interested in high individual effort,³⁶ then I conclude that the global organizer’s entry regulation has a negative externality on the local organizer. On the other hand, result (ii) shows that the large number of contestants not only guarantees maximized aggregate effort in all contests but also maximized aggregate effort in each contest (for a given prize allocation). Thus, if a local organizer is interested in high aggregate effort in its contest, then I conclude that the local organizer profits from the global organizer’s unrestricted entry regime.

5 Extension

As mentioned in Sect. 2, the model presented so far holds for a general cost function $\mathop {\sum }\nolimits _{k=1}^{K}C^{t}(x_{\ell ,k}^{t})=\mathop {\sum }\nolimits _{k=1}^{K}\frac{1}{\mu }c^{t}\left( x_{\ell ,k}^{t}\right) ^{\mu }$ for $t\in \{H,L\}$ and $\ell \in \{i,j\}$ with $\mu \in \{ \mathbb {R} \mid \mu >1\}$. According to this function, I excluded (i) constant marginal costs as well as (ii) fixed costs. Moreover, (iii) total costs were additively separable. In this section, I consider the consequences of each point (i) to (iii) in detail.

(i) Constant marginal costs

The model in the main part of this paper holds for $\mu >1.$ The case $\mu =1$ reflects the case of constant marginal costs such that costs are linear. Due to the ATB assumption, the expected revenue $\left( x_{\ell ,k}^{t}/X_{k}\right) V_{k}$ for type t in contest k is linear in $x_{\ell ,k}^{t}$. The linearity of costs and revenues results in corner solutions that are of no economic interest. Therefore, the contest literature with ATB usually excludes the linear case.³⁷

(ii) Fixed costs

Suppose that type t’s cost function equals $\hat{C}^{t}(x_{\ell ,k}^{t})= \frac{1}{2}c^{t}\left( x_{\ell ,k}^{t}\right) ^{2}+f$, where f represents the fixed cost to enter contest k for each $k\in \{1,\ldots ,K\}$. The implications are very intuitive under an unrestricted entry regime. A low value of f only decreases profits but has neither an effect on participation nor on contribution. A medium value of f decreases the participation of some low types in contests with low prizes as their expected profits would be negative. A higher value of f implies that some or even all high types (in addition to the low types) do not enter the low prize contests. If f is very high, no type enters a contest.

(iii) Interaction effects

Suppose that type t’s total cost function equals $\tilde{C}^{t}(x_{\ell ,1}^{t},\ldots ,x_{\ell ,K}^{t})=\frac{1}{2}c^{t}\left( \mathop {\sum }\nolimits _{k=1}^{K}x_{\ell ,k}^{t}\right) ^{2}$. Exemplarily, suppose that $K=2$ such that $\tilde{C}^{t}(x_{\ell ,1}^{t},x_{\ell ,2}^{t})=\frac{1 }{2}c^{t}\left( \left( x_{\ell ,1}^{t}\right) ^{2}+2x_{\ell ,1}^{t}x_{\ell ,2}^{t}+\left( x_{\ell ,2}^{t}\right) ^{2}\right)$. In this case, the interaction term $2x_{\ell ,1}^{t}x_{\ell ,2}^{t}$ is added in comparison to the model in the main part of this paper. Economically, the interaction term represents the additional costs of participating in multiple contests due to, for instance, extra organizational expenditures or exhaustion.

Under an unrestricted entry regime, contestants i and j maximize their expected profits

$$\begin{aligned} \pi _{i,k}^{H}=\mathop {\sum }\limits _{k=1}^{K}\frac{x_{i,k}^{H}}{X_{k}}V_{k}-\frac{1}{ 2}c\left( \mathop {\sum }\limits _{k=1}^{K}x_{i,k}^{H}\right) ^{2}\,\text { and }\,\pi _{j,k}^{L}=\mathop {\sum }\limits _{k=1}^{K}\frac{x_{j,k}^{L}}{X_{k}}V_{k}-\frac{1}{2} \left( \mathop {\sum }\limits _{k=1}^{K}x_{j,k}^{L}\right) ^{2}. \end{aligned}$$

Then, I get the following proposition:

Proposition 3

If total costs are a power function in the aggregate effort, then the following holds:

• (ia) Under an unrestricted entry regime, the aggregate effort of each type, aggregate effort in contest k and aggregate effort in all contests are lower compared to an unrestricted entry regime and additively separable cost function.

• (ib) Under an unrestricted entry regime, the results for the aggregate effort of each type, aggregate efforts in contest k and aggregate effort in all contests coincide with the results obtained under a restricted entry regime with an additively separable cost function.

• (ii) Under a restricted entry regime, the results are the same as under a restricted entry regime and additively separable costs.

Proof

See “Appendix”. $\square$

Result (ia) is very intuitive. Contestants reduce their investments if there exist interaction effects in the effort costs. Combining results (ib) with (ii), I observe that the results under an unrestricted entry regime coincide with the results under a restricted entry regime if the effort cost is a power function. Thus, the global organizer who aims to maximize aggregate effort in all contests, is indifferent with respect to a restricted or unrestricted entry regime. This finding is in contrast to the result in Proposition 2 with additively separable costs.

6 Conclusion

So far, the contest literature has neglected to study the entry regulation of heterogeneous contestants to parallel contests by a global contest organizer. In this paper, I assume that the global contest organizer controls access to the contests and determines the prize allocation between the contests. The local organizer of a specific contest is passive and takes the allocated prize money as given. Contestants’ participation is determined endogenously and depends on the entry regime. They anticipate the number and quality of their competitors within each contest when they make their entry decision.

I show that the global organizer selects an unrestricted entry regime and sets identical prizes across contests in order to maximize aggregate efforts over all contests. The decisions by the global organizer have consequences for the individual contests. The individual effort in a specific contest is smaller under this unrestricted entry regime compared to a situation with a restricted entry regime. Spillover effects between contests exist only under the restricted entry regime: if the prize in contest k increases (ceteris paribus), the individual (aggregate) effort increases (decreases) in the other contests.

Relative prizes in the contest do not provoke sorting effects of contestants with different abilities. Thus, a relatively large prize in a contest does not necessarily attract high ability contestants into its contest independent of the entry regulation. The reason is as follows for unrestricted entry regulations. All contestants have an incentive to participate in each contest. Under the restricted entry regime, however, multiple equilibria exist and the proportion of low and high types in a contest is randomly determined³⁸ as it depends on the realized equilibrium. Thus, the global organizer’s influence on the distribution of talent is limited.

The analysis in this paper is the first step towards understanding contestants’ behavior and the spillovers between parallel contests with endogenous but regulated entry in more depth. An analysis of parallel contests with more than two types of contestants and/or an active role of the local contest organizers seem to be promising and interesting and is left for future research.

7 Proofs

7.1 Proof of Lemma 1

Part (i) and (ii): Using the first-order condition (1), the condition (3) and assuming symmetry within types, I obtain the high type i’s positive effort in equilibrium:³⁹

$$\begin{aligned} \frac{V_{k}}{\mathop {\int }\limits _{i=0}^{1}x_{i,k}^{H}di+\mathop {\int } \limits _{j=0}^{1}x_{j,k}^{L}dj}= & {} cx_{i,k}^{H}\Leftrightarrow \frac{V_{k}}{ x_{k}^{H}\underset{=1}{\underbrace{\mathop {\int }\limits _{j=0}^{1}di}}+x_{k}^{L} \underset{=1}{\underbrace{\mathop {\int }\limits _{j=0}^{1}dj}}} =cx_{k}^{H} \\&\Leftrightarrow \frac{V_{k}}{x_{k}^{H}+cx_{k}^{H}}=cx_{k}^{H}\Leftrightarrow x_{k}^{H,M}=\frac{\sqrt{V_{k}}}{\sqrt{c\left( 1+c\right) }}>0 \end{aligned}$$

Using (3) and $x_{k}^{H,M}$, I obtain the low type j’s effort $x_{j,k}^{L,M}=x_{k}^{L,M}>0$ in equilibrium. Since the optimal effort is positive for all contestants in all contests, I conclude that each contestant participates in all the contests.

Part (iii): The aggregate effort of a high type i (low type j) is $X_{i}^{H,M}=\mathop {\sum }\nolimits _{k=1}^{K}x_{k}^{H,M}=\frac{1}{\sqrt{c\left( 1+c\right) }}\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}$ $\left( X_{j}^{L,M}=\frac{ \sqrt{c}}{\sqrt{1+c}}\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}~\right) .$

Part (iv): The aggregate effort in contest k is calculated as follows:

$$\begin{aligned} X_{k}^{M}=\mathop {\int }\limits _{i=0}^{1}x_{k}^{H,M}di+\mathop {\int } \limits _{j=0}^{1}x_{k}^{L,M}dj=\mathop {\int }\limits _{i=0}^{1}\frac{\sqrt{V_{k}}}{ \sqrt{c\left( 1+c\right) }}di+\mathop {\int }\limits _{j=0}^{1}\frac{\sqrt{c}}{\sqrt{1+c }}\sqrt{V_{k}}dj=\frac{\sqrt{1+c}}{\sqrt{c}}\sqrt{V_{k}} \end{aligned}$$

Part (v): The aggregate effort in all the contests is $X^{M}=\mathop {\sum }\nolimits _{k=1}^{K}X_{k}^{M}=\frac{\sqrt{1+c}}{\sqrt{c}} \mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}.$

7.2 Proof of Lemma 2

Part (i) and (ii): Using the high type i’s first-order condition (4), condition (6) and assuming symmetry within types, the individual effort of the high type i in contest k is derived as follows:

$$\begin{aligned} \frac{V_{k}}{\mathop {\int }\limits _{i\in G_{k}}x_{i,k}^{H}di+\mathop {\int }\limits _{j\in G_{k}}x_{j,k}^{L}dj}= & {} cx_{i,k}^{H}\Leftrightarrow \frac{V_{k}}{ n_{k}^{H}x_{k}^{H}+n_{k}^{L}x_{k}^{L}}=cx_{k}^{H} \nonumber \\\Leftrightarrow & {} \frac{V_{k} }{n_{k}^{H}x_{k}^{H}+n_{k}^{L}cx_{k}^{H}}=cx_{k}^{H} \nonumber \\\Leftrightarrow & {} x_{k}^{H}=\frac{\sqrt{V_{k}}}{\sqrt{c\left( n_{k}^{H}+n_{k}^{L}c\right) }} \end{aligned}$$

(7)

Using condition (6), condition (7) and assuming symmetry within types, I obtain the individual effort of the low type j in contest k.

Note that the individual effort endogenously depends on the shares $n_{k}^{H}$ and $n_{k}^{L}$. I will derive the shares in equilibrium next. Accordingly, I first have to calculate the expected profits, which in contest k are

$$\begin{aligned} \pi _{i,k}^{H}= & {} \frac{x_{k}^{H}}{\mathop {\int }\limits _{i\in G_{k}}x_{k}^{H}di+\mathop {\int }\limits _{j\in G_{k}}x_{k}^{L}di}V_{k}-\frac{1}{2} c\left( x_{k}^{H}\right) ^{2}=\frac{1}{2}\frac{V_{k}}{n_{k}^{H}+n_{k}^{L}c} \text { and }\\ \pi _{j,k}^{L}= & {} \frac{x_{k}^{L}}{\mathop {\int }\limits _{i\in G_{k}}x_{k}^{H}di+\mathop {\int }\limits _{j\in G_{k}}x_{k}^{L}di}V_{k}-\frac{1}{2} \left( x_{k}^{L}\right) ^{2}=\frac{1}{2}\frac{V_{k}}{n_{k}^{H}\frac{1}{c} +n_{k}^{L}}. \end{aligned}$$

I observe that $\pi _{i,k}^{H}$ is independent of i and $\pi _{j,k}^{L}$ is independent of j. Next, I assume that both types are present in each contest such that $\pi _{k}^{H}=\pi _{i,k}^{H}$ and $\pi _{k}^{L}=\pi _{j,k}^{L}$ must hold for all $k=1,\ldots ,K$.⁴⁰ If one contest is more or less profitable than the other, some contestants would have an incentive to switch to another contest.

$$\begin{aligned} \pi _{1}^{H}=\pi _{2}^{H}=\cdots =\pi _{k}^{H}=\cdots =\pi _{K}^{H}\text { and }\pi _{1}^{L}=\pi _{2}^{L}=\cdots =\pi _{k}^{L}=\cdots =\pi _{K}^{L} \end{aligned}$$

Using the former condition of the high types’ profits, I obtain:

$$\begin{aligned} \left| \begin{array}{c} \pi _{1}^{H}=\pi _{2}^{H} \\ \pi _{1}^{H}=\pi _{3}^{H} \\ \vdots \\ \pi _{1}^{H}=\pi _{k}^{H} \\ \vdots \\ \pi _{1}^{H}=\pi _{K}^{H} \end{array} \right| =\left| \begin{array}{c} \frac{V_{1}}{n_{1}^{H}+n_{1}^{L}c}=\frac{V_{2}}{n_{2}^{H}+n_{2}^{L}c} \\ \frac{V_{1}}{n_{1}^{H}+n_{1}^{L}c}=\frac{V_{3}}{n_{3}^{H}+n_{3}^{L}c} \\ \vdots \\ \frac{V_{1}}{n_{1}^{H}+n_{1}^{L}c}=\frac{V_{k}}{n_{k}^{H}+n_{k}^{L}c} \\ \vdots \\ \frac{V_{1}}{n_{1}^{H}+n_{1}^{L}c}=\frac{V_{K}}{n_{K}^{H}+n_{K}^{L}c} \end{array} \right| \end{aligned}$$

Note that all contestants enter one contest as profits are positive in equilibrium such that $\mathop {\sum }\nolimits _{k=1}^{K}n_{k}^{L}=\mathop {\sum } \nolimits _{k=1}^{K}n_{k}^{H}=1$ holds. Eliminating the denominators and replacing $n_{K}^{H}=1-\mathop {\sum }\nolimits _{k=1}^{K-1}n_{k}^{H}$ and $n_{K}^{L}=1-\mathop {\sum }\nolimits _{k=1}^{K-1}n_{k}^{L}$ in the last row results in:

$$\begin{aligned} \left| \begin{array}{c} n_{2}^{H}+n_{2}^{L}c=\frac{V_{2}}{V_{1}}\left( n_{1}^{H}+n_{1}^{L}c\right) \\ n_{3}^{H}+n_{3}^{L}c=\frac{V_{3}}{V_{1}}\left( n_{1}^{H}+n_{1}^{L}c\right) \\ \vdots \\ n_{k}^{H}+n_{k}^{L}c=\frac{V_{k}}{V_{1}}\left( n_{1}^{H}+n_{1}^{L}c\right) \\ \vdots \\ \left( 1-n_{1}^{H}-n_{2}^{H}-\cdots -n_{K-1}^{H}\right) +\left( 1-n_{1}^{L}-n_{2}^{L}-\cdots -n_{K-1}^{L}\right) c=\frac{V_{K}}{V_{1}}\left( n_{1}^{H}+n_{1}^{L}c\right) \end{array} \right| \end{aligned}$$

Reformulating the last equation, I obtain:

$$\begin{aligned}&V_{1}\left( \left( 1-n_{1}^{H}-n_{2}^{H}-\cdots -n_{K-1}^{H}\right) +\left( 1-n_{1}^{L}-n_{2}^{L}-\cdots -n_{K-1}^{L}\right) c\right) =V_{K}\left( n_{1}^{H}+n_{1}^{L}c\right) \\&\quad \Leftrightarrow V_{1}\left( 1+c\right) =V_{K}\left( n_{1}^{H}+n_{1}^{L}c\right) \\&\qquad +V_{1}\left( n_{1}^{H}+n_{1}^{L}c+n_{2}^{H}+n_{2}^{L}c+\cdots +n_{K-1}^{H}+n_{K-1}^{L}c\right) \\&\quad \Leftrightarrow V_{1}\left( 1+c\right) =V_{K}\left( n_{1}^{H}+n_{1}^{L}c\right) \\&\qquad +V_{1}\left( n_{1}^{H}+n_{1}^{L}c+\frac{V_{2}}{V_{1}}\left( n_{1}^{H}+n_{1}^{L}c\right) +\cdots +\frac{V_{K-1}}{V_{1}}\left( n_{1}^{H}+n_{1}^{L}c\right) \right) \\&\quad \Leftrightarrow V_{1}\left( 1+c\right) =V\left( n_{1}^{H}+n_{1}^{L}c\right) \Leftrightarrow n_{1}^{H}=\frac{V_{1}}{V}\left( 1+c\right) -cn_{1}^{L} \end{aligned}$$

Analogously, I obtain $n_{k}^{H}$ as a function in $n_{k}^{L}$ as follows:⁴¹

$$\begin{aligned} n_{k}^{H}=\frac{V_{k}}{V}\left( 1+c\right) -cn_{k}^{L} \end{aligned}$$

(8)

Using condition (8) in condition (7), I determine the high type’s individual effort in contest k : 

$$\begin{aligned} x_{k}^{H,S}=\frac{\sqrt{V_{k}}}{\sqrt{c\left( n_{k}^{H}+n_{k}^{L}c\right) }}= \frac{\sqrt{V}}{\sqrt{c\left( 1+c\right) }} \end{aligned}$$

Analogously, the low type j’s effort $x_{k}^{L,S}$ is derived.

Part (iii): The aggregate effort in contest k is calculated as follows:

$$\begin{aligned} X_{k}^{S}= & {} \mathop {\int }\limits _{i\in G_{k}}x_{i,k}^{H,S}di+\mathop {\int }\limits _{j\in G_{k}}x_{j,k}^{L,S}dj=n_{k}^{H}x_{k}^{H,S}+n_{k}^{L}x_{k}^{L,S}\\= & {} \left( \frac{ V_{k}}{V}\left( 1+c\right) -cn_{k}^{L}\right) \frac{\sqrt{V}}{\sqrt{c\left( 1+c\right) }}+n_{k}^{L}\sqrt{\frac{c}{1+c}}\sqrt{V} \\= & {} \frac{V_{k}}{\sqrt{V}}\sqrt{\frac{1+c}{c}} \end{aligned}$$

Part (iv): Using the last result for $X_{k}^{S}$, the aggregate effort in all the contests is $X^{S}=\mathop {\sum }\nolimits _{k=1}^{K}X_{k}^{S}=\sqrt{V}\sqrt{ \frac{1+c}{c}}.$

Finally, I prove that equilibria in which the expected profits differ between contests are impossible. Proof by contradiction: Suppose that $\pi _{1}^{H}=\cdots =\pi _{k}^{H}=\cdots =\pi _{K-1}^{H}>\pi _{K}^{H}$ and $\pi _{1}^{L}=\pi _{2}^{L}=\cdots =\pi _{k}^{L}=\cdots =\pi _{K}^{L}$ hold in equilibrium.⁴² In this case, high types would not enter contest K such that $n_{K}^{H}=0$.⁴³ Using the equations $\pi _{1}^{H}=\cdots =\pi _{k}^{H}=\cdots =\pi _{K-1}^{H},$ $n_{K-1}^{H}=1-\mathop {\sum } \nolimits _{k=1}^{K-2}n_{k}^{H}$, $n_{K-1}^{L}=1-\mathop {\sum } \nolimits _{k=1}^{K-2}n_{k}^{L}-n_{K}^{L}$ and $\pi _{1}^{L}=\pi _{K}^{L}$, it is easy to show that condition (8) still holds. However, condition (8) and $n_{K}^{H}=0$ imply that $n_{K}^{L}=\frac{V_{K}}{V} \frac{1+c}{c}$. Replacing this condition and $n_{K}^{H}=0$ in $\pi _{K}^{H}= \frac{V_{K}}{n_{K}^{H}+n_{K}^{L}c},$ I obtain $\pi _{K}^{H}=\frac{1}{1+c}V$.⁴⁴ On the other hand, using condition (8), I obtain $\pi _{K-1}^{H}=\frac{V_{K-1}}{n_{K-1}^{H}+n_{K-1}^{L}c}=\frac{V_{K-1} }{\frac{V_{K-1}}{V}\left( 1+c\right) -cn_{K-1}^{L}+n_{K-1}^{L}c}=\frac{1}{1+c }V,$ which is identical to $\pi _{K}^{H}$. Therefore, I find a contradiction to our assumption $\pi _{1}^{H}=\cdots =\pi _{K-1}^{H}>\pi _{K}^{H}$. I conclude that $n_{k}^{H}=0$ or $n_{k}^{L}=0$ is possible in equilibrium according to condition (8). However, the expected profits are equalized over all the contests, even if a type is not present in contest k.

7.3 Proof of Proposition 1

Part (i): Under an unrestricted entry regime, aggregate effort in all the contests is $X^{M}=\frac{\sqrt{1+c}}{\sqrt{c}}\mathop {\sum }\nolimits _{k=1}^{K} \sqrt{V_{k}}$ (see Lemma 1(v)) and therefore depends on $\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}$. Proposition 1(i) holds due to the concavity of $f(V_{k}):=\sqrt{V_{k}}$ and Jensen’s inequality $f(\mathop {\sum }\nolimits _{k=1}^{K}\lambda _{k}V_{k})\geqslant \mathop {\sum }\nolimits _{k=1}^{K}\lambda _{k}f\left( V_{k}\right)$ with $\mathop {\sum }\nolimits _{k=1}^{K}\lambda _{k}=1.$ If I set $\lambda _{k}=\frac{1}{K}$ $\forall k=1,\ldots ,K$ and apply Jensen’s inequality, I get $\sqrt{ \mathop {\sum }\nolimits _{k=1}^{K}\frac{1}{K}V_{k}}\geqslant \mathop {\sum }\nolimits _{k=1}^{K}\frac{ 1}{K}\sqrt{V_{k}}\Leftrightarrow \sqrt{\bar{V}}\geqslant \mathop {\sum }\nolimits _{k=1}^{K}\frac{1}{K}\sqrt{V_{k}}\Leftrightarrow K\sqrt{\bar{V}} \geqslant \mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}$ with $\bar{V}\equiv \mathop {\sum }\nolimits _{k=1}^{K}\frac{1}{K}V_{k}$. Therefore, if all contest prizes equal the average prize $\bar{V}$, then K times $\sqrt{\bar{V}}$ is at least as large as the sum of $\sqrt{V_{k}}$ with asymmetric prizes.

Part (ii): Under a restricted entry regime, the aggregate effort in all the contests is given by $X^{S}=\sqrt{V}\sqrt{\frac{1+c}{c}}$ according to Lemma 2(iv). Thus, $X^{S}$ depends only on the total prize money V but not on the distribution of V across the contests.

7.4 Proof of Proposition 2

In this subsection, I compare the outcomes under an unrestricted entry regime with the outcomes under a restricted entry regime. I prove that $X^{M}>X^{S}$ always holds such that the global organizer chooses an unrestricted entry regime to maximize aggregate effort:

$$\begin{aligned} X^{M}>X^{S}\Leftrightarrow \frac{\sqrt{1+c}}{\sqrt{c}}\mathop {\sum }\limits _{k=1}^{K} \sqrt{V_{k}}>\sqrt{V}\sqrt{\frac{1+c}{c}}\Leftrightarrow \mathop {\sum }\limits _{k=1}^{K}\sqrt{V_{k}}>\sqrt{V} \end{aligned}$$

Thus, I must prove that $\mathop {\sum }\nolimits _{k=1}^{K}\sqrt{V_{k}}>\sqrt{V}$ holds. I define $a_{k}\equiv V_{k}/V$ with $0<a_{k}<1$ and $\mathop {\sum } \nolimits _{k=1}^{K}a_{k}=1$. Moreover, I define the function $f(x):=\sqrt{x}$ with the following characteristics:

• (L1) f is monotonically increasing and concave.

• (L2) $f(0)=0$ and $f(1)=1.$

• (L3) $f(x)>x$ $\forall x\in (0,1)$ and $f(x)<x$ $\forall x\in (1,\infty ).$

• (L4) $f(a\cdot b)=f(a)\cdot f(b)$ $\forall a,b\in \mathbb {R} ^{+}.$

Using the definitions of f and $a_{k}$, I have to prove the following inequality:

$$\begin{aligned} \mathop {\sum }\limits _{k=1}^{K}\sqrt{V_{k}}>\sqrt{V}\Leftrightarrow \mathop {\sum }\limits _{k=1}^{K}f(V_{k})>f(V)\Leftrightarrow \mathop {\sum }\limits _{k=1}^{K}f(a_{k}V)>f(V) \end{aligned}$$

L4 implies

$$\begin{aligned} \mathop {\sum }\limits _{k=1}^{K}f(a_{k}V)=\mathop {\sum }\limits _{k=1}^{K}\left( f(a_{k})\cdot f(V)\right) =f(V)\cdot \mathop {\sum }\limits _{k=1}^{K}f(a_{k}). \end{aligned}$$

(9)

L3 and $0<a_{k}<1$ imply that $f(a_{k})>a_{k}$$\forall k=1,\ldots ,K$ and therefore $\mathop {\sum }\nolimits _{k=1}^{K}f(a_{k})>\mathop {\sum }\nolimits _{k=1}^{K}a_{k}=1.$ Using the last inequality in condition (9), I obtain

$$\begin{aligned} \mathop {\sum }\limits _{k=1}^{K}f(a_{k}V)=f(V)\cdot \mathop {\sum }\limits _{k=1}^{K}f(a_{k})>f(V)\cdot 1. \end{aligned}$$

Applying f in the last inequality, I observe that $\mathop {\sum }\nolimits _{k=1}^{K} \sqrt{V_{k}}>\sqrt{V}$ holds. Therefore, I conclude that $X^{M}>X^{S}$ holds. According to Proposition 1, $X^{M}$ itself is maximized for an identical distribution of the prize money V across the contests. This proves the claim of Proposition 2.

7.5 Proof of Proposition 3

Part (ia): The representative contestants i and j maximize their expected profits

$$\begin{aligned} \pi _{i,k}^{H}=\mathop {\sum }\limits _{k=1}^{K}\frac{x_{i,k}^{H}}{X_{k}}V_{k}-\frac{1}{ 2}c\left( \mathop {\sum }\limits _{k=1}^{K}x_{i,k}^{H}\right) ^{2}\,\text { and }\,\pi _{j,k}^{L}=\mathop {\sum }\limits _{k=1}^{K}\frac{x_{j,k}^{L}}{X_{k}}V_{k}-\frac{1}{2} \left( \mathop {\sum }\limits _{k=1}^{K}x_{j,k}^{L}\right) ^{2}. \end{aligned}$$

The first-order conditions are as follows:

$$\begin{aligned} \frac{\partial \pi _{i}^{H}}{\partial x_{i,k}^{H}}= & {} \frac{V_{k}}{X_{k}} -c\mathop {\sum }\limits _{k=1}^{K}x_{i,k}^{H}=0\quad \forall ~k=1,\ldots ,K \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial \pi _{j}^{L}}{\partial x_{j,k}^{L}}= & {} \frac{V_{k}}{X_{k}} -\mathop {\sum }\limits _{k=1}^{K}x_{j,k}^{L}=0\quad \forall ~k=1,\ldots ,K \end{aligned}$$

(11)

Suppose that all first-order conditions hold.⁴⁵ Solving equations (10) and (11) for $\mathop {\sum }\nolimits _{k=1}^{K}x_{i,k}^{H}$ and $\mathop {\sum }\nolimits _{k=1}^{K}x_{j,k}^{L}$, I obtain

$$\begin{aligned} X_{i}^{H}=\mathop {\sum }\limits _{k=1}^{K}x_{i,k}^{H}=\frac{V_{k}}{cX_{k}}\text { and } X_{j}^{L}=\mathop {\sum }\limits _{k=1}^{K}x_{j,k}^{L}=\frac{V_{k}}{X_{k}}. \end{aligned}$$

Integrating over all contestants, I calculate the aggregate effort in all the contests:

$$\begin{aligned} X=\int X_{i}^{H}di+\int X_{j}^{L}dj=\frac{V_{k}}{cX_{k}}+\frac{V_{k}}{X_{k}} \end{aligned}$$

(12)

Evaluating equation (10) for two arbitrary contests k and m and then combining these two equations, I obtain

$$\begin{aligned} \frac{V_{k}}{X_{k}}=\frac{V_{m}}{X_{m}}\Leftrightarrow X_{m}=\frac{V_{m}}{ V_{k}}X_{k}. \end{aligned}$$

Aggregating over m, I derive the aggregate effort in all the contests:

$$\begin{aligned} X=\mathop {\sum }\limits _{m=1}^{K}X_{m}=\frac{\mathop {\sum }_{m=1}^{K}V_{m}}{V_{k}}X_{k} \end{aligned}$$

Substituting the variable m by k, I obtain

$$\begin{aligned} X=\frac{V}{V_{k}}X_{k}. \end{aligned}$$

(13)

Combining equations (12) and (13), the following condition results:

$$\begin{aligned} \frac{V_{k}}{cX_{k}}+\frac{V_{k}}{X_{k}}=\frac{V}{V_{k}}X_{k}\Leftrightarrow X_{k}=\frac{V_{k}}{\sqrt{V}}\cdot \sqrt{\frac{1+c}{c}}. \end{aligned}$$

Using this condition, it is easy to derive contestants i’s and j’s effort and aggregate effort:

$$\begin{aligned} X_{i}^{H}=\frac{V_{k}}{cX_{k}}=\frac{\sqrt{V}}{\sqrt{1+c}}\cdot \frac{1}{ \sqrt{c}}, X_{j}^{L}=\frac{\sqrt{V}}{\sqrt{1+c}}\cdot \sqrt{c}\text { and }X=\mathop {\sum }\limits _{k=1}^{K}X_{k}=\sqrt{V}\cdot \sqrt{\frac{1+c}{c}} \end{aligned}$$

It is easy to see that the aggregate effort X, the efforts $X_{i}^{H}$ and $X_{j}^{L}$ of the two types and total effort $X_{k}$ in contest k in the Extension are lower than the corresponding values under an unrestricted entry regime and additively separable costs presented in Lemma 1.⁴⁶

Part (ib): It is easy to see that aggregate effort X, the efforts $X_{i}^{H}$ and $X_{j}^{L}$ of the two types and total effort $X_{k}$ in contest k in the Extension coincide with the results received in Lemma 2 under a restricted entry regime with additively separable costs.

Part (ii): Each contestant is allowed to enter at most one contest. Suppose that a high type (and analogously for a low type) enter contest k. Then, the expected profit is simplified as follows:

$$\begin{aligned} \pi _{i,k}^{H}=\frac{x_{i,k}^{H}}{X_{k}}V_{k}-\frac{1}{2}c\left( \mathop {\sum }\limits _{k=1}^{K}x_{i,k}^{H}\right) ^{2}=\frac{x_{i,k}^{H}}{X_{k}}V_{k}- \frac{1}{2}c\left( x_{i,k}^{H}\right) ^{2} \end{aligned}$$

Note that this profit function and the results coincide with the case analyzed in Sect. 3.2.