Introduction

Aquifer characterization is fundamental for developing effective engineering strategies and applications such as the planning of groundwater extraction or recharge systems and the assessment of spatiotemporal evolution of subsurface contaminants. However, suitable methods of identifying aquifer hydraulic and transport properties are still under investigation within the scientific community. Many of the associated parameters cannot be estimated directly and need to be inferred through inverse modelling. Several approaches have been developed to address the inverse problem; extensive reviews have been carried out by Zimmerman et al. (1998), Vrugt et al. (2008) and Zhou et al. (2014).

In the past years, ensemble Kalman filter-based methods gained increasing interest due to their efficiency and flexibility in data assimilation for large nonlinear models. In fact, aquifer characterization by inverse modelling using gradient-based optimization approaches needs massive computational effort for moderately large systems. The ensemble Kalman filter-based methods save considerable computing time compared to full Bayesian approaches. Hendricks Franssen and Kinzelbach (2009) studied the ensemble Kalman filter (EnKF) with a Monte-Carlo type inverse modelling technique, and the sequential self-calibration method (Gómez-Hernández et al. 2003), for inverse modelling of groundwater flow systems, to conclude that the two methods give similar results; although, the EnKF computational cost is 80 times lower than that required by the sequential self-calibration method.

Since the introduction of the ensemble Kalman filter (EnKF) by Evensen (1994), it has been widely used for data assimilation and inverse modelling in several fields, including aquifer characterization. Chen and Zhang (2006) applied the EnKF to continuously update the hydraulic conductivity values in both two-dimensional (2D) and three-dimensional (3D) synthetic models by assimilating dynamic pressure head observations. Camporese et al. (2011) applied the EnKF to infer the spatial distribution of hydraulic conductivity from electrical resistivity tomography data of a 3D synthetic tracer test experiment. Tong et al. (2013) used the EnKF in a synthetic 2D aquifer to identify the hydraulic conductivity distribution by assimilating solute concentration measurements. Xu and Gómez-Hernández (2018) used the restart normal-score EnKF for the simultaneous identification of a contaminant source and the spatially variable hydraulic conductivity in an aquifer. The method has been applied in synthetic aquifers by assimilating in time piezometric heads and concentrations from observation wells.

Many variants of the EnKF have been developed over time such as the ensemble smoother (ES) proposed by van Leeuwen and Evensen (1996). Unlike the EnKF, which sequentially assimilates data over time, the ES incorporates all available information into a single global update step. Bailey and Baù (2012) used the ES to estimate spatially variable hydraulic conductivity within a synthetic 3D tilted v-shaped catchment system by assimilating water-table elevation and streamflow data. Crestani et al. (2013) compared the capabilities of the EnKF and the ES to estimate the hydraulic conductivity assimilating observed concentrations. The two approaches have been tested in a 2D synthetic aquifer where a tracer test is simulated. The authors conclude that EnKF always outperforms the ES due to iterative assimilations of information, which helps to handle nonlinear and non-Gaussian conditions. With the aim to improve the ES performance for highly nonlinear applications, Emerick and Reynolds (2012, 2013) proposed the ensemble smoother with multiple data assimilation (ES-MDA), which iteratively assimilates the same data multiple times. The good performance of ES-MDA for inverse modelling have been confirmed in different studies (Todaro et al. 2019, 2021, 2022; Lam et al. 2020; D’Oria et al. 2021; Godoy et al. 2022). Xu et al. (2021) compared the ensemble smoother with multiple data assimilation (ES-MDA) and the restart EnKF for the simultaneous identification of a contaminant source and hydraulic conductivity using both piezometric heads and concentrations on a synthetic aquifer. The results showed that the ES-MDA performs better than the restart EnKF when using enough iterations, needing almost the same computational time.

While these studies have demonstrated the capability of ensemble-based methods to determine aquifer parameters, their application to real sites is still limited due to the complexity of field data collection. Chen et al. (2013) employed the parameter space EnKF and some variants of ES to characterize the hydraulic conductivity field of an aquifer by assimilating experimental tracer data obtained from the Integrated Field Research Challenge site in U.S. Department of Energy's Hanford 300 Area. Crestani et al. (2015) inferred the vertical hydraulic conductivity distribution of an alluvial unconfined aquifer located in northern Italy by assimilating electrical resistivity tomography data through an EnKF method. Panzeri et al. (2015) coupled a modified ensemble Kalman filter algorithm with stochastic moment equations to estimate aquifer transmissivities by assimilating drawdown data recorded during cross-hole pumping tests in a heterogeneous alluvial aquifer located in Germany. Zovi et al. (2017) combined the normal score EnKF with multiple point geostatistics to retrieve the spatially distributed hydraulic conductivity and the storage coefficients of the same aquifer investigated in Crestani et al. (2015) by assimilating measured groundwater levels. Duan et al. (2022) integrated the transition probability geostatistics and the discrete cosine transform with the ES-MDA to map the hydraulic conductivity of a real karst aquifer using the data from a multiple cross-hole pumping test.

In this work, the ES-MDA is employed to infer the properties of a binary aquifer from concentration data obtained via an experimental tracer test. The data are collected in a laboratory sandbox that mimics a vertical cross-section of an unconfined aquifer. Glass beads of two different diameters reproduce a heterogeneous binary field, and fluorescein sodium salt is used as a tracer. The groundwater flow and transport processes are modeled with MODFLOW (Harbaugh 2005) and MT3DMS (Zheng and Wang 1999), respectively. The software package genES-MDA (Todaro et al. 2022) was used to apply the ES-MDA procedure.

Different approaches are tested to estimate the aquifer parameters. First, the binary pattern of the true field is assumed unknown, and the ES-MDA is applied to directly estimate the hydraulic conductivity field. Another common approach to model subsurface characteristics is the conceptualization of the field using lithotypes or facies; constant properties are assigned to each lithotype. Kalman-based methods are optimal when working with Gaussian distributed parameters, and they are not suitable for estimating categorical variables such as geological lithotypes. To handle the categorical parameter estimation through ES-MDA, it can be coupled with a truncated Gaussian model (Matheron et al. 1987). The main key of the truncated Gaussian model is the definition of the proportion of facies and their spatial distribution. The application of this approach for inverse modelling was first introduced by Wen et al. (2002) as an extension of the self-calibrating approach (Capilla et al. 1998; Wen et al. 1999; Franssen and Gómez-Hernández 2002). Then, the truncated Gaussian models were linked to ensemble-based methods in history-matching problems (Liu and Oliver 2005; Zhao et al. 2008; Agbalaka and Oliver 2008; Zhang et al. 2015), but they have only been applied to synthetic cases and considering the properties of the facies known. In this work, the ES-MDA is coupled with a truncated Gaussian model (ES-MDA-T) to simultaneously estimate the pattern of the aquifer and the hydraulic and transport parameters of each facies.

Both ES-MDA and ES-MDA-T are applied using a fully parameterized approach and a pilot point approach. In the fully parameterized approach, parameters are estimated at each grid cell or element in the model domain. This approach can provide a high level of detail and accuracy, but it can be computationally intensive. In order to reduce the computational demands, a pilot point approach (RamaRao et al. 1995; Gómez-Hernández et al. 1997), which is commonly used for inverse modeling in groundwater (see, e.g. Alcolea et al. 2006; Li et al. 2013; Cao et al. 2018; Keller et al. 2021), can be employed. The pilot point approach involves selecting a few key locations in the model domain where parameters are estimated, and then, using interpolation methods, parameter values at other locations are inferred.

To validate the methods proposed, a synthetic case that reproduces the sandbox experiment is developed and used to test different configurations of the inverse procedures. Then the experimental tracer test data are used to infer the characteristics of the sandbox field.

The paper is organized as follows: the next section presents the ES-MDA procedure and its link with a truncated Gaussian model; section ‘Description of the experiment’ is followed by a summary of all the tests performed using synthetic and experimental data, and the results; and lastly, there is section ‘Discussion and conclusions’.

Methods

The methods applied in this work to solve the inverse problem are based on the ensemble smoother with multiple data assimilation (ES-MDA) technique, in some cases coupled with a Gaussian truncated model. The ES-MDA is a stochastic iterative approach that allows the estimation of a set of unknown parameters and their uncertainty from available observations on the state of the system. The description of the ES-MDA scheme is presented in detail by Emerick and Reynolds (2013), Evensen (2018) and Todaro et al. (2022); here, an overview of the method is given. Then, the link between the truncated Gaussian model and the ES-MDA is presented.

ES-MDA

The ES-MDA is used to solve the inverse problem aimed at estimating the aquifer parameters assimilating observed tracer breakthrough curve data. The vector \(\mathbf{X}\) \(\in {\mathbb{R}}^{{N}_{\mathrm{P}}}\) contains the \({N}_{\mathrm{P}}\) aquifer parameters to be estimated, while the vector of observations \(\mathbf{D}\) \(\in {\mathbb{R}}^{m}\) contains the \(m\) tracer concentrations measured at sparse sampling locations in the aquifer at different times. The method requires the relationship between parameters and observations to be known; this is given by a forward model that simulates the flow (MODFLOW) and transport processes (MT3DMS). The procedure consists of an initialization phase and then proceeds with an iterative loop made up of two steps.

Initialization phase

The first ingredient of the ES-MDA is the definition of an initial ensemble of parameters. The size of the ensemble, \({N}_{\mathrm{e}}\), should be large enough to be a statistical representation of the problem at hand and as small as possible with the aim to limit the computational burden. The characteristics of the initial ensemble of parameters allow one to take into account prior information, when available.

Another preliminary step is to specify an ensemble of measurement errors \({\varvec{\upvarepsilon}}\in {\mathbb{R}}^{m \times {N}_{\mathrm{e}}}\), which are usually assumed to be uncorrelated and drawn from a Gaussian distribution with zero mean and given standard deviation. The ES-MDA also requires defining a priori the number of iterations to be performed, \(N\), and a vector of coefficients \({{\varvec{\upalpha}}=(\alpha }_{1}, {\alpha }_{2}, \dots , {\alpha }_{N})\) that apply to the measurement errors and control the parameter change from one step to another. A gradual decrease of \({\varvec{\upalpha}}\) during the iterative process improves the performance of the method as it gradually reduces the measurement errors helping to avoid overfitting in the first updates. Several schemes can be used to define the set of α, but they must satisfy the condition:

$$\sum\nolimits_{i=1}^{N}\frac{1}{{\alpha }_{i}}=1$$
(1)

After the initialization step, the procedure follows with two iterative steps.

Forecast step

At each iteration \(i\), the state of the system coinciding with the available observations, \({\mathbf{Y}}_{j,i}\), are obtained for each realization \(j\) of the ensemble of parameters, \({\mathbf{X}}_{j,i}\), by means of the forward model:

$${\mathbf{Y}}_{j,i}=\mathrm{g}\left({\mathbf{X}}_{j,i}\right)$$
(2)

where the operator \(\mathrm{g}\left(\bullet \right)\) includes the forward model run and the functions used to extract the predictions at the same spacetime locations where observations were collected.

Update step

During the update step, the ensemble of parameters is updated following the equation:

$${\mathbf{X}}_{i+1}={\mathbf{X}}_{i}+\frac{{\mathbf{C}}_{\mathbf{X}\mathbf{Y}}^{i}}{{\mathbf{C}}_{\mathbf{Y}\mathbf{Y}}^{i}+{\alpha }_{i}\mathbf{R}}\times \left(\mathbf{D}+\sqrt{{\alpha }_{i}}{\varvec{\upvarepsilon}}-{\mathbf{Y}}_{i}\right)$$
(3)

where \({\mathbf{C}}_{\mathbf{X}\mathbf{Y}}^{i}\in {\mathbb{R}}^{{N}_{\mathrm{P}}\times m}\), \({\mathbf{C}}_{\mathbf{Y}\mathbf{Y}}^{i}\in {\mathbb{R}}^{m\times m}\) and \(\mathbf{R}\in {\mathbb{R}}^{m\times m}\) are the cross-covariance between parameters and predictions, the auto-covariance of the predictions and the auto-covariance of the measurement errors, respectively. \(\mathbf{R}\) is a diagonal matrix containing the error variances, \({\mathbf{C}}_{\mathbf{X}\mathbf{Y}}^{i}\) and \({\mathbf{C}}_{\mathbf{Y}\mathbf{Y}}^{i}\) are computed from the parameters and predictions ensembles as:

$${\mathbf{C}}_{\mathbf{X}\mathbf{Y}}^{i}=\frac{1}{{N}_{\mathrm{e}} -1}{\sum }_{j=1}^{{N}_{\mathrm{e}}}\left({\mathbf{X}}_{j,i}-{\overline{\mathbf{X}} }_{i}\right){\left({\mathbf{Y}}_{j,i}-{\overline{\mathbf{Y}} }_{i}\right)}^{\mathrm{T}}$$
(4)
$${\mathbf{C}}_{\mathbf{Y}\mathbf{Y}}^{i}=\frac{1}{{N}_{\mathrm{e}} -1}{\sum }_{j=1}^{{N}_{\mathrm{e}}}\left({\mathbf{Y}}_{j,i}-{\overline{\mathbf{Y}} }_{i}\right){\left({\mathbf{Y}}_{j,i}-{\overline{\mathbf{Y}} }_{i}\right)}^{\mathrm{T}}$$
(5)

where \({\overline{\mathbf{X}} }_{i}\) and \({\overline{\mathbf{Y}} }_{i}\) are the ensemble means of parameters and predictions, respectively.

The procedure repeats until the last iteration after making \({{\mathbf{X}}_{i}=\mathbf{X}}_{i-1}\).

To avoid the appearance of negative values during the update phase, which can be inconsistent for some types of parameters, a space transformation can be applied. In this study, the ensemble of parameters is transformed in the logarithmic space before the update and back-transformed into its physical space after the update.

The total number of runs of the forward model, \({n}_{t}\), required by ES-MDA depends on the ensemble size and the number of iterations: \({n}_{t}=N\cdot {N}_{\mathrm{e}}\). Therefore, it is crucial to use a small ensemble and at the same time avoid undersampling problems, leading to divergence and the appearance of long spurious correlations. Covariance localization approaches can be applied to mitigate the appearance of long-range spurious correlations and to increase the rank of the covariance matrices, which are rank deficient when the number of parameters is higher than the ensemble size (Hamill et al. 2001; Anderson 2007; Chen and Oliver 2010). Covariance localization is applied by element-wise multiplication of the original covariance matrices with chosen correlation matrices reducing the correlations between points for increasing distances and cutting off spurious long-range correlations beyond a specific distance. In this study, the Gaspari and Cohn (1999) fifth-order correlation function is used to compute the elements of the correlation matrices. Furthermore, to avoid overshooting, a linear relaxation can be applied to the ensemble of parameters at the end of each update step:

$${\widehat{\mathbf{X}}}_{i+1}=(1-w){\mathbf{X}}_{i+1}+w{\mathbf{X}}_{i}$$
(6)

where \(w\) is a relaxation coefficient between 0 and 1. The localization distance and the coefficient of the linear relaxation are important tuning parameters in the ES-MDA algorithm that ensure accurate and stable estimates of the state variables. The localization distance could be chosen based on prior information or empirical estimates of the spatial correlation of the system being modeled, such as through variogram analysis, while the coefficient of the linear relaxation should be chosen so as to prevent overcorrection and damping of the ensemble spread. In this study, a combination of a trial-and-error approach and prior knowledge was used to choose these parameters.

The ES-MDA-T: linking the ES-MDA and a truncated Gaussian model

In this paper, the ES-MDA is coupled with the truncated Gaussian model with the aim of characterizing a binary field. The spatial distribution of the two facies and their main properties are simultaneously estimated. The proportion of the two lithotypes is assumed known. The truncated Gaussian model consists of thresholding a Gaussian random function using a threshold defined to match the proportions of the facies.

In this case, the vector of unknown parameters is \(\mathbf{X}=\left({\mathbf{P}}_{1},{\mathbf{P}}_{2}, \mathbf{F}\right)\), where \({\mathbf{P}}_{1}\) and \({\mathbf{P}}_{2}\) are the properties of the two facies to be estimated (e.g. hydraulic conductivities, longitudinal dispersivities of the two facies, etc.), while \(\mathbf{F}=({F}_{1}, {F}_{2}, \dots , {F}_{{N}_{\mathrm{C}}})\) is the vector containing the categorical variables for each cell of the discretized domain. Therefore, the number of unknown parameters \({N}_{\mathrm{P}}\) is equal to the number of aquifer parameters to be estimated (for the two facies) plus the total number of cells of the model grid (\({N}_{\mathrm{C}}\)), corresponding to the categorical variables. The categorical variable can take the values 1 or 2. The cells with categorical value 1 assume the properties \({\mathbf{P}}_{1}\), while the cells with categorical value is 2 assume properties \({\mathbf{P}}_{2}\). The vector of observations \(\mathbf{D}\) is the same as in the previous section.

This procedure allows for estimating categorical variables using the ES-MDA. The modification to the ES-MDA loop to incorporate the truncated Gaussian model into the process is described in the following.

Initialization phase

The initial ensemble of parameters is generated using random values drawn from a Gaussian distribution for the realizations of the aquifer parameters (\({\mathbf{P}}_{1}\) and \({\mathbf{P}}_{2}\)) and random Gaussian fields for the definition of the spatial distribution of the facies; let this initial ensemble of Gaussian random fields be called \(\widetilde{\mathbf{F}}=({\widetilde{F}}_{1}, {\widetilde{F}}_{2}, \dots , {\widetilde{F}}_{{N}_{\mathrm{C}}})\). The proportion between facies must be defined a priori on the basis of available information and expert knowledge. The ensemble of measurement errors and the vector of coefficients \({\varvec{\upalpha}}\) are defined as described in the previous section. The following iterative loop is the same as the standard ES-MDA method, but an additional step named the “truncation step” is introduced before the forecast step.

Truncation step

The truncation step consists of thresholding the Gaussian field to obtain a binary field; this step allows one to transform the continuous variables estimated by ES-MDA into categorical variables. At each iteration \(i,\) and for each realization of parameters \(j\), the categorical field \({\mathbf{F}}_{i,j}\) is obtained by truncating the Gaussian field \({\widetilde{\mathbf{F}}}_{i,j}\) using as threshold the percentile corresponding to the facies proportion. Then, the continuous Gaussian field is transformed into a categorical one by replacing each value of \({\widetilde{\mathbf{F}}}_{i,j}\) with 1, if it is below or equal to the threshold, and 2 otherwise. It must be noted that the threshold is different for each realization and it changes at each iteration in such a way as to guarantee the selected proportion between the two facies, which is fixed. Figure 1 shows an example of a Gaussian field and the associated binary field after truncation.

Fig. 1
figure 1

Example of truncation of a Gaussian field performed considering a facies proportion equal to 76%. a Single realization of a Gaussian field, and b the corresponding lithotypes after truncation

Full size image

Forecast step

At each iteration \(i\), the predictions \({\mathbf{Y}}_{j,i}\) are obtained for each realization \(j\) of the ensemble of parameters, \({\mathbf{X}}_{j,i}=\left({\mathbf{P}}_{1},{\mathbf{P}}_{2}, \mathbf{F}\right)\),

$${\mathbf{Y}}_{j,i}=\mathrm{g}\left({\mathbf{X}}_{j,i}\right)$$
(7)

At each cell of the grid, \({\mathbf{P}}_{1}\) parameters are assigned if the categorical value of the cell is 1, and \({\mathbf{P}}_{2}\) are assigned if the categorical value of the cell is 2.

Update step

During the update step, the ensemble of parameters, \({\widetilde{\mathbf{X}}}_{j,i}=\left({\mathbf{P}}_{1},{\mathbf{P}}_{2}, \widetilde{\mathbf{F}}\right)\) is updated in the continuous space:

$${\widetilde{\mathbf{X}}}_{i+1}={\widetilde{\mathbf{X}}}_{i}+\frac{{\mathbf{C}}_{\mathbf{X}\mathbf{Y}}^{i}}{{\mathbf{C}}_{\mathbf{Y}\mathbf{Y}}^{i}+{\alpha }_{i}\mathbf{R}}\times \left(\mathbf{D}+\sqrt{{\alpha }_{i}}{\varvec{\upvarepsilon}}-{\mathbf{Y}}_{i}\right)$$
(8)

The key difference with the standard implementation is that the updates are applied to the underlying continuous Gaussian fields and not to the conductivity fields, which, in this case, are binary. Then the procedure repeats from the truncation step until the end of the iterative process.

Fully-parameterized and pilot point approaches

The ES-MDA and the ES-MDA-T inverse procedures are applied following a fully parameterized approach and a pilot point approach. In the first case, the aquifer parameters (ES-MDA) and the categorical variables (ES-MDA-T) are estimated at each cell of the grid of the numerical model. In the second case, aquifer parameters and categorical variables are estimated at some pilot points and then interpolated into the rest of the domain. The number and location of pilot points have to be chosen in order to ensure that they capture the relevant heterogeneity of the sandbox field. In this work, the pilot points are evenly distributed in space with a distance approximately equal to five times the spatial resolution of the model grid. After each update step, the full map of parameters is obtained by assigning to each cell of the model grid the value of the closest pilot point. This type of interpolation will result in a blocky distribution of the conductivities.

Description of the experiment

Sandbox experiment

The tracer test used to collect the observations to solve the inverse problem is performed in a laboratory sandbox set up in the hydraulic laboratory of the University of Parma, Italy (Fig. 2). The experimental device mimics a vertical cross-section of an unconfined heterogeneous aquifer and the device has been used to develop several laboratory tests (Citarella et al. 2015; Cupola et al. 2015; Chen et al. 2018, 2021, 2023; Todaro et al. 2021). The sandbox has a width of 120 cm, a height of 73 cm, and a thickness of 14 cm; it is made of polymethyl methacrylate (PMMA) plates with a thickness of 2 cm for the lateral sides and 3 cm for the bottom lid. The sandbox is divided into three parts along the longitudinal direction: an upstream tank, a central chamber that contains the porous medium and a downstream tank. The flow into the experimental device is governed by the water levels at the upstream and downstream tanks, which are equal to 62.5 and 61 cm above the horizontal bottom of the tank, respectively. The porous media consists of glass beads with two different diameters of about 1 and 4 mm, which reproduce a binary field. Fluorescein sodium salt is employed as the conservative tracer. The PMMA walls of the device allow one to collect concentration data by interpreting pictures taken during the experiment. The picture RGB values are converted to concentrations through an image processing technique (Citarella et al. 2015).

Fig. 2
figure 2

Picture of the front side of the experimental sandbox (photo by authors). The red rectangle outlines the area where experimental data are collected

Full size image

At the beginning of the experiment (initial condition) the porous medium within the sandbox had a homogeneous concentration of fluorescein sodium salt of 25 mg/L. The tracer test performed had a duration of 4,000 s; during this time the fluorescein concentration progressively decreases within the sandbox as clean water enters the system. The experiment ended when tracer concentration was zero everywhere. Pictures are collected with a time step of 5 s and converted in concentration data at each pixel of the images. Breakthrough curves recorded at 64 monitoring points with a discretization time of 75 s are used as observations in the inverse procedure. For example, Fig. 3 shows the concentration fields obtained from the analysis of the images in four instants from the beginning of the test.

Fig. 3
figure 3

Concentration field (C) from the image process collected a 250 s, b 500 s, c 1,500 s and d 2,250 s after the start of test. Flow direction is from left to right. The black dots indicate the monitoring points where observations are collected to perform the inverse procedure

Full size image

During the experiment, the flow stopped accidentally for about 855 s after 985 s since the start of the test. This was likely caused by a clogged drain in the downstream tank leading to a rise in the downstream water level and resulting in no gradient in the sandbox during the clogging period. The model that simulates the experiment also takes into account the period of no-flow considering a transient boundary condition downstream. Groundwater flow and mass transport were modeled with MODFLOW 2005 and with MT3DMS, respectively. The domain is discretized into a uniform grid of 1-cm resolution (70 layers, 97 columns and 1 row).

Synthetic experiment

Before applying the different methods to the sandbox experiment, a synthetic case was performed with the aim of evaluating the capability of the proposed approaches to infer the aquifer characteristics and find the optimal configuration of the inverse algorithm. The synthetic case mimics the sandbox experiment; the reference hydraulic conductivity field is depicted in Fig. 4. It is a binary field characterized by two different facies, named Facies 1 and Facies 2. The same numerical model developed to simulate the experimental test is used as a forward model; the reference solution is obtained using the parameters reported in Table 1. The observed concentrations used for the inverse modeling are collected at the same spacetime locations considered for the experimental data: 64 breakthrough curves discretized in 54 time steps.

Fig. 4
figure 4

Reference conductivity field of the synthetic case. Light gray represents Facies 1, dark gray represents Facies 2. Black squares indicate the monitoring points

Full size image
Table 1 Transport and hydraulic parameters of the numerical model used to set up the synthetic case study. HK is the horizontal hydraulic conductivity, VK is the vertical hydraulic conductivity, n is the porosity, Ss is the specific storage coefficient, αL is the longitudinal dispersivity and αT is the transverse dispersivity
Full size table

Applications

Several tests were performed to compare the different approaches and the different settings of the ES-MDA algorithm. The analyses were initially performed using the dataset of the synthetic experiment and then the laboratory data. For all tests, the observations used in the inverse modeling are the breakthrough curves collected at the 64 monitoring points depicted in Fig. 4 and discretized in 54 time steps (the number of observations m is 3,456). The first analyses employ the ES-MDA to estimate directly the hydraulic conductivity field (\({\mathrm{HK}}_{1}\), \({\mathrm{HK}}_{2}\), …, \({\mathrm{HK}}_{{N}_{\mathrm{P}}}\)), assuming the other parameters are known. Then, the ES-MDA-T method is used incorporating the extra information that the medium is binary and, therefore, it focuses on identifying the spatial distribution of the two facies (\({F}_{1}\), \({F}_{2}\), …, \({F}_{{N}_{\mathrm{C}}}\)) and five aquifer parameters: the hydraulic conductivity (HKF1 and HKF2) and longitudinal transport dispersivity (αL,F1 and αL,F2) of the two facies, as well as the ratio between the transversal and longitudinal dispersivity (αT/αL), which is equal for the two facies. The porosity is fixed and homogeneous over the entire domain, as it is determined by the packing method rather than the size of the glass beads. Previous studies demonstrated that the porosity of uniformly random-packed spherical beads is about 0.37 (Beavers et al. 1973; Citarella et al. 2015). The proportion between the two facies is assumed known for all tests and equal to 76% for Facies 1 and 24% for Facies 2.

Both the ES-MDA and the ES-MDA-T methods are applied using a fully parameterized approach and a pilot point method aimed at reducing the number of unknown parameters. For the fully parameterized approach, the parameters are estimated at each cell of the model grid (\({N}_{\mathrm{P}}\) = 6,790 for the ES-MDA, \({N}_{\mathrm{P}}\) = 6,795 for the ES-MDA-T); for the pilot point method, the parameters are estimated at 266 points uniformly distributed over the field (\({N}_{\mathrm{P}}\) = 266 for ES-MDA, \({N}_{\mathrm{P}}\) = 271 for ES-MDA-T). The ensemble size considered (number of realizations of parameters) is 1,000 for the fully parametrized approach and 100 for the pilot point one.

For all tests, the measurement error ε is normally distributed with zero mean and variance 5⋅10–2 mg/L. ES-MDA and ES-MDA-T are run with six iterations and decreasing α = [364; 121.3; 40.4; 13.5; 4.5; 1.5]. Covariance localization is applied considering the aforementioned tapering functions that gradually reduce the correlations based on the spatial distance between parameters and predictions and between predictions themselves. The covariance matrices are modified by applying scale factors from 1 (no-correction) to 0 (zero correlation) for distances from 0 to 120 cm. The linear relaxation is applied with the coefficient w = 0.2 for the synthetic data and with w = 0.25 for the experimental data. The specific configuration of each test and the results are presented in the following.

Synthetic case study

Test 1.1: ES-MDA for estimation of the hydraulic conductivity field following a fully parameterized approach

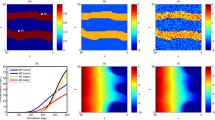
The ES-MDA is applied for the estimation of the hydraulic conductivity field in each cell of the model domain considering the remaining hydraulic and transport parameters are known. Two tests were performed starting from different types of an initial ensemble of parameters, all other variables being equal. The size of the ensemble is 1,000 for both tests. The first test (test 1.1A) uses homogeneous fields as the initial ensemble of parameters; the hydraulic conductivity of each realization is constant and selected randomly from a uniform distribution, HK ∈ U[0.1,9]. For the second test (test 1.1B), the initial ensemble of parameters is made up of Gaussian fields generated using isotropic exponential variograms with random parameters: the mean μ, variance σ and range of correlation h are drawn from the following uniform distributions: μ ∈ U[0.5,0.7], σ ∈ U[60,365], h ∈ U[0.05,2]. Figure 5 shows some realizations of the initial ensembles of parameters and the results of the inverse procedure for both tests. The results refer to the mean field obtained from the ensemble at the last iteration of the ES-MDA procedure. A map of the coefficient of variations is also reported. The RMSE between the observed and predicted concentrations is 2.7 and 2.1 mg/L for test 1.1A and test 1.1B, respectively.

Fig. 5
figure 5

Test 1.1: Examples of realizations of the initial ensemble of parameters for test 1.1A and test 1.1B (left); estimated horizontal hydraulic conductivity (HK) fields in terms of ensemble mean (middle) and map of the coefficient of variation (CV) (right). The black squares indicate monitoring points. The solid line reproduces the outline of the two facies of the actual field

Full size image

Test 1.2: ES-MDA for estimation of the hydraulic conductivity using a pilot point approach

The ES-MDA is applied for the estimation of the hydraulic conductivity field at 266 pilot points (Fig. 6). The ensemble size is 100; the initial realizations of parameters are a subset of the ensemble used in test 1.1B, from which the values at the pilot point locations were selected.

Fig. 6
figure 6

Test 1.2: Estimated binary field by means of ES-MDA using a pilot point approach: a the ensemble mean (horizontal hydraulic conductivity, HK) and b the coefficient of variation (CV). The black dots indicate the pilot points

Full size image

Figure 6 shows the mean field obtained from the ensemble at the last iteration and the map of the coefficient of variation computed from the ensemble. The RMSE between observed and predicted concentrations is 2.1 mg/L.

Test 1.3 ES-MDA-T for characterization of the binary field following a fully parameterized approach

The ES-MDA is linked with the truncated Gaussian model to simultaneously estimate the spatial distribution of the two facies and their main properties. In test 1.3, the fully parameterized approach is adopted. The ensemble size is 1,000 and the initial realizations of the hydraulic and transport parameters of the two facies are drawn from Gaussian distributions with different mean and variance defined as follows: HKF1 ∈ \(\mathcal{N}\)[0.7,0.01]; HKF2 ∈ \(\mathcal{N}\)[7,1]; αL,F1 ∈ \(\mathcal{N}\)[0.1,4·10–3]; αL,F2 ∈ \(\mathcal{N}\)[0.2,4·10–3]; αT /αL ∈ \(\mathcal{N}\)[0.05, 1·10–3]. The initial realizations of the field \(\widetilde{\mathbf{F}}\) are Gaussian random fields with zero mean and standard deviation of 1 generated using isotropic Gaussian variograms with correlation range randomly selected from a uniform distribution h ∈ U[10,60].

Figure 7 shows the solution in terms of the probability field derived from the ensemble of realizations. Each cell is assigned a value between 0 and 1, which represents the probability of that cell being associated with Facies 2. Since the field is binary, values close to 1 indicate a high probability of having Facies 2, while values close to 0 indicate a high probability of having Facies 1. For most cells, the true categorical variable is estimated in almost all realizations; the lowest agreement between the ensemble realizations, denoted by probabilities around 0.5, is found at the interface between the two materials. Table 2 summarizes the actual and estimated hydraulic and transport parameters with their uncertainty; the approach shows very good performance in reproducing all the properties of the two facies. The RMSE between the observed and predicted concentrations is equal to 1.53 mg/L.

Fig. 7
figure 7

Test 1.3: Probability field of Facies 2. Black squares indicate monitoring points. The solid line reproduces the outline of the two facies of the actual field

Full size image
Table 2 Test 1.3: Actual and estimated parameters of the two facies. The ensemble mean and the 95% uncertainty interval are reported
Full size table

Test 1.4 ES-MDA-T for characterization of the binary field using the pilot point approach

Test 1.3 is repeated using the pilot point method. The initial ensemble of parameters is made up of 100 realizations that are a subset of the initial ensemble of test 1.3: the values at the pilot point locations are extracted from the fully parametrized field. Figure 8 shows the resulting probability field. Most of the true categorical parameters are well reproduced by all the ensemble realizations in almost the whole field. The hydraulic and transport parameters of the two facies are reported in Table 3. The RMSE between the observations and predictions is equal to 2.2 mg/L.

Fig. 8
figure 8

Test 1.4: Probability field of Facies 2. Black dots indicate the pilot points. The solid line reproduces the outline of the two facies of the actual field

Full size image
Table 3 Test 1.4: Actual and estimated parameters of the two facies. The ensemble mean and the 95% uncertainty interval are reported
Full size table

Experimental case study

The results obtained from the synthetic case analyses pointed out that the best performance is achieved using the ES-MDA-T approach. Therefore, tests performed using data from the sandbox experiment only consider the approach that links ES-MDA with the truncated Gaussian model.

Test 2.1: ES-MDA-T for characterization of the binary field following a fully parameterized approach

The ES-MDA-T method is applied for the simultaneous estimation of the spatial distribution of the two facies and their properties using the experimental data. The same settings and ensembles of the synthetic test 1.3 are used. Figure 9 shows the estimated probability field. The estimated hydraulic and transport parameters with their uncertainty are reported in Table 4. The RMSE between the observed and predicted concentrations is equal to 3.2 mg/L.

Fig. 9
figure 9

Test 2.1: Probability field of Facies 2. The black squares indicate monitoring points; the dashed line denotes the portion of the field where experimental data are available. The solid line reproduces the outline of the two facies of the actual field

Full size image
Table 4 Test 2.1: Estimated parameters of the two facies. The ensemble mean and the 95% uncertainty interval are reported
Full size table

Test 2.2: ES-MDA-T for characterization of the binary field using a pilot point approach

In the second experimental case study, the same configuration of test 1.4 is employed. The inverse problem is solved by means of the pilot point method. The results are depicted in Fig. 10; only a portion of the field is well reproduced. In particular, the ES-MDA-T approach fails to correctly estimate the actual categorical variable for the upper part of the field where no observation data are available. Table 5 reports the estimated hydraulic and transport parameters with their uncertainty. The RMSE between the observed and predicted concentrations is equal to 2.9 mg/L.

Fig. 10
figure 10

Test 2.2: Probability field of Facies 2 Black dots indicate the pilot points; the dashed line denotes the portion of the field where experimental data are available

Full size image
Table 5 Test 2.2: Estimated parameters of the two facies. The ensemble mean and the 95% uncertainty interval are reported
Full size table

Test 2.3: ES-MDA-T for characterization of a three-facies field following a parameterized approach

The third test is performed considering that the experimental field is made of three materials. This follows the assumption that there is a mixing zone at the interface between the two facies made up of 1 mm or 4 mm diameter glass beads. The mixing zone, named Facies 3, has different characteristics from Facies 1 and Facies 2. The ES-MD-T is applied to estimate the spatial distribution of the three facies and their properties. The vector of unknown parameters is \(\mathbf{X}=\left({\mathbf{P}}_{1},{\mathbf{P}}_{2}, {\mathbf{P}}_{3}, \mathbf{F}\right)\), where \({\mathbf{P}}_{1}\), \({\mathbf{P}}_{2}\) and \({\mathbf{P}}_{3}\) are the vectors containing the parameters of the three facies, \(\mathbf{F}\) is the vector of categorical variables for each cell of the discretized domain. The categorical variable can take the values 1, 2 or 3. The cells with categorical value 1 assume the properties \({\mathbf{P}}_{1}\), the cells with categorical value 2 assume the properties \({\mathbf{P}}_{2}\), and when the value is 3, the parameters \({\mathbf{P}}_{3}\) are used. The vector of observations \(\mathbf{D}\) is the same as the previous experimental tests. The truncation of the Gaussian field is performed defining two thresholds that match the proportions between the three facies. It is assumed that the 75% of the field is occupied by Facies 1, 17% by Facies 2 and 8% by Facies 3. The two thresholds are equal to the 75th-percentile (Thr1) and 83th-percentile (Thr2) of the values of the Gaussian field to be truncated. The continuous variables of the Gaussian function are transformed into categorical variables replacing each value with 1 if it is below Thr1, 2 if it is above Thr2 and 3 otherwise. The same settings and initial ensemble of test 2.1 are employed, but two additional parameters are estimated: the hydraulic conductivity (HKF3) and longitudinal dispersivity (αL,F3) of Facies 3. The initial ensemble of the properties of Facies 3 are drawn from Gaussian distributions with different mean and variance defined as follows: HKF3 ∈ \(\mathcal{N}\)[5, 0.5] and αL,F3 ∈ \(\mathcal{N}\)[0.4,0.05].

Figure 11 reports the results of the inverse procedure in terms of the best estimate represented in each cell by the mode of the ensemble of parameters. Table 6 reports the estimated hydraulic and transport parameters with their uncertainty for the three facies. The RMSE between the observed and predicted concentrations is 3.2 mg/L.

Fig. 11
figure 11

Test 2.3: Estimated three-facies field by means of the ES-MDA-T method using experimental data. The black squares indicate monitoring points; the dashed line denotes the portion of the field in which experimental data are available. The solid line reproduces the outline of the two facies of the actual field

Full size image
Table 6 Test 1.3: Estimated parameters of the three facies. The ensemble mean and the 95% uncertainty interval are reported
Full size table

Discussion and conclusions

The ensemble smoother with multiple data assimilation was applied to characterize a binary aquifer by means of experimental tracer test data. First, the ES-MDA was used to infer the hydraulic conductivity field unaware that it was binary and assuming the rest of the hydraulic and transport parameters are known. Then, the ES-MDA was linked with a truncated Gaussian model for the simultaneous estimation of categorical variables, which reproduce the two-facies field, and the properties of each facies. A fully parameterized approach and a pilot point approach were considered in the analysis. Initially, a synthetic case study that mimics the laboratory experiment was developed to test the capability of the proposed procedures. It is noteworthy that the observation errors assumed for the synthetic case are large and comparable with the experimental ones used for the laboratory case study. Test 1.1 aimed at the estimation of the hydraulic conductivity field using a fully parameterized approach by assimilating observed breakthrough curves. The effect of the characteristics of the initial ensemble of parameters was investigated: test 1.1A was performed considering an initial ensemble consisting of random homogeneous fields, while test 1.1B considers Gaussian fields generated using exponential variograms with random parameters. The results show that test 1.1B performs better in terms of RMSE between the observed and predicted concentrations. Test 1.1A estimates a smoother field than test 1.1B; the portions of the field with low and high permeability are fairly identified, but not the actual distribution of the two facies. In contrast, test 1.1B better reproduces the complexity of the actual field and the discontinuities between the two facies. In both tests, the coefficient of variation is higher at the top and bottom of the field, due to the absence of observation points in these portions of the aquifer. Therefore, the initialization of the procedure, in terms of the initial ensemble of parameters, affects the solution. This is stressed by the ensemble size; the smaller it is, the more the solution may depend on the initial configuration. The size of the ensemble should be related to the number of parameters to be estimated; in this case, the number of realizations is equal to 1,000, and the number of parameters to be estimated is 6,795. This may lead to rank-deficient covariance matrices, since they are computed from the ensembles, and therefore covariance localization techniques must be used to mitigate this effect. Hence, the use of a well-defined initial ensemble of parameters and covariance localization techniques allows for reducing the number of realizations. This leads to a remarkable reduction of the computational burden. For instance, a gradient-based optimization method needs to run the forward model at least as many times as the number of parameters, per iteration. The ES-MDA requires running the forward model a number of times equal to the ensemble size, for each iteration. In this case, the ES-MDA computational effort is 85% less than that required by a gradient-based method.

With the aim to further reduce the computational time, test 1.2 was performed similarly to test 1.1, following a pilot point approach. The hydraulic conductivity is estimated in 266 pilot points applying the ES-MDA method with an ensemble size equal to 100. The performance metrics are comparable with those obtained with the fully parameterized approach. The main features of the binary field are reproduced, but the results are less accurate than the previous test.

The following tests were performed taking into account the binary distribution of the sandbox field. ES-MDA was coupled with a truncated Gaussian model to simultaneously estimate the distribution of the facies and their main hydraulic and transport parameters. ES-MDA-T was first applied following the fully parametrized approach (test 1.3). The results reproduce well the actual field with high accuracy as well as the true parameters of each facies. This test was repeated following the pilot point approach (test 1.4), reaching good results, but with a larger error in the reproduction of the breakthrough curves compared with test 1.3. Both test 1.3 and test 1.4 performed better than test 1.1 and test 1.2, suggesting that the ESMDA-T approach is better than the standard ES-MDA one in reproducing the characteristics of a binary field. In addition, ES-MDA-T has the advantage of being able to simultaneously estimate more properties of the aquifer. This estimation could be computationally prohibitive with the ES-MDA approach, as each aquifer parameter has to be estimated at each cell (or each pilot point), resulting in a huge number of parameters to be estimated. Furthermore, the estimation of different aquifer parameters for each cell can lead to equifinality problems and unreliable solutions. Test 2.1 and test 2.2 were performed using the experimental sandbox data using the optimal configuration obtained from the synthetic cases (test 1.3 and test 1.4). The ES-MDA-T method achieves good results, but with lower performance than that obtained for the synthetic cases. This could be due to epistemic errors in both the experimental data and the forward model structure. ES-MDA-T allows one to reproduce the main features of the field and the estimated hydraulic and transport parameters for the two facies are reasonable and close to those expected.

In general, the results obtained following the pilot point approach are comparable with those achieved by the fully parametrized one, but they show less detailed and less accurate representation of the parameter field. However, compared to the fully parameterized approach, the pilot point method significantly reduces the required computational time by up to 90%. It is noteworthy that the number and location of the pilot points, as well as the interpolation method adopted, may affect the final results of the inverse procedure. Further investigations will focus on varying the pilot point configuration with the aim to find the optimal one considering the trade-off between the computational cost and the accuracy of the results. The last test (test 2.3) was performed assuming that the actual field is made up of three materials, where the third material is generated by a mixing zone at the interface between the two facies. The ES-MDA-T approach is applied using a simple truncated Gaussian model that ensures that the three facies occur in the same sequential order; the results are comparable with those obtained for test 2.1.

For more complex fields, truncated pluri-Gaussian methods can be implemented to reproduce more than two facies and different types of contacts between them. Future work will investigate this aspect by carrying out new laboratory experiments on more complex fields.