Introduction

Aquitards are important hydrogeological features, as they play a key role in groundwater resource assessment (Gurwin and Lubczynski 2005), contamination transport (Ponzini et al. 1989), land subsidence (Zhuang et al. 2017), salinization (e.g. Van et al. 2022) subsurface energy storage (Sommer et al. 2015) and radioactive waste disposal (Hendry et al. 2015). Although the importance of aquitards is widely recognized (Hart et al. 2006; Keller et al. 1989), many stochastic evaluations of hydrogeological field studies focus on the characterization of aquifers and neglect aquitards (Fogg and Zhang 2016). This study aims to improve the stochastic parameterization of aquitards specifically.

To parameterize the hydraulic conductivity of hydrogeological units, typically in-situ-field-scale measurements, such as slug and pumping tests, are performed (Hantush and Jacob 1955; Keller et al. 1989; Neuman and Witherspoon 1972). However, the drawdown is generally only measured in the pumped aquifer and experiments are typically not run long enough to detect drawdowns outside the pumped aquifer, which results in poor estimates of aquitard parameters compared to aquifer parameters (Fogg and Zhang 2016; Neuzil 1986, 1994). Also, the aquifers and aquitards are typically assumed to be homogeneous and the flow to be axisymmetrical, yielding biased and ambiguous results (Berg and Illman 2015; Huang et al. 2011; Kuhlman et al. 2008; Wen et al. 2010; Wu et al. 2005). Thus, if identified at all, mean values of the aquitard’s hydraulic resistance do not provide information about spatial variability nor a measure of uncertainty of pumping test results. There are a few studies that performed stochastic analysis of pumping tests to identify correlation lengths (Demir et al. 2017; Firmani et al. 2006; Neuman et al. 2004; Zech et al. 2015); however, they focused on aquifers rather than aquitards. For cases where the description of the hydraulic conductivity of an aquitard needs to include spatial variability, methods have been developed to connect local measurements to a subregional variability or to regional-scale representative values within a geostatistical framework (De Marsily et al. 2005 and references therein). These local measurements typically consist of permeameter tests on core-scale samples (Alexander et al. 2011; Bierkens 1996; Keller et al. 1989). These tests may yield values that are not in line with field or model block-scale conductivities (Alexander et al. 2011; Batlle-Aguilar et al. 2016; Gerber et al. 2001; Hart et al. 2006; Zhao and Illman 2018), which can be caused by stress perturbations during collection, transportation and laboratory installation (Clark 1998) as well as geological heterogeneities which are not represented in the samples, such as fractures, dikes, sand streaks and interbeds (Hart et al. 2006; Keller et al. 1989; Van Der Kamp 2001; Bierkens and Weerts 1994; Meriano and Eyles 2009). Because of the latter, geostatistical upscaling is needed to relate the core-scale measurements to larger scales (Sanchez-Vila et al. 2006 and references therein), which is typically done by generating hydraulic conductivity realizations from core-scale measurement distributions with a certain spatial correlation, and running a groundwater flow model to derive the block-scale hydraulic conductivity (e.g. Pickup et al. 1994; Sarris and Paleologos 2004; Fleckenstein and Fogg 2008). In this way spatial variability in lithology and corresponding hydraulic conductivity can be accounted for; however, information about the vertical and lateral correlation lengths of the lithology or its corresponding hydraulic conductivity multi-point probability distributions needs to be known to adequately upscale the hydraulic conductivity from core to model block-scale within a geostatistical framework.

A large amount of data is needed to derive semivariograms (Weerts and Bierkens 1993) and accurate probability density functions (Khan and Deutsch 2016). If this is not available, estimates have to be used based on expert geological knowledge. However, inaccurate semivariograms, and in particular semivariogram ranges or correlation lengths, result in inaccurate block-scale hydraulic conductivity values. This is especially an issue with aquitards, as the core-scale hydraulic conductivity values of aquitard material, such as clay and peat, can vary several orders of magnitude (Neuzil 1994).

The objective of this study is to combine pumping tests and geostatistical upscaling to investigate whether pumping test observations can be used to obtain information about the spatial correlation of the lithology within aquitards. The procedure can be used to inversely estimate aquitard geostatistics. The paper is organized as follows. In the method section, the pumping test setup and the geological architecture of aquitards and aquifers at the site are described. Next, the core-scale conductivity data deemed representative of the aquitard under study, the groundwater flow model used and the stochastic method to estimate unknown correlation lengths of the aquitard are introduced. Following, the results are presented, which are then discussed in detail. The paper closes with a summary and conclusions.

Methods

Pumping test site and setup

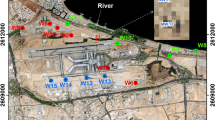
A pumping test was performed at a site in Schouwen-Duiveland, province of Zeeland, in the southwestern Netherlands (Figs. 1 and 2). Three aquifers and three aquitards are present at this location. A schematic profile of the geology and lithology at the test location is shown in Fig. 3. For the pumping test, one extraction well and four infiltration wells were installed in the second aquifer that lies directly below the aquitard under study (aquitard 2; Fig. 2). The wells were fully penetrating this aquifer. A total of 20 piezometers were installed in the first, second and third aquifers. Five pumping tests were performed with varying configurations concerning discharges and distribution of extracted water over infiltration wells. The discharges during the pumping periods are listed in Table 1.

Fig. 1
figure 1

Location of the pumping test site

Full size image
Fig. 2
figure 2

Configuration of pumping test wells and piezometers. The area as shown in the inset is 25 m × 25 m

Full size image
Fig. 3
figure 3

Hydrogeological schematization of the subsurface at the pumping test site

Full size image
Table 1 Well discharges during pumping tests. Negative values denote extraction, positive values infiltration
Full size table

The second aquitard, the one used for this study, is a Holocene tidal deposit stratigraphically classified as Wormer Member, which is part of the Naaldwijk Formation (TNO-GDN 2022). The well logs provide information about the depth of the aquitard’s top. A gradual transition from sandy to more clayey sediments is observed, while the base of the aquitard is much more pronounced, with an assumed thickness of 3 m (Fig. 3). The probability distribution of the measured core-scale hydraulic conductivities for this unit is bimodal, consisting of an approximately log-normal distribution for sand samples, and 4–5 orders of magnitude smaller log-normal distribution of clay, sandy clay and clayey sand samples (Fig. 4). The core-scale samples have not been collected at the test site, but rather in other locations where the Wormer Member is present. Correlation lengths cannot be directly determined from the samples as they have not been collected at the pumping test location. Instead, they originate from distributed locations several kilometers away from each other, thereby also disabling variogram analysis. The borelog descriptions from the drilling for the pumping test contained insufficient information for determining correlation lengths. The distributions are deemed representative, because of the similar composition and depositional environments between the pumping test site and the Wormer Member at other locations.

Fig. 4
figure 4

Core-scale hydraulic conductivity measurements for clay-rich and sand samples for the Wormer member (aquitard 2)

Full size image

Groundwater flow models

Two groundwater models were created for evaluating the pumping test using MODFLOW 6 (Langevin et al. 2017) with FloPy (Bakker et al. 2016). The first, a reference model, consists of five layers with homogeneous hydraulic conductivity values; the second model is set up with a heterogeneous second aquitard, consisting of multiple layers.

Reference model

The model domain is 4,000 m × 4,000 m and consists of five layers. The computational grid has cells of 160 m × 160 m at the boundaries. Cell size gradually decreases to 5 m × 5 m for the inner domain of 500 m × 500 m around the pumping and extraction wells. Within a radius of 20 m around the wells, the cell size further decreases gradually down to 0.07 m at the wells. All cells that fall within the borehole diameter of 324 mm are given a constant hydraulic conductivity of 500 m/day in the pumped aquifer.

No anisotropy was assumed, as during a pumping test the flow in aquifers is predominantly horizontal, and the flow in aquitards is mainly vertical. The model is calibrated using five periods of pumping. It is assumed the test reaches steady state within each period’s duration. The impact of this assumption is discussed in section ‘Discussion’, and results in five drawdown data points per piezometer. The hydraulic conductivity values for each model layer are obtained by calibration using the Levenberg–Marquardt algorithm (Levenberg 1944; Marquardt 1963) to obtain hydraulic conductivity values of the model layers. As an objective function for the calibration, the root mean squared error (RMSE) is minimized:

$$\mathrm{RMSE}= \sqrt{\frac{1}{5n}\sum\nolimits_{i=1}^{n}\sum\nolimits_{j}^{5}{\left({m}_{ij}-{o}_{ij0}\right)}^{2}}$$
(1)

where n is the number of piezometers, mij is the modelled drawdown and oij is the observed drawdown at piezometer i for configuration j. The piezometers in the active wells are not taken into account to prevent effects regarding non-Darcian flow and discretization issues due to the circular shape of the well, while the model grid consists of squared cells.

Heterogeneous model

The heterogeneous model is a refined version of the reference model. Heterogeneous distributions of hydraulic conductivity values were created for the aquitard of interest (aquitard 2) within the inner domain of 500 m × 500 m around the wells. The aquitard was also subdivided into 30 layers of 0.1 m to increase vertical resolution. All other layers were assigned the hydraulic conductivity values from the calibrated reference model.

The conductivity realizations for the aquitard section were generated by unconditional geostatistical simulation. According to borehole data in the area, the aquitard is composed of 56% clay (this class includes sandy clay and clayey sand) and 44% sand. These two contrasting lithologies result in two well-differentiated distributions of measured core-scale conductivities (Fig. 4). Due to the 4–5 orders of magnitude conductivity contrasts between the two classes, the lithology is assumed to be the main source of the conductivity heterogeneity of the aquitard. Thus, instead of generating hydraulic conductivities, the occurrence of sand and clay were simulated. A spherical indicator semivariogram model of sand/clay occurrence with geometric axisymmetric anisotropy was used, with a larger horizontal than vertical range. The semivariogram range is what is termed “correlation length” in the following. A sequential indicator simulation was applied (Journel and Alabert 1990) using gstat in R (Pebesma 2004) through the Python package rpy2. Horizontal and vertical correlation lengths ranging from 20 to 100 m and 0.5–2 m have been used, respectively. Examples of the generated fields are shown in Fig. 5. A total of 50 realizations were generated for each combination of correlation lengths adding up to 5,850 realizations in total. Because lithology is the dominant source of heterogeneity and because the variation of core-scale hydraulic conductivity within the lithoclasses can be assumed to be much smaller than the cell size (5 m × 5 m × 0.1 m; cf. Bierkens 1996), a constant representative value is assigned to each lithoclass. Here, an analytical formula was used to up scale the core-scale conductivity fluctuations that were proposed by Matheron (1967):

Fig. 5
figure 5

Examples realizations of the aquitard’s sand and clay distribution for three vertical and three horizontal correlation lengths used in the heterogeneous aquitard model. Green represents clay/sandy clay/clayey sand, and yellow represents sand

Full size image
$${K}_{\mathrm{cell}} = {K}_{\mathrm{g}} \times \mathrm{exp}({\sigma }_{Y}^{2}/6)$$
(2)

where Kcell is the resulting cell hydraulic conductivity, Kg is the geometric mean, and σY2 is the variance of the logarithm of the core-scale hydraulic conductivity distribution. This formula assumes the hydraulic conductivity variogram within the cell to be isotropic. Any anisotropy will follow from different horizontal and vertical correlation lengths at the scale of multiple cells and not from within the cells.

Assessment Framework

The performance of the simulated head distribution for each run of the heterogeneous aquifer model is evaluated and ranked according to the RMSE (Eq. 1) between the observed heads of the pumping test and each heterogeneous model realization.

Only the realizations with an RMSE lower than the RMSE of the reference model are evaluated. These realizations account for spatial variability and its uncertainty while outperforming the homogeneous model.

The representative hydraulic conductivities in the aquitard that belong to the best fitting realizations are determined in two ways. First, the drawdown results of each of the realizations are used as a synthetic reality, which are used to calibrate the reference model again to obtain a representative hydraulic conductivity for the entire aquitard. In addition, the representative vertical block hydraulic conductivity of the realizations was computed with a traditional numerical upscaling method. For this, a MODFLOW model with constant head boundaries on the top and bottom of the aquitard at hand is used to model flow through the aquitard under uniform flow conditions. The hydraulic conductivity is calculated from the average flux through the aquitard via Darcy’s law.

Results

Table 2 shows the details of the calibration of the homogenous model. The RMSE of the calibrated homogeneous model is 0.054 m, and there are 209 (out of 5,850) realizations of the heterogeneous model with a lower RMSE than this. Their correlation lengths (L) fall mostly within a range of LH = 20–60 m and LV = 0.875–2.0 m for horizontal and vertical directions, respectively. Details are displayed in Fig. 6. Note that the mean RMSE for each combination of correlation lengths is within a small range from 0.052 to 0.054 m. The maximum number of realizations with identical horizontal and vertical correlation lengths performing better than the homogeneous model is 10 with LH = 50 m and LV = 1.625 m. Low average RMSE values are also mainly located close to these values.

Table 2 Optimization results of homogeneous pumping test model
Full size table
Fig. 6
figure 6

Number of realizations that perform better than the homogeneous model (in terms of RMSE) for each combination of horizontal and vertical correlation length. The size of the dots indicates the number, while the colour indicates the mean RMSE of these realizations

Full size image

The representative aquitard conductivities K of the 209 best fitting realizations are calculated through two upscaling schemes. First, synthetic pumping tests are conducted on the heterogeneous fields and the corresponding representative conductivity for each realization identified. The second way is to run a flow simulation on each realization with a spatially uniform head distribution across the aquitard and identify the corresponding mean conductivity. The resulting frequency distributions of representative K values for the 209 realizations are shown in Fig. 7.

Fig. 7
figure 7

Histogram of hydraulic conductivity for the best fitting realizations using a spatially uniform head difference across the aquitard, and the hydraulic conductivity obtained with the interpretation of a synthetic pumping test. The black line shows the hydraulic conductivity value obtained by calibrating the homogeneous model for the observed drawdowns

Full size image

The results show that the hydraulic conductivity values from the synthetic pumping tests are close to the value found in the actual field pumping test which was identified by calibrating the homogeneous model. However, the upscaling scheme, assuming uniform flow conditions on average (typically the standard procedure), results in representative values spread out over several orders of magnitude, with higher values than found in the pumping tests.

Discussion

Best fits

The suite of best fitting realizations (Fig. 6) belongs to a range of correlation length values rather than a single optimum. There were also realizations with the same combination of correlation lengths that fit the pumping test worse than the homogeneous model. This is partly due to the probabilistic nature of the approach and partly related to the fact that a finite number of realizations have been used in the Monte Carlo approach. A larger number of realizations might have made the location of the optimal values more obvious, but the general pattern is clear. In addition, drawdowns were only measured above and below the aquitard so, in the model, the aquitard may be considered as a single layer. Averaging the internal heterogeneity causes large uncertainties in the correlation lengths. This was also observed in other studies that attempted to determine correlation lengths from field data such as Xiao et al. (2021), Abellan and Noetinger (2010); Gautier and Noetinger (2004); Hoeksema and Kitanidis (1984). The small variation in mean RMSE values in Fig. 6 is partly caused by the use of all piezometers, including those in the pumped aquifer (aquifer 2) and those in the aquifers above (aquifer 1) and below (aquifer 3; see Figs. 2 and 3). Particularly, drawdowns in aquifer 3 are insensitive to changes in the composition of the aquitard. In addition, the average RMSE values in Fig. 6 contain all fits better than the homogeneous model, including realizations that are just slightly better. The results show that for a horizontal correlation length, a limited range of vertical correlation lengths results in a good fit. Lower horizontal correlation lengths are associated with lower vertical correlation lengths; however, the broad range of results indicate that a single semivariogram model does not give the full uncertainty range of the model-block-scale hydraulic conductivity, as the uncertainty of the correlation lengths itself are usually not taken into account in upscaling procedures.

The modelled correlation lengths range from below to above the percolation threshold, which is the point where connected pathways of sand exist from the top to the bottom of the aquitard, forming a connected object (Colecchio et al. 2020, 2021). The results show that the aquitard is close to the percolation threshold as part of the ensemble realizations have percolation, but not in all of them, thus explaining the wide range of correlation lengths that result in good fits. Percolation at larger distances from the well can partially explain the difference between the two representative conductivities in Fig. 7, as it will result in high conductivities for the complete field with uniform flow, but is not observed in the pumping test. In aquitards where the hydraulic conductivity of the lithoclasses is not as well differentiated, percolation will be less of an issue and might lead to smaller ranges of correlation lengths that result in good fits. The representative hydraulic conductivity of the aquitard also depends on the flow pattern, as the interpreted hydraulic conductivity from a pumping test is not identical to that derived from uniform flow (Fig. 7). The representative conductivity from a pumping test is dominated by the heterogeneity close to the pumping wells due to the steep gradients during pumping. Thus, the selection of the best fitted realizations is insensitive to the existence of preferential flow paths in the aquitard at large distances (Copty et al. 2008). However, such high conductivity will increase the representative hydraulic conductivity under uniform flow conditions, which underlines previous findings (Sanchez-Vila et al. 2006; Bierkens and Van der Gaast 1998) that representative hydraulic conductivities are very sensitive to the flow geometry applied and essentially a non-local problem. As shown, this particularly applies to aquitards were differences between representative conductivity for uniform and radial flow can be of orders of magnitude. It is also akin to previous work on aquifer conductivities that distinguish between apparent values close to the pumping test being different than representative conductivities for larger scales (Dagan 2001). Thus, care should be taken when assessing the representative hydraulic conductivity of aquitards from a pumping test with a limited sphere of influence. It is likely that a larger pumping test would be needed to find representative conductivities for strictly vertical flow through the aquitard. For instance, with an aquitard thickness of ~3 m and an aquifer thickness of 11.8 m, the conductivities in Table 2 result in a leakage factor \(\sqrt{\mathrm{KD}\times c}=317\) m (in which KD is the transmissivity and c is the hydraulic resistance), while the dimension of the test site being monitored is 250 m × 250 m. It should be noted that the infiltration wells decrease the area in which vertical flow occurs, diminishing part of this discrepancy. However, the discrepancy suggests that a larger area should be monitored to find representative subregional-scale aquitard conductivities.

Model assumptions

Lithology and geometry of the aquitard

Lithology realizations with a fixed ratio between clay and sand are generated, with a single fixed ratio. The ratio was determined from well logs over the depth interval of the aquitard layer. Assuming this ratio as fixed is the source of uncertainty, as the composition of the subsurface, similar to the locations of the wells, is not randomly selected. Figure 7 shows a discrepancy between the hydraulic conductivity interpreted as a pumping test and with uniform flow conditions. This discrepancy could partially be caused by an overrepresentation of clay near the wells, which is compensated at a larger distance from the wells by an overrepresentation of sand.

A similar reasoning holds for the thickness of the aquitard, which is assumed constant. Assuming the aquitard to be thicker, i.e. counting the entire transition zone to the overlying aquifer, would result in a larger assumed sand fraction. In contrast, assuming a smaller thickness would result in a larger clay fraction, which would change the resulting correlation lengths.

In addition, the hydraulic conductivity is assumed to be constant within the lithology classes in each cell, based on the conductivity distributions of the Wormer Member. In reality the conductivity will differ throughout lithologies, which means additional information about the correlation within lithoclasses needs to be known. However, the variation between the conductivity distributions between the classes clay and sand is much larger than the variation within these classes, entailing that the correlation within the lithoclasses is of less importance for the hydraulic conductivity at field scale.

Also, the hydraulic conductivity at the test location might differ from the distribution of all samples within the Wormer Member. However, to develop a regional groundwater model, some assumptions have to be made; therefore, although the initial assumptions affect the correlation lengths, the proposed method results in correlation lengths that fit the assumed sand and clay fractions with the corresponding aquitard thickness and conductivity distributions.

Discretization

The cell size in the heterogeneous realizations is 5 m × 5 m × 0.1 m. Variation of hydraulic conductivity below that size are not resolved. Correlation lengths, particularly the best fitting ones LH = 20–60 m and LV = 0.875–2.0 m (Fig. 6), are well resolved over several cells to properly represent the variation in lithoclasses. A too small cell size would not only have resulted in much larger run times but would also have invalidated the assumption of a single representative hydraulic conductivity within a cell of a given lithoclass, which is based on the assumption that the correlation length of small-scale variation of conductivity within a lithoclass is smaller than the cell size.

Steady-state assumption

Steady state conditions are assumed, to forego the need for calibrating the specific storage. Reducing the number of parameters reduces the risk of nonuniqueness of the calibration result. The assumption is in line with the pumping test setup. The combination of extraction and re-infiltration results in a steady state after a shorter time period than a conventional pumping test with only extraction. Also, the first time period is long enough to reach steady state. The drawdown in the vicinity of the single extraction well does not change significantly between time periods; thus, the drawdown does not have to completely develop through the aquitard for every configuration.

Pumping test setup

The setting of the pumping test studied here, with multiple infiltration wells and several configurations, increases the model sensitivity to spatial variation in the aquitard beyond the pumping well, whereas it reduces the strong dependence on the composition of the aquitard close to the pumping well as described by Copty et al. 2008. A conventional pumping test, with a single extraction well, favours heterogeneous realizations where the harmonic mean of the hydraulic conductivity values directly at the well equal the conductance value, instead of inferring information about the larger-scale spatial variability. The use of multiple wells results in multiple sensitive regions, which narrows the range of possible heterogeneous realizations that fit the observed drawdowns.

The horizontal correlation lengths of the best fitting realizations are shorter than the distance between the wells, which leaves some uncertainty to the estimate of the correlation length. This uncertainty could be further reduced by increasing the number of infiltration and extraction wells at shorter distance as well as additional (independent) configurations with variations in infiltration and extraction wells—in a similar fashion to hydraulic tomography (Yeh and Liu 2000; Zhao and Illman 2018; Berg and Illman 2013; Poduri and Kambhammettu 2021). Also, the extent of the observation network should exceed the radius in which vertical flow caused by the wells occurs, as determined by the leakage factor, if the intent is to obtain a representative value of aquitard conductivity that represents subregional vertical flow.

The method can be improved for future application by taking additional measurements to assess heterogeneous realizations not only on drawdown observations, but also by including flow velocity and travel time data. This can be achieved by using, e.g., fiber optics (des Tombe 2021) and electromagnetic methods (e.g. Bonnett et al. 2019).

Implications for upscaling and regional parameterization

Correlation lengths of lithologies or hydraulic conductivities are useful information for the stochastic parameterization of heterogeneous aquitards. They also serve to assess the expected range of hydraulic conductivity values at locations where no field-scale data is available to include uncertainty.

The results of this study show that the representative hydraulic conductivity value obtained from a pumping test for a heterogeneous aquitard is not necessarily representative of other flow patterns. Particularly, it does not equal the representative value for uniform flow which is typically needed in regional groundwater flow models. The representative hydraulic conductivity values for uniform flow spread over several orders of magnitude for a limited number of realizations. Thus, its uncertainty is high and typically underestimated by conventional parameterization methods using a single correlation length.

The optimum correlation lengths identified may be transferred to unmonitored locations. A prerequisite is a similar distribution of lithoclasses and the same geological depositional environment. Uncertainty about correlation lengths should be taken into account.

Conclusions

The hydraulic conductivity of aquitards plays an important role in groundwater flow and transport models. The hydraulic parameterization of aquitards is typically done either by interpreting pumping tests, resulting in a single resistivity value, or by geostatistical upscaling, for which information about the scales of spatial variability is needed.

A method is presented to derive correlation lengths of lithoclasses with varying hydraulic conductivities in aquitards from a pumping and injection test. That way, the lithological variation and associated hydraulic conductivity of the aquitard can be parameterized, including spatial variability and uncertainty. Results show that it is not a single value for horizontal and vertical correlation lengths that fits best, but rather a range of equally eligible values. Thus, some uncertainty about the correlation lengths remains.

This information about spatial variability scale and uncertainty is transferable to aquitards of a similar depositional environment and can be used to improve the parameterization in regional groundwater flow models elsewhere.

This study also shows that the representative hydraulic conductivity for an aquitard obtained through a pumping test is not directly representative for other flow patterns. It should therefore be used with care in regional groundwater flow models assuming uniform flow. Thus, it is better to upscale the simulated hydraulic conductivity realizations to representative model block conductivities under the flow conditions expected to be simulated with the groundwater model.