Introduction

There have been numerous cases of environmental and socioeconomic damage resulting from land subsidence associated with groundwater overexploitation (Gambolati et al. 2005; Galloway and Burbey 2011; Bagheri-Gavkosh et al. 2021; Shirzaei et al. 2021). Although it is desirable to take a balance between the benefits of groundwater usage and the damage from land subsidence, it is often difficult to find the optimal groundwater pumping rate because of uncertainty in the hydrogeological structure and the complex mechanisms of land subsidence.

According to Nelson and Quevauviller (2016), the annual amount of groundwater abstraction has been often regulated in many countries to strike a balance between groundwater recharge and abstraction. These regulations aim to control the groundwater level to ensure that it is stable in the long term and to prevent and mitigate land subsidence. However, this kind of regulation has not worked well in terms of land subsidence in some places in which the long-term groundwater level is stable because groundwater recharge and abstraction are already balanced on an annual basis but the land subsidence is associated with seasonal groundwater-level drawdown. Such cases have been reported widely, for example, California (Helm 1975) and Las Vegas (Hoffmann et al. 2001) in the USA, and Shanghai (Liu and Helm 2008b; Ye et al. 2016) and Taiwan (Chang et al. 2004) in China. In such cases, a new groundwater regulation is necessary based on an understanding of the land subsidence mechanism; however, it has not been clear which specific regulations would be effective because the related studies were limited.

The northern Kanto Plain in Japan is one of the typical areas in which there is seasonally progressed subsidence, as described previously. Like large cities in other countries, the Kanto Plain has a large population in the lowland and experienced land subsidence caused by groundwater abstraction before the 1970s (Ishii et al. 1976; Endo 1992; Hayashi et al. 2007). In particular, land subsidence was significant in the coastal area (Ishii et al. 1976; Endo 1992). Various surveys on geology and groundwater use have been conducted, and ground level data, water-level monitoring data at observation wells, and monitoring data by Global Navigation Satellite System (GNSS) and Synthetic Aperture Rader (SAR) have been accumulated (e.g., Ishii et al. 1976; Endo 1992; Sugahara et al. 1992; Sugahara et al. 1995; Nakagawa et al. 2000; Ishitsuka et al. 2016). Because of these efforts and the regulations on groundwater abstraction (e.g., the Industrial Water Law in 1956, the Building Water Law in 1962, and the municipal ordinances), the land subsidence in the coastal area has been mitigated (Endo 1992; Yamamoto 1995; Nakagawa et al. 2000; Endo et al. 2001; Hayashi et al. 2007; Nakajima et al. 2010). However, since the 1970s, the subsidence area has moved northward, and the progress of land subsidence has been continuously observed in agricultural areas in the northern Kanto Plain even though the annual amount of groundwater abstraction is controlled by regulations following the methods used in the coastal areas (Sugahara et al. 1992; Sugahara et al. 1995; Nakagawa et al. 2000; Morita 2015; Ishitsuka et al. 2016).

As a possible cause of land subsidence in the northern Kanto Plain, Sugahara et al. (1995) and Morita (2015) have pointed out reduced recharge due to urbanization. However, this conflicts with the observed hydraulic head data given in Sugahara et al. (1995), where the hydraulic head is found to be stable in the long-term trend, meaning that the annual recharge is sufficient. Note that Morita (2015) did not refer to any hydraulic head data. On the other hand, Sugahara et al. (1992) mentioned that non-agricultural groundwater abstraction from depths of 150–300 m has caused land subsidence. However, Morita (2015) disagreed with this because the amount of groundwater used for industry has been small because of the strict regulations. Notably, existing studies and surveys have not successfully determined the mechanisms of land subsidence in this area, and a numerical model for land subsidence has not been established. Consequently, the current regulations on the total amount of annual groundwater abstraction have not been successful in stopping the land subsidence.

In order to clarify the land subsidence mechanisms and to plan groundwater management strategies affecting the control of future subsidence, numerical modeling, including calibration and application to the interpretation of monitoring data, is essential (Fokker et al. 2018). Consequently, various calibration techniques have been proposed and an appropriate method has been used depending on the situation and purpose—for example, Hoffmann et al. (2003) used UCODE (Poeter and Hill 1998) based on a modified Gauss-Newton method for a study in Antelope Valley, California. Liu and Helm (2008a) suggested the Newton-Raphson method with the initial parameters estimated by graphical preanalysis. Liu and Helm (2008b) and Luo et al. (2016) applied this method in the field at a site in Shanghai. Hung et al. (2012) used a genetic algorithm, one of the evolutionary algorithms, in combination with multilayer compaction monitoring data in central Taiwan. These studies succeeded in calibrating a land subsidence model that satisfactorily reproduced the observed subsidence. More recently, Zoccarato et al. (2016) used an ensemble smoother in the upper Adriatic sedimentary basin (Mediterranean region) and Aichi (2020) used the null-space Monte Carlo method in Kameido, Tokyo (Japan), both were utilized for considering the model’s predictive uncertainty.

The objectives of this study are to elucidate the land subsidence mechanisms in the northern Kanto Plain and to examine effective groundwater management strategies to mitigate the seasonally progressive land subsidence. For this purpose, this study also develops an inversion procedure of an evolutionary algorithm (EA) to calibrate the long-term land subsidence model. EA has an advantage over deterministic algorithms such as Gauss-Newton and Newton-Raphson when the target problem is disturbed by noise (Fogel 1994). The robustness of the EA is considered suitable for situations where available observation data are limited, which is a typical difficulty in land subsidence studies, including this study. Although a genetic algorithm has already been used to calibrate the land subsidence model (Hung et al. 2012), the details of the algorithm are not provided, and its performance is not clear. Therefore, this study provides valuable insight into the use of EA to calibrate the land subsidence model.

Study area

As a subsidence case typical of the northern Kanto Plain, Kawajima, a town located in Saitama prefecture, Japan, was chosen as the study site. Figure 1a–c shows the location and geological map of the Arakawa Lowland and surrounding area, and Kawajima is located in the middle part of the Arakawa Lowland. The Arakawa Lowland is orientated in the northwest–southeast direction along the Arakawa River. The eastern side is bordered by uplands of Pleistocene age, and the western side is bordered by uplands and hills also of the Pleistocene. To the northwest of Kawajima, consolidated sediments of Neogene and Pre-Neogene are found at the surface. The surface lithology can be confirmed from the surface geological map of the 1:50,000 Fundamental Land Classification Survey, Saitama, provided by the Ministry of Land, Infrastructure, Transport and Tourism (MLIT 1973). According to this map, Neogene and Pre-Neogene are composed of conglomerates. The surface of Pleistocene uplands is the Kanto Loam formation, composed of loamy sand and clay overlying the marine sediments of sand and clay alterations. Sediments covering the Arakawa Lowland are fluvial Holocene with 25–30 m thickness (Ando and Fujimoto 1990; Ando and Houtigai 1997; Ishihara et al. 2011; Komatsubara 2014). These Holocene sediments consist of soft layers of clay and sand overlying a basal gravel layer. As the hydrostratigraphic cross-section (Fig. 2a,b) shows, unconsolidated Holocene sediments are widely distributed in the surface layer of the Arakawa Lowland, which is confirmed by data from more than 3,000 shallow boreholes (Ishihara et al. 2011), indicating the high potential of land subsidence caused by the groundwater abstraction.

Fig. 1
figure 1

a Location of the Kanto Plain. b Location of the northern Kanto Plain. Modified from the 1:500,000 digital elevation topographic map of Kanto-Koushinetsu region provided by the Geospatial Information Authority of Japan (GIAJ 2021). The definition of the northern Kanto Plain in this study is based on the Outline of Measures to Prevent Land Subsidence by the Ministry of Land, Infrastructure, Transport and Tourism of Japan (MLIT 2008). c Geological map of the Arakawa Lowland and surrounding area, including study site, Kawajima, and the location of Kawajima land subsidence observatory. Modified from the 1:200,000 seamless digital geological map of Japan V2 provided by the National Institute of Advanced Industrial Science and Technology, Geological Survey of Japan (AIST 2017). The black solid line shows the border of Kawajima. The coordinate system is WGS 1984/UTM zone 54N. Line N–S and line E–W represent the traces of the hydrostratigraphic sections in Fig. 2

Full size image
Fig. 2
figure 2

Hydrostratigraphic cross-section across Kawajima in a east–west and b north–south directions, based on the geological map accompanying the Geological Survey Report of Kawajima Land Subsidence Observatory (WQCD 1985)

Full size image

A summary of the geological information and groundwater usage is represented in Fig. 3. Groundwater use in Kawajima is mainly for agriculture, derived from shallow wells (see section ‘Groundwater uses in Kawajima’ for details). The hydraulic head has been increasing long-term, but it contains significant seasonal fluctuations, decreasing between June and August (summer) and increasing between December and February (winter). These characteristics are common in significant subsidence areas in the northern Kanto Plain, northern Saitama, southern Gunma, and southwestern Tochigi prefectures (Sugahara et al. 1992). Therefore, the model for Kawajima is expected to contribute to the understanding of subsidence in other locations in the northern Kanto Plain. In addition, Kawajima has a land subsidence observatory near the center of the town (Fig. 1c), and a detailed geological column of the monitoring well shown in Fig. 4 is available (WQCD 1985). Since April 1987, the Kawajima land subsidence observatory has observed hydraulic head and land subsidence with an extensometer. The observatory has three observation wells of different depths: well No. 1 has 300 m depth, No. 2 has 190 m depth, and No. 3 has 80 m depth, which is the modeling target in this study (Fig. 5). A comparison of the subsidence at each well can help to characterize the deformation of the section between well-bottoms. For these reasons, Kawajima was chosen as the study site.

Fig. 3
figure 3

Summarized information from section ‘Study area’. Annual amount of groundwater abstraction and depth distributions of well screens for deep wells with unknown purpose, and wells for tap water supply and agriculture in Kawajima. Screen depth and stratigraphic column of well nos. 2 and 3 in Kawajima land subsidence observatory are also shown. Modeling target of this study is well No. 3 with 0–80 m depth

Full size image
Fig. 4
figure 4

Chronostratigraphy, hydrostratigraphy, and screen depths of three observation wells in Kawajima land subsidence observatory. Depth of screen is 249–258 and 274–287 m for well No. 1, 143–154 m for well No. 2, and 41–63 m for well No. 3

Full size image
Fig. 5
figure 5

Stratigraphy and conceptual model of well No. 3 in the Kawajima land subsidence observatory which is the modeling target in this study. Sediments were divided into nine layers based on their geologic and hydrogeologic characteristics

Full size image

Hydrogeological background of Kawajima

Much research has been conducted on the stratigraphy of Kawajima. Based on the results of existing investigations and their own paleomagnetic and pollen analyses, Naya et al. (2017) classified the stratigraphy of Kawajima as Holocene to 30 m depth, upper to middle Pleistocene to 90 m depth, and lower Pleistocene to around 590 m depth. Figure 4 shows chronostratigraphy, hydrostratigraphy, and screen depths of three observation wells at the Kawajima land subsidence observatory, based on Naya et al. (2017) and borehole data from the observatory. The layers from the surface to 200 m depth alternate between highly permeable and less permeable layers. Groundwater is accessed by humans to a depth of 200 m. Below that, thick fine-grained layers alternate with thicker aquifers that have not been accessed. Figure 5 shows the details of layers down to a depth of 80 m. The Holocene consists of fluvial sediments, and the Pleistocene is shallow marine sediments, both with a variety of grain sizes. These layers are classified into nine layers (S, F1–5, T1–3) according to the hydrogeologic characteristics. The surface soil is represented by “S”, the aquifer by “F”, and the aquitard by “T”. Layers F1, F2, and F3 are highly permeable and the main sources for groundwater abstraction. Layers F3, F4, F5 are mainly composed of sands and gravels but also include thin layers of fine grains. The layers T1, T2, and T3 are composed of fine grains and are soft. There are thick fine-grained layers below 80 m depth (Figs. 3 and 4), but these layers are marine sediments of the lower Pleistocene and are well consolidated.

Groundwater uses in Kawajima

Temporal changes in the amount of groundwater abstraction used for tap water supply, industry, and buildings

The Saitama prefectural ordinance requires groundwater users to report the monthly and annual amounts of groundwater abstraction for three usages: tap water supply, industry, and buildings (for air-conditioners). Figure 6 shows the temporal changes in the monthly amount of groundwater abstraction for the three usages from 1985 to 2010 in Kawajima. The data are summarized from the Saitama prefectural report on groundwater abstraction amount. Among the three usages, most of the groundwater abstraction is for tap water supply, and the abstraction amount for industry and buildings is minimal. The abstraction amount for tap water supply in 1990, when an intense drought occurred, is noticeable, but the overall abstraction amount was basically unchanged in other years.

Fig. 6
figure 6

Temporal changes in the monthly amount of groundwater abstraction for tap water supply, industry, and buildings in Kawajima

Full size image

Groundwater abstraction amount by use

There has been no continuous survey of agricultural groundwater use but surveys were conducted in 1985 and 1995 (KRAAO 1992, 2001). The amount of groundwater abstraction was then compared by the purpose of use based on the data in 1985 (Fig. 7a) and 1995 (Fig. 7b). The data are summarized from the Status of Utilization of Agricultural Groundwater in the Kanto region, published by the Kanto Regional Agricultural Administration Office (KRAAO) in 1992 and 2001 (KRAAO 1992, 2001). In both 1985 and 1995, groundwater abstraction for agriculture significantly exceeds that of the other three usages combined. The amount of groundwater abstraction for agriculture significantly increases during the flooding period of the paddy field, which is the primary agricultural land use in Kawajima. On the other hand, the total groundwater abstraction for tap water supply, industry, and buildings varies a little seasonally. Therefore, most of the groundwater used in Kawajima within 1 year is abstracted for agriculture during summer.

Fig. 7
figure 7

Monthly amount of groundwater abstraction for agriculture and the total of tap water supply, industry, and buildings in Kawajima a in 1985 and b in 1995. Note that the cold summer in 1985 is a reason for the smaller amount of groundwater abstraction for agriculture

Full size image

Depth distribution of well screens

The distribution of well-screen depth in the town of Kawajima is summarized in Fig. 3 based on the wells used for agriculture and tap water supply, and for deep wells. The list of wells for agriculture in 1985 was obtained from the Status of Utilization of Agricultural Groundwater in the Kanto region compiled by KRAAO in 1992 (KRAAO 1992). The list of wells for agriculture in 1995 was obtained from the same report compiled in 2001 (KRAAO 2001). The list of wells for tap water supply was obtained from the Geological Survey Report of Kawajima Land Subsidence Observatory, compiled by the Water Quality Conservation Division (WQCD), the Department of Environment of Saitama prefecture, in 1985 (WQCD 1985). The list of deep wells was obtained from the National Deep Well Reference Book compiled by the Ministry of Land Infrastructure, Transport and Tourism of Japan in 2009 (MLIT 2009).

As seen in Fig. 3, 91.5% of well screens of wells used for agriculture are concentrated in layers shallower than 50 m depth in 1985, and the same is found for 85.8% in 1995. A closer look within the 50 m depth shows that the agricultural well screens are evenly distributed in a depth of 0–10 m, 10–20 m, 20–30 m, and 30–50 m. Considering the stratigraphy in Fig. 5, agricultural abstraction is mainly conducted from aquifers F1, F2, and F3, and this situation was drawn as a conceptual model in Fig. 5. On the other hand, as seen in Fig. 3, well screens for wells used for tap water supply are distributed in deeper aquifers with a depth of 50–150 m. These aquifers are mainly distributed in the middle to late Pleistocene. Thus, the aquifers from which groundwater is withdrawn for tap water supply differ significantly from those of agricultural wells utilizing Holocene and upper to middle Pleistocene aquifers. In addition, five other deep wells were found in the list of deep wells in Kawajima (MLIT 2009). Although the purposes of these five deep wells are unknown, their screens are distributed through the same layers as wells for tap water supply.

Observed hydraulic head

In Kawajima, hydraulic heads of major aquifers have been observed hourly at three observation wells at the land subsidence observatory. Figure 8 shows the monthly averages of hydraulic heads observed from April 1987 to April 2019. The data are summarized from each edition of the Annual Report on Land Subsidence and Groundwater Level Observation from 1988–2019, published annually by WQCD (WQCD 1988–2019). As seen in Fig. 8, deeper aquifers have a lower hydraulic head and show the overall trends of recharge. Hydraulic heads of the three observation wells have been increasing in a long-term trend. In addition, the hydraulic heads of well nos. 2 and 3 show significant seasonal fluctuations, decreasing between June and August (summer) and increasing between December and February (winter). Declines in the hydraulic heads of well nos. 2 and 3 become significantly prominent in the years of drought (1987, 1990, 1994, and 1996) and intense heat (2004), reflecting higher groundwater demands than usual years.

Fig. 8
figure 8

Monthly averaged hydraulic heads of three observation wells at the Kawajima land subsidence observatory

Full size image

On the other hand, the long-term trend of the hydraulic head of well No. 1 is similar to that of well No. 2, but the seasonal fluctuation is slight, even in the year of drought and intense heat. A slight delay is also found in the phase of seasonal fluctuation of the hydraulic head of well No. 1 compared to well nos. 2 and 3. The different hydraulic head patterns between well No. 1 and well nos. 2 and 3 may have been due to the lack of groundwater use at the screen depth of well No. 1 (Fig. 4). Furthermore, there is a fine-grained layer about 40 m thick between the bottom of well No. 2 and the well-screen of No. 1. Therefore, it is unlikely that the seasonal hydraulic head patterns observed in well nos. 2 and 3 would penetrate this thick low-permeability layer and significantly affect the hydraulic head pattern in well No. 1. For this reason, the propagation of the hydraulic-head change of other aquifers with different depths, or distant places, is considered to be a cause of the slight seasonal fluctuation of the hydraulic head in well No. 1.

Observed cumulative deformation

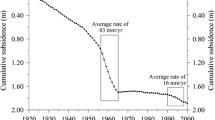
Figure 9 shows the cumulative deformation observed in Kawajima from April 1987 to April 2019 (WQCD 1988–2019). The curve for well No. 3 shows the monthly average of cumulative deformation based on daily observations of deformation with an extensometer in well No. 3 in the Kawajima land subsidence observatory. The curve for the layers between well nos. 2 and 3 shows the same information for layers from 80 to 190 m depth, which was calculated by subtracting the cumulative deformation observed in well No. 3 from that observed in well No. 2. The curves for two benchmarks, 49–17 and 49–18, points of elevation reference, show the cumulative deformations that were annually observed in two other locations within the town of Kawajima.

Fig. 9
figure 9

Observed cumulative deformation in Kawajima. Data for well No. 3 and layers between well nos. 2 and 3 are the monthly averages calculated from the daily observation at the Kawajima land subsidence observatory. Data for the benchmarks in Kawajima is annually observed in two different locations in Kawajima

Full size image

The curve for well No. 3 shows that land subsidence has progressed with repeated seasonal expansion and compaction, including plastic compaction. The seasonal compaction at well No. 3 reaches its maximum between May and August when the hydraulic head of well No. 3 declines the most. The most significant monthly expansion in a year tends to appear 1 month after the compaction period. Between November and April, a small expansion occurs. The curve of the layers between well nos. 2 and 3 shows that the elastic deformation has been repeated with little plastic deformation in the layers between well nos. 2 and 3 (from 80 to 190 m depth). In addition, the cumulative deformations at the benchmarks are smaller or almost the same compared to the cumulative deformation at well No. 3. These data suggest that the plastic deformation in Kawajima mainly occurs from 0 to 80 m depth in the layers associated with well No. 3 in the Kawajima land subsidence observatory.

Summary of observed information and modeling strategy

The characteristics of hydrogeology, groundwater use, and land subsidence in Kawajima can be summarized as follows. First, most groundwater is abstracted for agriculture from layers shallower than 50 m depth between May and August. Non-agricultural groundwater use does not have a significant impact on land subsidence because it is small in quantity and is pumped from the well-consolidated deep layers of the lower Pleistocene. Second, the hydraulic head has gradually increased with seasonal fluctuations consistent with seasonal groundwater use for agriculture. Third, the subsurface formations have gradually subsided with repeated elastic expansion and elastoplastic compaction consistent with seasonal fluctuations in the hydraulic head. Fourth, the plastic deformation is concentrated in the layers of well No. 3 (from 0 to 80 m depth).

Based on the preceding information, a modeling strategy is designed as follows. The modeling target is the layers of well No. 3 in the Kawajima land subsidence observatory (Fig. 5). Based on the horizontal continuity of the hydrogeological structure in the Arakawa Lowland (Ando and Fujimoto 1990; Ando and Houtigai 1997; Ishihara et al. 2011; Komatsubara 2014) and the homogeneously dense distribution of pumping wells for paddy fields, the process is likely to be homogeneous in the horizontal direction. Furthermore, groundwater flow in the clayey layers is essential when considering land subsidence. It is usually almost vertical to the bedding because the high hydraulic conductivity of the aquifer causes rapid and horizontally wide propagation of hydraulic head change in the aquifer, which is like a horizontally homogeneous boundary condition at the bottom or top of the aquitard. Then, a vertically one-dimensional (1D) model was adopted in this study. Although vertically 1D models have limitations (Gambolati and Freeze 1973), they have been applied and show good performance in previous studies for similar situations in California (Helm 1975), Mexico City (Ortega-Guerrero et al. 1999), Shanghai (Liu and Helm 2008b), Tokyo (Aichi 2020) and Kuki and Mobara (Joshi et al. 2020) in Japan, and central Taiwan (Hung et al. 2012).

Method

Governing equation of the vertically 1D land subsidence simulation

In this study, saturated groundwater flow and vertical uniaxial soil deformation were modeled. The deformation of mineral grains was assumed to be negligible compared to the deformation of the skeleton. Elastic deformation was modeled with linear elasticity, and plastic deformation was modeled with a modified Cam-clay model (Roscoe and Burland 1968). The change of the water density ρ (kg m–3) was assumed to be constant. Then, the governing equation of the groundwater mass conservation law was derived with Darcy’s law as follows:

$$\frac{1}{1+{e}_0}\frac{\partial e}{\partial t}=\frac{\partial }{\partial z}\left[K\left(\frac{1}{\rho \textrm{g}}\frac{\partial p}{\partial z}\right)+1\right]$$
(1)

where, e is the void ratio (-), K is the hydraulic conductivity (m s–1), g is the gravitational acceleration (m s–2), and p is the pore pressure (Pa). The change of void ratio was divided into the elastic component ∆ee and the plastic component ∆ep. The elastic change of void ratio ∆ee when the effective stress changes from \({\sigma}_0^{\prime }\) to σ′ was calculated with

$$\Delta {e}^{\textrm{e}}=-\frac{S_{\textrm{s}}}{\rho \textrm{g}}\left({\sigma}^{\prime }-{\sigma}_0^{\prime}\right)\left(1+{e}_0\right)$$
(2)

where Ss is a specific storage (m–1). Here, the compressional stress is taken to be positive while the expansion of void ratio is taken to be positive, and the effective stress is defined as

$${\sigma}^{\prime }=\sigma -p$$
(3)

where σ is total stress (Pa). The plastic deformation of porous media was calculated with the following formula,

$$e-{e}_{\textrm{pc}}=-{C}_{\textrm{c}}\left({\log}_{10}\;{\sigma}^{\prime }-{\log}_{10}\;{\sigma}_{\textrm{pc}}^{\prime}\right)$$
(4)

where epc is the void ratio at the effective stress is equal to the past-maximum effective stress (preconsolidation stress) \({\sigma}_{\textrm{pc}}^{\prime }\) and Cc is a compression index.

Equation (4) was also used to calculate the initial value of \({\sigma}_{\textrm{pc}}^{\prime }\) using e0 and the over consolidation depth (OCD, see Fig. 10), whereby OCD denotes the past-maximum thickness of overburden layers above the target layer in terms of the height from the current surface (Fig. 10), and was used to calculate the initial value of the preconsolidation stress. Since the preconsolidation stress is the maximum effective stress that the target layer experienced in the past, the initial value of preconsolidation stress can be calculated by estimating the former overburden pressure based on OCD and the assumed initial pore pressure distribution. Because OCD can be easily linked with the geological interpretation and it is convenient to set a vertically distributed preconsolidation stress within an aquitard, it is adopted in this model as a parameter.

Fig. 10
figure 10

Concept of over consolidation depth (OCD)

Full size image

Then, the plastic change of void ratio ∆ep was calculated with

$$\Delta {e}^{\textrm{p}}=\left\{\begin{array}{cc}-{C}_{\textrm{c}}\;{\log}_{10}\frac{\sigma^{\prime }}{\sigma_{\textrm{p}\mathrm{c}}^{\prime }}+\frac{S_{\textrm{s}}}{\rho \textrm{g}}\left({\sigma}^{\prime }-{\sigma}_{\textrm{p}\mathrm{c}}^{\prime}\right)\left(1+{e}_0\right)& {\sigma}^{\prime}\ge {\sigma}_{\textrm{p}\mathrm{c}}^{\prime}\\ {}0& {\sigma}^{\prime }<{\sigma}_{\textrm{p}\mathrm{c}}^{\prime}\end{array}\right.$$
(5)

and the total strain ε was calculated with

$$\varepsilon =\frac{\Delta {e}^{\textrm{e}}+\Delta {e}^{\textrm{p}}}{1+{e}_0}$$
(6)

where the extensional strain is taken to be positive. Once the total strain is calculated,

$$u={\int}_{z_1}^{z_2}\varepsilon dz$$
(7)

gives the change of thickness u (m) from z1 (m) to z2 (m).

In order to numerically solve the governing equation, the finite difference method was used for space and time derivatives, and the implicit method was used for time integration. The discretized governing equation becomes nonlinear simultaneous equations. The Newton-Raphson method was used to obtain the solution to solve it.

Parameter search with an evolutionary algorithm

Evolutionary algorithm

In order to calibrate the model parameters, this study focuses on an inversion procedure with an evolutionary algorithm (EA). The EA is a highly flexible optimization algorithm that mimics biological evolution (Whitley 1994; Fogel 1994). EA searches for solutions probabilistically, which gives it an advantage over deterministic algorithms, such as Gauss-Newton and Newton-Raphson, where the target problem is disturbed by noise (Fogel 1994). Therefore, this study adopted EA to calibrate the model parameters because little observation data is available.

Here, the basic concept of EA is introduced. Although EA requires iterative computation, EA has been used in many fields because it does not require continuity of the problem and differentiability assumptions (Whitley 1994). There are various types of EAs such as genetic algorithms (Goldberg 1989; Bäck and Schwefel 1993; Whitley 1994), evolution strategies (Bäck and Schwefel 1993; Beyer and Schwefel 2002), and evolutionary programming (Bäck and Schwefel 1993; Yao et al. 1999). Although each algorithm has similarities and differences in the optimization target, the way to express genes and the optimization procedure (Bäck and Schwefel 1993), the interaction of research communities since the 1990s has resulted in a variety of original algorithms that incorporate each other’s features. As a result, an umbrella term “evolutionary algorithm” has been more common in recent years, and thus it has been used in this study.

Figure 11 shows a procedure of parameter search common to many EAs. First, many individual solutions for a given problem are initially generated using random numbers (initialization). A set of solutions is called the population. Then, each solution is evaluated (evaluation). Evaluation does not have to be numerical, but it should at least determine the superiority between individual solutions. The iterative part starts with the next step. A pair of individual solutions (“parents”), which will generate a new solution (“offspring”), is selected from the population (selecting parents). Through genetic operations, i.e., crossover and/or mutation, an offspring inheriting its parents’ characteristics is generated (crossover; mutation). An offspring generation process is continuously conducted by selecting new parents until a pool of parents and offspring becomes a specific size. All offspring experience an evaluation step (evaluation). Then, individual solutions that consist of a new population are selected from the pool of parents and offspring (selection). The procedure returns to the beginning of the iterative part, selecting parents, and continues the loop until the end condition is satisfied. Typically, the average evaluation of the next generation is better than the one of the previous generation.

Fig. 11
figure 11

Procedure common to many evolutionary algorithms (EAs)

Full size image

Implemented inversion procedure

Figure 12 shows the inversion procedure of EA in this study, a detail of which is modified from the general procedure of EAs introduced in the previous section. The following five parameters are the target of this procedure: K, Ss, Cc, e0, and OCD. Here, the individual solution is a set of these parameters. All nontarget parameters were fixed. The number of sets in a generation was set to be 100. The detail of the procedure is as follows.

Fig. 12
figure 12

Inversion procedure of the EA in this study

Full size image

Initialization

One set of initially guessed parameters (in Table 1) was prepared. Then, this set was replicated for 100 sets as a first generation.

Table 1 Initially guessed parameter values. For layer type, see section ‘Hydrogeological background of Kawajima’ and Fig. 5
Full size table

Evaluation

The subsidence was computed using each set. For the objective function, the evaluation value of each set, the root mean square error (RMSE) between the observed subsidence and the simulated subsidence was adopted. The smaller RMSE was evaluated as the better agreement in observation and simulation. Here, the set with the smallest RMSE was guaranteed to be preserved in the next generation (preserved set).

Selecting parents

The parents were chosen by a virtual roulette wheel (Whitley 1994), the selection probability of which was proportional to the inverse of the RMSE. Therefore, the set with the smaller RMSE had a higher probability of being chosen as a parent.

Crossover and mutation

The offspring’s parameter values were the weighted averages of the parents’ parameter values with the random weight from a uniform distribution (0,1), letting the offspring inherit its parents’ characteristics. Then, a mutation was conducted. A mutation added a normally distributed random number of the standard deviation (in Table 2) to the offspring’s every parameter. Each parameter has an upper and lower limit regardless of sediment type. If the mutated parameter value exceeded its limit, the parameter value was pulled back to its closest limit. Setting an upper and lower limit aimed to avoid unrealistic convergence values. After generating 99 new offspring individually, the 100 sets, i.e., 99 offspring and the preserved set, replaced all the parents and become the next generation. Then, the procedure was repeated from the ‘evaluation’.

Table 2 Searched range of parameters
Full size table

The aforementioned procedure keeps a preserved set over generations until a better set appears. When a better set appears, the preserved set is replaced. Therefore, the preserved set is gradually improved over the generations. Because crossover and mutation use random numbers, this inversion procedure can probabilistically explore the parameter space near the preserved set, and the preserved set is updated as generations go by.

Model set up

The model was divided into 87 meshes, to which specific layer properties were assigned. Nine types of layers classified according to the hydrogeological characteristics (Fig. 5) were identified. The following parameters were set to all layers: hydraulic conductivity K (m day–1), specific storage Ss (m–1), compression index Cc (-), initial void ratio e0 (-), water density (kg m–3), solid density (kg m–3), and the over consolidation depth (OCD) (m). The water density was assumed to be constant at 1,000 kg m–3. The solid density was assumed to be constant at 2,600 kg m–3 based on the core soil tests (WQCD 1985). K, Ss, Cc, e0, and OCD were determined through an iterative inversion with EA, and the values shown in Table 1 are used as initial values. The initial values in Table 1 were estimated based on the geological survey and core soil tests. Considering that the Arakawa Lowland is a buried fluvial terrace, the OCD of Pleistocene can be estimated by the elevation of the past residual hill from the cross-sectional map in Fig. 2. Then, the OCD of Pleistocene was set to 3 m, and the OCD of Holocene was assumed to be 0 m considering the small erosion by the Arakawa River in this area.

Initial condition and boundary condition

As an initial condition, the pore pressure values of all meshes were specified to be hydrostatic with a hydraulic head of 13.35 m, according to the Geological Survey Report of the Kawajima Land Subsidence Observatory (WQCD 1985). As a boundary condition, the pore pressure value at 51.7 m depth, which is the center of the observation screen, was specified based on the observed hydraulic head. The simulation period was from January 1945 to April 2019, and the time step was fixed at 1 month. The observed data of the hydraulic head are available from April 1987; however, the hydraulic head must be inferred before that. Figure 13 shows the assumed hydraulic head for the boundary condition. The concept of these initial and boundary conditions is described as follows.

Fig. 13
figure 13

Boundary condition. The hydraulic head was assumed for January 1945–March 1987, and the observed hydraulic head was used for April 1987–April 2019

Full size image

The hydraulic head in the Kanto Plain had gradually declined from the 1950s to the 1970s due to increased groundwater use associated with urbanization (Ishii et al. 1976; Endo 1992; Hayashi et al. 2009). In the earlier years, the hydraulic head was considered to be higher because industrial groundwater use expanded after the Second World War (Ishii et al. 1976). Therefore, this study assumed that the initial pore pressure distribution was hydrostatic in 1945, the last year of the Second World War. The sinusoidal seasonal fluctuation in the hydraulic head was assumed and added to the long-term trend with an amplitude of typical value from the observed fluctuation. The long-term change in the hydraulic head was assumed to decrease and be the lowest in 1960–1970, a typical trend observed in the southern part of Saitama prefecture. After 1970, considering the start of groundwater regulations in the Kanto Plain, a slight increase was assumed so that the hydraulic head was smoothly connected with the observed hydraulic head. Although these are the best efforts to estimate the past hydraulic head, it is still highly uncertain. The effect of this uncertainty is expected to be assessed by a future study.

There are no observational data for the hydraulic head for the Holocene aquifer at 25–30 m depth. Sugahara et al. (1992) explained that in the paddy field area in Saitama prefecture, the hydraulic head within 30 m depth tends to be stable because the irrigation water quickly recharges the surface-water courses. Since Kawajima is one of such areas, for the Holocene aquifer, the temporal change in the hydraulic head was checked to be stable after the simulation instead of setting the boundary condition. For the same reason, the pore pressure at the land surface was expected to be stable. Then, the pore pressure of the land surface mesh was assumed to always coincide with atmospheric pressure. Although there is a thick aquitard beneath the model’s bottom, plastic compaction is rarely observed below the model, suggesting that little water is squeezed out from beneath the model. Therefore, the model’s bottom was assumed to have zero mass flux.

Results and discussion

Simulated subsidence and searched parameters

The iterative part of the inversion procedure was repeated 20,000 times (generations) until the change of the preserved set’s RMSE became stable. Figure 14 shows the preserved set’s RMSE for each generation. The preserved set’s RMSE improved rapidly in the first tens of generations (Fig. 14a) and then improved slowly after that (Fig. 14b). The preserved set’s RMSE of the 20,000th generation (model A) is 3.0 × 10–3 (m), about three-quarters of the RMSE by the initial guess of parameters set. Figure 15 shows the subsidence simulated by model A, and the simulated subsidence agrees satisfactorily with the observed subsidence. The simulated subsidence shows a seasonal expansion and compaction, and compaction becomes significant in the years of drought.

Fig. 14
figure 14

a Root mean square error (RMSE) for the first 150 generations. b RMSE for all generations

Full size image
Fig. 15
figure 15

Observed cumulative subsidence, simulated cumulative subsidence by model A, and the difference between them. A positive difference means that the simulation overestimates the subsidence by that value more than the actual subsidence

Full size image

The reproducibility of the observed subsidence by model A is generally good, but there are some points of concern—for example, the difference between observed subsidence and simulated subsidence becomes significant in the years of drought. As discussed in section ‘Study area’, in drought years, the hydraulic head drops sharply and a large plastic deformation is observed accordingly. The reason this phenomenon could not be reproduced well can be attributed to the reproduction of historical preconsolidation stress distribution. This problem could be solved by successfully estimating groundwater levels before 1987, when the observatory began operation.

Another concern is the change in the reproduction trend of observed subsidence around March 2011, when the Tohoku Earthquake occurred. The curve representing the difference between observed and simulated subsidence in Fig. 15 shows that before March 2011, subsidence was more dominant in the simulated curve than in the observed curve, but after March 2011, this is reversed. As a result, the long-term trend of simulated subsidence shows a continuous downward trend while the long-term trend of observed subsidence over the last 6 or 7 years has remained almost unchanged. This could have a negative impact on the model’s predictive performance in predicting long-term subsidence. The possibility that strong seismic activity from the Tohoku Earthquake affected the secondary consolidation of the Holocene has been noted by several studies (Imakiire and Koarai 2012; Yasuhara and Kazama 2015; Noda et al. 2017). Model A is likely to have been affected by the Tohoku Earthquake, and seismic effects on land subsidence modeling require further investigation.

Table 3 shows the parameter values of model A. The parameter values converged within a range of typical values in existing published papers (Freeze and Cherry 1979; Terzaghi et al. 1996; Wang 2000; Gregory et al. 2006). Table 3 shows that aquifers tend to be more permeable and stiffer than aquitards, implying that the inversion analysis found a solution within a reasonable trend. Although the aquitard T3 was estimated to be stiffer than the aquifer F2, it is not surprising because T3 is Pleistocene and F2 is Holocene.

Table 3 Parameter values of model A. See text for details
Full size table

Temporal change in the hydraulic head distribution and preconsolidation stress distribution

Figure 16a shows the temporal change in the hydraulic head distribution simulated by model A, whereas Fig. 17a shows the temporal change in the hydraulic head at 25, 35, and 55-m depth, simulated by model A. Since F3, F4, and F5 are hydraulically continuous, their hydraulic heads were common and followed the boundary conditions shown in Fig. 13. Similar behavior of the hydraulic head was confirmed in the lower part of T3. Due to the low hydraulic diffusivity, the seasonal fluctuation in the hydraulic head decayed in T3, and the hydraulic head in the upper part of T3 had a decreasing trend. The hydraulic head of T2 and F2 showed a decreasing trend and slight seasonal fluctuation, which is consistent with the expected stability of the hydraulic head in the Holocene aquifer discussed in section ‘Initial condition and boundary condition’. The decline of hydraulic heads in T2, F2, and T3 is slowing down year by year, whereas the hydraulic heads in S, T1, and F1 are stable, although they do not provide enough water to the lower layers to keep the hydraulic head of T2, F2, and T3 constant.

Fig. 16
figure 16

a Temporal change in the hydraulic head distribution. b Temporal change in the preconsolidation stress distribution from the initial preconsolidation stress distribution

Full size image
Fig. 17
figure 17

a Temporal change in the hydraulic head. b Temporal change in the preconsolidation stress at 25, 35, and 55-m depth

Full size image

Figure 16b shows the temporal change in the preconsolidation stress distribution from the initial preconsolidation stress distribution simulated by model A. Figure 17b shows the temporal change in the preconsolidation stress at 25, 35, and 55 m depth, respectively, simulated by model A. In F3, F4, and F5, the preconsolidation stress increased until 1960 and remained almost unchanged until 1987. After that, the preconsolidation stress increased in 1987, 1990, 1994, and 1996 when the drought increased groundwater demand, resulting in significant subsidence in the year of drought. Plastic compaction in the aquifer layers is interpreted as the plastic compaction of thin clay and silt within an aquifer, which often exists (Leake and Prudic 1991). Such clay and silt are thinner than mesh resolution or omitted in geological column descriptions and have little effect on the bulk permeability. However, the result suggested that they might play an important role in significant subsidence in a year of drought. In T2, F2, and T3, the preconsolidation stress has constantly increased regardless of drought, indicating the mechanisms of continuous plastic compaction every year.

Prediction

Predictive performance test

As seen in section ‘Simulated subsidence and searched parameters’, the simulation results for model A indicated that the Tohoku Earthquake may have affected the deformation conditions. In order to clearly examine whether or not the Tohoku Earthquake affected the deformation conditions, it is necessary to perform cross-validation by dividing the observed subsidence data into two periods, one affected by the Tohoku Earthquake and the other not. For this purpose, the predictive performance of the inversion procedure was tested. Parameters in Table 4 (model B) were calibrated using the first two-thirds of the observed data (April 1987–August 2008) and compared with the parameters of model A in Table 4. Table 1 was used for initial values, and the iterative part of the inversion procedure was repeated 20,000 times, then the subsidence is predicted for the remaining one-third (September 2008–April 2019) in Fig. 18.

Table 4 Comparison of parameters of models A and B. Model B is calibrated using the first two-thirds of the observed data (April 1987–August 2008). See section ‘Simulated subsidence and searched parameters’ for details on model A
Full size table
Fig. 18
figure 18

Observed cumulative deformation, cumulative deformation simulated by the parameter set calibrated for April 1987–August 2008, predictive subsidence for September 2008–April 2019, and the difference between observations and simulations

Full size image

The reproducibility of the observed subsidence by model B over the calibration period was as good as that of model A. The same characteristic of model A, in which the error between simulation and observation is larger in drought years, was also confirmed. Therefore, the large errors in drought years are systematic errors. In addition, many parameters of model B were estimated to be in the same order of magnitude as the parameters of model A, suggesting the possibility of successful convergence as seen in Table 4.

Over the prediction period, the prediction by model B agrees well with the observation from September 2008 to February 2011 (Fig. 18). However, since March 2011, the observed subsidence has been predominant over the predicted subsidence, with an average difference of 0.58 cm, which is very poor compared to the reproducibility of observed subsidence by model A over the same period. The poor predictive performance since March 2011 is clearly attributed to the Tohoku Earthquake, and it is confirmed that the Tohoku Earthquake affected the deformation conditions. In order to improve the predictive performance, subsidence due to groundwater abstraction needs to be separated from subsidence due to seismic activity. However, this problem cannot be solved immediately because the postseismic deformation model cannot be easily determined (Suito and Freymueller 2009).

Scenario analysis

Three future scenarios were prepared by assuming the boundary conditions after April 2019 (in Fig. 13) to obtain useful information for future land subsidence management. The assumed boundary conditions after April 2019 are shown in Fig. 19a. Scenario 1 assumes that the current hydraulic head fluctuations will continue, whereas scenario 2 assumes that the amplitude of the hydraulic head fluctuations in scenario 1 is reduced by half. Scenario 3 assumes to have the same amplitude as scenario 1, and also assumes the continuous recovery trend of hydraulic head since the 1970s (0.055 m year–1). As a result of the simulation using model A, the predictive subsidence was 1.3 mm year–1 for scenario 1, 0.7 mm year–1 for scenario 2, and 1.0 mm year–1 for scenario 3 (Fig. 19b), which suggests that scenario 2 succeeded the most in reducing land subsidence. This result indicates that groundwater management focusing on the summer season, which is not currently included in a rule, may effectively mitigate land subsidence caused by seasonal groundwater level fluctuations.

Fig. 19
figure 19

a Assumed boundary conditions and b Predictive deformation

Full size image

Attempts to control land subsidence by managing seasonal fluctuations in groundwater levels may be successful in other areas too. Land subsidence progressing due to seasonal groundwater level fluctuations has been reported in California (Helm 1975), Las Vegas (Hoffmann et al. 2001), Shanghai (Liu and Helm 2008b; Ye et al. 2016), and Taiwan (Chang et al. 2004). In these studies, numerical models have been constructed to elucidate the subsidence mechanism, and interest has been focused on groundwater management that can effectively control future subsidence. For example, Liu and Helm (2008b) analyzed three different scenarios of seasonal groundwater level fluctuations with the same amplitude and different long-term trends for the Shanghai model, as shown in scenarios 1 and 3 of this study (Fig. 19). However, none of the studies simulated land subsidence with varying amplitudes of seasonal groundwater level fluctuations. Although the amount of mitigated subsidence when the amplitude is varied depends on the characteristics of the aquifer system and requires further individual investigation, the scenario analysis of this study provided a new perspective for groundwater management.

Limitations

Limitations of evolutionary algorithm

Because EA searches for solutions probabilistically, it has a greater ability to escape from local solutions than deterministic algorithms, but multiple runs of EA from the same initial values do not necessarily yield the same solution. Also related to this problem is the lack of clear criteria to determine how many generations to discontinue the search for a solution. These problems can be solved by examining the validity of the final parameter values obtained and the convergence status of the model evaluation values, as this study has done.

Another drawback is the slow convergence of the EA. As seen in Fig. 14, the rate of improvement of the solution evaluation values slows down drastically as the generation progresses. This may give the modeler the illusion that the currently obtained solution is a global solution and may cause the modeler to discontinue the search for a solution in the middle of the generation. Another serious drawback is the need to introduce hyperparameters such as the number of solutions in one generation, the so-called population size. In order to solve these problems, while taking the advantages of EA, the combination of EA and other algorithms is studied. This is called a hybrid evolutionary algorithm, in which, for example, EA is used to locate a rough global solution and then a deterministic algorithm is used to refine the solution (El-Mihoub et al. 2006). The adoption of such advanced methods would broaden the scope of land subsidence research.

Limitations of the models

The subsidence models in this study were a vertical 1D model for the Holocene to upper and middle Pleistocene within 80 m depth. In general, the 1D subsidence model is available only when the horizontal strain is much smaller than the vertical strain. In this study, data collection justified a 1D model because the major deformations were confirmed only within 80 m depth, and because the horizontal continuity of the geology and stratigraphy was confirmed in the study area. Otherwise, a 3D model would be appropriate (e.g., Ochoa-Gonzalez et al. 2018). For the same reason, the model of this study would be inappropriate and would need to include deeper layers if plastic deformation occurred below 80 m depth, for example, because of a change in the groundwater abstraction situation for tap water supply. In addition, as noted in sections ‘Simulated subsidence and searched parameters’ and ‘Prediction’, earthquakes have a strong influence on the subsidence model, which remains unresolved.

Conclusions

There are three novel points in this study. The first is to clarify the land subsidence mechanism in the northern Kanto Plain, which has not been determined by previous studies, through data compilation. The second is to highlight the use of an inversion procedure of EA for the long-term land subsidence model calibration; the inversion procedure of EA is very flexible and can be applied to any other region. The third is to suggest possible groundwater regulations to effectively suppress land subsidence caused by seasonal groundwater level fluctuations. The result can be used as a reference for new regulatory planning in other countries that have experienced seasonal subsidence despite regulations on the annual amount of groundwater abstraction.

In order to understand the mechanisms of land subsidence in the northern Kanto Plain and contribute to mitigating land subsidence, this study compiled hydrogeological information, and well distribution and monitoring data, and it developed a numerical model with an evolutionary algorithm to simulate land subsidence.

The important findings from the data compilation are as follows. First, most of the groundwater used within 1 year is abstracted for agriculture from shallower layers less than 50 m depth between May and August. Second, the hydraulic head has gradually increased with seasonal fluctuations consistent with seasonal groundwater use for agriculture and strict regulation on the amount of annual groundwater abstraction. Third, the subsurface formations have gradually subsided with repeated elastic expansion and elastoplastic compaction corresponding to seasonal fluctuations in the hydraulic head. Fourth, the plastic deformation is concentrated in layers from 0 to 80 m depth.

The main results and implications from a numerical model were as follows. The parameters of model A converged within a range of typical values in the existing literature, and the simulated land subsidence satisfactorily agreed with observed subsidence. Estimated parameters reasonably reflected hydrogeological structures, indicating that the inversion analysis with the evolutionary algorithm successfully worked even though available observation data were limited. The simulation clarified that the plastic deformation had constantly occurred in aquitards T2, F2, and T3, while the sudden plastic deformation in aquifers F3, F4, and F5 occurred in the years of drought. Because of the long-term recovery trend of the hydraulic head in the aquifer, the decline of hydraulic head in the aquitard has slowed down.

In order to test the predictive performance of the inversion procedure, model B was calibrated using the first two-thirds of the observed data (April 1987–August 2008). As a result, it also succeeded in predicting the observed subsidence from September 2008 to February 2011. In addition, many parameters of model B converged to the same order of magnitude as the parameters of model A. However, the prediction became worse after March 2011, which suggests that more investigation is necessary on the possible effect of the Tohoku Earthquake in March 2011 on the consolidation of the layers. The 1D subsidence model of this study is valid only when the major deformations are contained within 80 m depth. Therefore, deeper layers need to be included in the model if the plastic deformation occurred below 80 m depth.

Finally, the scenario analysis indicated that reducing the amplitude of the hydraulic-head drop in the summer season is expected to reduce land subsidence, rather than maintaining the long-term recovery trend of the hydraulic head that has been observed. Similar results may be obtained in other countries that have experienced seasonally progressed land subsidence despite regulations on the annual amount of groundwater abstraction, and the result of the scenario analysis in this study may serve as a reference for new regulations.