Introduction

Continental surface-water bodies with salinities higher than 3 g L −1—g L −1 of total dissolved solids (TDS)—are considered salt lakes (Last and Schweyen 1983). While they account for less than 5% of the Earth’s surface, salt lakes store a volume of water (85,000 km3) close to that of freshwater lakes (105,000 km3; Williams 1996; Waiser and Robarts 2009). The classification of salt lakes varies depending on their relationship to local groundwater as recharge lakes, terminal discharge lakes and throughflow lakes (Cartwright et al. 2009). When a salt lake is connected to an aquifer, the difference in densities between groundwater and surface water enhances the development of a freshwater/salt-water interface (FSI). In addition, hypersaline wetlands provide habitats for microorganisms adapted to extreme salinity conditions such as high solar radiation, extreme temperatures and irregular water regimes. Therefore, these ecosystems show geochemical and biological peculiarities worth studying, with possible applications to different research fields of great scientific interest (Porter et al. 2005; Prieto-Ballesteros et al. 2003; Oren 2018, among many others). The natural behaviour of these wetlands is likely to be altered by anthropic actions such as agriculture, livestock, or wastewater spills, which may cause changes in both the quantity and quality of the wetland waters, threatening the survival not only of their biodiversity but also the ecosystem. When the connection between groundwater and wetlands is demonstrated, the resilience of the latter is determined by their relationship with groundwater (de la Hera-Portillo et al. 2020). For this reason, understanding hydrogeological system functioning and establishing the groundwater/surface-water relationships of the ecosystem is essential, especially in the context of waters with different salinities and densities.

Difficulties in understanding and managing these complex hydrogeological systems arise from the assumption that groundwater flow is driven towards a decreasing hydraulic potential direction. However, small variations in water density may produce a flow in directions that are not related to a decrease in hydraulic potential but rather to spatiotemporal differences in the concentration of dissolved solids. Groundwater density is a function of its total dissolved solids (TDS) content. Therefore, to characterize groundwater flow and its relationship with wetlands, the transport equation of dissolved species must be defined and coupled with the advective component of the flow (Voss 2016).

Some simple examples can be found in Glover (1959), Henry (1964) and Konikow et al. (1997), where the solutions of the equations of the state (flow and transport) and their coupling can be approximated by analytical methods. These examples have been used to test models that, through numerical methods, analyse the advective and dispersive mechanisms of groundwater flow in a more stable way, considering the effects caused by variable density (Voss 1984; Holzbecher 1998; Voss and Provost 2002; Guo and Langevin 2002). A generalized description can be found in previous studies such as Diersch and Kolditz (2002) or Heredia and Díaz (2007).

The aforementioned study cases have been characterized by their stability—freshwater, which is less dense, is usually found above denser saltwater, which generates a stable solution of the problem. Salt lakes, however, show the opposite situation, as the brine is located on the top and the relatively freshwater of the aquifer is below, resulting in a gravitational instability that can generate cells of convection (Wooding et al. 1997a). When the density differences between the two fluids are high enough, solute transport is the result of mixed convective flow (advection, dispersion and diffusion) until a stable density gradient is achieved (Simmons et al. 2001). Gravitational instability occurs in the form of lobes called “fingers” plunging into the relatively fresher water of the underlying aquifer (Fig. 1). An example of unstable flow is represented by the Elder problem (Elder 1967) carried out in Hele-Shaw cells. Although it was initially used to represent thermal convection, Voss and Souza (1987) and Simmons et al. (1999, 2010), among others, subsequently developed a method to represent density-driven flow.

Fig. 1
figure 1

Conceptual model of variable-density flow in a salt discharge lake in a closed basin. Water inputs to the lake come from groundwater inputs (shallow (Rfn) and regional (Rff)), surface runoff and springs (Ro), and direct precipitation over the lake (P). Evaporation (Ev) and evapotranspiration (Et) cause salts to concentrate and precipitate on the lake surface. A concentration gradient occurs between the saltwater and the fresh groundwater (above), which causes free convection cells to be formed by density-driven flow into the aquifer (DDF) in the form of “fingers” or “lobes”

Full size image

Duffy and Al-Hassan (1988) were pioneers in demonstrating how high-density groundwater recirculation can exist under playa lakes in closed basins that have been generated mainly by evaporation. Since then, there have been several studies on convection cells due to density-driven flow in closed basins. Of great interest in understanding these processes are the studies carried out by Fan et al. (1997) and Wooding et al. (1997a, b), which analysed the onset of instabilities in this type of system and the evolution of the lobes or fingers. Previous studies (Simmons et al. 1999) have presented a case study to represent unstable flows of different densities known as the salt lake problem, which was also conducted in Hele-Shaw cells. Based on these investigations, numerous authors have developed numerical models to simulate this theoretical process (see an extended summary in Holzbecher (1998); Diersch and Kolditz (2002); and Simmons et al. (2010)). Later studies applied these models to hydrogeological processes and analysing the salinity evolution of wetlands from their genesis to maturity. These studies are critically important for the correct interpretation of water and salt concentration budgets in this type of salt lake (Bauer et al. 2006; Zimmermann et al. 2006; Tyler et al. 2006; Nield et al. 2008; Geng and Boufadel 2015; Bentley et al. 2016).

A real example of density-driven flow (DDF) under salt lakes in closed basins is the endorheic basin of Pétrola Lake (SE, Spain). This example is one of the most representative of a hypersaline wetland in southern Europe, included in the RAMSAR catalogue and in the Spanish Natura 2000 network because of its great biological diversity (site code: ES4210004). This rich ecosystem and its environmental importance are closely associated with its geomorphological characteristics and hydrological regime and the chemical characteristics of its waters, with concentrations in TDS often exceeding 80 g L−1. These salinities cause density differences (up to 0.25 g cm−3) between the waters of the lake and those of the underlying aquifer (Gómez-Alday et al. 2014). The possible development of convection cells under this lake plays an important role in the transport of chemical species to other regions of the aquifer, exerting a great influence on the recycling of elements such as sulfur (Valiente et al. 2017) or nitrogen (Gómez-Alday et al. 2014; Valiente et al. 2018).

In order to determine the hydrogeological functioning of the system in a natural regime, as well as the behaviour and morphology of the FSI in the surrounding areas of Pétrola Lake, as a contribution for the understanding of the nitrate reduction processes described in the interface by previous research (Gómez-Alday et al. 2014; Valiente et al. 2018), a conceptual model was established based on the data collected. These data are the hydraulic characteristics of the materials, the hydraulic heads and the physico-chemical characteristics of the water, as well as data from a geoelectric prospecting campaign at the edges of the wetland, where the contrast between the different resistivities of the continuous current in saline and fresh groundwater is more pronounced. To validate the conceptual model, a mathematical groundwater-flow and solute-transport model, created in a coupled manner, was developed with the objective not only to define the geometry of the interface but also to establish the mixed convective flows.

Study area and hydrogeology

The endorheic basin of Pétrola Lake, with a surface area of 43 km2, is located in the southeastern part of the Iberian Peninsula in the Spanish province of Albacete (Fig. 2). There are numerous salt lakes in this endorheic region of Castilla - La Mancha, but the most permanent lake is Pétrola Lake, located 852 m above sea level (masl; Fig. 3) and with a water surface occupying an area of approximately 2 km2. The general hydroperiod of the lake presents a phase of high water level in early spring and a phase of depletion in late summer. The study area is influenced by both continental semiarid and Mediterranean climates. The average rainfall in the 2001–2018 period was 295 mm year−1. In the driest years, rainfall was on the order of 200 mm year−1, and in the wettest years, it reached 540 mm year−1. Rainfall is concentrated in the months of March, April, May and October, with the summer months representing the dry period. The annual mean temperature values (min-max) are 8.8 and 0.0 °C, respectively. Continentality is evident in the extreme temperatures that are recorded in the area, with maximum average values in summer of 38.8 °C. The maximum degree of insolation has reached 3,800 h year−1 (2012). The mean potential evapotranspiration in the same period was 1,226 mm year−1, with a difference between the maximum and minimum values of approximately 217 mm year−1. Meteorological data are available from the Pozo Cañada thermopluviometric station, located 15 km south from the study area.

Fig. 2
figure 2

Geological map modified from scale 1:50,000 from the MAGNA 50 project (IGME 1981). Groundwater-level contour map over hillshade from a digital elevation model from CNIG (2015). a Location of the study area. b Hydrochemical zonation. c Photographs 1 and 2 show the salt concentration process due to evaporation, and photographs 3 and 4 show the outcrops argillaceous sediments ranging in color from reddish to dark gray, respectively. Scale bar in photos: 1 m

Full size image
Fig. 3
figure 3

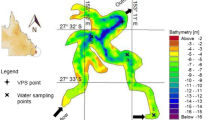
a Bathymetry of Pétrola Lake; the groundwater-level elevation contour lines are derived from a digital elevation model. The light-grey lines represent the bathymetric lines from CNIG (2015), and the red line represents the maximum flooding surface. b Agricultural-influenced sector (AiS), urban wastewater spill-influenced sector (UWiS) and mining-influenced sector (MiS). Locations of resistivity (ERT) sections measured (2012) close to the lake’s margins. WWTP (wastewater treatment plant). c Piezometers that monitor different depths of the aquifer, with the average value and confidence interval at a significance level of 95% (2008–2018) of TDS (g L−1) and tritium (TU, tritium units). The TDS values above 852 masl are from surficial lake water close to the piezometers, but other areas of the lake can reach 80 g L−1 of TDS. d Photograph of the location of the piezometers

Full size image

Based on data from regional geology (analysis of geological maps (1: 50,000) and associated report of the MAGNA series of the IGME (Geological and Mining Institute of Spain) and of the lithological columns of supply boreholes (outside of the study area), it has been possible to infer the composition and thickness of the aquifer materials. Hydrogeologically, the lake’s endorheic basin is formed by the superposition of at least two aquifers that, from bottom to top, are (1) an Upper Jurassic aquifer (confined) and (2) a Lower Cretaceous aquifer, over which the lake lies. The Jurassic aquifer is composed of fractured oolitic limestones up to 130 m thick, with an impermeable bottom formed by Lower Kimmeridgian marls (Gómez-Alday et al. 2014). An unconfined Cretaceous aquifer is present in most of the study area except at the eastern boundary, where Jurassic materials crop out through mechanical contact (direct fault). The Cretaceous aquifer is formed by siliciclastic sands, sandy-conglomerates, and reddish to dark gray clay to argillaceous sediments with thicknesses that can exceed 60 m and ages between Barremian and Albian. The hydraulic conductivity of these materials is low-mid for sandy sediments (10–80 m day−1) and low for argillaceous sediments (0.1–0.01 m day−1; see Table S2 in the electronic supplementary material (ESM); storage capacity is high (30–40%). Gray-to-black argillaceous sediments show noticeable lateral changes in thickness throughout the Pétrola Basin. Nevertheless, around Pétrola lake, these materials are found about 15 m deep, with 5–10 m thicknesses. The impermeable aquifer bottom is comprised of clay materials (more than 50-m thickness) that lack hydraulic connections between the Jurassic aquifer and Cretaceous aquifer (Gómez-Alday et al. 2014). A schematic cross-section that reflects the conceptual model of the available geological information is presented in Fig. 4.

Fig. 4
figure 4

aConceptual model of the endorheic basin of Pétrola Lake. The figure provides an overview on how the physical system works under natural conditions (observed groundwater head (Ho) represented by the mean value and confidence interval, and total dissolved solids (TDS) represented by the range). b Geometry, boundary conditions and hydraulic properties used in the two-dimensional numerical model. Kh and Kv denote horizontal and vertical hydraulic conductivity, respectively. Transport boundary conditions are given by a specified concentration (C and Co). D = longitudinal dispersivity, Gw: sample code. Location of the section is in Fig. 2

Full size image

The inventory of groundwater sampling points conducted in the Cretaceous aquifer, together with data on groundwater levels and springs, allowed one to infer radial and centripetal subsurface flow into the lake from the recharge zones (edges of the system). Around the lake, the water table of the Cretaceous aquifer is close to the topographic surface and several springs and streams drain the aquifer in this area. Surface runoff is not of significant importance, as the courses are irregular and even disappear depending on the geomorphology. However, the drainage-network flows converge to the lake and can function intensively in the case of significant rainfall events (Fig. 2). The water budget of the system is governed by a varied series of interrelated elements (recharge and discharge areas). In a natural regime, recharge occurs mainly through infiltration of rainwater and subsurface runoff into the lake. Research carried out by the Segura Hydrographic Confederation (CHS 2010), based on data from the SIMPA model “Spanish acronym meaning: Integrated System for Rainfall-Runoff Modeling”, for the determination of the ecological water needs in lakes and wetlands, estimate average inputs to the lake of about 2 hm3/year. As it is a closed system, the outputs are made directly by the direct evaporation of the water and the evapotranspiration of the vegetation surrounding the wetland.

Hydrochemically, the study area was divided into three different zones (see zoning and control points in Fig. 2; Gómez-Alday et al. 2014). Chemical analyses of water samples were conducted in the defined zones (zones 1–3) during two field campaigns (2008–2012 and 2013–2018; Valiente 2018; Valiente et al. 2018). Zone 1 corresponds to the recharge area of the unconfined aquifer in the north and east. The sampling points in zone 2 are close to the lake discharge zone (springs), and zone 3 is the lake itself. Zones 1 and 2 have similar characteristics with hydrofacies ranging between Mg–Ca–HCO3 and Mg–Ca–SO4. The electrical conductivity (EC) values ranged from 596 to 1,824 μS/cm in zone 1 to 1,504–3,760 μS/cm in zone 2. The lake water has a hydrofacies that can be classified as Mg–Na–SO4–Cl. The surface waters of the lake have EC values that can range between 59,300 μS/cm (April 2010) and 123,000 μS/cm (November 2010). The δ18OH2O in the water samples from zone 1 and zone 2 ranged from −5.4 to −7.6‰ (average of −6.5‰; n = 25), whereas samples from zone 3 varied from −7.4 to +4.2‰ (average of −4.6‰; n = 16). Therefore, the mixing line of water can be observed by the isotopic compositions of samples plotted along one of the flow lines (e.g., cross section in Fig. 2, see Valiente et al. 2018). That flow-line represents the conceptual model of hydrogeological behaviour.

In zone 3, within the edges of the lake, four piezometric wells were constructed in one of the artificial dikes of the lake, with the water intake zone (screened grates) located at different depths (Fig. 3). During the field campaigns (2008–2012 and 2013–2018), the TDS content and tritium activity in the sampled water were determined in each of them. TDS values at each sampled depth showed low-to-moderate variability throughout that sampling period, except in the surficial lake waters (influences of precipitation and direct evaporation). In order to represent these findings, statistical treatment of the data has been carried out, applying Student’s t-distribution suitable for the number of data points less than 50. The obtained mean TDS values, and the confidence intervals at a significance level of 95% for the mean of the population, are shown on Fig. 3. Thus, a salinity gradient can be observed from the lake surface (TDS varying between 80 and 22 g L−1 at 850 masl approximately) to a depth of 38 m (1 g L−1 at 810 masl). At a 12-m depth, there were high TDS values (50 g L−1 at 840 masl). With those salinities, water density in the area of the piezometers can vary between 1,037 kg m−3 in Gw-12 and almost 1,000 kg m−3 in Gw-38, taking an average value of 1,018 kg m−3. The tritium contents of the aquifer waters and of the lake brine indicate a possible mixing process between recent and old waters. The Cretaceous aquifer waters sampled in piezometers Gw-38 and Gw-34 (with values below 0.2 UT) indicate that they are old waters (infiltrated before 1950). However, tritium values of 4 TU (corresponding to recent waters) are found in the lake brine. In between, piezometers Gw-12 and Gw-26 show tritium values of 1.5 and 0.9 TU, respectively, corresponding to a mixture of recent and old water (Gómez-Alday et al. 2014).

Corine land cover inventory data for 2012 and 2018 (EEA 2018) in the endorheic basin show a significant increase in the area occupied by agricultural activities (from 75 to 84%). Approximately 19% of this area corresponds to irrigated crops supplied with water from the Jurassic aquifer, while the same irrigation returns are recharged to the Cretaceous aquifer. The average annual volume of groundwater abstracted from the Jurassic aquifer to irrigate the crops present in the endorheic basin is approximately 2 hm3 year−1, and irrigation returns can reach up to 15% of this value.

The most important threats and pressures on the wetland environment (Fig. 3), following the classification of Salafsky et al. (2008), are described in Table 1. The anthropic modifications of the wetland over time according to the typologies proposed by Camacho et al. (2009) would be hydrological, geomorphological, and those that alter water quality. These include (1) roads (southern area) and roads that border and artificially delimit the wetland, (2) discharge areas of the wastewater treatment plant in the town of Pétrola (WWTP: waste water treatment plant) with direct discharge to the wetland of water with EC below 800 μS cm−1 from a population of approximately 680 inhabitants, (3) a central dike of the lake (separates the wastewater input from the rest of the lake), and (4) a salt extraction area on the eastern edge of the lake (presence of at least four salt concentration ponds, separated from the rest of the lake by dikes). In this sense, three well-differentiated zones of influence can be established depending on the main anthropic activities in the wetland environment: (1) the northern and western agricultural-influenced sector (AiS); (2) the southern urban wastewater spill-influenced sector (UWiS); and (3) the eastern mining-influenced sector (MiS; see Fig. 3).

Table 1 Main threats and pressures estimated by the Spanish Natura 2000 network on the Pétrola lake environment (site code: ES4210004) EIONET (2000)
Full size table

Rank: H high, M medium, and L low

Electrical resistivity tomography

Geoelectrical prospecting methods are a powerful tool when studying aquifers with variable-density flows (different salinities), as the contrast between different direct-current resistivities in saline groundwater and fresh groundwater can be used (Bauer et al. 2006; Heagle et al. 2013; Bentley et al. 2016). If the porosity of the aquifer materials is homogeneous and/or the possible spatial distribution of other types of materials is known, the electrical conductivity found in the aquifer will be directly related to the concentration of total dissolved solids in the groundwater at a given temperature. Indeed, if the resistivity of the pore water (ρw) and the parameters of the saturated aquifer formation (porosity ϕ; tortuosity a; and the cementation factor m) are known, the resistivities of the aquifer (ρ) (matrix and fluids) can be determined by means of Archie’s law (Archie 1942).

$$ \rho =a\cdotp {\varphi}^{-m}\cdotp {\rho}_{\mathrm{w}} $$
(1)

To establish the distribution of aquifer resistivities around Pétrola Lake, an electrical resistivity tomography (ERT) survey was conducted during June 2012 (see location in Fig. 3). A total of four sections between 155 and 350 m in length were measured (two in the AiS zone, one in the UWiS zone and one in the MiS zone, Fig. 3; Table 2). A RESECS DMT resistivity meter equipped with 72 electrodes was used for this purpose. The acquisition was performed using a Wenner electrode device because it provides a higher SNR (SNR is defined as the ratio of signal power to noise power) and is more sensitive to vertical resistivity variations (Loke and Dahlin 2002). The spacing of the electrodes was 5 m, and the voltage used was 400 V. The depth reached ranged from 30 m for the shortest section to 60 m depth in the central part of the longest section. Two injection cycles were applied in each measurement, taking into account 700 values of spontaneous potential (SP), potential difference (V) and current intensity (I). For each apparent resistivity measurement, the RMS root mean square error was calculated, repeating the measurements until an RMS < 15% was reached at each point (Table 2). Topography was obtained from the CNIG digital elevation model data (CNIG 2015), with one datum every 5 m and was included in the inversion of the sections. Inversion of the field data was performed with Res2Dinv software (deGroot-Hedlin and Constable 1990; Loke and Barker 1996) using the same parameters in the inversion for all profiles. A least-squares algorithm was chosen for the inversion, and the final RMS errors calculated for the five sections were between 7.4 and 24.6% (Table 2).

Table 2 Information on the ERT profiles performed
Full size table

Groundwater model settings

To model the hydrogeological behaviour of the FSI, the SEAWAT code (Guo and Langevin 2002; Langevin et al. 2008) was used. This model combines the MODFLOW (McDonald and Harbaugh 1984) and MT3DMS (Zheng and Wang 1999) codes, which solve the groundwater flow and solute transport equations, respectively. For this purpose, they use a finite difference approximation under variable density conditions as a function of the concentration of TDS in a coupled manner.

SEAWAT is based on the concept of an equivalent freshwater head, i.e., at any point in a saline aquifer where water reaches a certain head, it is possible to find an equivalent freshwater head. The head reached by the saltwater depends not only on pressure and elevation but also on the density of the water. Formulating the flow equation as a function of this head means working with the density and its derivatives. Instead, if the groundwater flow equation is expressed in terms of the equivalent head of freshwater with constant density, this no longer happens. The groundwater flow equation in terms of equivalent freshwater head allows the calculation of volumetric flows using a form of Darcy’s law adapted for variable density but does not allow one to directly obtain the piezometric heights in the aquifer. To do so, equivalent freshwater heads must be converted to actual heads, which can be accomplished very easily with the chosen code.

SEAWAT has two procedures for coupling the groundwater flow equation with the solute transport equation: explicit and implicit. With the explicit procedure, within each stress period, the flow equation is solved for the first-time step, and the resulting advective velocity field is then used in the solution of the solute transport equation. The densities are updated, and if the stress period is not over, the next time step is taken and so on until the end of the stress period. This procedure, which alternately solves the flow and solute transport equations, is repeated for all stress periods until the simulation is completed. The implicit procedure is optional and consists of comparing the differences in densities between two successive transport solutions with a tolerance set by the user. If it is below the tolerance, the algorithm continues; otherwise, the flow is solved with new densities and so on—the reader interested in a detailed description of SEAWAT can refer to Guo and Langevin (2002).

Conceptual model, discretization and boundary conditions

The first phase to build a groundwater model is to define the conceptual model of the system, that is, how the hydrological system works in reality. This includes establishing the corresponding boundary conditions. The first conceptual model of hydrogeological behaviour of this aquifer and its relations with Petrola Lake was established by Gómez-Alday et al. 2014, and that has been expanded with the data provided in this study—sections ‘Study area and hydrogeology’ and ‘Electrical resistivity tomography’ (Fig. 4). As mentioned earlier, under natural conditions the water inputs of Pétrola Lake’s unconfined aquifer are mainly produced by recharge through infiltration of precipitation. The aquifer water outputs are by evapotranspiration from the surrounding vegetation and discharges through the lake where open water evaporation occurs. Figure 4 provides a general estimate of average water balance values, related to the boundary conditions imposed on the model. Recharge values used in this model were calibrated based on the values derived from the SIMPA model (2 hm3 year−1 in 43 km2), which are similar to 15% of the average annual precipitation for the 1990–2018 period (CHS 2010). Annual mean evaporation values were also calibrated to maintain the constant water level in the lake. Nevertheless, a prefixed water level condition was used (850 masl), obtaining stability between the inflows and outflows of the system during the simulated period.

From this conceptual model, to understand the morphology of FSI and hydrogeological behaviour, a mathematical simulation model was made by means of a two-dimensional (2D) section of the unconfined aquifer, which, with a SE–NW direction (see location in Fig. 2), almost represents one of the regional groundwater flow directions. As indicated by Anderson et al. (2015), cross-sectional or profile models are useful to test the validity of the conceptual model and are especially used when the vertical-flow component is important (e.g., case of mixed convective flows that may occur in this study). In addition, this type of 2D model reliably represents the behaviour of three-dimensional (3D) systems in a simple way, as indicated in studies by Knorr et al. (2016).

The model length is 7,000 m, and the depth is 60 m in the basin depocentre. The lateral and lower boundaries (impermeable boundaries) were treated as no-flow boundaries. The dimensions, boundary conditions and model parameters are shown in Fig. 4. The study area was horizontally discretized in two dimensions in 100 m cells with 20 layers of 5 m thickness. Neither kinetic nor sorption reactions were simulated and the longitudinal dispersivity in the model was 10 m. The initial concentration was 0.8 g L−1 for the entire aquifer, and a constant concentration (in TDS) was used for the lake (concentration reached by the brine was 80 g L−1). As indicated by Bentley et al. (2016), it is preferable to use constant values for all boundary conditions, rather than time-varying values, to maintain the simple scope of the numerical simulations. In this sense, the model was run for 10,000 years with annual time steps until reaching a TDS concentration similar to that found in the piezometers in Fig. 4 and obtaining a quasi-steady state that could explain the conceptual model in its natural (not influenced) state.

Model calibration

The calibration process consisted of adjusting the model inputs (within reasonable ranges) so that both the groundwater flow directions and the distribution of salinities were close to the field measurements. In this case it was achieved by a trial-and-error method. The model was run with initial estimates of the input parameter values (hydraulic conductivity of the materials, infiltration recharge and evaporation from the lake) and the differences between the observed (reality) and calculated (model) values were related to the groundwater head and the TDS content. This method is typically used to determine the optimal development of a groundwater flow model under natural conditions.

In the lake environment where DDF occurs, the observed values of groundwater head differ from the calculated ´equivalent freshwater head´ values used by SEAWAT (see section ‘Groundwater model settings’). This head would be defined as the level that would be observed in a piezometer if completely filled with freshwater. To determine this head, the pressure balance in the piezometer intake area must be considered, as shown in Eq. (1). Therefore, as mentioned by Guo and Langevin (2002), it is necessary to convert model results or field data, either during the model calibration or in the interpretation of the calculated results.

$$ \mathrm{Hf}=\left(\frac{\uprho \mathrm{s}}{\uprho \mathrm{f}}\right)H+\left(\frac{\uprho \mathrm{s}-\uprho \mathrm{f}}{\uprho \mathrm{f}}\right)Z $$
(2)

where Hf is equivalent freshwater head (L), H is groundwater head measured in any piezometer (L), ρs and ρf are the densities of salt water and freshwater respectively (M/L3) and Z is the reference elevation (L).

Calibration was performed in a quasi-stationary regime from model control points distributed along the aquifer section (Fig. 4). The observed groundwater heads and TDS in the control points were compared with the calculated ones. The result shows a mean absolute error between observed and calculated groundwater heads (Fig. 5) of less than 0.3 m from the mean absolute error, and between observed and calculated TDS values of 0.9 g /L, over the whole section.

Fig. 5
figure 5

Scatterplots showing calculated vs. observed a equivalent fresh groundwater heads and b TDS concentrations. Locations of observation wells are shown in Fig. 4. R2 is the determination coefficient. The mean absolute error is a 0.26 m and b 0.90 g L−1

Full size image

Results

Groundwater-flow and transport modelling under variable density effects can contribute significantly to an understanding and conceptual model of the aquifer system. The simulation shows that the hypersaline wetland is connected to the groundwater body through the interaction of interface waters with significant differences in salinity (60 g L−1 in the lake and 1 g L−1 in the aquifer). Consequently, these fluids have different densities and viscosities and, therefore, the type of flow is more complex than that produced in the case of diffusion mixing (Holzbecher 1998).

The main flow directions are centripetal towards the wetland, confirming the regional flow of the system. The regional flow velocities, with salinities of 1 g L−1 TDS, range from 0.02 to 0.04 m day−1, implying long periods of groundwater transit in the aquifer, thus confirming the tritium values found in the Gw-38 piezometer, representative of the regional flow (Fig. 5).

Beneath the wetland, the distribution of salinities resembles convection cells due to DDF, with the highest salinity values at the surface (60 g L−1 TDS). The modelling with variable density produces a situation of gravitational instability, in which the fluid with high density (heavier) is arranged over another of lower density (lighter) giving rise to mixed convective motions due to density gradients (see Fig. 6 detail). In this way, a denser saline waterfront is produced that penetrates the low-salinity water layer and can end up in a quasi-steady state forming convective cells that recirculate in the aquifer around the lake. The velocities of these convective flows range from 0.05 to 0.1 m day−1.

Fig. 6
figure 6

a Detail of the lake edges with simulation of DDF, with the presence of mixed convective flows. b Photograph showing reddish groundwater seeps related to the oxidation of metals such as iron, in the zones where the interaction between the freshwater (regional groundwater flow) and salt interface occurs (springs-seeps). c Computed morphology of the FSI, head potential and flow vectors for a 10,000-year time simulation

Full size image

As a result of the density difference between the water in the lake and the groundwater in the aquifer, a DDF into the underlying aquifer occurs up to a depth of 20 m (elevation 830 masl). At this depth, the saltwater front does not appear to advance because the DDF is affected by (1) the presence of low-permeability clay that reduces the flow velocity and (2) the hydraulic potential of the regional flow that balances the system.

There is an interface with salinities decreasing from 40 to 10 g L−1 TDS between the high-salinity zones and the relatively freshwater zones of the aquifer (Fig. 6). This wedge-shaped interface reaches from about 30 cm from the lake bottom into the interior of the aquifer for up to 200 m, with an approximate thickness of approximately 5–10 m. The simulated salinity distribution in this zone resembles the TDS profile found in the piezometers (see Fig. 3). Significant hydraulic gradients develop in this transition zone with flow velocities up to 0.1 m day−1. This effect causes vertical flows at the edges of the lake that reflect the exchange of fresh and saline groundwater and is evidenced by the presence of abundant springs and seeps in these areas (see spring distribution in Fig. 2, relationship with the conceptual model; see for example spring 2571 in Fig. 4, and seeps in Fig. 6, photo). The hydro-chemical characteristics of the springs are illustrated in the zone 2 cross-section. In addition, on these points, previous research described natural attenuation processes of nitrate pollution in the FSI (Gómez-Alday et al. 2014; Valiente et al. 2018). This research supports the hypothesis that the autochthonous reactive organic matter produced in the lake by biomass can be effectively transported by the DDF towards the interface areas (springs) where saline and polluted fresh groundwater mix.

Electrical resistivity tomography profiles were used in this study to delineate the spatial structure of the subsurface salinity of the lake environment at the time of the geophysical survey. Sections are located at the edges of the lake in each of the zones defined by the anthropogenic modifications and show, in general, different inversion results (Fig. 6). The inversion sections show resistivities ranging over several orders of magnitude (0.01 to >100 Ω-m). As pointed out by Zonge et al. (2005), the electrical resistivity of sediments depends on the salinity of the interstitial water, clay content and water content. Assuming in this case a homogeneous medium, completely saturated, and with porosities ranging between 10 and 30%, and using Eq. (1), (a = 1 and m = 2, see section ‘Electrical resistivity tomography’), and observing the resistivity of the ER aquifer (Ω-m), one can establish the average EC (mS/cm) of the water contained in the pores and therefore its TDS content (g L−1; Table 3).

Table 3 Empirical relationships between the electrical resistivity of the aquifer (ERaquifer, Ω-m), the electrical conductivity (ECwater, mS cm−1) and the salinity (TDSWater, g L−1) of the water in the pores of the aquifer according to Eq. (1). FSI freshwater/salt-water interface
Full size table

Section C is in the mining-influenced sector (MiS) (Fig. 7), where extremely low resistivity values (<10 Ω-m) are detected for almost the entire profile. According to Table 3, the EC of the pore water would be approximately 80–100 mS cm−1 (40 to >80 g L−1 TDS) due to the proximity of the salt concentration ponds. The ERT section in this area is 160 m long, and the elevations are from the surface of the lake at 850 to 830 masl. The resistivity throughout the section is very homogeneous. An additional ERT survey was carried out in 2008 in the same sector (right in the area where the piezometers are located) with three sections close to each other with 350 m length and 60 m depth. The results can be found in Gómez-Alday et al. (2014). This work interpreted a zone of the aquifer with relatively fresh water at a depth of approximately 30 m (820 masl) over which there is water of increasing salinity as a result of the salt concentration gradient in the lake. The thickness of the zone with higher salinity in these sections coincides with what was observed in the 2012 field survey.

Fig. 7
figure 7

Inverse models of resistivity distributions for 2D ERT profiles. Sections A–B: Agricultural-influenced sector (AiS). Section C: Mining-influenced sector (MiS). Section D: Urban wastewater-spill-influenced sector (UWiS). See Table 2 and Fig. 3 for cross-section locations. High resistivity (magenta-red) represents low electrical conductivity (EC), whereas low resistivity (blue-green) shows areas with high EC. Orange-yellow indicates the transition zone (see Table 3)

Full size image

Sections A and B are agricultural-influenced sectors (AiSs; Fig. 7). These sections start a few metres from the edge of the lake (860 masl) and present very varied electrical resistivities. In general, it can be inferred that high resistivities (>50 Ω-m) are observed in the lower part of the section, which would coincide with freshwater in the aquifer. According to Table 3, the electrical conductivity of the pore water would be approximately 1–20 mS cm−1 (<10 g L−1 TDS). On the other hand, in the upper part of both sections, much lower resistivities (<12.5 Ω-m) are observed, which would correspond to salt water (Table 3). Between the two zones, there is an area of variable thickness corresponding to the FSI (12.5–50 Ω-m). In the specific case of section B, the FSI in the area closest to the lake is produced by a very steep contact up to approximately 40 m depth (820 masl). At about x = 200 (from the beginning of the section), the interface is abruptly maintained until a depth of 20 m (elevation 840 masl). This wedging is not observed in section A, but a lobe with lower resistivity (<12.5 Ω-m) is detected in the centre of the section (x = 160 m), which enters the freshwater zone down to a depth of 30 m (830 masl). These very low resistivities measured in sections A–B can reach depths of 820 masl and can be considered an anomaly, while in the other ERT sections and in the groundwater model, the high resistivities do not fall below the level of 830–840 masl. This could be caused by aquifer heterogeneities, the presence of faults, and/or even a power line located in the area where the anomaly took place. Notably, changes in electrical resistivity are registered at the surface of both profiles (first 5–10-m depth), with resistivities below 50 Ω-m, corresponding to freshwater (Table 3). The location of these sections in the vicinity of irrigated crops (irrigation with freshwater from the Jurassic aquifer, Fig. 3) allows one to infer a freshwater input at the surface because of irrigation returns and surface runoff, which can modify the conductivity gradient.

Finally, in the urban wastewater-spill-influenced sector (UWiS), section D, although located on the edge of the wetland, resistivities well above 12.5 Ω-m throughout almost the entire section are detected, with electrical resistivity values at 15 m depth of more than 50 Ω-m—typical for freshwater (conductivities of less than 3 mS/cm and < 1 g L−1 TDS). The location of this section is in the vicinity of the wastewater discharge pond of the village of Pétrola (Fig. 7).

Discussion and conclusions

This study shows that coupling mathematical modelling with electrical tomography methods to study groundwater flow and solute transport is a useful method to understand the functioning of variable DDFs. Both methodologies enabled the establishment of not only a conceptual framework of the hydrogeological functioning of the hypersaline wetland in the closed basin of Pétrola in a quasi-stationary state, but also an understanding of the possible modifications due to different anthropic pressures.

The results show that the salinity of the surface waters changes with the lake hydroperiod (Fig. 3). At a certain depth, groundwater presents a low-moderate variability of salinity without statistically significant seasonal or interannual variations (see Fig. 3c), which allows inference of a salt-lake–aquifer system that was in a quasi-stationary state during the study period (2008–2018). This is the hydrogeological system behaviour simulated with groundwater-flow modelling, considering the variable density, using SEAWAT. The simulation results explain the general behaviour of the system, the spatial distribution of groundwater salinity, and the presence of mixed convective flows. The final system state across the studied cross-section lake is a saline wedge with a morphology reflecting the spatial distribution of salinity. In this sense, the results obtained not only represent an applied version of the Elder problem (Elder 1967) or “salt lake problem” (Simmons et al. 1999), but this real case study advances knowledge of the direction and magnitude of the flows of variable density. Furthermore, the study was carried out in a context where the hydrogeological heterogeneity and regional groundwater flow influence different aspects such as the presence of springs and seeps at the edge of the lake, which may govern the distribution of habitats and/or the transport of reactive substances and attenuation of pollutants at the FSI zone, as some of the mechanisms of resilience of the lake.

The quasi-steady-state simulation shows an FSI defined by a sharp salinity gradient from the surface (850 masl) to a 20–30 m depth below the lake (820 masl). From this zone onwards, the buoyancy of the saltwater, with respect to the freshwater coming from the regional flow, limits the impact of the mixed convective flows and, therefore, solute transport from the lake. Towards the edges of the lake, there is also a flow directed by density differences that extend hundreds of metres towards the recharge zones (see ERT profiles). Springs and/or seeps appear in these areas because of the bidirectional exchange between fresh and salty groundwater (Fig. 2). These processes can control not only the inflow rates of different chemical species (SO42−, NO3−, metals, microcontaminants, etc.) driven by the fresh groundwater into the lake, but also the outflow of other hydrochemical species, as for example organic matter contained by the saline water leaving the lake.

The distribution of electrical resistivities shows a snapshot of the morphology of the FSI, which confirms the influence of the DDF at the edges of the wetland. However, the interface morphology resulting from the modelling and the electrical tomography study do not coincide in all these areas (e.g. anomaly in sections A–B). Judging from the tomography data, the interface has significant lateral changes (medium heterogeneity). These lateral changes may be due to different variables such as the existence of heterogeneities in the distribution and properties of the geological materials. Both the ERT and the results of the model, within their complexity, reflect the contrast of salinities in the model and resistivities in the ERT down to approximately 830–840 masl. Also, in the urban wastewater-influenced sector (UwiS), the constant discharge of wastewater with low salinity (< 0.5 g L−1) from the nearby Pétrola municipality most probably modifies the expected salinity distribution under natural conditions.

Previous research (see Valiente et al. 2018) had postulated that the type of land use could have significant influence on the FSI geometries’ modification. In order to understand how land uses could influence the FSI, more information would be needed such as evolution of land uses over time and their correlation with ERT surveys carried out during different campaigns and modifications driven by irrigation return flows. The new information can be used to perform model validation, as boundary conditions will be applied that differ from those used for the calibration of the conceptual model.

Should the morphology of the FSI be conditioned by the dominant land use type, this might have important implications not only for the hydrogeological behaviour of the system but also for the dynamics of pollutant attenuation processes and, consequently, for the preservation of the saline ecosystems. Indeed, Pétrola Lake has proven to be an exceptional example of resilience to groundwater contamination by organic and inorganic compounds derived from agricultural and urban wastewaters. The FSI represents favourable conditions for chemical species, including contaminants, to react; at the FSI, heterotrophic denitrification occurs due to the DDF transport of autochthonous organic matter from surface water to the underlying groundwater (Gómez-Alday et al. 2014; Valiente et al. 2018). In addition, sulfur redox reactions can also occur at the FSI, exerting a strong influence on the recycling of nutrients in the human-modified system (Valiente et al. 2017).

In conclusion, the importance of the FSI in hypersaline wetlands (including coastal wetlands) as reactive zones is widely known and has been investigated in Pétrola Lake and other systems from many perspectives–see, among others, the work of Gunnars and Blomqvist (1997); Santoro (2010); Kim et al. (2011); Farajnejad et al. (2017). However, the following characteristics of the endorheic basin of Pétrola Lake make this wetland a unique study case: (1) the flow velocity of mixed flows in the interface zones (m day−1), (2) quasi-stationary state of the system, (3) presence of anthropogenic activities, including land-use influences that could modify the interfaces, and (4) knowledge of natural biodegradation processes. Therefore, future research on the coupling of reactive transport to DDF must be performed to provide new insights into the significant role of these important interfaces.