Characterization of the subsurface urban heat island and its sources in the Milan city area, Italy

Abstract

Urban areas are major contributors to the alteration of the local atmospheric and groundwater environment. The impact of such changes on the groundwater thermal regime is documented worldwide by elevated groundwater temperature in city centers with respect to the surrounding rural areas. This study investigates the subsurface urban heat island (SUHI) in the aquifers beneath the Milan city area in northern Italy, and assesses the natural and anthropogenic controls on groundwater temperatures within the urban area by analyzing groundwater head and temperature records acquired in the 2016–2020 period. This analysis demonstrates the occurrence of a SUHI with up to 3 °C intensity and reveals a correlation between the density of building/subsurface infrastructures and the mean annual groundwater temperature. Vertical heat fluxes to the aquifer are strongly related to the depth of the groundwater and the density of surface structures and infrastructures. The heat accumulation in the subsurface is reflected by a constant groundwater warming trend between +0.1 and + 0.4 °C/year that leads to a gain of 25 MJ/m² of thermal energy per year in the shallow aquifer inside the SUHI area. Future monitoring of groundwater temperatures, combined with numerical modeling of coupled groundwater flow and heat transport, will be essential to reveal what this trend is controlled by and to make predictions on the lateral and vertical extent of the groundwater SUHI in the study area.

Résumé

Les aires urbaines contribuent majoritairement à l’altération de l’environnement local atmosphérique et des eaux souterraines. L’impact de tels changements sur le régime thermique des eaux souterraines est illustré à l’échelle mondiale par une température des eaux souterraines dans les centres ville plus élevée que celle des zones rurales environnantes. La présente étude porte sur l’îlot de chaleur urbain souterrain (ICUS) formé dans les aquifères situés sous l’aire urbaine de Milan en Italie du Nord et évalue les contrôles naturels et anthropiques sur la température des eaux souterraines à l’intérieur de cette aire, en analysant les enregistrements de la charge hydraulique et de la température de ces eaux réalisés au cours de la période 2016-2020. Cette analyse montre l’occurrence d'un ICUS d’une intensité atteignant jusqu’à 3°C et révèle une corrélation entre la densité des bâtiments/ infrastructures souterraines et la température moyenne annuelle des eaux souterraines. Les flux thermiques verticaux vers l’aquifère sont fortement corrélés à la profondeur des eaux souterraines et à la densité des structures et infrastructures de surface. L’accumulation de la chaleur dans le sous-sol se traduit par la tendance à un réchauffement constant des eaux souterraines compris entre +0.1 et +0.4 °C/an, qui conduit à un gain en énergie thermique de 25 MJ/m² par an dans l’aquifère de surface à l’intérieur de la zone occupée par l’ICUS. La surveillance dans le futur de la température des eaux souterraines, combinée à une modélisation numérique couplée de l’écoulement souterrain et du transfert de chaleur, sera essentielle pour révéler les facteurs de contrôle de cette tendance et pour procéder à la prévision de l’extension latérale et verticale de l’ICUS des eaux souterraines dans la zone d’étude.

Resumen

Las zonas urbanas contribuyen en gran medida a la alteración del entorno local de las aguas atmosféricas y subterráneas. El impacto de estos cambios en el régimen térmico de las aguas subterráneas está documentado en todo el mundo por la elevada temperatura de las aguas subterráneas en los centros de las ciudades con respecto a las zonas rurales circundantes. Este estudio investiga la isla de calor urbana subsuperficial (SUHI) en los acuíferos bajo el área de la ciudad de Milán, en el norte de Italia, y evalúa los controles naturales y antropogénicos en las temperaturas de las aguas subterráneas dentro del área urbana mediante el análisis de los registros de carga y temperatura de las aguas subterráneas adquiridos en el período 2016-2020. Este análisis demuestra la ocurrencia de un SUHI con una intensidad de hasta 3° C y revela una correlación entre la densidad de las infraestructuras de construcción/subsuelo y la temperatura media anual de las aguas subterráneas. Los flujos de calor verticales hacia el acuífero están fuertemente relacionados con la profundidad de las aguas subterráneas y la densidad de las estructuras e infraestructuras de superficie. La acumulación de calor en el subsuelo se refleja en una tendencia constante de calentamiento de las aguas subterráneas entre +0,1 y +0,4 °C/año que conduce a una ganancia de 25 MJ/ m² de energía térmica al año en el acuífero poco profundo dentro de la zona del SUHI. El futuro monitoreo de las temperaturas de las aguas subterráneas, combinado con el modelado numérico del flujo de aguas subterráneas y el transporte de calor acoplados, será esencial para revelar por qué se controla esta tendencia y para hacer predicciones sobre la extensión lateral y vertical del SUHI de aguas subterráneas en el área de estudio.

摘要

城市地区是改变当地大气和地下水环境的主要因素。这种变化对地下水热状况的影响在世界范围内通过城市中心相对于周围农村地区的地下水温度升高而被关注。本研究调查了意大利北部米兰市区地下含水层中的地下城市热岛(SUHI),并通过分析 2016-2020 年获得的地下水水头和温度记录来评估了市区地下水温度的自然和人为控制。该分析表明,SUHI 的发生强度高达3° C,并揭示了建筑物/地下基础设施的密度与年平均地下水温度之间的相关性。含水层的垂直热通量与地下水的深度以及地表结构和基础设施的密度密切相关。地下的热量积累反映在+0.1 至+0.4 °C/年之间的地下水持续变暖趋势,导致 SUHI 区域浅层含水层中每年增加 25 MJ/m² 的热能。未来对地下水温度的监测,结合地下水流动和热传输耦合的数值模拟,对于揭示这种趋势是由什么控制并对研究区地下水 SUHI 的横向和纵向范围进行预测是必不可少的。

Riassunto

Le aree urbane sono soggette a una forte alterazione delle condizioni ambientali in superficie, nel sottosuolo e negli acquiferi. L’impatto di tali cambiamenti sul regime termico delle acque di falda è stato individuato in diverse parti del globo e si manifesta con temperature delle acque di falda presso il centro della città maggiori rispetto alle temperature nelle aree rurali circostanti. Si propone un’analisi dell’isola di calore urbana (SUHI) negli acquiferi sottostanti la città di Milano (Italia settentrionale) e, tramite l’analisi di serie temporali piezometriche e di temperatura acquisite tra il 2016 e il 2020, si valuta l’impatto naturale e antropico sulla temperatura dell’acqua di falda nell’area urbana. Negli acquiferi in analisi si osserva un marcato effetto isola di calore, di intensità fino a 3°C, e si mette in luce la relazione tra la densità di edificato/infrastrutture sotterranee e la temperatura media annua dell’acqua di falda. Inoltre, si osserva che l’intensità del flusso di calore verticale diretto verso l’acquifero è ben correlata con la profondità della tavola d’acqua e la densità di strutture e infrastrutture. Tale accumulo di calore nel sottosuolo causa il riscaldamento dell’acqua di falda a un tasso compreso tra +0.1 e +0.4 °C/anno, che si riflette nell’immagazzinamento di energia termica da parte dell’acquifero superficiale fino a 25 MJ/m² annui all’interno dell’isola di calore. Si ritiene che il monitoraggio continuo degli acquiferi urbani sia essenziale ai fini di valutare i fattori che controllano il trend sopra descritto e per prevedere, con l’ausilio di tecniche di modellazione numerica di flusso e trasporto di calore, l’estensione laterale e verticale dell’isola di calore negli acquiferi presenti nell’area di studio.

Resumo

As áreas urbanas são os principais contribuintes para a alteração do ambiente atmosférico local e das águas subterrâneas. O impacto de tais mudanças no regime térmico das águas subterrâneas é documentado em todo o mundo pela temperatura elevada das águas subterrâneas nos centros das cidades em relação às áreas rurais circundantes. Este estudo investiga a ilha de calor urbana subterrânea (ICUS) nos aquíferos abaixo da área da cidade de Milão, no norte da Itália, e avalia os controles naturais e antropogênicos sobre as temperaturas da água subterrânea dentro da área urbana, analisando a altura da água subterrânea e os registros de temperatura adquiridos no período de 2016-2020 período. Esta análise demonstra a ocorrência de uma ICUS com intensidade até 3 °C e revela uma correlação entre a densidade de edifícios/infraestruturas subterrâneas e a temperatura média anual da água subterrânea. Os fluxos verticais de calor para o aquífero estão fortemente relacionados com a profundidade da água subterrânea e a densidade das estruturas superficiais e infraestruturas. O acúmulo de calor na subsuperfície é refletido por uma tendência de aquecimento constante das águas subterrâneas entre +0.1 e +0.4 °C/ano que leva a um ganho de 25 MJ/m² de energia térmica por ano no aquífero raso dentro da área da ICUS. O monitoramento futuro das temperaturas da água subterrânea, combinado com a modelagem numérica do fluxo de água subterrânea acoplado e transporte de calor, será essencial para revelar o que essa tendência é controlada e fazer previsões sobre a extensão lateral e vertical da água subterrânea na área de estudo da ICUS.

Introduction

Highly urbanized areas rely on abundant and uncontaminated groundwater resources to withdraw drinking water and, more recently, the urban subsurface has been used to extract low enthalpy geothermal energy. However, urban areas are major contributors to local atmospheric and groundwater environment modifications (Oke 1973) since human activities can affect the air and groundwater natural physical-chemical conditions. Among these, the groundwater thermal regime is one of the most emergent issues in urban areas due to increasing awareness about the quality and the conservation of groundwater resources. Many recent studies have shown the extent and the intensity of the subsurface urban heat island (SUHI) effect in several cities worldwide (for a review, Bayer et al. 2019 and Zhu et al. 2011; Berlin, Cologne and Karlsruhe, Benz et al. 2016 and Menberg et al. 2013a; Basel, Epting and Huggenberger 2013; Cardiff, Farr et al. 2017; Paris, Hemmerle et al. 2019; Munich, Frankfurt and Darmstadt, Menberg et al. 2013a; Tokyo, Seoul, Osaka and Bangkok, Taniguchi et al. 2007; Amsterdam, Visser et al. 2020). The UHI is referred to as the air/ground/groundwater positive temperature anomaly encountered in the urban environment with respect to the surrounding rural areas. The UHI is often documented in densely populated and highly developed cities as its formation is related to the modifications of the environment due to urbanization such as land artificial covering/sealing with buildings, asphalt and surface infrastructures, and heat losses from anthropogenic sources. Such factors modify the solar radiation balance and the energy balance at the earth’s surface, leading to the local warming of the air and the ground temperature. Moreover, the shallow subsurface hosts several kinds of geothermal systems for heating and cooling purposes which cause thermal disturbances. For the aforementioned city sites, the shallow mean annual groundwater temperature is 2–8 °C warmer than in suburban areas and for some of them a warming trend was recognized due to global warming and urbanization effects. Benz et al. (2015) evaluated the thermal contribution of various anthropogenic heat sources for two European cities revealing the building basements and the elevated ground surface temperatures as the dominant heat sources on a citywide scale.

SUHIs were documented as an environmental issue since elevated temperatures can affect the groundwater quality in terms of chemical, physical and biological conditions (Blum et al. 2021) and living ecosystems (Brielmann et al. 2009). However, elevated groundwater temperatures may also represent an opportunity in areas with high energy demand since the thermal energy stored in the aquifers can be exploited by shallow geothermal systems (Arola and Korkka-Niemi 2014; Bayer et al. 2019). This, besides recovering part of the energy released by human activities and stored in the subsurface, might control the size and the intensity of the SUHI in large cities (and the aforementioned side effects). Thus, the analysis of the thermal regime is essential to a sustainable management of the subsurface thermal resource and, thus, to reach, by a cautious usage, a balance between the heat released by anthropogenic pollution and the heat extracted by geothermal installations. As an example, Zhu et al. (2011) estimated the thermal potential of SUHIs in several big cities due to elevated groundwater temperatures to be always higher than the total city heating demand.

The relevant studies about anthropogenic thermal pollution in the study area are focused only on the atmosphere and have pointed out the correlation between the size and the intensity of the UHI and the degree of urbanization during the evolution of city of Milan (Bacci and Maugeri 1992; Pichierri et al. 2012). In this context, a comprehensive analysis of the thermal status of the aquifers beneath the Milan city area (MCA) is still lacking but is pivotal to sustainable and efficient geothermal energy planning, considering the high density of subsurface infrastructures and the thermal demand of the city.

This study involves a detailed characterization of the subsurface thermal regime of Milan and evaluates the natural and anthropogenic controls on groundwater temperatures within the urban area, which are also fundamental for assessing the aquifer thermal potential and for the purpose of de-risking the development of shallow geothermal energy (Farr et al. 2017). The extent of the SUHI in the groundwater is outlined by analyzing high-resolution groundwater temperature data, collected by the authors since 2016, through spatio-temporal statistical techniques. The correlation between the groundwater thermal regime and various natural (e.g., depth to the water table, air temperature) and anthropogenic (e.g., percentage of area covered by buildings, sealed surfaces) indicators reveals a complex thermal framework, in which the local anthropogenic thermal contribution significantly affects the overall thermal regime by shaping the extent and the intensity of the SUHI.

Study area

The MCA (Fig. 1) is located in the northern portion of the Po plain (northern Italy) and covers an area of 181.7 km². The area is one of the most densely populated and industrialized regions in Italy and Europe (1,396,059 total inhabitants; mean population density: 7,684.6 inhabitants/km²; ISTAT 2020). In the MCA, the development of human infrastructures is extremely intensive both at the ground surface and in the subsurface reaching 35 and 50% of land covered by buildings and asphalt, respectively, in a 3-km-radius circle centered on the city (17 and 37% in the municipality). The city area hosts six underground metro lines (for a total length of 106 km), 414 deep water supply wells, 544 shallow geothermal wells, 311 ground-source heat pumps, and many deep foundations. In this context, the shallow aquifers are exploited for drinking, thermal energy production, and industrial purposes leading to a complex framework of positive and negative thermal sources.

Fig. 1

Maps showing the location of the Milan city area (MCA), the study area, with the main regional hydrological features. Country codes from ISO (2021)

Geology and hydrogeological settings

The northern portion of the Po plain represents the foreland basin of the Alpine collisional belt hosting a sequence of deposits up to 800 m thick. The various depositional events from early Pleistocene account for the creation of three main depositional sequences that correspond to as many aquifer complexes (Fig. 2; ISPRA, Regione Lombardia 2016). The deep confined aquifer (C) is characterized by continental-marine facies at the bottom, covered by a meandering river plain fining upward sequence of medium-fine sand layers interbedded with clay and silt layers and locally of conglomeratic units at the top (0.87 Ma). The overlaying semi-confined (SC) and phreatic (P) aquifers consist of fining-upward fluvioglacial sequences relative to the onset of the major glaciations and by the progradation of laterally extensive alluvial deposits and the coalescence of distal and proximal fluvioglacial outwash facies, while the deeper (SC) consists of sands and sandy gravels with a thickness between 50 m and 100 m, and the shallower (P) mainly consists of gravel with a sandy matrix 20–50 m thick. These two sequences are separated by a clayey silty regional aquitard (0.45 Ma) which shows a good continuity south of Milan and disappears moving northward.

Fig. 2

Simplified cross-section (A–A′) showing the aquifer complexes in the study area. See Fig. 1 for the section trace. The water-table elevation was obtained from the interpolation of piezometric values in 2019

The occurrence of lowland springs (called “Fontanili”) is observed across the entire Po plain (E–W for about 800 km) in a 20-km-wide belt (Fig. 1). These springs of phreatic water have been associated to a decrease of the grain size (from N to S), passing from high plain coarse sandy gravel to low plain medium-fine sand, and in the aquifer transmissivity.

In this study, only the shallow phreatic aquifer is considered, due to the lack of sufficient groundwater temperature data in the semi-confined aquifer below. However, the groundwater thermal regime below the aquitard is significantly less exposed to thermal pollution from the surface, as evidenced by deep temperature profiles. The depth of the water table ranges between 18 and 3 m from north to south, respectively, which is due to the urban drawdown cone caused by the extensive use of the groundwater in the urban area (and especially in the industrial districts located mostly to the north) and to the lower transmissivity of the shallow aquifer south of the city (De Caro et al. 2020).

Climate

The elevation of the study area ranges between 100 and 145 m asl. The climate is warm temperate with moderately cold winters, hot muggy summers and no dry season (Cfa according to the Köppen-Geiger classification; Peel et al. 2007). According to the meteorological records of the last 20 years, the mean annual precipitation is about 1,000 mm/year and the mean annual air temperature of the study area is about 14.5 °C with a minimum mean daily temperature of −5.4 °C and a maximum mean daily temperature of +31 °C (ARPA Lombardia 2020). These values are approximately constant in the whole study area, even if up to 3 °C warmer conditions can be found in the city center due to the heat island effect (Pichierri et al. 2012).

Materials and methods

Air temperature

Air temperature time series for the period 2016–2020 were obtained from the meteorological stations database managed by the regional environmental monitoring agency (ARPA Lombardia 2020). Seven monitoring stations located in the study area were used to obtain mean annual temperature maps. Data from two locations, in the suburban area to the north (A1) and in the city center (A2), respectively, are presented in Fig. 3 (see Fig. 4a for their location). The mean annual air temperature recorded in the city center is 16.0 °C, whereas outside the city is 14.7 °C. Direct air temperature measurements of the last 4 years well agree with the UHI intensity observed through remote sensing techniques by Pichierri et al. (2012) and show an average annual heat island of 1.8 °C with positive peaks during the cold season of about 5 °C (Fig. 3b).

Fig. 3

a Mean daily air temperature recorded by two meteorological stations in the Milan city area (A1: outside the city, A2: city center, see Fig. 4a for their location); b correlation between the temperature in the city center and outside the city

Fig. 4

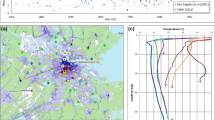
a Map of the study area showing the locations of the monitored piezometers (bubbles colored by the mean annual groundwater temperature and sized by the groundwater temperature standard deviation), the meteorological stations (A1, A2), the land use, the depth of the groundwater and the main groundwater flow direction. The 15 instrumented piezometers, referred as high-resolution (H-R) wells, are highlighted with a black star icon and numbered. b Mean annual temperature-depth profiles obtained by monthly manual measurements (lines are colored by the percentage of area covered by buildings inside a 500-m-radius-circle centered on each monitoring point). Some of the monitoring points shown in Fig. 1 are not visible in (a) but are plotted in (b) and included in the following analysis

Groundwater temperature

The shallow groundwater temperature has been monitored by the authors since 2016 with submersed automatic sensors at specific depth and with periodic temperature-depth manual logging. Open pipe piezometers were selected according to their location and depth, the degree of structural protection (i.e., within public parks and schools), and the integrity of the borehole structure. In total 61 open pipe piezometers (Fig. 4) have been monitored and, within 15 of them (“H-R wells” in Fig. 4a), submersible sensors were installed at specific depth to continuously monitor the pressure and the groundwater temperature. Groundwater vertical temperature profiles were acquired regularly in the 15 instrumented piezometers since 2016 and, from 2019, in another 46 piezometers located within and near the Milan municipality (Fig. 4b).

Temperature-depth profiles

Groundwater temperature vs depth profiles are a comprehensive tool to examine the thermal regime in space (both horizontally and vertically) and in time. They are often used to estimate subsurface water flow patterns and heat fluxes caused not only by conduction but also by advection processes (Kurylyk et al. 2019; Taniguchi et al. 1999; Zhu et al. 2015). The temperature-depth profiles presented in this study were recorded approximately every 3 months from June 2019 to September 2020 at 61 locations (five acquisitions each). Moreover, at the 15 instrumented piezometers, temperature-depth profiles have been collected since 2016, and 18 temperature-depth profiles are available for each location. The mean borehole depth from the ground surface is about 25 m (with a max of 100 m) covering mainly the shallow part of the phreatic aquifer (P); average water column of about 15 m with a max of 90 m. The temperature was recorded (accuracy of ±0.1 °C) by moving a submersible multimeter probe (In-Situ Aqua TROLL 600®) from the bottom of the piezometer to the water table with a 1-m vertical spacing. The temperature-depth profiles are presented in Fig. 4b colored by the degree of urbanization (the percentage of area covered by buildings inside a 500-m radius-circle centered on each monitoring point). The map in Fig. 4a shows the mean annual groundwater temperature of the shallowest portion of the temperature-depth profiles (i.e., first 2 m) together with the temperature standard deviation during the period 2019–2020.

Groundwater head and temperature time series

Temperature-depth profiles cover a significant portion of the study area, but their temporal resolution is very low due to the time required (about one week) to complete each measurement campaign. Groundwater levels have been recorded by the local water supply agency (MM spa) since early 1970 at many locations in the study area but, unfortunately, direct measurements of the groundwater temperature before 2016 were not available and, for this reason, the hydraulic head and groundwater temperature fluctuations were analyzed only for the period covered by continuous measurements. The selected piezometers (H-R wells in Fig. 4a) are equipped with submersible transducers (Van-Essen Instruments, Micro-Diver®) placed at constant depth by means of a stainless-steel cable of known length (L_cable) and autonomously record the pressure (±0.1 cmH2O) of the above water column (plus the atmospheric pressure) and the temperature (±0.01 °C) every 15 min. To compare temperature data from different piezometers, the monitoring devices were placed approximately at the same depth below the water table (between 3 and 5 m). Pressure data recorded by each sensor were corrected by the atmospheric pressure and converted into piezometric head (masl), knowing the ground surface elevation at each measuring location. The piezometric head is obtained through the following equation:

$$ H(t)={Z}_{\mathrm{sens}}+{P}_{\mathrm{tot}}(t)-{P}_{\mathrm{air}}(t) $$

(1)

where H(t) is the piezometric head (masl) at time t, Z_sens the elevation (masl) of the sensor obtained by subtracting L_cable to the ground surface elevation, P_tot(t) the pressure measured by the sensor at time t and P_air(t) the atmospheric pressure at time t.

Figure 5 shows the hydraulic head and temperature time series recorded at three piezometers located north of the city (No. 1), in the city center (No. 10), and south of the city (No. 15), respectively (see Fig. 4a for their locations). The configuration of each piezometer is summarized in Fig. 5a. Note that the depth of the groundwater changes substantially from north to south as outlined by contour lines in Fig. 4a.

Fig. 5

Time series at three selected locations (Nos. 1, 10 and 15 in Fig. 4a) for the period 2016–2020: a ground elevation (Z_g), water-table depth, hydraulic head as on March 2016 (Z₀) and sensor (black dots) elevation (Z_sens), b hydraulic head time series and 1-year moving average, referred to Z₀ (masl) reported in (a), and c groundwater temperature time series. Grey bars indicate the winter season

The unsaturated layer between the ground surface and the water table can be considered a thermal resistant material able to dampen the temperature signal coming from the surface and to shift it in time. Thus, the downward heat propagation depends essentially on the thickness of the unsaturated soil and the thermal properties of the soil but, in a densely urbanized environment, the input signal from the surface can be altered by site-specific anthropogenic heat sources located at the surface (e.g., heat losses from building foundations, land use and land cover materials) or in the subsurface (e.g., heat losses from underground structures, infrastructures or geothermal installations and water leakage from sewage and district heating systems; Attard et al. 2016; Benz et al. 2015; Epting et al. 2017).

Cross-correlation is used to quantify the similarity of two time series as a function of the displacement of one relative to the other. The cross-correlation (Cryer and Chan 2008) is a function of time shift (t) that expresses the covariance between the output signal (f; i.e., the groundwater temperature) and the input signal (g; i.e., surface air temperature) shifted by a time (t), divided by the square root of the product of the variance of the signals:

$$ \mathrm{CCF}(t)=\frac{\mathrm{Cov}\ \left[f(0),g\left(0+t\right)\right]}{\sqrt{\Big(\mathrm{Var}(f)\times \mathrm{Var}(g)}} $$

(2)

To assess the connection between the surface thermal regime and the groundwater thermal regime a cross-correlation analysis between the air temperature and the groundwater temperature time series recorded at the 15 instrumented piezometers was carried out.

Human-made structures and infrastructures

Urban areas are characterized by a dense texture of structures and infrastructures that modify the water infiltration and groundwater flow processes, the heat transfer between the surface and the subsurface, and eventually the heat transport in the aquifer. In this context, the groundwater thermal regime is affected by several natural and human-activities-related factors already identified by many authors (Benz et al. 2015; Epting and Huggenberger 2013; Ferguson and Woodbury 2004; Menberg et al. 2013b; Taylor and Stefan 2009) such as:

• 1. The thickness of the unsaturated zone that dampens the temperature fluctuations coming from the surface

• 2. The groundwater flow velocity that drives the heat transport in advective-dominated aquifers

• 3. The presence of surface water bodies and the degree of interaction with the groundwater

• 4. The percentage of buildings, surface infrastructures and sealed/cemented ground

• 5. The presence of underground structures/infrastructures (e.g., tunnels) or deep foundations

• 6. The use of low-enthalpy geothermal wells

In densely populated urban areas, the anthropogenic component of the subsurface thermal budget is nonnegligible or even prevailing (Epting and Huggenberger 2013). Thus, to characterize the influence of nonnatural thermal contributors on the groundwater thermal regime it was necessary to collected and homogenized information on the land cover, the surface/underground transport network (i.e., railway and metro lines), the location of water supply wells, shallow geothermal wells and ground source heat pumps (GSHP), the sewerage and the district-heating pipe distribution networks, the groundwater depth and hydraulic gradient, and on the mean annual air temperature (Fig. 6). Surface structure and infrastructure datasets were collected from the regional geographic database (Regione Lombardia 2020), whereas surface information (e.g., land cover) was derived from satellite image interpretation, while subsurface information (e.g., tunnels, district heating network) was collected and digitized from available thematic maps and technical drawings.

Fig. 6

Maps of the study area showing the spatial distribution of: a buildings and asphalted surfaces, b parks, croplands and bare soil, c surface waters and springs, d mean groundwater depth and hydraulic head isolines, e underground tunnels and surface railways, f water supply wells, geothermal wells and ground source heat pumps (GSHP), g district heating and sewer networks, and h mean annual air temperature

Results and discussion

Subsurface warming trends were observed in many big cities worldwide (Arola and Korkka-Niemi 2014; Epting and Huggenberger 2013; Farr et al. 2017; Menberg et al. 2013a; Taniguchi et al. 2007; Visser et al. 2020; Zhu et al. 2011). In those cities, the shallow mean annual groundwater temperature at urbanized locations is 2–8 °C warmer than less urbanized suburban areas. According to the mentioned studies, this is due to anthropogenic heat losses in the subsurface (e.g., from tunnels, foundations, GSHPs) and to indirect heat accumulation of urban surface structures and infrastructures (e.g., due to solar radiation on concrete structures). It has been demonstrated that the development of the SUHI is related to anthropogenic modifications of the land use and the percentage of area covered by buildings (Benz et al. 2015, 2018). On the other hand, in order to quantify the amount of heat released in the aquifer a robust knowledge of the hydrogeological setting of the area and of the conterminous regions is essential (Bidarmaghz et al. 2019). In this work, the groundwater level and the shallow groundwater temperature fluctuations observed in the MCA were analyzed by means of spatio-temporal statistical and correlation techniques, revealing a SUHI effect up to 3 °C intense. This value falls within the above cited range for the observed shallow groundwater UHI in large cities.

Section B–B′ across the Milan city area, shown in Fig. 7, summarizes the shallow groundwater thermal regime along the main groundwater flow direction and highlights the extent and the intensity of the SUHI effect in the groundwater.

Fig. 7

North–south cross-section (see Fig. 4a for its location) showing a the groundwater depth and the distribution of the mean annual groundwater temperature interpolated using data from temperature-depth profiles of 2020 within 500 m from both sides of the section line, and the temperature annual standard deviation; b the tunnels crossed by the section, the number of geothermal wells within 250 m from both sides of the section (biggest circle = 20 wells) and the building density

Spatial analysis

Shallow groundwater temperature-depth profiles in the study area show a significant variation within the thermal regime. To untangle this variability, the groundwater temperature-depth profiles were interpolated over time and, according to the shape of the profiles and the temperature fluctuations, four main groups were identified (Fig. 8): (1) undisturbed (i.e., the mean annual groundwater (GW) temperature is equal to the mean annual air temperature) profiles with shallow groundwater (<10 m), (2) undisturbed profiles with deep groundwater (>10 m), (3) disturbed (i.e., the mean annual GW temperature is more than 1 °C higher than the mean annual air temperature) profiles in highly urbanized areas and (4) profiles close to shallow water bodies.

Fig. 8

Groundwater temperature-depth profiles interpolated over time (2016–2020). Dates of sampling are highlighted with ticks at the top of each box. The location of the selected profiles is highlighted in Fig. 4a with the following codes (from left to right): 12, 1, 10 and 13

Spatial correlation

To assess the impact of natural and anthropogenic variables on the groundwater thermal regime the mean annual groundwater temperature (GW Temp) and the temperature standard deviation (SD), calculated using the data from the temperature depth profiles at the water-table depth, were compared to 12 site-specific parameters. These 12 parameters include, namely:

• 1. The mean annual groundwater depth (GW Depth) obtained from manual measurements

• 2. The mean annual air temperature (Air Temp) obtained from meteorological stations

• 3. The percentage of area covered by buildings

• 4. The percentage of area covered by asphalt

• 5. The percentage of area covered by railway ballast

• 6. The percentage of area covered by green areas

• 7. The upstream distance to underground tunnels along the main flow direction

• 8. The distance to the nearest river or canal

• 9. The number of GSHPs

• 10. The total length of district heating pipelines

• 11. The equivalent horizontal hydraulic conductivity (K) of the phreatic aquifer

• 12. The local hydraulic gradient

The values for 3, 4, 5, 6, 9 and 10 were computed over a 500-m-radius-circle centered on each monitoring point. The values for 11 and 12 were obtained from the work by De Caro et al. (2020).

To this aim, the correlation between each combination of GW Temp and SD with the 12 selected variables was evaluated by means of the Pearson’s correlation coefficient (R). Figure 9 shows the correlation of each pair, where the Pearson’s R is specified below each plot (which is emphasized in bold if the p value is lower than 0.05). The Pearson’s R is also represented by the color and the elongation of the ellipses, and the thick red lines indicate the linear best fit. It must be noted that the slope of the linear fit does not necessarily represent the correlation, and the scale of the variables varies significantly.

Fig. 9

Correlation between the mean annual groundwater temperature (GW Temp), the temperature standard deviation (SD) and the 12 selected variables. The red lines represent the linear best fit, the ellipsis color intensity and their elongation represent the Pearson’s R, which is also reported below each plot and emphasized in bold if the p value is lower than 0.05

The mean annual groundwater temperature is positively correlated to the air temperature and the percentage of buildings, and negatively to the groundwater depth, the distance from tunnels, and canals or rivers. These last ones are inversely correlated to the degree of urbanization as the canals crossing the city are typically culverted and sealed. A lower, but still significant (p < 0.05), inverse correlation is observed between the mean annual groundwater temperature, the hydraulic conductivity and the hydraulic gradient. The groundwater temperature standard deviation is inversely correlated to the groundwater depth and the percentage of area covered by asphalt and, directly, to the percentage of green unsealed areas. This suggests that, among natural variables, the thickness of the unsaturated zone dampens the amplitude of seasonal temperature fluctuations (Kurylyk et al. 2015) and the groundwater flow velocity controls the heat accumulation in the groundwater (Ferguson and Woodbury 2004; Zhu et al. 2015). In addition, human-related activities appear to strongly affect the shallow groundwater thermal regime. Among these, the percentage of built area and the distance from tunnels are the most correlated with the mean annual groundwater temperature. This is highlighted in Fig. 10 where the mean annual groundwater temperature and the standard deviation are summarized by means of a correlation plot against the groundwater depth, the building density and the upstream distance to tunnels along the main groundwater flow direction. Areas with a shallow water table and low building density show a very high temperature standard deviation (Fig. 10a), while the mean annual GW temperature is variable (but in general higher with respect to deeper locations) as the groundwater is more sensitive to thermal inputs from the surface. At deeper groundwater locations, the standard deviation is lower and the mean GW temperature is related to the building density and, thus, depends on the degree of urbanization. Due to the complexity of superimposed thermal contributors some outliers that are evident in Fig. 10a can be related to site-specific conditions, e.g. the proximity to specific heat/cool sources such as canals, geothermal reinjection wells and tunnels. As demonstrated by Attard et al. (2016), underground structures such as tunnels can generate a very strong heat flow, but their thermal perturbation is appreciable only at local scale (approximately within 200 m from the heat source, depending on the volume of the structure, the thermal properties and the groundwater flow velocity). Figure 10b shows the mean annual groundwater temperature and the SD at locations within 800 m downstream underground tunnels. Many points located at a distance smaller than 200 m from tunnels show mean annual temperatures higher than 18 °C. For those locations a strong thermal perturbation is observed but it should be noted that the perturbation caused only by tunnels in this area is difficult to disentangle as they are located near the city center where the mean annual groundwater temperature is above 18 °C and multiple heat sources act together to obtain a complex thermal regime.

Fig. 10

Correlation plots showing the relation between the mean annual groundwater temperature (color scale), the temperature standard deviation (dots dimension), the groundwater depth and: a the building density and b the distance from tunnels upstream the main groundwater flow direction

Vertical heat flow

Temperature-depth profiles were used to estimate the vertical heat flow in the shallow part of the aquifer by computing the thermal gradient between the groundwater temperature at the water table and 2 m below. With this assumption (which neglects the effects of horizontal advective flow) the vertical thermal gradient was considered an indicator of the thermal perturbation from above. The shallow thermal gradient was computed at 61 different locations for each of the five measurement campaigns. Figure 11 shows the statistical distribution of the thermal gradient for five groundwater depth intervals and three building density classes. Positive values indicate heat flow directed from the surface towards the aquifer and, vice versa, negative values indicate heat flow towards the surface. Shallow groundwater classes (from 0 to 10 m) show both positive and negative thermal gradient according to the season, while the thermal gradient of deep groundwater classes (more than 10 m) is slightly positive for all the seasons (i.e., there is a constant heat flow directed to the aquifer). Similarly, the thermal gradient is more sensitive to seasonality where the building density is lower and it is almost constant, with positive values, for high building-density classes. From the analysis of vertical profiles, it can be inferred that groundwater is undergoing warming in almost the entire study area. Seasonal fluctuations are more pronounced where the groundwater is shallow and where the urban density is low. At high urban density locations, a positive heat flow directed towards the aquifer is observed, due to heat losses from building basements/foundations and the heat accumulation in the shallow subsurface is reflected by a significant groundwater warming during all the seasons.

Fig. 11

Vertical thermal gradient computed as the difference between the groundwater temperature at the water table and the temperature 2 m below, classified by the groundwater depth and the building density (on the right the number of samples in each class). Positive values indicate heat flow directed from the surface to the aquifer and, vice versa, negative values indicate flow towards the surface

Temporal analysis

Cross-correlation

High-resolution groundwater head and temperature time series available from 2016 at a specific depth below the water table were used to estimate the link between the atmosphere and the groundwater by means of a cross-correlation analysis between the air and the groundwater temperature time series. Figure 12a,b show the air and the groundwater temperature signals at location No. 8 (Fig. 12c) and the cross-correlation function obtained by combining the time series, respectively. At each location, the time shift, also referred to as Lag (days), to which corresponds the best correlation between the signals (positive peaks) and the value of the cross-correlation function for that specific time shift t (referred to as cross-correlation coefficient: CCC) were derived. Figure 12c shows the spatial distribution of the calculated Lag and CCC, where the first indicates the delay between the signals and the second the similarity between the signals.

Fig. 12

Cross-correlation analysis: a air (red) and groundwater (black) temperature time series recorded at well No. 8, dashed line represents the difference between the groundwater temperature and the linear trend (thin line). b Example of the cross-correlation function at well No. 8, best correlation is observed with a lag of 285 days. c Map showing the spatial distribution of the lag times and the cross-correlation coefficients (CCC) for the high-resolution monitoring points in the study area. d Correlation between lag times, CCC, hydrogeological settings (GW depth, rivers, flow velocity) and variables related to urbanization (% of buildings, asphalt, railway and green areas, tunnels and district heating). The Pearson’s R is reported below each plot

Then, similarly as described in section ‘Spatial correlation’, the Lag and the CCC were compared to the groundwater depth, the groundwater flow velocity, and variables related to the urban density by means of a correlation analysis (Fig. 12d). In accordance with the theoretical hypothesis (Ferguson and Woodbury 2004; Kurylyk et al. 2015; Zhu et al. 2015), the depth to the water table and the groundwater flow velocity play a role in lowering the cross-correlation coefficient (i.e., by dampening the temperature fluctuations) and shifting the groundwater temperature signal in time. Urbanization also plays a significant role, leading to a decrease in correlation with the increase of the building density (small dots in Fig. 12c). Moreover, the percentage of green areas is inversely correlated to the lag times as progressive surface land covering with asphalt/concrete dampens the amplitude of groundwater temperature fluctuations.

Some anomalies with respect to the generally observed trend (governed by groundwater depth and urban density) were observed at specific locations (Nos. 3, 5 and 7), where a very high correlation coefficient (>0.6) and small lag times (<90 days) were observed despite deep groundwater (>15 m depth) and relatively dense urbanized conditions (building density > 30%). To untangle this unexpected regime the variables reported in Fig. 12d were analyzed revealing a strong effect of the percentage of area covered by railway ballast (at locations Nos. 3, 5 and 7 the highest percentage of railway was observed). A further analysis is needed as the railway ballast seems to improve the thermal link between the atmosphere and the groundwater, possibly by favoring both rainfall infiltration and air circulation. Moreover, at well No. 5, some very close (10 m) excavation works (open pit 20 × 20 m wide and 3–5 m deep) may have further influenced the natural water infiltration and heat transport processes.

Trend analysis

Figure 13a,b shows the hydraulic head and temperature fluctuations with respect to the hydraulic head as on March 2016 and to the mean annual temperature of 2016. During the monitored years, a general groundwater-level lowering was observed from 2016 to 2019 followed by a rising after 2019 (Fig. 13a). The analysis of groundwater temperature time series revealed a comprehensive warming trend at almost all the monitored locations (Fig. 13b). To assess the temperature trend for the period 2016–2020 the groundwater temperature time series were averaged by means of a 1-year moving window. Then, to compare the multi-annual temperature variation, each yearly averaged time series was fitted with a linear regression model, obtaining the temperature change rate at each location ranging from ~0 to ~0.5 °C/year in the city center (Fig. 13c). The yearly trend of the air temperature was calculated accordingly showing no significant variation for the period analyzed.

Fig. 13

a Hydraulic head and b temperature fluctuations with respect to the hydraulic head as on March 2016 and to the mean annual temperature of 2016. c Bar plot showing the linear fit trend of the groundwater temperature time series observed from 2016 to 2020; the gray scale represents the building density at each location. d Bar plot showing the hydraulic head lowering and rising rate observed from 2016 to 2019 (red) and from 2019 to 2020 (green), respectively, and e map showing the spatial distribution of the hydraulic head fluctuation rates in the study area

Similarly, the groundwater fluctuation rate was calculated at each location separately for the period 2016–2019 and 2019–2020 (Fig. 13d), showing rates up to 1 m/year to the north of the city where most of the industrial activities were located and the aquifer transmissivity is higher. Figure 13e shows the spatial distribution of the groundwater level change for the period 2016–2019 (red, decreasing) and 2019–2020 (green, rising).

The temperature trend obtained from the linear regression (Fig. 13c) was interpolated over the study area by means of ordinary kriging as shown in Fig. 14a. The difference between the mean daily groundwater temperature and the 1-year moving window average was computed for each day of the monitored period (from July 2016 to July 2020 to represent 4 full years) and summarized by the standard deviation of the computed differences at each location (size of the circles in Fig. 14a). Higher values indicate strong seasonal fluctuations around the 1-year moving window average value. An overall warming trend of about +0.15 °C/year was observed in the entire study area with positive exception in the city center (+0.44 °C/year) and in the northern and southern sectors (+0.24 °C/year). The slightly negative trend observed at well No.13 could be due to its proximity to one of the main canals of the city, which due to its periodic opening and closing can affect the temperature signal.

Fig. 14

Maps showing: a the groundwater temperature trend observed from 2016 to 2020 and the amplitude of the seasonal fluctuations expressed by the standard deviation of the differences between the daily groundwater temperature and the 1-year moving window average; b the energy gained yearly by the shallow aquifer and the energy content with respect to a reference temperature of 14.7 °C (mean annual air temperature). c Box and whiskers plots showing the distribution of the groundwater temperature during the continuous monitoring (2016–2020) at the labelled wells (a). The reader must be aware that the interpolations in these maps are only representative, and the heterogeneity of these variables is very high in such a complex environment

This positive warming trend leads to heat accumulation in the shallow aquifer. By considering a constant temperature variation along the entire shallow phreatic aquifer (i.e., considering only the shifting of temperature-depth profiles towards higher temperature as shown in Fig. 8) the energy gained per year by the shallow aquifer was estimated according to Eq. (3):

$$ {E}_{\mathrm{gain}}={C}_{\mathrm{bulk}}\times B\times \Delta T $$

(3)

where C_bulk is the equivalent thermal capacity of the bulk aquifer which, according to VDI 4640 (2001), was set 2.4 MJ/m³/K for the saturated portion of the phreatic aquifer; B is the saturated thickness of the phreatic aquifer, and ∆T is the mean annual temperature variation shown in Fig. 14a. The size of the circles in Fig. 14b represents the energy already stored in the shallow aquifer with respect to a constant reference temperature of 14.7 °C (mean annual air temperature, Fig. 14c) and was obtained for each location by replacing ∆T in Eq. (3) with the difference between the mean annual groundwater temperature of 2016 and the reference temperature. The statistics of the groundwater temperature for the period 2016–2020 are summarized through boxplots in Fig. 14c where the mean annual air temperature is also shown.

Since the analysis of the air temperature time series in the study area did not reveal a significant warming trend for the last 30 years, the warming rate observed from temperature-depth profiles and temperature time series (that is reflected by up to +25 MJ/year/m² of thermal energy gained by the shallow aquifer beneath the city center) must be mainly due to human-related heat sources. This value agrees with the estimates of +70 MJ/year/m² for the only urban area of Cologne (Zhu et al. 2011), +2.1 and + 1.0 × 10⁹ MJ/year for the municipalities of Karlsruhe (61.9 km², +33.9 MJ/year/m²) and Cologne (81.3 km², +12.3 MJ/year/m²; Benz et al. 2015).

Conclusions

This study reveals the extent and the intensity of the urban heat island effect in the groundwater beneath the Milan city area and attempts to identify the natural and anthropogenic controls on the thermal regime. High-resolution groundwater temperature data were collected by the authors since 2016 and analyzed for the first time in the study area. The integration from different sources of groundwater temperature data and the analysis of the spatial distribution of the mean annual groundwater temperature and the seasonal fluctuations revealed differences up to 3 °C between the city center and the surrounding rural areas located both upstream and laterally to the main groundwater flow direction. Downstream the city center, a superimposition of the effects due to the intense urbanization and the proximity of the water table to the surface is observed leading to higher groundwater temperature and strong seasonal fluctuations in the shallow portion of the aquifer. The impact of natural and human-related processes on the groundwater thermal regime was assessed by means of a bivariate and a cross-correlation analysis revealing the thickness of the unsaturated zone and the density of surface structures/infrastructures to be the most relevant parameters at controlling the vertical heat fluxes into the aquifer. The most relevant anthropogenic heat sources were identified as the percentage of building cover, the sealing of land with asphalt and concrete structures, and the presence of underground tunnels and geothermal systems. Their spatial density varies significantly in the study area but reaches the maximum simultaneously inside a 2-km-radius circle centered in the city center where the SUHI is observed. Inside this area a constant inverse thermal gradient (i.e., heat directed into the aquifer) of about +0.1 °C/m and a warming trend of +0.4 °C/year were observed, leading to a gain of thermal energy by the shallow aquifer beneath the SUHI up to +25 MJ/year/m².

Insights from this city-scale groundwater temperature analysis, which is original for the Milan city area, are useful to future research, including city-scale numerical modeling, about quantifying the contribution of single anthropogenic heat sources on the thermal regime of the shallow aquifers to delineate possible subsurface warming scenarios and support the sustainable development of shallow geothermal energy. In this context, a well-designed monitoring network would provide valuable data about changes in the groundwater environment linked to the changes in the natural and human-related surface thermal regime and is pivotal to estimate the heat accumulated in the SUHI and to assess the thermal potential upon realistic groundwater thermal conditions.