Abstract
Knowledge of the hydraulic and geological properties of karst systems is particularly valuable to hydrogeologists because these systems represent an important source of potable water in many countries. However, the high heterogeneity that characterizes karst systems complicates the definition of karst hydrogeological properties, and their estimation involves complex and expensive techniques. In this study, a workflow for karst spring characterization was used to analyze two springs, Nanto spring and Mossano spring, located in the Berici Mountains (NE Italy). Based on the data derived from 4 years of continuous hourly monitoring of discharge, water temperature and specific electrical conductivity, a hydrogeological conceptual model for the monitored springs was proposed. Flow rate measurements, which combined recession curve, flow duration curve and autocorrelation function techniques, were used to evaluate the spring discharge variability. Changes in spring discharge can be related both to the degree of karstification/permeability and to the size of the karst aquifer. Moreover, combining monitored parameters and rainfall—analyzed by the cross-correlation function and VESPA (Vulnerability Estimator for Spring Protection Areas) index approach—permitted assessment of the spring response to recharge and the behavior of the drainage system. Although the responses to the recharge events were quite similar, the two springs showed some differences in terms of the degree of karstification. In fact, Mossano spring showed a more developed karst system than Nanto spring. Three systems (two karsts and one matrix/fractured) are outlined for Mossano spring, while two systems (one karst and one matrix/fractured) are outlined for Nanto spring.
Résumé
La connaissance des propriétés hydrauliques et géologiques des systèmes karstiques est. particulièrement utile pour les hydrogéologues, car ces systèmes constituent des ressources en eau importantes dans de nombreux pays. Cependant, la grande hétérogénéité qui caractérise les systèmes karstiques rend difficile la définition des propriétés hydrogéologiques, et leur estimation implique la mise en œuvre de techniques complexes et onéreuses. Dans cette étude, une méthode de travail pour la caractérisation des sources karstiques a été utilisée pour l’analyse de deux sources (sources Nanto et Mossano), localisées dans les Monts Berici (Nord-Est de l’Italie). Sur la base des données issues de quatre ans de suivi horaire des débits, de la température et de la conductivité électrique de l’eau, un modèle hydrogéologique conceptuel des sources suivies a été proposé. Les mesures de débits, qui combinent les courbes de récession, les courbes de durée d’écoulement et les techniques de fonction d’autocorrélation, ont été utilisées pour évaluer la variabilité du débit des sources. Les changements du débit des sources peuvent être corrélés à la fois au degré de karstification/perméabilité et à la taille du système karstique. De plus, la combinaison des paramètres de suivi avec les données de pluie (analysée avec la fonction de corrélation croisée et l’approche indicielle VESPA - Estimateur de Vulnérabilité pour les Aires de Protection des Sources) a permis d’évaluer la réponse des sources à la recharge et le comportement du système de drainage. Bien que les réponses aux événements de recharge soient quasi similaires, les deux sources présentent certaines différences en termes de degré de karstification. En fait, la source Mossano montre un système karstique plus développé que la source Nanto. Trois systèmes (deux karstiques et un matriciel/fracturé) sont mis en évidence pour la source Mossano, alors que deux systèmes (un karstique et un matriciel/fracturé) caractérisent la source Nanto.
Resumen
El conocimiento de las propiedades hidráulicas y geológicas de los sistemas kársticos es especialmente valioso para los hidrogeólogos, ya que estos sistemas representan una importante fuente de agua potable en muchos países. Sin embargo, la gran heterogeneidad que caracteriza a los sistemas kársticos complica la definición de sus propiedades hidrogeológicas, y su estimación implica técnicas complejas y costosas. En este estudio, se utilizó un flujo de trabajo para la caracterización de manantiales kársticos para analizar dos de ellos, el manantial de Nanto y el manantial de Mossano, situados en las montañas Berici (NE de Italia). Basado en los datos derivados de cuatro años de monitoreo horario continuo de la descarga, temperatura del agua y conductividad eléctrica específica, se propuso un modelo conceptual hidrogeológico para los manantiales monitoreados. Se utilizaron medidas de caudal, que combinaron la curva de recesión, la curva de duración del caudal y técnicas de función de autocorrelación, para evaluar la variabilidad de la descarga de los manantiales. Los cambios en la descarga de los manantiales pueden estar relacionados tanto con el grado de karstificación/permeabilidad como con el tamaño del acuífero kárstico. Además, la combinación de los parámetros monitoreados y la lluvia—analizados por la función de autocorrelación y el enfoque del índice VESPA (Vulnerability Estimator for Spring Protection Areas)—permitió la evaluación de la respuesta del manantial en la recarga y del comportamiento del sistema de drenaje. Aunque las respuestas a los eventos de recarga fueron bastante similares, los dos manantiales mostraron algunas diferencias en términos del grado de karstificación. De hecho, el manantial de Mossano mostró un sistema kárstico más desarrollado que el de Nanto. Tres sistemas (dos kársticos y uno de matriz/fracturado) se perfilan para el manantial Mossano, mientras que dos sistemas (uno kárstico y otro de matriz/fracturado) son descriptos para el manantial Nanto.
摘要
了解岩溶系统的水力和地质特性对水文地质学家来说特别有意义, 因为这些系统是许多国家重要的饮用水来源。然而, 岩溶系统所具有的高度非均质性使得岩溶水文地质性质的定义变得复杂, 而岩溶水文地质性质的评价又涉及复杂而昂贵的技术。在本研究中, 应用岩溶泉水特征化的工作流程分析了位于Berici 山(意大利东北部)的Nanto泉和Mossano泉。根据连续4年逐时监测的流量、水温和比电导率数据, 提出了泉水监测的水文地质概念模型。采用流量测量方法, 结合衰退曲线、流量持续时间曲线和自相关函数技术, 对泉流量的变化进行了评价。泉水流量的变化既与岩溶作用/渗透能力有关, 也与岩溶含水层的大小有关。此外, 结合监测参数和降雨量(通过互相关函数和VESPA(泉保护区脆弱性估计)指数方法进行分析), 可以评估泉对补给的响应和排水系统的行为。结果显示两个泉尽管对补给的响应非常相似, 但在岩溶化程度方面表现出一些差异。事实上, Mossano泉比Nanto 泉有更好发育的岩溶系统。本研究对Mossano泉进行了3个系统(2个岩溶和1个基质/裂隙)的描述, 对Nanto泉进行了2个系统(1个岩溶和1个基质/裂隙)的描述。
Resumo
O conhecimento das propriedades hidráulicas e geológicas dos sistemas cársticos é particularmente valioso para os hidrogeólogos, porque esses sistemas representam uma importante fonte de água potável em muitos países. No entanto, a alta heterogeneidade que caracteriza os sistemas cársticos dificulta a definição das propriedades hidrogeológicas dos carstes e sua estimativa envolve técnicas complexas e caras. Neste estudo, um fluxo de trabalho para a caracterização das nascentes cársticas foi utilizado para analisar duas nascentes, nascente Nanto e nascente Mossano, localizadas nas montanhas Berici (NE Itália). Com base nos dados derivados de quatro anos de monitoramento horário contínua da descarga, temperatura da água e condutividade elétrica específica, foi proposto um modelo conceitual hidrogeológico para as nascentes monitoradas. Medidas de vazão, que combinaram curva de recessão, curva de duração de fluxo e técnicas de função de autocorrelação, foram usadas para avaliar a variabilidade da descarga da nascente. Alterações na descarga da nascente podem estar relacionadas tanto ao grau de carstificação/permeabilidade quanto ao tamanho do aquífero cárstico. Além disso, a combinação de parâmetros monitorados e chuvas—analisados pela função de correlação cruzada e abordagem de índice VESPA (Vulnerability Estimator for Spring Protection Areas/Estimador de Vulnerabilidade para Áreas de Proteção de Nascentes) permitiu avaliar a resposta da nascente à recarga e o comportamento do sistema de drenagem. Embora as respostas aos eventos de recarga tenham sido bastante semelhantes, as duas fontes mostraram algumas diferenças em termos do grau de carstificação. De fato, a nascente de Mossano mostrou um sistema cárstico mais desenvolvido que a nascente de Nanto. Três sistemas (dois cársticos e um matriz/fraturado) são delineados para a nascente Mossano, enquanto dois sistemas (um cárstico e um matriz/fraturado) são delineados para a nascente Nanto.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The analysis of karst springs behavior is a widespread activity in hydrogeology because karst aquifers are a primary source of human water supply in many countries (Ford and Williams 2007). The estimation of available water and the determination of water quality and vulnerability will play a growing strategic role in the future because of the increasing demand for water for drinking, irrigation, and industrial purposes (Assaad and Jordan 1994; Bakalowicz 2005; Crawford and Ulmer 1994; Field 1992; Goldscheider 2012; Kresic and Stevanović 2010). The quantitative characterization of karst systems requires the estimation of realistic hydraulic and geometric parameter values for both the rock matrix and the conduit network (Kovács and Perrochet 2008). Classical geological and hydrogeological surveys of karst (i.e., borehole tests, tracer experiments, speleological and geophysical observations) are not only expensive and sometimes inapplicable but also provide limited information due to the great heterogeneity of karst systems (Kovács et al. 2005).
The monitoring of spring discharge and water physical-chemical parameters (e.g., temperature and electrical conductivity), accompanied by analysis of the resulting hydrographs and chemographs, represents a classical hydrogeological prospection technique that is very helpful when detailed analyses such as tracer tests and speleological investigations, are not applicable. This approach allows for assessment of the basic hydrogeological characteristics of a karst aquifer that can be used for planning its utilization and protection. Necessary considerations regarding this method are as follows: (1) the spring hydrograph provides an integrated representation of the network of fractures and conduits transferring groundwater from the recharge to the outflow area and (2) the quality and quantity of groundwater are of diagnostic importance for understanding the functioning of the system (Dreiss 1982, 1989; Ford and Williams 2007; Knisel 1972).
Several authors have focused their attention on the analysis of recession curves. Considering a recharge event producing an increase in spring discharge, the recession curve describes the part of the hydrograph showing the progressive decrease in discharge from the peak of the discharge to the pre-storm outflow (Ford and Williams 2007). Starting with the works of Boussinesq (1877) and Maillet (1905), recession curve analysis (RCA) has been used to infer the geometrical or hydraulic properties of aquifers supplying springs (Bonacci 1993; Brutsaert and Nieber 1977; Covington et al. 2009; Dewandel et al. 2003; Fiorillo 2014; Kresic and Stevanović 2010; Padilla et al. 1994; Szilagyi et al. 1998; Troch et al. 1993) or to identify the flow-type induced by different degrees of aquifer karstification (Baedke and Krothe 2001; Birk and Hergarten 2010; Kovács and Perrochet 2008; Kovács et al. 2005; Malík and Vojtková 2012).
Another approach for hydrograph analysis, derived from hydrological practices, is the use of flow duration curves (FDCs). The FDC is a cumulative frequency curve showing the percent of time during which the discharge is equal to or exceeds a specified threshold in a given period. This approach has been used to assess the range and variability of spring discharge (Hartmann et al. 2013; Kovačič 2010; Malík 2015).
Drainage through a karst system can be represented as an impulse function that transforms the recharge input pulse into a flow rate variation at a spring recorded by a hydrograph. The analysis of this function permits the identification of the hydrogeological features of an aquifer and its degree of karstification (Ford and Williams 2007). Time series analysis is a signal processing method employed to explore impulse functions and to improve the understanding of the hydrogeological behavior of a karst system. Mangin (1984) was the first to apply this approach in karst hydrogeology, using autocorrelation and spectral density functions to analyze the spring discharge. Subsequently, different authors have extended the application of these methodologies to other parameters (e.g., precipitation, water temperature, electrical conductivity) by the introduction of other functions such as cross-correlation (Adji and Bahtiar 2016; Bailly-Comte et al. 2011; Fiorillo and Doglioni 2010; Kovačič 2010; Ladouche et al. 2014; Larocque et al. 1998; Mayaud et al. 2014; Zhang et al. 2013). The most widely used methodology consists of the concomitant utilization of autocorrelation functions (ACFs) and cross-correlation functions (CCFs); in particular, an ACF examines how a value depends on preceding values over a period of time (Larocque et al. 1998; Mayaud et al. 2014). The use of ACFs allows one to quantify the memory effect of a system (Mangin 1984; Panagopoulos and Lambrakis 2006), while in contrast, CCFs provide an overview of the interrelationship between the input and output series (Larocque et al. 1998; Panagopoulos and Lambrakis 2006). In karst hydrogeology, a CCF is usually employed to evaluate the correlation between rainfall and spring discharge, highlighting the response of a system to the recharge impulse (Chung et al. 2018; Fabbri et al. 2013; Fiorillo and Doglioni 2010; Liu et al. 2011; Tagne and Dowling 2018; Zhang et al. 2013).
The Vulnerability Estimator for Spring Protection Areas or VESPA index (Galleani et al. 2011) is a promising method used to assess the degree of vulnerability of a karst spring, but it can also be used to classify general hydrogeological behavior through the analysis of spring responses to recharge impulses. The prevailing behavior is identified considering two parameters: spring discharge and electrical conductivity (Banzato et al. 2017). Moreover, an advantage of this method is the ability to combine these two parameters with water temperature to assess spring vulnerability.
In this study, the RCA, FDC, ACF and CCF techniques were used to define the conceptual hydrogeological model of two springs located in the Berici Mountains (northeastern Italy). In addition, the parameters defined by the VESPA index were used to assess the type of flow and vulnerability of springs. Moreover, particular attention was paid to the meaning of the CCF analysis between spring discharge and electrical conductivity and between spring discharge and water temperature as an estimate of the minimum transit time inside the conduit network feeding the springs. These techniques enable use of only the monitoring parameters together with rainfall events to obtain qualitative information about the hydrogeological features characterizing the analyzed springs.
The objectives of this study are twofold: (1) outline a workflow for karst spring characterization and (2) contribute to highlighting the main features of groundwater circulation in a peculiar karst system. In fact, the Berici Mountains represent a peculiar karst system because they appear as a calcareous plateau, surrounded by the Venetian Plain and isolated from the nearby Prealps.
Materials and methods
Geological and hydrogeological settings
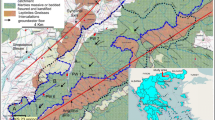
The Berici Mountains extend across the central part of the Veneto Region to the southwest of the city of Vicenza (Veneto, NE Italy; Fig. 1a). Together with the Lessini Mountains and the Euganei Hills, the Berici Mountains constitute a relatively undeformed foreland structural high known as the Lessini-Berici-Euganei block (LBE; Pola et al. 2014). Toward the east, the triangular-shaped LBE block is separated from the Eastern Southern Alps and their deformed foreland by the high-angle NE-dipping Schio-Vicenza fault (NW–SE trend; Fig. 1a). Within the LBE block, the Berici Mountains are separated from the Euganei Hills to the south by the high-angle Riviera Berica fault (NNE–SSW trend). These faults are buried beneath the Quaternary alluvial deposits (Benvenuti and Norinelli 1967; Mietto 1988a; Pola et al. 2014).
a Location of the Berici Mountains within the central part of the Veneto Region (NE Italy) and schematic structural sketch (SV Schio-Vicenza fault; RB Riviera Berica fault). b Geological sketch map of the Berici Mountains (Antonelli et al. 1990) showing the study area and the location of the monitoring springs. The springs located in the Berici area are reported subdivided on the basis of the flow rate regime (Permanent spring, Periodic spring, Episodic spring; Marcolongo 2005). The cave locations are defined utilizing the information achieved by the webgis of the Vicenza Province (2012). In legend, information about the permeability degree of each unit are presented (Fabiani 1911; ARPAV 2007). The coordinates are in UTM zone 32 N system using the WGS84 datum (expressed in km)
The Berici Mountains are an isolated plateau covering almost 200 km2 (Fig. 1b) with a maximum elevation of approximately 450 m above sea level (asl) (Monte Alto, elevation 444 m asl). Two long and deep valleys, Val Liona and Valle di Fimon (Fig. 1b), extend to the core of the complex, which can then be divided into two distinct sectors, the eastern and western sectors (Mietto 1988a; Mietto and Sauro 2000). The stratigraphic sequence is characterized by Upper Cretaceous to Miocene sedimentary rocks with subhorizontal or gently dipping beds and by basaltic rocks related to the Paleogene Lessini-Berici-Euganean volcanic cycle (Mietto 1988a).
The study area is located in the eastern sector of the Berici Mountains (Fig. 1b). The oldest outcropping rocks are represented by upper Cretaceous marly limestone of the Scaglia Rossa Formation (SR), with a thickness of some tens of meters, followed by middle Eocene marly arenaceous limestones (ML, maximum thickness of 35 m) and Nummulitic limestones (NL, 50–90 m in thickness). These are overlapped by upper Eocene marly limestones (Priabona Formation, PFm) that can reach a maximum thickness of approximately 200 m. The sedimentary sequence is closed by the Oligocene limestones of the Castelgomberto Formation (CFm), with a thickness ranging from 80 to 200 m. The whole succession was affected by a basaltic explosive volcanism (Oligocene), with the formation of several necks, volcanoclastic rocks and tuffites of variable thickness (BV; Fig. 2 and Table 1; Bassi et al. 2000; Mietto 1988a).
Geologic map of the study area. Lithologies were obtained from the lithological map of the Veneto Region (1:250,000; Antonelli et al. 1990), while the stratigraphic contacts between the different units were detailed during field work. From the bottom: Scaglia Rossa Formation (SR), Pelagic limestone containing planktonic foraminifera; Marly-arenaceous Limestone (ML), alternating marly limestone, calcareous marls, and calcarenites interbedded with tuffs; Nummulitic Limestone (NL) massive limestone rich in Nummulites; Priabona Formation (PFm), marly limestones with rich fossil content; Castelgomberto Formation (CFm), massive or irregularly bedded limestones and irregularly bedded calcarenites with miliolids and coralline red algae; basaltic volcanits (BV), basaltic explosive volcanism represented by necks, volcanoclastic rocks and tuffites (Bassi et al. 2000). Regarding settlements: Nt Nanto, Ms Mossano. In the top-left box is a rose diagram of the orientations of the maximum diameter directions of dolines (DMAX; Torresan 2016). The coordinates are in UTM-zone 32-N system using the WGS84 datum (expressed in m)
Karst phenomena played a significant role in the geomorphological evolution of the area, leading to the formation of both surficial and underground karst features. This phenomenon is particularly true for the high-karstified limestones of CFm, where the dolines are the most representative large-scale karst features (Castiglioni 1996; Mietto 1988b; Mietto and Sauro 2000; Sauro 2002, 2005). Considering the hypogean features, approximately 630 caves are present in the Berici Mountains, many of which are located in the CFm (Fig. 1). The spatial extension of these caves ranges between a few meters and approximately 1 km, while the maximum difference in elevation is approximately 100 m (Italian Speleological Society 2019). From a hydrogeological point of view, NL, PFm and CFm can be classified as aquifers because of their degree of karstification, while SR and ML can be considered aquitards due to their greater terrigenous composition. In addition, due to the low permeability of the volcanic products, BV can be considered a permeability barrier for the groundwater flow affecting the karst systems (ARPAV 2007; Fabiani 1911).
As typically occurs in karst environments, dolines represent a preferential path for the infiltration of meteoric water, even though their bottom can be infilled with fine sediments. As a consequence, the Berici Mountains landscape is characterized by the absence of any hydrographic network, and its recharge is exclusively of autogenic origin (Ford and Williams 2007). Diffuse autogenic recharge is channelized in a well-developed underground karst system that allows the circulation of infiltration waters through different-sized conduits, fractures, etc. Subsequently, water discharges from several springs located at the base of the Berici plateau and preferentially along the contact between permeable rock units (NL, PFm or CFm) and low-permeability layers (ML or SR; Fabiani 1911). This system generates a large number of springs, whereby approximately 166 springs are present in the Berici Mountains (Marcolongo 2005). Among these springs, 43 springs show a permanent regime, while the remaining 123 springs are periodic (periods without flow during the long dry season) or episodic (periods of activity in response to only main rainfall events). Most of the permanent springs have an average discharge that is generally lower than 2 L/s, while the maximum average discharge is approximately 20 L/s (Marcolongo 2005).
The monitored springs, called Nanto and Mossano, are two perennial springs located in the eastern part of the Berici Mountains in municipalities of the same names (Fig. 1b). The decision to monitor these two springs, among all the springs located in the Berici Mountains, is related to some pre-established requirements: (1) perennial regime; (2) accessibility; (3) presence of an intake capture structure; and (4) lack of water exploitation.
Nanto spring (Fig. 3a) discharges at the base of the slope of the Berici Mountains at an elevation of approximately 25 m asl The spring emerges at the contact between NL and the underlying ML (Figs. 2 and 3b).
a Nanto spring. The CTD-Diver is located in the collection chamber; b Geological cross-section of Nanto spring; c Mossano spring; CTD-Diver is located in the external storage tank; a data logger for the water temperature measurements was installed in the collection chamber. d Geological cross-section of Mossano Spring. Cross-section traces are shown in Fig. 2. In legend, AD alluvial deposits; BV basaltic volcanics; CFm Castelgomberto Formation; PFm Priabona Formation; NL nummulitic limestones; ML Marly-arenaceous Limestones
Mossano spring (Fig. 3c), located at an elevation of approximately 90 m asl, also discharges at the contact between NL and ML (Figs. 2 and 3d). Information about the monitored parameters for both springs are shown in the ‘Results and discussion’ section.
Dolines in the karst area surrounding the two springs were recognized by the analysis of satellite images (Landsat) and a digital elevation model (DEM) in a geographic information system (GIS) environment (Fig. 2). The alignment of several dolines leads to the assumption that some tectonic structures, i.e., fractures and faults, exist. The interaction between tectonics and karstification was confirmed upon considering the orientations of the maximum diameter directions of dolines (DMAX; Bondesan et al. 1992). As shown in Fig. 2, the DMAXs are preferentially WNW-oriented according to the direction of the identified structures (Torresan 2016). In addition, a structural field analysis performed near Mossano spring allowed these elements to be characterized as extensional faults related to Paleogene extensional tectonics (Zampieri 1995).
Monitoring data
Nanto and Mossano springs were continuously monitored for almost 4 years, from January 2015 to June 2018, by two high-accuracy multiprobe sensors (CTD-Diver). The recorded parameters were (1) water-level height above the diver (H in cm; range 0–1000 cm, accuracy ±0.5 cm and resolution 0.2 cm), (2) temperature (T in °C; range from −20 to +80 °C, accuracy ±0.1 °C and resolution 0.01 °C), and (3) specific electrical conductivity at 25 °C (EC in mS/cm; range 0–30 mS/cm, accuracy ±1% of reading and resolution ±0.1% of reading). An acquisition time interval of 1 h was chosen to register the effect of flood events during the hydrogeological year (Galleani et al. 2011). The water level measurements were converted to discharge (Q) values by two experimental level-discharge relations obtained through 57 flow-rate and level measurements collected from January 2015 to June 2018 (see the electronic supplementary material, ESM).
The time series of both springs were subject to several interruptions due to data logger malfunctions. The main monitoring interruptions for Nanto spring occurred from September 2015 to January 2016, from October 2016 to January 2017 (only for EC), and from February 2017 to April 2017. Mossano spring experienced only one long interruption, from September 2015 to January 2016. Moreover, both springs exhibited short interruptions during the monitoring period. It is worth mentioning that the CTD-Diver used in Mossano spring was located in an external storage tank (Fig. 3c), in which the water temperature was affected by atmospheric agents and by daily and seasonal air temperature variations. Conversely, the measurement of the water level was not directly influenced by rainfall events in the spring area. For this reason, a new data logger for Mossano spring was added on January 2018 with the aim of measuring only water temperature. This data logger was positioned in the collection chamber connected to the external storage tank (Fig. 3c), where it was impossible to conduct water level measurements.
Data collected by the Barbarano Vicentino meteorological station were used to evaluate the local precipitation and temperature and to perform the time series analysis. This station is part of a public monitoring network covering the Veneto Region, with 167 meteorological stations managed by the Regional Agency for Environmental Prevention and Protection (ARPAV). The Barbarano Vicentino meteorological station is located at an elevation of 16 m asl, 2.9 km from Mossano spring and 4.2 km from Nanto spring (Fig. 1b), representing the nearest station to the monitored springs. Although the infiltration area of the two karst systems is located at an elevation of approximately 300–400 m asl, there are no meteorological stations representative of these elevations close to the Berici Mountains.
Time series analysis and vulnerability
The workflow used to characterize the two monitored springs, starting from the monitored parameters, is schematized in Fig. 4. The analysis of the variations in spring discharge and the definition of the behavior of the springs were used to delineate the conceptual hydrogeological model.
The workflow adopted in this work to achieve the final definition of a hydrogeological conceptual model. Flow rate data are used to evaluate the spring discharge variations through recession curve analysis (RCA), flow duration curve (FDC) and auto-correlation function (ACF). The monitoring parameters (Q, T and EC) and the rainfall events (R) are used to evaluate the spring behavior by the cross-correlation function (CCF) and VESPA index approach. For each approach is defined the main parameter evaluated and the types of information that can be achieved
The discharge variations recorded in karstic springs are mainly related to the degree of recharge and karstification of the system. For this reason, a detailed analysis of spring discharge must be performed to assess some of the main features characterizing a given type of aquifer. In the proposed workflow, three methods were chosen to analyze the flow rate variability: (1) recession curves analysis (RCA), (2) flow duration curve (FDC) analysis, and (3) autocorrelation function (ACF) analysis.
The spring response in relation to rainfall events indicates the principal characteristics of the monitored karst system. To evaluate the spring behavior, the variations in the other monitored parameters (Q, T and EC) and their relationships to recharge were considered. Two types of analyses were performed: cross-correlation functions (CCFs) and VESPA index analysis.
Recession curves analysis allows for the study of variations in spring discharge as a consequence of recharge events. The analysis of the recession curves focused on the recession coefficient (α), which is qualitatively related to the degree of aquifer karstification (Baedke and Krothe 2001; Birk and Hergarten 2010; Dewandel et al. 2003; Fiorillo 2014; Kovács and Perrochet 2008; Kovács et al. 2005; Malík and Vojtková 2012; Tallaksen 1995) and, in part, to the size of the karst system (Bonacci 1993). The recession coefficient was used by Maillet (1905) to describe flow recession using a simple exponential equation (Bonacci 1993; Ford and Williams 2007):
where Qt is the discharge at time t, Q0 is the initial discharge at time t0 and α is the recession coefficient.
Boussinesq (1903, 1904) express the recession by a quadratic form:
Dewandel et al. (2003) pointed out that Eq. (1) provides an approximate analytical solution for the diffusion equation that describes flow in a porous medium, whereas Boussinesq’s quadratic equation provides an exact analytical solution (Ford and Williams 2007).
However, the mathematical properties of Eq. (1), in which the derivative is exponential and α is independent of Q0, are more convenient than the quadratic solution in Eq. (2), explaining the widest use of the Maillet formula (Dewandel et al. 2003).
Although Eq. (1) is useful for describing the baseflow recession of a karst system (Kovács and Perrochet 2008; Kovács et al. 2005; Malík and Vojtková 2012), many authors have proposed describing the cumulative effects of several reservoirs in order to interpret the entire recession curve (Amit et al. 2002; Dewandel et al. 2003; Ford and Williams 2007; Kovács and Perrochet 2008). As a matter of fact, the recession curve can be subdivided into multiple segments, describing different reservoirs with different hydrogeological properties (i.e., permeability, porosity, storativity), all contributing to spring discharge. For each segment, there is a corresponding α value obtained by the exponential Eq. (1). According to Taylor and Greene (2008), a difference in α exceeding one order of magnitude can be associated with different types of flow regimes and is used to describe spring behavior during the recession period. High values of α indicate fast drainage (conduit dominated flow) related to well-developed karst conduits and, thus, to a high degree of karstification. Conversely, low values of α are ascribable to diffuse flow into smaller fractures and pores (diffuse dominated flow), indicating a lower degree of karstification (Bagheri et al. 2016; Bonacci 1993; Ford and Williams 2007; Kovács and Perrochet 2008).
Flow duration curves analysis is a measure of the range and variability of spring discharge. FDC analysis represents the percentage of time during which the flow rates of a given spring exceed a specified threshold (Malík 2015). The discharges were ordered and plotted from the highest to the lowest values, without considering their chronological sequence. The obtained graph shows the discharge on the ordinate axis and the percentage of the monitoring time that exceeded the specified flow-rate threshold on the abscissa axis. FDC can be used to estimate principal karst system features by analyzing the slope of the curve. In fact, the presence of high slopes suggests well-developed karst conduits (conduit dominant flow), whereas low slopes indicate systems with a high storage capability and a lower degree of karstification (diffuse dominant flow; Malík 2015).
Moreover, the use of the autocorrelation function permits the definition of the memory of a karst system in terms of discharge variations. The ACF can be defined as a normalized measure r(k) of the linear dependence among successive values of the data series (discharge values in this case), and it is as described (Zhang et al. 2013):
in which:
where k is the time lag, n is the length of the time series, t is the time, x is a single event measurement, and \( \overline{x} \) is the mean of the event measurements. The related autocorrelogram is useful for evaluating the memory of a system, which is estimated through the decorrelation lag time. This lag time is defined as the time needed by the autocorrelation function to reach a determined value, usually between 0.1 and 0.2 (Mangin 1984; Liu et al. 2011; Panagopoulos and Lambrakis 2006; Tagne and Dowling 2018; Zhang et al. 2013). The autocorrelation values of an uncorrelated time series rapidly decrease (Chung et al. 2018; Liu et al. 2011), which can be interpreted as a system with short memory. Conversely, a high system memory results in a gentle decrease in the slope of the autocorrelation function; therefore, through autocorrelogram analysis, some consideration related to the degree of karstification and the size of the karst aquifer can be made (Liu et al. 2011; Mangin 1984; Padilla and Pulido-Bosch 1995).
To evaluate the springs’ responses over time with respect to recharge, CCFs were carried out with the monitored spring parameters (Q, T, EC) and rainfall (R). Cross-correlation is widely used in hydrogeology to analyze linear relationships between input and output signals (Chung et al. 2018; Fabbri et al. 2013; Fiorillo and Doglioni 2010; Liu et al. 2011; Tagne and Dowling 2018; Zhang et al. 2013).
This statistical analysis was performed using R code (R Core Team 2018). Before the application of the CCFs, the data series were filtered because the parameters Q, T and EC are usually autocorrelated. The filtering process was performed with the use of a simple filter and defined as the differences of one lag for every parameter. This approach corresponds to determining the difference between each value and its previous value, removing a trend and making stationary a nonstationary time series (R Core Time 2018). CCF represents the correlations between two different data series with respect to lag times. The cross-covariance function, where u is the input and y is the output, is given by Eqs. (6) and (7):
where \( \overline{u} \) and \( \overline{y} \) are the averages of the input and output parameters, respectively. CCF is defined as:
Equation (7) was used primarily to analyze the cross-correlation between R (input) and Q (output), to define the system response and to qualitatively evaluate the travel time of the meteoric water to cross the vadose zone. When there was a correlation to a certain lag, this was interpreted as the delay (expressed in hours) of the spring response to a recharge event. Furthermore, cross-correlations between spring parameters, i.e., Q vs. T and Q vs. EC, were performed to assess the spring behavior. Q vs. EC allows the evaluation of the minimum travel time of the neo-infiltrated water to transit through the conduits system and reach the point of emergence at the springs. Consequently, information about the size of the karst system can be obtained. Additionally, T vs. EC was calculated to evaluate whether these two parameters were synchronous. The CCF results were plotted in two-dimensional (2D) graphs, known as cross-correlograms, in which the correlation value (between −1 and +1) is reported on the y-axis, and the lag is shown on the x-axis. In addition, two confidence bands were displayed to graphically define whether or not the two analyzed series are correlated. If two series are correlated, the correlation value must be higher than the confidence bands. These bands, one negative and one positive, were defined as: \( -\frac{1.96}{\sqrt{n}} \) and \( \frac{1.96}{\sqrt{n}} \), respectively (R Core Team 2018).
Through the use of more than 1 year of continuous hourly monitoring data, the type of spring behavior was classified using parameters of the VESPA index (Galleani et al. 2011) based on the Q, EC and T values of the spring. The VESPA index V was defined by the following relationship (Banzato et al. 2017):
In Eq. (9), c(ρ) is the correlation factor, ranging from 1 to 0, defined as:
where ρ is the correlation coefficient between Q and EC, ranging between −1 and 1, calculated over more than 1 year of continuous hourly data. u(ρ) is the Heavside step function:
where α is a scale coefficient ranging from 0 and 1, which is normally assumed to be 0.5, and β and γ are the temperature and discharge factors, respectively, defined as:
where Tmax and Tmin are the maximum and minimum temperatures, respectively, and Qmax, Qmin and Qmed are the maximum, minimum and average discharge values recorded during the monitoring period, respectively. The use of Eq. (9) allows one to define the spring vulnerability degree, as shown in Table 1. Because Eq. (9) is related to the joint use of Q, T and EC, each factor can increase or decrease the spring vulnerability. No recharge measurements are required for the definition of the VESPA index, and there are no relationships between recharge and discharge. The four degrees of vulnerability shown in Table 1 are the result of experimental applications of the VESPA index and local regulations (Piedmont Region, NW Italy), defining the vulnerability of a karst spring area (Galleani et al. 2011).
By means of ρ and c(ρ), Galleani et al. (2011) proposed three different types of prevailing spring phenomena (Table 2):
- 1.
The type A “replacement” phenomenon represents a well-developed discharge system. The replacement effect produces an increase in Q, a variation in T according to the seasonal rainfall temperatures and a decrease in EC. This replacement effect is typical for highly karstified limestone aquifers.
- 2.
The type B “piston” phenomenon represents a moderate drainage system in which the hydrodynamic response can show impulse behavior. This phenomenon is typical for slightly karstified limestone aquifers with significant water storage. The piston effect produces increases in Q, T and EC.
- 3.
The type C “homogenization” phenomenon is characterized by a poorly developed drainage system, where the water response to rainfall is almost absent. The Q trend presents slow and modest fluctuations that are uncorrelated with T or EC.
Due to the differences in the development of the fracture network, the type A drainage systems are generally the most vulnerable, while type C drainage systems are the least vulnerable (Galleani et al. 2011).
The type of drainage system is inferable on the basis of c(ρ) and ρ, as in Table 2. In addition, because the coefficient ρ is defined as the correlation between Q and EC, a graphical comparison between these two parameters was performed to validate/deny the behavior classification and to explain the EC variations that are ascribable to the groundwater residence time in the karst aquifer. For this reason, the graphical comparison between Q and EC was not included in the workflow in Fig. 4 because it represents a supplementary analysis.
Results and discussion
The analyzed monitored period utilized to perform the statistical analyses was from April 2017 to June 2018. This period represents the longer-interval time without significant monitoring interruptions. From the analysis of summary statistics (Table 3) and histograms (Fig. 5) of the monitoring data, it is possible to highlight a difference in the distribution of data between Nanto and Mossano springs. In terms of discharge, the main differences are as follows: (1) the Mossano Q distribution is bimodal, while the Nanto Q distribution is unimodal; (2) the maximum value of Nanto is higher than the maximum value of Mossano; and (3) the median and mean are higher in Mossano than in Nanto. Likewise, the EC values of Nanto are bimodal, and the median and mean values in Nanto are higher than those in Mossano. Furthermore, the Mossano T values are lower than the Nanto T values, and both springs show a unimodal histogram distribution of T. Regarding the rainfall data, Table 4 shows a summary of the parameters recorded over the 4 years of monitoring by the Barbarano Vicentino meteorological station.
Histograms of the monitoring data in the period from April 2017 to June 2018. a Discharge of Nanto spring. b Temperature of Nanto spring. c Specific electrical conductivity of Nanto spring. d Discharge of Mossano spring. e Temperature of Mossano spring. f Specific electrical conductivity of Mossano spring
Spring discharge variations
Maillet’s equation was used to calculate the recession coefficient α for different segments of the analyzed discharge curves, which were individuated in the monitoring period (January 2015–June 2018). For this type of analysis, compared to the statistical method, the entire monitored period can be used because RCA is less influenced by data continuity. Two representative recession curves among those analyzed (see ESM), with the related α values, are shown in Fig. 6. The α values calculated for the Nanto and Mossano springs highlight the different karstification degrees of the lithologies forming the aquifer reservoir. The first system, described by α coefficients within 10−1 order of magnitude, is constituted by well-developed conduits, allowing for the rapid discharge of rainfall infiltration (conduit dominant flow; Taylor and Greene 2008). This system is probably more developed in the limestones of the CFm and NL formations than in the marly limestone of PFm. The second system is characterized by recession coefficients within 10−3 orders of magnitude, suggesting a slower circulation in fractured rocks (diffuse dominant flow; Taylor and Greene 2008) involving both NL. and PFm. The main difference between Nanto and Mossano is the existence of a recession value of 10−2 for Mossano spring, suggesting an intermediate or mixed flow system (i.e., a system bearing both karstic and fissured characteristics). This hydrogeological behavior represents a transition between the conduit system and the matrix-fracture system and could be related to a karstification degree of PFm that is possibly greater in the Mossano recharge area than in the Nanto recharge area, as testified by field observations (Torresan 2016). The calculated α values (Fig. 6) are greater than the recession coefficients that are commonly available in the literature—for example, the recession coefficients found by Amit et al. (2002) range from 0.1 to 0.0006, while Bagheri et al. (2016) showed α values ranging between 0.02 and 0.0002; furthermore, in Giacopetti et al. (2017), the recession coefficients ranged between 0.01 and 0.001. The differences in these α coefficients are probably due to both the geological and hydrogeological features of the recharge areas and to the small extension of the karst systems. As a matter of fact, as stated by several authors (Baedke and Krothe 2001; Bonacci 1993; Birk and Hergarten 2010; Fiorillo 2014; Kovács and Perrochet 2008; Kovács et al. 2005), the recession coefficient is inversely proportional to the area of the active aquifer and/or to the recharge area feeding the spring.
Recession curve analysis: a Nanto spring recession curve evaluated in the time interval between 17 February 2016 and 27 February 2016; b Mossano spring recession curve evaluated in the time interval between 25 March 2015 and 10 March 2015. Type of regime defined in accordance with Taylor and Green (2008)
The type of drainage system suggested by the RCA is also confirmed by the FDCs (Fig. 7). The steep slope of the upper end of the FDCs indicates the existence of karst conduits, resulting in a highly variable spring discharge. Conversely, the semiflat slope at the lower end of the curves indicates high water storage due to the low-permeability system (fracture-matrix system). In addition, differences in the behavior between the two springs are highlighted. Nanto spring shows essentially two components, while Mossano spring shows three components. This difference can be related to the existence of an intermediate system (mixed flow, shown in Fig. 6) with a remarkable capability of discharge (9.4–10.4 L/s, exceedance of 10–50%).
ACF analysis further confirms the different behaviors of the two monitored springs. The autocorrelogram analyses (Fig. 8) highlight an initial component characterized by a steeper slope. The ACFs quickly decrease in the first 50–70 h, indicating the existence of well-developed karst conduits that favor a rapid discharge flow. A second component is present only in the Mossano ACF (Fig. 8b) and shows an intermediate slope with a moderately slow reduction of the ACF ranging from approximately 50–900 h. This component can be ascribed to the existence of an intermediate flow system that is also distinguished by RCA (Fig. 6) and FDCs (Fig. 7). Finally, the third component, which reaches the threshold value of 0.2, developed from approximately 50–320 h (almost 13 days from lag 0) in Nanto spring and from approximately 900–1,000 h (approximately 40 days from lag 0) in Mossano spring. This third component confirms the presence of a low-permeability fracture network, which is more extensive in Nanto than in Mossano, that influences the storage capability, delaying the groundwater flow toward the springs.
The lag times required to reach the threshold value allow for some consideration of the size of the karst systems. When the flow rate in Nanto spring reaches the threshold value, Mossano spring has an autocorrelation of approximately 0.5. This difference can be related to the size of the hydrogeological system, which is probably greater in Mossano than in Nanto.
Spring behavior
To evaluate the spring responses, cross-correlation (CCF) analyses were performed considering the period from January 2018 to June 2018 (Figs. 9 and 10). This interval time represents the monitoring period in which the parameters Q, T and EC are representative for both springs and without missing data. The cross-correlation between R (input) and Q (output) allows one to identify the spring response in terms of discharge variations as a consequence of recharge events. Figure 9a clearly shows positive correlations at lags of 4 and 5 h for Nanto spring, meaning a response delay of discharge occurs 4–5 h after a rainfall event. Additionally, for Mossano spring, the significant positive correlations at lags of 5 and 6 h (Fig. 10a) define a response occurring with a delay of 5–6 h after a rainfall event. However, both springs also showed negative correlations (lags of 1 and 2 h for Nanto spring and lags of 3 h for Mossano spring). A possible interpretation of this result is that 1–3 h after rainfall events (increased R), the discharge is decreasing due to its natural trend before the recharge flow perturbation. This behavior is interpreted as the necessary travel time for neo-infiltrated water to cross the vadose percolation zone and reach the saturated zone of the karst aquifer, increasing its hydraulic head and, as consequence, the spring discharge.
Cross-correlation between the monitored parameters in Nanto spring in the period between January 2018 and June 2018. a Cross-correlation between R vs Q. b Cross-correlation between Q vs T. c Cross-correlation between Q vs EC. d Cross-correlation between T vs EC. The dashed blue lines represent the confidence bands
Cross-correlation between the monitored parameters in Mossano spring in the period between January 2018 and June 2018. a Cross-correlation between R vs Q. b Cross-correlation between Q vs T. c Cross-correlation between Q vs EC. d Cross-correlation between T vs EC. The dashed blue lines represent the confidence bands
The CCFs of Q vs. T and Q vs. EC are also useful for analyzing the springs’ behavior. Both springs showed only negative significant correlations (Figs. 9b,c and 10b,c), indicating a contrasting response between discharge and both temperature and specific electrical conductivity, traducing in a replacement behavior (type A drainage system). In particular, CCFs between Q and T indicate a maximum negative cross-correlation at a 1-h lag in Mossano and a 4-h lag in Nanto (Figs. 9b and 10b). Similarly, the CCFs between Q and EC show a maximum negative correlation at a 2-h lag in Mossano and a 4-h lag in Nanto (Figs. 9c and 10c). Of interest are the differences in the response delay between the input (Q) and output (T, EC). The Nanto negative correlations for T and EC have 2–6 h delays in comparison with the discharge (Fig. 9b,c), while they have 1–3 h delays in Mossano (Fig. 10b,c). Furthermore, the CCFs between T and EC showed a very high positive correlation at lags of 0 and 1 h (Fig. 9d and Fig. 10d), showing that these two parameters behave in the same way. The shortest delay in both springs can be considered an estimate of the minimum time needed by the infiltrated waters to transit through the conduit network and reach the point of emergence (e.g., the first arrival time of a tracer test; Ford and Williams 2007). Considering that EC is less subject to external agents compared to T, it is possible to demonstrate the different hydrogeological behaviors of the investigated system. In Nanto, the first negative correlation between Q and EC at lag 0 can be related to the fact that once the freshwater has infiltrated the karst aquifer, it reaches the spring in less than 1 h. All the negative correlations between lags 0 and 7 can be interpreted as the time needed for all of the neo-infiltrated water to reach the spring, with a maximum peak of concentration at 4-h lag. In Mossano spring, the first negative correlation is at a 1-h lag, indicating that after infiltration into the karst reservoir, the freshwater reaches the emergence point after 1 h. The total time required to deplete the neo-infiltrated water is 3 h, with a maximum peak at 2-h lag. Two main differences can be observed between Nanto and Mossano springs: (1) the instantaneous response in Nanto can be related to both the existence of a well-developed karst system and the size of the hydrogeological system (smaller in Nanto than in Mossano), and (2) the longer time needed to deplete the freshwater in Nanto is probably due to a high contribution of a fracture/matrix system rather than a conduit system. Conversely, the shorter time in Mossano may be related to the concomitant influence of three systems (instead of two), namely, the conduit system, the intermediate system and the fracture/matrix system, with the intermediate system developed inside the marly limestones of the PFm.
The VESPA index was calculated considering more than 1 year of continuous hourly monitoring data (April 2017–June 2018), without a large number of missing data, as suggested by Banzato et al. (2017). The results are summarized in Table 5. Nanto is classified as a highly vulnerable spring (V = 1.78; Table 1), which exhibits with homogenization behavior (ρ = 0.14; c(ρ) = 0.07; type C in Table 2). Conversely, Mossano is classified as a replacement spring (type A in Table 2) by the coefficient ρ and as a replacement/piston (type A/B) spring by the factor c(ρ), while the VESPA index (V = 13.04) points to a very high degree of vulnerability (Table 1). The VESPA index suggests different behavioral categories for Nanto spring and Mossano spring. Because the spring behavior is defined as the correlation between Q and EC, it is worth observing the related hydro- and chemo-graphs (Fig. 11). Both springs exhibit a comparable discharge trend (Fig. 11a), which is supported by the positive correlation of 0.66; however, Mossano spring shows a greater variability in the flow rate than that of Nanto spring. These discharge variations can explain the higher degree of vulnerability of Mossano spring (Table 5). Regarding the EC, both springs shown decrease in EC, corresponding to the main Q peaks (Fig. 11b), indicating a replacement behavior, as suggested by the CCFs analyses. This observation highlights the existence of well-developed karst conduits that rapidly discharge infiltrated waters and that are poor in ion content, as a consequence of recharge events. In addition to this behavior, Nanto spring show a general increasing trend, which is more prominent after the time 4,000 h (Fig. 11b), that is related to an increase in the ion content of the groundwater due to a low-permeability system (fractures/matrix system). In particular, the increase in EC is more accentuated after the EC negative peaks for Nanto spring. In terms of spring behavior, the conduit system shows a replacement behavior, while a homogenization behavior can be attributed to the fractures/matrix system. The VESPA index does not allow the separation of these two contributions; however, the results obtained by the analysis of the ρ and c(ρ) factors for Nanto spring emphasized that the homogenization drainage system prevails over the replacement system, confirming that the fractures/matrix system is more extensive than the karst system.
In contrast, excluding the EC negative peaks corresponding to the recharge events, Mossano spring shows a generally constant EC trend (Fig. 11b). In addition, after the decrease in EC corresponding to the Q peaks, the EC recovery is gradual. The difference between Nanto and Mossano springs can be explained by the presence of an intermediate system in Mossano, between the conduits system and the fractures/matrix system, producing a progressive transition from high flow to baseflow. The progressive recovery of EC values in Mossano spring defines three permeability systems that are responsible for the general replacement behavior individuated by the VESPA index analysis.
Hydrogeological conceptual model
According to the proposed workflow (Fig. 4), combining the performed analyses and results, a hydrogeological conceptual model for both springs can be delineated. The analysis of the variations in spring discharge, accomplished using the RCA, ACF and FDC techniques, allow one to obtain qualitative information about the permeability of the karst system, related to the degree of karstification, and to the size of the karst system. The study of the spring behavior, accomplished using the CCFs and VESPA index analyses combined with monitored parameters (Q, T, EC) and the recharge (R), allows information to be obtained about: (1) the spring response, which can be related to the neo-infiltrated water travel time across both the vadose zone and the saturated zone, (2) the size of the karst systems and (3) the degree of vulnerability of the karst springs.
Conceptually, it is possible to consider the two analyzed karst systems as a multi-reservoir system to explain their hydrogeological structure. In the case of Nanto spring, two reservoirs with different karstification degrees can be individuated. In fact, RCA, FDC and ACF analyses delineated the existence of both well-developed karst conduits and a fractures/matrix system of lower permeability. In addition, the fractures/matrix system is more developed in size than the conduit system, as indicated by the FDC and ACF results. After a rainfall event, the neo-infiltrated water requires 4–5 h to move across the unsaturated zone and reach the karst aquifer, as shown by the CCF between Q vs. R. Subsequently, freshwater reaches the point of emergence of the spring through the well-developed karst conduits in less than an hour (Q vs. EC). However, the contribution of karst conduits to the depletion of neo-infiltrated water is less than that of the fractures/matrix system, shown by the CCF between Q vs. EC. The abrupt increases in the EC after the EC negative peaks (Fig. 11b), in conjunction with the recharge events, are attributable to the net transition between a conduit-dominant flow to a diffuse-dominant flow.
The results obtained through the use of RCA, FDC and ACF analyses allowed for the identification of the existence of three reservoirs affecting Mossano spring. In particular, a karst conduit system and a fracture/matrix system, separated by an intermediate system, were individuated. The intermediate system is relevant in the existence of the Mossano spring. In fact, the intermediate system is active for a longer time compared to the other two systems, as indicated by the ACF and FDC analyses. The intermediate system, constituted by both karstic and fissured features, is more developed in size compared to the other two systems. During a recharge event, the infiltrated freshwater reaches the karst aquifer after 5–6 h, as indicated by the CCF between Q vs. R. Due to the high permeability of the karst conduits, the travel time of the neo-infiltrated water across the karst reservoir is shorter (about 1 h) and the water is depleted after approximately 3 h (the CCF between Q vs. EC). The existence of the intermediate system allows for the gradual recovery of the baseflow stage, as suggested by the progressive increase in EC after the negative peaks, related to infiltration processes (Fig. 11b).
Comparing Nanto spring and Mossano spring, some differences appear. In terms of the degree of karstification, the Mossano system is more karstified than the Nanto system. In fact, in the Nanto system, the fracture/matrix system prevails over the conduit system, while, in Mossano, an intermediate system exists. This conclusion is further emphasized by the results of the RCA, FDC and ACF analyses. The intermediate system affecting Mossano spring is probably due to the PFm that may be more permeable in the Mossano karst area.
Regarding the size of the karst domain, ACF analysis shows that the Mossano karst system is greater than the Nanto system. Additionally, the CCF between Q vs. EC confirms the different size by comparing the time of the first arrival of freshwater at the springs. However, the transit time needed for the water to infiltrate the epikarst is comparable (4–6 h). This last aspect is amenable to the same features of the recharge area, constituted by an alteration of the CFm with the formation of soil, mainly used for agricultural purposes.
Finally, other differences are highlighted by the VESPA index that identify Nanto as a highly vulnerable spring with a type C drainage system, while Mossano as a very highly vulnerable spring characterized by a type A drainage system.
Conclusions
In this study, a workflow for the hydrogeological characterization of karst springs was proposed. This workflow was applied to the study of two springs located in the Berici Mountains (Vicenza, NE Italy), with the aim of increasing the knowledge of groundwater circulation in a peculiar karst system.
A multi-approach for the analysis of spring discharge variations, using recession curve analyses, flow duration curves and auto-correlation function techniques, was employed to evaluated the karst degree and the size of the system. Moreover, by combining the monitoring parameters (Q, T, EC) with recharge events (R) through the joint use of cross-correlation functions and the VESPA index approach, it was possible to obtain qualitative information of: (1) the spring response to recharge events, (2) the travel time of meteoric water into both the vadose zone and the conduits network (3) the size/permeability of the karst systems, (4) the spring vulnerability and (5) the drainage system behavior. The information obtained by all the performed analyses allows one to define a hydrogeological conceptual model for each spring that can be used to explain the main features that characterize each karst system. In fact, the previously mentioned quantitative/qualitative information comprises peculiar points in the preliminarily studies of a karst spring, finalized to its potentiality assessment in the water supply.
The two monitored springs showed the same behavior as a consequence of the recharge events, as supported by both the CCFs and graphical comparison between Q and EC (Fig. 11). However, the analyses of spring discharge variations and the VESPA index highlighted some differences between Nanto and Mossano springs. In fact, Mossano spring is composed of three systems with different degrees of permeability, whereas the Nanto spring reservoir is characterized by two systems. Another difference is that karst behavior prevails in Mossano spring (the conduit and intermediate systems), while fracture/matrix behavior prevails in Nanto spring. This result is further supported by the VESPA index, which delineates Nanto spring as a type C drainage system and Mossano as a type A drainage system.
The results obtained can be extended to the other perennial springs affecting the south-eastern part of the Berici Mountains in which the geological and hydrogeological conditions are the same as the Nanto and Mossano karst systems. However, a monitoring program is indispensable in order to correctly establish the hydrogeological features affecting these perennial springs.
Although, in this work, 4 years of data of continuously monitored parameters were collected, only the continuous data from 1 year were indispensable to perform all of the analyses included in the proposed workflow.
The combined use of such methodologies allows for both support of the detail of the hydrogeological conceptual model and limitation of the loss of information or erroneous interpretation that can result from using only one technique. For example, the results achieved by the ρ coefficient do not allow the identification of the existence of the karst conduits for Nanto spring, delineating a type-C behavior ascribable to a matrix-fracture system. However, although the RCA, FDC and ACF individuated the existence of both karst conduits and the matrix-fracture system, the VESPA index approach allows one to confirm that the matrix-fracture system prevails over the conduit system.
References
Adji TN, Bahtiar IY (2016) Rainfall–discharge relationship and karst flow components analysis for karst aquifer characterization in Petoyan spring, Java, Indonesia. Environ Earth Sci 75:735. https://doi.org/10.1007/s12665-016-5553-1
Amit H, Lyakhovsky V, Katz A, Starinsky A, Burg A (2002) Interpretation of spring recession curves. Ground Water 40(5):543–551
Antonelli R, Barbieri G, Dal Piaz GV, Dal Prà A, De Zanche V, Grandesso P, Mietto P, Sedea R, Zanferrari A (1990) Carta geologica del Veneto 1: 250.000: una storia di cinquecento milioni di anni [Geological map of Veneto 1: 250.000: a history of five hundred million years]. Università di Padova, Padova, Italy
ARPAV (2007) Atlante delle sorgenti del Veneto [Atlas of Veneto springs]. Padova–Progetto SAMPAS, Area Tecnico-Scientifica, Servizio Acque Interne, Regione del Veneto, Venice, 144 pp
Assaad FA, Jordan H (1994) Karst terranes and environmental aspects. Environ Geol 23(3):228–237
Baedke SJ, Krothe NC (2001) Derivation of effective hydraulic parameters of a karst aquifer from discharge hydrograph analysis. Water Resour Res 37(1):13–19. https://doi.org/10.1029/2000WR900247
Bagheri R, Jafari H, Momeni A, Bagheri F (2016) Analysis of karst spring recession curves, west of Iran. Arab J Geosci 9(19):1–12. https://doi.org/10.1007/s12517-016-2754-6
Bailly-Comte V, Martin JB, Screaton EJ (2011) Time variant cross correlation to assess residence time of water and implication for hydraulics of a sink-rise karst system. Water Resour Res 47:W05547. https://doi.org/10.1029/2010WR009613
Bakalowicz M (2005) Karst groundwater: a challenge for new resources. Hydrogeol J 13:148–160
Banzato C, Butera I, Revelli R, Vigna B (2017) Reliability of the VESPA index in identifying spring vulnerability level. J Hydrol Eng 22(6):1–11. https://doi.org/10.1061/(ASCE)HE.1943-5584.0001498
Bassi D, Ćosović V, Pupazzoni CA, Ungaro S (2000) The Colli Berici. In: Bassi D. (ed) Shallow water benthic communities at the middle-upper Eocene boundary: southern and north-eastern Italy, Slovenia, Croatia, Hungary. Field trip guidebook of the 5th meeting IGCP 393 IUGS-UNESCO. Annali dell’Università di Ferrara, supplemento Scienze della Terra, UNIPI, Pisa, Italy, pp 43–57
Benvenuti G, Norinelli A (1967) Contributo alla conoscenza delle strutture sepolte tra i Colli Euganei e i Berici [Geophysical contribution to knowledge of buried structures between Euganean Hills and Berici Hills]. Boll Geofis Teor Appl 9:269–284
Birk S, Hergarten S (2010) Early recession behaviour of spring hydrographs. J Hydrol 387(1–2):24–32. https://doi.org/10.1016/j.jhydrol.2010.03.026
Bonacci O (1993) Karst springs hydrographs as indicators of karst aquifers. Hydrol Sci J 38:51–62. https://doi.org/10.1080/02626669309492639
Bondesan A, Meneghel M, Sauro U (1992) Morphometric analysis of dolines. Int J Speleol 21(1–4):1–55
Boussinesq MJ (1877) Essai sur la theorie des eax courantes [Essay on the theory of running waters]. Memoires presentes par divers savants a l’Academie des Sciences de l’Institut National de France, Tome XXIII, no. 1, Academy of Science, Paris
Boussinesq J (1903) Sur un mode simple d’écoulement des nappes d’eau d’infiltration à lit horizontal, avec rebord vertical tout autour, lorsqu’une partie de ce rebord Est enlevée depuis la surface jusqu’au fond [Groudwater flow within an aquifer limited by a horizontal impermeable layer, with a vertical no-flow boundary around, when one of then is removed]. C R Acad Sci 137:5–11
Boussinesq J (1904) Recherches théoretiques sur l’écoulement des nappés d’eau infiltrées dans le sol et sur le débit des sources [Theoretical research on the recharge of the groundwater infiltrated into the soil and the discharge of the springs]. J Mathemat Pures Appl 10:5–78
Brutsaert W, Nieber JL (1977) Regionalized drought flow hydrographs from a mature glaciated plateau. Water Resour Res 13(3):637–643
Castiglioni B (1996) Comparison of morphometric aspects of dolines between two zones in Berici Hills (Vicenza, Italy). Acta Carsolog XXV:69–87
Chung SY, Senapathi V, Sekar S, Kim TH (2018) Time series analyses of hydrological parameter variations and their correlations at a coastal area in Busan, South Korea. Hydrogeol J 26(6):1875–1885. https://doi.org/10.1007/s10040-018-1739-9
Covington MD, Wicks CM, Saar MO (2009) A dimensionless number describing the effects of recharge and geometry on discharge from simple karstic aquifers. Water Resour Res 45(11):W11410. https://doi.org/10.1029/2009WR008004
Crawford NC, Ulmer CS (1994) Hydrogeologic investigations of contaminant movement in karst aquifers in the vicinity of a train derailment near Lewisburg, Tennessee. Environ Geol 23(1):41–52
Dewandel B, Lachassagne P, Bakalowicz M, Weng P, Al-Malki A (2003) Evaluation of aquifer thickness by analysing recession hydrographs: application to the Oman ophiolite hard-rock aquifer. J Hydrol 274(1–4):248–269. https://doi.org/10.1016/S0022-1694(02)00418-3
Dreiss SJ (1982) Linear Kernels for karst aquifers. Water Resour Res 18(4):865–876
Dreiss SJ (1989) Regional scale transport in a karst aquifer: 1. component separation of spring flow hydrographs. Water Resour Res 25:117–125
Fabbri P, Ortombina M, Piccinini L, Zampieri D, Zini L (2013) Hydrogeological spring characterization in the Vajont area. Ital J Eng Geol Environ Book Ser 6:541–553
Fabiani R (1911) La Regione dei Berici [The Berici Region]. R Magistr Acque Uff Idrogr Venezia 28– 29:1–84
Field MS (1992) Karst hydrology and chemical contamination. J Environ Syst 22(1):1–26
Fiorillo F (2014) The recession of spring hydrographs, focused on karst aquifers. Water Resour Manag 28(7):1781–1805. https://doi.org/10.1007/s11269-014-0597-z
Fiorillo F, Doglioni A (2010) The relation between karst spring discharge and rainfall by cross-correlation analysis (Campania, southern Italy). Hydrogeol J 18(8):1881–1895. https://doi.org/10.1007/s10040-010-0666-1
Ford D, Williams P (2007) Karst hydrogeology and geomorphology. Wiley, West Sussex, England. https://doi.org/10.1002/9781118684986
Galleani L, Vigna B, Banzato C, Lo Russo S (2011) Validation of a vulnerability estimator for spring protection areas: the VESPA index. J Hydrol 396:233–245. https://doi.org/10.1016/j.jhydrol.2010.11.012
Giacopetti M, Materazzi M, Pambianchi G, Posavec K (2017) Analysis of mountain springs discharge time series in the Tennacola stream catchment (central Apennine, Italy). Environ Earth Sci 76(1):1–11. https://doi.org/10.1007/s12665-016-6339-1
Goldscheider N (2012) A holistic approach to groundwater protection and ecosystem services in karst terrains. AQUA Mundi 2:117–124
Hartmann A, Wagener T, Rimmer A, Lange J, Brielmann H, Weiler M (2013) Testing the realism of model structures to identify karst system processes using water quality and quantity signatures. Water Resour Res 49:3345–3358. https://doi.org/10.1002/wrcr.20229
Italian Speleological Society (2019) Catasto delle grotte del Veneto [Database of Veneto caves]. http://www.catastogrotteveneto.it/. Accessed September 2019
Knisel WG (1972) Response of karst aquifers to recharge. Hydrogeological paper 60, Colorado State University, Fort Collins, CO, 48 pp
Kovačič G (2010) Hydrogeological study of the Malenščica karst spring (SW Slovenia) by means of a time series analysis. Acta Carsolog 39(2):201–215. https://doi.org/10.3986/ac.v39i2.93
Kovács A, Perrochet P (2008) A quantitative approach to spring hydrograph decomposition. J Hydrol 352(1–2):16–29. https://doi.org/10.1016/j.jhydrol.2007.12.009
Kovács A, Perrochet P, Király L, Jeannin PY (2005) A quantitative method for the characterization of karst aquifers based on spring hydrograph analysis. J Hydrol 303(1–4):152–164. https://doi.org/10.1016/j.jhydrol.2004.08.023
Kresic N, Stevanović Z (2010) Groundwater hydrology of springs: engineering, theory, management, and sustainability. Butterworth-Heinemann, Oxford, 573 pp
Ladouche B, Marechal J-C, Dorfliger N (2014) Semi-distributed lumped model of a karst system under active management. J Hydrol 509:215–230. https://doi.org/10.1016/j.jhydrol.2013.11.017
Larocque M, Mangin A, Razack M, Banton O (1998) Contribution of correlation and spectral analyses to regional study of a large karst aquifer (Charentes, France). J Hydrol 205(3–4):217–231
Liu L, Chen X, Xu G, Shu L (2011) Use of hydrologic time-series data for identification of hydrodynamic function and behavior in a karstic water system in China. Hydrogeol J 19(8):1577–1585. https://doi.org/10.1007/s10040-011-0774-6
Maillet E (1905) Mécanique et physique du globe: essai d’hydraulique souterraine et fluviale [Mechanics and physiques of the world: an essay of subterranean and fluviatile hydraulics]. Hermann, Paris
Malík P (2015) Evaluating discharge regimes of karst aquifer. In: Stevanović Z (ed) Karst aquifers: characterization and engineering. Professional Practice in Earth Sciences, Springer, Heidelberg, Germany, 692 pp
Malík P, Vojtková S (2012) Use of recession-curve analysis for estimation of karstification degree and its application in assessing overflow/underflow conditions in closely spaced karstic springs. Environ Earth Sci 65(8):2245–2257. https://doi.org/10.1007/s12665-012-1596-0
Mangin A (1984) Pour une meilleure connaissance des systèmes hydrologiques à partir des analyses corrélatoire et spectrale [The use of autocorrelation and spectral analyses to obtain a better understanding of hydrological systems]. J Hydrol 67:25–43
Marcolongo E (2005) Studio idrogeologico di alcune sorgenti fredde Dei Colli Berici [Hydrogeological study of some cold springs of the Berici Hills]. MSc Thesis, Università di Padova, Padua, Italy
Mayaud C, Wagner T, Benischke R, Birk S (2014) Single event time series analysis in a binary karst catchment evaluated using a groundwater model (Lurbach system, Austria). J Hydrol 511:628–639. https://doi.org/10.1016/j.jhydrol.2014.02.024
Mietto P (1988a) Aspetti geologici dei Monti Berici [Geological aspects of the Berici Hills]. In: AA. VV. (ed) I colli Berici: natura e civiltà. Signum, Padua, Italy, pp 12–23
Mietto P (1988b) Carsismo e speleologia nei Monti Berici [Karst and speleology in the Berici Mountains]. In: AA. VV. (ed) II colli Berici: natura e civiltà. Signum, Padua, Italy, pp 226–241
Mietto P, Sauro U (2000) Grotte del Veneto: paesaggi carsici e grotte del Veneto [Veneto caves: karst landscapes and Veneto caves], 2nd edn. In: Regione del Veneto. La Grafica, Verona, Italy
Padilla A, Pulido-Bosch A (1995) Study of hydrographs of karstic aquifers by means of correlation and cross-spectral analysis. J Hydrol 168:73–89. https://doi.org/10.1016/0022-1694(94)02648-U
Padilla A, Pulido-Bosch A, Mangin A (1994) Relative importance of Baseflow and Quickflow from hydrographs of karst spring. Ground Water 32:267–277. https://doi.org/10.1111/j.1745-6584.1994.tb00641.x
Panagopoulos G, Lambrakis N (2006) The contribution of time series analysis to the study of the hydrodynamic characteristics of the karst systems: application on two typical karst aquifers of Greece (Trifilia, Almyros Crete). J Hydrol 329:368–376. https://doi.org/10.1016/j.jhydrol.2006.02.023
Pola M, Ricciato A, Fantoni R, Fabbri P, Zampieri D (2014) Architecture of the western margin of the north Adriatic foreland: the Schio-Vicenza fault system. Ital J Geosci 133:223–234. https://doi.org/10.3301/IJG.2014.04
R Core Team (2018) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/. Accessed February 2020
Sauro U (2002) The Monti Berici: a peculiar type of karst in the southern Alps. Acta Carsolog 31(3):99–114
Sauro U (2005) The Monti Berici guide of the field trip. Suppl Geograf Fisic Dinam Quatern VII:367–372
Szilagyi JM, Parlange B, Albertson JD (1998) Recession flow analysis for aquifer parameter determination. Water Resour 34:1851–1857
Tagne GV, Dowling C (2018) Inferring groundwater flow and recharge from time series analysis of storm responses in a karst aquifer of southeastern Kentucky (USA). Hydrogeol J 26(8):2649–2668. https://doi.org/10.1007/s10040-018-1837-8
Tallaksen LM (1995) A review of baseflow recession analysis. J Hydrol 165(1–4):349–370. https://doi.org/10.1016/0022-1694(94)02540-R
Taylor CJ, Greene EA (2008) Hydrogeologic characterization and methods used in the investigation of karst hydrology. In: Field techniques for estimating water fluxes between surface water and ground water. US Geol Surv Techniques Methods PNR61. pp 75–114
Torresan F (2016) Studio idrogeologico e geostrutturale di alcune sorgenti carsiche dei Monti Berici (VI) [Hydrogeological and geostructural study of some karst springs of the Berici Mountains (VI)]. MSc Thesis, Univ. di Padova, Padua, Italy
Troch PA, De Troch FP, Brutsaert W (1993) Effective water table depth to describe initial conditions prior to storm rainfall in humid regions. Water Resour Res 29:427–434
Vicenza Province (2012) Carta Geomorfologica 1: 60.000 [Geomorphological map 1: 60,000). Piano Territoriale di Coordinamento Provinciale Tav 2–4. http://geoportale.provincia.vicenza.it. Accessed September 2019
Zampieri D (1995) Tertiary extension in the southern Trento platform, southern Alps, Italy. Tectonics 14(3):645–657. https://doi.org/10.1029/94TC03093
Zhang Z, Chen X, Chen X, Shi P (2013) Quantifying time lag of epikarst-spring hydrograph response to rainfall using correlation and spectral analyses. Hydrogeol J 21(7):1619–1631
Acknowledgements
The authors would like to thank the editors, Prof. M. Petitta, and three anonymous reviewers for their constructive suggestions and remarks, which greatly improved this manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(PDF 940 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Torresan, F., Fabbri, P., Piccinini, L. et al. Defining the hydrogeological behavior of karst springs through an integrated analysis: a case study in the Berici Mountains area (Vicenza, NE Italy). Hydrogeol J 28, 1229–1247 (2020). https://doi.org/10.1007/s10040-020-02122-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-020-02122-0