Abstract
Toronto Springs is a complex distributary karst spring system with 11 perennial springs in the Missouri Ozarks, USA. Carroll Cave (CC) and Wet Glaize Creek (WG) were previously identified as principal recharge sources. This study (1) characterized physical and chemical properties of springs and recharge sources; (2) developed end-member mixing models to estimate contributing proportions of CC and WG; and (3) created a conceptual model for the system. Samples analyzed for major ions and specific conductivity, in conjunction with a rotating continuous monitoring program to identify statistically comparable baseflow conditions, were used to assess differences among the sites. Monitoring data showed that the springs differed depending upon recharge proportions. Cluster analysis of average ion concentrations supported the choice of CC and WG as mixing model end members. Results showed a range in the proportions of the recharge sources, from surface-water to groundwater dominated. A conceptual model suggests that a system of distinct conduits beneath the WG flood plain transmits water to the individual springs. These conduits controlled the end-member recharge contributions and water chemistry of the springs. Interpretation of relative proportions of recharge contributions extends existing knowledge of karst hydrologic geometry beyond that of point-to-point connections to revealing complex surface-water/groundwater mixing in heterogeneous distributary spring systems.
Résumé
Les sources Toronto constituent un système complexe de distribution de sources karstiques avec 11 émergences pérennes dans les Ozarks du Missouri, Etats-Unis d’Amérique. La grotte Carroll (CC) et la rivière Wet Glaize (WG) ont été au préalable identifiées comme constituant la principale recharge. La présente étude (1) caractérise les propriétés physiques et chimiques des émergences et des vecteurs de la recharge; (2) développe des modèles de mélange à polarités pour estimer les contributions de CC et de WG; et (3) élabore un modèle conceptuel pour le système. Des analyses d’échantillons pour les ions majeurs et la conductivité spécifique, conjointement à un programme de surveillance continu à rotation destiné à identifier des conditions d’écoulement de débit de base statistiquement comparables, ont été utilisées pour estimer les différences entre les sites. Les données de suivi montrent que les différences entre les émergences dépendent du pourcentage de recharge. L’analyse typologique des concentrations moyennes des ions permet de choisir CC et WG comme les pôles du modèle de mélange. Les résultats montrent une variation en terme de pourcentage des vecteurs de recharge, depuis les eaux de surface jusqu’à une dominante d’eaux souterraines. Un modèle conceptuel suggère que le système de conduits situé en-dessous de la plaine d’inondation WG assure le transfert de l’eau jusqu’aux émergences individualisées. Ces conduits contrôlent les contributions des différents pôles de recharge identifiés dans le modèle de mélange et l’hydrochimie des émergences. L’interprétation des pourcentages relatifs des contributions à la recharge étend la connaissance de la configuration hydrologique du karst au-delà de celle des connexions point à point, révélant un mélange complexe d’eaux de surface et d’eaux souterraines dans des systèmes hétérogènes de distribution d’émergences.
Resumen
Los manantiales de Toronto Springs constituyen un sistema distributario complejo de manantiales kársticos con 11 manantiales perennes en el Missouri Ozarks, EEUU. Carroll Cave (CC) y Wet Glaize Creek (WG) fueron previamente identificados como las principales fuentes de recarga. Este estudio (1) caracterizó las propiedades físicas y químicas de los manantiales y las fuentes de recarga; (2) desarrolló modelos de mezcla de los miembros extremos para estimar las proporciones contribuyentes de CC y WG; y (3) creó un modelo conceptual del sistema. Se utilizaron las muestras analizadas orientadas a iones mayoritarios y conductividad específica, en conjunción con un programa rotativo de monitoreo continuo para identificar condiciones estadísticamente comparables del flujo de base, con el objeto de evaluar las diferencias entre ambos sitios. Los datos de monitoreo mostraron que los manantiales diferían en función de las proporciones de la recarga. El análisis de cluster de las concentraciones promedio de los iones apoyó la elección de CC y WG como un modelo de mezcla de los miembros extremos. Los resultados mostraron un intervalo en las proporciones de las fuentes de recarga, desde ser dominadas por agua superficial a agua subterránea. Un modelo conceptual sugiere que el sistema de distintas conductos por debajo de la planicie de inundación de WG transmite agua a los manantiales individuales. Estos conductos controlaban las contribuciones a la recarga de los miembros extremos y de la química del agua de los manantiales. La interpretación de las proporciones relativas de las contribuciones de la recarga extiende el conocimiento existente de la geometría hidrológica del karst más allá que las conexiones punto a punto para revelar la complejas mezclas agua superficial/agua subterránea en sistemas distributarios heterogéneos de manantiales.
抽象
摘要:多伦多泉系统是一个复杂的支流泉系统,这个泉系统包括美国密苏里州欧扎克市11个常流泉。Carroll Cave 和 Wet Glaize Creek 曾被确认为主要补给源。这项研究(1)描述了泉和补给源的物理和化学特性;(2)开发了端元混合模型,以估算Carroll Cave 和 Wet Glaize Creek贡献比例;(3)创立了系统的概念模型。用于分析主要离子及电导率的样品,连同确认统计上可比较的基流条件的循环连续监测程序用来评价各地点的差别。监测资料显示,泉的差别取决于补给比例。平均离子浓度聚合分析支持选择Carroll Cave 和 Wet Glaize Creek作为混合模型端元。结果显示了从地表水到地下水主导的补给源比例范围。概念模型表明,Wet Glaize Creek洪泛平原之下的独特的管道系统向各泉输水。这些管道控制着端元补给贡献率及泉的化学成分。补给贡献率的相对比例论述不但扩充了岩溶水文化学现有的认知,而且还扩充了揭示异质支流泉系统中复杂的地表水/地下水混合点对点的连接认知。
Resumo
As nascentes Toronto correspondem a um sistema distributário cárstico complexo, com 11 nascentes perenes na porção Missouri dos montes Orzaks, EUA. As Cavernas Carroll (CC) e o Córrego Wet Glaize (WG) foram inicialmente identificadas como as principais fontes de recarga. Esse estudo (1) caracterizou propriedades físicas e químicas de nascentes e fontes de recarga; (2) desenvolveu um modelo misturado de membros finais para estimar a contribuição proporcional das CC e do WG; e (3) criou um modelo conceitual para o sistema. As amostras analisadas para os principais íons e condutividade específica, em conjunto com um programa de monitoramento contínuo de rotação para identificar as condições de escoamento de base estatisticamente comparáveis, foram utilizados para avaliar diferenças entre as áreas. Os dados de monitoramento mostraram que as nascentes diferiram dependendo das proporções de recarga. A análise de agrupamento das concentrações médias de íons apoiou a escolha das CC e do WG como um modelo misturado de membros finais. Os resultados mostraram uma faixa nas proporções das fontes de recarga, a partir de um domínio por parte das águas superficiais para um domínio por parte das águas subterrâneas. O modelo conceitual sugere que um sistema de condutos distintos sob a planície de inundação do WG transmite água para as nascentes individuais. Estes condutos controlam as contribuições dos membros finais de recarga e a química da água das nascentes. A interpretação de proporções relativas das contribuições de recarga estende-se ao conhecimento existente de geometria hidrológica do carste, além daquela de conexões ponto-a-ponto, ao revelar misturas complexas entre águas superficiais/águas subterrâneas em sistemas distributários heterogêneos de nascentes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Local hydrology in the Ozarks ecoregion of Missouri (USA) is dominated by karst features and processes such as losing streams, caves, and large spring flow systems. In Missouri, over 4,400 springs have been documented, including eight first-magnitude springs (Jackson 2013) that have an average discharge equal to or exceeding 100 ft3 s−1 (2.8 m3 s−1; Meinzer 1927). Recharge via losing streams is the common recharge mode for spring systems in the Ozarks and several of these systems have been well characterized by dye-tracing studies (Vandike 1992, 1996; Lerch et al. 2005; Mugel et al. 2009; Miller and Lerch 2011). Additionally, while distributary springs represent an important type of discharge feature observed within the Ozarks, typified by Montauk and Toronto Springs (Beckman and Hinchey 1944; Vineyard and Feder 1982), there are a limited number of studies documenting distributary and multiple outlet spring systems in karst settings (Quinlan and Ewers 1985; Quinlan 1990; Goldscheider 2005). Typically identified through dye-tracing work or contaminant transport investigations, distributary spring systems can have a variety of forms that may vary depending on hydrologic conditions, recharge area characteristics, and local hydrogeology (Quinlan and Ewers 1985; Quinlan 1990; J. Vandike, Water Resources Center-Missouri Department of Natural Resources, personal communication, 2014). Results of these studies show that multiple springs in such systems may receive positive traces from single tracer injections or may show similar levels of a particular contaminant. Quinlan and Ewers (1985) reported that distributary spring systems were a common feature in carbonate aquifers, and they described such systems as having four principal origins: (1) enlargement of pre-existing anastomoses due to large head differences between flooded passages and base level; (2) collapse and blockage of a spring orifice forcing alternate routes to develop; (3) diversion to lower routes as base level is lowered; and (4) backflooding from surface streams that forces undersaturated water into anastomoses at the potentiometric surface. However, the existing literature has few studies that quantitatively document distributary spring systems and their hydrogeological features, and there are no existing studies describing their geochemistry or documenting possible mixing of recharge sources within these systems. For the purposes of this report, the term distributary springs will be used to describe spring systems that have the following characteristics: (1) multiple springs in close geographic proximity to one another; (2) springs having shared recharge areas (whether in total or a portion of); and (3) flow through a shared conduit system.
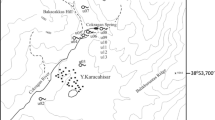
Wet Glaize Creek (WG) is located in the central Missouri Ozarks in southeastern Camden County (Fig. 1). The 332 km2 watershed is underlain by Ordovician age sandstones and dolomites and the majority of the streams in the watershed have significant losing reaches (Harvey et al. 1983). Toronto Springs is a distributary spring system, located in the northern portion of the watershed, which consists of numerous perennial spring outlets located along the north and south sides/banks of WG (Figs. 2 and 3). Carroll Cave (CC) is a stream cave with 32 km of known passages, located 4 km to the south of Toronto Springs, which provides a significant percentage of the flow discharging from Toronto Springs (Fig. 4) (Miller 2010). Dye tracing has positively traced CC to eight of the springs, and WG to ten springs (Fig. 3). Seepage runs—measuring loss of stream flow between upstream and downstream gaging stations (Lerner et al. 1990)—in streams of the WG watershed have also identified two major losing reaches along the WG main channel, downstream from dye injection locations shown to lose to Toronto Springs (Miller 2010). These results revealed that complex recharge relationships exist at Toronto Springs, and prompted the additional studies reported here. There are a number of different approaches that have been employed to obtain information on sources and other properties of recharge (Scanlon et al. 2002) and can be subdivided into physical (Lerner et al. 1990; Rushton 1997), tracing (e.g., Leaney and Allison1986; Ronan et al. 1998; Arnold and Allen 1996; Flint et al. 2002) and numerical methods (Singh 1995; Hatton 1998; Qian et al. 2006). Mixing models typically using two to six geochemical end member tracers (Christopherson and Hooper 1992; Doctor et al. 2006; Barthold et al. 2011) have been successfully used to determine sources of recharge (e.g., Liu et al. 2004, 2008a, b, 2013) that compare favorably to results using isotope analysis (Liu et al. 2004; Doctor et al. 2006).
Map of Wet Glaize Creek watershed, showing karst features, Carroll Cave, and known structural features. Labelled creeks include: Creek A = Traw Hollow, Creek B = Davis Hollow, Creek C = Barnett Hollow, Creek D = Mill Creek, Creek E = Wet Glaize Creek, Creek F = Sellars Creek, Creek G = Conns Creek. Spring, sinkhole, and structural feature data from Missouri Department of Natural Resources, Missouri Geological Survey (2007, 2010a, b)
The specific objectives of this research were to: (1) characterize the individual geochemistry of 11 springs within the Toronto Springs system and the two recharge sources through high-resolution monitoring of specific conductivity (SpC), temperature, and pH; (2) analyze major ion concentrations in the springs to develop end-member mixing models to estimate the proportion of CC and WG to the recharge of each spring; and (3) synthesize results of the mixing models and previously conducted dye tracing and seepage run studies to develop a conceptual model that describes the primary flow paths of the Toronto Springs system.
Materials and methodology
Setting
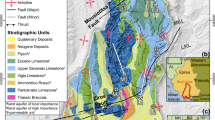
The WG drainage basin is located in the central Missouri Ozarks region and is within the Grandglaize Basin, which, in turn, is part of the Osage River Basin. The area is characterized by rolling hills dissected by meandering streams and local elevation varies from 213 to 348 m above sea level with total vertical relief of about 135 m. Land cover is dominated by grasslands and deciduous forests, which account for 91 % of the total land cover in the watershed (Missouri Resource Assessment Partnership 2005). The region is dominated by karst topography, with features that include springs, caves, and sinkholes (Fig. 2), and the majority of local surface drainages have losing stream reaches (Harvey et al. 1983). The underlying bedrock is Ordovician dolomites and sandstones, with the cave and karst areas mainly occurring within the Gasconade Dolomite. Overlying the Gasconade Dolomite is the Roubidoux Formation; a grouping of sandstone and chert with some dolomite interbeds, which is found primarily along the ridgetops, and the Jefferson City-Cotter Dolomite is exposed in a few areas near the Montreal Fault Block (Middendorf 1984), the major structural feature of the study area. Additional structural features include the Mill Creek Fault, the Mill Creek Syncline; and in the study area, the dip is generally 1° to the east (Helwig 1965). While many of the faults are minor in overall displacement, they play an important role in the loss of surface water to the subsurface environment.
Carroll Cave (Fig. 4) is a large stream cave system which has been mapped to a length of 32 km, though exploration and survey is still ongoing. The dendritic pattern and curvilinear passages are indicative of floodwater recharge from losing streams predominantly along bedding partings (Palmer 1991). The cave contains three streams that flow independently from one another, creating two in-cave drainage divides. The numerous side passages contribute flow as tributaries to these larger streams. Thunder River, the largest stream, flows through the cave for over 11 km, dropping 60 m in elevation, before reaching the water table at a large terminal lake room. Qualitative dye tracing has shown the surface recharge areas for Thunder River to be Traw Hollow (located to the south of the cave), Davis Hollow, and portions of south Barnett Hollow. Confusion Creek, the second largest stream, was discovered in 2009 and is reached via a large side passage within the cave known as DL7. Recharge to Confusion Creek is from a series of large sinkholes located to the west of the main cave system. Carroll River, the smallest of the three streams in terms of discharge, has been truncated by the downcutting of Thunder River and appears to currently receive recharge only from epikarstic aquifers located above and adjacent to the cave system (Miller 2010).
Toronto Springs (Fig. 3) is located in the northern portion of the WG drainage basin. The spring system consists of approximately 20 perennial and ephemeral springs which discharge from the alluvium of the WG floodplain. Two of the springs emerge from openings at the base of dolomite outcrops, with one known to be a cave (spring TS8). Eleven of the perennial springs were selected for monitoring, which had substantial flow and deep enough channels to accommodate deployment of dataloggers, seven of which were located on the south side of WG and four on the north side. Total average flow for the spring system is approximately 800 L s−1 with a flow range of 10–90 L s−1 for each spring (Miller 2010).
Methodology
Spring-water monitoring
Up to three YSI Sonde 6600 dataloggers (YSI, Yellow Springs, OH) were deployed for continuous, high-resolution monitoring of the 13 sites (11 springs, WG, and Thunder River in CC; Figs. 2 and 3). One site was chosen as a reference site (TS7) at which the YSI datalogger was continuously deployed while the other dataloggers were rotated among sites at 2–4-week intervals. Data were collected for pH, SpC (μs/cm), and temperature (°C) at 15-min intervals. Dataloggers were deployed from May 2009 through September 2010. The data were then examined for baseflow periods and statistical analyses (see ‘Methodology’, ‘Statistical analysis’) were used to determine if individual springs were significantly different from one another in these basic water quality parameters. Only baseflow conditions were examined as inundation of the springs by WG during high flow periods invalidated comparisons among the springs under high flow conditions. Baseflow YSI data were chosen using four criteria:
-
1.
The datalogger sensors had sufficient time to equilibrate to the surrounding spring water.
-
2.
No erratic readings existed or acceptable replacement data were available.
-
3.
SpC, pH, and temperature readings were stable or asymptotically approaching equilibrium following a runoff event.
-
4.
Once baseflow periods were identified, a 3-day interval was randomly chosen for each site.
Each of the selected data sets represented 288 individual data points (3 days × 96 readings per day) for each site. These data were then used to calculate ratios to the reference site at TS7 and for conducting statistical analyses. Each site in the study, where possible, had a datalogger deployed during cool months (October–March) and warm months (April–September) to examine possible seasonal variations. However, due to time and resource constraints, three sites (TS4, TS5, TS6) have two warm periods and no cool periods, and one site (TS2) had no warm season data. Data were downloaded, sensors calibrated, and maintenance performed twice per month.
Chemical analysis
Samples were collected for ion analyses twice per month from February to September 2010 from the 13 sites already described. Grab samples were collected under baseflow and runoff conditions in 500-ml plastic bottles and placed on ice during transport to the laboratory. A total of 167 samples were collected. Major cations, HCO3 −, and CO3 2− concentrations were determined within 24 h of collection; anion concentrations were determined within standard holding times (Eaton et al. 2005). Cations were analyzed by flame photometry (Na+ and K+) or by atomic absorption spectrometry (Ca2+and Mg2+) as described by Nathan et al. (2012). Bicarbonate (HCO3 −) and CO3 2− concentrations were determined by titration using H2SO4 along with indicators of phenolphthalein and methyl orange (Eaton et al. 2005). Anion analyses of NO3 −, SO4 2−, PO4 3−, Cl−, and F− were completed using ion chromatography with electrolytic suppression on a Dionex DX 600 system in accordance with methodologies described in Standard Methods for the Examination of Water and Wastewater (Eaton et al. 2005). Anion analyses were conducted for all sites during the first two sampling periods to ensure charge balance occurred (within 10 %), after which one site was randomly chosen for each sampling set. Coincident with the grab samples collected for ion analysis, instantaneous measurements of pH, temperature, and SpC were conducted. Additional details about the chemical analyses can be found in Miller (2010).
Statistical analysis
For the continuous monitoring data, statistical analyses were performed on datasets created by dividing the raw values of an individual spring by the corresponding values at reference site TS7, which was chosen as the reference since the site is a spring branch that integrates the flow from all springs on the south side of WG. Due to resource constraints, it was not possible to monitor all 13 sites simultaneously and, therefore, the computation of ratios to a common reference provided a means of standardizing the data so that site differences could be statistically analyzed. The ratio was computed for each individual spring to that of the reference site using
where R ij is the ratio for a value between a given spring and that for TS7, S ij is the i-th spring for parameter j, where j represents a value for pH, temperature, or SpC; STS7j is the value at reference site TS7 for the j-th parameter. The ratio data were not normally distributed according to the Kolmogorov-Smirnov test (p < 0.05 for all parameters); therefore, non-parametric statistical methods were used for determining differences between sites.
Mann–Whitney tests (U-tests) were used to determine if seasonal differences (cool vs. warm) for a site were significantly different (α = 0.05). If significant differences were found between seasonal datasets, then the seasonal data were analyzed separately. Due to the sampling periods, datalogger maintenance, and the time span of the research, some sites (TS2, TS4, TS5 and TS6) did not have both seasons represented. For those sites with two warm season datasets, the U-test was used to determine if the two warm season datasets were significantly different. Then the dataset closest to the mid-point of the season (i.e., the end of June) was chosen. One exception was made in splitting the seasonal datasets for spring TS2. The presumptive warm season data for the site exhibited unseasonably cool water temperature, even though the sampling periods were technically in the warm season. Because of this, it was ultimately decided to include the TS2 data only in the cool season analysis.
The Kruskal-Wallis test (H-test) was used to determine differences among sites using the ratio data for pH, SpC, and temperature (α = 0.05). Pair-wise comparisons were then made to determine significant differences in mean rank between sites based on critical difference values using the method of Chan and Walmsley (1997). The critical difference values are a function of the total number of observations in the data set, the number of comparisons, and the number of observations per site. Therefore, critical differences calculated for the cool season were smaller, compared to the warm season critical difference, due to the fact that fewer overall sites were monitored during the cool season. The major cation (Ca2+, Mg2+, Na+, K+) and HCO3 − data were normally distributed based on the Kolmogorov-Smirnov test (α = 0.05). Thus, one-way analysis of variance (ANOVA) was used for determining differences among sites (α = 0.05), and 95 % confidence intervals about the mean concentrations were computed for these data. In addition, cluster analysis by Ward’s method of agglomeration was used to determine groups of springs based on their average Ca2+, Mg2+, and HCO3 − concentrations and SpC to support the choice of end members for the mixing models. Ward’s method computes the distance between two groups as proportional to the change in the within group sum of squares that results when two groups are combined (Ward 1963).
Two-end-member mixing model analysis
Previous dye-tracing results (Miller 2010) demonstrated that CC and WG are the dominant recharge sources to Toronto Springs. The two-end-member mixing model developed here assumed that CC and WG were the primary end-members of the monitored springs at Toronto Springs and that other recharge sources were negligible. Two end members provide the minimum number of inputs into such hydrological mixing models (Christopersen and Hooper 1992) and such models have been successfully used to quantify source contributions in a variety of settings (e.g., Gong et al. 1995; Liu et al. 2008a) Thus, a simple two-end-member mixing model (Eq. 2) was developed:
where P iHM is the proportion of the highest valued end member contributing flow to spring, i; S ij is the i-th spring for parameter j, where j represents the cation or anion concentration, or SpC; HM j is the highest end member value for parameter j, represented by CC; and LM j is the lowest end member value for parameter j, represented by WG. Average site values for Ca2+, Mg2+, and HCO3 − concentrations and the instantaneous SpC data were used as the input for the mixing models. In an effort to provide robustness to the input datasets, SpC was included because it is an overall indicator of dissolved ion concentrations in the water samples and provided an independent measurement method from that of the specific ion concentrations. A mixing model representing the average of the proportions from these four parameters was also computed.
Results and discussion
Differences in physical and chemical characteristics among springs
Results of the U-tests for temperature, pH, and SpC values for all sites indicated significant seasonal differences with p-values <0.05. Monitoring data from springs TS1 and TS7 (reference site) showed slight, but significant, differences in temperature and larger differences in SpC and pH by season (Fig. 5). Also, note the observed diurnal fluctuations at the reference site for temperature and pH, while TS1 does not show such a pattern. Other sites showed similar seasonal patterns in all three parameters (data not shown), but temperatures generally showed greater differences between seasons than that of TS1. Because of these differences, the cool and warm season ratio datasets were analyzed separately to assess differences among the sites. Results of the H-tests for the warm and cool season datasets showed significant differences between sites with respect to pH, temperature, and SpC (Table 1). Major differences in temperature were observed between sites with WG having the highest mean rank in the warm season and the lowest mean rank in the cool season, an anticipated result for a surface stream. Conversely, CC had among the highest mean ranks for temperature in the cool season, grouped along with sites TS1 and TS13, indicating a more groundwater dominated flow regime. The datasets for pH showed similar results, with WG having the highest mean rank in both seasons (most basic) and spring TS12 the lowest mean rank in both seasons (most acidic). Specific conductivity showed differences among sites that were consistent with anticipated differences between surface stream and groundwater flow systems. WG had the lowest SpC in the warm season due to seasonally high flow, while spring TS8 and CC had the highest mean ranks. The H-test results clearly demonstrated that the springs had distinct chemical and physical properties. Furthermore, results of dye-tracing studies in an earlier phase of this research showed that springs with shared recharge areas were generally similar (i.e., not significantly different) in these three parameters (Fig. 3; Miller 2010). However, the dye traces only established point-to-point connections and could not be used to estimate the proportion of recharge sources to the springs.
Temperature, specific conductivity (SpC), and pH of Spring TS1 and the reference site, Spring TS7, in warm and cool seasons. a Warm season temperature; b Cool season temperature; c Warm season SpC; d Cool Season SpC; e Warm season pH; f Cool season pH. Vertical lines indicate 3-day period used for statistical analyses
Major ion concentrations
Of the major ions, only Ca2+ concentrations showed significant differences between sites, with average concentrations ranging from 0.802 to 1.00 mmol L−1 (Table 2). Spring TS8 and CC had the highest average Ca2+ concentrations, and both were significantly greater than TS2 and WG, while the other springs were intermediate in concentration. Concentrations of Ca2+, Mg2+, and HCO3 − showed considerable variation across sites (Table 2 and Fig. 6), but WG and TS2 consistently had the lowest concentrations of all three ions. CC and TS8 also had the highest average Mg2+ concentrations, and the highest or among the highest HCO3 − concentrations (Fig. 6). Average Mg2+ and HCO3 − concentrations of the remaining springs were generally between those of WG and CC. Figure 5a shows the average Mg2+ versus Ca2+ concentration data by site. Eight sites fell below the 1:1 line, three above the line, and two on the line, demonstrating that, overall, the sites had slightly greater average concentrations of Mg2+ (0.931 mmol L−1) than Ca2+ (0.918 mmol L−1). This indicated that the Gasconade dolomite is, at least locally, slightly enriched in Mg2+ compared to a 1:1 ratio. Concentrations of Na+ and K+ were very similar for all sites (Table 2). Average SpC ranged from 338 μS cm−1 at WG to 396 μS cm−1 at TS8, and there were no significant differences in average SpC between sites (Table 2). Similar to the major ion concentrations, WG and TS2 had the lowest SpC. In contrast, CC had an average SpC (364 μS cm−1) that was intermediate among the sites and similar to several springs that were intermediate in major ion concentrations (TS1, TS4, TS10, TS11, and TS13; Table 3). Overall, WG and CC generally encompassed the range of observed Ca2+, Mg2+, and HCO3 − concentrations, but not the range of SpC.
Average concentrations and 95 % confidence intervals (gray error bars) for 11 springs, Carroll Cave, and Wet Glaize Creek. a Ca2+ and Mg2+ concentrations by site. b HCO3 − and Mg2+ concentrations by site. Symbol colors indicate relative concentration groups based on cluster analysis of average Ca2+ (a) or HCO3 − (b) concentrations— red = high; orange = intermediate; and yellow = low
Cluster analysis was used to determine major groups among the sites based on their average ion concentrations and SpC. Resulting dendrograms for all four parameters showed three distinct clusters (Fig. 7). For Ca2+ and SpC, a reduction in the number of clusters from >4 to 3 occurs at a distance of <0.5 for both parameters (Fig. 7), and subsequent reduction from three to two clusters occurs at distances that are much greater than that required for previous combinations. In the Ca2+ dendrogram (Fig. 7), for example, this indicated that sites CC, TS8, and TS12 were a distinct cluster (i.e., distance of 4.4 was required for combining) from the eight sites in the adjacent cluster. Similarly for the SpC dendrogram (Fig. 7), the six-site cluster including CC was distinctly different (i.e., distance of 3.3) from the five-site cluster that included WG. Dendrograms for Mg2+ and HCO3 − (not shown) were very similar to that of Ca2+ and resulted in similar groups (Table 3). Overall, the results of the cluster analysis indicated the existence of three distinct groups—low, intermediate, and high concentration or conductivity (Table 3 and Fig. 6). However, SpC showed a very different arrangement of sites within each group compared to that of the ion concentrations (Table 3). For SpC, CC was in the intermediate conductivity group and was included with a large group of springs (TS1, TS4, TS10, TS11, and TS13) that were in the intermediate concentration group for the ion data. Further, three sites that were in the intermediate group based on ion concentrations (TS5-7), were included in the low conductivity group along with TS2 and WG. In contrast, groups based on ion concentrations showed that WG and TS2 were always in the low concentration group, and CC and TS8 were always in the high concentration group (Table 3 and Fig. 6). Most of the remaining springs were in the intermediate group. These results were consistent with earlier dye-tracing studies (Miller 2010) demonstrating that CC and WG were the primary recharge sources to the springs. The ion data also supported the choice of CC and WG as end members in the mixing models, and indicated that ion-specific data were more discriminating than SpC for identifying recharge sources to the springs. This research supports the use of major ion concentrations as a valid and simple approach for discriminating recharge sources in distributary spring systems.
Two-end-member mixing model
Mixing model results showed that the springs represented a range from groundwater to surface-water-dominated recharge sources. Results of the Ca2+ mixing model showed a range of values from 27 to 107 % of the recharge contributed by CC (Table 4). However, all of the springs except TS2 were estimated to have >50 % contribution from CC, and among the ion-specific models, the Ca2+ model gave the highest estimated proportion of CC to the springs, with an average of 63 % for all sites. The Mg2+ mixing model had the narrowest spread of estimates for end-member contributions compared to the other models with the estimated CC contribution ranging from 4 to 78 % (Table 4). In contrast to the Ca2+ model results, the proportion of recharge from CC estimated by the Mg2+ model was <40 % for seven of the sites, and all sites except TS13 resulted in lower proportions of recharge from CC. The Mg2+ model resulted in the highest estimates of surface-water contribution to the springs with an average of 58 % of the spring recharge attributed to WG. Results of the HCO3 − model were generally intermediate to that of the Ca2+ and Mg2+ models. Estimated recharge proportions of CC ranged from −4 to 136 %, but the average overall sites for the HCO3 − model showed slightly greater groundwater inputs (55 % CC) than surface water. For eight of the springs (TS1, TS4-7, TS10, TS11, TS13), the HCO3 − model estimated the proportion of CC recharge to be in a relatively narrow range (37–50 % CC), and all of these springs, except TS13, were intermediate to that of the Ca2+ and Mg2+ model results.
The model for SpC showed very different results in the end-member proportions from the ion-specific models because of the narrow range (340–397 μS cm−1) of the data and the fact that CC was not the high end member. As a result, estimated recharge proportions from the SpC model were inconsistent with the ion-specific models and tended to greatly over-estimate CC recharge contribution compared to them. Overall, the SpC model estimated that 92 % of the recharge was attributed to CC, but comparisons of specific sites showed large differences between results of the ion-specific and SpC models. For several springs (TS4, TS10, TS11, and TS13), the SpC model indicated that CC dominated the recharge to these springs, but the ion-specific models showed more equal contributions of recharge from CC and WG. Further, differences between the results of the SpC and ion-specific models for TS8 and TS12 were much larger. While results of the Ca2+ and Mg2+ models were seemingly inconsistent for TS8, they reflected the similarity in ion concentrations between CC and TS8, demonstrating that the site was dominated by groundwater recharge (see the following discussion). Thus, the mean of the ion-specific models was considered to be the most robust estimate of the recharge proportions, and the SpC data were not included in the mean model. Results of the mean model showed that eight of the springs (TS1, TS4-7, TS10, TS11, TS13) had nearly equal proportions of recharge from CC and WG, one spring (TS2) was dominated by recharge from WG, and two springs (TS8 and TS12) were dominated by recharge from CC. Viewed spatially (Fig. 8), the eight springs with similar recharge proportions, and therefore ion concentrations, were distributed throughout the flood plain and on both sides of the WG channel. Spring TS12, dominated by CC recharge, is located on the north side of the WG channel, yet CC flow is from the south. These observations provided evidence for the existence of separate sub-surface conduits flowing to specific springs or groups of springs (see the following). Moreover, the ion-specific mixing models illustrate that the Toronto Springs system represents an active groundwater/surface-water mixing zone between a karst aquifer and a surface stream channel. This work builds upon recent advances in karst hydrogeology that reveal complexities in recharge–discharge relationships and surface stream-conduit exchange within aquifer systems (Moore et al. 2009; Gulley et al. 2010; Luhman et al. 2012).
While the ion-specific mixing models were useful for describing recharge source mixing for the majority of the monitored springs, the fact that the model was not applicable for some springs suggested the influence of other recharge sources to these springs. Spring TS8 was one example for which the average Ca2+ and HCO3 − concentrations were greater than CC and, thus, resulted in >100 % apparent contribution from groundwater. However, previous groundwater tracing indicated that TS8 was not positively traced from CC, and recharge to this spring apparently represents contribution from a separate karst aquifer, also formed in Gasconade dolomite, which resulted in very similar ion concentrations to that of CC. In addition, WG was not traced to spring TS8, yet the Mg2+ mixing model indicated that 22 % of the recharge was derived from the creek. Given the location and chemical characteristics of TS8, any source of surface recharge was likely from lower Barnett Hollow Creek; however, no dye tracing has been conducted to confirm this connection. Spring TS12 gave a similar result to that of TS8 for the HCO3 − model because the spring had slightly greater average HCO3 − concentrations than CC. In contrast to TS8 though, TS12 has been traced from CC, and the ion-specific models estimated that CC was the dominant recharge source to this spring. Spring TS2 also had a result inconsistent with the HCO3 − mixing model because the site had an average HCO3 − concentration slightly lower than that of WG. Analogous to TS12, spring TS2 has been traced from WG, and the mean model estimated the creek to account for 91 % of the recharge to this spring. In contrast, the Ca2+ and Mg2+ mixing model results for TS2 indicated contributions from CC, but the cave was not positively traced to the spring. Apparently, other groundwater sources may provide a small proportion of the recharge to TS2. The mixing model results demonstrate that the ion concentrations of CC and WG are representative of local groundwater and surface streams, respectively, and support the hypothesis that WG and CC are the two primary recharge sources to the Toronto Springs system.
Development of a conceptual model for the Carroll Cave–Toronto Springs system
Distributary spring systems have often been viewed in a simplistic manner in which the various springs were presumed to derive from a common recharge source, resurging through the alluvium at various locations. Results from this study show that this view is incorrect for Toronto Springs, and the individual springs can represent different mixing zones with distinct water chemistry. Results of the mixing models along with previous dye-tracing studies, seepage runs, geological mapping, detailed survey of the CC system, and known structural features of the WG watershed (Helwig 1965; Middendorf 1984; Miller 2010; Fig. 2), support the hypothesis that distinct conduits recharge the springs or groups of springs and that surface and subsurface water interactions occur along these complex flowpaths. Furthermore, it is proposed that springs with common proportions of end-member recharge, even when on opposite sides of the base level stream, were supplied by the same conduit or fracture and these flow paths controlled the contribution of the end-member recharge. This represents a new conceptual model for distributary spring systems in that the water discharging from the 11 springs at Toronto Springs is not geochemically homogenous but is dependent on the complex mixing of groundwater and surface stream-flow systems. Detailed studies of the hydrology and hydrochemistry of distributary spring systems are lacking in the literature and, therefore, no conceptual models exist to describe the physical setting or the nature of recharge source mixing occurring within these systems.
The conceptual model developed here to describe this system includes the major known recharge sources to Carroll Cave via losing streams in Traw and South Barnett hollows (Figs. 9 and 10). These losing streams recharge either Thunder River, a Thunder River tributary (DL7), or Confusion Creek within Carroll Cave, but eventually converge into a single large conduit at the water table that extends for approximately 4 km northeast towards Toronto Springs. The lower portion of this large conduit is viewed as the major mixing zone of WG with CC groundwater (Fig. 9). Structural faults of the Montreal Fault Block and cutoff springs along WG provide the probable conduits that facilitate the mixing of surface and ground waters that subsequently resurge as distinct spring outlets along the north and south sides of WG. Toronto Springs represents a unique distributary spring system created by the unusual combination of a large karst recharge area in close proximity to a major fault block.
Conceptual model of the Carroll Cave–Toronto Springs system, showing recharge sources to Carroll Cave (CC) and the mixing of groundwater and surface-water systems contributing flow to Toronto Springs (TS). Flow direction in the model is indicated alongside each flow line in the model and is generally southwest to northwest. Spring and sinkhole feature data from Missouri Department of Natural Resources, Missouri Geological Survey (2007, 2010a)
Conclusions
Intensive monitoring of 11 springs and their two principal recharge sources demonstrated that the springs were distinctly different in terms of temperature, pH, and SpC, and these differences also varied seasonally among the springs. Mean ion concentrations were not significantly different between sites, except for Ca2+, but cluster analysis of Ca2+, Mg2+, HCO3 −, and SpC among sites demonstrated the existence of three distinct groups and supported the use of CC and WG as recharge end members in the mixing models. Results of the mixing models indicated a broad range of end-member proportions for the springs, from surface water to groundwater dominated, and elucidated the complex mixing that can occur within a distributary spring setting. Two springs, TS2 and TS8, provided additional support for the development of the generalized mixing models, showing that CC and WG were representative of local groundwater and stream flow regimes, respectively. Results from multiple lines of evidence combining this and previous work—mixing model results, dye tracing, seepage runs, cave survey, and known structural features of WG watershed—support the hypothesis that distinct conduits supplied flow to the springs or groups of springs, and these conduits controlled the end-member recharge contributions and geochemistry of the springs. This represents a new understanding of the complexities that can exist within distributary spring systems, and a conceptual model of the hydrogeologic setting of this conduit structure has been proposed to synthesize these results. Toronto Springs represents a complex distributary spring system where groundwater from the CC karst aquifer mixes with surface water from the WG stream channel to discharge via distinct conduits within the flood plain of WG. This study provides another methodological tool for examining karst aquifer flow systems and groundwater/surface-water interactions in large drainage basins to aid in better understanding the recharge sources and discharge characteristics of complex distributary spring systems.
References
Arnold JG, Allen PM (1996) Estimating hydrological budgets for three Illinois watersheds. J Hydrol 176:57–77
Barthold FK, Tyralla C, Schneider K, Vaché KB, Frede HG, Breuer L (2011) How many tracers do we need for end member mixing analysis (EMMA)? A sensitivity analysis. Water Resour Res 47:W08519
Beckman HC, Hinchey NS (1944) The large springs of Missouri. Missouri Geol Surv Water Resour XXIX (2):63
Chan Y, Walmsley RP (1997) Learning and understanding the Kruskel-Wallis one-way analysis-of variance-by-ranks test for differences among three or more independent groups. Phys Ther 77:1755–1761
Christophersen N, Hooper RP (1992) Multivariate analysis of stream water chemical data: the use of principal components analysis for the end-member mixing problem. Water Resour Res 28(1):99–107
Doctor D, Alexander C, Petric M, Kogovsek J, Urbanc J, Lojen S, Stichler W (2006) Quantification of karst aquifer discharge components during storm events through end-member mixing analysis using natural chemistry and stable isotopes as tracers. Hydrogeol J 14(7):1171–1191
Eaton AD, Clesceri LS, Greenburg AE (eds) (2005) Standard methods for the examination of water and wastewater, 20th edn. American Public Health Association, Washington, DC
Flint AL, Flint LE, Kwicklis EM, Fabryka-Martin JT, Bodvarsson GS (2002) Estimating recharge at Yucca Mountain, Nevada, USA: comparison of methods. Hydrogeol J 10:180–204
Goldscheider N (2005) Fold structure and underground drainage pattern in the alpine karst system Hochifen-Gottesacker. Eclogae Geol Helv 98(1):1–17
Gong GC, Liu KK, Pai SC (1995) Prediction of nitrate concentration from two end member mixing in the southern East China Sea. Cont Shelf Res 15:827–842
Gulley J, Martin JB, Screaton EJ, Moore PJ (2010) River reversals into karst springs: a model for cave enlargement in eogenetic karst aquifers. Geol Soc Am Bull 123(3–4):457–467
Harvey EJ, Skelton J, Miller DE (1983) Hydrology of Carbonate Terrane–Niangua, Osage Fork, and Grandglaize basins, Missouri. Missouri Department of Natural Resources, Division of Geology and Land Survey, Water Resources Report no. 35. http://www.dnr.mo.gov/pubs/WR35.pdf. Accessed October 2010
Hatton T (1998) Catchment-scale recharge modelling, part 4: the basics of recharge and discharge. CSIRO, Collingwood, Australia
Helwig JA (1965) Geology of Carroll Cave, Camden County, Missouri. Bull National Speleol Soc 27(11):11–26
Jackson J (2013) Missouri Spring Database. Primary Database. Missouri Department of Natural Resources, Missouri Geological Survey, Rolla, MO
Leaney FW, Allison GB (1986) Carbon-14 and stable isotope data for an area in the Murray Basin: its use in estimating recharge. J Hydrol 88:129–145
Lerch RN, Wicks CM, Moss PL (2005) Hydrologic characterization of two karst recharge areas in Boone County, Missouri. J Cave Karst Stud 67:158–173
Lerner DN, Issar AS, Simmers I (1990) Groundwater recharge: a guide to understanding and estimating natural recharge. Int Assoc Hydrogeologists Rep. 8, IAH, Kenilworth, UK, 345 pp
Liu F, Williams MW, Caine N (2004) Source waters and flow paths in an alpine catchment, Colorado Front Range, United States. Water Resor Res 40:W09401
Liu F, Bales RC, Conklin MH, Conrad ME (2008a) Streamflow generation from snowmelt in semi-arid, seasonally snow-covered, forested catchments, Valles Caldera, New Mexico. Water Resour Res 44:W12443
Liu F, Parmenter R, Brooks PD, Conklin MH, Bales RC (2008b) Seasonal and interannual variation of streamflow pathways and biogeochemical implications in semi-arid, forested catchments in Valles Caldera, New Mexico. Ecohydrology 1:239–252
Liu F, Hunsaker C, Bales RC (2013) Controls of streamflow generation in small catchments across the snow–rain transition in the southern Sierra Nevada, California. Hydrol Process 27:1959–1972
Luhmann AJ, Covington MD, Alexander SC, Chai SY, Schwartz BF, Groten JT, Alexander EC (2012) Comparing conservative and nonconservative tracers in karst and using them to estimate flow path geometry. J Hydrol 448–449: 201–211
Meinzer OM (1927) Large springs in the United States. US Geol Surv Water-Supply Paper 557, 94 pp
Middendorf M (1984) Bedrock geology of the Montreal Quadrangle, Missouri: geologic map. Missouri Division of Geology and Land Survey, Rolla, MO
Miller BV (2010) The hydrology of the Carroll Cave–Toronto Springs System: identifying and examining source mixing through dye tracing, geochemical monitoring, seepage runs, and statistical methods. MSc Thesis, Western Kentucky University, USA. http://digitalcommons.wku.edu/theses/216. Accessed January 2014
Miller BV, Lerch RN (2011) Delineating recharge areas for Onondaga and Cathedral Caves using groundwater-tracing techniques. Mo Speleol 51(2):1–36
Missouri Dept. of Natural Resources (2007) Sinkhole areas for the State of Missouri. Missouri Geological Survey, Rollo, MO. http://www.dnr.mo.gov/geostrat/. Accessed October 2014
Missouri Dept. of Natural Resources (2010a) Spring locations for the State of Missouri. Missouri Geological Survey, Rollo, MO. http://www.dnr.mo.gov/geostrat/. Accessed October 2014
Missouri Dept of Natural Resources (2010b) Structural features for the State of Missouri. Missouri Geological Survey, Rollo, MO. http://www.dnr.mo.gov/geostrat/. Accessed October 2014
Missouri Resource Assessment Partnership (2005) Land use/land cover for Camden County, Missouri. MoRAP, Columbia, MO. ftp://msdis.missouri.edu/pub/lulc/lulc0. Accessed August 2010
Moore PJ, Martin JB, Screaton EJ (2009) Geochemical and statistical evidence of recharge, mixing, and controls on spring discharge in an eogenetic karst aquifer. J Hydrol 376(3–4):443–445
Mugel DN, Richards JM, Schumacher JG, (2009) Geohydrologic investigations and landscape characteristics of areas contributing water to springs, the Current River, and Jacks Fork, Ozark National Scenic Riverways, Missouri. US Geol Surv Sci Invest Rep 2009-5138, 80 pp
Nathan MV, Stecker JA, Sun Y (2012) Soil testing in Missouri: a guide for conducting soil tests in Missouri. Extension Circular 923, University of Missouri Extension, Columbia, MO. http://soilplantlab.missouri.edu/soil/ec923.pdf. Accessed October 2010
Palmer AN (1991) Origin and morphology of limestone caves. Geol Soc Am Bull 103:1–21
Qian J, Zhan H, Wu Y, Li F, Wang J (2006) Fractured-karst spring-flow protections: a case study in Jinan, China. Hydrogeol J 14:1192–1205
Quinlan JF (1990) Special problems of ground-water monitoring in karst terranes. In: Ground water and vadose zone monitoring. ASTM STP 1053:275–304
Quinlan JF, Ewers RO (1985) Groundwater flow in limestone terrains: strategy rationale for reliable, efficient monitoring of ground water quality in karst areas. In: Proceedings of the 5th National Symposium on Aquifer Restoration and Ground Water Monitoring, National Water Well Association, Dublin, OH, pp 197–234
Ronan AD, Prudic DE, Thodal CE, Constantz J (1998) Field study and simulation of diurnal temperature effects on infiltration and variably saturated flow beneath an ephemeral stream. Water Resour Res 34:2137–2153
Rushton K (1997) Recharge from permanent water bodies. In: Simmers I (ed) Recharge of phreatic aquifers in (semi)arid areas. Balkema, Rotterdam, pp 215–255
Scanlon BR, Healy RW, Cook PG (2002) Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol J 10:18–39
Singh VP (1995) Computer models of watershed hydrology. Water Resources, Littleton, CO
Vandike JE (1992)The hydrogeology of the Bennett Spring area: Laclede, Dallas, Webster, and Wright counties, Missouri. Water Resour. Rep. no. 38, Missouri Dept. of Natural Resources, Division of Geology and Land Survey, Columbia, MO. https://www.dnr.mo.gov/pubs/WR38.pdf. Accessed October 2010
Vandike JE (1996) The hydrology of Maramec Spring. Water Resour. Rep. no. 55. Missouri Dept. of Natural Resources, Division of Geology and Land Survey, Columbia, MO. https://www.dnr.mo.gov/pubs/WR55.pdf. Accessed October 2010
Vineyard JD, Feder GL (1982) Springs of Missouri. Water Resour. Rep. no. 29, Missouri Geological Survey and Water Resources, Columbia, MO. https://www.dnr.mo.gov/pubs/WR29.pdf. Accessed October 2010
Ward JH (1963) Hierarchical grouping to optimize an objective function. J Am Statist Assoc 58(301). doi 10.1080/01621459.1963.10500845
Acknowledgements
The authors would like to thank the following organizations for their funding support of the project: Missouri Speleological Survey; Cave Research Foundation; Carroll Cave Conservancy; National Speleological Society; and Western Kentucky University. Special thanks to: Amber Spohn for her field work support in sample collection and datalogger maintenance, Lee Anne Bledsoe and Priscilla Baker from the Crawford Hydrology Laboratory for all of their assistance in the various aspects of the groundwater tracing, and Jeffery Crews with the Missouri Geological Survey for his assistance in obtaining information regarding geological mapping that had occurred in the study area. The authors would also like to thank the various landowners who provided access to many of the recharge features and to the numerous cavers who assisted in charcoal packet retrieval, dye injection assistance, and in the ongoing mapping of Carroll Cave.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Miller, B.V., Lerch, R.N., Groves, C.G. et al. Recharge mixing in a complex distributary spring system in the Missouri Ozarks, USA. Hydrogeol J 23, 451–465 (2015). https://doi.org/10.1007/s10040-014-1225-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-014-1225-y