Abstract
In the literature on the definition of urban areas, the methodological approaches are divided into formalist (aggregation by density thresholds) and functionalist (aggregation by commuting quotas). This paper proposes a mixed approach, in which the territorial density threshold from the lower-level administrative unit is combined with the brightness of nighttime satellite imagery, intended as a proxy variable for the functional links. The objective is to attain a method for the delimitation of urban areas, to be used by various States and Regions across the world in an iterative procedure, for the delimitation of urban areas as connected topological spaces. This represents an independent method, compared to the various standards adopted by national and regional statistics bureaus, which allows comparing the infrastructural, economic, and social data of different cities in the world. Such cities are hence described in terms of the “real” dimension of the urban areas, partially correcting the bias related to the adoption of administrative perimeters as a “fact” when local authorities make decisions regarding them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A fast and significant demographic growth started in the 19th century and is still ongoing. This has been compounded by a phenomenon of concentration of population in cities. The estimates of the Population Department of the United Nations state that, in 1950, just 29 inhabitants of the Earth out of 100 lived in urban areas. In 1990, this percentage reached 45%, while the urban population more than tripled, for a total of 2.4 billion. Nowadays, around 3.5 billion people live in urban areas. Around 2030, when the world population will presumably reach 8 billion, 5 billion people are estimated to live in cities. In this framework, cities tend to expand, leading to the minimization of commuting times and distances between them. Throughout history, urban expansion has always been related to urban population growth. Conversely, nowadays urban expansion continues even if local demographic growth has stopped, for the purpose of improving life quality, which is lower in peripheral areas.
The result seems to be a modern revival of the age of medieval communes, with the competition between cities replacing the competition between States. The comparison between cities is an increasingly essential need and does not match the sectorial perimeter of urban geography. Economic, social, and—finally—environmental sciences need to compare cities according to their real dimension. This requires integrating the administrative delimitation with a proxy datum for the definition of the shape of the urban area in a homogeneous way. A proxy variable is required because the proposed method is meant to be simple and easily applicable, even when there are no detailed local datasets—such as, for example, commuting movements. The chosen variable is the brightness of nighttime satellite imagery, intended as a signal of human activity, and hence a parameter for the intensity of daily exchanges between the administrative unit of the central city and the other contiguous administrative units. This leads to the definition of a wider urban zone—through an iterative process articulated into several calculation procedures—intended as the summation of multiple local administrative units, and as the estimate of the real dimension of a city. In this process, the urban area is determined as the aggregation of single local administrative units: this produces an overestimation of the real urban area. However, the objective is not to perform an accurate delimitation of urban areas but to transpose all the available local sets of indicators on a common base, to perform mutual comparisons between wider urban zones. These “urban zones” are “wider” in relation to the extension/expansion of the functional scope that keeps together the area. This expression is here introduced and preferred to the more common “larger urban zones” as the first adjective recalls the measurement of land, with a focus on physical space and surfaces. Instead, “wider” recalls connections and links, which define the real interrelation within an area and reveal its “diffuse” nature.
2 Literature review
2.1 The traditional use of aggregation thresholds
An urban agglomeration is a territory that hosts a set of municipalities with intense—especially economic—relationships with a given city, which represents the agglomeration center (pivot). Their interdependence is characterized by the presence of daily commuters between the single municipalities and the pivot city. When no single city is prevalent in size and/or importance within the agglomeration, the latter is referred to as a (urban) conglomeration.
Agglomerations and conglomerations have been intimately related to the progress of urbanization and the development of urban public transport in the late nineteenth century. The term, which appeared at the end of the nineteenth century, did not raise great interest until the early decades of the twentieth century. Urban morphology became a field of interest following the diffusion of private cars and the functionalists’ new urban planning approaches. This concept was systemically defined in the first half of the 20th century. For example, in Switzerland, in 1930, the Federal Statistical Office (Bundesamt für Raumentwicklung ARE 2006) defined an “urban agglomeration” as a seamlessly built area, consisting of a center and an urban belt, where at least 20% of the population had to work in the primary sector and at least 30% of the active population had to be commuters. In the USA (Adams et al. 1999) and Canada (Statistics Canada 2011), the aggregation of administrative units into Metropolitan Statistical Areas is performed only according to the demographic size, without taking into account functional parameters. This approach originated in the United Kingdom (UK Official Statistics 2011), in an attempt at finding a measure of the real size of urban areas. However, it did not lead to an evolution in the administrative division. Only in France (2015), a (simplified) statistical model has been the basis for a revision of the administrative division. The French model is only based on additive heuristics, without considering commuting flows. Similar approaches also followed this trend in Germany (DESTATIS Statistiches Budensamt 2019) and Japan (Institute for Urban Strategies The Mori Memorial Foundation 2019); however, these analyses are limited to the main urban areas (over 500,000 inhabitants).
The purpose of discretizing urban and non-urban space has already been discussed in the context of the modifiable areal unit problem (MAUP, (Gehlke and Biehl 1934)). Openshaw (Stan 1983) observed that “the areal units (zonal objects) used in many geographical studies are arbitrary, modifiable, and subject to the whims and fancies of whoever is doing, or did, the aggregating”. The issue is still relevant for regional political economy, with special regard for the functional delineation of the urban segments. The use of small-scale spatial data plays a major role in that research field (Rüdiger and Neumann 2019) both for socio-economic (Wong 2009) and transport analyses (Viegas et al. 2009).
The basic algorithm for economic analyses has been devised in the ’80s for the analysis of Travel-to-Work Areas in Great Britain (Coombes et al. 1986). It is a classical constructive heuristic, while the contiguity constraint of the districts is estimated a posteriori. This approach is used also in Italy (ISTAT Istituto Nazionale di Statistica 2017) with commuting geography.
The issue of the definition of metropolitan areas is taken up by Tonev et al. (Tonev et al. 2017), who investigate the methodological approaches related to the functional integration of regional units and inter-regional relations. They focus on those used within Integrated Territorial Investments (ITI) to delimit the metropolitan areas analyzing the functional integration of regional units and inter-regional relations. ITI (“Community Led Local Development”, (European Urban Knowledge Network 2018)) has been introduced by the EU, encouraging member states to define and study their metropolitan areas. Galdo et al. (2019) propose a method to identify urban areas by combining data from the ground (Census) and space (Google Earth). Bosker et al. (2020) focus on Indonesia and make use of data on commuting flows, spatially fine-grained population, and remotely sensed nighttime lights to define metropolitan areas using several approaches from the literature. Moreno-Monroy et al. (2020) present a method to delimit metropolitan areas—as functional urban areas (FUAs)—by analyzing the effects of the thresholds (density, commuting share). Maravalle and Simeone (1995) considered the problem of subdividing a region into districts—formed by geographically contiguous sites—with the highest possible homogeneity concerning a certain set of characteristics. Hansen et al. (2003) provided an exact algorithm for regional clustering. On the same path, Duque et al. (2011) introduced a new spatially constrained clustering problem called the max-p-regions problem. It involves clustering a set of geographic areas into the highest possible number of homogeneous regions so that the values of spatially extensive regional attributes are above a set threshold.
A standard definition of the metropolitan area was developed by OECD (2012), (Veneri 2016) and Eurostat (Schiavina et al. 2019; Eurostat 2019a): it is based on the aggregation of municipalities around a pivot city following functional thresholds (e.g., a minimum share of daily trips toward the pivot).
2.2 From static satellite data acquisition to AI procedures
As in the rest of geographic sciences, the availability of satellite data has also been discontinuous across human geography. Kim (1890) proposed the first study on US metropolitan areas, using both cartographic and satellite data. Uchida et al. (Uchida and Nelson 2011), in absence of O‑D commuting flow data, introduced the Agglomeration Index (AI) to measure the “thickness” of urban concentration. Duranton (2015) adopted a functional approach, by proposing a commuting algorithm. Following a series of complex procedures (Bankert et al. 2011) to clean the white noise of natural and anthropogenic—non-urban—light sources, nighttime satellite images can be the main tool for the analysis of cities (Chen et al. 2017). Smith (2016) investigated applications and techniques for socio-economic research with online interactive thematic mapping using post-processed satellite images. Freire et al. (2016) investigated the relationship between territorial density and size of the spatial sampling grid used for satellite images. Bennet & Smith (2017)’s reviews develop the use of multitemporal DMSP-OLS and VIIRS imagery to analyze urbanization, economic, and population dynamics across a range of geographic scales. The second-generation NASA “Black Marble” images (Román et al. 2018) offer a greater definition and are also provided as a georeferenced raster for GIS analysis. They allow multiple outputs, ranging from verisimilitude (Roychowdhury et al. 2011) to machine learning-aided linear discretization techniques (Rybnikova et al. 2021).
2.3 Why adopt a simplified approach?
The definition of the functional space of cities is still a trending topic in regional political economy, especially in the framework of a functional delimitation of urban segments. The use of small-scale spatial data plays a key role in this research area (Budde and Neumann 2019). In addition to the socio-economic studies based on the definition of territorial grids, several studies use sensor-generated data, such as daytime and nighttime satellite images, for the segmentation and classification of urban and non-urban space (Skyglowberlin 2022). Elvidge et al. (2021) have carried out an in-depth investigation of the opportunities provided by the satellite dataset for the detailed delimitation of urban areas, reducing signal interferences in (Zhou et al. 2015), they provide a high-detail global mapping. However, the more detailed satellite images are, the lower the compatibility with local datasets is, as these are based on local administrative divisions. The subdivision of these data, which is virtually possible, would make multi-national comparisons much more complex. Different needs must be balanced to achieve the set goal: that is, to provide a methodology for statistical and analytical comparisons between the different cities in the world.
The difference between “administrative” and “real” cities is inversely proportional to their size, as will be demonstrated in the following paragraphs. This law has a global validity, despite some differences between continents.
3 Methodology
The proposed method adopts local subdivisions to delimit urban areas as wider urban zones, instead of administrative division. In this way, the statistical bias of the MAUP is kept but no new perimeters are identified, preserving the connection with the local geostatistical history. Urban areas, defined by a double threshold (territorial density and average brightness from satellite nighttime images) are treated as topological spaces.
In this sense, an urban area is an out-and-out topological space formed by the aggregation of several local administrative units. This allows transposing the intuitive concepts of “distance” and “continuity” from the frontier into the study of urban areas.
3.1 From the agglomeration to the connected domain of LAUs
The proposed method operates on the minimum territorial divisions, that is Local administrative units (LAUs); it performs the discretization of urban areas through the identification of homogeneous areas by territorial density. These elements are urban islands characterized by a good degree of urbanistic homogeneity. Each island is a geographical space with the following characteristics:
-
homogeneous urban structure, related to the homogeneity of territorial distribution;
-
possibility of being topologically represented by a simply connected domain (that is, a density-connected domain).
Starting from the main LAU—the pivot—, urban zones can be delimited in two ways:
-
1.
by aggregating contiguous LAUs;
-
2.
by disaggregating contiguous LAUs that do not meet aggregation conditions, and then by aggregating only the urban portions of the LAU to the pivot.
3.2 The density threshold
The first step is the definition of a density threshold to discriminate whether an LAU may or may not be part of the examined urban zone. The density threshold is not a standard assumption: it depends on the density of the upper administrative level (national/regional). So, the urban threshold of a region with a low density will be lower than for a region characterized by a higher density. Of course, this is a necessarily simplified procedure, as this numerical threshold approximates a much more complex real situation. Urban structures are interrelated by multiple elements: population density (conceived as an approximation of the contiguity of the built-up area) is just one of them. The key issue is the motorization rate of the population: the higher it is, the more land-rarefied (sprawling) urban structures will be. A city does not exist as a fixed entity (built-up area) but as a cloud of high-density relational paths.
In this sense, the subordination of one municipality to another is also described by the ratio between the mean number of daily trips between the two areas, divided by the total value. There are several values in the technical literature, but generally, a level of 30% is assumed to define urban contiguity and a level of 10% for metropolitan-level contiguity. In general, the existence of both spatial and functional contiguity (percentage of trips) is well approximated when fulfilling a set density threshold density. This approximation is acceptable (i.e., trips are underestimated by about 5–7% and not overestimated) for transport simulation. Given the density d [people/km2] of the third-level administrative subdivision (NUT3 or NUT2 [Eurostat 2021], as in European NUTSFootnote 1), of the examined urban zone, the density threshold Θ is defined as (Fig. 1):
The analysis of the different local conditions has led to the choice of a dynamic, rather than static, density threshold. As shown in Rüdiger and Neumann, changes in the threshold lead to changes in the granularity of the analysis. (Table 1).
3.3 Data sources
The data used to apply the described procedure have been obtained from the following sources:
-
World national and administrative boundaries, FAO (2020)
-
VIIRS Nighttime Light (VNL) satellite images (2020)
-
Gridded Population of the World (GPW), version 4 (2019)
3.4 WUZ building procedure
The method is iterative. Let the m zones of a given country with a third-level administrative subdivision NUT3 (or NUT2) be called regions Ri. Regardless of the local denomination, the model recognizes for each country, the subdivision into regions and the division of each region into local administrative units. Each region Ri contains n LAUs ordered from 1 to n in descending order based on the resident population. The procedure is iterative and is repeated for each LAU0 of Ri with a population greater than 50,000 inhabitants. The method is aimed at estimating the effective size of a city as the aggregation of several LAUs. Of course, if the urban zone is all contained within the LAU boundary, the method will not provide any aggregation.
The proposed procedure is an evolution of the pure topological model based on the density threshold—proposed in (Spinosa 2017)—integrated with the acquisition of average brightness within the perimeter of LAUs. For each region Ri and for each LAUk with more than 50,000 inhabitants and with a density d, the following additive algorithm (Fig. 2a) is performed to build the wider urban zone WUZj:
-
1.
Acquire the administrative boundary of LAUk
-
2.
Acquire the average brightness Bk calculated within the boundary of LAUk
-
3.
Calculation of the threshold density Θ as in (1)
-
4.
n = total number of LAUs in the region Ri
-
5.
v = 1
-
6.
w = 1
-
7.
\(\mathrm{WUZ}_{j}=\mathrm{LAU}_{k}\)
-
8.
For v = 1 to n repeat the following cycle:
-
9.
m = number of LAUs adjacent to LAUk
-
10.
For w = 1 to m repeat the following cycle:
-
11.
Acquire the administrative boundary of LAUw
-
12.
Acquire the average brightness Bw calculated within the boundary of LAUw
-
13.
Acquire the density dw of LAUw
-
14.
If \(B_{w}\geq 0,5B_{0}\) then
15. If \([d_{w}\geq \Uptheta\) and \(\mathrm{LAU}_{w}\notin (\mathrm{WUZ}_{k},k=1toj)]\) then \(\mathrm{WUZ}_{j}=\mathrm{WUZ}_{j}+\mathrm{LAU}_{w}\)
-
16.
w = w + 1
-
17.
v = v + 1
-
11.
-
18.
End.
a The example represents a simplified administrative district with four distinct urban zones. For the first area, a.1, the WUZ is derived from the aggregation of three LAUs with different densities. In the area a.2, the WUZ is formed through the incorporation of two municipalities by density and annexation of a third one (with a density below Θ) by contiguity. a.3 and a.4 are mononuclear urbanisms: that is, single cities with a single municipality. b The second example shows how an urban zone can be formed even by disaggregation of a demographically inhomogeneous LAU boundary. A common non-simply connected boundary is divided into two sub-domains. One of them hosts the main urban nucleus, and the other one represents the remaining non-urban land. In b.4 the WUZ coincides only with the urban sub-domain. In the case of additive procedure: the core municipality (pivot)—considered a topographic space—is aggregated to the municipality in the concave space. The density of the resulting WUZ is lower than the original ones
The WUZ building process by disaggregation (Fig. 2b) consists in repeating the aggregation process on a single LAU scale. The reference unit is the minimum investigation radius ϱR. Given a LAU, if R0 is the administrative division of higher level (NUT3 or NUT2), made up of n LAUh with a surface σh [km2], then ϱR is:
Given a LAUh boundary (with a population Πh and a surface σh [km2]) adjacent to a forming UAo, LAUh is considered anomalous if:
In this case, LAUh is divided into η regular square portions \({\mathrm{LAU}}_{h}^{k}\) [k = 1,η] with a side ϱR [km] and an area \({\varrho _{R}}^{2}\) [km2]. At this point, the procedure continues as in the additive case. Each of the η \({\mathrm{LAU}}_{h}^{k}\) parts has:
Of course, \(\sigma _{h}=\upeta \cdot {\delta }_{h}^{k}\).
The aggregation gradually incorporates the individual \({\mathrm{LAU}}_{h}^{k}\) parts that meet the density threshold:
LAUh is demographically inhomogeneous if not all the η parts \({\mathrm{LAU}}_{h}^{k}\) are incorporated in the formed UAo. In algorithmic form, the disaggregation procedure for LAUh is as follows:
-
1.
Calculate ϱR as in (2)
-
2.
k = 1
-
3.
\(\upeta =\sigma _{h}/4{\varrho _{R}}^{2}\)
-
4.
If \(\upeta \geq 4\) then
-
5.
Divide LAUh into η equal parts
-
6.
For k from 1 to η then
-
7.
if \({\delta }_{h}^{k}\geq \Uptheta\) then \(\mathrm{LAU}_{0}=\mathrm{LAU}_{0}+{\mathrm{LAU}}_{h}^{k}\)
-
8.
k = k + 1
-
7.
-
5.
-
9.
End.
The last step is to make the LAU0 a connected topological domain. LAU0 could have holes or points or, again, concave areas. Given the n administrative units of R0 not included in LAU0 (internal, as holes, or external):
-
1.
\(\mathrm{U}=\mathrm{LAU}_{0}\)
-
2.
i = 1
-
3.
If U is a connected topological space or i = n
-
4.
Then go to end
-
5.
else while U is not a connected topological space
-
6.
\(\mathrm{U}=\mathrm{U}+h_{i}\)
-
7.
\(\mathrm{i}=\mathrm{i}+1\)
-
5.
-
8.
End.
This sub-procedure is a morphological homogenization process, which can include the addition of other LAUs or previously discarded (due to the low density) parts of LAU.
3.5 Conflict points
The WUZ building procedure has two possible ordinary conflict points, which occur when the aggregative process:
-
a)
meets the boundary of the region Ri
-
b)
meets a LAU that has already been incorporated into another WUZ
Conflict (a) is resolved by continuing the procedure in the adjacent region. This conflict also results to be avoided by applying the procedure simultaneously to the entire State, without operating region by region. However, there will still be anomalies in cross-border WUZs between two neighboring states; the best solution is to proceed on a case-by-case basis by incorporating the foreign region into the WUZ building procedure.
Conflict (b) is resolved in two steps. The procedure is run on the LAUs ordered from the largest to the smallest population. Given a WUZj, the algorithm positively verifies the aggregation of LAUw, but LAUw is part of a previous formed WUZk. Then the following sub-procedure is:
-
1.
If the density \(\sigma (\mathrm{WUZ}_{k})\geq \Uptheta\) then
-
2.
If the population of the pivot city (WUZj) > 1.5 · population of pivot city (WUZk) then
-
3.
\(\mathrm{WUZ}_{j}=\mathrm{WUZ}_{j}+\mathrm{WUZ}_{k}\)
-
4.
Else if the population of pivot city (WUZk) > 1.5 · population of pivot city (WUZj) then \(\mathrm{WUZ}_{k}=\mathrm{WUZ}_{k}+\mathrm{WUZ}_{j}\)
-
3.
-
2.
-
5.
End.
Therefore, the adjacency of two WUZs implies that the largest one incorporates the other if two conditions are met: that is, the fulfillment of the density threshold and a ratio between the population of the respective pivot cities > 1.5. Conversely, the two areas, although adjacent, remain separate.
4 Results
This repository contains the tables—available for consultation—that result from the application of the proposed method for all the countries of the world. Considering the homogeneity of data availability, the year 2015 has been chosen as the demographic horizon. The tables, arranged by continent and macro-region, show the following data: name of the WUZ, region (NUT3 or NUT2), area (in km2), population as of 1/1/2005 and as of 1/1/2015, annual growth rate (AGR), territorial density (pop. per km2).
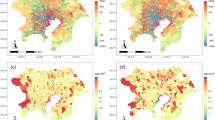
The following images show the comparison between the satellite images and the aggregated perimeter of WUZs with a population exceeding 200,000 inhabitants. The colors—increasing from yellow to red—indicate territorial density. (Figs. 3, 4 and 5).
a Northern Italy, nighttime satellite image (Nasa 2017). b Northern Italy, model results for the main WUZs
a Central Italy, nighttime satellite image (Nasa 2017). b Central Italy, model results on the main WUZs
a Southern Italy and isles, nighttime satellite image (Nasa 2017). b Southern Italy and isles, model results on the main WUZs
5 Discussion
The results of the proposed procedure for the delimitation of urban zones with an additive method based on brightness and density thresholds strongly differ from those obtained with commuter flow-based methods. This matches the purpose of this work, which is to define a heuristic for the identification of Local administrative units in relation to the built environment. Fig. 6 shows the results of the proposed model for the Italian case. This method overcomes the issues related to the availability of commuting matrices; moreover, the methods that adopt aggregation thresholds linked to dynamic factors are more suitable for simulating the metropolitan area, that is, the space of a city.
Italy, comparison between the boundaries of the main urban areas according to (a) the proposed methodology and (b) a functionalist approach such as the “Local labor system” of Istat (2011)
The use of LAUs produces a less pleonastic perimeter. On average, in the Italian case, the perimeters produced by the proposed method are characterized by a built/green area ratio of 1: 0.75/0.90. According to the “Local labor system” (LLS) of Istat the ratio is 1:0.7–8.5 (mean 1.87). The mean Jaccard distance dJ between the WUZs and the LLSs is 0.715. Despite the irregularity of the progression, Fig. 7 shows that the differences between the two methodologies tend to decrease as territorial density grows. This confirms the confidence level of satellite image brightness as an alternative to commuting intensity, which is at the base of the Istat functionalist model.
The use of local territorial distribution does not solve the MAUP bias, as the small case of the Italian case already shows: the average size of the LAU (Comune) varies between 15.8 km2 in Lombardy and 76.1 km2 in Apulia. However, this allows working with the calculated urban zones, using the existing databases, which must not be divided and projected on a different territorial division.
The application on the Italian case shows that the aggregated zones generated by the proposed model are more extended than the real urban area, and less extended than the metropolitan area. The comparison with the French “Unité urbaine” (I.n.d.l.s.e.d.é. économiques 2022), based on a formalist approach (density thresholds and number of workers) reported a value of dJ = 0.455. Instead, the comparison with the perimeters of the Travel to Work Areas (TTWAs) of the United Kingdom (O.f.N. Statistics 2016), which are determined through a functionalist approach, showed dJ = 0.765. In general, the estimations produced by the WUZ method seem to be 10–50% lower than those obtained with a formalist method. When comparing the results with the areas obtained through a functionalist approach, the (negative) difference is higher (beyond 50%).
Future research will include an in-depth comparison with the models based on the (fixed or dynamic) commuting threshold instead of the density threshold. It seems necessary to investigate the propensity to commuting within the WUZs to examine the circadian physiology of inner versus outer LAUs. In particular, the observations on the Italian case have suggested future research on the variation of brightness in relation to the number of commuting movements between a pivot city and the aggregated LAUs. This will contribute to the objective of standardizing the interpretation model of urban areas on a general and extra-national base.
Notes
Nomenclature of Territorial Units for Statistics or NUTS is a geocode standard for referencing the subdivisions of countries. The standard, adopted in 2003 (Eurostat 2019b), is developed and regulated by the European Union, but it is general and easily applicable anywhere else in the world.
References
(2015) “Les zonages d’étude de l’Insee. Une histoire des zonages supra communaux définis à des fins statistiques,” INSEE Méthods, Institut national de la statistique et des études économiques, no. 129. https://www.epsilon.insee.fr/jspui/bitstream/1/29553/1/imethode129.pdf. Accessed 13 May 2022
(2020) “Earth Observation Group, Payne Institute for Public Policy,” VIIRS Nighttime Light (VNL) V2. https://eogdata.mines.edu/products/vnl/#annual_v2. Accessed 13 May 2022
“Sistemi locali del lavoro (SLL),” Istat, 2011–2016. https://www.istat.it/it/informazioni-territoriali-e-cartografiche/sistemi-locali-del-lavoro. Accessed 13 May 2022
Adams JS, Drasek BJV, Phillips EG (1999) Metropolitan area definition in the United States. Urban Geogr 20(8):695–726. https://doi.org/10.2747/0272-3638.20.8.695
Bankert R, Solbrig J, Lee T, Miller S (2011) Automated lightning flash detection in nighttime visible satellite data. Weather Forecast 26:399–408
Bennett MM, Smith LC (2017) Advances in using multitemporal night-time lights satellite imagery to detect, estimate, and monitor socioeconomic dynamics. Remote Sens Environ 192:176–197. https://doi.org/10.1016/j.rse.2017.01.005
Bosker M, Park J, Roberts M (2020) Definition matters. Metropolitan areas and agglomeration economies in a large-developing country. J Urban Econ. https://doi.org/10.1016/j.jue.2020.103275
Budde R, Neumann U (2019) The size ranking of cities in Germany—caught by a MAUP? GeoJournal 6(84):1447–1464
Bundesamt für Raumentwicklung ARE (2006) Monitoring urbaner Raum. https://www.are.admin.ch/are/de/home/staedte-und-agglomerationen/grundlagen-und-daten/monitoring-urbanerraum.html. Accessed 13 May 2022
Center for International Earth Science Information Network (CIESIN)—Columbia University (2019) Gridded population of the world (GPW), version 4. https://sedac.ciesin.columbia.edu/data/collection/gpw-v4. Accessed 13 May 2022
Chen H, Xiong X, Sun C, Chen X, Chiang K (2017) Suomi-NPP VIIRS day—night band on-orbit calibration and performance. J Appl Remote Sens 11:Art 36019
Coombes MG, Green AE, Openshaw S (1986) An efficient algorithm to generate official statistical reporting areas: the case of the 1984 travel-to-work areas revision in Britain. J Oper Res Soc 37(10):943–953
DESTATIS Statistiches Budensamt (2019) Städte-Boom und Baustau: Entwicklungen auf dem deutschen Wohnungsmarkt 2008–2018
Duque JC, Church RL, Middleton RS (2011) The p‑regions problem. Geogr Anal 43(1):104–126
Duranton G (2015) Delineating metropolitan areas: measuring spatial labour market networks through commuting patterns. Econ Interfirm Netw Adv Jpn Bus Econ 4:107–133. https://doi.org/10.1007/978-4-431-55390-8_6
Elvidge C, Zhizhin M, Ghosh T, Hsu F‑C, Taneja J (2021) Annual time series of global VIIRS nighttime lights derived from monthly averages: 2012 to 2019. Remote Sens 13(5):922–927
European Urban Knowledge Network (2014–2016 (2018) Community Led Local Development (CLLD) for Integrated Territorial Investment (ITI). https://www.eukn.eu/fileadmin/Lib/files/EUKN/2013/Factsheet%20CLLD.pdf. Accessed 13 May 2022
Eurostat (2019a) City, functional urban area and greater city. https://ec.europa.eu/eurostat/web/cities/spatial-units. Accessed 13 May 2022
Eurostat (2019b) Hystory of NUTS. https://ec.europa.eu/eurostat/web/nuts/history. Accessed 13 May 2022
Eurostat (2021) NUTS 2021 classification. https://ec.europa.eu/eurostat/web/nuts/background. Accessed 13 May 2022
FAO (2020) National and administrative boundaries, interactive repository. http://www.fao.org/geonetwork/srv/en/main.home?uuid=ac02a460-da52-11dc-9d70-0017f293bd28. Accessed 13 May 2022
Freire S, MacManus K, Pesaresi M, Doxsey-Whitfield E, Mills J (2016) Development of new open and free multi-temporal global population grids at 250m Resolution. In: Proceedings of the 19th AGILE conference on geographic information science Helsinki
Galdo V, Li Y, Rama M (2019) Identifying urban areas combining data from the ground and from outer space: an application to India. J Urban Econ. https://doi.org/10.1016/j.jue.2019.103229
Gehlke CE, Biehl K (1934) Certain effects of grouping upon the size of the correlation coefficient in census tract material. J Am Stat Assoc 185A(29):169–170
Hansen P, Jaumard B, Meyer C, Simeone B, Doring V (2003) Maximum split clustering under connectivity constraints. J Classif 20:143–180
I. n. d. l. s. e. d. é. économiques (2022) “Base des aires d’attraction des villes 2020,” Insee. https://www.insee.fr/fr/information/4803954. Accessed 4 Dec 2022
Institute for Urban Strategies The Mori Memorial Foundation (2019) Japan power cities databook 2019. http://morim-foundation.or.jp/english/ius2/jpc2/. Accessed 13 May 2022
ISTAT Istituto Nazionale di Statistica (2017) Forme, livelli e dinamiche dell’urbanizzazione in Italia. https://www.istat.it/it/archivio/199520. Accessed 13 May 2022
Kim S (2007) Changes in the nature of urban spatial structure in the United States, 1890–2000. J Reg Sci 47:273–287
Maravalle M, Simeone B (1995) A spanning tree heuristic for regional clustering, communications in statistics. Theory Methods 24(3):625–639
Moreno-Monroy AI, Schiavina M, Veneri P (2020) Metropolitan areas in the world. Delineation and population trends. J Urban Econ. https://doi.org/10.1016/j.jue.2020.103242
NASA (2017) 2016 archive from Suomi NPP-VIIRS. https://earthobservatory.nasa.gov/features/NightLights
O. f. N. Statistics (2016) Travel to work area analysis in Great Britain: 2016,” ONS. https://www.ons.gov.uk/employmentandlabourmarket/peopleinwork/employmentandemployeetypes/articles/traveltoworkareaanalysisingreatbritain/2016. Accessed 12 Apr 2022
OECD (2012) Redefining ‘urban’. A new way to measure metropolitan areas. OECD Publishing https://doi.org/10.1787/9789264174108-en
Román MO, Wang Z, Sun Q, Kalb V, Miller SD, Molthan A, Schultz L, Belle J, Stokes EC, Pandeyg B, Setog KC, Hall D, Oda T, Wolf RE, Lin G, Golpayegani N et al (2018) NASA’s Black Marble nighttime lights product suit. Remote Sens Environ 10:113–143
Roychowdhury K, Taubenböck H, Jones S (2011) Delineating urban, suburban and rural areas using Landsat e DMSP-OLS night-time images. In: Joint Urban Remote Sensing Event Munich
Rüdiger B, Neumann U (2019) The size ranking of cities in Germany: caught by a MAUP? GeoJournal 84:1447–1464
Rybnikova N, Portnov B, Charney I, Rybnikov S (2021) Delineating functional urban areas using a multi-step analysis of artificial light-at-night data. Remote Sens 13(18):3714. https://doi.org/10.3390/rs13183714
Schiavina M, Moreno-Monroy A, Maffenini L, Veneri P (2019) “GHS-FUA R2019A—GHS functional urban areas, derived from GHS-UCDB R2019A,” European Commission, Joint Research Centre (JRC). https://data.jrc.ec.europa.eu/dataset/347f0337-f2da-4592-87b3-e25975ec2c95. Accessed 13 May 2022
Skyglowberlin “Peer reviewed literature about artificial light at night,” Zotero. https://www.zotero.org/groups/2913367/alan_db. Accessed 4 Apr 2022
Smith DA (2016) Online interactive thematic mapping: applications and techniques for socio-economic research. Comput Environ Urban Syst 57:106–117
Spinosa A (2017) A new algorithm for the city: the use of topology and transport modeling to make urban areas more equitable. In: World Engineering Forum Roma
Stan O (1983) The modifiable areal unit problem. Concepts and techniques in modern geography, no. 38
Statistics Canada (2011) Standard Geographical Classification (SGC). https://www.statcan.gc.ca/eng/subjects/standard/sgc/geography. Accessed 13 May 2022
Tonev P, Dvořák Z, Šašinka P, Kunc J, Chaloupková M, Šilhan Z (2017) Different approaches to defining metropolitan areas (case study: cities of Brno and Ostrava, Czech republic). Geogr Tech 12:108–120. https://doi.org/10.21163/GT_2017.121.11
Uchida H, Nelson A (2011) Agglomeration index: towards a new measure of urban concentration, urbanization and development: multidisciplinary perspectives. Oxford University Press https://doi.org/10.1093/acprof:oso/9780199590148.003.0003
UK Official Statistics (2011) The rural-urban definition—detailed guidance on the rural-urban definition and how and when to apply it. https://www.gov.uk/government/statistics/the-rural-urban-definition. Accessed 13 May 2022
Veneri P (2016) City size distribution across the OECD. Does the definition of cities matter? Comput Environ Urban Syst 59:86–94
Viegas JM, Martinez LM, Silva AE (2009) Effects of the modifiable areal unit problem on the delineation of traffic analysis zones. Environ Plan B Urban Anal City Sci 36(4):625–643
Wong D (2009) The modifiable areal unit problem (MAUP). In: The SAGE handbook of spatial analysis Los Angeles, pp 105–124
Zhou Y, Smith S, Zhao K, Imhoff M, Thomson A, Bond-Lamberty B, Asrar G, Zhang X, He C, Elvidge C (2015) A global map of urban extent from nightlights. Environ Res Lett. https://doi.org/10.1088/1748-9326/10/5/054011
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
A. Spinosa declares that he has no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
10037_2022_169_MOESM1_ESM.ods
That tables result from the application of the proposed method for all the countries of the world. The tables, arranged by continent and macro-region, show the following data: name of the WUZ, region (NUT3 or NUT2), area (in square km), population as of 1/1/2005 and as of 1/1/2015, annual growth rate (AGR), territorial density (pop. per square km).
000_synthesis
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Spinosa, A. Wider urban zones: use of topology and nighttime satellite images for delimiting urban areas. Rev Reg Res 42, 141–159 (2022). https://doi.org/10.1007/s10037-022-00169-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10037-022-00169-y