An inclusion model for predicting granular elasticity incorporating force chain mechanics

Abstract

Granular media is ubiquitous, playing a vital role in a diverse set of applications. The complex microstructure of granular media results from assorted particle shapes, morphologies, and packings, make it difficult to predict its macroscopic behavior. Under compression, these complex microstructures enable highly anisotropic and heterogenous behaviors, including creation of highly-loaded particles (i.e. force chains) supported by clusters of minimally-loaded particles. While many existing constitutive models relate state variables describing microscale behavior to continuum properties, these models do not generally consider the mesoscale interactions between the force chain network and minimally-loaded particles. Here, we develop a micromechanics model that connects micro-scale force chain mechanics to macro-scale mechanical behavior through explicit consideration of the interaction between force chains and minimally-loaded particles. We first examine the elastic behavior of a force chain using a spring model, explicitly considering the mesoscale interactions between the force-chains and surrounding regions. We then construct an equivalent inclusion problem to calculate macroscopic mechanical response as analytical functions of microscopic properties, with proper consideration of mesoscale interactions. We present our calibration and validation approaches, showing the model’s predictive abilities. Finally, we examine the effect of relevant microscopic quantities on macroscopic response, demonstrating the importance of these mesoscale interactions on bulk deviatoric behavior.

Appendices

Appendix 1: Eshelby tensor for an orthotropic matrix

When creating the equivalent inclusion problem, an orthotropic matrix is assumed. Such an assumption affects the form of the Eshelby tensor. Previous work has found a closed-form solution for the Eshelby tensor through use of Airy stress functions paired with a complex variable formulation [59, 60]. The Eshelby tensor for an inclusion in an orthotropic matrix can be expressed as follows. We note that the expansion for $S_\alpha$ reported in Chiang et al. is corrected here [59, 60].

$$\begin{aligned} \begin{aligned}&S_{1111} = P_\alpha \left( e^2 C_{1111} + \frac{e\lambda \left( \sqrt{C_{1111}C_{2222}}-C_{1122} \right) }{2C_{1212}S_\alpha }\right. \\&\quad \left. \left( \sqrt{C_{1111}C_{2222}} + C_{1122} + C_{1212} \right) \right) \\&\quad S_{1122} = P_\alpha \left( e^2 C_{1122} - \frac{e \left( \sqrt{C_{1111}C_{2222}}-C_{1122} \right) }{2\lambda S_\alpha } \right) \\&\quad S_{2211} = P_\alpha \left( \lambda ^2 C_{1122} - \frac{e \lambda ^3 \left( \sqrt{C_{1111}C_{2222}}-C_{1122} \right) }{2 S_\alpha } \right) \\&\quad S_{2222} = P_\alpha \left( \lambda ^2 C_{1111} + \frac{e\lambda \left( \sqrt{C_{1111}C_{2222}}-C_{1122} \right) }{2C_{1212}S_\alpha }\right. \\&\quad \left. \left( \sqrt{C_{1111}C_{2222}} + C_{1122} + C_{1212} \right) \right) \\&\quad 2 S_{1212} = \frac{P_\alpha }{S_\alpha } \left( 1 + e^2 \lambda ^2 \right) S_\alpha \sqrt{C_{1111}C_{2222}} \\&\quad + e\lambda \left( \sqrt{C_{1111}C_{2222}}-C_{1122} \right) \end{aligned} \end{aligned}$$

(A.1)

$$\begin{aligned} \begin{aligned}&\text {where, }\quad e = \frac{b}{a},\quad \lambda = \left( \frac{C_{1111}}{C_{2222}}\right) ^{1/4},\\&\quad S_\alpha = \sqrt{1 + \frac{C}{4}},\quad P_\alpha = \frac{1}{Q\sqrt{C_{1111}C_{2222}}}, \\&\quad C = \frac{(\sqrt{C_{1111}C_{2222}} + C_{1122})(\sqrt{C_{1111}C_{2222}} - C_{1122} - 2C_{1212})}{C_{1212}\sqrt{C_{1111}C_{2222}}}, \\&\quad Q = 1 + e^2 \lambda ^2 + 2 e \lambda S_\alpha \end{aligned} \end{aligned}$$

(A.2)

Appendix 2: Buckling criterion for a triplet

The potential energy density for a triplet in terms of the degrees of freedoms of the particles is given in Eq. 11. Looking at the potential energy itself, we have

$$\begin{aligned} \psi = k^n \left( \delta n\right) ^2 + \frac{1}{2} k^s \left( \delta l \cos \theta d\theta \right) ^2 \end{aligned}$$

(B.1)

To find instabilities, we obtain an energy expression that incorporates virtual work performed on the system.

$$\begin{aligned} \begin{aligned} V&= \psi - W \\ V&= k^n \left( \delta n\right) ^2 + \frac{1}{2} k^s \left( \delta l \cos \theta d\theta \right) ^2 - F^t\Delta \\ V&= k^n \left( \delta n\right) ^2 + \frac{1}{2} k^s \left( \delta l \cos \theta d\theta \right) ^2 \\&\quad - F^t\left( 4R \cos \theta - 2 \delta l \cos (\theta + \delta \theta ) \right) \end{aligned} \end{aligned}$$

(B.2)

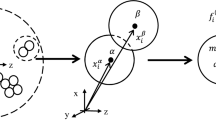
$F^t$ represents a force along the triplet direction, $\textbf{n}$, as shown in Fig. 1, while $\Delta$ represents the displacement associated with $F^t$. Recasting $\delta l$ in terms of particle radius and perturbation from it, we take $\delta l = 2R - \delta n$. Furthermore, using the definition of a derivative $\cos \theta d\theta \approx \sin (\theta + d\theta ) - \sin \theta$, we can re-express Eq. B.2 as

$$\begin{aligned} \begin{aligned} V = k^n \left( \delta n\right) ^2&+ \frac{1}{2} k^s \left( \left( 2R - \delta n \right) \left( \sin \left( \theta + d\theta \right) - \sin \theta \right) \right) ^2 \\&- F^t\left( 4R \cos \theta - 2 \left( 2R - \delta n \right) \cos (\theta + \delta \theta ) \right) \end{aligned} \end{aligned}$$

(B.3)

We take derivatives of Eq. B.3 with respect to the degrees of freedom in the triplet system - $\delta n$ and $\delta \theta$. Using these derivatives, we obtain a system of two equations.

$$\begin{aligned} \begin{aligned}&2 k^n \delta n - 2 F_c \cos \left( \theta + \delta \theta \right) \\&\quad - k^s (2R - \delta n) (\sin \left( \theta + \delta \theta \right) - \sin \theta )^2 = 0 \\&\quad -2 F_c (2R - \delta n) \sin \left( \theta + \delta \theta \right) \\&\quad + k^s (2R - \delta n)^2 \cos \left( \theta + \delta \theta \right) \left( \sin \left( \theta + \delta \theta \right) - \sin \theta \right) = 0 \end{aligned} \end{aligned}$$

(B.4)

For a triplet with a given configuration angle, $\theta$, we can compute the corresponding $F_c$. In most cases, the system in B.4 would need to be solved numerically. However, an analytical solution can be obtained for the special case of a triplet with $\theta = 0$. This simplifies the system given in B.4 to

$$\begin{aligned} \begin{aligned}&2 k^n \delta n - 2 F_c \cos \left( \delta \theta \right) - k^s (2R - \delta n) \sin ^2 \left( \delta \theta \right) = 0 \\ -&2 F_c (2R - \delta n) \sin \left( \delta \theta \right) + k^s (2R - \delta n)^2 \cos \left( \delta \theta \right) \sin \left( \delta \theta \right) = 0 \end{aligned} \end{aligned}$$

(B.5)

Solving the system of equations in B.5 gives a simplified expression for the critical buckling load.

$$\begin{aligned} F_c = \frac{k^nk^s R\cos (\delta \theta )}{2k^n + k^s} \approx \frac{k^nk^s R}{2k^n + k^s} \end{aligned}$$

(B.6)

For a given $k^s$, if a load along the triplet exceeds $F_c$, the triplet is not considered to be a part of the strong network.

Appendix 3: Testing result chart

Table 3 For the validation process, 26 unique loading paths were chosen. The strains were chosen by varying the principal strains ($\epsilon _1$ and $\epsilon _2$) and the angle between $\epsilon _1$ and the x-axis (the angle $\beta$). These strains were then transformed accordingly (to $\epsilon _{xx}$, $\epsilon _{yy}$, $\epsilon _{xy}$) and imposed on the assembly (Fig. 8). The listed errors are between model prediction and mean response measured from five DEM simulations. The median error for $\tilde{E}_x$, $\tilde{E}_y$, and $\tilde{G}_{xy}$ are 13%, 13%, and 9% respectively. The large errors shown are due to increased sensitivity in error measurement due to lower stiffness values and stochasticity of the system