DEM-simulation of thin elastic membranes interacting with a granulate

Abstract

For a wide range of applications, we need DEM simulations of granular matter in contact with elastic flexible boundaries. We present a novel method to describe the interaction between granular particles and a flexible elastic membrane. Here, the standard mass-spring model approach is supplemented by surface patches given by triangulation of the membrane. In contrast to standard mass-spring models, our simulation method allows for an efficient simulation even for large particle size dispersion. The novel method allows coarsening of the mass-spring system leading to a substantial increase in computation efficiency. The simulation method is demonstrated and benchmarked for a triaxial test.

1 Introduction

For many applications in granular matter research, the system boundaries are given by deformable containers, which may be modeled as elastic membranes. Of particular interest are jamming systems where the granulate changes its mechanical properties drastically when the particle number density in the system is changed [1,2,3], which is frequently achieved by evacuating the air from a deformable container partly filled by granulate. Prominent examples are granular robotic grippers [4], where this mechanism is used to grip and manipulate objects, granular paws [5] and similar [6].

In these cases, the system dynamics is determined by two-way coupling, that is, the deformation of the membrane (e.g., caused by external air pressure) implies forces on the granular particles, and the membrane is deformed under the action of the granular packing.

Such membranes can be modeled within the discrete element method (DEM) as mass-spring systems (MSS), e.g., [7], or with a coupling between the finite element method (FEM) and DEM, e.g., [8]. In an MSS, the membrane is described as a regular or irregular graph whose vertices are particles and whose edges are linear or non-linear elastic springs. The elastic behavior is, thus, described by the springs. FEM directly solves the elasticity problem from the problem’s constituent equations on the material discretized by a mesh. It is, therefore, considered to more accurately predict the membrane’s deformation. However, FEM requires a computationally costly recalculation of the mesh if the mesh has low-quality elements (e.g., obtuse triangles) or topological changes (e.g. tearing or pinching) occur. An MSS does not suffer these costs and has, thus, the advantage of faster computations [9,10,11]. Hence, we rely on MSS for our work.

For an MSS, the contacts between the membrane and the enclosed granular particles are described by the contacts between the membrane’s particles and the particles of the granulate. The choice of the membrane’s structure is critical: If the meshes are too coarse, particles can penetrate the membrane. Therefore, the mesh width has to be chosen according to the smallest particles in the system [7, 12]. This is problematic for several reasons: First, in the course of the simulation, when the membrane and the granulate particles interact, the mesh width may change which is difficult to predict. Second, for the simulation of a highly disperse granulate, the number of membrane particles and springs can be very large, resulting in an inefficient simulation. The problem can be solved by artificially increasing the sizes of the non-interacting membrane particles (overlapping particles) [13] which, however, introduces an undesired thickness of the membrane. All MSS models are problematic for the modeling of tangential (frictional) forces along the membrane since the contacts of the membrane particles and the granular particles depend on the concrete arrangement of the particle positions.

In the current paper, we describe a novel type of MSS which allows for the simulation of impenetrable flexible elastic boundaries requiring a moderate number of membrane particles. This model does not suffer from the drawbacks discussed above. Since, by construction, the membrane is impenetrable, the mesh width can be chosen large which makes our method computationally efficient. The proposed model was used recently to simulate a granular gripper [14] and a bending beam of granular meta-material [15].

2 Model description

2.1 Particle: particle interaction

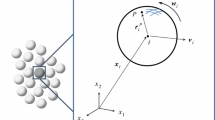
The discrete element method (DEM) solves Newton’s equation for the position $\varvec{r}_i$ and the angular orientation $\varvec{\varphi }_i$ of each particle, i, of mass $m_i$ and tensorial moment of inertia, ${\hat{J}}_i$:

$$\begin{aligned} m_i\frac{\text {d}^2\varvec{r}_i}{\text {d}t^2}&= \varvec{F}_i = \sum \limits _{j\ne i} \varvec{F}_{ij} + \varvec{F}_i^\text {ext}\,, \end{aligned}$$

(1)

$$\begin{aligned} {\hat{J}}_i\frac{\text {d}^2\varvec{\varphi }_i}{\text {d}t^2}&=\varvec{M}_i = \sum \limits _{j\ne i} \varvec{M}_{ij}\,. \end{aligned}$$

(2)

Here, $\varvec{F}_i^\text {ext}$ is an external force, e.g., gravity, and $\varvec{F}_{ij}$ and $\varvec{M}_{ij}$ are the force and torque acting on particle i due to contacts with particles j. There are several models for $\varvec{F}_{ij}$ and $\varvec{M}_{ij}$ as functions of the relative position, orientation, velocity and angular velocity of the involved particles, i and j, for an extended discussion see, e.g., [16,17,18,19,20].

2.2 Membrane: topology

In the current paper, we focus on the description of an ambient membrane and its interaction with the granular particles. In our model, the elastically deformable membrane is modeled by mass-carrying particles that are connected by viscoelastic springs (mass-spring system, MSS). The topology of the membrane is given by a mathematical graph whose vertices and edges are represented by particles and springs, respectively.

The positions of the membrane particles (here called vertex particles), thus, describe the shape of the membrane (Fig. 1). They are subject of Newton’s equations, where the forces acting on the vertex membrane particles originate from four contributions: (a) viscoelastic stretching of the membrane, (b) moments due to bending of the membrane, (c) interaction of granular particles with the membrane, and (d) external forces. We shall discuss these contributions in Sects. 2.3–2.6. The total force acting on the vertex particles is the sum of these four contributions.

Fig. 1

Sketch of the MSS

The particle-based representation of the membrane allows for easy integration within DEM: the treatment of membrane particles and granular particles differs only in the forces acting on them, their dynamics are handled identically.

2.3 Membrane: stretching

Given two adjacent vertex particles i, j at positions $\varvec{\rho }_{i}$, $\varvec{\rho }_{j}$ and velocities $\dot{\varvec{\rho }}_{i}$, $\dot{\varvec{\rho }}_{j}$, we define the relative quantities

$$\begin{aligned} \varvec{\rho }_{ij}&\equiv \varvec{\rho }_{i} - \varvec{\rho }_{j}, \end{aligned}$$

(3)

$$\begin{aligned} \dot{\varvec{\rho }}_{ij}&\equiv \dot{\varvec{\rho }}_{i} - \dot{\varvec{\rho }}_{j} \end{aligned}$$

(4)

and the unit vector

$$\begin{aligned} \hat{\varvec{\rho }}_{ij}&\equiv \frac{\varvec{\rho }_{ij}}{\rho _{ij}}\,. \end{aligned}$$

(5)

The interaction between particles i and j is due to a linear elastic spring. Particle i feels the force

$$\begin{aligned} \varvec{F}_{ij}^{\,\text {spring}} = \hat{\varvec{\rho }}_{ij}\left[ k\left( \rho _{ij} - \rho _{ij}^0\right) - 2\gamma \sqrt{k\,m_{ij}^\text {eff}} \,\hat{\varvec{\rho }}_{ij}\cdot \dot{\varvec{\rho }}_{ij} \right] , \end{aligned}$$

(6)

which is the force of a damped harmonic oscillator, with equilibrium length, $\rho _{ij}^0$, effective mass, $m_{ij}^\text {eff}=m_im_j/(m_i+m_j)$, damping coefficient, $\gamma$, and spring constant, k.

To relate the spring constant, k, to material characteristics, we notice that each realistic membrane has a finite width, d, and the elasticity of the membrane material is characterized by its elastic modulus E. For our idealized two-dimensional membrane of vanishing thickness, one obtains the elastic constant [21, 22]

$$\begin{aligned} k=\frac{\sqrt{3}}{2}E\,d. \end{aligned}$$

(7)

2.4 Membrane: flexibility

To explain the description of membrane flexibility, we consider four adjacent vertex particles at positions $\varvec{\rho }_{1}$, $\varvec{\rho }_{2}$, $\varvec{\rho }_{3}$, $\varvec{\rho }_{4}$ [23], see Fig. 2. The vertex particles span two triangles with normal vectors

$$\begin{aligned} \varvec{n}_1&= (\varvec{\rho }_1 - \varvec{\rho }_3)\times (\varvec{\rho }_1 - \varvec{\rho }_4) \end{aligned}$$

(8)

$$\begin{aligned} \varvec{n}_2&= (\varvec{\rho }_2 - \varvec{\rho }_4)\times (\varvec{\rho }_2 - \varvec{\rho }_3)\,. \end{aligned}$$

(9)

The corresponding angle $\theta _{12}$

$$\begin{aligned} \cos \theta _{12}\equiv \varvec{n}_1 \cdot \varvec{n}_2 \end{aligned}$$

(10)

characterizes the flection of the triangles, with respect to their common edge $\varvec{\rho }_{43} = \varvec{\rho }_4 - \varvec{\rho }_3$. The restoring torque counteracting the flection can be expressed by elastic and dissipative forces, $\varvec{F}_{i}^\text {el}$, acting on the involved vertex particles, $i\in \{1,2,3,4\}$ [23],

$$\begin{aligned} \varvec{F}_{i}^\text {el}&= k^\text {el} \frac{\left| \varvec{\rho }_{43}\right| ^2}{|\varvec{n}_1|+|\varvec{n}_2|} \left( \sin {\frac{\theta _{12}}{2}}-\sin {\frac{\theta _{12}^0}{2}}\right) \varvec{u}_i, \end{aligned}$$

(11)

$$\begin{aligned} \varvec{F}_{i}^\text {diss}&= -k^\text {diss}\,|\varvec{\rho }_{43}|\,{\dot{\theta }}_{12}\varvec{u}_i\,, \end{aligned}$$

(12)

where $k^\text {el}$ and $k^\text {diss}$ are material parameters.

Fig. 2

The deformation of the membrane is described by the angle $\theta _{12}$ between the normal vectors of adjacent triangles $\triangle 134$ and $\triangle 243$. $\theta _{12}$ is extremely exaggerated in this sketch

The directions of the forces are linear combinations of the triangles’ normal vectors given by

$$\begin{aligned} \varvec{u}_1&= |\varvec{\rho }_{43}|\frac{\varvec{n}_1}{|\varvec{n}_1|^2}, \end{aligned}$$

(13)

$$\begin{aligned} \varvec{u}_2&= |\varvec{\rho }_{43}|\frac{\varvec{n}_2}{|\varvec{n}_2|^2},\end{aligned}$$

(14)

$$\begin{aligned} \varvec{u}_3&= \frac{(\varvec{x}_1-\varvec{x}_4)\cdot \varvec{\rho }_{43}}{|\varvec{\rho }_{43}|}\frac{\varvec{n}_1}{|\varvec{n}_1|^2} + \frac{(\varvec{x}_2-\varvec{x}_4)\cdot \varvec{\rho }_{43}}{|\varvec{\rho }_{43}|}\frac{\varvec{n}_2}{|\varvec{n}_2|^2},\end{aligned}$$

(15)

$$\begin{aligned} \varvec{u}_4&= \frac{(\varvec{x}_1-\varvec{x}_3)\cdot \varvec{\rho }_{43}}{|\varvec{\rho }_{43}|}\frac{\varvec{n}_1}{|\varvec{n}_1|^2} + \frac{(\varvec{x}_2-\varvec{x}_3)\cdot \varvec{\rho }_{43}}{|\varvec{\rho }_{43}|}\frac{\varvec{n}_2}{|\varvec{n}_2|^2}\,. \end{aligned}$$

(16)

Each vertex particle is involved in 6 different pairs of triangles, see Fig. 1. The total force acting on a vertex particle is, thus, the sum of the 6 corresponding forces given by Eqs. (11, 12).

2.5 Membrane: granulate-membrane interaction

For the description of the interaction between the membrane and the confined granular particles, we assume triangular patches spanned between the time-dependent momentary positions of adjacent vertex particles, Fig. 3, similar to the approach used in [24]. The interaction of the granular particles with the membrane is then described by contacts between the granular particles and the patches. This assures that the patches are always impenetrable disregarding the sizes of the particles and the deformation of the membrane.

Fig. 3

Sketch of a contact between a granular particle and a triangular patch. The resulting force, $\varvec{F}_c$, is mapped to the involved vertex particles $\varvec{\rho }_{1}$, $\varvec{\rho }_{2}$, $\varvec{\rho }_{3}$, according to the barycentric weights, $a_{1}$, $a_{2}$, $a_{3}$, of the contact point, $\varvec{x}_c$, with respect to the locations of the vertex particles

Contacts between a patch and a granular particle are classified as vertex, edge, or face contact:

$$\begin{aligned} \begin{aligned} \text {vertex contact if ~}&\varvec{x}_c=\varvec{\rho }_i ;~i\in \{1,2,3\}\\ \text {edge contact if~}&\left( \varvec{x}_c-\varvec{\rho }_j\right) \times \left( \varvec{\rho }_i-\varvec{\rho }_j\right) = \varvec{0} ;\\&~i,\,j\in \{1,2,3\} ;~i \ne j \\ \text {face contact~}&\text {else} \end{aligned} \end{aligned}$$

(17)

In case a granular particle contacts multiple neighboring patches, A and B, we chose the adequate contacts according to Table  1 in dependence on whether these contacts are face, edge, or vertex contacts [25]. These selection rules do only apply if the patches A and B have a common vertex. Otherwise, all contacts are handled regularly.

Table 1 Selection of contacts for the case that a granular particle is in contact with two adjacent patches, A and B

In case a granular particle contacts multiple neighboring patches at their common vertex, one of these contacts is selected randomly, and the others are disregarded.

Contacts of the membrane with itself may be calculated from contacts between vertex particles and triangular patches.

Once the contact point is defined, we compute the force according to the specified contact law. The relative velocity of the granular particle and the membrane at the contact point which enters the force is interpolated from the velocities of the vertex particles using barycentric weights, as sketched in Fig. 3. Similarly, the obtained force is distributed to the involved vertex particles with barycentric weights $a_1$, $a_2$, $a_3$. The positions and velocities of the vertex particles and, thus, the dynamics of the membrane are obtained by numerical integration in the same way as the granular particles.

The selection rules above in combination with the barycentric partition of the force lead to smooth and physically plausible forces acting on the vertex particles  [25].

2.6 Membrane: external forces

External forces are directly applied to the vertex particles of the membrane. For an external confining stress $\sigma$, we consider a vertex particle i which is part of the triangular patches j of area $A^w_j$ and normal unit vector $\hat{\varvec{n}}^{\,w}_j$. We calculate the forces

$$\begin{aligned} \varvec{F}^{\,w}_j=A^{\,w}_j\sigma \,\hat{\varvec{n}}^{\,w}_j\, \end{aligned}$$

(18)

acting on the triangular patches, where $\hat{\varvec{n}}^{\,w}_j$ are defined such that forces act from outside the membrane to the granulate located inside. The force acting on vertex particle i is then obtained by summing the individual forces

$$\begin{aligned} \varvec{F}^{\,\text {stress}}_i=\sum _{j}\frac{1}{3}\varvec{F}^{\,w}_j. \end{aligned}$$

(19)

The factor 1/3 is used because a triangular patch is made up of three vertex particles, each bearing its external load equally.

3 Applications

We implemented the described flexible wall into the DEM program MercuryDPM [26]. Here, we present two examples of its application.

3.1 Triaxial test

The triaxial test is commonly used to investigate the mechanical properties of a granular sample. To that aim, the sample is placed between two parallel platens and wrapped by a cylindrical membrane, see Fig. 4. A confining stress $\sigma _{\text {c}}$ in radial direction is applied through the membrane. By controlling the initial distance $h=h_0$ between the platens, an initial stress $\sigma _{\text {p}}=\sigma _{\text {c}}$ is applied in axial direction. Then, the platens are displaced at constant relative velocity $\varvec{v_p}$ to apply a strain $\epsilon =\log (h_0/h)$. We record the corresponding deviatoric stress $\sigma _{\text {d}} = \sigma _{\text {p}}-\sigma _{\text {c}}$.

Fig. 4

A triaxial test cell in its initial and final states

In the simulation, we represent the platens by rigid walls and the membrane by an MSS. We place small particles at random positions inside the membrane such that they do not contact one another. To generate the initial conditions, we apply the Lubachevsky–Stillinger algorithm [27]. We then gradually apply the initial stress, $\sigma _p$, to the platens and the confining stress, $\sigma _{\text {c}}$, to the membrane. After this initialization, we displace the platens at relative velocity $\varvec{v}_{\text {p}}$ and record the deviatoric stress, $\sigma _{\text {d}}$. Figure 4 shows the initial and final states of such a simulation.

To demonstrate the performance of our model, we perform simulations for two different cases:

• 1. We describe the membrane by an MSS where the confining stress of the membrane is provided by contacts between vertex particles and granular particles. This approach was used before, e.g., in [12]. We term this setup $\text {MSS}_{\text {particle}}$.

• 2. We describe the membrane as described in Sect. 2. Here the confining stress of the membrane is provided by contacts between the granular particles and the triangular patches. We term this setup $\text {MSS}_{\text {patch}}$.

For $\text {MSS}_{\text {particle}}$, we place the vertex particles of the membrane spaced by $s=1.33\,\text {mm}$, such that the radius of a vertex particle is about 1/3 the radius of a granular particle. This value is a trade-off between keeping the computational cost low and having a smooth membrane that prevents penetration of granular particles [7, 12]. For $\text {MSS}_{\text {patch}}$, we use $s=4.0\,\text {mm}$ because the membrane has a smooth surface and is impenetrable by design.

We perform the triaxial test at velocity $v_{\text {p}}=0.05\,\text {m}/\text {s}$ and confining pressure $\sigma _{\text {c}}=100\,\text {kPa}$. The material parameters are given in Table 2. Furthermore, we choose the parameters $\gamma \approx 0.15$, $k^\text {el}=10^{-3}\,\text {N/m}$ and $k^\text {diss}=10^{-4}\,\text {Ns/m}$. Using the initial areas of the triangles, we use Eqs. (11–16) to compute the confining forces.

Table 2 Material parameters used in the simulation

We consider two different systems: case 1—a cylinder of initial height $100\,\text {mm}$ and radius $25\,\text {mm}$, and case 2—a cylinder of initial height $140\,\text {mm}$ and radius $35\,\text {mm}$. The numbers of particles used for the membrane and the granulate are given in Table 3.

Table 3 Number of granular and membrane particles in the simulations

Figure 5 shows the deviatoric stress, $\sigma _{\text {d}}$, as a function of the axial strain, $\epsilon$. The different membrane representations, $\text {MSS}_{\text {particle}}$ and $\text {MSS}_{\text {patch}}$, do not lead to significant differences in the stress–strain behavior.

Fig. 5

Deviatoric stress against axial strain for two different geometries

Table 4 compares the computer time used to simulate a real-time of $20\,\text {ms}$. The reduced number of particles in $\text {MSS}_{\text {patch}}$ accelerates the simulations by about the factor 5, compared to simulations using $\text {MSS}_{\text {particle}}$.

Table 4 Computer time used for different membrane representations

3.2 Friction test

A correct representation of frictional forces at contacts with the membrane is important for many applications. For instance, one of the mechanisms allowing a granular gripper to grasp an object relies on frictional forces [4]. By construction, an object gliding on a membrane modeled by particles cannot feel a constant (or, at least, smooth) force.

We demonstrate the smoothness of a membrane modeled by the here described model, and the resulting frictional forces by means of a simple sliding test: In $\text {MSS}_{\text {particle}}$, a membrane is modeled by vertex particles with spacing $1.33\,\text {mm}$ and radius $r=0.67\,\text {mm}$. In $\text {MSS}_{\text {patch}}$, the membrane is modeled by patches of side length $1.33\,\text {mm}$.

For the test, we place a spherical particle of radius $2\,\text {mm}$ on a membrane, the free motion of this particle is restricted to the vertical coordinate, perpendicular to the membrane. Its horizontal motion at constant velocity, $0.05\,\text {m/s}$, is enforced externally. Figure 6 shows the particle’s vertical position and the frictional force in sliding direction.

Fig. 6

The frictional force in horizontal direction felt by a particle when moving on the surface of a membrane (upper image) and corresponding vertical position (lower image) vs the horizontal position for both considered membrane models. Rolling degree of freedom was suppressed

For $\text {MSS}_{\text {particle}}$, we see oscillations in both horizontal force and vertical position. For $\text {MSS}_{\text {patch}}$, we instead observe constant vertical position and constant friction force, as expected when a particle slides on an even plane.

4 Conclusions

Previous work using MSS for representing membranes within DEM simulations describe contacts between the granulate and confining membranes through contacts between the membrane’s particles and the particles of the granulate. In this paper, we introduced a membrane model using surface patches. Contacts between the granulate and the membrane are described by contacts between surface patches constituting the membrane and the particles of the granulate.

The novel model describes a closed surface by design, therefore, the number of particles in the MSS can be reduced drastically. In a sample simulation modeling a triaxial test, we obtained an acceleration of the numerical method by about the factor 5. The comparison of our results with the results using a traditional membrane description did not reveal significant differences in the physical behavior. We further demonstrated the new model’s ability to represent smooth surfaces.