1 Introduction

When the particle number density of a granular system increases, granular packings change their properties drastically. This change is termed the jamming transition [8, 26]. While loose granulate can behave fluid-like or gaseous, under the action of stress in the jammed state, the relative particle positions are essentially persistent, and a granulate is stable against externally applied stress; thus, it behaves solid-like. The granular jammed state and the corresponding jamming transition were intensively studied in the literature, e.g. [10, 19, 30].

Granular jamming can be observed in many systems. Here, we consider a granulate embedded within an elastic membrane. Jamming is achieved by evacuating the air from the system such that the granulate is compressed by the action of the differential pressure between the beam’s interior and the ambient air (termed “confining pressure” in the following). Such systems are also of technical interest as the jamming can be conveniently controlled by the amount of air in the system. By applying a confining pressure, one can, thus, achieve flexible structures that solidify when needed.

Technical applications of granular jamming are ubiquitous and range from endoscopic applications in medical engineering [2, 9, 27, 37] to variable stiffness wings for aerospace applications [5] and many more. In particular, in the context of robotics, these structures find various applications [12], e.g. for granular grippers [7, 14, 23], granular paws [15], or swarm robots [24].

Since jammed granulates behave in many ways similar to solids, they can be considered as meta-materials. The properties of the meta-material are determined by the grain material, the elastic properties of the surrounding membrane, and the applied confining pressure [7, 12, 14, 16, 21]. Structural features as, e.g., fabric reinforcement [16] can also affect the overall mechanical behavior of a given jammed structure.

To analyze the properties of a granular meta-material, in the current paper, we study the response of a beam made from granular meta-material (termed “granular beam” in the following) under the action of load. In general, the response of a granular beam will be viscoelastic or plastic due to the dissipative nature of particle interaction. Here, we restrict ourselves to small and quasistatic deformation; that is, we study the elastic response. Plastic deformations that occur for larger load and viscoelastic effects that occur for larger deformation rates are not considered here.

A granular beam is an ideal paradigm to characterize a material under the influence of compressive, tensile, and also flexural stress. Comparing the experimentally measured or via numerical simulations obtained response of the granular beam with the results for beams of homogeneous materials, e.g. a Timoshenko-beam, we can assign the granular meta-material properties such as an effective Young’s modulus, Poisson’s ratio, and others [1, 22].

So far, most results published in the literature concern experimental investigations of the granular beam under bending load for varying particle material, size, surface properties, and shape [5, 17, 20] as well as varying membrane properties and confining pressures [5, 16, 20]. Granular beams have also been studied numerically using DEM in 2d concerning the elastic modulus of the particle and membrane material [16]. Going beyond the analysis of force-displacement relations, Bridigo et al. analyzed the surface of the beam to study the position of the neutral axis [5] and the change of the beam cross-section due to bending [4]. They extended the Timoshenko beam theory to account for the non-linear force-bending relation at higher load. The force network in such 2d granular beams under stress was also studied [16]. Most numerical studies are performed for 2d systems using regular particle packings.

Common to the mentioned experiments is the challenge of systematically investigating the influence of a single parameter, e.g., particle stiffness, on the beam’s response while keeping the other parameters invariant. Moreover, most experimental techniques are restricted to measuring global quantities, such as force-deformation relations, and observing the response of the packing at the visible surfaces. Here, numerical particle simulations such as DEM can provide insight. Therefore, we apply 3d DEM simulations to investigate the response of a granular beam under load to characterize the elastic properties of the granular meta-material in the viscoelastic regime.

2 System setup

Fig. 1
figure 1

Sketch of the system: A simply supported beam is deformed by a central load, F

Full size image

Our setup is sketched in Fig. 1: We consider a simply supported beam of quadratic cross-section (\(8\,\text {cm}\times 8\,\text {cm}\)) and length 40 cm, subjected to a central load, leading to bending. The granulate is enclosed in a membrane, Fig. 2, modeled by a triangular mesh with a hexagonal unit cell made up of 1792 vertex particles and 3580 faces. The membrane is shaped like a beam with rounded corners. We place small particles inside the membrane at random positions such that they do not contact one another. To generate the initial conditions, we apply the Lubachevsky-Stillinger algorithm [28]. The entire system is contained in a cuboid-shaped solid mold to ensure that the beam keeps its shape and does not increase in size by deforming the elastic membrane. Figure 3 shows the initial setup obtained by this process.

Fig. 2
figure 2

Membrane enclosing the granular beam. Solid and dotted rectangles indicate the region where external forces apply. The dashed rectangle indicates the region of vertex particles used to measure the displacement

Full size image
Fig. 3
figure 3

Initial beam setup (the rectangular solid mold is not shown)

Full size image

We then gradually apply an isotropic confining pressure \(\varDelta p\) to the membrane. To this end, each triangular wall element of area \(A^w_i\) and normal unit vector \(\varvec{e}^{\,w}_i\) is loaded with a force \(\varvec{F}^{\,w}_i=A^{\,w}_i\varDelta p\,\varvec{e}^{\,w}_i\), where \(\varvec{e}^{\,w}_i\) is defined such that force acts from outside the membrane to the granulate located inside. In the process of initial pressure application, the granulate is compressed such that the volume of the granular beam shrinks. To ensure that the shrinking granular beam keeps its cuboid shape, during the gradual increase of the pressure, the planes constituting the solid mold are moved such that the granular beam stays in contact with the mold.

After applying the isotropic confining pressure, we continue the DEM simulation for some time to ensure that a stationary state is reached. The mold is then no longer needed.

The external force, F, (see Fig. 1) and the corresponding counter-forces at the supports apply to the granular beam similar to the confining pressure: We fix the positions of some membrane particles on the bottom close to the beam ends. These fixed particles located in the dotted rectangle in Fig. 2 model the simple supports of the beam. Similarly, we choose membrane particles on the top of the beam to apply the force F. These membrane particles are located in the solid rectangle in Fig. 2. Finally, we use the membrane particles in the dashed rectangle in Fig. 2 at the bottom side of the granular beam to determine the beam’s deflection.

The material properties of the membrane and the granular particles are specified in Table 1. Since we are interested in quasistatic deformations of the granular beam but not in dynamic features (like oscillations), the value of the damping constant, \(\gamma _\text {m}\), of the membrane springs is unimportant. It serves only for numerical stability.

We simulate the granular beam in zero gravity conditions.

Table 1 Material parameters used in the simulation
Full size table

3 Simulation method

3.1 Granular particles

The motion of the granular particles is determined by the external forces, namely, the applied load F, and the confining pressure \(\varDelta p\). For the simulation of the particle dynamics, we use the discrete element (DEM) program MercuryDPM [36]. For the details of DEM, we refer, e.g., to [31, 33]. For the particle-particle interaction force, we assume the Hertz-Mindlin no-slip contact model [11].

DEM solves Newton’s equation for the position \(\varvec{r}_i\) and the angular orientation \(\varvec{\varphi }_i\) of each particle, i, of mass \(m_i\) and tensorial moment of inertia, \(\hat{J}_i\):

$$\begin{aligned} m_i\frac{\text {d}^2\varvec{r}_i}{\text {d}t^2}&= \varvec{F}_i = \sum \limits _{j\ne i} \varvec{F}_{ij} + \varvec{F}_i^\text {ext}\,. \end{aligned}$$
(1)
$$\begin{aligned} \hat{J}_i\frac{\text {d}^2\varvec{\varphi }_i}{\text {d}t^2}&=\varvec{M}_i = \sum \limits _{j\ne i} \varvec{M}_{ij}\,. \end{aligned}$$
(2)

\(\varvec{F}_i^\text {ext}\) is an external force, e.g., gravity, and \(\varvec{F}_{ij}\) and \(\varvec{M}_{ij}\) are the force and torque acting on particle i due to its contact with particle j. We calculate the force \(\varvec{F}_{ij}\) with

$$\begin{aligned} \varvec{F}_{ij} = \varvec{F}_{ij}^\text {n} + \varvec{F}_{ij}^\text {t}, \end{aligned}$$
(3)

consisting of forces along the normal and tangential direction of the contact. For the contact we define the compression \(\xi _{ij}=R_i + R_j - |\varvec{r}_i-\varvec{r}_j|\), the normal unit vector \(\hat{\varvec{r}}_{ij}= (\varvec{r}_i-\varvec{r}_j)/|\varvec{r}_i-\varvec{r}_j|\), and the relative velocity \(\dot{\varvec{r}}_{ij} = \dot{\varvec{r}}_i - \dot{\varvec{r}}_j\). The normal force is [6, 33]

$$\begin{aligned} \varvec{F}_{ij}^\text {n}&= \max \left( 0,\, k_{ij}^\text {n}\xi _{ij}^{\frac{3}{2}} - \frac{3}{2}k_{ij}^\text {n}A_{ij} \sqrt{\xi _{ij}}\dot{r}^\text {n}_{ij}\right) \hat{\varvec{r}}_{ij}, \end{aligned}$$
(4)

with the normal relative velocity \(\dot{r}^\text {n}_{ij} = \hat{\varvec{r}}_{ij}\cdot \dot{\varvec{r}}_{ij}\) and the effective radius \(R_{ij}^\text {eff}=R_iR_j/(R_i+R_j)\). The elastic spring constant \(k_{ij}\) is given by

$$\begin{aligned} k_{ij}^\text {n}&= \frac{4}{3}\left( \frac{1-\nu _i^2}{E_i} + \frac{1-\nu _j^2}{E_j}\right) ^{-1}\sqrt{R_{ij}^\text {eff}}, \end{aligned}$$
(5)

where \(E_i\) and \(\nu _i\) are the elastic modulus and the Poisson’s ratio of the material of particle i. Further, we use the damping constant \(A_{ij}=4.3\cdot 10^{-6}\). This corresponds to a coefficient of restitution of 0.875 for two granular particles with elastic modulus \(E=100\,\text {MPa}\) and radius \(2.7\,\text {mm}\) impacting at a velocity of \(2\,\text {m/s}\) [32].

We model tangential forces arising from friction between two particles. The tangential relative velocity at the point of contact is a function of the relative velocity of the particle centers and the particles’ angular velocity \(\varvec{\omega }_{i}\):

$$\begin{aligned} \dot{\varvec{r}}^\text {t}_{ij}&= (\dot{\varvec{r}}_{i} + \varvec{\omega }_i\times \varvec{b}_{ij}) - (\dot{\varvec{r}}_{j} + \varvec{\omega }_j\times \varvec{b}_{ji}) - \dot{r}_{ij}^\text {n}\hat{\varvec{r}}_{ij}. \end{aligned}$$
(6)

The vector \(\varvec{b}_{ij} = -(R_i-\xi _{ij}/2)\hat{\varvec{r}}_{ij}\) points from the center of particle i towards the contact point. For the contact, we define a vector of tangential compression \(\varvec{\xi }^\text {t}_{ij}\), which is set to zero on contact formation and integrated using \(\dot{\varvec{r}}^\text {t}_{ij}\). Throughout the duration of the contact, we assure that the tangential compression remains normal to \(\hat{\varvec{r}}_{ij}\) by appropriately rotating \(\varvec{\xi }^\text {t}_{ij}\) [29].

The tangential force is [11]

$$\begin{aligned} \varvec{F}_{ij}^\text {t} = -\textrm{min}\left( \frac{2}{3}k_{ij}^\text {t}\xi ^\text {t}_{ij},\,\mu F_n\right) \hat{\varvec{\xi }}^\text {t}_{ij}, \end{aligned}$$
(7)

with \(\xi ^\text {t}_{ij} = |\varvec{\xi }^\text {t}_{ij}|\) and the tangential unit vector \(\hat{\varvec{\xi }}^\text {t}_{ij}=\varvec{\xi }^\text {t}_{ij}/\xi ^\text {t}_{ij}\). If the particles are sliding against each other, i.e. \(|\varvec{F}_{ij}^\text {t}|=\mu |\varvec{F}_{ij}^\text {n}|\), we include sliding dissipation and modify the tangential force:

$$\begin{aligned} \varvec{F}_{ij}^\text {t} = -\mu F_n\hat{\varvec{\xi }}^\text {t}_{ij} - \gamma \sqrt{m_{ij}^\text {eff} k_{ij}^\text {t}} \dot{\varvec{r}}_{ij}^\text {t}. \end{aligned}$$
(8)

The tangential stiffness is given by

$$\begin{aligned} k_{ij}^\text {t}=8 \left( \frac{2-\nu _i}{G_i} + \frac{2-\nu _j}{G_j}\right) ^{-1} \sqrt{R^\text {eff}_{ij}\xi _{ij}}, \end{aligned}$$
(9)

where we used the shear modulus \(G_{i} = \frac{E_{i}}{2(1+\nu _{i})}\), assuming isotropic particles. The quantities \(\mu\), \(\gamma\), and \(m_{ij}^\text {eff}=m_im_j/(m_i+m_j)\) are the friction coefficient, the tangential damping coefficient, and the effective mass, respectively.

The tangential force at the contact point causes a torque

$$\begin{aligned} \varvec{M}_{ij} = - \varvec{b}_{ij} \times \varvec{F}_{ij} \end{aligned}$$
(10)

acting on the particles.

3.2 Membrane

The flexible elastic membrane was modeled as a two-dimensional mass-spring system (MSS) [25]. In the standard implementation, the force exerted by the membrane onto the enclosed granulate results from the interaction between the membrane’s vertex particles and granular particles, similar to contacts among the granular particles. This approach was used to simulate triaxial tests in 3d [3, 34] and 2d [16] (where the membrane is a 1d object). Albeit this method reliably describes flexible membranes, it also entails problems: First, a fine-meshed grid is required to reliably assure that no granular particle can escape the system through the meshes. In particular, for a polydisperse granulate, the mesh size must be chosen to account for the smallest grains, even if their mass fraction is small. This leads to a large amount of computer time spent on the membrane simulation. Since the mesh size changes during the simulation due to the elastic deformations of the membrane, care must be taken throughout the entire simulation to prevent particles from passing through the mesh of the membrane. Second, since granular particles can contact different numbers of membrane vertex particles, isotropy of the confining pressure is difficult to assure.

Therefore, we use an alternative model for the membrane [13], that avoids the mentioned drawbacks: In our model, the membrane’s vertex particles are mathematical points without any extension. These points define the vertices of triangles, and the interaction between the membrane and the granular particles is computed through repulsive forces between these triangles and the granular particles, similar as described in Sect. 2. Contacts between the vertex particles of the membrane and the granular particles are, thus, disregarded. Quantities such as velocities and forces at the contact point are interpolated to and from the vertex particles using barycentric interpolation. This novel concept allows to reduce the number of membrane particles drastically and, moreover, assures an isotropic confining pressure. For a detailed description of the membrane model, we refer to [13].

4 Results

4.1 Timoshenko beam theory

In the following Section, we determine the characteristics of a granular beam by comparison with a homogeneous beam of linear-elastic material. Therefore, in the current Section, we summarize the relevant theory. The Timoshenko beam theory for small deformation describes the bending of a beam as sketched in Fig. 4.

Fig. 4
figure 4

Sketch to introduce the variables describing the bending beam using the Timochenko theory

Full size image

When a beam of length L, constant cross-section A, and area moment of inertia I, is loaded by q(x) along the x-coordinate, its deformation, \(\varDelta z(x)\), obeys

$$\begin{aligned} EI\frac{\text {d}^4\varDelta z(x)}{\text {d}x^4} = q(x)-\frac{EI}{\kappa AG}\frac{\text {d}^2q(x)}{\text {d}x^2}\,, \end{aligned}$$
(11)

with the elastic modulus, E, the shear modulus, G, and the Timoshenko shear coefficient \(\kappa =5/6\) for a rectangular cross-section [18]. With the load function

$$\begin{aligned} q(x) = F\delta (L/2 - x), \end{aligned}$$
(12)

where \(\delta\) is the Dirac \(\delta -\)function, we can integrate Eq. (11) with appropriate boundary conditions [35]. At the position \(x=L/2\), we obtain the displacement

$$\begin{aligned} \varDelta z\left( \frac{L}{2}\right) = \frac{FL^3}{48EI}+\frac{FL}{4\kappa GA}. \end{aligned}$$
(13)

In the following, we use this relation to determine the effective elastic modulus of the simulated granular beam.

4.2 Granular bending beam

Fig. 5
figure 5

Displacement as a funtion of the applied force, \(\varDelta z(F)\), as sketched in Figs. 2, 4 for different elastic modulus of the particle material and confining pressures \(\varDelta p\), and a constant elastic modulus of the membrane, \(E_\text {m}=100\,\text {MPa}\). Dots show the function for increasing load; crosses show the function for decreasing load

Full size image

We simulate a simply supported granular jamming beam under the action of a central load, Fig. 2. In particular, we study the influence of the elastic modulus of the membrane, the elastic modulus of the particle material, and the confining pressure. Figure 5 shows the central displacement as a function of the load, \(\varDelta z(F)\), for an elastic modulus of the membrane \(E_\text {m}=100\,\text {MPa}\) and various values of the elastic modulus of the particle material, \(E_\text {p}\), and confining pressure, \(\varDelta p\). We find the beam becoming stiffer with increasing pressure, as expected. That is, for a given external load, F, the displacement decreases with increasing pressure. Similar for the elastic modulus of the membrane, see Fig. 6: The larger \(E_\text {m}\), the stiffer the granular beam.

Fig. 6
figure 6

Displacement as a function of the applied load, \(\varDelta z(F)\), for \(\varDelta p = 50\,\text {kPa}\) and different elastic modulus of the particle material, \(E_\text {p}\), and different elastic modulus of the membrane, \(E_\text {m}\). Dots show the function for increasing load; crosses show the function for decreasing load

Full size image

We start with the smallest force F, then run the DEM simulation until all fluctuations have faded away. Then we determine the resulting deformation, \(\varDelta z(F)\), and increase F to the next value. Upon reaching the maximal F we repeat the procedure but for a decreasing value of F. Only for a small confining pressure \(\varDelta p\), we notice sizeable hysteresis. Noticeable hysteresis as revealed by the curve for \(\varDelta p=10\,\text {MPa}\) in the upper panel of Fig. 5 indicates that the domain of linear elastic deformation was left, demarcating the limit of validity of our study. For all other combinations of parameters, no hysteresis is noticeable.

The approximately linear dependence \(\varDelta z(F)\) shown in Figs. 5 and 6 allows us to determine an effective elastic modulus of the granular beam material, thus, to consider the jammed granulate as a meta-material. To this end, we fit Eq. (13) describing \(\varDelta z(F)\) obtained from Timoshenko’s theory to the simulation result with \(E=2G(1+\nu )\). From the optimal fit, we obtain the elastic modulus, \(E_\text {gr}\), and the Poisson ratio, \(\nu _\text {gr}\), of the granular beam material. Together these allow us to calculate the beam’s effective elastic modulus

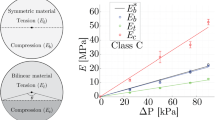
$$\begin{aligned} E_\text {gr}^\text {eff}=\frac{E_\text {gr}}{1-\nu _\text {gr}^2}\,. \end{aligned}$$
(14)

Figure 7 displays the relation between \(E_\text {gr}^\text {eff}\) and the particle’s effective elastic modulus

$$\begin{aligned} E_\text {p}^\text {eff}= \frac{E_\text {p}}{1-\nu _\text {p}^2}\,. \end{aligned}$$
(15)
Fig. 7
figure 7

Effective elastic modulus of the granular beam material as a function of the elastic modulus of the particle material, \(E_\text {gr}=f(E_\text {p})\), for different values of the elastic modulus of the membrane and confining pressure \(\varDelta p\). The lines show power-law fits to the data

Full size image

Note, that we disregard data for \(\varDelta p=10\,\text {kPa}\), as we observed significant hysteresis in this case.

The data shown in Fig. 7 suggests a power law relation between the elastic moduli: Including data for two additional confining pressure values \(\varDelta p=30\,\text {kPa}\) and \(\varDelta p=70\,\text {kPa}\), Figure 8 indeed shows that all data points collapse on a line if we plot the relation

$$\begin{aligned} \frac{E_\text {gr}^\text {eff}}{E_\text {p}^\text {eff}} = \alpha \left( \frac{E_\text {m}^\text {eff}}{E_\text {p}^\text {eff}}\right) ^\beta \left( \frac{\varDelta p}{E_\text {p}^\text {eff}}\right) ^\gamma \end{aligned}$$
(16)

with

$$\begin{aligned} E_\text {m}^\text {eff}\equiv \frac{E_\text {m}}{1-\nu _\text {m}^2}\,, \end{aligned}$$
(17)

and

$$\begin{aligned} \alpha = 0.29;\qquad \beta = 0.41;\qquad \gamma = 0.36. \end{aligned}$$
(18)
Fig. 8
figure 8

The relation of the granular beam’s effective \(E_\text {gr}^\text {eff}\) to the studied parameters as described by Eq. (16)

Full size image

5 Summary

We studied the elastic response of a granular bending beam by means of three-dimensional DEM simulations. We performed bending simulations while varying particle stiffness, membrane stiffness, and differential pressure. Using Timoshenko beam theory we calculated an effective elastic modulus of the beam. We found a power law relating the beam’s effective modulus to the studied parameters.