1 Introduction

A PD device is a particularly convenient way of introducing damping in a system because of its intrinsic robustness, compatibility with high-temperature environments, manufacturability, simplicity, and durability. A significant advantage of this technology is the possibility of retrofitting existing structures, thus limiting problems related to the design and certification because the PD device needs not to deal with operative loads.

PDs are made by an enclosure connected to a vibrating structure and filled with relatively small particles. The particles are not constrained to the case; rather, they can freely move inside it. Collisions arise between particles and the inner walls of the cavity and among particles themselves. Damping is generated by the impacts, due to relative speeds of the parts, and by dissipation due to friction.

Impact and particle dampers are known since the middle of the past century, but in recent years this technology has received renewed attention, as attested by the number of recent papers cited in two recent reviews [1, 2].

Many device configurations were studied analytically and experimentally using particles of different materials, sizes, numbers, and shapes, and enclosures of various geometry, mass ratios, and collocation on the host structures. Despite the variety of investigations and applications, a general-purpose analytical model of the behavior of a PD, suitable to be used in a design phase, is still not available, mainly due to the strong non-linear behavior. Some characteristics, such as the sensitivity to the mass of the particles, the amplitude of the input level, or the size of the enclosure, are nowadays understood, but the non-linear effect of many parameters is still not adequately described by analytical models, especially because of the mutual interaction among the design variables. Therefore, the prediction of the actual performance of a generic installation can be quite difficult.

Recently, however, numerical simulation methodologies such as the Discrete Element Method (DEM) are becoming more and more convenient, as testified in the literature reviews [1, 2]. These numerical simulations allow the analysis of different, complex configurations and to evaluate the effect of the most important parameters driving the design phase.

Unfortunately, even the simulation of basic test cases remains difficult: the need to tune a high number of parameters is challenged by incomplete data sets from the literature and results are often presented indirectly after significant post-processing analysis. Furthermore, the parameters describing the overall damping of the host structure are often presented with little information concerning the motion of the particles enabling it, thus preventing any possibility of a more extensive correlation; the cases typically studied in literature cover only a few possible installation configurations, and the tests do not account for the strongly non-linear behavior of such systems.

The authors performed a new analysis of the papers referred to in two recent review papers and of more recent published works; the described experimental setups have been classified according to different parameters; the analysis showed that the available literature does not adequately cover the whole design domain of such devices, thus tuning the simulation tools can be difficult because of the lack of some relevant effect.

For all these reasons the authors decided to perform a set of experiments exploring a wider design space for PDs with spherical particles and to make available not only the post-processed overall damping parameters but also all the raw measurements. All the experimental data are made available on Zenodo [3].

The tests are focused on two aspects that are not widely examined in literature: the effects of the mutual orientations between the gravity acceleration, the imposed motion, and the PD axis, as well as the effects of different kinds of forcing terms time histories.

A cylindrical enclosure has been adopted to emphasize the effect of the case geometry and of its orientation with respect to both the gravity and the motion directions on the motion regime of particles. A slender metallic beam was equipped with the PD and used in two setups. Three installation angles were used for the PD (0°, 45°, and 90°) to activate all the mechanisms involved in damping generation.

The system was tested in two configurations (motion parallel and normal to gravity) to analyze the effect of gravity on the particles’ motion. For all the configurations, the system was excited with two different kinds of inputs: controlled amplitude stepped sines and band-limited random excitations. The sensitivity to the input level was also studied.

2 Analysis of the current experimental domain

This section shows the results of the analysis of papers referred to in the two cited recent review papers [1, 2] and of more recent published works. Among the considered papers, the described experimental setups have been classified according to different parameters, such as shape and orientation of the cavity, the direction of gravity, direction of motion, and kind of input.

The papers included in such classification are focused on the experimental analysis of the dynamics of particle dampers; therefore, the papers related to specific applications have been discarded for the lack of information and some very specific parameters, e.g., the actual geometry of cavities. Many papers concerning the application of PD for seismic purposes were discarded as well, as they all belong to the case with motion normal to gravity, do often make use of a reduced number of particles, consider a limited frequency range and employ devices that can be classified as non-packed particle dampers [4].

The literature shows that many configuration parameters play a significant role in the design of an effective device; for instance, the mass ratio, that is the ratio between the mass of particles and the effective mass of the host structure, is widely recognized as a relevant design parameter.

Since the motion of the particles is significantly affected by gravity, a first classification is presented according to the relative direction of motion with reference to the gravity: motion parallel to the gravity (58 papers), motion perpendicular to it (34 papers), different constant or relative angle (3 papers). The different performance and the different motion of particles within the case caused by this operative condition are discussed in a few papers [5,6,7,8]. Depending on the mutual interactions of the orientation of the case geometry, the direction of imposed motion, and the direction of the gravity acceleration, see Fig. 1, the motion of the particles can change dramatically, e.g. from the bouncing of the grouped particle bed to a fluid-like sloshing. These effects can be expected to have a reduced influence at higher frequencies, but not to vanish.

Fig. 1
figure 1

Possible trajectories of particles (low frequency)

Full size image

The experimental works were further classified according to the shape of the PD’s enclosure; most of the papers deal either with a box-shaped or a cylindrical enclosure. The studies concerning box-shaped PD’s enclosures are equally divided into experiments with motion parallel to gravity and with motion normal to it (19 each); while, in the case of a cylindrical enclosure, most of the papers (37) exploit a motion parallel to gravity, with only 15 papers referring to motion perpendicular to the gravity.

The attitude of the PD is irrelevant in the case of a box-shaped cavity, provided that one of the axes of the enclosure is parallel to motion. In the case of a cylindrical enclosure, instead, the direction of the axis plays a significant role, modifying the motion of the particle bed inside the PD; considering this aspect, in the case of motion parallel to gravity, the PD axis lies in the same direction in 36 setups, and only in one it is orthogonal. Among 15 setups exploiting motion normal to the gravity, 5 have the axis aligned with the gravity (normal to the motion), 10 with the axis aligned with motion (normal to the gravity); no one normal to both.

A deformable structure is often exploited to drive the PD; this is because the host structure amplifies, when close to resonance, the motion applied to the PD and also because the performance of the PD can be measured in terms of structural damping, that is the desired effect on the host structure. Mostly two kinds of hosting structures are used: a simply cantilever beam and a leaf spring structure. The difference between them is basically related to the lack of rotation of the free end in the second case; usually, the first mode of the host structure is used to assess the performances of the PD.

The papers were also classified according to the input used to activate the particles’ dynamics and the method adopted to measure the effectiveness of the damper. Among 119 experimental setups, 71 exploited sinusoidal inputs (most of them a narrow sweep, 9 a stepped sine, and only 2 a controlled input), 25 various initial conditions (mostly displacement, some others impact), and 17 random input signals.

An aspect not addressed in the literature is the effect of a superposition of different kinds of motions due to either complex or broadband input disturbances. This is related to the dynamics of the hosting structure, which can lead to operative conditions that can be significantly different from those that can be achieved with the single-tone sinusoidal input often considered in the literature.

The classification shows that mainly two aspects were not sufficiently examined in the literature: the effects of the mutual orientations between the gravity acceleration, the imposed motion, and the PD axis, particularly when those orientations are oblique, and the effects of different kinds of forcing terms time histories.

3 Test description and setup

The testing activities were carried out on a slender beam with a thin rectangular cross-section, clamped at one end. As already mentioned in the introduction, two configurations are considered: one with the out-of-plane bending direction aligned with gravity and the other with the out-of-plane bending direction normal to gravity, see Fig. 2.

Fig. 2
figure 2

Installation of the hosting structure. Motion oriented as gravity acceleration vector (up); motion oriented orthogonal al the gravity acceleration vector (down)

Full size image

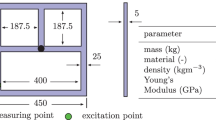
The beam is made of aluminium alloy; the relevant data are listed in Table 1.

Table 1 Geometrical and material data of the host structure
Full size table

A cylindrical geometry was adopted so that a preferential working direction is obtained, along the axial direction; the curved lateral surface significantly influences the motion of particles when the case is not mounted parallel to the gravity. The PD lateral wall is made of PMMA, to observe the particles’ motion, while the top and bottom walls are made of aluminum alloy. The installation of the cylinder enclosure on the beam was implemented in 3 different ways: one with the cylindrical enclosure’s axis aligned with the transversal motion of the beam, the other two with the cylindrical axis rotated with respect to the transversal motion of the beam, to couple the dynamics of particles with the shape of the cavity; the axis is rotated (45° and 90°) toward the beam axis to preserve the symmetry of the system.

To install the PD with these angles, a 20 mm sided 45–45–90 triangular base steel prism, with a mass of 31 g, has been used. The center of the external base of the cylindrical enclosure in the aforementioned configurations is located at distances of 10 mm, 10 mm, and 0 mm, respectively, from the free end of the beam (Fig. 3). The dynamic properties of the system are slightly changed by the installation of a small additional mass and by the change in the position of the center of gravity of the particle damper; therefore the experimental results, and the particle damper performance, cannot be compared directly for different configurations. Nevertheless, these small discrepancies are considered acceptable, since the goal of the activities is to outline the differences in the global behavior of the system.

Fig. 3
figure 3

Installation of the particle damper in the configuration orthogonal to the gravity. 0° (left). 45° (middle). 90° (right)

Full size image

Particle damper’s dimensions and mass are listed in Table 2; the overall experimental setup is sketched in Fig. 4.

Table 2 Geometrical and material data of the particle damper case
Full size table
Fig. 4
figure 4

Particle damper experimental setup

Full size image

The cavity was filled with 120 steel spheres, with a nominal diameter of 3 mm and a mass of 0.110 g each.

An electromechanical shaker (Bruel & Kjaer Type 4809) was used to dynamically load the structure, maintaining complete control of the excitation. This allows for the investigation of the effect of different kinds of input signals, sweep, random and stepped-sine, in an open-loop or with a closed control loop. Load is transferred from the shaker to the beam by a very flexible nylon stinger that permits the transmission of only an axial force. The force transmitted from the shaker to the beam is measured by a load cell (PCB 208C01) connected by a screw to the hosting structure. Four piezoelectric accelerometers (PCB 333B32) are installed too along the beam. A SIEMENS-LMS SCADAS 316 frontend, with built-in amplifiers and anti-aliasing filters, and driven by the SIEMENS-LMS Testlab software, was used for data acquisition and signal post-processing, including the estimation of the system damping properties.

Information concerning sensors’ positions and masses, accounting also for the effective masses of cables, are reported in Table 3 for correlation purposes. The experiments with controlled amplitude and motion parallel to gravity were performed on a slightly different sensor setup, reported in Table 4, and a slightly lower cantilever length equal to 538 mm.

An high speed camera was used to record the particles movement for a selected set of configurations. Unfortunately the hardware at hand does not allow to synchronize the camera frames with the time history data sampled by the SCADAS system.

Table 3 Geometrical and mass data of the sensors
Full size table
Table 4 Geometrical and mass data of the sensors, for the experiments with controlled amplitude and motion parallel to gravity
Full size table

3.1 Hosting structure characterization

The dynamical behavior of the reference structure was investigated by considering the hosting beam with installed sensors and the empty case of the particle damper. The latter was glued to the structure near the free end, with the cylinder axis parallel to the transversal displacement and at a distance of 10 mm from the free end section.

A single dummy mass of 13.2 g, approximatively equivalent to the overall mass of the particles, was fixed to the beam at the same position of the axis of the cylinder in order to account for the inertia of the particles. The structure was loaded with a random signal in the band 0–256 Hz. The signal was acquired for 10 s, leading to a frequency resolution of \(\Delta f=\mathrm {0.1}\) Hz. The acquisition was then repeated in the band 2–10 Hz centered around the first mode, using a stepped sine and a frequency resolution equal to \(\Delta f=\mathrm {0.02}\) Hz, to better estimate the damping. Modal frequencies and damping, calculated starting from the Frequency Response Functions (FRFs) by resorting to the Polymax algorithm [9], are reported in Table 5.

Table 5 Experimental modes of reference configuration
Full size table

A finite element model of the beam has been realized using three-node beam elements within the open-source multibody software MBDyn [10], and accounting for the sensors and PD as lumped masses.

Matching the model’s natural frequencies alone is not sufficient for a significant correlation; since the PD’s behavior is very sensitive to the amplitude of the motion, it is of paramount importance to match the magnitude of the response of the underlying structure at every frequency. Therefore, a correct tuning of the mass distribution, stiffness, and structural damping was required.

Figure 5 depicts the correspondence between the experimental and numerical FRFs around the first mode for the accelerometer near the free end, after the correlation of the finite element model on the experimental result. Following this procedure, the finite element model may be coupled to a specialized discrete element code and used for the simulation of the experiments with the particles as shown in [11].

Fig. 5
figure 5

Comparison of experimental and numerical FRFs around the first mode. Accelerometer 4

Full size image

3.2 Types of input signals employed

The test setup was subjected to two kinds of inputs, which are described and motivated in this section:

  1. 1.

    Controlled amplitude stepped sine excitation

  2. 2.

    Band-limited random excitation

The damping sensitivity to the input level is also investigated, and attention is given to the particles’ motion inside the box.

3.2.1 Controlled amplitude stepped sine excitation

In the stepped sine technique, the FRFs are built line by line, by using a pure sine to excite the structure. Only the spectral line at the excitation frequency is considered in the response, thus ignoring the non-linear contribution of the other harmonics. This means that their energy contribution is lost; nevertheless, their amplitude is small compared to that of the main tone and decreases as the frequency increases [7, 12]. The testing controller adjusts the forcing term magnitude in order to achieve, for each spectral line, the same acceleration measure from the sensor positioned near the free end of the beam. This is necessary since the shaker is driven by a sinusoidal voltage generator; thus, by keeping a constant voltage for different forcing frequencies, the force exciting the hosting structure, and consequently the accelerations, would be dependent on the structural impedance and would vary with the frequency.

The motion of the particles is also highly sensitive to the acceleration of the particle damper’s enclosure; therefore, a controlled amplitude stepped sine excitation method was chosen to partially circumvent the problem.

This activity is focused on the first bending mode of the beam: this allows to reduce the influence of the installation point rotation on the motion imposed at the enclosure.

The structure was excited in the frequency range around the first mode (4–9 Hz), with a 0.02 Hz resolution. Different controlled acceleration ranges were used depending on the direction of motion relative to gravity to better analyze how the controlled acceleration drives the behavior of the particles for different directions of motion; a range between 0.5 g and 5.0 g was selected for the configurations where the motion is aligned with gravity and a range from 0.25 g and 2.5 g for the configurations were the motion is normal to gravity.

3.2.2 Band-limited random excitation

A pure harmonic input usually leads to a clearly identifiable motion of particles. Multi-tonal input and band-limited random input, instead, do not lead to clearly identifiable particles’ periodic motions. The effects of a complex and more realistic excitation on the motion of the particles and, consequently, on the PD damping capacity are thus investigated. Damping must be defined in an averaged sense and its measure can be very different from the previously identified ones since the particle bed inside the enclosure experience different motion regimes. The input levels during these tests are not directly comparable with the values of the previous experiments with purely harmonic inputs. In unsteady signals, the root mean square (RMS) value is generally employed to normalize the FRFs, but in the case of strong non-linearity, such as the one studied here, it can hide important information.

The use of unsteady inputs offers the possibility to employ very different kinds of excitation signals encompassing both multi-tonal inputs, with various relative phases, and white or pink random signals, possibly limited in bandwidth. The authors decided to investigate the effect of band-limited excitation since this is deemed as the most different from a harmonic input. Also for these tests, the beam was installed in two configurations: beam bending displacement parallel to the gravity acceleration and normal to it. In both configurations, the particle damper axis was mounted normal to the beam motion direction.

The damping sensitivity to the input level is investigated for two different white noise inputs: the first was a narrow band random noise centered around the first mode of the host structure (3–20 Hz); the second one was a wider band noise (3–256 Hz), able to excite the resonance of higher flexural structural modes. In the latter case, the response is characterized by contributions from many modes contributing not only to the displacement of the free end of the beam but also to a significant rotation of the free end. Also, the motion of the particles inside the case is studied for the different tests.

3.3 Digital signal processing (DSP) post-processing

One of the main difficulties in the study of the effects of a PD is related to its strong non-linear behavior. At higher input levels, the collisions of the particles, both among them and with the box, generate acceleration patterns that are superimposed over the basic signal. The system is non-linear, and standard digital signal processing techniques, like FRFs, are unable to analyze all the aspects of the system at hand. For instance, Fig. 6 shows the acceleration time history and its related spectrum, obtained by exciting the host structure with a PD by a single tone and with an input force of magnitude sufficient to produce collisions with the case. The sine is at 6.25 Hz and the dynamic response is acquired with a 10240 Hz sampling rate and with a 0.3125 Hz frequency resolution to limit leakage effects on the FRF shapes. The effects of the impacts, evident from the time history, can be seen in the Fourier’s transform as a series of peaks that are equally spaced by the frequency of the input harmonic. Therefore, the relation between a sinusoidal input and the output at the same frequency is no longer linear and the interpretation of the results in the frequency domain is biased.

Fig. 6
figure 6

Time history (up) and magnitude of the spectrum (down) of a structure with particle damper excited with a single sine

Full size image

The motion of the particles is also highly sensitive to the acceleration of the particle damper’s enclosure: this can be problematic in the interpretation of the experimental results obtained with non-periodic inputs. Non-periodic inputs can cause responses entailing different kinds of motion of particles and damping mechanisms, thus generating damping estimations that are not linked to a specific operating mode of the damper; this could be the case with an impulsive response, or a random excitation.

In case of an impulsive response, damping can be computed either by employing the half-power bandwidth method (or similar methods) on the acceleration/force FRFs, or by using a logarithmic decrement in the time domain. During the observation period of the response, different motion regimes of the particles can be found, and consequently different damping mechanisms: for instance, the particles could undergo energetic impacts immediately after the impulse, and come to rest with respect to the PD enclosure toward the end of the transient, thus reducing their dissipative capacity. Extracting data from this time history brings to merge in a single parameter all such different behaviors and to obtain a not clearly ascribable number. Some more insight could perhaps be gained by analyzing the trajectories of each particle through a suitable post-processing of high speed films, taken from different point of views; however, the short duration of the particle dynamics, coupled with the significant non-linearity of the particle behavior with respect to the acceleration level and the excitation frequency, strongly limits, in the authors’ opinion, the effectiveness of impulsive response analysis for PDs. The post-processing of high-speed films remains a valid avenue that warrants to be explored for periodic and random sustained excitation.

This non-linear behavior cannot be fully characterized using unsteady excitations; a better method to study the damping performance of these devices would be to use periodic inputs at different frequencies and levels. Nevertheless, unsteady excitations can be more realistic.

4 Test campaign results

In this section, some results of the test campaign are shown for illustration and validation purposes; the analysis reported in this section is also focused on aspects not widely examined in the literature: the effects of the mutual orientations between gravity, imposed motion, and PD’s axis, as well as the effects of different kinds of forcing terms time histories.

As anticipated in the introduction, the full results and acquisitions of the performed tests are made available on Zenodo [3].

4.1 Stepped sine controlled experimental results: sensitivity to geometrical orientation

The case with gravity, the motion of the first mode, and PD axis orientation aligned was thoroughly investigated in different literature papers and is useful to better understand the basic mechanisms generating damping.

Fig. 7
figure 7

Tip accelerometer FRFs trend at different acceleration levels for different orientations, vertical motion

Full size image

For that setup, the comparison of the obtained FRFs of the accelerometer near the free end is depicted in Fig. 7a. The first mode natural frequency and damping variation trends are reported in Fig. 8a and b respectively.

Fig. 8
figure 8

Comparison of the trends of first mode frequencies and damping versus tip acceleration and relative directions, vertical motion

Full size image
Fig. 9
figure 9

Video sequence of the motion of the spheres inside the enclosure. All directions aligned. Tip acceleration of 1.9 g, 6.4 Hz

Full size image

The sequence of pictures in Fig. 9 shows the motion of the particles inside the enclosure. Figure 10 shows time histories acquired at various levels of acceleration; they refer to three periods of the accelerometer near the beam’s free end and have been sampled at a high rate (40960 Hz) in order not to filter the effects of the impacts. Here, and in the following experiments, the impact events are loosely identified by vertical colored lines, and linked to the corresponding different video frames; the correspondence is merely qualitative because it was not possible to synchronize the camera with the data acquisition system.

Fig. 10
figure 10

Time histories of the acceleration at the tip. Gravity and structure motion aligned, PD aligned. Dashed red vertical line: impact on the lower cap, frame 4 of Fig. 9; green vertical line: impact on the upper cap, frame 3 of Fig. 9 (color figure online)

Full size image

By analyzing videos and time histories, the different motions of the particles were correlated with the damping. When gravity is aligned with the beam tip displacement and the PD axis, the main phenomenon is the impact of particles with the floor and the ceiling of the case, while a negligible interaction occurs with the lateral surface of the cavity. Observing the damping trend of Fig. 8b three different working conditions can be identified:

  1. 1.

    The acceleration imposed on the enclosure is smaller than 1 g. The spheres remain on the floor for the whole period; there is no relative motion, and no extra damping is generated.

  2. 2.

    The spheres detach from the case floor as a single body and impact the case only once for each period. The damping ratio, the distance from the floor reached by the spheres, and the energy exchanged at each collision increase with the input acceleration level.

  3. 3.

    As shown in Fig. 9, particles hit both the case floor and the ceiling as a single body, once per period. However, the damping ratio, and the amount of net energy extracted from the system, diminishes with increasing acceleration levels. The phase between the impacts of the particles on the floor and with the ceiling, and the relative velocity between the particles and the enclosure, play an important role in the drop of the damping ratio.

The three conditions above also explain why the system’s first natural frequency changes for different values of the input. The results do agree with the theoretical model of Friend and Kinra [13].

Changing the alignment of the particle damper with respect to the motion entails different dynamics of the particles within the case and leads to a significant reduction of the damping efficiency, as is clear by comparing the 0°, 45°, and 90° curves of Fig. 8b. The damping trends are similar, with the 45° one being smoother near its maximum. A deeper investigation of the data shows different typologies of motion for the spheres.

In the 90° configuration, the motion is qualitatively equal to that of the 0° configuration; the smaller damping is both because of the smaller distance between the free surface of the particles and the facing side of the enclosure and the fact that the distance between the upper layer of spheres and the curved ceiling surface is not constant. The particles keep moving like a single mass, just like an impact damper, but the variable width introduces some radial motion in the particle bed. The rising part of the damping curve after 1 g level has the same slope obtained at 0°, confirming the analytical results of [13].

When the PD is oriented at 45° the damping curve of Fig. 8b doesn’t show an increment with respect to the 90° case, even if the free space in the direction of motion lasts longer. The effect of the interaction with the enclosure can be evaluated by analyzing the videos, see Fig. 11, and the time histories, Fig. 12.

Fig. 11
figure 11

Video sequence of the motion of the spheres inside the enclosure. Gravity and structure motion aligned, PD 45°. Tip acceleration of 1.7 g, 6 Hz

Full size image
Fig. 12
figure 12

Time histories of the acceleration at the tip. Gravity and structure motion aligned, PD 45°. Dashed red vertical line: impact on the lower left cap, frame 4 of Fig. 11; green vertical line: impact on the upper cap, frame 2 of Fig. 11 (color figure online)

Full size image

In this situation, the spheres don’t move in the same way and along a straight path. Once the input level is above 1 g, impacts happen in a distributed manner with the bottom of the enclosure and the side surface. Collisions are not synchronized and occur during the whole descendent motion half period. Starting from 1.5 g at 6 Hz, also impacts with the upper inner surfaces were observed. Since the particles’ motion is not bounded by a flat surface but by the ceiling and the curved upper part of the side each particle has a different free space and exchanges a different amount of energy with the system. Further increasing the acceleration, the whole behavior tends to resemble the one already seen for the 0° and 90° cases: two impacts for every period, separated by half a cycle. Even in this situation, however, the collision strength appears to be smaller than those of the 0° and 90° cases. Clearly, a given PD enclosure can lead to significantly different results depending of the relative orientation between the acceleration and the enclosure spatial orientation, since this changes the overall shape as seen by the particles throughout their motion.

The effects of the mutual orientations between gravity, structural motion, and particle damper’s axis were further investigated by rotating the hosting structure as shown in Fig. 2b, so that the imposed motion is normal to the direction of gravity. The FRFs of the accelerometer near the PD, obtained at different orientations, are visible in Fig. 13, while a video sequence and the time histories relative to motion perpendicular to gravity and aligned to the PD’s axis are shown in Figs. 15 and 16 respectively.

After the damping peak, the damping curves relative to the orthogonal or parallel to gravity experiments follow a similar dropping trend, as shown in Fig. 14; the motions of the particles inside the enclosure become similar between the two configurations for increasing imposed acceleration and a steady condition is established for which two hits for period occur. However, the experiments with motion orthogonal to gravity show that when the particle bed moves from one side to the other of the PD enclosure, it does not behave as a solid body: gravity, which is perpendicular to the motion, induces a wave-like movement, where some balls climb onto the others (Figs. 15, 16).

Fig. 13
figure 13

Tip accelerometer FRFs trend at different acceleration levels for different orientations, horizontal motion

Full size image
Fig. 14
figure 14

Comparison of the trends of first mode frequencies and damping versus tip acceleration and relative directions, horizontal motion

Full size image
Fig. 15
figure 15

Video sequence of the motion of the spheres inside the enclosure. Gravity and structure motion orthogonal, PD 0\(^\circ\) wrt motion. Tip acceleration of 1.25 g, 6.3 Hz

Full size image
Fig. 16
figure 16

Time histories of the acceleration at the tip. Motion and PD axis aligned, perpendicular to gravity. Dashed red vertical line: impact on the right cap, frame 1 of Fig. 15; green vertical line: impact on the upper cap, frame 4 of Fig. 15 (color figure online)

Full size image

At low excitation levels the particles keep laying on the case floor, the bouncing mode is not active and only the particles in the upper layers can move and dissipate energy. The particles are forced into a sloshing mode that generates considerable damping even before the 1.0 g threshold found in the experiments with the motion parallel to gravity. For relatively small accelerations, e.g. 0.5 g, some spheres of the upper layer move around damping the system. Increasing the acceleration level, the number of moving spheres increases, and, at 1.0 g, all of them take a synchronous motion superimposed with some random movement of the upper particles. Such random displacement becomes less and less significant, for increasing inputs, compared to the sloshing. A simple analytical model capable of modeling these different motion regimes and the ensuing damping is unknown; a numerical simulation is likely the unique possibility to have useful predictions on the efficiency of PD.

The results and the videos of the experiments with the enclosure rotated by 45° and 90° with respect to the direction of motion showed that the particles experienced similar dissipative mechanisms. However, since the enclosure’s size along the motion direction was reduced, the particles had less free space to move, thus causing less damping due to impacts with a less optimal phase. This situation applied both for partial fluidization of the upper layers at low accelerations and for global fluidization at high accelerations; hence, both the initial damping’s sensitivity to acceleration and the maximum damping have been affected negatively by the reduction of the enclosure’s size along the motion in these cases. It has to be remarked that the maximum in the damping curve of Fig. 14b, when the PD is oriented at 45°, is not greater than that of the 90° case, despite the free space in the direction of motion lasting longer; this result once again demonstrates the importance of considering the actual PD motion and shape in order to obtain a correct estimation of its damping capability.

As most of the literature results do not consider the mentioned different motion conditions and enclosure orientations, the authors believe that the results of the experiments hereby reported can be representative of phenomena that a numerical simulation needs to be able to reproduce.

4.2 Random signal experimental results: effects of a different excitation input signal

The random signal experiments are carried out with the PD enclosure axis aligned with the motion direction. Figure 17 shows the damping ratio of the first mode found with different levels of excitation using a random signal in a limited frequency band (3–20 Hz). The RMS reference acceleration level is calculated in the loaded band from the full history response, and it is influenced by the interaction with the beam. Since the system was loaded with an open-loop strategy, the input force content is not constant with frequency, but it is affected by the dynamics of the hosting structure; in particular, a drop at the resonance frequency is evident.

Since the input bandwidth is limited around the first resonance, phenomena that are very similar to those already seen for the stepped sine excitation tests are triggered. In the parallel-to-the-gravity scenario, the particles stay on the bottom of the enclosure as the input level is usually not sufficient to win the gravity and to generate relative motion. Nevertheless, given the randomness of the forcing signal, some spheres occasionally detach from the base, even for low levels of input. Increasing the load, the number and the strength of the collisions increases as witnessed by the 5 s time histories of Fig. 18. In the evaluated range of RMS acceleration, the damping curve doesn’t show the same decreasing trend of the stepped sine controlled experiments after reaching its maximum; a maximum can be assumed to exist at higher RMS accelerations.

When the beam’s motion is orthogonal to gravity, the particles’ motion resembles what is already seen with stepped sine excitation: for very low input levels only the balls on the free surface move, while increasing the input level a progressively more significant sloshing motion was noted. This dissipation mechanism is more efficient than the parallel-to-gravity scenario, as energy was subtracted from the system also for low inputs. The maximum value of damping is lower than that of the stepped sine experiments since the input signal was unsteady and the impacts with the enclosure don’t happen always with the same phase. Figure 19 shows 5 s time histories of the acceleration at the free end when the motion is perpendicular to gravity.

Fig. 17
figure 17

Comparison of the trends of first mode dampings versus tip acceleration and relative directions. Random signal in the 3–20 Hz band

Full size image
Fig. 18
figure 18

Time histories of the acceleration at the tip. All directions aligned. Random input 3–20 Hz

Full size image
Fig. 19
figure 19

Time histories of the acceleration at the tip. Motion and particle enclosure aligned, perpendicular to gravity. Random input 3–20 Hz

Full size image

A wider excitation band was employed to measure the effect of the PD on the damping of the higher bending modes (Fig. 20). The damping trend with respect to the acceleration level is similar to that previously observed for the first mode: after an initial high slope ramp, the damping curve reaches a maximum and decays, with asymptotic residual damping that is higher than the initial one.

Time histories acquired with the wide-band excitation appear random, as steady or repetitive patterns could not be recognized; the particles did not impact the enclosure’s walls agglomerated as a single body, but they had a chaotic and independent motion. This situation was noted both for the parallel and the perpendicular cases. The images sequence of Fig. 21, extracted from the video of the 9.222 g RMS experiment with motion parallel to gravity, shows the spheres scattered inside the enclosure and hitting each other and the sides of the box in an unpredictable manner.

Fig. 20
figure 20

Comparison of the trends of dampings of different modes versus tip acceleration and relative directions. Random signal in 3–256 Hz band

Full size image
Fig. 21
figure 21

Video sequence of the motion of spheres inside the enclosure. Motion and enclosure’s axis aligned to gravity. Random signal in 3–256 Hz band

Full size image

5 Concluding remarks

The results of the experimental campaign highlight the strong influence of the investigated parameters on the overall behavior of a particle damper. Leaving apart already studied factors, such as mass and dimensions, the authors have shown that the mutual orientations between the PD, the imposed motion, and gravity have an important impact on the motion of the particles inside the enclosure and the resulting damping. The strong non-linearity of the system has been explored with respect to both the sensitivity to the imposed acceleration level and the loss of the classical relationship between input and output. The experimental strategy based on controlled stepped sine excitation has been identified as the best candidate to limit bias and to make the acquired information usable for different setups and repeatable for correlation purposes. Tests with limited or broadband white noise random signals have confirmed the strong link between the PD damping efficiency and its orientation. Furthermore, they have shown that a dispersion of the forcing term in a larger band alters dramatically the movements of the spheres inside the enclosures and their capability to generate damping.