Approximate coefficient of restitution for nonlinear viscoelastic contact with external load

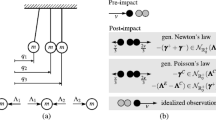
Abstract

We derive an approximate coefficient of restitution (CoR) for a single bead impacting the ground when a constant external load acts upon the colliding body. Some of the main applications concern classical nonlinear viscoelastic models such as the Kuwabara-Kono model, Simon-Hunt-Crossley model, and Hertzian stiffness with linear damping, however the proposed approach applies to a wide class of nonlinear viscoelastic contact models. It is shown that suitable expansions allow to derive a computable expression of the CoR which provides accurate predictions for a valuable range of external loads, viscosity coefficients and impact velocities.

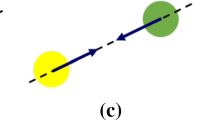
Graphical abstract

Appendices

Appendix A${\mathcal {O}}(\gamma )$ expansion of the squared CoR and large $\tilde{g}$ limit

In this appendix we examine the ${\mathcal {O}}(\gamma )$ expansion (10) of the squared CoR obtained for $\gamma \ll 1$ :

$$\begin{aligned} e^2 = 1 - 2 \gamma \beta \mathcal {I}_0(\tilde{g}) + \mathrm{H.O.T.}, \end{aligned}$$

(A1)

where

$$\begin{aligned} \mathcal {I}_0(\tilde{g}) = \int _0^{T_0} {\left( \frac{du_0}{d \tau } \right) }^2 u_0^{\beta - 1} d \tau \end{aligned}$$

(A2)

and $T_0 >0$ corresponds to the end of impact in the absence of dissipation ($u_0(T_0)=0$, $\frac{du_0}{d \tau }(T_0)=-1$). We shall simplify the integral coefficient (A2) for arbitrary $\tilde{g}$ and investigate the large $\tilde{g}$ limit.

Due to the symmetry $u_0 \left( \frac{T_0}{2} + \tau \right) = u_0 \left( \frac{T_0}{2} - \tau \right)$ about the maximal compression in the nondissipative case, we can rewrite the integral in (A2) as

$$\begin{aligned} \mathcal {I}_0(\tilde{g}) = 2 \int _0^{\frac{T_0}{2}} {\left( \frac{du_0}{d \tau } \right) }^2 u_0^{\beta - 1} d \tau . \end{aligned}$$

(A3)

Multiplying (9) by $\frac{du_0}{d \tau }$ and integrating from $\tau = 0$ yields the energy conservation equation

$$\begin{aligned} \frac{1}{2} \left[ {\left( \frac{du_0}{d \tau } \right) }^2 - 1 \right] + \frac{{u_0}^{\alpha + 1}}{\alpha +1 } = \tilde{g} u_0 , \end{aligned}$$

which can be used to solve for $\frac{d u_0}{d \tau }$ in the compression phase,

$$\begin{aligned} \frac{du_0}{d \tau } = {\left[ 1 + 2 \left( \tilde{g} u_0 - \frac{{u_0}^{\alpha +1}}{\alpha + 1} \right) \right] }^{\frac{1}{2}}. \end{aligned}$$

(A4)

At the maximum compression one has $\frac{du_0}{d \tau }(T_0/2) = 0$, therefore the maximal deformation $u_M=u_0(T_0/2)$ satisfies

$$\begin{aligned} \frac{1}{\alpha + 1} {u_M}^{\alpha + 1} = \tilde{g} u_M + \frac{1}{2}. \end{aligned}$$

(A5)

Considering the integral in (A3) and changing integration variable ($\tau \rightarrow u_0$), we get using (A4)

$$\begin{aligned} \mathcal {I}_0(\tilde{g}) = 2\int _0^{u_M} {\left[ 1 + 2 \left( \tilde{g} u_0 - \frac{{u_0}^{\alpha +1}}{\alpha + 1} \right) \right] }^{\frac{1}{2}} u_0^{\beta - 1} d u_0 . \end{aligned}$$

(A6)

Let us now investigate the large $\tilde{g}$ limit. Equation (A5) yields

$$\begin{aligned} \frac{1}{\alpha + 1} {u_M}^{\alpha + 1} \approx \tilde{g} u_M \end{aligned}$$

which suggests to introduce the new unknown y defined by

$$\begin{aligned} u_M = \tilde{g}^{\frac{1}{\alpha }} y . \end{aligned}$$

(A7)

Substituting $u_M$ from (A7) back into (A5), we obtain

$$\begin{aligned} \frac{1}{\alpha + 1} y^{\alpha + 1} - y = \frac{\epsilon }{2}, \end{aligned}$$

(A8)

where $\epsilon = \frac{1}{{\tilde{g}}^{1 + \frac{1}{\alpha }}}$ is a small parameter when $\tilde{g}\gg 1$. This yields

$$\begin{aligned} y= & {} {(1 + \alpha )}^{\frac{1}{\alpha }} + {\mathcal {O}}(\epsilon ), \\ u_M= & {} {\left[ \tilde{g} (1+\alpha ) \right] }^{\frac{1}{\alpha }} + {\mathcal {O}}\left( \frac{1}{\tilde{g}}\right) . \end{aligned}$$

In order to study the behavior of integral (A6) for $\tilde{g}\gg 1$, we perform the change of variable $u_0 = {\tilde{g}}^{\frac{1}{\alpha }} y_0$, which leads to

$$\begin{aligned} \begin{array}{ccl} \mathcal {I}_0(\tilde{g}) &{} = &{} \displaystyle 2 {\tilde{g}}^{\frac{\beta }{\alpha } + \frac{1}{2 \alpha } + \frac{1}{2}} \\[12pt] &{} &{} \displaystyle \times \int _0^y {\left[ \epsilon + 2 \left( y_0 - \frac{y_0^{\alpha + 1}}{\alpha + 1} \right) \right] }^{\frac{1}{2}} {y_0}^{\beta - 1} d y_0 . \end{array} \end{aligned}$$

(A9)

When $\epsilon \approx 0$, the integral (A9) can be approximated as

$$\begin{aligned} \begin{array}{ccl} \mathcal {I}_0(\tilde{g}) &{} = &{} \displaystyle 2\sqrt{2} {\tilde{g}}^{\frac{\beta }{\alpha } + \frac{1}{2 \alpha } + \frac{1}{2}} \\[12pt] &{} &{} \displaystyle \times \int _0^{{\left( 1 + \alpha \right) }^{\frac{1}{\alpha }}} \left( 1 - \frac{y_0^{\alpha }}{\alpha + 1} \right) ^{\frac{1}{2}} {y_0}^{\beta - \frac{1}{2}} d y_0 \\ &{} &{} + \mathrm{H.O.T.} \end{array} \end{aligned}$$

(A10)

Now we can consider another change of variable $t=\frac{{y_0}^{\alpha }}{ \alpha + 1 }$, which yields using (19)

$$\begin{aligned} \mathcal {I}_0(\tilde{g}) = \frac{2\sqrt{2}}{\alpha } {(\alpha + 1)}^{\frac{\beta + 1/2}{\alpha }} {\tilde{g}}^{\frac{2 \beta + \alpha + 1}{2 \alpha }} \, \mathrm{B}\;\, \left( \frac{\beta + \frac{1}{2}}{\alpha }, \frac{3}{2} \right) . \end{aligned}$$

(A11)

Thus, substituting (A11) into (A1) yields the large $\tilde{g}$ limit of the CoR expansion

$$\begin{aligned} e^2 \approx 1 - 2 \gamma C \tilde{g}^{\left( \frac{\beta }{\alpha } + \frac{1}{2 \alpha } + \frac{1}{2} \right) }, \end{aligned}$$

(A12)

where

$$\begin{aligned} C = 2\sqrt{2} \frac{\beta }{\alpha } {\left( \alpha + 1 \right) }^{\left( \frac{\beta }{\alpha } + \frac{1}{2 \alpha } \right) } \mathrm{B}\; \left( \frac{\beta + \frac{1}{2}}{\alpha }, \frac{3}{2} \right) . \end{aligned}$$

Appendix B Proof of Proposition 1

In this appendix we establish the ${\mathcal {O}}(\gamma ^2)$ approximation of the CoR e stated in Proposition 1.

We start from the expansion (35) of $e^2$, where the integral $\frac{\partial \mathcal {I}}{\partial \gamma } (\gamma ,\tilde{g})$ given in (34) needs to be computed at $\gamma =0$. This step quite technical, therefore we shall summarize the main steps of the computation and refer to the technical report [41] for details.

Let us denote by $u_0$ the solution of (30)-(31) in the non-dissipative case $\gamma = 0$ and consider the corresponding impact duration $T_0$. In (35), we need to evaluate $\frac{\partial \mathcal {I}}{\partial \gamma }$ for $\gamma =0$, so using (34) we can write

$$\begin{aligned} \begin{array}{ccl} \displaystyle \frac{\partial \mathcal {I}}{\partial \gamma }(0,\tilde{g}) &{} = &{} \displaystyle \frac{1}{\beta } \int _0^{T_0} u^0_{\gamma } \left[ (\beta + \alpha ) u_0^{\beta + \alpha -1} \right. \\[12pt] &{} &{} \displaystyle \left. - \tilde{g} \beta u_0^{\beta - 1} \right] d \tau , \end{array} \end{aligned}$$

(B13)

where we note $u^0_{\gamma }(\tau ) = \frac{\partial u}{\partial \gamma }(0,\tau )$. We need to compute $u^0_{\gamma }$ to further evaluate (B13). Differentiating (30)-(31) with respect to $\gamma$ at $\gamma =0$, we obtain the linear non-homogeneous problem

$$\begin{aligned} \begin{array}{c} \displaystyle \frac{d^2 u^0_{\gamma }}{d \tau ^2} + \alpha u_0^{\alpha - 1} u^0_{\gamma } + \frac{d}{d \tau } (u_0^{\beta }) = 0, \end{array} \end{aligned}$$

(B14)

with

$$\begin{aligned} \begin{array}{ccc} \displaystyle u^0_{\gamma } (0) = 0& \mathrm{and}& \displaystyle \frac{d u^0_{\gamma }}{d \tau } (0) = 0 . \end{array} \end{aligned}$$

This problem can be solved using the variation of constants formula. One obtains after lengthy but straightforward computations (see the technical report [41]):

$$\begin{aligned} u^0_{\gamma } = - u_{0}^{\prime } \int _0^{\tau } \frac{d }{d s}(u_0^{\beta }) u_1 ds + u_1 \int _0^{\tau } \frac{d }{d s}(u_0^{\beta }) u_{0}^{\prime } ds , \end{aligned}$$

(B15)

where $u_{0}^{\prime }=\frac{d u_0}{d \tau }$, $u_1$ is the solution to

$$\begin{aligned}&\frac{d^2 u_1}{d \tau ^2} + \alpha u_0^{\alpha -1} u_1 = 0, \end{aligned}$$

(B16)

$$\begin{aligned}&u_1 (T_0 /2) = (\tilde{g} - u_M^{\alpha })^{-1}, \quad \frac{d u_1}{d \tau } (T_0 /2) = 0, \end{aligned}$$

(B17)

and $u_M = u_0 (\frac{T_0}{2})$ satisfies (13) (hence $\tilde{g} - u_M^{\alpha }<0$ in (B17)). Note that $u_{0}^{\prime }$ and $u_1$ are independent solutions to the homogeneous problem (B16).

Substitution of (B15) in (B13) yields after lengthy algebraic manipulations (see [41])

$$\begin{aligned} \frac{\partial \mathcal {I}}{\partial \gamma }(0,\tilde{g}) = - \beta \, \mathcal {I}_0 \, \mathcal {Q}_0 , \end{aligned}$$

(B18)

where $\mathcal {I}_0$ is given by (A3) and

$$\begin{aligned} \mathcal {Q}_0= & {} -\beta ^{-1} \int _0^{T_0/2}{ u_1 u_0^{\beta -1} [ (\beta + \alpha ) u_0^{\alpha } - \tilde{g} \beta ] d\tau } \\= & {} \beta ^{-1}\int _0^{T_0/2}{ \frac{u_1}{u_0^\prime }\, \frac{d}{d\tau } ( u_0^\beta u_0^{\prime \prime } ) \, d\tau } \end{aligned}$$

(the second identity follows from (9)). This integral can be further simplified using the fact that

$$\begin{aligned} \frac{d }{d \tau }\left( \frac{u_1}{ u_0^\prime } \right) = -\frac{1}{ { \left( u_0^\prime \right) }^2 } \end{aligned}$$

(B19)

and integrating twice by parts (see [41]), which yields finally

$$\begin{aligned} \mathcal {Q}_0 = \int _0^{T_0/2}{u_0^{\beta -1} d\tau } . \end{aligned}$$

(B20)

This integral can be rewritten in the form (40) by changing the integration variable ($\tau \rightarrow u_0$) and using (A4).

Now that $\frac{\partial \mathcal {I}}{\partial \gamma }(0,\tilde{g})$ has been computed with (B18)-(B20), substitution into (35) yields the squared restitution coefficient

$$\begin{aligned} e^2 = 1 - 2\beta \mathcal {I}_0 \gamma + 2 \beta ^2 \mathcal {I}_0 \mathcal {Q}_0 \gamma ^2 + o(\gamma ^2), \end{aligned}$$

(B21)

where $\mathcal {I}_0, \mathcal {Q}_0 >0$ are given in (A3), (B20). Dropping the $o(\gamma ^2)$ remainder in (B21) and taking the square root, one obtains the following approximation of the CoR

$$\begin{aligned} e \approx \left( 1 - 2\beta \mathcal {I}_0 \gamma + 2 \beta ^2 \mathcal {I}_0 \mathcal {Q}_0 \gamma ^2 \right) ^{1/2} . \end{aligned}$$

(B22)

For this approximation to be meaningful, it is necessary to have $1--2\beta \mathcal {I}_0 \gamma + 2 \beta ^2 \mathcal {I}_0 \mathcal {Q}_0 \gamma ^2 \ge 0$, and we shall set $e=0$ if this condition is not satisfied. This leads us to an approximation $e\approx e_+$ valid for $\gamma \approx 0$, where

$$\begin{aligned} e_+ = \max { \left( 1 - 2\beta \mathcal {I}_0 \gamma + 2 \beta ^2 \mathcal {I}_0 \mathcal {Q}_0 \gamma ^2,0 \right) }^{1/2} . \end{aligned}$$

(B23)

Moreover, expanding the right side of (B22) at order 2 in $\gamma$ yields the simplified approximation

$$\begin{aligned} e \approx 1 - \beta \mathcal {I}_0 \gamma + \beta ^2 \mathcal {I}_0 ( \mathcal {Q}_0 - \frac{1}{2}\mathcal {I}_0 ) \gamma ^2 \end{aligned}$$

(B24)

for $\gamma \approx 0$. We thus have another approximation $e\approx e_s$ at hand, given by

$$\begin{aligned} e_s = \max {\left( 1 - \beta \mathcal {I}_0 \gamma + \beta ^2 \mathcal {I}_0 ( \mathcal {Q}_0 - \frac{1}{2}\mathcal {I}_0 ) \gamma ^2 ,0 \right) } . \end{aligned}$$

(B25)

In numerical computations we observe that approximations (B22) and (B24) tend to overestimate the CoR, hence it is interesting to choose the smallest approximation. This leads us to consider

$$\begin{aligned} e \approx \min {(e_+,e_s)}. \end{aligned}$$

(B26)

In particular, if $1--2\beta \mathcal {I}_0 \gamma + 2 \beta ^2 \mathcal {I}_0 \mathcal {Q}_0 \gamma ^2 \ge 0$ and (B24) is positive, (B26) corresponds to $e \approx e_s$ if

$$\begin{aligned} \big ( \mathcal {Q}_0 - \frac{\mathcal {I}_0}{2} \big ) \, \left( \, \beta {\big ( \mathcal {Q}_0 - \frac{\mathcal {I}_0}{2} \big )} \gamma - 2 \, \right) \le 0 \end{aligned}$$

and $e \approx e_+$ otherwise.