1 Introduction

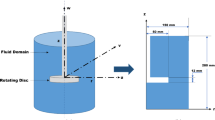
Pelletizing is a process, in which fine disperse granular materials, e.g. iron ore concentrates or fly ash, are agglomerated to form larger particles during the continuous circulation of the bed of material mixed with the particular binder [1,2,3]. It is carried out with pelletizing discs, see the schematic drawing on Fig. 1, or pelletizing drums where the material performs a rolling motion. Pelletizing is used particularly for the processing of mineral raw materials through the rolling of fine dispersed material. Typically, final pellets leave the process space by falling over the board of the disc once they reach desired size with a narrow, close to monodisperse grain size distribution.

Pelletizing is required in many industries to generate certain materials of coarser particle sizes for generating a certain permeability or increase flowability of a bulk material, reduce dust emissions on transfer points or storage heaps etc.

Fig. 1
figure 1

Basic features of a pelletizing disc: a cylindrical vessel rotates around its inclined axis, small pellets grow to large ones during the rolling motion (\(\beta\) - inclination angle. \(\mathbf {g}\) - gravity vector)

Full size image

New applications of pelletizing processes (e.g. in the fertilizer industry, production of aggregates from demolition waste for the construction industry etc.) require a better understanding of the whole process and its complexity. It will help to achieve an integration of a smart process control to increase throughput and pellet quality; reduce binder, power and water consumption [3].

2 Disc pelletezing process

The pelletizing process implies the agglomeration of very fine (sometimes just several microns) particles to pellets of some millimeters in diameter in a humid particle bed. The acting binding mechanisms are desribed among others in [1, 2]. The basic geometrical construction of a pelletizing disc is a cylindrical vessel. The cylinder is inclined to the horizontal plane with the angle \(\beta\) typically in the range of \(\beta =35\ldots 55^\circ\) [1].

While the process itself has been used for a long time, the details of different influences such as feed particle size distribution, binder type and a quality, amount of the liquid added at a certain position, pelletizing disc speed and inclination angle, scraper position etc., in particular the various combinations thereof, are still not completely understood. Moreover, pelletizing is a dynamic process and understanding of the internal states of pellets (velocities, forces, number of contacts in different regimes etc), is needed to tune the pelletizing disc operation and improve the automatization efforts.

The large number of parameters influencing the complex process would make systematic experimental investigations for modelling the whole process very challenging and expensive. For this reason, there is a high interest to use numerical simulations for the analysis of pelletizing processes. Simulations may help to develop models and to determine an optimum combination of the various parameters for each specific application.

Optimization of pelletizing process is aimed at reducing the energy consumption, increasing the quality of the obtained product and limiting the time, needed to produce pellets with the required parameters. Automatization of pelletizing discs is an ongoing challenge, which can help to improve the process. Nowadays, machine settings are continuously adjusted on the base of digital data from cameras and sensors. Nevertheless, a modell is required to use these data for online process control.

Particle motion and resulting contact forces play in combination with other parameters an important role for porocity, initial sterength and sphericity of the particles. Therefore, the paper presents the discrete element model (DEM) for the partile motion and contact forces on the disc as a first step towards more complex models.

The discrete element method (DEM) is a particle based simulation technique, which can be applied for the numerical simulation of the agglomeration process. In the last decade, several investigations of similar processing machines, where particles are moving inside a rotating drum, have been done. Such machines can be divided into two groups:

  1. 1.

    machines, where the rotation axis of the vessel is orthogonal to the direction of gravity vector. Most of them are so-called “ball mills” and are used for the raw material processing [4,5,6,7,8,9].

  2. 2.

    machines, where the rotation axis of the vessel is parallel to the direction of gravity vector. An example of such machine are spheronizers, which are used in pharmaceutical industry [10, 11].

Numerical simulations of the particle behavior inside these machines can help to enlighten the internal processes and to optimize existing machines. In order to do so, DEM simulation of the complete process must capture not only the dynamics of the multi-disperse particle assembly, but also agglomeration and attrition of the pellets. Particle dynamics and the knowledge of resulting forces acting on the particles are the basics and substantially influence agglomeration and attrition processes. Therefore, particle dynamics are in the focus of this paper and agglomeration and attrition are disregarded in both, experiments and numerical simulations presented.

The outline of the paper is as follows. Section 2 introduces in brief the pelletizing process. Section 3 gives a short description of some reference experiments, which have been done on a laboratory-scale pelletizing disc in order to validate the results from corresponding numerical simulations. Section 4 introduces the DEM model of the pelletizing disc. Section 5 gives a qualitative comparison of experimental and numerical results. Based on the numerical simulations, some quantitative measures are introduced, which characterize the dynamic state of the bed of materials on the investigated pelletizing disc. Finally, the findings of the present study are summarized in Section 6.

3 Experiments

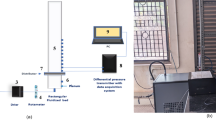
Some benchmark experiments are done to understand the behavior of pellets inside the pelletizing disc. Dry spherical glass particles are used as model pellets on a pelletizing disc with a diameter D=400mm (see an example on Fig. 2). It rotates with various rotational speeds n and at various inclination angles \(\beta\). Rotational speeds and inclination angles are controlled by electronics. An additional supporting construction for a camera is mounted on top in order to record images and video sequences of the rolling pellet motion. The distance between disc and camera is about 600mm, a plexiglas cover above the disc prevents the loss of material and protects the camera.

Fig. 2
figure 2

Pelletizing disc from company “HAVER”

Full size image

The used spherical glass particles are nearly monodisperse, particle diameters vary from 4mm to 5mm with a mean size \(\bar{d_{p}} = {4.54}\,{\text{mm}}\) (see particle size distribution on Fig. 3). The bulk mass of particles in each test is about \(m\approx {0.8}\,{\text{kg}}\), the particle material density is \(\rho \approx {2500}{\hbox {kg m}}^{-3}\) and the particle number is \(N_{p}\approx {6700}\,{\text{pcs}}\).

Spherical glass particles “Diamond pearls” (Company Mühlmeier GmbH & Co. KG) are chosen since size, density, sphericity, friction coefficint young modulus etc. vary only within a small range, thus reliably facilitating the comparison between experiment and model.

Fig. 3
figure 3

Particle size distribution of the monodisperse packing of spherical glass particles

Full size image

Near-monodisperse particle size distribution (prior to polydisperse one) was chosen to keep an experimental setup as simple as possible. Also it allows to prevent the influence of particle segregation on obtained results in these initial experiments.

From literature [1], the critical rotational speed \(n_{crit}\), at which the particles are expected to centrifugate on the disc, can be found with the help of an empirical equation as:

$$\begin{aligned} n_{crit} \approx \frac{42.3}{\sqrt{D}}\sqrt{\sin {\beta }} \end{aligned}$$
(1)

with D in [m] and \(n_{crit}\) in [rpm]. Equation (1) does not consider specific characteristics and shear properties of the bulk solid material or individual pellets.

For industrial applications it is recommended to use rotational speeds n of the pelletizing disc with so called “operating speed factor” (OSF, \(\psi\)). This factor is used usually in the range \(\psi =0.6\ldots 0.75\) and applies to the critical rotational speed \(n_{crit}\):

$$\begin{aligned} n = \psi \cdot n_{crit} \end{aligned}$$
(2)

In our experiments, the following values of \(\psi ^{exp}\) are employed: [0.5, 0.6, 0.7 and 1.0], i.e. experiments are carried out with varying rotational speeds n from 26.8 rpm to 62.2 rpm.

The main objective of the experiments is to get snapshots which capture the behavior of rotating material. After an initial startup period, it is assumed that the material is in a quasi-steady state, i.e. the kinetic energy of the whole system is approximately constant. More detailed quantitative evaluation of obtained results is not planned with the actual setup of the experiment.

4 DEM model

DEM simulations can help to understand details of material bed behavior, i.e. particle movement on pelletizing disc and to investigate e.g. different rotational regimes of the bulk solid. The obtained numerical data is analyzed to discover dependencies between particle dynamics and machine parameters. These correlations are difficult to get from experiments (i.e. number of contacts, pellet’s velocities inside the bulk etc).

The DEM model is based on the equations of motion of an individual rigid ball-shaped agglomerate P:

$$\begin{aligned} m_{P}\dfrac{d^{2}\mathbf {x}}{dt^{2}}&=\sum _{c}\mathbf {f}_{c}+m_{P}\mathbf {g} \end{aligned}$$
(3)
$$\begin{aligned} I_{P}\dfrac{d\mathbf {\omega }}{dt}&=\sum _{c}\mathbf {t}_{c} \end{aligned}$$
(4)

here \(m_{P}\) and \(I_{P}\) are the mass and moment of inertia of pellet P; \(\mathbf {x}\) and \(\mathbf {\omega }\) describe its location and angular velocity, \(\mathbf {f}_{c}\) and \(\mathbf {t}_{c}\) are the force and torque transferred in each contact c of P with one of its neighbors and \(\mathbf {g}\) is the gravity vector. The torque \(\mathbf {t}_{c}=\mathbf {l}_{c}\times \mathbf {f}_{c}\) can be calculated from the branch vector \(\mathbf {l}_{c}\), i.e. the distance vector from the pellet center to the contact point c, and \(\mathbf {f}_{c}\), see e.g. [12] for details.

In the simulations, the contact force between two model pellets made of glass is given by the linear viscoelastic contact model:

$$\begin{aligned} \mathbf {f}_{c}&=f_{n}{\hat{n}}+f_{t}{\hat{t}} \end{aligned}$$
(5)
$$\begin{aligned} f_{n}&=-k_{n}\delta _{n}-c_{n}\frac{d\delta _{n}}{dt} \end{aligned}$$
(6)
$$\begin{aligned} f_{t}&=\text{ min }\left[ -k_{t}\delta _{t}-c_{t}\frac{d\delta _{t}}{dt},\,\mu f_{n}\right] \end{aligned}$$
(7)

which divides the contact force in a normal \(f_{n}\) and tangential \(f_{t}\) components with respect to the normal unit vector \({\hat{n}}\) from the center of pellet P to the center of the contacting pellet. Here, \(f_{t}\) is limited to Coulomb friction, which is given by the friction coefficient \(\mu\). The model parameters, i.e. the spring stiffness \(k_{n}\) and \(k_{t}\) and the viscous damping \(c_{n}\) and \(c_{t}\), have been deduced according to Pournin [13]Footnote 1 from the restitutional coefficients \(e_{n}\), \(e_{t}\) and the contact time \(t_{c}\) of the pellet.

$$\begin{aligned} k_{n}&= \frac{m}{{t_{c}}^{2}}\left( \pi ^{2}+\ln ({e_{n}})^{2}\right) , \end{aligned}$$
(8)
$$\begin{aligned} c_{n}&= -\frac{2m}{t_{c}}\ln ({e_{n}}), \end{aligned}$$
(9)
$$\begin{aligned} k_{t}&= \frac{2m}{7{t_{c}}^{2}}\left( \pi ^{2}+\ln ({e_{t}})^{2}\right) , \end{aligned}$$
(10)
$$\begin{aligned} c_{t}&= -\frac{4m}{7{t_{c}}}\ln ({e_{t}}) \end{aligned}$$
(11)

This scheme worked well in DEM simulations under similar conditions [12, 15,16,17]. The normal \(\delta _{n}\) and tangential \(\delta _{t}\) overlaps of two pellets in contact and the corresponding time derivatives are evaluated from the DEM results, see e.g. [12] for details.

The model equations (5) to (11) are implemented in the DEM software YADE [18]. The mesh of the pelletizing disc is generated by the open-source finite element generator Gmsh [19]. All important model parameters are summarized in Table 1. Please note, that the stiffness of the model pellets has been reduced in order to increase the time step width \(\Delta t\) of the DEM simulations. The stiffness reduction is a known technique which allows to speed-up the simulations without a significant influence on the dynamic behavior of a dense granular material [20]. Restitution and friction coefficients of different materials is a topic of many researches. Values used for this work reflect the results of recent studies for a similar simulation condition [21,22,23]. Chosen parameters do not fully reflect the real physical properties of the simulated material, but still provide realistic numerical data within an appropriate range of time.

Table 1 Parameters and their values in simulations
Full size table

The procedure for each parameter set of numerical simulations is as follows. At the beginning of the simulation the pelletizing disc is being filled by particles according to the PSD presented in Fig. 3. The kinetic energy of all elements in the simulation is monitored. After it has reached the steady state, positions, velocities and contact characteristics of model pellets (stresses, directions etc.) are captured for the further analysis. An exemplary snapshot of the pelletizing disc simulation is presented in Fig. 4.

Fig. 4
figure 4

Pelletizing disc, snapshot from simulation. Color shows velocity values of particles

Full size image

The simulation data is analyzed in a similar manner as described in [12, 17]. DEM data is averaged and a micro-macro transition is performed. For that purpose, the whole simulation region is divided along r (50 zones), z (20 zones) and \(\phi\) (50zones). All rotating particles are grouped into zones depended on their instantaneuos positions.

5 Rotational regimes of granular material on the pelletizing disc

Fig. 5
figure 5

Qualitative comparison of experimental data (top row) and simulation results (bottom row) with the inclination angle of the pelletizing disc \(\beta = {40}^{\circ }\) and \(\psi =\) 0.5,0.7 and 1.0 (from left to right column). The color scale is used the same as for Fig. 4. An angle between red lines on all images is \({60}^{\circ }\) and serves for better visual comparison

Full size image

A qualitative comparison of experimental (photo images) and simulation data (snapshots) for inclination angle \(\beta = {40}^{\circ }\) and \(\psi =\) 0.5, 0.7 and 1.0 is presented in Fig. 5. For a better visual comparison of the experimental and simulation data, two additional red lines with an angle of \({60}^{\circ }\) in between are added to all images. The form of the rotating bed of material appears to be similar in both: experiments and simulations. For low rotational speed (\(\psi =0.5\)), the characteristic kidney-shaped form of the bed of material can be clearly identified. When the rotational speed is increased (\(\psi =0.7\)), some particles are detaching from the dense bed at the upper part of the bulk. Near the critical value \(n_{crit}\) at \(\psi =1.0\), much more particles are out of the bed of material, but many of them are still dense packed.

Particles in the upper part of a pelletizing disc are packed more loosely as in the bottom part. At higher rotational speeds this effect is more visible and for industrial applications it is in most of cases an undesirable behavior.

Fig. 6
figure 6

Length \(\phi\) of rotational body in degrees along the disc edge as a function of operating speed factor \(\psi\) for different inclination angles \(\beta\). Arrow shows increasing \(\beta\) values

Full size image

Figure 6 gives the opening angle \(\phi\) of the bed of material. This angle characterizes the length of the rolling body along the disc edge expressed in degrees and, respectively, the motional regime of the particle on the disc. It is obtained through the analysis of particle informations from DEM simulations.

The two legs of \(\phi\) embrace only the part of the bed of material with a particle volume fraction above 0.3. The zones with more loosely particle packings are not considered. In Fig. 6, the relationship \(\phi \left( \psi \right)\) is shown for different values of \(\beta\). A clear jump from \(\phi \simeq {130}^{\circ }\) to \(\phi \simeq {360}^{\circ }\) is found for each configuration with \(\beta \le {40}^{\circ }\). In these configurations, the \(\phi\)-jump increases with higher \(\beta\). Here, \(\phi \simeq {130}^{\circ }\) is characteristic for a kidney-shaped bed of materials like in the inlay of Fig. 6, whereas \(\phi \simeq {360}^{\circ }\) indicates a ring-shaped one. Therefore the switch from \(\phi \simeq {130}^{\circ }\) to \(\phi \simeq {360}^{\circ }\) correlates with the actual critical OSF \(\psi _{crit}\) (critical rotational speed) of the pelletizing disc.

Interestingly, with the pre-calculated critical speed (\(\psi =1.0\)) particles do not reach the centrifugation neither in simulations nor in experiments. Thus they do not reach the pre-calculated critical speed. It can be explained by the ideal spherical form of the bodies and their permanent rotation, which is not considered in the equation (1).

Fig. 7
figure 7

Length \(\phi\) of rotational body in degrees along the disc edge as a function of operating speed factor \(\psi\) for inclination angles \(\beta = {40}^{\circ }\) and different contact times \(t_c\)

Full size image

As noted above the stiffness of simulated material was reduced to enlarge the time step and increase the calculation speed. Though this technique is known and provides in most of cases reliable results, verification simulations were performed with smaller contact times (\(t_c = {10^{-4}}\,{s}\) and \(t_c = {10^{-5}}\,{s}\)) and correspondingly higher stiffnesses. The simulation with inclination angle \(\beta = {40}^{\circ }\) and different rotational speeds were done. Simulation step \(\Delta t\) was reduced to ensure the system stability. The macro-parameter of the system, length of the rotational body \(\phi\) was monitored and results are presented in Fig. 7. It can be seen that there are only minimal visible differences between the simulations with varied contact times. So the overall system behavior is not changing with the higher stiffnesses.

Fig. 8
figure 8

Probability distribution of contact duration \(t_{d}\) for different operating speed factors \(\psi\). The inlet zooms the area from 0 to 0.002s for better visibility. The data is obtained from simulations with \(\beta = {40}^{\circ }\)

Full size image

In Figs. 8 and  9, the contact duration time \(t_{d}\) between individual pellets and the coordination number \(N_{c}\), i. e. the instant number of contacts for each pellet, are examined in order to characterize the state of the bed of materials more quantitatively.

This information demostrates, how long particles are being in contact and it helps to characterize the bulk solid behavior. Fig. 8 shows the probability distribution of contact durations \(P\left( t_d\right)\) for \(\beta = {40}^{\circ }\) and different values of \(\psi\). This information was analyzed for the last 2 seconds of each simulation setup. It is found that the most of contacts in the bulk are very short-time ones with the duration \(t_d \le {0.001}{\text{s}}\) in a normal operation mode (\(\psi\) with \(\psi <\psi _{crit}\)). This time matches exactly contact time \(t_{c}\), which was used as a material parameter (see the Table 1). It verifies the correctness of the model and its implementation in simulation software.

On the contrary, the number of long-lasting contacts increases slightly while the number of short-time contacts decreases for over-critical rotational speeds (\(\psi >\psi _{crit}\), see the dashed line in the Fig. 8).

Figure 9 presents the probability distribution of instant contact numbers per particle (coordination number) \(P(N_{c})\) for different operating speed factors \(\psi\). Here, only the contacts between spherical elements are considered. Contacts between disc and particles are ignored for this analysis to escape the influence of border effects.

Fig. 9
figure 9

Probability distribution of contact numbers per particle \(N_{c}\) for different operating speed factors \(\psi\). The data is obtained from simulations with \(\beta = {40}^{\circ }\). Inlets a–g are showing snapshots of simulations in different regimes. Black arrows show the direction of increasing \(\psi\) values

Full size image

It is found that pellets in the bulk have predominantly few contacts (\(N_{c}\le 2\)) for sub-critical speeds (\(\psi <\psi _{crit}\)) and most pellets have no contacts to other pellets at all. It can also be seen, that the number of particles with two contacts and more (\(N_{c}>=2\)) decreases with increasing rotational speeds \(\psi\) in the range \(0.5\dots 1.15\) (see the direction of black arrow). The situation changes fundamentally for \(\psi >1.20\), where the disc exceeds the critical speed and particle start to centrifugate. Here, the number of pellets with \(N_{c}>=2\) rose visibly (see the curve with \(\psi = 1.25\)).

The curve \(\psi = 1.25\) shows the probability distribution of contact numbers per particle for overcritical speed. It is clearly seen that this distribution is different in compare to states with lower rotational speeds. Much more particles are having more than 1 contact.

In Fig. 9, the inlets a–g give corresponding snapshots of the bed of material on the pelletizing disc. The transition from the rolling movement of the loosened kidney-shaped bed of material (inlets a – d) to the solid-body like rotation of the ring-shaped bed of material (inlets f – g) is evident. It correlates with the characteristic changes in \(P\left( t_{d}\right)\) and \(P\left( N_{c}\right)\) as discussed above. Note that similar observations of a step by step loosening of the bed of materials for the sub-critical configurations have been also made in the experiments, see Fig. 5.

For a more compact analysis of the state of the bed of materials, the integrated contact number \(p_{c}\), is used and is defined as follows:

$$\begin{aligned} p_{c} = \int \limits _{2}^{N_{c,max}}P\left( N_{c}\right) \,dN_{c} \end{aligned}$$
(12)

Based on this definition, all pellets with at least two contacts to other pellets up to the maximum contact number \(N_{c,max}\) in the bed are taken into account (see hatched area on Fig. 9 as an example for the curve \(\psi =1.0\)).

Fig. 10
figure 10

Integrated contact number \(p_{c}\) as a function of operating speed factor \(\psi\) for different inclination angles \(\beta\)

Full size image
Fig. 11
figure 11

Critical velocity of pelletizing disc predicted by empirical equation (1) as a function of inclination angle \(\beta\) (violet line). Green and blue lines are critical speeds \(n_{crit}\) from DEM-simulations for friction coefficients \(\mu =0.5\) and \(\mu =0.7\)

Full size image

Figure 10 visualizes the dependencies \(p_{c}\left( \psi ,\,\beta \right)\) for all investigated configurations of the pelletizing disc. It can be seen, that configurations with \(\beta \le {40}^{\circ }\) exhibit a switch in the development of \(p_{c}\) from descending behavior to ascending behavior. Contrary the configurations with \(\beta >{40}^{\circ }\) do not show such a switch: \(p_{c}\) decreases approximately linearly with increasing \(\psi\). Therefore, the integrated contact number gives a nice, compact characterization of the bulk solid behavior on the pelletizing disc. It is also possible to deduce the critical OSF \(\psi _{crit}\) of a specific configuration from this chart, i. e. \(\psi _{crit}\left( \beta ={30}^{\circ }\right) =0.9\), \(\psi _{crit}\left( \beta ={35}^{\circ }\right) =1.05\) and \(\psi _{crit}\left( \beta ={40}^{\circ }\right) =1.25\). Exactly these values are taken as a base for the following analysis.

In the Fig. 11, the critical rotational speed \(n_{crit}\left( \beta \right)\) of the investigated configurations is compared to the prediction based on the empirical correlation from eq. (1). Here, we give \(n_{crit}\left( \beta \right)\) for two different pellet materials with two different friction coefficient \(\mu =0.5\) and \(\mu =0.7\). Note that in Figs. 5 - 11, only results from DEM simulations with \(\mu =0.5\) have been presented.

Clearly, both correlations \(n_{crit}^{\mu =0.5}\left( \beta \right)\) and also \(n_{crit}^{\mu =0.7}\left( \beta \right)\) deduced from the simulations do not fit to the prediction of the empirical correlation in eq. (1). Summarizing these observations it can be concluded, that the bulk solid behavior on a pelletizing disc must be described by more elaborated correlations than given in eq. (1). This is in agreement with findings of other authors, e.g. Fayed and Otten [24]. The micro-mechanics between individual particles must be taken into account, and characteristic properties of their dynamics cannot linked directly to global process or machine parameters.

6 Conclusions

In this work DEM simulations are used to investigate the particle dynamics on the pelletizing disc numerically. The model is tested through the qualitative visual comparison of an experimental data with the simulation. The DEM model can be used to investigate the internal dynamics of more realistic granular materials in the pelletizing process, e.g. during the production of iron ore pellets.

As a model pellets glass particles of the size 4–5 mm with the total mass of 0.8 kg are used, which corresponds to about \(N_{p}\approx {6700}\,{\text{particles}}\). The linear viscoelastic contact model is employed for the description of pellet-pellet contacts.

Visual comparison of experimental and simulation data showed a good conformity. For qualitative determination of the critical rotational speed with DEM simulation several quantities were proposed:

  • length of rotating body \(\phi\) along the edge of pelletizing disc is reaching the value \({360}^{\circ }\) if particles centrifugate.

  • Most of contacts in the bulk are very short in a normal operational mode of pelletizing disc. In an over-critical state the duration of contacts increases.

  • Integrated contact number \(p_{c}\), which characterizes the state of the particle system regarding the portion of particles with contact number \(N_{c} \ge 2\). This value is getting significantly higher (when the system is reaching the critical state) in comparison to a normal rotational mode.

The critical rotational speed of the pelletizing disc is investigated with different measures which are applied to the simulation data. It is found, that the micro-mechanics in the bed of materials changes rapidly near the critical state. Both, the contact duration and the number of contacts between pellets, decrease below the critical rotational speed. On the opposite side these both parameters rise, when the disc is rotating over the critical rotational speed.

The integrated number of contacts \(p_{c}\) is introduced as a measure, which can be used to characterize the bulk solid behavior on different configurations of a pelletizing disc in a compact manner. It is also possible to identify the critical state of a configuration with the help of \(p_{c}\). It is shown, that the critical rotational speed of the pelletizing disc is not only a function of machine and global process parameters, but also of the properties of individual pellets.

It is also found that the critical speed calculation should not only consider the machine parameters like it is done in the equation (1), but it should include bulk material properties and the form of rotating particles to able to predict the critical rotational speed more precisely.

DEM simulations were carried out with some simplifications like a reduced material stiffness. The real stiffnesses of glass beads used in experiments is very expensive to simulate due to a very small time steps needed for that. Verification simulations were done and proved the stability of the macro-parameter of the rotational body even with much softer material. To study the influence of the friction coefficient two different values were employed: 0.5 and 0.7. Higher friction coefficients decrease the rotational speed, where the critical state is reached (see Fig. 11). It happens due to the higher friction forces, which are pushing particles along the border of a pelletizing disc. Lower restitution coefficients relax the particle behavior, making it smoother. The influence of this parameter is the topic of ongoing studies.

Further investigations should be done with other model pellet materials, which reflect better the properties of real green pellets. Additional, agglomeration and attrition processes, which have been neglected in the present study, should be incorporated into the simulation approach. Finally, more detailed experiments should be done at laboratory-scale pelletizing discs for a better validation of the proposed DEM model.