Un-jamming due to energetic instability: statics to dynamics

Abstract

Jamming/un-jamming, the transition between solid- and fluid-like behavior in granular matter, is an ubiquitous phenomenon in need of a sound understanding. As argued here, in addition to the usual un-jamming by vanishing pressure due to a decrease of density, there is also yield (plastic rearrangements and un-jamming that occur) if, e.g., for given pressure, the shear stress becomes too large. Similar to the van der Waals transition between vapor and water, or the critical current in superconductors, we believe that one mechanism causing yield is by the loss of the energy’s convexity (causing irreversible re-arrangements of the micro-structure, either locally or globally). We focus on this mechanism in the context of granular solid hydrodynamics (GSH), generalized for very soft materials, i.e., large elastic deformations, employing it in an over-simplified (bottom-up) fashion by setting as many parameters as possible to constant. Also, we complemented/completed GSH by using various insights/observations from particle simulations and calibrating some of the theoretical parameters—both continuum and particle points of view are reviewed in the context of the research developments during the last few years. Any other energy-based elastic-plastic theory that is properly calibrated (top-down), by experimental or numerical data, would describe granular solids. But only if it would cover granular gas, fluid, and solid states simultaneously (as GSH does) could it follow the system transitions and evolution through all states into un-jammed, possibly dynamic/collisional states—and back to elastically stable ones. We show how the un-jamming dynamics starts off, unfolds, develops, and ends. We follow the system through various deformation modes: transitions, yielding, un-jamming and jamming, both analytically and numerically and bring together the material point continuum model with particle simulations, quantitatively.

Graphic abstract

1 Introduction

The macroscopic Navier-Stokes equations allow one to describe Newtonian fluids with constant transport coefficients (e.g., viscosity). In many non-Newtonian systems, complex fluids [1], colloidal suspensions, review [2,3,4], and especially granular matter [5] in its flowing state [6], the transport coefficients depend on various state-variables such as the density and the granular temperature [7]. This interdependence and the presence of energy dissipation is at the origin of many interesting phenomena: clustering [8], shear-band formation [9], jamming/un-jamming [10], dilatancy [11], shear-thickening [3, 4, 12, 13] or shear-jamming [10, 14], plastic deformations [15,16,17,18,19,20,21], related also to creep/relaxation [11, 22,23,24,25], and many others. The research on granular matter in the last decades—to a good fraction inspired by works of Bob Behringer and co-workers—will be briefly reviewed next.

1.1 A brief history of granular research

In order to describe solid-like granular matter on the macroscopic scale, concepts from elasto- and visco-plastic theories were used [15, 16, 21, 26,27,28,29,30,31,32,33,34,35] including instabilities, yield and failure [29, 36,37,38,39,40,41,42,43,44,45]. Recently, statistical mechanics/physics concepts [19, 46], helped to better understand the probabilities for plastic deformations [17,18,19,20,21, 34, 47,48,49], force network change/growth [50, 51], stress-based meso ensembles [52], or stress-relaxation [11, 22,23,24]. A traditional subject of research are stress-fluctuations [53,54,55,56], and the quest for the “effective temperature” [47, 48, 57, 58] of thermal or a-thermal granular packings [48, 52, 59]. Most recently, universal scaling laws [60] were reported, and compression and shear in particularly small systems [61] could be understood. Considering granular solids, their stiffness, and the elastic moduli [31, 62, 63] have to be considered in the presence of non-affine deformations [63]. For this, over-compression [45, 49] and shear [49, 60, 62, 64,65,66] cyclic loading [66, 67] or even thermal cyclic loading [68] were applied.   When sheared granular matter starts to flow and (for large enough strain) reaches a steady state, or critical state [69,70,71], the nowadays widely accepted “classical” $\mu (I)$-rheology [72] holds. It was recently extended to include friction, softness and cohesion [2, 12, 13, 69, 70, 73,74,75], but it does not have a fully tensorial form [76, 77], and doubts about its well-posed-ness are still discussed [78,79,80].   Modern experimental techniques [25, 71, 81, 82], also with focus on low confining stress [83], shed new light on classical works on the response to local perturbations [84], jamming and un-jamming [23, 84,85,86,87], in particular by shear [10, 49, 60, 65, 88,89,90], and transient fabric/micro-structure evolution [31, 49, 55, 91,92,93,94]. One of the classical experimental techniques involves photoelastic materials that allow to visualize stress [95,96,97], as complemented by a huge amount of particle simulations, e.g., see Ref. [9], or for a most recent example, see Ref. [98] and references therein.   One important success of granular research was to bring solid-like and flowing behavior of granular matter together, e.g., in a continuum theory with fluidity [18, 47, 48, 99], and to understand anisotropy [70, 91, 93, 94], also shape induced [100, 101], as well as involving the rotational degrees of freedom and micro-polar models [2, 102,103,104,105,106], not to forget wet particle systems [3, 4], for which a thermodynamically consistent theory [21, 107] and numerical solutions [108] were recently proposed.

1.2 Open challenges

Some open questions are: How can we understand phenomena that originate from the particle- or meso-scale, which is intermediate between atoms and the macroscopic, hydrodynamic scale? And how can we formulate a theoretical framework that takes the place of the Navier-Stokes equations?

A universal theory must involve all states granular matter can take, i.e., granular gases, fluids, and solids, as well as the transitions between those states. What are the state-variables needed for such a theory? And what are the parameters (that we call transport coefficients) and how do they depend on the state-variables?

Main goal of this paper is to propose a minimalist candidate for such an universal theory, able to capture granular solid, fluid, and gas, as well as various modes of transitions between these states. The model, remarkably, involves only four state-variables, density, momentum density (vector), elastic strain (tensor), and granular temperature. It is a boiled down, simplified case of the more complete theory GSH [47, 48, 109,110,111,112], complemented by insights based on DEM, see Ref. [49] and references therein, modified such that it works below, above and during transitions. For the sake of transparency and treatability, whenever possible, we reduce most transport coefficients and parameters to constants—without loss of generality.

Each transport coefficient is related to the propagation or evolution of one (or more) of the state-variables that encompass the present state of the system. For simple fluids [1, 113], it is possible to bridge between the (macroscopic) hydrodynamic and the (microscopic) atomistic scales; as an example, the diffusion coefficient quantifies mass-transport mediated by microscopic fluctuations.

In the case of low density gases, the macroscopic equations and the transport coefficients can be obtained using the Boltzmann kinetic equation as a starting point. For moderate densities, the Enskog equations provide a good, quite accurate description of dense gases (or fluids) of hard atoms [1], or of particles including the effects of dissipation, which results in what is nowadays referred to as standard kinetic theory (SKT) [7, 114]. Beyond SKT one can only reach out (empirically) towards realistic systems [8, 115, 116], and beyond, see, e.g., [4, 12]. The limit of granular fluids is where transport coefficients, like the viscosity, deviate from SKT. This involves a divergence [12, 117, 118] when the granular fluid becomes denser [8, 116, 118], approaching the jamming density from well below, i.e., the state that we could call a granular solid, as described by classical solid mechanics [120]. Recent research also considers soft particles [74, 118, 121] for which jamming changes from a sharp to a rather smooth transition. One objective of this paper is to bring together fundamental theoretical concepts of continuum mechanics [21, 32, 35, 48, 107, 122, 123] with observations made from particle simulations for simple granular systems in the gas, fluid, and solid states, including also the transitions between those states [8, 49, 116, 118, 124,125,126].  

1.3 About states of granular matter

When exposed to external stresses, grains are elastically deformed at their contacts. In static situations, there is only elastic energy; in flowing states, some of the elastic energy is transferred to kinetic energy and back¹, as sketched in Fig. 1 for the example of slow isotropic jamming, and—after an overcompression cycle—eventually un-jamming. Note that the jamming transition at small (yet finite) compression rate appears smooth/continuous, whereas the un-jamming transition is rather sharp/discontinuous [127].

Grains yield differently for vanishing or finite $T_g$. In motion, for $T_g\not =0$, yield is a continuous phenomenon, i.e., state-variables vary continuously. If the grains are at rest initially, $T_g=0$, yield is discontinuous—as evidenced by a layer of grains on a tilted plane. Discontinuity is mainly in the equilibrium value of the elastic stress. It is finite in the convex region and zero in the concave one, as it always relaxes away there. Any discontinuity of a phase transition is always in the equilibrium values of some quantities.

Fig. 1

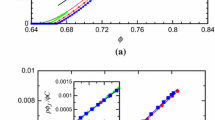
Sketch of isotropic jamming and un-jamming, with dimensionless compression rate $I_v < I_v(\phi _J^{0}=0.6608)={\dot{\varepsilon }}_v d_p/\sqrt{P_{\mathrm{sim}}\rho _p}=1.2\times 10^{-5}$, of frictionless, polydisperse particles, from simulations in Ref. [49], with reversal at maximal density $\phi _{\mathrm{max}}=0.9$, so that unjamming occurs at $\phi _J^{1}=0.666$. Displayed from particle simulations are the coordination number Z (green, scaled as $Z/4-1$) that defines dynamic initial jamming at $Z(\phi _J^{0})=Z_0\,=\,6$, the dimensionless elastic pressure $P_{\mathrm{sim}} d_p/k_n$ (blue, scaled by a factor of 3000), with magnitude $4\times 10^{-5}$ at $\phi _J^{0}$, and the fraction of kinetic energy $K/(1+K)$ (red), as discussed in footnote 1: For initial jamming, the yellow area designates the dense collisional flow state ($K\sim 1$), while the cyan area designates the quasi-static (isotropic) state ($K\ll 1$). The thin magenta line is a fit to Eq. (11) in Ref. [49] of all solid-like high-pressure data (using $K<5\times 10^{-4}$, i.e., $\phi \ge 0.665$), on the initial compression branch (data out of this plot, well above the rather unstable cyan area, up to much larger $\phi _{\mathrm{max}}$), yielding an extrapolated jamming density of $\phi _J^{P}=0.66125$ (around which the cyan area is centered), and a dimensionless modulus $p_0 = 0.06272$ (note that $p_0 \rightarrow p_0/\phi _J^{P}$ in Ref. [49]), and the nonlinear coefficient $\gamma _p=0.179$ that accounts for the large overlaps of particles in the simulation, for more details see Ref. [49]. Note that this full-range fitting perfectly collapses with the unloading branch (not visible), agrees with the loading branch for $P>0.001$ (out of range), but is fundamentally different from the calibrated comparison between simulation and model solution, as presented in Sect. 6

Particle systems, compressed and decompressed with different rates, are discussed in Ref. [127]. Here, a rather slow rate is chosen and the system response is plotted in Fig. 1. Even such little dynamics allows for a rich phenomenology below and above jamming, where the yellow area corresponds to a dense fluid with solid features—just below jamming, while the cyan area corresponds to a solid with fluid features—jammed, but strongly unstable (see the steps and wiggles in pressure and coordination number) [88].

The capability of granular solids to remain quiescent, in mechanical equilibrium, under a given finite stress is precarious. For small perturbations they will return to their original state. If pressure or shear stress become too large, the grains will, suddenly, start moving—either locally or globally [17, 127]—with a decaying elastic stress. This qualitative change in behavior is an unambiguous phase transition. We shall refer to the region capable of maintaining the global, overall equilibrium of static grains as elastic, and its boundary (in the space spanned by the state-variables) as the yield surface. For local loss of elasticity we rather use the term plastic, irreversible events, see Refs. [19, 61].

Granular systems will also un-jam for vanishing pressure and a continuous reduction of density, though we reserve the term yield for the (sudden) loss of elastic stability: Grains un-jam in either case, they yield only when the elastic stress, in particular the pressure, is finite.

Starting from the elastic region, decompression (tension) reduces the density and the elastic deformations of the grains—until the latter vanish and the system un-jams. Decompressing further just reduces the density accordingly. The system is now un-jammed in the sense that one can change the density without any restoring force, i.e., the elastic energy remains zero. In reverse, compression only increases the density, as long as it is smaller than the jamming density. At jamming both the elastic deformations and the associated energy start to increase with density. In contrast, there is a discontinuity leaving the elastic regime at finite values of elastic stress. It is a sudden transition from quiescent, enduringly deformed grains, to moving ones oscillatorily deformed due to “jiggling” particle motions. This transition needs to be explained, to have a model for. And it is clear that the transition must be encoded in the elastic energy—the only quantity characterizing the quiescent state—not in the dynamic/fluctuating contributions to energy.

In the elastic region, grains appear solid when at rest, but they will flow if subject to an imposed finite shear rate, and appear liquid. Such a continuous change in appearance is well accounted for by any competent dynamic theory or rheology, it is not a transition² . Moreover, flowing grains in the elastic region do feature a macroscopic elastic shear stress, with an associated elastic energy (even though granular contacts switch continually), something no Newtonian liquid is capable of. Also, the shear stress remains finite when the grains stop flowing, which is not the case in Newtonian fluids.

So there are two different flowing states, either with finite elastic stress/strain, or with vanishing ones, which includes granular gases, as accounted for by the kinetic theory, see Refs. [8, 116] and references therein. There is also a transition between them, as possibly related to (dry) liquefaction [37], but not to be confused with liquefaction due to a fluid between the particles, which is completely disregarded in this study of dry granular matter (even though the fluid stress can be considerable in wet system). We take both transitions, either leaving the quiescent state, or the flowing one, as the same transition, with the same underlying physics. In fact, encoding the transition in the elastic energy certainly affects the flowing state as well. The mechanism for yield is here related to elastic energy (irrespective whether the pressure or the shear stress is too large, or the density too small), as traditionally encompassed by concepts like plastic potentials, yield functions, or flow rules [21, 30, 32, 34, 106, 122], see Fig. 2 and textbooks like Ref. [122].

1.4 Relation to other systems in physics

We do not think that the transition is due to spontaneously broken translational symmetry—the usual mechanism giving rise to static shear stresses, as in any fluid-solid transition. The quick argument is: Consisting of solid, grains already break translational symmetry. More importantly, the loss of equilibrium and granular statics is caused by the shear stress or pressure being too strong.

This is an indication of an over-tightening phenomenon, of which the (pair-breaking) critical current is a prime example. If a superconductor conducts electricity without dissipation, it is in a current-carrying equilibrium state. If, however, the imposed current exceeds a maximal value, the system leaves equilibrium and enters a dissipative, resistive state. The superfluid velocity, $v_{sf}\sim \nabla \varPsi _q$, given by the gradient of a quantum mechanical phase, $\varPsi _q$, is the analogue of the strain. The dissipationless current, $j_{sf}=\partial w/\partial v_{sf}$, given by the derivative of the energy with respect to $v_{sf}$, is the analogue of the elastic stress. The over-tightening transition in superconductivity is well accounted for by an inflection point, at which the energy turns from stably convex to concave, see the classic paper by Bardeen [130]. The close analogy between the two systems is a good reason to employ the same approach here, to postulate that the surface of the cone in Fig 2 can be related to an inflection surface of the elastic energy.

1.5 About elastic granular matter

The granular solid state is contingent on granular matter capable of being elastic, for which there is ample evidence, see e.g. Refs. [6, 52, 84, 95, 125, 131,132,133,134] and references therein. In addition to the material stiffness, many other material properties (including cohesion, friction, surface-roughness, particle-shape) determine the elastic response of granular matter. For soft and stiff materials the deformations are, respectively, considerable and slight, but never zero. Because of their Hertz-like non-linear contacts, grains are infinitely soft in the limit of vanishing contact area (deformation). Therefore, at any given finite force, deformations are always sufficiently large to display the full spectrum of elastic behavior, including a considerable static shear stress (enabling a tilted surface), and elastic waves. Even the simplest model material, consisting of perfectly smooth spheres of isotropic, linearly elastic material, displays non-linearity due to their Hertz-type contacts, on-top of the contact network (fabric) and its re-structuring. Only in computer simulations is it possible to remove the first and focus on the second, see e.g. Ref. [49].

Elastic waves propagate in granular media, displaying various non-linear features, including anisotropy, dispersion and rotations, see e.g. Refs. [104,105,106, 135,136,137,138,139,140] and references therein. The discreteness and disorder of granular media add various phenomena—already for tiny amplitudes—such as dispersion, low-pass filtering and attenuation [104, 140,141,142]. With increasing amplitudes, a wide spectrum of further phenomena is unleashed, among which the beginning of irreversibility and plasticity, see Ref. [20] in this topical issue, and references therein, and the loss of mechanical stability [143], what we call “yield” in the following.

1.6 Yield: About the limits of elasticity

To envision the yield surface, we consider the space spanned by three parameters: pressure P, shear stress $\sigma _s$, and void ratio $e=(1-\phi )/\phi$ (where $\rho =\rho _p \phi$, with material density $\rho _p$ and volume fraction $\phi$), ignoring the granular temperature (i.e., fluctuations of kinetic and potential energy), as discussed in Ref. [144] and so many papers following. Based on the observation of the Coulomb yield and the virgin consolidation line, we assume that the yield surface is as rendered in Fig. 2. Elastic, jammed states, maintained by deformed grains, are stable and static only inside it³.

Fig. 2

Granular yield surface, or the jamming phase diagram, for $T_g=0$, as a function of the pressure P, shear stress $\sigma _s$, and void ratio e, as rendered by an energy expression in [112]. Panel c is the 3D combination of a and b; with b depicting how the straight Coulomb yield line bends over, depending on the void ratio e—a behavior usually accounted for by cap models in elasto-plastic theories; while a depicts the maximal void ratio $e=1/\phi -1$ (equivalent to the inverse density) plotted against pressure P, or the so-called virgin consolidation line (VCL). In panel (a), the dotted line is an empirical relation, $e=e_1-e_2 \log (P/P_0)$, with $P_0=0.5$ MPa, $e_1=0.679$ and $e_2=0.097$, approximating the VCL, but not valid for $P \rightarrow 0$. The thick solid line cuts the e-axis at $e_0$, with the intersection being the lowest possible, random loosest packing value, see Ref. [112] for details, where also the thin solid line is discussed. Thus $e_0$ also defines the lowest possible jamming volume fraction, $\phi _{J0}=1/(1+e_0)$, see Ref. [49], with static, elastic states possible only below the VCL, as will be shown in Sect. 5 and 6

The Coulomb yield line, see Fig. 2b, can be reached by increasing the shear stress at given confining pressure. When the shear stress exceeds a certain level, the system yields, un-jams and becomes dynamic. No static, stable elastic state exists above the Coulomb yield line, as evidenced by a sand pile’s steepest slope.

It is imperative to realize that (what we call) the Coulomb yield line is conceptually different from the peak shear stress achieved during the approach to the critical state at much larger strains. Coulomb yield is the collapse of static states—such as when one slowly tilts a plate carrying grains until they start to flow (max. angle of stability). Its behavior is necessarily encoded in the system’s energy, because this phenomenon does not at all involve the system’s dynamics. The critical state, including the peak shear stress—though referred to as “quasi-static”—is a fully dynamic and irreversible effect. It is accounted for by the stationary solution at given strain rates in GSH. The angle of repose (always smaller than the max. angle of stability) is in GSH given by the critical friction angle [47, 48].

In the absence of shear stresses, the maximally sustainable pressure depends on the void ratio, e, as rendered in Fig. 2a. Starting from a given e, slowly increasing P, the grain-structure will collapse and yield at this pressure, to a smaller value of e, such that the final state is stable, static, and below the curve of Fig. 2a. This is because when applying a slowly increasing pressure, the point of collapse is (ever so) slightly above the curve; and the end point below it is typically also close. This evolution resembles a stair-case, with the granular medium increasing its density by hugging this curve, which frequently referred to as the virgin/primary consolidation line, or simply the pressure yield line. The line cuts the e-axis at the random loosest void ratio, $e_0$, above which no elastic stable states exists.

Because of the pressure yield line, the Coulomb yield curve cannot persist for arbitrarily large P at given e. Rather, it bends over to form a “cap”, as rendered in Fig. 2b, since an additional shear stress close to the pressure yield line will also cause the packing to collapse. (The shape of the cap depends on the interplay of isotropic and deviatoric deformations as well as the probability for irreversible, possibly large-scale re-structuring events of the micro-structure, i.e., the contact network, including also the sliding of contacts, but also breakage of particles, which is, however, excluded from this study. Whether the picture sketched here is sound without breakage remains an open question [21].)

Merging Figs. 2a and 2b yields the elastic region below the yield surface, as given in Fig. 2c. Although the e-axis, for $P,\sigma _s=0$, is also referred to as the loci of (isotropic) un-jamming, the elastic stress goes continuously to zero here, because the grains are successively less deformed. There is, as already discussed above in Sect. 1.3, no discontinuous phase transition or yield here, except for the coordination number, see Fig. 1. Point is, concerning only this one point of the plot, if the elastic stresses vanish, both in the convex and concave region, nothing much resembling a discontinuous transition happens there. Isotropic jamming and un-jamming, as well as the discontinuity in the coordination number on the isotropic e-axis is discussed in detail at various spots in this paper, see Sects. 1.3, 3.2.3, and 4.1.1.

Next, all different symbols and nomenclatures are summarised.

1.7 Notation and symbols

This paper is a cooperation of co-authors, whose notational baggage from past publications clash with one another. In the dire need to compromise, we ask the readers to suffer—with us—using varying symbols and notations. Our state-variables are: density, $\rho$, momentum density, $\rho v_i$, granular temperature, $T_g$, and the elastic (true) strain, as summarized here.

• 1. The bulk density, $\rho$, is related to the volume fraction, $\phi =\rho /\rho _p$ (with $\rho _p$ the particles’ material density), the porosity $1-\phi$, and the void ratio $e=(1-\phi )/\phi$. (Later, we shall choose units such that $\rho _p=1$, so that volume fraction and bulk density are identical⁴.)

• 2. The conserved momentum density defines the velocity $v_i=( \rho v_i ) / \rho$. The symmetric part of the velocity gradient is

  $$\begin{aligned} v_{ij}:=v_{(i,j)} = -{\dot{\varepsilon }}_{ij} = D_{ij} = \textstyle \frac{1}{2}(\nabla _iv_{j}+\nabla _jv_{i}) \,, \end{aligned}$$

  where differences between finite and linear strain theory are detailed, e.g., in Refs. [145,146,147]. Eigenvalues of the total strain rate ${\dot{\varepsilon }}_{ij}$ are positive for compression and negative for tension.

  The symbol $v_{ij}$ is usual in condensed matter physics [113, 120, 145, 148]; it is also the one employed in most previous GSH-publications. The notation ${D_{ij}}$ is common in theoretical mechanics [32, 107, 146], while ${\dot{\varepsilon }}_{ij}$, or ${\dot{\gamma }}$, are used, e.g., in soil mechanics and related literature [106, 122].

• 3. Subscripts, such as i,j,k,l, refer to components of tensors in the usual index notation, with double-indices implying summation, the comma indicating a partial derivative, as in $v_{(i,j)}$; the superscript $^{*}$ denotes the respective traceless (deviatoric) tensor. Using the summation convention, the volumetric strain rate is abbreviated as: ${\dot{\varepsilon }}_v={\dot{\varepsilon }}_{ll}=-v_{ll}=-D_{ll}=-\mathrm{tr}{} \mathbf{D}$, where the last term is in symbolic tensor notation. The deviatoric strain rate is thus ${\dot{\varepsilon }}_{ij}^{*}=-v^{*}_{ij}=-D_{ij}^{*}$, with the norm $v_s:=\sqrt{v^{*}_{ij}v^{*}_{ij}} =D_s={(2 J^{D}_2)^{1/2}}$, where $J^{D}_2$ is the second deviatoric invariant, insensitive to the sign convention.

• 4. The elastic (true) strain, $\varepsilon ^{e}_{ij} \equiv - u_{ij}$, as properly defined in theoretical mechanics, e.g., see Refs. [145, 147], even for large deformations (implying the logarithmic definition due to its additivity, reversibility, and split-ability into isotropic and deviatoric contributions), is the tensorial state-variable on which the elastic (potential) energy depends. It is always well-defined and unique, in contrast to the total or plastic strains, which are not, and thus will not be used as state-variables for (constitutive) modeling. The respective strain rates, however, are well-defined and thus are used. The strain rate was already given (see item 2.), ${\dot{\varepsilon }}_{ij}=-v_{ij}$, so that the plastic strain rate is defined as: $\textstyle {\dot{\varepsilon }}^{p}_{ij} ={\dot{\varepsilon }}_{ij}-\frac{d}{dt}\varepsilon ^{e}_{ij}$ (see also item 7.).

• 5. The isotropic elastic strain

  $$\begin{aligned} \varDelta := -u_{ll} = \varepsilon ^{e}_{ll} = \varepsilon ^{e}_v = \log \left( \rho /\rho _J\right) \end{aligned}$$

  is positive for compression⁵. It may be seen as the true (finite) strain relative to a stress-free reference configuration—for finite $\varDelta > 0$. Arriving at $\varDelta =0$, the system un-jams at $\rho _J^{u}=\rho$ and the jamming density remains the actual one.⁶

• 6. The norm of the deviatoric elastic strain is, in accordance to the general scheme, $u_s=\sqrt{u_{ij}^*u_{ij}^*}=(2 J^{u}_2)^{1/2}$.

• 7. In general, we take $\frac{\partial }{\partial t}$ as the partial time derivative, and $\frac{d}{dt}$ as the total one, including all convective terms. Hence, with the vorticity tensor given as $\varOmega _{ij} \equiv v_{[i,j]} \equiv \textstyle \frac{1}{2}(\nabla _iv_j-\nabla _jv_i)$, one has (as example) the total time derivative of the elastic strain

  $$\begin{aligned} \textstyle { \frac{d}{dt} }\varepsilon _{ij}^e=\left( \textstyle { \frac{\partial }{\partial t}}+v_k \nabla _k\right) \varepsilon ^e_{ij}+\varOmega _{ik}\varepsilon ^e_{kj} -\varepsilon ^e_{ik}\varOmega _{kj} ~. \end{aligned}$$

  (1)

  Being off the focus here, the convective and vorticity terms are neglected, so that $\textstyle {\frac{d}{dt} \equiv \frac{\partial }{\partial t}}$. The dots in ${\dot{\varepsilon }}^p_{ij}$ and ${\dot{\varepsilon }}_{ij}$ are only a (convention preserving) indication of rates, but do not represent the mathematical operation above.

• 8. The total stress is not an independent state-variable, but rather given by the energy density and entropy production, as discussed in the classical GSH literature. In the simplified version, it may be written as $\sigma _{ij}=\pi _{ij}+P_T\delta _{ij}+\sigma _{ij}^{\mathrm{visc.}}$, with elastic, kinetic/granular temperature and viscous contributions. The isotropic stress is referred to as pressure, $P=\frac{1}{3}\sigma _{kk}$, the elastic pressure is $P_\varDelta =\frac{1}{3}\pi _{kk}$, for three dimensions ${{\mathcal{D}}}=3$, and the deviatoric elastic stress is denoted as $\pi ^*_{ij}=\sigma ^{e*}_{ij}$, with norm $\pi _s = \sqrt{\pi ^*_{ij}\pi ^*_{ij}} = \sqrt{2 J_2^\pi }$.

  Note that there are alternative definitions for shear/deviatoric stress⁷.

• 9. The symbols B and G are used in the definitions of, respectively, isotropic and deviatoric (shear) elastic energy density, $w_e = w - w_T$, defined as the total minus the thermal energy density. In previous GSH-papers [47, 48, 112], the symbol A was used instead of G, but since A is here referred to as anisotropy, see Ref. [49], we stick to G⁸.

• 10. The granular temperature used in GSH is $T_g \propto \sqrt{w_T}$, encompassing both kinetic and potential fluctuating energy contributions. The granular temperature used in kinetic theory and DEM is different, denoted as $T_G = T_K = 2E_{\mathrm{kin}}/M{{\mathcal{D}}}$, with total mass of all particles, M, in dimension ${{\mathcal{D}}}$, ignoring the potential part. Comparing GSH-formulas in the gas limit to those of kinetic theory [7, 8, 114, 116, 119], one should remember

  $$\begin{aligned} T_g^2\sim T_G ~. \end{aligned}$$

  (2)

  In the following, we will use $T_{g}$⁹, with units of velocity, i.e., if scaled by the particle diameter, that of an inverse time, or a rate, very similar to the fluidity, g, studied and discussed in Ref. [18], and references therein^{10, 11}.

1.8 Overview

In what follows, we shall, in Sect. 2, consider the significance of an inflection surface, of a convex-concave transition in the energy, as relevant for classical systems, transiently elastic systems and granular matter. We then present a review of GSH and new constitutive relations based on particle simulations, as well as a minimalist version, in Sect. 3, allowing for analytic solutions in Sect. 4, and numeric calculations to catch some transitions in Sect. 5. A quantitative comparison and calibration with particle simulations is carried out in Sect. 6, before we conclude in Sect. 7.

2 Equilibrium conditions and dissipative terms

In this section, we first revisit the reason for thermodynamic energy’s convexity, and derive the equilibrium conditions for three systems: elastic, transiently elastic and granular media. There is one equilibrium condition for each state-variable, that maximizes its contribution to entropy or, equivalently, minimizes its contribution to energy. Examples for equilibrium conditions are uniform temperatures and stress gradients proportional to density. As these conditions represent extremal points, the energy needs to be convex to be minimal, for the system to be stable.

Then we make the general point that every equilibrium condition, if not satisfied, is a dissipative channel that gives rise to a negative/dissipative term in the evolution equation of the associated state variable. As a result, the state-variable relaxes, towards satisfying the condition. In a closed system, all variables will eventually satisfy all their respective conditions, which is the state we called equilibrium.

If the energy is concave, equilibrium conditions represent maxima of the energy with respect to variation of a state-variable ¹². The dissipative terms can thus drive the system away from equilibrium, producing, e.g., non-uniformity in temperature and non-equilibrium stress fields. When this happens, what micro-mechanical mechanisms it originates from, is necessarily more specific. How the dynamics further evolves depends on the system one considers. In the classical van der Waals theory of the gas-liquid transition, droplet formation is the basic mechanism. In granular media, we propose the following mechanism.

In the stable region, within the cone of Fig 2, the dissipative term in the equation for the elastic strain serves to maintain stress equilibrium. It remains inconspicuous as long as one studies the evolution of stresses close to equilibrium.

Outside the cone, beyond stability, it can force the system to leave equilibrium. Non-equilibrium stresses accelerate grains in varying directions, producing jiggling and thus granular temperature which, in turn, allows the stress to relax, pushing the system back into the convex region.

This is what we believe happens in grains at yield and beyond the transition. Setting up a dynamical model for following the system through the transition to different states is the main purpose of this paper.

2.1 Classical view on equilibrium states

Consider a system characterized by the state-variables density, $\rho$, entropy density, s, and elastic strain,

$$\begin{aligned} - \varepsilon ^e_{ij} \equiv u_{ij} \approx {\textstyle \frac{1}{2}}(\nabla _iU_j+\nabla _jU_i), \end{aligned}$$

(3)

with elastic displacement vector (field) $U_i$, relative to the stress-free reference configuration, and a thermodynamic energy density that is a function of all state-variables, $w=w(\rho ,s,u_{ij})$ [113, 120].

Note that, for convenience, we spell out only the small-strain approximation in Eq. (3) [145,146,147], however, throughout, we work with the (logarithmic) Hencky finite (true) strain definition, due to its more favorable properties: additivity, reversibility, split-ability into isotropic and deviatoric parts, which allows the interpretation of $\rho _J$ as the stress-free reference density, and thus allows us to work not only with hard but also with very soft materials.

A textbook proof of energy convexity considers only the entropy as a variable, and involves that the system is connected to a heat bath. A temperature fluctuation (associated to entropy fluctuations) vanishes only if the energy is larger with it than without, which is shown to imply convexity [149].

In a more general consideration, we start with the assumption that the system is stable and has an equilibrium for given values of $\rho$, s and $u_{ij}$. Since the elastic stress, $\pi _{ij}\equiv -\partial w/\partial u_{ij}$ is symmetric, $\pi _{ij}=\pi _{ji}$, we may write the total differential of the energy density as:

$$\begin{aligned} \mathrm{d}w&= T\mathrm{d}s - \pi _{ij}\mathrm{d} u_{ij} {+ (\mu + \varPhi ) \mathrm{d}\rho } \, , \end{aligned}$$

(4)

with gravitational potential $\varPhi$, chemical potential $\mu =\partial (w-\rho \varPhi )/\partial \rho$¹³, and temperature $T=\partial w/\partial s$.

Varying this energy by  

(i):

keeping $\int s\,\mathrm{d}V=const.$, or $\delta \int \left( w-T_Ls\right) \,\mathrm{d}V = 0$, with Lagrange parameter $T_L=const.$;

(ii):

keeping $\int \rho \,\mathrm{d}V=const.$, or $\delta \int \left( w-\mu _L \rho \right) \,\mathrm{d}V = 0$, with Lagrange parameter $\mu _L=const.$;

(iii):

forbidding external work, i.e., assuming a closed system: $\oint {\pi _{ij}}\delta U_i\,\mathrm{d}A _j=0$; and

(iv):

using Gauss’ theorem¹⁴, yields

$$\begin{aligned} 0 =&\int \left[ {T}\delta s -\pi _{ij}\delta \nabla _jU_i + (\mu +\varPhi ) \delta \rho - T_L\delta s - \mu _L \delta \rho \right] \,\mathrm{d}V \nonumber \\ =&\int \left[ \left( {T}-T_L\right) \delta s + {(} \nabla _j{\pi _{ij}} {)} \delta U_i + \left( {\mu }+\varPhi -\mu _L\right) \delta \rho \right] \,\mathrm{d}V \, , \end{aligned}$$

(5)

with either $\delta \rho$, $\delta s$ or $\delta U_i$ varying independently, while keeping the others constant. The split-up equilibrium (extremal) conditions may now be written as:

$$\begin{aligned} \nabla _iT=0 \,, ~~ {\nabla _i\mu = - \nabla _i \varPhi = - g_i \,, ~~} {\nabla _j\sigma ^{eq}_{ij}=\rho g_i \,, } \end{aligned}$$

(6)

with the total equilibrium stress $\sigma ^{eq}_{ij}$¹⁵. They represent an energy minimum—and stable equilibrium—only if deviations from them yield an energy increase.

2.2 The limit of solid elasticity

Elasticity (reversibility) corresponds to the unique dependence between density and isotropic elastic strain increment, $\delta u_{ii} = - \delta \rho / \rho$, or, integrated, $\varDelta = - u_{ii} = \log (\rho /\rho _0)$, the logarithmic (true) isotropic elastic strain, where $\rho _0$ is the density of the stress free reference configuration¹⁶. This allows to rewrite¹⁷ the integral

$$\begin{aligned} \int dV (\mu +\varPhi ) \delta \rho = \int dV \rho g_i \delta U_i~, \end{aligned}$$

(7)

which now implies, in conjunction with Eq. (5):

$$\begin{aligned} \nabla _iT=0, ~~ \nabla _i P_T + \nabla _j\pi _{ij} = \rho g_i \,, \end{aligned}$$

(8)

(or $\nabla _j\pi _{ij} = \rho g_i$, for $P_T=0$), with the thermal contribution to stress, $P_T = - \partial ((w-w_e)/\rho ) / \partial (1/\rho )$, using volume, i.e., inverse density $1/\rho \propto V$, as state-variable, as discussed in more detail in Sect. 3.1.1.

Next, inserting $T=T^{eq}+\delta T$, $\pi _{ij}=\pi _{ij}^{eq}+\delta \pi _{ij}$, with $\nabla _iT^{eq}=0$ and $\nabla _j\pi _{ij}^{eq}= {\rho g_i}$, we require

$$\begin{aligned} \delta ^2 w=\delta T\delta s-\delta \pi _{ij}\delta u_{ij}>0. \end{aligned}$$

(9)

Assuming first $\delta u_{ij}\equiv 0$, we may write $\delta ^2 w=\delta T\delta s=({\partial T}/{\partial s})(\delta s)^2>0$, implying

$$\begin{aligned} \frac{\partial ^2 w}{\partial s^2}=\frac{\partial T}{\partial s}>0, \end{aligned}$$

or that the energy w is a convex function of s. As a result, temperature fluctuations will diminish, and the state characterized by a uniform temperature is a stable equilibrium. Conversely, if the energy is concave, $\partial ^2 w/\partial s^2<0$, the condition $\nabla _iT=0$ represents a maximum of energy, and the system is unstable. Any fluctuations in entropy will move it away from uniform temperature. In the case of the van der Waals transition between gas and liquid, a uniform single-phase system is moved to the coexistence of two phases, with different entropy densities, but the same temperature.

Next, assuming $\delta s\equiv 0$, as used explicitly below, in Sect. 3.2.2 and 3.2.3, we order the six components of $\pi _{ij}$ and $u_{ij}$ each as a 6-tuple vector, denoted by Greek letters, and require

$$\begin{aligned} \delta ^2 w=-\delta \pi _{ij}\delta u_{ij}=-\delta \pi _{\alpha }\delta u_{\alpha }=\frac{\partial \pi _{\alpha }}{\partial u_{\beta }}\delta u_{\alpha }\delta u_{\beta }>0. \end{aligned}$$

(10)

This implies that the $6\times 6$ Hessian matrix

$$\begin{aligned} \frac{\partial ^2w_e}{\partial u_{\alpha }\partial u_{\beta }}=-\frac{\partial \pi _{\alpha }}{\partial u_{\beta }} \quad \text {has only positive eigenvalues,} \end{aligned}$$

(11)

implying that the elastic energy $w_e$ is a convex function of the elastic strain $u_{ij}$. If there is at least one negative eigenvalue, the condition $\nabla _j\pi _{ij}= {\rho g_i}$ no longer represents a stable state, because along the associated eigenvector, the energy is a maximum. The system can and will depart from its previously stable elastic state, initially by violating $\nabla _j\pi _{ij}= {\rho g_i}$, typically rendering the stress in non-equilibrium.

To obtain stable, static elastic solutions, one has to solve $\nabla _j\pi _{ij}= {\rho g_i}$ for given boundary conditions. This is equivalent to looking for minima of the elastic energy. The solutions are stable if the elastic energy is convex and unstable otherwise.

The more general consideration, including both $\delta s$ and $\delta u_{ij}$, leads to a $7\times 7$ matrix that, for stable equilibria, must possess seven positive eigenvalues.

A complete consideration for elasticity requires also the inclusion of density, $\rho$, and momentum density $\rho v_i$ (conjugate to $v_i$) as the energy’s variables. This, being somewhat more lengthy, would distract from the present concern. The associated equilibrium conditions, with the chemical potential, $\mu =\partial w/\partial \rho$ (conjugate to $\rho$, see Refs. [123, 150]), are:

$$\begin{aligned} \nabla _i\mu&=g_i , \end{aligned}$$

(12)

$$\begin{aligned} -{\dot{\varepsilon }}_{ij}&\equiv v_{ij}\equiv \textstyle \frac{1}{2}(\nabla _iv_j+\nabla _jv_i)=0, \end{aligned}$$

(13)

$$\begin{aligned} {\nabla _j\pi _{ij}}&+ s\nabla _iT+\rho \nabla _i\mu =\rho g_i ~. \end{aligned}$$

(14)

All three equations, together, express minimal energy, or maximal entropy.

If any of the equilibrium conditions¹⁸ are not satisfied, dissipative currents appear to counteract: heat diffusion $\sim \nabla _iT$ in the evolution equation for s, viscous stress $\sim v_{ij}$ in the evolution equation for $\rho v_i$, and a term $\sim {\nabla _k\pi _{ik}-\rho g_i = \nabla _k\pi _{ik}-\rho \nabla _i \mu }$, in the equation for the “dissipative displacement rate”:

$$\begin{aligned} \textstyle Y_i := V_i - v_i = \frac{\partial }{\partial t}U_i-v_i = - \beta \left( \nabla _k\pi _{ik} { -\rho g_i} \right) \, . \end{aligned}$$

(15)

Analogous to heat-conductivity, $\beta$ quantifies the strength of the dissipation, carrying units of time divided by density, a mere abbreviation; taking it as a scalar is a simplification. All these terms serve the sole purpose of restoring the respective equilibrium conditions: ${\nabla _iT=0, ~v_{ij}=0, ~\nabla _k\pi _{ik}=\rho g_i}$.

The dissipative displacement rate, as a necessary result of thermodynamics, has been first recognized in the classical 1972-paper: “The unified hydrodynamic theory for crystals, liquid crystals, and normal fluids”, by Martin et al. [148]. It drives the system, boundary conditions permitting, towards a constant stress gradient, $\nabla _k\pi _{ik}=\rho g_i$. If on top of this equilibrium state, the stress varies, such as in elastic waves, the dissipative displacement rate, contributes to wave damping. If one concentrates on the evolution of stresses in equilibrium, this term vanishes and is irrelevant. However, if the energy is concave, this term can drive the system away from equilibrium and even can result in instabilities (numerical as well as physical). Writing the elastic stress gradient in the notation of the $6\times 6$ matrix, see Eq. (11), as:

$$\begin{aligned} \nabla _k\pi _{jk} \rightarrow \nabla _k\pi _\alpha =\partial \pi _{\alpha }/\partial u_{\beta }\nabla _k u_{\beta } ~, \end{aligned}$$

(16)

since $\partial \mu /\partial u_\beta = \partial \varPhi /\partial u_\beta = 0$, we see that, if the matrix, $\partial \pi _{\alpha }/\partial u_{\beta }$, has a negative eigenvalue, the corresponding term will flip its sign. Instead of keeping maintaining stress equilibrium, it can drive the stress away from equilibrium. This, in turn, accelerates mass points, possibly leading to non-uniform velocities, $v_i$, and thus finite strain rates, $v_{ij}\equiv -{\dot{\varepsilon }}_{ij}$. Initially, the stress perturbation will grow along the direction associated with the negative eigenvalue, but for finite times, this is by no means true, as the system will try to move towards a new stable equilibrium state, whatever that is. See the next Sect. 4 and 5 about what happens in granular matter without gradients. Discussing the possibility of a relation to gradient plasticity is beyond the scope of this paper.

Inserting Eq. (15) in the definition of the elastic strain, Eq. (3), reads

$$\begin{aligned} {\dot{\varepsilon }}^p_{ij}&:= \textstyle {\frac{\partial }{\partial t}} u_{ij} - v_{ij} \equiv - {\frac{\partial }{\partial t}}\varepsilon _{ij}^e+{\dot{\varepsilon }}_{ij} \equiv \psi _{ij} ~\nonumber \\&= - \textstyle {\frac{1}{2}} \left( \nabla _i[\beta ( \nabla _k\pi _{jk} {-\rho g_j} )] + \nabla _j[\beta ( \nabla _k\pi _{ik} {-\rho g_i} )] \right) ~, \end{aligned}$$

(17)

which seems to suggest that the “dissipative current”, $\psi _{ij}$, is simply the plastic strain rate, $\psi _{ij} ={\dot{\varepsilon }}^p_{ij}$, which apparently exists even in classical solids if the stress is not in equilibrium. This could be confusing, as it is not related to typical plasticity formulations, and neither is it connected to concepts of plastic potentials or flow functions (see Refs. [32, 34, 122]). The term plastic strain rate is more appropriate for the other dissipative contributions discussed in the next two sections, on transient elasticity and granular media.

Note that heat diffusion and viscous stress exist in any system, in which entropy and momentum are state-variables: liquids, solids, granular media, irrespective of the microscopic interaction. Same holds for the dissipative term $\psi _{ij}$, which exists in any system in which the elastic strain is a variable. This is the reason it also exists in granular media. Generally speaking, every dissipative term strives to satisfy its equilibrium condition by changing the value or distribution of the associated state-variable. Equilibrium is achieved if all equilibrium conditions are satisfied, as entropy is then maximal.

2.3 Transient elasticity and plasticity

There are many transiently elastic systems in nature. If quickly deformed, they are elastic and capable of restoring their original shape. But this does not happen if the deformation is kept longer; then the deformation is irreversible, plastic. One example are polymeric melts that consist of entangled elastic strands, which elastically deform, but disentangle if given enough time. This leads to a reduction, and eventually vanishing, of the elastic stress. For such systems, the equilibrium condition is:

$$\begin{aligned} \pi _{ij}=0, \qquad \text {or,~equivalently}\quad u_{ij}=0 ~. \end{aligned}$$

(18)

Consequently, Eq. (17) takes the form:

$$\begin{aligned} {\dot{\varepsilon }}^p_{ij} = \textstyle {\frac{\partial }{\partial t}}&u_{ij}-v_{ij} \equiv -\textstyle {\frac{\partial }{\partial _t}}\varepsilon _{ij}^e+{\dot{\varepsilon }}_{ij} =-\lambda _e u_{ij} ~, \end{aligned}$$

(19)

with the plastic strain rate now a relaxation term, with a positive coefficient $\lambda _e$. Employing essentially this equation, including the convective terms of Eq. (1), a wide range of polymer behavior including shear thinning/thickening and the Weissenberg or rod-climbing effect were reproduced [151, 152].

It is noteworthy that the plastic strain rate in the form ${\dot{\varepsilon }}^p_{ij} = -\lambda _e u_{ij}$ is a diagonal Onsager term, quantify dissipative currents that drive the system towards the respective equilibrium, in this case of the elastic strain. Hence, off-diagonal ones such as

$$\begin{aligned} {\dot{\varepsilon }}^p_{ij} = \textstyle {\frac{\partial }{\partial t}} u_{ij} - v_{ij} = -\lambda _e T_g{u _{ij}} - p_{ijkl} v_{kl} \end{aligned}$$

(20)

are also permitted (in this case strain-rate causes dissipative currents that drive elastic strain to equilibrium). They will turn out to be useful in granular physics, see below, Eq. (26), and the discussion below it.

The close link, even identity, between transient elasticity and strain relaxation on one hand, and plastic behavior of irreversible shape change on the other, is a useful insight. Similarly useful is the understanding of the difference between elasticity and transient elasticity. For the latter to be in equilibrium, the elastic stress has to vanish, while a constant stress suffices for the former. For verbal clarity, we denote

$$\begin{aligned} \text {elastic equilibrium}&:\quad \nabla _j\pi _{ij}= {\rho g_i}\,, \nonumber \\ \text {``plastic equilibrium''}&:\quad u_{ij}\equiv -\varepsilon ^e_{ij}=0 ~, \end{aligned}$$

(21)

where “plastic equilibrium” is short for “transiently elastic, long-term equilibrium”.

There is a further subtlety that we must address here. If the polymer energy depends on both the density and the elastic strain, there are two contributions in the stress: the pressure as given by Eq. (14) and the elastic stress. Then the system may possess an equilibrium pressure even when Eq. (21) holds. However, if the density is not an independent state-variable, implying $P\equiv 0$, an equilibrium pressure needs a finite $\varDelta \equiv -u_{ll}$ to be sustained, and $u_{ij}=0$ cannot be the equilibrium condition. Rather, it is given as

$$\begin{aligned} u^*_{ij}\equiv -\varepsilon ^{e*}_{ij}=0,\quad \text {implying}\quad {\dot{\varepsilon }}^p_{ij} =-\lambda _e u_{ij}^* ~, \end{aligned}$$

(22)

the vanishing of the deviatoric part, while the trace $\varDelta$, not independent from the density, simply follows the dynamics of the density. It does not relax.

Note that the relaxation time of $\varDelta$ and $u_s$ need not be the same. If that of $\varDelta$ is especially long, it may be neglected for certain phenomena, for which the dynamics is governed by ${\dot{\varepsilon }}^p_{ij} =-\lambda _e u_{ij}^*$ alone.

When the system is crossing an inflection surface, the term $-\lambda _e u_{ij}$, in Eq. (19) is not affected, and continues to push the elastic strain towards $u_{ij}=0$.

2.4 Granular matter

GSH was set up in compliance with thermodynamics and conservation laws. Here, we discuss its structural part, necessary if one is to be consistent with the general principles of physics. In Sect. 3, a reduced complete version of GSH is presented, including a few, as simple as possible constitutive choices, which will be employed later to study the jamming and un-jamming dynamics.

Two basic pieces of physics characterize granular media: (1) They have two entropies: $s_g$ for the granular degrees of freedom and s for the much more numerous microscopic ones. (2) Depending on circumstances, granular media may be elastic or transiently elastic. Both elastic and plastic equilibria of Eqs. (21) are therefore relevant. However, note that the equilibrium (limit) state is not necessarily ever reached, neither under permanent deformation, nor under free relaxation. In the former case, the system is permanently pulled away from the equilibrium (steady state is not equal to equilibrium), while in the latter, if $T_g$ relaxes fast enough, the equilibrium cannot be realized by the other state-variables either.

Including $s_g$ as an extra state-variable, with $T_g \equiv \partial w/\partial s_g$, the equilibrium condition is $T=T_g$, obtained by maximizing $\int (s+s_g)\mathrm{d}V\approx \int s\,\mathrm{d}V$, where $s_g \ll s$ may be ignored. The equilibrium condition implies that all degrees of freedom, microscopic as well as granular ones, will eventually equilibrate with one another. Furthermore, since for particles of grain size well above molecular size, already for tiny velocity fluctuations (jiggling), one typically has $T_g \gg T$ by many orders of magnitude, $\sim 10^{10}$, see item 10. in Sect. 1.7, we may set the equilibrium granular temperature to zero,

$$\begin{aligned} T_g =T \approx 0 ~. \end{aligned}$$

(23)

In analogy to the relaxation terms discussed above, the evolution equation for $s_g$ must therefore possess a relaxation term $\sim T_g$, pushing $s_g$ towards $s_g \propto T_g=0$. This dissipation/relaxation takes place due to collisions, with rate $\sim T_g$, in the collisional gas- and fluid-like regime. In addition, analogous to the viscous heating term in the hydrodynamic theory of Newtonian fluids, which transfers kinetic energy into heat, via $\eta v_{ij}^*v_{ij}^*\equiv \eta v_s^2 \rightarrow T \textstyle {\frac{\partial }{\partial t}} s$, there is a term that transfers kinetic energy into “granular heat”, $\eta _gv_s^2\rightarrow T_g\textstyle {\frac{\partial }{\partial t}} s_g$. Therefore, assuming $\nabla _i T_g=0$, and ignoring other gradients, the evolution equation for granular energy reads

$$\begin{aligned} T_g \textstyle {\frac{\partial }{\partial t}} s_g = - \gamma T_g^2 + \eta _g v_s^2 ~, \end{aligned}$$

(24)

with coefficient $\gamma =\gamma (T_g)$ dependent on $T_g$, and the compressional viscosity neglected, like convective and diffusive terms, for the sake of brevity. To be used in the following, after division by $T_g$ and some re-writing, the evolution equation for granular temperature reads:

$$\begin{aligned} {b\rho } \textstyle {\frac{\partial }{\partial t}}T_g=-\gamma _1T_g^* T_g+\eta _1v_s^2. \end{aligned}$$

(25)

The effective rate of dissipation $T_g^* = T_g + T_e$ is discussed in more detail¹⁹ below in Sects. 3.1 and 4.

For given deviatoric (shear) strain rate, $v_s=|v_{ij}^*|=|-{\dot{\varepsilon }}_{ij}^*|$, the steady state solution is given and discussed in Sect. 4.6 in the limit cases $\gamma _0\ll \gamma _1T_g$ and $T_e \ll T_g$:

$$\begin{aligned}T_g=T_g^{(ss)} = v_s\sqrt{\frac{\eta _g}{\gamma }} \approx v_s\sqrt{\frac{\eta _1}{\gamma _1}} , \end{aligned}$$

a result known to hold in granular gases²⁰, up to moderate densities [7, 8, 116]. In this case, the system is in the rate-independent elasto-plastic regime, where the granular temperature is proportional to the strain rate. For diminishing $T_g \ll T_e$ and $\gamma _0\gg \gamma _1T_g$, we have an exponential and much faster decay, ${\frac{\partial }{\partial t}}T_g \propto -T_g$, however, also here the steady state granular temperature persists and remains relevant, as $T_g^{(e)} \approx (T_g^{(ss)})^2/T_e$, see Sect. 4.6.

Returning to the elastic strain $u_{ij}$, we note that granular media are elastic for quiescent grains, $T_g=0$, as slopes of sand-piles demonstrate. If the particles “jiggle”, $T_g\not =0$, the elastic shear strain and stress will diminish, and eventually vanish: Tapping a vessel of grains (with a finite number) long (and strong) enough results in a flattened granular surface, like in transient elasticity. Combining both conditions of Eqs. (21), the evolution equation for the elastic strain contains different types of plastic strain rates, see also Ref. [21, 107] and Eqs. (17), and (20),

$$\begin{aligned} {\dot{\varepsilon }}^p_{ij}&= {\dot{\varepsilon }}_{ij} - \textstyle {\frac{\partial }{\partial t}} \varepsilon ^e_{ij} = \lambda T_g \varepsilon ^e_{ij}+ p_{ijkl} {\dot{\varepsilon }}_{kl} + \psi _{ij} \nonumber \\&= - v_{ij} + \textstyle {\frac{\partial }{\partial t}} u_{ij} = -\lambda T_g{u _{ij}} - p_{ijkl} v_{kl} + \psi _{ij} ~, \end{aligned}$$

(26)

where the first term on the right, pushing $u_{ij}$ towards the plastic minimum $u_{ij}=0$, operates only for $T_g\not =0$, representing the fluctuation driven plastic strain rate.  

The second term represents strain-driven plastic deformations. Note that the probabilities $p_{ijkl}$ occur well within the macroscopic, elastically stable regime—involving possibly local events, on the particle scale—and will be simplified²¹ using only the respective purely isotropic and deviatoric (shear) plastic deformation probabilities, $p_v$ and $p_s$, see Sect. 4.1²². The micro-mechanical origins of these probabilities, are not addressed here, rather see Refs. [14, 18,19,20, 28, 34, 49, 129] and many more references therein. There—among other considerations—it is shown that (finite) granular systems can remain elastic for tiny strain, then have localized plastic events at larger strain with probability increasing, before (global) yield takes place with particular probabilities as cast into a meso-scale, stochastic master-equation approach, in Refs. [50, 153, 154].

The third term, the dissipative current, $\psi _{ij}$, depends on the equilibrium condition for the gradient of the elastic stress, see Refs. [47, 112], and thus vanishes for stress in equilibrium—or constant stress, for homogeneous/uniform systems in the absence of gravity—as relevant in the following sections. As discussed above, around Eq. (17), the dissipative current, $\psi _{ij}$, pushes $u_{ij}$ towards the elastic equilibrium in the energetically convex region, and away from it in the concave one, since it changes sign at the transition.

2.4.1 Dynamics at constant shear rate or stress

Equation (26), in addition to the dynamics of $T_g$, Eq. (24), render granular behavior rather more complex than the superposition of behavior from polymers and elastic media. Imposing either a constant shear rate or a constant elastic stress in a polymer melt, Eq. (19), the steady state result is the same, $v_s=\lambda _e u_s$, in either case.

This symmetry does not hold for granular media—not even for the simplest case with $T_e=0$, and $p=0$. A constant shear rate, ${\hat{v}}_s$, where the hat indicates the fact that this quantity is fixed/controlled, with the stationary solution $T_g^{(s)}={\hat{v}}_s\sqrt{\eta _1/\gamma _1}$ inserted into Eq. (26), ignoring the p-terms on the r.h.s., leads to a rate-independent evolution equation for $u_{ij}$ that possesses the hypoplastic structure [155], since $T_g$ is taking a value proportional to the absolute value of the strain rate. The steady state elastic shear strain is thus: $u_s^{(s)}=\sqrt{\gamma _1/\eta _1}/\lambda$. It accounts well for elasto-plastic motion [156], including the approach to the critical state and shear jamming [47, 48, 157, 158].

On the other hand, controlling the stress or, equivalently, holding the elastic strain, ${\hat{u}}_s$, constant and inserting the stationary limit of Eq. (26), $v_s^{(u)}=\lambda T_g {\hat{u}}_s$, into Eq. (24), yields the relaxation rate: $\gamma _c = ( \gamma _1 - \eta _1 \lambda ^2 u_s^2) = \gamma _1 [ 1 - (u_s/u_s^c)^2 ]$, negative if ${\hat{u}}_s < u_s^{c}=u_s^{(s)}=\sqrt{\gamma _1/\eta _1}/\lambda$, the case when we find $T_g$ to relax to zero, pushing the system into a static state, $v_s^{(u)} \rightarrow 0$.

The relaxation rate vanishes (i.e., the relaxation time diverges) as the stress (or elastic strain) approaches the critical value, $u_s^c$. With a further increase of $u_s$, the rate flips sign to positive above the critical value, see [47, 48], creating an ever increasing strain rate $v_s^{(u)}$. Accordingly, switching from an imposed shear rate (say during an approach to the critical state) to an imposed sub-critical stress will render the system static due to the relaxation of $T_g$, whereas a critical or super-critical stress will create $T_g$ and thus accelerate the flow, since $v_s \propto T_g$.

2.4.2 Dynamics in the concave region

Within the cone of Fig. 2, in the energetically convex region, as long as one considers only the evolution of stress close to equilibrium, the dissipative current, $\psi _{ij}={\textstyle \frac{1}{2}} \left( \nabla _i[\beta (\nabla _k\pi _{jk} {-\rho g_j}) ]+\nabla _j[\beta (\nabla _k\pi _{ik} {-\rho g_j}) ] \right) ,$ remains close to zero, see also Eq. (26) and the discussion below it. Serving to maintain stress equilibrium, it may simply be neglected. Perturbing the system by a (local) stress, $\delta \pi _{ij}$, from a static situation, in the convex, stable region, results in a relaxation of the elastic strain, due to the sign of $\psi _{ij}$. In contrast, in the concave region, because of Eq. (16), the relaxation turns into an explosion, and can drive the stress towards further, stronger non-uniformity.

This accelerates the grains, locally, leading to non-uniform velocities $v_i$ and finite strain rates, $v_{ij}\equiv -{\dot{\varepsilon }}_{ij}\not =0$. The latter serve as a source for granular heat, see Eq. (24), and create considerable $T_g$, which activates the first plastic term of Eq. (26), which relaxes the stress back into the stable, convex region. Hence, although the imposed perturbation creates a local stress response along the direction associated with the negative eigenvalue initially, it is the stress relaxation back to the convex region that dominates for finite times. If not strong/fast enough, the system will yield or un-jam dynamically. This is one way how GSH accounts for stability and un-jamming dynamics by instability, both mediated by the granular temperature

Unfortunately, including the elastic stress-gradient driven plastic strain rate renders Eq. (26) an unstable partial differential equation, the solution of which requires increased technical efforts. This is undesirable in a first, qualitative study, and an approximation scheme may prove useful. We suggest to go on neglecting the elastic dissipative terms, and to add a stress term to Eq. (24), such that $T_g$ is directly produced by an elastic stress. The balance equations for $s, s_g$, for the energetically convex region, are given as

$$\begin{aligned} T\textstyle {\frac{\partial }{\partial t}} s=\,&R=\gamma T_g^2+\beta _{ijkl}\pi _{ij}\pi _{kl}+\cdots , \end{aligned}$$

(27)

$$\begin{aligned} T_g\textstyle {\frac{\partial }{\partial t}} s_g=\,&R_g=-\gamma T_g^2+\eta _gv_{ij}v_{ij}. \end{aligned}$$

(28)

The equally permissible alternative,

$$\begin{aligned} T\textstyle {\frac{\partial }{\partial t}} s&=\gamma T_g^2+\cdots , \end{aligned}$$

(29)

$$\begin{aligned} T_g\textstyle {\frac{\partial }{\partial t}} s_g&=-\gamma T_g^2+\eta _gv_{ij}v_{ij} +{\bar{\beta }}_{ijkl}\pi _{ij}\pi _{kl}, \end{aligned}$$

(30)

was not adopted, because any static $\pi _{ij}$ would then produce $T_g$, leading to its decay. This is not observed in static granular media that can sustain finite stresses indefinitely (see sand-piles)—if not perturbed externally. Yet the reasoning is not valid outside the cone, where static stresses are not stable. Hence we combine Eq. (27) with (30), noting

$$\begin{aligned} {\bar{\beta }}_{ijkl}=0\,\,\text {inside,}\quad \text {and}\,\, \beta _{ijkl}=0\,\,\text {outside,} \end{aligned}$$

(31)

the elastically stable cone. The explicit forms for $\beta _{ijkl}$ and ${\bar{\beta }}_{ijkl}$, which carry the units of inverse stress (compliance) rate, are constitutive choices that will be discussed in the next section in some detail for $\beta _{ijkl}$, while a very simple model for ${\bar{\beta }}_{ijkl}$ will be presented in Sect. 4.9 and studied in Sect. 5.

2.5 Second law of thermodynamics

The second law of thermodynamics (the balance of thermal and granular entropy) from Eqs. (27) and (28) can be summarized as $R>0$ and $R_g+\gamma T_g^2>0$ (since both represent dissipative, irreversible processes), or combined:

$$\begin{aligned} R+R_g = (\beta _{ijkl}+ {\bar{\beta }}_{ijkl}) \pi _{ij}\pi _{kl} + \eta _gv_{ij}v_{ij} + \ldots \ge 0 ~, \end{aligned}$$

(32)

noting that the dissipation of granular energy $-\gamma T_g^2$ irreversibly enters the thermal energy, thus cancelling itself in $R+R_g$.   More general, the total production of entropy can be re-phrased [48, 107, 109, 110] as:

$$\begin{aligned} R+R_g&= \pi _{ij} {\dot{\varepsilon }}^p_{ij}+ \sigma ^D_{ij} {\dot{\varepsilon }}_{ij}{+ Y_i \left( \nabla _j \pi _{ij} - \rho g_i \right) } \ge 0 ~, \end{aligned}$$

(33)

where the dissipative displacement rate, $Y_i$, as defined above in Eq. (15), being proportional to $\nabla _k \pi _{ik}- \rho g_i$ itself, renders the last term positive. Next, more complex expressions are needed for the evolution of the elastic strain, $\varepsilon ^e_{ij}= {\dot{\varepsilon }}_{ij}- {\dot{\varepsilon }}^p_{ij}$, and the a-priori unknown viscous/dissipative stress, $\sigma ^D_{ij}$, for both of which the isotropic and deviatoric parts can—and are assumed to—evolve independently from each other. As example, where the dissipative stress and the dissipative current are not shown for the sake of brevity, inserting the constitutive relation from Eq. (26), leads to the following split-up:

$$\begin{aligned}&R+R_g \approx \pi _{ij} {\dot{\varepsilon }}^p_{ij}+ \ldots \nonumber \\&\approx \lambda _1 T_g P_\varDelta \varDelta + \lambda T_g \pi ^*_{ij} \varepsilon ^{e*}_{ij}+ \pi _{ij} \left( {p_v} {\dot{\varepsilon }}_v \delta _{ij} + {p_s} {\dot{\varepsilon }}^*_{ij} \right) + \ldots ~, \end{aligned}$$

(34)

where the dots remind us of ignored terms (all $\ge 0$).

The first and second term in Eq. (34) represent entropy production by fluctuation driven relaxation and are always positive. In general, the isotropic term can have a different coefficient, $\lambda _1 \ne \lambda$. In contrast, the third and fourth term are due to plastic (re-arrangements) driven by isotropic and deviatoric strain, respectively. They can be either positive or negative, dependent on the direction of the strain rate²³. The third term is negative for extension (${\dot{\varepsilon }}_{v}<0$), while the fourth term is negative, in particular, at strain reversal. If negative, these contributions must be compensated by positive production terms, as derived next²⁴, or the probabilities could be set to zero, as will be discussed in more detail in Sect. 4.

The general approach to construct the viscous/dissipative stress from an inserted plastic strain rate is using the Onsager matrix (also to establish time-inversion symmetry, which is not discussed here), from the appendix in Ref. [107]. After ignoring gradients of temperature and thus heat fluxes, as well as all associated terms, one can transform all tensors into eigen-value form²⁵, which also implies a signed variable $\alpha _s$²⁶. This results in only two independent invariants per state-variable tensor, ignoring the third for the sake of simplicity, yielding a $4 \times 4$ matrix form to determine plastic strains and dissipative stresses:

$$\begin{aligned}&\left( \begin{array}{c} {\dot{\varepsilon }}^p_v \\ {\dot{\varepsilon }}^p_s \\ \sigma ^D_v \\ \sigma ^D_s \end{array} \right) = {\aleph } \cdot \left( \begin{array}{c} \varDelta \\ \varepsilon ^e_s \\ {\dot{\varepsilon }}_v \\ {\dot{\varepsilon }}_s \end{array} \right) ~,~~\mathrm{with}~~ \nonumber \\&{\aleph } = \left( \begin{array}{c c c c} e_{vv} &{} e_{vs} &{} h_{vv} &{} h_{vs} \\ e_{sv} &{} e_{ss} &{} h_{sv} &{} h_{ss} \\ \alpha _s \pi _s - h_{vv} {{\mathcal{B}}}_\varDelta &{} -h_{sv} {{\mathcal{G}}}_\varDelta &{} \eta _{vv} &{} 0 \\ -h_{vs} {{\mathcal{B}}}_\varDelta &{} \alpha _1 P_\varDelta - h_{ss} {{\mathcal{G}}}_\varDelta &{} 0 &{} \eta _{ss} \end{array} \right) \nonumber \\&~ = \left( \begin{array}{c c c c} \lambda _1 T_g &{} - \alpha _1 {\dot{\varepsilon }}_s &{} {p_v} &{} {p_s} \alpha _1 \varepsilon ^e_s \\ - \alpha _s {\dot{\varepsilon }}_v &{} \lambda T_g &{} {p_v} \alpha _s \varDelta &{} {p_s} \\ \alpha _s \pi _s - {p_v} {{\mathcal{B}}}_\varDelta &{} -{p_v} \alpha _s \varDelta {{\mathcal{G}}}_\varDelta &{} \eta _v &{} 0 \\ - {p_s} \alpha _1 \varepsilon ^e_s {{\mathcal{B}}}_\varDelta &{} \alpha _1 P_\varDelta - {p_s} {{\mathcal{G}}}_\varDelta &{} 0 &{} \eta _s \end{array} \right) \end{aligned}$$

(35)

with 4-tuple vectors of the invariants of the state-variables or their conjugates (pressure $P_\varDelta = {{\mathcal{B}}}_\varDelta \varDelta$ and shear stress norm $\pi _s=\pm |\pi _{ij}| = \mathrm{sign}(\pi )|\pi _{ij}|={{\mathcal{G}}}_\varDelta \varepsilon ^e_s$), with secant moduli assumed constant in the momentary configuration, above jamming (cases below jamming, $\varDelta <0$, are briefly discussed at the end of this section).

One can interpret the diagonal (off-diagonal) terms as quantifying the dissipative currents that drive the system towards its equilibrium—of the respective (cross-coupled) state-variable. For example, $e_{ss}$ quantifies the dissipative current caused by $\varepsilon ^e_s$, driving itself to equilibrium, while $e_{vs}$ quantifies the dissipative current caused by $\varepsilon ^e_s$, driving the volumetric elastic strain, $\varepsilon ^e_v$, to equilibrium.

Other terms, like $\eta _{vv}$ ($\eta _{ss}$), quantify the volumetric (deviatoric) dissipative stresses, i.e., momentum current density, caused by isotropic (shear) strain, driving themselves to equilibrium, while cross-terms are ignored here²⁷. The off-diagonal terms are non-symmetric, e.g., $h_{vs}$ cross-couples plastic strain (dissipative current) caused by shear strain that drives volumetric elastic strain to equilibrium and, at the same time, cross-couples dissipative shear stress with isotropic elastic stress, involving the modulus ${{\mathcal{B}}}_\varDelta$²⁸. The diagonal term $-\gamma T_g$ driving granular temperature to equilibrium, represents a source term for temperature, T, and is not shown here, like all related off-diagonal terms (set to zero).

The plastic strain rates (placeholder for strain-rate minus elastic strain, which is the state-variable) are thus:

$$\begin{aligned} {\dot{\varepsilon }}^p_v = \lambda _1 T_g \varDelta - \alpha _1 \varepsilon ^e_s {\dot{\varepsilon }}_s (1-{p_s}) + {p_v} {\dot{\varepsilon }}_v \,, \end{aligned}$$

and

$$\begin{aligned} {\dot{\varepsilon }}^p_s = \lambda T_g \varepsilon ^e_s - \alpha _s \varDelta {\dot{\varepsilon }}_v (1-{p_v}) + {p_s} {\dot{\varepsilon }}_s \,, \end{aligned}$$

while the dissipative stresses are

$$\begin{aligned} \sigma ^D_v = \eta _v {\dot{\varepsilon }}_v - {p_v} P_\varDelta + \alpha _s \pi _s \varDelta (1- {p_v}) \,, \end{aligned}$$

and

$$\begin{aligned} \sigma ^D_s = \eta _s {\dot{\varepsilon }}_s - {p_s} \pi _s + \alpha _1 P_\varDelta \varepsilon ^e_s (1- {p_s}) \,, \end{aligned}$$

where the probabilities ${p_v}$ and ${p_s}$ vanish if the strain-rate is zero, i.e., they represent strain-activated dissipative stresses, different from the strain-rate activated viscous stresses, as in the first terms.

For the sake of brevity, some of the above terms are not used further on, i.e., while the $\alpha _1$-term will be used, only a placeholder is given for ${\alpha _{sv}}=\alpha _s \varDelta {\dot{\varepsilon }}_v(1-{p_v})$; similarly, for the dissipative stresses, only the first terms are used in some (numerical) solutions (even though small), while the other terms are subject to ongoing studies. The only non-classical term used is the granular energy creation, active outside the elastically stable regime, abbreviated as ${f_g} = {\bar{\beta }}_{ijkl} \pi _{ij} \pi _{kl}$, defined in subsection 2.4.2, and used below in Sect. 4.

Inserting the above expressions into Eq. (33) results in an always positive total entropy production:

$$\begin{aligned} R+R_g&= P_\varDelta {\dot{\varepsilon }}^p_v + \pi _s {\dot{\varepsilon }}^p_s + \sigma ^D_v {\dot{\varepsilon }}_v + \sigma ^D_s {\dot{\varepsilon }}_s ~\nonumber \\&= \lambda _1 T_g \varDelta P_\varDelta + \lambda T_g \varepsilon ^e_s \pi _s + \eta _v {\dot{\varepsilon }}_v^2 + \eta _s {\dot{\varepsilon }}_s^2 \nonumber ~\\&= \beta _v P_\varDelta ^2 + \beta _s (\pi _s)^2 + \eta _v {\dot{\varepsilon }}_v^2 + \eta _s {\dot{\varepsilon }}_s^2 \ge 0 \,, \end{aligned}$$

(36)

which is true by construction, since all terms are quadratic in either elastic strains (stresses) or strain rates. The first two terms are a simple constitutive choice for the more general forms in Eq. (32), with purely isotropic, $\beta _v = \lambda _1 T_g / {{\mathcal{B}}}_\varDelta$, and deviatoric, $\beta _s=\lambda T_g / {{\mathcal{G}}}_\varDelta$, compliance rates.

Below jamming, one has (per definition) no elastic stress with purely plastic deformations, with probabilities, ${p_v}={p_s}=1$, and thus only the viscous terms survive in Eq. (36). On the other hand, in the ideal elastic limit, above jamming, one has no plastic deformations, ${p_v}={p_s}=0$, so that the classical GSH shows up with only the $\lambda$-preceded relaxation terms surviving (and the $\alpha$-preceded terms in plastic strains and dissipative stresses cancelling each other).

The question how to split up R and $R_g$, as well as related questions about the discrete nature of plastic (re-arrangement) events, and the principle of time-reversal symmetry are subject of ongoing research [21, 159].

3 Granular solid hydrodynamics (GSH)

As review, GSH is a continuum mechanical theory for granular media, set up in compliance with thermodynamics and conservation laws. GSH possesses the state-variables:

(i):

density, $\rho$, or volume fraction, $\phi =\rho /\rho _p$,

(ii):

momentum density, $\rho v_i=0$, neglected here,

(iii):

elastic isotropic strain $\varDelta =-u_{ll}=\varepsilon ^e_v=\log \left( \rho /\rho _J \right)$,

(iv):

elastic deviatoric (shear) strain $u_s=\sqrt{2 J^{u}_2}$,

(v):

granular temperature $T_G \propto T_g^2$, and

(vi):

temperature T, not used in the following, conventions/nomenclature are given in Sect. 1.7.

The GSH used here reduces to various different, more classical theories, in the respective limits—when set appropriately, as was shown in: Refs. [156] for hypoplasticity, [160] for the $\mu (I)$-rheology, and [47] for fluidity, etc. The question is now if it is possible to catch the complex phenomenology at yielding, jamming, un-jamming, elasticity and loss of elasticity with a simple model that only knows about four state-variables: $\rho$, $\varDelta$, $u_s$, and $T_g$.

For the sake of completeness, we first recollect the more complex, more complete classical GSH, as published in the previous years, in Sect. 3.1, before we reduce GSH to an over-simplified minimal model in Sect. 3.2, which will allow for a better understanding of the structure of GSH. Note that the nomenclature of classical GSH is applied in Sect. 3.1, whereas we switch to the positive compressive strain convention and nomenclature in Sect. 3.2.

3.1 About classical GSH

The complete equations of GSH may be found in Refs. [47, 112], a simplified version in Ref. [48], from which we boil down to a minimalistic version in Sect. 3.2, ignoring not only momentum density and gradients, but also the density dependence of most transport coefficients and parameters, since those represent top-down constitutive assumptions, rather than basic (qualitative, bottom-up) theory. First, we discuss a few complications in the classical GSH nomenclature, that are not necessary for our present focus, but will become important if a more quantitative model is the goal, so that we keep them as reference for the sake of completeness.

3.1.1 The classical GSH constitutive model

The energy density has a granular thermal and an elastic part:

$$\begin{aligned} w&=w_T+w_\varDelta , \qquad w_T={s_g^2}/{(2\rho b)} ~, \nonumber \\ w_\varDelta&=\sqrt{\varDelta }[2 {B}(\rho ) \varDelta ^{2}/5+ G(\rho )u_s^2],\quad {B},G>0 ~.\end{aligned}$$

(37)

This represents the first constitutive assumption at the core of classical GSH. In the following, we drop the explicit $\rho$-dependence of B and G for convenience, but keep in mind and used it whenever needed. (In previous GSH-publications, G was denoted as ${{\mathcal{A}}}$.). The elastic stresses are defined as the derivatives of w with respect to the elastic strain $u_{ij}$:

$$\begin{aligned} \pi _{ij}&\equiv -{\partial w}/{\partial u_{ij}} = P_\varDelta \delta _{ij} - \pi _s u^*_{ij}/u_s ~, \end{aligned}$$

(38)

$$\begin{aligned} P_\varDelta&=\sqrt{\varDelta }({B}\varDelta +G{u_s^2}/{2\varDelta }),\quad \pi _s=2G \sqrt{\varDelta }\, u_s ~, \end{aligned}$$

(39)

$$\begin{aligned} 4&P_\varDelta /{\pi _s}=2({B}/G)(\varDelta /u_s)+{u_s}/{\varDelta } ~, \end{aligned}$$

(40)

with $P_\varDelta \equiv \pi _{\ell \ell }/3,$ which represent no constitutive assumptions, but are just a consequence of Eq. (37). Like the elastic stress, being conjugate to the elastic strain, the granular temperature is conjugate to the granular entropy, which allows to define the thermal pressure, $P_T$, as the derivative of the granular thermal free energy with respect to volume, at constant $s_g$ or $T_g$, as:

$$\begin{aligned} T_g&\equiv {\partial w_T}/{\partial s_g}={s_g}/{\rho b} ~, \quad \rightarrow \quad w_T={\rho b T_g^2}/{2} ~, \end{aligned}$$

(41)

$$\begin{aligned} P_T&=-\left. \frac{\partial [ w_T/\rho ]}{\partial (1/\rho )}\right| _{s_g} \equiv - \left. \frac{\partial [(w_T-T_g s_g)/\rho ]}{\partial [1/\rho ]}\right| _{T_g} \nonumber \\&= \frac{T_g^2}{2}\frac{\partial b}{\partial (1/\rho )} = \frac{T_g^2}{2}\frac{\partial b}{\partial \rho }\frac{1}{(-1/\rho ^2)} = - \frac{\rho ^2T_g^2}{2}\frac{\partial b}{\partial \rho } ~, \end{aligned}$$

(42)

where we note that the granular entropy is not needed, replaced by the density dependent (positive) function $b=b(\rho )$, decaying with density, $\partial b/\partial \rho < 0$.

The elastic energy $w_\varDelta$ has been tested for: (1) static stress distributions in silos, sand piles, point loads on a granular sheet [161]; (2) incremental stress-strain relations from varying static stresses [162]; (3) propagation of elastic waves at varying stresses [163].

As already observed in Ref. [112], $w_\varDelta$ is convex if:

$$\begin{aligned} u_s/\varDelta&\le \sqrt{2{B}/G} =:g_e, \text { or } \nonumber \\ \pi _s / P_\varDelta&\le \sqrt{2G/{B}}=2/g_e ~. \end{aligned}$$

(43)

For more details see Sect. 3.4. Because the macroscopic friction, or yield limit, $\mu _0 \sim \sqrt{2G/{B}}$, is observed to be not (or only weakly) density dependent, in steady state, at least for cohesionless granular media, the next constitutive model assumption used is: $G/{B}=const.$, and

$$\begin{aligned} {B}={B}_0 \left[ ({\rho -{\bar{\rho }}})/({\rho _{cp}-\rho })\right] ^{0.15}, \end{aligned}$$

(44)

where ${B}_0>0$ is a constant, and ${\bar{\rho }}\equiv \frac{1}{9}(20\rho _{\ell p}-11\rho _{cp})$, with $\rho _{cp}-\rho _{\ell p}\approx \rho _{\ell p} -{\bar{\rho }}$. ($\rho _{cp}$ is the random-close packing density, the highest one at which grains may remain uncompressed, $\rho _{\ell p}$ is the random-loose packing density, the lowest one at which grains may stay static.) The expression for B was empirically constructed to account for three granular characteristics: (1) It provides concavity, for any density smaller than $\rho < \rho _{\ell p}$, and convexity between $\rho _{\ell p}$ and $\rho _{cp}$, ensuring the stability of elastic solutions in this region. (2) The density dependence of sound velocities, c (as measured by Hardin and Richart [164]), is well approximated by $c=\sqrt{{{\mathcal{B}}}/\rho } \approx \sqrt{B\varDelta ^{1/2}/\rho }$. (3) The slow divergence at $\rho _{cp}$ mimics the fact that the system is much stiffer for $\rho =\rho _{cp}$ than at loose packing $B(\rho = \rho _{\ell p})$. Comparing these constitutive assumptions for G and B with particle simulations is subject of ongoing work²⁹.

Finally, in 3D, the function b was chosen [47] as:

$$\begin{aligned} b={b_1}/\rho +b_0\left[ 1-{\rho }/{\rho _{cp}}\right] ^a, \end{aligned}$$

(45)

with another small power law, $a\approx 0.1$, such that $P_T \approx w_T$ for $\rho \rightarrow 0$, and $P_T \approx w_T/(1-\rho /\rho _{cp})$ for $\rho \rightarrow \rho _{cp}$, limits which reduce b to first or second term, respectively.

The thermal pressure, explicitly given as:

$$\begin{aligned} P_T =\frac{\rho T_g^2}{2} \left[ \frac{b_1}{\rho }+\frac{\rho }{\rho _{cp}}\frac{ab_0 }{(1-\rho /\rho _{cp})^{1-a}}\right] =: \frac{{\mathcal{D}}}{2} \rho T_g^2 G_p ~, \end{aligned}$$

(46)

defines the (positive, dimensionless) abbreviation

$$\begin{aligned} G_p=G_p(\rho ) :=- \frac{\rho \, \partial b}{2\, \partial \rho } = - \frac{\phi \, \partial b}{2 \, \partial \phi } = G_p(\phi ) \, \end{aligned}$$

for the term in brackets, as set to constant in the following sections, a good approximation only for low densities, where the ideal gas pressure, $P_T=\textstyle {\frac{{\mathcal{D}}}{2}}\rho T_g^2$, with $G_p \approx 1$, defines the coefficient $b_1={{\mathcal{D}}} \rho _p$, so that $b=b_1/(2\rho ) = {{\mathcal{D}}}/(2\phi )$ .

In the regime of standard kinetic theory being valid, and with $T_g$ carrying units of diameter, d, and rate, i.e., inverse time, one has a different, analytically known $G_{\mathrm{SKT}}=\left[ 1+({{\mathcal{D}}}-1) (1+r) \phi g_2(\phi ) \right]$, with restitution coefficient r and pair correlation at contact, $g_2(\phi )$.³⁰ For more details, in particular for the other transport coefficients, see Refs. [8, 116, 118, 166].

Adding some speculative connection to other works, the function b is qualitatively similar to the density dependence, $F=gd/\delta v$, of the scaled fluidity, g, as reported in Ref. [18]. However, note that the fluidity is based on shear stress and shear strain only, whereas the thermal stress, $P_T/G_p = \rho T_g^2 = \rho (\delta v/d)^2 \sim \rho (g/F)^2$ is also defined for isotropic deformations, i.e., non-sheared systems. Whether g and $F(\rho )$ are truly related with $T_g$ and $G_p(\rho )$, and how exactly, is subject of ongoing research and goes beyond the scope of this paper.

3.1.2 The evolution equations

For completeness, we specify the evolution equations in the classical GSH nomenclature, where we note the sign conventions $\varDelta =\varepsilon ^e_v$, $u_{ij}=-\varepsilon ^e_{ij}$ and $v_{ij}=-{\dot{\varepsilon }}_{ij}$, see Sect. 1.7. For the elastic strain one has:

$$\begin{aligned} \textstyle {\frac{\partial }{\partial t}}&u^*_{ij}=v^*_{ij}-\lambda T_gu^*_{ij}, \end{aligned}$$

(47)

$$\begin{aligned} \textstyle {\frac{\partial }{\partial t}}&\varDelta +v_{\ell \ell }=\alpha _1u^*_{ij}v^*_{ij}-\lambda _1 T_g\varDelta , \end{aligned}$$

(48)

with $\alpha _1$ as an off-diagonal Onsager coefficient, see Sect. 2.5, accounting for Reynolds dilatancy.

Mass and momentum conservation read:

$$\begin{aligned} \textstyle {\frac{\partial }{\partial t}}&\rho +\nabla _i(\rho v_i)=0, \end{aligned}$$

(49)

$$\begin{aligned} \textstyle {\frac{\partial }{\partial t}}&(\rho v_i)+\nabla _j(\sigma _{ij}+\rho v_iv_j) = \rho g_i, \end{aligned}$$

(50)

with the total stress: $\sigma _{ij}=\pi _{ij}+P_T\delta _{ij}-\eta _1T_g v^*_{ij}$, with viscosity, $\eta _g=\eta _1 T_g$.

Finally, the evolution equation for $T_g$, with b as given by Eq. (41) and $T_g^*\equiv T_g+\gamma _0/\gamma _1=:T_g+T_e$, is given by Eq. (25).

The coefficients $\alpha _1,\gamma _0,\gamma _1,\eta _1$, and $\rho b$ are all functions of the state variables, especially the density, which would require many more constitutive assumptions, so that they are over-simplified and taken as constants in the following sections. Alternative energy densities are compared next.

3.2 Minimal GSH type model for a material point

At the core of GSH, assuming a homogeneous representative volume, without convection, $\rho v_i = 0$ and gradients, $\nabla _i (...) = 0$, one has a postulated energy density,

$$\begin{aligned} w = w_e + w_{T} ~, \end{aligned}$$

(51)

with an elastic and a dynamic, kinetic/granular contribution. The total stress is thus not an independent (state) variable, but can be abbreviated as

$$\begin{aligned} \sigma _{ij}= & {} \pi _{ij} + P_T \delta _{ij} + \sigma _{ij}^{\mathrm{visc.}} \nonumber \\=: & {} P_\varDelta \delta _{ij} + \pi ^*_{ij} + \rho T_g^2 G_p \delta _{ij} + \chi {\dot{\varepsilon }}_{v}\delta _{ij} + \eta {{\dot{\varepsilon }}}^*_{ij}~, \end{aligned}$$

(52)

where the five terms represent isotropic and deviatoric elastic stresses, kinetic/granular stress (with an over-simplified $G_p=1$, which should depend—at least—on density, see Eq. (46)), and isotropic (v=volumetric) and deviatoric (s=shear) viscous stresses, with viscosities $\chi =\eta _v$ and $\eta =\eta _1=\eta _s$, respectively, where the subscript 1 was used above. Additional dissipative stresses are derived and shown in Sect. 2.5, but are mostly ignored further on.

Now, a few versions of the energy density are discussed, before elastic energy stability is considered in the next Sect. 3.4.

3.2.1 The linear elastic energy

For completeness, in the (too) simple case of a linear elastic energy density:

$$\begin{aligned} w_{lin}=\left( (1/2) B_{lin} \varDelta ^2 + G_{lin} u_s^2 \right) \quad \mathrm{if}~ \varDelta >0 ~, \end{aligned}$$

(53)

and $w_{lin}=0 ~\mathrm{if}~ \varDelta \le 0$, with $u_s^2=\varepsilon ^{e*}_{ij}\varepsilon ^{e*}_{ij}$, one can easily derive the elastic stress $\pi _{ij}=\partial w/\partial u_{ij}$. The parameters $B_{lin}$, $G_{lin}$ carry the units of stress, while their possible dependencies on other state-variables (like density) are ignored here.

The isotropic elastic pressure (defined in ${{\mathcal{D}}}$ dimensions) is:

$$\begin{aligned} P_\varDelta ^{lin} = \frac{\pi _{ll}}{{{\mathcal{D}}}} = \frac{\partial w_{lin}}{\partial \varDelta } = B_{lin} \varDelta ~, \end{aligned}$$

and the deviatoric elastic stress is:

$$\begin{aligned} {\pi ^*_{ij}}^{lin} := \frac{\partial w_e}{\partial \varepsilon ^{e*}_{ij}} = 2 G_{lin} \varepsilon ^{e*}_{ij}\, . \end{aligned}$$

Further differentiation yields the (constant) moduli: ${{\mathcal{B}}}_{lin}=B_{lin}$, ${{\mathcal{G}}}_{lin}=2G_{lin}$, and no anisotropy ${{\mathcal{A}}}_{lin}=0$, which is surely too simple for granular matter.

The anisotropic linear elastic energy density:

$$\begin{aligned} w_{A}=\left( (1/2) B_{lin} \varDelta ^2 + A_{lin} \varDelta \varepsilon ^{e*}_{ij}{\hat{\varepsilon }}^e_{ij} + G_{lin} u_s^2 \right) ~, \end{aligned}$$

(54)

if $\varDelta >0$ with ${\hat{\varepsilon }}^e_{ij}=\varepsilon ^{e*}_{ij}/|\varepsilon ^{e*}_{ij}|$, as proposed in Refs. [91, 125, 167]. yields:

$$\begin{aligned} P_\varDelta ^{A} = \frac{\pi _{ll}}{{{\mathcal{D}}}} = \frac{\partial w_A}{\partial \Delta}= B_{lin} \varDelta + A_{lin} \varepsilon ^{e*}_{ij}{\hat{\varepsilon }}^e_{ij}~, \end{aligned}$$

and the deviatoric elastic stress:

$$\begin{aligned} {\pi ^*_{ij}}^{A} = \frac{\partial w_e}{\partial \varepsilon ^{e*}_{ij}} = 2 G_{lin} \varepsilon ^{e*}_{ij}+ A_{lin} \varDelta {\hat{\varepsilon }}^e_{ij}\, . \end{aligned}$$

Further differentiation yields the (constant) moduli: ${{\mathcal{B}}}_{A}=B_{lin}$, ${{\mathcal{G}}}_{A}=2G_{lin}$, and anisotropy ${{\mathcal{A}}}_{A}=A_{lin} {\hat{\varepsilon }}^e_{ij}$, which is the simplest possible anisotropic elastic model, with cross-coupling between isotropic and deviatoric elastic strains and stresses, as compared to particle simulations and discussed in detail in Refs. [91, 125, 167]. However, the anisotropy modulus is not constant and thus requires an evolution or state equation by itself, e.g., $A_{lin}/B_{lin}=F_{dev}$, with deviatoric fabric, $F_{dev}$, as observed from 3D particle simulations in Refs. [31, 125].

3.2.2 The non-linear (Hertzian) elastic energy

One can derive the elastic stress $\pi _{ij}=\partial w/\partial u_{ij}$, from the simplest (non-linear) elastic energy density:

$$\begin{aligned} w_e=\sqrt{\varDelta } \left( (2/5) B \varDelta ^2 + G u_s^2 \right) \quad \mathrm{if}~ \varDelta >0 ~, \end{aligned}$$

(55)

and $w_e=0 ~\mathrm{if}~ \varDelta \le 0$, with $u_s^2=\varepsilon ^{e*}_{ij}\varepsilon ^{e*}_{ij}$, and $B=B(\rho )$, $G=G(\rho )$ carrying the units of stress, while their possible functional dependencies on other state-variables (like density) are not carried along in the rest of this study. Two choices (out of many more) of the density dependence of the energy density (and its coefficients) are discussed below, where appropriate, but in other cases the density dependence is avoided completely in order to learn what the effect of this simplifaction would be. The isotropic elastic pressure (defined in ${{\mathcal{D}}}$ dimensions) is:

$$\begin{aligned} P_\varDelta = \frac{\pi _{ll}}{{{\mathcal{D}}}} = \frac{\partial w_e}{\partial \varepsilon ^e_{v}} = B \varDelta ^{3/2} + {\frac{1}{2}} Gu_s^2\varDelta ^{-1/2} =: {{\mathcal{B}}}_\varDelta \varDelta \, , \end{aligned}$$

and the deviatoric elastic stress is:

$$\begin{aligned} \pi ^*_{ij} := \frac{\partial w_e}{\partial \Delta} = 2 G \varDelta ^{1/2} \varepsilon ^{e*}_{ij}=: {{\mathcal{G}}}_\varDelta \varepsilon ^{e*}_{ij}\, , \end{aligned}$$

implicitly defining the ($\varDelta$-dependent) bulk and shear secant moduli ${{\mathcal{B}}}_\varDelta$ and ${{\mathcal{G}}}_\varDelta$, which mimic a linear $\varDelta$- or $\varepsilon ^{e*}_{ij}$-dependence of isotropic or deviatoric stress, respectively, not to be confused with the (true) tangent moduli:

${{\mathcal{B}}}= B \varDelta ^{1/2} \left[ (3/2) - (1/4) (G/B) (u_s / \varDelta )^2 \right] \ne {{\mathcal{B}}}_\varDelta$,

${{\mathcal{G}}}=2G\varDelta ^{1/2} = {{\mathcal{G}}}_\varDelta$, and ${{\mathcal{A}}}_{ij}=G\varDelta ^{1/2} (u_s/\varDelta ) {\hat{\varepsilon }}^e_{ij}$, where the tensor nature of ${{\mathcal{A}}}$ is often dropped.

In absence of deviatoric elastic strain, $u_s=0$, using the proportionality of pressure, $P_\varDelta \propto \varDelta ^{3/2}$, this results in a pressure dependence of the moduli

$$\begin{aligned} {{\mathcal{B}}} \propto {{\mathcal{G}}} \propto \varDelta ^{1/2} \propto P_\varDelta ^{1/3} ~. \end{aligned}$$

The notation details and alternative definitions of the state-variables $\varepsilon ^e_{v}=\varDelta$ and $u_s = |\varepsilon ^{e*}_{ij}|=|-u^*_{ij}|$ are given in Sect. 1.7.

3.2.3 The granular linear elastic energy

From particle simulations, using the linear contact model, see Refs. [49, 125, 168, 169] and references therein, the (linear) elastic energy density is complemented by a pre-factor, dependent (non-linearly) on the coordination number

$$\begin{aligned} C:=C(\phi ,\phi _J)=C(\varDelta )=C_0+C_1 \varDelta ^{\alpha _C} ~, \end{aligned}$$

(56)

with positive constants³¹ , see Sect. 6, so that:

$$\begin{aligned} w_C= \phi C \, \textstyle {\frac{c(\varDelta )}{2}} B_C \varDelta ^2 + \phi C_2 G_C \varDelta u_s^2 \,, ~ \mathrm{if}~ \varDelta >0 ~, \end{aligned}$$

(57)

and $w_C=0,~\mathrm{if}~ \varDelta \le 0$, with $u_s^2=\varepsilon ^{e*}_{ij}\varepsilon ^{e*}_{ij}$, and $B_C$, $G_C$ carrying the units of stress, while their possible dependencies on other state-variables are ignored in the rest of this study; density-dependent coefficients are discussed in the context of the Hertzian energy density. The nonlinear function

$$\begin{aligned} c(\varDelta )=1-\textstyle {\frac{1}{5}\,\frac{C_1}{C_0} \, \varDelta ^{\alpha _C}} \,, \end{aligned}$$

is empirically chosen—to leading order—such that elastic pressure is proportional to $\phi C$ and dimensionless functions proportional to powers of elastic strain, 0, 1, and higher, i.e., $[1+{{\mathcal{O}}}(\varDelta ) + \ldots ]$, constructed to remove the lowest order non-linearity $\propto \varDelta ^{\alpha _C}$, for $\alpha _C=1/2$³². The shear contribution to elastic energy is inspired by reasonable agreement with experimental data [21], and involves an additional coefficient $C_2$. Assuming an ideally elastic system, i.e., $\partial \phi /\partial \varDelta =\phi$, the isotropic elastic pressure becomes:

$$\begin{aligned} P^C_\varDelta&= \frac{\partial w_C}{\partial \varDelta } \nonumber \\&= \phi B_C \varDelta \left[ \, C c + \textstyle {\frac{1}{2}} (Cc+(Cc)') \varDelta \right] + \phi C_2 G_C u_s^2 \left[ 1+\varDelta \right] \nonumber \\&= \phi C B_C \varDelta \left[ 1 + \textstyle \frac{\varDelta }{2} \left( 1 - \textstyle {\frac{6}{10}} (\textstyle {\frac{C_1}{C_0}})^2 \right) + \textstyle {\frac{1}{10}} \textstyle {\frac{C_1}{C_0}} \varDelta ^{3/2} \right] \nonumber \\&~~~~ + \phi C_1 B_C \textstyle {\frac{3}{10}} (\textstyle {\frac{C_1}{C_0}})^2 \varDelta ^{5/2} + \phi C_2 G_C {u_s^2} \left[ 1+\varDelta \right] \nonumber \\&\approx \phi C B_C \varDelta + \phi C_2 G_C {u_s^2} + \ldots ~~\mathrm{for}~\varDelta \ll 1 \, , \end{aligned}$$

(58)

and the deviatoric elastic granular stress is:

$$\begin{aligned} {\pi ^*_{ij}}^C = \frac{\partial w_C}{\partial \varepsilon ^{e*}_{ij}} = 2 \phi C_2 G_C \varDelta \varepsilon ^{e*}_{ij}\, , \end{aligned}$$

(59)

qualitatively different from the Hertzian type energy density. The tangent moduli are thus:

$$\begin{aligned} {{\mathcal{B}}}_C&= \phi B_C \left\{ C + \varDelta ^{1/2} \textstyle {\frac{C_1}{2}} + 2 \varDelta (C_0-\textstyle {\frac{3 C_1^2}{10 C_0}}) + 2 \varDelta ^{3/2} C_1 \right. \nonumber ~\\&\left. + \textstyle {\frac{1}{2}} \varDelta ^2 (C_0-\textstyle {\frac{6 C_1^2}{5 C_0}}) + \textstyle {\frac{2}{5}} \varDelta ^{5/2} (C_0-\textstyle {\frac{6 C_1^2}{5 C_0}}) - \textstyle {\frac{1}{10}} \varDelta ^3 \textstyle {\frac{C_1^2}{C_0}} \right\} \nonumber ~\\&+ 2 \phi C_2 G_C {u_s^2} [ 1+\varDelta /2 ] \nonumber ~\\&\approx \phi B_C ( C_0 + \textstyle {\frac{3 C_1}{2}} \varDelta ^{1/2} ) + 2 \phi C_2 G_C {u_s^2} \, , \mathrm{~ for ~ } \varDelta \ll 1 \nonumber ~\\ {{\mathcal{G}}}_C&= 2 \phi C_2 G_C \varDelta \, , \mathrm{~ and ~ } \nonumber ~\\ {{\mathcal{A}}}_C&= 2 \phi C_2 G_C u_s (1+\varDelta ) {\hat{\varepsilon }}^e_{ij} ~, \end{aligned}$$

(60)

where the tensor nature of ${{\mathcal{A}}}_C$, the unit tensor, ${\hat{\varepsilon }}^e_{ij}$, is mostly ignored in the following. In absence of deviatoric elastic strain, $u_s=0$, and $\varDelta \ll 1$, using the pressure, $P_\varDelta /(\phi C B_C) \approx \varDelta$, results in a pressure dependence of the moduli ${{\mathcal{B}}}_C \propto P_\varDelta ^0$, and ${{\mathcal{G}}}_C \propto P_\varDelta$, or ${{\mathcal{G}}}_C/{{\mathcal{B}}}_C \propto P_\varDelta$. For small $\varDelta$ this results in ${{\mathcal{G}}}_C/{{\mathcal{B}}}_C \propto \varDelta (1-\textstyle \frac{C_1}{2C_0}\varDelta ^{1/2})$, i.e., the shear modulus decreases with increasing compression, relative to the bulk modulus, as is also observed from particle simulations with a linear contact model [49, 125], see Sect. 3.5.

3.2.4 Granular Hertzian energy density

The combination (superposition) of the two previous subsections, i.e., non-linear contacts combined with the granular (coordination number dependent) energy,

$$\begin{aligned} w_1= \phi \left( \textstyle {\frac{2}{5}} C B_C \varDelta ^{5/2} + C_2 G_C \varDelta u_s^2 \right) ~ \mathrm{if}~ \varDelta >0 ~, \end{aligned}$$

(61)

is quite similar (different only in its dependence on $\phi$ and C) to the energy density proposed in Ref. [21], but goes beyond the scope of this study and will be discussed elsewhere.

3.3 Simplest GSH equations and discussion

For a material point, in absence of gradients, using $\partial _t \sim \partial /\partial t \sim d/dt$, the evolution of density with strain rate:

$$\begin{aligned} \partial _t \rho = \rho {\dot{\varepsilon }}_{v} \end{aligned}$$

(62)

has no free parameters. Here, positive strain rate corresponds to compression and negative to extension, i.e., density increase and decrease, respectively; density can also be seen as the volume fraction, related to each other by the (constant) material density, i.e., $\phi = \rho /\rho _p$. Later, in Sect. 5, units will be chosen explicitly, such that $\rho _p=1$, so that $\phi =\rho$, as implied from now on.

In the evolution equation for the isotropic elastic strain:

$$\begin{aligned} \partial _t \varDelta = {\dot{\varepsilon }}_{v}- \lambda _1 T_g \varDelta + \alpha _1 \varepsilon ^{e*}_{ij}{{\dot{\varepsilon }}}^*_{ij} \end{aligned}$$

(63)

the first term couples elastic and total strain together, while the second term is relaxing $\varDelta$ towards zero³³—in case of finite $T_g$, with rate $\lambda _1 T_g$. The third term can be positive (or negative, e.g., at strain reversal³⁴ ), and thus works against (or with) the relaxation term.

The third equation defines the evolution of the deviatoric (shear) elastic strain

$$\begin{aligned} \partial _t \varepsilon ^{e*}_{ij}= {{\dot{\varepsilon }}}^*_{ij}- \lambda T_g \varepsilon ^{e*}_{ij}+ {\alpha _{sv}} ~, \end{aligned}$$

(64)

where the first term creates deviatoric elastic strain, co-linearly with the strain rate, while the second term relaxes the deviatoric elastic strain, with rate $\lambda T_g$. A third (dilatancy) term, ${\alpha _{sv}}$, analogous to the third term in Eq. (63), is permitted by the Onsager relation, and was previously added for symmetry in Refs. [47, 48, 125], as discussed in Sect. 2.5, and used in Sect. 4, but not discussed here.

The fourth equation represents the evolution of the granular temperature

$$\begin{aligned} \partial _t T_g= & {} - R_T T_g {T_g^*} + f_T({\dot{\varepsilon }}_{ij}) \nonumber \\=\, & {} R_{T0} \left[ - (1-r^2) T_g {T_g^*} + f_s^2 {{\dot{\varepsilon }}}^*_{ij}{{\dot{\varepsilon }}}^*_{ij}+ f_v^2 {\dot{\varepsilon }}_{v}{\dot{\varepsilon }}_{v}\right] \end{aligned}$$

(65)

with ${T_g^*}=T_g+{T_e}$, as specified in Sect. 4, and the abbreviation for the dissipation rate, $R_T = \gamma _1/(\rho b) = R_{T0} (1-r^2)$, proportional to the energy dissipation factor $(1-r^2)$, where r is the (effective) restitution coefficient. The energy creation terms are condensed into the tensor function $f_T({\dot{\varepsilon }}_{ij})$, independent on r, so that one could separate them into two energy creation rates, $R_{T0} f_s^2 = \eta _s/(\rho b)$ and $R_{T0} f_v^2=\eta _v/(\rho b)$, for shear and volumetric strain rates, respectively, with further terms from Sect. 2.5 ignored here.

3.4 Minimal elastic model with two variables

One could decompose the elastic stress and strain tensors into invariants (and their orientations). Under the assumption of fixed and co-linear tensor-eigensystems, and ignoring the third invariant for the sake of brevity, what remains are the isotropic and deviatoric stresses, $\sigma _\alpha = \{ P_\varDelta ,\pi _s = \pi ^*_s \}$, and elastic strains, $u_\alpha =\{ \varDelta , u_s = u^*_s \}$, each as 2-tuple vectors, denoted by Greek indices. This provides the criteria for energy minima:

$$\begin{aligned} \delta ^2 w=-\delta \pi _{ij}\delta u_{ij} = \delta \pi _{\alpha }\delta u_{\alpha } = \frac{\partial \pi _{\alpha }}{\partial u_{\beta }}\delta u_{\alpha }\delta u_{\beta }>0. \end{aligned}$$

(66)

Using the (positive) invariants yields the simple 2 × 2 Hessian matrix (for second order elastic work):

$$\begin{aligned} \frac{\partial^{2}w_{e}}{\partial u_{\alpha }\partial u_{\beta }} = \frac{\partial \pi _{\alpha }}{\partial u_{\beta }}= & {} \left( \begin{array}{c c} \partial P_\varDelta /\partial \varDelta &{} \partial P_\varDelta /\partial u_s \nonumber \\ \partial \pi _s/\partial \varDelta &{} \partial \pi _s/\partial u_s \end{array} \right) \\=: & {} \left( \begin{array}{c c} {{\mathcal{B}}} &{} {{\mathcal{A}}} \\ {{\mathcal{A}}} &{} {{\mathcal{G}}} \end{array} \right) = {\bf C} ~. \end{aligned}$$

(67)

If it has only positive eigenvalues, the (elastic) energy $w_{e}$ is a convex function of the elastic strain-invariants $\varDelta$ and $u_{s}$. With other words, the elastic stability criterion is $\det ({\bf C}) = {{\mathcal{BG}}} - {{\mathcal{A}}}^{2} > 0$, where ${{\mathcal{A}}}$ is a scalar in the rest of this subsection.

3.4.1 Eigen-values and -vectors at elastic instability

First, we compute the eigen-values and -vectors from the matrix $\mathbf {C}$, before we introduce constitutive assumptions about the energy density and discuss those, separately, in the next sub-subsections.

Basic linear algebra yields the two eigen-values, $C_{1,0} = ({{\mathcal{B}}} + {{\mathcal{G}}})/2 \pm \sqrt{({{\mathcal{B}}} - {{\mathcal{G}}})^2/4 + {{\mathcal{A}}}^2}$, as solution of the quadratic equation $0 = ({{\mathcal{B}}}-C)({{\mathcal{G}}}-C)-{{\mathcal{A}}}^2 = C^2 - C ({{\mathcal{B}}} + {{\mathcal{G}}}) + {{\mathcal{B}}}{{\mathcal{G}}} - {{\mathcal{A}}}^2$, with $C_1={{\mathcal{B}}} + {{\mathcal{G}}}$ and $C_0=0$, at the point of instability, where ${{\mathcal{B}}}{{\mathcal{G}}}={{\mathcal{A}}}^2$.

Using $C_1$, and ${{\mathcal{A}}}=\sqrt{{{\mathcal{G}}}{{\mathcal{B}}}}$, with the two equations $- {{\mathcal{G}}} {\hat{n}}^{(1)}_1 + {{\mathcal{A}}} {\hat{n}}^{(1)}_2 = 0$ and ${{\mathcal{A}}} {\hat{n}}^{(1)}_1 - {{\mathcal{B}}} {\hat{n}}^{(1)}_2 = 0$, results in the corresponding eigen-vector (with ${\hat{n}}^{(1)}_2 = {\hat{n}}^{(1)}_1 {{\mathcal{G}}}/{{\mathcal{A}}} = {\hat{n}}^{(1)}_1 {{\mathcal{A}}}/{{\mathcal{B}}} = {\hat{n}}^{(1)}_1 \sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}}$), which defines the “direction” (in elastic strain invariants) of maximal stability: ${\hat{n}}^{(1)} = \pm (1,\sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}}) / \sqrt{1+{{\mathcal{G}}}/{{\mathcal{B}}}}$³⁵.

Using $C_0=0$, and ${{\mathcal{A}}}=\sqrt{{{\mathcal{G}}}{{\mathcal{B}}}}$, with the two equations ${{\mathcal{B}}} {\hat{n}}^{(0)}_1 + {{\mathcal{A}}} {\hat{n}}^{(0)}_2 = 0$ and ${{\mathcal{A}}} {\hat{n}}^{(0)}_1 + {{\mathcal{G}}} {\hat{n}}^{(0)}_2 = 0$, results in the corresponding eigen-vector (with ${\hat{n}}^{(0)}_2 = - {\hat{n}}^{(0)}_1 {{\mathcal{B}}}/{{\mathcal{A}}} = - {\hat{n}}^{(0)}_1 {{\mathcal{A}}}/{{\mathcal{G}}} = - {\hat{n}}^{(0)}_1 \sqrt{{{\mathcal{B}}}/{{\mathcal{G}}}}$), which gives the “direction” of instability (in the space of elastic strain-invariants): ${\hat{n}}^{(0)} = \pm (-\sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}},1) / \sqrt{1+{{\mathcal{G}}}/{{\mathcal{B}}}}$, perpendicular to the direction of maximal stability. Note the special role the ratios of moduli take in this analysis.

More explicitly, considering elastic energy, incremental changes in the elastic strain space, in directions ${\hat{n}}^{(0)}$, i.e., $\delta u^{(0)}_\alpha = (\delta \varDelta ^{(0)},\delta u^{(0)}_s) = \delta \varepsilon ^e \, {\hat{n}}^{(0)}_\alpha$, at the point of elastic instability, can be done without change of elastic stress, $\delta \pi ^{(0)}_\alpha =0$, and energy, $\delta ^2 w^{(0)} = ( \delta \varepsilon ^e )^2 {\hat{n}}^{(0)}_\alpha {\hat{n}}^{(0)}_\beta C_{\alpha \beta } = 0$. Such increments are thus permitted from energy/thermodynamic arguments; for examples, see Fig. 4. With other words, any other elastic strain increment will require energy; for further energy considerations, see also Refs. [21, 44, 106, 107] and references therein.

3.4.2 GSH with Hertzian type elastic instability

In the case of a Hertzian type elastic energy density, $w_e$, see Eq. (55), as typically used in the GSH literature [47], one has:

${{\mathcal{B}}}=(3/2) B \varDelta ^{1/2} - (1/4) G u_s^2 \varDelta ^{-3/2} \ne {{\mathcal{B}}}_\varDelta$,

${{\mathcal{G}}}=2G\varDelta ^{1/2}$, and ${{\mathcal{A}}}=G\varDelta ^{-1/2}u_s$,

i.e., the stability condition, ${{\mathcal{B}}}{{\mathcal{G}}} - {{\mathcal{A}}}^2 > 0$, translates to

$$\begin{aligned} (u_s/\varDelta )^2 < g_e^2 := 2B/G ~, \end{aligned}$$

(68)

as previously shown in Eq. (12) in Ref. [48], and in Eq. (43) above, for elastic, static systems above jamming, for $\varDelta > 0$. Below jamming, for $\varDelta \le 0$, one has $w_e=0$ and thus trivially $\det (\boldsymbol{\mathcal{\rm C}}) = 0$, while at the point of instability: $\sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}} = {{\mathcal{A}}}/{{\mathcal{B}}} = {{\mathcal{G}}}/{{\mathcal{A}}} = 2\varDelta /u_s = 2/g_e$.

Using $w_e$ in Eq. (55), the non-zero eigenvalue can be re-written as: $C_1 = [B + 2G] \varDelta ^{1/2} = B [1 + 4/g_e^2 ] \varDelta ^{1/2}$, with $g_e=\sqrt{2B/G}$, while the zero eigenvalue will be more relevant for understanding failure mechanisms at elastic instability.

The eigen-vectors in elastic strain space are: ${\hat{n}}^{(1)} = \pm (1,2/g_e) /\sqrt{1+4/g_e^2}$, and ${\hat{n}}^{(0)} = \pm (2/g_e,-1) /\sqrt{1+4/g_e^2}$, at the point of elastic instability, where incremental elastic strains parallel to ${\hat{n}}^{(0)}$ change neither stress, $\delta \pi ^{(0)}_\alpha =0$, nor energy, $\delta ^2 w^{(0)} = ( \delta \varepsilon ^e )^2 {\hat{n}}^{(0)}_\alpha {\hat{n}}^{(0)}_\beta C_{\alpha \beta } = 0$, and are thus permitted.

In other words, considering the shear vs. normal stress space, one could see the limit of elasticity as one possible definition of the maximal (elastic) macroscopic (bulk) friction, defined by the ratio: $\mu _e := \pi ^*_s/P_\varDelta = {{\mathcal{G}}}_\varDelta u_s / ({{\mathcal{B}}}_\varDelta \varDelta )$, with the limit value taken at the loss of elastic stability: $\mu ^0_e = \sqrt{2G/B} = 2/g_e$. Incremental changes of elastic strain along the eigenvector ${\hat{n}}^{(1)}$, with norm $\delta \varepsilon ^e$, result in stress increments, $\delta \pi ^{(1)}_\alpha =C_1 \delta \varepsilon ^e {\hat{n}}^{(1)}_\alpha$, parallel to the slope $\mu ^0_e = \sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}}$.

3.4.3 GSH with granular elastic energy instability

In the case of a granular (coordination number dependent) elastic energy density, $w_C$, see Eq. (57), and the respective moduli, see Eq. (60), the stability condition, ${{\mathcal{B}}}_C{{\mathcal{G}}}_C - {{\mathcal{A}}}_C^2 > 0$, divided by ${{\mathcal{G}}}_C$, translates to:

$$\begin{aligned} C_2 [1+(1+\varDelta )^2] \frac{G_C u_s^2}{B_C \varDelta }&< \frac{{{\mathcal{B}}}_C(u_s=0)}{\phi B_C} \nonumber \\&\approx [ C_0 + {{\mathcal{O}}}(\varDelta ^{\alpha _C}) ] \, , \end{aligned}$$

(69)

or a condition for the elastic shear strain:

$$\begin{aligned} u_s^2&\le (u_s^e)^2 := \frac{{{\mathcal{B}}}_C(u_s=0) \, \varDelta }{2 \phi C_2 G_C [1+\varDelta +\varDelta ^2/2]} \nonumber \\&= \frac{B_C C_0 \, \varDelta }{2 C_2 G_C} \left[ 1 + \textstyle {\frac{3C_1}{2C_0}} \varDelta ^{1/2} +(1 - \textstyle {\frac{3C_1^2}{5C_0^2}}) \varDelta +\textstyle {\frac{C_1}{2C_0}} \varDelta ^{3/2} - \varDelta ^2 \right] \nonumber \\&\approx \frac{ B_C [ C_0 + \textstyle {\frac{3}{2}} C_1 \varDelta ^{\alpha _C} + \ldots ]}{2 C_2 G_C} \, \varDelta \, , \end{aligned}$$

(70)

which simplifies in leading order to $u^e_s \propto \sqrt{\varDelta }$ , very close to jamming, $\varDelta \ll 1$. This renders $w_C$ a choice qualitatively different to the Hertzian energy density, with respect to the elastic instability; note that the term $\propto \varDelta ^{1/2}$ kicks in quite strongly already for small $\varDelta$. Some of the higher order terms are negative and drag down the limit of stability at higher density, i.e., at higher isotropic elastic strain³⁶.

The eigen-vectors in elastic strain space are: ${\hat{n}}^{(1)} = \pm (1,\textstyle {\frac{{\mathcal{G}}_C}{{\mathcal{A}}_C}}) /\sqrt{1+(\textstyle {\frac{{\mathcal{G}}_C}{{\mathcal{A}}_C}})^2} = \pm \textstyle {\frac{1}{u_C}} (u_s^e(1+\varDelta ),{\varDelta })$, ${\hat{n}}^{(0)} = \pm (-1,\textstyle {\frac{{\mathcal{A}}_C}{{\mathcal{G}}_C}}) /\sqrt{1+(\textstyle {\frac{{\mathcal{A}}_C}{{\mathcal{G}}_C}})^2} = \pm \textstyle {\frac{1}{u_C}} (-\varDelta ,u_s^e(1+\varDelta ))$, with $u_C=\sqrt{(u_s^e)^2(1+\varDelta )^2+\varDelta ^2}$, at the point of elastic instability, where incremental elastic strains parallel to ${\hat{n}}^{(0)}$ change neither stress, $\delta \pi ^{(0)}_\alpha =0$, nor energy, $\delta ^2 w^{(0)} = ( \delta \varepsilon ^e )^2 {\hat{n}}^{(0)}_\alpha {\hat{n}}^{(0)}_\beta C_{\alpha \beta } = 0$, and are thus permitted.

In other words, considering the shear vs. normal stress space, one could see the limit of elasticity as one possible definition of the maximal (elastic) macroscopic (bulk) friction, defined by the ratio: $\mu _C^e := {\pi ^*_s}^C/P_\varDelta ^C$, with the limit value taken at the loss of elastic stability. $\mu _C^{e0} = {{\mathcal{G}}_C} u_s^e / ({{{P}}}_\varDelta^C )$. Incremental changes of elastic strain along the eigenvector ${\hat{n}}^{(1)}$, with norm $\delta \varepsilon ^e$, result in stress increments, $\delta \pi ^{(1)}_\alpha =C_1 \delta \varepsilon ^e {\hat{n}}^{(1)}_\alpha$, parallel to the slope.

Rather than detailing the elastic instability further, refer to the following subsection, which relates to particle simulations and is qualitatively similar to the present energy density for small $\varDelta$, see Fig. 3. Finding an energy density in even better agreement with particle simulations, in particular improving the empirical $c(\varDelta )$, is work in progress.

3.5 Anisotropic, elastic-plastic moduli from DEM

In Refs. [49, 125, 167], an incremental (athermal) elasto-plastic evolution model for the isotropic and deviatoric stresses was proposed (in their eigen-system, p and $\tau$) as

$$\begin{aligned} \partial _t p&= {{\mathcal{B}}} {\dot{\varepsilon }}_v (1-p_v) + {{\mathcal{A}}}_s {\dot{\varepsilon }}_s (1-p_s) \,, \end{aligned}$$

(71)

$$\begin{aligned} \partial _t \tau&= {{\mathcal{A}}}_s {\dot{\varepsilon }}_v (1-p_v) + {{\mathcal{G}}} {\dot{\varepsilon }}_s (1-p_s) \,, \end{aligned}$$

(72)

with additional evolution equations for the anisotropy modulus ${{\mathcal{A}}}_s$ (with subscript s indicating its tensor nature) [125, 167], with eigen-directions of ${{\mathcal{A}}}_s$ (fabric) and $\tau$ not necessarily identical, and the jamming density [49]—not detailed further here. In order to relate this model to the present GSH based evolution equations, assume (overly simplified, for the sake of clarity) that $\partial _t p \approx {{\mathcal{B}}} \partial _t \varDelta$ and $\partial _t \tau \approx {{\mathcal{G}}} \partial _t \varepsilon ^e_s$, to arrive at the evolution equations of the elastic strains:

$$\begin{aligned} \partial _t \varDelta&= {\dot{\varepsilon }}_v (1-p_v) + \frac{{{\mathcal{A}}}_s}{{\mathcal{B}}} {\dot{\varepsilon }}_s (1-p_s) \,, \end{aligned}$$

(73)

$$\begin{aligned} \partial _t \varepsilon ^e_s&= {\dot{\varepsilon }}_s (1-p_s) + \frac{{{\mathcal{A}}}_s}{{\mathcal{G}}} {\dot{\varepsilon }}_v (1-p_v) \,, \end{aligned}$$

(74)

where the first terms represent their elastic and plastic responses, with probabilities for plastic deformations $p_v$ (see Sect. 4.1.1) and $p_s$ (see Sect. 4.1.2), while the second terms are anisotropy terms, cross-coupling isotropic and deviatoric strain actions and reactions.

In Ref. [125], the elements of the constitutive moduli matrix, $\mathbf {C}$, were directly deduced from particle simulations, and took a form (slightly simplified here by implying that the fabric and the elastic strain are proportional): ${{\mathcal{B}}} = p_0 \phi Z$ (with the product of volume fraction, $\phi$, and coordination number, Z, which is a non-linear function of $\varDelta$), ${{\mathcal{G}}}/{{\mathcal{B}}} = G_0(\varDelta ) (1 - g_s (u_s/\varDelta )^2)$, and ${{\mathcal{A}}}_s/{{\mathcal{B}}} = u_s/\varDelta$, with $G_0(\varDelta )=g_0 (1-\exp (-\varDelta /\varDelta _g))$ and constants $p_0$, $g_0$, $g_s$ and $\varDelta _g$.

The (elastic) shear modulus is plotted in Fig. 3, as obtained from the (elastic response only) particle simulation data (no details shown),

$$\begin{aligned} \frac{{{\mathcal{G}}}^c}{{\mathcal{B}}} := \frac{1}{{\mathcal{B}}} \frac{\partial \pi _s}{\partial \varepsilon^e _s} = g_0 \left( 1 - \exp \left( \frac{\varDelta ^c }{ \varDelta ^c_g} \right) \right) \,, \end{aligned}$$

(75)

with the (critical state) calibrated material parameters, $p_0 \approx 0.065$ (from above ${{\mathcal{B}}}$), maximal (scaled) shear modulus, $g_0 p_0 = 0.036 \pm 0.001$, i.e., $g_0 \approx 1/2$, characteristic elastic isotropic strain, $\varDelta ^c_g = 0.070 \pm 0.005$, and the (extrapolated) unjamming density, $\phi _J^c \approx 0.655 \pm 0.001$, in $\varDelta ^c=\log (\phi /\phi _J^c)$, where the superscript, c, implies the critical state. Note that for this model no energy density is available so far—work in progress.

Fig. 3

Shear modulus at critical state, scaled as $G_c = ({{\mathcal{G}}}^c/{{\mathcal{B}}}) / p_0$, from DEM simulations, with fit to Eq. (75) in Sect. 3.5, parameters are given in the main text, similar to Ref. [125] (raw data details not shown here). The other curves represent $({{\mathcal{G}}}_C/{{\mathcal{B}}}_C) / p_0$ from Sect. 3.2.3, with $C_2=C_0=5.1$ and $u_s=0$, where the labels indicate the complete model (C) or lowest order in $\varDelta$ (0)

In the elastic limit case one has $p_v=p_s=0$, and can identify the cross-term in Eq. (73) with the last term in Eq. (63), i.e., $\alpha _1 \varepsilon ^e_s {\dot{\varepsilon }}_s = \frac{{{\mathcal{A}}}_s}{{\mathcal{B}}} {\dot{\varepsilon }}_s$, causing pressure dilatancy under shear strain. From the second cross-term in Eq. (74), one can deduce a missing cross-term in Eq. (64), as $\alpha \varDelta {\dot{\varepsilon }}_v = \frac{{{\mathcal{A}}}_s}{{\mathcal{G}}} {\dot{\varepsilon }}_v$, causing shear stress “dilatancy” under isotropic strain.

From this, the condition for elastic instability, ${{\mathcal{G}}}/{{\mathcal{B}}}-({{\mathcal{A}}}/{{\mathcal{B}}})^2=0$, with ${{\mathcal{A}}}=|{{\mathcal{A}}}_s|$, translates to: $g_e^2:=(u^g_s/\varDelta )^2 = G_0(\varDelta )/[1+g_s G_0(\varDelta )]$, which implies a very narrow elastic regime for small $\varDelta$, since $G_0(\varDelta ) \rightarrow g_0 \varDelta /\varDelta _g$, for vanishing $\varDelta /\varDelta _g \ll 1$, so that $g_e \propto \sqrt{\varDelta /\varDelta _g}$. For large $\varDelta /\varDelta _g \gg 1$, one has instead $g_e^2 \approx 1/[g_s+1/g_0]$, independent of $\varDelta$.

The “direction” (in elastic strain invariants) of maximal stability becomes: ${\hat{n}}^{(1)} = \pm (1,\sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}}) / \sqrt{1+{{\mathcal{G}}}/{{\mathcal{B}}}} = \pm (\varDelta ,u^g_s) / \sqrt{\varDelta ^2+(u^g_s)^2}$, and with the perpendicular “direction” of maximal in-stability: ${\hat{n}}^{(0)} = \pm (-\sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}},1) / \sqrt{1+{{\mathcal{G}}}/{{\mathcal{B}}}} = \pm (-u^g_s,\varDelta ) / \sqrt{\varDelta ^2+(u^g_s)^2}$, after using $\sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}}={{{\mathcal{A}}}/{{\mathcal{B}}}}=u^g_s/\varDelta$.

This model, derived from frictionless particle simulations [125], thus would result in a non-linear $u^g_s=g_e\varDelta$ in Fig. 4—different from the other models presented before in this section. However, all models have in common that the stress response to a strain-increment in the direction of the unit-vector ${\hat{n}}^{(1)}$, is parallel to the slope $\mu _e^0=\sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}}$ in stress space.

Further consideration of this particle simulation based constitutive model for stress and fabric—and the question if an additional fabric state variable (tensor) is needed at all—go beyond the scope of the present study, but are subject of ongoing research. Nevertheless, anisotropy cross terms, as those discussed above, will be considered in the next section in some situations.

3.6 Special cases

In order to reduce the model complexity, and to understand what the eigen-vectors from the last subsection mean, it is instructive to consider a few simple special cases. Some of these cases will be later studied analytically and numerically. They represent simplifications that boil down a complicated theoretical framework to a simpler, possibly even transparent form that allows for better understanding and sometimes even for analytical solutions. We propose to apply those special cases to any new theory before one really applies the whole framework. Furthermore, the special cases allow to isolate a few of the terms and possibly calibrate the model parameters one by one. One traditional work on more complex, so-called proportional loading paths is Ref. [37], however, we reduce ourselves to the simplest cases only.

For the rest of this section, we use the stability results from the Hertz-like elastic energy density, as discussed in Sect. 3.4.2. Most of the cases are illustrated schematically in Fig. 4. Except for a few cases, most start from a jammed, elastically stable state with finite initial elastic strains $\varDelta (0) > 0$ and $u_s(0) > 0$.

Fig. 4

Sketch of (strain-driven) deformation cases in the space of the elastic strain invariants, i.e., $u_s$ plotted against $\varDelta$. The slope $g_e$ indicates the elastic instability limit. The numbers at the black arrows indicate the case-number, where dashed, thin lines are continuing the trends outwards into the concave zone (elastically instable). The blue and red arrows give the eigen-vectors of stability ${\hat{n}}^{(1)}$, and instability, ${\hat{n}}^{(0)}$, respectively, where their unspecified direction $(\pm )$ maybe directed outwards or into the convex zone (elastically stable), dependent on the situation and the boundary conditions. Note that in elastic stress space, the blue and red arrows are parallel and perpendicular to the slope $\mu _e^0 = \pi _s^*/P_\varDelta = \sqrt{{{\mathcal{G}}}/{{\mathcal{B}}}}$, respectively, for the models presented above.

(case 0) Assume the system unjammed, $\varDelta (0) < 0$, and apply a constant compressive strain rate, ${\dot{\varepsilon }}_{v}=-v_{ll}>0$. The density and the elastic strain, $\varDelta =\log (\rho /\rho _J)$, will grow together until the system jams at $\rho _J$, from which on its evolution equation kicks in. It was shown in Refs. [170, 171], and earlier works cited therein, that already below jamming, the jamming density (and thus $\varDelta$) depends on the procedure of preparation, in particular on the strain rate and on the granular temperature, however, this fact goes beyond the present focus and is thus not studied further.

(case 1) Assuming a purely isotropic de-compression, ${\dot{\varepsilon }}_{v}=-v_{ll}<0$, from a jammed state, one expects the elastic isotropic strain, $\varDelta$, to decrease faster than its deviatoric (shear) counterpart, $u_s$, until at $u_s^2 = (2B/G) \varDelta ^2$, or $u_s=g_e \varDelta$, the looser system cannot sustain the shear-stress anymore, so that un-jamming due to instability with respect to shear occurs. In order to remain at least marginally stable, one needs a decrease of $u_s \rightarrow u_s^0 = g_e \varDelta$, a situation that could be referred to as shear-yielding [10, 49, 100].

(case 1b) In the situation without initial elastic shear strain, $u_s(0)=0$, the stability criterion is always true and the system remains stable until isotropic un-jamming takes place at $\varDelta =0$.

(case 2) In the case of isotropic compression, the model remains stable, unless the virgin consolidation line is reached, where the system restructures to be able to carry the increasing stress. This situation is not detailed further, but the (case 2b) of loading without shear is studied in Sect. 4.1 to display the role of plastic deformations due to isotropic compression.

(case 3) Assuming a purely deviatoric (volume conserving) shear strain rate, ${{\dot{\varepsilon }}}^*_{ij}=-v^*_{ij}$, from a jammed state, one expects the elastic deviatoric (shear) strain, $u_s$, to increase faster than its isotropic counterpart, $\varDelta$, could build up, until at $\varDelta \rightarrow \varDelta _0 (1+\epsilon _\varDelta ) = u_s/g_e$, the system cannot sustain pressure (isotropic stress) anymore, so that an instability with respect to volume change occurs, and one has a consequent decrease of $\phi _J$, due to a possible further increase of $\varDelta$, i.e., one origin of dilatancy. The evolution of $\varDelta$ inside the cone and at the limit of elastic stability are qualitatively different, as will be studied numerically later on.

(case 3b) Under the same purely deviatoric deformation, the isotropic elastic strain $\varDelta$ could also decrease, corresponding to $\phi _J$ increasing. This leads to elastic instability at smaller elastic strains, $\varDelta \rightarrow \varDelta _0 (1-\epsilon _\varDelta ) = u_s/g_e$, not much changing the considerations in case 3, but rather leading to compactancy instead of dilatancy, as to be expected for very loose packings. Furthermore, this could lead to isotropic unjamming, if $\phi _J$ drops below $\phi$.

Several of the cases discussed above will be next studied analytically (as far as possible) and numerically in Sect. 5.

4 Analytical results for special cases

After a summary of the equations that will be used in this section, we take several special cases, starting from the athermal limit, $T_g=0$ to highlight the probabilities for strain-induced irreversible deformations in Sect. 4.1. Various versions and limits of the (over-simplified) classical GSH model from Sects. 3.2.2 and 3.4.2, are discussed and analytically treated (in some special cases where this is possible), with focus on the effect of $T_g$, while also several new terms and regularization schemes are proposed, to be later used in the numerical solutions.

The set of model equations is summarized here for reference, with extensions from classical GSH (model 0):

$$\begin{aligned} \partial _t \rho= & {} \rho {\dot{\varepsilon }}_{v} ~, \end{aligned}$$

(76)

$$\begin{aligned} \partial _t \varDelta= & {} {\dot{\varepsilon }}_{v}{\left( 1 - p_v \right) } - \lambda _1 T_g \varDelta {p_g} + \alpha _1 \varepsilon ^{e*}_{ij}{{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) } ~, \end{aligned}$$

(77)

$$\begin{aligned} \partial _t \varepsilon ^{e*}_{ij}= & {} {{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) } - \lambda T_g \varepsilon ^{e*}_{ij}{+ \alpha _{sv}} ~, \end{aligned}$$

(78)

$$\begin{aligned} \partial _t T_g= & {} - R_T T_g^2 {(T_g^*/T_g)} + f_T({\dot{\varepsilon }}_{ij}) + {f_g(g_*)} ~, \end{aligned}$$

(79)

before some meaningful special cases (purely isotropic and deviatoric loading) are discussed below, for which analytical solutions are provided, if possible.

The elastic strains, for the sake of brevity, are to be read as deviations from the equilibrium, i.e., as: $\varDelta \rightarrow \varDelta -\varDelta ^{eq}$ and $\varepsilon ^{e*}_{ij}\rightarrow \varepsilon ^{e*}_{ij}-\varepsilon ^{e*}_{ij}\,^{eq}$, accounting for the stress equilibrium condition, $\nabla _j \pi _{ij}^{eq} = \rho g_i$, and other boundary conditions.

Avoiding the terms not present in the original Eqs. (62)-(65), one arrives at what we refer to model 0 (having thus no valid athermal limit), which is used as starting point to study transients in Sect. 5. The terms ${p_g}$ and ${\alpha _{sv}} = \alpha _s \varDelta {\dot{\varepsilon }}_v(1-{p_v})$, as defined in Sect. 2.5, are introduced here as place-holders for elements discussed below, in Sect. 4.7, or to be added in future, as introduced in Refs. [49, 125, 167].

The rate of cooling is modified in the elastic, jammed state ($\varDelta > 0$) by adding an “elastic dissipation rate” $T_e$, referred to as model e, as ${T_g^*/T_g} = 1 + T_e/T_g = 1 + T_{e0} \varDelta ^h / T_g$ where only the special case $h=0$, i.e., $T_e=T_{e0}$, will be treated below³⁷. The presence of $T_e$ does not affect the dynamics too much for finite $T_g \gg T_e$ (Haff’s free homogeneous cooling state (HCS), well below jamming), but in the limit of very small $T_g \rightarrow 0$, for elastic, jammed systems, this (phonon/wave-driven) dissipation becomes important, generalizing HCS, providing an exponential decay of $T_g \rightarrow 0$ in absence of other driving mechanisms (and $\varDelta >0$), see Sect. 4.4. The dissipated granular energy $\partial _t w = \rho b T_g \partial _t T_g = - \rho b R_T T_g^3 {(T_g^*/T_g)}$ is balanced by an equal positive term creating thermal energy or entropy, i.e., this term does not contribute to the second law of thermodynamics, see Sect. 2.5.

The new term ${ f_g(g_*) }$, in Eq. (79), is only active if the system is outside of the elastically stable regime, where $g_* = u_s/\varDelta - g_e > 0$, with the limit of elastic stability $g_e$. It is continuous, inactive in the convex region, active outside. This term generates more granular temperature, jiggling, the more the system gets elastically unstable, due to concavity of the elastic energy.

The terms ${\left( 1 - p_v \right) }$ and ${\left( 1 - p_s \right) }$ represent the new probabilities for elastic deformations, with ${p_v}$ and ${p_s}$ the new probabilities for isotropic/deviatoric plastic deformations, respectively, see Ref. [49], as specified in Sect. 2.4, Eq. (26), and discussed next, in Sect. 4.1.

4.1 The granular athermal limit $T_g=0$

Enforcing the athermal case, $T_g=0$, the system of equations reduces to:

$$\begin{aligned} \partial _t \varDelta= & {} {\dot{\varepsilon }}_{v}{\left( 1 - p_v \right) } + \alpha _1 \varepsilon ^{e*}_{ij}{{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) } ~, \end{aligned}$$

(80)

$$\begin{aligned} \partial _t \varepsilon ^{e*}_{ij}= & {} {{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) } { + \alpha _{sv}} ~, \end{aligned}$$

(81)

see Eqs. (73) and (74), where the cross-term ${\alpha _{sv}}$ is usually neglected, and the off-diagonal Onsager coefficients ${p_v}$ and ${p_s}$ were previously introduced in Ref. [112], but taken equal to $\alpha _1$, while here they are, alternatively, interpreted as the probabilities for (isotropic and deviatoric) plastic (re-structuring) events in the packing, as in Sect. 2.4, Eq. (74), and in Refs. [49, 167]. Note that in Eqs. (80) and (81), the probabilites for isotropic and deviatoric plastic deformations are systematically attached to isotropic and deviatoric strain rates, respectively.

In the few plots in this section, dimensionless units are used, such that $\rho =\phi$, and stress is in units of 1 MPa, as discussed in detail at the beginning of Sect. 5. The quantitative calibration of the GSH based theory by particle simulation data, as well as an alternative choice of units, are discussed in Sect. 6.

4.1.1 Athermal isotropic loading

For isotropic loading (${{\dot{\varepsilon }}}^*_{ij}=0$), the system of equations reduces even further to $\dot{\varepsilon }_v^p :={\dot{\varepsilon }}_{v}-\partial _t{\varDelta } = {\dot{\varepsilon }}_{v}-\partial _t{\varepsilon ^e_v} = {\dot{\varepsilon }}_{v}{p_v} = \partial _t \log (\rho _J)$³⁸.

The elastic limit, with probability ${p_v}=0$, translates to constant $\rho _J$, whereas the fully plastic limit, ${p_v}=1$, translates to $\dot{\varepsilon }_v^p={\dot{\rho }}/\rho ={\dot{\varepsilon }}_{v}$.

Relating this to the classical cam-clay model [122], where $\dot{\varepsilon }_v^p ={\dot{\varepsilon }}_v \, (\lambda -\kappa )/\lambda$, allows to identify ${p_v}=1-\kappa /\lambda$ as constant. However, in the following we will derive a more complex model, where ${p_v}$, the probability for plastic deformations, is a function of the state-variables and the sign of deformation rate (i.e., compression or tension).

A simple constitutive assumption, ${p_v} {\dot{\varepsilon }}_{v}= - \lambda _1 T_e \varDelta$, could be directly merged into the relaxation term as $-\lambda _1 T_g^* \varDelta$, with $T_g^*=T_g+T_e$, and solved analytically³⁹. This model displays the transient elastic behavior of polymer melts or glasses for which (in absence of any isotropic strain rate, for finite, constant $T_e$) $\varDelta \rightarrow 0$. However, since the reality of granular matter, as measured from particle simulations in Ref. [49], is somewhat more complex, already for frictionless spheres—and even more for realistic frictional non-spherical particles—we have to come up with a better relation for the probability for isotropic plastic rearrangements.

The (un-)jamming density was reported, see Eq. (5) in Ref. [49], to reach after infinitely many isotropic loading/unloading cycles the limit density:

$$\begin{aligned} \rho _\infty = \rho _{J0} + b_\infty \left[ \frac{\rho }{\rho _{J0}} - 1 \right] _+ ^{\beta _\infty } ~, \end{aligned}$$

(82)

with the half-sided linear function $[x>0]_+=x$, and $[x \le 0]_+=0$, otherwise, $\rho _\infty = \rho _{J0}$ for $\rho <\rho _{J0}$  ⁴⁰. Using Eq. (82), and noting that the first loading is characterized by $\rho _J-\rho _{J0} = \rho _J^{(1)}-\rho _{J0} = p_{v0} (\rho _\infty -\rho _{J0})$, with $p_{v0}=1-e^{-1}$, see Eq. (6) in Ref. [49], one can deduce the probability for plastic deformations from:

$$\begin{aligned} \frac{\partial \log (\rho _J)}{\partial t} = \frac{1}{\rho _J} \frac{\partial \rho _J}{\partial t} = \frac{\rho }{\rho _J} \frac{\partial \rho _J}{\partial \rho } \, \frac{1}{\rho } \frac{\partial \rho }{\partial t} = {p_v} {\dot{\varepsilon }}_{v}~, \end{aligned}$$

(83)

yielding:

$$\begin{aligned} {p_v}= & {} \frac{\rho }{\rho _J} \frac{\partial \rho _J}{\partial \rho } = p_{v0} \beta _\infty \frac{\rho }{\rho _J} \frac{\rho _\infty - \rho _{J0}}{\rho - \rho _{J0}} \nonumber \\= & {} { \frac{p_{v0}}{1-p_{v0}} \beta _\infty \frac{\rho _\infty / \rho _J - 1}{1 - \rho _{J0}/\rho } \approx c_{v0} \frac{\varDelta - \varDelta _\infty }{1 - \rho _{J0}/\rho } }~, \end{aligned}$$

(84)

expressed in terms of the difference between the limit and the actual jamming density $\rho _\infty -\rho _J = e^{-1} (\rho _\infty -\rho _{J0})$, or the elastic strain difference, $\varDelta -\varDelta _\infty = \log (\rho /\rho _J)-\log (\rho /\rho _\infty ) = \log (\rho _\infty /\rho _J) \approx \rho _\infty /\rho _J-1$, with a constant $c_{v0} = p_{v0} \beta _\infty /(1-p_{v0}) \approx 1/2$.

Cast into a pseudo-code, as implemented for the numerical solutions, see Figs. 5 and 6, the isotropic plastic strain-rate is computed from Eq. (84):

Fig. 5

Jamming density $\rho _J=\rho \exp (-\varDelta )$, plotted against density, $\rho$, during loading up to $\rho _{max}=0.66$, 0.67, 0.69, 0.72 and 0.90, with subsequent un-/re-loading cycles with amplitude, $\delta \rho =0.01$. The cycles on top correspond very much to the case $\rho _{max}=0.90$ and $\delta \rho =0.25$ displayed in Fig. 2a in Ref. [49]. The solid red line represents $\rho _\infty$ in Eq. (82), with $\rho _{J0}=0.6567$, and coefficients: $p_{v0}=1-e^{-1}$, $p_v^-=0$, $b_\infty = 0.02$, $\beta _\infty = 0.30$. Note the flat blue lines for unloading and for $\rho _J<\rho _\infty$, i.e., cases where one has ${p_v}=0$ for unloading and in unjammed situations. The jamming density can be deduced from simulations, using Eq. (107), see Sect. 6

Fig. 6

Pressure plotted against density, $\rho$, similar as in Fig. 5, but with $\rho _{J0}=0.60$, during loading up to $\rho _{max}=0.62$, 0.64, 0.66, and 0.68, with subsequent un-/re-loading cycles with amplitude, $\delta \rho =0.01$. The horizontal blue lines on top correspond to $\rho _{max}=0.68$ and $\delta \rho =0.08$. The dashed green curve represents the initial loading, up to $\rho _{max}$ (green dots), with six un-/re-loading cycles, ending at the magenta dots. Note that the lowest $\rho _{max}=0.62$ is un-jamming and re-jamming during the cycles. The upper (blue) curve represents the elastic limit case, with ${p_v}=0$, i.e., without plastic rearrangements and the analytical pressure state-line: $P_\varDelta = B \varDelta ^{3/2}$, with $B=1$. The lowermost curves represent cyclic un-/re-loading from $\rho _{max}=0.68$ with large amplitude, $\delta \rho =0.08$, down to $\rho _{min}=0.60$, well below the jamming-point, un-jamming and re-jamming during every cycle. The inset represents the void fraction, e, plotted against (logarithmic) pressure, P, similar to Fig. 2a

$$\begin{aligned}&{p_v} = \mathtt{\min } \left[ 1, \theta \, {p_v} \right] \nonumber \\&\mathtt{if~} {p_v} < 0 \mathtt{~then} \nonumber \\&~~~ {p_v} = \mathtt{\max } \left[ p_v^{-}, - {p_v} \right] \nonumber \\&\mathtt{else~} ~ \nonumber \\&~~~ \mathtt{if~} {\dot{\varepsilon }}_{v}\le 0 \mathtt{~then~} {p_v} = 0 \nonumber \\&\mathtt{endif} ~ \nonumber \\&\mathtt{if~} \rho _J \le \rho _{J0} \mathtt{~then~} {p_v} = 1 ~ \nonumber \\&\mathtt{if~} {\dot{\varepsilon }}_{v}= 0 \mathtt{~then~} {p_v}=0 ~, \end{aligned}$$

(85)

with a regularizing step-function

$$\begin{aligned} \theta =\theta (\varDelta /\varDelta _\theta )=(1/2)[1+\tanh (\varDelta /\varDelta _\theta )] \,, \end{aligned}$$

smoothed around $\varDelta =0$, with $\varDelta _\theta =2\times 10^{-5}$.

In words, the different terms/factors mean:

(i):

First, the step function takes care that below jamming, one has no strain-driven plastic deformations.

(ii):

Just above jamming, the denominator in Eq. (84) leads to a divergence, but is limited to ${p_v} \le 1$.

(iii):

Second, in cases where the probability would become negative, typically for large $\rho _J > \rho _\infty$, the system is set to be reversible, with positive probability, ${p_v}=-{p_v}$, and limited by a small constant slope, $p_v^{-} \ge 0$.

(iv):

For positive, ${p_v}$, the system is partly plastic during loading, but set to be elastic for unloading.

(v):

If the jamming density is below its isotropic lower limit, $\rho _{J0}$, the system is set to be perfectly plastic.

(vi):

The last line makes sure that there is no strain-driven contribution to dissipative stress if static.

For some more details, see Sect. 6.2, and for the statistical analysis of the probability, see Refs. [18, 19, 159], and references therein. For experimental calibration of the model, and its relation to classical models, see Refs. [21, 122].

4.1.2 Athermal deviatoric (pure shear) loading

Another special case that allows for analytical treatment is pure deviatoric (isochoric) shear, ${\dot{\varepsilon }}_{v}=0$, the elastic strains develop as $\partial _t \varDelta = \alpha _1 \varepsilon ^{e*}_{ij}{{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) }$ and $\partial _t\varepsilon ^{e*}_{ij}= {{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) }$ or, equivalently, for the plastic strain rate $\dot{\varepsilon }_{ij}^p = {{\dot{\varepsilon }}}^*_{ij}- \partial _t\varepsilon ^{e*}_{ij}= {{\dot{\varepsilon }}}^*_{ij}{p_s} \sim v_s {p_s}$.

Postulating the existence of a constant “critical” steady state for the (elastic) macroscopic friction, $\mu \approx \mu ^e=\pi _s/P_\varDelta$, i.e., the quasi static limit stress ratio, $\mu ^c_0 := \mu ^c(v_s \rightarrow 0) = {{\mathcal{G}}}_\varDelta ^c u^c_s/({{\mathcal{B}}}^c_\varDelta \varDelta ^c)$⁴¹$^,$⁴², this allows to express the probability for plastic (shear) events as:

$$\begin{aligned} {p_s} = \frac{\mu }{\mu ^c_0} \left[ {{\hat{\varepsilon ^{e*}_{ij}}}} \hat{{\dot{\varepsilon }}}^*_{ij} \right] _{+} := \frac{1}{\mu _0^c} \frac{{{\mathcal{G}}}_\varDelta }{{{\mathcal{B}}}_\varDelta } \frac{ \left[ \varepsilon ^{e*}_{ij}{{\dot{\varepsilon }}}^*_{ij}\right] _+}{\varDelta v_s} \approx \frac{u_s}{u_s^c} ~, \end{aligned}$$

(86)

for $\varDelta >0$, and ${p_s}=1$ otherwise, where the hats denote unit-tensors, the ratio of the tangent moduli depends on the constitutive choice of the energy density, and the last approximation is only valid after sufficiently long steady shear, close to the critical state, and/or if $\varDelta \approx \varDelta ^c$ vanishes from Eq. (86), but not for strain reversal, similar to Eqs. (28) and (31) in Ref. [47]. The term in brackets limits ${p_s} \ge 0$, as to keep it positive, i.e., $[x>0]_{+} = x$, and $[x\le 0]_{+}=0$, with ${p_s}=0$ in the absence of shear, $v_s=0$, and thus valid also for strain-reversal and during early transients, for which negative argument values result in perfectly elastic response, ${p_s} = 0$, as done similarly in Refs. [49, 125, 167] and references therein—based on, and in agreement with, DEM simulations⁴³. The probability for plastic events in Eq. (81), specified above in Eq. (86), can be very small at the beginning of shear, but increases due to the build-up of elastic shear strain, $u_s$, before it asymptotically approaches ${p_s}=1$, for large strain in the perfectly plastic, critical state. At reversal of shear, the argument of the bracket-function becomes negative, i.e., the system is elastic with ${p_s}=0$, until the shear strain adjusts to the new direction⁴⁴. When stopping shear, $v_s=0$, the system also becomes elastic, ${p_s}=0$.

In cases where density and thus $\varDelta$ is reduced in magnitude after the system has reached the critical state (not studied here), also $u_s^c \propto \varDelta ^c$ will reduce, and terms with $(1-{p_s})$ could become negative, resulting in the decay of elastic strains, however, this is skipped here for the sake of brevity.

Analytical treatment is possible close to steady state, for $\varDelta \approx \varDelta ^c$ assumed constant, where the deviatoric elastic strain evolves as: $\partial _t u_s = v_s {\left( 1 - p_s \right) } \approx v_s (1-u_s/u_s^c)$, with analytical solution:

$$\begin{aligned} u_s(t) = u_s^c - [u_s^c - u_s(0)] \exp (-v_s t/u_s^c) ~, \end{aligned}$$

(87)

and critical state elastic shear strain:

$$\begin{aligned} u^c_s = \varDelta ^c \left[ 2/\mu ^c_0 - \sqrt{(2/\mu ^c_0)^2 - g_e^2} \right] ~, \end{aligned}$$

as plotted in the inset of Fig. 7 as dashed lines, for the initial shear stress evolution $\sigma _{\mathrm{dev}}=\pi ^*_s = 2G\varDelta ^{1/2} u_s$. This analytical solution is very similar to the solutions presented in Refs. [49, 125, 167], however, further discussion is beyond the scope of this paper⁴⁵.

Fig. 7

Shear stress, $\sigma _{\mathrm{dev}} \approx \pi _s=|\pi _{ij}^*|$ (units are specified in Sect. 5 and a comparison to particle simulations is presented in Sect. 6), plotted against pressure, P, from athermal solutions to slow shear from initially isotropic states, compressed up to $\rho _{max}=0.61$, 0.63, 0.65, 0.67, and 0.69 (green dots), and subsequent cyclic pure shear with amplitude, $\delta \gamma \sim 0.28$, where the magenta dots represent the end-situation after six forward-backward shear cycles. The dashed line indicates the pre-set slope $\mu _0^c=\sigma _{\mathrm{dev}}^c/P^c=0.5$. The only other parameter active in this model is $\alpha _1=2$, where the case $\rho _{max}=0.65$ was simulated with two other values of $\alpha _1=0.5$ and 8, to display the enhancing effect on pressure-dilatancy of this parameter. Note that the imposed macroscopic friction, here $\mu _0^c=0.5$ (dash-dotted blue line), is chosen smaller than the elastic stability limit, $2/g_e=1$ (dashed blue line), such that the latter is never reached. The inset represents the shear stress evolution with strain, during the cyclic forward-backward shearing, where the higher density cases reach larger stress levels; the thick dashed lines represent the analytical solutions from Eq. (87) during initial shear from the isotropic states

What remains is to also consider the variation/evolution of $\varDelta$ during pure (volume conserving) shear, due to variations in the jamming density. Noting the similarity between ${p_s}$ and the $\alpha _1$-term in Eq. (80), in order to solve the problem analytically, one can rewrite the evolution equation for the isotropic elastic strain as: $\partial _t{\varDelta } = \alpha _1 u_s v_s {\left( 1 - p_s \right) } \approx \alpha _1 u_s^c v_s {p_s} {\left( 1 - p_s \right) } \approx \alpha _1 u_s^c {p_s} \partial _t u_s \approx \alpha _1 u_s \partial _t u_s$, for constant $v_s$ (not valid for strain-reversal). This equation has a critical state solution, $\varDelta =\varDelta ^c$, due to the term ${\left( 1 - p_s \right) } \approx 0$, as well as a stable elastic solution with $\partial _t \varDelta \approx 0$ for ${p_s} \propto u_s \approx 0$, in an initial isotropic state, see the infinite slopes in Fig. 6, for small shear strain and thus small shear stress. Due to the quadratic proportionality to $u_s$, the variation in $\varDelta$ is much smaller than the variation in $u_s$ itself—at least as long as $u_s/\varDelta < 1$. During shear starting from an isotropic state, the variation in $\varDelta$ is strictly positive, in the athermal limit, corresponding to dilatancy, i.e., the jamming density decreases, while at shear strain-reversal the evolution is opposite, changing sign during evolution, allowing for “butterfly-shape” loading-unloading cycles of $\varDelta$ or $P_\varDelta$, see the inset in Fig. 8, as consistent with particle simulations [125]. Note that the above assumptions are reasonable well above jamming, $\varDelta >0$, but not close to jamming, where the un-jamming can happen during every branch of the cycles, as shown in Ref. [49].

Fig. 8

Pressure plotted against density, from the same model solution as in Fig. 6. The lower curve represents the initial loading, up to $\rho _{max}$ (green dots), with six cyclic forward-backward shear cycles, ending at the magenta dots, displaying the pressure-dilatancy caused by isochoric shear. The upper (dashed blue) curve represents the elastic limit compression, with ${p_v}=0$. The inset displays the pressure during the shear cycles for the largest two densities

4.2 The granular thermal limit ${\dot{T}}_g=0$

Assuming that one could maintain a constant granular temperature steady state, e.g., by homogeneous driving/tapping, see Refs. [172], this would result in the set of equations:

$$\begin{aligned} \partial _t \varDelta= & {} {\dot{\varepsilon }}_{v}{\left( 1 - p_v \right) } - \lambda _1 T_g \varDelta {p_g} + \alpha _1 \varepsilon ^{e*}_{ij}{{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) } \end{aligned}$$

(88)

$$\begin{aligned} \partial _t \varepsilon ^{e*}_{ij}= & {} {{\dot{\varepsilon }}}^*_{ij}{\left( 1 - p_s \right) } - \lambda T_g \varepsilon ^{e*}_{ij}{+ \alpha _{sv}} ~. \end{aligned}$$

(89)

For vanishing strain rate ${\dot{\varepsilon }}_{ij}=0$, the equations decouple and only the relaxation terms survive, This corresponds to the “plastic equilibrium” limit case $\varDelta =0$, $\varepsilon ^{e*}_{ij}=0$, which is approached exponentially fast, with rates $\lambda _1 T_g$ and $\lambda T_g$. The term ${p_g}=1$ allows to choose the plastic equilibrium of transiently elastic systems, for which $\varDelta \rightarrow 0$, or is needed in a form ${p_g}=1-\varDelta _\infty /\varDelta$, or ${p_g}=1-{p_v}$, so that a granular type plastic limit with $\varDelta > 0$ can be achieved, see Sect. 4.7.

For finite ${\dot{\varepsilon }}_{ij}$, the system will establish thermal, elasto-plastic dynamic states that are not discussed further for the sake of brevity.

Strictly controlling density, i.e., fixing e, the situation is interesting again for granular matter. Any perturbation, as tapping or small-amplitude cyclic shear, will typically result in a decrease of both the elastic strain, $\varDelta$, and consequently the pressure, $P_\varDelta = {{\mathcal{B}}}_\varDelta \varDelta$. In this situation, the pressure curve shifts to smaller densities (larger e), and changes slope, both moving it away further from the elastic state-line, like shown in Fig. 6 (which represents a zoom into the previous Fig. 5, but with different parameter $\rho _{J0}=0.60$, which would more resemble frictional granular material. On the other hand, large strain shear results in (pressure) dilatancy, shifting the state-line to higher densities (or the void fraction to the right, towards the VCL, but not beyond), defining the critical state line (CS)—see magenta points in Fig. 8. The amplitude of pressure dilatancy increases with density (pressure), and so does the characteristic shear strain at which the system transits into a new state.

4.3 Isotropic jamming/un-jamming in minimal GSH

The model equations for isotropic compression/tension, with strain rates $\partial _t \rho = {\dot{\varepsilon }}_{v}\ne 0$, and ${{\dot{\varepsilon }}}^*_{ij}=0$, reduce to:

$$\begin{aligned} \partial _t \varDelta= & {} {\dot{\varepsilon }}_{v}{\left( 1 - p_v \right) } - \lambda _1 T_g \varDelta \end{aligned}$$

(90)

$$\begin{aligned} \partial _t \varepsilon ^{e*}_{ij}= & {} - \lambda T_g \varepsilon ^{e*}_{ij}{+ \alpha _{sv}} \end{aligned}$$

(91)

$$\begin{aligned} \partial _t T_g= & {} - R_T T_g^2 {(T_g^*/T_g)} + f_T({\dot{\varepsilon }}_{ij}) + {f_g(g_*)} \end{aligned}$$

(92)

The density is coupled to strain rate directly, while the second equation (91) is decoupled (for ${\alpha _{sv}} = 0$) just relaxing an existing elastic shear strain to zero. The coupled evolution equations (90) and (92) could be (quantitatively) calibrated to particle simulations like in Ref. [49], in a future study, however, in Sect. 6 they are calibrated to the athermal case, that isolates the evolution of $\varDelta$, as is relevant also for extremely small compression rates, ${\dot{\varepsilon }}_v$, and thus $T_g \approx 0$, if ${p_v}\ne 0$. For finite positive (compressive) strain rate, the inhomogeneous solution leads to a divergent increase of $T_g$ with time due to the continuous energy input. The energy production term due to elastic instability in Eq. (92) would become active for finite $u_s$, when $\varDelta < g_e u_s$, but is ignored here, assuming $u_s=0$ (which is not strictly true in real systems, where there can be some small, local, random elastic deviatoric strain).

For finite positive (compressive) strain rate, one has a continuous energy input due to the viscous source term $f_T$, that can lead to increase or decrease of $T_g$, and thus affects also the evolution of $\varDelta$. For negative (expansive) strain rate, the same is true, however, as soon as the system approaches un-jamming, the behavior qualitatively changes due to $T_e \rightarrow 0$, which is qualitatively, not quantitatively accounted for in the present version with constant parameters, in particular $f_v$ and $R_{T0}$; more details are beyond the scope of this study.

4.4 Homogeneous cooling below and above jamming

In the absence of any strain-rate mode, or other means of energy input [172], and assuming that $T_g$ is so small that $\varDelta$ is practically constant, the evolution equation for $T_g$, abbreviating $\gamma =R_T=R_{T0} (1-r^2)$, and assuming $T_e=0$, results in an algebraic evolution:

$$\begin{aligned} \frac{T_g}{T_g^0}= & {} \frac{1}{1 + R_T T_g^0 t} ~, \end{aligned}$$

(93)

in the free, homogeneous cooling state, as relevant for systems below jamming in the granular gas state⁴⁶. On the other hand, assuming the simplest model for $T^*_g \approx T_e$, with $h=0$ (or for constant $\varDelta$), for a small perturbation from an elastic base state, one has

$$\begin{aligned} \frac{T_g}{T_g^0}= & {} \exp {(-R_T {T_e} t)} ~, \end{aligned}$$

(94)

as relevant for elastically stable systems, well above the jamming density, for which small perturbations decay exponentially fast.

4.5 Pure shear transients from an isotropic state

This case was studied in detail by particle simulations in Refs. [49, 125], and should be studied analytically too with respect to questions about the build-up of anisotropy, and the degradation of the (shear) modulus, but is skipped for the sake of brevity.

4.6 Steady state pure shear (model 0 and e)

In case of deviatoric pure shear, the density equation vanishes, since $v_{ll}=0$ the density is conserved, $\partial _t \rho = 0$, and the terms with isotropic strain rate in the equations drop out. The remaining equations yield the steady state solution for the granular temperature:

$$\begin{aligned} \partial _t T_g = 0 = R_{T0} \left[ - (1-r^2) T_g {T^*_g} + f_s^2 {{\dot{\varepsilon }}}^*_{ij}{{\dot{\varepsilon }}}^*_{ij}\right] \end{aligned}$$

with $T^*_g=T_e+T_g$, so that (for $T_e = 0$):

$$\begin{aligned} (T_{g0}^{(ss)})^2 = \frac{f_s^2 ( {{\dot{\varepsilon }}}^*_{ij}{{\dot{\varepsilon }}}^*_{ij})}{ (1-r^2) } = \frac{f_s^2 v_s^2}{(1-r^2)} ~, \end{aligned}$$

(95)

or (for $T^*_g = T_g+T_e$):

$$\begin{aligned} (T_{g}^{(ss)})^2 + T_{g}^{(ss)} {T_e} - (T_{g0}^{(ss)})^2 = 0 ~, \end{aligned}$$

yields

$$\begin{aligned} T_{g}^{(ss)} = \pm \sqrt{({T_e}/2)^2 + (T_{g0}^{(ss)})^2} - {T_e}/2 ~, \end{aligned}$$

(96)

where only the positive solution is reasonable.

In the “collisional” limit $T_g \gg {T_e}$, one has the dynamic steady state: $T_{g}^{(ss)} \approx T_{g0}^{(ss)} \propto v_s$, while for $T_g \ll {T_e}$, the steady state temperature in the “elastic” steady state is: $T_{ge}^{(ss)} \approx (T_{g0}^{(ss)})^2/{T_e} \propto v_s^2$, i.e., it vanishes quadratically for $v_s \rightarrow 0$.

For the deviatoric elastic strain one has:

$$\begin{aligned} \partial _t \varepsilon ^{e*}_{ij}= 0 = {{\dot{\varepsilon }}}^*_{ij}- \lambda T_g \varepsilon ^{e*}_{ij}~, \end{aligned}$$

so that:

$$\begin{aligned} u^{(ss)}_s = v_s / ( \lambda T_g^{(ss)} ) \mathrm{~and~} u^{(ss)}_{s0} = \sqrt{ 1-r^2} / (\lambda f_s) ~, \end{aligned}$$

(97)

while for the isotropic elastic strain one has:

$$\begin{aligned} \partial _t \varDelta = 0 = - \lambda _1 T_g \varDelta + \alpha _1 \varepsilon ^{e*}_{ij}{{\dot{\varepsilon }}}^*_{ij}~, \end{aligned}$$

so that inserting Eqs. (95) and (97) yields the isotropic elastic strain in steady state:

$$\begin{aligned} \varDelta ^{(ss)} = \frac{ \alpha _1 v_s^2 }{ \lambda _1 \lambda (T_g^{(ss)})^2 } \mathrm{~and~} \varDelta _0^{(ss)} = \frac{ \alpha _1 (1-r^2) }{ \lambda _1 \lambda f_s^2 } ~, \end{aligned}$$

(98)

the former valid for model e, the latter for the simplest model 0, where the subscript 0 indicates $T_e=0$; model e is not indicated since it represents the default case.

In the “elastic” limit $T_g \ll {T_e}$, for $v_s \rightarrow 0$, the other two state-variables, in model e, behave as: $u_s^{(ss)} \rightarrow v_s^{-1}$, $\varDelta ^{(ss)} \rightarrow v_s^{-2}$, and thus $g^{(ss)} = u_s/\varDelta \rightarrow v_s$, i.e., a leading order linear increase with (shear) strain rate.

4.7 Steady state pure shear (model 1)

In model 1, only the evolution equation of the isotropic elastic strain has to be modified:

$$\begin{aligned} \frac{d}{dt}\varDelta = 0 = - \lambda _1 T_g \varDelta {p_g} + \alpha _1 u^*_{ij} v^*_{ij} \end{aligned}$$

so that inserting Eqs. (95) and (97) yields the isotropic elastic strain in steady state:

$$\begin{aligned} \varDelta _1^{(ss)} = \frac{ \alpha _1 v_s^2 }{ \lambda \lambda _1 (T_g^{(ss)})^2 {p_g} } = \frac{ \varDelta ^{(ss)} }{ {p_g} } ~, \end{aligned}$$

(99)

for model 1 for constant or $\varDelta$-independent ${p_g}$.

In some of the numerical implementations, we used ${p_g=\varDelta - \varDelta _\infty }$, in order to make $\varDelta$ relax towards a finite value, with $\varDelta _\infty =\log (\rho _\infty /\rho )$, as defined in Eq. (82). This allows to re-write ${p_g=\log (\rho _J/\rho _\infty )}$, which makes the relaxation term vanish for $\rho _J=\rho _\infty$, negative for larger values and increasingly positive for smaller jamming densities. Unfortunately, it also requires to solve a quadratic equation, resulting in

$$\begin{aligned} \varDelta ^{(ss)}=(1/2)\varDelta _\infty [1 + \sqrt{1+4\varDelta ^{(ss)}/\varDelta _\infty }] ~, \end{aligned}$$

i.e., an increased steady state elastic strain, representing strain-dilatancy. Note that this approach to achieve finite $\varDelta$ under steady state shear, increasing with density—as to be expected—is different in philosophy than making the bulk modulus factor B density dependent.

In other of the numerical implementations, we used ${p_g=1 - \varDelta _\infty /\varDelta }$, in order to make $\varDelta$ relax towards a finite value, resulting in the simpler steady state expression:

$$\begin{aligned} \varDelta ^{(ss)}_1 =\varDelta ^{(ss)} - \varDelta _\infty = \log (\rho _\infty /\rho _J^{(ss)})~, \end{aligned}$$

with $\varDelta _\infty <0$ for $\rho >\rho _\infty$, which even can change sign dependent on the relative magnitudes of $\varDelta ^{(ss)}$ and $\varDelta _\infty$. Note that this approach to achieve finite $\varDelta$ under steady state shear, increasing with density—as to be expected—is different in philosophy than making the bulk modulus factor B density dependent.

4.8 Discussion of the steady state rheology

Dividing Eq. (97) by (98) yields the deviatoric to elastic strain ratio in steady state (in order to evaluate whether the system is elastically stable or not):

$$\begin{aligned} g^{(ss)} := \frac{u_s^{(ss)}}{\varDelta ^{(ss)}} = \frac{\lambda _1 T_g^{(ss)}}{\alpha _1 v_s} ~. \end{aligned}$$

(100)

If the ratio of elastic strains in Eq. (100) is smaller than the elastic stability limit $g^{(ss)} \le g_e = \sqrt{2B/G}$ the system remains in a possibly stable (elastic, jammed) state, while it looses stability if the ratio reaches and/or exceeds the limit value.

Solving numerically the system of equations, including the transient evolution, confirms that the steady state is independent of the density, for model 0, see Sect. 5, as $\rho$ does not appear in the steady state solutions above.

The elastic strain ratio, Eq. (100), which determines whether the system becomes elastically instable in steady state, is not the same as the macroscopic friction at which the material flows plastically. Dividing the steady state shear stress by pressure defines the macroscopic (bulk) “friction”: $\mu = \sigma ^*_{ij} / P$, which results in the steady state bulk friction:

$$\begin{aligned} \mu ^{(ss)} = \frac{ \sigma ^*_{ij} }{ P } = \frac{ {\pi ^*_{ij}}^{(ss)} + \eta v^*_{ij} }{ P_\varDelta + P_T } = \frac{ {{\mathcal{G}}}_\varDelta u_{ij}^{(ss)} + \eta v^*_{ij} }{ {{\mathcal{B}}}_\varDelta \varDelta ^{(ss)} + P_T } ~. \end{aligned}$$

(101)

In the slow strain rate limit, ${\dot{\varepsilon }}_{ij}\rightarrow 0$, of Eq. (101), above jamming, $\varDelta > 0$, the second terms in nominator and denominator vanish, linearly and quadratically with $T_g \rightarrow 0$, respectively, and one has

$$\begin{aligned} \mu _0^{(ss)}= & {} \frac{ {{\mathcal{G}}}_\varDelta u_{s}^{(ss)} }{ {{\mathcal{B}}}_\varDelta \varDelta ^{(ss)} } \nonumber \\= & {} \frac{ 2 (G/B) (\varDelta ^{(ss)})^{-1} u_{s}^{(ss)} }{ 1 + (1/2) (G/B) (u_s^{(ss)})^2 (\varDelta ^{(ss)})^{-2} } \nonumber \\= & {} \frac{ 4 (G/2B) g^{(ss)} }{ 1 + (G/2B) (g^{(ss)})^2 } = \frac{ 4 g^{(ss)} }{ g_e^2 + (g^{(ss)})^2 } ~. \end{aligned}$$

(102)

For the special case $g^{(ss)} = g_e$, when the elastic limit of stability and the steady state ratio of elastic strains coincide, this translates to: $\mu _0^{(ss)}=2/g_e$.

4.9 Temperature unjam-regularization (model g)

In order to regularize the elastic unjamming instability, we introduce a measure for the distance from the elastic limit $g_s = (g - g_e) = (u_s/\varDelta - \sqrt{2B/G})$, which influences the temperature evolution

$$\begin{aligned} \frac{d}{dt} T_g = R_{T} \left[ - T_g^2 \right] + f_T( {\dot{\varepsilon }}_{ij}) + {f_g(g_*)} ~, \end{aligned}$$

(103)

with ${f_g(g_*)}=f_g \theta (g_s) g_s$, and the step-function $\theta (g_s>0)=1$, and 0 else, so that one has for steady-state pure shear (with model 0):

$$\begin{aligned} (T_g^{(ss)})^2 = \frac{f_s^2 v_s^2 + f_g \theta (g_s) g_s}{(1-r^2)} ~, \end{aligned}$$

(104)

i.e., just an elevated granular temperature that affects, in turn, the other state-variables (elastic strains) via their respective relaxation terms, as will be shown in the next Sect. 5.

5 Numerical solutions of GSH

In order to better understand GSH, including transients and transitions, and to validate the analytical solutions in the previous Sect. 4, we solve the system of equations numerically (with matlab, using ode45) and—focusing on a few terms only—discuss the features of the simplest GSH type model with mostly constant coefficients, see table 1, and the energy density from Eqs. (55). Symbols with a prime are dimensional, whereas all presented results are dimensionless (without prime), as explained next.

Table 1 Summary of parameters used for the numerical solutions of GSH, in the classical version without plastic deformation probabilities, $p_v=p_s=0$, where m. indicates the model version used, and dots replace varied values. The last three columns contain the elastic stability limit $g_e$, and the analytical solution to the steady state for shear to normal elastic strain and stress, respectively

Units are indicated by subscript-u and are here chosen as particle diameter, e.g., $x^{'}_u=d^{'}_p=10^{-3}$m, and density, $\rho ^{'}_u=\rho ^{'}_p=m^{'}_p/V^{'}_p=2000$ kg $\hbox {m}^{-3}$, with volume, $V^{'}_p$, of a single particle, so that its mass is: $m^{'}_p=\rho ^{'}_p V^{'}_p=(\pi /6) \rho ^{'}_p (d^{'}_p)^3 =(\pi /6) m^{'}_u \approx 10^{-6}$ kg, with unit of mass: $m^{'}_u=\rho ^{'}_u (x^{'}_u)^3=2 \times 10^{-6}$ kg. When the final unit is chosen as stress, $\sigma ^{'}_u = 1$ MPa (or 10 kPa), this results in the unit of time being: $t^{'}_u=(m^{'}_u/x^{'}_u/\sigma ^{'}_u)^{1/2} \approx 50 \times 10^{-6}$ s $=50$ $\mu$s (or $t^{'}_u=500$ $\mu$s).

The protocol of the numerical solutions consists of three stages: The initial preparation by isotropic compression (green) is followed by the testing mode (various colors for different parameters), and finally by a relaxation phase without any strain rate (magenta). The testing mode is in the following examples pure deviatoric (volume-conserving) shear, for large strains, to approach the critical state.

5.1 Effect of elastic dissipation and unjamming

Next goal is to understand the behavior of the simplest version of the classical GSH model, see Sects. 3.2.2 and 3.4.2, and the effects of both elastic dissipation parameter, $T_e$, and temperature regularization, $f_g$, that controls the dynamics at elastic unjamming.

The initial preparation starts from an un-jammed state at $\rho (0)=0.58$, with isotropic jamming taking place at density $\rho _{J0}=0.60$, up to different target densities $\rho =0.61$, 0.62, 0.63, 0.68, 0.74, and 0.80 during $t_p=1000$. From this point on, pure shear is applied for $t_s=5000$ and the final relaxation is applied for $t_r=4000$.

First, the effect of $T_e$ on the system is studied in Figs. 9 and 10, by plotting shear stress against pressure and the ratio of the deviatoric-to-isotropic elastic strains against time. Due to the density-independent parameters, in particular B, all the different density configurations approach to the same steady state, as analytically predicted (solid point in upper panel). The overshoot in the transient decreases with increasing density, before the steady state ratio of $u_s/\varDelta$ is reached, and the relaxation kicks in after shear is stopped. In the former, Fig. 9, $T_e=10^{-6}$ (case A) is practically zero and has no effect, whereas in the latter, Fig. 10, the finite $T_e$ (case B) causes a reduced $T_g$ in steady state, as well as a much more rapid relaxation (exponential due to $T_e$, instead of algebraic, like in the free cooling granular gas) to the static state (shorter magenta lines). Due the decreased $T_g$, in steady state, the other state-variables $\varDelta$ and $u_s$ are increased, whereas their ratio is slightly decreased, see Eq. (100).

Fig. 9

Case A (model 0): Shear stress plotted against pressure (top) and deviatoric-to-isotropic elastic strain ratio plotted against time (bottom). The green lines (on the horizontal axis) represent the isotropic preparation, the magenta lines (overlapping) the final relaxation, and the big solid (cyan) dot, or dashed cyan line in the lower panel, show the theoretically predicted steady state $\sigma _{\mathrm{dev}} = \mu _0^{(ss)} p$, Eq. (102), being density-independent for the over-simplified models. The dash-dotted (blue) lines represent the elastic stability limit $g_e$, Eqs. (43) and (68), while the dashed thin blue line indicates $\mu _0=0.5$ (not relevant here, because ${p_s}=0$.) for negligible $T_e = 10^{-6}$

Fig. 10

Case B (model 0e with $T_e = 2.10^{-4}$): Same model as in Fig. 9, with only difference the elastic dissipation active. Meaning of colors, lines is the same as in Fig. 9

The effect of the new temperature production term with $f_g=4.10^{-4}$ is then tested in Fig. 11 (case C), with otherwise the same settings as in case B. Only those cases that overshoot $g_e$ are affected. One of them, the lowermost density case, is completely destabilized by the increase in $T_g$ in the unstable regime, reaching a completely different steady state (far out of plot range), and returning rapidly to elastic stability as soon as the shear strain is stopped. Another case (second lowest density) remains above, but moves closer to $g_e$ and remains there for some longer time before it reaches the analytically predicted steady state. This proofs that the production term of $T_g$, due to the elastic instability, allows to regularize the systems behavior by dynamic means: Counterintuitively, an increased generation of $T_g$ can keep the system closer to the elastic instability, however, if too much $T_g$ is produced, this destabilizes the system and allows it to explore the plastic, collisional steady state with very large $T_g$ and—at the same time—comparatively small $u_s$ and $\varDelta$ (see the lower left corner in the upper panel and the out-of-bounds data in the lower panel).

Fig. 11

Case C (model 0eg with $T_e = 2.10^{-4}$ and $f_g=4.10^{-4}$): Same as in Fig. 9, with difference the elastic dissipation and the granular temperature creation both active. Meaning of colors, lines is the same as in Fig. 9

5.2 Effect of dilatancy and dynamics

Next goal is to understand the behavior of the model at constant density, with different dilatancy parameters, $\alpha _1$, and the effects of the elastic dissipation parameter $T_e$ and the temperature regularization $f_g$.

The initial preparation starts from an un-jammed state at $\rho (0)=0.58$, and is applied up to target density $\rho =0.65$, during $t_p=1000$. From this point on, pure shear is applied for $t_s=5000$ and the final relaxation is applied for $t_r=4000$, like before.

The values of $\alpha _1$ are chosen such that a few of the data remain within the elastic instability limit $u_s/\varDelta <g_e$, but a few overshoot, as can be seen in the lower panels of Figs. 12, 13, and 14.

Fig. 12

Case D1 (model 0): Shear stress plotted against pressure (top) and deviatoric-to-isotropic elastic strain ratio plotted against time (bottom), for the same density, $\rho =0.65$ for pure shear, with parameters given in table 1, in particular, for $T_e = 0$, and $f_g=0$, for different values of $\alpha _1=0.75$, 1, 1.25, 1.5, 2 (from top to bottom). The green lines (on the horizontal) represent the isotropic preparation, the curves the evolution during pure shear up to the dots, representing the analytical steady state solution, $\sigma _{\mathrm{dev}} = \mu _0^{(ss)} P$, see Eq. (102), while the magenta lines show the final relaxation, starting from the dots, without shear. The slopes in the top panel correspond to $\mu _0^{(ss)}=1$ and $\mu _c=0.5$, to guide the eye, and the dashed horizontal lines in the lower panel represent the analytical values $g_e=2$ (dash-dotted, blue), see Eqs. (43) and (68), and various $g^{(ss)}$ (cyan and thin dots), see Eq. (100)

Fig. 13

Case D2 (model 0): Shear data as in Fig. 12, where all parameters are the same, except for $f_g=5.10^{-5}$, which determines the granular temperature production in the instable regime, see Eq. (104) (not shown explicitly), which causes the different behavior of the upper curves. Meaning of colors, lines is the same as in Fig. 12

First, the effect of $f_g$ on the system is studied in Figs. 12, 13, and later the effect of $T_e$ in Fig. 14. Again, shear stress is plotted against pressure and the ratio of the deviatoric-to-isotropic elastic strains is plotted against time. In the former, Fig. 12, $T_e$ and $f_g$ are practically zero and have no effect at all, but an increasing dilatancy parameter, $\alpha _1$ causes the system into decreasing levels of $g=u_s/\varDelta$ during shear steady state (ss). The two lowermost curves remain within the elastic instability limit, the intermediate value $\alpha _1=1.25$ displays a slight overshoot but hits $g_e=2$ in steady state, wheras the upper two curves are clearly beyond the elastically stable regime $g>g_e$. In the shear stress to normal stress plot, the different $\alpha _1$ values lead to different steady states (thick dots) and a slow relaxation (magenta lines).

When temperature regularization is active in Fig. 13, the curves in the stable regime are not affected, the intermediate case is slightly modified and the upper two curves (smaller two $\alpha _1$) are, again, considerably affected by the generation of $T_g$, i.e., the much larger $T_g$ causes both elastic strains to relax towards the plastic limit—see the curves in the lower left corner of the shear to normal stress plot.

In the last Fig. 14, the finite $T_e$ causes a reduced $T_g$ in steady state, which results also in smaller $u_s^{(ss)}/\varDelta$, see Eq. (100). During final relaxation, $T_e$ is also causing a much more rapid (exponential) relaxation to the static state (shorter magenta lines).

Fig. 14

Case D3 (model 0): Shear data as in Fig. 13, where all parameters are the same, except for $T_e = 2.10^{-4}$, which leads to slightly lower steady states, and a much more rapid (exponential) dissipation of energy. Meaning of colors, lines is the same as in Fig. 12

Note that the elastic dissipation term, with finite $T_e$, is reducing granular temperature within and outside, whereas the thermal activation, $f_g$, increases $T_g$, but only outside the elastically stable regime.

6 DEM particle simulations

The particle simulations to be compared to the GSH solutions are the simplest possible element tests in a periodic cubical cell, with only diagonal components of the strain-rate active (isotropic compression/tension and pure shear). The $N=4913$ frictionless particles ($\mu _p=0$), with particle diameters drawn from a random homogeneous size distribution with maximum to minimum width, $d_p^{max}/d_p^{min}=3$, are the same as used in Ref. [49], even though the simulations were re-run slower for the first compression and de-compression cycle, see Fig. 1.

6.1 Non-dimensionalization of DEM

The parameters given in the following with a prime, e.g., $\rho ^{'}_p=2000$ or $d^{'}_p=2$, are used in the simulations shown in this paper. For working with units, there are two alternatives: Either one can read the numbers in chosen units⁴⁷ or the units are chosen based on physical properties to achieve non-dimensional quantities. The latter option is adopted here, i.e., the unit of length is chosen as the mean particle diameter, $x^{'}_u = \langle d^{'}_p \rangle = 2$, so that $\langle d_p \rangle = 1$ is the dimensionless diameter. The second unit is the material density, $\rho ^{'}_u = \rho ^{'}_p = 2000$, so that one has the dimensionless density, $\rho =\phi$, and thus the unit of mass, $m^{'}_u = \rho ^{'}_u (x^{'}_u)^3$, i.e., the particle mass, $m_p = (\pi /6)$. For the third unit one has several choices, where we adopt here the units of elastic stress, $\sigma ^{'}_u = k^{'}_n/d^{'}_p$, with the linear normal contact stiffness, $k^{'}_n = 10^5$, which yields the dimensionless stress $\sigma = \sigma ^{'} d^{'}_p / k^{'}_n$, and results in the unit of time $t^{'}_u = ( m^{'}_u / k^{'}_n )^{1/2} = 0.4$⁴⁸. In the chosen units, the dimensionless linear stiffness is $k_n = k^{'}_n (t^{'}_u)^2 / m^{'}_u = 1$, and the linear contact viscosity, $\gamma ^{'}_n=10^3$, becomes $\gamma _n =\gamma ^{'}_n t^{'}_u / m^{'}_u =\gamma ^{'}_n /[k^{'}_n t^{'}_u]=4\times 10^{-3}$, with background viscosity, $\gamma ^{'}_b=10^2$, or $\gamma _b=\gamma ^{'}_b t^{'}_u / m^{'}_u = 4\times 10^{-4}$.

The consequent physically relevant properties are the restitution coefficient $r = \exp (-\eta t_c) \approx 0.855$, with damping factor $\eta =\gamma _n/(2m_{12})$, reduced mass, $m_{12}=0.063$, and contact duration, $t_c=\pi /\sqrt{k_n/m_{12}-\eta ^2}=0.79$, or $t^{'}_c = t_c t^{'}_u = 0.316$, all considered for a contact between the largest and the smallest particle, with the larger viscous damping time-scale, $t_v = 2m_{12}/\gamma _n \approx 5$, and the even larger background damping time-scale $t_b = 2m_{12}/\gamma _b \approx 50$. Note that this choice of units corresponds to setting $t^{'}_u \propto t^{'}_c$, which corresponds to collapsing different stiffness simulations in the elastic regime [77, 118].

6.2 Calibration of GSH with DEM

The energy density has the same units as stress,

$$\begin{aligned} w^{'}_C = \frac{E^{'}_{pot}}{V^{'}} = \frac{\phi }{N V^{'}_p}\sum _{c=1}^{M} \frac{1}{2} k^{'}_n (\delta ^{'}_c)^2 \approx \frac{\phi C k^{'}_n}{4 V^{'}_p} \langle (\delta ^{'})^2 \rangle ~, \end{aligned}$$

(105)

with the particle volume, $V^{'}_p=\phi V'/N=(\pi /6) \langle (d^{'}_p)^3 \rangle$, and the contact number per particle $C=2M/N$, given the total number of contacts, M. The fraction of rattlers, $f_r$, that relates C to the coordination number $Z=C/(1-f_r)$, is not studied here, as it was discussed in detail in Ref. [49] and references therein.

The dimensionless energy density is thus:

$$\begin{aligned} w_C= & {} w^{'}_C d^{'}_p / k^{'}_n = \frac{\phi C}{4 V^{'}_p} d^{'}_p \langle (\delta ^{'})^2 \rangle = \frac{3 \phi C \langle d^{'}_p \rangle ^3}{2 \pi \langle (d^{'}_p)^3 \rangle } \langle \delta ^2 \rangle \nonumber \\= & {} \frac{3 \phi C}{2 \pi \langle d_p^3 \rangle } \langle \delta ^2 \rangle = \frac{B_0\phi C}{2} \langle \delta ^2 \rangle \end{aligned}$$

(106)

with all lengths non-dimensionalized by $d^{'}_p$, and $B_0 = \frac{3}{\pi \langle d_p^3 \rangle } \approx 0.766$, accounting for the third non-dimensional moment of the size distribution $\langle d_p^3 \rangle \approx 1.245$ (equals unity for monodisperse particles), for more details see Refs. [31, 168, 169, 171, 174].

Fig. 15

Scaled energy density, $w^*_{\mathrm{sim}} = w / (B_0 \phi C)$, plotted against density (volume fraction), $\phi =\rho =\rho '/\rho ^{'}_p$, for three models as introduced in Sects. 3.2.2 (Hertzian, $w^*_e=(2/5) \langle B \rangle \varDelta ^{5/2}$—yellow lines), 3.2.3 (granular, linear, $w^*_C=\langle B \rangle \varDelta ^{2} /2$—blue lines), as well as perfectly elastic, $w^*_{J0}=\langle B \rangle \varDelta _0^2 /2$ (dashed line), with $\varDelta _0=\log (\phi /\phi _{J0})$, and fixed jamming point, $\phi _{J0}=0.6567$, representing the VCL in Fig. 2. Both $w^*_e$ and $w^*_C$ are based on the same solution of $\varDelta$, for several large-amplitude, isotropic, loading-unloading cycles, see Sect. 4.1.1, where $w^*_C$ is almost in agreement with $w^P_{\mathrm{sim}} = w^*_{\mathrm{sim}}/h_{21}^2$ (large circles), see main text

Various energy densities are plotted in Fig. 15. Note that up to the second-last term in Eq. (106), one has exact identities, with $w^* = w_C/(B_0 \phi C) = \langle \delta ^2 \rangle /2$ (small circles and magenta line), whereas the transformation to $\varDelta ^2$ is one ambiguous choice out of many, which only holds approximately (large circles and blue lines).

How to compute $\varDelta$ is actually based on the analysis of the incremental (tangent) stress-strain evolution in the elastic regime (details not shown—work in progress). For observing the (smoothed) non-dimensional bulk modulus: $\langle B \rangle = \partial P^*_\varDelta / \partial \varepsilon _v \approx {const.}$, very slow isotropic compression simulation data are analyzed at finite, small strain-steps, $\partial \varepsilon _v \approx 10^{-4}$, with $P_\varDelta ^* = P_\varDelta / (B_0 \phi C h_{21}) = \langle B \rangle \varDelta$, ignoring data below jamming or during plastic, dynamic events with $K>10^{-5}$, which also assures that $P \approx P_\varDelta$, due to negligible kinetic and dissipative stresses.

The elastic strain, $\varDelta$, based on the re-scaled pressure, $P^*_\varDelta /\langle B \rangle$, is plotted in Fig. 16, showing that the linear contact model particle simulation data agree perfectly well with the linear granular model prediction from Sect. 3.2.3, with one adjustable parameter $p_0 \approx 0.0645$ (and the correction term $h_{21}$). Note that the Hertzian model predicts a qualitatively different non-linear behavior of the re-scaled pressure, proportional to $\varDelta ^{3/2}$. Crucial here is the overlap-correction for stress, $h_{21}=1- \langle \delta ^2 \rangle / (a d_p \langle \delta \rangle )$ with $a = 2$, accounting for the reduced particle center-distances, see Ref. [168], for very soft, deformable particles that do not break/fracture under strong compression⁴⁹.

Fig. 16

Pressure scaled such that it resembles the isotropic elastic strain, $\varDelta = P/(p_0 \phi C h_{21})$, with $p_0=B_0 \langle B \rangle \approx 0.0645$, from the same data as in Fig. 15, where the uppermost, dashed line represents the perfectly elastic limit case, $\varDelta _0=\log (\phi /\phi _{J0})$, with $\phi _{J0}=0.6567$—where the logarithm is the reason for pressure appearing non-linear. The circles and triangles represent loading and unloading, respectively, perfectly fitting the numerical solution of the elastic strain, $B_C \varDelta$ (blue lines), with $B_C=1$. The yellow lines represent the Hertzian model, $B \varDelta ^{3/2}$, with $B=1$. For a zoom into the small pressure range, see Fig. 1, where the left-most point is non-zero due to the initial condition with large kinetic energy

The coordination number that is an essential ingredient of the linear granular model, see Sect. 3.2.3, is plotted in Fig. 17, requiring three parameters $C_0$, $C_1$, and $\alpha _C$, as given in the inset. The particle simulation data are in perfect agreement with the analytical form of $C(\varDelta )$, from Eq. (56), during both loading and unloading.

Fig. 17

Coordination number $C=C_0+C_1 \varDelta ^{\alpha _C}$, from the same data as in Fig. 15; circles and triangles correspond to the first loading and unloading branch, respectively

This also allows to deduce the jamming density from the elastic strain, $\varDelta$, or from the average contact overlap $\langle \delta /d_p \rangle / d_1$, representing the (virtual) stress-free reference configuration, directly measurable only at unjamming, as plotted in Fig. 18:

$$\begin{aligned} \phi _J = \phi / \exp (\varDelta ) \approx \phi \exp (-\langle \delta /d_p \rangle / d_1 ) \,, \end{aligned}$$

(107)

which eventually allows to compare its evolution with the theoretical predictions for arbitrary strain paths, see also Fig. 5. In Eq. (107), the approximation deteriorates for large overlaps, where there are various similar, not exactly identical choices to (directly) deduce $\phi_J$ from elastic strain, $\Delta$, that can be approximated (indirectly) from overlap, $\delta$.

Fig. 18

Jamming density, $\phi _J=\rho _J$, with $\varDelta$ deduced from the pressure, in Fig. 16, from the same data as in Fig. 15, with simulation data for two loading-unloading cycles, and model data for three cycles. The parameters in the constitutive model introduced in Sect. 4.1.1, which lead to this good quantitative match with simulations are: $\rho _{J0} = 0.6567$, $b_\infty =\alpha _{\mathrm{max}}=0.021$, $\beta _\infty = 0.30$, as taken from Ref. [49] (where $b_\infty =\alpha _{\mathrm{max}}$), and slope of the reversible branch, $p_v^-=0.02 \approx b_\infty$. Unjamming takes place when the jamming density hits the density (green line), and due to $T_g \approx 0$, here, there is no evolution of $\rho _J$ below jamming

7 Conclusion and Outlook

The focus of this paper was on yielding and un-jamming/jamming of granular matter, a study inspired by the late Bob Behringer, to whom this work is dedicated. In an attempt to combine theoretical considerations with numerical/experimental observations on granular matter, the authors propose a minimalist macroscopic model to capture qualitatively all states of granular matter, and which even can be solved analytically in various special cases. Furthermore, the paper contains a review of literature on GSH as well as on particle simulations, which are compared in relation to each other and eventually used to quantitatively calibrate the GSH theoretical model with existing numerical results from a simple, frictionless, soft particle model.

The system considered was a representative volume element (RVE) of granular matter, homogeneous, i.e., without gradients and with no walls. The granular material was considered in fluid-like and solid-like states, as well as during continuous changes between these states. Particular focus was on the transition from elastically stable to instable, which is a novel contribution since the latter states can be highly dynamic, a situation that is not treatable by, e.g., standard elasto-plastic approaches or critical state theory.

Based on the rather complex, but versatile granular solid hydrodynamics (GSH), a much simplified qualitative model that includes un-jammed, gas- or fluid-like states as well as jammed solid-like states (elastically stable) was proposed and studied both analytically as well as numerically. Furthermore, various transitions and intermediate states could be identified and better understood in the framework of this simple GSH type model, which has only four state-variables, density, elastic strain (isotropic and deviatoric) and granular temperature, unifying all the states and transitions of granular matter that we could imagine. In order to keep this universal model attempt transparent, the model equations were often over-simplified by setting most parameters constant, so that the structure of the model equations rather than the consequences of additional constitutive assumptions could be tested. Analytical solutions of the model were possible for cases where either one or more state-variables was fixed or set to zero, while other cases involved either purely isotropic or pure shear modes of deformation, which typically removes considerable fractions from the equations to render them solvable.

The model was generalized to include soft particle phenomenology, and even quantitative rheology, elastic and dissipative responses, as inspired by recent soft particle simulations. Also a strictly non-thermal limit (removing the granular temperature) was considered, as well as perfectly plastic, elastic or intermediate states—possibly related to the critical state and the elastic instability, which was actually the main focus and reason to start this research. A major open question about the size of the volume in which such instabilities occur, cannot be answered in this study, since we assumed homogeneity inside the RVE on the continuum theory level.

Even though rather simple, the minimal universal model is capable of following the granular system from very low (dilute granular gas) to very high densities (dense jammed granular solid), including various transitions and all the transients. In order to limit complexity, the model was considered for a homogeneous (gradient-free) system that could be either seen as a RVE, or as material point of a full continuum model. However, it is not clear which size this material element should have. From particle simulations with a few 1000 particles, it is clear (data not shown here) that the system is never really homogeneous, and that zones of plastic deformations can range from a few particles up to system spanning events. This inhomogeneity within the RVE was enclosed in the probabilities for plastic deformations that are an extension to the classical GSH.

Considering jamming, we report a very slow, “half-hearted” transition to the jammed state, as observed in both particle simulations and GSH, where the true jamming density $\phi _J$, is established above, not at the minimal possible jamming density $\phi _{J0} < \phi _J$, even in the absence of perturbations due to granular temperature, $T_g$, just due to the occurrence of plastic (irreversible) deformations that lead to better, more efficient packing during compression. A more detailed study of the rate dependence and thus dependence on $T_g$, was beyond the scope of this study.

7.1 Modes of un-jamming

Once jammed, the first mode of isotropic un-jamming appears trivial: decompression of the system makes the density decrease and un-jamming takes place when the elastic strain vanishes. However, the density at which un-jamming takes place is not the same as the jamming density, it rather depends on the history of the packing. Perturbations by tapping or over-compression both can result in un- and re-jamming densities considerably larger than the lowest possible, the random loose packing density. The longer/stronger the system is perturbed, the larger the jamming density will be, but the approach to this upper limit is realized very slowly, so slow that it requires very many cycles to be reached. Whether there are well defined random loose and random close packing densities, below/above which the system cannot jam/un-jam anymore is an important open question. Both limit densities are very sensible to the protocol one uses to approach and realize/measure them, especially in the absence of friction as relevant for soft, gel-like particles that resemble many of the simulations referred to in this study.

The second mode of un-jamming is by plastic yielding, which involves irreversible deformations/re-structuring of the solid granular matter, but does not involve dynamics or granular temperature—at least not in the classical picture. Plastic events occur with a certain probability, see Ref. [49], which is larger the closer the system is to un-jamming or the larger the elastic shear strain (and/or stress) is, which was previously accumulated. This mode involves the more classical world of elasto-plastic continuum mechanics and rheology for example see Refs. [4, 30, 175]. The evident lack of a dynamic state-variable is at the origin of many difficulties with those elasto-plastic concepts, in particular when the deformation rates become larger and larger. Modern concepts like fluidity or non-local models have been proposed during the last years to overcome this problem [18, 70, 99, 116, 175, 176], however, the proper account for the granular temperature in the elastic regime, and for unjamming, is still an open issue that is at least partly solved now.

The third mode of un-jamming is a transition occuring via an elastic instability, i.e., the loss of convexity, and then involves deformations of the solid granular matter that can occur without penalty (work), at the onset of concavity (elastic instability) or, are even activated/pushed by the external stresses (in the concave regime, or closeby). This mode is seemingly different from plastic yielding, since it allows for dynamics (granular temperature) to build up, grow, and eventually push back the system into a mechanically stable elastic state before/while it is dissipated.

How much different—if at all—plastic and elastic yielding really are has to be seen, and is subject of ongoing research.

7.2 Outlook and open questions

Besides extending the theory to general, inhomogeneous systems with gradients, further research is also needed to:

• Generalize the present version to arbitrary tensorial form in three dimensions, involving also the so far lacking third invariant of the tensors.

• Connect quantitatively the granular gas and fluid (standard) kinetic theory (SKT) with GSH.

• Determine the proper shape of the energy density for granular solids from particle simulations, and for more realistic materials with friction, cohesion, polydispersity, etc.

• Sort out if the present version of GSH without a micro-structural (fabric) tensor is sufficient or needs to be improved—is the elastic strain enough?

• Find the different mechanisms of relaxation, creation and destruction of energy in the elastic strain degrees of freedom as well as the dynamic, kinetic, granular ones.

• Identify the relaxation/evolution dynamics and the interplay of the multiple mechanisms, represented by the various different terms, of the state-variables below, above and during un-jamming/jamming?

• Find out how to bridge the gap between the discrete (in time) local and global plastic events (re-arrangements of the micro-structure) and the macroscopic/continuum picture presented here.

• Discussion of the fundamental principles of time-reversal symmetry and other items related to relaxation, entropy production, etc., goes beyond the scope of this paper, but is subject of ongoing discussions/collaborations.

Present research is aimed to address the remaining challenging questions: What are the differences and similarities of the driving forces/mechanisms? And, can they indeed all be combined in a single universal model as attempted in this study?