1 Introduction

Slope failures often result in the mobilisation of soils and sediments in the form of landslides, debris flows, and rock avalanches, among others [14]. These types of mass movements are a major source of hazard in mountainous areas. They are particularly dangerous because the transported granular material can travel long distances at high speed, with destructive consequences on communities and on impacted infrastructure [23].

Obtaining a deeper understanding of the rheological behavior of mass flows, and consequently of their runout dynamics, is of fundamental importance. It aids in drawing more accurate hazard maps, and in designing more effective mitigation measures [21]. However, experimental evidence is difficult to obtain in the field. Mass flows are thus typically studied as simplified models of granular flows created in laboratory flumes or chutes [3]. Physical models of this type are based on Froude similarity scaling [1, 2, 9, 28]. However, they create stress fields that only roughly approximate field conditions [15]. Since the length-scale is reduced by the scaling factor N, frictional stresses play a less important role (scaling as 1/N), and collisional stresses become the main source of energy dissipation (scaling as N). Moreover, the excess pore pressure is upscaled, resulting in a dramatic alteration of its rheological contribution [15].

The geotechnical centrifuge produces stress conditions that are closer to those observed in the field [5, 7, 26, e.g.], allowing the study of saturated flow and its interaction with obstacles [12, 17, 20, 22, e.g.]. Granular flows, however, pose technological and conceptual challenges to the geotechnical centrifuge. Flows triggered in the scaled model can hardly achieve steady conditions in the small space of a centrifuge model box. Drum-type centrifuges partially solve this problem [4], but are more complex to interpret, and typically limited in size. Most importantly, all grains are subject to an apparent Coriolis acceleration when moving within the spinning reference frame [6]. Because of this issues, a unified interpretation framework is still missing.

Recently, [8] explored the scaling principles of granular flows under a centrifugal acceleration field. The study was performed with a numerical model based on the Discrete Element Method (DEM). The numerical environment allows to bypass the many technological issues that affect physical models in real centrifuges. In particular, it allows to generate flows that reach steady conditions. They confirmed that traditional scaling holds for granular flows under a centrifugal acceleration field [11], assuming that the centrifuge radius R is sufficiently large (\(R>50h\), with h being the granular flow height). However, a small variation of the Inertial number must be factored in the scaling law. Most importantly, it was also found that secondary effects induced by the apparent Coriolis acceleration often obscure these results. Thus, identifying measures to reduce, or at least understand, the effects of the Coriolis acceleration is a key issue for enabling to use the geotechnical centrifuge with confidence.

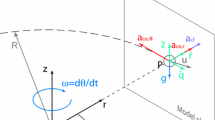
Consider a steady-state granular flow, such as the one illustrated in Fig. 1. The flow is located inside a centrifuge with radius R, spinning with rotational velocity \(\varvec{\omega }\). The Cartesian reference frame xyz rotates together with the box containing the flow. Placed in this reference frame, the particle mean flow is in the positive x direction, driven by the centrifugal acceleration \(a_\mathrm {cf}\). This system is analogous to a long chute, where the gravity vector is aligned with r. The overall acceleration \(\varvec{a}\) experienced by a particle moving with speed \(\varvec{u}\) at a distance r from the rotation axis is complemented by the Coriolis acceleration \(\varvec{a}_\text {Co}\):

$$\begin{aligned} \varvec{a} = \varvec{a}_\mathrm {cf} + \varvec{a}_\text {Co} = -\varvec{\omega } \times (\varvec{\omega }\times \varvec{r})-2\varvec{\omega } \times \varvec{u}. \end{aligned}$$
(1)

The centrifugal acceleration \(\varvec{a}_\text {cf}\) is aligned with r and always directed outwards. Conversely, the Coriolis acceleration is aligned with y, see Fig. 1, and its direction is a function of the sign of \(\omega \). It can be directed outward, compressing the flow, or inward, dilating it (thus, we refer to it as “compressive” or “dilative”, respectively). Note that, in practice, this choice pertains to the user, as long as the main flow direction can be switched with respect to \(\omega \).

Fig. 1
figure 1

The DEM simulation domain, with 7956 particles flowing over a rough inclined surface (1.2d thick, in grey) and made of immobile particles, with mean tilt \(\zeta =24^\circ \). The periodic boundaries are illustrated with grey planes. The insets show the direction of the Coriolis acceleration \(\varvec{a}_{\mathrm {Co}}\) as a function of the direction of the rotational velocity \(\omega \) and the flow direction \(\varvec{u}\)

Full size image

The Coriolis acceleration has profound, yet poorly understood, effects on the flow structure. When it is dilative, it can increase the flow speed, and potentially cause instabilities [6]. However, threshold operational conditions that lead to a loss of stability have not yet been determined precisely. In this paper, we address this issue, analysing a set of numerical experiments where the effects of the Coriolis acceleration are identified and quantitatively analyzed.

2 Numerical model and simulation campaign

A DEM flume simulation environment is set up, based on the model by [19]. We generate an assembly of particles and place them on an inclined plane with constant slope \(\zeta =24^\circ \) and with prescribed roughness, as in [25]. We aim at reproducing the simplest granular flow that exhibits Coriolis-induced effects, in order to magnify the effects themselves. We therefore adopt spherical monodisperse particles, and neglect the presence of an interstitial fluid. The particles have mean diameter \(d=0.1~\mathrm {mm}\) (\(\pm 10\%\)). The setup is illustrated in Fig. 1.

All material parameters are listed in Table 1. The particle contact model is linear and elasto-viscous in the normal and tangential directions, with a prescribed restitution coefficient. In the tangential direction, contact forces are capped by Coulomb friction [18]. The inter-particle friction coefficient is relatively high (0.5) with respect to real grains, e.g. sand [13]. However, this allows to benchmark the simulations with the data from [25]. The contact stiffness, like the friction coefficient, does not refer to any specific material. It is however sufficiently high to make compressibility effects negligible [24], and the particles can thus be considered rigid.

Table 1 Material parameters used in the numerical simulations
Full size table

The model boundaries in x and z are periodic (see Fig. 1). Flow dimensions are of the order of 20d in x, 10d in z, and \(h=35d=35~\mathrm {mm}\) in y. In these conditions, [25] showed that stable flows can be obtained if \(22< \zeta < 26 \), with limited finite particle size effects. The particles are immersed in a centrifugal acceleration field generated by the rotation of the reference frame. The conditions in the model are equivalent to an increased-gravity environment, in the form of \(Ng \equiv \omega ^2 R\).

The DEM simulations are launched with the initial steady-state conditions obtained with a simple 1g gravity field (\(N=1, R\rightarrow \infty \)). Then, the flow is accelerated with the prescribed centrifugal acceleration \(a_\mathrm {cf}=Ng\) until convergence of mean flow variables (mean speed \(u_x\), obtained by ensemble-averaging over all particles, and mean solid volume fraction \(\phi \)) is achieved. All simulations are performed without a gravitational acceleration g along the z-axis.

In this paper, we analyze simulated flows obtained with different values of \(\omega \), tuned to obtain different scaling factors \(N=[1,~2,~5,~10,~20,~50]\). Each acceleration state is in turn tested within centrifuges with normalized radius R/h increasing from 10 to \(10^5\). Due to the shape of the centrifugal acceleration field, the particles experience a sudden change in centrifugal acceleration when crossing the periodic boundaries in x. However, this difference is minimal, and reduces dramatically as the radius increases. For \(R/h=10^2\), it is already smaller than \(2\%\), and drops to \(0.002\%\) for \(R/h=10^5\). Therefore, the system approximates uniform-acceleration conditions increasingly well even with periodic boundaries.

All geotechnical centrifuges currently available in laboratories worldwide have sizes that fall within the simulated range [29, sites.google.com/view/issmgetc104/facilities/statistics]. This range includes also simulations that feature very large radii, up to \(R=350~\mathrm {m}\). While these values are clearly beyond the typical size of laboratory equipment, they are still interesting, because they represent ideal systems where the Coriolis-induced effects are minimal.

3 Coriolis-induced flow instability

Under the assumption that the flow is in a dense state and with constant solid fraction \(\phi =\phi _0\), a simplified continuum approach can be used to describe the flow using field variables [10]. When \(R\gg h\), the normal stress \(\sigma _{y}\) can be approximately written, from Eq. 1, as a function of depth:

$$\begin{aligned} \sigma _{y}(y) = \int _y^h \rho \phi _0 a_y \mathrm {d}y = \rho \phi _0 \left( u^{*2}\frac{h-y}{h} - 2\omega \int _y^h u(y)\mathrm {d}y\right) , \end{aligned}$$
(2)

with \(u^*=\sqrt{\omega ^2 Rh\cos \zeta }\) as the flow characteristic velocity. The exact profile of u(y) can however be hardly guessed a priori. [8], confirmed that a Bagnold-like profile \(u\propto y^{2/3}\) can be recovered only if the Coriolis acceleration is negligible. However, this particular case has limited practical relevance, because the Coriolis acceleration is always present.

In dense granular flows the main resistance to shear is provided by friction:

$$\begin{aligned} \tau _{xz}(y)=\mu (I) \sigma _{y}(y), \end{aligned}$$
(3)

where \(\mu \) is the bulk friction coefficient, which is a function of the Inertial number I [16]. In the DEM simulations presented here, \(\omega \) is negative and the Coriolis acceleration is dilative. Consequently, the normal stress \(\sigma _{y}(y)\) is diminished. This is accompanied by a reduction in shear resistance \(\tau _{xz}\), which causes the flow to accelerate, reaching steady state for lower values of \(\sigma _{y}(y)\), see Eq. 2.

A sample of steady-state surface velocities, \(u(y=h)\), obtained in DEM simulations with three different setups are presented in Fig. 2. The gray line reports results obtained by [8] when turning off the Coriolis acceleration in the simulations. In this simplified benchmark, the acceleration field is constant and uniform, and can be written as an amplification of gravity by the scaling factor N: \(a=Ng\). These conditions are ideal: the flow remains in a dense state, the dependence between normal and shear stress is linear, and the velocity field can be predicted by:

$$\begin{aligned} u(y) = \frac{2}{3}\frac{I h}{d}u^*\left( 1-\left( 1-\frac{y}{h}\right) ^{3/2}\right) , \end{aligned}$$
(4)

However, this setup cannot be reproduced in physical experiments, where the Coriolis acceleration cannot be neglected, and therefore has only value as a theoretical benchmark.

Figure 2 also reports with red lines the results obtained by [8] with the full acceleration field (Eq. 1), including of a compressive Coriolis acceleration (\(\omega ^+\)). The comparison between this data set and the \(a=Ng\) benchmark highlights the effect of the Coriolis acceleration: the flow is dense and stable, but markedly slower, due to the enhanced normal stress. Simple scaling does not hold true, because the velocity exhibits a dependence on the radius, in addition to N.

Finally, Fig. 2 displays with blue lines the results we obtained with the full acceleration field, and a dilative Coriolis acceleration (\(\omega ^-\)). In this case, the normal stress is reduced, and shear stresses are less effective in dissipating energy. This results in faster, and potentially unstable, flows with respect to the \(a=Ng\) benchmark. In fact, the figure only reports those simulations that reached a stable stationary state, such as the one graphically illustrated in Fig. 3a. In these cases, the Coriolis acceleration does not significantly alter the flow fabric, \(\phi \) is not changed significantly, and the flow is still in a dense state.

The increase in R reduces the effects of both compressive and dilative Coriolis accelerations, and the results move closer to the \(a=Ng\) benchmark. It can be noted that prohibitively large values of R are required for obtaining a good approximation of Coriolis-free conditions.

Fig. 2
figure 2

Variation of the surface velocity as a function of the equivalent scaling factor N, for all simulations where a dense, stable configuration has been achieved. Results obtained in simulations without the Coriolis acceleration (\(a=Ng\)), and those obtained using a compressive Coriolis acceleration (\(\omega ^+\)), are reported from [8]

Full size image
Fig. 3
figure 3

Illustration of the dilative effect of the Coriolis acceleration. The three snapshots depict flows obtained within a centrifuge with radius \(R=11.1~\mathrm {m}\) (\(R/H\approx 3000\)), which is spinning at different speeds corresponding to \(N=5,20,50\). Depending on this velocity, the Coriolis acceleration can a have a minimal effect on the flow structure, which remains dense, b promote the development of a dilute upper layer, or c disrupt the flow coherence, with particles moving chaotically over the domain. All snapshots are taken at identical simulation time \(t=1.2~\text {s}\), measured from the instant of application of the centrifugal acceleration field. The simulations at \(N=5\) and \(N=20\) (dense and dilute, respectively), are in steady state at this time

Full size image

When the Coriolis acceleration is dilative, its effect can also be seen as a reduction of the particles’ self weight. Consider Fig. 3a. Here, the Coriolis acceleration is larger for those particles that flow with the highest velocity u, i.e. those at the top (\(y=h\)). When the Coriolis acceleration is high, these particles can reach the condition \(a_{y}=0\) (see Eq. 1), losing contact with the flow body. This has the potential to disrupt the flow structure by causing the formation of a dilute layer at the top, as illustrated in Fig. 3b.

Whether dense or dilute, the flows exhibit velocity profiles at steady state that are severely affected by the Coriolis acceleration. In Fig. 4a, the velocity profiles obtained with and without the Coriolis acceleration are compared. The profiles are extracted from the same simulations described in Fig. 3a–b, and are scaled by \(u^*\). Equation 4 describes the profile that develops in the \(a=Ng\) benchmark. Although all curves exhibit similar shapes, reminiscent of the Bagnold profile, those obtained with the Coriolis acceleration are faster. This is in agreement with Fig. 2. Another evident effect induced by the Coriolis acceleration is a generalized dilation of the flow. This is evident from Fig.  4b, which shows the variation of \(\phi \) over height. The simulation with \(N=20\) is far more dilute, with \(\phi \) overall lower than the reference mean volume fraction \(\phi _0=0.565\), which is obtained in the \(a=Ng\) benchmark. The dilute layer, where the particle fabric is looser covers the upper half of the profile. These effects are much less marked at \(N=5\), where \(\phi \) exhibits a reduced variability over the height, and is overall very close to \(\phi _0\).

Fig. 4
figure 4

Samples of the scaled velocity \(u/u^*\) (a) and solid volume fraction \(\phi \) (b) profiles obtained at steady-state for simulations in the dense and dilute regime. For reference, the dashed lines show the profiles that would develop if the Coriolis acceleration were to be neglected (the \(a=Ng\) benchmark)

Full size image

Within the dilute layer, the only source of energy dissipation is the mutual collision of the saltating particles, which is much less effective in decelerating the flow than friction. Thus, once the dilute layer has formed, the flow typically accelerates indefinitely, with a growing thickness of the dilute layer. This is graphically illustrated in Fig. 5. The simulations with the largest radius quickly achieve steady conditions, while those with the smaller radius exhibit an exponential growth in velocity together with a drastic dilation of the flow (\(\phi \rightarrow 0\)), and are therefore labelled as unstable, see Fig. 3c.

Fig. 5
figure 5

Variation in time of surface velocity and solid fraction of the flow. Different lines correspond to different values of the centrifuge radius R for simulations at \(N=50\)

Full size image

In a real centrifuge, an unstable flow of this type not only invalidates the test, but also causes the grains to disperse within the model box, moving chaotically at high speed. This comes with high risk of damaging the model and its instrumentation. It is therefore a condition that should be carefully avoided. Unfortunately, a secondary effect of the flow transition from dense to dilute is the impossibility to describe its rheology using a simple constitutive model. A unified framework able to describe the rheology both in the dense and in the dilute regime is still under development [27]. For this reason, we use the DEM simulations to empirically determine which centrifuge operative conditions are potentially dangerous.

To do this, we collect the results obtained with the parametric matrix, grouped in three categories that correspond to the states described in Fig. 3: dense, dilute, and unstable. The result of this procedure is illustrated in Fig. 6. For a given N, if the centrifuge radius R is large, the Coriolis acceleration is small (ideally, \(a_\text {Co}=0\) for \(R\rightarrow \infty \)). Thus, simulations are stable (dense, as in Fig. 3a), and the system well approximates the desired scaled field conditions. Conversely, when the radius is small, the centrifuge must spin at a higher velocity to achieve the prescribed scaling factor N. As a consequence, the Coriolis acceleration increases, not only in absolute terms, but also with respect to the centrifugal acceleration. If the radius is small (red area in Fig. 6), the Coriolis acceleration leads the system towards the unstable state described by Fig. 3c. The narrow yellow band in Fig. 6 gathers all dilute simulations.

Fig. 6
figure 6

Phase diagram of flow states (dense, dilute, unstable) within a centrifugal acceleration field with a dilative Coriolis acceleration

Full size image

To quantitatively determine the threshold conditions between dense and unstable flow, we refer to the analytical solution for the surface velocity conditions derived by [8] for the dense state:

$$\begin{aligned} u(h) = \frac{2}{3}\frac{I h}{d}u^*(1+\frac{1}{3} \phi \mathrm {Co}), \end{aligned}$$
(5)

where \(\mathrm {Co}=I u_\mathrm {Co} / u^*\) is the dimensionless group that measures the influence of the Coriolis acceleration on the velocity field. The term \(u_\mathrm {Co} = -\omega h^2/d\) is the Coriolis characteristic velocity. The Inertial number has been empirically found to grow as \(I=I_0 N^{1/6}\) [8], with \(I_0=0.08\) as the Inertial number measured at simple gravity (\(N=1\)).

The applicability of Eq. 5 is severely limited by the assumption of a constant volume fraction \(\phi =\phi _0\); our analysis clearly illustrates that this is not always the case. Even the simulations that achieve a steady state exhibit flows with a lower density with respect to the reference case (\(a=Ng\)), albeit slightly. Thus, Eq. 5 cannot be used to predict the flow velocity quantitatively. Nevertheless, \(\text {Co}\) is found to be a good indicator of the degree of alteration of the velocity field induced by the Coriolis acceleration. This is because its formulation takes into account the mutual dependence of velocity and stresses described by Eq. 2, and is therefore capable of qualitatively capture many flow features, including the limit conditions that determine instability. In our case, we find that all simulations with \(\mathrm {Co}<0.06\) are in the dense regime, and a dilute layer does not form. Additionally, we find that all simulations with \(\mathrm {Co}>0.1\) are unstable. This is graphically illustrated by Fig. 7, where the mean solid volume fraction of the flow at steady state is plotted as a function of \(\mathrm {Co}\). This threshold helps in avoiding unsafe or, at a minimum, unrepresentative conditions in the centrifuge.

Fig. 7
figure 7

Final, steady-state values of mean volume fraction for all DEM simulations as a function of the Coriolis factor \(\mathrm {Co}\). The color corresponds to the type of achieved steady-state conditions: dense, dilute, and unstable (see Fig. 6). The vertical line points to the identified threshold value for dense flows (\(\mathrm {Co} = 0.1\)), and the dashed line provides a guide of the flows state transition

Full size image

4 Conclusions

In this paper, we present a numerical study of granular flows within a centrifugal acceleration field, exploring the effects of a dilative Coriolis acceleration. The numerical model mimics the conditions of a geotechnical centrifuge. While still relying on approximations, the numerical environment has the advantage of simplifying many technological issues that affect geotechnical centrifuges. Most importantly, it provides guidance on how to reach steady-state conditions in real centrifuge experiments.

Using this tool, we described and quantitatively estimated the consequences of the Coriolis acceleration on the type of achieved steady conditions. We performed a parametric study by varying the scaling factor N and the centrifuge radius R. The conclusions can be summarized as follows:

  • The Coriolis acceleration can have either dilative or compressive effects on the flow. When compressive, it can aid in stabilizing the flow (as shown by [8]). When dilative, it allows to obtain faster flows, but it also becomes a potential source of instability.

  • When the Coriolis acceleration is dilative, it is still possible to obtain stable flows. However, only a limited set of possible operational conditions appear to guarantee stability. These however demand the use of a very large centrifuge radius, which becomes even larger if the experiments aim at achieving high scaling factors N.

  • The reference value of the Coriolis factor \(\mathrm {Co}<0.1\) can be used for a preliminary assessment of whether the flow will achieve steady dense conditions or not.

In the future, it would be of great interest to verify these results experimentally, although we recognize that performing physical tests with different centrifuge radii might be prohibitively complex. In any case, running such tests would require to deal with potentially unstable flows. We recommend to pay meticulous attention at confining the flow, in order to avoid damage to the experimental apparatus and model instrumentation. Furthermore, the analytical results show that changing the particle diameter could have an influence on the flow conditions. Future work aims at clarifying this aspect.