Abstract
This paper presents the numerical modelling of initial powder compaction and pressure-assisted sintering performed by original viscoelastic discrete element model. The research is focused on the influence of the type of the model representing an elastic part of interparticle force. Two elastic contact models—linear and nonlinear Hertz model—have been implemented and used to analyse interaction of NiAl powder particles during compaction and sintering process. Numerical models have been validated using own experimental results. Microscopic effects (particle penetration) and macroscopic changes (relative density) have been compared. It has been shown that although both models represent properly macroscopic behaviour of the material at the sintering process, the Hertz model produces the results closer to the real experimental ones during the initial compaction stage. Evaluation of macroscopic quantities enables implementation of the discrete element model in the framework of the multiscale modelling framework which is currently developed for sintering processes.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
The discrete element method (DEM) is a relatively new numerical method developed intensively at present time by many investigators [1,2,3]. In DEM, a material is represented by a large assembly of particles interacting among one another with contact forces. A particle interaction model in the DEM can take into account different effects, which are related to the specific model application. The formulation of appropriate contact interaction of particles seems to be an essential requirement to model properly the material behavior in the macroscopic scale. Currently, DEM is a widely acceptable method and has become a popular and useful tool for modeling discrete systems, such as a powder particles interactions in the powder metallurgy processes [4,5,6]. Generally, the manufacturing process of powder metallurgy consists of initial powder compaction and pressure-assisted sintering, which is the most important stage of powder metallurgy processes. It involves the consolidation of bonded powders at elevated temperatures, close to the melting temperature. Modelling of powder metallurgy and sintering processes requires a special constitutive model for particle contact interaction in which the sintering driving forces, viscosity, elasticity, cohesive and thermal interactions play a significant role. Although deformation during sintering itself is governed mainly by the viscosity, the material does maintain certain elasticity [7, 8]. Elastic effects influence the distribution of forces in the heterogeneous particulate material and have some importance to the evaluation of stresses during the initial compaction and pressure-assisted sintering process.
Rheological schemes of: a cohesionless contact model with friction, b viscoelastic model of sintering [16]
Elastic (or elastoplastic) effects modeled by DEM can be represented by several models. The most basic one—linear model, assumes the linear relation between the elastic normal force and particles penetration. The non-linear Hertz model was performed on the majority of elastic or elasto-plastic models of powder compaction, such as [9]. More complicated (representing also plastic deformation) is the linear hysteretic spring model [1, 10, 11], which is the simplest version of some more complicated nonlinear-hysteretic force laws [10, 12]. A simple linear elastoplastic and adhesive contact model for spherical particles has been proposed in [13]. Plastic deformation of contacts during loading and elastic unloading, accompanied by adhesion are considered, for which the pull-off force increases with plastic deformation. A model assuming rigid plastic behaviour according to the Hollomon stress–strain curve has been developed by Storåkers et al. [14, 15].
In the following paper the theoretical and numerical results from two most popular/classic elastic models employed as a components of viscoelastic discrete element model of powder metallurgy have been compared. The influence of linear and nonlinear Hertz model on the densification during initial compaction and sintering stage has been investigated. Moreover, the numerical results have been compared and validated by own experimental results. Proposed work is an extension of original viscoelastic discrete element model of sintering presented in [16].
2 Formulation of discrete element model
The numerical model of initial compaction and pressure-assisted sintering has been implemented within the framework of the discrete element method (DEM), which assumes that a particulate material can be represented as a collection of spherical particles interacting among one another. In the discrete element method, the motion of rigid spherical elements (particles) is governed by the standard equations of rigid body dynamics.
The presented discrete element model is a combination of the cohesionless contact model with friction (the Kelvin–Voigt system—Fig. 1a) for the initial powder compaction, heating (before sintering) and cooling (after sintering), and the viscoelastic model of sintering (the Maxwell system—Fig. 1b) with the addition of thermal element related to the effect of thermal expansion. The equations of motion has been integrated in time using an explicit central difference type algorithm, the so-called leap-frog method. The detailed formulation of models is described in [16].
The normal contact interaction for the initial powder compaction consists of a spring and a dashpot connected in parallel, thus the normal contact force \(F_\mathrm{n} \) is a sum of the elastic force in the spring \(F_\mathrm{n}^\mathrm{e} \) and the viscous component \(F_\mathrm{n}^\mathrm{d}\):
Presented research considers two elastic models—linear (LM) and nonlinear Hertz model (HM)—as a components of the Kelvin–Voigt and Maxwell models. In the case of LM, the relation between the elastic normal force \(F_\mathrm{n}^\mathrm{e} \) and penetration \(u_\mathrm{n}^\mathrm{e}\) of outer particles surfaces is linear and it can be represented by the formula [17]:
where \(k_\mathrm{n}\) is the particles stiffness determined similarly to [17]:
where \(\beta \) is the scaling parameter, E is Young’s modulus, \(r_{\mathrm{eff}}\) is the effective radius:
where \(r_i \) and \(r_j \) are particles radii.
Alternatively, the elastic part of the normal contact force \(F_\mathrm{n}^\mathrm{e} \) can be presented in the form of the Hertz interaction model, which is the most classical nonlinear model used in particle collisions:
where \(E_{\mathrm{eff}}\) is the effective modulus of elasticity defined in terms of the Young’s moduli, \(E_{i}\) and \(E_{j}\), and the Poisson’s ratios, \(\nu _{i}\) and \(\nu _{\mathrm{j}}\), of the two contacting particles:
The normal stiffness \(k_{\mathrm{n}}\) of Hertz model depends on the particle penetration \(u_\mathrm{n}^\mathrm{e}\) and it can be obtained as the derivative of the relationship (5):
Penetration for particles indicating a spherical shape \(u_\mathrm{n}^\mathrm{e}\) is given by following equation consistent for both linear and Hertz model:
where d is the distance between particles centers, \({\upalpha }\) is thermal expansion coefficient and \(\Delta T\) is temperature increment.
The second component of Kelvin–Voigt model is the viscous one \(F_\mathrm{n}^\mathrm{d} .\) It can be assumed to be a linear function of the normal relative velocity \(\hbox {v}_{\mathrm{rn}} \):
where \(c_\mathrm{n} \) is the viscosity coefficient given as a fraction \({\upxi }\) of the system of two rigid bodies with the masses of \(m_i \) and \(m_j\) connected with a spring with the stiffness \(k_\mathrm{n} \), which is given by Eqs. (3) or (7) for linear and Hertz models, respectively.
The tangential force in the Kelvin–Voight model has been calculated using an algorithm based on the Mindlin and Deresiewicz non-slip solution of the contact problem [18], which is commonly used in the framework of the DEM, cf. [19]. The tangential force \(F_{\mathrm{s}}\) is calculated incrementally, and its increments are given by the following expression:
where \(k_{\mathrm{s}}\) is the tangential stiffness described in [20], \(\hbox {v}_{\mathrm{rs}}\) is the relative tangential velocity and \(\Delta t\) is the time step.
The tangential stiffness \(k_\mathrm{s} \) depends on the equivalent shear modulus \(G_{\mathrm{eff}}\) and the particle overlap h:
The tangential force \(F_{\mathrm{s}}\) is limited by the Coulomb friction:
where \(\mu \) is the Coulomb friction coefficient.
The formulation of initial compaction model has considered only the elastic deformation of particles. Presented analysis concerns the relatively low values of external pressure and the hard and brittle NiAl material, thus the contribution of elastic deformation in the total one is a predominant. This effect has been studied in [20].
The viscoelastic model of sintering considers both elastic \(F_\mathrm{n}^\mathrm{e}\) and viscous \(F_\mathrm{n}^\mathrm{v}\) element connected in series (Fig. 1b). Presented Maxwell model indicates the equality of elastic and viscous forces and additive decomposition of the relative normal velocity between particles \(v_{\mathrm{rn}} \) into the elastic and viscous parts, \(v_{\mathrm{rn}}^\mathrm{e}\) and \(v_{\mathrm{rn}}^\mathrm{v}\), respectively. Taking into account following assumptions, we obtain the evolution equation for the force in the Maxwell branch:
where \(F_\mathrm{n}^\mathrm{v}\) is the viscous force resulting from the mass transport mechanism of grain boundary diffusion during sintering process [6]:
where \(\eta \) is the viscosity coefficient, a is the radius of cohesive neck and \(D_{\mathrm{eff}}\) is the effective grain boundary diffusion coefficient:
where \(\delta \) is the thickness of the grain boundary, \({\varOmega }\) is atomic volume, k is the Boltzmann constant, T is the temperature and. \(D_{\mathrm{gb}}\) is grain boundary diffusion coefficient dependent on temperature:
where \(D_{\mathrm{0gb}}\) is the pre-exponential factor of grain boundary diffusion, \({\varDelta } H_{\mathrm{gb}}\) is the activation enthalpy of grain boundary diffusion, R is the gas constant.
The force in Maxwell branch is balanced by sintering driving force \(F_\mathrm{n}^{\mathrm{sint}} \) resulting from surface tension on particles grain boundary [6]:
where \({\varPsi }\) is the dihedral angle and \({\upgamma }_{\mathrm{s}}\) is the surface energy.
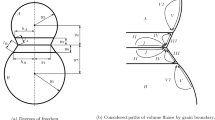
The initial neck radius \(\hbox {a}_0 \) depends on the initial penetration \(\hbox {u}_0 \) induced by the compaction. From simple geometrical considerations we have:
The growth of the radius of the interparticle grain boundary is governed by the following evolution law:
The grain boundary radius a grows until the sintering process is stopped. Its maximum at the equilibrium state is given by the following geometric relationship:
where \(\Psi \) is the dihedral angle determined according to the Young’s law which assumes that in the system consisting of two grains and a gas in the pore in the equilibrium we have equilibrium of surface tensions. The geometric parameters are defined in Fig. 2.
Following Martin et al. [21] the rotational motion of the particles and tangential interaction has been neglected in the present formulation of sintering. This should be favorable for particle rearrangements.
3 Numerical results and discussion
Analogously to work performed in [20], a detailed investigation of interaction of two equal NiAl particles (with radii \(\hbox {R} = 10 {\upmu }\hbox {m}\)) under compression has been carried out using the two elastic contact models presented earlier. The purpose of this study was to compare the force–penetration relationships for different models and model parameters (Table 1). In order to estimate of the external pressure exerted on the particle assembly, which is illustrated graphically in Fig. 3, the equations of LM and HM (Eqs. 2 and 5) have been transformed by dividing both sides by \(4R^{2}\):
It can be seen in Fig. 4 that the HM predicts a softer behavior in the standard range of hot pressing pressure up to 50 MPa. In the case of LM, it indicates much higher stiffness, thus it produces higher resistance for particle penetration in the standard range of hot pressing pressure. Presented micromechanical analysis can be helpful to explain the mechanism during DEM simulations of initial powder compaction and further sintering of large particle assembly.
Maintaining the original particle size and particle size distribution (Fig. 5) determined experimentally [20], a cylindrical container of diameter \(200 \,{\upmu }\hbox {m}\) has been filled with 1751 particles (Fig. 6). Due to the size of DE model, the temperature evolution is prescribed and uniformly distributed in the specimen (heat transfer is neglected) similarly as in [21, 22]. It has been assumed that such a reduced geometric model with real particles size represents correctly initial compaction and sintering process in a real specimen with diameter of 120 mm. Moreover, intermetallic NiAl particles indicate the spherical shape (Fig. 7). This particular feature of applied powder can be great advantage of application of discrete element method and further validation of experimental and numerical results.
The particle specimen has been used in simulations of the die compaction and sintering. The powder placed in the cylinder has been subjected to the uniaxial compression exerted by the top plate loaded with a linearly rising pressure. Figure 8 presents the temperature and pressure profiles of simulation in sintering temperature of \(1400\,{^{\circ }}\hbox {C}\), sintering time of 30 min and external pressure of 30 MPa. As it can be seen, the transition of DEM models (from KV to Maxwell) occurs at the 0.5 of the melting point which corresponds to activation of grain boundary diffusion processes. From this point, the sintering starts, which is accompanied by activation of sintering driving force.
The values of parameters has been determined by own reference studies presented in [23] and confirmed with experimental data giving good correspondence [24,25,26]. The activation enthalpy of grain boundary diffusion, \(\Delta \hbox {H}_{\mathrm{gb}}\), has been treated as a fitting parameter. The obtained value of \(\Delta \hbox {H}_{\mathrm{gb}}\) of intermetallic material is in correspondence with experimental measurements [27] and the empirical approximation for BCC materials (NiAl) [28].
Figure 9 presents the evolution of relative density of NiAl specimen during initial powder compaction and pressure-assisted sintering. Moreover, the graph shows the experimental results obtained by own studies, which have been widely described in [16, 20, 29]. The whole simulation has been divided into subsequent stages: loading, heating, sintering, cooling and unloading. The results show that the discrete element model reproduces correctly macroscopic behavior of the material during each stages of hot pressing process. It can be seen the substantial growth of relative density during initial compaction (loading) and sintering stage just after transition from Kelvin–Voigt to Maxwell model. As it can be expected, the heating and cooling stages are accompanied by keeping the relative density at the same level.
Numerical simulations have been performed by both HM and LM as elastic part of Kelvin Voight and Maxwell models. Analyzing the simulation performed in 30 MPa of pressure, it can be seen visible change of material densification between HM and LM during the loading stage (Fig. 10). From the beginning we have a high densification rate for both models in the initial phase caused by particle rearrangement and the density changes slower in the later phase, at a higher density, when the rearrangement of the particles is more difficult. In the intermediate and final stage the deformation of the particles becomes a more important densification mechanism. The evolution of the relative density predicted by HM is similar to that determined experimentally in the contrast to LM. Due to the lower stiffness, the densification of HM specimen is higher and before heating and sintering process the material indicates the relative density close to the experimental one. Differences between the numerical results obtained with different models are relatively large. This is because the differences between the force–indentation curves predicted by the compared models in the range of contact pressure in our studies are relatively high, cf. Fig. 4.
Evolution of relative density of NiAl specimen as a function of pressure for the linear and Hertz model. Comparison of numerical and experimental results [20]
Obtained results of LM have been performed by taking \(\beta \) parameter as 0.5. Better agreement between results from LM model and experiment can be achieved, however it requires the performance of calibration procedure by fitting numerical results to experimental one by changing value of \(\beta \). The advantage of Hertz model refers to the fact, that it does not require the calibration and predicts the powder densification without any parameter variation.
The sintering stage brought the similar results between two considered models (Fig. 9). Both LM and HM represent quite well density changes. At the initial stage relative density increase faster due to the lower material resistance caused by low viscosity. As the temperature achieves the sintering temperature, the material density stabilizes. The numerical results of 5 and 30 MPa are compared with the experimental data showing quite a good agreement.
4 Conclusions
This paper presents the numerical and experimental analysis of hot pressing of NiAl powder with an emphasis on the best possible representation of its main stages: initial powder compaction and pressure-assisted sintering. The numerical study has been performed within the discrete element framework. In the paper, an original viscoelastic model of hot pressing has been used. The present work has been aimed to compare the elastic linear and Hertz models as the components of discrete element models of initial powder compaction and pressure-assisted sintering. Numerical models have been validated using own experimental results. Microscopic effects (particle penetration) and macroscopic changes (relative density) have been compared. As the numerical results are quite similar in the sintering stage, the initial compaction (loading stage) indicates the substantial differences in the case of higher external pressure (30 MPa). Especially for these conditions, Hertz model is more realistic and gives better agreement with experimental results. Due to the higher stiffness, linear model shows less penetration relative to Hertz one, which was confirmed by simply analysis of two-particle compression.
References
Luding, S.: Cohesive frictional powders: contact models for tension. Granul. Matter 10(4), 235–246 (2008)
Antony, S.J., Kruyt, N.P.: Role of interparticle friction and particle-scale elasticity in the shear-strength mechanism of three-dimensional granular media. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 79, 031308 (2009)
Balakrishnan, A., Pizette, P., Martin, C.L., Joshi, S.V., Saha, B.P.: Effect of particle size in aggregated and agglomerated ceramic powders. Acta Mater. 58, 802–812 (2010)
Martin, C.L., Schneider, L.C.R., Olmos, L., Bouvard, D.: Discrete element modeling of metallic powder sintering. Scr. Mater. 55, 425–428 (2006)
Martin, S., Guessasma, M., Léchelle, J., Fortin, J., Saleh, K., Adenot, F.: Simulation of sintering using a non smooth discrete element method. Application to the study of rearrangement. Comput. Mater. Sci. 84, 31–39 (2014)
Parhami, F., McMeeking, R.: A network model for initial stage sintering. Mech. Mater. 27, 111–124 (1998)
Langlois, V., Jia, X.: Ultrasonic monitoring of the elastic properties of PMMA bead packings and their rearrangement during pressure sintering. Powder Technol. 208, 509–514 (2011)
Latella, B.A., Liu, T.: High-temperature Young’s modulus of alumina during sintering. J. Am. Ceram. Soc. 88, 773–776 (2005)
Martin, C.L., Bouvard, D., Shima, S.: Study of particle rearrangement during powder compaction by the discrete element method. J. Mech. Phys. Solids 51, 667–693 (2003)
Walton, O.R., Braun, R.L.: Viscosity, granular-temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. J. Rheol. 30(5), 949–980 (1986)
Luding, S.: Collisions & Contacts between two particles. In: Herrmann, H.J., Hovi, J.-P., Luding, S. (eds.) Physics of Dry Granular Media—NATO ASI Series E350, p. 285. Kluwer Academic Publishers, Dordrecht (1998)
Zhu, C.Y., Shukla, A., Sadd, M.H.: Prediction of dynamic contact loads in granular assemblies. J. Appl. Mech. 58, 341 (1991)
Pasha, M., Dogbe, S., Hare, C., et al.: A linear model of elasto-plastic and adhesive contact deformation. Granul. Matter 16, 151 (2014). doi:10.1007/s10035-013-0476-y
Storåkers, B., Biwa, S., Larsson, P.-L.: Similarity analysis of inelastic contact. Int. J. Solids Struct. 34, 3061–3083 (1997)
Storåkers, B., Fleck, N.A., McMeeking, R.M.: The viscoplastic compaction of composite powders. J. Mech. Phys. Solids 47, 785–815 (1999)
Nosewicz, S., Rojek, J., Pietrzak, K., Chmielewski, M.: Viscoelastic discrete element model of powder sintering. Powder Technol. 246, 157–168 (2013)
Rojek, J., Labra, C., Su, O., Oñate, E.: Comparative study of different discrete element models and evaluation of equivalent micromechanical parameters. Int. J. Solids Struct. 49, 1497–1517 (2012)
Mindlin, R.D., Deresiewicz, H.: Elastic spheres in contact under varying oblique forces. ASME J. Appl. Mech. 20, 327–344 (1953)
Di Renzo, A., Di Maio, F.P.: Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 59, 525–541 (2004)
Rojek, J., Nosewicz, S., Jurczak, K., Chmielewski, M., Bochenek, K., Pietrzak, K.: Discrete element simulation of powder compaction in cold uniaxial pressing with low pressure. Comput. Part. Mech. (2016). doi:10.1007/s40571-015-0093-0
Martin, C.L., Schneider, L.C.R., Olmos, L., Bouvard, D.: Discrete element modeling of metallic powder sintering. Scr. Mater. 55, 425–428 (2006)
Henrich, B., Wonisch, A., Kraft, T., Moseler, M., Riedel, H.: Simulations of the influence of rearrangement during sintering. Acta Mater. 55, 753–762 (2007)
Nosewicz, S.: Discrete element modeling of powder metallurgy processes. Ph.D. thesis, Institute of Fundamental Technological Research, Warsaw, Poland (2016). doi:10.13140/RG.2.1.5102.7444
Kitabjian, P.H., Nix, W.D.: Atomic size effects in Nial based solid solutions. Acta Metall. 46, 701–710 (1998)
Frank, S., Divinski, S.V., Sodervall, U., Herzig, Ch.: Ni tracer diffusion in the B2-compound NiAl: influence of temperature and composition. Acta Mater. 49, 1399–1411 (2001)
Amouyal, Y., Rabkin, E., Mishin, Y.: Correlation between grain boundary energy and geometry in Ni-rich NiAl. Acta Mater. 53, 3795–3805 (2005)
Hancock, G.F., McDonnel, B.R.: Diffusion in the intermetallic compound NiAl. Phys. Status Solidi (A) 4(1), 143–150 (1971)
Brown, A.M., Ashby, M.F.: Correlations for diffusion constants. Acta Metall. 28, 1085–1101 (1980)
Chmielewski, M., Nosewicz, S., Pietrzak, K., Rojek, J., Strojny-Nędza, A., Mackiewicz, S., Dutkiewicz, J.: Sintering behavior and mechanical properties of NiAl, Al\(_{2}\)O\(_{3}\), and NiAl-Al\(_{2}\)O\(_{3}\) composites. J. Mater. Eng. Perform. 23, 3875–3886 (2014)
Acknowledgements
The scientific work funded by the National Science Centre within a project awarded by Decision Number DEC-2013/11/B/ST8/03287 and DEC-2012/05/N/ST8/03376.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The kinetics of sintering during experiments have been evaluated by the study of the densification change in time. The sintering processes in sintering temperature of \(T_{\mathrm{S}} =1400\,{^{\circ }}\hbox {C}\) and external pressure of 5 and 30 MPa were interrupted at different time instants (measurement points) in order to study the evolution of density. The measurement points have been selected basing on the scheme in Fig. 11. The sintering degree was assessed based on the relative density, \(\rho _{\mathrm{rel}}\), defined as the ratio of the measured bulk (apparent) density \(\rho \) to the theoretical density \(\rho _{\mathrm{theo}}\) for the fully dense material:
Results of density measurements are provided in Table 2.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nosewicz, S., Rojek, J., Chmielewski, M. et al. Application of the Hertz formulation in the discrete element model of pressure-assisted sintering. Granular Matter 19, 16 (2017). https://doi.org/10.1007/s10035-016-0699-9
Received:
Published:
DOI: https://doi.org/10.1007/s10035-016-0699-9