Abstract
Extracting features from original signals is a key procedure for traditional fault diagnosis of induction motors, as it directly influences the performance of fault recognition. However, high quality features need expert knowledge and human intervention. In this paper, a deep learning approach based on deep belief networks (DBN) is developed to learn features from frequency distribution of vibration signals with the purpose of characterizing working status of induction motors. It combines feature extraction procedure with classification task together to achieve automated and intelligent fault diagnosis. The DBN model is built by stacking multiple-units of restricted Boltzmann machine (RBM), and is trained using layer-by-layer pre-training algorithm. Compared with traditional diagnostic approaches where feature extraction is needed, the presented approach has the ability of learning hierarchical representations, which are suitable for fault classification, directly from frequency distribution of the measurement data. The structure of the DBN model is investigated as the scale and depth of the DBN architecture directly affect its classification performance. Experimental study conducted on a machine fault simulator verifies the effectiveness of the deep learning approach for fault diagnosis of induction motors. This research proposes an intelligent diagnosis method for induction motor which utilizes deep learning model to automatically learn features from sensor data and realize working status recognition.
Similar content being viewed by others
1 Introduction
Failures often occur in manufacturing machines, which may cause disastrous accidents, such as economic losses, environmental pollution, and even casualties. Effective diagnosis of these failures is essential in order to enhance reliability and reduce costs for operation and maintenance of the manufacturing equipment. As a result, research on fault diagnosis of manufacturing machines that utilizes data acquired by advanced sensors and makes decisions using processed sensor data has been seen success in various applications [1,2,3]. Induction motors, as the source of actuation, have been widely used in many manufacturing machines, and their working states directly influence system performance, thus affecting the production quality. Therefore, proper grasping of data reflecting the working states of induction motors can obtain early identification of potential failures [4]. During recent years, various approaches for induction motor fault diagnosis have been developed and innovated continuously [5,6,7,8].
Artificial intelligence (AI)-based fault diagnosis techniques have been widely studied, and have succeeded in many applications of electrical machines and drives [9, 10]. For example, a two-stage learning method including sparse filtering and neural network was proposed to form an intelligent fault diagnosis method to learn features from raw signals [11]. The feed-forward neural network using Levenberg-Marquardt algorithm showed a new way to detect and diagnose induction machine faults [12], where the results were not affected by the load condition and the fault types. In another study, a special structure of support vector machine (SVM) was proposed, which combined Directed Acyclic Graph-Support Vector Machine (DAG-SVM) with recursive undecimated wavelet packet transform, for inspection of broken rotor bar fault in induction motors [13]. Fuzzy system and Bayesian theory were utilized in machine health monitoring in Ref. [14]. Although these studies have shown the advantages of AI-based approaches for induction motor fault diagnosis, most of these approaches are based on supervised learning, in which high quality training data with good coverage of true failure conditions are required to perform model training [15]. However, it is not easy to obtain sufficient labelled fault data to train the model in practice.
Furthermore, many fault diagnosis tasks in induction motors depend on feature extraction from the measured signals. The feature characteristics directly affect effectiveness of fault recognition. In the existing literature, many feature extraction methods are suitable for fault diagnosis tasks, such as time-domain statistical analysis, frequency-domain spectral analysis [16], and time-scale/frequency analysis [17], among which wavelet analysis [18], which belongs to time-scale analysis, is a powerful tool for feature extraction and has been well applied to processing non-stationary signals. Whereas, the problem is that different features extracted from these methods may affect the classification accuracy. Therefore, an automatic and unsupervised feature learning from the measured signals for fault diagnosis is needed.
Limitations above can be overcome by deep learning algorithms which follow an effective way of learning multiple layers of representations [19]. Essentially, a deep learning algorithm uses deep neural networks which contain multiple hidden layers to learn information from the input, but was not put into practice because of its training difficulty until Geoffrey Hinton proposed layer-wise pre-training algorithm to effectively train deep networks in 2006 [20]. Since then, deep learning techniques have been advanced significantly and their successful applications have been seen in various fields [21], including hand written digit recognition [22], computer vision [23,24,25,26], Google Map [27], and speech recognition [28,29,30]. In addition, For natural language processing (NLP), deep learning has achieved several successful applications and made significant contributions to its progress [31,32,33]. In the area of fault diagnosis, deep learning theory also has many applications. For example, deep neural network built for fault signature extraction was utilized for bearings and gearboxes [34], while a classification model based on deep network architecture was proposed in the task of characterizing health states of the aircraft engine and electric power transformer [35]. The deep belief network (DBN) was also used for identifying faults in reciprocating compressor valves [36]. Sparse coding was used to built deep architecture for structural health monitoring [37], and a unique automated fault detection method named “Tilear” using deep learning concepts was proposed for the quality inspection of electromotor [38]. Furthermore, auto-encoder based DBN model was successfully applied to quality inspection [39], while a sparse model based on auto-encoder was shown to form a deep architecture, which realized induction motor fault diagnosis [40].
Inspired by the prior research, this paper presents a deep learning model based on DBN for induction motor fault diagnosis. The deep model is built on restricted Boltzmann machine (RBM) which is the building unit of a DBN and by stacking multiple RBMs one by one, the whole deep network architecture can be constructed. It can learn high-level features from frequency distribution of measured signals for diagnosis tasks. Including this section, this paper is organized with 5 sections. Section 2 provides theoretical background of the deep learning algorithm. Section 3 presents the proposed fault diagnosis approach, where the deep architecture based on DBN is described in detail. Experiments are carried out in Section 4 to verify the effectiveness of the proposed deep model, where classification performance is discussed. Section 5 summarizes the whole study and gives future directions.
2 Theoretical Framework
The DBN is a deep architecture with multiple hidden layers that has the capability of learning hierarchical representations automatically in an unsupervised way and performing classification at the same time. In order to accurately structure the model, it contains both unsupervised pre-training procedure and supervised fine-tuning strategy. Generally, it is difficult to learn a large number of parameters in a deep architecture which has multiple hidden layers due to the vanishing gradient problem. To address this issue, an effective training algorithm, which learns one layer at a time and each pair of layers is seen as one RBM model, is proposed and introduced in Refs. [41, 42]. As DBN is formed by units of RBM, the basic unit of DBN, i.e., RBM, is introduced first.
2.1 Architecture of RBM
The RBM is a common used mathematical model in probability statistics theory and follows the theory of log-linear Markov Random Field (MRF) [36] which has several special forms and RBM is one of them. A RBM model contains two layers: One layer is the input layer which is also called visible layer, and the other layer is the output layer which also called hidden layer. RBM can be represented as a bipartite undirected graphical model. All the visible units of the RBM are fully connected to hidden units, while units within one layer do not have any connetion between each other. That is to say, there are no connection between visible units or between hidden units. The architecture of a RBM is shown in Figure 1.
In Figure 1, v represents the visible layer, i is the ith visible unit, h is the hidden layer, and j is the jth hidden unit. Connections between these two layers are undirected. An energy function is proposed to describe the joint configuration (v, h) between them, which is expressed as
Here, v i , and h j represent the visible unit i and hidden unit j respectively; a i , and b j are their biases. w ij denotes the weight between these two units. Therefore, the joint distribution of this pair can be obtained using the energy function where θ is the model parameter set containing a, b, and w:
Due to the particular connections in RBM model, it satisfies conditional independent. Therefore, conditional probability of this pair of layers can be written as:
Mathematically,
where σ(x) is the activation function. Generally, σ(x)=1/(1+exp(-x)) is adopted.
2.2 Training RBM
In order to set the model parameters, the RBM needs to be trained using training dataset. In the procedure of training a RBM model, the learning rule of stochastic gradient descent is adopted. The log-likelihood probability of the training data is calculated, and its derivative with respect to the weights is seen as the gradient, shown in Eq. (8). The goal of this training procedure is to update network parameters in order to obtain a convergence model.
Parameter update rules are originally derived by Hinton and Sejnowki, which can be written as:
where ε is the learning rate, the symbol <·> data represents an expectation from the data distribution while the symbol <·> model is an expectation from the distribution defined by the model. The former term is easy to compute exactly, while the latter one is intractable to compute [43].
An approximation to the gradient is used to obtain the latter one which is realized by performing alternating Gibbs sampling, as illustrated in Figure 2(a).
Later, a fast learning procedure is proposed, which starts with the visible units, then all the hidden units are computed at the same time using Eq. (6). After that, visible units are updated in parallel to get a “reconstruction” by Eq. (7), as illustrated in Figure 2(b), and the hidden units are updated again [44]. Model parameters are updated as:
In addition, for practical problems that come down to real-valued data, Gaussian-Bernoulli RBM is introduced to deal with this issue. Input units of this model are linear while hidden units are still binary. Learning procedure for Gaussian-Bernoulli RBM is very similar to binary RBM introduced above.
2.3 DBN Architecture
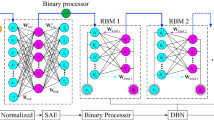
DBN model is a deep network architecture with multiple hidden layers which contain many nonlinear representation. It is a probabilistic generative model and can be formed by RBMs as shown in Figure 3. It illustrates the way of stacking one RBM on top of another. DBN architecture can be built by stacking multiple RBMs one by one to form a deep network architecture.
As DBN has multiple hidden layers, it can learn from the input data and extract hierarchical representation corresponding to each hidden layer. Joint distribution between visible layer v and the l hidden layers h k can be calculated mathematically from conditional distribution P(h k−1 |h k) for the (k–1)th layer conditioned on the kth layer and visible-hidden joint distribution P(h n−1, h n):
For deep neural networks, learning such amount of parameters using traditional supervised training strategy is impractical because errors transferred to low level layers will be faint through several hidden layers and the ability to adjust the parameters is weak for traditional back propagation method. It is difficult for the network to generate globally optimal parameters. Here the greedy layer-by-layer unsupervised pre-training method is used for training DBNs. This procedure can be illustrated as follows: The first step is to train the input units (v) and the first hidden layer (h 1) using RBM rule(denoted as RBM1). Next, the first hidden layer (h 1) and the second hidden layer (h 2) are trained as a RBM (denoted as RBM2) where the output of RBM1 is used as the input for the RBM2. Similarly, the following hidden layers can be trained as RBM3, RBM4,…, RBMn until the set number of layers are met. It is an unsupervised pre-training procedure, which gives the network an initialization that contributes to convergence on the global optimum.
For classification tasks, fine-tuning all the parameters of this deep architecture together is needed after the layer-wise pre-training, as shown in Figure 4. It is a supervised learning process using labels to eliminate the training error and improve the classification accuracy [45, 46].
3 DBN-based Fault Diagnosis
Based on the DBN, a fault diagnosis approach for induction motor has been developed, as illustrated in Figure 5, where the DBN model is built to extract multiple levels of representation from the training dataset.
Vibration signals are selected as the input of the whole system for fault diagnosis as they usually contain useful information that can reflect the working state of induction motors. However, there exists correlation between sampled data points. This is difficult for DBN architecture to model as it does not have the ability to function the correlation between the input units which may influence the following classification task. Therefore, in this study the vibration signals are transformed from time domain to frequency domain using Fast Fourier Transform (FFT), and then frequency distribution of each signal is used as the input of the DBN architecture. This is beneficial to classification task during the training procedure. Specifically, DBN learns a model that generates input data, which can obtain more intrinsic characteristics of the input, thus improving classification accuracy eventually. In this module, DBN stacked by a number of RBMs is built and then trained by training dataset from data preparation module to obtain the model parameters. The DBN training process is shown in Figure 6. Input parameters of the architecture will be first initialized including a set of neuron numbers and hidden layer numbers, together with training epochs. Each layer of the architecture is then trained as a RBM unit, and the output of lower-layer RBM is used as the training input for the next layer RBM.
After layer-by-layer learning, synaptic weights and biases are settled and the basic structure is determined. Classification process is then followed to predict the fault category. It is a supervised fine-tuning procedure and the proposed method adopts the back-propagation training algorithm to realize fine-tuning which uses labeled data for training, so that it can improve the discriminative ability for classification task. The unsupervised training process trains one RBM at a time and afterwards supervised fine-tuning process using labels adjusts weights of the whole model. The difference between DBN outputs and the target label is regarded as training error. In order to obtain the minimum error, the deep network parameters will be updated based on learning rules.
After training the DBN model, all the DBN parameters are fixed, and the next procedure is to test the classification capability of the trained DBN model and classification rate is calculated as an index for evaluation. The vibration signal is the input of the constructed fault diagnosis system, and its output indicates working states of the induction motor.
4 Experimental Verification
4.1 Experimental Setting
To evaluate the proposed approach for fault diagnosis of induction motors, experimental studies are conducted using a machine fault simulator illustrated in Figure 7. It simulates six different conditions during motor operation and vibration signals are measured corresponding to different working states. The descriptions of each operation conditions are listed in Table 1 [47].
Experimental facility [47]. 1. Opera meter, 2. Induction motor, 3. Bearing, 4. Shaft, 5. Loading disc, 6. Driving belt, 7. Data acquisition board, 8. Bevel gearbox, 9. Magnetic load, 10. Reciprocating mechanism, 11. Variable speed controller, 12. Current probe
These acquired vibration signals are used to test the DBN-based fault diagnosis system. These vibration signals are divided into training datasets and testing datasets separately, and both datasets are randomized before being used in the DBN model.
4.2 Comparison Approaches
According to Hinton’s theory [30], parameters of the DBN architecture are initialized in advance. The input layer has 1000 units for vibration signals, and the output layer is built with 6 neurons indicating the target classes corresponding to six different operation conditions. The deep model has 4 hidden layers with each containing 500 neurons. Training epochs is set to be 100, and learning rate of the RBM learning process and fine-tuning procedure are set as 0.01 and 0.1, respectively. Threshold value of training error is set to be 0.12.
For the number of hidden units in each layer, networks with small number of hidden units may not learn enough representations for future tasks while networks with large numbers of neurons may increase the possibility of overfitting, which cause poor generalization in untrained dataset. From the literature, there is no formula to calculate an exact number of neurons being used, but the number of neurons within a range is effective in practice. As the input neurons are 1000, number of units for each hidden layer is selected as 500 to avoid both too narrow and too complicated network structures. In addition, the relationship between numbers of hidden units and classification performance of the network are also discussed in the next section.
In order to verify the effectiveness of the proposed approach in actual applications of fault diagnosis for induction motors, comparative experiments have been carried out, and some are listed here:
-
(1)
Original vibration signals are used directly as input of soft-max function;
-
(2)
Original vibration signals are used directly as input of the BP network with one hidden layer;
-
(3)
Original vibration signals are preprocessed to extract time domain features including mean value, root mean square (RMS) value, shape factor, skewness, kurtosis, impulse factor and crest factor [3], then 7 selected features are used as input of the BP network;
-
(4)
4 features including shape factor, impulse factor, crest factor and kurtosis are used as input of the BP network,
-
(5)
Signals are preprocessed with 5-layer wavelet packet decomposition to get 63 sub-frequency bands, then the energy features at all sub-frequency bands are used as input of the BP network.
In addition, another comparative experiment is carried out where unprocessed raw vibration signal is used directly as the input data.
4.3 Results and Discussion
In this validation experiment, training dataset and testing dataset contain vibration signals from all six working states. The proposed DBN-based fault diagnosis system is used to classify these six different working states at the same time. All learning algorithms are repeated 50 times and the average classification rates are calculated, as listed in Table 2. In this case, training dataset has 1200 samples (200 samples for each working state), while testing dataset has 600 samples (100 samples for each working state). 99.98% classification rate is achieved in testing datasets.
The results from a comparative study are also listed in Table 2. From the diagnosis results, the first method failed in the fault diagnosis task. Using original vibration signals without preprocessing, BP network with 1 hidden layer cannot achieve accurate classification. For time domain analysis, different features used in the tests give different results, which mean accurate classification needs manual intervention to pick proper features to do the task of fault diagnosis. The wavelet analysis method provided similar results as compared to the DBN using unprocessed vibration data, but it needs the signal preprocessing first and the results also rely on whether the extracted features are good for the task, while the DBN using frequency distribution of the signals achieved the highest classification rate in all experiments. In addition, the proposed DBN-based approach combines feature learning and classification together to improve the efficiency of fault diagnosis. These experiments proved that proposed approach is an effective way for fault diagnosis of induction motors.
For traditional fault diagnosis approaches, as the raw vibration signal always contains many noise interference, one essential step is the data preprocessing to eliminate noise and extract the relevant information from them for classification. Hence, a robust and effective feature extraction requires some high-quality engineering experience and professional knowledge that are often challenging and hard to be obtained. Compared with traditional fault diagnosis approaches, DBN-based deep learning architecture can automatically learn representations from the input and reduce the manual work so that it can reduce the influence of artificial factors.
Figure 8 shows the detailed label distribution in the verification experiment using DBN model and FFT-DBN model, respectively. The results indicate that FFT-DBN model has better classification capability in the task of fault diagnosis for induction motors than DBN model as FFT-DBN model only has 1 misclassification sample while DBN model has confusion in label 2, 3 and 5. It also illustrates that frequency distribution of the signal is suitable in the application of DBN model, while DBN architecture cannot well model the temporal information of input data which may influence the following classification process.
In Figure 9, the training error and the classification rates of these two model are shown. From the comparison, FFT-DBN model has faster convergence and better classification rate. There is a fluctuation during the learning process in DBN model which means the architecture may not be stable enough to learn an accurate model for the classification task.
4.4 Effects of Scales and Depths of DBN Architecture
Experiments are conducted in this section to study the relationship between classification performance and different deep architectures in induction motor applications. Both DBN model using time-domain signals and FFT-DBN model using frequency distribution of the signals are investigated, and the comparison results are provided and discussed.
In the experiment, hidden neurons from 10 to 100 and from 100 to 1500 are considered. The hidden layers are explored as deep as 6 layers. Each group of experiments are repeated 50 times and the average classification rates are calculated as the evaluation index for deep architecture. Both DBN model and FFT-DBN model are tested, and the results are shown in Figure 10.
From the results, DBN model is sensitive to the scales and depths of the architecture as there are obvious differences between the classification rates from different networks. DBN architecture with 4 hidden layers (green line in Figure 10(a)) has the best classification rate. DBN with only 1 hidden layer cannot model the input data exactly, and when the hidden layers are increased to 5 and 6, the classification results become unstable which indicates the model encounters the problem of overfitting. In other words, the trained model is too complex to model the input so that the generalization ability becomes worse. On the other hand, when neuron number is under 100, the classification rates from DBN model are below 90%. As the number of neurons increases, the classification rate improves and when the number of neurons increases to 1000, the classification rate begins to decrease, indicating too much neurons may cause overfitting that influences classification capability of the model.
Compared with classification results of the DBN model, the results of the FFT-DBN model is much stable, shown in Figure 10(b). There is little fluctuation with the increase of hidden neurons, but the classification rates are all above 99% except two extreme individuals. One is a network with 6 hidden layers and each hidden layer has 10 hidden units which is too narrow to learn enough representations and the other is the network of 5 hidden layers with 1500 neurons at each hidden layer which has the possibility of overfitting as the input data is not so complex. However, generally, FFT-DBN model performances well in various network structures, both in accuracy and stability.
From the comparison, DBN model using time-domain signals has less classification rates in various architectures than the one using frequency distribution of the signals, which means DBN architecture cannot well model signals that correlate between input units. Lacking of time-domain information leads to an inaccurate model of the input data. Therefore, using frequency distribution as input to the DBN architecture gives a good alternative solution in fault diagnosis task for induction motors.
5 Conclusions
This paper presents a deep learning model based on DBN, where frequency distribution of the measured data is used as input, for fault diagnosis of induction motors in manufacturing. The construction of this deep architecture uses restricted Boltzmann machine as a building unit, and uses greedy layer-wise training for model construction. The presented approach makes use of strong capabilities of DBN, which can model high-dimensional data and learn multiple layers of representation, thus can reduce training error and improve classification accuracy. Experimental studies are carried out using vibration signals to verify the effectiveness of the DBN model for feature learning, providing a new way of feature extraction for automatic fault diagnosis in manufacturing.
In future work, methods to improve the performance of the DBN model in fault diagnosis will be explored. Generalization ability of the model will also be investigated to overcome the problem of overfitting. Using both labeled and unlabeled datasets to train the DBN model is also of interest. In addition, the performances corresponding to different model parameters need to be further researched.
References
H Gao, L Liang, X Chen, et al. Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization. Chinese Journal of Mechanical Engineering, 2015, 28(1): 96–105.
G Chen, L Qie, A Zhang, et al. Improved CICA algorithm used for single channel compound fault diagnosis of rolling bearings. Chinese Journal of Mechanical Engineering, 2016, 29(1): 204–211.
M Riera-Guasp, J A Antonino-Daviu, G A Capolino. Advances in electrical machine, power electronic, and drive condition monitoring and fault detection: state of the art. IEEE Transactions on Industrial Electronics, 2015, 62(3):1746–1759.
M H Drif, A J Cardoso. Stator fault diagnostics in squirrel cage three-phase induction motor drives using the instantaneous active and reactive power signature analyses. IEEE Transactions on Industrial Informatics, 2014, 10(2):1348–1360.
Y Wang, F Zhang, T Cui, et al. Fault diagnosis for manifold absolute pressure sensor (MAP) of diesel engine based on Elman neural network observer. Chinese Journal of Mechanical Engineering, 2016, 29(2): 386–395.
J Antonino-Daviu, S Aviyente, E G Strangas, et al. Scale invariant feature extraction algorithm for the automatic diagnosis of rotor asymmetries in induction motors. IEEE Transactions on Industrial Informatics, 2013, 9(1): 100–108.
J Faiz, V Ghorbanian, BM Ebrahimi. EMD-based analysis of industrial induction motors with broken rotor bars for identification of operating point at different supply modes. IEEE Transactions on Industrial Informatics, 2014, 10(2): 957–966.
P Karvelis, G Georgoulas, I P Tsoumas, et al. A symbolic representation approach for the diagnosis of broken rotor bars in induction motors. IEEE Transactions on Industrial Informatics, 2015, 11(5): 1028–1037.
M Zhang, J Tang, X Zhang, et al. Intelligent diagnosis of short hydraulic signal based on improved EEMD and SVM with few low-dimensional training samples. Chinese Journal of Mechanical Engineering, 2016, 29(2): 396–405.
D Matić, F Kulić, M Pineda-sánchez, et al. Support vector machine classifier for diagnosis in electrical machines: Application to broken bar. Expert Systems with Applications, 2012, 39(10): 8681–8689.
Y Lei, F Jia, J Lin, et al. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3137–3147.
T Boukra, A Lebaroud, G Clerc. Statistical and neural-network approaches for the classification of induction machine faults using the ambiguity plane representation. IEEE Transactions on Industrial Electronics, 2013, 60(9): 4034–4042.
H Keskes, A Braham. Recursive undecimated wavelet packet transform and DAG SVM for induction motor diagnosis. IEEE Transactions on Industrial Informatics, 2015, 11(5): 1059–1066.
C Chen, B Zhang, G Vachtsevanos. Prediction of machine health condition using neuro-fuzzy and Bayesian algorithms. IEEE Transactions on Instrumentation and Measurement, 2012, 61(2): 297–306.
Y L Murphey, M A Masru, Z Chen, et al. Model-based fault diagnosis in electric drives using machine learning. IEEE/ASME Transactions on Mechatronics, 2006, 11(3): 290–303.
J Wang, R X Gao, R Yan. Multi-scale enveloping order spectrogram for rotating machine health diagnosis. Mechanical Systems and Signal Processing, 2014, 46(1): 28–44.
B Boashash. Time-frequency signal analysis and processing: A comprehensive reference. Academic Press, 2015.
R Yan, R X Gao, X Chen. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Processing, 2014, 96: 1–15.
G E Hinton. Learning multiple layers of representation. Trends in Cognitive Sciences, 2007, 11(11): 428–34.
G E Hinton, R R Salakhutdinov. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504–507.
I Arel, D C Rose, T P Karnowski. Research frontier: deep machine learning–a new frontier in artificial intelligence research. IEEE Computational Intelligence Magazine, 2010, 5(4): 13–18.
Y Bengio. Learning deep architectures for AI. Foundations & Trends® in Machine Learning, 2009, 2(1): 1–55.
Y Jia, E Shelhamer, J Donahue, et al. Caffe: Convolutional architecture for fast feature embedding. Proceedings of the 22nd ACM international Conference on Multimedia, Orlando, Florida, USA, November 3-7, 2014: 675–678.
K He, X Zhang, S Ren, et al. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, June 27-30, 2016: 770–778.
C Szegedy, W Liu, Y Jia, et al. Going deeper with convolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, June 7–12, 2015: 1–9.
Y Cai, H Wang, X Chen, et al. Vehicle detection based on visual saliency and deep sparse convolution hierarchical model. Chinese Journal of Mechanical Engineering, 2016, 29(4): 765–772.
G E Hinton. To recognize shapes, first learn to generate images. Progress in Brain Research, 2007, 165(6): 535–47.
Q V Le. Building high-level features using large scale unsupervised learning. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, May 26-31, 2013: 8595–8598.
L Deng, G Hinton, B Kingsbury. New types of deep neural network learning for speech recognition and related applications: An overview. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, May 26-31, 2013: 8599–8603.
Y LeCun, Y Bengio, G Hinton. Deep learning. Nature, 2015, 521(7553): 436–444.
L Deng, D Yu. Deep learning: methods and applications. Foundations and Trends® in Signal Processing, 2014, 7(3–4): 197–387.
C Xiong, S Merity, R Socher. Dynamic memory networks for visual and textual question answering//Proceedings of the International Conference on Machine Learning, New York City, NY, USA, June 19-24, 2016: 2397–2406.
K S Tai, R Socher, C D Manning. Improved semantic representations from tree-structured long short-term memory networks. arXiv preprint arXiv: 1503.00075, 2015.
[34] F Jia, Y Lei, J Lin, et al. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mechanical Systems and Signal Processing, 2016, 72: 303–15.
P Tamilselvan, P Wang. Failure diagnosis using deep belief learning based health state classification. Reliability Engineering & Systems Safety, 2013, 115(7): 124–135.
V T Tran, F Althobiani, A Ball. An approach to fault diagnosis of reciprocating compressor valves using Teager–Kaiser energy operator and deep belief networks. Expert Systems with Applications, 2014, 41(9): 4113–4122.
J Guo, X Xie, R Bie, et al. Structural health monitoring by using a sparse coding-based deep learning algorithm with wireless sensor networks. Personal and Ubiquitous Computing, 2014, 18(8): 1977–1987.
A Steinecker. Automated fault detection using deep belief networks for the quality inspection of electromotors. tm - Technisches Messen. tm - Technisches Messen, 2014, 81(5): 255–263.
J Sun, A Steinecker, P Glocker. Application of deep belief networks for precision mechanism quality inspection. Precision Assembly Technologies and Systems, 2014: 87–93.
W Sun, S Shao, R Zhao, et al. A sparse auto-encoder-based deep neural network approach for induction motor faults classification. Measurement, 2016, 89: 171–178.
X W Chen, X Lin. Big data deep learning: challenges and perspectives. IEEE Access, 2014, 2: 514–525.
A R Mohamed, D Yu, L Deng. Investigation of full-sequence training of deep belief networks for speech recognition. Proceedings of the International Speech Communication Association Annual Conference, Makuhari, Chiba, Japan, September 26-30, 2010: 2846–2849.
R Salakhutdinov, G Hinton. Deep Boltzmann Machines. Journal of Machine Learning Research, 2009, 5(2): 1967–2006.
G E Hinton. A practical guide to training restricted Boltzmann machines. Momentum, 2010, 9(1): 599–619.
B Schölkopf, J Platt, T Hofmann. Greedy layer-wise training of deep networks. Advances in Neural Information Processing Systems, 2007, 19: 153–160.
G E Hinton, S Osindero, Y W Teh. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527–1554.
X Yang, R Yan, R X Gao. Induction motor fault diagnosis using multiple class feature selection. Proceedings of 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Pisa, Italy, May 11-15, 2015: 256–260.
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by National Natural Science Foundation of China (Grant No. 51575102), Fundamental Research Funds for the Central Universities of China, and Jiangsu Provincial Research Innovation Program for College Graduates of China (Grant No. KYLX16_0191).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shao, SY., Sun, WJ., Yan, RQ. et al. A Deep Learning Approach for Fault Diagnosis of Induction Motors in Manufacturing. Chin. J. Mech. Eng. 30, 1347–1356 (2017). https://doi.org/10.1007/s10033-017-0189-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10033-017-0189-y