Meyer (2022, herein M22) critically examines a number of assumptions behind the social cost of carbon (SCC) calculations in Dayaratna et al. (2020, herein D20), which made use of the Framework for Uncertainty, Negotiation, and Distribution (FUND) model due to Anthoff and Tol (2013). He argues that our most important assumptions “are either not as important or strong as the authors suggest, outdated, or not supported by published literature.” Meyer lists a number of alternative assumptions which he suggests would be more appropriate to apply but does not present any new calculations. Herein we assess his recommendations and discuss the changes they imply for the SCC calculation. Altogether, we find that the results do not materially differ from the implications of D20.

The claims in D20 subject to criticism by M22 fall into four groups, two of which are particularly consequential. (1) Climate risks associated with very high Equilibrium Climate Sensitivity (ECS) outcomes are improperly handled in probabilistic Integrated Assessment Model (IAM) simulations because they fail to adjust the processes governing time-to-equilibrium to be consistent with ECS as it varies, resulting in physically impossible parameter combinations; (2) agricultural damages in FUND (and by implication other IAMs) are overstated because they failed to take account of accumulated evidence regarding gains from CO2 fertilization; (3) conventional ECS values in IAMs are too high compared to those estimated in recent climatological literature; (4) translating SCC estimates from IAMs into an optimal carbon price requires dividing by the Marginal Cost of Public Funds (Sandmo 1975). Of these topics, (2) and (3) are the most important.

Item (1) was pointed out by Roe and Bauman (2013). D20 noted that the ECS estimation method in Lewis and Curry (2018) jointly conditioned climate sensitivity with evidence on the rate of ocean heat uptake, thus yielding a probability distribution that did not violate physical limits on adjustment speeds. M22 did not critique the argument of Roe and Bauman (2013) or the estimation method of Lewis and Curry (2018), instead he argued that the ECS issue does not matter because other uncertainties in SCC calculations are at least as important, and a subsequent study by Calel et al. (2015) did not find variations in the tail thickness of the ECS distribution mattered much for estimating mean damages when using the Nordhaus damage function in the DICE-2009 model (Nordhaus 2008). Regarding the first point, we agree that there are many important assumptions involved in IAM simulations but our own simulations in D20 and the new ones we present herein, nonetheless, show that the choice of ECS is among the most influential. Regarding the second, Fig. 3 in Calel et al. (2015) shows that use of fat-tailed ECS distributions increases the spread of warming estimates but leaves the mean largely unchanged, which is the basis of their claim regarding robustness of estimated damages. However, while they discuss the role of the parameter governing adjustment speed, those simulations allow ECS to vary while leaving adjustment speed fixed, which is precisely the point of criticism in Roe and Bauman (2013).Footnote 1 When they allow it to vary (see their Table 2), the mean damages change dramatically. But they still do not constrain the speed of adjustment to be consistent with ECS, so not all the outcomes in their simulations are physically possible.

In any case, this issue does not affect our simulations in D20 nor those we present herein so we will leave it aside. Regarding (2), M22 says “Dayaratna et al. (2020) cite a few papers published in the past decade showing a new high-CO2-adapted rice variety and larger estimates of the CO2 fertilization. They suggest that the agriculture parameter \({\gamma }_{t}\) in FUND should be at least 30% larger.” This is an incomplete summary of our argument. While we discussed rice, we also discussed evidence covering all major crop types as well as satellite-based measurements of leaf-area index which tracks rising yields of grasslands, which are essential for livestock productivity.

Part of our argument was based on a meta-analysis by Challinor et al. (2014). M22 points to the Moore et al. (2017) meta-analysis, noting the size of their data set and suggesting it supersedes the Challinor et al. analysis. In fact, both studies used the same dataset. Moore et al. simply applied a different estimating equation than Challinor et al. and obtained results that implied worse climate impacts on agriculture. Unfortunately, they did not report their econometric estimates nor present any hypothesis testing to defend their modeling decisions. They used a functional form that, compared to Challinor et al., strongly dampens the gains from CO2 fertilization but they did not report sensitivity analysis to this assumption. Challinor et al. estimated and presented separate response functions for data subsets based on whether the underlying study considered adaptation or not. Moore et al. did not do this and indeed constrained the adaptation effect in their simulation model into a form that largely eliminates it. The response functions shown in the Moore et al. paper (see their Fig. 1) include warming but leave out CO2 fertilization and adaptation altogether. Since this implausibly pairs large increases in temperature with no change in CO2, the functions are irrelevant to understanding the net effects of CO2-induced climate change on agriculture. Moreover, experimental studies published subsequently to both papers (e.g., Lenka et al. 2017, 2019; Qiao et al. 2019) have continued to report large net gains from combined warming and CO2 fertilization, in line with the Challinor et al. findings.

Fig. 1
figure 1

SCC estimates 2020–2050 using 2.5% discount rate and ECS distributions from Roe and Baker (“Roe–Baker”, 2007), Lewis (2022, “L22”) and Lewis and Curry (2018, “LC18”). Also shown are L22 with FUND agriculture productivity parameter boosted by 15 or 30%

Full size image

Nevertheless, we do not require a reader to assume that CO2 and temperature co-movements will always yield net benefits in the future. Our position is that evidence shows the gains from CO2 fertilization are probably higher than those assumed by the original parameterization in FUND, so a sensitivity analysis to stronger CO2 growth effects is warranted. This is even more the case for other IAMs that assume away the CO2 fertilization effect altogether. M22 sets this concern aside on the grounds that IAMs differ for a host of reasons besides failure to include CO2 fertilization effect. Be that as it may, there is no reason to ignore the effect, and opens up IAMs to easily avoidable criticism.

Turning to item (3), M22 criticizes our use of the Christy and McNider (2017) ECS estimate, since it is based on sampling of the lower- and mid-troposphere. He argues in favor of estimates based on surface measurements on the grounds that “many of the historic surface temperature measurements were taken in populated cities” making them more relevant for estimating the effect of warming on the economy. But it is precisely the fact that the measurements are largely taken from populated cities that poses a problem for ECS estimation, since significant amounts of warming in that record is attributable to urbanization, not climate change (e.g., Fall et al. 2010; McKitrick and Nierenberg 2010; He et al. 2013; Li et al. 2013 etc.).Footnote 2 IAMs try to isolate the economic effect of CO2-induced warming, not warming due to urban heat island effects, because the intended output is the social cost of carbon. Since climate model simulations show that CO2-induced warming should be stronger in the troposphere than at the surface (Santer et al. 2005) especially in the tropics, and tropospheric data sets are not contaminated by urbanization bias at the surface, the Christy and McNider (2017) study is ideally suited for our purpose.

M22 also notes that multiple different surface temperature data sets strongly agree with each other and he implies this argues in favor of preferring them. But the data sets in question are not independent, instead they all use the same underlying surface data archive known as the Global Historical Climatology Network or GHCN (McKitrick 2010). By contrast, the various tropospheric data products come from two largely independent measurement platforms, namely weather satellites and weather balloons, so the agreement between them is further grounds for taking note of the troposphere-based ECS estimate.

M22 discusses the ECS estimate of Sherwood et al. (2020) and notes that the IPCC (2021) Sixth Assessment Report provided a very similar best estimate. It should be noted, however, that the IPCC based its best estimate on Sherwood et al. (2020) so they are not independent. M22 also takes note of Lewis (2022) which updates the Sherwood et al. data and incorporates some small methodological improvements, yielding an ECS best estimate of 2.2 K, which is higher than the 1.5 K best estimate of Lewis and Curry (2018) which we used.Footnote 3 The difference arises mostly due to assimilation of paleoclimatological data: Lewis (2022) reports that using only post-1869 instrumental data to match Lewis and Curry (2018) yields a best estimate of 1.8 K. These points aside, we agree that Lewis (2022) is an important contribution to the ECS estimation literature and should be incorporated into IAMs. To that end, we obtained the complete density function from Lewis and re-ran our analysis.

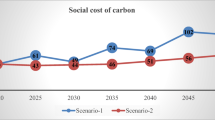
As we did with Christy and McNider (2017) and Lewis and Curry (2018) in D20, we sampled Lewis (2022) using the technique of inverse transform sampling. We ran the FUND model for 10,000 Monte Carlo simulations under the five separate economic growth scenarios assumed by the U.S. Interagency Working Group (US Interagency Working Group 2013). Table 1 lists the results from these simulations over the 2020–2050 interval for discount rates from 2.5 to 7.0%, leaving the FUND agricultural CO2 fertilization parameter unchanged or increasing it by, respectively, 15 and 30%. Columns 1–4 show the central SCC estimate and columns 5–8 show the associated probability of SCC being negative. Figure 1 summarizes the best estimate results for a 2.5% discount rate. The results using the Lewis (2022) sensitivity distribution lie mid-way between the results using Roe-Baker (2007) and those using Lewis and Curry (2018). Since the ECS best estimate likewise is mid-way between them (2.2, 3.0, and 1.5 K, respectively), this shows that ECS is an extremely influential parameter for estimating the SCC in IAMs. Figure 1 shows that increases to the CO2 fertilization parameter, as expected, also reduce the SCC, such that a 30 percent increase in the parameter cuts the SCC by 30 to 40 percent over the 2020–2050 interval.

Table 1 Median social cost of carbon estimates (Cols 1–4) and portion of the distribution below $0.00 (Cols 5–8) 2010–2050 in FUND
Full size table

M22 finds the Lewis (2022) ECS distribution to be an appropriate choice, recommends not adjusting the CO2 fertilization parameter, and recommends use of a 5% discount rate as being in the middle of the range in guidance of the US Office of Management and Budget, and also close to that used in DICE based on empirical considerations. Figure 2 shows the 2050 SCC best estimates using a 5% discount rate, no CO2 fertilization adjustment, and ECS distributions from, respectively, Roe and Baker (2007), Lewis (2022), Lewis and Curry (2018), and Christy and McNider (2017). The Lewis and Curry (2018) estimate is included both for comparison and also because it is close to the ECS distribution obtained by Lewis (2022) using only post-1869 temperature data. As of 2050 under M22’s preferred configuration, the SCC is $3.39 and has a 33.4 percent chance of being negative. Using the Christy and McNider (2017) ECS estimate, the ECS mean value is slightly negative. Either way, these values imply that the SCC is close enough to zero through 2050 as to make it difficult to justify even moderate climate mitigation policies, much less those needed for Paris compliance or achievement of Net Zero by 2050.

Fig. 2
figure 2

SCC estimates for 2050 using 5.0% discount rates and 4 different ECS estimates assuming no increase in the FUND CO2 fertilization effect

Full size image

Finally, with regard to application of the Sandmo (1975) formula, in which the optimal carbon tax is the SCC divided by the Marginal Cost of Public Funds (MCPF), estimation of the MCPF is an empirical matter and results can vary widely among and within countries. Dahlby and Ferede (2018), for example, estimate the MCPF’s for factor income taxes among Canadian provinces and find they vary from 1.4 to 6.8. A value of 2.0 is on the low end yet implies that the optimal carbon tax should only be half the SCC, which is a consequential change. Thus, it is not possible to claim the issue never matters. However, as a practical matter, using the parameter choices recommended by M22, the SCC is so small through 2050 that the precise value of the MCPF is, in this case, moot.