Capital markets and the costs of climate policies

Abstract

Globalization is accompanied by increasing current account imbalances. They can undermine the positive impacts of increasing international cooperation and trade on economic growth and income convergence. At the same time, climate change challenges the global community and requests for co-operative action. Regional energy transformation due to climate policies and the resulting regional mitigation costs are key variables of climate economic analysis. This study is the first that include current account imbalances and imperfect capital markets to investigate potential market feedback mechanisms between climate policies, energy sector transformation and capital markets. Furthermore, it answers the question whether the capital-intensive transformation towards zero-carbon economies increases the policy cost of mitigation under the condition of imperfect capital markets. First results demonstrate a dominant baseline effect of capital market imperfections on macroeconomic variables, and moderate effects on mitigation costs in global climate policy scenarios. For some regions (e.g. Middle East) estimates of relatively high mitigation costs are revised downwards, if imperfect capital markets are considered.

1 Introduction

In assessing the potential impacts of climate change, a majority of climatologists and climate impact researchers conclude that a stabilization of the climate system below a temperature change of 2 $^{\circ }$C (compared to the preindustrial level) has to be achieved. While current climate policies focus on national contributions (NDCs), a number of recent studies (e.g. Kriegler et al. 2018; Robiou du Pont et al. 2017; Rogelj et al. 2017) show that greenhouse gas emission reductions in line with NDCs will not be sufficient to achieve a long-term climate stabilization below 2 $^{\circ }$C. International co-operation and multilateral actions are needed to intensify national mitigation efforts. The transfer of financial means and physical capital can be considered as part of the portfolio of international climate change mitigation measures. The purposeful allocation of capital can help to increase the effictiveness and fairness of mitigation efforts.

However, capital flows may generate or intensify current account imbalances and are subject of capital market imperfections. Capital market constraints can be expected to increase the costs of transformation towards carbon-free economies, because renewable energy technologies are more capital-intensive than fossil-based technologies. This may increase mitigation costs and reduce the incentive of capital-constrained countries to join international efforts of fighting climate change. This all is not yet discussed in the climate economics literature. This paper fills this gap and in particular asks to which extent the representation of capital markets and capital market imperfections changes the global and regional costs of climate change mitigation.

To answer this question, the present study makes use of the Integrated Assessment (IA) model REMIND. We improve the methodology of this model by explicitly representing capital market imperfections and make the model’s macro-economic dynamics consistent with empirical current account imbalances. By embedding an economic growth model that requests for long-term compensation of short-term current account deficits, REMIND derives patterns of long-term international trade and current accounts. The simulation of the current account structure and net foreign assets in this model is related to intertemporal trade and capital trade, respectively. Intertemporal trade helps to balance needs of financing consumption and investments in countries with different demographic dynamics or at different stages of development, hence contributes to economic growth.

The issue of capital trade is weakly represented in applied economic modelling studies. With respect to IA models, it has hardly been addressed since (Manne and Rutherford 1994) and Nordhaus and Yang (1996)—on the one hand, because of the numerical demands on solving large-scale models with capital trade, on the other hand, because of the peculiarity of resulting trade flow patterns. In a model with perfect competition and free trade, simulated trade flows may deviate by an order of magnitude from empirical data. The standard theory predicts capital flows from rich to poor countries which is in contrast to observed patterns of international current accounts and which is known as the Lucas paradox (Lucas 1990).

In this paper, we discuss how this problem manifests in an IA model. We demonstrate how the model can be improved by applying a wedge analysis and integrating capital market imperfections that redirect trade flows to be consistent with observed data. With the specified capital market representation, the model is able to deal with the Lucas paradox and prepared for improved projections of energy sector transformations and mitigation cost estimates. By similar intent as the present study, Iyer et al. (2015) apply an IA model to assess mitigation cost changes due to the representation of instititutional differences between countries. Unlike the present study, Iyer et al. (2015) do not model the capital market directly, but implemented region-specific risk mark-ups for investments into different electricity generation technologies. They find that this change yield increasing mitigation costs.

When running experiments with the REMIND model, we start by analyzing the impacts of representing imperfect capital markets on the baseline dynamics. Changes in the baseline have a direct impact on the costs of climate policies because the reference case is shifted against which policy scenarios are compared. The second part of the numerical analysis starts with the hypothesis that simulated climate policy costs depend on the representation of the capital market. We quantify this effect and demonstrate mitigation cost changes of opposite signs across regions.

The paper is structured as follows. In Sect. 2, we highlight the role of capital trade in shaping long-term growth dynamics. Challenges of modelling capital trade are linked to the Lucas paradox for which we provide alternative explanations. A method to represent capital market imperfections and to solve the Lucas paradox is presented. In Sect. 3, we introduce the trade module of the REMIND model and its integration in an intertemporal welfare-maximizing model framework. Disclosing the nature of trade as control variable and the meaning of the intertemporal budget constraint is crucial. This also applies to the representation of the time preference structure and imperfect capital market features. We discuss the major differences in consumption and current account patterns between baseline scenarios with and without capital market imperfections in Sect. 6. The impact of climate policies is analyzed in Sect. 7 where we answer the question to which extent the estimation of mitigation costs is distorted by the assumption of perfect and uniform capital markets. We summarize in Sect. 8 and identify future research demand.

2 Capital trade and saving

Globalization is linked to an increasing international flow of goods and capital and has the potential to increase welfare by allowing resources to be allocated more efficiently. Speller (2011) point to the importance of capital trade by detecting an increase of capital flows from 5 to 7% of world GDP between 2002 and 2007. At the same time global current account imbalances (the sum of deficits and surpluses) doubled from 3 to 6% of world GDP. Standard economic theory suggests that in the presence of perfect capital markets the net allocation of capital across countries reflect productivity differentials (Lucas 1990). Under neoclassical assumptions, capital flows from advanced economies to emerging and developing economies. Theory, furthermore, emphasizes the particular relation between capital trade and the intertemporal consumption smoothing requirements of countries (Sachs 1982). In standard growth models with equal preference structure across countries, all countries show the same consumption growth rates disregarding any differences in GDP growth. This is due to capital trade.

However, as was first noted by Lucas (1990), and therefore called Lucas paradox, the prediction that capital will flow from advanced to emerging and developing economies is at odds with the observed global pattern of net capital flows. A bulk of economic literature tries to explain this paradox (e.g. Chinn and Prasad 2003; Gruber and Kamin 2007; Alfaro et al. 2008; Caballero et al. 2008; Mendoza et al. 2009; Campa and Gavilan 2011). Gourinchas and Jeanne (2013) show in a more recent study that capital does not flow to a larger extent to countries that invest and grow more. They identify a number of factors, but see no main explanation for what they call “allocation puzzle”. Fan et al. (2009) and Ndikumana et al. (2002) explain capital outflows from the perspective of China and Sub-Saharan Africa, respectively. While a number of studies investigated the fundamental drivers of capital trade—differences in productivity and consumption time preferences—other drivers came into the focus as well: information assymetries, missing markets, weak financial institutions and home biases.

Speller (2011) highlight two explanations. The first is that cross-country productivity differentials are mismeasured and that greater capital scarcity in emerging and developing economies does not translate into a higher marginal product of capital and larger investment returns. The second explanation are frictions that exist in reality but are not captured by the simple neoclassical model. Frictions are in particular related to cross-country differences in financial market development. Residents in countries with underdeveloped financial markets will have restricted access to instruments that allow them to hedge risk. Risk-adjusted investment returns and risk premiums are suggested to be used to take frictions into account (e.g. Gertler and Rogoff 1990). Capital market imperfections also result from the home bias in investors portfolio allocation preferences.

A prominent subject of explaining capital trade flows and the Lucas paradox, respectively, are differences in the countries’ savings decisions. These differences depend amongst others on the stage of economic development of countries or their socioeconomic and cultural characteristics. Demographic factors are important in this context (e.g. Marchiori 2011; Niemelainen 2021). According to the standard theory of consumption (Modigliani 1970), households borrow when they are young, save in working age, and dissave when they retire. This implies that countries with a relatively high share of old population will save less than those with a relatively high share of young people.

In an economic growth model, the decision about the savings rate is mainly determined by the pure rate of time preference. In most applied economic models, like Integrated Assessment models, by default, equal time preferences are assumed across regions.¹ Differences in time preferences can cause trade flows in opposite directions (Leimbach et al. 2015). A strong argument in favor of a regional differentiation of time preferences is the fact that savings rates are heterogenous (Marchiori 2011; Aizenman and Sun 2010; Lengwiler 2005; Caroll et al. 2000). Choi et al. (2008), for example, find that international differences in subjective discounting display increasing relative U.S. impatience and create current account imbalances that match patterns observed in the data. An alternative way of representing differences in preferences is adopted by Rebelo (1992) using a Stone-Geary utility function.

The assumption of regionally differentiated time preference rates can be combined with the assumption of either being constant or varying over time. Time inconsistency is a major counter-argument with regard to the latter (Groom et al. 2005).² Optimal growth with endogenously determined rates of time preferences is examined by Uzawa (1996) and Das (2003) who adopts the idea that the time preference varies with increasing income.

The discussion in this section reveals a variety of factors explaining why observed capital flows may deviate from projections of neoclassical growth models with perfect capital market assumptions. Recent studies (Gourinchas and Jeanne 2013; Rothert 2016; Kehoe et al. 2018; Steinberg 2019) try to establish a method to deal with this modelling challenge. They apply a wedge analysis. Kehoe et al. (2018) and Steinberg (2019) use this tool in order to explain the huge current account imbalance of the USA. The methodological approach of the wedge analysis identifies and adjusts different model parameters, that affect capital flows, until selected model output (e.g. current accounts) match observed data. Steinberg (2019), for example, implemented five wedge components: domestic and foreign savings wedges, domestic and foreign investment wedges and a trade wedge. The savings wedge is most prominent in all studies.³ While it points to deficits in the representation of the savings behavior in the applied models, it incorporates a manifold of single components like the institutional and demographic settings discussed above. Whereas Steinberg (2019) implemented the savings wedge as a tax on savings in the budget equation, Kehoe et al. (2018) implemented this wedge as a change of the discount factor and time preference, respectively. We will apply the wedge analysis method to the REMIND model that is introduced next.

3 The trade module of REMIND

3.1 Basic structure with perfect capital market

In this study we improve and apply the REMIND model. It is a global, multi-regional, energy-economy-climate model (Leimbach et al. 2010) used in long-term analyses of climate change mitigation (e.g. Bauer et al., 2012; Bertram et al., 2015; Luderer et al., 2018). A detailed model description is provided by Luderer et al. (2015)⁴.  For the purpose of this paper we will focus on those parts of the model that are most relevant for the discussion of trade issues.

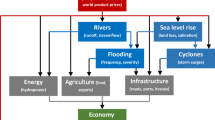
REMIND couples an economic growth model with an energy system model and a simple climate model (see Fig. 1). Technological change in the energy sector is embedded in a macroeconomic environment that by means of investment and trade decisions as well as assumptions on technical progress (in particular labor efficiency growth) governs long-term regional development. REMIND is suited to analyse long-term trade patterns as it allows for intertemporal trade and current account imbalances. It, furthermore, separates the component of fossil fuel trade in the current account that can be expected to have a sustained impact under climate policies in a number of countries.

Fig. 1

Structure of REMIND

The applied version of REMIND includes twelve world regions:

• 1. USA - USA

• 2. EUR - EU27

• 3. JPN - Japan

• 4. CHA - China and Hongkong

• 5. IND - India

• 6. REF - Reforming economies including Russia

• 7. SSA - Sub-Saharan Africa (including Republic of South Africa)

• 8. MEA - Middle East and North Africa

• 9. LAM - Latin America

• 10. OAS - Other Asia (Central and Pacific Asia)

• 11. CAZ - Canada, Australia, New Zeeland

• 12. NEU - Non-EU European countries.

World-economic dynamics is simulated in REMIND over the time span 2005 to 2100, with five-year time steps until 2060 and ten-year time steps thereafter. The model runs until 2150 to avoid distortions due to terminal effects. Major parts of the model are fixed to empirical data until 2015. In each region, a representative household maximizes utility U(r) that depends upon per capita consumption:

$$\begin{aligned} U(r)=\sum _{t=t_0}^{T} \left( G(t,r) \cdot L(t,r)\cdot \left( \frac{\left( \frac{C(t,r)}{L(t,r)}\right) ^\frac{1}{\gamma (r)}-1}{1-\frac{1}{\gamma (r)}}\right) \right) ~~~~\forall r . \end{aligned}$$

(1)

with

$$\begin{aligned} G(t,r) =e^{-\rho (r) \cdot (t-t_0)} ~~~~\forall t,r . \end{aligned}$$

(2)

C(t, r) represents consumption in time-step t and region r, L(t, r) represents population, G(t, r) the discount factor, $\gamma (r)$ the intertemporal elasticity of substitution and $\rho (r)$ the pure rate of time preference.

Each region generates macro-economic output (i.e. GDP) based on a nested “constant elasticity of substitution” (CES) production function of the production factors labor, capital, and final energy. The parameters of the production function are calibrated to replicate a prescribed baseline scenario of GDP, final energy use and labor, which is - for this study - an updated SSP2⁵ version of those in Kriegler et al. (2017). GDP (Y) is available for consumption C, investments I into the macroeconomic capital stock, energy system expenditures E and for the export of composite goods $X_G$ (net of imports $M_G$).

$$\begin{aligned} Y(t,r) = C(t,r) + I(t,r) + X_G(t,r) - M_G(t,r) + E(t,r). \end{aligned}$$

(3)

Equation (3) assumes that the macroeconomic production sector is flexible in producing consumption and investment goods as they are perfect substitutes. Macro-economic investments as control variable enter a common capital stock equation with assumed depreciation rate of 5$\%$.

While the above formulation of the welfare function considers regionally differentiated preference parameters $\gamma$ and $\rho$, the original version of REMIND assumes uniform values of 1.0 and 0.03, respectively, across regions. Trade between regions is first of all induced by differences in factor endowments and technologies. Trade in a composite good is supplemented by the possibility of intertemporal trade. Capital mobility is represented by free trade in the composite good. It is weak capital mobility as only new capital, i.e. investment goods, is mobile. Capital mobility and intertemporal trade cause equalization of the return rates on capital and guarantee an intertemporal and interregional equilibrium. Trade is modeled as export in and import from a common pool. There is no bilateral trade. Both trade variables represent control variables. Apart from trade in the composite good, there is trade in different primary energy goods e (coal, oil, gas, biomass, uranium) entering the equation that describes primary energy supply:

$$\begin{aligned} PE_e(t,r) = EX_e(t,r) - X_e(t,r) + M_e(t,r). \end{aligned}$$

(4)

PE(r, t) represents the regional supply and EX(t, r) the domestic extraction of primary energy of type e.

While the trade of physical capital is linked to trade in the composite good, any goods and energy trade implies trade in financial capital and in case of current account imbalances net flows of financial capital. This is accounted for in an intertemporal budget constraint, which requests the accumulated net foreign assets B of each region to converge to zero:

$$\begin{aligned} B(r) = N(r) + \sum _{t} \sum _{j} \left( p_{j}(t) \cdot [{X}_{j}(t,r) - {M}_{j}(t,r) ]\right) ~~~~\forall ~r \end{aligned}$$

(5)

and

$$\begin{aligned} B(r)=0~~~~~\forall ~r, \end{aligned}$$

(6)

$p^i_j(t)$ represents present value world market prices derived iteratively by a Walrasian type tatonnement process (see Leimbach et al. 2016, for the details of price adjustment). N(r) represents the intial net foreign asset of region r.

The trade patterns simulated by the model are subject to the regional intertemporal budget constraints that allow for huge flexibility in allocating investment, saving and consumption over time. But they also put a limit on this flexibility because balancing of the current accounts is enforced and no region can accumulate infinite debts. Each export of the composite good qualifies the exporting region for a future import (of the same present value), but implies for the current period a loss of consumption. Imports increase current consumption but imply the accumulation of debts that have to be cleared in the long run according to the intertemporal budget constraint. The selection of the time horizon for clearing all debts is arbitrary and will likely have an impact on the resulting trade patterns. We decided to use the models’ time horizon 2150 as the terminal period to settle the intertemporal budget constraints in each region.

If we accept that indebtedness is part of the real-world dynamics that should be represented in such kind of economic growth model, an alternative to Eq. (6) in balancing capital trade would be to follow the historic trend of the current account pattern. In essence, this would imply to assume sustained current account surplus for China and increasing debts of the USA. Within the literature that tries to explain current account imbalances, there is some indication (e.g. Aizenman and Sun 2010; Chen 2011) that this cannot be a sustainable pattern.

3.2 Representation of imperfect capital market in REMIND

The model as presented in the previous section features a perfect capital market facing the problem of capital flows in the wrong direction (cf. Lucas paradox as discussed in Sect. 2). In order to overcome this misfeature, we implement components in the model that are suited to correct capital flows and represent imperfect capital markets. In a first step, we impose debt constraints - demanding each model region to keep their additional current account deficits and surpluses accumulated over the five year model time step below 20% of GDP. When we look at the historical data from 1980 until today (PWT8.1), the 20% limit holds for almost all world regions. Just the accumulated trade deficit of the US slightly exceeds this bound between 2004 and 2008.

With D(t, r) as the level of foreign debts (i.e. the accumulated and discounted current account deficits), international capital flows are restricted by constraints on the change $\Delta {D}$ of assets and indebtedness, respectively:

$$\begin{aligned} D(\tau ,r)&= \sum ^{\tau }_{t=1} \sum _{j} \left( p_{j}(t) \cdot [{M}_{j}(t,r) - {X}_{j}(t,r) ]\right) - N(r) ~~~~\forall ~ \tau ,r \end{aligned}$$

(7)

$$\begin{aligned} \Delta {D}(t,r)&= \sum _{j} p_{j}(t) \cdot [{M}_{j}(t,r) - {X}_{j}(t,r) ] ~~~~\forall ~ t,r \end{aligned}$$

(8)

with prices $p_{j}$ normalized by the price of the composite good

$$\begin{aligned} -0.2 \cdot Y(t,r)< \Delta {D}(t,r) < 0.2 \cdot Y(t,r) ~~~~~~~\forall ~ t,r. \end{aligned}$$

(9)

We can show that these constraints already help to close the gap between observed and simulated capital flows (see next section), yet considerable differences remain. Therefore, in a next step, we adopt conceptual ideas of the empirical studies by Gourinchas and Jeanne (2013), Rothert (2016), Kehoe et al. (2018) and Steinberg (2019) to further improve the matching of model results and empirical data and to resolve the Lucas paradox. For this purpose, we perform a wedge analysis.

Within this wedge analysis, we apply a trade and a savings wedge. They are attached to selected model parameters that have a major impact on capital trade flows. The wedges distort the original model such that the new simulation results match observed capital flow data and associated variables (consumption shares, current accounts), respectively, in the base year. The savings wedge has two components: a wedge attached to the intertemporal elasticity of substitution (cf. Eq. 1) and a wedge attached to the pure rate of time preference (cf. Eq. 2). We use the latter in a similar way as Kehoe et al. (2018), which, however, differs from the approach of other models in dealing with these parameters. Van der Ploeg and Rezai (2019), for example, define them as ethical parameters.

The trade wedge represents a mark-up on capital imports. As financial capital is used to balance net trade in general, it is applied to the trade of the composite good $M_G$ as well as to trade of energy resources $M_e$. This mark-up is implemented as a trade cost equivalent $\mu (r)$ in the budget constraint:

$$\begin{aligned} Y(t,r) = C(t,r) + I(t,r) + X_G(t,r) - M_G(t,r) \cdot \left( 1 - \mu (r) \right) + E(t,r) + \sum _{e}\mu (r) M_e(t,r). \end{aligned}$$

(10)

It can also be interpreted as a risk mark-up and risk premium,⁶ respectively, which high-risk capital importing countries have to pay in order to compensate for a potential default of repayment.

While the default values of the parameters $\rho$, $\gamma$ and $\mu$ are 0.03, 1.0 and 0.0, respectively, the estimated wedges are presented in Table 1. Details of the numerical algorithm to estimate the wedges are described in the Appendix. As expected, the largest wedges emerge for regions with huge gaps between model and empirical data under the perfect capital market setting (cf. Sect. 6). For most regions, the two wedges attached to the preference parameters show the opposite sign, with a large negative wedge attached to the time preference parameter for China, MEA and REF, and a large positive wedge for USA. Risk mark-ups are high for Sub-Saharan Africa, China, India, MEA and REF, while completly in line with real-world experiences, no risk mark-ups are estimated by the algorithm of the wedge analysis for developed economies.

Table 1 Wedge estimation

While we acknowledge that elements of the present capital market modelling, mainly the savings wedge, do not represent imperfections in a narrow sense, we subsume them under this term also in the following. The savings wedge is induced by changes in preference parameters that summarize various institutional factors that have influence on saving decisions and cover market imperfections (cf. Sect. 2). A full representation of the institutional diversity is not possible. The wedges are implemented and estimated in a way that the model as a whole reproduces observed data which are related to a world that include these imperfections. As institutional factors are not explicitly represented, the present approach does not allow a targeted analysis of financial market reforms.

4 Baseline results

Figure 2 shows a comparison of results from running REMIND with the different representations of the capital market as introduced in the previous section.

Running REMIND with a perfect capital market configuration yields trade projections with short-term capital flows from developed to developing and emerging economies. This results in strong current account deficits in the base year in Sub-Saharan Africa, China and other developing and emerging world regions, while current account surpluses are for example simulated for the USA. While the results are soundly explained by the theory (cf. Sect. 2), for most regions, the model results are in significant contrast with the empirical data as shown in Fig. 2. This also applies to the consumption shares. Most striking is the deviation in Sub-Saharan Africa. Consumption in Sub-Saharan Africa in the base year 2005 is almost 40% higher than the produced GDP. Imposing growth constraints on accumulated debts and assets help reducing the gap between historic and model data, in particular in the case of Sub-Saharan Africa and China, but also for India and USA (see Fig. 2). Significant differences remain for these regions, and also for MEA, OAS and REF.

Fig. 2

Comparison of empirical data and simulation results (history - empirical data, Base - baseline with perfect capital market, Base$\_$debt - baseline with debt constraints, Base_imp - baseline with impefect capital market)

The third projection line in Fig. 2 is based on running REMIND featuring all imperfect capital market elements, including the debt and assets growth constraints as well as all wedges estimated. This setting results in more realistic short-term capital flows. The gap between historical data and model results is closed for the current account and consumption shares. We see lower initial consumption levels and higher consumption growth rates in most developing countries. Triggered by the savings and trade wedges, investments during early periods in developing countries are based more on domestic savings than on foreign capital flows. This improves the current account balance of affected developing countries, which can use short-term surpluses to increase consumption in the long run.

Fig. 3

Differences in terms of aggregated consumption between a perfect capital market and an imperfect capital market solution (REMIND results)

Despite of large differences of the consumption trajectories between the perfect and imperfect capital market implementation, the cumulated discounted consumption effects are relatively small.⁷ Globally, aggregated consumption differences of the imperfect capital market solution compared to the perfect capital market one amounts to 0.5$\%$ (see Fig. 3). We see somewhat larger differences between 2 and 6$\%$ for China, India, MEA and REF. They can mainly be explained by reduced growth and investment dynamics due to capital market effects, i.e. due to changes in capital flows and capital market prices as well as capital losses triggered by risk premiums.

Applying the improved version of REMIND, featuring an imperfect capital market representation, we are able to simulate long-term trade patterns of the represented regions. The resulting cluster of trade patterns and the composition of the current accounts of all regions is presented and discussed in the Appendix. In summary, we identify four clusters in a baseline scenario:

• (1) CAZ, MEA, REF - resource owners with large amounts of foreign assets in the short term.

• (2) China, India, OAS accumulate substantial net foreign assets by goods exports that in the mid-term overcompensate large imports of energy.

• (3) Europe, Japan - large imports of energy that possibly are accompanied by imports of goods, and hence negative foreign assets, in the short to mid term.

• (4) USA, LAM - large amounts of goods imports and capital inflows yield substantial negative net foreign assets in the short term and challenge a long-term trade balance.

As a final baseline result, Fig. 4 highlights the isolated impact of a single component of the imperfect capital market implementation - the capital market risk premiums. While this impact of the risk premiums does not change the qualitative trade pattern as discussed before, it causes considerable changes of consumption and other variables to which consumption differences can be decomposed.⁸ As expected, regions with large risk premium are most negatively affected. In the case of China, higher capital costs reduce investments and induce long-term reduction of GDP. This applies also to India and Sub-Saharan Africa, where the direct capital market effect (i.e. higher implicit costs of credits and debt repayment) is more pronounced and causes additional losses in consumption. Overall, the demand on fossil fuels at the international market declines, in particular with coal. For developing and emerging economies facing higher international capital costs, reducing imports is a mean to balance the current accounts. Due to decreasing demand and decreasing fossil fuel prices, resource exporting world regions like MEA and REF forfeit revenues from the resource markets, which can only partly be compensated by lower spendings on domestic fuels (labeled by “ESM$\_$var”).

Fig. 4

Decomposition of consumption losses from imposing a risk premium on capital imports; contributing factors are labeled in the legend with $ESM\_fixed$ representing energy system investments and $ESM\_var$ representing fuel costs plus operation and maintenance costs in the energy system (positive values denote contributions that reduce consumption in the scenario with risk premium)

While the use of domestic fuels is significantly increased in most countries, the change pattern is not unique for the investments in energy conversion capacities. They are commonly expected to decrease with higher capital costs. Corresponding to this expectation, higher consumption due to savings of energy system investments (labeled as “ESM$\_$fixed”) can be seen for regions with high risk premium. However, it is not a dominant effect. Consequently, energy system investments into more capital-intensive renewable energy technologies are not stronly reduced with risk premiums taken into account.⁹

5 Costs of climate policies

To analyse the impact of capital market imperfections on the mitigation costs, we run a climate policy scenario.¹⁰ Climate policies are simulated by imposing a global carbon price which regulates all greenhouse gases, and hence is related to CO$_2$ equivalents. The endogenously derived carbon price ensures the model to stabilize the climate system below 2 $^{\circ }$C.

Whereas baseline emissions increase to more than 80 GtCO$_2$eq, net emissions have to be reduced to a level of nearly 0 Gt in the climate policy scenario (see Fig. 5). The resulting mitigation gap is huge, and can only be closed by drastic reductions in the consumption of fossil energy resources. This requires a massive use of carbon free technologies, for example renewable energy technologies and electric vehicles in the energy conversion and transportation sector, respectively. Depending on the state of technological development, on the characteristic of the energy resource basis including its valuation, and on how the global mitigation efforts are distributed, the low carbon transition of economies can generate additional capital needs. For example, renewable energy technologies are more capital intensive than fossil-based technologies. Market imperfections may impede and delay the provision of capital, and hence increase the costs of climate policies.

Fig. 5

Total greenhouse gas emissions under baseline scenarios with perfect capital market (Base) and imperfect capital market (Base_imp), and under 2 $^{\circ }$C climate policy scenario

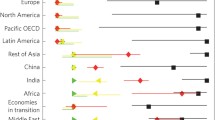
According to simulation results of REMIND with a perfect capital market, global mitigation costs are around 1.4% for the 2 $^{\circ }$C scenario (Fig. 6). Regional mitigation costs are low for developed countries and above average for developing and emerging economies. The values are comparable with those from previous studies (e.g. Luderer et al. 2011; Aboumahboub et al. 2014; Tavoni et al. 2015).

The global mitigation costs derived in the context of imperfect capital markets only marginally increase compared to the case with perfect capital markets. The baseline effect between the cases with and without perfect capital markets has been larger (compare Fig. 3). This confirms the robustness of mitigation cost estimates of previous studies that assumed perfect capital markets. However, cost differences between the perfect and imperfect capital market scenarios are identified at the regional level. Higher mitigation costs under imperfect capital markets can be observed for India, OAS and China, but also USA and LAM. Higher costs (CHA, IND, OAS) and lower revenues (USA) from the capital market as well as less benefits from decreasing prices on the fossil markets (CHA, IND, OAS, LAM) are the main factors of mitigation cost increases with imperfect capital markets.

Fig. 6

Regional and global mitigation costs for 2 °C scenario with perfect and imperfect capital market

Most remarkably, there are some regions with significantly lower mitigation costs in the imperfect capital market scenario. This in particular applies to the resource exporting regions REF, MEA and CAZ, which in general are amongst those regions that face highest mitigation costs (see Fig. 6). The main reason for this reduction in mitigation costs is strongly related to the baseline dynamics. The imperfect capital market under baseline conditions results in a reduction of trade activities which also affect the trade of fossil resources. Consumption and import of coal show largest reduction under imperfect capital markets. This is also indicated by the comparatively large consumption effects due to coal trade demonstrated in Fig. 4. While coal use for electricity production can easily be substituted by renewables and natural gas under perfect as well as imperfect capital market conditions, this substitution is more strongly used when capital markets are imperfect and net importers are looking for opportunities to avoid costly foreign liabilities. In consequence, with imperfect capital markets we see a reduced level of energy resource revenues in the baseline and less additional losses of these revenues in a climate policy scenario.

Simultaneously, the reduced consumption of fossils in the baseline results in a slightly lower mitigation gap (see Fig. 5). That explains why we see at the global level no increase of mitigation costs despite the increased capital costs of investing in low carbon technologies. If one of the two opposing effects were stronger than the other, the global mitigation costs would show a larger difference.

Changes in the net foreign assets due to climate policies are small. This applies to both the scenarios with and without perfect capital markets and indicates robustness of long-term trade and growth patterns (see Appendix).

6 Conclusions

This study investigates the effects of representing imperfect capital markets in a large scale IA model. It turns out that major variables of the model are affected quite differently. The presented approach, that is based on a wedge analysis, yields strong impacts on the simulated consumption and current account paths. Moderate changes result regarding the consumption of fossil resources and baseline greenhouse gas emissions. Both are somewhat lower under imperfect capital market conditions. Otherwise, the use of energy technologies as well as the trajectories of macroeconomic and energy investments are quite robust. The same applies to the mitigation costs of climate policies. On the global level, cost differences between the perfect and imperfect capital market implementation are negligible. Reduced costs, that can be expected from the smaller mitigation gap under imperfect capital markets, are counterbalanced by higher costs for financing the capital-intensive transformation of the energy system. Overall, the baseline effect dominates, i.e. a comparison of climate policy scenarios with and without capital market imperfections reveals only slight differences that go beyond those that already can be seen when comparing the respective baseline scenarios. Yet, differences exist with regard to regional mitigation costs. In particular, resource exporting countries are shown to experience substantial mitigation cost reductions with capital market imperfections represented.

While the results from this study substantiate cost estimates of previous studies that assumed perfect capital markets, further research is needed to qualify them. A first extention of the present approach is to shift from constant wedges to wedges that fade out over a certain time horizon. Another strand of future research should face the challenge of weakening the assumption of perfect foresight. Under the standard assumption of perfect foresight, the effect of capital market imperfections is contained and differences in rate of returns between regions are equalized relatively fast without substantial failures in investment decisions. More substantial changes of the investment dynamics, on the macro-economic as well as energy system level, can be expected under imperfect foresight or with a model that includes explicitly a financial sector with interest rates as policy control variable.

In this study we assumed exogenous parameter variations and constraints to close the gap between model variables and statistical data. In future research, it would be useful to model capital market imperfections in an endogenous manner. For example, national financial markets that are open to foreigners show significant economies of scale and positive network externalities. These effects can give rise to an endogenous specialization and concentration dynamics that are not captured by exogenous assumptions applied in the present study. Such improved model framework would provide a tool to explain financial market imperfections as the result of spillovers and natural monopolies rather than exogenous constraints.

From a welfare perspective it is also interesting to improve research on the merits of capital market liberalization. The results presented here show that the mutually beneficial capital trade can help developing countries with a relatively young population to finance consumption and investment in the near term, which generates capital income for aging popluations in advanced economies in the medium to longer term. These welfare analysis need to be based on improved modelling of financial markets to provide well-informed advice to policy makers.

Appendix

1.1 Numerical algorithm of wedge analysis

The wedge analysis serves to estimate wedges that are used in the model (REMIND) to correct capital trade flows. These wedges represent either autonomous new parameters (risk premiums) or additive components of existing parameters (pure rate of ime preference, intertemporal elasticity of substitution). The applied approach of wedge analysis, furthermore, includes two targets - current account and consumption in 2005, both as share on GDP. The two targets have a counterpart variable in the model. Within the developed numerical algorithm, the targets are used to adjust the wedges. This adjustment is an iterative process which is illustrated by Fig. 7 and take the general form of ($\Delta$x - wedge, T - target, M - model variable, w - adjustment weight, i -iteration index, j - wedge type):

$$\begin{aligned} \Delta x^{i+1}_j = \Delta x^{i}_j \pm w_j \cdot \sqrt{\mid T_j - M^i_j \mid } ~~~~~~~~\forall ~i,j . \end{aligned}$$

(11)

Fig. 7

Flow chart of algorithm to estimate wedges

In the following, we provide the details of the implemented algorithm structured along the three components of Fig. 7.

1. Initialization:

The savings and trade wedges are initialized by

$$\begin{aligned} \Delta \rho ^0 = 0 , \Delta \gamma ^0 = 0 , \Delta \mu ^0 = 0 \end{aligned}$$

(12)

and the adjustment weights are assigned a value that does not change between iterations:

$$\begin{aligned} w_{\Delta \rho } = 0.001 , w_{\Delta \gamma } = 0.01 , w_{\Delta \mu } = 0.005. \end{aligned}$$

(13)

2. Evaluation of deviation:

The model is run with the updated wedges included in eqs. (1), (2) and (10). Subsequently, the difference between the model and the target value of the consumption share variable and current account share variable, respectively, is calculated:

$$\begin{aligned} \Delta C^i&= C_{targ} - C^i_{mod} \end{aligned}$$

(14)

$$\begin{aligned} \Delta {CA}^i&= {CA}_{targ} - CA^i_{mod} \end{aligned}$$

(15)

3. Adjustment of wedges:

The model runs until the markets clear and the deviation of target values and model variables is close to zero. Whenever convergence is not yet concluded, a new set of wedges is computed according to the following relations.

If $\Delta C^i < -\epsilon$

$$\begin{aligned} \Delta \rho ^{i+1}&= \Delta \rho ^{i} + w_{\Delta \rho } \cdot \sqrt{-\Delta C^i} ~~~~~~~~\forall ~i \end{aligned}$$

(16)

$$\begin{aligned} \Delta \gamma ^{i+1}&= \Delta \gamma ^{i} - w_{\Delta \gamma } \cdot \sqrt{-\Delta C^i} ~~~~~~~~\forall ~i \end{aligned}$$

(17)

$$\begin{aligned} \Delta \mu ^{i+1}&= \Delta \mu ^{i} - w_{\Delta \mu } \cdot \sqrt{-\Delta C^i} ~~~~~~~~\forall ~i . \end{aligned}$$

(18)

If $\Delta C^i > \epsilon$

$$\begin{aligned} \Delta \rho ^{i+1}&= \Delta \rho ^{i} - w_{\Delta \rho } \cdot \sqrt{\Delta C^i} ~~~~~~~~\forall ~i \end{aligned}$$

(19)

$$\begin{aligned} \Delta \gamma ^{i+1}&= \Delta \gamma ^{i} + w_{\Delta \gamma } \cdot \sqrt{\Delta C^i} ~~~~~~~~\forall ~i \end{aligned}$$

(20)

$$\begin{aligned} \Delta \mu ^{i+1}&= \Delta \mu ^{i} + w_{\Delta \mu } \cdot \sqrt{\Delta C^i} ~~~~~~~~\forall ~i . \end{aligned}$$

(21)

If $\Delta CA^i < -\epsilon$

$$\begin{aligned} \Delta \rho ^{i+1}&= \Delta \rho ^{i} - w_{\Delta \rho } \cdot \sqrt{-\Delta CA^i} ~~~~~~~~\forall ~i \end{aligned}$$

(22)

$$\begin{aligned} \Delta \gamma ^{i+1}&= \Delta \gamma ^{i} + w_{\Delta \gamma } \cdot \sqrt{-\Delta CA^i} ~~~~~~~~\forall ~i \end{aligned}$$

(23)

$$\begin{aligned} \Delta \mu ^{i+1}&= \Delta \mu ^{i} + w_{\Delta \mu } \cdot \sqrt{-\Delta CA^i} ~~~~~~~~\forall ~i . \end{aligned}$$

(24)

If $\Delta CA^i > \epsilon$

$$\begin{aligned} \Delta \rho ^{i+1}&= \Delta \rho ^{i} + w_{\Delta \rho } \cdot \sqrt{\Delta CA^i} ~~~~~~~~\forall ~i \end{aligned}$$

(25)

$$\begin{aligned} \Delta \gamma ^{i+1}&= \Delta \gamma ^{i} - w_{\Delta \gamma } \cdot \sqrt{\Delta CA^i} ~~~~~~~~\forall ~i \end{aligned}$$

(26)

$$\begin{aligned} \Delta \mu ^{i+1}&= \Delta \mu ^{i} - w_{\Delta \mu } \cdot \sqrt{\Delta CA^i} ~~~~~~~~\forall ~i . \end{aligned}$$

(27)

1.2 International trade patterns

We present patterns of long-term trade based on the level of net exports of the tradable goods in REMIND. By measuring the present value of trade flows, we combine different types of trade to a projection of current accounts. The resulting composition of the current accounts of all regions, as simulated by the revised version of REMIND, is shown in Figs. 8 and 9 for the baseline and climate policy scenario, respectively.

Fig. 8

Current account structure (baseline)

Discontinuities, in particular in the initial years, are due to strong transition effects. Starting at a level close to empirical values, all regions first try to approach a steady state characterized by macro-economic variables, such as consumption growth rates and capital labor ratios, to be on a balanced growth path. Capital (composite good) trade across regions is used to bridge the transition period as fast as possible. In addition, exogenously assumed labor productivities take effect. For example, productivity growth rates are comparatively high in India between 2020 and 2030 causing additional demand (import) on capital and a temporary decline of the current account. While the results presented do not claim for high predictive power, which in particular applies to the time and the level when the current accounts turn around, they nevertheless provide a possible qualitative pattern of future development. Four regional clusters can be identified. The first group comprises the resource owners (CAZ, REF, MEA). Their current accounts are characterized by energy resources exports and composite good imports. These regions generate a large amount of foreign assets in the short-term and have quite balanced current accounts in the mid and long term. This, however, depends on a sustained future demand on resources and changes if climate change will request for a reduction of the fossil-fuel intensive way of global energy production. The simulated differential effects are moderate.

China, OAS and India as fast growing economies form the second group. A pronounced intertemporal current account structure is associated with mid-term export surpluses and long-term import surpluses. India and OAS follow the pattern of China with some delay in time. Due to large fossil resource imports they accumulate debts that turn in the mean time into substantial surplusses by extensive goods exports. SSA shares some characteristics with the first and second group. While it starts with a current account surplus based on energy exports, it follows more and more the pattern of the developing Asian economies with large shares of energy imports and goods exports. The third group, composed of Europe and Japan, is also characterized by substantial energy resources imports that, however, are accompanied by mid term imports of the composite good. These regions shift in early periods from net exporters of goods to a net importers, therefore accumulate a large amount of debts. This net import position turns around again later in the century.

Finally the USA and LAM represent a group for which intertemporal trade is very important. Part of current economic growth and consumption is based on capital inflow and goods imports. Regarding USA, favorable institutional conditions support this way of growth, but it is questionable that it can be sustained over the century (cf. Aizenman and Sun 2010; Chen 2011). A pattern as simulated by the model is more likely. Huge initial current account deficits have to be cut back in the long run. Changes due to climate policies are small. Nevertheless, in the short term (until 2040) the U.S. have to generate an additional current account surplus of more than 500 billion Dollar US2005 (net present value) in the climate policy scenario compared to the baseline scenario.

Fig. 9

Current account structure (2 $^{\circ }$C policy scenario)