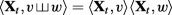Smooth Rough Paths, Their Geometry and Algebraic Renormalization

Abstract

We introduce the class of “smooth rough paths” and study their main properties. Working in a smooth setting allows us to discard sewing arguments and focus on algebraic and geometric aspects. Specifically, a Maurer–Cartan perspective is the key to a purely algebraic form of Lyons’ extension theorem, the renormalization of rough paths following up on [Bruned et al.: A rough path perspective on renormalization, J. Funct. Anal. 277(11), 2019], as well as a related notion of “sum of rough paths”. We first develop our ideas in a geometric rough path setting, as this best resonates with recent works on signature varieties, as well as with the renormalization of geometric rough paths. We then explore extensions to the quasi-geometric and the more general Hopf algebraic setting.

1 Introduction

Recent years led to a remarkable convergence of different streams of mathematics. At the center of it is the notion of path $X: [0, T]\to \mathbb {R}^{d}$ and the “stack” of its iterated integrals

$$ \mathbf{X}_{T} :=\text{Sig}(X |_{[0,T]}) := {\sum}_{n \ge 0}~\underset{0 \le u_{1}\leq {\cdots} \leq u_{n} \le T}{\int {\ldots} \int}dX_{u_{1}}\otimes {\cdots} \otimes dX_{u_{n}}, $$

commonly called the signature of X over [0,T], which takes values in $T((\mathbb {R}^{d}))$, the space of tensor series over $\mathbb {R}^{d}$. It is easy to see that the signature of a path segment actually takes its values in a very special curved subspace of the tensor (series) algebra, $G(\mathbb {R}^{d}) \subset T((\mathbb {R}^{d}))$, with a natural group structure. This construction, which originates in Chen’s fundamental work [14], is central to the theory of rough paths and stochastic analysis [29, 41, 43]. Specifically, the path t↦X_t := Sig(X|_[0,t]) is the canonical rough path lift of X, for any sufficiently smooth path X to make the signature well-defined. These ideas have proven useful in a remarkable variety of fields, stretching from machine learning [15] to algebraic geometry and renormalization theory. More specifically, we mention:

Signature varieties

In [1], Améndola, Sturmfels and one of us study the geometry of signatures tensors. The signatures of a given class of smooth paths parametrize an algebraic variety inside the space of tensors, derived from the free nilpotent Lie group, with surprising analogies with the Veronese variety from algebraic geometry. These signature varieties provide both new tools to investigate paths and new challenging questions about their behaviour. In [1] piecewise linear paths and polynomial paths are investigated. In a later work by Galuppi [30], and in the terminology of this paper, the role of classical smooth paths has been replaced by certain smooth rough paths, see Definition 2.1. Related recent works on signature varieties include [18, 49].

Rough paths and renormalization

Rough paths were famously used to solve the singular KPZ stochastic partial differential equation [33] and subsequently led to the theory of regularity structures for general singular SPDEs [34], with precise correspondences to rough paths highlighted e.g. in [26, Sec. 13.2.2]. The central topic of renormalization of singular SPDEs [8] was revisited from a rough path perspective in [6], which notably introduced pre-Lie algebras, and further inspired progress in the field [7], see also Otto et al. [40].

We cannot possibly expose in full the subtle intertwining of probabilistic, analytic, geometric and algebraic techniques of the above works, but still, sketch the general idea in a simple setting. If X models a realization of noise, such as Brownian sample paths, then the very notion of Stieltjes integration against dX_u is ill-defined (with probability one, such paths are not of locally bounded variation). The stochastic analysis provides probabilistic solutions: Stratonovich integration amounts to work with mollified X, followed by taken limits in probability, whereas Itô integration respects the martingale structure of such processes. Rough path theory (later: regularity structures) understands that these different calculi can be hard-coded imposing the first N-iterated integrals of X. The resulting object, an enhancement of X, is called a rough path (resp. model in the context of regularity structures).

There are situations—notably the KPZ equation—when the Stratonovich solution diverges, whereas the correct and desired object is given by the Itô solution. From a rough paths perspective, this amounts to adjusting (“renormalize”) the higher levels of the aforementioned enhancement. Doing so in an algebraically consistent way is a highly non-trivial task, and was achieved in a rough path, resp. regularity structure, set in the afore-mentioned works. In particular, [8] develops the algebraic theory of renormalization exclusively for smooth models, to which our study of smooth rough paths is aligned.

In this paper, we look at the indefinite signature path t↦X_t := Sig(X|_[0,t]), also known as canonical rough path lift, of a $\mathbb {R}^{d}$-valued smooth path X, as the solution of the linear differential equation

$$ \dot{\mathbf{X}}_{t} = \mathbf{X}_{t} \otimes \dot{X}_{t}, \qquad \mathbf{X}_{0} = \mathbf{1} \in \mathcal{G}, $$

(1)

with, as is well-known (see e.g. [41, Section 2.1.1] or [29, Chapter 7]) $\mathcal {G} := G(\mathbb {R}^{d} ) = \exp _{\otimes }(\mathfrak {g}) \subset T((\mathbb {R}^{d}))$, where $\mathfrak {g} := {\mathscr{L}}((\mathbb {R}^{d})) = \mathbb {R}^{d} \oplus [\mathbb {R}^{d},\mathbb {R}^{d}] \oplus {\cdots }$ denotes the space of Lie series. The same construction in the quotient (or level-N truncated) algebra

$$ (T^{N}(\mathbb{R}^{d}),\otimes_{N}, \mathbf{1}) $$

yields a finite-dimensional Lie group $\mathcal {G}^{N} := G^{N}(\mathbb {R}^{d} )= \exp _{\otimes _{N}}(\mathfrak {g}^{N}) \subset T^{N} (\mathbb {R}^{d})$ with Lie algebra $\mathfrak {g}^{N} := {\mathscr{L}}^{N} (\mathbb {R}^{d})$, the Lie polynomials of degree less equal N.

This yields an increasing family of Lie algebras (resp. groups) with inclusion maps i_N (resp. j_N), and Lie exponentials $\exp _{\otimes N}$ and $\exp _{\otimes }$, N in $\mathbb {N}$, see Section 2.

Cartan’s classical development of a smooth $\mathfrak {g}^{N}$-valued path $\mathfrak {y}$ is precisely given by solving the differential equation

$$ \dot{\mathbf{X}}_{t} = \mathbf{X}_{t} \otimes_{N} \mathfrak{y} (t), \qquad \mathbf{X}_{0} = \mathbf{1} \in \mathcal{G}^{N}. $$

Basic results on linear differential equations in finite dimensions guarantee a unique and global solution. This gives a well-defined “projective” way to solve for $\dot {\mathbf {X}}_{t} = \mathbf {X}_{t} \otimes \mathfrak {y} (t)$, $\mathbf {X}_{0} = \mathbf {1} \in \mathcal {G}$, for any $\mathfrak {g}$-valued path $\mathfrak {y}$. This is a precise generalization of (1) and leads us to the class of smooth rough paths¹. In infinite-dimensional Lie group theory, solvability of such equations has led to the notion of regular Lie group [47]. However, this is of no concern to us and we refer to [3, 4] for the subtleties of infinite groups like $\mathcal {G}$.

Conversely, every smooth $\mathcal {G}^{N}$-valued path X_t is the Cartan development of

$$ \mathfrak{y} (t) := \langle\omega_{\mathbf{X}_{t}}, \dot{\mathbf{X}}_{t} \rangle = \mathbf{X}_{t}^{-1} \otimes \dot{\mathbf{X}}_{t} = \partial_{h} |_{h=0} {\mathbf{X}_{t,t+h}} \in \mathfrak{g}^{N}. $$

Here ω_x is the $\mathfrak {g}^{N}$-valued (left invariant) Maurer–Cartan form, given at $\mathbf {x} \in G^{N}(\mathbb {R}^{d})$, by

$$ \omega_{\mathbf{x}} := \mathbf{x}^{-1} \otimes d\mathbf{x}, $$

which can be viewed as left logarithmic derivative of the identity map of $G^{N}(\mathbb {R}^{d})$, see also [42]. The reason we encounter the left invariant Maurer–Cartan form, rather than its right invariant counterpart ((dx) ⊗x^− 1) can be traced back to the order of interated integrals in the definition of the signatures, i.e. $u_{1} \le {\dots } \le u_{n}$ rather than $u_{n} \le {\dots } \le u_{1}$. We recall also that the Maurer–Cartan form has appeared in previous works of rough paths on manifolds [11], as well as signature based shape analysis [12]. We shall see in Sections 2.4 and 3.4 that renormalization of rough differential equations, in the spirit of [6], can much benefit from this geometric viewpoint. (For earlier use in the context of renormalization see also [16].) In the context of renormalization of rough differential equations however, its use appears to be new.

The geometry of $\mathcal {G}$ encodes validity of a chain rule, equivalently expressed in terms of shuffle identities, that in turn exhibits $\mathcal {G}$ as a character group of the shuffle Hopf algebra. This suggests correctly that the Maurer–Cartan perspective is not restrictive to $G(\mathbb {R}^{d})$-valued (“geometric”) rough paths, but valid for “general” rough paths, in the sense of [54], with values in the character groups of a general graded Hopf algebra. However, too much generality does not allow for some of the concrete applications we have in mind, notably an understanding of differential equations driven by rough paths and their renormalization theory. We thus commence in Chapter 2 with smooth instances of geometric rough paths (in short: grp), which can be thought of as a multidimensional path enhanced with iterated integrals with classical integration by parts (shuffle) relations, together with suitable analytic conditions. A typical (non-smooth) example is given by Brownian motion with iterated integrals in the Stratonovich sense, see e.g.[26, Sec. 2.2] for precise definitions, see also [26, 29, 35, 41, 43]. (We will review what we need in the main text below, cf. Definitions 2.1 and 2.3.) Another aspect concerns the sub-Riemannian structure of $G^{N}(\mathbb {R}^{d} )$, the state space of (level-N) geometric rough paths, see e.g. in [29, Remark 7.43] or [25].

The indefinite signature of a $\mathbb {R}^{d}$-valued path always stays tangent to the left-invariant vector fields generated by the d coordinate vector fields. In sub-Riemannian geometry, such paths are called horizontal. The study of smooth geometric rough paths is effectively the study of (possibly non-horizontal) smooth paths on $\mathcal {G}$. It is classical in geometric rough path theory to equip this space with the Carnot–Caratheodory metric. A generic smooth geometric rough path then has infinite length and is thus a genuine and interesting example of rough paths. We then continue to extend smooth rough paths in a more general setting:

Quasi-geometric theory

A quasi-geometric rough path should then be thought of as a multidimensional path enhanced with iterated integrals with classical integration by parts (shuffle) relation replaced by a generalized integration by parts rule known as quasi-shuffle. A typical example is given by Brownian motion with iterated integrals in the Itô sense. This structure also arises naturally when dealing with discrete sums (cf. [22] for signature sums) or piecewise constant paths, as well as Lévy processes [19], general semimartingales and finally rough path analysis [2, 7]. We also note unpublished presentations on quasi-rough paths by D. Kelly, who first introduced the concept, following his work [35, 38]. The very influential article [35] focused on the interplay between geometric and branched rough paths, introduced in [32], not central to this work. We note that quasi-shuffle structures have emerged independently in renormalization theory, see e.g. [17, 39, 45, 46] and the references therein.

Hopf algebra constructions

We finally revisit the previous constructions from a general Hopf algebra construction. In view of [6] we do not single out the case of branched rough paths. Our gradual approach to treat first geometric (Chapter 2), then quasi-geometric (Chapter 3) and finally the Hopf algebra case (Chapter 4) is a choice we made for essentially two reasons: (i) The material of Chapter 2 remains accessible to readers with a minimum on prerequisites and is also the setting that is most used in the context of signatures, including the recent developments in algebraic geometry. (ii) Not every result obtained in the (quasi-)geometric setting has a precise counter-part in the Hopf algebraic generality. For instance, as already observed in [6] in the context of branched rough paths, one loses certain uniqueness properties of renormalization operators when passing to more general structures.

Let us list the main contributions of this work with some detailed pointers to the main text.

• With Definitions 2.1, also 3.8, 4.1 we introduce the class of smooth rough paths in their respective setting and show in Theorems 2.8, also 3.10, 4.2 that level-N smooth rough paths have a lift whose uniqueness hinges on some algebraic/geometric minimality. (This is in contrast to the classical Lyons lift of level-N rough paths, where uniqueness depends on analytical conditions, see e.g. [29, Chapter 9].) We note that a related minimality condition appeared in the context of rough paths with jumps [27].

• An interesting insight is then that smooth rough paths, the resulting space of which is by nature non-linear, can be given a canonical linear structure. (This should be contrasted with ad hoc linearizations based on Lyons–Victoir extension, see e.g. [26, Ex. 2.4] and especially [54].)

• We finally revisit differential equations driven by our classes of rough paths, followed by their renormalization as initiated in [6]. Specifically, in Theorem 2.26 we highlight the role of smooth rough paths in the argument. Our subsequent extensions in Sections 3 and 4 complements (and differ from) existing results, notably [6], with a sole focus on geometric and branched structures, and related works [7, 9] that involve/pass through branched constructions.

2 Smooth Geometric Rough Paths

2.1 Definitions and Fundamental Properties

Let $(T((\mathbb {R}^{d})), +, \otimes )$ denote the algebra of tensor series over $\mathbb {R}^{d}$, equipped with the standard basis e₁,…,e_d. Elements of $T((\mathbb {R}^{d}))$ are of the form

$$ \mathbf{x} = \sum \mathbf{x}^{w} e_{w}, $$

with summation over all words w = ℓ₁…ℓ_n with letters ℓ_j ∈{1,…,d}, scalars x^w and $e_{w} := e_{l_{1}} \otimes {\dots } \otimes e_{l_{n}}$. The summation includes also 1, the empty word. There is a natural pairing of $T((\mathbb {R}^{d}))$ with $T(\mathbb {R}^{d})$, the space of tensor polynomials linearly spanned by the e_w so that

$$ \langle \mathbf{x}, w \rangle := \langle \mathbf{x}, e_{w} \rangle = \mathbf{x}^{w}. $$

(2)

The same pairing applies to the truncated space $T^{N}(\mathbb {R}^{d})$, consisting of tensor polynomials of degree at most $N\in \mathbb {N}$, spanned by pure tensors e_w whose word w has length |w|≤ N. We denote the canonical projection onto $T^{N}(\mathbb {R}^{d})$ as $\textsf {proj}_{N}\colon T((\mathbb {R}^{d}))\to T^{N}(\mathbb {R}^{d})$. Equivalently, we can introduce $T^{N}(\mathbb {R}^{d})$ as a quotient algebra. Indeed, introducing the ideal $T^{>N}((\mathbb {R}^{d})) := {\bigoplus }_{n> N}^{\infty }(\mathbb {R}^{d})^{\otimes n}$ one immediately has the following isomorphism

$$ T^{N}(\mathbb{R}^{d}) \cong T((\mathbb{R}^{d})) / T^{>N}((\mathbb{R}^{d})). $$

We write ⊗_N for the induced truncated tensor product.

Using the identification between words and tensors, we denote by the shuffle product on words , defined by for any word w and the recursive definition

(3)

for any couple of words w, v and letters i,j ∈{1,…,d}. The product induces a commutative algebra² on $T(\mathbb {R}^{d})$.

There are several Lie algebras we want to look at which stem from the algebra $(T((\mathbb {R}^{d})),\otimes )$; we use the notation ${\mathscr{L}}(\mathbb {R}^{d})$ for the Lie algebra generated by the letters $\mathbb {R}^{d}$ (the space of Lie polynomials), ${\mathscr{L}}^{N}(\mathbb {R}^{d})$ for the projection of ${\mathscr{L}}(\mathbb {R}^{d})$ into $T^{N} (\mathbb {R}^{d})$, and ${\mathscr{L}}((\mathbb {R}^{d})) \subset T((\mathbb {R}^{d}))$ the Lie series. We define the tensor and truncated tensor exponentials $\exp _{\otimes }\colon T^{>0}((\mathbb {R}^{d})) \to T((\mathbb {R}^{d}))$, $\exp _{\otimes _{N}}\colon T^{N}(\mathbb {R}^{d})\cap T^{>0}((\mathbb {R}^{d}))\to T^{N}(\mathbb {R}^{d})$ given respectively by

$$ \exp_{\otimes}\mathbf{x}= {\sum}_{n \ge 0}\frac{\mathbf{x}^{\otimes n}}{n!}, \qquad \exp_{\otimes_{N}}\mathbf{x}= {\sum}_{n=0}^{N}\frac{\mathbf{x}^{\otimes_{N} n}}{n!}. $$

(4)

Then it is well known ([43, 53]) that $G(\mathbb {R}^{d})= \exp _{\otimes } {\mathscr{L}}((\mathbb {R}^{d}))$ is a group with operation ⊗ which satisfies

Similar results hold for $G^{N}(\mathbb {R}^{d})$, now in terms of words with joint length ≤ N and as the image of ${\mathscr{L}}^{N}(\mathbb {R}^{d})$ under $\exp _{\otimes _{N}}$ respectively. We note that $(G^{N}(\mathbb {R}^{d}), \otimes _{N})$ is a bona fide finite-dimensional Lie group with Lie algebra ${\mathscr{L}}^{N}(\mathbb {R}^{d})$.

The following definitions are standard (as e.g. found in [35]), but with analytic Hölder / variation type conditions replaced by a smoothness assumptions.

Definition 2.1

We call level-N smooth geometric rough path (in short: N-sgrp) over $\mathbb {R}^{d}$ any non-zero path $\mathbf {X}: [0,T] \to T^{N}(\mathbb {R}^{d})$ such that

• (a.i) The shuffle relation holds for all times t ∈ [0,T]

  

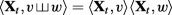  (5)

  for all words with joint length |v| + |w|≤ N.

• (a.ii) For every word of length |w|≤ N, the map t↦〈X_t,w〉 is smooth. We write

  $$ \dot{\mathbf{X}}_{t} = {\sum}_{|w|\le N} \langle\dot{\mathbf{X}}_{t},w\rangle e_{w} $$

  for the derivative of X.

By smooth geometric rough path (in short: sgrp) we mean a path with values in $T((\mathbb {R}^{d}))$ with all defining “≤ N” restrictions on the word’s length omitted.

Remark 2.2

By Proposition 2.14 below N-sgrp are smooth $G^{N}(\mathbb {R}^{d})$-valued paths, thus (with respect to the appropriate Carnot–Caratheodory metric [29]) genuine 1/N-Hölder regular rough paths, which justifies our terminology. Similarly, sgrps are nothing but smooth $G(\mathbb {R}^{d})$-valued paths, provided $G(\mathbb {R}^{d})$ is equipped with a suitable “weak” differential structure to make it a topological Lie group, see [4].

The shuffle relation applied to empty words and the demand that X is non-zero imply together with continuity in t that 〈X_t,1〉 = 1 for all t ∈ [0,T], hence X is (similar to formal power series) invertible with respect to ⊗_N. Every N-sgrp gives then rise to increments, $(s,t) \mapsto \mathbf {X}_{s}^{-1} \otimes _{N} \mathbf {X}_{t}$. This motivates the following definition.

Definition 2.3

We call level-N smooth geometric rough model (in short: N-sgrm) over $\mathbb {R}^{d}$ any non-zero map $\mathbf {X}: [0,T]^{2} \to T^{N}(\mathbb {R}^{d})$ such that

• (b.i) the shuffle relation (5) holds with X_t replaced by X_s,t, any s,t.

• (b.ii) Chen’s relation holds, by which we mean

  $$ \mathbf{X}_{s,u} \otimes_{N} \mathbf{X}_{u,t}=\mathbf{X}_{s,t} $$

  (6)

  for any s,u,t ∈ [0,T].

• (b.iii) For every word of length |w|≤ N, the map ↦〈X_s,t,w〉 is smooth, for one (equivalently: all) base point(s) s ∈ [0,T].

By smooth geometric rough model (in short sgrm) we mean a map with values in $T((\mathbb {R}^{d}))$, with all “≤ N” quantifiers omitted and (6) with ⊗_N replaced by ⊗.

Remark 2.4

The terminology “model” is consistent with that of Hairer’s regularity structures. More specifically, given a N-sgrm X = X_s,t we have the map

$$ s \mapsto \{T^{N}(\mathbb{R}^{d}) \ni \mathbf{u} \mapsto \langle \mathbf{X}_{s,\cdot}, \mathbf{u} \rangle \} $$

which together with Chen’s relation yields precisely a model in the sense of regularity structures. See e.g. [26, Sec. 13.2.2], [50, Theorem 5.15] and [6, Proposition 48]. Our use of the adjective “smooth” is also consistent with the notion of smooth model, used by Hairer and coworkers and central to the algebraic renormalization theory of [8].

It follows from (5), resp. (b.i), and the non-zero condition that N-smooth geometric rough paths and models actually take values in $G^{N}(\mathbb {R}^{d})$; similarly for (tensor series) smooth rough paths and models and $G(\mathbb {R}^{d})$. Clearly, every level-N smooth geometric rough path $\mathbf {X}:[0,T]\to T^{N}(\mathbb {R}^{d})$ induces a level-N smooth geometric rough model $\mathbf {X}: {[0,T]^{2}} \to T^{N}(\mathbb {R}^{d})$ in the above sense, by considering the increments

$$ \mathbf{X}_{s,t} := \mathbf{X}_{s}^{-1} \otimes_{N} \mathbf{X}_{t}. $$

(7)

Conversely, every level-N smooth geometric rough model defines a level-N smooth geometric rough path X_t := X_0,t so that N-sgrp and N-sgrm are equivalent modulo a starting point in $G^{N} (\mathbb {R}^{d})$.

Definition 2.5

A sgrp X is called extension of some N-sgrp Y if

$$ \langle \mathbf{X}_{t}, w \rangle = \langle \mathbf{Y}_{t}, w \rangle \qquad \text{for all \textit{t} and whenever $|w| \le N$;} $$

if this holds for a $N^{\prime }$-sgrp X, with $N < N^{\prime } < \infty$, we call it $N^{\prime }$-extension of Y. We adopt also the same denomination if Y is a N-sgrm and X is a sgrm ($N^{\prime }$-sgrm) and one has the same relation above for any s,t ∈ [0,T].

When d = 1, the situation is trivial, and sgrps are in one-to-one correspondence with smooth scalar paths: An arbitrary scalar path Y with initial point Y₀ = 0 has a (unique) extension given by

$$ \mathbf{X}_{t} = \mathbf{1} + Y_{t} e_{1} + \frac{(Y_{t})^{2}}{2!} e_{11}+ {\cdots} =\exp_{\otimes}{Y_{t}} \in T((\mathbb{R})). $$

Conversely, every sgrp with X₀ = 1 must be of this form, as a consequence of the shuffle relations. When d > 1 such extensions are never unique. For instance, given the two basis vectors $e_{1},e_{2}\in \mathbb {R}^{2}$ and denoting by 0 the common zero of $T(\mathbb {R}^{2})$, we see that $t \mapsto (1,\mathbf {0},\mathbf {0})\in T^{2}(\mathbb {R}^{2})$ and $t \mapsto (1,\mathbf {0}, t[e_{1},e_{2}]) \in T^{2}(\mathbb {R}^{2})$ are both 2-sgrps over $\mathbb {R}$, and hence level-2 extensions of the trivial 1-sgrp t↦(1,0).

In classical rough path analysis [29, 41], a graded p-variation (or Hölder) condition is enforced, which guarantees a unique extension. We give here a novel algebraic condition that enforces uniqueness, somewhat similar in spirit to the minimal jump extension of cadlag rough paths in [27]. This condition is motivated by the following result.

Proposition 2.6

Given a sgrm X over $\mathbb {R}^{d}$, the diagonal derivative defined for all times s by

$$ \dot{\mathbf{X}}_{s,s}:= \partial_{t} |_{t=s} \mathbf{X}_{s,t} $$

lies in ${\mathscr{L}}((\mathbb {R}^{d})) \subset T((\mathbb {R}^{d}))$. The analogue statement holds for N-sgrm’s, with ${\mathscr{L}}((\mathbb {R}^{d}))$ replaced by its truncation ${\mathscr{L}}^{N}(\mathbb {R}^{d})$ (the Lie polynomials).

Proof

A geometric proof is not difficult. We define the $G^{N}(\mathbb {R}^{d})$-valued path X_t := X_0,t so that $\dot {\mathbf {X}}_{s,s}:= \mathbf {X}_{s}^{-1} \otimes \dot {\mathbf {X}}_{s}$ which is exactly the Maurer–Cartan form at X_s, evaluated at the tangent vector $\dot {\mathbf {X}}_{s}$. This results in an element in the Lie algebra, which here is identified with ${\mathscr{L}}^{N}(\mathbb {R}^{d})$. Since N is arbitrary, this also implies the first claim. □

Remark 2.7

Let us illustrate the previous proposition in the case N = 2. The defining shuffle relation of sgrm’s applied to single letter words i and j yields

$$ \langle\mathbf{X}_{s,t},i \rangle\langle\mathbf{X}_{s,t},j \rangle= \langle \mathbf{X}_{s,t},ij\rangle+\langle\mathbf{X}_{s,t},ji\rangle. $$

Dividing this identity by t − s > 0, followed by sending t ↓ s, one has immediately

$$ \langle \dot{\mathbf{X}}_{s,s},ij\rangle+\langle\dot{\mathbf{X}}_{s,s},ji\rangle=0 $$

so that the second tensor level of $\dot {\mathbf {X}}_{s,s}$ is anti-symmetric, hence $\dot {\mathbf {X}}_{s,s} \in \mathbb {R}^{d} \oplus [\mathbb {R}^{d},\mathbb {R}^{d}]$.

Theorem 2.8 (Fundamental theorem of sgrm)

Given an N-sgrm Y for some $N \in \mathbb {N}$, there exists exactly one sgrm extension X of Y which is minimal in the following sense:

$$ \dot{\mathbf{X}}_{s,s} \in \mathcal{L}^{N} (\mathbb{R}^{d}) \subset \mathcal{L} ((\mathbb{R}^{d}))\quad \forall \in[0,T]. $$

This unique choice then in fact satisfies $\dot {\mathbf {X}}_{s,s}=\dot {\mathbf {Y}}_{s,s}$. We call MinExt(Y) := X the minimal extension of Y and also $\mathrm {MinExt^{\textit {N}^{\prime }}(Y)} := \text {\textsf {proj}}_{N^{\prime }} \mathbf {X}$, for $N^{\prime } > N$, the $N^{\prime }$-minimal extension of Y. For a fixed interval [s,t] ⊂ [0,T], X_s,t only depends on {Y|_[u,v] : s ≤ u ≤ v ≤ t} and we introduce the signature of Y on [s,t] defined by

$$ \text{Sig}(\mathbf{Y}|_{[s,t]}) := \mathbf{X}_{s,t} \in G(\mathbb{R}^{d}). $$

Proof

(Existence) Thanks to the previous proposition

$$ \mathfrak{y} (t) := \dot{\mathbf{Y}}_{t,t} \in \mathcal{L}^{N} (\mathbb{R}^{d}) $$

defines a smooth path with values in the Lie algebra ${\mathscr{L}}^{N} (\mathbb {R}^{d})$. Its Cartan development into $G(\mathbb {R}^{d})$ amounts to solving $\dot {\mathbf {X}}_{t} = \mathbf {X}_{t} \otimes \mathfrak {y} (t)$ with $\mathbf {X}_{0} = \mathbf {1} \in G(\mathbb {R}^{d})$. It is enough to do this in finite dimensions, say in $G^{N^{\prime }}(\mathbb {R}^{d})$ for arbitrary $N^{\prime }>N$, in which case such differential equations have a unique and global solution. Indeed, existence of a unique local solution is clear from ODE theory, whereas non-explosion is a consequence of linearity of this equation. See also a much more general reference [37]. Since the natural projections from $G^{N^{\prime }+1}(\mathbb {R}^{d}) \to G^{N^{\prime }}(\mathbb {R}^{d})$ are Lie group morphisms, we obtain a consistent family of $N^{\prime }$-extensions which defines t↦X_t in the projective limit. The minimal extension is then given by $\mathbf {X}_{s,t} = \mathbf {X}_{s}^{-1} \otimes \mathbf {X}_{t}$, where we note that

$$ \dot{\mathbf{X}}_{t,t} = \mathbf{X}_{t}^{-1} \otimes \dot{\mathbf{X}}_{t} = \mathfrak{y} (t) \in \mathcal{L}^{N} (\mathbb{R}^{d}). $$

(Uniqueness) It is sufficient to consider $N^{\prime }=N+1$. In this case two level-$N^{\prime }$ extensions X, $\bar {\mathbf {X}}$, differ by an element in the center of $G^{N^{\prime }}(\mathbb {R}^{d})$, so that ${\varPsi }_{s,t} := \langle \mathbf {X}_{s,t} -\bar {\mathbf {X}}_{s,t}, w \rangle$ is additive for every word |w|≤ N + 1. We need to show that Ψ ≡ 0. By assumption, Ψ vanishes on words of length |w|≤ N, so we can assume $|w| = N^{\prime }=N+1$. With Ψ_t := Ψ_0,t note that Ψ_s,t = Ψ_t −Ψ_s. Write X_t = X_0,t, and similarly for $\bar {\mathbf {X}}$, and also $\sim$ for equality in the limit t ↓ s. Then

$$ \dot{{\varPsi}}_{s} \sim \frac{{\varPsi}_{s,t}}{(t-s)} = \frac{\langle \mathbf{X}^{-1}_{s}\otimes (\mathbf{X}_{t} - \mathbf{X}_{s}) -\bar{\mathbf{X}}^{-1}_{s} \otimes (\bar{\mathbf{X}}_{t} -\bar{\mathbf{X}}_{s} ), w \rangle }{(t-s)} \sim \langle \mathbf{X}^{-1}_{s}\otimes \dot{\mathbf{X}}_{s} -\bar{\mathbf{X}}^{-1}_{s} \otimes \dot{\bar{\mathbf{X}}}_{s} , w \rangle $$

and in view of the minimality assumption of order N of both X, $\bar {\mathbf {X}}$, with the condition |w| = N + 1, we see that $\dot {\varPsi }$ is zero, hence Ψ ≡Ψ₀ = 0 which concludes the argument for uniqueness. □

Remark 2.9

(Computing the minimal extension) Note that the existence part of this proof is constructive and gives the minimal extension via a solution of a linear differential equation. To make this explicit in case of a N-sgrp Y, it suffices to solve

$$ \dot{\mathbf{X}} = \mathbf{X} \otimes (\mathbf{Y}^{-1} \otimes_{N} \dot{\mathbf{Y}}), \qquad \mathbf{X}_{0} = \mathbf{1} \in T((\mathbb{R}^{d})). $$

To compute the signature on [s,t], it suffices to start at the initial condition X_s = 1.

It follows automatically from the proof of Theorem 2.8 that, defining MinExt(N) as the class of sgrms which arise as minimal extension of some N-sgrms over $\mathbb {R}^{d}$, we have the inclusions

$$ \begin{array}{@{}rcl@{}} &\text{MinExt}(1) \subset \text{MinExt}(2) \subset {\cdots} \subset \text{MinExt}(N ) \subset {\cdots} \subset \{\text{sgrm over}~ \mathbb{R}^{d}\},&\\ &\bigcup_{N\geq 1}\text{MinExt}(N)\subset \{\text{sgrm over}~ \mathbb{R}^{d} \}.& \end{array} $$

When d > 1, all inclusions above are strict. For instance, take a non-finite Lie series, i.e. $\mathfrak {v} \in {\mathscr{L}}((\mathbb {R}^{d})) \backslash {\mathscr{L}}(\mathbb {R}^{d})$. Then $\mathbf {X}_{s,t} = \exp _{\otimes }(\mathfrak {v}(t-s))$ defines a sgrm, which is not a minimal extension of any N-sgrm. These strict inclusions motivate the following finer subset of sgrms.

Definition 2.10

A sgrm X over $\mathbb {R}^{d}$ is called a good sgrm if X = MinExt(Y) for some N-sgrm Y, $N \in \mathbb {N}$.

Recalling that a minimal extension has the same diagonal derivative as the underlying N-sgrm, one has the immediate characterisation of good sgrms.

Lemma 2.11

A sgrm X is good if and only if for all times s ∈ [0,T] one has

$$ \dot{\mathbf{X}}_{s,s} \in \mathcal{L}(\mathbb{R}^{d}). $$

We link the notion of minimal extension with previous constructions in the literature.

Example 2.12

Every smooth path $Y: [0,T] \to \mathbb {R}^{d}$ can be regarded (somewhat trivially) as 1-sgrp Y = (1,Y ). The solution to

$$ \dot{\mathbf{X}} = \mathbf{X} \otimes (\mathbf{Y}^{-1} \otimes_{1} \dot{\mathbf{Y}}) = \mathbf{X} \otimes \dot{Y}, \qquad {\mathbf{X}}_{0} = \mathbf{1} \in T((\mathbb{R}^{d})) $$

is then precisely given by the stack of iterated integrals

$$ \mathbf{X}_{t} = \text{Sig}\left( Y|_{[0,t]}\right) = \left( 1, \int dY, \ldots, \int (dY)^{\otimes n}, \ldots\right) \in T((\mathbb{R}^{d})) $$

with n-fold integration over the n-simplex over [0,t], i.e. $0 \le u_{1} \le {\dots } \le u_{n} \le t$. The signature of Y on [s,t] coincides then with the usual definition of signature of Y, see e.g. [43], modulo a choice of unit initial data at time s, which entails integration over simplices over [s,t].

Example 2.13

Fix a step-2 Lie element over $\mathbb {R}^{d}$,

$$ \mathfrak{v} = (\mathfrak{a},\mathfrak{b}) \in \mathbb{R}^{d} \oplus [\mathbb{R}^{d}, \mathbb{R}^{d}] \equiv \mathcal{L}^{2} (\mathbb{R}^{d}), $$

where $[\mathbb {R}^{d}, \mathbb {R}^{d}]$ stands for the set of anti-symmetric 2-tensors over $\mathbb {R}^{d}$. Consider the example of a 2-sgrm given by

$$ \mathbf{Y}_{s,t}= \left( 1, \mathfrak{a}(t-s),\mathfrak{b}(t-s) + \tfrac{1}{2} \mathfrak{a}^{\otimes 2}(t-s)^{2}\right) = \exp_{\otimes_{2}} (\mathfrak{v}(t-s)) \in T^{2} (\mathbb{R}^{d}). $$

One easily sees that $\dot {\mathbf {Y}}_{t,t}= \mathfrak {v}$ for all t ∈ [0,T]. Since $\mathfrak {v}$ is constant in time, the differential equation

$$ \dot{\mathbf{X}} = \mathbf{X} \otimes \mathfrak{v}, \qquad \mathbf{X}_{s} = 1 \in T((\mathbb{R}^{d})) $$

has an explicit exponential solution at any time t given by

$$ \mathbf{X}_{s,t} = \exp_{\otimes} (\mathfrak{v}(t-s)) = 1 + \mathfrak{v}(t-s) + \tfrac{1}{2} \mathfrak{v}^{\otimes 2}(t-s)^{2} + {\dots} \in T((\mathbb{R}^{d})). $$

(8)

This is precisely the signature of Y on [s,t] and X is the minimal extension of Y. Modulo a starting point in the group such a construction is well-known as a log-linear rough path, here the special case of second order logarithm. The case $\mathfrak {v} = (\mathfrak {a},0)$ is covered in Example 2.12 via the constant velocity path $\dot {Y} \equiv \mathfrak {a}$. By taking $\mathfrak {v} = (0,\mathfrak {b})$ the minimal extension coincides with a pure area rough path, see [30] for an algebraic geometric perspective on these structures. Giving the explicit exponential solution (8) is possible here thanks to the constant velocity $\mathfrak {v}$. In a general situation, with time-dependent $\mathfrak {v}=\mathfrak {v} (t)$ the solution has exponential form given by Magnus expansion and additional commutator terms will appear, see e.g. [37].

We finish this subsection by relating sgrp to (weakly) geometric rough paths in the sense of standard definitions as found e.g. in [29, 35].

Proposition 2.14

One has the following properties:

• (i) Every N-sgrp X is a 1/N-Hölder weakly geometric rough path. Consequently, X is also a γ-Hölder geometric rough path, for any 1/γ ∈ (N,N + 1), and the set of N-sgrps is dense therein.

• (ii) The minimal extension of some N-sgrp X coincides with the Lyons lift of X, as constructed e.g. in [29, Chapter 9].

Proof

(i) We only need to discuss the analytic regularity, which is formulated for the increments $\mathbf {X}_{s,t} = \mathbf {X}^{-1}_{s}\otimes \mathbf {X}_{t}$, i.e. the associated rough model. Thanks to (b.iii), we have $|\langle \mathbf {X}_{s,t},w\rangle | \lesssim |t-s| \lesssim |t-s|^{|w|(1/N)}$ uniformly over s,t ∈ [0,T], using that |w|≤ N. The consequence follows from well-known relations between geometric and weakly geometric rough paths [29, Chapter 9]. The final density statement is clear, since already the minimal level-N extensions of smooth paths (a.k.a. canonical lifts) are dense in this level-N rough paths space, cf. [29].

(ii) We remark that the minimal extension of X can be constructed by solving a linear differential equation driven by X, in the sense of Definition 2.18 below, whereas the Lyons lift solves the analogous rough differential equations. □

2.2 Canonical Sum and Minimal Coupling of Smooth Geometric Rough Models

As was pointed out, the state space of a sgrp is $G(\mathbb {R}^{d})$, a non-linear subset of $T((\mathbb {R}^{d}))$. In particular, the pointwise sum X_t + Y_t of any given two sgrps X, Y does not generally make sense as a sgrp. From a classical rough path perspective, the obstruction to making sense of the addition of rough path increments lies in its possible dependence on (a priori) missing mixed iterated integrals. For smooth rough paths, however, it turns out that there is a canonical way to add smooth geometric rough models and, more generally a scalar multiplication.

Definition 2.15

For any fixed sgrms X, Y let $t\mapsto \mathbf {Z}_{t} \in T ((\mathbb {R}^{d}))$ be the Cartan development of $\dot {\mathbf {X}}_{s,s}+\dot {\mathbf {Y}}_{s,s}$, i.e. the unique solution to

$$ \dot{\mathbf{Z}}_{t}= \mathbf{Z}_{t}\otimes \left( \dot{\mathbf{X}}_{t,t}+\dot{\mathbf{Y}}_{t,t}\right), \quad \mathbf{Z}_{0} = \mathbf{1}. $$

We then write $\mathbf {Z} := \mathbf {X} \boxplus \mathbf {Y}$ for the associated sgrm and call it the canonical sum of X and Y. For any $\lambda \in \mathbb {R}$ we define also the sgrm $\mathbf {Z}=\lambda \boxdot \mathbf {X}$ via the Cartan development of $\lambda \dot {\mathbf {X}}_{s,s}$, we call it the canonical scalar multiplication.

We will see later that this addition of sgrm overlaps non-trivially with the renormalization of rough path. Operations $\boxdot$ and $\boxplus$ equip the space of sgrps with a vector space structure and by Lemma 2.11 good sgrps form a linear subspace.

For some general comments on these operations we refer to Remark 4.15 in the more general framework of roughs path associated to a Hopf algebra. We simply remark that in the smooth geometric setting the canonical sum coincides with a construction of Lyons for p-variation weakly geometric rough paths, see [41, Section 3.3.1 B].

Proposition 2.16

For any fixed couple of sgrms X, Y a map $\mathbf {Z}\colon [0,T]^{2}\to G(\mathbb {R}^{d})$ coincides with $\mathbf {X} \boxplus \mathbf {Y}$ if and only if Z satisfies Z_s,t = Z_s,u ⊗Z_u,t for s,u,t ∈ [0,T] and one has for any s ∈ [0,T]

$$ \mathbf{Z}_{s,t}=\mathbf{X}_{s,t}\otimes \mathbf{Y}_{s,t}+R_{s,t}, $$

(9)

for some $R_{s,t}\in T((\mathbb {R}^{d}))$ such that for all $x\in T(\mathbb {R}^{d})$ one has 〈R_s,t,x〉 = o(|t − s|) as t → s. Moreover, we have the relations

$$ \mathbf{X}_{s,t}\otimes\mathbf{Y}_{s,t} = \mathbf{Y}_{s,t}\otimes\mathbf{X}_{s,t}+r_{s,t} = \mathbf{X}_{s,t}+\mathbf{Y}_{s,t}-\mathbf{1}^{\ast}+r^{\prime}_{s,t}, $$

(10)

for some r_s,t, $r^{\prime }_{s,t} \in T((\mathbb {R}^{d}))$ such that for all $x\in T(\mathbb {R}^{d})$ one has $\langle r_{s,t},x\rangle ,\langle r^{\prime }_{s,t},x\rangle = o(|t-s|)$ as t → s.

Proof

See the more general Proposition 4.16. □

Remark 2.17

Looking back at [41, Section 3.3.1 B] and Proposition 2.14, we actually conclude that it is possible to sum a N-sgrm X to any general γ-Hölder weakly geometric rough path W for any γ ∈ (0,1) in a canonical way, though the construction is not obtained via diagonal derivatives but via the demand $(\mathbf {X}\boxplus \mathbf {W})_{s,t}=\mathbf {X}_{s,t}\otimes \mathbf {W}_{s,t}+o(|t-s|)$ and a sewing lemma argument. This gives a strong motivation of looking at smooth rough paths as “universal perturbations” (accordingly to [41, Section 3.3.1 B]) of γ-Hölder weakly geometric rough paths.

The canonical sum can now be used to define a minimal coupling in the case of a finite number of smooth geometric rough models $\mathbf {X}^{i}:[0,T]\to G(\mathbb {R}^{d_{i}}),~i=1,\dots ,m$. Set d = d₁ + ⋯ + d_m and consider the linear embedding

$$ \mathbb{R}^{d_{i}} \cong \{ 0\} \oplus {\cdots} \oplus \{ 0 \} \oplus \mathbb{R}^{d_{i}} \oplus \{ 0 \} \oplus {\cdots} \oplus \{ 0 \} \subset \mathbb{R}^{d_{1}} \oplus {\cdots} \oplus \mathbb{R}^{d_{m}} \cong \mathbb{R}^{d}. $$

This extends uniquely to an injective algebra homomorphism

$$ \iota_{i}:\quad T((\mathbb{R}^{d_{i}}))\to T((\mathbb{R}^{d})), $$

equipped with the tensor product ⊗, and hence (by restriction) also to a group homomorphism from $G(\mathbb {R}^{d_{i}})$ into $G(\mathbb {R}^{d})$. (See also [28, Section 7.5.6] for a more general discussion how to lift linear maps to group homomorphisms.) Then we can consider the sgrms $\iota _{i}\mathbf {X}^{i}:[0,T]\to G(\mathbb {R}^{d})$ and we define the minimal coupling of the Xⁱ as the canonical sum of the $\iota _{i}\mathbf {X}^{i}$

$$ (\mathbf{X}^{1},\dots,\mathbf{X}^{m})_{\min}:=\iota_{1}\mathbf{X}^{1}\boxplus\cdots\boxplus \iota_{m}\mathbf{X}^{m}. $$

(11)

The name minimal coupling amounts to the fact that we are choosing a sgrm which involves the least possible information on mixed iterated integrals. This construction can also be seen as partial generalization of Lyons–Young “(p,q)” pairing discussed in [29].

2.3 Differential Equations Driven by SGRP

Let $(f_{1},\dots ,f_{d}) \in (\text {Vect}^{\infty }(\mathbb {R}^{e}))^{d}$ be a collection of smooth vector fields, with bounded derivatives of all orders, so that all stated operations and differential equations below make sense. For the empty word 1, set f₁ = id, the identity vector field. For a word w = ℓ₁…ℓ_n with |w| = n > 0 letters ℓ_j ∈{1,…,d}, define the vector field

$$ f_{w} :=f_{\ell_{1}}\vartriangleright({\cdots} \vartriangleright(f_{\ell_{n-1}}\vartriangleright f_{\ell_{n}})\cdots), $$

(12)

where $\vartriangleright$ is the following operation of two vector fields: i.e. using Einstein summation over i,j = 1,…,e we set

$$ f \vartriangleright g := f^{i} (\partial_{i} g^{j}) \partial_{j}, $$

where f = (fⁱ∂_i), and g = (g^j∂_j). Using tensor calculus notation, we can equivalently set $f \vartriangleright g = (\nabla g) f$ where ∇g is the Jacobian matrix of g. The operation $\vartriangleright$ is also a classical example of pre-Lie product (see Section 4.2) for which one has the usual identity of commutators

$$ f\vartriangleright g -g\vartriangleright f=[f,g], $$

(13)

for any couple of vector fields f,g. The resulting family of maps {y↦f_w(y)}_w is represented by a linear map $f\colon T (\mathbb {R}^{d}) \to \text {Vect}^{\infty }(\mathbb {R}^{e})$ such that

$$ T(\mathbb{R}^{d})\in \mathbf{x} ~\mapsto~ f_{\mathbf{x}} (\cdot) = \langle f (\cdot),\mathbf{x} \rangle, $$

(14)

where the final pairing amounts to viewing f as (formal) sum $\sum f_{w} e_{w}$, with summation over all words. Importantly, this map, restricted to Lie polynomials induces a Lie algebra morphism

$$ \mathcal{L}(\mathbb{R}^{d} ) \ni \mathfrak{u} ~\mapsto~ f_{\mathfrak{u}} \in \text{Vect}^{\infty}(\mathbb{R}^{e}). $$

This morphism is uniquely determined by its values on the canonical basis of $\mathbb {R}^{d}$, since ${\mathscr{L}}(\mathbb {R}^{d})$ is isomorphic to the free Lie algebra over $\mathbb {R}^{d}$. From an intrinsic geometric point of view, $f_{\mathfrak {u}}$ is a vector field over $\mathbb {R}^{e}$ interpreted as a manifold. This holds only to the extent that one uses the flat connection on $\mathbb {R}^{e}$.

In what follows, we equip $T(\mathbb {R}^{d})$ with an inner product structure, by declaring orthonormal the basis vectors $e_{w} \in T(\mathbb {R}^{d})$, induced by distinct words w. Viewing $T(\mathbb {R}^{d})$ as subspace of $T((\mathbb {R}^{d}))$, this is consistent with the readily used pairing 〈x,z〉 with $\mathbf {x} \in T((\mathbb {R}^{d}))$, $\mathbf {z} \in T(\mathbb {R}^{d})$. In particular {e_w : |w|≤ N} yields an orthonormal basis in the level-N truncated space $T^{N}(\mathbb {R}^{d})$, with inner product 〈⋅,⋅〉 = 〈⋅,⋅〉_N. We now introduce a natural notion of differential equation associated to sgrms and a class of vector fields $(f_{1}, {\dots } ,f_{d})$.

Definition 2.18

Let X be N-sgrm or a good sgrm such that $\dot {\mathbf {X}}_{s,s}\in {\mathscr{L}}^{N}(\mathbb {R}^{d})$. We say that a smooth path $Y\colon [0,T]\to \mathbb {R}^{e}$ is the solution of a differential equation driven by X with vector fields $(f_{1},\dots ,f_{d})\in (\text {Vect}^{\infty }(\mathbb {R}^{e}))^{d}$ if it satisfies the differential equation

$$ \dot{Y}_{s}= \langle f (Y_{s}), \dot{\mathbf{X}}_{s,s}\rangle_{N}={\sum}_{|w|\le N} f_{w} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},w\rangle, $$

(15)

where f : x↦f_x is given in (12). We will refer to (15) with the shorthand notation

$$ dY=f(Y)d\mathbf{X}. $$

(16)

Remark 2.19

We remark that the equation (16) generalises the known notion of controlled ODE. Indeed, $\langle \dot {\mathbf {X}}_{s,s},\mathbf {1}\rangle =0$ for any N-sgrm or a good sgrm and if X is the minimal N-extension of a smooth path $X={\sum }_{i=1}^{d} X^{i} e_{i}$, obtained by classical iterated integration in Example 2.12, then Definition 2.18 collapses to the usual definition of controlled equation

$$ \dot{Y} = {\sum}_{i=1}^{d} f_{i}(Y) \dot{X}^{i}, $$

thereby obtaining a consistent definition. However, the richer structure of smooth geometric rough paths in Example 2.13 extends this framework.

Given a generic initial condition $Y_{0}\in \mathbb {R}^{e}$ and vector fields $(f_{1}, {\dots } , f_{d})$ on $\mathbb {R}^{e}$, it follows from standard properties on classical differential equations that there exists a unique solution with initial condition Y₀. For a N-sgrp X, the notion of solution of differential equation driven by a sgrp is furthermore consistent with the notion of rough differential equation solution à la Davie [21] when the driver X is interpreted as a 1/N-Hölder weakly geometric rough path.

Proposition 2.20

A path $Y\colon [0,T]\to \mathbb {R}^{e}$ is a solution of a differential equation driven by a N-sgrp X with vector fields $(f_{1}, {\dots } , f_{d})$ if and only if for all s,t ∈ [0,T]

$$ Y_{t}-Y_{s}={\sum}_{1\leq |w|\leq N}f_{w}(Y_{s})\langle \mathbf{X}_{s,t},w\rangle+r_{s,t}, $$

(17)

where X_s,t is the geometric rough model associated to X_t and r is a remainder such that r_s,t = o(|t − s|) as t → s.

Proof

Supposing the property (17), we first observe, since f₁ = 0 and 〈X_s,s,w〉 = 0 for any non-empty word w,

$$ \lim_{t\downarrow s}\frac{Y_{t}-Y_{s}}{t-s}=\lim_{t\downarrow s}{\sum}_{1\leq |w|\leq N}f_{w}(Y_{s})\left\langle \mathbf{X}_{s}^{-1}\otimes_{N}\frac{\mathbf{X}_{t}-\mathbf{X}_{s}}{t-s},w\right\rangle={\sum}_{1\leq |w|\leq N}f_{w}(Y_{s})\langle \dot{\mathbf{X}}_{s,s},w\rangle. $$

We thus conclude that Y is differentiable and obtain (15). (With f and $s \mapsto \dot {\mathbf {X}}_{s,s}$ smooth, it is then clear that Y is not only differentiable but in fact smooth.) Conversely, supposing that Y is a solution of (15), we apply Taylor’s formula to Y and t →〈X_s,t,w〉 for any |w|≤ N obtaining for all s,t ∈ [0,T].

$$ Y_{t}-Y_{s}={\sum}_{1\leq |w|\leq N}f_{w}(Y_{s})\langle \dot{X}_{s,s},w\rangle(t-s)+r^{\prime}_{s,t}={\sum}_{1\leq |w|\leq N}f_{w}(Y_{s})\langle X_{s,t},w\rangle+r^{\prime\prime}_{s,t} $$

for some $r^{\prime }_{s,t}$, $r^{\prime \prime }_{s,t}$ satisfying both $r^{\prime }_{s,t}, r^{\prime \prime }_{s,t}= o(|t-s|)$ as t → s. □

Using the properties of the diagonal derivative, we can restate the identity (15) with respect to the Lie algebra ${{\mathcal L}}^{N}(\mathbb {R}^{d})$.

Lemma 2.21

Let X be N-sgrm or a good sgrm such that $\dot {\mathbf {X}}_{s,s}$ lies in ${\mathscr{L}}^{N}(\mathbb {R}^{d})$ and consider an orthonormal basis $\mathfrak {B}^{N}$ for ${\mathscr{L}}^{N}(\mathbb {R}^{d}) \subset T^{N}(\mathbb {R}^{d})$. The following equivalence holds:

$$ dY = f (Y) d \mathbf{X} \quad \text{ if and only if }\quad\dot{Y}_{s} = {\sum}_{\mathfrak{u} \in \mathfrak{B}^{N}} f_{\mathfrak{u}} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},\mathfrak{u} \rangle. $$

Proof

Complete $\mathfrak {B}=\mathfrak {B}^{N}$ to an orthonormal basis $\bar { \mathfrak {B}} = \mathfrak {B} \cup \mathfrak {B}^{\perp }$ of $T^{N}(\mathbb {R}^{d})$. In that basis

$$ \dot{Y}_{s} = \langle f (Y_{s}), \dot{\mathbf{X}}_{s,s}\rangle_{N} ={\sum}_{\mathbf{x} \in \bar{\mathfrak{B}}} f_{\mathbf{x}} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},\mathbf{x} \rangle. $$

We now observe that $\dot {\mathbf {X}}_{s,s} \in {\mathscr{L}}^{N}(\mathbb {R}^{d})$, thanks to Proposition 2.6. Consequently, there is no contribution from any $\mathbf {x} \in \mathfrak {B}^{\perp } \subset {\mathscr{L}}^{N}(\mathbb {R}^{d})^{\perp }$. □

Example 2.22

In the case N = 2 a natural orthonormal basis for ${\mathscr{L}}^{2}(\mathbb {R}^{d})$ is given by

$$ \left\{i, \frac{1}{\sqrt{2}}[i,j]\colon i,j \in \{1, \ldots,d \}, i<j\right\} $$

and the previous lemma asserts that dY = f(Y )dX is equivalent to the following higher order controlled equation

$$ \begin{array}{@{}rcl@{}} \dot{Y}_{s} &=& {\sum}_{i=1}^{d} f_{i} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},i\rangle + {\sum}_{i<j} \frac{1}{2} f_{[i,j]} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},[i,j]\rangle\\ &=& {\sum}_{i=1}^{d} f_{i}(Y_{s})\langle \dot{\mathbf{X}}_{s,s},i\rangle+ {\sum}_{i<j} \frac{1}{2} [f_{i}, f_{j}] (Y_{s})\langle \dot{\mathbf{X}}_{s,s},[i,j]\rangle. \end{array} $$

This also follows directly by applying Remark 2.7 to the equation (15) with N = 2.

Remark 2.23

Even if a differential equation driven by a N-sgrm can be viewed as a Davie solution, we note however that Lemma 2.21 is a particular property of differential equations driven by N-smooth geometric rough paths which does not hold for RDEs driven by a generic 1/N-Hölder weakly geometric rough path.

Indeed, working with one-dimensional 1/2-Hölder weakly geometric rough path³ and a generic vector field $f\in \text {Vect}^{\infty }(\mathbb {R})$ one has the trivial identities

$$ \begin{array}{@{}rcl@{}} {\sum}_{1\leq|w|\leq 2}f_{w}(Y_{s})\langle\mathbf{X}_{s,t},w\rangle &=& f(Y_{s})(X_{t}-X_{s})+(f\cdot f^{\prime})(Y_{s})\frac{(X_{t}-X_{s})^{2}}{2},\\ {\sum}_{\mathfrak{u} \in \mathfrak{B}^{2}} f_{\mathfrak{u}} (Y_{s})\langle \mathbf{X}_{s,t},\mathfrak{u}\rangle &=& f(Y_{s})(X_{t}-X_{s}). \end{array} $$

Therefore there is no r_s,t = o(|t − s|) such that

$$ {\sum}_{|w|\leq 2}f_{w}(Y_{s})\langle\mathbf{X}_{s,t},w\rangle= {\sum}_{\mathfrak{u} \in \mathfrak{B}^{2}} f_{\mathfrak{u}} (Y_{s})\langle \mathbf{X}_{s,t},\mathfrak{u}\rangle+ r_{s,t}. $$

2.4 Algebraic Renormalization of SGRP

Consider a collection of Lie series $v = (v_{1},\ldots , v_{d})\subset {\mathscr{L}} ((\mathbb {R}^{d}))$, and let T_v be the ⊗-endomorphism on $T((\mathbb {R}^{d}))$, obtained by extending the translation map e_i↦e_i + v_i. We call T_v the translation map. When the v_i’s are all Lie polynomials, we remark that T_v maps $T^{N}(\mathbb {R}^{d})$ to $T^{M}(\mathbb {R}^{d})$ with $M=N\cdot N^{\prime }$ where $N^{\prime }$ denotes the smallest integer such that $v_{i}\in {\mathscr{L}}^{N^{\prime }}(\mathbb {R}^{d})$. By restriction to Lie series, ${\mathscr{L}} ((\mathbb {R}^{d}))\subset T((\mathbb {R}^{d}))$, we can and will view T_v also as Lie algebra endomorphism, still denoted by T_v. We first give a dynamic view on the higher-order translation of sgrp.

Theorem 2.24

• (i) Let $v=(v_{1},\dots ,v_{d})$ be a collection of elements in ${\mathscr{L}}((\mathbb {R}^{d}))$. Given a sgrp X over $\mathbb {R}^{d}$, the unique solution to

  $$ \dot{\mathbf{Z}}_{t} = \mathbf{Z}_{t} \otimes (T_{v} \dot{\mathbf{X}}_{t,t}), \qquad \mathbf{Z}_{0} = T_{v} \mathbf{X}_{0} $$

  (18)

  takes values in $G(\mathbb {R}^{d})$ and is again a sgrp, and we have the explicit form

  $$ \mathbf{Z}_{t} = T_{v} (\mathbf{X}_{t}), \quad \mathbf{Z}_{s,t} = {T}_{v} (\mathbf{X}_{s,t}). $$

  (19)

  Starting with a sgrm X over $\mathbb {R}^{d}$, the above applies to t↦X_0,t and we obtain a sgrm Z with explicit form given by

  $$ \mathbf{Z}_{s,t} = {T}_{v} (\mathbf{X}_{s,t}). $$

• (ii) Let now $v=(v_{1},\dots ,v_{d})$ be a collection of elements in ${\mathscr{L}}(\mathbb {R}^{d})$ and X be a good sgrm over $\mathbb {R}^{d}$. Then Z as constructed in (i) is also a good sgrm. More specifically, let $N^{\prime }$ be the smallest integer such that v_i lies in ${\mathscr{L}}^{N^{\prime }}(\mathbb {R}^{d})$ for all i and assume X is the minimal extension of some N-sgrm Y over $\mathbb {R}^{d}$. Let $M = N\cdot N^{\prime }$. The unique solution to

  $$ \dot{\mathbf{W}}_{t} = \mathbf{W}_{t} \otimes_{M} (T_{v} \dot{\mathbf{Y}}_{t,t}), \qquad \mathbf{W}_{0} = 1, $$

  defines a M-sgrp, given by $\mathbf {W}_{s,t} = \mathbf {W}_{s}^{-1}\otimes _{M} \mathbf {W}_{t}$, which we call $\mathcal {T}_{v}[\mathbf {Y}]$. Moreover, we have the explicit form

  $$ \mathcal{T}_{v}[\mathbf{Y}]_{s,t} = {T_{v}^{M}} (\mathbf{Y}_{s,t}^{M}) = \text{\textsf{proj}}_{M}{T}_{v}(\mathbf{X}_{s,t}) $$

  (20)

  with algebra endomorphism ${T_{v}^{M}} := \text {\textsf {proj}}_{M} T_{v}\mathfrak {i}^{M}$ of $(T^{M}(\mathbb {R}^{d}),\otimes _{M})$, using the (linear) embedding $\mathfrak {i}^{M}: T^{M}(\mathbb {R}^{d})\to T((\mathbb {R}^{d}))$, and Y^M = MinExt^M(Y).

Remark 2.25

Note that the map $\mathbf {Y} \mapsto \mathcal {T}_{v}[\mathbf {Y}]$ for an N-sgrm Y is neither a linear nor a pointwise map, in contrast to X↦T_vX for sgrps or sgrms, which underlies the convenience of working with “genuine” sgrm’s, with full state space $T((\mathbb {R}^{d}))$ (rather than some level-N truncation thereof). With regard to [6, 8] we may view T_v and $\mathcal {T}_{v}$ renormalization maps, acting on non-linear spaces of sgrm’s and N-sgrm’s respectively. We shall discuss in Theorem 2.26 below how this action effects differential equations driven by sgrm’s.

Proof

(i) Fix a sgrp X and write

$$ \dot{\mathbf{X}}_{t} = \mathbf{X}_{t} \otimes (\mathbf{X}^{-1}_{t}\otimes \dot{\mathbf{X}}_{t})= \mathbf{X}_{t} \otimes \dot{\mathbf{X}}_{t,t}. $$

Since T_v commutes with derivation and is an algebra morphism, then Z_t = T_v(X_t) clearly satisfies the differential equation (18). The algebraic properties of T_v together with Proposition 2.6 imply that T_v(X_t) belongs to $G(\mathbb {R}^{d})$ and $T_{v}(\dot {\mathbf {X}}_{t,t})$ belongs to ${\mathscr{L}}((\mathbb {R}^{d}))$ respectively. Therefore T_v(X_t) must coincide with the Cartan development of $T_{v}(\dot {\mathbf {X}}_{t,t})$, thereby yielding (19). Similar results hold with a sgrm.

(ii) Fix a good sgrm and apply part (i) to the path t↦X_0,t. Since v contains only Lie polynomials the map T_v becomes an algebra morphism $T_{v}\colon T(\mathbb {R}^{d})\to T(\mathbb {R}^{d}s)$. Using Lemma 2.11 and this last property one has $T_{v}(\dot {\mathbf {X}}_{t,t})\in {\mathscr{L}}(\mathbb {R}^{d})$, which implies that T_v(X_s,t) is a good sgrm. In the specific case of a collections of elements belonging to ${\mathscr{L}}^{N^{\prime }}(\mathbb {R}^{d})$, we consider Y^M = MinExt^M(Y). The path $t\mapsto \mathbf {Y}^{M}_{0,t}=\mathbf {Z}_{t}$ will satisfy the following equation

$$ \dot{\mathbf{Z}}_{t} = \mathbf{Z}_{t} \otimes_{M} \dot{\mathbf{Y}}^{M}_{t,t}, \qquad \mathbf{Z}_{0} = \mathbf{1}. $$

(21)

Using standard properties of tensors, ${T_{v}^{M}}$ is an algebra endomorphism of $(T^{M}(\mathbb {R}^{d}),\otimes _{M})$. Indeed for any $x,y\in T^{M}(\mathbb {R}^{d})$

$$ \begin{array}{@{}rcl@{}} ({T_{v}^{M}} x)\otimes_{M}({T_{v}^{M}} y)&=&\textsf{proj}_{M}(({T_{v}^{M}} x)\otimes ({T_{v}^{M}} y))=\textsf{proj}_{M}((T_{v} x)\otimes (T_{v} y))\\ &=&\textsf{proj}_{M} T_{v}(x\otimes y) = \textsf{proj}_{M} T_{v} \mathfrak{i}^{M} \textsf{proj}_{M}(x\otimes y)={T_{v}^{M}} (x\otimes_{M} y), \end{array} $$

where we used in the fourth equality the fact that $T_{v} z\in T^{>M}((\mathbb {R}^{d}))$ for all $z\in T^{>M}((\mathbb {R}^{d}))$ (T_v is not lowering the grade). Applying ${T^{M}_{v}}$ to both sides of (21), we obtain that ${T^{M}_{v}}(\mathbf {Z}_{t})$ coincides with the Cartan development in $G^{M}(\mathbb {R}^{d})$ of ${T_{v}^{M}} \dot {\mathbf {Y}}^{M}$. By uniqueness of this we can express $\mathcal {T}_{v}[\mathbf {Y}]_{s,t}$ as ${T^{M}_{v}}(\mathbf {Z}_{s})^{-1}\otimes _{M}{T^{M}_{v}}(\mathbf {Z}_{t})= {T}_{v}^{M} (\mathbf {Y}_{s,t}^{M})$, obtaining (20). The identity ${T_{v}^{M}} (\mathbf {Y}_{s,t}^{M}) =\textsf {proj}_{M}{T}_{v}(\mathbf {X}_{s,t})$ follows trivially. □

Combining the properties of translation operators T_v with the differential equation (16), we can describe the effect of translation on smooth geometric rough paths in the same way as [6]. Given $v=(v_{1},\dots ,v_{d})$ a collection of elements in ${\mathscr{L}}(\mathbb {R}^{d})$ and $(f_{1}, \ldots , f_{d})\in (\text {Vect}^{\infty }(\mathbb {R}^{e}))^{d}$ we consider the collection of vector fields $({f^{v}_{1}},\ldots , {f^{v}_{d}})\in (\text {Vect}^{\infty }(\mathbb {R}^{e}))^{d}$ given for each i = 1,…,d by

$$ {f^{v}_{i}}= f_{i} + f_{v_{i}}, $$

where $f_{v_{i}}$ was given in (14). Starting from this collection of translated vector fields on d directions, we can consider the linear map $f^{v}\colon T (\mathbb {R}^{d}) \to \text {Vect}^{\infty }(\mathbb {R}^{e})$, extending the family $({f^{v}_{1}},\ldots , {f^{v}_{d}})$ on any word like in (12). This operation allows to transfer the action of the translation at the level of differential equations.

Theorem 2.26

Let X be a good sgrm and W a N-sgrm. For any given collection v = (v₁,…,v_d) of elements in ${\mathscr{L}}(\mathbb {R}^{d})$ a path $Y\colon [0,T]\to \mathbb {R}^{e}$ solves one of the equations

$$ dY = f(Y) d (T_{v}(\mathbf{X})), \quad dY = f (Y) d (\mathcal{T}_{v}[\mathbf{W}]); $$

if and only if it solves respectively

$$ dY = f^{v} (Y) d \mathbf{X}, \quad dY = f^{v} (Y) d\mathbf{W}. $$

Remark 2.27

The differential equations in the above statement are understood, in the sense of Definition 2.18, as equations driven by a N-sgrm W, a $(N\cdot N^{\prime })$-sgrm $\mathcal {T}_{v}[\mathbf {W}]$ (when the directions v = (v₁,…,v_d) are all contained in ${\mathscr{L}}^{N^{\prime }}(\mathbb {R}^{d})$) and a good sgrm T_vX, respectively.

Proof

Writing X as the minimal extension of a M-sgrm for some $M\in \mathbb {N}$, the result follows by showing only the equivalence for W. We present here two possible proofs.

(First argument) Fix s and y = Y_s and $\mathfrak {w} := \dot {\mathbf {W}}_{s,s} \in {\mathscr{L}}^{N}(\mathbb {R}^{d})$ and $M=N\cdot N^{\prime }$, where $N^{\prime }$ is the minimal integer such that $v_{i}\in {\mathscr{L}}^{N^{\prime }}(\mathbb {R}^{d})$ for all i = 1,…,d. By Theorem 2.24, the diagonal derivative of $\mathcal {T}_{v}[\mathbf {W}]$ at time s is precisely $T_{v} \mathfrak {w} \in {\mathscr{L}}^{M}(\mathbb {R}^{d})$ up to minimal extension. Using Lemma 2.21, the result follows once we check that

$$ {\sum}_{\mathfrak{u}\in \mathfrak{B}^{M}} f_{\mathfrak{u}} (y )\langle T_{v} \mathfrak{w},\mathfrak{u} \rangle = {\sum}_{\mathfrak{v} \in \mathfrak{B}^{N}} f^{v}_{\mathfrak{v}} (y)\langle \mathfrak{w},\mathfrak{v}\rangle. $$

To prove this identity, we use an argument already contained in [6]. Let $f : \mathfrak {x} \mapsto f_{\mathfrak {x}}$ be the induced Lie algebra morphism from ${\mathscr{L}}^{M}(\mathbb {R}^{d})$ into $\text {Vect}^{\infty }(\mathbb {R}^{e})$. Hence, whenever f is smooth, the maps $f_{T_{v}}$ and f^v are both Lie algebra morphisms from ${\mathscr{L}}^{M}(\mathbb {R}^{d})$ into $\text {Vect}^{\infty }(\mathbb {R}^{e})$, which furthermore agree on the generators e_i. Thus $f_{T_{v}\mathfrak {x}}(z) = f^{v}_{\mathfrak {x}}(z)$ for any $z\in \mathbb {R}^{e}$ and any $\mathfrak {x}\in {\mathscr{L}}^{M}(\mathbb {R}^{d})$ thanks to the universal property of ${\mathscr{L}}^{M}(\mathbb {R}^{d})$ so

$$ {\sum}_{\mathfrak{u} \in \mathfrak{B}^{M}}f_{\mathfrak{u}} (y )\langle T_{v} \mathfrak{w},\mathfrak{u} \rangle = f_{T_{v}\mathfrak{w}}(y) = f^{v}_{\mathfrak{w}}(y) ={\sum}_{\mathfrak{v}\in \mathfrak{B}^{N}} f^{v}_{\mathfrak{v}} (y)\langle \mathfrak{w},\mathfrak{v}\rangle. $$

(Second argument) The identity $f_{T_{v}}(z)=f^{v}(z)$ does not hold simply over ${\mathscr{L}}(\mathbb {R}^{d})$ but over all $T(\mathbb {R}^{d})$. For that, we first show that in fact for any $u\in {\mathscr{L}}(\mathbb {R}^{d})$ and any $x\in T^{>0}((\mathbb {R}^{d}))$ we have $f_{u}\vartriangleright f_{x}=f_{u x}$. We do so completely analogously to [51, Lemma 2.5.11], proceeding by induction over the length of u. For u a letter, the statement holds by definition of w↦f_w. Assume the statement holds for all u of length n. Then, to check it for all homogeneous Lie elements of word length n + 1, since left bracketings span the free Lie algebra, it suffices to look at Lie elements of the form [u,i]. So,

$$ \begin{array}{@{}rcl@{}} f_{[u,i] x} &=& f_{u i x}-f_{iux}=f_{u}\vartriangleright(f_{i}\vartriangleright f_{x})-f_{i}\vartriangleright(f_{u}\vartriangleright f_{x})\\ &=&(f_{u}\vartriangleright f_{i} -f_{i}\vartriangleright f_{u})\vartriangleright f_{x} =[f_{u},f_{i}]\vartriangleright f_{x} = f_{[u,i]}\vartriangleright f_{x}, \end{array} $$

where for the third equality, we used the identity (13). Then, since $v_{i}\in {\mathscr{L}}(\mathbb {R}^{d})$, indeed we get, again via induction over the length of words,

$$ f_{iw}^{v}={f_{i}^{v}}\vartriangleright {f_{w}^{v}} =f_{T_{v} i}\vartriangleright f_{T_{v} w} =f_{v_{i}}\vartriangleright f_{T_{v} w}=f_{v_{i} T_{v}(w)} =f_{T_{v} (iw)}. $$

We finally obtain the general identity by linearity. Thus for any $\mathbf {x} \in T^{N}(\mathbb {R}^{d})$ we have

$$ {\sum}_{w}\langle \mathbf{x},w\rangle {f_{w}^{v}} = f_{\mathbf{x}}^{v}=f_{T_{v} \mathbf{x}}= {\sum}_{w}\langle T_{v} \mathbf{x},w\rangle f_{w}. $$

Then, by Proposition 2.20 we have the desired equivalence of differential equations through the following equality, for any smooth path $Y:[0,T]\to \mathbb {R}^{e}$ and s,t ∈ [0,T], using the notation $\mathbf {W}^{\infty }:=\text {MinExt}(\mathbf {W})$ one has

$$ \begin{array}{@{}rcl@{}} Y_{t}-Y_{s}&=&{\sum}_{1\leq |w| \leq N} \langle{\mathbf{W}_{s,t},w}\rangle {f^{v}_{w}}(Y_{s}) = {\sum}_{1\leq |w|} \langle{\textsf{proj}_{N}\mathbf{W}^{\infty}_{s,t},w}\rangle {f^{v}_{w}}(Y_{s})\\ &=&{\sum}_{1\leq |w|} \langle{T_{v}\textsf{proj}_{N}\mathbf{W}^{\infty}_{s,t},w}\rangle f_{w}(Y_{s}) = {\sum}_{1\leq |w|} \langle{\textsf{proj}_{M}T_{v}\mathbf{W}^{\infty}_{s,t},w}\rangle f_{w}(Y_{s})+R_{s,t}\\ &=&{\sum}_{1\leq |w|\leq M}\langle{(\mathcal{T}_{v}[\mathbf{W}])_{s,t},w}\rangle f_{w}(Y_{s})+R_{s,t}, \end{array} $$

with

$$ \begin{array}{@{}rcl@{}} R_{s,t} &=& {\sum}_{1\leq|w|\leq M}\langle{T_{v}\textsf{proj}_{N}\mathbf{W}^{\infty}_{s,t}-T_{v}\mathbf{W}^{\infty}_{s,t},w}\rangle f_{w}(Y_{s}) \\ &=&-{\sum}_{1\leq |w|\leq M} \langle{\textsf{proj}_{>N}\mathbf{W}^{\infty}_{s,t},T_{v}^{\ast} w}\rangle f_{w}(Y_{s})=o(|t-s|), \end{array} $$

as $\langle \mathbf {W}^{\infty }_{s,t},w\rangle =O(|t-s|^{2})$ for all w with |w| > N, since then $(s,t)\mapsto \langle \mathbf {W}^{\infty }_{s,t},w\rangle$ is a smooth function on the compact domain [0,T]² with $\langle \mathbf {W}^{\infty }_{t,t},w\rangle =0$ and $\partial _{s}|_{s=t}\langle \mathbf {W}^{\infty }_{s,t},w\rangle =\langle \dot {\mathbf {W}}^{\infty }_{t,t},w\rangle =0$. □

Remark 2.28

The second argument in the above proof is valid for genuine (non-smooth) γ-Hölder weakly geometric rough paths, with N = ⌊1/γ⌋, $Y:[0,T]\to \mathbb {R}^{e}$ an arbitrary continuous path and choosing MinExt(W) as the Lyons extension of W, see Proposition 2.14. There, it again correctly identifies the respective rough differential equations via Davies’ expansion.

This argument first presented in [51, Section 2.5.2] fills a gap left in the proof of [6, Theorem 38] where it is misleadingly suggested that a Lie algebraic argument can be used. Indeed, as noted in Remark 2.23 there is no Davie-type definition of RDE solution where the sum is restricted to a Lie basis.

As final application of the section we combine Theorems 2.24 and 2.26 with the notion of minimal coupling and sum to obtain a “smooth geometric” renormalization along a time component, see [6, Theorem 38]. Consider a time-space path of the form

$$ \bar{X}_{t} = (t, X_{t}) = ({X^{0}_{t}},{X^{1}_{t}}) \in \mathbb{R} \oplus \mathbb{R}^{d} = \mathbb{R}^{1+d} $$

for some smooth path $X^{1}\colon [0,T]\to \mathbb {R}^{d}$ (the first component of canonical basis of $\mathbb {R}^{d+1}$ will be denoted by e₀). Assume also that there exists a good sgrm $\mathbf {X}^{1}:[0,T]^{2} \to G (\mathbb {R}^{d})$ extending X¹. Then we can introduce the usual signature of time component $\mathbf {X}^{0}:[0,T]^{2} \to G (\mathbb {R})$ defined by

$$ \mathbf{X}^{0}_{s,t}=\exp_{\otimes}((t-s)e_{0}) $$

and the choice

$$ \bar{\mathbf{X}}:=(\mathbf{X}^{0},\mathbf{X}^{1})_{\min} $$

constitutes a canonical way to extend $\bar {X}$. Choosing then a Lie polynomial $v_{0}\in {\mathscr{L}}(\mathbb {R}^{d+1})$, we can also consider the translation map $T_{v_{0}}$ obtained by the identity action on $e_{1},\dots , e_{d}$, and e₀↦e₀ + v₀. Then we can explicitly describe $T_{v_{0}}\bar {\mathbf {X}}$ and differential equations driven by that.

Corollary 2.29

Let X¹ be a good sgrm and $v_{0}\in {\mathscr{L}}(\mathbb {R}^{d+1})$. Then the translation $t\mapsto T_{v_{0}}\bar {\mathbf {X}}_{0,t}$ can be described as the sum $\mathbf {V}_{0}\boxplus \bar {\mathbf {X}}$, where V₀ is given by

$$ (\mathbf{V}_{0})_{s,t}=\exp_{\otimes}(v_{0}(t-s)). $$

Moreover, for any given family of vector fields (f₀,f₁,…,f_d) one has the equivalence

$$ dY = \bar{f} (Y) d (T_{u_{0}}(\bar{\mathbf{X}}))\quad \text{if and only if} \quad dY = (f_{0} + \bar{f}_{u_{0}})(Y) dt+ f (Y) d \mathbf{X}^{1}, $$

where $\bar {f}\colon T(\mathbb {R}^{d+1})\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ and $f\colon T(\mathbb {R}^{d})\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ are defined like in (14), starting respectively from $(f_{0}, {\dots } , f_{d})$ and $(f_{1}, {\dots } , f_{d})$.

Proof

The proof follows by applying the results in the section. By construction of $\bar {\mathbf {X}}$, one has the following diagonal derivative $\dot {\bar {\mathbf {X}}}_{t,t}=e_{0}+\dot {\mathbf {X}}^{1}_{t,t}$. Then by construction of $T_{v_{0}}$ and Theorem 2.24, we have

$$ \frac{d}{dt}(T_{v_{0}}(\bar{\mathbf{X}})_{s,t})|_{t=s}=T_{v_{0}}(e_{0}+\dot{\mathbf{X}}^{1}_{s,s})=v_{0}+e_{0}+\dot{\mathbf{X}}^{1}_{s,s}=\frac{d}{dt}(\mathbf{V}_{0}\boxplus\bar{\mathbf{X}})_{s,t}|_{t=s}. $$

Since the diagonal derivative identifies uniquely $T_{v_{0}}(\bar {\mathbf {X}})$ we conclude. Passing to the differential equation, we remark from Definition 2.18 that a smooth path $Y\colon [0,T]\to \mathbb {R}^{e}$ is a solution of $dY=\bar {f}(Y)d\bar {\mathbf {X}}$ if and only if

$$ dY = f_{0}(Y) dt+ f (Y) d \mathbf{X}^{1}. $$

Moreover, the map $\bar {f}^{v_{0}}$ satisfies trivially $\bar {f}^{v_{0}}_{0}=f_{0} + \bar f_{v_{0}}$, $\bar {f}^{v_{0}}_{i}=f_{i}$ for any i = 1,…,d. We conclude then by Theorem 2.26. □

3 Smooth Quasi-geometric Rough Paths

In the sequel, we extend the previous results and notions of smooth rough paths in the context of quasi-geometric rough paths, the natural generalisation of rough paths when we consider an underlying quasi-shuffle algebra, see [36]. Quasi-geometric rough paths were first introduced in talks by David Kelly and properly studied in [2].

3.1 Quasi-shuffle Algebras

We briefly review quasi-shuffle algebras in the version of [36]. Their origin can be traced back to [10] and we also refer the reader to [24, 46]. We shall use Hoffman’s isomorphism in the context of stochastic integration (‘Itô vs. Stratonovich’) which was discussed in detail in [23].

Let us start from a generic vector space $\mathbb {R}^{A}$ where A is a locally finite (with respect to the weight function ω below) set called alphabet. To link this space with the previous section, we assume the inclusion {1,…,d}⊂ A, which induces a canonical inclusion $\mathbb {R}^{d}\subset \mathbb {R}^{A}$. Given an alphabet A, with a slight abuse of notation we will denote by T(A) and T((A)) the spaces of tensor polynomials and tensor series over $\mathbb {R}^{A}$ respectively. To simplify the notation, in what follows we will also identify elements of T((A)) as words, as explained in the previous section, i.e.

$$ e_{a_{1}}\otimes {\cdots} \otimes e_{a_{n}}\longleftrightarrow a_{1}{\ldots} a_{n}, $$

for any a₁,…,a_n ∈ A. Moreover, we use the same symbol ⊗ to denote the tensor product operation of T((A)) and the “external” algebraic tensor product of two vector spaces.

The quasi-shuffle product relies on the existence of a commutative bracket, i.e. a map $\{ ,\}\colon \overline {A}\times \overline {A}\to \overline {A}$, where $\overline {A}=A\cup \{0\}$ such that

$$ \{ a ,0\}= \{ 0 ,a\}=0, \quad \{ a ,b\}= \{ b ,a\}, \quad \{ a ,\{b, c\}\}= \{ \{a ,b\}, c\}. $$

(22)

We adopt the notation {a} = a, for a ∈ A, and more generally, for any word w = a₁…a_n we set {a₁…a_n} := {a₁,{…{a_n− 1,a_n}}…} independently of the order of the letters in the word and the brackets. Together with the choice of a commutative bracket {,} we also fix a weight ω which is compatible with {,}, i.e. ω is a function $\omega \colon A\to \mathbb {N}^{\ast }$ satisfying

$$ \omega(\{ab\})=\omega(a)+ \omega(b) $$

(23)

when {ab}≠ 0. Note that there could be several weights compatible with a given bracket and the definition of bracket does not need a weight.

Given a word $w=a_{1} {\dots } a_{n}$ we denote by |w| = n the length of w and introduce its weighted length ∥w∥ = ω(a₁) + ⋯ + ω(a_n). Since ω(a) ≥ 1 for all a ∈ A we have trivially |w|≤∥w∥. The weighted length induces a grading on T(A). To stress this property, we also use the notations T_ω(A) and T_ω((A)) when we grade these vector spaces according to the weighted length. e.g.

$$ T_{\omega}(A)= \underset{n=0}{\overset{\infty}{\bigoplus}} \langle\text{\{words $w\colon \|w\| =n$\}}\rangle. $$

Moreover, for any $N\in \mathbb {N}$ we define the truncated space $T_{\omega }^{N}(A)$ by taking words of weighted length at most N, we denote the projection on $T_{\omega }^{N}(A)$ by proj_N,ω. Using the weighted length, we can view $T^{N}_{\omega }(A)$ as a quotient algebra and introduce the corresponding truncated tensor product ⊗_N,ω. The pairing 〈,〉 between $T((\mathbb {R}^{d}))$ and $T(\mathbb {R}^{d})$ generalises to the pairing $\langle , \rangle \colon T_{\omega }((A))\times T_{\omega }(A)\to \mathbb {R}$ for any alphabet A. Its restriction T(A) × T(A) ⊂ T((A)) × T(A) yields a scalar product on T(A). We denote by 〈⋅,⋅〉_N the restriction to truncated spaces $T^{N}_{\omega }(A)\times T^{N}_{\omega }(A)$. As before, the set {w : ∥w∥≤ N} is an orthonormal basis of $T^{N}_{\omega }(A)$. Combining {,} and the shuffle product, we introduce the quasi-shuffle product.

Definition 3.1

The quasi-shuffle product is the unique bilinear map in T(A) satisfying the relation for any v ∈ T(A) and the recursive identity

(24)

for any words v, w in T(A) and letters a, b in A.

Example 3.2

If A = {1,…,d} and the commutative bracket is trivial, i.e. {ab} = 0 for any a, b in A, then the recursive relation (24) reduces to

so that coincides with the standard shuffle product in (3). Observe that setting ω(i) = 1 for all i ∈ A, one has ∥w∥ = |w| and T_ω({1,…,d}) is exactly $T(\mathbb {R}^{d})$ but in general we can consider the shuffle algebra over a generic alphabet with a weight which is not identically 1, see e.g. in [35].

Example 3.3

For fixed integers M,d ≥ 1, we define the alphabet $\mathbb {A}_{M}^{d}$ as

$$ \mathbb{A}_{M}^{d}=\left\{\alpha\in \mathbb{N}^{d}\setminus \{0\}\colon {\sum}_{i=1}^{d} \alpha_{i}\leq M\right\}, $$

as well as the weight $\omega (\alpha )= {\sum }_{i=1}^{d} \alpha _{i}$. We also define the bracket $\{,\}_{M}\colon \overline {\mathbb {A}_{M}^{d}}\times \overline {\mathbb {A}_{M}^{d}}\to \overline {\mathbb {A}_{M}^{d}}$ as the unique bilinear map satisfying the property

$$ \{\alpha,\beta\}_{M}: =\left\{ \begin{array}{ll} \alpha +\beta &\quad \text{if} \alpha+\beta\in \mathbb{A}_{M}^{d}, \\ 0 &\quad \text{otherwise}, \end{array} \right. $$

for any $\alpha , \beta \in \mathbb {A}_{M}^{d}$. The sum arising in this expression is the intrinsic sum between multi-indices. The set {1,…,d} embeds in $\mathbb {A}_{M}^{d}$ for any M ≥ 0 by simply sending every i ∈{1,…,d} to the i-th element of the canonical basis. Using this inclusion the letter {112} is identified with the multi-index (2,1,0,…,0) and e have {i₁…i_n} = 0 for any n > M and i_j ∈{1,…,d}. It follows from standard properties on multi-indices that {,} and ω satisfy properties (22) and (23). The associated quasi-shuffle algebra $T_{\omega }(\mathbb {A}_{M}^{d})$ is used to define the notion of quasi-geometric bracket extension in [2]. We can also drop the finite index M and consider the infinite alphabet $\mathbb {A}^{d}= \mathbb {N}^{d}\setminus \{0\}$ with the same weight. This alphabet is then isomorphic to the free semi-group generated over d elements. The associated quasi-shuffle algebra was intensively used in [22].

For any choice of {,} the quasi-shuffle product is a well-defined commutative product on T(A), see [36]. It further defines a product on the graded algebra T_ω(A) for a given compatible weight function $\omega \colon A\to \mathbb {N}^{\ast }$. The product is also compatible with the weighted length on T_ω(A). From a Hopf algebraic point of view, see Section 4 for the general framework, we can equip T_ω(A) with the deconcatenation coproduct Δ: T_ω(A) → T_ω(A) ⊗ T_ω(A) and the counit $\mathbf {1}^{\ast }\colon T_{\omega }(A) \to \mathbb {R}$ defined respectively by

$$ {\Delta} (a_{i_{1}}{\ldots} a_{i_{n}})=\mathbf{1} \otimes a_{i_{1}}{\ldots} a_{i_{n}}+ {\sum}_{k=1}^{n} a_{i_{1}}{\ldots} a_{i_{k}}\otimes a_{i_{k+1}}{\ldots} a_{i_{n}}+ a_{i_{1}}{\ldots} a_{i_{n}} \otimes \mathbf{1}, $$

$$ \mathbf{1}^{\ast}(w): =\left\{ \begin{array}{ll} 1 &\quad \text{if} w=\mathbf{1}, \\ 0 &\quad \text{otherwise}. \end{array} \right.$$

Both the triples and are graded Hopf algebras, see [36]. A fundamental result is the existence of an explicit isomorphism between these two Hopf algebras for any commutative bracket {,}, see [36, Theorem 3.3].

Theorem 3.4 (Hoffman Isomorphism)

For any commutative bracket {,} we define the Hoffman “exponential” and “logarithm” Φ_H, Ψ_H: T(A) → T(A) on any word as

$$ {\varPhi}_{H}(w)={\sum}_{I\in C(|w|)}\frac{1}{I!}\{w\}_{I}, \quad{\varPsi}_{H}(w)={\sum}_{I\in C(|w|)}\frac{(-1)^{|w|-|I|}}{I}\{w\}_{I}, $$

(25)

where C(|w|) is the set of compositions of order |w|, i.e. the multi-indices I = (i₁,…,i_m) such that i₁ + ⋯ + i_m = |w| and

$$ I!= i_{1}!{\ldots} i_{m}!,\quad I= i_{1}{\ldots} i_{m}, \quad |I|= m. $$

Moreover, we denote by {w}_I the word

$$ \{w\}_{I}:= \{w_{1}{\ldots} w_{i_{1}}\}\{w_{i_{1}+1}{\ldots} w_{i_{1}+i_{2}}\}\ldots\{w_{i_{1}+{\cdots} +i_{m-1}+1} {\ldots} w_{n}\}. $$

The map is an isomorphism of graded Hopf algebras such that ${\varPsi }_{H}= {\varPhi }_{H}^{-1}$.

With Φ_H and Ψ_H as in (25), two explicit formulae were shown in [36] for the adjoint maps ${\varPhi }_{H}^{\ast }, {\varPsi }_{H}^{\ast } \colon T_{\omega }(A)\to T_{\omega }(A)$ with respect to scalar product 〈,〉. Indeed, for any word w = a₁…a_n we have

$$ {\varPhi}^{\ast}_{H}(w)= {\varPhi}^{\ast}_{H} (a_{1}) {\ldots} {\varPhi}^{\ast}_{H}(a_{n}), \quad {\varPsi}^{\ast}_{H}(w)= {\varPsi}^{\ast}_{H} (a_{1}) {\ldots} {\varPsi}^{\ast}_{H}(a_{n}) $$

(26)

and for each letter a ∈ A, the following identity holds:

$$ {\varPhi}^{\ast}_{H}(a)={\sum}_{n\geq 1}{\sum}_{\{a_{1}{\ldots} a_{n}\}=a}\frac{1}{n!}a_{1}{\ldots} a_{n}, \quad{\varPsi}^{\ast}_{H}(a)={\sum}_{n\geq 1}{\sum}_{\{a_{1}{\ldots} a_{n}\}=a}\frac{(-1)^{n-1}}{n}a_{1}{\ldots} a_{n}, $$

(27)

where the underlying set of summation {a₁…a_n} = a involves all possible ways of writing the letter a in terms of brackets of the word a₁…a_n. By simply considering the graded dual of the shuffle and quasi-shuffle Hopf algebras (see Section 4) in Theorem 3.4, the map ${\varPhi }_{H}^{\ast }$ becomes an isomorphism where are the dual coproducts associated to the shuffle and quasi-shuffle operation. To extend ${\varPhi }^{\ast }_{H}$ and ${\varPsi }_{H}^{\ast }$ to the whole set T((A)), we observe that the concatenation product ⊗ easily extends to T_ω((A)). However, the coproducts and do not make sense on T_ω((A)) ⊗ T_ω((A)), see e.g. [50, Theorem 3.6] for a counterexample on $T((\mathbb {R}^{1}))$. They need to be extended to the completed tensor space, see [53, Section 1.4]

$$ T_{\omega}((A)){\overline{\otimes}}T_{\omega}((A)):= {\prod}_{k,m=0}^{\infty} \langle \text{\{words $w\colon \|w\| =k$\}}\rangle \otimes \langle \text{\{words $w \colon \|w\| =m$}\rangle, $$

leading to two topological graded coalgebras and .

Proposition 3.5

The maps ${\varPhi }^{\ast }_{H}$ and ${\varPsi }^{\ast }_{H}$ defined by (26) and (27) uniquely extend to two linear maps ${\varPhi }^{\ast }_{H},{\varPsi }^{\ast }_{H} \colon T_{\omega }((A))\to T_{\omega }((A))$, for which we shall use the same notation. The map ${\varPhi }^{\ast }_{H}$ gives rise to a graded automorphism of the algebra (T_ω((A)),⊗) as well as an isomorphism between the two topological graded coalgebras and . In both cases one has ${\varPsi }_{H}^{\ast }= ({\varPhi }_{H}^{\ast })^{-1}$.

Proof

It is sufficient to build the extension of ${\varPhi }^{\ast }_{H}$. Combining properties (26) and (27), for any series $S={\sum }_{w} \alpha _{w} w\in T_{\omega }((A))$ we define

$$ {\varPhi}^{\ast}_{H}(S):={\sum}_{w}{\sum}_{n_{1}\geq 1}{\sum}_{\{{a_{1}^{1}}{\ldots} a_{n_{1}}^{1}\}=w_{1}} \ldots{\sum}_{n_{m}\geq 1}{\sum}_{\{{a_{1}^{m}}{\ldots} a_{n_{m}}^{m}\}=w_{m}}\alpha_{w} \frac{1}{n_{1}!}\cdots\frac{1}{n_{m}!} {a_{1}^{1}}{\ldots} a_{n_{m}}^{m}, $$

where w = w₁…w_m. Thanks to property (23) and the assumption $\omega (A)\subset \mathbb {N}^{\ast }$, the terms in the series ${\varPhi }^{\ast }_{H}(S)$ are locally finite, i.e. for any word u there is only a finite number of non-zero terms in the bracket $\langle {\varPhi }^{\ast }_{H}(S),u\rangle$. It follows from property (26) that ${\varPhi }^{\ast }_{H}$ extended to infinite series is also an algebra morphism. The other properties easily follow from the fact that T_ω(A) and T_ω(A) ⊗ T_ω(A) are dense subsets of T_ω((A)) and $T_{\omega }((A)){\overline {\otimes }}T_{\omega }((A))$. □

The Hoffman isomorphism allows to define Lie groups and Lie algebras from the corresponding Lie groups and Lie algebras built from the corresponding shuffle structures.

In what follows, we use the notations ${\mathscr{L}}^{N}(A)$, G^N(A), ${\mathscr{L}}(A)$, ${\mathscr{L}}((A))$ and $G(A)= \exp _{\otimes } {\mathscr{L}}((A))$ to denote respectively the N-step Lie polynomials, the free step-N Lie group, the Lie polynomials and Lie series generated by $\mathbb {R}^{A}$ and $G(A)= \exp _{\otimes } {\mathscr{L}}((A))$, where $\exp _{\otimes }$ is given in (4). If we fix a generic weight ω and $N \in \mathbb {N}$, we denote by ${\mathscr{L}}^{N}_{\omega }(A)$ and $G^{N}_{\omega }(A)$ the following quotients

$$ \mathcal{L}^{N}_{\omega}(A)= \mathcal{L}(A)/\mathcal{L}^{\omega}_{>N}(A),\quad G^{N}_{\omega}(A)= G(A)/G^{\omega}_{>N}(A), $$

where ${\mathscr{L}}^{\omega }_{>N}$ and $G^{\omega }_{>N}(A)$ are respectively the Lie ideal and normal subgroup

$$ \mathcal{L}^{\omega}_{>N}(A):=\langle\{ w : \|w\| > N \}\rangle \cap \mathcal{L}(A), \qquad G^{\omega}_{>N}:=\langle\{ w : \|w\| > N \}\rangle \cap G(A). $$

(These last two properties follow trivially from (23)). Moreover, passing to the quotient gives rise to the identification

and the property $G^{N}_{\omega }(A) =\exp _{\otimes _{N,\omega }}({\mathscr{L}}^{N}_{\omega }(A))$ where $\exp _{\otimes _{N,\omega }}\colon T^{N}_{\omega }(A)\to T^{N}_{\omega }(A)$ is the exponential associated with the truncated product ⊗_N,ω

$$ \exp_{\otimes_{N,\omega}}v= {\sum}_{n\geq 0}^{N}\frac{v^{\otimes_{N, \omega}^{n}}}{n!}, $$

thereby obtaining that ${\mathscr{L}}^{N}_{\omega }(A)$ is the Lie algebra of $G^{N}_{\omega }(A)$. Similar objects can be defined in the quasi-shuffle context via the map ${\varPsi }^{\ast }_{H}$. The proof of the following corollary is a straightforward application of Proposition 3.5 combined with the usual properties of Lie series and the group G(A).

Corollary 3.6

• (i) The set $\hat {G}(A) := {\varPsi }_{H}^{\ast } G(A)=\{{\varPsi }_{H}^{\ast } \beta , \beta \in G(A)\}$ with the operation ⊗ is a group which has the following description

  

  We call $\hat {G}(A)$ the group of quasi-shuffle characters.

• (ii) The sets $\hat {{\mathscr{L}}}((A))= {\varPsi }_{H}^{\ast }{\mathscr{L}}((A))$ and $\hat {{\mathscr{L}}}(A):= {\varPsi }_{H}^{\ast } {\mathscr{L}}(A)$ with the commutator of ⊗ are two Lie algebras, which satisfy $\hat {{\mathscr{L}}}(A)\subset \hat {{\mathscr{L}}}((A))$ and $\hat {G}(A)=\exp _{\otimes }{\mathscr{L}}((A))$. We call them the quasi-shuffle Lie series and quasi-shuffle Lie polynomials respectively and they coincide with the free Lie algebra and Lie series generated by the set $\mathfrak {A}=\{{\varPsi }_{H}^{\ast }(a)\colon a\in A\}$.

• (iii) The set $\hat {G}^{N}_{\omega }(A):= {\varPsi }_{H}^{\ast } G^{N}_{\omega }(A)$ with the operation ⊗_N,ω is a Lie group whose Lie algebra is given by $\hat {{\mathscr{L}}}^{N}_{\omega }(A):= {\varPsi }_{H}^{\ast } {\mathscr{L}}^{N}_{\omega }(A)$ and one has $\hat {G}^{N}_{\omega }(A)= \exp _{\otimes _{N,\omega }}(\hat {{\mathscr{L}}}^{N}_{\omega }(A))$ and the identification

  

Example 3.7

Let us spell out the primitive elements of $\hat {{\mathscr{L}}}_{\omega }^{3}(\mathbb {A}_{2}^{d})$. Starting from the definition of ${\mathscr{L}}_{\omega }^{3}(\mathbb {A}_{2}^{d})$ and using the notations [,] for the Lie bracket, one has that ${\mathscr{L}}_{\omega }^{3}(\mathbb {A}_{2}^{d})$ is generated as vector space by the following elements

$$ \left\{i, [i,j], \{ij\}, [[i,j],k],[i,\{jk\}]\right\}, $$

where i,j,k ∈{1,…,d}. It follows from the definition of ${\varPsi }^{\ast }_{H}$ that

$$ {\varPsi}_{H}^{\ast}(i)= i, \qquad {\varPsi}_{H}^{\ast}(\{ij\})=\{ij\} - \frac{1}{2}(ij+ij)\mathbf{1}_{i\neq j} - \frac{1}{2} ii \mathbf{1}_{i= j}. $$

We therefore obtain that $\hat {{\mathscr{L}}}_{\omega }^{3}(\mathbb {A}_{2}^{d})$ is generated as vector space by

$$ \left\{i, [i,j], {\varPsi}_{H}^{\ast}(\{ij\}), [[i,j],k],[i,{\varPsi}_{H}^{\ast}(\{jk\})]\right\}. $$

3.2 Smooth Quasi-geometric Rough Paths

The notion and properties of smooth rough paths can be transposed to the quasi-shuffle context leading to equivalent concepts.

Definition 3.8

We call level-N smooth quasi-geometric rough path over the alphabet A with weight ω (in short: N-sqgrp) any non zero path $\mathbf {X}: [0,T] \to T^{N}_{\omega }(A)$ satisfying the following properties:

• (a’ i) For all times t ∈ [0,T] and all words v and w such that ∥w∥ + ∥v∥≤ N

  

  (28)

• (a’ ii) For every word of weighted length ∥w∥≤ N, the map t↦〈X_t,w〉 is smooth and we write $\dot {\mathbf {X}}_{t}$ for the derivative of X.

We call level-N smooth quasi-geometric rough model (in short: N-sqgrm) any map $\mathbf {X}: [0,T]^{2} \to T^{N}_{\omega }(A)$ such that the property (28) holds for all X_s,t and the properties (b.ii), (b.iii) in Definition 2.3 hold on a set of weighted words with the operation ⊗_N,ω. By smooth quasi-geometric rough path (model) (in short: sqgrp and sqgrm) we mean a path (map) with values in the full space of tensor series T_ω((A)) where (28) hold for any w,v ∈ T_ω((A)) and relation (b.ii) hold with ⊗.

It follows immediately from Definition 3.8 that sqgrps and N-sqgrps are identified with smooth paths with values in the groups $\hat {G}(A)$ or $\hat {G}^{N}_{\omega }(A)$ and we can pass to the associated models by considering the increments with respect to ⊗_N,ω. Similarly we can easily adapt the notion of extension of a sqgrp and the diagonal derivative of a sqgrm, which takes value in $\hat {{\mathscr{L}}}((A))$ or $\hat {{\mathscr{L}}}^{N}_{\omega }(A)$. Since the shuffle product is a specific case of the quasi-shuffle product, Definition 3.8 extends also the notions of N-sgrps and N-sgrms in a presence of a generic alphabet A and weight ω, we will call these objects weighted N-sgrps and weighted N-sgrms.

Thanks to the properties of the Hoffman isomorphism, we can easily relate smooth (resp. truncated) quasi-geometric rough paths and models with some corresponding weighted geometric objects by simply composing these objects with the appropriate version of the Hoffman isomorphism.

Theorem 3.9

Let N ≥ 0 and $\mathbf {X}\colon [0,T]\to T^{N}_{\omega }(A)$. Then X is a N-sqgrp if and only if $\hat {\mathbf {X}}={\varPhi }_{H}^{\ast }\mathbf {X}$ is a weighted N-sgrp. Conversely, $\hat {\mathbf {X}}$ is a weighted N-sgrp if and only if $\mathbf {X}={\varPsi }_{H}^{\ast }\hat {\mathbf {X}}$ is a N-sqgrp. The same result applies to N-sqgrms, sqgrps and sqgrms.

Proof

The result follows easily from combining the properties of the maps ${\varPhi }_{H}^{\ast }$ and ${\varPsi }_{H}^{\ast }$ in Theorem 3.4 with the conditions in Definition 2.1 and Definition 3.8. E.g. starting from a N-sqgrp X one has

for all words with joint weighted length ∥w∥ + ∥v∥≤ N. Moreover, restricting ${\varPhi }^{\ast }_{H}\mathbf {X}_{t}$ to all words with joint weighted length ∥w∥≤ N, it will be a finite linear combination of the functions 〈X_t,v〉 with ∥v∥≤ N, which are all smooth functions. The same considerations apply to N-sqgrms, sqgrps and sqgrms trivially. The converse case with ${\varPsi }_{H}^{\ast }$ follows from the properties in Corollary 3.6. □

Thanks to this one-to-one correspondence between quasi-geometric rough paths and geometric rough paths, we can import all the constructions of the previous section by simply checking that they preserve the maps ${\varPhi }_{H}^{\ast }$ and ${\varPsi }_{H}^{\ast }$. In particular, the notion of minimal extension for sgrms can easily be transposed to sqgrms.

Proposition 3.10

Given an N-sqgrm Y for some $N \in \mathbb {N}$, there exists exactly one sqgrm extension X of Y which is minimal in the sense that for all s ∈ [0,T] one has

$$ \dot{\mathbf{X}}_{s,s} \in \hat{\mathcal{L}}^{N}_{\omega} (A). $$

We call q MinExt(Y) := X the quasi-geometric minimal extension of Y and also $q\text {MinExt}^{N^{\prime }}(Y) := \text {\textsf {proj}}_{N^{\prime },\omega } \mathbf {X}$, for $N^{\prime } > N$, the $N^{\prime }$-minimal extension of Y. For a fixed interval [s,t] ⊂ [0,T] it holds that X_s,t only depends on {Y|_[u,v] : s ≤ u ≤ v ≤ t} and we introduce the quasi-signature of Y on [s,t] by $q\text {Sig}(\mathbf {Y} |_{[s,t]}) := \mathbf {X}_{s,t} \in \hat {G}(A)$. Moreover, we have the identities

$$ q\text{MinExt}(\mathbf{Y})= {\varPsi}^{\ast}_{H} \text{MinExt}({\varPhi}^{\ast}_{H}\mathbf{Y}),\qquad q\text{Sig}(\mathbf{Y}|_{[s,t]})={\varPsi}^{\ast}_{H}\text{Sig}({\varPhi}^{\ast}_{H}\mathbf{Y}|_{[s,t]}). $$

(29)

A sqgrm X is called a good sqgrm if X = q MinExt(Y) for some N-sqgrm Y.

Remark 3.11

The existence and uniqueness of a minimal extension for sqgrg hold on general grounds thanks to properties of Hopf algebras, see Theorem 4.2. However, Hoffman isomorphism gives us in (29) an explicit solution of the minimal extension in terms of the minimal extension related to a geometric rough path.

Proof

Thanks to Theorem 3.9, the map $\hat {\mathbf {Y}}={\varPhi }^{\ast }_{H}\mathbf {Y}$ is a weighted N-sgrp. Since the proof of Theorem 2.8 applies to any alphabet A and any weight on letters ω, there exists a unique minimal extension $\hat {\mathbf {X}}$ of $\hat {\mathbf {Y}}$. Beyond the fact that the function $\mathbf {X}:={\varPsi }_{H}^{\ast } \hat {\mathbf {X}}$ is a quasi-geometric rough path, its diagonal derivative satisfies

$$ \dot{\mathbf{X}}_{s,s} = {\varPsi}_{H}^{\ast}\dot{\hat{\mathbf{X}}}_{s,s} = {\varPsi}_{H}^{\ast}\dot{\hat{\mathbf{Y}}}_{s,s}={\varPsi}_{H}^{\ast}{\varPhi}_{H}^{\ast}\dot{\mathbf{Y}}_{s,s} = \dot{\mathbf{Y}}_{s,s}. $$

The uniqueness of $\hat {\mathbf {X}}$ follows from the uniqueness of the minimal extension in the geometric case and the isomorphism properties of ${\varPsi }^{\ast }_{H}$ and ${\varPhi }^{\ast }_{H}$. From this uniqueness we deduce also the identities (29) straightforwardly. □

In the same way as for geometric rough paths, the notion of smooth quasi-geometric rough path is consistent with its equivalent γ-Hölder version as introduced in [2]. The proof of the following corollary is left to the reader.

Corollary 3.12

Every N-sqgrm X is a 1/N-Hölder quasi-geometric rough path and its minimal extension X coincides with the lift of X, as constructed in [2, Proposition 3.9].

Remark 3.13

Even if there is no distinction in the literature between γ-Hölder quasi-geometric rough paths and weakly γ-Hölder quasi-geometric rough paths, the techniques in [29] can easily be adapted to introduce these concepts. Once done, N-sqgrm’s $\hat {\mathbf {X}}$ should also be 1/N-Hölder weakly quasi-geometric rough paths and form a dense subset among γ-Hölder quasi-geometric rough paths for 1/γ ∈ (N,N + 1).

The existence of a minimal extension allows to define a vector space structure over sqgrms and weighted sgrps. Indeed given two smooth quasi-geometric rough models $\mathbf {X},\mathbf {Y}:[0,T]^{2}\to \hat {G}(A)$ and $\lambda \in \mathbb {R}$, we define their canonical sum $\mathbf {X}\boxplus \mathbf {Y}$ and their scalar multiplication $\lambda \boxdot \mathbf {X}$ like in Definition 2.15.

Since the operation of taking the diagonal derivative of a sqgrm commutes with the linear maps ${\varPhi }_{H}^{\ast }$ and ${\varPsi }_{H}^{\ast }$, from Proposition 4.16 we deduce the following corollary.

Corollary 3.14

Let X, Y be smooth quasi-geometric rough paths/models. Then the map (s,t) →X_s,t ⊗Y_s,t and $\mathbf {X}\boxplus \mathbf {Y}$ satisfy the same relations in (10) and (9) respectively. Moreover ${\varPhi }_{H}^{\ast }$ is a linear isomorphism with inverse ${\varPsi }_{H}^{\ast }$ between the vector space of sqgrms and weighted sgrms endowed with $\boxplus$ and $\boxdot$.

Remark 3.15

The sum of smooth quasi-geometric rough paths/models can be used to define a notion of minimal coupling like in (11). In this case, the elements of the sum are smooth geometric rough paths/models $\mathbf {X}^{i}:[0,T]\to \hat {G}(A_{i})$, where A_i, i = 1,…,m form a partition of A where each A_i is closed under the commutative bracket {,}.

3.3 Differential Equations Driven by SQGRP

We introduce the notion of differential equation driven by a smooth quasi-geometric rough path. Since we replaced our initial directions on $\mathbb {R}^{d}$ with an alphabet A, we assume the existence of a wider collection of smooth vector fields $(f_{a}\colon a\in A)\subset \text {Vect}^{\infty }(\mathbb {R}^{e})$. Moreover, in the same way as {1,…,d}⊂ A we further fix a family (f₁,…,f_d) ⊂ (f_a: a ∈ A). As before, we can apply the operation $\vartriangleright$ to the elements (f_a: a ∈ A) obtaining again a linear map $f\colon T_{\omega }(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ defined by (12). This map induces a morphism of Lie algebras $f\colon {\mathscr{L}}(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$, which is uniquely determined by his values on A. By means of the adjoint Hoffman exponential ${\varPhi }^{\ast }_{H}$, we can uniquely define a map similar to f, which preserves the quasi-shuffle Lie polynomials.

Proposition 3.16

Given a family of vector fields $(f_{a}\colon a\in A)\subset \text {Vect}^{\infty }(\mathbb {R}^{e})$, there exists a map $\hat {f}\colon T_{\omega }(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ whose restriction on $\hat {{\mathscr{L}}}(A)$ is the unique morphism of Lie algebras $\hat {f}\colon \hat {{\mathscr{L}}}(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ which satisfies $\hat {f}({\varPsi }^{\ast }_{H}(a))=f_{a}$ for any a ∈ A. This map is explicitly given by $\hat {f}= f_{{\varPhi }^{\ast }_{H}}$.

Proof

By the definition of $\hat {{\mathscr{L}}}(A)$, the map $f_{{\varPhi }^{\ast }_{H}}$ satisfies clearly the properties of the statement. Moreover, thanks to the free structure of $\hat {{\mathscr{L}}}(A)$ described in Corollary 3.6, the condition $\hat {f}({\varPsi }^{\ast }_{H}(a))=f_{a}$ uniquely determines a morphism of Lie algebras $\hat {f}\colon \hat {{\mathscr{L}}}(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$. □

Using the explicit definitions of f and ${\varPhi }^{\ast }_{H}$, we can then describe $\hat {f}$ as the unique linear map satisfying the conditions

$$ \hat{f}_{w}=(\hat{f}_{a_{1}}\vartriangleright({\ldots} \vartriangleright(\hat{f}_{a_{n-1}}\vartriangleright \hat{f}_{a_{n}})\ldots), \quad \hat{f}_{a}={\sum}_{n\geq 1}{\sum}_{\{a_{1}{\ldots} a_{n}\}=a}\frac{1}{n!}f_{a_{1}{\ldots} a_{n}}, $$

(30)

for any words w = a₁…a_n and a ∈ A. We are now ready to introduce the notion of differential equation in the quasi-geometric context.

Definition 3.17

Let X be N-sqgrm or a good sgrm such that $\dot {\mathbf {X}}_{s,s}\in {\mathscr{L}}^{N}_{\omega }(A)$. We say that a smooth path $Y\colon [0,T]\to \mathbb {R}^{e}$ is the solution of a differential equation driven by X and the vector fields (f_a: a ∈ A) if it satisfies

$$ \dot{Y}_{s} = \langle \hat{f} (Y_{s}), \dot{\mathbf{X}}_{s,s}\rangle_{N} ={\sum}_{\|w\|\le N} \hat{f}_{w} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},w \rangle, $$

(31)

where $\hat {f}:\mathbf {x}\mapsto \hat {f}_{\mathbf {x}}$ is given in (30). We will refer to (31) as

$$ dY=\hat{f}(Y)d\mathbf{X}. $$

(32)

Remark 3.18

This definition leaves the open problem for future work how to canonically define a notion of differential equation, when only given d vector fields $f_{1},\dots ,f_{d}$, without the need to always individually define a case-specific extension to (f_a : a ∈ A), and how to define this notion at best in such a way that it is consistent with geometric and branched d dimensional differential equations.

Combining the results in Proposition 2.20, Lemma 2.21 and Proposition 3.5, we can summarise three equivalent characterisations of (32) in the quasi-geometric context.

Proposition 3.19

Given a path $Y\colon [0,T]\to \mathbb {R}^{e}$ a N-sqgrp X and a family of vector fields (f_a: a ∈ A), one has the following equivalent conditions:

• i) Y solves $dY=\hat {f}(Y)d\mathbf {X}$.

• ii) Y solves $dY = f (Y) d \hat {\mathbf {X}}$, where $\hat {\mathbf {X}}={\varPhi }_{H}^{\ast } \mathbf {X}$ is the N-level weighted geometric rough path obtained via Theorem 3.9.

• iii) For all s,t ∈ [0,T]

  $$ Y_{t}-Y_{s}={\sum}_{1\leq \|w\|\leq N}\hat{f}_{w}(Y_{s})\langle \mathbf{X}_{s,t},w\rangle+r_{s,t}, $$

  where X is the smooth quasi-geometric rough model associated to X and r is a remainder such that r_s,t = o(|t − s|) as t → s.

• iv) For any $\hat {\mathfrak {B}}^{N}$ orthonormal basis of $\hat {{\mathscr{L}}}^{N}_{\omega }(A) \subset T^{N}_{\omega }(A)$ one has

  $$ \dot{Y}_{t} = {\sum}_{\mathfrak{u} \in \hat{\mathfrak{B}}^{N}} \hat{f}_{\mathfrak{u}} (Y_{s})\langle \dot{\mathbf{X}}_{t,t},\mathfrak{u}\rangle. $$

The results i), ii) and iii) hold also if X is a good sqgrm.

Proof

The equivalence i) ⇔ iii) follows in the same way as in Proposition 2.20 and the equivalence i) ⇔ iv) is a consequence of the property $\dot {\mathbf {X}}_{s,s}\in \hat {{\mathscr{L}}}_{\omega }^{N}(A)$. To prove the last equivalence i) ⇔ ii) it is sufficient to prove the identity

$$ {\sum}_{\mathfrak{u} \in \hat{\mathfrak{B}}^{N}} \hat{f}_{\mathfrak{u}}(y)\langle \mathfrak{x},\mathfrak{u}\rangle = {\sum}_{\mathfrak{v} \in \mathfrak{B}^{N}} f_{\mathfrak{v}} (y)\langle {\varPhi}^{\ast}_{H}\mathfrak{x},\mathfrak{v}\rangle, $$

for any $\mathfrak {x}\in \hat {{\mathscr{L}}}_{\omega }^{N}(A)$, $y\in \mathbb {R}^{e}$ and any orthonormal basis $\mathfrak {B}^{N}$ of ${\mathscr{L}}_{\omega }^{N}(A)$. However, by the definition of $\hat {f}$ and using the property ${\varPhi }^{\ast }_{H}\mathfrak {x}\in {\mathscr{L}}_{\omega }^{N}(A)$ one has

$$ {\sum}_{\mathfrak{u} \in \hat{\mathfrak{B}}^{N}} \hat{f}_{\mathfrak{u}} (y)\langle \mathfrak{x},\mathfrak{u}\rangle=\hat{f}_{\mathfrak{x}} (y)= f_{{\varPhi}^{\ast}_{H}(\mathfrak{x})}(y) ={\sum}_{\mathfrak{v} \in \mathfrak{B}^{N}} f_{\mathfrak{v}} (y)\langle {\varPhi}^{\ast}_{H}\mathfrak{x},\mathfrak{v}\rangle. $$

The case of a smooth model follows straightforwardly. □

Example 3.20

Let us check how some properties of Proposition 3.19 appear when we fix $A=\mathbb {A}_{2}^{d}$ from Example 3.3, a sqgrm X over A and a generic family of vector fields (f₁,…,f_d) extended to A by setting f_{ij}≡ 0. The differential equation

$$ dY= f(Y_{t})d\hat{\mathbf{X}} $$

is equivalent to

$$ \dot{Y}_{s}= {\sum}_{|w|\le N} f_{w} (Y_{s})\langle \dot{\hat{\mathbf{X}}}_{s,s},w \rangle, $$

(33)

where w is a word with values in the alphabet {1,…,d}. Using the identity $\hat {\mathbf {X}}:= {\varPhi }^{\ast }_{H} \mathbf {X}$, we can rewrite (33) as

$$ \dot{Y}_{s} = {\sum}_{|w|\le N} f_{w} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},{\varPhi}_{H}w \rangle. $$

It follows from the definition of Φ_H in (25) that it is possible to write down a general combinatorial formula for Φ_H(w), see [23, Proposition 4.10]

$$ {\varPhi}(w)= {\sum}_{u\in \{w\}}\frac{1}{2^{|w|-|u|}} u, $$

where {w} consists of the words we can construct from w by successively replacing any neighbouring pairs ij in w by {ij}. Switching the sum on w and u, (33) becomes

$$ \dot{Y}_{s} = {\sum}_{|w|\le N}{\sum}_{u\in \{w\}}\frac{1}{2^{|w|-|u|}} f_{w} (Y_{s})\langle \dot{\hat{\mathbf{X}}}_{s,s},u \rangle={\sum}_{\|u\|\le N}{\sum}_{\{w\}_{p}= u}\frac{1}{2^{|w|-|u|}} f_{w} (Y_{s})\langle \dot{\hat{\mathbf{X}}}_{s,s},u \rangle, $$

(34)

where the sum over {w}_p = u involves all the ways one can write a word u as {w}_I of a word w whose letters are in the alphabet {1,…,d} and I ∈ C(|w|). The element

$$ {\sum}_{\{w\}_{p}= u}\frac{1}{2^{|w|-|u|}} f_{w}, $$

then corresponds to the expression $\hat {f}_{u}$ for any word u.

Using the shorthand notations $\langle \dot {\mathbf {X}}_{s,s}, a \rangle =\langle \dot {\hat {\mathbf {X}}}_{s,s}, a\rangle =\dot {X}_{s}^{a}$ for any a ∈ A, the expressions (33) and (34) in case N = 2 become respectively

$$ \dot{Y}_{s}={\sum}_{i=1}^{d} f_{i} (Y_{s}) \dot{X}_{s}^{i} + {\sum}_{i,j=1}^{d} f_{ij} (Y_{s})\langle \dot{\hat{\mathbf{X}}}_{s,s},ij \rangle $$

and

$$ \begin{array}{@{}rcl@{}} \dot{Y}_{s} &=& {\sum}_{i=1}^{d} \hat{f}_{i} (Y_{s})\dot{X}_{s}^{i} + {\sum}_{i,j=1}^{d} \hat{f}_{ij} (Y_{s})\langle\dot{\mathbf{X}}_{s,s},ij\rangle + {\sum}_{i\leq j}^{d} \hat{f}_{\{ij\}} (Y_{s})\dot{X}_{s}^{\{ij\}} \\ & =& {\sum}_{i=1}^{d} f_{i} (Y_{s})\dot{X}_{s}^{i}+ {\sum}_{i,j=1}^{d} f_{ij} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},ij \rangle \\&&+ \frac{1}{2}\left( {\sum}_{i=1}^{d} f_{ii}(Y_{s})\dot{X}_{s}^{\{ii\}}+{\sum}_{i<j}^{d} (f_{ij}+f_{ji})(Y_{s})\dot{X}_{s}^{\{ij\}} \right)\\ & =&{\sum}_{i=1}^{d} f_{i} (Y_{s})\dot{X}_{s}^{i}+ {\sum}_{i,j=1}^{d} f_{ij} (Y_{s})\langle \dot{\mathbf{X}}_{s,s},ij \rangle + \frac{1}{2}{\sum}_{i,j=1}^{d} f_{ij} (Y_{s})\dot{X}_{s}^{\{ij\}}. \end{array} $$

Interpreting Xⁱ and X^{ij} as the components of a semimartingale and his quadratic variations, we obtain an algebraic version of the Itô-Stratonovich correction among semi-martingales at level of SDEs, see [23] for further applications.

3.4 Algebraic Renormalization of SQGRP

We now want to adapt the notion of translation discussed for geometric rough paths to the context of quasi-geometric rough paths. Adapting the same arguments in Section 2.4, for any family $(v_{a} \colon a\in A )\subset {\mathscr{L}}((A))$, a translation map T_v: T_ω((A)) → T_ω((A)) can easily be defined on any alphabet A. In the case of a family $(v_{a} \colon a\in A )\subset {\mathscr{L}}(A)$ it follows from the properties of any weight ω, that T_v sends $T^{N}_{\omega }(A)$ to $T^{M}_{\omega }(A)$ with $M=N\cdot N^{\prime }$, where $N^{\prime }$ is the smallest integer such that $v_{i}\in {\mathscr{L}}^{N^{\prime }}_{\omega }(A)$. Passing to the quasi-shuffle context, the natural direction to perform a translation must be done along the Lie algebra $\hat {{\mathscr{L}}}((A))$. To define a proper notion, Corollary 3.6 tells us the set $\hat {{\mathscr{L}}}(A)$ consists of Lie series obtained from the set $\mathfrak {A}= \{{\varPsi }^{\ast }_{H}(a)\colon a\in A\}$. Therefore, fixing a subset $u = (u_{a} \colon a\in A)\subset \hat {{\mathscr{L}}}((A))$, there is a unique morphism of Lie algebras $\hat {T}_{u}\colon \hat {{\mathscr{L}}}((A))\to \hat {{\mathscr{L}}}((A))$ such that

$$ \hat{T}_{u}\left( {\varPsi}_{H}^{\ast}(a)\right) = {\varPsi}_{H}^{\ast}(a) + u_{a}. $$

Using the translation maps T_v and the maps ${\varPsi }^{\ast }_{H}$, ${\varPhi }^{\ast }_{H}$ we see that $\hat {T}_{u}$ uniquely extends to an endomorphism of T_ω((A)) with respect to the product ⊗.

Theorem 3.21

For any collection $u = (u_{a} \colon a\in A )\subset \hat {{\mathscr{L}}}((A))$ there exists a unique ⊗-endomorphism over T_ω((A)) which extends $\hat {T}_{u}\colon \hat {{\mathscr{L}}}((A))\to \hat {{\mathscr{L}}} ((A))$. We call it the quasi-translation map and we denote it by the same symbol $\hat {T}_{u}$. In particular, one has the explicit relation

$$ \hat{T}_{u} = {\varPsi}^{\ast}_{H} T_{\hat{u}}{\varPhi}^{\ast}_{H}, $$

(35)

where $\hat {u}$ is given by the family $\hat {u}= ({\varPhi }^{\ast }_{H}(u_{a}) \colon a\in A )\subset {\mathscr{L}}((A))$. Moreover, if $(u_{a} \colon a\in A)\subset \hat {{\mathscr{L}}} (A)\hat {T}_{u}$ sends $T^{N}_{\omega }(A)$ to $T^{M}_{\omega }(A)$ with $M=N\cdot N^{\prime }$, where $N^{\prime }$ is the smallest integer such that $v_{i}\in \hat {{\mathscr{L}}}^{N^{\prime }}_{\omega }(A)$.

Proof

Thanks to Proposition 3.5 and the properties of the translation map, the map ${\varPsi }^{\ast }_{H} T_{\hat {u}}$ ${\varPhi }^{\ast }_{H}$ is a ⊗-endomorphism satisfying

$$ {\varPsi}^{\ast}_{H} T_{\hat{u}}{\varPhi}^{\ast}_{H}({\varPsi}_{H}^{\ast}(a))= {\varPsi}^{\ast}_{H}T_{\hat{u}}(a)={\varPsi}^{\ast}_{H}(a+{\varPhi}_{H}^{\ast}(u_{a}))={\varPsi}^{\ast}_{H}(a)+u_{a}. $$

Moreover, from Corollary 3.6 we also deduce that ${\varPsi }^{\ast }_{H} T_{\hat {u}}{\varPhi }^{\ast }_{H}$ is a Lie endomorphism of $\hat {{\mathscr{L}}}((A))$. Therefore we conclude from the freeness of $\hat {{\mathscr{L}}}((A))$ that the definition (35) is a bona fide extension of $\hat {T}_{u}$. Concerning the uniqueness of $\hat {T}_{u}$, let Γ: T_ω((A)) → T_ω((A)) be an ⊗-endomorphism extending $\hat {T}_{u}$. Considering the map ${\varPhi }^{\ast }_{H} {\Gamma }{\varPsi }^{\ast }_{H}$ we can easily check on any a ∈ A the property

$$ {\varPhi}^{\ast}_{H} {\Gamma} {\varPsi}^{\ast}_{H}(a)= a+ {\varPhi}^{\ast}_{H} (u_{a}). $$

Using the fundamental property of T((A)), ${\varPhi }^{\ast }_{H} {\Gamma } {\varPsi }^{\ast }_{H}$ must coincide with $T_{\hat {u}}$ and we obtain the uniqueness. The last properties of $\hat {T}_{u}$ follows from the fact that ${\varPhi }^{\ast }_{H}$ and ${\varPsi }^{\ast }_{H}$ are graded maps. □

Remark 3.22

The procedure outlined in this section still leaves open the question as how to define a family of Lie endomorphisms $(\hat {T}_{u})_{u}$, $\hat {T}_{u}: T_{\omega }((A))\to T_{\omega }((A))$ which only takes as input a finite family $u=(u_{1},\dots ,u_{d})$ of primitive elements and the demand that T_ui = i + u_i for $i=1,\dots ,d$. This further question, which is similar in nature and connected to what was described in Remark 3.18, is motivated by the fact that such translations coming from (only) d choices of Lie elements exist canonically in the geometric and branched case, see [6] where they were introduced. It would be desirable to have a translation map in the d-dimensional quasi-geometric setting (which is T_ω((A)) with |{a ∈ A|ω(a) = 1}| = d) that works fully analogously, and at best is consistent with both the geometric and the branched d-dimensional setting.

The quasi-translation maps now at hand can be applied to sqgrps/sqgrms and their truncated versions as in Theorem 2.24. Indeed for any $u = (u_{a} \colon a\in A )\subset \hat {{\mathscr{L}}}((A))$ and sqgrp/sqgrm X we can actually define the compositions $\hat {T}_{u} (\mathbf {X}_{t})$ and $\hat {T}_{u} (\mathbf {X}_{s,t})$. In addition, for any $u = (u_{a} \colon a\in A)\subset \hat {{\mathscr{L}}}(A)$ and N-sqgrm Y we define

$$ \hat{\mathcal{T}}_{u}[\mathbf{Y}]_{s,t} := \hat{T}_{u}^{M} (q\text{MinExt}^{M}(\mathbf{Y})) = \textsf{proj}_{M, \omega}\hat{T}_{u}(q\text{MinExt}(\mathbf{Y})_{s,t}), $$

(36)

where $M=N\cdot N^{\prime }$ with $N^{\prime }$ the smallest integer such that $u_{a}\in \hat {{\mathscr{L}}}^{N^{\prime }}_{\omega }(A)$ for all a ∈ A and $\hat {T}_{v}^{M} :=\textsf {proj}_{M,\omega } \hat {T}_{u}\mathfrak {i}^{M}$ with the embedding $\mathfrak {i}^{M}: T^{M}_{\omega }(A)\to T_{\omega }((A))$. These two operations have equivalently a dynamical reinterpretation like Theorem 2.24.

Proposition 3.23

Given a sqgrp (sqgrm) X over A with weight ω and $u = (u_{a} \colon a\in A )\subset \hat {{\mathscr{L}}} ((A))$, the composition $\hat {T}_{u} (\mathbf {X}_{t})~(\hat {T}_{u} (\mathbf {X}_{s,t}))$ is again a sqgrp (sqgrm) which coincides with the solution of

$$ \dot{\mathbf{Z}}_{t} = \mathbf{Z}_{t} \otimes (\hat{T}_{u} \dot{\mathbf{X}}_{t,t}), \qquad \mathbf{Z}_{0} = \hat{T}_{u} \mathbf{X}_{0}. $$

(37)

The same result applies to good sqgrms when $u\subset \hat {{\mathscr{L}}} (A)$. In addition, for any $u = (u_{a} \colon a\in A)\subset \hat {{\mathscr{L}}} (A)$ and N-sqgrm Y the path $t\to \hat {\mathcal {T}}_{u}[\mathbf {Y}]_{0,t}$ is a sqgrp coinciding with the solution of

$$ \dot{\mathbf{W}}_{t} = \mathbf{W}_{t}\otimes_{M, \omega} (\hat{T}_{u} \dot{\mathbf{Y}}_{t,t}), \qquad \mathbf{W}_{0} = \mathbf{1}, $$

(38)

where $M\in \mathbb {N}$ is contained in the definition of $\hat {\mathcal {T}}_{u}[\mathbf {Y}]$ in (36).

Proof

Choosing the family $\hat {u}=({\varPhi }^{\ast }_{H}(u_{a}) \colon a\in A )$, we can apply Theorem 2.24 to the weighted sgrp (sgrm) $\hat {\mathbf {X}}={\varPhi }^{\ast }_{H} \mathbf {X}$ and $\hat {\mathbf {Y}}={\varPhi }^{\ast }_{H} \mathbf {Y}$. Then the paths associated to ${T}_{\hat {u}}(\hat {\mathbf {X}})$ and $\mathcal {T}_{\hat {u}}[\hat {\mathbf {Y}}]$ solve respectively the equations

$$ \begin{array}{@{}rcl@{}} \dot{\hat{\mathbf{Z}}}_{t} &=& \hat{\mathbf{Z}}_{t} \otimes (T_{\hat{u}} \dot{\hat{\mathbf{X}}}_{t,t}), \qquad \hat{\mathbf{Z}}_{0} = T_{\hat{u}} \hat{\mathbf{X}}_{0};\\ \dot{\hat{\mathbf{W}}}_{t} &=& \hat{\mathbf{W}}_{t}\otimes_{M, \omega} (T_{\hat{u}} \dot{\hat{\mathbf{Y}}}_{t,t}), \qquad \hat{\mathbf{W}}_{0} = \mathbf{1}. \end{array} $$

Using the identity (35) and the properties of ${\varPhi }^{\ast }_{H}$, ${\varPsi }^{\ast }_{H}$ of preserving the weighted length, we deduce that $\hat {T}_{u}(\mathbf {X})={\varPsi }^{\ast }_{H}{T}_{\hat {u}}(\hat {\mathbf {X}})$ and $\hat {\mathcal {T}}_{u}[\mathbf {Y}]={\varPsi }^{\ast }_{H}\mathcal {T}_{\hat {u}}[\hat {\mathbf {Y}}]$. Looking at the equation of the paths ${\varPsi }^{\ast }_{H} \hat {\mathbf {Z}}$ and ${\varPsi }^{\ast }_{H} \hat {\mathbf {W}}$, we obtain the equations (37) and (38). □

We conclude the section with a summary of the properties of translation operators $\hat {T}_{u}$ together with the differential equation (16). For any collection of Lie polynomials with values in A given by $v = (v_{a} \colon a\in A )\subset {\mathscr{L}}(A)$ and any family of vector fields (f_a: a ∈ A), we consider the collection of vector fields $({f^{v}_{a}}\colon a\in A)$ defined on any a ∈ A as

$$ {f^{v}_{a}}:=f_{a}+ f_{v_{a}}, $$

where $f\colon {\mathscr{L}}(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ is the natural definition on an alphabet A of the Lie algebra morphism defined in (12). Extending $({f^{v}_{a}}\colon a\in A)$ to all T_ω(A), we obtain a map $f^{v}\colon T_{\omega }(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ which satisfies the identity $f^{v}= f_{T_{v}}$ over ${\mathscr{L}}(A)$, as it was already shown in the proof of Theorem 2.26, when A = {1,…,d}. By replacing the directions of translations v with $u= (u_{a} \colon a\in A)\subset \hat {{\mathscr{L}}}(A)$ we can uniquely define a Lie algebra morphism $\hat {f}^{u}\colon \hat {{\mathscr{L}}}(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ such that on any a ∈ A one has as

$$ \hat{f}^{u}_{{\varPsi}^{\ast}_{H}(a)}:=\hat{f}_{{\varPsi}^{\ast}_{H}(a)}+ \hat{f}_{u_{a}}. $$

Extending $\hat {f}^{u}$ to all T_ω(A) and applying the definition of $\hat {f}$ with formula (35), we also obtain a map $\hat {f}^{u}\colon T_{\omega }(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$. Both maps $\hat {f}^{u}$ and f^v allow to write the effect of translation at the level of differential equations.

Theorem 3.24

Let X be a good sqgrm and W a N-sqgrm. For any given $u=\{u_{a}\colon a\in A\}\subset \hat {{\mathscr{L}}}(A)$ a path $Y\colon [0,T]\to \mathbb {R}^{e}$ solves one of the equation

$$ dY = \hat{f} (Y) d (\hat{T}_{u}(\mathbf{X})), \quad dY = \hat{f} (Y) d (\hat{\mathcal{T}}_{u}[\mathbf{W}]); $$

if and only if it solves respectively

$$ dY = \hat{f}^{u} (Y) d \mathbf{X}, \quad dY =\hat{f}^{u} (Y) d \mathbf{W}. $$

(39)

Alternatively, by setting $\hat {u}=\{{\varPhi }^{\ast }_{H}(u_{a})\colon a\in A\}\subset {\mathscr{L}}(A)$ and $\hat {\mathbf {X}}= {\varPhi }^{\ast }_{H}\mathbf {X}$, $\hat {\mathbf {W}}= {\varPhi }^{\ast }_{H}\mathbf {W}$ then Y solves also equivalently

$$ dY = f^{\hat{u}} (Y) d \hat{\mathbf{X}}, \quad dY = f^{\hat{u}} (Y) d \hat{\mathbf{W}}. $$

(40)

Proof

Equivalences (39) and (40) follow by combining the proof of Theorem 2.26 and Proposition 3.19. The only thing to check is to describe the relations between the maps $\hat {f}^{u}$ and $f^{\hat {u}}$ and the translations $T_{\hat {u}}$ and $\hat {T}_{u}$. Indeed, it follows from the definition of $\hat {T}_{u}$ and $\hat {f}^{u}$ that one has

$$ \hat{f}^{u}= \hat{f}_{\hat{T}_{u}} $$

on any element ${\varPsi }^{\ast }_{H}(a)$ and consequently over all $\hat {{\mathscr{L}}}(A)$. Following the first argument in Theorem 2.26 we get the first equivalence (39). Using the explicit definition of $\hat {f}$ and identity (35), we deduce also the following equality on $\hat {{\mathscr{L}}}(A)$

$$ \hat{f}_{\hat{T}_{u}}= f_{{\varPhi}^{\ast}_{H}\hat{T}_{u}}= f_{T_{\hat{u}}{\varPhi}^{\ast}_{H}}= f^{\hat{u}}_{{\varPhi}^{\ast}_{H}}. $$

Applying the same argument as in the proof of (ii) in Proposition 3.19, we conclude. □

We conclude the section by extending the time translation of Corollary 2.29 in the quasi-shuffle context. For these purposes, we suppose given a generic alphabet A¹ with commutative bracket {,}₁ and weight ω₁. Then we simply add an extra time component as new letter $\hat {0}$ and we define the extended alphabet $\bar {A}=\{\hat {0}\}\cup A^{1}$ together with weight $\omega \colon \bar {A}\to \mathbb {N}^{\ast }$ defined by extending ω₁ and putting $\omega (\hat {0})=1$ and the extended commutative bracket {,} given for any a,b ∈ A¹

$$ \{a,\hat{0}\}=\{\hat{0},a\}=\{\hat{0},\hat{0}\}= 0,\quad \{a,b\}=\{a,b\}. $$

Under these conditions the signature of the time component $\mathbf {X}^{0}\colon [0,T]^{2}\to G(\mathbb {R})$

$$ \mathbf{X}^{0}_{s,t}:=\exp_{\otimes}((t-s)\hat{0}) $$

can be easily embedded in $\hat {G}(\bar {A})$ and for any good sqgrm $\mathbf {X}^{1}:[0,T]^{2} \to \hat {G} (A_{1})$ we can introduce again

$$ \bar{\mathbf{X}}:=(\mathbf{X}^{0},\mathbf{X}^{1})_{\min}; $$

(see also Remark 3.15). Since ${\varPsi }^{\ast }_{H}(\hat {0})= \hat {0}$, for any given a $u_{0}\in \hat {{\mathscr{L}}}(\bar {A})$, we choose the translation $\hat {T}_{u_{0}}\colon T(A)\to T(A)$ such that $\hat {T}_{u_{0}}\hat {0}=\hat {0}+u_{0}$ and such that $\hat {T}_{u_{0}}({\varPsi }^{\ast }_{H}(a))={\varPsi }^{\ast }_{H}(a)$. Then one has trivially $\hat {T}_{u_{0}}=$ id over the subalgebra of $T_{\omega }(\bar {A})$ isomorphic to $T_{\omega _{1}}(A^{1})$ and we can describe the relations for equations driven by $\bar {X}$. The proof follows easily from Corollary 2.29, Theorem 3.24 and Proposition 3.19.

Corollary 3.25

Let X¹ be a good sqgrm and $u_{0}\in \hat {{\mathscr{L}}}(A)$. Then the translation $t\mapsto \hat {T}_{u_{0}}\bar {\mathbf {X}}_{0,t}$ can be described as the sum $\mathbf {U}_{0}\boxplus \bar {\mathbf {X}}$, where U₀ is given by

$$ (\mathbf{U}_{0})_{s,t}=\exp_{\otimes}(u_{0}(t-s)). $$

Moreover, for any given family $(f_{\hat {0}}, f_{a} \colon a\in A^{1})$ we define $\bar {f}\colon T(A)\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ and $f\colon T(A_{1})\to \text {Vect}^{\infty }(\mathbb {R}^{e})$ like in (14) starting from $(f_{\hat {0}}, f_{a} \colon a\in A^{1})$ and (f_a: a ∈ A¹) respectively and using the notations $\hat {u}_{0}= {\varPhi }^{\ast }_{H}u_{0}$, $\hat {\mathbf {X}}^{1}= {\varPhi }^{\ast }_{H}\mathbf {X}^{1}$ equation

$$ dY = \hat{\bar{f}} (Y) d (\hat{T}_{u_{0}}(\bar{\mathbf{X}})) $$

is equivalent to

$$ dY = (f_{\hat{0}} + \hat{\bar{f}}_{u_{0}})(Y) dt+ \hat{f} (Y) d \mathbf{X}^{1},\qquad dY = (f_{\hat{0}} + \bar{f}_{\hat{u}_{0}})(Y) dt+ f (Y) d \hat{\mathbf{X}}^{1}. $$

Remark 3.26

Note that we recover in this smooth quasi-geometric rough path setting a property like the final statement of [6, Theorem 30 (ii)]: The smooth rough path increment/model $T_{v_{0}}\mathbf {Z}_{t}$ does not depend on the precise choice of the Hopf algebra homomorphism $T_{u_{0}}$, as long as $T_{u_{0}} \hat {0}=\hat {0}+u_{0}$ and $T_{u_{0}}=\text {id}$ on $T_{\omega _{1}}(A^{1})$.

4 Recast in an Abstract Hopf Algebra Framework

Many of the above constructions can be formulated in the abstract framework of Hopf algebras following the approach adopted in [54] and [20]. In this section, we introduce the notion smooth rough paths over a Hopf algebra and we will discuss their renormalization. An interesting operation arises at this level: the canonical sum of rough paths, which is applied to present an alternative construction to renormalization of branched rough paths, along the lines of [6].

4.1 Smooth Rough Paths on a Hopf Algebra

In what follows we fix $(\mathcal {H}, \cdot , {\Delta })$ a connected, $\mathbb {N}$-graded and locally finite commutative Hopf algebra over $\mathbb {R}$. That is to say there is a sequence of finite-dimensional vector spaces $\{{\mathscr{H}}_{n}\}_{n\geq 0}$ such that

$$ \mathcal{H}=\underset{n=0}{\overset{\infty}{\bigoplus}} \mathcal{H}_{n}, \quad \mathcal{H}_{0}\approx \mathbb{R}= \langle \mathbf{1}\rangle, $$

where 1 is the unit of ${\mathscr{H}}$. For any given Hopf algebra in this class, we introduce two different notions of dual space: the full dual ${\mathscr{H}}^{\prime }$ and the graded dual ${\mathscr{H}}^{\ast }$ respectively defined by

$$ \mathcal{H}^{\prime}:=\text{Hom}(\mathcal{H}, \mathbb{R})=\text{Hom}\left( \underset{n=0}{\overset{\infty}{\bigoplus}} \mathcal{H}_{n}, \mathbb{R}\right),\quad\mathcal{H}^{\ast}:=\underset{n=0}{\overset{\infty}{\bigoplus}} \mathcal{H}_{n}^{\prime}= \underset{n=0}{\overset{\infty}{\bigoplus}} \text{Hom}(\mathcal{H}_{n}, \mathbb{R}), $$

where $V^{\prime }=\text {Hom}(V, \mathbb {R})$ stands for the space of continuous $\mathbb {R}$-valued linear forms on V. There is a canonical pairing 〈⋅,⋅〉 between ${\mathscr{H}}^{\prime }$ and ${\mathscr{H}}$ and the space ${\mathscr{H}}^{\ast }$ lies dense in ${\mathscr{H}}^{\prime }$ by equipping ${\mathscr{H}}^{\prime }$ with the weak topology, i.e. the weakest topology for which the evaluation maps v^∗↦〈v^∗,u〉, $u\in {\mathscr{H}}$ are continuous, see [3, Lemma 1.7], [4].

Using the grading of ${\mathscr{H}}$, we can also define for any $N\in \mathbb {N}$ the truncated spaces

$$ (\mathcal{H}^{\ast})^{N}:=\underset{n=0}{\overset{N}{\bigoplus}} \mathcal{H}_{n}^{\ast},\quad \mathcal{H}^{N}:=\underset{n=0}{\overset{N}{\bigoplus}} \mathcal{H}_{n}, $$

which yield two natural filtrations and $\{({\mathscr{H}}^{\ast })^{N}\colon N\in \mathbb {N}\}$, $\{{\mathscr{H}}^{N}\colon N\in \mathbb {N}\}$ for the vector spaces ${\mathscr{H}}^{\ast }$ and ${\mathscr{H}}$. We note that $({\mathscr{H}}^{\ast })^{N}=({\mathscr{H}}^{N})^{\ast }$ and will henceforth write ${\mathscr{H}}^{\ast N}$.

The coproduct Δ of ${\mathscr{H}}$ induces by duality a product ⋆ in ${\mathscr{H}}^{\prime }$ and a fortiori on ${\mathscr{H}}^{\ast }$ defined on any $\alpha , \beta \in {\mathscr{H}}^{\prime }$ and $h\in {\mathscr{H}}$ via the identity

$$ \langle \alpha\star \beta, h\rangle := \langle (\alpha \otimes \beta),{\Delta} h\rangle_{2}, $$

where 〈⋅,⋅〉₂ is the canonical pairing between ${\mathscr{H}}^{\prime }\otimes {\mathscr{H}}^{\prime }$ and ${\mathscr{H}}\otimes {\mathscr{H}}$ induced by the canonical dual pairing 〈⋅,⋅〉. Moreover it is also possible to define a coproduct Δ^∗ only on ${\mathscr{H}}^{\ast }$ from the identity

$$ \langle {\Delta}^{\ast} w,u\otimes v \rangle_{2}:= \langle w,u v \rangle, $$

obtaining the dual Hopf algebra $({\mathscr{H}}^{\ast }, \star , {\Delta }^{\ast })$. The coproduct Δ is compatible with the filtration and hence so is the product ⋆, which maps ${\mathscr{H}}^{\ast M}\times {\mathscr{H}}^{\ast N}$ to ${\mathscr{H}}^{*M+N}$. The projections $\pi _{N}: {\mathscr{H}}\longrightarrow {\mathscr{H}}/\oplus _{n=N+1}^{\infty } {\mathscr{H}}_{n}$ onto the quotient by the ideal $\oplus _{n=N+1}^{\infty } {\mathscr{H}}_{n}$ is an algebra morphism so that ⋆_N := π_N ⋆ restricted to ${\mathscr{H}}^{*N}$ defines a truncated product $\star _{N}: {\mathscr{H}}^{*N}\times {\mathscr{H}}^{*N}\to {\mathscr{H}}^{*N}$. Much in the same way as rough paths over a Hopf algebra ${\mathscr{H}}$ were defined, see [20, 54], we now define smooth rough paths and models.

Definition 4.1

We call a level-N smooth ${\mathscr{H}}$ rough path (in short: N-s${\mathscr{H}}$rp) any non zero path $\mathbf {X}: [0,T] \to {\mathscr{H}}^{*N}$ satisfying the following properties:

• (a” i) For all times t ∈ [0,T] and for all $h\in {\mathscr{H}}^{K}$, $k\in {\mathscr{H}}^{L}$, with K + L = N one has

  $$ \langle\mathbf{X}_{t},v \cdot w\rangle = \langle \mathbf{X}_{t},v\rangle \langle\mathbf{X}_{t},w\rangle. $$

  (41)

• (a” ii) For every word $h\in {\mathscr{H}}^{N}$, the map t↦〈X_t,h〉 is smooth.

We call level-N smooth ${\mathscr{H}}$ rough model (in short: N-s${\mathscr{H}}$rm) any map $\mathbf {X}: [0,T]^{2} \to {\mathscr{H}}^{*N}$ which satisfies property (41) for all X_s,t as well as the following properties:

• (b’ i) The following abstract Chen relation holds:

  $$ \mathbf{X}_{s,u} \star_{N} \mathbf{X}_{u,t}=\mathbf{X}_{s,t} $$

  (42)

  for any s,u,t ∈ [0,T].

• (b’ ii) For every $h \in {\mathscr{H}}^{N}$, the map t↦〈X_s,t,w〉 is smooth, for one (equivalently: all) base point(s) s ∈ [0,T].

By smooth ${\mathscr{H}}$ rough path (model) (in short: s${\mathscr{H}}$rp and s${\mathscr{H}}$rm), we mean a path (map) with values in ${\mathscr{H}}^{\prime }$ for which (41) holds for any $w,v\in {\mathscr{H}}$ and relation (42) holds with ⋆.

Algebraic properties of smooth ${\mathscr{H}}$ rough paths are encoded in the specific Lie group (Lie algebra) structures of ${\mathscr{H}}^{\prime }$. Following [54, Definition 2.6], property (41) (in the case when $v,w\in {\mathscr{H}}$), amounts to X_t belonging to the group of N-truncated characters $G^{N}(\mathcal H)$ or the group of characters $G(\mathcal H)$, for any t. The $(G({\mathscr{H}}), \star )$ is a topological Lie group when equipped with the topology of pointwise convergence, see [3] and by quotienting $(G^{N}(\mathcal H), \star _{N})$ is a finite-dimensional Lie group. Their Lie algebras can be explicitly described by the set ${\mathfrak g}^{N}({\mathscr{H}})$ of level-N truncated infinitesimal characters, resp. the set ${\mathfrak g}({\mathscr{H}})$ of infinitesimal characters, i.e. of elements $\alpha \in {\mathscr{H}}^{\star N}$, resp. $\alpha \in {\mathscr{H}}^{\star }$ such that for all $(h, k)\in {\mathscr{H}}^{K}\times {\mathscr{H}}^{L}$ with K + L = N, resp. $(h, k)\in {\mathscr{H}}^{2}$, the following property holds:

$$ \langle \alpha, h \cdot k\rangle=\langle \alpha, h \rangle \langle \mathbf{1}^{\ast}, k \rangle + \langle \mathbf{1}^{\ast}, h \rangle \langle \alpha,k\rangle, $$

where 1^∗ is the counit of ${\mathscr{H}}$. The Lie brackets $[\cdot , \cdot ]_{\star _{N}}$ on ${\mathfrak g}^{N}({\mathscr{H}})$ and [⋅,⋅]_⋆ on ${\mathfrak g}({\mathscr{H}})$ are given by the commutators of ⋆_N and ⋆. The pair $({\mathfrak g}({\mathscr{H}}),[\cdot , \cdot ]_{\star })$ defines a topological Lie algebra, see [4]. A special role is played by the set of primitive elements $P({\mathscr{H}}^{\ast })= {\mathfrak g}({\mathscr{H}})\cap {\mathscr{H}}^{\ast }$ which is a Lie algebra with the induced Lie brackets. To relate these Lie algebras with the character groups we introduce the exponential and truncated exponential map $\exp _{\star }:{\mathscr{H}}^{\prime }\to {\mathscr{H}}^{\prime }$, $\exp _{\star _{N}}:{\mathscr{H}}^{*N}\to {\mathscr{H}}^{*N}$ defined by

$$ \exp_{\star} \textbf{x}:={\sum}_{n=0}^{\infty}\frac{\textbf{x}^{\star n}}{n!}, \quad \exp_{\star_{N}}\textbf{x}= {\sum}_{n\geq 0}^{N}\frac{\mathbf{x}^{\star n}}{n!}|_{\mathcal{H}^{N}}. $$

When restricted to the Lie algebras, they induce bijections $\exp _{\star _{N}}: {\mathfrak g}^{N}({\mathscr{H}})\to G^{N}({\mathscr{H}})$ and the $\exp _{\star }: {\mathfrak g}({\mathscr{H}})\to G({\mathscr{H}})$, turning $G({\mathscr{H}})$ into an analytic Lie group, see [3, Theorem 3.7 and Appendix B] and [4, Theorem 3.9] for the properties of $\exp _{\star }$ and $G({\mathscr{H}})$.

In practice, we can identify N-s${\mathscr{H}}$rp X_t and N-s${\mathscr{H}}$rm X_s,t with the same equivalence properties of N-sgrp and N-sgrm by using the group structure induced by ⋆, see (7). Similarly to Definition 2.5, we define the extension of a N-s${\mathscr{H}}$rp. The diagonal derivative

$$ \dot{\mathbf{X}}_{s,s}:= \partial_{t} |_{t=s} \mathbf{X}_{s,t}= \mathbf{X}_{s}^{-1} \star \dot{\mathbf{X}}_{s} $$

of any given X in s${\mathscr{H}}$rp lies in the Lie algebra $g({\mathscr{H}})$. These properties allow to extend Theorem 2.8 on any smooth ${\mathscr{H}}$-rough path.

Theorem 4.2 (Fundamental Theorem of s${\mathscr{H}}$rp)

Let $N \in \mathbb {N}$. Any Y in N-s${\mathscr{H}}$rp uniquely extends to some X in s${\mathscr{H}}$rp which is minimal in the sense that

$$ \mathbf{X}_{s}^{-1} \star \dot{\mathbf{X}}_{s} \in \mathfrak{g}^{N} (\mathcal{H}) $$

for all s ∈ [0,T]. We call ${\mathscr{H}}\text {MinExt}(\mathbf {Y}) := \mathbf {X}$ the ${\mathscr{H}}$-minimal extension of Y and also ${\mathscr{H}}\text {MinExt}^{N^{\prime }}(Y) := \pi _{N^{\prime }} \mathbf {X}$, for $N^{\prime } > N$, the $N^{\prime }$-minimal extension of Y. Moreover, for any [s,t] ⊂ [0,T] the associated sgrm of X_s,t only depends on Y|_[s,t]. We call this object the ${\mathscr{H}}$ signature of Y on [s,t], in symbols $\text {Sig}_{{\mathscr{H}}}(\mathbf {Y}|_{[s,t]})$. A s${\mathscr{H}}$rm X is called a good s${\mathscr{H}}$rm if it satisfies $\mathbf {X}= {\mathscr{H}}\text {MinExt}(\mathbf {Y})$ for some N-s${\mathscr{H}}$rm Y.

Proof

The proof of the result goes as that of Theorem 2.8, modulo the replacement of ⊗ by ⋆. The only properties to check in this generalised context is the existence and uniqueness of a smooth solution for the initial value problem

$$ \dot{\gamma}(t) = \gamma(t)\star \eta(t), \quad \gamma(0)=\mathbf{1}^{\ast} $$

for any given smooth curve $\eta :[0, T]\to {\mathfrak g}({\mathscr{H}})$. Moreover, we need to prove that for any given couple $X, \bar {X}\in G^{N+1}({\mathscr{H}})$ such that $\langle X,h\rangle = \langle \bar {X}, h\rangle$ for any $h\in {\mathscr{H}}_{N}$ then $X-\bar {X}$ belongs to the center of $G^{N+1}({\mathscr{H}})$. The first property follows from the regularity in the sense of Milnor, see [47], of the Lie group $G({\mathscr{H}})$, see [5, Theorem B] and references therein. The second property follows from [54, Proposition 2.10]. □

Example 4.3

Setting and we recover respectively Theorems 2.8 and 3.9. In this identification, the operation ⋆, depending on Δ is identified with the concatenation product ⊗ see [53]. As recalled in Theorem 3.4, the Hoffman’s exponential and logarithm (25) yield an isomorphism of graded Hopf algebras . Hence the basic properties of these maps follow from the general fact that for any given Hopf algebra isomorphism ${\Gamma }\colon {\mathscr{H}}\to \mathcal {\mathcal {K}}$ among two Hopf algebras ${\mathscr{H}}$ and $\mathcal {K}$ with the properties listed at the beginning, the adjoint map ${\Gamma }^{\ast }\colon {\mathscr{H}}^{\ast }\to \mathcal {K}^{\ast }$ is also an isomorphism. We observe also that the scalar product 〈⋅,⋅〉 defined on $T(\mathbb {R}^{d})$ and T_ω(A) can be used to identify the graded dual ${\mathscr{H}}^{\ast }$ with ${\mathscr{H}}$ by means of the Riesz lemma, so that it is not necessary to introduce the notion of graded dual in that context.

Example 4.4

Another relevant example in the context of renormalization of rough paths arising in [6] is the Butcher–Connes–Kreimer Hopf algebra $\mathcal {H}_{BCK}(\mathbb {R}^{d})$ consisting of polynomials of rooted forests τ with nodes decorated by the finite set {1,…,d} together with the empty forest 1. A forest f is graded accordingly to |f|, the number of its nodes and the coproduct Δ is defined on each tree τ as

$$ {\Delta}(\tau)={\sum}_{c} P_{c}(\tau)\otimes R_{c}(\tau), $$

(43)

where the sum is taken over a specific set of admissible cuts over the tree. The result of each cut produces a polynomial of trees P_c(t) and R_c(t) a tree corresponding to the root. We call the N-s${\mathscr{H}}$rp or s${\mathscr{H}}$rp in this context level-N smooth branched rough paths and smooth branched rough paths (in short: N-sbrp and sbrp), see [32]. The operation ⋆ induced by the coproduct (43) coincide with the so called Grossman–Larson algebra of forests [31] and $P({\mathscr{H}}^{\ast }_{BCK}(\mathbb {R}^{d}))$ coincides with the free vector space $\langle \mathfrak {T}_{d}\rangle$ generated by $\mathfrak {T}_{d}$, the set of dual trees decorated by the finite set {1,…,d} and $\mathfrak {g}(\mathcal {H}_{BCK}(\mathbb {R}^{d}))$ is the vector space $\langle \mathfrak {T}^{\prime }_{d}\rangle$ of tree series.

In adequacy with the previously results, level-N smooth ${\mathscr{H}}$-rough models are a special case of γ-Hölder ${\mathscr{H}}$-rough paths introduced in [20].

Proposition 4.5

Every N-s${\mathscr{H}}$rm X is a 1/N-regular N-truncated ${\mathscr{H}}$ rough path, see [20, Definition 4.3] and its minimal extension $\tilde {\mathbf {X}}$ coincides with the lift of X, as constructed in [20, Theorem 4.4].

Remark 4.6

The same considerations of Remark 3.13 apply also to the class of γ-regular N-truncated ${\mathscr{H}}$ rough paths.

4.2 Translation of Smooth Rough Paths on a Hopf Algebra

We now extend to the framework of smooth ${\mathscr{H}}$-rough paths the notion of translation discussed in Theorems 2.24 and 3.21. To specify in which direction we can perform a translation, we choose a generic finite-dimensional subspace $\mathcal {D}\subset P({\mathscr{H}}^{\ast })$. Fixing a basis {h₁,…,h_e} of $\mathcal {D}$, we obtain a fixed set of directions to apply a translation. By assigning an element of $P({\mathscr{H}}^{\ast })$ to each direction, we introduce an abstract notion of translation.

Definition 4.7

Given a family of primitive elements $v=\{v_{i}\colon i=1,\ldots ,e \}\subset \mathfrak {g}({\mathscr{H}})$ we call a translation map over $\mathcal {D}$ any continuous Lie algebra homomorphism $M_{v}\colon \mathfrak {g}({\mathscr{H}})\to \mathfrak {g}({\mathscr{H}})$ such that M_vh_i = h_i + v_i for any i = 1,…,e.

Remark 4.8

Using the topological properties of $\mathfrak {g}({\mathscr{H}})$, if $v=\{v_{i}\colon i=1,\ldots ,e\}\subset P({\mathscr{H}}^{\ast })$ to define a continuous Lie algebra homomorphism M_v it is sufficient to have a Lie homomorphism $M_{v}\colon P({\mathscr{H}}^{\ast })\to \mathfrak {g}({\mathscr{H}})$ since the Lie algebra $P({\mathscr{H}}^{\star })$ is dense in ${\mathfrak g}({\mathscr{H}})$, see [4, Remark 3.11]. Note that Definition 4.7 only gives a pointwise definition for a fixed v. As in the cases studied in this paper, in practice, we need a map v → M_v with certain consistency properties like $M_{v} M_{u}=M_{v+M_{v} u}$, a condition we do not impose here. More generally we hope to investigate in future work, what properties one should impose on $\mathcal {D}$ and v in a general Hopf algebra framework. A first suggestion of such a set of axioms was very recently given in [52, Definitions 6 and 7].

Remark 4.9

The previous translation maps T_v and $\hat {T}_{\hat {v}}$ in the geometric and quasi-geometric setting are specific examples of translation over two different subspaces of primitive elements, i.e. the vector space $\mathbb {R}^{d}$ and the free vector space generated by $\mathfrak {A}= \{{\varPsi }^{\ast }_{H}(a)\colon a\in A\}$. This is a very specific situation one uses the specific structure of $P({\mathscr{H}}^{\ast })$ as a free Lie algebra, which ensures both the existence and the uniqueness of a translation map. However, it was shown in [6, Example 9] that one can construct two different translation maps over the same vector space $\mathcal {D}$ when ${\mathscr{H}}=\mathcal {H}_{BCK}(\mathbb {R}^{d})$. The Lie structure of $\mathfrak {g}({\mathscr{H}})$ is therefore not sufficient to determine a unique translation. Hence the idea of a definition which does not involve a uniqueness of the translation in its formulation.

Once given $v=\{v_{i}\colon i=1,\ldots ,e \}\subset \mathfrak {g}({\mathscr{H}})$ and a translation map M_v over $\mathcal {D}$, we can actually uniquely extend M_v to a continuous ⋆ morphism $M_{v}\colon {\mathscr{H}}^{\prime }\to {\mathscr{H}}^{\prime }$ the full translation map which we denote in the same way. The extension is purely algebraic and follows by standard Milnor–Moore theorem [48]. Indeed any translation map defines uniquely a Lie algebra morphism $M_{v}\colon P({\mathscr{H}}^{\ast })\to {\mathscr{H}}^{\prime }$ which is compatible with the product ⋆. Using the universal property of the universal enveloping algebra $\mathcal {U}(P({\mathscr{H}}^{\ast }))$ and the Milnor–Moore theorem, the map M_v uniquely extends to a ⋆ morphism $M_{v}\colon \mathcal {H}^{\ast }\to {\mathscr{H}}^{\prime }$ which by density can be defined over ${\mathscr{H}}^{\prime }$. This map allows us to perform translation of s${\mathscr{H}}$rms like in Theorem 2.24 and Proposition 3.23.

Theorem 4.10

Given a s${\mathscr{H}}$rp (s${\mathscr{H}}$rm), a family $v=\{v_{i}\colon i=1,\ldots ,e \}\subset \mathfrak {g}({\mathscr{H}})$ and a translation map M_v over $\mathcal {D}$, the composition M_v(X_t), (M_v(X_s,t)) is again a s${\mathscr{H}}$rp (s${\mathscr{H}}$rm) which coincides with the solution of

$$ \dot{\mathbf{Z}}_{t} = \mathbf{Z}_{t} \star (M_{v} \dot{\mathbf{X}}_{t,t}), \qquad \mathbf{Z}_{0} = M_{v}\mathbf{X}_{0}. $$

(44)

The same result applies to good s${\mathscr{H}}$rms when $v\subset P({\mathscr{H}}^{\ast })$. Supposing also that for any $N\in \mathbb {N}$ there exists an integer L ≥ N depending on v such that $M_{v}\colon {\mathscr{H}}^{*N}\to {\mathscr{H}}^{*L}$, then for any N-s${\mathscr{H}}$rp Y the unique solution to

$$ \dot{\mathbf{W}}_{t} = \mathbf{W}_{t} \star_{L}(M_{v} \dot{\mathbf{Y}}_{t,t}), \qquad \mathbf{W}_{0} = \mathbf{1}^{\ast}, $$

defines a L-s${\mathscr{H}}$rm, given by $\mathbf {W}_{s,t} = \mathbf {W}_{s}^{-1}\otimes _{M} \mathbf {W}_{t}$, which we call ${\mathscr{M}}_{v}[\mathbf {Y}]$. Moreover, we have the explicit form

$$ \mathcal{M}_{v}[\mathbf{Y}]_{s,t} = {M_{v}^{L}} (\mathbf{Y}_{s,t}^{L}) = \pi_{L}{M}_{v}(\mathbf{X}_{s,t}) $$

(45)

with algebra endomorphism ${M_{v}^{L}} := \pi _{M} M_{v}\mathfrak {i}^{M}$ of $({\mathscr{H}}^{*M},\star _{M})$, using the (linear) embedding $\mathfrak {i}^{M}: {\mathscr{H}}^{*M}\to {\mathscr{H}}^{\prime }$, and $\mathbf {Y}^{M}={\mathscr{H}}\text {MinExt}^{M}(\mathbf {Y})$.

Proof

The theorem is then concluded by checking that M_vX and ${\mathscr{M}}_{v}[\mathbf {Y}]$ solves the equation (44) and (45) for any s${\mathscr{H}}$rp X and N-s${\mathscr{H}}$rp Y. This last check follows like in the proof of Theorem 2.24 by replacing ⊗ with ⋆. □

As direct application of Theorem 4.10, we present a characterisation of the renormalization of branched rough paths introduced in [6] when ${\mathscr{H}}=\mathcal {H}_{BCK}(\mathbb {R}^{d})$. In that case, the authors provided the existence a translation map $M_{v}\colon \mathfrak {T}_{d}\to \mathfrak {T}_{d}$ over the subspace $\mathcal {D}$ generated by the dual trees $\{\bullet _{i}^{\ast }\colon i=1,\ldots ,d\}$ by using a specific property of the Lie algebra $(\langle \mathfrak {T}_{d}\rangle , [ ,]_{\star })$, which we briefly sketch.

Recall that a (left) pre-Lie algebra is a vector space V equipped with a bilinear map $\curvearrowright :V\otimes V\to V$ whose associator

$$ (x,y,z)=(x\curvearrowright y)\curvearrowright z-x\curvearrowright (y\curvearrowright z) $$

is invariant under the exchange of the two variables y and z, see [44]. Given a pre-Lie algebra, one can construct a Lie bracket via its anti-symmetrisation

$$ [x,y]_{\curvearrowright}= (x\curvearrowright y) - (y\curvearrowright x). $$

It turns out that $\langle \mathfrak {T}_{d}\rangle$ admits an explicit pre-Lie algebra structure $\curvearrowright$ which as well as satisfying $[ ,]_{\curvearrowright }=[ ,]_{\star }$, also has the property that $(\langle \mathfrak {T}_{d}\rangle , \curvearrowright )$ is isomorphic to the free pre-Lie algebra over d elements, see [13].

Thanks to this property for any given family of tree series $v= (v_{1}, \ldots , v_{d} )\subset \mathfrak {T}^{\prime }_{d}$, it is then possible to fix a unique translation map $M_{v}\colon \langle \mathfrak {T^{\prime }}_{d}\rangle \to \langle \mathfrak {T^{\prime }}_{d}\rangle$ which satisfies

$$ M_{v}\bullet_{i}^{\ast}= \bullet_{i}^{\ast} + v_{i}, \quad M_{v}(x\curvearrowright y)= (M_{v}x)\curvearrowright (M_{v}y), $$

(46)

for any i = 1,…,d. It follows from the standard properties of the operation $\curvearrowright$ and the Grossmann-Larson product on the grading on trees |⋅| that for any given $v= (v_{1}, \ldots , v_{d} )\subset \mathfrak {T}_{d}$ M_v maps $\mathcal {H}^{*N}_{BCK}(\mathbb {R}^{d})$ to ${\mathscr{H}}^{*L}_{BCK}(\mathbb {R}^{d})$ where $L=N\cdot N^{\prime }$ with $N^{\prime }$ the smallest integer such that $|v_{i}|\leq N^{\prime }$ for any i = 1,…,d. From Theorem 4.10 we deduce the following corollary.

Corollary 4.11

Given a sbrp (sbrm) X and $v = (v_{1},\ldots , v_{d})\subset \mathfrak {T}^{\prime }_{d}$, the composition M_v(X_t) (M_v(X_s,t)) with M_v uniquely defined by (46) is again a sqgrp (sqgrm) which coincides with the solution of

$$ \dot{\mathbf{Z}}_{t} = \mathbf{Z}_{t} \otimes (M_{v} \dot{\mathbf{X}}_{t,t}), \qquad \mathbf{Z}_{0} = M_{v} \mathbf{X}_{0}. $$

(47)

The same result applies to good sqgrms when $v\subset \mathfrak {T}_{d}$. Under the same restriction on v, for any N-sbrm Y the path $t\to {\mathscr{M}}_{u}[\mathbf {Y}]_{0,t}$ is a L-sbrp coinciding with the solution of

$$ \dot{\mathbf{W}}_{t} = \mathbf{W}_{t}\otimes_{L} (M_{v} \dot{\mathbf{Y}}_{t,t}), \qquad \mathbf{W}_{0} = \mathbf{1}^{\ast}, $$

(48)

where $L\in \mathbb {N}$ is the smallest integer such that $|v_{i}|\leq N^{\prime }$ for any i = 1,…,d.

Remark 4.12

Conditions (46) identify uniquely a full translation map M_v whose explicit calculation on forest is not direct. In [6] the authors obtained a dual description of the dual map $M^{\ast }_{v}\colon {\mathscr{H}}_{BCK}(\mathbb {R}^{d})\to {\mathscr{H}}_{BCK}(\mathbb {R}^{d})$ using coalgebraic tools related to extraction and contraction of trees but an explicit expression of M_v is still unknown. Looking at (47), (48) we realize that in case of smooth branched rough paths it is sufficient to compute M_v only on trees, which should slightly simplify the computations. Moreover, when M_v coincides with the addition in (51), then we obtain an explicit equation which does not involve any coalgebraic tool.

Remark 4.13

Concerning the question of defining translation maps for more general Hopf algebras ${\mathscr{H}}$, the example of the free pre-Lie algebra points towards the general approach of using some ’free’ algebraic structure on the Lie algebra $P({\mathscr{H}}^{\ast })$, if it is available, to define the translation map as a universal homomorphism of the free object. Ideas to this regard were proposed in [51, Definition 5.2.1] and [52, Definition 8]. In the latter, this basic idea is also applied to the case of the free post-Lie algebra taking the role of $P({\mathscr{H}}^{\ast })$.

4.3 Canonical Sum and Minimal Coupling of Smooth Rough Paths

We pass now to the notion of sum in the generalised context of s${\mathscr{H}}$rms, extending Definition 2.15 to a generic Hopf algebra as before.

Definition 4.14

For any fixed s${\mathscr{H}}$rms $\mathbf {X}, \mathbf {Y}:[0,T]^{2}\to {\mathscr{H}}^{\prime }$ let $t\mapsto \mathbf {Z}_{t} \in {\mathscr{H}}^{\prime }$ be the Cartan development of $\dot {\mathbf {X}}_{s,s}+\dot {\mathbf {Y}}_{s,s}$, i.e. the unique solution to

$$ \dot{\mathbf{Z}}_{t}= \mathbf{Z}_{t}\star \left( \dot{\mathbf{X}}_{t,t}+\dot{\mathbf{Y}}_{t,t}\right), \quad \mathbf{Z}_{0} = \mathbf{1}^{\ast}. $$

We then write $\mathbf {Z} := \mathbf {X} \boxplus \mathbf {Y}$ for the associated sgrm and call it the canonical sum of X and Y. For any $\lambda \in \mathbb {R}$ we define also the sgrm $\mathbf {Z}=\lambda \boxdot \mathbf {X}$ via the Cartan development of $\lambda \dot {\mathbf {X}}_{s,s}$, we call it the canonical scalar multiplication.

Remark 4.15

This scalar multiplication yields a new scaling device for smooth rough paths which strongly differs from the well-known dilation δ_λ, where the latter is defined for any $x\in {\mathscr{H}}_{n}$ by $\langle \delta _{\lambda }\mathbf {X}_{s,t},x\rangle =\langle \mathbf {X}_{s,t},\lambda ^{n} x\rangle =\lambda ^{n}\langle \mathbf {X}_{s,t},x\rangle$. In contrast to the pointwise scaling δ_λ, this new scaling is a dynamical way to scale a smooth rough path. However, we observe that $(0\boxdot \mathbf {X})_{s,t}=\delta _{0}\mathbf {X}_{s,t}=\mathbf {1}^{\ast }$ and that $\overleftarrow {\mathbf {X}}$ (the backward⁴ rough path), δ_− 1X and $(-1)\boxdot \mathbf {X}$ are pairwise distinct. We expect this to have interesting applications to the theory of signatures of rough paths in the geometric setting.

From the vector space structure of the Lie algebra ${\mathfrak g}(\mathcal H)$, we easily deduce that the set of all smooth ${\mathscr{H}}$ rough models forms itself a vector space when equipped with the sum $\boxplus$ and the scalar multiplication $\boxdot$, with the set of all good smooth ${\mathscr{H}}$ rough models forming a subspace. In particular, for any real numbers λ₁, λ₂, λ we have

$$ \begin{array}{@{}rcl@{}} &\mathbf{X}\boxplus\mathbf{Y}=\mathbf{Y}\boxplus\mathbf{X},\quad\lambda\boxdot(\mathbf{X}\boxplus\mathbf{Y})=(\lambda\boxdot\mathbf{X})\boxplus(\lambda\boxdot\mathbf{Y}),&\\ &(\lambda_{1}+\lambda_{2})\boxdot\mathbf{X}=(\lambda_{1}\boxdot\mathbf{X})\boxplus(\lambda_{2}\boxdot\mathbf{X}).& \end{array} $$

This is very much in contrast to the spaces of γ-Hölder or bounded p-variation rough paths for γ ≤ 1/2 and p ≥ 2, where it is basic folklore by now that such a vector space structure does not exist in any meaningful sense.

It is then possible to characterise the sum $\boxplus$ via the group operation ⋆ up to some small remainder. The following theorem is an extension in a Hopf algebra and smooth case of [41, Section 3.3.1 B], which was stated in the context of geometric p-variation rough paths.

Proposition 4.16

For any fixed couple of s${\mathscr{H}}$rms X, Y a map $\mathbf {Z}\colon [0,T]^{2}\to G({\mathscr{H}})$ coincides with $\mathbf {X} \boxplus \mathbf {Y}$ if and only if Z satisfies Z_s,t = Z_s,u ⋆ Z_u,t for s,u,t ∈ [0,T] and one has for any s ∈ [0,T]

$$ \mathbf{Z}_{s,t}=\mathbf{X}_{s,t}\star \mathbf{Y}_{s,t}+R_{s,t}, $$

(49)

for some $R_{s,t}\in {\mathscr{H}}^{\prime }$ such that for all $x\in {\mathscr{H}}$ one has 〈R_s,t,x〉 = o(|t − s|) as t → s. Moreover, we have the relations

$$ \mathbf{X}_{s,t}\star\mathbf{Y}_{s,t} = \mathbf{Y}_{s,t}\star\mathbf{X}_{s,t}+r_{s,t} = \mathbf{X}_{s,t}+\mathbf{Y}_{s,t}-\mathbf{1}^{\ast}+r^{\prime}_{s,t}, $$

(50)

for some r_s,t, $r^{\prime }_{s,t} \in {\mathscr{H}}^{\prime }$ such that for all $x\in {\mathscr{H}}$ one has $\langle r_{s,t},x\rangle ,\langle r^{\prime }_{s,t},x\rangle = o(|t-s|)$ as t → s.

Proof

Let us start by formula (49). We fix $\mathbf {Z}:[0,T]^{2}\to G({\mathscr{H}})$ any map with Z_s,t = Z_s,u ⋆ Z_u,t and for all $x\in {\mathscr{H}}$ one has 〈Z_s,t −X_s,t ⋆ Y_s,t,x〉 = o(|t − s|). Then, by considering the path t →Z_0,t and fixing s ∈ [0,T], we use the continuity of the map ${\mathscr{H}}^{\prime }\ni \mathbf {x}\mapsto \mathbf {Z}_{0,s}\star \mathbf {x}$, for the weak convergence with respect to the duality pairing of ${\mathscr{H}}^{\prime }$ with ${\mathscr{H}}$ to have the equalities

$$ \begin{array}{@{}rcl@{}} \lim_{t\to s}\frac{\mathbf{Z}_{0,t}-\mathbf{Z}_{0,s}}{t-s}&=&\mathbf{Z}_{0,s}\star\lim_{t\to s}\frac{\mathbf{Z}_{s,t}-\mathbf{1}^{\ast}}{t-s} =\mathbf{Z}_{0,s}\star\lim_{t\to s}\frac{\mathbf{X}_{s,t}\star\mathbf{Y}_{s,t}-\mathbf{1}^{\ast}}{t-s}\\ &=&\mathbf{Z}_{0,s}\star\partial_{t}|_{t=s}(\mathbf{X}_{s,t}\star\mathbf{Y}_{s,t})=\mathbf{Z}_{0,s}\star(\dot{\mathbf{X}}_{s,s}+\dot{\mathbf{Y}}_{s,s}). \end{array} $$

Thus the path s↦Z_0,s is differentiable with derivative $s\mapsto \mathbf {Z}_{0,s}\star (\dot {\mathbf {X}}_{s,s}+\dot {\mathbf {Y}}_{s,s})$, implying $\dot {\mathbf {Z}}_{s,s}=\dot {\mathbf {X}}_{s,s}+\dot {\mathbf {Y}}_{s,s}$, i.e. $\mathbf {Z}=\mathbf {X}\boxplus \mathbf {Y}$. On the other hand, assuming that Z is given by $\mathbf {X}\boxplus \mathbf {Y}$, for all $x\in {\mathscr{H}}$ there are remainders $\theta ^{x}_{s,t}= o(|t-s|)$, ${\theta }^{\prime x}_{s,t}= o(|t-s|)$ such that

$$ \begin{array}{@{}rcl@{}} \langle\mathbf{Z}_{s,t},x\rangle&=&\langle\dot{\mathbf{Z}}_{s,s},x\rangle (t-s)+\theta^{x}_{s,t}\\ &=&\langle\dot{\mathbf{X}}_{s,s}+\dot{\mathbf{Y}}_{s,s},x\rangle (t-s)+\theta^{x}_{s,t}\\ &=&\langle\mathbf{X}_{s,t}+\mathbf{Y}_{s,t}- \mathbf{1}^{\ast},x\rangle+{\theta}^{\prime x}_{s,t}. \end{array} $$

Therefore the equivalence (49) will follow from equivalence (50). Recall that for X_s,t, Y_s,t in $G({\mathscr{H}})$ and x in ${\mathscr{H}}$, we have $\langle \mathbf {X}_{s,t}\star \mathbf {Y}_{s,t},x\rangle = \langle \mathbf {X}_{s,t} \hat {\otimes } \mathbf {Y}_{s,t},{\Delta } x\rangle$, where $\hat {\otimes }$ is the completed external tensor product, and furthermore 〈X_s,t,1〉 = 〈Y_s,t,1〉 = 1. Hence,

$$ \langle\mathbf{X}_{s,t}\star\mathbf{Y}_{s,t},\mathbf{1}\rangle = \langle\mathbf{Y}_{s,t}\star\mathbf{X}_{s,t},\mathbf{1}\rangle = \langle\mathbf{Y}_{s,t}+\mathbf{X}_{s,t}-\mathbf{1}^{\ast},\mathbf{1}\rangle = 1. $$

Furthermore, for every $x\in {\mathscr{H}}^{\geq 1}={\sum }_{n=1}^{\infty }{\mathscr{H}}_{n}$, i.e. 〈1^∗,x〉 = 0, we write ${\Delta } x=\mathbf {1}\otimes x+x\otimes \mathbf {1}+{\sum }_{i=1}^{n} y_{i}\otimes z_{i}$ for some n and $y_{i},z_{i}\in {\mathscr{H}}^{\geq 1}$, thereby obtaining

$$ \begin{array}{@{}rcl@{}} \langle\mathbf{X}_{s,t}\star\mathbf{Y}_{s,t},x\rangle &=& \langle \mathbf{X}_{s,t} \hat{\otimes} \mathbf{Y}_{s,t},{\Delta} x\rangle = \langle\mathbf{X}_{s,t},x\rangle+\langle\mathbf{Y}_{s,t},x\rangle+{\sum}_{i=1}^{n}\langle\mathbf{X}_{s,t},y_{i}\rangle\langle\mathbf{Y}_{s,t},z_{i}\rangle\\ &=&\langle\mathbf{X}_{s,t}+\mathbf{Y}_{s,t}-\mathbf{1}^{\ast},x\rangle +\underbrace{{\sum}_{i=1}^{n}\langle\mathbf{X}_{s,t},y_{i}\rangle\langle\mathbf{Y}_{s,t},z_{i}\rangle}_{o(|t-s|)}. \end{array} $$

The fact that this last term is of order o(|t − s|) follows from the smoothness of X and Y and 〈X_t,t,y_i〉 = 〈Y_t,t,z_i〉 = 0, which for any index i, actually yields the existence of a constant C_i > 0 such that |〈X_s,t,y_i〉〈Y_s,t,z_i〉|≤ C_i(t − s)² for all t,s ∈ [0,T]. Similarly, one shows that $\langle \mathbf {Y}_{s,t}\star \mathbf {X}_{s,t}-\mathbf {X}_{s,t}-\mathbf {Y}_{s,t}+\mathbf {1}^{\ast },x\rangle = o(|t-s|)$. □

Remark 4.17

As pointed out in Remark 2.17 with reference to [41, Section 3.3.1 B] for smooth geometric rough paths, we strongly conjecture that one can add the minimal extension of a N-s${\mathscr{H}}$rm X to any general γ-Hölder ${\mathscr{H}}$ rough path W for any γ ∈ (0,1), via the requirement $\langle (\mathbf {X}\boxplus \mathbf {W})_{s,t},x\rangle =\langle \mathbf {X}_{s,t}\star \mathbf {W}_{s,t},x\rangle +o(|t-s|)$ using the sewing lemma.

The canonical sum can now be used to define a minimal coupling of smooth rough paths in the situation where we have connected graded commutative Hopf algebras $(\mathfrak {H}^{i})_{i=1,\dots ,m}$ of the form

$$ \mathfrak{H}^{i}= \underset{j=0}{\overset{\infty}{\bigoplus}} \mathfrak{H}_{j}^{i} $$

together with embeddings $\iota _{i}:(\mathfrak {H}^{i})^{\ast }\to ({\mathscr{H}})^{\ast }$ which are injective graded Hopf algebra homomorphisms, such that the sum of the non-unital parts (the kernels of the counit of ${\mathscr{H}}^{\ast }$) of the images $\hat {\mathfrak {H}}^{i}:=\iota _{i}(\mathfrak {H}^{i})^{\ast }$ and $\hat {\mathfrak {H}}^{i}_{j}:=\iota _{i}(\mathfrak {H}^{i})^{\ast }_{j}$ inside ${\mathscr{H}}^{\ast }$ forms a direct product, i.e.

$$ {\sum}_{i=1}^{m} \hat{\mathfrak{H}}^{i,\geq 1}=\underset{i=1}{\overset{m}{\bigoplus}} \hat{\mathfrak{H}}^{i,\geq 1}, $$

where $\hat {\mathfrak {H}}^{i,\geq 1}:={\bigoplus }_{j=1}^{\infty } \hat {\mathfrak {H}}_{j}^{i}=\{x\in \hat {\mathfrak {H}}^{i}\colon \langle x,\mathbf {1}\rangle =0\}$, and such that the first level of ${\mathscr{H}}^{\ast }=\oplus _{n=0}^{\infty } {\mathscr{H}}^{\ast }_{n}$ is actually spanned by the first levels of the $\hat {\mathfrak {H}}^{i}$, i.e.

$$ \mathcal{H}^{\ast}_{1}=\underset{i=1}{\overset{m}{\bigoplus}} \hat{\mathfrak{H}}^{i}_{1}. $$

Any s$\mathfrak {H}^{i}$rp $\mathbf {X}^{i}:[0,T]\to G(\mathfrak {H}^{i})$ is trivially mapped via the embedding ι_i and extended by continuity inside ${\mathscr{H}}^{\prime }$ to a s${\mathscr{H}}$rp $\iota _{i} \mathbf {X}^{i}:[0,T]\to G({\mathscr{H}})$. We define then the minimal coupling of the Xⁱ as

$$ (\mathbf{X}^{1},\dots,\mathbf{X}^{m})_{\min}:=\iota_{1} \mathbf{X}^{1}\boxplus\cdots\boxplus \iota_{m}\mathbf{X}^{m}. $$

As a special case, we consider two connected graded commutative Hopf algebras $\mathfrak {H}^{0}$, $\mathfrak {H}^{1}$ with embedded graded dual spaces $\hat {\mathfrak {H}}^{0}=\iota _{0}(\mathfrak {H}^{0})^{\ast }$, $\hat {\mathfrak {H}}^{1}=\iota _{1}(\mathfrak {H}^{1})^{\ast }$ such that

$$ \hat{\mathfrak{H}}^{0,\geq 1}+\hat{\mathfrak{H}}^{1,\geq 1}=\hat{\mathfrak{H}}^{0,\geq 1}\oplus\hat{\mathfrak{H}}^{1,\geq 1}, \quad \mathcal{H}_{1}^{\ast}=\hat{\mathfrak{H}}^{0}_{1}\oplus\hat{\mathfrak{H}}^{1}_{1}. $$

By taking $\hat {\mathfrak {H}}^{0}$ the unital subalgebra generated by just a single element $x_{0}\in ({\mathscr{H}})^{\ast }_{1}$ (which is automatically a graded sub Hopf algebra of ${\mathscr{H}}^{\ast }$), the only smooth rough models $\mathbf {X}^{0}:[0,T]\to G(\mathfrak {H}^{0})$ are of the form

$$ \iota_{0}\dot{\mathbf{X}}^{0}_{s,s}=\psi(s)x_{0} $$

for some smooth $\psi \colon [0,T]\to \mathbb {R}$. Then one easily checks that

$$ \iota_{0}\mathbf{X}^{0}_{s,t}=\exp_{\star}\left( \left( {{\int}_{s}^{t}}\psi(u)du\right) x_{0}\right). $$

By taking ψ = 1, we find that for any s$\mathfrak {H}^{1}$rp $\mathbf {X}^{1}:[0,T]\to G(\mathfrak {H}^{1})$ the minimal coupling ${\bar {\mathbf {X}}}:=(\mathbf {X}^{0},\mathbf {X}^{1})_{\min \limits }$ is uniquely determined by

$$ \dot{\bar{\mathbf{X}}}_{s,s}=x_{0}+\dot{\mathbf{X}}^{1}_{s,s}. $$

In this situation, we can directly reinterpret $\bar {\mathbf {X}}$ as a specific type of full translation.

Corollary 4.18

Let X¹ be a good s${\mathscr{H}}$rm, $v_{0}\in \mathfrak {g}({\mathscr{H}})$ and $M_{v_{0}}\colon {\mathscr{H}}^{\ast }\to {\mathscr{H}}^{\ast }$ a full translation map such that $M_{v_{0}}x_{0}=x_{0}+v_{0}$ and $M_{v_{0}}$ restricted to $\iota _{1}(\mathfrak {H}^{1})^{\ast }$ is the identity. Then the translation $t\mapsto M_{v_{0}}\bar {\mathbf {X}}_{0,t}$ can be described as the sum $\mathbf {V}_{0}\boxplus \bar {\mathbf {X}}$, where V₀ is given by

$$ (\mathbf{V}_{0})_{s,t}=\exp_{\star}(v_{0}(t-s)). $$

Proof

We obviously have

$$ \partial_{t}|_{t=s}(M_{v_{0}}{\bar{\mathbf{X}}}_{s,t}) = M_{v_{0}}\dot{\bar{\mathbf{X}}}_{s,s} = x_{0} + v_{0} + \dot{\mathbf{X}}^{1}_{s,s}=v_{0}+\dot{\bar{\mathbf{X}}}_{s,s}, $$

(51)

which shows $M_{v_{0}}{\bar {\mathbf {X}}}=\mathbf {V}_{0}\boxplus \bar {\mathbf {X}}$. □

Remark 4.19

In this general connected graded commutative Hopf algebra setting, we once again recover a property similar to the final statement of [6, Theorem 30 (ii)]: the s${\mathscr{H}}$rp $M_{v_{0}}{\bar {\mathbf {X}}}_{t}$ does not depend on the precise choice of the Hopf algebra homomorphism $M_{v_{0}}$, as long as $M_{v_{0}} x_{0}=x_{0}+v_{0}$, $M_{v_{0}}|_{\hat {\mathfrak {H}}^{1}}=\text {id}$.