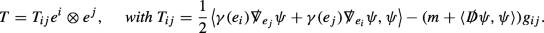A Spin-Perturbation for Minimal Surfaces

Abstract

We investigate the coupling of the minimal surface equation with a spinor of harmonic type. This arises as the Euler–Lagrange equations of the sum of the volume functional and the Dirac action, defined on an appropriated Dirac bundle. The solutions show a relation to Dirac-harmonic maps under some constraints on the energy-momentum tensor, extending the relation between Riemannian minimal surface and harmonic maps.

1 Introduction

Among many interesting and rich structures of the Dirac-harmonic maps introduced in [4], we are interested in those with special domain metrics. The properties of the domain metrics can be reflected by the energy-momentum tensor of the corresponding Lagrangian. Here we will see that, in special cases, the Dirac-harmonic maps admit another geometric interpretation, which is similar to minimal surface and will be called SP-minimal surfaces. This is the object we are going to study.

As a motivation, recall that the energy-momentum tensor for the Dirichlet energy along a harmonic map u: M → N from a Riemann surface M gives rise to a holomorphic quadratic differential over M, which represents a cotangent vector in the Teichmüller space of M [11, 22]. In particular, when the metric is critical with respect to variations, the energy-momentum tensor vanishes and the map u is weakly conformal (“weakly” means it can admit ramifications). But for a weakly conformal map u from a Riemann surface, it is a harmonic map iff it is a branched minimal immersion. This key observation provides an effective way to obtain minimal surfaces via harmonic maps, see e.g. [8, 21].

The supersymmetric nonlinear sigma model gives rise to the fermionic analogue of the harmonic maps, namely we couple a map u: M → (N, h) with a spinor field ψ along it and consider the action

where g is a fixed Riemannian metric on is the canonical Dirac operator defined for such spinors. The critical points of this action functional are known as Dirac-harmonic maps. They are reduced to harmonic maps if the spinor field ψ is turned off. The energy-momentum tensor of this functional is given by a symmetric 2-tensor $\mathcal {T}=\mathcal {T}_{ij} e^{i}\otimes e^{j}$ where (eⁱ) is a local orthonormal coframe and

(1)

See [4] for more details.

Now it is natural to wonder to what the solutions would be reduced if the associated energy-momentum tensor of the Dirac-harmonic functional vanishes. This leads us to consider a perturbation of the volume functional of an immersion $u\colon M^{m}\to (\overline {M},\overline {g})$ by a Dirac action:

(2)

where ψ is a spinor along the map u, see Section 2. The critical points, which we might call “Dirac-minimal surfaces” at first glance, would be a good candidate. But we will save the name until it is formally judged; rather, let us be modest and call it a spin-perturbed minimal surface, or SP-minimal surface. The technical problem was the dependence of the spinor bundles on the pull-back metrics, but this can be handled with the well-known Bourguignon–Gauduchon approach [3, 13]. We will see that there do exist relations between the SP-minimal surfaces and the Dirac-harmonic maps similar to that between minimal surfaces and harmonic maps, provided that the energy-momentum tensor satisfies certain constraints. The vanishing of the energy-momentum tensor is sufficient but more than necessary. More precisely, our main result is the following

Theorem 1.1

Let $u\colon M^{m}\to (\overline {M},\overline {g})$ be an isometric immersion from a Riemannian spin manifold and $\psi \in {{\varGamma }}({{\varSigma }}_{g} M\otimes u^{\ast } T\overline {M})$. Let $\mathcal {T}(u,\psi )$ be the energy-momentum tensor (1) for the Dirac-harmonic map functional.

• 1. Suppose $\mathcal {T}=(2-m) g$. Then (u, ψ) is a Dirac-harmonic map iff $(u,\sqrt {m/2}\psi )$ is an SP-minimal surface.

• 2. More generally, if $-\mathbb {I}(T)=2\sigma \textup {\textbf {H}}$ for some σ ≥ 0, then (u, ψ) is a Dirac-harmonic map iff $(u,\sqrt {\sigma }\psi )$ is an SP-minimal surface, where $\mathbb {I}$ (resp. H) are the second fundamental form (resp. mean curvature vector of the immersion), and T is the energy-momentum tensor for (2) given by

  

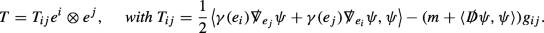
  Here (e_i) is a local orthonormal frame and (eⁱ) is the dual coframe.

Note that in dimension two we may relax u to be a conformal immersion, since the Dirac-harmonic functional is conformally invariant. Furthermore, the energy-momentum tensor for the Dirac-harmonic functional gives rise to a holomorphic quadratic differential along Dirac harmonic maps [4] in dimension two. However for a general supersymmetric nonlinear sigma model [5, 9, 17] and for the Riemannian versions (e.g. a nonlinear sigma model with gravitino as in [12,13,14]), there are only conservation laws weaker than being holomorphic, except in some special cases as e.g. [16]. In this sense, the above generalized conditions for the energy-momentum tensor may be useful in understanding the associated quadratic differentials.

As another motivation, the volume of a super Riemann surface is not fully understood. The critical point there might be more appropriate to be called a Dirac-minimal surface. Note that the area or volume functional corresponds to the simplest Nambu–Goto invariant action in bosonic string theory [20]. The equation that we are going to study may only be a Riemannian simplification of the physics-relevant one. It is anyway interesting and heuristic to study our spin-perturbed area functional if we defend ourselves by the commuting and anti-commuting variables argument, which is well-known in the community. The main point here is to search for a reasonable geometric description of the Dirac-harmonic maps which may give rise to a moduli-type theory.

The paper is organized as follows. First we introduce the spin-perturbed volume functional whose critical points are the SP-minimal surfaces. Then we investigate the relations of such surfaces with Dirac-harmonic maps. In the end we also discuss some known examples.

When I was a student in Jürgen’s group, he brought up the topic of supersymmetric variational problems. I had this question from him during the project on the nonlinear sigma models with gravitinos. This note is dedicated to him as a partial answer. I would like to take this chance to thank him for his constantly inspiring and encouraging discussions during the last years.

2 The Spin-perturbed Volume Functional

In this section we introduce the spin-perturbed volume functional and calculate the Euler–Lagrange equations for its critical points. Before turning to the perturbed case, we recall some basics of minimal surfaces in order to fix the notation. The spin-perturbed action functional shows some similarities to the Dirac-harmonic map functional, but note that the metric on M varies along with the variation of the immersions, while in the harmonic maps and Dirac-harmonic maps setting the domain metrics are fixed. This difference has to be handled by introducing contractions of the energy-momentum tensor, as explained in the sequel.

2.1 Review of the Minimal Surface Equation

Here, we recall the first variation of the volume functional for an immersion and the variational field of the Riemannian metric.

Let $(\overline {M}^{m+m^{\prime }},\overline {g})$ be a Riemannian manifold and $u\colon M^{m}\to \overline {M}$ an immersion of codimension $m^{\prime }\ge 1$. With respect to the pull-back metric $g\equiv u^{\ast }\overline {g}$, the map u is then an isometric immersion. The volume (or area) of (M, g) is

$$ \mathcal{A}(u):={\int}_{M}\text{dvol}_{g}. $$

Consider a smooth variation (u_t) of u = u₀, with variational field

$$ V:= \frac{\partial u_{t}}{\partial t}\Big|_{t=0}\in {{\varGamma}}(u^{\ast} T\overline{M}). $$

Assume that for each t ∈ (−ε, ε), the map u_t is a smooth immersion. This gives rise to a smooth variation $g(t)\equiv u_{t}^{\ast }\overline {g}$ of the metric g = g(0).

Let $(e_{1},\dotsc , e_{m},e_{m+1},\dotsc , e_{m+m^{\prime }})$ be an oriented $\overline {g}$-orthonormal frame in a local neighborhood $U\subset \overline {M}$ such that e_i, 1 ≤ i ≤ m are tangential to u₀(M) and e_α, $m+1\le \alpha \le m+m^{\prime }$ are normal to u₀(M). We may further assume that the tangent frame $(e_{1},\dotsc , e_{m})$ is geodesic at x₀ = u₀(x₀) ∈ M≅u₀(M) with respect to $g=u_{0}^{\ast }\overline {g}$. Denoting the Levi-Civita connection of g by ∇, and that of $\overline {g}$ by $\overline {\nabla }$, then

$$ \nabla_{e_{i}} e_{j}(x_{0})=\left( \overline{\nabla}_{e_{i}} e_{j}\right)^{\top}(x_{0})=0. $$

This is equivalent to that the Christoffel symbols of $\overline {g}$ with tangential indices vanish: ${{\varGamma }}^{i}_{jk}(x_{0})=0$. Similarly, we may assume that the normal frame $(e_{m+1},\dotsc , e_{m+m^{\prime }})$ is chosen such that

$$ \left( \overline{\nabla}_{e_{i}} e_{\alpha}\right)^{\bot}(x_{0})=0, \qquad \text{ or equivalently: } \quad {{\varGamma}}^{\beta}_{i\alpha}(x_{0})=0. $$

We will use the Einstein summation convention wherever there is no confusion: any index appearing twice (not necessarily in upper and lower positions) is meant to be summed.

With respect to this frame,

$$ g(t)_{ij}=\left( u_{t}^{\ast} \overline{g}\right)_{ij}(x) = \overline{g}_{u_{t}(x)}\left( \mathrm{d} u_{t}(e_{i}),\mathrm{d} u_{t}(e_{j})\right) $$

and the linearization of the metric is

$$ \begin{array}{@{}rcl@{}} \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} g(t)_{ij}(x) &=& \frac{\partial\overline{g}_{u_{t}(x)}}{\partial t}(e_{i},e_{j})\Big|_{t=0} + \overline{g}_{u(x)}\left( \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0}\mathrm{d} u_{t}(e_{i}), \mathrm{d} u_{t}(e_{j})\right) \\ &&+\overline{g}_{u(x)}\left( \mathrm{d} u_{t}(e_{i}),\frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} \mathrm{d} u_{t}(e_{j})\right), \end{array} $$

which is a symmetric 2-tensor. Since $\overline {g}$ is $\overline {\nabla }$-parallel, we have

$$ \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} g(t)_{ij}(x) = \overline{g}_{p}(\overline{\nabla}_{e_{i}}V, e_{j}) + \overline{g}_{p}(e_{i},\overline{\nabla}_{e_{j}}V), $$

where we have used [e_i,V ] = [du_t(e_i),du_t(∂_t)] = 0 and hence $\overline {\nabla }_{V} e_{i}=\overline {\nabla }_{e_{i}} V$. Write V = V^le_l + V^αe_α = V^⊤ + V^⊥, then at x₀,

$$ \overline{\nabla}_{e_{i}} V = e_{i}(V^{l}) e_{l} + V^{l}\overline{\nabla}_{e_{i}} e_{l} + e_{i}(V^{\alpha}) e_{\alpha}+V^{\alpha}\overline{\nabla}_{e_{i}} e_{\alpha}. $$

Thus

$$ \begin{array}{@{}rcl@{}} \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} g(t)_{ij}(x) &=& e_{i}(V^{j})+V^{l}\left<\overline{\nabla}_{e_{i}}e_{l}, e_{j}\right> + V^{\alpha}\left<\overline{\nabla}_{e_{i}}e_{\alpha}, e_{j}\right> \\ && +e_{j}(V^{i})+V^{l}\left<\overline{\nabla}_{e_{j}}e_{l}, e_{i}\right> + V^{\alpha}\left<\overline{\nabla}_{e_{j}}e_{\alpha}, e_{i}\right> \\ &=&\left( e_{i}(V^{j})+e_{j}(V^{i})\right) - 2V^{\alpha} \mathbb{I}^{\alpha}_{ij} \equiv k_{ij}, \end{array} $$

where $\mathbb {I}^{\alpha }_{ij}$ are the coefficients of the second fundamental form $\mathbb {I}$:

$$ \mathbb{I}^{\alpha}_{ij} = \left<\overline{\nabla}_{e_{i}}e_{j},e_{\alpha}\right>, \quad 1\le i,j\le m, \quad m+1\le \alpha\le m+m^{\prime}. $$

Thus the variational field of g(t) is given by $k=k_{ij}e^{i}\otimes e^{j}\in \text {Sym}^{2}(T^{\ast } M)$ with

$$ k_{ij}=e_{i}(V^{j})+e_{j}(V^{i})-2V^{\alpha} \mathbb{I}^{\alpha}_{ij}, \qquad 1\le i,j\le m. $$

Let $\textbf {H}:= \text {tr}(\mathbb {I})$ be the mean curvature vector.¹ It follows that

$$ \text{tr}(\dot{g}(0))\equiv \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} g(t)_{ii}(x) = 2\text{div}_{g}(V^{\top})-2\langle V^{\bot},\textbf{H}\rangle. $$

Now let (eⁱ) be the dual frame for the cotangent bundle of M. The volume form for the metric g(t) can be locally expressed as

$$ \text{dvol}_{g(t)} = \sqrt{\det(g(t))}e^{1}\wedge {\cdots} \wedge e^{m}. $$

Recall that

$$ \begin{array}{@{}rcl@{}} \frac{\mathrm{d}}{\mathrm{d} t}\sqrt{\det(g(t))} &=&\frac{1}{2}\frac{1}{\sqrt{\det(g(t))}} \frac{\mathrm{d}}{\mathrm{d} t}\det(g(t)) =\frac{1}{2}\frac{1}{\sqrt{\det(g(t))}} \det(g(t))\text{tr}\left( g(t)^{-1}\frac{\mathrm{d}}{\mathrm{d} t}g(t)\right) \\ &=& \frac{1}{2}\sqrt{\det(g(t))} \text{tr}\left( g(t)^{-1}\frac{\mathrm{d}}{\mathrm{d} t}g(t)\right). \end{array} $$

At t = 0, we have g(0)_ij = δ_ij, hence

$$ \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0}\sqrt{\det(g(t))} = \frac{1}{2}\text{tr}(\dot{g}(0)) = \text{div}_{g}(V^{\top})-\left<V^{\bot},\textbf{H}\right>. $$

Therefore, the first variation formula for the volume functional is given by

$$ \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} \mathcal{A}(u_{t}) = {\int}_{M} -\left<V^{\bot},\textbf{H}\right> + \text{div}_{g}(V^{\top})\text{dvol}_{g}. $$

In the case where M is either closed or complete and V has compact support, then

$$ \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} \mathcal{A}(u_{t}) = {\int}_{M} -\left<V^{\bot},\textbf{H}\right>\text{dvol}_{g}. $$

Therefore u is a critical point of $\mathcal {A}$ iff H = 0, i.e. u is minimal.

2.2 Spin-perturbation of the Volume Functional

Now we are going to consider the coupling with a spinor field. From now on assume that (M, g) is spin, with a fixed spin structure and with associated spinor bundle Σ_gM, where $g=u^{\ast }\overline {g}$. It has a canonical spin connection ∇^s = ∇^ΣM and a Riemannian inner product g^s, together with a compatible Clifford map γ: TM →End(Σ_gM) which satisfies the following Clifford relation

$$ \gamma(X)\gamma(Y)+\gamma(Y)\gamma(X)=-2g(X,Y)\text{Id}, \qquad \forall X,Y\in{{\varGamma}}(TM). $$

Then the spin Dirac operator is canonically defined as for any spinor φ ∈Γ(Σ_gM). For more material on spin geometry we refer to [7, 10, 18].

For the family of metrics g(t), the associated spinor bundles are isomorphic, and there are isometries

$$ b_{t}\colon (TM, g(0)) \to (TM, g(t)) \qquad \text{ and } \qquad \beta_{t}\colon {{\varSigma}}_{g(0)}M\to {{\varSigma}}_{g(t)}M $$

with respect to the corresponding inner products on the bundles [13, 23] and

$$ \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0}b_{t}=-\frac{1}{2}K\in \text{End}(TM), $$

where k is the variational field of the metric and K the associated endomorphism on TM. Moreover, pulling back the spin Dirac operator via the above isometry β_t, we obtain a differential operator

The linearization of was computed in [3, Theorem 21] (see also [19, Section 2])

(3)

where the divergence div_g on symmetric 2-tensors is as in [13, 22] and ♯: T^∗M → TM denotes the musical isomorphism.

Given an isometric immersion $u\colon M\to \overline {M}$, consider the bundle²${{\varSigma }}_{g} M\otimes u^{\ast } T\overline {M}$. The connection, inner product and Clifford multiplication are naturally extended on this product bundle, denoted by and³γ respectively. Thus it becomes a Dirac bundle in the sense of [18, Def. 5.2] and we have as well the Dirac operator

which is a formally self-adjoint, first order elliptic differential operator. In terms of the local orthonormal frame (e_a), we can write a spinor $\psi \in {{\varGamma }}({{\varSigma }}_{g} M\otimes u^{\ast } T\overline {M})$ as

$$ \psi=\psi^{a}\otimes e_{a}=\psi^{i}\otimes e_{i} + \psi^{\alpha}\otimes e_{\alpha}, $$

(4)

where the index a runs through 1 to $m+m^{\prime }$. Then the Dirac operator acts as

(5)

or, in terms of the tangent and normal frames,

The spin-perturbation of the volume functional that we are going to consider has the form

(6)

Here $m=\dim M$ and if u is an isometric immersion then |du|² = m. In contrast to the Dirac-harmonic map functional in [4], there is no conformal symmetry for $\mathcal {A}_{S}$, because of the presence of the Riemannian volume part. Nevertheless it is invariant under diffeomorphisms: for f ∈Diff(M) which preserves the orientation and the spin structure, we have

$$ \mathcal{A}_{S}(f^{\ast} u, f^{\ast}\psi)=\mathcal{A}_{S}(u,\psi). $$

(7)

2.3 The Variation Formulas

Here, we derive the Euler–Lagrange equations for (6). The calculation is similar to that in [12]. We remark that there is an alternative method adopted in [2] which gives another viewpoint of such problems.

Let (u, ψ) be a critical point and let (u_t,ψ_t)_−ε<t<ε be a variation of (u, ψ), where u₀ = u, ψ₀ = ψ, and for each t ∈ (−ε, ε), u_t is an immersion, and $\psi _{t}\in {{\varGamma }}({{\varSigma }}_{g(t)}M\otimes u_{t}^{\ast } T\overline {M})$. As we have seen the variation of the volume of (M, g(t)), it remains to compute the variation of the Dirac action:

We need to compute the first term in the RHS. Note that e_i(t) = b_t(e_i) are g(t)-orthonormal, and the b_t can be extended to the normal bundle such that e_α(t) = b_t(e_α) form an orthonormal frame along u_t for the normal bundle. Also note that γ_t(b_t(e_i)) can be taken to be t-independent. In terms of (4) and (5), noting that (e_a(t)) are orthonormal, we have

Writing $\beta _{t}^{-1}{\psi _{t}^{a}}\equiv {\phi _{t}^{a}}$, the variational field of ψ is given by

$$ \eta:= \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0}{\phi_{t}^{a}}\otimes e_{a}(t) \in {{\varGamma}}({{\varSigma}}_{g} M\otimes u^{\ast} T\overline{M}). $$

Then we take the t-derivatives at t = 0:

For the first term, we use (3) and the skewness of the Clifford multiplication to get

Viewing the t-derivatives as a covariant derivative on the product manifold $\mathbb {R}\times \overline {M}$ whose connection will still be denoted by $\overline {\nabla }$ (see e.g. [12] and also compare with [2]), we have

$$ \partial_{t}\overline{\nabla}_{e_{i}(t)}e_{a}(t) = \overline{R}(\mathrm{d} u_{t}(\partial_{t}),e_{i}(t)) e_{a}(t) + \overline{\nabla}_{e_{i}(t)}\left( \overline{\nabla}_{\partial_{t}}e_{a}(t)\right) + \overline{\nabla}_{[\partial_{t},e_{i}(t)]} e_{a}(t). $$

At t = 0, this is

$$ \left( \partial_{t}\overline{\nabla}_{e_{i}(t)}e_{a}(t)\right)_{t=0} = \overline{R}(V, e_{i})e_{a} + \overline{\nabla}_{e_{i}(t)}\left( \overline{\nabla}_{\partial_{t}}e_{a}(t)\right)_{t=0} - \frac{1}{2}\overline{\nabla}_{K(e_{i})} e_{a}. $$

Note that

$$ 0=\frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0}\delta_{ab} = \left<\frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0} e_{a}(t), e_{b}\right> + \left<e_{a}, \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0}e_{b}\right>. $$

Plugging these into the t-derivative of and evaluating at t = 0, we get

where we have used the abbreviation

$$ \mathscr{R}\equiv \langle\psi^{a},\gamma(e_{i})\psi^{b}\rangle\overline{R}(e_{a}, e_{b})e_{i} $$

so that

$$ \langle\gamma(e_{i})\psi^{a},\psi^{b}\rangle\langle\overline{R}(V,e_{i})e_{a}, e_{b}\rangle = \langle\mathscr{R}, V\rangle. $$

Define a symmetric 2-tensor $T=T_{ij}e^{i}\otimes e^{j}\in \text {Sym}^{2}(T^{\ast } M)$ by

(8)

This is the energy-momentum tensor for the functional (6). Then

Therefore,

where denotes the contraction of T and $\mathbb {I}$.

To summarize, we have

Proposition 2.1

(First variation formula) For a smooth variation (u_t,ψ_t) of (u, ψ) with variational field (V, η), where each u_t is an immersion, the first variation formula for the functional $\mathcal {A}_{S}$ is

Corollary 2.2

If M is a closed manifold, then

In case M is complete and non-compact, if the variational field (V, η) is compactly supported, the above formula still holds.

Some comments are in order. The above first variation formulas tell us that for a critical point (u, ψ), it is necessary that namely ψ is a harmonic spinor along the immersion u. The symmetric tensor T in (8) is the energy-momentum tensor for the functional $\mathcal {A}_{S}$ in the following sense: given (u, ψ) where u is an immersion, $g=u^{\ast }\bar {g}$, and given an arbitrary smooth symmetric 2-tensor h, let g(t) = g + th and b_t,β_t as before, then

$$ \frac{\mathrm{d}}{\mathrm{d} t}\Big|_{t=0}\mathcal{A}_{S}(u,(\beta_{t}\otimes b_{t})\psi;g(t)) = {\int}_{M}-\frac{1}{2}\langle h,T\rangle\text{dvol}_{g}. $$

In particular, the diffeomorphism invariance (7) implies that

$$ \text{div}_{g}(T)=0. $$

Now suppose V^⊤ has compact support in the interior of M such that it generates a local one-parameter flow, then the diffeomorphism invariance (7) together with Corollary 2.2 (where V^⊥ = 0 and η = 0) implies that

$$ 0={\int}_{M} \langle\mathscr{R}+\text{div}_{g}(T)_{\sharp}, V^{\top}\rangle \text{dvol}_{g}. $$

By decomposing the vector ${\mathscr{R}}$ into the tangent and normal components, i.e. ${\mathscr{R}}={\mathscr{R}}^{\top }+{\mathscr{R}}^{\bot }$, we have

$$ \langle\mathscr{R},V\rangle = \langle\mathscr{R}^{\top}, V^{\top}\rangle + \langle\mathscr{R}^{\bot}, V^{\bot}\rangle. $$

Since V^⊤∈Γ(TM) can be arbitrary, we conclude that there always holds

$$ \mathscr{R}^{\top}=-\text{div}_{g}(T)_{\sharp}=0\qquad \text{ and hence } \quad \mathscr{R}=\mathscr{R}^{\bot}. $$

Corollary 2.3

The variation formula for $\mathcal {A}_{S}$ on closed manifolds, or on complete manifolds with compact supported variations, has the form

Proposition 2.4

The Euler–Lagrange equations for the functional $\mathcal {A}_{S}$ are⁴

(9)

Solutions of (9) will be called a SP-minimal surface. Note that since ψ is harmonic, we have

The regularity theory for minimal surface operator (e.g. [6]) and for Dirac operator (e.g. [12]) can be applied to the system (9), and we expect that if M is a surface and u is an immersion of class W^1,2 while ψ is of class $H^{\frac {1}{2}}$, then the solution (u, ψ) is smooth. But the regularity theory is not our concern here. We will assume the solutions under consideration are smooth in the sequel, at least in lower dimensions.

3 Relation to Dirac-harmonic Maps

A C²-map $u\colon (M,g)\to (\overline {M},\overline {g})$ (not necessarily an immersion) is called harmonic if it is a critical point of the Dirichlet energy functional

$$ E(u)=\frac{1}{2}{\int}_{M} |\mathrm{d} u|^{2} \text{dvol}_{g}. $$

Let τ(u) = tr(∇du) be the tension field of u, then the harmonic map equation is τ(u) = 0. Note that for an isometric immersion $u\colon M\to \overline {M}$, the tension field is the same as the mean curvature vector: τ(u) = H.

A pair (u, ψ), where $u\colon (M,g)\to (\overline {M},\overline {g})$ is a C² map and $\psi \in {{\varGamma }}({{\varSigma }} M\otimes u^{\ast } T\overline {M})$, is called a Dirac-harmonic map if it is a critical point of

The metric g on the domain manifold is fixed. The Euler–Lagrange equations are

(10)

where $\mathcal {R}\equiv \mathcal {R}(u,\psi )$ is defined in the same way as ${\mathscr{R}}$ in the previous section; namely, with respect to a local frame (𝜖_a) of $T\overline {M}$, we can write ψ = ψ^a ⊗ 𝜖_a, and then with respect to a local orthonormal frame (e_i) of (M, g),

$$ \mathcal{R}(u,\psi):= \langle\psi^{a},\gamma(e_{i})\psi^{b}\rangle\overline{R}(\epsilon_{a},\epsilon_{b})\mathrm{d} u(e_{i}), $$

see [4] for more details. The energy-momentum tensor $\mathcal {T}=\mathcal {T}_{ij}e^{i}\otimes e^{j}$ for ${\mathscr{L}}_{D}$ is given by

The question of interest is: suppose (u, ψ) is a Dirac harmonic map, i.e. it solves (10), and suppose that the energy-momentum tensor vanishes $\mathcal {T}(u,\psi )=0$, what would the geometry specialized by (u, ψ) be?

As said, if u is a harmonic map from a Riemannian surface (so $m=\dim M=2$) with vanishing energy-momentum tensor, then u is weakly conformal and hence a branched minimal immersion. However, in the Dirac-harmonic map case, the vanishing of the energy-momentum tensor $\mathcal {T}$ does not guarantee that u is a branched immersion. This prevents further investigation. But if we restrict ourselves to considering those which are immersions, we have the following

Theorem 3.1

Let $u\colon (M^{2},g)\to (\overline {M},\overline {g})$ be a smooth isometric immersion from a surface M and $\psi \in {{\varGamma }}({{\varSigma }}_{g} M\otimes u^{\ast } T\overline {M})$. Suppose $\mathcal {T}(u,\psi )=0$. Then (u, ψ) is a Dirac-harmonic map iff (u, ψ) is an SP-minimal surface.

Proof

Since u is an isometric immersion, du(e_i) = e_i, thus the ${\mathscr{R}}$-operator for Dirac-harmonic maps and the $\mathcal {R}$-operator for SP-minimal surfaces coincide. The energy density of u is constant:

$$ |\mathrm{d} u|^{2} =\sum\limits_{i} \langle\mathrm{d} u(e_{i}), \mathrm{d} u(e_{i})\rangle = \overline{g}_{ii}=m=\dim(M)=2. $$

Hence together with $\mathcal {T}=0$ implies that

$$ \frac{1}{2}\langle\gamma(e_{i})\nabla_{e_{j}}\psi+\gamma(e_{j})\nabla_{e_{i}}\psi,\psi\rangle=0. $$

Therefore T_ij = − 2g_ij and

$$ -\mathbb{I}(T)=2\textbf{H}=2\tau(u). $$

The conclusion follows. □

Since the functional ${\mathscr{L}}_{D}$ is not conformally invariant in dimensions m ≥ 3, the energy-momentum tensor $\mathcal {T}$ cannot vanish on-shell in higher dimensions. Indeed, in dimension m ≥ 3, if u is an isometric immersion, then

If furthermore Note that in case $\mathcal {T}=\lambda g$, then necessarily λ = 2 − m < 0.

Proposition 3.2

Let $u\colon M^{m}\to \overline {M}$ be an isometric immersion, with m ≥ 2 and $\psi \in {{\varGamma }}({{\varSigma }}_{g} M\otimes u^{\ast } T\overline {M})$ so that

$$ \mathcal{T}(u,\psi)=-(m-2) g. $$

(11)

Then (u, ψ) is a Dirac-harmonic map if and only if $(u,\widetilde {\psi })$ is an SP-minimal surface, where $\widetilde {\psi }=\sqrt {m/2}\psi$.

The proof is similar to that of Theorem 3.1 and is omitted.

Recall that for a conformal field theory the energy-momentum tensor is always perpendicular to the metric tensor, while this fails if the action is not conformally invariant. It remains unclear to us when the two symmetric tensors $\mathcal {T}$ and g would be aligned. We suspect this would also be rare and rigid.

Furthermore, notice that the ${\mathscr{R}}$ operator and the $\mathcal {R}$ operator has the same structure which are quadratic in the spinor part, and τ = H for isometric immersions, we immediately get

Corollary 3.3

Let $u\colon M^{m}\to \overline {M}$ be an isometric immersion and $\psi \in {{\varGamma }}({{\varSigma }}_{g} M\otimes u^{\ast } T\overline {M})$. Let T be defined as (8). If

$$ -\mathbb{I}(T)=2\sigma\textbf{H} \qquad \text{ for some } \sigma>0, $$

then (u, ψ) is a Dirac-harmonic map iff $(u,\widetilde {\psi }=\sqrt {\sigma }\psi )$ is an SP-minimal surface.

This includes Proposition 3.2 as a special case where σ = m/2.

Finally, we discuss some explicit examples based on the ansatz in [15] and [1]. Consider a pair (u, Φ) where $u\colon M^{m}\to \overline {M}^{m+1}(c)$ is an isometrically immersed hypersurface into a space of constant sectional curvature c, with global unit normal ν, and the spinor component has the form

$$ {\varPhi}=\gamma(e_{j})\psi\otimes e_{j} +\varphi\otimes \nu $$

(12)

for some pure spinors ψ, φ ∈Γ(ΣM). The conditions for (u, Φ) to be a Dirac-harmonic map are clarified in [1, Theorem 1.1, Theorem 1.5]. Writing H = |H| as the mean curvature where $\textbf {H}=\text {tr}(\mathbb {I})$ (so H = Hν), we have

where P is the Penrose operator on Γ(Σ_gM) defined by

that is, for any X ∈Γ(TM),

In the case m ≥ 3 and that u is a totally umbilical immersion which is non-minimal, as in the discussion of [1], we actually have

If in addition then

(13)

From (13) we obtain

It follows that

and hence

$$ \mathbb{I}(T)=-m\textbf{H}. $$

Thus in this case the Dirac-harmonic maps and the SP-minimal surfaces are equivalent.

In the surface case, if φ = 0 in (12), then again the Dirac-harmonic maps and the SP-minimal surfaces are equivalent. While in the general case, whether the equivalence holds or not remains unclear. Note that when M is a closed surface, there are no known examples with φ≠ 0.

Thus, on one side, we can get some examples directly from [1]; on the other hand, we cannot obtain new examples using the ansatz (12). It is also unclear whether the condition (11) is satisfied in the higher dimensional case.